Widespread Allelic Heterogeneity in Complex Traits

Abstract

Recent successes in genome-wide association studies (GWASs) make it possible to address important questions about the genetic architecture of complex traits, such as allele frequency and effect size. One lesser-known aspect of complex traits is the extent of allelic heterogeneity (AH) arising from multiple causal variants at a locus. We developed a computational method to infer the probability of AH and applied it to three GWASs and four expression quantitative trait loci (eQTL) datasets. We identified a total of 4,152 loci with strong evidence of AH. The proportion of all loci with identified AH is 4%–23% in eQTLs, 35% in GWASs of high-density lipoprotein (HDL), and 23% in GWASs of schizophrenia. For eQTLs, we observed a strong correlation between sample size and the proportion of loci with AH (R² = 0.85, p = 2.2 × 10⁻¹⁶), indicating that statistical power prevents identification of AH in other loci. Understanding the extent of AH may guide the development of new methods for fine mapping and association mapping of complex traits.

Introduction

Genome-wide association studies (GWASs) have successfully identified many loci associated with various diseases and traits.^{1, 2, 3, 4} Unfortunately, interpreting the detected associated genes is challenging due to two facts. First, most of the associated variants fall in non-coding regions of the genome.^{5, 6, 7, 8, 9, 10} Second, for only a handful of GWAS loci was a causal sequence variant detected that underlies the trait or disease susceptibility. Therefore, it is challenging to identify the relevant genes, which is the first step to understanding the biological mechanisms of the disease.

Detecting the causal variants is complicated by the fact that most significant associated variants may not be causal, but instead are in linkage disequilibrium (LD) with unknown functional variants. In general, sequence variants, with respect to a trait, can be grouped into three categories. The first category contains causal variants that have a biological effect on the trait and are responsible for the association signal. The second category contains variants that are statistically associated with the trait due to high LD with the causal variants. The third category contains variants that are not statistically associated with the trait and are not causal. Fine-mapping methods aim to distinguish between the two first categories (causal variants versus correlated variants). One way to link the causal variant with a particular gene is by colocalization methods that determine whether a single variant is responsible for both variation in the trait and variation in expression of a gene at the same locus (expression quantitative trait loci, eQTLs).

Fine-mapping and colocalization methods are designed to identify the causal variant and the associated gene at a locus, but in many cases, they assume a single causal variant. In the presence of multiple causal variants, those fine-mapping and colocalization methods^{11, 12, 13} will have a lower accuracy to detect the true causal variants and genes. Thus, a fundamental question is how many different causal variants are present in a locus.

The presence of multiple causal variants at the same locus that influence a particular disease or trait is known as allelic heterogeneity (AH). AH is very common for Mendelian traits. Clearly, many different mutations in the same gene may cause loss or gain of function leading to a specific Mendelian disease. For example, approximately 100 distinct mutations are known to exist at the cystic fibrosis locus,¹⁴ and even more are present at loci causing inherited hemoglobinopathies.¹⁵ In contrast to Mendelian traits, the extent of AH at loci contributing to common, complex disease is almost unknown. Hermani et al.¹⁶ have shown in their study the existence of multiple reproducible epistatic effects that influence gene expression. However, a recent study has shown that most of these epistatic effects can be explained by a third variant in that locus.¹⁷ Thus, it is of utmost importance to detect loci that harbor AH in order to avoid considering them as epistatic interactions.

Identifying the number of causal variants in complex traits is difficult because of extensive LD and small effect sizes. The standard approach to identify AH is to use conditional analysis. In conditional analysis, the independent association of multiple SNPs is tested after conditioning on other SNPs, which are more significant. The conditional analysis lacks power because it requires multiple variants to have a strong effect and to be independently significant. When several associated variants are highly correlated, the conditional analysis will not detect multiple independent associations, but we cannot rule out the existence of AH. Thus, the extent of AH in complex traits is unknown. AH could substantially influence our ability to explain the missing heritability and to identify causal genes.

We developed and applied a method to quantify the number of independent causal variants at a locus responsible for the observed association signals in GWASs. Our method is incorporated into the CAVIAR (causal variants identification in associated regions) software.¹⁸ The method is based on the principle of jointly analyzing association signals (i.e., summary level Z-scores) and LD structure in order to estimate the number of causal variants. Our method computes the probability of having multiple independent causal variants by summing the probability of all possible sets of SNPs for being causal. We compared results from our method to results produced using the standard conditional method (CM),¹⁹ which tests for independent association of a variant after conditioning on its significantly associated neighbors. Using simulated datasets, we illustrate that CAVIAR tends to outperform CM. We observed a very low false positive rate for CAVIAR to detect loci with AH even when the true causal variant is not included in our dataset. We applied CAVIAR to both eQTL and GWAS datasets. Our results indicate that in the Genotype-Tissue Expression (GTEx) dataset,²⁰ 4%–23% of eGenes harbor AH. We observed a high correlation between the number of loci with AH and sample size. In addition, we replicated a significant fraction of the loci with AH in three other existing eQTL studies. We also applied CAVIAR to three GWAS datasets: schizophrenia (SCZ),³ high-density lipoprotein (HDL),²¹ and major depression disorder (MDD),²² where we observed 23%, 35%, and 50% of loci (respectively) with strong evidence for AH.

Subjects and Methods

Joint Distribution of Observed Statistics in Standard GWASs

In this section, we provide a brief description of statistical tests that are performed in GWASs and the joint distribution of computed marginal statistics. These statistics are used as an input to CAVIAR. We consider GWASs on a quantitative trait for n individuals. Let Y be a vector of (n × 1) where y_i indicates phenotypic value for the i^th individual. Moreover, we genotype all the individuals for all the m variants. Let $G\in {\left\{\mathrm{0,1,2}\right\}}^{\left\{n\times m\right\}}$ be a matrix of genotypes for all the individuals where g_ij is the minor allele count for the i^th individual at the j^th variant. We standardize the minor allele count for each variant to have mean of 0 and variance of 1. We use X_j to indicate the standardized minor allele count for all the individuals at the j^th variant. We have $1^T{X}_i=0$ and $X_i^T{X}_i=n$ as the genotypes are standardized.

We assume that phenotypic values follow the linear model and the c variant is the causal variant. Thus, we have:

$$\begin{array}{c}Y=\mu 1+{\beta }_c{X}_c+\mathit{e}\end{array}$$

where μ is the phenotypic mean value, β_c is the effect size of the variant X_c, 1 is a (n × 1) vector of ones, and e is a (n × 1) vector to model the environment contribution and error in the measurement. In this model, we assume the error is i.i.d. and follows a normal distribution with mean of zero and variance of ${\sigma }_e^2\mathit{I}$, where I is a (n × n) matrix of identity and σ_e is the variance scalar of e. From the model explained above, we have $Y\sim N\left(\mu 1+{\beta }_c{X}_c,{\sigma }_e^2\mathit{I}\right)$. We use the maximum likelihood to compute the estimated β_c and σ_e which are denoted by ${\hat{\beta }}_c$ and ${\hat{\sigma }}_e$. Thus, we have:

$$\begin{array}{c}\mathrm{ℒ}\left(Y|\mu ,{\beta }_c,{\sigma }_e^2\right)=|{2\pi {\sigma }_e^2\mathit{I}|}^{-\frac{1}{2}}\text{exp}\left(-\frac{1}{2{\sigma }_e^2}{\left(Y-\mu 1-{\beta }_c{X}_c\right)}^T\left(Y-\mu 1-{\beta }_c{X}_c\right)\right),\\ \hat{\mu }=\frac{1}{n}{1}^{T}Y,\hat{\mu }\sim \mathcal{N}\left(\mu ,\frac{{\sigma }_e^2}{n}\right),\\ {\hat{\beta }}_c=\frac{X_c^T\mathit{y}}{n},\sqrt{n}\frac{{\hat{\beta }}_c}{{\sigma }_e}\sim \mathcal{N}\left(\frac{{\beta }_c}{{\sigma }_e}\sqrt{n},1\right).\end{array}$$ (Equation 1)

The association statistic for SNP c, denoted by S_c, follows a non-central t-distribution, which is the ratio of a normally distributed random variable to the square root of an independent chi-square distributed random variable. As shown in previous works, if the number of individuals are large enough,¹⁸ we can assume the marginal statistics follows a normal distribution with mean equal to ${\lambda }_c=\frac{\hat{\beta }}{\hat{\sigma }}\sqrt{n}$ and variance of 1:

$$\begin{array}{c}{S}_c\sim t_{{\lambda }_c,n}\approx \mathcal{N}\left({\lambda }_c,1\right).\end{array}$$ (Equation 2)

We assume that variant i is correlated with the causal variant c and the correlation between the two variants is r where $r=\frac{1}{n}{X}_i^T{X}_c$. Then, the marginal statistic estimated at variant i is equal to the marginal statistics for the causal variant that is scaled by r. We compute the covariance of the marginal statistics between two variants where the LD between the two variants is r.

$$\begin{array}{c}\text{Cov}\left(\sqrt{n}\frac{{\hat{\beta }}_i}{\sigma },\sqrt{n}\frac{{\hat{\beta }}_c}{\sigma }\right)=\frac{1}{n{\sigma }^2}{X}_i^T\text{Var}\left(Y\right)X_c=r.\end{array}$$

We compute the joint distribution of the marginal statistics for two variants i and j as follows:

$$\begin{array}{c}\left[\begin{array}{c}{S}_i\\ S_j\end{array}\right]\sim \mathcal{N}\left(\left[\begin{array}{c}{\lambda }_i\\ {\lambda }_j\end{array}\right],\left[\begin{array}{cc}1& r_{ij}\\ r_{ij}& 1\end{array}\right]\right),\end{array}$$ (Equation 3)

where ${\lambda }_j=r{\lambda }_i$ if the variant i is causal and the variant j is not causal or ${\lambda }_i=r{\lambda }_j$ if the variant j is causal and the variant i is not causal.

Computing the Likelihood of Causal Configuration

We can extend the joint distribution of marginal statistics for two variants to a more general case. Assume we have m variants and the pairwise correlation between each variant is denoted by Σ. Let $S={\left[S_1,S_2,S_3,\cdots S_m\right]}^T$ be the vector of marginal statistics obtained for each variant. The joint distribution of the marginal statistics for all the m variants is computed as

$$\begin{array}{c}\left(S|\text{Λ}\right)\sim \mathcal{N}\left(\text{ΣΛ},\text{Σ}\right),\end{array}$$ (Equation 4)

where Λ is (m × 1) is a vector of normalized effect sizes and ${\lambda }_i$ is the normalized effect size of the i^th variant. We introduce a parameter C that indicates the causal status of each variant. Each variant can have two possible causal status. We have c_i = 1 if the i^th variant is causal and c_i = 0 if the i^th variant is not a causal variant. We define a prior probability on the vector of effect size Λ for a given causal status using a multivariate normal distribution,

$$\begin{array}{c}\left(\text{Λ}|C\right)\sim \mathcal{N}\left(0,{\text{Σ}}_c\right),\end{array}$$ (Equation 5)

where Σ_c is a (m × m) matrix. The off diagonal elements of Σ_c are set to zero. The diagonal elements are set to σ or zero. We set the i^th diagonal element to σ if the i^th variant is causal and we set the i^th diagonal element to zero if the i^th variant is not causal. Thus, the joint distribution follows a multivariate normal distribution,

$$\begin{array}{c}\left(S|C\right)\sim \mathcal{N}\left(0,\text{Σ}+{\text{ΣΣ}}_c\text{Σ}\right)\end{array}.$$ (Equation 6)

Computing the Number of Independent Causal Variants in a Locus

In this section, we provide the formula to compute the probability of having i causal variants in a locus. We compute the probability of having i causal variants in a locus by summing over all the possible causal configurations where only i variants are causal. Let N_c indicates the number of causal variants in a locus. We have,

$$\text{Pr}\left(N_c=i|S\right)=\frac{{\sum }_{|\mathit{c}|=i}P\left(S|C\right)P\left(C\right)}{{\sum }_{C\in \mathcal{C}}P\left(S|C\right)P\left(C\right)}$$ (Equation 7)

where P(C) is the prior on the causal configuration C, $\mathcal{C}$ is the set of all possible causal configurations, including the configuration of all the variants that are not causal, and $\left|C\right|$ indicates the number of causal variants in the causal configuration C. The numerator in the above equation considers all possible causal configurations that have i causal variants, and the denominator is a normalization factor to ensure that the probability definition holds.

In this paper, we use a simple prior for a causal status. We assume that the probability of a variant to be causal is independent from other variants and that the probability of a variant to be causal is γ. Thus, we compute the prior probability as $\text{P}\left(C^{\ast }\right)=\prod {\gamma }^{\left|c_i\right|}{\left(1-\gamma \right)}^{1-\left|c_i\right|}$. We utilize different values for γ as shown in Figure S2. In our experiment, we set γ to 0.001.^{23, 24, 25} It is worth mentioning that, although we use a simple prior for our model, we can incorporate external information such as functional data or knowledge from previous studies. As a result, we can have variant-specific prior where ${\gamma }_i$ indicates the prior probability for the i^th variant to be causal. Thus, we can extend the prior probability to a more general case, $\text{P}\left(C^{\ast }|\text{Γ}=\left[{\gamma }_1,{\gamma }_2,\cdots {\gamma }_{\ell }\right]\right)=\prod {\gamma }_i^{\left|c_i\right|}{\left(1-{\gamma }_i\right)}^{1-\left|c_i\right|}$.

Reducing the Computational Complexity for Computing the Likelihood of a Causal Status

Unfortunately, the time complexity to compute the likelihood of a causal status using Equation 6 is O(m³). In this section, we provide a sped-up process that reduces the time complexity to O(m²k), where k is the number of causal variants (k is the number of variants that their causal status is 1). The number of causal variants is smaller than the total number of variants in a locus $\left(k\ll m\right)$. Thus, we can speed up the likelihood computation by a factor of $\left(m/k\right)$.

According to Equation 6, to compute the likelihood of a causal status, we must compute the quantity

$${\left(2\pi \right)}^{-\frac{m}{2}}\text{det}|\text{Σ}+{\text{ΣΣ}}_c{\text{Σ}|}^{-\frac{1}{2}}\text{exp}\left\{-\frac{1}{2}{S}^T{\left(\text{Σ}+{\text{ΣΣ}}_c\text{Σ}\right)}^{-1}S\right\}$$ (Equation 8)

where $\text{det}|.|$ denotes the determinant of a matrix. First, we speed up the exponential part. Thus, we have:

$$S^T{\left(\text{Σ}+{\text{ΣΣ}}_c\text{Σ}\right)}^{-1}S=S^T{\text{Σ}}^{-1}{\left(I_{m\times m}+{\text{Σ}}_c\text{Σ}\right)}^{-1}S$$ (Equation 9)

where $S^T{\text{Σ}}^{-1}$ is independent from the causal status and can be computed once and used many times. As a result, the most time-consuming part is to compute ${\left(I_{m\times m}+{\text{Σ}}_c\text{Σ}\right)}^{-1}$. We set elements of U_m×k and V_k×m such that Σ_cΣ = UV. Let ${\alpha }_i$ indicate the index of i^th causal variant. We set elements of V as follows: $V\left(i,j\right)=r_{{\alpha }_i,j}$. Let $U\left({\alpha }_i,i\right)=\sigma$, and we set the rest of elements of U to zero. Thus, we have:

$${\left(I_{m\times m}+{\text{Σ}}_c\text{Σ}\right)}^{-1}={\left(I_{m\times m}+UV\right)}^{-1}$$ (Equation 10)

We use the Woodbury matrix identity formula to compute the inverse. We have

$${\left(A+UEV\right)}^{-1}=A^{-1}-A^{-1}U{\left(E^{-1}+V{A}^{-1}U\right)}^{-1}V{A}^{-1}.$$ (Equation 11)

We set A to I_m×m and E to I_k×k, so the left side of the Woodbury matrix identity formula converts to ${\left(I_{m\times m}+{\text{Σ}}_c\text{Σ}\right)}^{-1}$. From the right side of the Woodbury matrix identity formula, we have:

$${\left(I_{m\times m}+{\text{Σ}}_c\text{Σ}\right)}^{-1}={\left(I_{m\times m}+UV\right)}^{-1}$$ (Equation 12)

$$=I_{m\times m}^{-1}-I_{m\times m}^{-1}U{\left(I_{k\times k}^{-1}+V{I}_{m\times m}^{-1}U\right)}^{-1}V{I}_{m\times m}$$ (Equation 13)

$$=I_{m\times m}-U{\left(I_{k\times k}+VU\right)}^{-1}V$$ (Equation 14)

where ${\left(I_{k\times k}+VU\right)}^{-1}$ requires inverting a (k × k) matrix that is much faster than inverting a (m × m) matrix.

Similarly, the naive method to compute $\text{det}\left|\text{Σ}+{\text{ΣΣ}}_c\text{Σ}\right|$ requires O(m³). We utilize the Sylvester’s determinant identity that is as follows:

$$\text{det}|I_{m\times m}+UV|=\text{det}|I_{k\times k}+VU|.$$ (Equation 15)

Thus, instead of computing the determinant of a (m × m) matrix, we can compute the same value by computing the determinant of a (k × k) matrix. We have

$$\text{det}\left|\text{Σ}+{\text{ΣΣ}}_c\text{Σ}\right|=\text{det}\left|\text{Σ}\right|\text{ det}\left|I_{m\times m}+{\text{Σ}}_c\text{Σ}\right|$$ (Equation 16)

$$=\text{det}\left|\text{Σ}\right|\text{ det}\left|I_{m\times m}+UV\right|$$ (Equation 17)

$$=\text{det}\left|\text{Σ}\right|\text{ det}\left|I_{k\times k}+VU\right|.$$ (Equation 18)

In the above equation, we can compute $\text{det}\left|\text{Σ}\right|$ once and use it for different causal statuses. In addition, the computational complexity of $\text{det}\left|I_{k\times k}+VU\right|$ is O(k³). Thus, the time complexity to compute $\text{det}\left|\text{Σ}+{\text{ΣΣ}}_c\text{Σ}\right|$ is O(k³).

Conditional Method

A standard method to detect allelic heterogeneity (AH) is the conditional method (CM). CM is an interactive process. In each iteration of CM, we identify the SNP with the most significant association statistics. Then, conditioning on that SNP and all SNPs that are selected in previous steps, we re-compute the marginal statistics of all remaining variants in the locus. After the first iteration of CM, we consider a locus to have AH when the re-computed marginal statistics for at least one of the variants is more significant than a predefined threshold. Similarly, we consider a locus to not have AH when the re-computed marginal statistics of all variants is not significant. The predefined threshold is referred to as the stopping threshold for CM. We set the stopping threshold to be $\left(0.05/m\right)$ (stopping threshold is based on p value). Thus, we perform CM until there is no significant variant in a locus. This standard method can be applied to either summary statistics or individual-level data. GCTA-COJO¹⁹ performs conditional analysis while utilizing the summary statistics.

When applying CM to individual-level data, we re-compute the marginal statistics by performing linear regression where we add the set of variants that are selected as covariates. We utilize the LD between the variants, which we obtain from a reference dataset, when applying CM to summary statistics data. In this case, we re-compute the marginal statistics for the i^th variant as follows:

$$Z_i^{new}=\frac{\left(z_i-z_j{r}_{ij}\right)}{\sqrt{1-r_{ij}^2}}$$ (Equation 19)

when we have selected the j^th variant as causal. Let z_i indicate the marginal statistics for the i^th variant and r_ij the genotype correlations between the i^th and j^th variants.

Datasets

We obtained the summary statistics for GTEx eQTL dataset (release v6p, dbGaP: phs000424.v6.p1). We estimated the LD structure using the available genotypes in the GTEx dataset. We considered 44 tissues and applied our method to all eGenes in order to detect loci that harbor allelic heterogeneity. eGenes are genes that have at least one significant eQTL (p value < 10⁻⁵). The number of individuals ranges from 70 to 361 depending on the tissues of interest.

We obtained the summary statistics of blood eQTL for 373 European individuals from the GEUVADIS (Genetic European Variation in Disease) website. We approximated LD structure from the 1000G European population. We applied our method to the 2,954 eGenes in GEUVADIS to detect AH loci.

We obtained the summary statistics from the MuTHER (Multiple Tissue Human Expression Resource) website and utilized the skin and fat (adipose) tissues. MuTHER dataset consist of 856 individuals. We then approximated LD from the 1000G European population. We obtained 1,433 eGenes for skin and 2,769 eGenes for adipose.

We used the high-density lipoprotein cholesterol (HDL-C) trait.²¹ We considered only the GWAS hits, which are reported in a previous study. We applied ImpG-Summary²⁶ to impute the summary statistics with 1000G as the reference panel. We used the 1000G European population to estimate the LD. HDL-C consists of around 100,000 individuals. We used the 37 loci that is reported in previous study,²¹ which have at least one significant variant (genome-wide significance level of 5 × 10⁻⁸), as an input to CAVIAR. Following common protocol in fine-mapping methods, we apply CAVIAR to loci that have at least one statistically significant variant.

We analyzed the recent GWASs on major depression disorder (MDD)²² and schizophrenia.³ The major depression disorder study has 2 and the schizophrenia study has 108 loci identified to contain at least one significant variant. We utilized the summary statistics provided by each study and approximated the LD using the 1000G populations. SCZ consists of 36,989 case subjects and 113,075 control subjects, and MDD consists of 5,303 case subjects and 5,337 control subjects.

Data Simulation

Simulating Genotypes

We first simulated genotypes using HAPGEN2,²⁷ where we utilized the 1000G CEU population as initial reference panels. We simulated 1,000 individuals. We focus on the chromosome 1 and the GWAS variants that are obtained from the NHGRI catalog.²⁸ We filter out monomorphic SNPs and SNPs with low minor alley frequency (MAF ≤ 0.01).

Simulated Summary Statistics with No Epistasis Interaction

We simulated the summary statistics using LD structure and effect size for causal variants. It is known that summary statistics follows a MVN distribution $\left(S\sim N\left(\text{ΣΛ},\text{Σ}\right)\right)$. The mean of statistics is ΣΛ and the variance of statistics is Σ. As mentioned above, Σ is the LD structure and $\text{Λ}=\left[{\lambda }_1,{\lambda }_2,\mathrm{..}{\lambda }_m\right]$ is the true effect size used to simulate data. For variants that are non-causal, we set the effect size to zero. This process of simulating summary statistics is used in our previous studies.^{18, 29, 30, 31, 32, 33} Effect size for the causal variants is set to obtain the desired power. In our simulated datasets, effect size is computed for the genome-wide significant level $\left(\alpha ={10}^{-8}\right)$. We use binary search to compute the value of the effect size for a desired statistical power. The statistical power is defined as

$$\text{Power}=1-\frac{1}{\sqrt{2\pi }}{\int }_{{\text{Φ}}^{-1}\left(\alpha /2\right)+{\lambda }_i}^{{\text{Φ}}^{-1}\left(1-\alpha /2\right)+{\lambda }_i}{e}^{-\frac{1}{2}{x}^2}dx=\text{Φ}\left({\text{Φ}}^{-1}\left(\alpha /2\right)+{\lambda }_i\right)+1-\text{Φ}\left({\text{Φ}}^{-1}\left(1-\alpha /2\right)+{\lambda }_i\right)$$

where α is the significant threshold. Moreover, $\text{Φ}$ and ${\text{Φ}}^{-1}$ denote the cumulative density function (CDF) and inverse of CDF for the standard normal distribution.

We use false positive (FP) and true positive (TP) as metrics to compare different methods. FP indicates the fraction of loci that harbor one causal variant and are incorrectly detected as loci that harbor AH. TP indicates the fraction of loci that harbor AH and are correctly detected.

Simulating Summary Statistics with Epistasis Interaction

We simulated the genotypes similar to the case where we have no epistasis interaction, which is mentioned above. Then, we simulated phenotypes using the following model:

$$Y=x_i{x}_j{\beta }_{ij}+e,$$ (Equation 20)

where x_i and x_j indicate the standardized genotypes for i^th and j^th variants, respectively. Moreover, β_ij is the epistasis interaction effect size. We set β_ij such that we obtained the desired heritability for the simulated phenotype. Then, we computed the marginal statistics for each variant utilizing the linear regression single variant testing.

Results

Overview of Identifying Allelic Heterogeneity

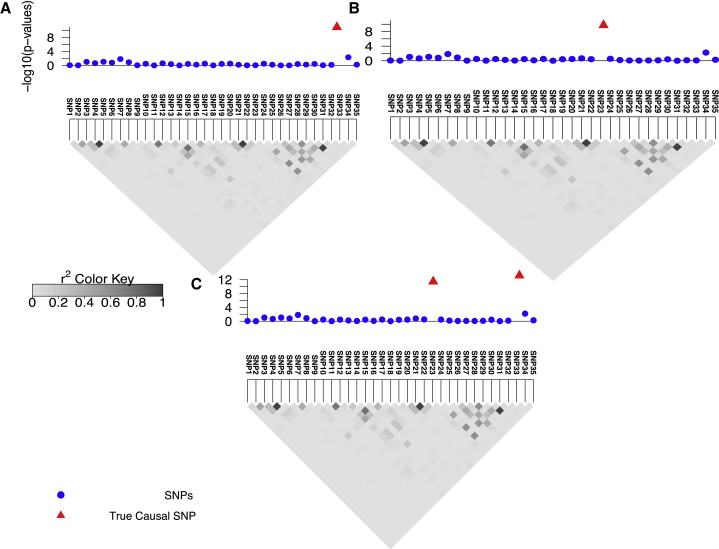
Our method utilizes the shape of marginal statistics (statistics obtained from GWASs such as z-score) and the patterns of LD to detect whether or not there is evidence for AH. In Figures 1A and 1B, we illustrate a simple example with no AH. However, we can guess that the region shown in Figure 1C harbors AH; here, we observe two high independent peaks in the region. Unfortunately, detecting AH is less intuitive in regions that are more complicated.

Figure 1.

Overview of CAVIAR for Detecting Allelic Heterogeneity Regions

(A and B) The marginal statistics for a locus where we have implanted one causal variant. In (A), SNP33 is causal and in (B), SNP23 is causal.

(C) The same locus where both SNP23 and SNP33 are causal.

In these figures, the x axis is the negative logarithm of the p values for each locus to indicate the strength of the marginal statistics. The gray triangle below each figure indicates the LD pattern. Each square indicates the correlation between two variants, and the magnitude of the correlation is shown by the color intensity of the square. The darker the square, the higher the correlation between two variants.

The input to our method is the LD structure of the locus and the marginal statistics for each variant in the locus. The LD between each pair of variants is computed from genotyped data or is approximated from HapMap or 1000G data.^{34, 35} We use the fact that the joint distribution of the marginal statistics follows a multivariate normal distribution (MVN)^{18, 30, 36, 37} to compute the posterior probability of each subset of variants being causal, as described below. Then, we compute the probability of having i independent causal variants in a locus by summing the probability of all possible subsets of size i (sets that have i causal variants). We consider a locus to be AH when the probability of having more than one independent causal variant is more than 80%.

We would like to emphasize that using only summary statistics and LD information is insufficient for differentiating tightly linked variants. For example, if two variants are in perfect pairwise LD (correlation of 1), it is impossible to detect with just the summary statistics whether only one of the variants is causal or both are causal. Therefore, our estimates are just a lower bound on the amount of loci with AH for a given complex trait.

CAVIAR Is More Accurate than Existing Conditional Method

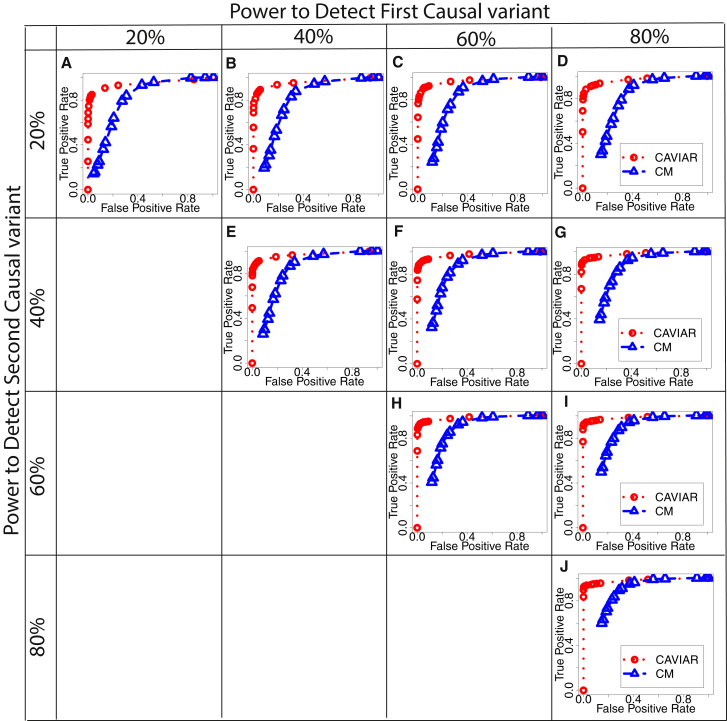
In order to assess the performance of our method, we generated simulated datasets. We used HAPGEN2,²⁷ a widely used software, to generate a case-control study using the European population obtained from the 1000G. Then, we implanted one or two causal variants in a region and generated marginal statistics for each variant (described in the Subjects and Methods). We applied CAVIAR to all the simulated datasets to detect loci that harbor AH. We generated two datasets. In the first dataset, we set power to detect the causal variants at 10%, 30%, 50%, or 70%. In the second dataset, we set power to detect the causal variants at 20%, 40%, 60%, or 80%. We compared our results with the conditional method (CM). We use false positive (FP) and true positive (TP) as metrics for comparison. FP indicates the fraction of loci with one causal variant that are incorrectly detected as loci with AH. TP indicates the fraction of loci with AH that are correctly detected. We found that our method has higher TP compared to CM for the same FP rate. Figures 2 and S1 illustrate the ROC curves for the first and second simulated datasets. In all these experiments, we set γ to 0.001.

Figure 2.

ROC Curve for CAVIAR and CM

We implant one causal variant to compute the false positive (FP) rate. FP indicates loci that harbor one causal variant; however, these loci are detected as AH. We implant two causal variants to compute the true positive (TP) rate. TP indicates loci that harbor AH and are detected correctly. We range the effect size such that the power at the causal variant is 20%, 40%, 60%, and 80% at the genome significant level 10⁻⁸. We obtain these results from simulated data with no epistasis interaction. We simulated data using 1,000 individuals and set γ to 0.001.

It is possible that the most significant variant is not causal.^{18, 30} In some cases, there may exist more than one causal variant in a locus; however, a variant that is in tight LD with the two causal variants tends to have higher marginal statistics.¹⁸ This phenomenon is recently known as “ghost effect.”³⁸ In fact, in the above simulation when we simulate more than one causal variant in a locus, we observed a ghost effect in few loci. However, the chance of a ghost effect occurring in simulated data is small. Thus, we extend our simulation to address this issue. We simulated data where we have more than one causal variant and generated cases only where a ghost effect occurs in a locus. We simulated cases where the power to detect the first causal variant is 50% and the power to detect the second causal variant ranges between 10%, 30%, 50%, and 70%. We observed that CAVIAR tends to have high recall rate even when the locus has ghost effect (see Table S1).

CAVIAR running time depends on the number of variants (m) in a locus and the maximum number of causal variants allowed. In our simulation, we set the maximum number of causal variants as six. In a locus with 50 variants where the maximum number of causal variants is 6, CAVIAR takes 26 min to finish. CAVIAR runs in less than 3 min for loci with 50 variants where the maximum number of causal variants is set to 5 or fewer (see Table S2). These results are obtained by running CAVIAR on a MacBook Air with 1.4 Ghz Intel Core i5 CPU. CAVIAR memory footprint is less than 1 Gb.

CAVIAR Has a Low False Positive even When the Causal Variant Is Not Included

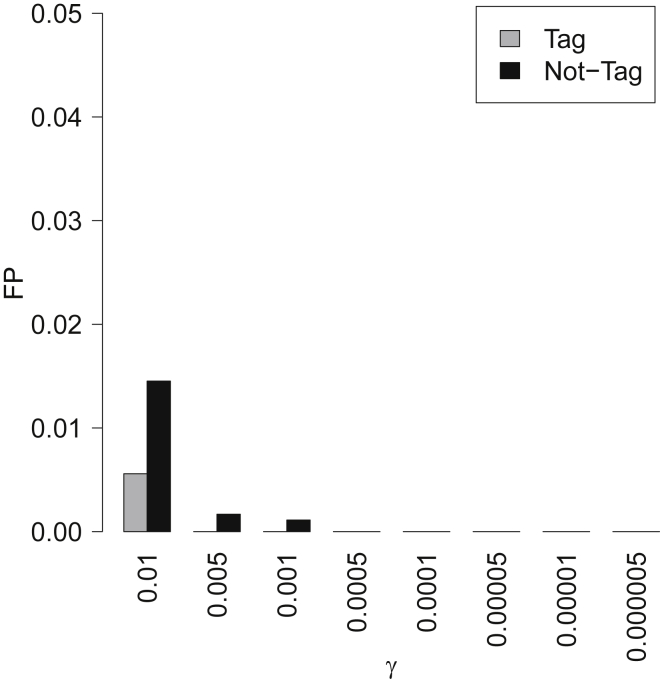
In the previous section, we show CAVIAR has an extremely low FP and a high TP rate in detecting loci with AH. In the simulated data, the causal variant was included. However, in real datasets we cannot guarantee that information will exist for all the causal variants. One possible reason for detecting a locus as AH could be that the actual causal variant is not included or tagged in the data. In this section, we show that loci detected by CAVIAR with AH are rarely due to the fact that the actual causal variant is not included.

We simulate datasets where we implant one causal variant in a locus and generate marginal statistics in a method similar to the previous section. Next, we remove the causal variant from our analysis and use the remaining variants in the locus as an input to CAVIAR. We observe the FP is extremely low (FP < 0.015), even when the causal variant was not included in the analyzed data (see Figure 3). Our conclusion is that CAVIAR may fail to detect AH in some loci, but a very small proportion of loci where we detected AH are incorrect.

Figure 3.

CAVIAR Has Low FP Even When the True Causal Variant Is Not Collected

Thus, most loci that are detected by CAVIAR to harbor AH are most probably true. x axis indicates the prior probability of causal variant (γ). We set γ to 0.01, 0.005, 0.001, 0.0005, 0.0001, 0.00005, 0.000001, and 0.000005.

Setting CAVIAR Parameters to Detect Loci that Harbor AH

There are two main input parameters for CAVIAR, excluding the summary statistics of a locus: the prior probability that a variant is causal (γ) and AH posterior probability (AHPP) threshold. We consider a locus to harbor AH when the summation of posterior probability for two and more causal variants exceed AHPP threshold. To select γ and AHPP, we simulated data as mentioned above for different ranges of causal variants. We simulated datasets where the power to detect the causal variants is 10%, 30%, 50%, or 70%. In all these simulations, we implanted one or two causal variants and computed the FP and TP. The results of these experiments are shown in Figures S2–S11. We observed that to obtain extremely low FP and high TP, the best range for γ is 0.01 to 0.0001, where AHPP is set to 0.7 to 0.8. We set the γ to 0.001 from our previous results in fine-mapping.^{18, 30} Thus, we can apply CAVIAR to perform fine-mapping as well as to detect the loci that harbor AH. Furthermore, to be extremely stringent, we set AHPP to 0.8.

In addition, when we set AHPP to 0.8, we vary γ among 0.01, 0.005, 0.001, 0.0005, 0.0001, 0.00005, 0.000001, and 0.000005. We observed that for different values of γ, CAVIAR tends to have extremely low FP (FP ≤ 0.001) and high TP. The result for this experiment, when the power to detect the causal variants is 50%, is shown in Figure S12.

CAVIAR Is Robust to Out-of-Sample LD Structure

The LD structure can be computed from raw genotypes when they are available (in-sample LD). However, in most datasets, we do not have access to the raw genotypes. Thus, we approximate the LD utilizing the 1000G^{34, 35} or HapMap³⁹ datasets. Estimating the LD structure from a reference panel is known as out-of-sample LD.

In this experiment, we want to investigate the effect of using misspecified LD structures. We simulated the marginal statistics by utilizing the LD structure (LD matrix) obtained from HAPGEN2. Next, we simulate the marginal statistics and generate a misspecified LD by adding standard Gaussian noise, $N\left(0,\tau \right)$, to each element of the original LD matrix. We use the simulated marginal statistics and the misspecified LD as an input to CAVIAR. We simulated 10,000 loci with one causal variant to compute the FP, and we simulated 10,000 loci with two causal variants to measure TP. We vary the variance of the Gaussian noise (τ) between 0.01, 0.02, 0.05, 0.1, 0.2, 0.25, and 0.3. In this experiment, we observed low FP and high TP for CAVIAR results. The result for this experiment is shown in Figure S13. It is worth mentioning that the probability of observing a τ greater than 0.1 is extremely low.

CAVIAR Accurately Detects the Number of Causal Variants in a Locus when All the Variants Are Collected

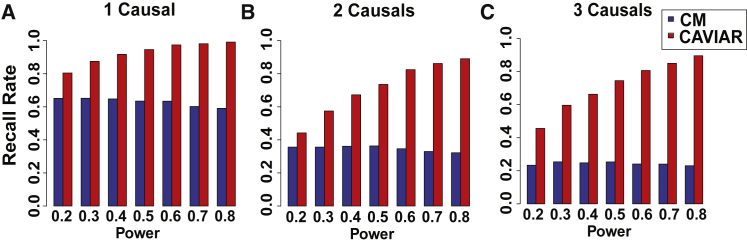
In the previous sections, we have shown that CAVIAR is accurate in detecting loci that harbor AH. An additional benefit of our method is that it can accurately detect the number of causal variants in a locus. We simulated the phenotypes similar to the previous sections. In these experiments, we implanted one, two, and three causal variants in a locus. We set the effect size of the causal variant such that the statistical power to detect all causal is 20%, 30%, 40%, 50%, 60%, 70%, and 80%. In these experiments, power is the total probability to detect all causal variants. In this case, we have k causal variants, and we want the statistical power to be p. We set the effect size of k causal variants such that the summation of the power for all causal variants is equal to p. We use 1,000 individuals in our experiments.

As CAVIAR provides probability values for different number of causal variants, we consider a locus to have i independent causal variants where the probability of having i causal variants is the maximum probability for different numbers of causal variants. We allow up to six causal variants when applying CAVIAR. In the case of CM, the number of causal variants in a locus is equivalent to the number of conditional steps that we perform until the p value of all variants is higher than $\left(\alpha /m\right)$ (Bonferroni correction), where m is the total number of variants in a locus and α is 0.05. We compute the recall rate as the fraction of simulations where a method correctly predicted the number of causal variants in a locus. In Figure 4, we plot the recall rate of CAVIAR and CM in detecting the number of causal variants. We observe that, in comparison to CM, CAVIAR has a much higher recall rate in detecting the true number of causal variants in a locus.

Figure 4.

CAVIAR Is More Accurate than CM to Detect the Number of Causal Variants

The x axis is the power of causal variants, and the y axis is the accuracy to detect the number of causal variants in a locus. We implanted one, two, and three causal variants. We compute the recall rate as the fraction of simulations where the number of causal variants in a locus is predicted correctly. Recall rate of each method for different number of causal variants: (A) one causal variant, (B) two causal variants, and (C) three causal variants. We vary the statistical power to detect the causal variant among 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, and 0.8.

CAVIAR Distinguishes between Epistatic Interaction and Allelic Heterogeneity

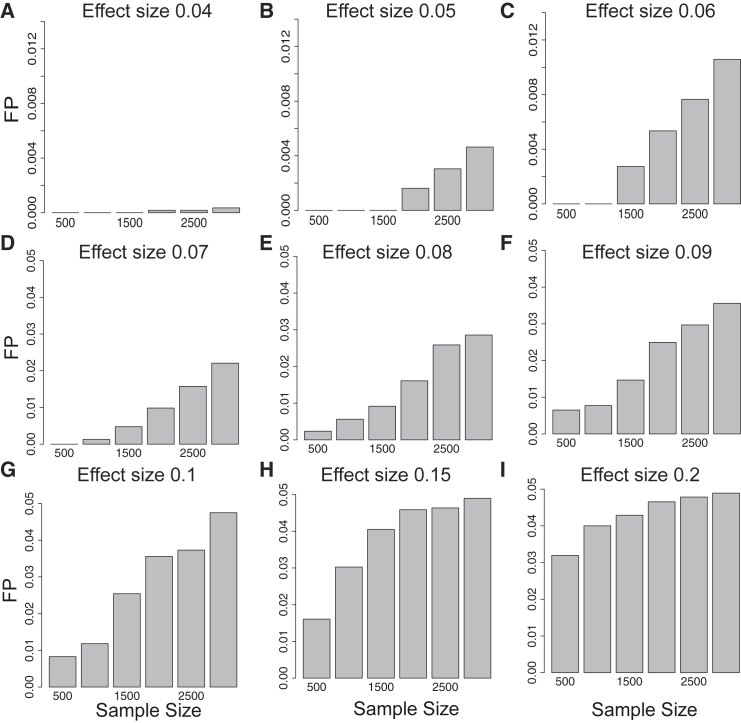
It is possible to incorrectly detect a locus with AH due to the epistatic interaction in that locus. In this section, we utilize simulated data to illustrate that CAVIAR rarely detects AH in loci where the true genetics architecture is epistasis. We simulated different datasets where we implanted epistatic interactions between two randomly selected variants in a locus. Then, we generated simulated phenotypes using the linear additive model (described in the Subjects and Methods). We vary the number of individuals in each dataset among 500, 1,000, 1,500, 2,000, 2,500, and 3,000. In addition, for each dataset, we vary the effect size among 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, 0.1, and 0.2. For each simulated dataset, we simulated 5,000 different marginal statistics. CAVIAR has an extremely low false positive rate in these experiments (see Figure 5). In Figure 5, we show the results for the effect size of 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, 0.1, and 0.2. The results for effect size of 0.01, 0.02, and 0.03 are not shown because the FP is zero for these values. As a result, CAVIAR detects only a small fraction of epistatic interactions as AH. It is worth mentioning that the amount of epistatic interactions for different traits is very low. Thus, these results indicate that the loci that harbor AH and are detected by CAVIAR are not artifacts of epistatic interaction.

Figure 5.

CAVIAR Distinguishes between Epistatic Interaction and Allelic Heterogeneity

The x axis is the sample size that we vary between 500, 1,000, 1,500, 2,000, 2,500, and 3,000 individuals. The y axis is the false positive (FP) rate. We simulated datasets where we have epistatic interaction and compute the FP as the number of cases where CAVIAR incorrectly detects these loci to harbor AH. Shown are the FP for different effect sizes of the epistatic interaction.

Prevalence of Allelic Heterogeneity in eQTL Datasets

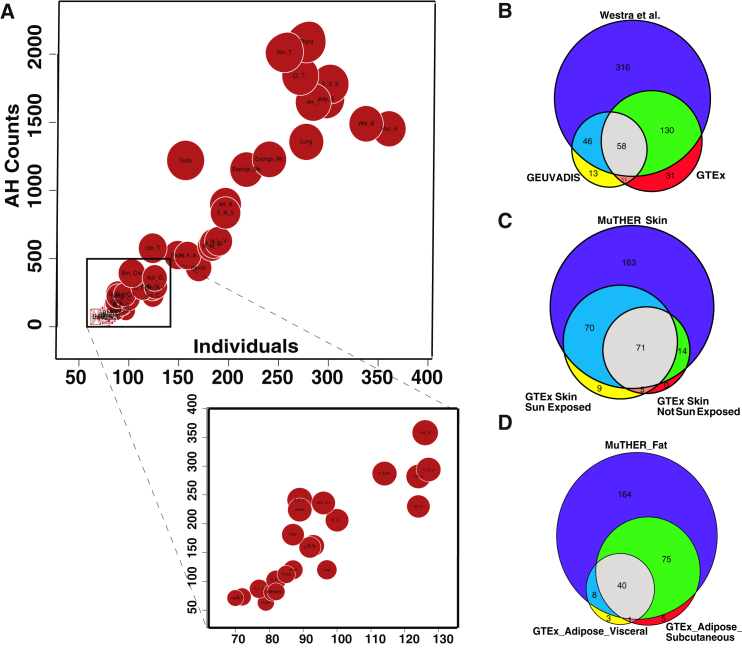
We used four datasets to examine the extent of AH in eQTL datasets (GTEx,²⁰ GEUVADIS,⁴⁰ MuTHER,⁴¹ and Wester et al.⁴²). In the GTEx dataset,²⁰ we have access to 44 tissues. In each tissue, we have around 22,000 genes (probes). We obtained the marginal statistics and genotypes from the GTEx project²⁰ for each gene in all tissues. Then, we filtered out genes lacking at least one significant SNP. We set the significant cut-off threshold to a p value of 10⁻⁵. Genes that have a significant cis-eQTL SNP are known as eGenes. We applied our method to detect AH loci only to eGenes. We found that 4%–23% of the eGenes show evidence for AH (with probability >80%) (Figure 6, Table 1). In addition, we applied the CM to the same set of eGenes. We observed that 50%–80% of loci detected by the CM to have AH were also detected by CAVIAR (see Table 1). Furthermore, we observed that CM detects 13.6%–44% of loci detected by CAVIAR as AH.

Figure 6.

Levels of Allelic Heterogeneity in eQTL Studies

(A) Linear relationship between the amount of AH and sample size. Each red circle indicates a different type of tissue from the GTEx dataset. The size of each red circle is proportional to the number of genes that harbor a significant eQTL (eGenes).

(B–D) Significant overlap between AH estimations for different eQTL datasets, shown for (B) blood (p = 7.9 × 10⁻⁹⁷), (C) skin (p = 4.9 × 10⁻⁶³), and (D) adipose (p = 1.1 × 10⁻⁶⁹) tissue. p values are computed using a hypergeometric test that is implemented in the SuperExactTest⁴³ software.

Table 1.

List of 44 Tissues in GTEx

Tissue	#Individual	#eGene	#AH (CAVIAR)	#AH/#eGene	#AH (CM)	#Overlap between (%) CAVIAR & CM
Vagina	79	1,535	63	0.0410	26	13 (50.0%)
Brain, anterior cingulate cortex BA24	72	1,745	73	0.0418	27	10 (42.4%)
Small intestine terminal ileum	77	1,978	87	0.0439	32	17 (53.1%)
Brain, hypothalamus	81	1,750	81	0.0462	31	17(54.8%)
Uterus	70	1,504	71	0.0472	33	14(42.4%)
Brain, putamen basal ganglia	82	2,144	102	0.0475	52	24 (46.1%)
Brain, hippocampus	82	1,713	82	0.0478	35	13 (37.1%)
Liver	97	2,148	120	0.0558	40	18 (45.0%)
Prostate	87	2,088	120	0.0574	31	21 (67.7%)
Brain, nucleus accumbens basal ganglia	93	2,596	162	0.0624	70	41 (58.5%)
Brain, frontal cortex BA9	92	2,547	159	0.0624	70	40 (57.1%)
Ovary	85	1,776	112	0.0630	58	30 (51.7%)
Pituitary	87	2,708	181	0.0668	71	39 (54.9%)
Brain, cerebellar hemisphere	89	3,455	241	0.0697	115	59 (51.3%)
Brain, caudate basal ganglia	100	2,939	206	0.0700	95	54 (56.8%)
Spleen	89	3,141	224	0.0713	107	59 (55.1%)
Brain, cortex	96	3,009	236	0.0784	91	51 (56.0%)
Artery coronary	124	2,897	230	0.0793	119	65 (54.6%)
Colon sigmoid	124	3,247	282	0.0868	130	87 (66.4%)
Cells, EBV transformed lymphocytes	114	3,280	287	0.0875	126	81 (64.2%)
Esophagus, gastresophageal junction	127	3,231	294	0.0909	138	100 (72.4%)
Brain, cerebellum	103	4,278	393	0.0918	181	119 (65.7%)
Adrenal gland	126	3,636	358	0.0984	189	110 (58.2%)
Stomach	170	4,007	433	0.1080	146	103 (70.5%)
Pancreas	149	4,372	526	0.1203	235	153 (65.1%)
Colon transverse	124	4,771	576	0.1207	279	203 (72.7%)
Heart, atrial appendage	159	4,174	522	0.1250	192	125 (65.1%)
Breast mammary tissue	183	4,600	590	0.1282	246	178 (72.3%)
Adipose visceral omentum	185	4,611	611	0.1325	296	223 (75.3%)
Heart, left ventricle	190	4,526	627	0.1385	278	205 (73.7%)
Testis	157	8,333	1,220	0.1464	349	257 (73.6%)
Artery aorta	197	5,850	898	0.1535	435	338 (77.7%)
Skin, not sun exposed, suprapubic	197	5,371	835	0.1554	180	138 (76.6%)
Esophagus muscularis	218	6,431	1,153	0.1792	515	411 (79.8%)
Esophagus mucosa	241	6,849	1,228	0.1792	605	480 (79.3%)
Lung	278	7,026	1,356	0.1929	662	537 (81.1%)
Adipose, subcutaneous	298	7,806	1,669	0.2138	870	714 (82.6%)
Muscle, skeletal	361	6,687	1,452	0.2171	715	614 (85.8%)
Whole blood	338	6,822	1,489	0.2182	792	656 (82.8%)
Skin, sun exposed, lower leg	302	8,093	1,780	0.2199	549	467 (85.0%)
Artery, tibial	285	7,443	1,647	0.2212	796	653 (82.0%)
Cells, transformed fibroblasts	272	7,915	1,841	0.2325	965	798 (82.6%)
Thyroid	278	8,931	2,088	0.2337	932	786 (84.3%)
Nerve tibial	256	8,429	2,012	0.2386	1,075	881 (81.9%)
Total	7,014		28,717

Tissues are sorted based on the number of samples. #Individual indicates the number of samples for each tissue. #AH (CAVIAR) is the number of loci detected by CAVIAR that harbor AH. #AH(CAVIAR)/#eGene is the fraction of eGenes that are detected to harbor AH. #AH(CM) is the number of loci detected by the conditional method (CM) to harbor AH.

The number of eGenes detected in a tissue depends on the statistical power to detect a significant variant associated with the gene expression. The statistical power is highly correlated to the number of samples for that tissue. We hypothesized that there might also exist correlation between the sample size and the number of loci with AH. Indeed, we observed that the proportion of eGenes with AH for each tissue is in a linear relationship with the sample size, as shown in Figure 6A (R² = 0.85, p = 2.2 × 10⁻¹⁶). This result indicates that statistical power prevents the identification of AH at other loci.

To check the reproducibility of the AH detection, we compared the results from GTEx blood data with results from two other blood eQTL studies: GEUVADIS⁴⁰ and Wester et al.⁴² We tested the overlap between genes with AH for skin and adipose tissues based on the GTEx²⁰ and MuTHER⁴¹ datasets. We only considered eGenes that are common between the studies. In all comparisons, we observed a high reproducibility rate for the detection of AH in blood (Figure 6B, p = 7.9 × 10⁻⁹⁷), skin (Figure 6C, p = 4.9 × 10⁻⁶³), and adipose (Figure 6D, p = 1.1 × 10⁻⁶⁹) tissues. We compute the significant overlap between AH estimations for different eQTL datasets. We compute the p values using a hypergeometric test that is implemented in the SuperExactTest⁴³ software. In addition, Jansen et al.⁴⁴ recently performed CM on a blood eQTL dataset to detect AH genes. We computed the overlap for AH loci detected by CAVIAR in GTEx blood tissue. We observed that 492 AH loci are common between CAVIAR and the Jansen et al.⁴⁴ results. CAVIAR detected 1,489 AH loci and Jansen et al.⁴⁴ detected 2,496 AH loci (see Figure S14).

Prevalence of Allelic Heterogeneity in GWAS Datasets

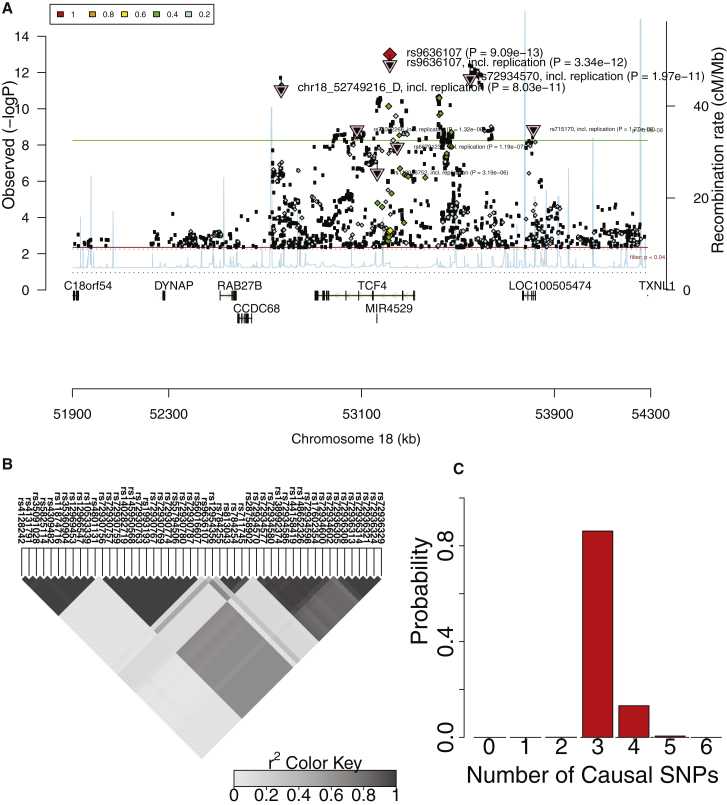
To measure the level of AH in a human quantitative trait, we applied our method to a GWAS of high-density lipoprotein (HDL).²¹ We obtained the summary statistics available for HDL from the ImpG-Summary²⁶ webpage. There are 37 loci that are reported as significant for HDL.²¹ Out of 37 loci, 13 (35%) showed evidence for AH with probability ≥80% (see Table S3). We also studied the results of GWASs focused on two psychiatric diseases: major depression disorder (MDD)²² and schizophrenia (SCZ).³ For MDD, we found evidence for AH at one of two loci. For SCZ, we identified 25 loci out of 108 (23%) with high probability of AH (see Table S4). One example of AH in SCZ is the locus on chromosome 18 that includes TCF4 (MIM: 602272) (Figure 7A). The locus contains multiple associated SNPs that are distributed in different LD blocks (Figure 7B). According to our analysis, there are three or more causal variants in this locus with high probability (Figure 7C) (for similar results in other loci, see Figures S15–S51 for HDL and Figures S52–S179 for SCZ).

Figure 7.

Allelic Heterogeneity in the TCF4 Locus Associated with Schizophrenia

(A) Manhattan plot obtained from Ricopili consists of all the variants (7,193 variants) in a 1 Mbp window centered on the most significant SNP in the locus (rs9636107). We use PGC-SCZ52-may13 version of the data. This plot indicates multiple significant variants that are not in tight LD with the peak variant.

(B) LD plot of the 50 most significant SNPs showing several distinct LD blocks.

(C) Histogram for the probability of having different number of causal variants.

Discussion

We have proposed a novel probabilistic method to detect loci with AH. Our results show that our method is more accurate than the standard conditional method (CM). One of the main benefits of our method is that it requires only summary statistics. Summary statistics of a GWAS or eQTL study are widely available, so our method is applicable to most existing datasets. We have shown that AH is widespread and more common than previously estimated in complex traits, both in GWASs and eQTL studies. Since our method is influenced by statistical power and uncertainty induced by LD, the proportions of loci with AH detected in this study are just a lower bound on the true amount of AH. Thus, our study suggests that many, and maybe even most, loci are affected by AH.

Our results highlight the importance of accounting for the presence of multiple causal variants when characterizing the mechanism of genetic association in complex traits. Falling to account for AH can reduce the power to detect true causal variants and can explain the limited success of fine mapping of GWASs. It is worth mentioning that methods for fine-mapping^{38, 45, 46} exist that allow for more than one causal variant in a locus; however, these methods require access to raw genotypes and phenotypes. One of the advantages of CAVIAR is that it requires only the existing summary statistics (e.g., marginal statistics per-SNP obtained from GWASs). Thus, methods such as CAVIAR are applicable to most GWAS datasets. Similarly, attempts to explain GWASs using eQTL data should be more successful with methods that assume some loci may include multiple causative variants (e.g., eCAVIAR³¹ and RTC⁴⁷).

One of the limitations of our method is that we assume that the observed marginal statistics are corrected for the population using PCA-based methods. Recently, linear mixed models (LMMs)^{48, 49, 50, 51, 52, 53} have become a popular correction for population structures that have cryptic relationships. Thus, the current version of our method is not applicable to summary statistics that have been corrected for population structure using LMM. However, we have shown in our previous works^{30, 36} that the same statistical model can be extended to incorporate the summary statistics that have been corrected for population structure using LMM. Unfortunately, in this case, the study’s raw genotypes and phenotypes should be available in order to perform the desired analysis.

In summary, we have developed a method to detect the presence of AH in loci of complex traits. We show that, while the method may fail to detect AH in some loci, the false positive rate is very low. Thus, when our method detects a locus to have AH with a high probability, the prediction is very reliable. Since the amount of AH detected in our study is just a lower bound on the number of loci with AH, we suggest that AH is widespread in complex traits.

Published: May 4, 2017

Web Resources

• Blood eQTL browser, http://genenetwork.nl/bloodeqtlbrowser/

• CAVIAR, http://genetics.cs.ucla.edu/caviar/

• Complex Traits Genomic Group, http://www.cnsgenomics.com/software/

• dbGaP, http://www.ncbi.nlm.nih.gov/gap

• GEUVADIS, ftp://ftp.ebi.ac.uk/pub/databases/microarray/data/experiment/GEUV/E-GEUV-1/analysis_results/

• GTEx Portal (release v.6, dbGaP: phs000424.v6.p1), http://www.gtexportal.org/home/

• HapGen2, http://mathgen.stats.ox.ac.uk/genetics_software/hapgen/hapgen2.html

• ImpG Summary, http://bogdan.bioinformatics.ucla.edu/software/impg/

• LocusZoom, http://locuszoom.sph.umich.edu/locuszoom/

• MDD summary statistics, https://www.med.unc.edu/pgc/files/resultfiles/converge.MDD.summary_stats.2Sep2015.tbl.gz

• MuTHER, http://www.muther.ac.uk/Data.html

• OMIM, http://www.omim.org/

• Ricopili, http://data.broadinstitute.org/mpg/ricopili

• SCZ summary, https://www.med.unc.edu/pgc/files/resultfiles/scz2.snp.results.txt.gz

• SuperExactTest, https://cran.r-project.org/web/packages/SuperExactTest/index.html