Abstract
Atrial fibrillation (AF) usually manifests as reentrant circuits propagating through the whole atria creating chaotic activation patterns. Little is yet known about how differences in electrophysiological and ionic properties between patients modulate reentrant patterns in AF. The goal of this study is to quantify how variability in action potential duration (APD) at different stages of repolarization determines AF dynamics and their modulation by ionic block using a set of virtual whole-atria human models. Six human whole-atria models are constructed based on the same anatomical structure and fiber orientation, but with different electrophysiological phenotypes. Membrane kinetics for each whole-atria model are selected with distinct APD characteristics at 20, 50, and 90% repolarization, from an experimentally calibrated population of human atrial action potential models, including AF remodeling and acetylcholine parasympathetic effects. Our simulations show that in all whole-atria models, reentrant circuits tend to organize around the pulmonary veins and the right atrial appendage, thus leading to higher dominant frequency (DF) and more organized activation in the left atrium than in the right atrium. Differences in APD in all phases of repolarization (not only APD90) yielded quantitative differences in fibrillation patterns with long APD associated with slower and more regular dynamics. Long APD50 and APD20 were associated with increased interatrial conduction block and interatrial differences in DF and organization index, creating reentry instability and self-termination in some cases. Specific inhibitions of IK1, INaK, or INa reduce DF and organization of the arrhythmia by enlarging wave meandering, reducing the number of secondary wavelets, and promoting interatrial block in all six virtual patients, especially for the phenotypes with short APD at 20, 50, and/or 90% repolarization. This suggests that therapies aiming at prolonging the early phase of repolarization might constitute effective antiarrhythmic strategies for the pharmacological management of AF. In summary, simulations report significant differences in atrial fibrillatory dynamics resulting from differences in APD at all phases of repolarization.
Keywords: arrhythmia, human atria, electrophysiology, variability, model populations, electrical propagation, fibrillatory patterns
Introduction
Reentrant circuits are one of the main manifestations of the most commonly diagnosed arrhythmia in the human heart: atrial fibrillation (AF) (Fuster et al., 2011). Chronic AF causes electrical remodeling in cardiac tissue, resulting in short refractory periods and slow conduction favoring reentries (Nattel et al., 2008), as well as structural remodeling, including fibrosis that alters atrial tissue composition (Burstein and Nattel, 2008; Harrison et al., 2015; Miragoli and Glukhov, 2015). AF frequently arises by rapid ectopic activity around the pulmonary veins (PV) generating stable reentrant circuits combined with short duration wavelets that propagate through the whole atria (Nattel et al., 2008). Reentrant sources are usually generated in the left atrium (LA) with propagation of the fibrillatory waves to the right atrium (RA) (Haïssaguerre et al., 1998). Its underlying mechanisms are not completely understood yet due to the complexity of teasing out structural and electrophysiological contributors (Burstein and Nattel, 2008; Nattel et al., 2008; Harrison et al., 2015; Miragoli and Glukhov, 2015).
Current anti-AF therapies aim at decreasing heart rate, blocking reentrant pathways, and isolating ectopic foci [normally ablation combined with antiarrhythmic drugs (Ames and Stevenson, 2006)]. Their efficacy is, however, limited (Jais and Packer, 2007). Further improvements in the management of AF will be facilitated by a better characterization of atrial dynamics and electrophysiological substrates through the analysis of specific measurable indices. As an example, the frequency of tissue activation or the organization in atrial activation can be quantified from electrograms (EGMs) measured on the atrial surface. Heterogeneity in these indices is considered putative of the complex spatiotemporal patterns that characterize AF, including multiple self-sustained rotors driving fibrillatory conduction (Berenfeld and Jalife, 2011; Atienza et al., 2015; Benharash et al., 2015), collision of the resulting wavefronts (Narayan et al., 2011), and disorganized local activation due to rotor meandering (Zlochiver et al., 2008; Berenfeld and Jalife, 2011). Importantly, all these measurable indices (and hence AF characteristics) present significant variability between different patients, but the implications of this variability are not well understood (Habel et al., 2010; Britton et al., 2013; Sánchez et al., 2014; Kogawa et al., 2015; Muszkiewicz et al., 2016).
In this study, we investigate AF dynamics in virtual patients exhibiting intersubject variability in atrial electrophysiological properties and differences in their response to ionic block used for antiarrhythmic therapy. In order to isolate the contribution of the electrophysiological properties from the anatomical substrate, we recreated these patients by constructing realistic 3D human atrial models with different action potential duration (APD) properties but with the same anatomy and structure (Seemann et al., 2006). Rotor dynamics for each virtual patient were analyzed using EGM maps distributed through the whole atria and validated through comparison against clinical EGM recordings. Specifically, we quantified how key intersubject differences in the repolarization of the action potential (AP) affected atrial activation patterns in AF. The potential effect of antiarrhythmic strategies on each virtual patient was assessed through the simulation of specific ionic blocks.
Materials and Methods
Construction of Six Human Whole-Atria Electrophysiology Models
The human whole-atria anatomical model described in Seemann et al. (2006) was used as the basis to construct the six virtual human patient models of AF. The whole-atria anatomical model includes fiber orientation, conduction anisotropy, and spatial heterogeneities in ionic currents and conduction velocity (CV) in the main atrial structures: LA, RA, sinoatrial node (SAN), cresta terminalis, pectinate muscles, fossa ovalis, Bachmann’s bundle, cavotricuspid isthmus, left atrial appendage (LAPG), right atrial appendage (RAPG), atrioventricular ring, and interatrial bridges (Seemann et al., 2006; Krueger et al., 2011; Tobon et al., 2013). Anisotropic ratio (transversal to longitudinal ratio of conductivity) and spatial heterogeneities are summarized in Table S1 in Supplementary Material.
Each human whole-atria model was assigned a different AP phenotype with human atrial membrane kinetics based on the Maleckar et al. model (Maleckar et al., 2009), but with ionic conductances calibrated to account for AF remodeling and intersubject variability in APD using an experimentally calibrated population of human AP models as described in Sánchez et al. (2014). In short, a population of 2,275 AP atrial models was constructed based on an AF-remodeled version of the Maleckar et al. model (70% decrease in ICaL, 50% decrease in Ito, 50% decrease in IKur, and 100% increase in IK1), considering variability in six ionic current conductances (IK1, INaK, ICaL, Ito, IKur, and INaCa) and calibrated using AP recordings from human atrial trabeculae (Wettwer et al., 2004, 2013). In order to evaluate effects of differences in APD90, APD50, or APD20 values on atrial dynamics, the human AP models (Figure 1A) were classified into six subpopulations based on whether they exhibited long or short APD90, APD50, or APD20 values (Figures 1B–D). For each degree of repolarization (APD90, APD50, or APD20), the human atrial models yielding APD within the first quartile in the overall population were classified as “short APD,” and the models above the third quartile as “long APD.” For example, the short APD90 subpopulation included all models with APD90 shorter than 172.6 ms and the long APD90 subpopulation those with APD90 longer than 222.3 ms (first and third APD90 quartiles, respectively, Figure 1B).
Figure 1.
Considered atrial fibrillation (AF) phenotypes based on cellular repolarization characteristics. (A) Population of simulated AF cell models calibrated against experimental recordings (black). The baseline Maleckar et al. model after chronic-AF remodeling (magenta) is provided for comparison. (B–D) First (blue) and fourth (red) quartile subpopulations according to APD90, APD50, and APD20, respectively, together with the corresponding histograms. Note magnification in time axis in panel (D). (E) Scatter plots of experimentally measured APD90, APD50, and APD20. Dotted lines represent first and third quartile values for each group of experimental action potential durations (APDs). (F) Venn diagrams with the number of action potential (APs) belonging to one, two, or three subpopulations of models for different intersections of short and long APD phenotypes.
In human atrial cardiomyocytes, APD90, APD50, and APD20 are frequently (although not always) related with each other, i.e., long APD90 is in general associated with long APD50 and long APD20, as shown in Figure 1E via scatter plots of experimentally measured APD90 vs APD50, APD90 vs APD20, and APD50 vs APD20. The scatter plots of Figure 1E further illustrate natural overlaps between short/long APD categories (e.g., long APD90 vs short APD50; Figure 1E, left panel) and less likely intersections (e.g., long APD20 vs short APD50; Figure 1E, right panel). Such overlaps are also captured in the six generated model subpopulations as illustrated in the Venn diagrams displayed in Figure 1F, showing frequency of intersections in number of APs between the different (and more largely sampled) APD subpopulations.
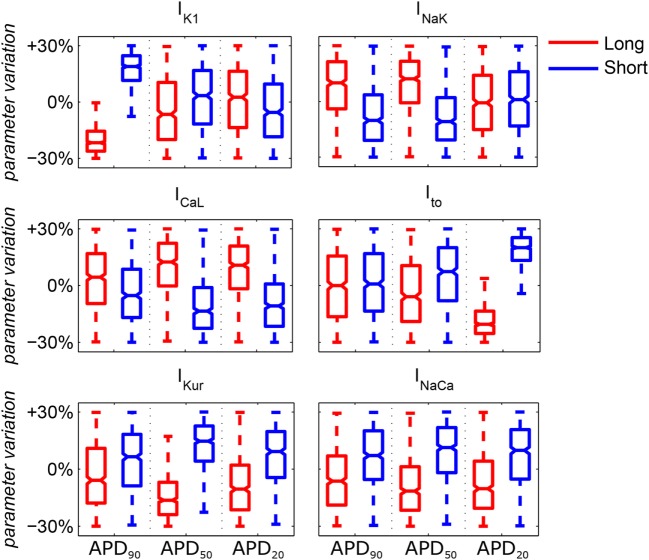
The distributions of ionic current conductances in each of the short/long APD90, APD50, and APD20 subpopulations are shown in Figure 2. This is in agreement with experimental studies showing variability in cellular electrophysiology in human cardiomyocytes and, specifically, in the atria (Wang et al., 1993). Each subpopulation of human AP models was used to assign membrane kinetics in one of the six human whole-atria models, by randomly assigning an AP model of the corresponding subpopulation to each cell (once per whole-atrial model). Figure S1 in Supplementary Material shows APD distributions in the six whole-atria models in sinus rhythm. These distributions indicate that the effect of APD heterogeneity due to the existence of different atrial structures has a stronger impact on APD dispersion than the random APD variability within each subpopulation. This means that tissue coupling and macrostructural regional differences in the anatomical model (Table S1 in Supplementary Material) attenuate cell-to-cell differences in APD due to random sampling from the AP subpopulations.
Figure 2.
Median values and ranges of variability in ionic conductances in the six subpopulations of human atrial action potential models under atrial fibrillation remodeling. Blue and red indicates short and long APD90, APD50, and APD20, respectively. Each boxplot represents the range covered by the ionic conductances: the edges of the box are the first and third quartiles, whiskers extend to the most extreme data points, the estimated median physiological value is the central horizontal line and the notch around the median is the 5% significance level.
Our simulations also incorporate the effect of a concentration of 1 nM acetylcholine ([ACh]) in the whole models, simulated as in previous studies (Kneller et al., 2002), in order to facilitate the inducibility of arrhythmic behavior (Pandit et al., 2011) and to incorporate electrophysiological heterogeneities in the different atrial structures (Table S1 in Supplementary Material). Given the uncertainty on exact distributions of ACh release in the human atria (Kneller et al., 2002; Jones et al., 2012), we adopted a simplified approach for its modeling, accounting for left and right atrial (LA/RA) differences on IKACh as reported in Sarmast et al. (2003). Larger ACh concentrations yielded an overall reduction in the regularity indices described below, with similar spatial distributions (Figure S2 in Supplementary Material).
Stimulation Protocol
A preliminary conditioning of each whole-atria model was performed by applying a train of 40 periodic stimuli at the SAN site at a cycle length of 500 ms. Then, six extra-stimuli were applied near the right pulmonary veins (RPV) in the LA to generate reentries and fibrillatory behavior. The cycle length of these six extra-stimuli was different for each AP phenotype (in the range 130–180 ms). All externally applied stimuli were 2-ms duration and twice diastolic threshold current pulses.
Simulated Ionic Current Reduction
In order to investigate how APD differences may modulate the response to antiarrhythmic therapies, the effects of ionic current block on fibrillatory dynamics and reentrant properties were quantified. Given their importance in atrial dynamics, as identified in previous studies (Kneller et al., 2005; Pandit et al., 2005, 2011; Sánchez et al., 2012), 30% IK1 block, 30% INaK block, and 15% INa block were simulated in all six whole-atrial models. These degrees of block allow the analysis of fibrillatory properties without critical alterations in cellular electrophysiology and/or electrical propagation (Sánchez et al., 2012), in agreement with experimental studies on the inhibition of IK1 with barium (Wu et al., 1999), INa with flecainide (Barekatain and Razavi, 2012), and INaK with digitalis (Wasserstrom and Aistrup, 2005). Furthermore, similar degrees of block have been widely used in sensitivity analysis studies (Romero et al., 2009, 2011; Keller et al., 2010; Sánchez et al., 2012; Chang et al., 2015). Simulation of these ionic blocks was initiated 3 s after arrhythmia generation in each of the six AF virtual models.
Whole-Atria Model Evaluation Based on EGMs of AF Patients
The EGM indices obtained from the six human whole-atria models were compared to intracardiac recordings from AF patients included in the Ann Arbor database (Ann Arbor EGM Libraries, Chicago, IL, USA) (see Figures S3 and S4 in Supplementary Material). We considered only the unipolar EGMs registered on the atrial surface, i.e., those in the high RA and the RAPG. The sampling rate for signal acquisition was 1,000 Hz. The signal processing techniques described in the following section and the Supplementary Material for the simulated EGMs were also applied to calculate dominant frequency (DF), organization index (OI), and regularity index (RI) in the EGM database. Further details in metrics calculation are provided in the Supplementary Material. Coupling index (CP) was not calculated as only one EGM signal per patient was available (Faes and Ravelli, 2007).
In the six virtual models, EGMs were obtained in 49 electrodes covering both the LA and the RA and located at a distance of about 2 mm from the endocardial surface, as in unipolar EGM recordings (Plonsey and Rudy, 1980; Gima and Rudy, 2002; Baher et al., 2007). A fourth-order Butterworth band-pass-filter (fc1 = 40 Hz; fc2 = 250 Hz), followed by a signal-rectifier and a fourth-order Butterworth high-pass-filter (fc = 20 Hz), were applied to the EGMs in order to minimize spectral components different from those of the main activation wavefront (Botteron and Smith, 1995). The four indices mentioned in the previous paragraph, DF, OI, RI, and CP, were extracted from the 49 EGM signals and interpolated to the whole-atrial tissue for representation.
Computational Tools
Whole-atrial simulations were conducted using the ELVIRA code, which solves the monodomain equation using the finite element method as described in Heidenreich et al. (2010), with a time step of 0.04 ms ensuring numerical convergence of the results (Figure S5 in Supplementary Material) and minimizing computation time. Signal processing techniques were implemented using Matlab.
Results
Modulation of AF Dynamics by Electrophysiological Phenotypic Differences
Figure 3 illustrates the strong effect of differences in APD in the dynamics of human AF through quantification of DF, RI, and OI in the six virtual patients. AF dynamics were modulated by differences in all three phases of repolarization, as shown in Figure 3 for the models with short vs long APD90, APD50, and APD20. Furthermore, the computed EGMs in the six whole-atria models yielded all arrhythmia-related indices in agreement with those in the Ann Arbor EGM database, as shown in the Supplementary Material.
Figure 3.

Modulation of atrial fibrillation reentrant dynamics by intersubject variability in action potential phenotype. Interpolated maps show dorsal views of the atria for dominant frequency (DF), organization index (OI), regularity index (RI), and coupling index (CP) between adjacent electrogram (thick white lines represent CP > 0.9, thin solid lines represent 0.75 ≤ CP < 0.9, and soft gray lines represent 0.6 ≤ CP < 0.75. CP < 0.6 is represented by absence of lines) for short and long APD90, APD50, and APD20 virtual phenotypes.
Fibrillatory dynamics in the human long APD90 whole-atria model was sustained by a single stable rotor in the RA, with slower DF than in the short APD90 atrial model (top-left panel in Figure 3). The short APD90 model exhibited more chaotic AF dynamics (sustained by several reentrant rotors) with high DF values, particularly in the LA and low RI (reflecting changes in activation patterns in different cycles). OI was generally high for both phenotypes, meaning that reentrant rotors presented no frequential components significantly different from DF and its harmonics.
The human model with long APD50 exhibited smaller values of DF (1.77 Hz lower in average) and OI (0.42 smaller in average) in the RA than the model with short APD50 (second row-left panels in Figure 3). The main reason was a block of interatrial propagation occurring in one out of three wavefronts from the LA to the RA for the long APD50 simulation. However, RI and CP were similar for both human models, suggesting local morphological changes of similar magnitude in the EGMs over time and between neighboring regions (second row-right panels in Figure 3).
Interestingly, AF dynamics in human atrial models with short vs long APD20 displayed notable differences in fibrillatory patterns. The human atrial long APD20 model was associated with very organized and regular activation patterns (OI and RI indices) as compared with those in the human atrial short APD20 model. AF dynamics in the short APD20 model were similar to those in the short APD50 model but with a more chaotic propagation in the RA due to the wavefront meandering, as shown by the lower values of both OI and RI (second and third rows, middle panels in Figure 3). Regarding the long APD20, there was only one main rotor, with low DF, high OI, high RI, and high CP in all the tissue (third row in Figure 3), which stopped propagating after 6.3 s of simulation due to interatrial conduction block.
Modulation of Fibrillatory Behavior in the Six Models by Ionic Blocks
In spite of differences in atrial dynamics shown in Figure 3, ionic current block yielded similar propagation patterns in all six virtual whole-atria models, as illustrated in Figure 4. The cores of the main reentrant rotors were usually located near the RPV, the LPV, the LAPG, and the RAPG, and secondary rotors usually appeared close to the SVC and the MV. Some particular cases, such as IK1 block in the short APD50 virtual phenotype as well as INaK block in both short and long APD50 virtual phenotypes, presented significant wave meandering and temporary rotors in the RA. In 17 out of the 18 considered interventions, the fibrillatory behavior remained self-sustained for the duration of the simulation. Only 30% INaK block in the long APD90 virtual model led to arrhythmia termination. Complete information about the number of rotors and reentrant circuits, i.e., those without phase singularities but rotating around an anatomical structure, in the LA and the RA are displayed in Table S2 in Supplementary Material classified by duration and path length for each simulation. The antiarrhythmic effect of the ionic current blocks simulated was, therefore, limited in the simulations, even though the complexity of the arrhythmia was decreased.
Figure 4.

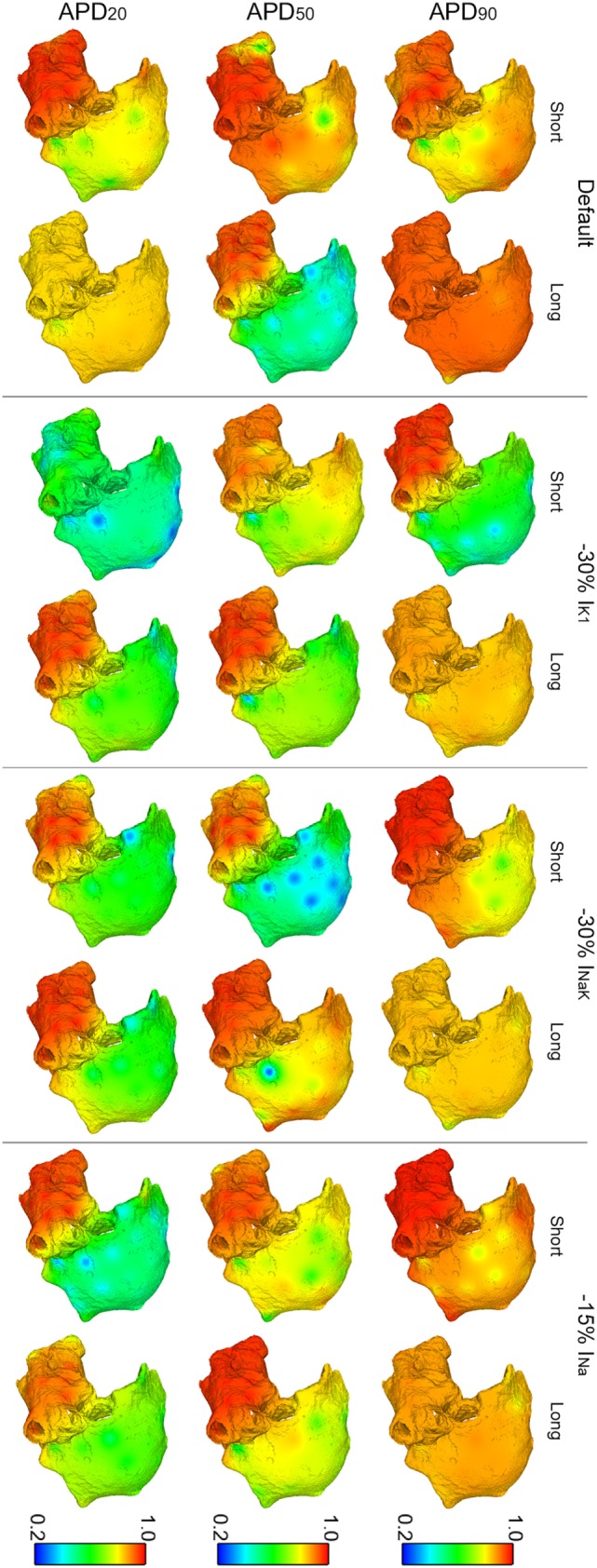
ContinuedModulation of dominant frequency (DF) of reentry in atrial fibrillation by intersubject variability in action potential phenotype in response to ion channel block. Interpolated DF maps (dorsal view of the atria) are shown for short and long APD90, APD50, and APD20 subpopulations of models before (default) and after 30% IK1 inhibition, 30% INaK inhibition, and 15% INa inhibition, respectively.
Overall, IK1, INaK, or INa block led to smaller DF and more uniform DF distributions in the six virtual phenotypes (Figure 4). This was due to the predominance of the main rotors over secondary rotors entailing additional periodicity of atrial tissue activation. However, significant LA–RA gradients in DF arose in some scenarios due to interatrial propagation block. This was the case in simulations with INaK and INa blocks in the short APD20 virtual phenotype (third row, right panels in Figure 4). Both IK1 block in the short APD50 phenotype and INaK block in the long APD50 phenotype entailed low DF in most atrial tissue except for high DF in reduced areas close to the junctions between the LA and the RA (second row, middle panels in Figure 4). This regional high DF was produced by a different delay in the wavefronts propagating and reentering in each atrium due to the APD alterations derived from the ionic blocks. Two depolarizations per rotor cycle were observed in the two cases: one due to the propagation wavefront rotating in the RA and the other due to the income of an earlier wavefront from the LA, colliding afterward with the RA wavefront. These areas did not have time to repolarize completely after their activation by each wavefront and, therefore, depolarizations were locally less prominent.
Regarding OI distributions, OI was higher in the LA than in the RA in all the simulated conditions due to the wave meandering and generation of secondary wavelets in the RA. This, thus, led to more disorganized activation patterns in RA than in LA (Figure 5). A significant reduction of OI in the LA was only observed after inhibition of IK1 in the short APD20 phenotype (third row in Figure 5). The highest OI values were obtained when IK1, INaK, or INa were inhibited in the long APD90 phenotype, although these were slightly smaller than those in the phenotype when no ionic blocks were simulated (first row in Figure 5).
Figure 5.
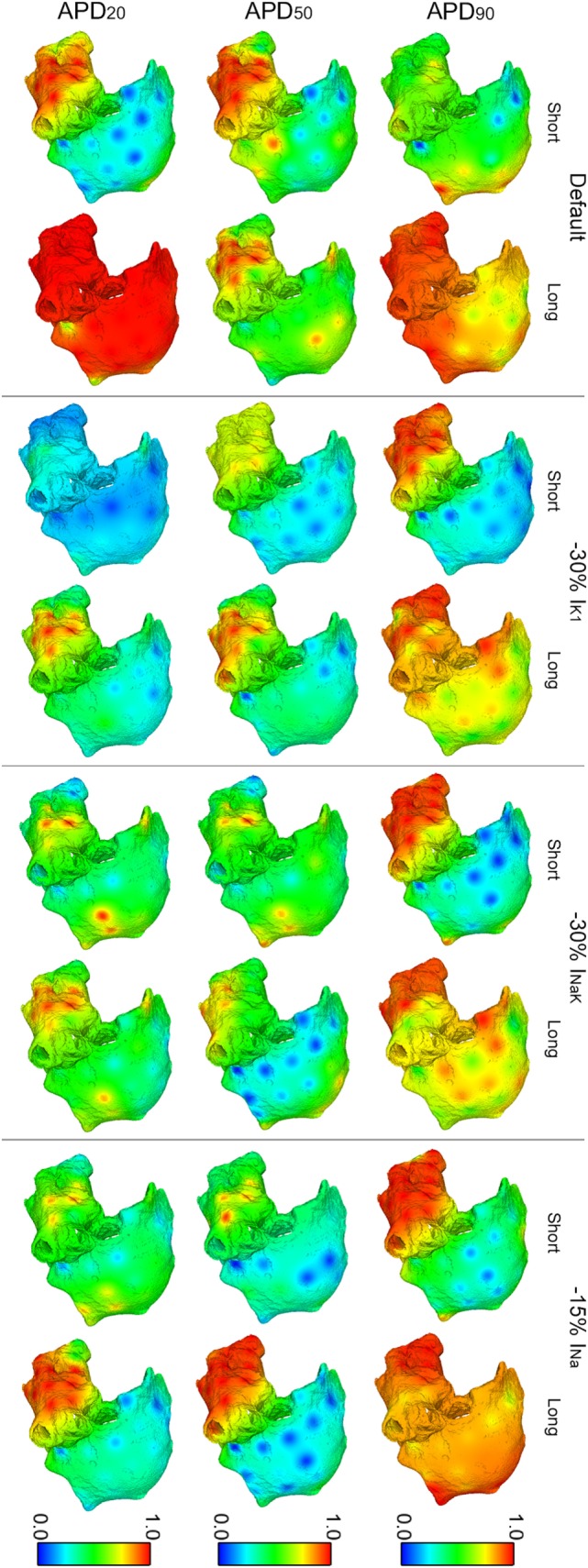
Modulation of organization index (OI) of reentry in atrial fibrillation by intersubject variability in action potential phenotype in response to ion channel block. Interpolated OI maps (dorsal view of the atria) are shown for short and long APD90, APD50, and APD20 subpopulations of models before (default) and after 30% IK1 inhibition, 30% INaK inhibition, and 15% INa inhibition, respectively.
Figures 6 and 7 show results of RI distributions and CP between adjacent electrodes, respectively. RI values after ionic inhibition were all smaller than in their respective default cases. Furthermore, they were generally higher in the LA than in the RA, highlighting important LA–RA gradients in most of the simulated cases because of the presence of RA rotors with acute meandering, whereas LA activation was usually more stable. As for OI, inhibition of IK1 in the short APD20 phenotype led to very irregular activation patterns, i.e., low RI, in both atria (third row, second column in Figure 6). The most regular activation patterns were obtained following INa block in the long APD90 phenotype (top-right panel in Figure 6). Regarding CP, a decrease in coupling with respect to the default cases was generally observed after the simulations of ionic blocks (Figure 7). The strongest couplings were observed in the LA after inhibiting INa in four of the six virtual phenotypes, whereas they were very weak in both atria for the short APD50 and APD20 phenotypes after blocks of any of the three ionic currents (Figure 7).
Figure 6.
Modulation of regularity index (RI) of reentry in atrial fibrillation by intersubject variability in action potential phenotype in response to ion channel block. Interpolated RI maps (dorsal view of the atria) are shown for short and long APD90, APD50, and APD20 subpopulations of models before (default) and after 30% IK1 inhibition, 30% INaK inhibition, and 15% INa inhibition, respectively.
Figure 7.
Modulation of coupling index (CP) of reentry in atrial fibrillation by intersubject variability in action potential phenotype in response to ion channel block. Dorsal views of the left atrium (left) and right atrium (right) are shown. CP between electrogram in adjacent electrodes (thick white lines represent CP > 0.9, thin solid lines represent 0.75 ≤ CP < 0.9, and soft gray lines represent 0.6 ≤ CP < 0.75. CP < 0.6 is represented by absence of lines) for short and long APD90, APD50, and APD20 subpopulations of models before (default) and after 30% IK1 inhibition, 30% INaK inhibition, and 15% INa inhibition, respectively.
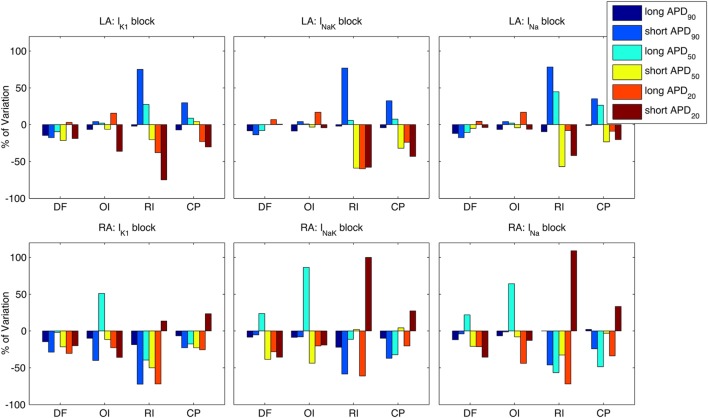
Percentual variations of the analyzed indices following the three ionic blocks with respect to the averaged values in the six virtual phenotypes are shown in Figure 8 for both the LA (top panels) and the RA (bottom panels). Bars of the same color in Figure 8 represent each virtual phenotype, whereas the analyzed indices are shown in the horizontal axis. The effects of these ionic blocks were qualitatively similar between virtual phenotypes, except for some particular cases. For example, the block of any of the three ionic currents promoted interatrial differences in RI and CP in the short APD90 phenotype by increasing both indices in the LA and decreasing them in the RA. The opposite occurred in the short APD20 phenotype, in which RI and CP were decreased in the LA and increased in the RA.
Figure 8.
Modulation by action potential (AP) phenotype in intra-subject and intersubject variability in response to drug block. Percentages of variation of average indices of atrial fibrillation reentrant dynamics [dominant frequency (DF), organization index (OI), regularity index (RI), and coupling index (CP) x-axes] are presented for the six considered AP phenotypes. Top and bottom rows show results for left atrium (LA) and right atrium (RA), under partial block of IK1 (left column), INaK (middle column), and INa (right column), respectively.
Discussion
In this study, six 3D human atrial models with different AP phenotypes were constructed to quantify differences in patterns, regularity, and organization of AF dynamics in control and following ionic inhibition. The AF dynamics in the human atrial models are shown to yield quantified indices in agreement with those obtained from AF patients in the Ann Arbor database. This supports the credibility of human atrial models to be used as test beds for antiarrhythmic therapy. Through analysis of fibrillatory electrical activation in the six human atrial models, we provide novel findings on patterns of human atria fibrillatory dynamics in different electrophysiological phenotypes and their response to ionic current block.
In our simulations, human atria with long vs short APD90 yielded significantly different fibrillatory patterns, with clear differences in DF and RI. Longer APD90 was associated with slower and more regular fibrillatory patterns. This is in good agreement with the close correlation between APD90 and effective refractory period (ERP) and their strong effects on tissue wavelength, which determines reentrant dynamics.
Importantly, differences in APD50 and APD20 also highly influenced the propagation patterns. Long APD50 resulted in interatrial conduction block, and this led to significant interatrial differences in DF and OI. Long APD20 phenotype also led to interatrial propagation block of the reentrant circuits, resulting in self-termination of the arrhythmia. This suggests that therapies aiming at prolonging the early phase of repolarization might constitute novel antiarrhythmic strategies for the pharmacological management of AF. Simulations also show that virtual phenotypes with short atrial AP present rapid reentrant rotors, highly stable in the LA, and more irregular in the RA, which is larger and, therefore, allows coexistence of a higher number of wavelets and wave meandering. For all AP phenotypes investigated, electrical activation in the LA is generally faster and more organized than in the RA, irrespective of specific AP differences considered.
The selective ion channel inhibitions considered in this study yielded similar propagation patterns qualitatively consistent between virtual AP phenotypes: inhibition of IK1, INaK, or INa entailed a more notable wave meandering that reduces the organization of the arrhythmia for all the AP phenotypes, either by slowing down electrical propagation in the human atria (INa block) or enlarging the propagation wavefront (IK1 and INaK block). The results are consistent with previous studies (Murgatroyd and Camm, 1993; Kneller et al., 2005; Pandit et al., 2005; Noujaim et al., 2007; Comtois et al., 2008), lending further credibility to the simulation results. Our study, therefore, illustrates how human whole-atria models provide a test-bed in which to test antiarrhythmic strategies, importantly accounting for phenotypic differences in atrial electrophysiological as observed across human individuals.
Our simulations also show that IK1 inhibition had a more prominent antiarrhythmic decrease effect in DF than INaK or INa reduction, which is explained by the importance of IK1 in ERP modulation in human atrial cardiomyocytes. Block of IK1 was also proven to be more effective to terminate AF than block of INa in the sheep heart (Filgueiras-Rama et al., 2012). Furthermore, in mouse hearts, upregulation of IK1 increased velocity and stability of reentrant rotors (Noujaim et al., 2007) and downregulation of IK1 was effective to terminate some arrhythmias (Noujaim et al., 2011).
Furthermore, our simulation results indicate larger disorganizations of reentry (reduced OI) for short APD50 and APD20 phenotypes in response to any of the three interventions compared to the effects of these interventions in the other APD phenotypes. Such a reduced organization has been previously related with less stable reentrant circuits (antiarrhythmic), but paradoxically with a larger number of secondary wavelets (pro-arrhythmic) (Everett et al., 2001). This suggests the importance of different electrophysiological substrates and early repolarization in determining the response to drug therapy.
Activation patterns become more irregular with inhibition of IK1, INaK, or INa in the simulations, and CP between pairs of adjacent EGMs became weaker after ionic current block. This is explained by increased wave meandering and, therefore, decreased morphological similarity between adjacent atrial EGMs. Wave meandering was more pronounced in the RA than in the LA due to its larger size and the larger distance to the ectopic foci near the PV in our simulations. Our simulation results are in agreement with previous studies showing decreased stability of rotors in the human atria due to IK1 and INa inhibition (Kneller et al., 2005; Ehrlich and Nattel, 2009; Pandit and Jalife, 2013) as well as variable efficacy of these pharmacological interventions in the conversion of AF, likely due to differences in underlying electrophysiological substrates.
INa inhibition effectively slowed CV in both LA and RA for the six virtual phenotypes, increased wavelength of reentrant circuits via strong prolongation of ERP, and reduced DF in the whole atria for all AP phenotypes, as previously established in both computational and experimental studies (Pandit et al., 2005; Burashnikov et al., 2007; Antzelevitch and Burashnikov, 2010; Sánchez et al., 2012). However, the possible side effects of sodium channel blockers on ventricular electrophysiology highlight the necessity of finding more effective atrial-selective therapies.
Finally, INaK inhibition in the human virtual atrial models, with the exception of the long APD90 phenotype in which the arrhythmia terminated, led to an overall less notable modulation of fibrillatory dynamics and organization indices than those associated to IK1 or INa, regardless of the atrial AP phenotype. This was in spite of evidence supporting the role of the NaK pump in modulating atrial APD and its rate adaptation (Grandi et al., 2011; Koivumäki et al., 2011; Sánchez et al., 2012; Bueno-Orovio et al., 2013), as well as the long standing use of digoxin in the cardio-conversion of AF (Lévy, 1997). The slow adaptation of APD secondary to INaK block could, therefore, entail important contributions to the efficacy of pharmacological inhibition of the NaK pump (Sánchez et al., 2012). However, these would take place at time scales much longer than the acute inhibitions considered here for reasons related to computational tractability of whole atria simulation studies at the whole-atrial level.
Limitations
In this study, the Maleckar et al. model (Maleckar et al., 2009) was used to simulate cellular electrophysiology, given its improved representation of human atrial repolarization dynamics. The choice of a different human atrial cell model could make results be different from those shown in this study. Nevertheless, AP phenotypes in AF with other human atrial cell models (Courtemanche et al., 1998; Grandi et al., 2011) after experimental calibration were shown to be similar to those with the Maleckar et al. model in a previous study (Sánchez et al., 2014).
Reentrant behavior was generated using a particular stimulation protocol consisting of periodic stimuli applied at the SAN followed by six extra-stimuli near the RPV. However, AF in clinical practice may present multiple ectopic foci that trigger and sustain the arrhythmia, and their location may be variable as well (Jalife et al., 2002). Furthermore, a healthy atrial anatomical model was used in this study, in order to focus on the effects of AF-induced electrophysiological rather than structural remodeling (like fibrosis), which would also affect arrhythmia generation and maintenance (Burstein and Nattel, 2008).
The effects of selective ionic blocks were analyzed individually in this study. However, many antiarrhythmic drugs, such as flecainide, digitalis, or barium, have multiple ionic targets and their simultaneous inhibitions could have synergistic and/or non-linear effects on arrhythmic markers. Therefore, a multi-target approach like that used in Sivagangabalan et al. (2014) could be interesting to explore in future studies. In addition, we only simulated moderate selective ion channel inhibitions (30% IK1 block, 30% INaK block, and 15% INa block). Larger ion channel blocks might lead to a successful termination of atrial fibrillatory dynamics in more virtual patients, but they would also have stronger effects in the ventricles, raising potential safety concerns.
The relatively small number of virtual electrodes used (49) led to visible interpolation artifacts in the figures. Nevertheless, this precision was high enough to allow proper characterization of arrhythmic behavior, since the electrical propagation wavefronts were much wider than the separation between adjacent electrodes.
As a final remark, the random assignment of a specific model within each subpopulation to each cell in the 3D model could potentially lead to neighboring cells with very different electrophysiological properties. This effect was, however, reduced for two reasons: (1) variability in the AP within each subpopulation was relatively small (first and fourth quartiles of the subpopulations were chosen to represent the slight variability present within one subject); (2) the electrotonic coupling between cells strongly smoothed electrical gradients during propagation (Figure S1 in Supplementary Material).
Conclusion
Inter-patient variability in cell repolarization entails notable differences in the organization and stability of arrhythmias in AF-electrophysiologically-remodeled tissue. Specific ionic blocks of IK1, INaK, and INa reduce the regularity of fibrillation patterns and promote interatrial differences, especially for the phenotypes with short APD at 20, 50, and/or 90% repolarization.
Author Contributions
All authors equally contributed to the conception of the work, revising it critically for important intellectual content, and final approval of the version to be published, ensuring that questions related to the accuracy or integrity of any part of the work were appropriately investigated and resolved. EP and BR acted as supervisors of the research, AB-O mainly contributed in methodological aspects, and CS was responsible for conducting all the simulations, analysis of results, and drafting the work.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to acknowledge Martin Krueger, Gunnar Seemann, and Olaf Dössel from the Karlsruhe Institute of Technology for providing us with their human atrial model.
Funding
This work was supported by project TIN2013-41998-R and DPI2016-75458-R from Spanish Ministry of Economy and Competitiveness (MINECO), Spain, MULTITOOLS2HEART from CIBER-BBN through Instituto de Salud Carlos III, Spain and by Aragón Government, Spain, and European Social Fund (EU) through Biomedical Signal Interpretation and Computational Simulation (BSICoS) group. The computation was performed at the High Performance computing platform of the NANBIOSIS ICTS, Biomedical Research Networking Center in Bioengineering, Biomaterials and Nanomedicine (CIBER-BBN) and Aragón Institute of Engineering Research (I3A), Zaragoza, Spain. BR and AB-O were supported by BR’s Wellcome Trust Senior Research Fellowship in Basic Biomedical Sciences, the NC3R Infrastructure for Impact Award (NC/P001076/1) and the CompBioMed project.
Supplementary Material
The Supplementary Material for this article can be found online at http://journal.frontiersin.org/article/10.3389/fbioe.2017.00029/full#supplementary-material.
References
- Ames A., Stevenson W. G. (2006). Cardiology patient page. Catheter ablation of atrial fibrillation. Circulation 113, e666–e668. 10.1161/CIRCULATIONAHA.105.613083 [DOI] [PubMed] [Google Scholar]
- Antzelevitch C., Burashnikov A. (2010). Atrial-selective sodium channel block as a novel strategy for the management of atrial fibrillation. Ann. N. Y. Acad. Sci. 1188, 78–86. 10.1111/j.1749-6632.2009.05086.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atienza F., Climent A. M., Guillem M. S., Berenfeld O. (2015). Frontiers in non-invasive cardiac mapping: rotors in atrial fibrillation-body surface frequency-phase mapping. Card. Electrophysiol Clin. 7, 59–69. 10.1016/j.ccep.2014.11.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baher A., Qu Z., Hayatdavoudi A., Lamp S. T., Yang M.-J., Xie F., et al. (2007). Short-term cardiac memory and mother rotor fibrillation. Am. J. Physiol. Heart Circ. Physiol. 292, H180–H189. 10.1152/ajpheart.00944.2005 [DOI] [PubMed] [Google Scholar]
- Barekatain A., Razavi M. (2012). Antiarrhythmic therapy in atrial fibrillation. Tex. Heart Inst. J. 39, 532–534. [PMC free article] [PubMed] [Google Scholar]
- Benharash P., Buch E., Frank P., Share M., Tung R., Shivkumar K., et al. (2015). Quantitative analysis of localized sources identified by focal impulse and rotor modulation mapping in atrial fibrillation. Circ. Arrhythm. Electrophysiol. 8, 554–561. 10.1161/CIRCEP.115.002721 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berenfeld O., Jalife J. (2011). Complex fractionated atrial electrograms: is this the beast to tame in atrial fibrillation? Circ. Arrhythm. Electrophysiol. 4, 426–428. 10.1161/CIRCEP.111.964841 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Botteron G. W., Smith J. M. (1995). A technique for measurement of the extent of spatial organization of atrial activation during atrial fibrillation in the intact human heart. IEEE Trans. Biomed. Eng. 42, 579–586. 10.1109/10.387197 [DOI] [PubMed] [Google Scholar]
- Britton O. J., Bueno-Orovio A., Van Ammel K., Lu H. R., Towart R., Gallacher D. J., et al. (2013). Experimentally calibrated population of models predicts and explains intersubject variability in cardiac cellular electrophysiology. Proc. Natl. Acad. Sci. U.S.A. 110, E2098–E2105. 10.1073/pnas.1304382110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bueno-Orovio A., Sánchez C., Pueyo E., Rodriguez B. (2013). Na/K pump regulation of cardiac repolarization: insights from a systems biology approach. Pflugers Arch. 466, 183–193. 10.1007/s00424-013-1293-1 [DOI] [PubMed] [Google Scholar]
- Burashnikov A., Di Diego J. M., Zygmunt A. C., Belardinelli L., Antzelevitch C. (2007). Atrium-selective sodium channel block as a strategy for suppression of atrial fibrillation: differences in sodium channel inactivation between atria and ventricles and the role of ranolazine. Circulation 116, 1449–1457. 10.1161/CIRCULATIONAHA.107.704890 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burstein B., Nattel S. (2008). Atrial fibrosis: mechanisms and clinical relevance in atrial fibrillation. J. Am. Coll. Cardiol. 51, 802–809. 10.1016/j.jacc.2007.09.064 [DOI] [PubMed] [Google Scholar]
- Chang E. T. Y., Strong M., Clayton R. H. (2015). Bayesian sensitivity analysis of a cardiac cell model using a Gaussian process emulator. PLoS ONE 10:e0130252. 10.1371/journal.pone.0130252 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comtois P., Sakabe M., Vigmond E. J., Munoz M., Texier A., Shiroshita-Takeshita A., et al. (2008). Mechanisms of atrial fibrillation termination by rapidly unbinding Na+ channel blockers: insights from mathematical models and experimental correlates. Am. J. Physiol. Heart Circ. Physiol. 295, H1489–H1504. 10.1152/ajpheart.01054.2007 [DOI] [PubMed] [Google Scholar]
- Courtemanche M., Ramirez R. J., Nattel S. (1998). Ionic mechanisms underlying human atrial action potential properties: insights from a mathematical model. Am. J. Physiol. 275, H301–H321. [DOI] [PubMed] [Google Scholar]
- Ehrlich J. R., Nattel S. (2009). Novel approaches for pharmacological management of atrial fibrillation. Drugs 69, 757–774. 10.2165/00003495-200969070-00001 [DOI] [PubMed] [Google Scholar]
- Everett T. H., IV, Kok L. C., Vaughn R. H., Moorman J. R., Haines D. E. (2001). Frequency domain algorithm for quantifying atrial fibrillation organization to increase defibrillation efficacy. IEEE Trans. Biomed. Eng. 48, 969–978. 10.1109/10.942586 [DOI] [PubMed] [Google Scholar]
- Faes L., Ravelli F. (2007). A morphology-based approach to the evaluation of atrial fibrillation organization. IEEE Eng. Med. 26, 59–67. 10.1109/MEMB.2007.384097 [DOI] [PubMed] [Google Scholar]
- Filgueiras-Rama D., Martins R. P., Mironov S., Yamazaki M., Calvo C., Ennis S. R., et al. (2012). Chloroquine terminates stretch-induced atrial fibrillation more effectively than flecainide in the sheep heart. Circ. Arrhythm. Electrophysiol. 5, 561–570. 10.1161/CIRCEP.111.966820 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuster V., Rydén L. E., Cannom D. S., Crijns H. J., Curtis A. B., Ellenbogen K. A., et al. (2011). 2011 ACCF/AHA/HRS focused updates incorporated into the ACC/AHA/ESC 2006 Guidelines for the management of patients with atrial fibrillation: a report of the American College of Cardiology Foundation/American Heart Association Task Force on practice guidelines developed in partnership with the European Society of Cardiology and in collaboration with the European Heart Rhythm Association and the Heart Rhythm Society. J. Am. Coll. Cardiol. 57, e101–e198. 10.1016/j.jacc.2010.09.013 [DOI] [PubMed] [Google Scholar]
- Gima K., Rudy Y. (2002). Ionic current basis of electrocardiographic waveforms: a model study. Circ. Res. 90, 889–896. 10.1161/01.RES.0000016960.61087.86 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grandi E., Pandit S. V., Voigt N., Workman A. J., Dobrev D., Jalife J., et al. (2011). Human atrial action potential and Ca2+ model: sinus rhythm and chronic atrial fibrillation. Circ. Res. 109, 1055–1066. 10.1161/CIRCRESAHA.111.253955 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Habel N., Znojkiewicz P., Thompson N., Müller J. G., Mason B., Calame J., et al. (2010). The temporal variability of dominant frequency and complex fractionated atrial electrograms constrains the validity of sequential mapping in human atrial fibrillation. Heart Rhythm 7, 586–593. 10.1016/j.hrthm.2010.01.010 [DOI] [PubMed] [Google Scholar]
- Haïssaguerre M., Jaïs P., Shah D. C., Takahashi A., Hocini M., Quiniou G., et al. (1998). Spontaneous initiation of atrial fibrillation by ectopic beats originating in the pulmonary veins. N. Engl. J. Med. 339, 659–666. 10.1056/NEJM199809033391003 [DOI] [PubMed] [Google Scholar]
- Harrison J. L., Sohns C., Linton N. W., Karim R., Williams S. E., Rhode K. S., et al. (2015). Repeat left atrial catheter ablation. Circ. Arrhythm. Electrophysiol. 8, 270–278. 10.1161/CIRCEP.114.002066 [DOI] [PubMed] [Google Scholar]
- Heidenreich E. A., Ferrero J. M., Doblaré M., Rodríguez J. F. (2010). Adaptive macro finite elements for the numerical solution of monodomain equations in cardiac electrophysiology. Ann. Biomed. Eng. 38, 2331–2345. 10.1007/s10439-010-9997-2 [DOI] [PubMed] [Google Scholar]
- Jais P., Packer D. L. (2007). Ablation vs. drug use for atrial fibrillation. Eur. Heart J. Suppl. 9, G26–G34. 10.1093/eurheartj/sum050 [DOI] [Google Scholar]
- Jalife J., Berenfeld O., Mansour M. (2002). Mother rotors and fibrillatory conduction: a mechanism of atrial fibrillation. Cardiovasc. Res. 54, 204–216. 10.1016/S0008-6363(02)00223-7 [DOI] [PubMed] [Google Scholar]
- Jones D. L., Tuomi J. M., Chidiac P. (2012). Role of cholinergic innervation and RGS2 in atrial arrhythmia. Front. Physiol. 3:239. 10.3389/fphys.2012.00239 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller D. U. J., Weber F. M., Seemann G., Dossel O. (2010). Ranking the influence of tissue conductivities on forward-calculated ECGs. IEEE Trans. Biomed. Eng. 57, 1568–1576. 10.1109/TBME.2010.2046485 [DOI] [PubMed] [Google Scholar]
- Kneller J., Kalifa J., Zou R., Zaitsev A. V., Warren M., Berenfeld O., et al. (2005). Mechanisms of atrial fibrillation termination by pure sodium channel blockade in an ionically-realistic mathematical model. Circ. Res. 96, e35–e47. 10.1161/01.RES.0000160709.49633.2b [DOI] [PubMed] [Google Scholar]
- Kneller J., Zou R., Vigmond E. J., Wang Z., Leon L. J., Nattel S. (2002). Cholinergic atrial fibrillation in a computer model of a two-dimensional sheet of canine atrial cells with realistic ionic properties. Circ. Res. 90, E73–E87. 10.1161/01.RES.0000019783.88094.BA [DOI] [PubMed] [Google Scholar]
- Kogawa R., Okumura Y., Watanabe I., Kofune M., Nagashima K., Mano H., et al. (2015). Spatial and temporal variability of the complex fractionated atrial electrogram activity and dominant frequency in human atrial fibrillation. J. Arrhythm. 31, 101–107. 10.1016/j.joa.2014.08.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koivumäki J. T., Korhonen T., Tavi P. (2011). Impact of sarcoplasmic reticulum calcium release on calcium dynamics and action potential morphology in human atrial myocytes: a computational study. PLoS Comput. Biol. 7:e1001067. 10.1371/journal.pcbi.1001067 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krueger M. W., Schmidt V., Tobón C., Weber F. M., Lorenz C., Keller D. U. J., et al. (2011). “Modeling atrial fiber orientation in patient-specific geometries: a semi-automatic rule-based approach,” in Functional Imaging and Modeling of the Heart Lecture Notes in Computer Science, eds Metaxas D. N., Axel L. (Berlin, Heidelberg: Springer; ), 223–232. [Google Scholar]
- Lévy S. (1997). Intravenous digoxin: still the drug of choice for acute termination of atrial fibrillation? Eur. Heart J. 18, 546–547. 10.1093/oxfordjournals.eurheartj.a015293 [DOI] [PubMed] [Google Scholar]
- Maleckar M. M., Greenstein J. L., Giles W. R., Trayanova N. A. (2009). K+ current changes account for the rate dependence of the action potential in the human atrial myocyte. Am. J. Physiol. Heart Circ. Physiol. 297, H1398–H1410. 10.1152/ajpheart.00411.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miragoli M., Glukhov A. V. (2015). Atrial fibrillation and fibrosis: beyond the cardiomyocyte centric view. Biomed Res. Int. 2015, e798768. 10.1155/2015/798768 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murgatroyd F. D., Camm A. J. (1993). Atrial arrhythmias. Lancet 341, 1317–1322. 10.1016/0140-6736(93)90824-Z [DOI] [PubMed] [Google Scholar]
- Muszkiewicz A., Britton O. J., Gemmell P., Passini E., Sánchez C., Zhou X., et al. (2016). Variability in cardiac electrophysiology: using experimentally-calibrated populations of models to move beyond the single virtual physiological human paradigm. Prog. Biophys. Mol. Biol. 120, 115–127. 10.1016/j.pbiomolbio.2015.12.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayan S. M., Wright M., Derval N., Jadidi A., Forclaz A., Nault I., et al. (2011). Classifying fractionated electrograms in human atrial fibrillation using monophasic action potentials and activation mapping: evidence for localized drivers, rate acceleration, and nonlocal signal etiologies. Heart Rhythm. 8, 244–253. 10.1016/j.hrthm.2010.10.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nattel S., Burstein B., Dobrev D. (2008). Atrial remodeling and atrial fibrillation mechanisms and implications. Circ. Arrhythm. Electrophysiol. 1, 62–73. 10.1161/CIRCEP.107.754564 [DOI] [PubMed] [Google Scholar]
- Noujaim S. F., Pandit S. V., Berenfeld O., Vikstrom K., Cerrone M., Mironov S., et al. (2007). Up-regulation of the inward rectifier K+ current (IK1) in the mouse heart accelerates and stabilizes rotors. J. Physiol. 578, 315–326. 10.1113/jphysiol.2006.121475 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noujaim S. F., Stuckey J. A., Ponce-Balbuena D., Ferrer-Villada T., López-Izquierdo A., Pandit S. V., et al. (2011). Structural bases for the different anti-fibrillatory effects of chloroquine and quinidine. Cardiovasc. Res. 89, 862–869. 10.1093/cvr/cvr008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pandit S. V., Berenfeld O., Anumonwo J. M. B., Zaritski R. M., Kneller J., Nattel S., et al. (2005). Ionic determinants of functional reentry in a 2-D model of human atrial cells during simulated chronic atrial fibrillation. Biophys. J. 88, 3806–3821. 10.1529/biophysj.105.060459 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pandit S. V., Jalife J. (2013). Rotors and the dynamics of cardiac fibrillation. Circ. Res. 112, 849–862. 10.1161/CIRCRESAHA.111.300158 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pandit S. V., Zlochiver S., Filgueiras-Rama D., Mironov S., Yamazaki M., Ennis S. R., et al. (2011). Targeting atrioventricular differences in ion channel properties for terminating acute atrial fibrillation in pigs. Cardiovasc. Res. 89, 843–851. 10.1093/cvr/cvq359 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plonsey R., Rudy Y. (1980). Electrocardiogram sources in a 2-dimensional anisotropic activation model. Med. Biol. Eng. Comput. 18, 87–94. 10.1007/BF02442485 [DOI] [PubMed] [Google Scholar]
- Romero L., Carbonell B., Trenor B., Rodríguez B., Saiz J., Ferrero J. M. (2011). Systematic characterization of the ionic basis of rabbit cellular electrophysiology using two ventricular models. Prog. Biophys. Mol. Biol. 107, 60–73. 10.1016/j.pbiomolbio.2011.06.012 [DOI] [PubMed] [Google Scholar]
- Romero L., Pueyo E., Fink M., Rodríguez B. (2009). Impact of ionic current variability on human ventricular cellular electrophysiology. Am. J. Physiol. Heart Circ. Physiol. 297, H1436–H1445. 10.1152/ajpheart.00263.2009 [DOI] [PubMed] [Google Scholar]
- Sánchez C., Bueno-Orovio A., Wettwer E., Loose S., Simon J., Ravens U., et al. (2014). Inter-subject variability in human atrial action potential in sinus rhythm versus chronic atrial fibrillation. PLoS ONE 9:e105897. 10.1371/journal.pone.0105897 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sánchez C., Corrias A., Bueno-Orovio A., Davies M., Swinton J., Jacobson I., et al. (2012). The Na+/K+ pump is an important modulator of refractoriness and rotor dynamics in human atrial tissue. Am. J. Physiol. Heart Circ. Physiol. 302, H1146–H1159. 10.1152/ajpheart.00668.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarmast F., Kolli A., Zaitsev A., Parisian K., Dhamoon A. S., Guha P. K., et al. (2003). Cholinergic atrial fibrillation: I(K,ACh) gradients determine unequal left/right atrial frequencies and rotor dynamics. Cardiovasc. Res. 59, 863–873. 10.1016/S0008-6363(03)00540-6 [DOI] [PubMed] [Google Scholar]
- Seemann G., Höper C., Sachse F. B., Dössel O., Holden A. V., Zhang H. (2006). Heterogeneous three-dimensional anatomical and electrophysiological model of human atria. Philos. Trans. A Math. Phys. Eng. Sci. 364, 1465–1481. 10.1098/rsta.2006.1781 [DOI] [PubMed] [Google Scholar]
- Sivagangabalan G., Nazzari H., Bignolais O., Maguy A., Naud P., Farid T., et al. (2014). Regional ion channel gene expression heterogeneity and ventricular fibrillation dynamics in human hearts. PLoS ONE 9:e82179. 10.1371/journal.pone.0082179 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tobon C., Ruiz-Villa C. A., Heidenreich E., Romero L., Hornero F., Saiz J. (2013). A three-dimensional human atrial model with fiber orientation. Electrograms and arrhythmic activation patterns relationship. PLoS ONE 8:e50883. 10.1371/journal.pone.0050883 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z., Fermini B., Nattel S. (1993). Delayed rectifier outward current and repolarization in human atrial myocytes. Circ. Res. 73, 276–285. 10.1161/01.RES.73.2.276 [DOI] [PubMed] [Google Scholar]
- Wasserstrom J. A., Aistrup G. L. (2005). Digitalis: new actions for an old drug. Am. J. Physiol. Heart Circ. Physiol. 289, H1781–H1793. 10.1152/ajpheart.00707.2004 [DOI] [PubMed] [Google Scholar]
- Wettwer E., Christ T., Endig S., Rozmaritsa N., Matschke K., Lynch J. J., et al. (2013). The new antiarrhythmic drug vernakalant: ex vivo study of human atrial tissue from sinus rhythm and chronic atrial fibrillation. Cardiovasc. Res. 98, 145–154. 10.1093/cvr/cvt006 [DOI] [PubMed] [Google Scholar]
- Wettwer E., Hála O., Christ T., Heubach J. F., Dobrev D., Knaut M., et al. (2004). Role of IKur in controlling action potential shape and contractility in the human atrium: influence of chronic atrial fibrillation. Circulation 110, 2299–2306. 10.1161/01.CIR.0000145155.60288.71 [DOI] [PubMed] [Google Scholar]
- Wu M. H., Su M. J., Sun S. S. (1999). Electrophysiological profile after inward rectifier K channel blockade by barium in isolated rabbit hearts. Altered repolarization and unmasked decremental conduction property. Europace 1, 85–95. 10.1053/eupc.1998.0022 [DOI] [PubMed] [Google Scholar]
- Zlochiver S., Yamazaki M., Kalifa J., Berenfeld O. (2008). Rotor meandering contributes to irregularity in electrograms during atrial fibrillation. Heart Rhythm 5, 846–854. 10.1016/j.hrthm.2008.03.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.