Front–Rear Polarization by Mechanical Cues: From Single Cells to Tissues

Abstract

Directed cell migration is a complex process that involves front–rear polarization, characterized by cell adhesion and cytoskeleton-based protrusion, retraction, and contraction of either a single cell or a cell collective. Single cell polarization depends on a variety of mechanochemical signals including external adhesive cues, substrate stiffness, and confinement. In cell ensembles, coordinated polarization of migrating tissues results not only from the application of traction forces on the extracellular matrix but also from the transmission of mechanical stress through intercellular junctions. We focus here on the impact of mechanical cues on the establishment and maintenance of front–rear polarization from single cell to collective cell behaviors through local or large-scale mechanisms.

Front–Rear Polarity in Single Cells and Cell Ensembles

One of the most striking features of animal cells is their ability to acquire and sustain an asymmetric shape in response to environmental cues. This cellular property, called cell polarization, is fundamental to the function of most eukaryotic cells, and it is particularly relevant for shaping tissues during development. Cell polarization also plays a pivotal role in intracellular transport, cell division, differentiation, and directional cell movement. Front–rear cell polarity occurs in both single cells and cell collectives. Front–rear cell polarity is spontaneously acquired by migrating isolated cells as well as by cohesive cells during wound healing, epithelial gap closure [1–3], development, and cancer invasion [4,5]. During migration a single cell must first polarize and form its front or leading edge, which is characterized by cytoskeleton assemblies that produce a protrusion. At the leading edge, actin projections known as lamellipodia (see Glossary) form associated to nascent cell–extracellular matrix (ECM) contacts, which leads to the stabilization of an oriented internal actin rearward flow and ultimately cell protrusion [6]. At the rear of lamellipodia, anchoring of mature cell–ECM contacts to actomyosin allows the formation of longitudinal stress fibers. Consequently, the rear, or uropod, is established under strong tension and adhesion sites are disassembled [7], leading to cell retraction. Cell polarity is thus associated with a particular organization and orientation of the cytoskeleton and adhesive structures.

Glossary.

Actomyosin: contractile cellular network formed by the association of nonmuscle actin fibers and myosin motors, mostly myosin II.

Adherens junctions: actin-associated intercellular junctions, part of the apical junctional complex of epithelial cells. They are recognized at the ultrastructural level by electrondense accumulation at the inner face of the plasma membrane of apposed cells.

Cadherins: conserved transmembrane proteins having an activity of homophilic Ca²⁺-dependent cell–cell adhesion. They constitute the intermembrane link of adherens junctions and cadherin adhesions.

Cadherin adhesions: cadherin-mediated cell–cell contacts observed between cells or between cells and cadherin-coated surfaces.

Durotaxis: tendency of cells to move from soft to stiff ECM.

Extracellular matrix (ECM): fibrous material constituted by cell-driven polymerization of an ensemble of proteins, glycoproteins, and proteoglycans secreted by cells and filling the intercellular space in vivo and coating the cell culture substratum in vitro.

Focal adhesions: micrometric focal points of interaction of cells with the ECM made of pleomorphic multiprotein complex linking the ECM to the actomyosin cytoskeleton via adhesion receptors of the integrin family.

Lamellipodia: large cell membrane protrusion, usually found at the front of migrating cells, characterized by a dynamic rearward flow of branched actin filaments.

Mechanotransduction: literally, transduction of forces across the plasma membrane or other cell compartment (nuclear envelope). It can be associated with the transformation of mechanical work into a biochemical signal.

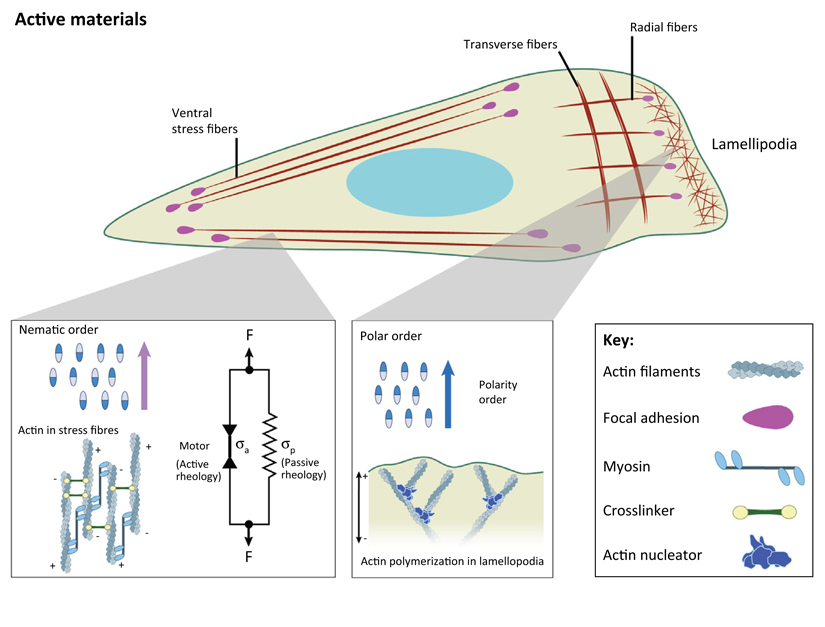
Nematic phase: the liquid crystal state is a distinct phase of matter observed between crystalline (solid) and isotropic (liquid) states. For a material made of rod-like molecules, the crystalline state corresponds to molecules regularly placed on lattice sites and aligned, whereas the position and orientation are randomly distributed in the liquid state. A liquid crystal is a material where molecules are intermediately ordered between solid and liquid states. A class of liquid crystals, called nematics, corresponds to molecules that display an orientational order with no positional order.

Plithotaxis: tendency of cells to align and migrate along the direction of maximum intercellular tension.

Viscoelasticity: property of a material with rheological properties of both elastic solids and liquids upon deformation. The Basic rheological models refer to the Voigt solid or the Maxwell liquid in which the system either does not undergo any deformation or flows as a liquid at long time scales, respectively. A simplified view of biological networks as physical gels, characterized by turnover and remodeling, describes them as Maxwell liquids, that is, elastic at short times and viscous at longer times.

Front–rear polarization of single cells can be elicited by chemical signals such as chemokines and morphogens [8]. For instance, reaction–diffusion processes can lead to pattern formation and trigger cell polarity as described by the pioneering work from Alan Turing [9]. However, it can also be acquired constitutively by isolated fibroblasts or keratocytes likely as a result of spontaneous changes in intracellular biochemical signaling and/or mechanics [10,11]. Indeed, many biochemical cues are involved in the establishment of cell polarity: diffusing factors such as morphogens and chemokines, Rho family GTPases, as well as plasma membrane determinants such as par complex proteins, as reviewed in [12]. Front–rear polarization has also recently been shown to be elicited by external force application [13], indicating that mechanical cues control at least some aspects of the establishment of front–rear polarization. This could be achieved through changes in the cytoskeleton, focal adhesions (FAs), and contractility [6,14–16]. As opposed to passive materials, living cells actively respond to mechanical perturbations occurring in their environment. Cell adhesion to the surrounding ECM is an example of a mechanical process whose cell-generated forces adapt to the mechanical properties of their microenvironment [17]. Accordingly, front–rear polarity can emerge from a symmetry breaking mechanism whose origin can be determined by the mechanochemical properties of the ECM and the preferential orientation of adhesion complexes, cytoskeletal structures, and traction forces.

Motile clusters of cells have additional strategies over single cells to polarize and migrate. In some processes, such as vascular sprouting, only the front cell of the cluster shows clear front–rear polarity [18]. By contrast, in other processes all cells within the motile group exhibit front–rear polarization, even if they retain stable cell–cell junctions [19–22]. This is the case of cell monolayers invading a free space, a process in which nearly every cell is able to extend lamellipodia and generate traction forces on its underlying substrate [23]. Polarity in cell collectives can also involve the appearance of highly motile cells at the front of the tissue called leader cells [1,24], followed by the organization of small cohorts of cells locally guided by these leaders [25]. Importantly, bulk cellular motions also display large-scale coordinated movements of cell clusters that can be seen as the emergence of large-scale polarization within the tissues [1,26]. This type of organization allows cell clusters to act as multifunctional entities in which some cells are specialized in migration while others carry out distinct functions such as differentiation or division [19]. Thus, polarized and unpolarized cells may coexist during collective cell migration.

Despite these differences, some features of collective cell polarization can be understood using the same framework as single cell polarization. For example, the emergence of large-scale polarized movements within epithelial cell sheets largely depends on external geometrical and mechanical constraints [21,27–30]. In analogy with single cells, cell polarization can be defined by cytoskeleton ordering [30,31], as well as correlated orientation over multiple cells [32]. However, the transmission of stresses through cell–cell junctions and its propagation through cellular assemblies provides an additional layer of regulation that is absent in single cells [23,26,30,33]. The present review focuses on this novel paradigm: the influence of the mechanical environment on the acquisition of polarization. In line with current understanding of active matter physics, polarization can be defined as the emergence of order and quantified by different order parameters, such as cytoskeleton organization [30,34,35], velocity correlation [26,36], cellular forces [21,34], and cell shape [37], at various length scales from the single cell [38] to multicellular assemblies [39].

Single Cell Polarization by Mechanical Cues

We first discuss how mechanical cues may direct front–rear polarization and migration of single cells (Figures 1 and 2). Cell adhesion and migration of an isolated cell on a rigid ECM revealed an intrinsic capacity of cell–ECM adhesion sites and cytoskeleton to self-polarize, that is, spontaneously organize in an anisotropic manner in the absence of external biochemical or mechanical cues [38,40]. Fibroblasts spreading on ECM-coated rigid surfaces are initially isotropic, surrounded by a circular lamellipodium in the absence of polarization [41]. Over time the evolution of isotropic radial self-organized F-actin leads, by a symmetry breaking process, to the orientation of actin fibers along a preferential direction of the lamellipodium–uropod axis [38]. This process of polarization requires cell contraction [42], FA proteins such as talin [43] and ∝-actinin [44], and depends on substrate compliance [34,42].

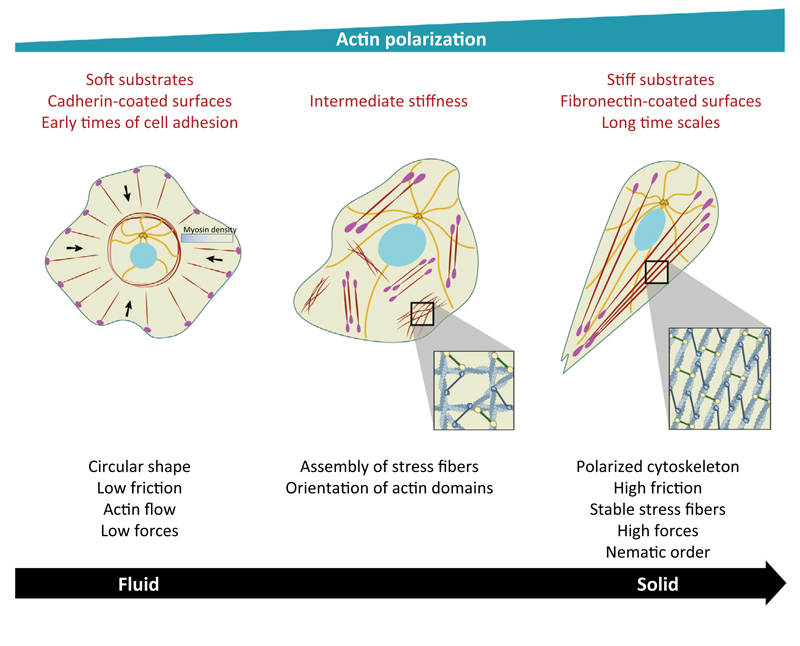
Figure 1. Single Cell Polarization by Biomechanical Cues.

(Left) Circular shape of a single cell under various conditions with the formation of noncontractile actin radial fibers at the edge and transverse arcs at the back (actin filaments are in dark red). Microtubules (MTs; orange) are confined in the central region. Light red dots represent focal adhesions (FAs) and black arrows represent the direction of the actin retrograde flow. (Middle) Appearance of ventral stress fibers that are organized in local domains on substrate of intermediate stiffness. The order parameter, S, that characterizes actin orientation is low. Note MTs reaching the edge of the cells. (Right) Actin polarization characterized by a large-scale alignment of actin filaments on stiff substrates, at long time scales and/or on fibronectin-coated surfaces (S = 1).

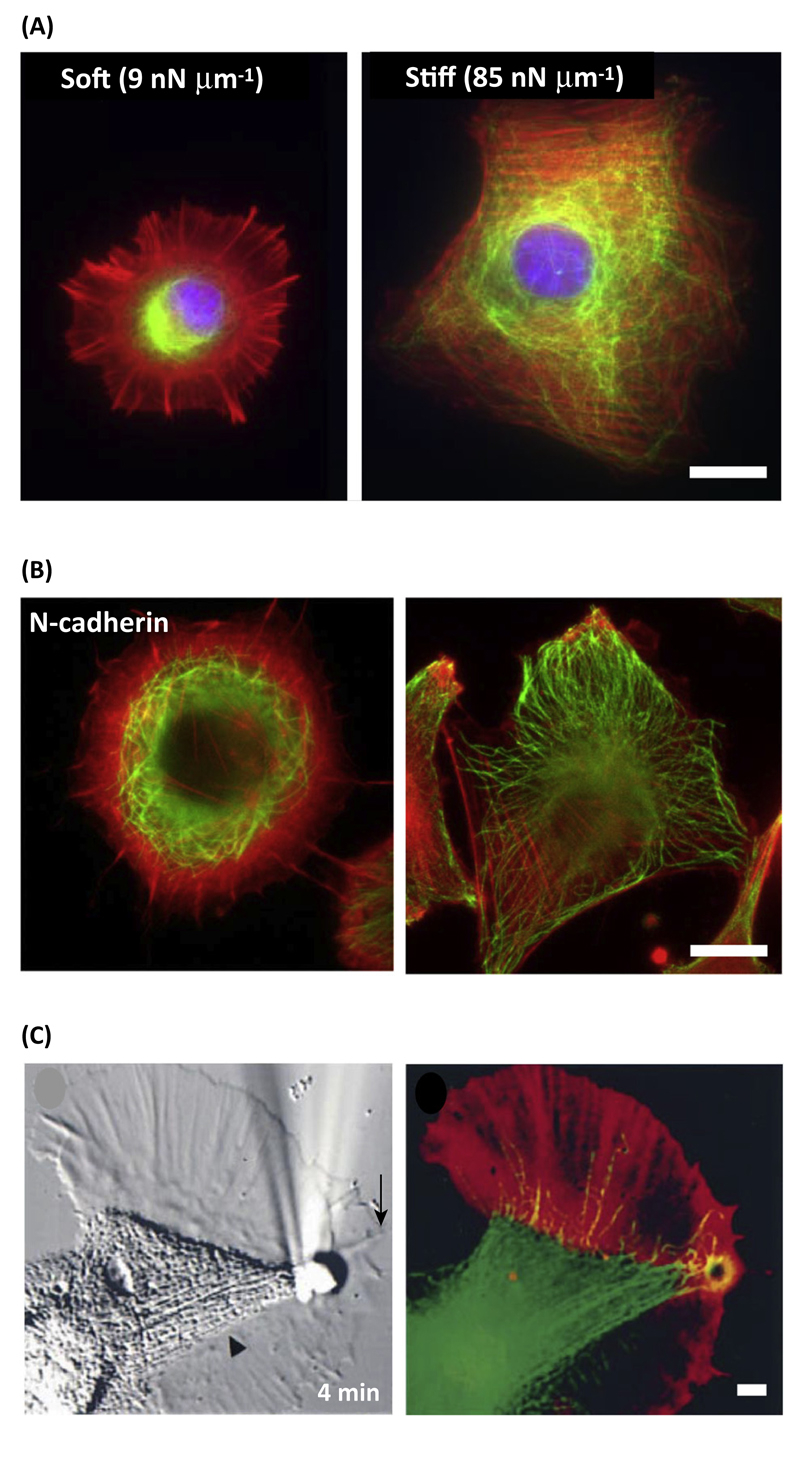
Figure 2. Response of Single Cell Actomyosin and Microtubule (MT) Organization to Adhesion and Mechanical Cues.

(A) Rat embryonic fibroblast (REF52) cells seeded on soft and stiff fibronectin-coated surfaces (M. Gupta et al., unpublished) [61]. (B) Double staining for F-actin (red) and MTs (green) of C2C12 cells spread on N-cadherin or fibronectin substrates [61]. (C) Aplysia growth stirred for 4 min with an adhesion molecule-coated bead was stained for F-actin (red) and MTs (green) [67]. Scale bars: A,B = 20 µm; C = 5 µm.

Self-polarization can also be driven by adhesive patterns imposing specific distribution of FAs [45,46], and by anisotropies in substrate stiffness, which favor cell elongation and FA orientation in the direction of highest stiffness [47,48]. In this connection, the seminal work by Lo et al. [17] demonstrated that cells migrate toward stiffer regions in a mechanism called durotaxis. The measurements of traction forces on substrates of various stiffness revealed a positive correlation between cell-generated forces and substrate rigidity [17,49]. The temporal redistribution of FAs during cell polarization on rigid matrices appeared to precede cell elongation leading to the idea of a local regulation of mechanosensing at the scale of FAs [42]. Cell–matrix adhesions composed of clusters of proteins are able to dynamically adjust both their size and shape to the applied stress through, for instance, protein phosphorylation or conformational changes [50,51]. During durotaxis, both the distribution and the dynamics of local traction forces within a single FA may explain rigidity sensing and cell migration along stiffness gradients [52]. Thus, at the single cell level, the well-described mechanosensing of FAs appears as a trademark of polarization together with actin cytoskeleton remodeling.

Along this line, early work [53] determined a direct correlation between FA size and mechanical force. The stress applied at the adhesion site, defined by $\sigma =\frac{\text{F}}{\text{A}}$ (where F is the traction force and A the FA area) kept a constant value showing a concomitant evolution of both quantities. However, recent studies describe a more complex relationship between traction forces and FA areas showing that this relationship either remains valid only during the initial stages of FA growth [54] or varies with substrate elasticity [55], suggesting that FAs could not be the only mechanosensors responsible for rigidity sensing. Among other possibilities of mechanosensing regulation, the actomyosin cytoskeleton appears as a good candidate because it has been shown to react, remodel, and polarize under mechanical signals [35,52,56–58]. Actomyosin bundles, formed by actin filaments maintained under tension by myosin II force generating dipoles, can act as large-scale mechanosensitive units by exhibiting a higher degree of polarization in response to stiffer substrates, characterized by a higher orientational order parameter [35,55]. In addition, cell migration from soft to stiff has been shown to be regulated by an enrichment of the nonmuscle myosin IIB isoform at the rear of the cell, which may explain the persistent migration of cells on matrix gradients [56]. On soft substrates, actin cytoskeleton is highly dynamic exhibiting a rearward flow of circumferential F-actin toward the nucleus, whereas stable stress fibers coupled to FAs are formed on stiffer substrates [34]. Increasing substrate stiffness correlates with the emergence of an orientational order in F-actin, which may be explained by an isotropic to nematic transition that could be compared with phase transitions described in passive materials such as liquid crystals (Box 1). Such behavior has been observed for different cell types including stem cells and fibroblasts [35,42,55]. Contractile cellular subunits could thus reorganize over time to produce an adequate force response required for intracellular polarization because the alignment of actin fibers favors a cooperative effect of pulling forces through myosin motors along the same direction. In other words, the internal active force produced by actomyosin contractility is directly coupled to the orientational ordering of actin filaments.

Box 1. Mechanics of Passive Materials.

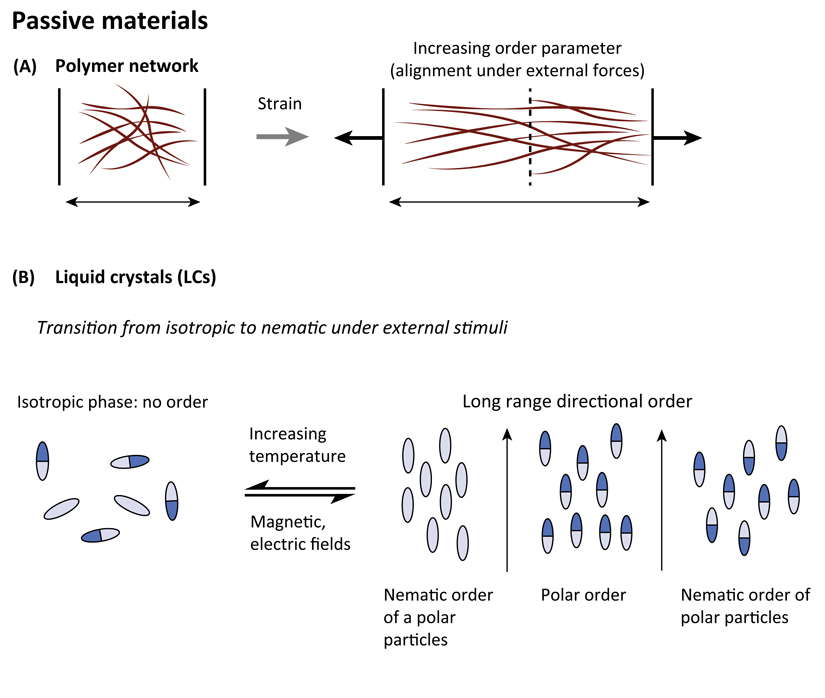
At the level of single cells, mechanical properties are controlled by the cytoskeleton, which is composed of a polymeric network made of semiflexible filaments crosslinked by other proteins through low energy chemical interactions such as dipolar or ionic, or hydrogen bonds having a finite bound time. This property makes this physical gel different from a chemical gel in which crosslinks are made of stable covalent bonds. For standard passive polymeric gels, the application of external strain induces an alignment of filaments along the direction of the strain (Figure IA). The degree of alignment can be quantified by measuring the order parameter of fiber alignment, S, where S = 0 for isotropic distribution; S = 1 for perfectly aligned fibers along a particular direction).

Cytoskeletal filaments are elongated objects that present a polarity that may be reminiscent of passive systems such as liquid crystals that may be rod-shaped molecules with elongated and anisotropic geometry. Similar to cytoskeleton filaments, liquid crystal molecules can be polar molecules with distinct heads and tails (Figure IB). In response to various stimuli such as temperature, magnetic or electric fields, or an increase in density, these systems can cooperatively order either in a polar or in a nematic phase. In a polar phase, the molecules are on average aligned in the same direction such as actin orientation in lamellipodia, whereas in a nematic phase, polar objects are aligned but with random head–tail orientations such as in the organization of antiparallel actin filaments within stress fibers (Figure IB). It is worth noting that nematic ordering can be also obtained with elongated apolar particles. This distinction may be important in understanding the organization of collective cell behaviors because single cells can exhibit elongated shapes with or without front–back polarity.

Figure I. Properties of Passive Systems.

(A) Response of polymer networks under directional external constraint. (B) Examples of phase transitions in liquid crystal materials in response to external stimuli including apolar and polar particles.

As opposed to passive materials, this active feedback between internal stress and polarization reinforces cellular mechanosensitivity to substrate elasticity. From a theoretical view, this large-scale mechanical response can be explained in the framework of continuum elasticity [35] or active gel theory [34,59]. In the first case, cells are represented by elliptical inclusions onto an elastic and deformable matrix. The active actomyosin forces in the cytoskeleton are modeled by ‘force dipoles’ that arise from the equal and opposite forces exerted by myosin motors at two nearby points on actin filaments. The internal cellular stress promotes polarization and orientation of these dipoles along their principal direction, leading to a correlation among actin polarization, cell shape anisotropy, and substrate elasticity [35]. Similarly, an approach based on active gels that assumes the cytoskeleton behaves as an elastic nematic gel can explain the emergence of order at the cellular scale (Box 2). In such cases, the coupling between substrate stiffness and order induced by gel activity is responsible for a substrate stiffness-dependent transition from isotropic to nematic order (Figure 1). This phase transition may be governed by the density of F-actin within the cell: as substrate rigidity increases, actin filament density increases and reaches a critical value over which nematic order appears, causing the stress to become anisotropic [34].

Box 2. Rheological Properties of Cytoskeleton Gels.

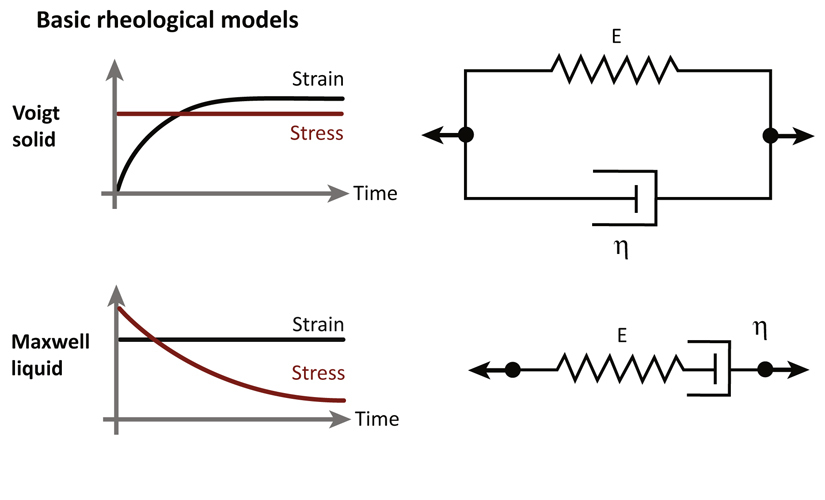
Depending on the lifetime of crosslinks, physical properties of gels may vary over time. Measurements of rheological properties are important for characterizing the mechanical behavior of materials. This can be done by applying a stress and measuring the resultant deformation. The application of a stress σ^p induces a change in length, ΔL, of the material. The strain is defined as $\gamma =\frac{\Delta L}{L}$ and the strain rate is defined as the temporal derivative of the strain $\dot{\gamma }=\frac{\Delta \gamma }{\Delta t}.$ The elastic response is characterized by resistance of the material to deformation, like a spring: σ^p = Eγ where E is Young's modulus. The viscous component allows the material to flow as a fluid and the resistance depends on the strain rate leading to ${\sigma }^{\text{p}}=\eta \dot{\gamma }$ where η is the viscosity. The Basic rheological models refer to the Voigt solid or the Maxwell liquid in which the system either does not undergo any deformation or flows as a liquid over long periods of time, respectively (Figure I). These models are represented by a purely viscous damper, η, and a purely elastic component, E, connected either in parallel or in series, respectively. A simplified view of cytoskeletons as physical gels, characterized by short crosslinker lifetimes, describes them as Maxwell liquids, that is, elastic at short times and liquid at longer times (viscoelasticity). This approach thus relies on hydrodynamic theories at macroscopic scales. By applying a sudden and constant deformation, the characteristic relaxation time given by τ = n/E is obtained by measuring the resulting stress over time. In the absence of ATP, the mechanical properties of cellular cytoskeletons could be studied using well-established methods of polymer rheology and hydrodynamics. This passive description does not incorporate active processes at work in the cytoskeleton. Indeed, more complex behaviors have been found to describe living cells and cytoskeleton remodeling including nonlinear elasticity, power laws, and fluidization [99].

In contrast to passive systems, living systems have another important characteristic: they are controlled by out-of-equilibrium processes using ATP hydrolysis as the main energy source. Mechanical properties of cells are also driven by out-of-equilibrium processes. For instance, cytoskeleton components such as actin and MTs continuously experience a polymerization/depolymerization process (dynamic instability) and interact with force-generating molecular motors. Thus, the active gel theory may well apply to the cytoskeleton. The active gel theory combines the hydrodynamic properties of passive materials together with an active stress reflecting, for instance, the activity of molecular motors such as myosins. As such, the cytoskeleton is described at large length scales compared with the mesh size of the gel, and at long time scales compared with the typical relaxation times of the actin filaments [59].

Figure I. Basic Rheological Models.

For the Voigt solid, the system does not undergo any deformation at long time scales. It is represented by a purely viscous damper and a purely elastic component connected in parallel. For the Maxwell liquid, the system flows as a liquid over long periods of time. It is represented by a purely viscous damper and a purely elastic component connected in series.

On soft substrates, the lifetime of actin structures is smaller than the one observed on stiffer surfaces, leading to polymerization-driven actin flows from the cell edge as opposed to the emergence of stable stress fibers. This suggests that increasing matrix stiffness can trigger changes in cell mechanical properties from a fluid-like behavior on soft substrates to a more solid-like behavior on stiff substrates (Box 3). Interestingly, cell shape appears to be also affected by substrate stiffness, leading to circular shapes on soft substrates and more polarized cell shapes as stiffness increases, indicating that changes in cell polarization as a function of substrate stiffness accompany changes in cell rheology from viscous on soft substrates to elastic on stiff substrates (Figure 1). The transition from a fluid to a more elastic-like response may come from the dynamics of FAs on soft and stiff substrates. On soft substrates, FAs are short-lived structures leading to low friction with the substrate. Since FAs serve as mechanical links between actin cytoskeleton and underlying substrate, this low friction favors actin flows in response to contractile stress which, in turn, contributes to destabilizing FAs. By contrast, solid-like behavior on stiffer substrates promotes FA assembly, and more generally stabilizes cross-linked actin structures. Along this line, it appears that changing the dynamics of actin cross-linkers can tune the solid and fluid-like behaviors of living cells [60]. This finding suggests that actin remodeling through force generation and FA assembly could involve a feedback loop that drives rigidity mechanosensing.

Box 3. Mechanical Properties of Active Systems.

The active gel theory results in the generalization of hydrodynamic theory that takes into account the out-of-equilibrium nature of the systems. This active stress is associated with the actomyosin network to explain cell-generated forces and contractility. The model can be obtained by coarse-graining the molecular complexity of the cytoskeleton and thus provides phenomenological equations for the description of macroscopic continuous variables such as density, velocities, and orientation field of cytoskeletal filaments (for a complete description of the different approaches of active gel theories see the review by Marchetti et al. [100]). The hydrodynamic active gel theory can be applied to generic active viscoelastic materials such as active Maxwell liquids. As such, it can describe the short-time elastic behavior and the long-time active liquid crystal behavior. The global stress within the material in the long-time limit is composed of two components in a tensorial relationship:

$${\sigma }_{ij}={\sigma }_{ij}^p+{\sigma }_{ij}^a$$

where ${\sigma }_{ij}^p$ corresponds to a passive system ${\sigma }_{ij}^a$ and to the active contribution (Figure I).

The active part is given by the following relationship:

$${\sigma }_{ij}^a=\zeta {\delta }_{ij}+{\zeta }^{\prime }{Q}_{ij}$$

where the first term corresponds to the isotropic part (the system contracts for ζ < 0 and expands for ζ > 0) and the second term corresponds to the orientational ordering of filaments (Q_ij is the nematic order parameter). An increase of alignment of the actomyosin contractile units induces an increase of active contribution of the stress. In the case of the actin cytoskeleton, this approach can be used, for instance, to describe the emergence of spontaneous flows within the cytoskeleton that are crucial for lamellipodium motion [101], as well as for cytoskeleton rheology and polarization in response to various chemical and physical cues (Figure 2). This approach recently described the large-scale responses of F-actin polarization within single cell to substrate stiffness [34]. Theoretical modeling based on this active gel approach demonstrates a biphasic rheology of the actin cytoskeleton, which transitions from fluid on soft substrates to solid on stiffer ones.

Interestingly, this approach can be used not only to describe the internal cytoskeleton but also at a larger scale, cellular assemblies [100]. During collective cell behaviors, different processes occur including division, extrusion, and rearrangements that may be described on a large scale by such a hydrodynamic approach even though the components in these situations are cells instead of filaments. More generally, this approach can be used to model active systems such as bird flocks, bacterial colonies, fish schools, and cell ensembles.

Figure I. Actin Architecture in a Single Migrating Cell including Actin Cortex, Lamellipodia, and Different Types of Stress Fibers.

Actin organization within the cell and its link to filament ordering. Ventral stress fibers: antiparallel filaments and contribution of both active and passive stresses to contractility. Organization of branched actin network in lamellipodial structures.

Cell–Cell Interactions, Mechanics, and Polarization

The emergence of ordering and polarization is a multiscale feature spanning from the subcellular cytoskeletal filament to the multicellular tissue. Whether cell colonies migrate spontaneously or in response to a chemical or a mechanical gradient, their polarization strategies integrate the generation of intercellular physical forces with upstream and downstream biochemical events. In light of single cell polarization elicited by cell–ECM interactions, we review some strategies that involve cell–cell interactions.

Single Cell Actomyosin and Microtubule Regulation by Cadherin Adhesions

To test whether the mechanisms described for single cell polarization scale to the supracellular length, studies have analyzed the spreading and actin organization of mesenchymal and epithelial cells on recombinant cadherin-coated glass surfaces, mimicking the formation of actual cadherin-mediated cell–cell contacts [61,62]. These studies revealed a behavior similar to cells seeded on ECM-coated compliant surfaces [34,38]. Despite the formation of actin-anchored cadherin adhesions, cells remain round and isotropic, with no sign of anisotropic distribution of the actin cytoskeleton (Figures 1 and 2A,B). The rearward flow of circumferential F-actin becomes elevated, as in cells spread on fibronectin-coated soft surfaces, suggesting cells on cadherin-coated substratum apply low friction forces and have a fluid-like behavior [61]. Although cadherin adhesions are mechanotransduction adhesion complexes, several mechanical/biochemical properties distinguish them from FAs: the amplitude of forces transduced at cadherin adhesions is lower than those transduced at FAs [63,64] and cadherin adhesions disassemble in conditions where cell contractility is increased, suggesting that they cannot sustain the force threshold required by the actomyosin network to undergo a fluid-to-solid phase transition.

In addition, it appears that mutual influence of actin and microtubule (MT) organization is important to drive cell polarization. The isotropic, rapid rearward flow of actomyosin has a negative effect on the penetration of MTs at the leading edge both in cells seeded on stiff cadherin substrates and on soft ECM-coated surfaces [61] (Figure 2A,B). Conversely, cells seeded on ECM-coated glass surfaces, unconstrained or confined on micropatterns, display MTs oriented parallel to stress fibers reaching the FA zone at the leading edge [61,65], a situation that is only achieved in cells adhering to cadherin surfaces when the tangential actomyosin arcs are destroyed by cytochalasin treatment [61]. Here it is important to note similarities with the polarization of growth cones in neurons (Figure 2C), which have a similar distribution and dynamics of actomyosin and MTs to fibroblasts on compliant matrices [66]. The application of an external outward directed force induces a local reduction in retrograde actin flow and a concomitant distal penetration of MTs, which precede preferential migration of the growth cone in the pulling force direction [67]. Altogether, these observations support the notion that actomyosin polarization is controlled at the single cell level by the biomechanical properties of both cell–matrix and cell–cell adhesions, and that this anisotropy impacts a major polarity marker, the MT network.

Tensional Symmetry Breaking in Cell Collectives

The biomechanical mechanisms mentioned earlier are clearly understood in minimal cell assemblies such as cell doublets with a single junction. A number of groups have shown [68–72] that these reductionist systems are strongly polarized in an antiparallel geometry characterized by an asymmetric position of the nucleus toward cell–cell contacts and an opposite orientation of the nucleus–centrosome axis and of the MT network toward cell–matrix adhesions. Interestingly, actomyosin distribution was also polarized but opposed to that of actin filaments, with enrichment toward cell–cell junctions. Cadherin and actomyosin were both involved in some aspects of this polarization such as the positioning of the nucleus [68,69].

In the context of a larger cell cluster, however, these mechanisms can only occur if symmetry is broken so that tension at the front and rear of a constituent cell is distinct. An appealing mechanism to achieve such tensional symmetry breaking is the existence of supracellular gradients in intercellular tension within the cell collective. This type of gradient has been demonstrated in epithelial cell sheets where they result from an imbalance of traction forces at the cell–matrix interface (Figure 3A) [23]. Intercellular tension differentials can vary dynamically across cell clusters of different sizes as a consequence of a mechanical wave propagating between the edges of the cluster [73]. Whether cells are able to sense these tension differentials and translate them into polarization through the mechanisms described earlier remains unknown.

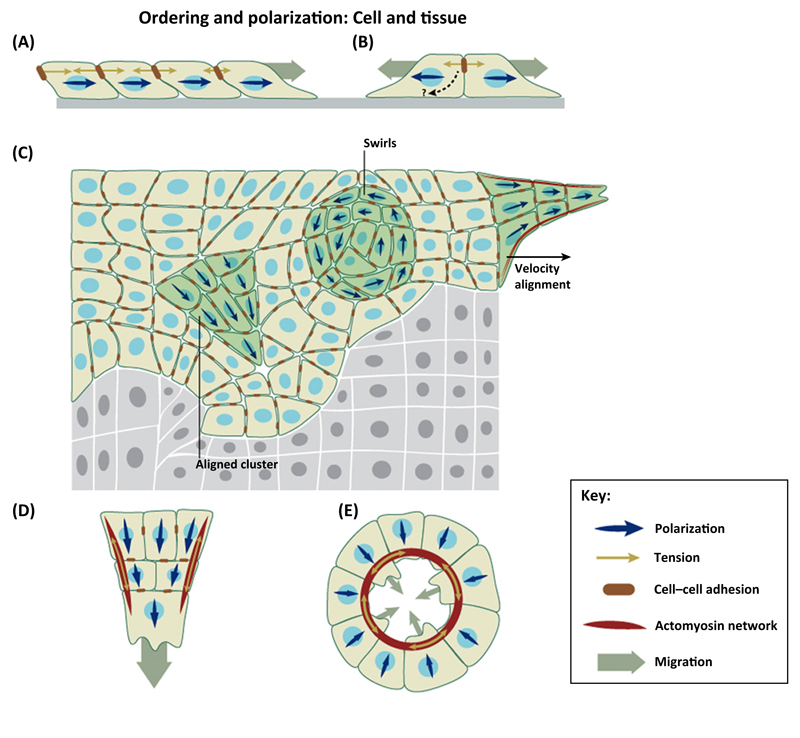
Figure 3. Mechanisms of Collective Cell Polarization by Mechanical Cues.

(A) Cells polarize downstream of a gradient of intercellular tension at the leading edge of expanding cell monolayers. (B) Cell doublets repolarize away from their intercellular contact. Under certain conditions, such repolarization leads to cell repulsion through contact inhibition of locomotion (CIL) interactions. (C) Spontaneous polarization of cell clusters and swirls within cohesive monolayers. These polarized structures emerge as a function of cell density, tension fluctuations, and confinement. (D) Contractile cables lining the leading front of cell monolayers coordinate cell polarization and Rho-GTPase activation at a supracellular length scale. (E) Contractile cables coordinate cell polarization at the leading front of a wound.

Coordinated Polarization in Multicellular Assemblies: Plithotaxis, Cell Crawling, and Supracellular Contractile Cables

The advent of techniques to measure cell–cell forces has unveiled new mechanisms for the collective orientation and polarization of cells within large multicellular collectives (Figure 3C) [21]. Tension is highly heterogeneous and anisotropic within epithelial and endothelial cell monolayers; however, cells tend to move along the lines in which tension is maximal. This mechanism is called plithotaxis and is dependent on the integrity of cell–cell junctions. It is important to note that tension is not a vector and, as such, it can define the lines along which cells move but not the direction in which they move. Thus, plithotaxis requires similar symmetry breaking mechanisms as those described earlier to fully define polarity of a cell moving in a collective.

Besides plithotaxis, a widespread mechanism for the coordination of collective cell migration is the formation of supracellular actomyosin cables (Figure 3C,D). These cables line the concave edge of gaps within epithelial layers and contract like a purse-string to drive cells forward and seal gaps [74]. Supracellular actomyosin cables have been widely reported during developmental processes such as dorsal closure in Drosophila or epiboly in zebrafish [75,76], as well as during epithelial wound healing both in vivo and in vitro [77,78]. In some of these processes, such as wound healing in the early embryo, contraction of the supracellular cable is the only mechanism behind collective cell movements, but in most processes cells exhibit both a supracellular cable and lamellipodial or filopodial protrusions at their leading edge (Figure 3D,E) [22].

The coexistence of these mechanisms can be regulated by the geometry of the cell boundary through a coupling between local curvature and actin organization, which drives a large-scale process linking cell crawling and actin-based purse-string mechanisms [3,79]. A clear example of this cooperative mechanism was recently reported in supracellular fingers at the leading edge of advancing cell monolayers [22]. These fingers are usually led by a large and highly protrusive cell that acts as a leader cell, which is mechanically linked to several rows of follower cells through a contractile actomyosin cable that lines the edge of the finger (Figure 3D). Besides coordinating cell movement, this cable defined patterns of Rho-GTPase activation, effectively converting the finger into a ‘super cell’. Additionally, leading cells may be linked through the nonclassical cadherin, Pcdh17, which accumulates at a cell–cell contact specifically in the lamellipodia of comigrating cells to create effective ‘super lamellipodia’ [80]. These super lamellipodia might provide higher migration coordination by tightly coupling protrusion of adjacent cells. These supracellular structures are emergent properties that enable groups of cells to exhibit supracellular polarization patterns that might provide cells with higher migration efficiency.

Polarization Downstream of Attractive versus Repulsive Cell–Cell Interactions

Beyond attractive, adhesive, cell–cell interactions, for certain mechanisms of collective cell polarization, it is becoming increasingly clear that repulsive forces are required to explain cell sorting, pattern formation, and collective migration of weakly adherent cells [81]. The simplest case of a repulsive interaction is volume exclusion, that is, the inability of two cells to occupy the same volume at the same time. When a cluster increases its density to become tightly packed, volume exclusion places constituent cells in a jammed state. Nontrivial emergent features of cell jamming include divergent correlation lengths, dynamic heterogeneities, and force chains [21,82]. Each of these physical features provides cells with the ability to interact with their neighbors over distances that grow with cell density, and thus offers the possibility to mediate polarization of cell collectives. Importantly, it is worth noting that jamming is not restricted to responses to increasing cell density; jamming transitions may also occur as a mere consequence of monolayer topology, that is, the average number of neighbors in a monolayer [83].

Besides volume exclusion, adjacent cells can also repel each other through contact inhibition of locomotion (CIL). CIL was first described in the 1950s following the phenomenological observation that when two cells collide they repolarize to migrate away from each other [84]. Thus, rather than forming stable adhesions, cells exhibiting CIL repel each other upon collision. Because cells are not inertial systems, repulsion should not be interpreted as a physical collision between passive elastic objects but rather as a complex mechanically active process involving the repolarization of the migratory machinery (Figure 3B). Little is known about the mechanisms behind repolarization during CIL, but current evidence indicates a transient involvement of N-cadherin homophilic adhesion between colliding cells. Experiments during neural crest development in Xenopus laevis showed that these adhesions transmit transient but significant cell–cell forces before cells separate [85]. This finding was later confirmed in Drosophila hemocytes by an elegant observation of actin flow dynamics [86]. In Xenopus neural crest cells, CIL is specifically acquired upon epithelial–mesenchymal transition (EMT) and E- to N-cadherin switch [87]. CIL has also been shown to be mediated by Eph/Ephrin [88] and Slit–Robo repulsive cues [89], but the link between these interactions and physical forces is unknown.

Repolarization downstream of a tugging force is not restricted to forces applied through actinbased adhesions. Using Xenopus laevis mesendoderm cells as a model, it was shown that pulling on magnetic beads coated with the protein C-cadherin causes cells to repolarize in the opposite direction of the pulling force [90]. This response involved intermediate filaments (keratin) and the desmosomal protein plakoglobin rather than the actin cytoskeleton. The fact that both actin and intermediate cytoskeleton are involved in force-dependent polarization responses suggests the existence of either common mechanotransduction pathways or redundant mechanisms of polarization.

Molecular Mechanisms of Front–Rear Polarization Downstream of Cell–Cell Forces

The search for molecular pathways responsible for the link between cell–cell adhesion forces and front–rear polarization has just started. Candidate pathways include mechanical sensors residing at cell–cell junctions [90–92] and downstream regulators of Rho-GTPases [22,93,94]. Recently, the tumor-suppressor protein Merlin was shown to localize at intercellular junctions in nonmotile monolayers of MDCK cells but become cytoplasmic at the onset of collective cell migration [95]. Merlin has been shown to regulate Rac1 function, thus potentially becoming a key candidate to explain coordination and polarization in monolayers. Experiments during neural crest development in Xenopus suggested that the Wnt/PCP pathway is activated downstream of a physical force applied through N-cadherin adhesions, which could inhibit Rac1 at a cell–cell contact and explain repolarization [96]. During Xenopus mesendoderm migration, a key molecular player contributing to cell polarity downstream of a physical force is plakoglobin [90], which has been shown to negatively regulate Rac1. Thus, Rac1 emerges as a key hub that regulates polarization downstream of the activation of distinct mechanosensors.

Concluding Remarks

In conclusion, we reviewed the bases of conceptual framework(s) to understand, model, and direct polarization from the subcellular to the tissue scale. The understanding of these processes takes into consideration both biochemical reactions and material mechanics. Knowledge on cytoskeleton, cell, and environment mechanics and crosstalk with more classical biochemical processes are still largely fragmented. Further understanding will require a more profound insight into active and passive properties of actomyosin as well as intermediate and MT networks at various time and length scales. It will also require a more precise determination of force transmission at cell–cell contacts and its regulation by ECM mechanical properties and cell–matrix adhesion.

There is also an urgent need to progress in the molecular understanding of cellular and subcellular mechanosensing at cell–cell and cell–matrix contacts and on instructive biochemical cues mobilized at the various scales. Clearly, we are at early ages of the understanding of this multiscale polarization by mechanical cues. This is, however, a crucial bottleneck in understanding cell and tissue polarization in 2D layers and 3D matrices in reconstituted tissues as well as in understanding the general principles underlying morphogenetic movements (see Outstanding Questions). We anticipate that the ideas reviewed here can be extended to 3D matrices as suggested by a previous study [97]. This understanding will have high incidence also in cancer biology [98] since changes in 3D environmental stiffness modulate cellular morphology of epithelial cell colonies leading to a more invasive behavior with a loss of apicobasal polarity in favor of front–back polarity and actin stress fiber formation.

Outstanding Questions.

How is local sensing through FAs and global sensing through cell cytoskeleton coupled in time and space to regulate rigidity sensing?

What are the molecular mechanisms that drive actin polarization over time, in response to adhesive cues and to matrix stiffness?

What controls coupling between actin and MT cytoskeleton in the emergence of cell polarity?

What drives the emergence of supra-cellular length scales and coordinated movements during collective cell migration?

What are the molecular mechanisms that control the crosstalk between cell–cell and cell–substrate adhesions during collective cell migration?

Can cell polarization mechanisms obtained on 2D surfaces be extended to 3D matrices?

Trends.

Physical properties of the environment have functional roles in cell polarization.

Rigidity sensing is not only governed by local dynamics of focal adhesions but also by large-scale actin cytoskeleton polarization.

Matrix stiffness regulates the internal rheological properties of the cytoskeleton.

Single cell polarization depends on the coupling between actin and microtubule cytoskeletons.

Polarization within multicellular assemblies is regulated by a crosstalk between cell–matrix and cell–cell adhesions.

Large-scale coordinated movements within epithelial cell sheets depend on external physical constraints.