Uncovering a Third Dissolved-phase ¹²⁹Xe Resonance in the Human Lung: Quantifying Spectroscopic Features in Healthy Subjects and Patients with Idiopathic Pulmonary Fibrosis

Abstract

Purpose

To accurately characterize the spectral properties of hyperpolarized ¹²⁹Xe in patients with idiopathic pulmonary fibrosis (IPF) compared to healthy volunteers.

Methods

Subjects underwent hyperpolarized ¹²⁹Xe breath-hold spectroscopy, during which 38 dissolved-phase free induction decays (FIDs) were acquired after reaching steady state (TE/TR=0.875/50 ms, BW=8.06 kHz, flip angle≈22°). FIDs were averaged and then decomposed into multiple spectral components using time-domain curve fitting. The resulting amplitudes, frequencies, linewidths, and starting phases of each component were compared among groups using a Mann–Whitney–Wilcoxon U-test.

Results

Three dissolved-phase resonances, consisting of red blood cells (RBCs) and two barrier compartments, were consistently identified in all subjects. In subjects with IPF relative to healthy volunteers, the RBC frequency was 0.70 ppm more negative (P=0.05), the chemical shift of barrier 2 was 0.6 ppm more negative (P=0.009), the linewidths of both barrier peaks were ~2 ppm narrower (P<0.001), and the starting phase of barrier 1 was 20.3 degrees higher (P=0.01). Moreover, the ratio RBC:barriers was reduced by 52.9% in IPF (P<0.001).

Conclusions

The accurate decomposition of ¹²⁹Xe spectra not only has merit for developing a global metric of pulmonary function, but also provides necessary insights to optimize phase-sensitive methods for imaging ¹²⁹Xe gas-transfer.

INTRODUCTION

Hyperpolarized (HP) ¹²⁹Xe MRI has emerged as a viable alternative to ³He for functional pulmonary MRI. This transition has created growing interest in exploiting the solubility of ¹²⁹Xe and its ~200 ppm in vivo chemical shifts to comprehensively assess lung function. This enormous range of chemical shifts is caused by the large and polarizable electron cloud of xenon, through which the ¹²⁹Xe atom experiences changes in the degree of nuclear shielding as it transiently binds to various macromolecules within the body (1). Conveniently, the ¹²⁹Xe binding affinities and degree of chemical exchange are governed by tissue properties; therefore the anatomical and physiological state of the lung determines the ¹²⁹Xe spectral characteristics.

The chemical shifts of ¹²⁹Xe have been investigated by spectroscopic techniques both in vitro and in vivo. Early in vitro studies of ¹²⁹Xe dissolved in human blood revealed two distinct dissolved-phase resonances (2). By separating red blood cells (RBCs) from plasma, ¹²⁹Xe resonances from these two compartments were found to be separated by roughly 22 ppm. Later in vitro work refined the assignment of plasma to 198 ppm and RBC to 217 ppm (3–6). Interestingly, Wolber et al. found that the linewidth of the plasma peak increases linearly with hematocrit, and also demonstrated that the chemical shift of the RBC peak is strongly and nonlinearly affected by oxygenation level (6,7). These oxygenation effects were recently confirmed by Norquay et al., who measured a 5.5 ppm range of ¹²⁹Xe-RBC chemical shifts when in vitro blood s0₂ values ranged from 0.1 to 1 (8).

Subsequent in vivo studies found that ¹²⁹Xe in the lung had similar spectral characteristics to those reported in vitro. Despite significant spectral broadening imparted by the inhomogeneous susceptibility environment in the lung, two dissolved-phase ¹²⁹Xe resonances could be readily observed. The RBC peak has been generally reported at 217 ppm in humans, while the 198 ppm peak has been assigned to ¹²⁹Xe dissolved in both plasma and other pulmonary tissues. This latter resonance is therefore commonly referred to as the “tissue/plasma” or “barrier” peak. By monitoring how these dissolved-phase peaks vary in vivo, ¹²⁹Xe has begun to show promise as a biomarker for multiple diseases and physiological processes. These have included measures of blood oxygenation (7,8), brain perfusion (9,10), and weight regulation through brown adipose tissue stimulation (11). However, the most widely investigated application has been the characterization of pulmonary gas-transfer (12–15). These studies exploit the fact that individual ¹²⁹Xe resonances directly reflect the dynamics of ¹²⁹Xe diffusing between the airspaces, interstitial barrier tissues, and capillary blood. For example, Kaushik et al. investigated ¹²⁹Xe spectra from subjects with idiopathic pulmonary fibrosis (IPF) and reported that the ratio of the RBC to barrier signal was reduced by more than 3-fold relative to that in healthy subjects (16). Moreover, this work demonstrated that the ratio of ¹²⁹Xe uptake in RBC versus barrier correlated strongly with the diffusing capacity for carbon monoxide (DL_CO), the most common clinical marker of gas-transfer. Kaushik also found that subjects with IPF exhibited a negative frequency shift in the RBC peak, which was interpreted as reflecting diminished blood oxygenation in the capillary beds.

Such spectroscopic findings not only provide sensitive measurements of lung function at a global scale, but they are also key to enabling phase-sensitive imaging techniques that spatially resolve gas-transfer. Recently, several such techniques, originally developed for fat-water separation, were extended to separate the ¹²⁹Xe signal in RBCs from that in barrier tissues (17,18). Such methods generally require acquiring dissolved-phase images at sufficient SNR and then using prior spectral knowledge to decompose images of the constituent resonances. The challenges of acquiring high-quality dissolved-phase images in vivo have been overcome by pairing an undersampled 3D radial acquisition with an optimized reconstruction (19,20). However, the second step of decomposing the dissolved-phase image remains an active area of research. Proper decomposition requires accurate information about the spectral characteristics of each resonance. However, such spectral characterization remains challenging because the resonances are broad and overlapping in the lung.

To date, the methods to decompose the dissolved-phase ¹²⁹Xe spectral properties have been somewhat rudimentary relative to ¹H and ¹³C spectroscopy, where sophisticated modeling techniques have been developed that incorporate knowledge of the coupling between protons and carbon atoms in various compounds (21,22). However, these advanced tools have not been readily applied to ¹²⁹Xe spectra. That is because ¹²⁹Xe is an inert gas with no J-coupling, but it does exhibit significant exchange and susceptibility broadening. Therefore, its spectrum can be accurately modeled by just two phenomena—precession and exponential decay. The challenge with ¹²⁹Xe spectroscopy lies in accurately accounting for the broad and overlapping nature of these resonances, as well as the substantial phase variation between them.

This work seeks to introduce techniques to better analyze ¹²⁹Xe spectra acquired in human lungs. Using non-linear curve fitting to decompose complex ¹²⁹Xe free induction decays (FIDs) in the time domain, we demonstrate that the spectrum of ¹²⁹Xe in human lungs is accurately characterized by not two, but three dissolved-phase resonances. We report the frequencies, linewidths, and phases of these three resonances in a cohort of healthy normal and IPF subjects. We then illustrate the key differences in spectral characteristics between the two populations. This work suggests that incorporating the knowledge that three dissolved-phase ¹²⁹Xe resonances arise within the lung could offer not only additional functional information in its own right, but could also improve the quality of phase-sensitive gas-transfer imaging.

METHODS

Subject Recruitment

This study was approved by the Duke Institutional Review Board. Prior to participating, all subjects provided written informed consent. The population consisted of 12 healthy normal (8 males, 4 females, 32.1 ± 13.8 years old) and 12 volunteers with IPF (10 males, 2 females, 68.5 ± 7.2 years old) who underwent HP ¹²⁹Xe spectroscopy as part of a broader imaging protocol. Prior to spectroscopy, all subjects completed pulmonary function testing, which included measuring the total lung capacity (TLC), functional residual capacity (FRC), forced vital capacity (FVC), and DL_CO.

Xenon Polarization and Delivery

Using a commercially available polarizer (Model 9810, Polarean, Inc., Durham, NC), 300 mL of isotopically enriched ¹²⁹Xe (85%) was hyperpolarized to ~20% via spin-exchange optical pumping. HP ¹²⁹Xe was cryogenically accumulated, thawed into a 1-L Tedlar bag, and diluted with 700 mL of ultra-high-purity N₂ to achieve a net 1-L volume with a 51 mL dose equivalent of HP ¹²⁹Xe (23). Immediately preceding delivery to the subject, the polarization of each dose was measured and recorded by a polarimeter (Model 2881, Polarean, Inc.).

¹²⁹Xe Spectroscopy

Both gas- and dissolved-phase spectra were acquired on a 1.5 T GE Healthcare 15M4 EXCITE MRI scanner using a quadrature ¹²⁹Xe vest coil (Clinical MR Solutions, Brookfield, WI). For each subject, heart rate and oxygen saturation were monitored using an MR-compatible monitoring system (Expression Model 865214, Invivo Corporation, Orlando, FL). Each subject was instructed to twice inhale to TLC, then exhale to FRC before inhaling the 1-L gas mixture for the 13-second breath hold. The spectroscopic parameters for the gas- and dissolved-phase ¹²⁹Xe FIDs were: 512 samples per FID, TE/TR = 0.875/50 ms, BW = 8.06 kHz, 1.2 ms 3-lobe sinc pulse, flip angle ≈ 0.5/22°. Since this scan also served as a calibration for subsequent imaging, we used a 22° dissolved-phase flip angle to maintain consistent scan parameters between both sequences. In lieu of using a 90° flip angle to eliminate magnetization that had accumulated downstream of the capillary beds, we instead discarded the first 48 dissolved-phase FIDS. We then averaged the 38 remaining steady-state frames in order to maximize FID SNR prior to curve fitting.

Spectroscopic processing

The complex FIDs from the single gas-phase and averaged dissolved-phase excitations were individually decomposed using a custom MATLAB^® toolkit (The MathWorks, Inc., Natick, MA). This open-source code is available for research use from www.civm.duhs.duke.edu/NmrSpectroscopy. The toolkit models each FID as a summation of precessing and exponentially decaying components (24). Each component signal is described by four parameters: an amplitude (a_n), starting phase (ϕ_n), resonant frequency (f_n), and linewidth (w_n). Using these parameters, the fitted signal, s_fit, can be calculated at any time, t, according to:

$$S_{fit}(t)=\sum _{n=0}^{n_{\mathit{\text{components}}}}{a}_n{e}^{i{\varphi }_n}{e}^{2\pi i{f}_{n}t}{e}^{-\pi w_{n}t}$$ (1)

Using a trust-region-reflective algorithm, this code iteratively solves for the parameters that minimize the least squares error between the measured and fitted data in the time domain (25). Unlike more common frequency-domain fitting methods, this approach does not require using linebroadening, zeropadding, or parameter constraints. However, to preserve convention, spectra are shown in the frequency domain. We also note that because of properties of the Fourier transform, the time domain amplitude is equivalent to the spectral peak area in the frequency domain. Fit results were compared after allowing for either 2 or 3 dissolved-phase resonances. Because the RBC resonance was most straightforward to isolate, its starting phase was set to zero and the those of the barrier resonances were reported relative to it.

In order to establish an absolute frequency reference against which to report the chemical shift of each component, we decomposed the dedicated gas-phase spectrum into two resonances, representing ¹²⁹Xe in the airways and alveoli (26). The stability of these resonances was evaluated in a subpopulation of 7 subjects by comparing their relative gas-phase frequencies to those of both thermally polarized ¹²⁹Xe in a phantom and hyperpolarized ¹²⁹Xe in a dose bag. We found that in humans, unlike in mice (26), the airway peak exhibits the most stable frequency. After correcting for shifts from Xe-Xe collisions (0.03 ppm for 0.3 atm Xe partial pressure), the frequency of the airway resonance was assigned to 0 ppm. With this reference, the alveolar peak appeared, on average, at −2.3ppm. This is reasonably close to the −2.9 ppm predicted from bulk magnetic susceptibility shifts (−3.02 ppm) for a spherical alveolus (26) corrected for Xe-O₂ (0.09 ppm) and Xe-Xe (0.03 ppm) collisions.

Statistical Analysis

All statistical analysis was performed in MATLAB. Differences between healthy normal and IPF cohorts were evaluated using a Mann–Whitney–Wilcoxon U-test, and determined to be statistically significant if P < 0.05. The coefficient of determination (r²) was used to assess correlations between spectroscopically-derived metrics and pulmonary function test (PFT) results.

RESULTS

Decomposing the Dissolved-Phase ¹²⁹Xe Spectrum

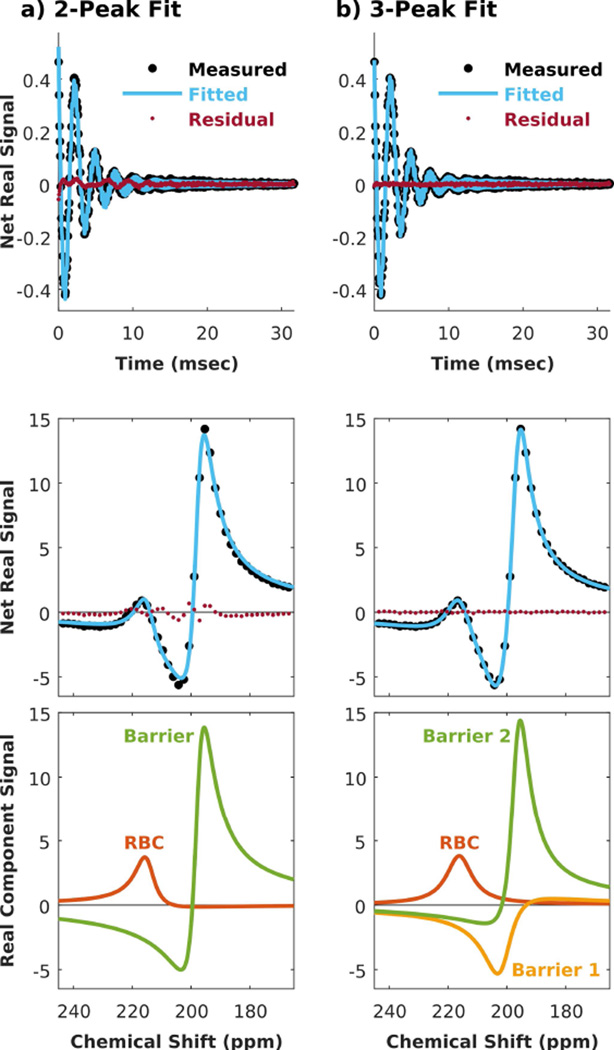
When fitting the ¹²⁹Xe spectrum from both subject groups, significant and patterned residual error persisted until three dissolved-phase resonances were included in the fit. This is illustrated in Figure 1a, showing a representative dissolved-phase ¹²⁹Xe FID (top) and spectrum (bottom) from a subject with IPF. Although the net-fitted signal from 2 peaks (blue line) appears to match the measured spectrum (large black circles at discrete spectral sampling points) reasonably well, the residual error (small red circles) shows distinct spectral oscillation in the region of dissolved-phase signal. When a third peak was introduced into the fit (Figure 1b), these fluctuations were eliminated and the residual error dropped to the noise floor. Using the 3-peak fit, the RBC resonance maintained similar amplitude and phase, but its linewidth became broader and its frequency shifted positively by ~3.5 ppm relative to the 2-peak fit results. This was related to a second observation that fitting to 3 peaks caused the barrier peak to split into two resonances that were ~5 ppm apart. These two peaks individually had smaller amplitudes than the single barrier peak derived from the 2-peak fit; they were both broader, and their starting phases were strikingly different considering their proximal frequencies. Throughout this work, we refer to the higher-frequency peak as barrier 1, and to the lower-frequency as barrier 2.

Figure 1.

Decomposing the dissolved-phase ¹²⁹Xe spectrum of a representative IPF subject. (a) Using 2 peaks resulted in non-negligible and patterned error in both the time and spectral domains. (b) The error was largely eliminated when decomposed into 3 peaks consisting of one RBC and two barrier resonances.

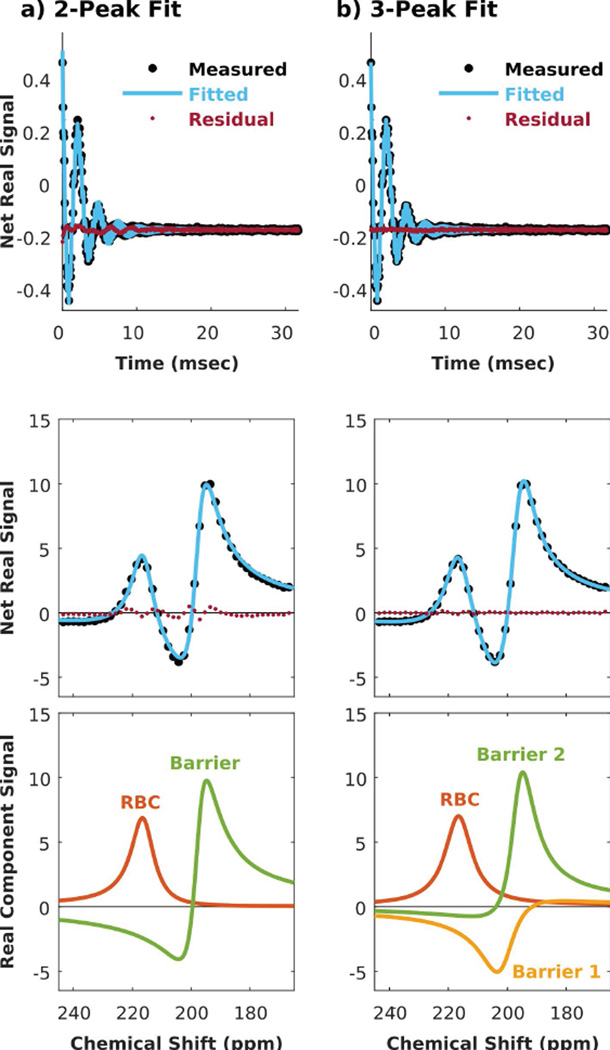
Allowing for 3 dissolved-phase peaks also improved the fit quality in healthy subjects, although less dramatically than for subjects with IPF. This is illustrated in Figure 2, depicting a representative dissolved-phase ¹²⁹Xe FID and spectrum decomposed into 2 versus 3 peaks. Fitting only 2 peaks resulted in residual error with a similar oscillating pattern, although of smaller magnitude than for the IPF subject. This was again eliminated by decomposing the FID into 3 resonances. As with the IPF subject, the 3-peak fitting also found the chemical shift of the RBC peak to be more positive than the 2-peak fitting. In the healthy subject, the linewidth and phase of the RBC peak were similar between the 2- and 3-peak fits. The 2-peak barrier resonance again split into two resonances that were individually less intense, broader, and ~4.7 ppm apart.

Figure 2.

Decomposing the dissolved-phase ¹²⁹Xe spectrum in a representative healthy subject. a) Using 2 peaks resulted in residual error that was small, but patterned in the time and spectral domains. b) The error was reduced to the noise floor by decomposing the spectrum into 3 peaks.

Quantifying Spectral Parameters from 2- and 3-Peak Fits

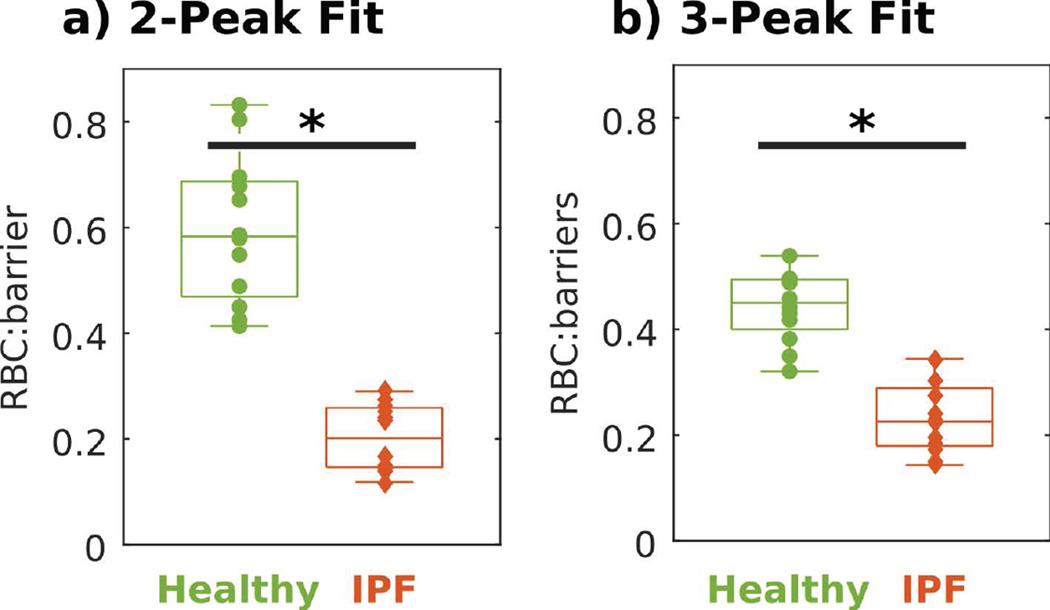
Figure 3 compares RBC:barrier ratios derived from 2- and 3-peak fits; in the latter case, termed RBC:barriers for clarity, this ratio is calculated by dividing the RBC amplitude by the sum of both barrier peak amplitudes. In the 2-peak fit, RBC:barrier was reduced by 65.1% in IPF vs healthy subjects (P < 0.001), whereas in the 3-peak fit the reduction was only 47.1% lower (P < 0.001). This difference is driven by the inclusion of the third dissolved-phase peak, which yielded lower RBC:barrier(s) in healthy subjects, but did not substantially affect the ratio in subjects with IPF.

Figure 3.

For both 2- and 3-peak fits, the RBC:barrier ratio is statistically reduced in IPF subjects relative to healthy subjects. * indicates a statistical difference between groups (P < 0.05).

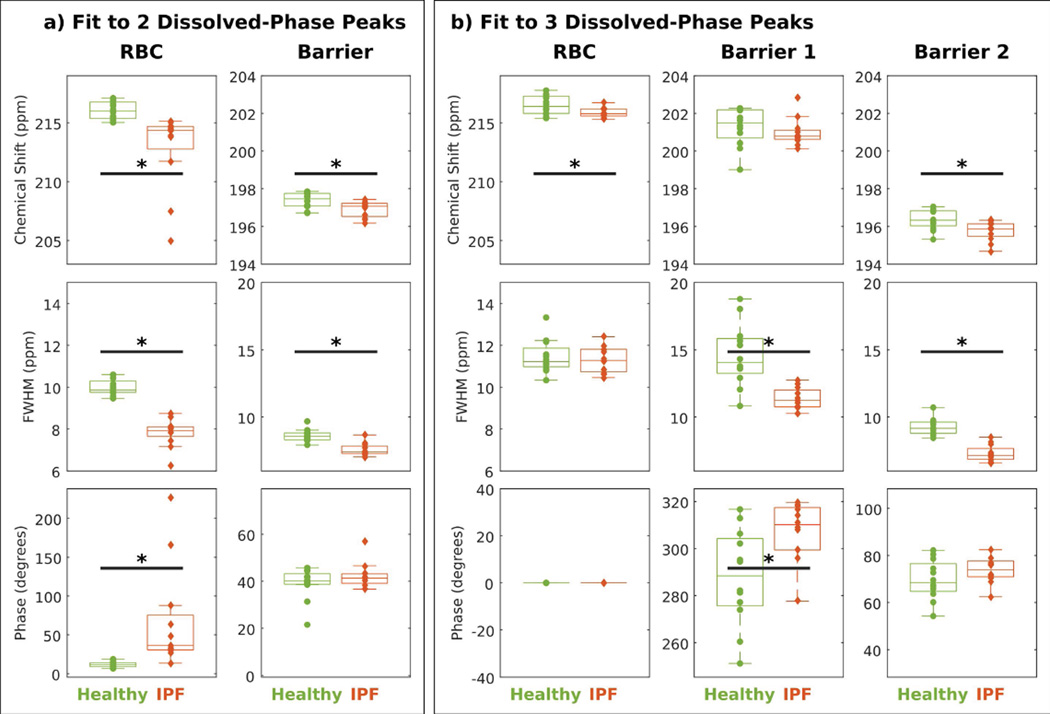
Figure 4 illustrates how the chemical shifts, linewidths, and starting phases varied when the FID was decomposed into 2 vs. 3 peaks in our healthy normal and IPF cohorts. Using a 2-peak fit (Figure 4a) found the RBC peak to be 3.15 ppm more negative (P < 0.001) and the barrier peak to be 0.45 ppm more negative in IPF versus healthy subjects (P = 0.03). Similarly, 2-peak fitting reported linewidths that were 2.15 ppm narrower for the RBC peak (P < 0.001) and 1.04 ppm narrower for the barrier peak (P < 0.001) in subjects with IPF versus healthy subjects. Using only a 2-peak fit caused the starting phase of the RBC peak to be highly variable in subjects with IPF. Moreover, this starting phase was 54.9 degrees higher (P < 0.001) in subjects with IPF relative to healthy subjects.

Figure 4.

Comparing 2- vs 3-peak fits among healthy subjects (green) and subjects with IPF (red). * indicates a statistical difference between groups (P < 0.05).

Using a 3-peak fit instead, the RBC resonance in subjects with IPF was only 0.70 ppm more negative than in healthy volunteers (P = 0.05). The chemical shift of barrier 1 was not statistically different between the two cohorts (P = 0.21), but barrier 2 was 0.6 ppm more negative (P = 0.009). Using the 3-peak fit, the linewidth of the RBC peak was indistinguishable between groups (P = 0.80). However, 3-peak fitting reported linewidths for barrier 1 and barrier 2 that were 3.2 ppm narrower (P < 0.001) and 2.0 ppm narrower (P < 0.001) in IPF versus healthy subjects. In patients with IPF, the phase of the barrier 1 peak was 20.2 degrees higher compared to healthy normal subjects (P = 0.01). The phase of barrier 2 was consistent between subjects with IPF versus healthy subjects (P = 0.19).

Spectroscopic Measurements Illustrate Differences Between IPF and Healthy Subjects

Because decomposing the FIDs into 3 peaks eliminated residual error and patterns in both groups, only 3-peak fit parameters and spectral SNR are summarized in Table 1. Spectral SNR was defined as the magnitude of the fitted signal divided by the magnitude of the residual error. Pulmonary function test results are also included for each subject.

Table 1.

Subject demographics, PFT results, and spectral parameters.

				PFTs (% pred)		Intensity	Frequency (ppm)			Linewidth (ppm)			Phase (degrees)
	Subject ID	Sex	Age	DLCO mL/min/mmHg	FVC L	RBC:barriers	RBC	Barrier 1	Barrier 2	RBC	Barrier 1	Barrier 2	RBC	Barrier 1	Barrier 2	SNR
Healthy	1	M	26	25.1 (79%)	4.4 (90%)	0.496	216.8	202.2	196.9	11.1	15.3	9.1	0.0	282.2	67.5	28.2
	2	M	65	27.9 (113%)	3.7 (97%)	0.418	216.6	201.2	196.1	11.1	13.6	9.4	0.0	302.1	80.4	30.6
	3	F	29	14.9 (76%)	2.8 (103%)	0.431	215.4	201.3	195.8	13.3	14.3	9.8	0.0	295.2	82.2	24.0
	4	M	27	26.5 (92%)	3.2 (65%)	0.539	216.1	200.1	195.9	11.3	13.8	9.0	0.0	306.3	67.0	22.0
	5	F	21	20.7 (94%)	2.8 (83%)	0.442	215.8	202.2	196.8	12.2	15.7	9.7	0.0	274.0	69.5	29.8
	6	F	21	20.4 (91%)	4 (112%)	0.488	217.4	201.0	196.4	11.1	12.1	8.5	0.0	316.6	78.7	31.5
	7	F	22	24.7 (102%)	4.2 (97%)	0.382	215.8	201.8	196.3	11.6	13.6	8.6	0.0	281.3	63.7	33.8
	8	M	24	32.2 (97%)	4.5 (82%)	0.458	217.1	202.3	196.2	12.2	16.0	10.7	0.0	277.2	72.7	26.3
	9	M	37	16.8 (55%)	3.3 (67%)	0.321	217.8	201.6	196.9	11.5	12.9	9.2	0.0	294.5	74.4	27.1
	10	M	54	23.2 (83%)	5.1 (106%)	0.349	216.2	199.0	195.3	10.9	10.8	8.8	0.0	312.9	65.9	31.6
	11	M	29	36.2 (112%)	5.6 (103%)	0.494	215.5	200.4	196.3	10.3	18.0	8.8	0.0	251.2	54.3	31.1
	12	M	30	30.5 (95%)	5 (103%)	0.495	217.4	202.2	197.1	10.8	18.8	9.6	0.0	260.5	60.1	32.3
	Mean		32	24.9 (90.8%)	4 (92.3%)	0.443	216.5	201.3	196.3	11.5	14.6	9.3	0.0	287.8	69.7	29.0
	Std Dev		13.8	6.3 (16.1%)	0.9 (15.2%)	0.066	0.8	1.0	0.5	0.8	2.3	0.6	0.0	20.4	8.4	3.6

				PFTs (% pred)		Intensity	Frequency (ppm)			Linewidth (ppm)			Phase (degrees)
	Subject ID	Sex	Age	DLCO mL/min/mmHg	FVC L	RBC:barriers	RBC	Barrier 1	Barrier 2	RBC	Barrier 1	Barrier 2	RBC	Barrier 1	Barrier 2	SNR
IPF	13	M	57	6.1 (23%)	1.78 (42%)	0.152	215.6	200.7	195.6	12.4	11.1	6.9	0.0	308.2	76.7	31.5
	14	M	68	10.2 (41%)	1.25 (29%)	0.143	215.4	200.8	195.4	11.8	10.7	6.6	0.0	318.1	78.7	21.8
	15	M	79	7.2 (31%)	2.27 (55%)	0.186	215.8	200.6	195.1	12.0	11.3	7.2	0.0	309.1	76.3	35.8
	16	F	60	11.9 (65%)	2.51 (85%)	0.196	215.9	200.1	194.7	11.8	12.5	8.5	0.0	314.3	82.5	32.9
	17	M	68	11.6 (48%)	1.86 (49%)	0.300	215.6	202.8	196.3	10.8	12.2	7.9	0.0	277.6	62.4	31.8
	18	M	70	17 (72%)	4.3 (99%)	0.240	215.7	200.8	196.1	10.6	11.2	7.3	0.0	299.3	71.8	31.9
	19	M	62	12.8 (47%)	3.1 (62%)	0.344	215.8	201.0	195.6	10.8	10.3	6.9	0.0	319.7	79.0	33.4
	20	F	67	8.9 (54%)	1.68 (77%)	0.173	216.7	201.2	196.3	11.2	10.8	7.1	0.0	311.2	71.8	35.9
	21	M	66	14.8 (59%)	2.67 (64%)	0.277	216.3	201.8	196.1	11.7	11.8	8.1	0.0	296.0	71.3	31.2
	22	M	69	13.6 (53%)	3.55 (76%)	0.344	216.2	201.0	195.9	11.3	10.3	7.0	0.0	318.8	76.0	33.3
	23	M	81	13.3 (59%)	2.46 (61%)	0.221	215.3	200.3	195.9	10.6	12.8	6.7	0.0	316.7	70.6	19.0
	24	M	75	11.4 (48%)	2.31 (54%)	0.230	216.1	200.8	195.8	10.5	11.4	7.4	0.0	299.4	68.8	33.3
	Mean		69	11.6 (50%)	2.5 (62.8%)	0.234	215.8	201.0	195.7	11.4	11.4	7.3	0.0	308.1	74.3	30.8
	Std Dev		7.2	3.1 (13.8%)	0.9 (19.3%)	0.073	0.4	0.8	0.5	0.6	0.9	0.6	0.0	12.7	5.4	5.4

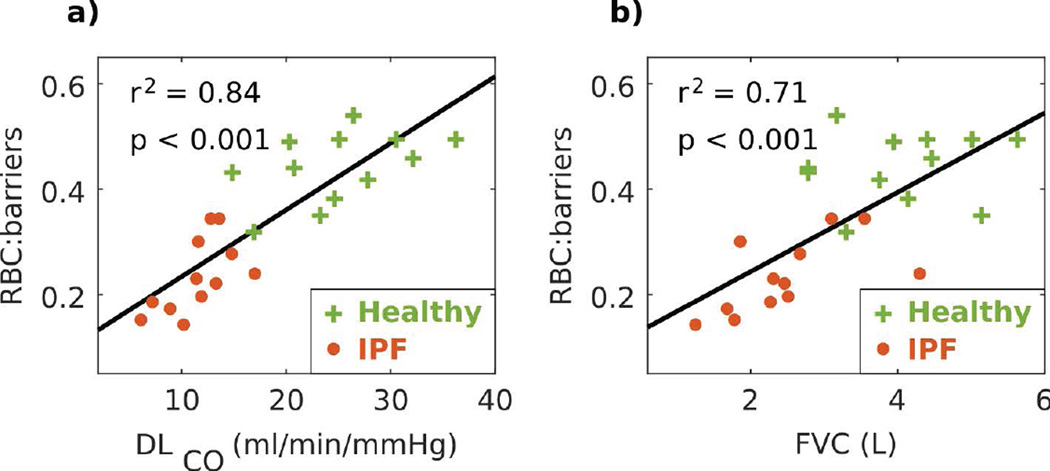
Figure 5 shows that the 3-peak RBC:barriers ratio strongly correlated with both DL_CO and FVC. The correlation was stronger with DL_CO (r² = 0.84, P < 0.001) than with FVC (r² = 0.71, P < 0.001). Both correlation plots separated the cohorts of IPF and healthy subjects, although they were further separated in the DL_CO correlation.

Figure 5.

3-peak RBC:barriers ratio correlated strongly with DL_CO and FVC. Green crosses represent healthy volunteers, red circles represent subjects with IPF, and black line represents the linear fit.

DISCUSSION

Modeling the Dissolved-Phase ¹²⁹Xe Spectrum

To date, the in vivo ¹²⁹Xe spectrum in human lungs has been reported to consist of only two dissolved-phase resonances. This is likely due, in part, because previous studies involved primarily healthy subjects, where the two barrier resonances are much broader. Thus, the presence of three dissolved-phase peaks is less evident than it is in IPF subjects where both barrier resonances become narrower, and barrier 2 shifts slightly away from barrier 1. An additional reason this third peak has likely eluded detection is because robust curve fitting methods have not generally been applied to ¹²⁹Xe spectroscopy.

The most prevalent method for decomposing the dissolved-phase ¹²⁹Xe spectrum has been to phase-correct the spectrum to first order and visually identify peaks. For each resonance, its signal amplitude is estimated by integrating the peak area, its frequency is determined by the location of the local peak maxima, and its linewidth is approximated from the measured peak full width at half maximum. This approach, while readily available, has several limitations. First, because the dissolved ¹²⁹Xe resonances are broad and close in frequency, it is difficult to accurately identify resonant frequencies visually. The high degree of overlap and differences in starting phase can obscure peaks entirely, or the tails of a nearby resonance can shift local maxima away from their true positions. Second, when peaks overlap significantly, calculating linewidths from FWHMs becomes impossible. Third, this overlap reduces the accuracy of area under the curve measurements. Fourth, applying only zeroth- and first-order phase corrections does not allow the multiple dissolved-phase peaks to be simultaneously in-phase with the receiver, making measurements of peak integrals, frequencies and linewidths impossible to quantify accurately.

Although recent years have seen increasingly more sophisticated approaches to fitting ¹²⁹Xe spectra (8,16,27), the model used in this work has three key advantages: 1) fitting is performed in the time domain; 2) it accounts for differences in starting phase among individual peaks; and 3) it simultaneously considers both the real and imaginary signals to minimize the complex error. By fitting in the time domain, we minimize the error between the fitted model and the actual acquired data. Furthermore, time domain fitting avoids artifacts that can be introduced by additional processing steps such as zeropadding and linebroadening (16). Zeropadding in the time domain, particularly with long-lived signals that have not fully decayed by the end of the FID, can introduce spectral ringing as an artifact of truncating the FID. Therefore, spectral-domain fitting seeks to reduce such truncation artifacts by line broadening the signal, which apodizes the long-lived FID using an exponential decay function prior to Fourier transformation. By contrast, fitting in the time domain eliminates the need for Fourier transformation, rendering it immune to these truncation artifacts. In addition, the fitting method used here allows each peak to retain an individual starting phase. This is particularly important since acquiring dissolved-phase ¹²⁹Xe spectra without contamination from the much more abundant gas-phase signal requires using long, frequency-selective pulses. This delays the start of FID acquisition, during which each peak accumulates significant additional phase. Therefore, it is essential that the fitting routine incorporate different starting phases for each resonance by fitting the absorptive and dispersive components in the real and imaginary channels simultaneously.

Fitting the ¹²⁹Xe Spectrum Requires Three Dissolved-Phase Resonances

Including a third dissolved-phase peak into the spectral decomposition more accurately fit the measured signal for both subject groups. Although the magnitude of the net residual error could have been decreased further by introducing additional spectral components, we found them to have areas on the order of the noise floor, while their other spectral characteristics varied widely across subjects. Thus, error reduction achieved by decomposing more than three dissolved-phase peaks is attributable to overfitting. In contrast, three dissolved-phase peaks were consistently necessary to eliminate the structure seen in the residual error, and all three peaks had reproducible frequencies and linewidths. This suggests that our findings are not merely a consequence of overfitting, and rather that the dissolved-phase ¹²⁹Xe spectrum consists of three resonances. We can further conclude that this evidence of third dissolved-phase peak is not a consequence of averaging FIDs because we were able to decompose single FIDs into three dissolved-phase peaks with reasonable agreement between subsequent FIDs. However, we suggest averaging at least 5 FIDs to obtain sufficient SNR to reproducibly characterize all of the dissolved-phase peaks.

Decomposing the FIDs into three dissolved-phase resonances also made the spectral parameters of the RBC peak more consistent across subjects. As seen in Figure 4, without the third resonance, the RBC frequency and starting phase were highly variable among IPF subjects. Including the third peak caused both the RBC frequency and its starting phase to become stable across subjects. Moreover, it eliminated differences in RBC linewidth between IPF patients and healthy subjects. This suggests that when using only 2-peak fits, the RBC peak must absorb part of the signal from the missing barrier peak, causing its spectral parameters to become sensitive to changes in barrier signal. By introducing the third dissolved-phase resonance, the RBC peak becomes untangled from barrier 1, and its spectral parameters become stable across subjects. While including a third peak improves the fit of the RBC peak, it also must split the single barrier peak into two. Given that they are broad and close in frequency, this makes them difficult to fit in healthy subjects. As a result, the spectral parameters of the barrier peaks varied slightly more in healthy subjects using the 3-peak fit than the 2-peak fit.

RBC:barriers is reduced in IPF

In aggregate, 3-peak fitting has identified six spectral parameters that exhibited statistically significant changes between IPF and healthy subjects. This speaks to the rich information contained in the dissolved-phase ¹²⁹Xe spectrum. The most significant of these changes was that RBC:barriers was 47.1% lower in IPF versus healthy subjects (P < 0.001). This reduction was less than the 65.1% difference obtained using only a 2-peak fit. This difference is caused predominantly by 3-peak fits producing larger barrier amplitudes in healthy subjects. Because barrier 1 and barrier 2 are nearly perfectly out of phase, this causes the 2-peak fit to underestimate the overall barrier signal and consequently overestimate RBC:barrier. Nonetheless, RBC:barriers strongly correlated with DL_CO (r² = 0.84, P < 0.001), which is similar to the correlation of 0.89 we previously reported using 2-peak fits (16). Such strong correlations with the primary marker of gas transfer suggests that this reduction in RBC:barriers reflects on a combination of interstitial thickening, that restricts the diffusion of ¹²⁹Xe into the RBCs, and diminished capillary blood volume, caused by regional perfusion deficits.

RBC frequency is decreased in IPF, while RBC linewidth remains unchanged

Further insights into the gas exchange dynamics can be gained by examining both the RBC linewidth and frequency. By using 3-peak fits, the RBC peak linewidth remained consistent between IPF and healthy subjects at ~11.5 ppm. This stands in contrast to the apparent narrowing that had previously been reported in IPF when using the 2-peak fit (16). This suggests that RBCs experience essentially the same physical environment in the capillary beds of healthy and IPF subjects. However, the in vivo RBC line width we measure here is still broader than the 8.6 ppm linewidth reported for ¹²⁹Xe in RBCs in vitro (6). This broadening likely arises from the inhomogeneous lung environment.

Similarly, the 3-peak fits reduced the magnitude of the apparent RBC frequency shift in patients with IPF. We did observe a 0.7 ppm negative shift for the RBC peak in IPF, but this was much smaller than reported in our initial studies, which used 2-peak fits to report a shift of −2.4 ppm in subjects with IPF (16). In fact, applying the same 2-peak fits to the present study, we measured a similar, albeit more pronounced −3.15 ppm negative shift of the RBC peak in IPF subjects. Thus, it now appears that this larger apparent RBC shift in the 2-peak fits was primarily a consequence of incompletely decomposing the spectrum. We now understand from our 3-peak fit that the barrier consists of 2 resonances, which in IPF, are both more intense and narrower. Therefore, when the dissolved-phase spectrum was fit to only 2-peaks, a portion of the missing barrier peak was allocated to the RBC resonance. This caused the least squares fitting solution to miscalculate both the frequency, linewidth, and phase of the RBC resonance.

The RBC frequency shift is of particular importance in light of in vitro work demonstrating that this resonance can shift by as much as 5.5 ppm, depending on blood oxygenation (5). Thus, the relatively modest negative shift of 0.7 ppm for the RBC resonance we now report, suggests that capillary blood in IPF patients is not as poorly oxygenated as previously thought. While we must acknowledge that there may still be local regions where blood is poorly oxygenated, our whole-lung spectroscopic measure of blood oxygenation indicates that even in IPF, the RBCs are on average still well-oxygenated. Nonetheless, temporal changes in oxygenation should be observable in ¹²⁹Xe spectra acquired during prolonged breath-hold. This was demonstrated in healthy volunteers by Norquay et al., where a decrease of up to 1 ppm in RBC frequency was detected over the course of a 35-second breath-hold (8).

Possible Origins of the Two Barrier Peaks

While the physical origin of the two barrier peaks remains to be confirmed, this work provides important clues to their sources. The acquisition methods used here were designed to minimize downstream magnetization such that the measured signal, and its constituent resonances, must spatially originate near the lung’s gas-exchange regions. We can also deduce how the barrier peaks interact physiologically by noting that, unlike the RBCs, the linewidths of the barrier resonances became significantly narrower in IPF. This narrowing could be caused by diminished chemical exchange between these compartments or decreased susceptibility-driven distortions of the local magnetic field. Diminished chemical exchange could be the result of the two barrier compartments becoming physically larger and more spatially separated in IPF. Alternatively, spectral narrowing could be caused by the reduced surface area and geometric changes of the air-tissue interfaces as barrier tissues occupy an increasingly larger fraction of the lungs in IPF subjects. This possibility is bolstered by changes in the starting phases of barrier 1 and barrier 2 during the sub-millisecond delay between excitation and readout. First, the two barrier resonances were ~100 degrees out of phase with one another. This phase dispersion cannot be explained by chemical shifts alone because the two peaks are separated by only 83 Hz (4.7 ppm). Instead, we hypothesize that the phase differences between these two components arise during the long duration of RF excitation in the presence of the inhomogeneous magnetic field environment of the lung. Second, the starting phase of barrier 1 was 20.2 degrees higher in IPF subjects versus healthy subjects (P = 0.01). This leads us to suspect that barrier 1 may originate from areas closest to the lung’s air-tissue interfaces, where susceptibility differences are greatest. This premise is further reinforced by the linewidth of barrier 1 being broader than that of barrier 2. Therefore, we hypothesize that the barrier 1 peak represents tissue residing close to the alveolar wall and its associated large susceptibility gradient caused by neighboring airspaces. Barrier 2 is substantially narrower, with a linewidth in IPF patients that is nearly identical to the 7.2 ppm in vitro linewidth measured in plasma (6). Moreover, it also has a chemical shift near that of ¹²⁹Xe in water (196 ppm) (1). For these reasons, we postulate that barrier 2 arises from both plasma and aqueous inflammatory processes residing in the interstitial space.

Study Limitations

In this work, we administered a fixed gas volume for all subjects, regardless of individual lung volumes. Ideally, each subject would have inhaled a gas volume equal to a known proportion of their TLC, in order to control for lung inflation effects. However, breath-coaching subjects to an exact lung inflation level is challenging without resorting to more invasive means such as mechanical ventilation. Moreover, recent work by Qing et al. found that the effects of lung inflation are most severe at residual volume, most strongly affect the dissolved:gas ratios, and do not affect measures of alveolar septal thickness (28). Because our interest here is in the dissolved-phase compartments, and since our spectra were acquired at ~60% of TLC for healthy volunteers and ~80% for subjects with IPF, we expect inflation effects to affect our results only modestly.

Given the difficulty of normalizing dissolved-phase spectra to the gas-phase signal, we instead chose to normalize our spectral intensities to the sum of both barrier signals. Our findings clearly indicate that RBC:barriers is reduced in IPF; however, they are not able to reliably inform on whether RBC signal is diminished or the barrier signals are increased. If gas-phase signal could be acquired such that it originates only from the gas-exchange regions, this would serve as a better quantitative reference, since it represents the source magnetization for RBC and barrier peaks (16,28). To this end, future studies should strive to spatially constrain the gas-phase signal either by selective excitation or perhaps by applying diffusion weighting to preserve ¹²⁹Xe signal from the alveoli, while suppressing signal from large airways. Alternatively, we can exploit the spatial information afforded by imaging to only calculate these ratios within the gas-exchange regions on a voxel-by-voxel basis.

And finally, our healthy and IPF populations had significant differences in mean age, thus our findings must be attributed to a combination of age and disease effects. It would be useful in the future to acquire additional data from a cohort of healthy volunteers that are age-matched to the IPF subjects. This would enable us to compare both the age effects between the two healthy cohorts, as well as the effects of disease between the IPF subjects and age-matched controls.

CONCLUSION

In this work, we illustrated the advantages of using complex time-domain fitting to decompose ¹²⁹Xe FIDs acquired in the human lung. By employing these sensitive spectroscopic techniques, we uncovered evidence of a third dissolved-phase resonance, which aids in characterizing the spectral differences between healthy subjects and subjects with IPF. We confirm that the RBC:barriers ratio continues to be significantly reduced in subjects with IPF compared to healthy subjects. However, we reconsider the magnitude of our previously reported negative frequency shifts in the RBC resonance among subjects with IPF. We now suggest that the magnitude of these shifts may have been overestimated as a result of decomposing a 3-peak spectrum using only 2 peaks. This small change in global oxygenation, combined with no detectible change in the RBC linewidth suggests that the diffusional limitation imposed by IPF at rest may not be as significant as previously thought.

The wealth of functional information in these FIDs leaves a vast space for future spectroscopic research including temporal dynamics, longitudinal changes, regional variation, and applicability to other diseases. The existence of a third dissolved-phase peak also necessitates investigating the impact on the 1-point Dixon methods for decomposing RBC and barrier images. It may suggest that, to the extent possible, and given the very short T2* of these components, separate imaging of these resonances may be improved by multi-echo imaging techniques methods such as IDEAL (18).