Integrin extension enables ultrasensitive regulation by cytoskeletal force

Significance

There are competing conceptual models of integrin activation. Recent measurements of conformational equilibria and intrinsic affinities of integrins on the cell surface enable quantitative evaluation of these models. We show that among these models, only the combination of adaptor binding and cytoskeletal force provides ultrasensitive regulation of integrin activation and occurs in a range of force experienced by most ligand-bound integrins. Switch-like activation by force relies on the large change in length in integrin extension and explains why integrins extend and why their domain organization is so conserved.

Abstract

Integrins undergo large-scale conformational changes upon activation. Signaling events driving integrin activation have previously been discussed conceptually, but not quantitatively. Here, recent measurements of the intrinsic ligand-binding affinity and free energy of each integrin conformational state on the cell surface, together with the length scales of conformational change, are used to quantitatively compare models of activation. We examine whether binding of cytoskeletal adaptors to integrin cytoplasmic domains is sufficient for activation or whether exertion of tensile force by the actin cytoskeleton across the integrin–ligand complex is also required. We find that only the combination of adaptor binding and cytoskeletal force provides ultrasensitive regulation. Moreover, switch-like activation by force depends on the large, >130 Å length-scale change in integrin extension, which is well tailored to match the free-energy difference between the inactive (bent-closed) and active (extended-open) conformations. The length scale and energy cost in integrin extension enable activation by force in the low pN range and appear to be the key specializations that enable cell adhesion through integrins to be coordinated with cytoskeletal dynamics.

Integrins undergo larger and more complex conformational changes upon activation than other known cell surface receptors (1) (Fig. 1 A–C). In a resting, bent-closed conformation, the ligand-binding site lies close to the plasma membrane. In two extended states, the ligand-binding site faces away from the cell surface and extends 150–200 Å above it (Fig. 1 A–C). Activation requires the extended-open state, which binds ligand with >1,000-fold higher affinity than the bent-closed and extended-closed states (1, 3). Fusion proteins are the cell surface glycoprotein class that most closely rival integrins in the distances they span between conformational states (4). In fusion proteins, distal regions that integrate into host cell membranes must move adjacent to the membrane envelope in which the fusion protein is natively embedded to promote fusion of the two membranes. In contrast, the function supported by large-scale movements in integrin ectodomains has been mysterious and is addressed in this paper.

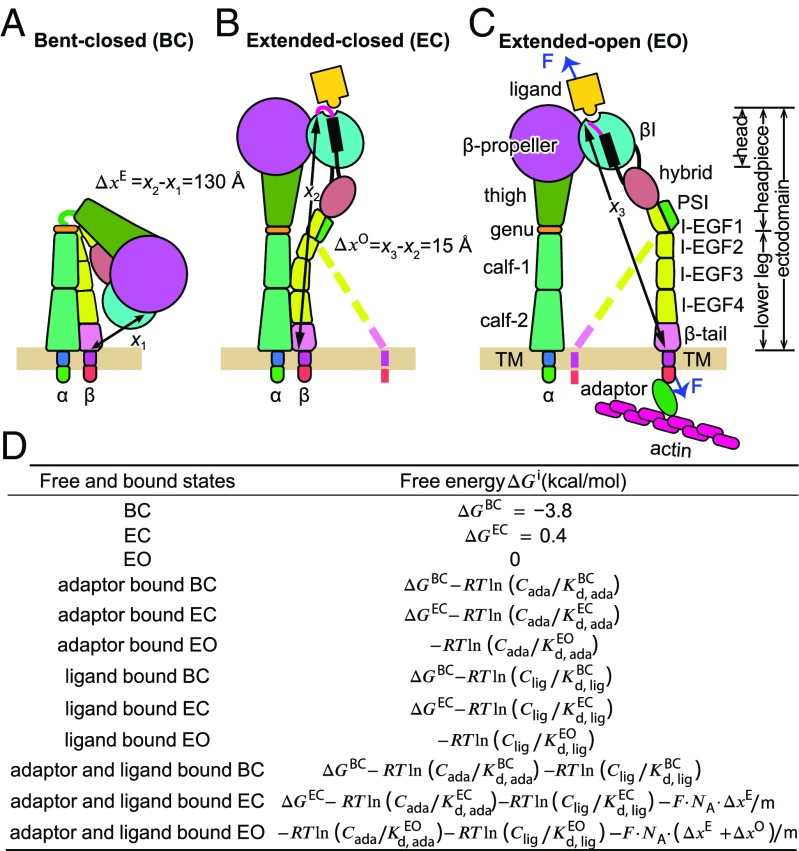
Fig. 1.

Integrin conformation and free energies. (A–C) Three overall conformational states. Domains are shown schematically approximately to scale. The distances in the force-bearing pathway between the ligand-binding site and the C terminus of the β-tail domain known from structures and molecular dynamics (see main text) are shown with arrows (x₁, x₂, and x₃). The complete force-transmission pathway includes the β-subunit transmembrane and cytoplasmic domains, which should have similar lengths in each state. All three conformations are arbitrarily shown with the lower legs normal to the membrane; however, flexible segments before the transmembrane domains enable integrins to tilt (2) so that x₁, x₂, and x₃ are parallel to the direction of applied force. (D) Free energies of each state either bound or unbound to adaptor or ligand and with and without force. ΔG^BC, ΔG^EC, and ΔG^EO values for integrin α₅β₁ on the surface of K562 cells are from ref. 3. C_ada and C_lig are concentrations of free active intracellular adaptor and free extracellular ligand, respectively. $K_{d,\hspace{0.17em}ada}^{BC}$, $K_{d,\hspace{0.17em}ada}^{EC}$, and $K_{d,\hspace{0.17em}ada}^{EO}$ are adaptor dissociation constants for the cytoplasmic tail of each integrin conformation. $K_{d,\hspace{0.17em}lig}^{BC}$, $K_{d,\hspace{0.17em}lig}^{EC}$, and $K_{d,\hspace{0.17em}lig}^{EO}$ are intrinsic dissociation constants for extracellular ligand of each integrin conformation. For α₅β₁ and fibronectin binding, $K_{d,\hspace{0.17em}lig}^{BC}$ = 4 μM, $K_{d,\hspace{0.17em}lig}^{EC}$ = 4 μM, and $K_{d,\hspace{0.17em}lig}^{EO}$ = 1.4 nM (3). F is the tensile force transmitted through integrin, R is the gas constant in kcal/(K·mol), m is the constant, 4184, to convert the energy unit from Joule/mol to kcal/mol, and N_A is the Avogadro constant.

In many biological systems, cells must respond to small changes in the magnitude of a signal input to drive switch-like cellular outputs. For example, integrin-dependent adhesion of platelets and leukocytes is “off” in the vasculature and “on” when these cells are activated. Furthermore, to mediate cell migration, integrins must be on in cellular regions that provide traction and off in other regions to allow the membrane to move relative to the substrate. Adhesion through integrins must also be coordinated with cytoskeletal dynamics to enable integrins to link to the force-exerting actin cytoskeleton to provide the traction for cell migration (1, 5–7). In the absence of special regulatory features, binding of a ligand to a receptor gives a graded response in which the output signal is only proportional, or lower, than the input signal. Such responses are not suited for biological regulation. Ultrasensitive responses, with the switch between on and off occurring over a narrow range of signal input, are highly desirable because of their noise resistance and high sensitivity, but require biological specializations. Such specializations include positive cooperativity in binding of ligands to multimeric proteins, sequential coupled activation of sets of components in kinase cascades, and feedback regulation (8).

Here, we demonstrate that large-scale conformational change enables integrin activation to be exquisitely regulated by cytoskeletal adaptor binding and the force applied by the actin cytoskeleton to an integrin and resisted by its ligand. Recent measurements of the free energies of the three overall conformational states of integrin α₅β₁ measured on intact, live cells (3) enable us to quantitatively assess competing models of integrin activation that either require (2, 9–11) or do not require (12, 13) the application of force. We show that among models proposed to date, only force-dependent activation enables ultrasensitive integrin activation. The large length scale of extension of >130 Å in integrins achieves complete shift from low to high affinity with only a twofold change in signal (force) input, a hallmark of ultrasensitive systems (8). Our results explain many of the unique features of integrins including their large scale of conformational change and the conservation of their domain organization from the dawn of metazoans.

Biological System

Integrins are heterodimers composed of $\mathrm{\alpha }$ and β- subunits that associate over a large interface in the head to form the ligand-binding site (Fig. 1 A–C). The head connects through multiple leg domains in each subunit to a single-span transmembrane domain and a cytoplasmic domain. The ectodomain may be divided into the headpiece (head plus upper legs) and the lower legs, which meet at knees in each subunit. In the bent-closed (BC) conformation, the headpiece and lower legs interact over an extensive interface. Two types of conformational change occur in integrins (1, 14). In the transition from the bent-closed to the extended-closed (EC) conformation, the angle at the knees changes from flexed to extended and the headpiece swings away from the lower legs (Fig. 1 A and B). In headpiece opening, conformational change occurs in the β-subunit βI domain. Movements at the interface of the βI domain with the α-subunit β-propeller domain at the ligand-binding site increase affinity for ligand ∼4,000-fold in the extended-open (EO) conformation (3). These rearrangements are coupled through α-helix pistoning to the βI domain interface with the hybrid domain, so that the hybrid domain swings away from the α-subunit (headpiece opening, Fig. 1 B and C).

It has been known for some time that headpiece opening is stabilized by ligand binding and can be induced by allosteric antibodies that activate integrins. It also has been clear that basally, integrins are largely bent-closed and that the bent-closed conformation represents a low-affinity state (1, 14, 15). However, quantitative measurements of the relative stabilities (free energies) and binding affinities of specific conformational states only became available recently (3). Use of Fabs to distinct epitopes to stabilize the closed, open, and extended states enabled measurement of the intrinsic affinity for ligand of each state and the free energy of each state of integrin α₅β₁. Affinity for ligand was found to be solely dependent on whether the headpiece was open or closed and to be 4,000 higher for the extended-open than the extended-closed and bent-closed conformations. On the surface of K562 cells the free energies of the bent-closed, extended-closed, and extended-open states of α₅β₁ are −3.8, 0.4, and 0 kcal/mol, respectively (3). The corresponding populations of the three states on the cell surface are 99.75%, 0.1%, and 0.15%, respectively. When extended, α₅β₁ is more stable in the high-affinity extended-open than the low-affinity, extended-closed state. Thus, extension is the main energy barrier to activation.

As validated in other biological systems (8), we use equilibria to understand regulation of integrin activation. In this paragraph, we briefly consider the kinetics of integrin conformational change and dissociation from ligand and adaptor and the kinetic regimes in which our analysis is valid. Our calculations assume that the lifetime of the ligand–integrin–adaptor complex is longer than the time required for equilibration between conformational states. This assumption is justified by the timescales typical for conformational change and ligand and adaptor dissociation. The free-energy gap between the bent-closed and extended-open states of α₅β₁ on K562 cells is less than the typical free-energy difference (ΔG = ∼5–15 kcal/mol) between folded and unfolded conformations of a globular protein (16); the typical timescale for protein folding is in the microsecond to millisecond range (17). Similarly, conformational interconversion rates between active and inactive states in G protein-coupled receptors (18–20) and ion channels (21, 22) are in the microsecond to millisecond range. In contrast, the lifetime of the fibronectin–integrin α₅β₁ complex is much longer, 70–150 s (23–25). Similarly, kinetics measured for dissociation of the integrin cytoplasmic domain from the cytoskeletal adaptor talin show a bond residence time in the range of 180–1,000 s (26–28). The rapidity of conformational change compared with bond residence time is also indirectly demonstrated by the finding that integrin–fibronectin complexes can be rapidly disrupted by allosteric inhibitors that stabilize the closed integrin conformation but not by ligand-mimetic inhibitors (29). We also consider the influence of force on bond residence timescales. We approximate bond dissociation kinetics in presence of force, k_off (F), as k_off ·Exp(F·σ/k_BT), where k_B is Bolzmann’s constant and σ represents the mechanical stability of receptor–ligand bonds (30). We use a value of σ = 15 Å, which is in the range found in experiments with fiducial markers for ligand–receptor and adaptor–receptor dissociation (31, 32). This value results in a 12-fold decrease in integrin–ligand and integrin–adaptor bond lifetimes at a force of 7 pN, which is the maximal force experienced by ∼90% of integrin-bound ligands (5). Even after such a decrease, bond lifetimes remain longer than estimated for conformational state lifetimes, and therefore the system can still be approached using thermodynamic equilibria. Thus, we may think of integrins as rapidly sampling different conformational states, whether bound or unbound to extracellular ligand and intracellular cytoskeletal adaptors, and experiencing tensile force. Therefore, we may neglect kinetics and use equilibria to compare alternative models of integrin activation by asking how ligand binding, adaptor binding, and force application by the actin cytoskeleton regulate integrin conformation and linkage to the extracellular environment and actin cytoskeleton, i.e., integrin activation.

Quantitative Comparison of Models for Integrin Activation

We first examine integrin activation by binding of a cytoskeletal adaptor such as talin to the integrin β-subunit cytoplasmic tail (12, 13, 33). This model assumes that there is a mechanism for allosterically coupling adaptor binding to the β-subunit cytoplasmic tail to integrin extension or integrin extension plus opening. One proposed mechanism involves coupling of α- and β-subunit TM domain separation to talin binding (12, 13). The physical mechanism for coupling does not matter to our calculations. We assume that all of the binding energy of the adaptor is coupled to integrin conformational equilibria through the very simple assumption that binding of the adaptor inside the cell is selective for integrin ectodomain conformation outside the cell. This allows us to quantitate with thermodynamics what is meant by the statement that “talin binding to the integrin β cytoplasmic tail is the final common step for integrin activation (ref. 12, p. 329).” Adaptor binding lowers the energy of specific conformational state(s) by the stabilizing term −R·T·ln(C/K_d) where R is gas constant, T is temperature, C is the concentration of the active intracellular adaptor such as talin, and K_d is the dissociation constant of the adaptor for the integrin conformational state(s) for which it is specific. Fig. 1D shows how adaptor and ligand binding modulate the free energies of each of the three integrin conformational states, in four different binding states: free, adaptor-bound, ligand-bound, and adaptor and ligand-bound (12 different conformation/binding states altogether). These free energies together with the thermodynamic partition function are used to calculate the proportion (probability) of each of the 12 states in the integrin cell surface ensemble.

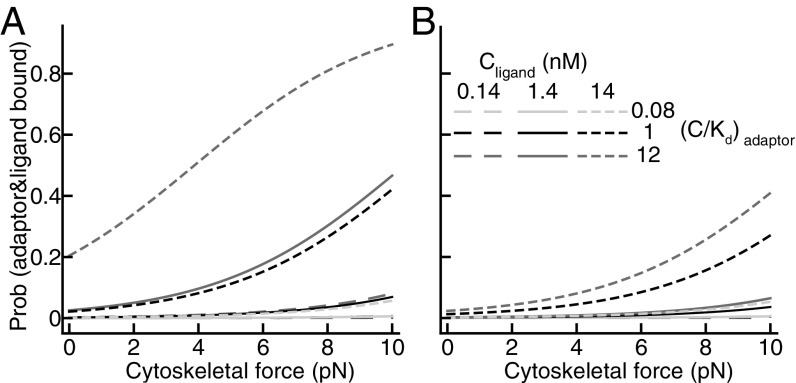
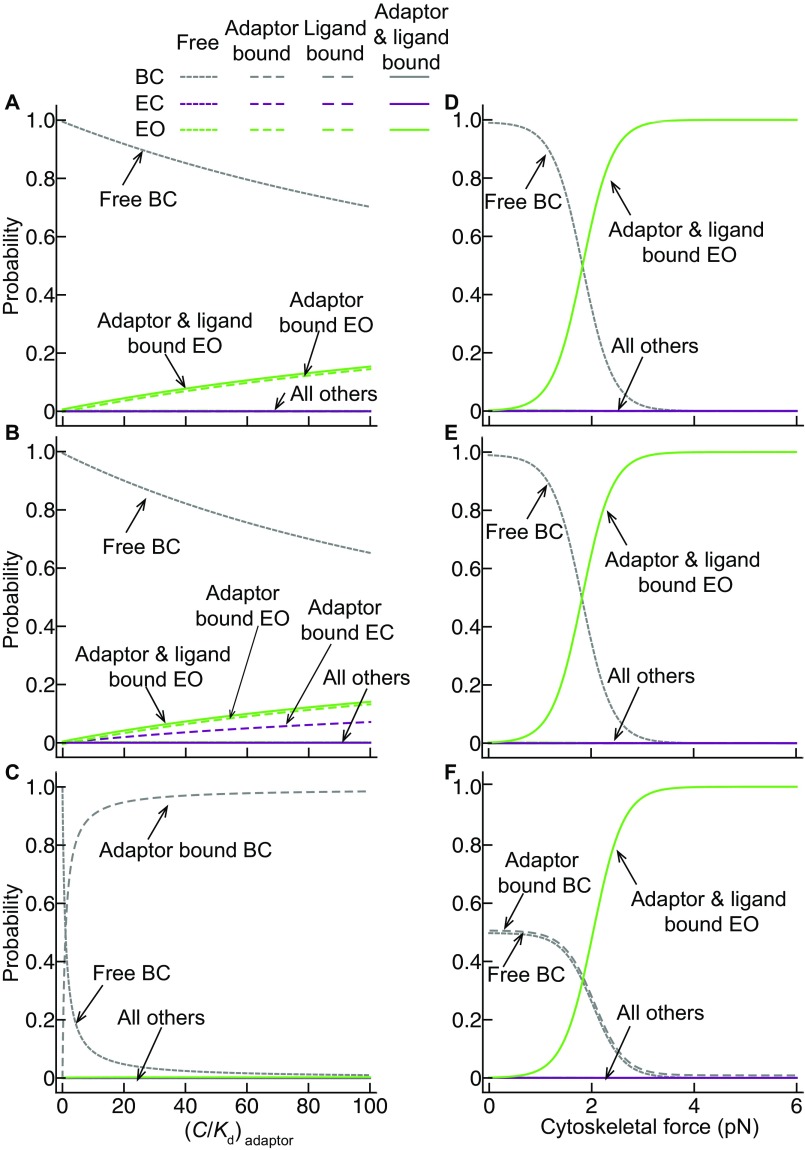
To encompass different meanings in the field of “integrin activation”, we have calculated it in different ways here. Activation may be defined as the sum of the probabilities of the ligand and adaptor-bound states of all three conformations because this enables linkage of the extracellular and intracellular environments, irrespective of integrin conformation. The sum of the adaptor–ligand-bound states of all three integrin conformations is graphed on the y axis of Figs. 2 and 3. However, because the extended-open state has so much higher affinity than the other states for ligand, it accounts for essentially all of the adaptor–ligand-bound integrin (Fig. S1).

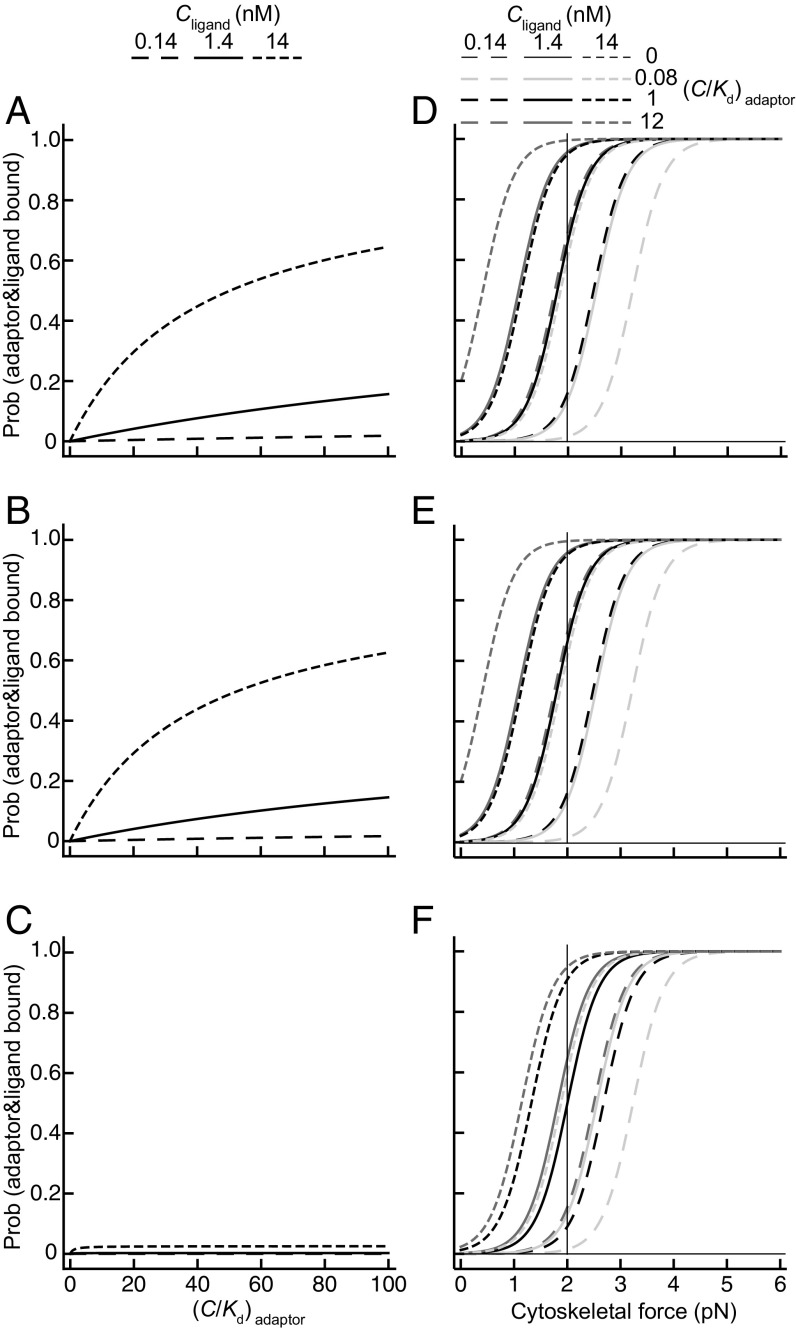
Fig. 2.

Comparison of integrin activation by adaptor binding alone or adaptor binding with force. (A–C) The model where only the adaptor binding gives activation. (D–F) The model where adaptor binding and cytoskeletal force combine to give activation. For each model, three scenarios are shown, where the cytoskeletal adaptor binds only the extended-open conformation (A and D), the two extended conformations (B and E), or all three conformations (C and F). Adaptor concentration is expressed relative to its K_d. The proportion of integrin bound to both adaptor and ligand is calculated using the terms and equations shown in Fig. 1D together with the intrinsic affinities for fibronectin and free energies of integrin α₅β₁ conformational states on K562 cells (3), as detailed in Calculations. Plots show results for three different concentrations of fibronectin in the extracellular matrix. (A–C) Results with continuous variation in adaptor concentration. (D–F) Results with continuous variation of force at four different adaptor concentrations. The vertical line at 2 pN in D–F is discussed in the text and indicates how variation in adaptor concentration at a fixed force affects integrin activation.

Fig. 3.

Ultrasensitive integrin activation by cytoskeletal force is dependent on transition from bent to extended states. Only the two extended states, EC and EO, are used, and the free energy of the BC state is used for the EC state. (A and B) Two scenarios are shown where the cytoskeletal adaptor binds only the EO conformation (A) or both EC and EO conformations (B). Other details are as in Fig. 2.

Fig. S1.

Influence of adaptor binding (A–C) and cytoskeletal force models (D–F) on the probability of integrin conformational states. Three scenarios are shown where the cytoskeletal adaptor binds only the extended-open conformation (A and D), the two extended conformations (B and E), and all three conformations (C and F). (A–C) Results for a fibronectin concentration of 1.4 nM (equal to the K_d of the EO conformation). (D–F) Results for a fibronectin concentration of 1.4 nM and an adaptor concentration equal to its K_d (C/K_d = 1).

Given the free energies of the three overall integrin α₅β₁ conformational states and their intrinsic affinities for ligand (3), we may now realistically evaluate the adaptor-binding model of integrin activation. Fig. 2 A–C plots the effect of increasing the active concentration of intracellular adaptor from zero to 100-fold above its K_d. Models are shown where the adaptor is specific for the EO state (Fig. 2A), binds both the EO and EC states (Fig. 2B) or all three states (Fig. 2C). Results are similar for binding to only EO or both EO and EC states, because the largest energy difference is between the extended and bent states, and EO has much higher affinity for ligand than EC. As expected, adaptor binding to all three states has no activating effect. At extracellular fibronectin concentrations of 0.14, 1.4, and 14 nM that span its K_d of 1.4 nM for the EO state of α₅β₁, integrin activation showed graded responsiveness to adaptor concentration. With increasing adaptor concentration, the proportion of adaptor–ligand-bound states increased linearly at low adaptor concentrations and then less than linearly at higher concentrations (Fig. 2 A and B). Even a huge increase in adaptor concentration from zero to 100-fold above its K_d was insufficient to achieve full integrin activation. Additional binding of adaptors to independent sites, such as kindlins (6), would only shift the dose–response by a factor of two on the x axis of Fig. 2 A–C. Furthermore, the magnitude of activation was heavily dependent on the concentration of extracellular ligand fibronectin, providing little scope for the adaptor to similarly regulate integrin activation in environments with different fibronectin contents.

We next examined the ability of tensile force to regulate integrin activation. Once an integrin binds both ligand and the adaptor, force is applied to the adaptor by the actin cytoskeleton and resisted at the point of attachment of fibronectin to the extracellular matrix. Force thus passes through the integrin β-subunit between the extracellular ligand-binding site in the βI domain and the adaptor-binding site in the cytoplasmic domain (Fig. 1C). The same stabilizing term [−R·T·ln(C/K_d)] for adaptor binding was used as in the adaptor model. Additionally, for adaptor–ligand-bound states, the force-dependent stabilizing term −N_A·F·Δx was added, where N_A is the Avogadro number, F is force, and Δx is the change in distance between the states (Fig. 1D). Δx is measured between the membrane-proximal portion of the integrin β-subunit and the ligand-binding site because tensile force applied by the actin cytoskeleton and resisted by fibronectin in the matrix is exerted through the integrin between these sites. To calculate Δx, we used x₁, x₂, and x₃ values measured from bent ectodomain and open and closed headpiece crystal structures, from EM of bent and extended integrins, and from steered molecular dynamic-based atomic models of extended-closed and extended-open ectodomains (1, 2, 9, 14) (Fig. 1 A–C). Integrins have flexible linkers between their extracellular portions and transmembrane domains in each subunit (34), and thus can orient in the same direction as the applied force, enabling us to assume that the distances x₁, x₂, and x₃ are parallel to the applied force. Length increases in extension (Δx^E) and opening (Δx^O) are 130 Å and 15 Å, respectively. The effect of force is to tilt the energy landscape to make the more extended states lower in energy.

Remarkably, integrin activation is sigmoidally responsive to force regulation, whether adaptor binding is selective for integrin conformation (Fig. 2 D and E) or not (Fig. 2F). Force-dependent activation gives all-or-none regulation of integrin activation over a narrow range of tensile force of 2 pN. This corresponds to a change in the level of force of only approximately twofold (Fig. 2 D–F). All-or-none regulation by a change in the input signal of only twofold is considered a hallmark of ultrasensitive regulatory systems (8). Moreover, force dependence shows other highly desirable attributes for biological regulation. (i) Variation in fibronectin concentration over a 100-fold range only moderately shifted the force dependence by ∼2 pN (Fig. 2 D–F). (ii) Similarly, a 144-fold change in intracellular adaptor concentration only shifted force dependence by ∼2 pN. Thus, force dependence makes the system robust to wide variation in ligand and adaptor concentration and affinity for integrin. (iii) Force-dependent regulation makes integrin activation exquisitely sensitive to variation in adaptor concentration in the range from well below to near adaptor K_d for integrin. Thus, at a force of 2 pN, an increase in adaptor concentration from 0 to 0.08 to 1 × its K_d value increases the population of activated (ligand and adaptor-bound) integrins from 0 to 14% to 66%, respectively (vertical line in Fig. 2D with similar results in Fig. 2 E and F). We conclude that stabilization of the extended states by force enables force exerted on the integrin to strongly regulate integrin activation and further enables regulation of integrin activation by concentrations of adaptors near their K_d values.

To examine the importance of extension to integrin activation, we consider a model in which integrins do not extend, and only the smaller increase in distance with headpiece opening, Δx^O, contributes to force-dependent regulation. We use a difference in energy between the open, high-affinity and closed, low-affinity states (O and C, respectively) identical to that between the EO and BC states. Stabilization by force of the conformational equilibrium toward the high affinity state (−N_A·F·Δx^O) shows graded response to the increase of force (Fig. 3). Because Δx^E is much greater than Δx^O, extension provides much greater sensitivity to force as well as to adaptor concentration (Fig. 2 D–F). Thus, integrin extension is crucial to cytoskeleton-dependent regulation of integrin activation. Additionally, the larger scale of Δx^E (130 Å) than mechanical bond stability (σ, 15 Å) enables integrin extension to dominate mechanical bond stability in regulating integrin adhesiveness.

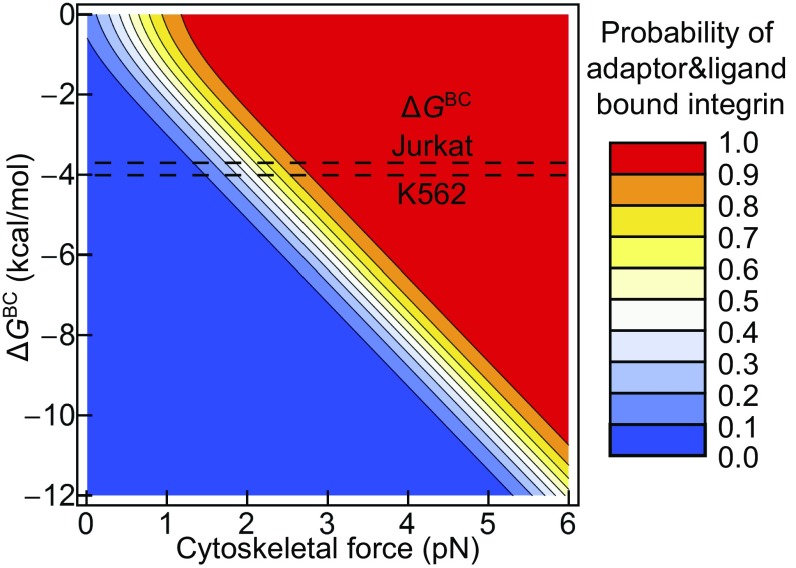
To quantitatively understand the requirements for force-dependent ultrasensitive activation, we also consider how the stability of the bent conformation (ΔG^BC) influences the responsiveness to cytoskeletal force application. The dashed lines in Fig. 4 show the range of ΔG^BC values measured for integrin α₅β₁ on K562 and Jurkat cells (3). Notably, measured integrin ΔG^BC values, together with structurally observed Δx^E and Δx^O values, give ultrasensitive all-or-none integrin activation in the range of forces that have been measured to be exerted on integrins and their ligands with live cells (5–7). Thus, the difference in free energy between the BC and EO states is tuned to the large 145 Å length-scale change between these two states to provide exquisite regulation of activation by the actin cytoskeleton.

Fig. 4.

Free energies observed for the BC conformation of integrin α₅β₁ on cell surfaces are ideally suited for ultrasensitive regulation of integrin activation by 0–4 pN of force. The proportion of integrin bound to both adaptor and ligand is calculated as in Fig. 2F using a fibronectin concentration of 1.4 nM (equal to the K_d of the EO conformation) and an adaptor concentration equal to its K_d (C/K_d = 1). Dashed lines show the range of free-energy values (−4.0 to −3.7 kcal/mol) measured for integrin α₅β₁ on the surface of K562 and Jurkat cells (3).

Perspectives

Activation models in the integrin field have previously been discussed conceptually, but not tested quantitatively. Here we have bridged this gap using recent measurements of the intrinsic ligand-binding affinity and free energies of integrin conformational states on cell surfaces (3). To examine one model in which adaptor binding alone activates integrins, we enforced complete allosteric linkage between adaptor binding and integrin activation by making adaptor binding selective only for the EO conformation among the three integrin states. Our results show that in the absence of force exertion, binding of an adaptor such as talin, even when completely linked allosterically to stabilizing the high-affinity integrin EO state, gives graded regulation of activation. Graded regulation is often termed sluggish because activation increases less than the increase in adaptor concentration. In contrast, application of force by the actin cytoskeleton to adaptor and ligand-bound integrins greatly stabilizes integrin extension and gives ultrasensitive integrin activation. All-or-none responsiveness occurs within a range of forces between 0–4 pN and with only a twofold change in the input (force), a hallmark of biological ultrasensitivity (8). Moreover, our results complement previous findings that talin exists in both autoinhibited and activated states (6). When modest levels of cytoskeletal force are applied to ligand–integrin–adaptor complexes, integrin activation becomes highly sensitive to changes in the localized concentration in cells of adaptors such as talin. Maximal sensitivity occurs when adaptor concentrations change in the range from 10-fold below to equal to their K_d; similarly, other ultrasensitive biological systems operate at effector concentrations near their K_d values (8).

Bacterial chemotaxis and eukaryotic MAP kinase pathways achieve all-or-nothing responsiveness over only a twofold change in the signal input. Notably, both systems use ATP as an energy donor to drive protein phosphorylation, and the MAP kinase pathway uses a cascade of three such phosphorylation steps. ATP is also the energy input for force application by the actin cytoskeleton; both actin polymerization and myosin-dependent actin contraction are driven by ATP. Positive cooperativity in ligand binding is another biological mechanism for driving sensitive, sigmoid responses. However, even with four subunits, hemoglobin only achieves all or nothing responsiveness (oxygen loading) with about a 10-fold change in oxygen concentration and thus is less sensitive than the above ATP-dependent systems (8).

Force represents a distinct mechanism for achieving biological regulation. A change in force is a more potent regulator than a change in effector (adaptor) concentration alone, because force directly decreases free energy, whereas effector concentration only logarithmically decreases free energy (Fig. 1D). Although we do not believe this has previously been pointed out, this direct relation of force to free energy is likely relevant to many systems in which mechanobiology is important.

Many studies have emphasized the importance of force in regulating integrin adhesiveness (2, 6, 7, 9, 10). Stimuli such as chemokines activate strong integrin adhesiveness and the extended-open, high-affinity integrin conformation when integrins bind to immobilized ligands, but fail to do so when integrin activation is measured by binding to soluble ligands or conformation-reporting antibodies, implicating the importance of force resistance by immobilized ligand for the high affinity state (11). The results here emphasize the importance of integrin extension in regulating integrin activation and make specific predictions about the range of force required to stabilize integrin extension and the high affinity state. Forces exerted within integrins, on their ligands, and within intracellular adaptors to actin, have been measured. As reviewed (5, 6), estimates on forces exerted by integrins on ligands have ranged from 1 to 100 pN and varied in whether ensemble averages or single molecules were measured. Furthermore, single molecule measurements vary in whether they are dynamic or measure the largest force exerted over time. The most recent dynamic single-molecule measurements, using a Forster resonance energy probe in an integrin ligand, show that 1–3 pN, 3–7 pN, and >7 pN forces were experienced by ∼70%, ∼25%, and <10% of integrin-bound ligands, respectively (5). Insertion of Forster resonance energy probes in the integrin β-subunit cytoplasmic domain between the ligand and talin-binding sites demonstrated that tensile force is applied to integrins when they simultaneously bind to specific ligand and to talin during cell migration (7). The average force exerted on the integrin cytoplasmic domain in these ensemble measurements was 1.5 pN, and the maximum force measured reached the upper dynamic range of the probe of 6 pN. Our calculations based on intrinsic affinity and free-energy measurements on cell surfaces suggest that α₅β₁ transitions between an off-state and a ligand and adaptor-bound on-state at forces between 1 and 3 pN. Our results suggest that the major population of integrin-bound ligands in single-molecule experiments (5) are experiencing forces in the sweet spot for regulation and are equilibrating between bound and unbound states, whereas a smaller subset of ligands experiencing higher forces are more stably bound. The overlap between the forces that we calculate regulate integrin adhesiveness and those measured on integrins and their ligands is most interesting. It is important to note that in contrast to many models, none of the parameters used were derived by fit to the model; the affinities, free energies, and distance parameters are all derived from experiment.

Integrins appear wonderfully evolved for actin cytoskeleton-dependent activation. Quantitation here helps explain both why integrins extend and why their domain organization is so conserved. Integrins are present in the most primitive metazoans (35, 36), and the number of integrin leg domains, 3 in α and 7 in β, is invariant in metazoa. The only innovation in chordates, the αI domain present in half of mammalian α-subunits, is present in the head and does not affect integrin extension or the path that force takes through the β-subunit (1). The NP(I/L)(Y/F) motif in the β-subunit cytoplasmic domain to which talin binds is present in the most primitive metazoans (36), suggesting that integrins evolved to be activated by actin cytoskeletal adaptors.

In summary, the remarkably long distance by which integrins extend may specialize them for activation by the actin cytoskeleton and enable cell adhesion through integrins to be coordinated with cytoskeleton dynamics. Cells rapidly form and break nascent adhesions at their leading edges during cell migration. Integrin adhesiveness must be coordinated with cytoskeletal dynamics so that cells can explore their environments and migrate (1, 6). The ability of localized actin polymerization and contraction to activate integrins enables coordination of the complex machinery required for cell migration within metazoan organisms and relaxes the requirement for centralized control of the multiple pathways involved. Force-dependent integrin activation also makes integrins sensitive to small localized changes in concentrations of the active states of adaptors such as talin and kindlin that link integrins to the actin cytoskeleton. This enables two mechanisms by which cytoskeletal dynamics can regulate integrin adhesiveness: (i) alterations in localized concentrations of effectors or inhibitors of integrin coupling to the actin cytoskeleton and (ii) alterations in the force that actin polymerization and actin–myosin contractility apply to integrins. Integrins appear to be unique among adhesion molecules in metazoans for their ability to provide the traction for migration of individual cells within the organism. Extension appears to be the key integrin evolutionary adaptation that enables ultrasensitive regulation of integrin activation by the actin cytoskeleton. The necessity to conserve this large conformational change may explain the absolute conservation of the domain architecture of integrins since the emergence of metazoa.

Calculations

Free energies (ΔGⁱ) of the 12 states, either bound or unbound with adaptor or ligand, were calculated as shown in Fig. 1D. Briefly, the ΔG of the unbound states were determined experimentally (3). Adaptor or ligand binding lowers the energy of the specific conformational state by the stabilizing term −R·T·ln(C/K_d), where R is gas constant, T is temperature, C is the concentration of the active intracellular adaptor or extracellular ligand concentration, and K_d is the dissociation constant between adaptor or ligand and the integrin conformational state(s) for which it is specific. In presence of force, for states bound to both adaptor and fibronectin, the force-dependent stabilizing term −N_A·F·Δx was added, where N_A is the Avogadro number, F is force, and Δx is the change in distance between the states.

The statistical weight of each state (Sⁱ) was calculated according to Sⁱ = exp[−ΔGⁱ/(R·T)]. The probability of each state was calculated as its statistical weight over the partition function, which is the sum of the statistical weights of all states in the ensemble (3).