Optimization of identity operation in NMR spectroscopy via genetic algorithm: Application to the TEDOR experiment

Abstract

Identity operation in the form of π pulses is widely used in NMR spectroscopy. For an isolated single spin system, a sequence of even number of π pulses performs an identity operation, leaving the spin state essentially unaltered. For multi-spin systems, trains of π pulses with appropriate phases and time delays modulate the spin Hamiltonian to perform operations such as decoupling and recoupling. However, experimental imperfections often jeopardize the outcome, leading to severe losses in sensitivity. Here, we demonstrate that a newly designed Genetic Algorithm (GA) is able to optimize a train of π pulses, resulting in a robust identity operation. As proof-of-concept, we optimized the recoupling sequence in the transferred-echo double-resonance (TEDOR) pulse sequence, a key experiment in biological magic angle spinning (MAS) solid-state NMR for measuring multiple carbon-nitrogen distances. The GA modified TEDOR (GMO-TEDOR) experiment with improved recoupling efficiency results in a net gain of sensitivity up to 28% as tested on a uniformly ¹³C, ¹⁵N labeled microcrystalline ubiquitin sample. The robust identity operation achieved via GA paves the way for the optimization of several other pulse sequences used for both solid- and liquid-state NMR used for decoupling, recoupling, and relaxation experiments.

1. Introduction

In NMR spectroscopy, an ideal RF pulse flips the spin uniformly throughout the spectral and spatial dimensions of the sample. However, field inhomogeneities, RF pulse miscalibrations and offset can dramatically reduce both sensitivity and resolution. In the past years, advanced pulse techniques such as composite and adiabatic pulses have been designed to improve the performance of pulse sequences using self-compensation mechanisms [1]. However, it has been challenging to optimize pulse sequences compensating for experimental errors that originate from different sources. Recently, we began to analyze the experimental errors affecting the most elementary RF pulse operations including flipping spin magnetization, decoupling, recoupling, etc. For their optimization, we proposed the use of a Genetic Algorithm (GA) that has been successful for designing new experiments [2] improving excitation and inversion of RF pulses [3], as well as optimizing existing pulse sequences [4]. More recently, GA optimization was used to optimize chemical exchange saturation transfer in MRI [5]. GA is a stochastic global search method based on Nature's evolutionary process [6] that was originally introduced by Holland and co-workers [7]. GA operates on a specific problem by encoding its solutions into a simple chromosome-like data structure and applying recombination operators to optimize the outcomes in an iterative manner. As with the natural selection, the solutions from each generation with the greatest fitness have a higher probability to be transmitted on to the next generation until the optimal solution is reached.

In this paper, we developed a new GA to optimize a series of π pulses, which are widely used in NMR pulse sequence design. In fact, series of pulses with an effective nutation of 2nπ are common elements in both solution and solid-state NMR experiments and are utilized for decoupling [8], recoupling [9], as well as Carr-Purcell-Meiboom-Gill (CPMG) relaxation dispersion experiments [10]. An ideal nutation of 2π along a fixed axis performs an identity operation, which leaves the spin state essentially unaltered. In reality, these π pulses accumulate experimental imperfections, causing the magnetization to deviate substantially from its ideal path. Substitution of these elements with robust composite π pulses is ineffective as these pulses are too long to perform an effective identity operation under the constraints of RF power and pulse length. In principle, phase optimization of these π pulses could alleviate the effects of these imperfections. However, simultaneous compensation of offset and RF inhomogeneity/miscalibrations has been challenging. Using our new GA optimization, we generated phase modulations that achieve a robust identity operation. We applied GA optimization to the transferred-echo double-resonance (TEDOR) [11] experiment, which is widely used for structure determination of biopolymers in solid-state NMR spectroscopy [12]. In the TEDOR sequence, rotor synchronized π pulses recouple the MAS-averaged heteronuclear dipolar couplings. Both TEDOR and its predecessor, rotational-echo double resonance (REDOR) [13] use XY8/XY16 phase-modulated sequences to compensate for both offset and flip angle errors [14]. In the case of REDOR, the rotor-synchronized π pulses were also replaced by composite pulses [15]. Here, we demonstrate that GA optimization of TEDOR outperforms XY8/XY16 phase-modulated sequences without increasing the length of the pulses or using composite pulses. Specifically, we used GA optimization to generate pulses of universal rotation (or type A [1a]) that are independent of the initial spin state, showing an improvement in the signal-to-noise ratio of up to 28% with respect to XY8/XY16 phase-modulated sequences as demonstrated for a U-¹³C, ¹⁵N-labeled microcrystalline ubiquitin sample. We anticipate that GA optimization will be utilized in the optimization of several solution and solid-state NMR experiments that utilize trains of π pulses, such as decoupling, recoupling, and CPMG relaxation dispersion experiments.

2. Theory

In NMR spectroscopy, identity operations can be obtained using a spin-echo sequence [16], which refocuses the evolution caused by nuclear spin Hamiltonian or by evolving the spin system for a time equivalent to the period of the corresponding propagator [17]. For instance, a single spin system with on-resonance constant amplitude RF irradiation (B₁) repeats its state at times n/B₁, where n = 0, 1, 2, … (Eq. (1)).

$$\begin{array}{c}{\mathbb{I}}_2=exp\{-i0I_x\}=exp\{-i2\pi I_x\}=exp\{-i4\pi I_x\}\\ {\mathbb{I}}_4=exp\{-i02I_z^1{I}_z^2\}=exp\{-i4\pi 2I_z^1{I}_z^2\}=exp\{-i8\pi 2I_z^1{I}_z^2\}\end{array}$$ (1)

where 𝕀₂ and 𝕀₄ are identity operations in two and four dimensions, respectively. I_x is a single spin operator in the x phase and $I_z^1{I}_z^2$ are the spin operators (spin 1 and spin 2) for the scalar coupling interactions. Therefore, a sequence with an even number (2n) of π pulses at constant phase performs a nutation of 2nπ, leaving the initial density matrix essentially unchanged. In order to design a robust identity operation, we explored the space of 2n phase values of π pulses to find a phase modulation, which can compensate these imperfections simultaneously using GA optimization.

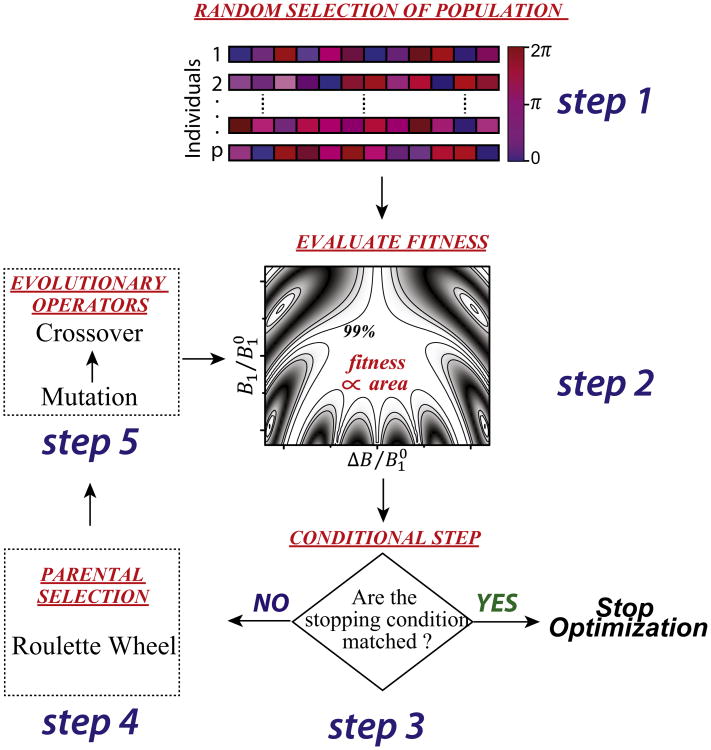
To understand GA optimization, let's consider a function, f(x) with a set of constraints on x. The nature of the function as well as the set of constraints on x dictates the extent of the challenge for reaching the global minimum (x_min) off. GA utilizes a stochastic global search method that overcomes local minima with a probability-based selection procedure as well as recombination operators (i.e., mutations and crossover) until the global minimum is reached. Typical GA optimizations include seven steps (Scheme 1). Our new GA optimization starts with an ‘encoding procedure’ that defines how each individual in the simulated natural evolution represents a valid solution to the problem. Step 1 initializes the search with a random population with P individuals. To reduce the total computational time, an educated guess of the initial population must be provided. In step 2, the fitness of each individual is evaluated using the fitness function that quantifies the optimality of a solution or individual. This is the most computationally-demanding step. Step 3 is the conditional step, where the algorithm checks multiple conditions on fitness to select the best individual, maximum number of generations, total computational time, etc. The optimization procedure terminates when the stopping conditions are satisfied; otherwise, the algorithm proceeds to step 4, which involves parental selection to create the next generation. A probabilistic selection (Roulette Wheel) based on the fitness values is used to create the new parent population. Step 5 applies recombination operators such as mutations and crossover to all of the selected parents creating a new generation of individuals. Then the algorithm proceeds to step 2 and continues the search until the stopping conditions are satisfied. A similar procedure can be used to optimize a population of pulses. Let 2n (where n = 1, 2, 3 …) be the number of π pulses in the identity sequence. We use a floating-point array of size 2n for representing an individual, where each element represents the phase value of the π pulses. The unitary operator (U_I) for a sequence of 2n number of π pulses with phase array {φ_k} can be written as

Scheme 1.

Flow chart representation of the genetic algorithm used for robust identity optimization. We have used an initial population of 50 random individuals evolved for 10⁴ generations. For a gene size of 200, the optimization took around 2 days to find the optimal individual or phase modulation set on a personal computer with an Intel Corei7 (2.7 GHz) processor.

$$U_I(\phi )-\prod _{k=1}^{2n}exp\{-i\pi (I_x\mathit{Cos}{\phi }_k+I_y\mathit{Sin}{\phi }_k)\}$$ (2)

We have used the fidelity formula (ℱ(φ), Eq. (3)) to estimate how these operators (U_I) approximate the identity operation.

$$\mathcal{F}(\phi )=\mathit{\text{Trace}}\{U_1(\phi )\}$$ (3)

The maximum value of (ℱ(φ) is 1 and corresponds to the identity U_I(φ) = 𝕀. A theoretical fidelity of 99% or more is considered ideal.

3. Materials and methods

To design dual compensated pulses, we used the global optimization toolbox included in the Matlab^® software. The simultaneous optimization of 200 parameters required approximately 2 days to find the optimal phase modulation on a personal computer with an Intel Corei7 (2.7 GHz) processor. For most calculations, we used a population size of 50 evolved for 10⁴ generations with a random phase set as the initial population. For the population type, we used doubleVector and performed parental selection via Roulette Wheel with an elite count of 2. For all optimizations, we used uniform mutation with a rate of 0.05 and the Arithmetic routine as the crossover function [18]. The NMR experiments were performed on a uniformly-¹³C, ¹⁵N labeled microcrystalline ubiquitin. All the experiments were acquired on a 700 MHz Bruker spectrometer with 12 kHz MAS spinning rate and at a temperature of 298 K. We used a 3.2 mm Bruker E-free^® MAS probe that includes a low inductance proton coil to reduce the ¹H RF heating, and a high efficiency solenoid coil for the observed frequency [19]. The sample were packed in a 3.2 mm thin-walled Bruker rotor with top and bottom spacers to position the sample in the center of the coil. RF pulse lengths were calibrated by placing the sample in the center of the coil and determined the π pulse length using the Bruker ‘cp-calib’ pulse program sequence, (π/2)^1H – CP – (6)^{13C or 15N} – with acquisition of either ¹³C or ¹⁵N and ¹H decoupling. The pulse length or RF amplitude of θ was varied systematically for ¹³C/¹⁵N calibration. ¹H RF calibration were performed using the CP pulse program, (θ)^1H – CP – with ¹³C acquisition and ¹H decoupling.

Each 1D with varying RF power or offset was acquired as pseudo 2D with 256 scans, 8 dummy scans and 2 s relaxation delay. A SPINAL64 sequence was used on the ¹H during both recoupling and acquisition periods. The calibrated powers for the p/2 pulses were 42.8 kHz (200 W) and 50 kHz (88.9 W) for ¹⁵N and ¹³C, respectively.

4. Results and discussion

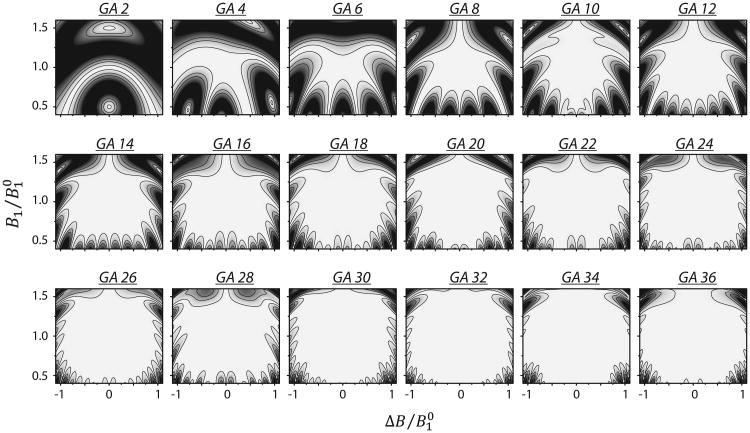
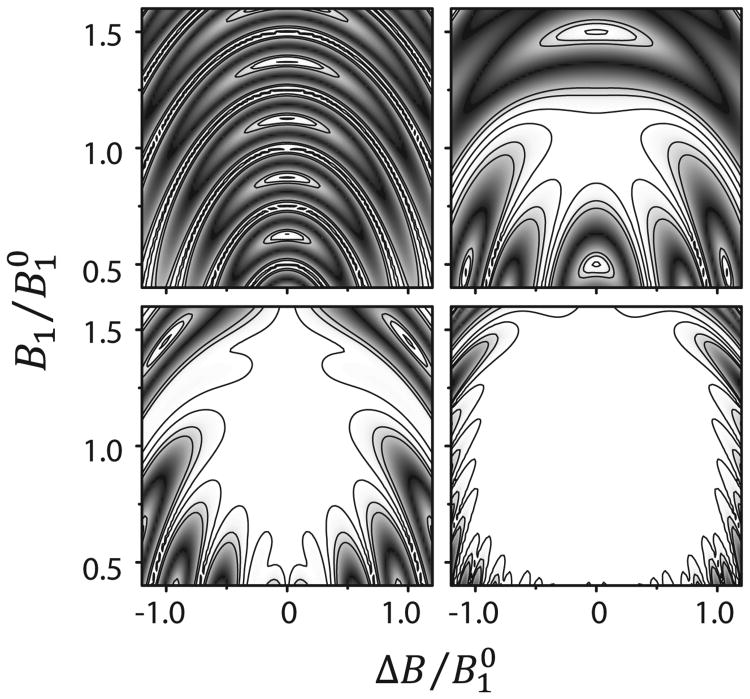
Using the procedure highlighted in Scheme 1, we have performed a global search over the parameter space of 2n phase values for a dual compensated π sequence for n = 1,…,18. The phase modulations obtained for all the cases are shown in Table 1. Since a fidelity of 99% can be considered ideal for most experimental cases, the area inside the 99% contour of the fidelity profile is a direct measure of the robustness of the phase modulation, which is maximized using the GA optimization (Scheme 1). The fidelity profiles for n = 2,…,36 are shown in Fig. 1 with contour levels at 99%, 90%, and 80%. Note that super-cycling these sets of phases creates identity operations for higher values of n. To show the improvements generated by the GA-optimized identity p sequence, we have performed a comparative study with XX (constant phase) and XY phase modulations. The XY phase modulation has XY8, i.e., X-Y-X-Y-Y-X-Y-X, while XY16 consists of $\text{XY}8-\overline{\text{XY}8}$[20]. Constant-phase sequences have the same phase for all of the π pulses. In this case, we used an X phase for all the pulses and labeled as XX8 for a sequence with 8 pulses. Theoretically, all these phase-modulated π sequences perform an effective identity operation. Fig. 2 shows the comparison of the simulated fidelity profiles of the identity operations obtained with the XX8, XY8 and GA optimized 10 (GA10) and 32 (GA32) phase modulations (Table 1). The area inside the 99% contour is greatly improved in the case of GA optimized phase modulations. While the XY8 phase modulation is robust up to a relative offset of ±0.3 along, with a ±10% change in RF amplitude, GA10 and GA32 are robust up to offsets of ±0.3 and ±1.0, respectively, with simultaneous errors in RF amplitude of ±40% and ±50%.

Table 1.

GA-optimized phase modulation set for a sequence of ‘2n’ number of π pulses. All the phase values are in degrees.

Number of pulses (2n)	GA-optimized phases (in degree)
2	0, 0
4	0, 90, 0, 90
6	0, 124, 0, 0, 124, 0
8	90, 0, 0, 90, 270, 180, 180, 270
10	72, 110, 0, 110, 72, 252, 290, 180, 290, 252
12	180.5, 61.5, 0, 0, 61.5, 180.5, 360.5, 241.5, 180, 180, 241.5, 360.5
14	0, 132.5, 215, 245, 215, 132.5, 0, 180, 312.5, 395, 425, 395, 312.5, 180
16	95, 47.5, 145, 0, 0, 145, 47.5, 95, 275, 227.5, 325, 180, 180, 325, 227.5, 275
18	126.5, 20.5, 0, 66.5, 202, 66.5, 0, 20.5, 126.5, 306.5, 200.5, 180, 246.5, 382, 246.5, 180, 200.5, 306.5
20	0, 70, 31.5, 202, 113.5, 113.5, 202, 31.5, 70, 0, 180, 250, 211.5, 382, 293.5, 293.5, 382, 211.5, 250, 180
22	71, 191, 242, 223, 136, 0, 136, 223, 242, 191, 71, 251, 371, 422, 403, 316, 180, 316, 403, 422, 371, 251
24	111, 64, 188, 115, 180, 0, 0, 180, 115, 188, 64, 111, 291, 244, 368, 295, 0, 180, 180, 0, 295, 368, 244, 291
26	74, 33, 125, 0, 17, 169, 108, 169, 17, 0, 125, 33, 74, 254, 213, 305, 180, 197, 349, 288, 349, 197, 180, 305, 213, 254
28	137, 129, 0, 98, 30, 104, 217, 217, 104, 30, 98, 0, 129, 137,
	317, 309, 180, 278, 210, 284, 37, 37, 284, 210, 278, 180, 309, 317
30	29, 108, 91, 0, 149, 217, 170, 52, 170, 217, 149, 0, 91, 108, 29, 209, 288, 271, 180, 329, 37, 350, 232, 350, 37, 329, 180, 271, 288, 209
32	139, 156, 27, 83, 0, 109, 74, 224, 224, 74, 109, 0, 83, 27, 156, 139, 319, 336, 207, 263, 180, 289, 254, 44, 44, 254, 289, 180, 263, 207, 336, 319
34	92, 161, 146, 0, 114, 116, 30, 196, 237, 196, 30, 116, 114, 0, 146, 161, 92, 272, 341, 326, 180, 294, 296, 210, 16, 57, 16, 210, 296, 294, 180, 326, 341, 272
36	141, 167, 81, 186, 189, 14, 81, 0, 142, 142, 0, 81, 14, 189, 186, 81, 167, 141, 321, 347, 261, 6, 9, 194, 261, 180, 322, 322, 180, 261, 194, 9, 6, 261, 347, 321

Fig. 1.

Identity operation fidelity profile of GA-optimized phase modulation sets GA2, GA4, GA6, …, GA36. All these phase modulations are shown in Table 1. The three contours (from the inner to outer contour) indicate 99%, 90% and 80% fidelity levels.

Fig. 2.

Identity operation fidelity map of phase modulation sets XX8, XY8, GA10 and GA32 (Left to Right, Top to Bottom). Three contours (from inner to outer) indicate 99%, 90% and 80% fidelity levels. We have used these phase modulations for recoupling in TEDOR experiment.

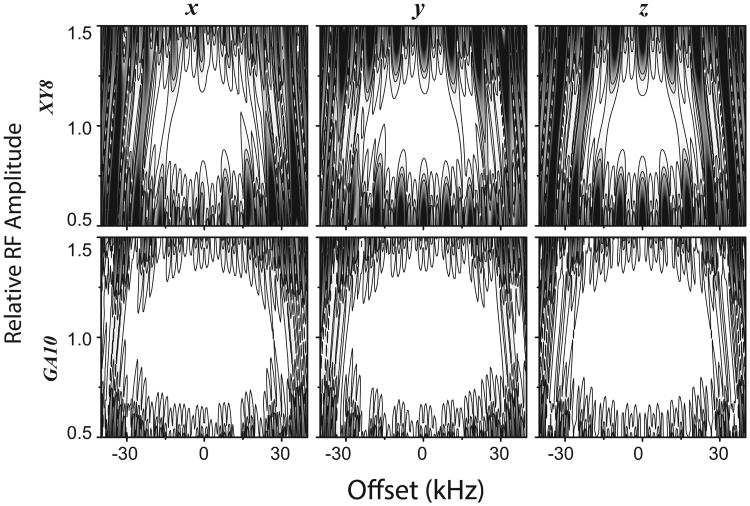
We have simulated the performance of these GA-optimized pulses in a spin-echo sequence using XY8 and GA10 phase modulations (Fig. 3). Starting from x, y and z magnetization, we measured the respective component in the final state of the spin-echo sequences. For the simulations, we used 50 kHz RF power and 100 μs spin echo delay. As shown in Fig. 3, 99% fidelity area of the GA10 sequence is more than two times of that obtained with XY8 for the three components of magnetization.

Fig. 3.

The fidelity profile response of XY8 (Top Row) and GA10 (Bottom Row) phase modulations in a spin echo pulse sequence. The response for x, y and z magnetization components are shown in columns from left to right. Simulations were performed for an RF amplitude of 50 kHz and a spin echo delay of 100 μs. Three contours (from inner to outer) indicate 99%, 90% and 80% fidelity levels.

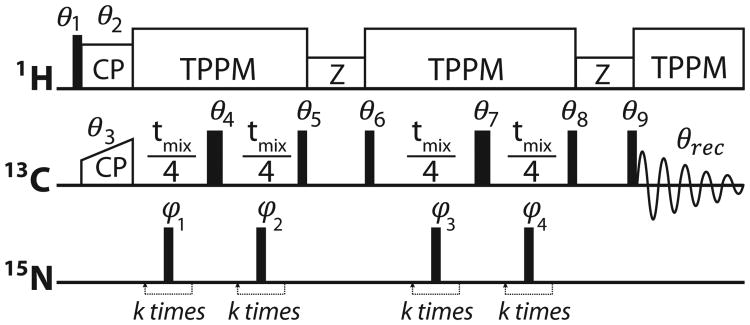
REDOR experiments typically employ phase-alternated π pulse scheme such as XY4, and XY8 [13,14]. TEDOR [11], on the other hand, utilizes an INEPT-type coherence transfer mechanism [21], where the two-spin interaction for polarization transfer is the dipolar coupling reintroduced by using two REDOR decoupling periods (Fig. 4). In order to study the experimental robustness of the GA-optimized identity sequence, we performed a ¹³C detected 1D ¹³C – ¹⁵N GMO-TEDOR experiment using the pulse sequence shown in Fig. 4. Starting with a CP transfer from ¹H to ¹³C, carbon magnetization is evolved under the recoupled heteronuclear dipolar coupling of ¹⁵N and ¹³C by applying a rotor-synchronized sequence of π pulses on ¹⁵N. The INEPT-type polarization transfer is achieved using π/2 pulses between the two REDOR periods. The accumulation of errors originating from all the π pulses in the recoupling sequence causes a severe loss of signal during the REDOR recoupling. In particular, the recoupling efficiency varies with the different phase modulations of φ₁, φ₂, φ₃ and φ₄. To better understand this phenomenon, we analyzed the effects of RF amplitude and offset response of the GA-optimized π sequence when applied to ¹⁵N in a rotor-synchronized manner. Indeed, we found that the intensity of the ¹³C signal depends on the recoupling efficiency. Specifically, we performed different experiments using four different sets of phase-cycling schemes used for the REDOR π sequences:

1. XX8 (no phase cycling or same phase for all pulses)

   $${\phi }_1={\phi }_2={\phi }_3={\phi }_4=\{0°,0°,0°,0°,0°,0°,0°,0°\}$$

2. XY8

   $${\phi }_1={\phi }_2={\phi }_3={\phi }_4=\{0°,90°,0°,90°,90°,0°,90°,0°\}$$

3. GA8x4 (uses GA32 phases, distributed in all four REDORsegments)

   $$\begin{array}{c}{\phi }_1=\{139°,156°,27°,83°,0°,109°,74°,224°\}\\ {\phi }_2=\{224°,74°,109°,0°,83°,27°,156°,139°\}\\ {\phi }_2=\{319°,336°,207°,263°,180°,289°,254°,44°\}\\ {\phi }_4=\{44°,254°,289°,180°,263°,207°,336°,319°\}\end{array}$$

4. GA10 display

   $${\phi }_1={\phi }_2={\phi }_3={\phi }_4=\{72°,110°,0°,110°,72°,252°,290°,180°,290°,252°\}$$

Fig. 4.

1D GMO-TEDOR pulse sequence used for finding the offset and RF power response of GA-optimized phase modulation set. We studied the offset and RF power response for XX8, XY8, GA8x4 and GA10 phase modulations by using these phase values at φ_{1 to 4}. The responses were measured by varying the offset and RF power of the recoupling π sequences on the ¹⁵N channel. A weak proton field of strength ω_rf = ω_r during the z-filters facilitates rapid dephasing of ¹³C spin coherences. The narrow and wide filled rectangles represent π=2 and π pulses respectively. The adopted phase cycles are: θ₁ = 1111, θ₂ = 2222, θ₃ = θ₆ = 1111, θ₄ = θ₇ = 1111, θ₅ = 1111, θ₈ = 2244, θ₉ = 1111, θ_rec = 4224.

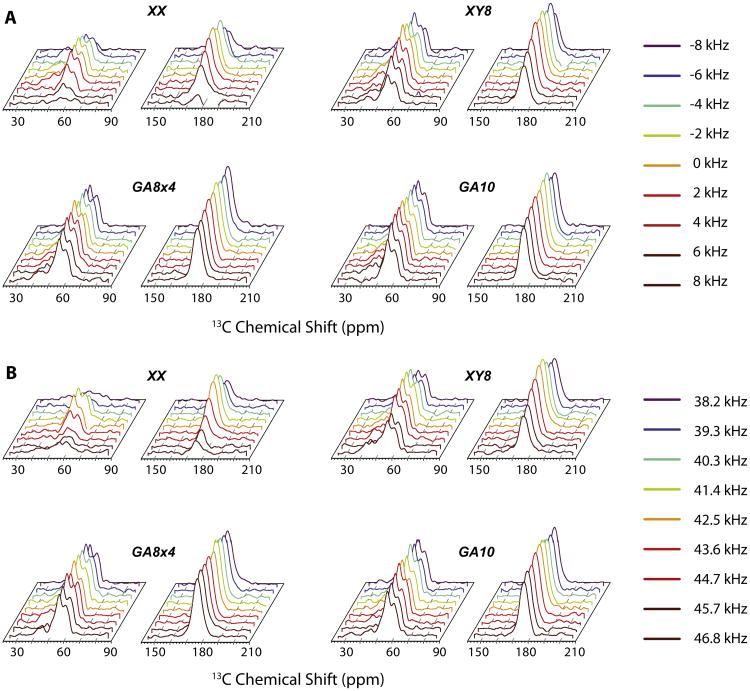
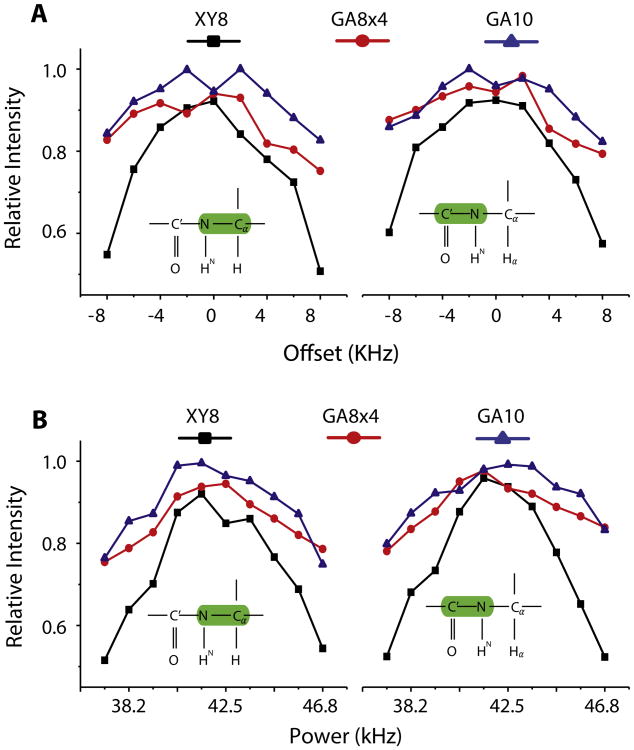
With 2 pulses per rotor period and 12 kHz spinning, the optimal recoupling delay for maximum polarization transfer can accommodate 8 to 10 pulses. This number also depends on the dipolar coupling, which is 2.5 kHz in our case (¹⁵N-¹³C). For weakly coupled system or higher spinning rates, one should use GA phase modulation of more than 10 pulses (e.g., GA16). The experimental intensity responses of CO and C_α upon changing the offset and RF power with XX8, XY8, GA8x4 and GA10 phase modulations are shown in Fig. 5A and B respectively. In order to study the ‘offset-intensity’ response, we have varied the ¹⁵N offset from –8 kHz to +8 kHz. For ‘RF power-intensity’ response, we have varied the ¹⁵N RF power from 160 to 240 W (200 W is the optimal power). Substituting the phase modulation of REDOR π sequence with that of robust identity operator reduces the error accumulated by experimental imperfections, improving the recoupling. We used the ¹³C intensity response as a measure of the efficiency of the recoupling sequence. Indeed, we observe a clear enhancement of the polarization transfer from ¹⁵N to ¹³C and vice versa via dipolar recoupling. From these experimental plots, we can conclude that GA-optimized phase modulation sets are less sensitive to offset and RF power for the GMO-TEDOR recoupling. Fig. 6 summarizes the overall GMO-TEDOR intensity response of GA optimized phase modulation sets (GA8x4 and GA10) over the conventional XY8 phases. The sensitivity enhancement of GA-optimized phase modulations in comparison to XY8 is summarized in Table 2. We found an offset averaged signal enhancement of 10.2% for GA8x4 and 15.9% for GA10. The power response shows an average enhancement of 14.5% and 12.4% for GA8x4 and GA10, respectively.

Fig. 5.

Spectral response of CO and C_α signal intensities upon changing (A) offset and (B) RF power of ¹⁵N recoupling π sequence. The response is shown for phase modulation XX8 (Top Left), XY8 (Top Right), GA8x4 (Down Left) and GA10 (Down Right).

Fig. 6.

(A) Offset response and (B) RF power of C_α (Left) and CO (Right) peak intensity under XY8, GA8x4 and GA10 phase modulations for ¹⁵N recoupling π sequences. Robust response is observed for the GA-optimized sequence.

Table 2.

Sensitivity enhancement TEDOR experiments with GA-optimized phase modulation in comparison to XY8. The response curves are shown in Fig. 6.

Phase modulation	Type	Gain in peak intensity (%) of 15N power and offset response (in comparison with XY8)
		Power	Offset
GA8x4	Max	28.4	27.7
	Mean	14.5	10.2
GA10	Max	27.9	26.1
	Mean	12.4	15.9

Trains of π pulses are basic and essential elements of many NMR pulse sequences. Starting from the Carr-Purcell sequence [10], many improved pulse trains such as CPMG, MLEV, and XY8 have been devised for various applications in liquid and solid-state NMR [8,20,22]. The applications of these pulse sequences are based on their response observed for the x, y and z magnetization components. Using GA optimization, we identified dual compensated identity operators, which preserve all these components of magnetization over a reasonable range of offset and RF inhomogeneity. Unlike gradient ascent [23] and the Nelder–Mead simplex algorithm [24], GA overcomes local barriers and finds global minima more efficiently. Importantly, the GA-optimized identity operation has a substantially improved 99% fidelity profile contour area (see Table 1 and Fig. 1). Conventional iterative pulse trains possess basic elements of 4, 8 or 16 pulses. In order to construct a pulse train of 10 π length, one has to combine 8 and 2 pulse trains, which dramatically reduces the total efficiency to less than that of individual pulse train. In contrast, using GA identity optimization, we have generated robust phase modulations for pulse length ranging from 2 to 36 π pulses, with a significant improvement for the 10 pulse version used in the GMO-TEDOR pulse sequence. This has no counterpart in conventional iterative pulse trains. Although TEDOR experiments are ideal to determine dipolar interactions (i.e., distances) in biomacromolecules, its utilization has been limited. This is due to the inherent insensitivity of these experiments. Specifically, the ¹³C–¹⁵N TEDOR experiments utilized a rotor-synchronized sequence of π pulses to recouple the MAS averaged ¹³C–¹⁵N dipolar couplings. In spite of the XY modulations used to compensate for pulse imperfections, these experiments are still prone to errors due to offset and RF pulse miscalibrations [13,14]. Here, we used GA10 and GA32 phase modulation sets replacing the XY8 sequence in the ¹³C detected ¹³C–¹⁵N GMO-TEDOR experiment (Fig. 4), with a remarkable improvement in sensitivity. We found a maximum sensitivity enhancement of 27.7% in offset response and a power response up to 28.4%. Compensating for pulse imperfections in REDOR recoupling was previously addressed using composite pulses [25] and correction sequences [26]. Indeed, these methods are complementary to the GA-optimized phase cycling and can be combined to obtain further improvements.

5. Conclusion

GA optimization makes it possible to improve the performance of REDOR and TEDOR experiments. This approach used for the newly designed phase modulation set using GA optimization in GMO-TEDOR has the potential to improve the experiments involving a sequence of π pulses with an effective pulse action of identity. These identity operators are dual compensated and initial state independent. Sequence of π pulses which preserves x, y and z components of magnetization is crucial to various applications in solid and liquid-state NMR as well as in MRI. We anticipate that GA optimization of identity operations will have a strong impact for various spectroscopic applications.