How many more? Sample size determination in studies of morphological integration and evolvability

Abstract

1. The variational properties of living organisms are an important component of current evolutionary theory. As a consequence, researchers working on the field of multivariate evolution have increasingly used integration and evolvability statistics as a way of capturing the potentially complex patterns of trait association and their effects over evolutionary trajectories. Little attention has been paid, however, to the cascading effects that inaccurate estimates of trait covariance have on these widely used evolutionary statistics.

2. Here, we analyze the relationship between sampling effort and inaccuracy in evolvability and integration statistics calculated from 10-trait matrices with varying patterns of covariation and magnitudes of integration. We then extrapolate our initial approach to different numbers of traits and different magnitudes of integration and estimate general equations relating the inaccuracy of the statistics of interest to sampling effort. We validate our equations using a dataset of cranial traits, and use them to make sample size recommendations.

3. Our results suggest that highly inaccurate estimates of evolvability and integration statistics resulting from small sample sizes are likely common in the literature, given the sampling effort necessary to properly estimate them. We also show that patterns of covariation have no effect on the sampling properties of these statistics, but overall magnitudes of integration interact with sample size and lead to varying degrees of bias, imprecision, and inaccuracy.

4. Finally, we provide R functions that can be used to calculate recommended sample sizes or to simply estimate the level of inaccuracy that should be expected in these statistics, given a sampling design.

Introduction

Though previous researchers hypothesized on the implications of correlations between traits for evolution (e.g. Darwin 1859), it was Olson and Miller (1958) who presented the hypothesis that traits that are related through function or development may be correlated phenotypically and can evolve together - the concept of morphological integration. Olson and Miller (1958) suggested that measuring the overall level of phenotypic correlation among traits, defined as the magnitude of integration, could provide insights into the underlying associations among traits and how these associations affect evolution (Olson and Miller 1958). The last three decades saw an explosion in interest in quantifying how associations between traits affect and reflect evolution (Polly 2005; Goswami 2006; Klingenberg 2008; Marroig et al. 2009; Adams & Felice 2014), spurred on by the work of Cheverud (1982) and Lande (1979; Lande and Arnold 1983) who placed Olson and Miller’s (1958) ideas within a quantitative genetics framework. This explosion led to a wide variety of different conceptualizations of integration in the literature. While integration has been defined by some authors purely in terms of covariation among traits within populations (e.g. Klingenberg 2008), others have described integration as the propensity of a developmental system to produce phenotypic covariation in populations (Hallgrimsson et al. 2009). In this latter definition, genetic and environmental influences, channeled through developmental processes that influence multiple traits, can lead to covariation among traits in a population. Integration of developmental processes is a feature of individuals, covariation is a feature of populations that results from variation in integrated developmental systems. It is this latter definition of integration we use here, but note that use of the term integration in statistics that measure phenotypic associations between traits is unavoidable.

Generally, studies of trait covariation focus on one of two related directions – testing a priori hypotheses about developmental or functional relationships among traits (e.g. modularity, the propensity for traits to covary more with traits within a module than between modules; Klingenberg 2008; Porto et al. 2009; Goswami & Polly 2010) or testing how covariance matrices may affect and reflect evolutionary forces and evolutionary change ( Marroig & Cheverud 2004; Gratten et al. 2008; Hansen & Houle 2008; Adams & Felice 2014; Goswami et al. 2014). While both directions are fundamentally important for our understanding of evolution, the last direction is our focus here. Though considerable effort has been devoted to understanding the role of trait covariation in evolution (Ackermann and Cheverud 2000; Marroig and Cheverud 2004; Porto et al. 2009; Marroig et al. 2009; Williams 2010; Berner et al. 2010; Grabowski et al. 2011; Villmoare et al. 2011; Hansen and Voje 2011;Gómez-Robles & Polly 2012; Klingenberg & Marugan-Lobon 2013; Goswami et al. 2014) the statistical issues associated with estimating high dimensional covariance matrices received comparatively less attention in evolutionary biology, save for a few notable exceptions (Meyer and Kirkpatrick 2008; Haber 2011; Marroig et al. 2012; Houle and Meyer 2015; Adams 2016). As a consequence, most researchers deal with statistical issues a posteriori (e.g., including standard error estimates). However, in the presence of bias, true population parameter values can fall outside of the confidence interval of sample estimates of the parameter, rendering the results meaningless with regards to the original research questions. While unbiased estimators of trait variance/covariance are available, most commonly used evolutionary statistics represent statistical transformations of such matrices. Statistical transformations, when applied to unbiased estimators, do not necessarily lead to unbiased estimators of the corresponding statistic (Gourieroux & Monfort 1995; Morrisey, 2016). For example, most evolvability statistics are based on the distribution of eigenvalues of covariance matrices, which can be substantially biased at small samples (Lawley 1956; see Supporting Information).

A few studies have explored the effects of sample size on various evolutionary statistics arising from sample covariance matrices (e.g. Polly 2005; Goswami 2006; Goswami & Polly 2010) and have provided us with important insights into the effects of sampling in statistics measuring the magnitude of morphological integration (Haber 2011). However, there is nothing comparable for statistics that quantify the role of covariation in biasing or constraining evolution – i.e. evolvability statistics (Hansen & Houle 2008). Likewise, we are not aware of any systematic approach to extrapolating sample size recommendations for a wide array of study designs, or even approaches that allow researchers to estimate a priori the amount of inaccuracy that a certain sampling design would incur. While the statistical issues discussed here can seem slight in comparison to the large evolutionary questions being asked, how one treats data and interprets analytical results may affect whether the findings are meaningful with regards to the original research question (Houle et al. 2011; Grabowski et al. 2016).

This study systematically explores the assumption that evolutionary statistics (e.g., evolvability, integration) of sample covariance matrices are adequate descriptions of the ‘true’ population values, and the cascading effect of sampling error on the accuracy of statistics used to quantify evolvability and integration. As our study employs several statistics that might not be familiar to researchers outside the field of multivariate evolution, we provide a detailed description of these statistics, together with a preliminary assessment of how sampling error might affect them statistically, as part of our Supplemental Information. Figure 1 and Table 1 also provide a quick introduction to evolvability and integration statistics, and they will also be discussed further below. For further details, see Hansen and Houle (2008) and Marroig et al. (2009).

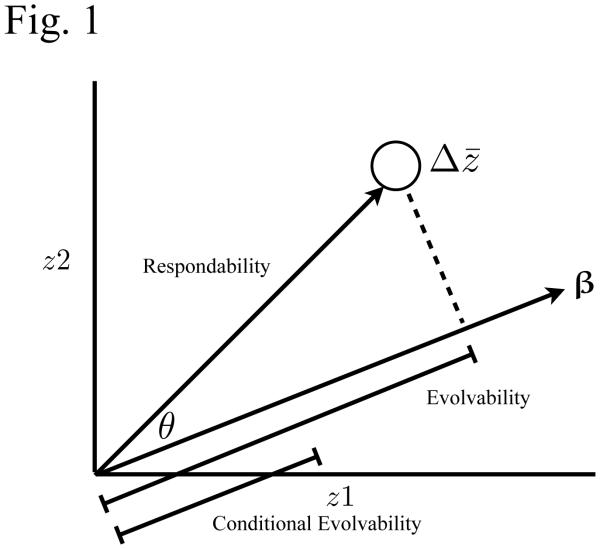
Fig. 1.

Modified from Hansen and Houle (2008) Fig. 1. Graphic shows the response (?z) of a population (open circle) when selection (β) is on two integrated traits. Respondability is the length of the predicted response to selection. Evolvability (e) is measured as the length (magnitude) of the projection of the response vector on the selection vector, and reveals the magnitude of the evolutionary response in the direction of selection. Conditional evolvability (c) is the length (magnitude) of the hypothetical response to selection (closed circle) when the response cannot deviate from the direction of selection. Integration (i) reveals the relative reduction in evolvability due to stabilizing selection. Finally, flexibility (f) is the cosine of the angle between the selection and response vectors.

Table 1.

Statistics, symbols, and their meanings in this analysis. From Hansen and Houle (2008) except where noted.

Statistic	Symbol	Equation	Definition
Magnitude of integration	r2	$\frac{1}{n}{\sum }_{i=1}^n\left(r^2\right)$	Average of squared correlations among traits (Cheverud et al. 1989)
Mean integration	i	$1-\text{E}\left[{\left(\beta P\beta {\beta }^{\prime }{P}^{-1}\beta \right)}^{-1}\right]$	Average relative degree to which evolvability is reduced due to conditioning on other traits over a large number of random direc- tions
Mean respondability	r	$E\left[\sqrt{{\beta }^{\prime }{P}^2\beta }\right]$	Average length of the predicted response to selection and measures how rapidly a popula- tion can respond to selection.
Mean flexibility	f	$\text{E}[\parallel \beta \parallel \parallel \Delta z\parallel cosϴ]$	Average cosine of angle between direction of selection and re- sponse vector over a large number of random directions (Marroig et al. 2009).
Mean evolvability	e	$\text{E}\left[{\beta }^{\prime }P\beta \right]$	Average length of the multivariate response in the direction of selec- tion for a given P over a large number of random directions.
Mean conditional evolvability	c	$\text{E}\left[{\left({\beta }^{\prime }{P}^{-1}\beta \right)}^{-1}\right]$	Average length of the multivariate response in the direction of selec- tion for a given P when all other traits are not allowed to change over a large number of random directions

r=correlation coefficient; β =selection gradient; P=phenotypic V/CV matrix; Δz = selection response; ϴ=angle between the selection gradient and selection response

We begin the empirical part of our study by simulating populations under different patterns of covariance and different magnitudes of integration. Next, we explore the relationship between sampling effort and accuracy under different numbers of traits and different magnitudes of integration. We then validate our model using a dataset of mammalian cranial traits. Finally, sample size requirements for reliable estimates of evolutionary statistics are suggested based on these findings. We also provide two R functions. Function howmany.R allows researchers to calculate the recommended sample sizes for certain level of inaccuracy, given any number of traits. Function howInaccurate.R estimates the expected degree of inaccuracy of a wide variety of sampling designs.

Materials and methods

Layout of analyses

The simulation protocol is broken into four parts. First, we construct sets of simulated covariance matrices with known parameter values of evolvability and integration statistics, and then use these matrices to describe the effects of sampling error on these statistics. Second, we break down the results seen in step one by describing how differences in sampling effort, in combination with population-level patterns of covariance and magnitudes of integration, affect evolvability and integration statistics by quantifying the statistics’ bias, imprecision and inaccuracy (see below). Third, we repeat step one but encompass a larger array of trait numbers and a broader range of integration magnitudes. Finally, we validate our results using a dataset of mammalian cranial traits.

Generating matrices

All simulations were performed using two different sets of randomly generated matrices. In the first set, matrices differ only in their pattern of covariation among traits. In the second set, matrices differ only in their integration magnitudes. To avoid underestimating the amount of sampling error associated with each covariance matrix, we filtered all random matrices in terms of their log-eigenvalue distribution. In particular, matrices whose last eigenvalue were exceedingly small were filtered out to prevent an underestimation of the amount of sampling error. Details of random matrix generation can be found in the S.I. - Generating matrices.

The first set of matrices (pattern matrices, PAT-1,PAT-2,PAT-3; see Table 2) corresponds to 10-trait covariance matrices with an average squared correlation coefficient r² of 0.17, corresponding to the mean of the distribution of integration magnitudes observed in a large dataset of mammalian cranial traits (Porto et al. 2013). To better sample the matrix space, 1,000 random covariance matrices were generated using the same parameters as above and their average simulation results will be presented in this manuscript as belonging to ‘matrix’ PAT 1,000.

Table 2.

Matrices, number of traits in each, magnitude of integration (r²), and individual number where sample matrix computed from this 'parameter' matrix becomes full rank.

Matrix	Number of traits	Description	Magnitude of Integration	Full rank
MAG-1	10	Matrix with low magnitude of integration and the same pattern as other MAGs	0.07	11
MAG-2	10	Matrix with intermediate magnitude of integration and the same pattern as other MAGs	0.17	11
MAG-3	10	Matrix with high magnitude of integration and the same pattern as other MAGs	0.50	11
PAT-1	10	Matrix with intermediate magnitude of integration and random pattern	0.17	11
PAT-2	10	Matrix with intermediate magnitude of integration and random pattern	0.17	11
PAT-3	10	Matrix with intermediate magnitude of integration and random pattern	0.17	11
PAT 1,000	10	Average of the results ob- tained for 1,000 PAT- matrices	0.17	11
Monodelphis	30	30 skull traits from a sample of Monodelphis from Porto et al. (2015)	0.27	31
Callithrix	30	30 skull traits from a sample of Callithrix from Marroig and Cheverud (2001)	0.08	31

The second set of matrices (magnitude matrices, MAG-1, MAG-2, MAG-3; see Table 2) are all modifications of a single random matrix, following Marroig et al. (2012). Briefly, a single matrix was generated and posteriorly had its first eigenvalue scaled up or down in such a way as to make the three matrices encompass the total distribution of integration magnitudes observed in a large dataset of mammalian cranial traits (MAG-1=lower bound, MAG-2=mean, MAG-3=higher bound; Porto et al., 2013).

It should be noted that the results presented in this manuscript are robust to the method used to generate the two matrix sets, as other approaches, such as the creation of matrices with known patterns of covariance (Marroig et al., 2012), present equivalent results.

Simulation approach

The simulation involved four main steps. The first step was to simulate a population based on each covariance matrix (PAT1, etc.). The second step was to calculate the parameter values of each statistic based on the known population covariance matrix. The third step was to calculate covariance matrices based on differing sample sizes of “individuals” drawn from the main population. The final step was to calculate the statistics of interest for each of the sampled matrices and compare the values of each to the known parameter values.

To make simulated populations in step one, 10,000 individuals were drawn from a multivariate normal distribution based on the simulated matrices with null mean. These 10,000 individuals are meant to be the effective size of a natural population from which samples can be drawn. Samples were taken from this population following the simulation routine described below.

For each sample size capable of producing full rank matrices, a sample of that number of individuals was drawn from the population, a covariance matrix was estimated, and then each statistic was calculated. This was repeated 100 times and the values were saved. Then the sample size was increased by 1 and the whole procedure was repeated again. The mean value of the statistics at each sample size was considered the best estimate of the statistic at that sample size, and 95% confidence intervals were calculated around this best estimate based the standard error of the iterations. Here, the confidence intervals are showing the range of the statistic that 95% of the repeated samples will fall in. They also provide the 95% confidence interval in which studies at that particular sample size would predict the parameter value to be.

An additional step is needed to calculate the evolvability statistics that is not present when calculating r². Because these statistics rely on the average response of covariance matrices to simulated selection vectors, random selection vectors were created by drawing from a random normal distribution with a mean of 0 and a standard deviation of 1, normalized to unit length, and then applied to the covariance matrix for each sample using the equations in Table 1 (Hansen and Houle 2008) to calculate the statistic of interest. The mean values for each statistic were calculated by repeating this procedure 1,000 times and taking the mean value of the repetitions (Hansen and Houle 2008). Since matrix inversion in highly multidimensional systems is a time consuming step in the calculations, the results for mean conditional evolvability and mean integration presented for ‘matrix’ PAT 1,000 were produced using analytical approximations from Hansen and Houle (2008), rather than the simulation approach. For all other matrices, all statistics were calculated using the simulation approach.

Quantifying error

We quantify three different aspects of error: bias, imprecision, and inaccuracy. Bias is the difference between the expected value of a parameter and the true parameter value. Imprecision is the distance of repeated measurements to each other and can be described as variance of an estimate and reflected in standard errors or confidence intervals. Inaccuracy is the distance of a measured value to its parameter value, and takes into account both bias and imprecision. The metric of inaccuracy used here is the mean squared distance of the estimate from the parameter, and as described here has the following relationship:

$$\text{Inaccuracy=Imprecision}+{\text{Bias}}^2$$ (Equation 1)

Although we calculated these three metrics here, we will only report our inaccuracy metric in a figure. Imprecision and bias in the statistics described in this manuscript can be observed in our plots of the simulation results. To allow for comparison between sets of results and evolvability and integration statistics, inaccuracy was scaled by the square of its parameter value. Inaccuracy can therefore be thought of as a proportion of the squared mean.

Since it is particularly useful to place measurements of inaccuracy in the context of between-species variation in these statistics, the squared coefficient of variation (CV²) of each statistic in a large sample of mammals are also reported in this manuscript (Porto et al. 2013). The reasoning to do so is simple. If the statistics included here vary considerably across species, one might be willing to accept a larger amount of inaccuracy when estimating them, as that inaccuracy is unlikely to lead a researcher to different conclusions. If these statistics are very similar across species, on the other hand, one might want these statistics to be estimated more accurately.

All simulations were run in the R statistical programming language (R Development Core Team 2011) using programs written by the authors (see associated Dryad package for the R codes). The simulations were run on the parallel computational resource Lifeportal (Formerly Bioportal; Kumar et al. 2009) at the University of Oslo. Rank was tested using the “rank.condition” function of the “corpcor” package (Schaefer et al. 2012).

Expanding the usefulness of the simulations

Determining adequate sample size for studies of multivariate evolution requires recommendations that can be extrapolated across studies with different designs. So far, all analyses were made under the assumption that a researcher is studying 10 traits with specific magnitudes of integration. In the attempt of making these results more general, the same simulation protocol described above was used to estimate the relationship between inaccuracy and sampling effort under different numbers of traits (from 10 to 100) and different magnitudes of morphological integration (MI; r² varying from 0.02 to 0.5). For each MI and trait number, a power function of the form ax^b was fitted to the simulation data, relating sampling effort to inaccuracy. Symbolic regressions were then used to search for models that describe the relationship between the exponent (b), the constant (a) and our variables (MI and number of traits) using Eureqa (Schmidt and Lipson 2013). Symbolic regressions search the mathematical space to find models that best fit a given dataset, while taking into account both the accuracy of the model and its simplicity. In our case, symbolic regressions were run until the model’s mean absolute error flatlined. Whenever more than one adequate model were found, models were chosen based on complexity, with simple models being favored against more complex ones. These models were then embedded in two R codes: (1) one that can be used to calculate the recommended sampling effort necessary to achieve a certain level of inaccuracy in the statistic of interest (howmany.R); (2) and another that estimates the level of inaccuracy that would be observed in evolutionary statistics, given a sampling design (howInaccurate.R).

To illustrate the sensitivity of the statistics of interest to changes in the number of traits and MI, 3D surfaces that relate recommended sampling effort, number of traits and MI were also generated using the howInaccurate function.

Validating the model

The strength of the models generated above depend on how well they predict real-world values for under-sampled species. Thus, it is particularly important for us to validate our model by testing whether the amount of inaccuracy in each statistic, as predicted by the equations in the R code, corresponds to what would be observed in real-world applications. To do so, we selected two genera of mammals that had more than two hundred individuals measured for 30 cranial traits - Callithrix and Monodelphis - (Marroig and Cheverud 2001; Porto et al 2015) and used them to test our models. There are two main reasons for choosing these two genera. First, due to their high sample sizes, we had accurate estimates of the evolvability and integration statistics for both genera. Second, they represent a broad range of integration magnitudes among mammals, with values of 0.08 and 0.27 for r² (Table 2), respectively (Porto et al. 2013). While individual trait pairs can have r² values higher than 0.27, it is rarely the case that a truly multivariate system will have values much higher than that for average squared correlation coefficients, and such systems would have such low underlying dimensionality that statistical bias would likely be small. Here, inaccuracies as predicted by our models were compared to inaccuracies obtained by bootstrap resampling their corresponding skull database while varying sample sizes. The main advantage of bootstrap is that it does not require any assumption of normality (Efron 1982) and produces results that would be equivalent to a situation in which someone under-sampled a particular species. The fit of inaccuracy predictions to the inaccuracies of the bootstrapped data was evaluated in terms of r² goodness-of-fit (as implemented in Schmidt and Lipson (2013)). Goodness-of-fit values above 0.9 were seen as the model fitting the data adequately. Values between 0.5 and 0.9 were considered minimally acceptable, but had their biases highlighted. Values below 0.5 were considered poor fit.

Results

Effects of sampling error on integration statistics

Moving from smaller to larger sample size generally has a large effect on the statistical measures of integration included here (r², and mean integration) for all simulated matrices (Fig. 2). The best estimates of all integration statistics are biased upward at small sample sizes for the two matrices with low to moderate levels of integration (MAG-1,MAG-2), with the statistic becoming generally unbiased for the matrix with the highest level of integration (MAG-3) for r² (Fig. 2B ). Mean integration (Figs. 2C, D) is biased upward for all the matrices at small sample sizes, and at the smallest the estimate does not contain the parameter value. This effect decreases (i.e. less individuals are needed to reach a point where the confidence interval contains the parameter) with increasing integration.

Fig. 2.

Best estimates (symbols) and 95% confidence intervals (lines) for Mean r² and Mean Integration using subsets ranging from 11-150 individuals from a simulated population of 10,000. Results are shown for populations with different patterns of integration (PAT) or different magnitudes of integration (MAG).

Imprecision increases with increasing the level of integration for r² (Fig. 2B). At the smallest sample sizes, r² estimates for MAG-3 can differ from each other by a factor of 3 to 4 times. Even at the highest sample size, there is considerable imprecision in these statistics. On the other hand, imprecision in mean integration is not significantly affected by the overall magnitude of integration (Fig. 2D).

Changes in the pattern of covariation do not appear to significantly affect integration statistics, with all best estimates for each matrix falling within the 95% confidence interval of the other matrices, at any sample size (Fig. 2).

Effects of sampling error on evolvability statistics

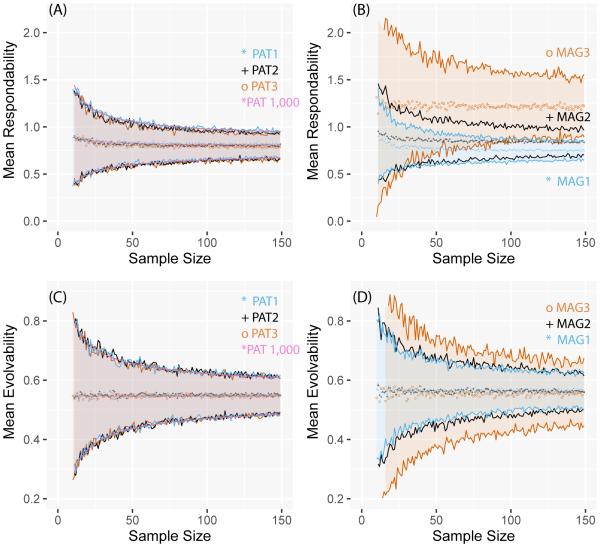
The mean respondability results (Fig. 3B) suggest a slight positive bias at the smallest sample sizes given little to moderate integration (MAG-1,MAG-2), with the statistic becoming generally unbiased for the matrix with the highest level of integration (MAG-3). Imprecision greatly increases with increased level of integration. Changing the pattern of covariation does not appear to affect the statistic, with all four PAT-matrices being indistinguishable in their sampling properties (Fig. 3A).

Fig. 3.

Best estimates (symbols) and 95% confidence intervals (lines) for Mean Respondability and Mean Evolvability using subsets ranging from 11-150 individuals from a simulated population of 10,000. Results are shown for populations with different patterns of integration (PAT) or different magnitudes of integration (MAG).

The mean evolvability plots for all seven matrices (PAT+MAG; Fig. 3C,D) indicate that this statistic has virtually zero sampling bias under any pattern of covariation and magnitude of integration. However, imprecision is stronger for matrices with high overall level of integration (MAG-3). At the smallest sample sizes, mean evolvability 95% confidence intervals for MAG-3 includes values that differ from each other by a factor of 3 to 4 times. At small sample sizes and given a matrix with little or moderate integration, mean flexibility (Fig 4A,B) is negatively biased, but bias is diminished substantially as integration level increases (MAG-3). Like mean evolvability, imprecision is highest in more integrated matrices (MAG-3), diminishing in MAG-1. Changing the pattern of covariation has slight to no effect on mean flexibility results (Fig. 4A), with best estimates for one matrix falling within the 95% confidence interval of the other matrices at any sample size.

Fig. 4.

Best estimates (symbols) and 95% confidence intervals (lines) for Mean Flexibility and Mean Conditional Evolvability using subsets ranging from 11-150 individuals from a simulated population of 10,000. Results are shown for populations with different patterns of integration (PAT) or different magnitudes of integration (MAG).

Finally, for mean conditional evolvability, all MAG-matrices (Fig. 4C,D) show strong negative bias in the best estimates at small sample sizes to the extent that the confidence interval does not contain the parameter until around 30-40 individuals for the matrix with a low level of integration (MAG-1). Changes in the pattern of covariation has little to no effect on this statistic, with best estimates for one PAT-matrix falling within the 95% confidence interval of the other three matrices, especially at high sample sizes (Fig.4C).

Not surprisingly, increasing sample size decreases the level of imprecision for all evolvability and integration statistics included here, regardless of magnitude or pattern of covariation. A summary of the effects of sampling error and level on integration over bias and imprecision estimates for each statistic can be found in Table 3.

Table 3.

- Summary of the effects of reduced sampling (Reducing N_ind) and increased integration magnitude (Increasing r²) over bias and imprecision estimates for each statistic.

Statistic	Bias		Imprecision
	Reducing Nind	Increasing r2	Reducing Nind	Increasing r2
r2	↑	↓	↑	↑
Integration	↑	↓	↑
Respondability	↑	↓	↑	↑
Evolvability			↑	↑
Flexibility	↑(−)	↓	↑	↑
Conditional Evolvability	↑(−)		↑

↑=increase; ↓=decrease;↑(−)=increase (negative bias);-------neutral effect

Inaccuracy in evolvability and integration statistics

For the integration statistics, increasing the magnitude of integration decreases inaccuracy (Fig 5A, B). The matrix with the highest magnitude of integration (MAG-3) is estimated more accurately than the least integrated ones, even when the latter are estimated with three times as many ‘individuals’. This is true regardless of the integration statistic being used. The level of inaccuracy observed for the r² statistic in matrices MAG-2 and MAG-3 is smaller than the squared coefficient of variation of this statistic among mammals (CV²; Porto et al. 2013) at any sample size. The opposite is true for matrix MAG-1. For the mean integration statistic, most matrices present values above the CV² at some sample size.

Fig. 5.

Plots of inaccuracy for evolvability and integration statistics at sample sizes from 11-150 for all 7 simulated population covariance matrices (PAT+MAG). Matrices PAT and MAG-2 were pooled together for simplicity, as their values are broadly the same. The squared coefficient of variation of each statistic (CV²) among dozens of species of mammals (Porto et al. 2013) are shown as dashed lines.

The mean respondability and mean evolvability results (Fig 5C,D) show that the level of inaccuracy varies with the magnitude of integration, though substantial convergence among all matrices is observed at the smallest sample sizes. Contrary to integration statistics, inaccuracy in mean respondability and mean evolvability is highest in matrices with moderate to high magnitude of integration (MAG-2,MAG-3), owing to the high imprecision previously observed. The level of inaccuracy observed for these statistics tend to be smaller than their CV² among mammals, except at the smallest sample sizes.

For mean flexibility (Fig. 5E), the most integrated matrix is the most accurate (MAG-3) at small sample sizes, and inaccuracy is inversely related to the magnitude of integration. The level of inaccuracy observed for this statistic tends to be smaller than CV² of this statistic among mammals, at any sample size.

Finally, for mean conditional evolvability (Fig. 5F), the magnitude of integration does not affect the level of inaccuracy, with all three matrices presenting the exact same sampling behavior. The level of inaccuracy observed for this statistic is smaller than CV² of this statistic among mammals at any sample size.

Expanding the usefulness of the simulations

Figure 6 illustrates the sampling effort necessary for obtaining, at most, 0.05 inaccuracy in the statistics of interest, given a particular number of traits (from 10 to100) and a particular level of morphological integration (measured as r², from 0.02 to 0.5). It’s worth noting that sampling effort here is illustrated as the ratio between the number of individuals and the number of traits. This was done for illustrative purposes only. The R code used to generate these plots, which contains the equations resulting from the symbolic regressions, can be found in the associated Dryad package.

Fig.6.

3D surface plots illustrating the recommended sampling effort necessary to obtain at most 0.05 inaccuracy in the statistics of interest, given different numbers of traits and different population-level magnitudes of integration (level of MI). Sampling effort is measured, in the 3D plots, as the ratio between the number of individuals sampled and the number of traits measured (for illustrative purposes only).

Four major features of the sampling properties of these statistics are worth highlighting. Firstly, only mean conditional evolvability requires similar sampling effort, regardless of the integration magnitude. Second, increasing the number of traits causes all statistics to require a proportionally smaller number of individuals to be measured (even though the number of individuals is still higher in absolute terms). Third, integration statistics tend to be more sensitive to change in the level of morphological integration and trait number than evolvability statistics, as evidenced by their higher multipliers. Finally, integration statistics require exponentially higher sampling effort at low integration magnitudes, while evolvability and respondability require larger sampling effort at high integration magnitudes.

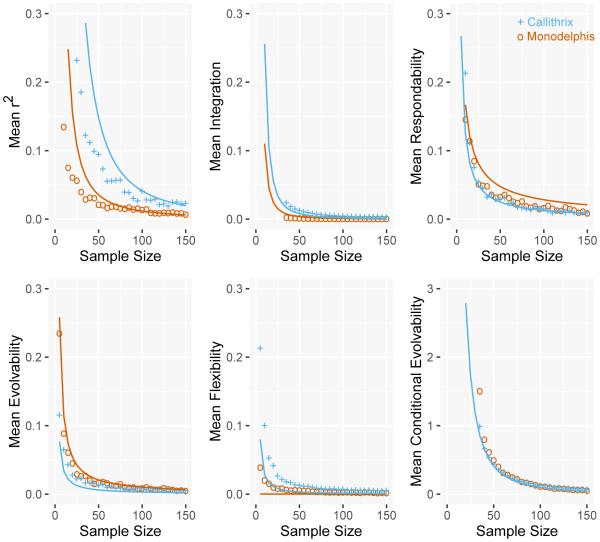
Validating the model

Figure 7 illustrates the fit of the inaccuracies as predicted by the models resulting from the symbolic regressions when compared to the inaccuracies estimated based on bootstrap resampling a database of 30 cranial traits for two species of mammals with different integration magnitudes. With the exception of mean integration and mean flexibility in Monodelphis, all other statistics present acceptable estimates of r² goodness of fit when constrained to be within the bounds in which the models were generated (Table 4). A total of 75% of the models also produce acceptable estimates of goodness of fit when extrapolated for the whole range of bootstrap resamples. The model fit for Callithrix was, on average, higher than Monodelphis. Only the model for mean flexibility tended to significantly underestimate the amount of inaccuracy (Figure 7). It should be noted that the sample sizes for statistics that require matrix inversion were constrained to the range Number of Individuals>Number of Traits.

Fig. 7.

Plots of inaccuracy for evolvability and integration statistics estimated based on bootstrap resamples from a large dataset of cranial traits measured in two species of mammals with different integration magnitudes (Porto et al 2013). The amount of inaccuracy that would be predicted by our models, in each species, is shown as a solid line. The overall fit of our models to the bootstrap resamples can be seen in Table 4.

Table 4.

Overall fit of our models to the bootstrap resamples from a large dataset of cranial traits measured in two species of mammals with different integration magnitudes (Porto et al 2013). The overall fit is illustrated for each statistic as the r² goodness-of-fit of the model to the data. The overall fit is reported for two ranges. Total range includes data points outside the range in which the models were generated (N_ind= 5-180). Limited range only includes the data points within the range in which the models were generated (i.e., the range in which matrices are full rank; N_ind=31-180). The Limited range overall goodness-of-fit is only reported for models that were considered to have poor fit in the Total range.

Statistic	Monodelphis		Callithrix
	Total Range	Limited	Total Range	Limited
r2	<0.5	0.55	0.81
Integration	<0.5	<0.5	0.88
Respondability	0.92		0.75	0.91
Evolvability	0.97		0.79
Flexibility	<0.5	<0.5	0.5
Conditional Evolvability	0.83		0.98

Discussion

What sample size is needed to adequately estimate a covariance matrix and calculate accurate evolvability and integration statistics? Based on the findings here, calculating accurate estimates of these statistics involves considering not only the sample size, but also the true magnitude of integration of the population, and the statistic of interest. Estimating a population covariance matrix based on a sample size of 40 individuals, which is commonly cited as the minimum requirement since Cheverud’s (1988) classic analysis, can be too few to accurately estimate a number of the metrics tested here because of substantial bias and/or lack of precision of these metrics. This is especially true now that there is increased use of semi-landmarks to characterize morphology and some of these statistics are being used in the context of gene expression data (see Ayroles et al. 2009), all of which entail measuring hundreds or even thousands of traits. In particular, the field would largely benefit from abandoning the notion of a universal minimum sample size, instead favoring careful consideration of the sampling properties of these statistics. The reason for this can be seen on the results for one matrix, MAG-1, with a parameter mean integration (Hansen & Houle 2008) value of 0.53. Given a sample of 40 individuals, this statistic is positively biased to up to around 20% of the parameter value. This upward bias would be separate from the imprecision at that sample size, which falls somewhere around 8% of the parameter value. Together this means that, on average, the best estimate of mean integration has a 95% confidence interval of 0.55 - 0.72. Note that the confidence interval does not even contain the parameter value of 0.53. This situation, with the confidence interval not containing the known parameter value due to bias in the statistic at small sample sizes, occurred for a number of the statistics included here for a range of patterns of covariation and magnitudes of integration.

Effects of sampling error - is bias pervasive?

As all matrices here become full rank when the number of individuals is one more than the number of traits (Table 2), the major source of inaccuracy in calculated evolvability and integration statistics is sampling error in the estimated covariance matrix. Bias seems to be pervasive among the evolvability and integration statistics (Table 3). As mentioned above, the 95% confidence intervals of some statistics explored here (mean conditional evolvability, mean flexibility, and mean integration) may only contain the parameter value at larger sample sizes. This observation indicates that, although consistent (i.e., they converge at the parameter value at higher sample sizes), these estimators are highly biased. These three statistics deserve, therefore, extra attention in any study attempting to estimate their mean values in high dimensional systems (e.g. Hansen et al. 2003a; Marroig et al. 2009; Roseman et al. 2010; Grabowski 2013). It’s important to emphasize that imprecision is as important a source of inaccuracy for all statistics as is bias. Imprecision, however, can be partially taken into account by a posteriori uncertainty estimates (such as standard errors).

It should also be noted that sampling error is particularly relevant to the extent that it influences our ability to detect significant differences in the parameter values of integration and evolvability statistics between two or more species. In a comparative framework, the amount of inaccuracy one should be willing to accept depends on how different the parameter values are between the groups of interest. Our results comparing the coefficient of variation of these statistics across mammals (CV²) with their sampling inaccuracy suggest that researchers wanting to compare these statistics among very diverse groups might be less stringent in sampling. For these groups, evolvability and integration statistics vary between groups to a greater extent than between samples at most sample sizes. On other hand, if a comparison is being made between groups with very similar parameter values for these statistics (e.g. among primates, Grabowski et al. 2011), more attention to sampling is advised. Since the true parameter values can never be known a priori, an approach that takes into account the sampling properties of these statistics, both prior to the study (e.g. via the sample size suggestions given here) and after results were obtained (e.g., standard errors), is advisable.

Effects of population-level patterns of covariation and magnitudes of integration

In general, changing patterns of covariation does not substantially affect bias, imprecision or inaccuracy of all statistics. This is not to imply that changes in patterns of integration are not important to evolution. Rather, the results presented here suggest that patterns of integration do not significantly affect the sampling properties of V/CV matrices, as long as the distribution of eigenvalues is contained within a certain range (see Supporting Information). On the other hand, as the magnitude of integration of the population increases, bias, imprecision and inaccuracy of statistics change considerably, with each statistic behaving in a different way. The main contrast in behavior is found between integration statistics, on one side, and mean evolvability plus mean respondability on the other. Inaccuracy in integration statistics is negatively correlated to the magnitude of integration and, is, therefore, lower at higher integration magnitudes. Inaccuracy in mean evolvability and in mean respondability, on the other hand, is positively correlated to the magnitude of integration and is, therefore, higher at lower integration magnitudes. In other words, certain statistics are most accurately estimated in the exact same conditions as other statistics are most inaccurately estimated. Since information about integration magnitudes can rarely be known a priori, researchers should take into account both scenarios (low and high integration) when using our R code to make sample size recommendations.

Sample size recommendations

Given what is currently known as the upper and lower boundaries of integration magnitudes, our results suggest that a sample size of 108 individuals is adequate to meet the 0.05 cutoff for inaccuracy for all statistics explored here between 10-20 traits. Importantly, though the absolute number of individuals required to meet the cutoff generally increases given a larger number of traits for all statistics, the relative sampling effort (N_IndividualsN_Traits) goes down considerably as the number of traits increases. The overall reduction of this relative sampling effort as the number of traits increases is particularly interesting as it’s driven by a drastic increase in both bias and imprecision, given a reduction in the number of traits.

There is wide variation in the number of individuals required to meet this criterion for the statistics explored here given differences in magnitudes of integration and the number of traits (Fig. 6). The 108 individuals mentioned above is driven by the mean r² statistic given a matrix of 20 traits with a low parameter value for r²(=0.05). It is important to note that this r² value is exactly what was found for the cranial traits of modern humans and bats in recent analyses (Marroig et al. 2009; Porto et al. 2013), making the case that such values can potentially be found in empirical analyses. Mean flexibility seems to require a particularly low number of individuals, but this is also the statistic for which our models fit the worst. Caution is advised when using recommendations for mean flexibility based on the attached R code and larger sample sizes are likely warranted.

Here, r² and mean conditional evolvability emerge as the most sensitive of all statistics (as seen by their high multipliers, Fig. 6). Most of the time, these statistics can be used as reference for sampling effort, meaning that as long as they are well estimated, other statistics should be too.

Larger context and general conclusions

Studies that use multivariate data to provide information about evolvability and integration of populations rely on accurate estimates of trait covariance. So far, little attention has been paid to how sensitive these summary statistics are to changes in sampling effort. Overall, the results of our analysis suggest that small sample sizes lead to inadequate, even if unbiased, estimates of population covariance, and this can lead to inaccurate and biased estimates of evolvability and integration statistics. Importantly, our results also suggest that one can predict the amount of inaccuracy that would be expected for these statistics, given a sampling design, and here we provide researchers with tools to allow for an a priori assessment of inaccuracy and thus formulate the best sampling designs for their research questions.