Hierarchical Models for Multiple, Rare Outcomes Using Massive Observational Healthcare Databases

Abstract

Clinical trials often lack power to identify rare adverse drug events (ADEs) and therefore cannot address the threat rare ADEs pose, motivating the need for new ADE detection techniques. Emerging national patient claims and electronic health record databases have inspired post-approval early detection methods like the Bayesian self-controlled case series (BSCCS) regression model. Existing BSCCS models do not account for multiple outcomes, where pathology may be shared across different ADEs. We integrate a pathology hierarchy into the BSCCS model by developing a novel informative hierarchical prior linking outcome-specific effects. Considering shared pathology drastically increases the dimensionality of the already massive models in this field. We develop an efficient method for coping with the dimensionality expansion by reducing the hierarchical model to a form amenable to existing tools. Through a synthetic study we demonstrate decreased bias in risk estimates for drugs when using conditions with different true risk and unequal prevalence. We also examine observational data from the MarketScan Lab Results dataset, exposing the bias that results from aggregating outcomes, as previously employed to estimate risk trends of warfarin and dabigatran for intracranial hemorrhage and gastrointestinal bleeding. We further investigate the limits of our approach by using extremely rare conditions. This research demonstrates that analyzing multiple outcomes simultaneously is feasible at scale and beneficial.

I. Introduction

Adverse drug events (ADEs) pose a serious public health risk. While clinical trials remain the gold standard for evaluating drug safety and efficacy, the emergence of massive healthcare repositories, in the form of longitudinal observational databases (LODs), introduces a novel resource for asking and answering drug safety questions. These databases contain insurance claims and electronic medical records, with time-stamped patient data that include drug exposures and diagnoses. The scale of these datasets is remarkable, with hundreds to thousands of observations on tens of millions of patients. These resources can potentially support post-approval surveillance for ADEs, where we can monitor the relative safety of drugs after they are clinically available. The development of a common data model (CDM) for LODs through the Observational Medical Outcomes Partnership (OMOP) experiment facilitates statistical methods implementation using these data to address pertinent questions about health practices, including comparative drug safety [Overhage et al., 2012]. The OMOP experiment has demonstrated the value and efficacy of competing analytical approaches [Stang et al., 2010]. While observational studies may be vulnerable to variability of study design, and the OMOP community produced the first steps toward systematic statistical evaluation of observational evidence [Madigan et al., 2014].

Commensurate with its considerable promise, analysis of LODs presents a significant statistical and computational challenge. Patients have different levels of illness and compliance that are not readily identifiable from the LODs. Observations are incomplete and inhomogeneous over time. In addition, the scale of the data creates a massive, but extremely sparse, resource. Not only are LODs massive in the number of patients recorded, they also contain the full spectrum of medical products, interventions, and diagnoses. This scale precludes many analytic approaches.

ADEs are clinical manifestations of specific pathologies. For example, hypocoagulability affects the entire body, creating a general increased risk of bleeding. However, the clinician will identify the results of hypocoagulability by the anatomic location where a bleeding event occurs. If the bleeding occurs in the brain, the diagnosis will be an intracranial hemorrhage. If the bleeding occurs in the stomach, the diagnosis will be a gastric hemorrhage. The clinician will identify the outcome but may not identify the pathology. The drug-specific effect often occurs at the level of the pathology, but the identified ADEs appear at finer granularity. Connecting outcomes and drugs without considering shared pathology ignores a crucial component of the pathophysiology.

Currently, most analytical approaches consider one outcome at a time, ignoring relationships among the outcomes. In particular, we miss an opportunity to "borrow strength" [DuMouchel, 2012] across outcomes where there is shared pathophysiology. Dealing with multiple ADE outcomes remains of critical importance to epidemiology and data mining [Thuraisingham et al., 2009, DuMouchel, 2012]. DuMouchel [2012] and Crooks et al. [2012] approach this problem by borrowing strength across outcomes to construct a multivariate logistic regression.

A common method for avoiding multiple outcomes is aggregating all the outcomes of interest into one overarching category, essentially considering different outcomes as exchangeable. Selecting which outcomes are related often follows directly from how clinicians codify diseases. For example, the International Classification of Diseases version 9 (ICD-9) code 432 represents “other and unspecified intracranial hemorrhage," of which 432.1 “subdural hemorrhage" is a subtype. Using all 432.* ICD-9 codes would capture all the subtypes of “other and unspecified intracranial hemorrhage" the ICD-9 considers, essentially aggregating all subtypes under the 432 code. The OMOP Standard Vocabulary encompasses multiple disease relationship representations, including the Systematized Nomenclature of Medicine-Clinical Terms (SNOMED-CT) vocabulary. However, determining which outcomes are related by shared pathology need not be limited to disease codes; the discretion of a clinical expert should guide their selection.

Aggregating outcomes produces drug risk estimates that reflect a weighted average of the risk for each outcome separately. This may introduce bias into outcome-specific risks. Prevalence differences underscore this bias, with high prevalence outcomes driving risk estimates. When considering outcomes with low prevalence, we would like to combine information about them with closely related common outcomes. However, aggregating these rare outcomes with common ones overwhelms the drug-outcome specific relationship. Therefore, we would like a way to treat similar outcomes as distinct while still respecting their relatedness.

In this paper we move beyond focusing on one outcome at a time. Specifically, we seek to reduce the bias that arises when we aggregate multiple, related outcomes into one synthetic outcome. To do this, we develop a set of open-source statistical tools relying on LODs structured according to the OMOP common data model. We integrate a hierarchy of pathology and outcomes into ADE detection.

II. The SCCS Model

I. SCCS Framework

The most common approaches to analyzing outcomes from LODs include cohort, case-control, and case-crossover methods [Maclure, 1991, Rothman et al., 2008]. However, other approaches have gained popularity in recent years. Farrington [1995] proposes the self-controlled case series (SCCS) method in order to estimate the relative incidence of rare drug-specific outcomes to assess vaccine safety. Simpson et al. [2013] and Suchard et al. [2013] use this model successfully in ADE detection. A significant benefit of the SCCS model is that it reduces the sample size to exposed patients experiencing at least one adverse event. Adverse event risk is a function of drug-specific effects and patient-specific risks, including underlying conditions. However, we are only interested in the drug-specific effects, and the SCCS model allows us to focus our statistical power on estimating these covariates of interest. These benefits make the SCCS model ideal for pharmacovigilance. A major limitation of the SCCS remains its formulation around one outcome at a time, a situation we will rectify by splicing our hierarchical model into an SCCS framework.

The SCCS model assumes that ADEs arise according to an inhomogeneous Poisson process. For a given LOD, let P count the number of outcome types we are considering, and let p = 1, …, P index these outcomes. For a given drug j, let Q_j equal the number of outcomes where at least one patient who has that outcome consumed that drug. Let j_p = 1, …, J_p index the drugs where there is at least one exposure to a patient with outcome p, such that J₁, …, J_P count the total number of drugs observed in the exposure set for each outcome. Parameters β = (β₁, …, β_P)′ where β_p = (β_p1, …, β_pJp)′ measure the instantaneous, unknown, log relative risks given exposure for each drug with respect to each outcome. Under the model, let patient i = 1, …, N for outcome p = 1, …, P have a baseline risk e^ϕ_ip. We consider drug eras as intervals of exposure over which the drugs a patient takes remains constant. Let the drug exposures multiplicatively modulate the underlying instantaneous event intensity λ_ikp during constant drug exposure era k.

We consider drug eras as intervals of exposure over which the drugs a patient takes remain constant. This aspect of the OMOP CDM requires special attention. We use the OMOP CDM 4 definition of a drug era. A drug era is a combination of individual drug exposures, such as individual prescription fills. For example, if the same medication is refilled routinely at the end of its 30 day supply for 3 refills, this appears as a single 90 day drug era. Our constant eras are intervals of time where patients remain on the same combination of medication. For example, consider a patient who takes drug A from July 5, 2009 through July 20, 2009 and drug B from July 10, 2009 to July 17, 2009. Three distinct drug eras emerge: one era from July 5 to July 9; another from July 10 to July 17; and the last era from July 18 to July 20.

Let K_ip be the total number of drug eras for person i in condition p. Following the notation of Suchard et al. [2013] and Simpson et al. [2013], the intensity arises as ${\lambda }_{ikp}=e^{{\varphi }_{ip}+{\mathbf{x}}_{ikp}^{\prime }{\mathit{\beta }}_p}$, where x_ikp = (x_ikp1, …, x_ikpJp)′ and x_ikpj indicates exposure to drug j in era k for outcome p. The exposure duration for exposure era k of patient i is l_ikp. The number of ADEs in era k of patient i for outcome p is y_ikp ~ Poisson(l_ikp × λ_ikp). The SCCS method conditions on the total number of events for a particular outcome n_ip = ∑_k y_ikp that a patient experiences over her total observation period. For multiple outcomes, (n_i1, …, n_ip) remain sufficient statistics for the subject’s baseline risks (ϕ_i1, …, ϕ_ip). By conditioning on these statistics, the baseline risks fall out of the conditional likelihood of the data regardless of their correlation and hence greatly reduce the number of parameters to estimate:

$$\prod _{i=1}^N\prod _{p=1}^{P}P(y_{ip}|x_{ip},n_{ip})=\prod _{i=1}^N\prod _{p=1}^P\frac{P(y_{ip}|x_{ip})}{(n_{ip}|x_{ip})}\propto \prod _{i=1}^N\prod _{p=1}^P\prod _k^{K_{ip}}{\left(\frac{e^{{\mathbf{x}}_{ikp}^{\prime }{\mathit{\beta }}_p}}{{\sum }_{k\prime }^{K_{ip}}{l}_{ik\prime p}{e}^{{\mathbf{x}}_{ik\prime p}^{\prime }{\mathit{\beta }}_p}}\right)}^{y_{ikp}}.$$ (1)

Taking the log of Equation (1) yields the log-likelihood under our model

$$L(\mathit{\beta })=\sum _{n=1}^N\left\{\sum _{p=1}^P\right[\sum _{k=1}^{K_{ip}}\left(y_{ikp}{\mathbf{x}}_{ikp}^{\prime }{\mathit{\beta }}_p\right)-n_{ip}\text{ log }\left(\sum _{k=1}^{K_{ip}}{l}_{ikp}{e}^{{\mathbf{x}}_{ikp}^{\prime }{\mathit{\beta }}_p}\right)\left]\right\}$$

that forms only part of our objective function of interest. Specifically we work in a Bayesian framework and choose to specify a prior distribution for the covariates.

Bayesian techniques are ideal for pharmacovigilance, succinctly capturing clinical prior knowledge of drug safety, and are common in the field, as seen in Curtis et al. [2008], Madigan et al. [2011]. Furthermore, the Bayesian approach mitigates many of the challenges of massive sparse data. Simpson et al. [2013] reduce overfitting under a maximum likelihood approach by assuming a prior over the drug effect parameter vector, constructing a Bayesian SCCS. We assume a priori that most drugs are safe and therefore assume a prior that shrinks the parameter estimates toward 0.

II. Disease Hierarchies

To analyze a group of related outcomes, we follow DuMouchel [2012] in framing our approach as a hierarchical multivariate regression, where the specific outcomes are related under their shared pathology. Each adverse event has a separate representation of each shared drug, a drug-outcome effect estimate. We rely on our Bayesian perspective and project that idea onto multiple ADE outcomes by extending our prior.

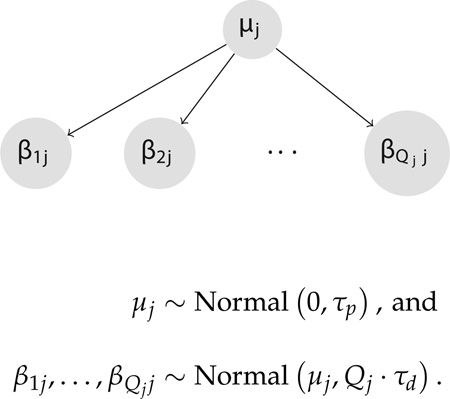
In the original Bayesian SCCS formulation applied to LODs, there can exist upwards of J_p ~ 10, 000 drug covariates. Multiple outcomes exacerbate this extreme dimensionality. Namely, we need to compute $ℐ={\sum }_{p=1}^P{J}_p$ covariates, roughly P-fold more covariates. To cope with this ultra high dimensionality, we model the effects of the same drug across outcomes hierarchically. We represent each drug-outcome effect as inheriting from a drug-pathology effect. We extend the prior structure of the original Bayesian SCCS model by using a hierarchical prior that shares information across regression coefficients (β_1j, …, β_Qjj) that measure the association of a single drug j across all Q_j outcomes where drug j appears in the records. The drug-level precision is τ_d, and the pathology-level precision is τ_p.

Not all drugs need be present across all outcomes. Therefore, we scale the prior precision for each drug by the number of outcomes in which the drug appears as a non-zero covariate. For example, if drug A appears among the patients with intracranial hemorrhage and gastric hemorrhage, while drug B appears only among patients with gastric hemorrhage, we seek to compensate for this mismatch by scaling the universal drug-level precision when approaching each outcome specific risk estimate. Specifically, we model

$${\mu }_j~\text{Normal }(0,{\tau }_p),\text{ and}$$ (2)

$${\beta }_{1j},\dots ,{\beta }_{Q_{j}j}~\text{Normal }({\mu }_j,Q_j·{\tau }_d).$$

III. Computational Swindle

As described, the hierarchical model imposes greater dimensionality, a more cumbersome log-likelihood, and a host of new parameters to track, suggesting that we will require new inference equipment that scales for LODs. However, a redefinition of parameters demonstrates that our more complex model easily compresses into a form that allows for inference with the existing high performance SCCS tools of Suchard et al. [2013]. We concatenate outcome specific event counts vectors ỹ = (y₁, y₂, …, y_P)′ and time of exposure vectors l̃ = (l₁, l₂, …, l_P) into new vectors representing the adverse events and exposure times across all outcomes.

In practice, we take our data, a set of event counts and drug exposures, for each outcome and add an outcome-specific tag to each of the drug exposures. That is, each drug exposure now has an associated outcome. For example, if we look at bleeding events, with outcomes intracranial hemorrhage and gastric hemorrhage, and drug warfarin, a covariate would be warfarin-intracranial hemorrhage or warfarin-gastric hemorrhage. Considering β̃ = (β₁, β₂, …, β_P), covariates for the same event are consecutive. We construct a new design matrix X̃,

$$\tilde{\mathit{X}}=\left[\begin{array}{cccc}\hfill {\mathit{X}}_1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathit{X}}_2\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill {\mathit{X}}_P\hfill \end{array}\right].$$

This design matrix is necessarily block diagonal, since the outcome-specific covariates are not represented in other outcomes. For example, the warfarin-intracranial hemorrhage covariate is not present among the data on patients who have gastric hemorrhage events. Given this structure, the resulting log-likelihood is

$$L(\mathit{\beta })=\sum _{i=1}^N[\sum _{k=1}^{{𝒦}_i}({ỹ}_{ik}{\tilde{\mathbf{x}}}_{ik}^{\prime }\tilde{\mathit{\beta }})-n_i\text{log }(\sum _{k=1}^{{𝒦}_i}{\tilde{l}}_{ik}{e}^{{\tilde{\mathbf{x}}}_{ik}^{\prime }\tilde{\mathit{\beta }}}\left)\right].$$ (3)

Under this reindexed representation, log-likelihood (3) matches the expression in Suchard et al. [2013], enabling us to recycle existing computational infrastructure. Furthermore, each X_p is extremely sparse, and the computational approach of Suchard et al. [2013] efficiently represents and computes over sparse systems. While creating X̃ increases the dimensionality, it is a sparse expansion, mitigating the computational demand. Thus, we can leverage the extant sparse computing solutions to evaluate this more sophisticated model, without drastically increasing the computational demand.

IV. Maximum A Posteriori Estimation using Cyclic Coordinate Descent

Given the reformulation, the changes to the univariate Bayesian SCCS framework remain in the prior. For notation, we consider the set G_j of covariates representing the same drug across all conditions we consider. The cardinality of G_j is Q_j. Let G_j{p} be this set excluding β_pj. We consider the induced prior distribution,

$$p({\beta }_{G_j})=\int p({\beta }_{G_j}|{\mu }_j)p({\mu }_j)\mathrm{d}{\mu }_j.$$ (4)

Taking the log of the integrand and recalling that all coefficients are independent given the pathology effect yields:

$$\text{log }[p({\mu }_j)]+\text{log }[p({\beta }_{G_j}|{\mu }_j)]=[f_1({\tau }_p)-\frac{{\tau }_p}{2}{({\mu }_j-0)}^2]+[f_2({\tau }_d)-\frac{Q_j{\tau }_d}{2}\sum _{g\in G_j}{({\beta }_g-{\mu }_j)}^2]=f_3({\tau }_p,{\tau }_d)-\frac{{\tau }_p}{2}{({\mu }_j-0)}^2-\frac{Q_j{\tau }_d}{2}\sum _{g\in G_j}{({\beta }_g-{\mu }_j)}^2=f_3({\tau }_p,{\tau }_d)-\frac{1}{2}[(Q_j^2{\tau }_d+{\tau }_p){\mu }_j^2-2Q_j{\tau }_d{\mu }_j\sum _{g\in G_j}{\beta }_g+Q_j{\tau }_d\sum _{g\in G_j}{\beta }_g^2].$$

In this construction, f₁(τ_p), f₂(τ_d), and f₃(τ_p, τ_d) are constants with respect to μ_j and G_j employed to simplify notation.

Completing the square to perform the integral returns

$$\text{log }[p({\beta }_{G_j})]=f_4({\tau }_p,{\tau }_d)-\frac{1}{2}[Q_j{\tau }_d(\sum _{g\in G_j}{\beta }_g^2)-\frac{{(Q_j{\tau }_d\sum _{g\in G_j}{\beta }_g)}^2}{Q_j^2{\tau }_d+{\tau }_p}],$$ (5)

where f₄(τ_p, τ_d) is a constant with respect to μ_j and G_j that remains after integrating over μ_j.

The implementation of Suchard et al. [2013] uses cyclic coordinate descent (CCD) to find the maximum a posteriori (MAP) estimates through optimizing the model log posterior P(β) = L(β) + log[p(β)]. Our approach amounts to regularized regression, for which CCD has been heavily employed [Friedman et al., 2010, Wu and Lange, 2013]. CCD circumvents the need to invert the full Hessian at each step [Wu et al., 2009]. At each CCD iteration, the updates are a function of the log-likelihood gradient ∂L/∂β_pj and Hessian ${\partial }^{2}L/\partial {\beta }_{pj}^2$ as well as the penalty gradient ∂log[p(β)]/∂β_pj and Hessian ${\partial }^2\text{log}[p(\mathit{\beta })]/\partial {\beta }_{pj}^2$. A single Newton step is taken along each coordinate and proves extremely efficient when X is sparse [Genkin et al., 2009, Suchard et al., 2013].

Working in the CCD framework, we require the gradient and the Hessian contributions to the log-likelihood and log-priors. Fortunately, the log-likelihood remains unchanged using our computational swindle. However, the penalty component does change under the hierarchical model, with both the gradient and the Hessian a function of the pathology precision. The forms of the penalty components in the Newton steps are

$$\frac{\partial \text{log}(p({\beta }_{pj}|{\beta }_{G_{j\{p\}}}))}{\partial {\beta }_{pj}}=-Q_j{\tau }_d{\beta }_{pj}+\frac{{(Q_j{\tau }_d)}^2({\sum }_{g\in G_j}{\beta }_g)}{Q_j^2{\tau }_d+{\tau }_p}\text{and}$$ (6)

$$\frac{{\partial }^2\text{log}(p({\beta }_{pj}|{\beta }_{G_{j\{p\}}})}{\partial {{\beta }_{pj}}^2}=-Q_j{\tau }_d+\frac{{(Q_j{\tau }_d)}^2}{Q_j^2{\tau }_d+{\tau }_p}.$$

V. Hyperparameter Selection

We use cross-validation based on the predictive log-likelihood of the hold-out set to select the hyperparameters τ_p and τ_d. Suchard et al. [2013] use a log-scale grid search that is computationally expensive even with only a single parameter. When we add a second parameter, this method becomes impractically slow. The additional parameter τ_p increases overall computing cost by an order of magnitude. However, it remains desirable to use cross-validation to select both τ_d and τ_p.

To help overcome this burden, we turn to Genkin et al. [2009] in implementing an "autosearch" for hyperparameter selection. We start with an initial guess and then increase or decrease our guess by one log unit until we have bracketed the maximum of the hold-out set predicted log-likelihood. Then we compute a quadratic approximation to the predicted log-likelihood. The maximum of this approximate surface becomes our estimate. To find both hyperparameters, we alternate between them, fixing one and finding the conditional maximum of the other, and then fixing to that new conditional solution and finding the conditional maximum of the other. We continue this process until both previous and proposed hyperparameters are within an order of magnitude. We prefer using this flexible tolerance method to a fixed tolerance method, in which finding the appropriate fixed tolerance would be difficult considering the log-scale of the search space.

III. Demonstration

I. Synthetic Study: Biased Risk Estimates

To evaluate the bias that arises when using aggregated outcomes, we simulate a small dataset with three conditions of interest. For the first and third conditions, the prevalence of these diagnoses is extremely low, with only 20 and 10 patients having these conditions, respectively. For the second condition, the prevalence is much higher, with 1000 patients present in our hypothetical dataset. We expose these synthetic patient groups to 10 drugs. Two drugs are positively associated with all conditions. However, the risk for these two drugs varies drastically among the three groups. In particular, the two dangerous drugs present a log relative risk of 0.5 for the first, rare condition, a log relative risk of 1 for the second common condition, and a log relative risk of 2 for the third, rare condition.

In our simulations, we first draw a patient-specific underlying risk from a Normal(−1,0.5) distribution. Then, for each patient, we uniformly select between 1 and 10 observations, or drug exposure eras, as well as an observation length per observation. In each observation, we assign between 1 and 10 drugs to the patient. For each drug, we know the log relative risk for the given event. Armed with the underlying risk rate as well as the drugs per observation, we compute the overall risk rate for each observation and draw from a Poisson distribution with that intensity to get the event count during that observation.

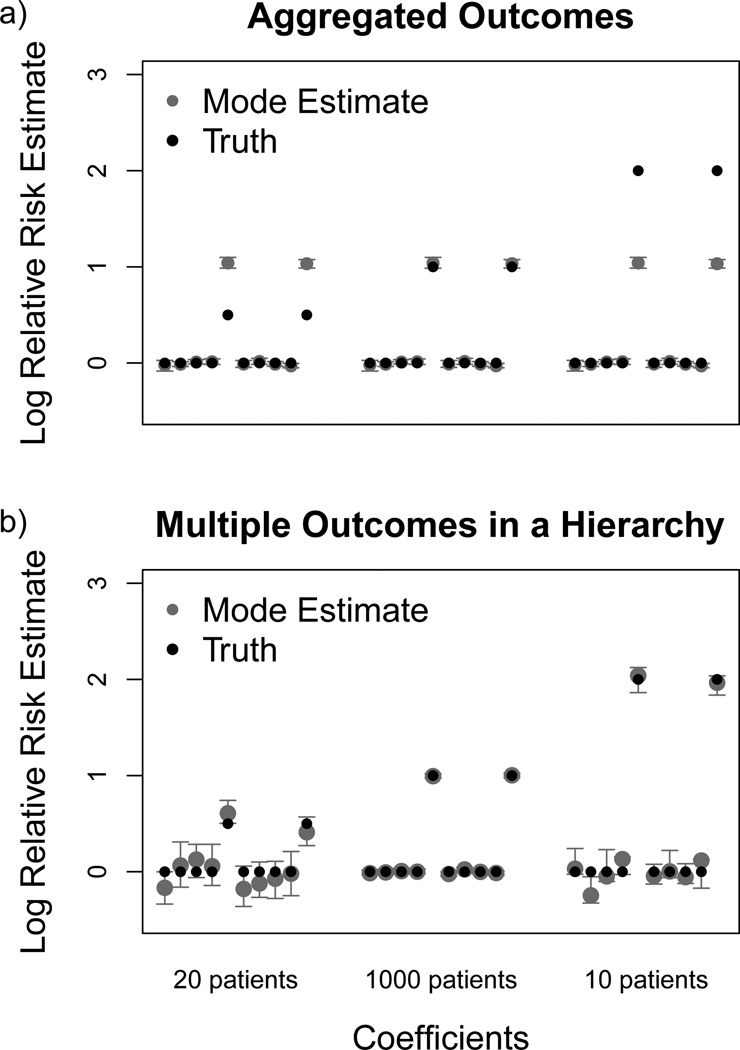
We compare the marginal estimates of the relative risks in both the aggregated data situation and using our hierarchical model. We first run our analysis considering all conditions exchangeable, extracting one risk estimate per drug. Effectively, when we aggregate data, the log relative risk among these three populations becomes a weighted average risk estimate. In Figure (1 a) we see that the analysis of the aggregated data slightly underestimates the log relative risk of the dangerous drugs in the large population. In the 20 patient and 10 patient populations, the method seriously overestimates and underestimates, respectively, the log relative risk of the dangerous drugs. In contrast, the estimates from modeling these outcomes together under a hierarchical structure avoid this problem. Separate risk estimates for each drug-outcome pairs demonstrate much less bias, as seen in Figure (1 b).

Figure 1.

Mode estimates and 95% bootstrap confidence intervals (gray) of the log relative risk for each drug and their simulated relative risk (black) across two conditions with different prevalence. The first 10 covariates represent the estimates from one condition with a prevalence of 20 patients; the second 10 represent estimates from the condition with high prevalence, affecting 1000 patients; and the last 10 covariates represent a second condition with low prevalence, affecting 10 patients. Using the multiple outcomes in an aggregated approach (a) produces less appropriate estimates than the hierarchical outcomes approach (b).

We compare the model fitting times for each of these datasets, including cross-validation and bootstrapping with 200 replicates. For the cross-validation, we averaged the predicted log-likelihood over 6 permutations of the 10-fold sampling of the data. Fitting the aggregated dataset took 5 seconds, and the cross-validation variance was 0.1. Using the autosearch cross-validation method, fitting the hierarchical model took 9 seconds. We also fit the model using the grid search cross-validation method. Specifically, we used a 10 by 10 grid ranging from 10⁻⁴ to 10⁵ for both ${\tau }_p^{-1}$ and ${\tau }_d^{-1}$. Using this grid, fitting the model took 32 seconds. The results from the autosearch, with starting estimates of 100, produced estimates of ${\tau }_p^{-1}$ and ${\tau }_d^{-1}$ at 1.1 and 2.2; the results from the grid search produced estimates of ${\tau }_p^{-1}$ and ${\tau }_d^{-1}$ at 100 and 1.

The difference between the estimates for ${\tau }_p^{-1}$ from the autosearch method and the grid-search method is noteworthy. The autosearch method finds a value beyond a grid point of 100. This results from two effects. First, both the autosearch and grid-search estimates may be sensitive to fitting parameter choices, like the number of permutations over which to average. This reflects the relatively flat topology of the predictive log-likelihood in this small dataset, where chance selections of data for cross-validation can move our perceived apex. We remedy this partly by averaging over multiple data permutations. Second, this difference underscores the inability of the grid method to adjust resolution as needed. The grid-search method is bound by our decision of grid size. Resolving the method using a finer grid is computationally daunting. The autosearch method avoids this problem, adjusting resolution as needed without the computational tax. However, the difference we see between the search methods in this case fails to appreciably change the estimated relative risks, with no risk estimates changing by more than 0.015. This result highlights the stability of our risk estimates to different hyperprior estimates.

II. Real World Study: Warfarin and Dabigatran

The standard for outpatient anticoagulation is warfarin, an inhibitor of vitamin K metabolism. Clinically, warfarin is difficult to use, requiring frequent laboratory tests to identify its sensitive, patient-specific dosing. Alternatives to warfarin present an opportunity for improving anticoagulation care. In 2009, a randomized, controlled, noninferiority trial suggested that dabigatran etexilate has a comparable treatment effect to warfarin [Connolly et al., 2009]. Furthermore, the manufacturer claims that dabigatran requires less clinical attention than warfarin to find the appropriate dose. Although this trial also found grossly similar risk profiles for dabigatran and warfarin, there were notable differences. In particular, warfarin posed a greater overall risk of major bleeding. However, dabigatran posed a significantly elevated risk of gastrointestinal hemorrhage (GIH). Among the worst outcomes for patients on anticoagulation therapy with warfarin is intracranial hemorrhage (ICH). The rate of this ADE among dabigatran patients was one third that of warfarin patients. Thus, for one ADE, dabigatran appears to increase risk; for another, it appears to be safer. Many concerns about this trial have surfaced [Charlton and Redberg, 2014]. New events of interest from the trial emerged later [Connolly et al., 2010]. Reilly et al. [2014] produced better dose-risk trade-off results. Subsequent clinical trials have reexamined the risk of major bleeding events. The results of these trials are equally inconclusive, with greater transfusion needs among dabigatran treated patients counterbalanced by lower intensive care stay and lower mortality [Majeed et al., 2013].

We contribute to this debate by considering a real world equivalent of the simulated study above. We want to use our hierarchical model to tease out the risk profiles for both warfarin and dabigatran while reflecting the shared pathology of bleeding events. Thus, we consider each of these outcomes under our hierarchical model. Furthermore, we explore what would happen if we aggregated these data, considering GIH and ICH exchangeable.

To perform these studies, we examine the MarketScan Lab Results (MSLR) dataset, maintained by the Reagan-Udall Foundation Innovation in Medical Evidence Development and Surveillance project. This dataset comprises 1.5 million patient lives. We depend on the OMOP common data model version 4 for representation of concepts of interest. To examine GIH and ICH, we select all patients who experienced a diagnosis that the OMOP common data model version 4 considered a subset of GIH or ICH. There are 37,909 patients who had GIH and 2,893 patients who had ICH.

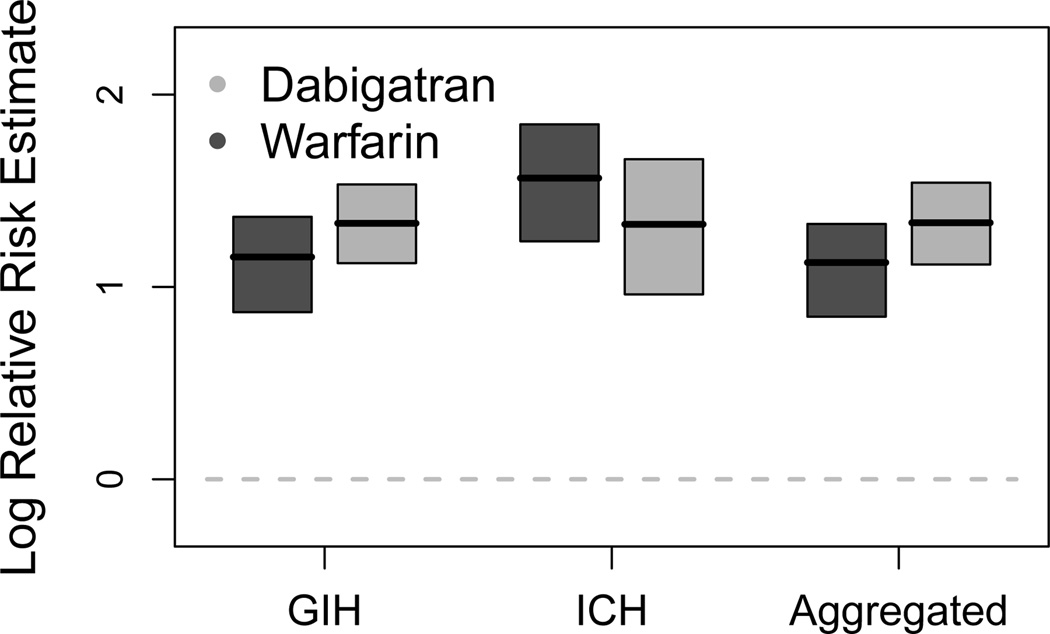
Figure (2) demonstrates our results. Grossly, three trends appear. First, we see that warfarin presents a lower risk for GIH than dabigatran. Second, this risk pattern reverses for ICH. This replicates trends previously found in the literature. Third, we see that considering these outcomes as exchangeable seriously masks the ICH estimates. The larger population of GIH patients overwhelms the analysis.

Figure 2.

Mode estimates and 95% bootstrap confidence intervals for the effect of dabigatran (light gray) and warfarin (dark gray) on gastrointestinal hemorrhage (GIH) and intracranial hemorrhage (ICH), compared to an aggregated outcome where GIH and ICH are exchangeable.

We again consider the computation time for each analysis, including cross-validation and bootstrapping. We used 200 replicates for the bootstrapping and averaged over 20 permutations of the cross-validation sampling data. Analyzing the GIH and ICH datasets independently took 124 and 9 seconds producing single variance estimates of 5.28 and 29.06 using one dimensional autosearch with a starting value of 0.1. Analyzing the aggregated dataset using one dimensional autosearch required 111 seconds and produced a single variance estimate of 1.1. Under the hierarchical model, the 10 by 10 log grid-search approach with a range of 10⁻³ to 10⁶ took 4735 seconds and produced estimates of ${\tau }_p^{-1}$ and ${\tau }_d^{-1}$ of 1 and 0.1. Using the two dimensional autosearch approach with an initial value of 0.001 took 2163 seconds and produced estimates of ${\tau }_p^{-1}$ and ${\tau }_d^{-1}$ of 4.15 and 0.18.

III. Real World Study: Extreme Prevalence Differences

In some cases, we want to evaluate the risk of extremely rare events, which may contain very little information about each drug risk pair. To explore what happens in this situation, we return to the MarketScan Lab Results (MSLR) dataset. Specifically we focus on two conditions: chronic gastrojejunal ulcer with hemorrhage and obstruction (CGJUHO) and vomiting blood (VB). Both of these diagnoses inherit from the OMOP common data model version 4 representation of upper gastrointestinal bleeding. We produce risk estimates from modeling these two categories as exchangeable, and we contrast our results when treating these two categories hierarchically. To construct our patient population, we select all patients who have had either of those diagnoses delivered in an inpatient, emergency department, or outpatient setting. There are only 24 patients with CGJUHO; there are 16,062 patients with VB. We consider the entire spectrum of drugs for both conditions.

Using 10-fold cross-validation with the predictive log likelihood averaged over two permutations and the one dimensional autosearch with an initial value of 0.1, analyzing the CGJUHO data alone produces a single prior variance estimate of 0.060 in 4 seconds, and analyzing the VB data produces a single prior variance estimate of 0.0076 in 200 seconds. The aggregated model required 200 seconds to find the point estimates, with a variance estimate of 0.0077. Under the hierarchical model, using a 10 by 10 log-scale grid of variance values ranging from 10⁻⁸ to 10¹, we find ${\tau }_p^{-1}$ and ${\tau }_d^{-1}$ maximize the predicted log-likelihood at 0.01 and 0.0001, respectively. Using the autosearch method, we find the optimal ${\tau }_p^{-1}$ and ${\tau }_d^{-1}$ to be 0.019 and 0.00017, respectively. The autosearch required 10,500 seconds; the grid search required 209,500 seconds.

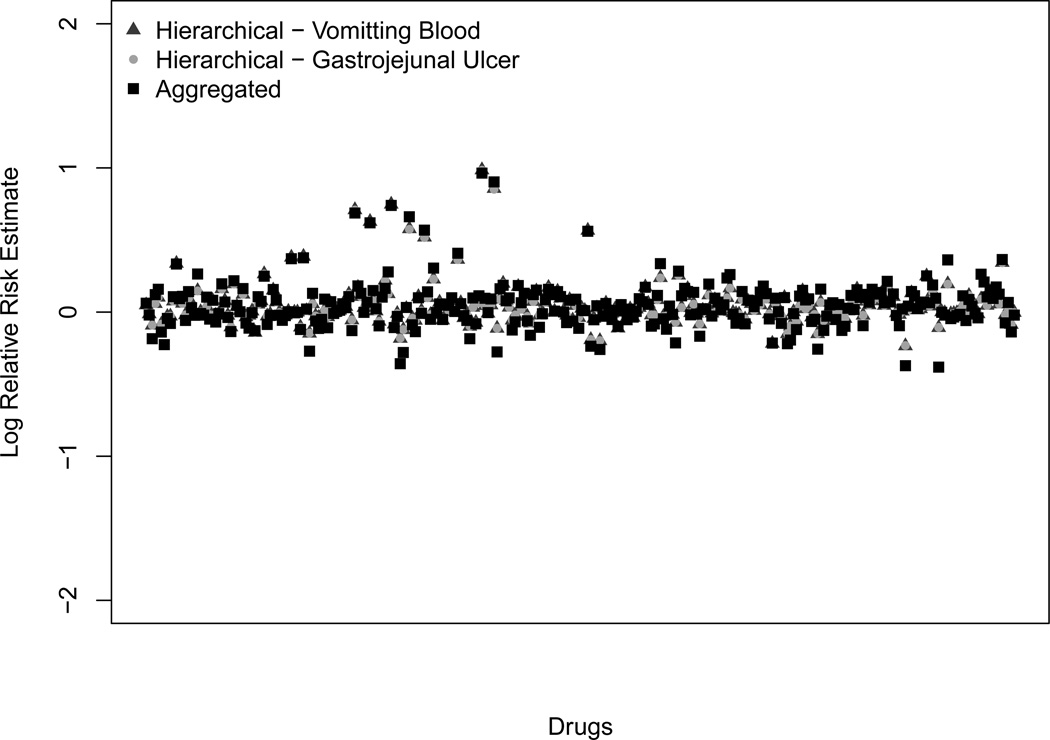
Although we consider all drugs for each condition of interest, it is most interesting to look at the drugs that are present among both the set of patients with CGJUHO and the set of patients with VB. The 288 drugs that fit this criterion have non-trivial hierarchies. From Figure (3), we see that under the hierarchical model, the condition-specific risk estimates are very close. Furthermore, the estimates under the hierarchical model are very close to those under the aggregated model.

Figure 3.

Mode estimates of the log relative risk for each drug for a common, rare, or aggregated outcome. The common outcome is vomiting blood (VB), dark gray triangles. The rare outcome is chronic gastrojejunal ulcer with hemorrhage and obstruction (CGJUHO), light gray circles. The aggregated outcome is CGJUHO or VB, black squares. The estimates for CGJUHO and VB rely on the hierarchical structure.

Ostensibly, this result undercuts the purpose of the hierarchical modeling. However, there are notable differences between this study and both the previous simulated study and the warfarin and dabigatran study. In this case, CGJUHO had drastically fewer patients than VB. Given the stark contrast in prevalences, it is reasonable for the very common condition to dominate the risk estimates of both the hierarchical and aggregated models. This suggests that the hierarchical model will correct for risk estimate bias as long as the prevalence differences between two conditions are not extreme. But, in the case of extreme prevalence differences, the results will be similar to aggregating the data. While the greedy iterative two dimensional autosearch approach greatly reduces computational time relative to the exhaustive search, it is still faster to compute a single hyperprior. Therefore, the differences in prevalence should guide the user in determining whether using the hierarchical model is warranted in her analysis.

IV. Discussion

In this work, we have developed a novel hierarchical framework for analyzing multiple outcomes in the setting of massive observational data. We have demonstrated that we can easily restructure this framework to leverage extant inference tools that mitigate the dimensional explosion of analyzing multiple outcomes. Furthermore, we have shown the value of such a framework in better discrimination of dangerous drugs and in better risk identification in small populations.

There are challenges in working with observational data [Ryan, 2013]. Inter-database variation in reported risk estimates can be considerable [Madigan et al., 2013]. Bias in the recording of the data percolates through all analyses. Assumptions regarding the uniformity of treatment and diagnosis decisions among physicians are almost certainly incorrect. The time-invariant risk assumption underlying the SCCS model is almost certainly false for some drug and disease pairs.

However, the quantity of data from observational healthcare datasets will not decrease, and the promise of these data remains strong. One hope for success in this field is to channel the information present in these databases into a framework that optimally allows for signal detection and noise reduction. One method for achieving this goal effectively is to integrate more biological and medical knowledge into the models. The simple hierarchical model of disease, which matches both disease biology and clinical perspectives of disease, is one modest example of such structural knowledge motivating advances in modeling.

In the future, hierarchical modeling can extend beyond diseases. Drugs also follow a natural hierarchical structure. Physicians and pharmacologists use drug classification heavily to group medications with similar modes of action together. These classification systems form a natural framework for understanding drug risk. The post-approval withdrawal of Vioxx (rofecoxib) has been one of the highest profile cases of a drug with insidious side effects. The medical community did not fully appreciate the cardiac effects of rofecoxib until after the drug had been released to the market. It is thought that the entire class of COX-2 inhibitors puts patients at risk for cardiovascular events [Cannon and Cannon, 2012]. While traditional NSAIDs inhibit COX-1 and COX-2, COX-2 selective inhibitors have negligible effects on COX-1. One could consider the hierarchical structure of the drugs following a similar model as suggested here. Each of the drugs could inherit a class-specific risk. For example, all of the COX-2 inhibitors would share a greater risk for MI than the COX-1 inhibitors. This would allow the model to capture class specific effects that are currently inefficiently estimated independently.