Abstract
Based on a fully coupled computational model for esophageal transport, we analyzed the role of the mucosa (including the submucosa) in esophageal bolus transport and how bolus transport is affected by mucosal stiffness. Two groups of studies were conducted using a computational model. In the first group, a base case that represents normal esophageal transport and two hypothetical cases were simulated: 1) esophageal mucosa replaced by muscle and 2) esophagus without mucosa. For the base case, the geometric configuration of the esophageal wall was examined and the mechanical role of mucosa was analyzed. For the hypothetical cases, the pressure field and transport features were examined. In the second group of studies, cases with mucosa of varying stiffness were simulated. Overall transport characteristics were examined and both pressure and geometry were analyzed. Results show that a compliant mucosa helped accommodate the incoming bolus and lubricate the moving bolus. Bolus transport was marginally achieved without mucosa or with mucosa replaced by muscle. A stiff mucosa greatly impaired bolus transport due to lowered esophageal distensibility and increased luminal pressure. We conclude that mucosa is essential for normal esophageal transport function. Mechanically stiffened mucosa reduces the distensibility of the esophagus by obstructing luminal opening and bolus transport. Mucosal stiffening may be relevant in diseases characterized by reduced esophageal distensibility, elevated intra-bolus pressure, and/or hypertensive muscle contraction such as eosinophilic esophagitis and jackhammer esophagus.
Keywords: Esophageal mucosa, Fibrosis, Dysphagia, Esophageal transport
1 Introduction
The primary function of the esophagus is bolus transport from pharynx to stomach, a function dependent on the mechanical-physiological properties of its multilayered wall consisting of longitudinal muscle (LM), circular muscle (CM), submucosa and mucosa. The active and passive properties of the muscular layers have been relatively well studied (Nicosia and Brasseur 2002; Jung et al 2004; Ghosh et al 2005; Mittal et al 2006; Brasseur et al 2007; Zhao et al 2007; Kou et al 2015a). However, the submucosa and mucosa, here collectively called mucosa, has been the object of relatively little research relating to bolus transport. Most studies of the mucosa relate to changes in its permeability as a defense mechanism against intraluminal acidity (Sarosiek and McCallum 2000; Orlando 2006), and biomechanical studies mainly focused on its geometry and material properties from in-vitro tests (Gregersen et al 2000; Yang et al 2006a,b, 2007; Zhao et al 2007; Natali et al 2009; Stavropoulou et al 2009; Li et al 2011a). The mucosa is generally modeled as an anisotropic elastic material, but presumably due to the complexity of biological tissues and of in-vitro testing, the reported material properties vary substantially among studies (Yang et al 2006a; Zhao et al 2007; Natali et al 2009; Stavropoulou et al 2009). Mucosal folding, which probably originates from residual stress in the esophageal wall, has also attracted substantial interest among researchers (Gregersen et al 2000; Yang et al 2007; Li et al 2011a,b). Residual stress is evident experimentally when tissue rings are cut radially and allowed to open up into sectors as the stress is relieved (Gregersen et al 2000). Both mucosal folding and residual stress are hypothesized to result from active contraction, tissue growth, or inflammation, each with distinct physiological implications (Yang et al 2007; Li et al 2011a). Despite the above research efforts, the role of the mucosa in esophageal bolus transport remains essentially unstudied. Our first aim was to address that issue. In addition, recent studies utilizing high-resolution impedance planimetry have found esophageal distensibility to be an important determinant of dysphagia in patients with eosinophilic esophagitis (EoE) and achalasia (Pandolfino et al 2002; Kwiatek et al 2010, 2011; Nicodeme et al 2013; Pandolfino et al 2013). Esophageal distensibility is a measurement that reflects stiffness of the esophageal wall. Hence, we hypothesized that mucosal stiffness is an important determinant of esophageal wall distensibility and increased mucosal stiffness will adversely impact bolus transport. This hypothesis was tested in the second part of this work by case studies of increased mucosal stiffness. All studies were conducted using a fully resolved computational model that we developed as explained in the following section.
2 Materials and methods
2.1 Esophageal transport model
We conducted simulations based on a fully resolved computational model of esophageal transport (Kou et al 2015a). The model integrates three essential aspects (liquid-like bolus, esophageal wall, and muscle activation) into a single simulation and is therefore capable of fully resolving interactions among the three. The model has been validated (Kou et al 2015a) and used to study the role of muscle activation in esophageal transport (Kou et al 2015b). Hence, we provide here only a brief discussion on our computational model and refer to our previous work (Kou et al 2015a) for details.
2.1.1 Immersed boundary method
Our esophageal transport model was developed based on the immersed boundary (IB) method. The IB method is both a mathematical formulation and a numerical method that was initially introduced to handle fluid-structure interactions (Peskin 1972, 1977). The IB method uses an Eulerian description of the momentum and incompressibility of the coupled fluid-structure system, and a Lagrangian description of the structural forces produced by the passive elasticity and active tension. Following the conversion, we let x = (x, y, z) ⊂ U denote fixed Cartesian coordinates, in which U ⊂ ℝ3 denotes the fixed domain occupied by the entire fluid-structure system. We let s = (s1, s2, s3) ⊂ Ω denote the Lagrangian coordinates attached to the immersed structure, in which Ω ⊂ ℝ3 denotes the immersed structure. For simplicity, we consider that the fluid-structure system possesses a uniform mass density ρ and dynamic viscosity μ. This simplification implies that the immersed structure is neutrally buoyant and viscoelastic rather than purely elastic. Then the equations of motion of the coupled fluid-structure system used in the IB method are (Peskin 2002),
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
Eqs. (1) and (2) are the incompressible Navier-Stokes equations. u(x, t) is the Eulerian velocity, p(x, t) is the pressure, and g(x, t) is the Eulerian elastic force density. Eq. (5) represents the material model of the immersed structure that computes G(s, t), the Lagrangian elastic force density, based on the current configuration. The material model is described by a time-dependent functional, 𝒢 : X ⟼ G. Eqs. (3) and (4) are interaction equations that transfer information between the Lagrangian and Eulerian systems via Dirac delta function kernel δ(x) = δ(x)δ(y)δ(z). Specifically, eq. (3) converts the Lagrangian force density G(s, t) into an equivalent Eulerian force density g(x, t), and eq. (4) determines the physical velocity of each Lagrangian material point from the Eulerian velocity field, thereby effectively imposing the no-slip condition along the fluid-solid inter-face. More discussions on those equations can be found in the literature, such as (Peskin 2002).
2.1.2 Problem setup
In our esophageal transport model, the immersed structure was a multiple-layered tubular esophagus that was immersed into a fluid box (see Figure 6 in (Kou et al 2015a)). The esophageal top end was anchored in place to consider the constraints of the upper esophageal sphincter, and its lower end was free to move. The esophagus was 18-cm long, consistent with clinical data (Meyer et al 1986). The thickness of each esophageal layer was calculated based on clinical data (Puckett et al 2005). Initially, the proximal esophageal section was distended by a swallowed liquid bolus. Distal to the bolus, the esophageal wall was at rest with a thin liquid film lining the lumen. The specific problem we were trying to simulate is: How is the bolus transported to the distal esophagus after muscle activation wave is initiated?
2.1.3 Material models
The bolus was modeled as a Newtonian fluid with a viscosity of 10 centipoise and a volume of about 1ml. This is within the range of properties used in clinical studies (Dantas et al 1990). The multiple-layered esophagus was modeled as an immersed structure with additional structural forces from the passive elasticity and activate tension. The modeled esophageal wall was composed by mucosal, CM and LM layers. Experiments show that the mucosal layer is composed by collagen fibrils and connective tissue (Natali et al 2009). The CM and LM layers consist of circumferentially and longitudinally oriented muscle fibers, respectively (Gilbert et al 2008). Correspondingly, we modeled each layer as a 3D axially-circumferentially-radially arranged fiber networks. Those fibers could assume an elastic force when subjected to tension, compression or bending. Thus the material elasticity of each esophageal layer could be characterized by the summation of a stretching strain-energy functional, Es[X(·, t)], and a bending strain-energy functional, Eb[X(·, t)]. Consequently, the specified form of the mapping function 𝒢 : X ⟼ G in eq. (5) could be given as below,
| (6) |
| (7) |
E = E[X(·, t)] is the total strain-energy functional. ℘E[X(·, t)] is the Fréchet derivative of E, in which ℘ denotes the perturbation of a quantity. To facilitate the characterization of stretching and bending energy of each esophageal layer, the fiber-based structure was further discretized into families of two-node spring segments and three-node beam segments. Details on the discretization can be found in our previous work (Kou et al 2015a).
Besides the passive elasticity, both the CM and LM layers also have active tension resulting from muscle activation, referred to as the CM contraction and LM shortening, respectively. The CM contraction involves the sequential contraction and relaxation of circumferentially oriented muscle fibers in the CM layer, whereas the LM shortening involves the sequential contraction (i.e. shortening) and relaxation of longitudinally oriented muscle fibers in the LM layer. These two types of muscle activation occur in almost perfect synchrony based on experimental studies (Pouderoux et al 1997; Nicosia et al 2001; Mittal et al 2006). We modeled the muscle fiber contraction and relaxation by dynamically changing the rest lengths of the corresponding muscle fibers in the corresponding muscle layer. We mimicked the neurally-controlled muscle contraction wave by specifying a sequential wave of changing fiber rest lengths. The technical details can be found in our previous work (Kou et al 2015a). An application study on roles of each type of muscle activation and the impact of their dis-coordination has been reported in our work (Kou et al 2015b). In this work, we conducted cases studies to understand the role of esophageal mucosa.
2.2 Methods for case studies
An important determinant of esophageal transport is the tissue property of the esophageal wall. In the computational model, we modeled the mucosa, CM, and LM layers as fiber networks. The stiffness (or compliance) of each layer was characterized by the modulus of the fiber network. To understand the influence of esophageal mucosa on esophageal transport, two groups of studies were conducted. In Group 1, a base case that represents normal esophageal transport and two hypothetical cases were simulated: one with the mucosal layer replaced by an active muscle layer and one with no mucosal layer. In the normal case or base case we used the same mucosal stiffness and muscle activation model as in our previous work (Kou et al 2015b). In Group 2, cases with mucosa of varying stiffness were simulated. Overall transport characteristics were examined and both pressure and geometry were analyzed.
All cases were simulated using IBAMR (Griffith et al 2007) software which is a parallelized code to simulate large systems involving fluid-structure interactions. For each case, we solved 100,000 time steps to advance the simulation of bolus transport by 2 seconds in physical time. The solution of each time step involved several million variables in both the fluid and the structure (i.e. the multi-layered esophagus). As the computational cost is very high, Northwestern University supercomputer, Quest, was used. Running each case on Quest needed 72 processors and took around 100 hours to finish. For studies involving varying mucosal stiffness, we simulated cases where the mucosal layer was 10, 100, and 1000 times stiffer than the normal case. Table 1 specifies moduli of mucosal layer fibers used in each simulation.
Table 1.
Values used for the modulus of the 3D mucosal fiber network in simulations of normal and increased mucosal stiffness.
| Modulus (KPa) |
Base case |
Case 1 (10×) |
Case 2 (100×) |
Case 3 (1000×) |
|---|---|---|---|---|
| Circumferential fibers | 0.004 | 0.04 | 0.4 | 4 |
| Radial fibers | 0.004 | 0.04 | 0.4 | 4 |
| Axial fibers | 0.04 | 0.4 | 4 | 40 |
3 Results
3.1 Group 1 cases
3.1.1 Normal esophagus
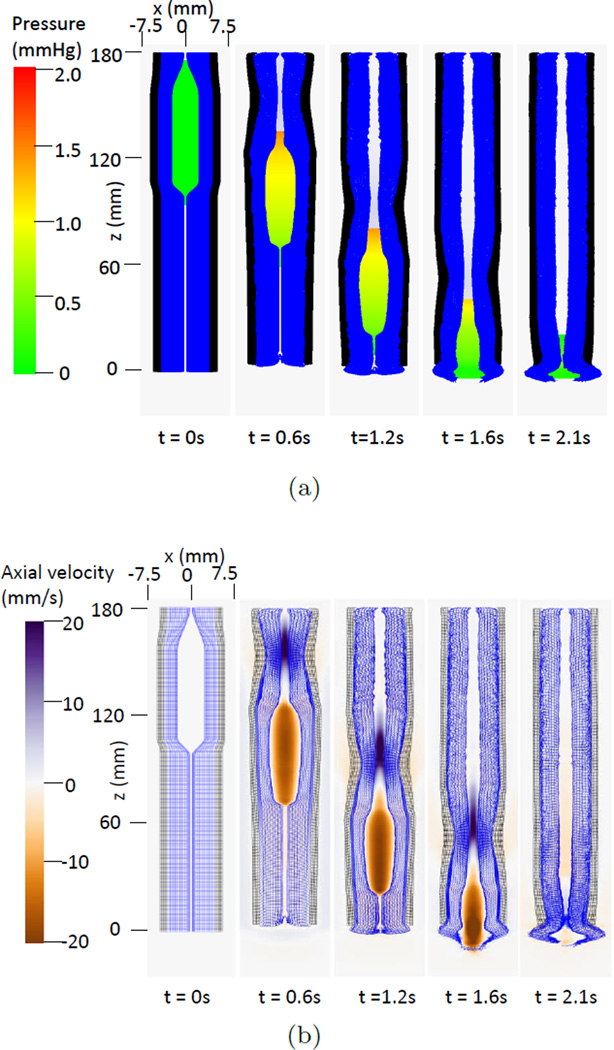
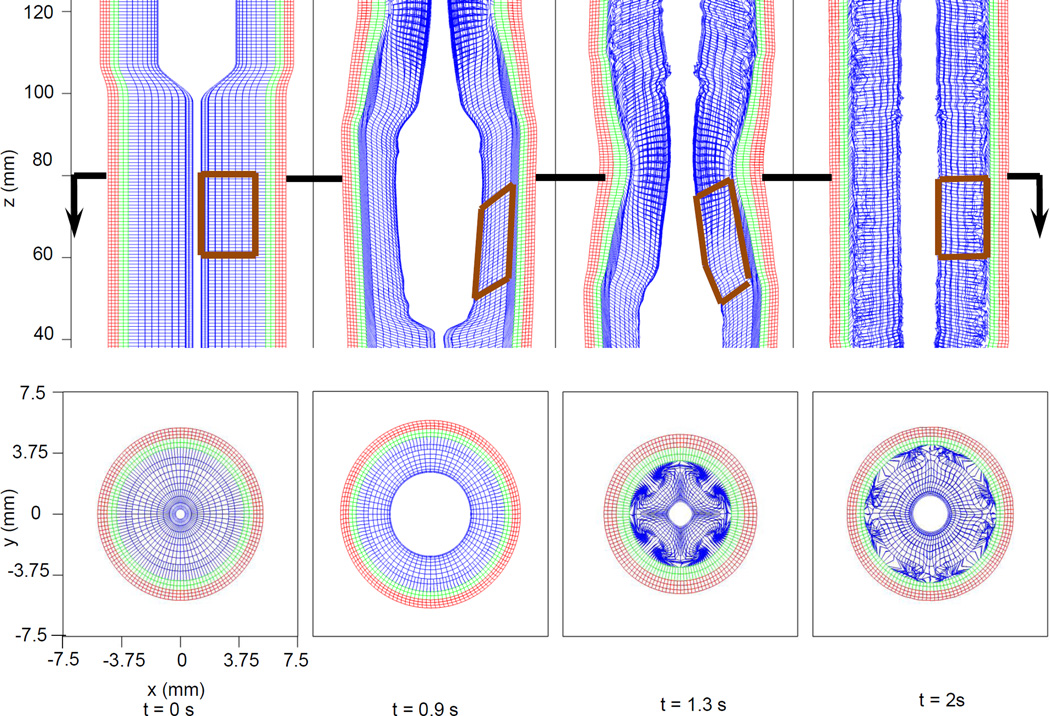
Fig. 1(a) and Fig. 1(b) depicts pressure and axial velocity during bolus transport in the base case (i.e. the case reported in our previous work (Kou et al 2015b)). Pressure generated by muscle activation propelled the bolus through the esophagus. Fig. 2 shows details of the deformation of the esophageal wall during bolus transport. Four distinctive states of a representative esophageal segment were observed: rest, dilatation, contraction, and relaxation. Although the muscle layer generated the active force from neurally-controlled muscle fiber contraction, the mucosal layer showed greatest deformation. Specifically, the mucosal layer underwent substantial distention to accommodate the incoming bolus. Subsequently, during muscle contraction, the mucosa was squeezed causing buckling in the cross-sectional plane. Fig. 2 (Upper) also shows pronounced axial displacement of the mucosa which is evident from the elongation of the segment of the mucosa outlined by the brown polygon. This suggests that axial movement of the mucosal layer lubricates the moving bolus.
Fig. 1.
Overall features of esophageal transport plotted in the plane y=0 (i.e. x-z plane) at different times for the base case. In the 3D model, the z axis represents the axial direction and the x and y axes represent the two orthogonal lateral directions. The esophageal wall is colored as a two-layered wall for better visualization. The outer layer denotes the CM and LM layers and is colored black; the inner layer denotes the mucosa and is colored blue. (a) The pressure field. (b) The axial velocity.
Fig. 2.
Kinematics of the esophageal layers at four different stages: at rest (t=0 s); at dilatation (t=0.9 s); at contraction (t=1.3 s); and at relaxation (t=2 s) for the base case. Blue, green and red mesh from the inside to the outside, denote the mucosal, CM and LM layers, respectively. (Upper) Side view of an esophageal section in the plane y=0 mm. The brown closed polygons illustrate the displacement of a mucosal segment over time. (Lower) Cross-sectional view of a section of the esophagus in the plane z=80 mm, indicated by the arrow in the upper panel.
3.1.2 Hypothetical cases with mucosa replaced by muscle or removed
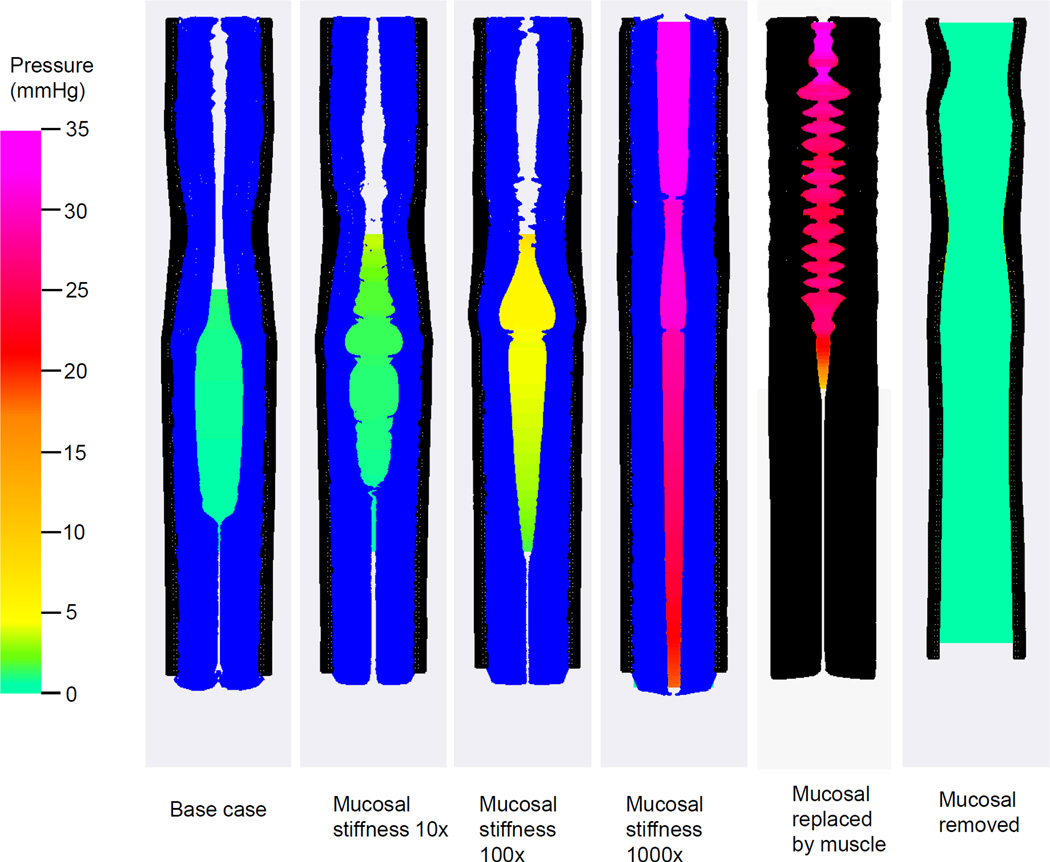
The two rightmost plots in Fig. 3 show two hypothetical cases. In the first hypothetical case, the mucosal layer was replaced by an active muscle layer. Bolus transport failed because the esophageal lumen was too stiff to accommodate the bolus. This was also evident from the greatly increased intrabolus pressure. In the second hypothetical case, in which the mucosal layer was totally removed, bolus transport failed because the lumen was wide-open. The axial velocity of the bolus was found to be minimal.
Fig. 3.
Intraluminal pressure field with the deformed esophageal wall in the plane y = 0 (i.e. x-z plane) for modeled cases. From the left to the right, the first four cases and the last case are plotted at time =0.9 s. The fifth case (i,e, the case with mucosal replaced by muscle) is plotted at time 0.1 s, as this case failed to run longer. The esophageal wall is colored with black depicting the CM and LM layers and blue depicting the mucosal layer.
3.2 Group 2 cases
3.2.1 Influence of mucosal stiffness (or compliance) on bolus transport
Fig. 3 illustrates bolus transport for cases with increasing mucosal stiffness. It was found that with increasing mucosal stiffness there was a rapid increase in intrabolus pressure and irregularity in the shape of the mucosa. This culminated in increasingly inefficient transport of the bolus compared to the normal case.
3.2.2 Mechanistic analysis of all cases
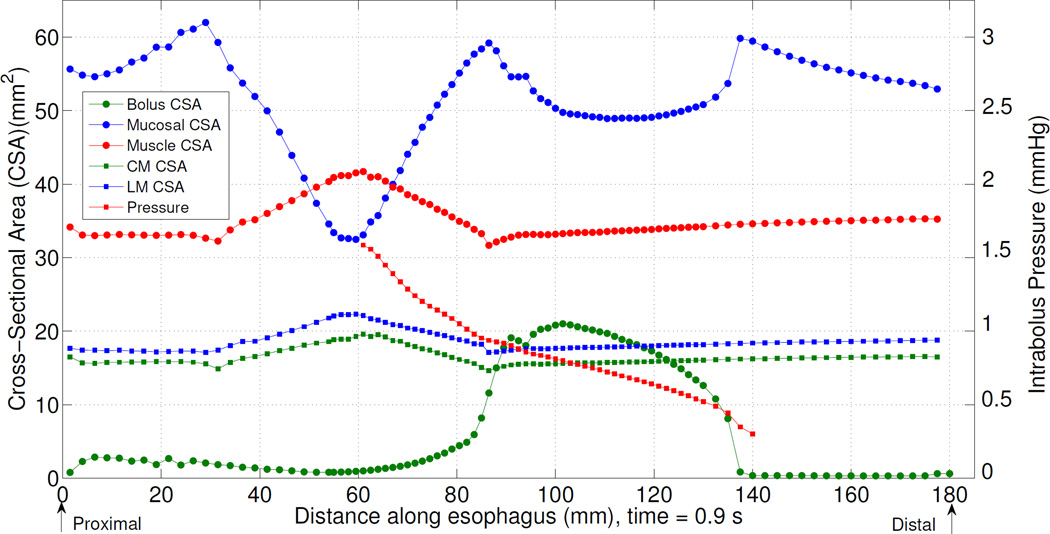
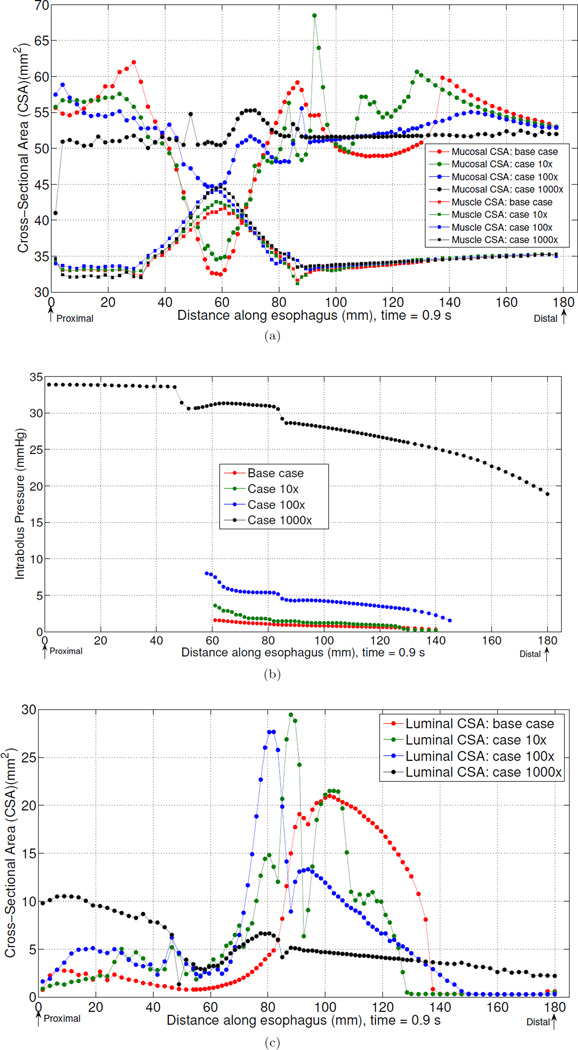
Fig. 2 and Fig. 3 highlight mucosal deformation as an essential aspect of normal esophageal bolus transport. Fig. 4 illustrates the interrelationship between mucosal deformation, muscle activation, and bolus disposition along the esophagus at time t = 0.9 s in the base case. Mucosal cross-sectional area (CSA) and thickness decreased in two regions: 1) the contracting region (i.e. the region with peak muscle contraction) and 2) the bolus region (i.e. the region where bolus CSA is greatest). The decrease in the first region was synchronized with muscle contraction as evidenced by the presence of an intrabolus pressure peak. The decrease in the second region was due to luminal dilatation because the lumen needs space to accommodate the incoming bolus. Note that during normal bolus transit the intrabolus pressure was relatively low. As noted above, Fig. 3 demonstrates that increased mucosal stiffness resulted in compromised bolus transit. Fig. 5(a) suggests that a possible mediator of that effect was diminished mucosal deformation caused by increased mucosal stiffness. Note that there was virtually no change in muscle CSA when the mucosal stiffness was progressively increased. However, there was progressive reduction, and finally elimination, of mucosal deformation. Fig. 5(b) depicts intrabolus pressure while Fig. 5(c) shows bolus CSA and consequently bolus disposition at time 0.9 s. Consistent with Fig. 3, it is seen that increased mucosal stiffness was associated with progressive elevation of intrabolus pressure. In extreme cases with 100× and 1000× mucosal stiffness, some or all of the bolus failed to be propelled by muscle contraction.
Fig. 4.
Intrabolus pressure and esophageal geometry for the base case at time = 0.9 s.
Fig. 5.
Mucosal and muscle CSA (a), intrabolus pressure (b), and (c) for the base case, case 10×, case 100×, case 1000× at time =0.9 s.
4 Discussion
We used a fully resolved computational model of esophageal transport to analyze the role of the esophageal mucosa and the effect of increased mucosal stiffness on esophageal transport. Our findings suggest that the mucosa plays an essential role in accommodating and lubricating the moving bolus by exhibiting the greatest deformation among all layers of the esophageal wall. In modeled cases without mucosa, with the mucosa replaced by muscle, or with very stiff mucosa, bolus transport was hardly achieved.
Based on high-resolution impedance manometry and fluoroscopy, Lin et al.(Lin et al 2014) characterized four phases of esophageal bolus transit. Phase I is esophageal accommodation, during which esophageal filling occurs with a minimal increase in intrabolus pressure. Phase II is compartmentalization during which the bolus is compartmentalized between the upper esophageal sphincter and the esophagogastric junction. For these two phases it is critical for the mucosal layer to be easily deformed by the incoming bolus. This is similar to the dilatation state during peristalsis (see Fig. 2). Phase III is esophageal peristalsis that corresponds to our simulation. Phase IV represents ampullary emptying, during which the lower esophageal sphincter (LES) relaxes and the bolus is emptied from the distal esophagus into the stomach. Future studies will address the role of the mucosa during bolus emptying.
At normal physiological condition, the esophageal mucosa is very compliant compared to muscle layers; a compliant material is easily dilated or compressed. As in our simulation, a compliant mucosa is readily squeezed, axially displaced by muscle contraction, and easily dilated to accommodate the incoming bolus. On the other hand, if the mucosal layer were stiffer than the muscle layer, the mucosal layer would not exhibit this accommodation and there would be no distinct bolus region. This is seen in the panel of Fig. 3 for 1000× mucosal stiffness. High mucosal compliance is also evident in clinical studies. For example, clinical endoscopy shows that the esophageal lumen always readily opens during the procedure. High-resolution impedance manometry shows that during Phase I of bolus transit, the bolus fills the upper esophageal segment without significant increase in pressure. The ease of lumen opening and bolus filling is a function of mucosal compliance. Note that certain in-vitro tests report that esophageal mucosa is of a higher stiffness. That is probably because the in-vitro mechanical properties of esophageal mucosa, depending on the test procedure and tissue preparation, are quite different from in-vivo ones at normal physiological conditions. This might also explain why the reported in-vitro material properties vary substantially among studies (Yang et al 2006a; Zhao et al 2007; Natali et al 2009; Stavropoulou et al 2009).
Stiffening of the esophageal mucosa can impair bolus transport leading to dysfunction. The compliance of the mucosal layer likely dominates the overall distensibility of the esophagus, as the stretching is the greatest in the mucosal layer in the dilation stage. Therefore, stiffened mucosa will reduce esophageal distensibility. The expected characteristics of this abnormality would be elevated luminal pressure, a narrowly distended lumen, and an elongated bolus region. This increased resistance to bolus passage might lead to hypertensive muscle contractility and hypertrophy as seen in jackhammer esophagus. Although the cases with abnormal mucosal stiffness studied here do not represent any specific clinical scenarios, the adverse impact of esophageal mucosal stiffening demonstrated by this simulation may be relevant to mucosal changes in eosinophilic esophagitis (EoE) patients who experience dysphagia and food impactions due to diminished esophageal distensibility (Kwiatek et al 2011; Nicodeme et al 2013). It is likely that the mucosal remodeling or inflammation associated with EoE (Aceves and Ackerman 2009) might change the mechanical property of mucosa to make it stiffer. Further test on esophageal mucosal biopsy for the stiffness or fibrosis is likely valuable.
Our computational model has limitations similar to those reported in our previous work (Kou et al 2015b). First, we considered bolus transport in the supine position to rule out the influence of the gravitation. Second, we modeled a wave speed of muscle activation that is faster than what is observed in clinical studies. We did this to reduce computational expense. Third, for simplicity, we assumed that muscle tension is from the contraction of muscle fibers with the same stiffness as that in the passive state. This may under-predict the magnitude of muscle tension and luminal pressure. However, we present our results and conclusions in such a way that they do not depend on the absolute magnitude of pressure. Fourth, we modeled the mucosal- submucosal layer collectively as a combined structure for simplicity, although histologically these layers are distinct. Very likely, they have different mechanical properties requiring separate material models. In conclusion, based on a fully coupled computational model for esophageal transport, we found that mucosa plays an important role in bolus transport. A stiffened mucosa adversely impacts bolus transport. We speculate that mucosal stiffening may be relevant in diseases characterized by reduced esophageal distensibility, elevated intra-bolus pressure, and/or hypertensive muscle contraction such as EoE and jackhammer esophagus.
Acknowledgments
Funding This work was supported by Public Health Service grants DK056033 (to P.J.K) and DK079902 (to J.E.P.).
John E. Pandolfino discloses consulting and educational association with Given Imaging and Sandhill Scientific.
Footnotes
Compliance with Ethical Standards
Conflicts of Interest Wenjun Kou, Peter J. Kahrilas and Neelesh A. Patankar declare that they have no conflict of interest.
Contributor Information
Wenjun Kou, Theoretical and Applied Mechanics, Northwestern University, 2145 Sheridan Road, Evanston, Illinois 60208, USA.
John E. Pandolfino, Department of Medicine, Feinberg School of Medicine, Northwestern University, 676 North Saint Clair Street, 14th Floor, Chicago, Illinois 60611, USA
Peter J. Kahrilas, Department of Medicine, Feinberg School of Medicine, Northwestern University, 676 North Saint Clair Street, 14th Floor, Chicago, Illinois 60611, USA
Neelesh A. Patankar, Department of Mechanical Engineering, Northwestern University, 2145 Sheridan Road, Evanston, Illinois 60208, USA.
References
- Aceves SS, Ackerman SJ. Relationships between eosinophilic inflammation, tissue remodeling, and fibrosis in eosinophilic esophagitis. Immunology And Allergy Clinics of North America. 2009;29(1):197–211. xiii–xiv. doi: 10.1016/j.iac.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brasseur JG, Nicosia MA, Pal A, Miller LS. Function of longitudinal vs circular muscle fibers in esophageal peristalsis, deduced with mathematical modeling. World Joural of Gastroenterology. 2007;13(9):1335–1346. doi: 10.3748/wjg.v13.i9.1335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dantas RO, Kern MK, Massey BT, Dodds WJ, Kahrilas PJ, Brasseur JG, Cook IJ, Lang IM. Effect of swallowed bolus variables on oral and pharyngeal phases of swallowing. American Journal of Physiology-Gastrointestinal and Liver Physiology. 1990;258(5 Pt 1):G675–G681. doi: 10.1152/ajpgi.1990.258.5.G675. [DOI] [PubMed] [Google Scholar]
- Ghosh SK, Kahrilas PJ, Zaki T, Pandolfino JE, Joehl RJ, Brasseur JG. The mechanical basis of impaired esophageal emptying postfundoplication. American Journal of Physiology-Gastrointestinal and Liver Physiology. 2005;289(1):G21–G35. doi: 10.1152/ajpgi.00235.2004. [DOI] [PubMed] [Google Scholar]
- Gilbert RJ, Gaige TA, Wang R, Benner T, Dai G, Glickman JN, Wedeen VJ. Resolving the three-dimensional myoarchitecture of bovine esophageal wall with diffusion spectrum imaging and tractography. Cell and Tissue Research. 2008;332(3):461–468. doi: 10.1007/s00441-008-0601-0. [DOI] [PubMed] [Google Scholar]
- Gregersen H, Kassab GS, Fung YC. The zero-stress state of the gastrointestinal tract: biomechanical and functional implications. Digestive Diseases and Sciences. 2000;45(12):2271–2281. doi: 10.1023/a:1005649520386. [DOI] [PubMed] [Google Scholar]
- Griffith BE, Hornung RD, McQueen DM, Peskin CS. An adaptive, formally second order accurate version of the immersed boundary method. Journal of Computational Physics. 2007;223(1):10–49. [Google Scholar]
- Jung HY, Puckett JL, Bhalla V, Rojas M, Bhargava V, Liu JM, Mittal RK. Discoordination between circular and longitudinal muscle contractions in patients with high amplitude esophageal contractions. Gastroenterology. 2004;126(4):A637–A637. [Google Scholar]
- Kou W, Bhalla APS, Griffith BE, Pandolfino JE, Kahrilas PJ, Patankar NA. A fully resolved active musculo-mechanical model for esophageal transport. Journal of Computational Physics. 2015a;298:446–465. doi: 10.1016/j.jcp.2015.05.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kou W, Pandolfino JE, Kahrilas PJ, Patankar NA. Simulation studies of circular muscle contraction, longitudinal muscle shortening, and their coordination in esophageal transport. American Journal of Physiology-Gastrointestinal and Liver Physiology. 2015b;309(4):G238–G247. doi: 10.1152/ajpgi.00058.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwiatek MA, Pandolfino JE, Hirano I, Kahrilas PJ. Esophagogastric junction distensibility assessed with an endoscopic functional luminal imaging probe (endoflip) Gastrointestinal Endoscopy. 2010;72(2):272–278. doi: 10.1016/j.gie.2010.01.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwiatek MA, Hirano I, Kahrilas PJ, Rothe J, Luger D, Pandolfino JE. Mechanical properties of the esophagus in eosinophilic esophagitis. Gastroenterology. 2011;140(1):82–90. doi: 10.1053/j.gastro.2010.09.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li B, Cao YP, Feng XQ. Growth and surface folding of esophageal mucosa: a biomechanical model. Journal of Biomechanics. 2011a;44(1):182–188. doi: 10.1016/j.jbiomech.2010.09.007. [DOI] [PubMed] [Google Scholar]
- Li B, Cao YP, Feng XQ, Gao H. Surface wrinkling of mucosa induced by volumetric growth: theory, simulation and experiment. Journal of the Mechanics and Physics of Solids. 2011b;59(4):758–774. [Google Scholar]
- Lin Z, Yim B, Gawron A, Imam H, Kahrilas PJ, Pandolfino JE. The four phases of esophageal bolus transit defined by high-resolution impedance manometry and fluoroscopy. American Journal of Physiology-Gastrointestinal and Liver Physiology. 2014;307(4):G437–G444. doi: 10.1152/ajpgi.00148.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer GW, Austin RM, Brady rCE, Castell DO. Muscle anatomy of the human esophagus. Journal of Clinical Gastroenterology. 1986;8(2):131–134. doi: 10.1097/00004836-198604000-00005. [DOI] [PubMed] [Google Scholar]
- Mittal RK, Padda B, Bhalla V, Bhargava V, Liu JM. Synchrony between circular and longitudinal muscle contractions during peristalsis in normal subjects. American Journal of Physiology-Gastrointestinal and Liver Physiology. 2006;290(3):G431–G438. doi: 10.1152/ajpgi.00237.2005. [DOI] [PubMed] [Google Scholar]
- Natali AN, Carniel EL, Gregersen H. Biomechanical behaviour of oesophageal tissues: Material and structural configuration, experimental data and constitutive analysis. Medical Engineering & Physics. 2009;31(9):1056–1062. doi: 10.1016/j.medengphy.2009.07.003. [DOI] [PubMed] [Google Scholar]
- Nicodeme F, Hirano I, Chen J, Robinson K, Lin Z, Xiao Y, Gonsalves N, Kwasny MJ, Kahrilas PJ, Pandolfino JE. Esophageal distensibility as a measure of disease severity in patients with eosinophilic esophagitis. Clinical Gastroenterology and Hepatology. 2013;11(9):1101–1107. e1. doi: 10.1016/j.cgh.2013.03.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicosia MA, Brasseur JG. A mathematical model for estimating muscle tension in vivo during esophageal bolus transport. Journal of Theoretical Biology. 2002;219(2):235–255. doi: 10.1006/jtbi.2002.3118. [DOI] [PubMed] [Google Scholar]
- Nicosia MA, Brasseur JG, Liu JB, Miller LS. Local longitudinal muscle shortening of the human esophagus from high-frequency ultrasonography. American Journal of Physiology - Gastrointestinal and Liver Physiology. 2001;281(4):G1022–G1033. doi: 10.1152/ajpgi.2001.281.4.G1022. [DOI] [PubMed] [Google Scholar]
- Orlando RC. Esophageal mucosal defense mechanisms. GI Motility. 2006 online. [Google Scholar]
- Pandolfino JE, Shi G, Curry J, Joehl RJ, Brasseur JG, Kahrilas PJ. Esophagogastric junction distensibility: a factor contributing to sphincter incompetence. American Journal of Physiology - Gastrointestinal and Liver Physiology. 2002;282(6):G1052–G1058. doi: 10.1152/ajpgi.00279.2001. [DOI] [PubMed] [Google Scholar]
- Pandolfino JE, de Ruigh A, Nicodme F, Xiao Y, Boris L, Kahrilas PJ. Distensibility of the esophagogastric junction assessed with the functional lumen imaging probe (flip) in achalasia patients. Neurogastroenterology & Motility. 2013;25(6):e496–e368. doi: 10.1111/nmo.12097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peskin CS. Flow patterns around heart valves: A numerical method. Journal of Computational Physics. 1972;10(2):252–271. [Google Scholar]
- Peskin CS. Numerical analysis of blood flow in the heart. Journal of Computational Physics. 1977;25(3):220–252. [Google Scholar]
- Peskin CS. The immersed boundary method. Acta numerica. 2002;11:479–517. [Google Scholar]
- Pouderoux P, Lin S, Kahrilas PJ. Timing, propagation, coordination, and effect of esophageal shortening during peristalsis. Gastroenterology. 1997;112(4):1147–1154. doi: 10.1016/s0016-5085(97)70125-2. [DOI] [PubMed] [Google Scholar]
- Puckett JL, Bhalla V, Liu J, Kassab G, Mittal RK. Oesophageal wall stress and muscle hypertrophy in high amplitude oesophageal contractions. Neurogastroenterology & Motility. 2005;17(6):791–799. doi: 10.1111/j.1365-2982.2005.00693.x. [DOI] [PubMed] [Google Scholar]
- Sarosiek J, McCallum RW. Mechanisms of oesophageal mucosal defence. Best Practice & Research Clinical Gastroenterology. 2000;14(5):701–717. doi: 10.1053/bega.2000.0119. [DOI] [PubMed] [Google Scholar]
- Stavropoulou EA, Dafalias YF, Sokolis DP. Biomechanical and histological characteristics of passive esophagus: Experimental investigation and comparative constitutive modeling. Journal of Biomechanics. 2009;42(16):2654–2663. doi: 10.1016/j.jbiomech.2009.08.018. [DOI] [PubMed] [Google Scholar]
- Yang W, Fung TC, Chian KS, Chong CK. 3D mechanical properties of the layered esophagus: experiment and constitutive model. Journal of Biomechanical Engineering. 2006a;128(6):899–908. doi: 10.1115/1.2354206. [DOI] [PubMed] [Google Scholar]
- Yang W, Fung TC, Chian KS, Chong CK. Directional, regional, and layer variations of mechanical properties of esophageal tissue and its interpretation using a structure-based constitutive model. Journal of Biomechanical Engineering. 2006b;128(3):409–418. doi: 10.1115/1.2187033. [DOI] [PubMed] [Google Scholar]
- Yang W, Fung TC, Chian KS, Chong CK. Instability of the two-layered thick-walled esophageal model under the external pressure and circular outer boundary condition. Journal of Biomechanics. 2007;40(3):481–490. doi: 10.1016/j.jbiomech.2006.02.020. [DOI] [PubMed] [Google Scholar]
- Zhao J, Jorgensen CS, Liao D, Gregersen H. Dimensions and circumferential stress-strain relation in the porcine esophagus in vitro determined by combined impedance planimetry and high-frequency ultrasound. Digestive Diseases and Sciences. 2007;52(5):1338–1344. doi: 10.1007/s10620-006-9238-6. [DOI] [PubMed] [Google Scholar]