The Choice of a Constitutive Formulation for Modeling Limb Flexion-Induced Deformations and Stresses in the Human Femoropopliteal Arteries of Different Ages

Abstract

Open and endovascular treatments for Peripheral Arterial Disease are notorious for high failure rates. Severe mechanical deformations experienced by the femoropopliteal artery (FPA) during limb flexion and interactions between the artery and repair materials play important roles and may contribute to poor clinical outcomes. Computational modeling can help optimize FPA repair, but these simulations heavily depend on the choice of constitutive model describing the arterial behavior. In this study Finite Element model of the FPA in the standing (straight) and gardening (acutely bent) postures was built using Computed Tomography data, longitudinal pre-stretch and biaxially determined mechanical properties. Springs and dashpots were used to represent surrounding tissue forces associated with limb flexion-induced deformations. These forces were then used with age-specific longitudinal pre-stretch and mechanical properties to obtain deformed FPA configurations for seven age groups. Four commonly used invariant-based constitutive models were compared to determine the accuracy of capturing deformations and stresses in each age group. The four-fiber FPA model most accurately portrayed arterial behavior in all ages, but in subjects younger than 40 years, the performance of all constitutive formulations was similar. In older subjects, Demiray (Delfino) and classic two-fiber Holzapfel-Gasser-Ogden formulations were better than the Neo-Hookean model for predicting deformations due to limb flexion, but both significantly overestimated principal stresses compared to the FPA or Neo-Hookean models.

1. INTRODUCTION

Atherosclerotic obstruction of the femoropopliteal artery (FPA) that reduces blood flow to the lower limbs (Peripheral Artery Disease, PAD) is a major contributor to morbidity, mortality and impairment in quality of life (Mahoney et al. 2010). Per-patient costs of PAD treatment are higher than those for coronary artery and cerebrovascular diseases (Mahoney et al. 2008) primarily due to high numbers of failed interventions that require repetitive treatment (Adam et al. 2005; Schillinger et al. 2006; Conte et al. 2006; Schillinger et al. 2007). Within just two years, hemodynamically significant restenosis develops in 27% of patients treated with a bypass (Siracuse et al. 2012), and in more than 45% of patients treated with angioplasty and stenting. This can lead to re-intervention in almost half of the treated patients (Schillinger et al. 2007).

Though exact reasons for poor clinical results in this arterial bed are not completely clear, deformations of the FPA during limb flexion and extension have been suggested to play a significant role (Ansari et al. 2013). The FPA undergoes severe bending, twisting and compression, challenging repair materials and devices to function at their limits. Furthermore, inability of certain materials and device designs to accommodate these deformations can lead to arterial injury, deleterious cellular and biochemical responses, culminating in restenosis and reconstruction failure.

Patient-specific computational modeling can help select the appropriate repair material or device for a specific segment of the FPA that experiences certain range of deformations. However, these simulations heavily depend on constitutive models used to describe arterial behavior. Recent experimental work (Kamenskiy et al. 2014b; Kamenskiy et al. 2015; Kamenskiy et al. 2016a) using the Holzapfel-Gasser-Ogden (HGO) model expanded (Baek et al. 2007) to account for longitudinal elastin and circumferential smooth muscle cells, demonstrated accurate portrayal of passive elastic FPA properties in different age groups. However, the model has eight constitutive parameters that need to be determined from extensive multi-ratio biaxial tests, preferably using non-parametric bootstrapping to assess uniqueness. Though theoretically possible, use of this complex model in conjunction with in vivo pressure-diameter data obtained in clinical environments is challenging due to the risk of overparameterization.

Other constitutive models with less parameters, such as the four-parameter classic HGO (Holzapfel et al. 2000), two-parameter Demiray (Delfino) (Delfino 1996), or a single-parameter Neo-Hookean formulation could potentially be used with less extensive experimental datasets, but their performance to describe the behavior of the FPA under limb flexion-induced deformations has not been evaluated. Furthermore, since the anisotropy of the FPA changes with age (Kamenskiy et al. 2015), this investigation should be performed for FPAs in different age groups. The goal of this work was to perform such analysis and determine which of the commonly used constitutive formulations adequately describe the complex FPA behavior under limb flexion-induced deformations.

2. METHODS

2.1 Characterization of limb flexion-induced FPA deformations in a lightly embalmed cadaver

Custom-made retrievable nitinol markers were deployed under fluoroscopic guidance into the FPA of a lightly embalmed human cadaver (89 year-old male) through a suprainguinal retroperitoneal approach without disturbing the surrounding tissues (MacTaggart et al. 2014). Use of lightly embalmed cadaver as opposed to fully embalmed, allowed better preservation of natural tissue properties (Wadman et al. 2010),(MacTaggart et al. 2014). Computerized Tomography (CT) images were acquired with the limb in the straight (180°, standing) and acutely bent (60°, gardening) postures with 0.625mm axial resolution. Image segmentation and analysis allowed comparison of the relative spatial locations of each intra-arterial marker to determine limb flexion-induced deformations (MacTaggart et al. 2014). Coordinates of the arterial centerline and marker positions were extracted for both straight and bent limb postures.

2.2 In situ longitudinal pre-stretch and mechanical properties of the FPA

After CT imaging, the FPA was retrieved for in situ pre-stretch measurement and mechanical characterization. In addition to testing the FPA from the lightly embalmed cadaver, fresh FPA properties and in situ pre-stretch were obtained from n=351 human tissue donors 13-82 years old (Kamenskiy et al. 2015; Kamenskiy et al. 2016a). The in situ pre-stretch was measured using an umbilical tape. The tape and the artery were cut together and while the umbilical tape maintained its length, the artery shortened due to in situ longitudinal pre-stretch ${\lambda }_z^{\text{in situ}}$. This pre-stretch was then defined as the ratio of the umbilical tape length to the excised artery length.

Mechanical characterization was performed with planar biaxial extension (Kamenskiy et al. 2014a; Kamenskiy et al. 2014b; Kamenskiy et al. 2015) using CellScale biotester. Twenty-one stretch-controlled protocols ranging from 1:1 to 1:0.01 ratios on each axis were executed at 0.01s⁻¹ strain rate and used to determine constitutive parameters for the models described below using non-parametric bootstrapping (Ferruzzi et al. 2011) with Levenberg-Marquardt minimization. Constitutive parameters were determined for seven age groups (11-20, 21-30, 31-40, 41-50, 51-60, 61-70, 71-80 years old). Details of mechanical testing and derivation of age group-specific mechanical properties for the human FPA are provided elsewhere (Kamenskiy et al. 2016b).

2.3 Constitutive models

Four invariant-based constitutive formulations for the FPA wall were compared. Neo-Hookean model was the simplest of all four describing the mechanical properties with a linear function of a single parameter. Demiray (Delfino) (Demiray et al. 1988; Delfino 1996) model accounted for the exponential stiffening and included two parameters yet assumed isotropic response. Classic two-fiber family HGO (Holzapfel et al. 2000) model had four parameters and accounted for both non-linearity and anisotropy. The FPA model was an expanded version of the HGO to include four fiber directions (Baek et al. 2007), and included eight parameters accounting for the isotropic contribution of ground substance, longitudinally oriented elastin, circumferential smooth muscle cells, and two families of collagen fibers as suggested by the FPA intramural structure (Kamenskiy et al. 2015; Kamenskiy et al. 2016a).

The Neo-Hookean model was chosen in the form (1). A single constitutive parameter C₁₀ is equal to half of the initial shear modulus: C₁₀ = C₀/2.

$$U=C_{10}({\stackrel{‒}{I}}_1-3)+\frac{1}{D_1}{(J-1)}^2$$ (1)

where ${\stackrel{‒}{I}}_1$ the first strain invariant, and J is a determinant of the deformation gradient tensor. Here and below bar denotes deviatoric portion of the tensor.

Demiray (Delfino) model was chosen in the form (2), where a > 0 is a stress-like material parameter and b > 0 is a non-dimensional material parameter.

$$U=\frac{a}{b}\left\{\mathrm{ex}p\left[\frac{b}{2}({\stackrel{‒}{I}}_1-3)\right]-1\right\}+\frac{1}{D_1}{(J-1)}^2$$ (2)

The classic two-fiber HGO model and the four-fiber FPA model were considered in the forms (3) and (4), respectively, without taking into account fiber dispersion. C₀ is the initial shear modulus of the isotropic ground substance, $C_1^i$ > 0 is a stress-like material parameter for the i^th fiber family, $C_2^i$ is a dimensionless material parameter for the i^th fiber family, and $I_4^i$ is a fourth invariant, equal to the square of the stretch in the i^th fiber direction $I_4^i={\mathbf{M}}^i{\left(\mathit{C}{\mathbf{M}}^i\right)}^2={\lambda }_i{\left({\mathbf{M}}^{\mathbf{i}}\right)}^2$. Mⁱ is a unit vector of the i^th fiber direction in the reference configuration, making an angle γⁱ with the longitudinal direction. C denotes the right Cauchy-Green tensor. In the case of two-fiber HGO model, fibers were assumed to represent collagen that is symmetric about the longitudinal axis with angle γ³ = −γ⁴ = γ. Collagen fibers were assumed to be mechanically equivalent such that parameters $C_1^3=C_1^4=C_1^{\mathit{col}}$ and $C_2^3=C_2^4=C_2^{\mathit{col}}$.

In the case of the four-fiber FPA model, we follow fiber notations representing histological FPA structure (Kamenskiy et al. 2016a). Those include elastin oriented longitudinally (γ¹ = 0) with $C_{1,2}^1=C_{1,2}^{\mathit{el}}$; smooth muscle cells oriented circumferentially (γ² = π/2) with $C_{1,2}^2=C_{1,2}^{\mathit{smc}}$; and two families of collagen fibers oriented helically at angles γ³ = −γ⁴ = γ to the longitudinal direction with $C_1^3=C_1^4=C_1^{\mathit{col}}$ and $C_2^3=C_2^4=C_2^{\mathit{col}}$ similar to the HGO model.

$$U=\frac{C_0}{2}({\stackrel{‒}{I}}_1-3)+\frac{1}{D_1}\left(\frac{J^2-1}{2}-\ln J\right)+\frac{c_1^{\mathit{col}}}{2c_2^{\mathit{col}}}{\Sigma }_{i=3,4}\left\{\exp \left[c_2^{\mathit{col}}{(I_4^i-1)}^2\right]-1\right\}$$ (3)

$$U=\frac{C_0}{2}({\stackrel{‒}{I}}_1-3)+\frac{1}{D_1}\left(\frac{J^2-1}{2}-\ln J\right)+{\Sigma }_{i=1}^4\frac{c_1^i}{4c_2^i}\left\{\exp \left[c_2^i{(I_4^i-1)}^2\right]-1\right\}$$ (4)

2.4 VUMAT material user subroutines

Simulations were performed using Abaqus 6.14/Explicit (Simulia, Dassault Systemes, Waltham, MA) which does have a built-in Neo-Hooken and two-fiber HGO constitutive models, but lacks Demiray (Delfino) and the four-fiber FPA formulations. The built-in HGO model however, utilizes conventional compressible formulation of invariant-based anisotropic hyperelastic material that can lead to incorrect representation of behavior under certain loading conditions (Vergori et al. 2013; Nolan et al. 2014). To avoid this behavior, a modified anisotropic formulation that uses full anisotropic invariants proposed by Nolan et al (Nolan et al. 2014) was adopted through VUMAT material user subroutine to model slightly compressible response. VUMAT subroutines were also written for isotropic Demiray (Delfino) and Neo-Hookean models, with latter written for consistency of comparison. Compressibility was introduced through an additional constitutive parameter D₁. The value of D₁ was chosen such that the ratio of initial bulk modulus to shear modulus was K₀/C₀ = 20 according to Abaqus recommendation for explicit analysis. Out of plane shear stiffness, that needs to be defined for shell elements that use user material subroutine, was set as k₁₁ = k₂₂ = 1 MPa and k₁₂ = 0. Local material orientation was set along the longitudinal (axis 1), circumferential (axis 2), and transverse (axis 3) directions.

VUMAT subroutines were verified by simulating planar biaxial tensile tests on three arterial samples. Samples were modelled as 15×15mm squares that were loaded in a displacement control manner with displacements applied to the rigid body circles representing specimen attachment points. Quarter-symmetry was utilized to increase computational efficiency, and stresses and strains calculated in the middle of the sample were compared against the experimental data.

2.5 Finite Element Model

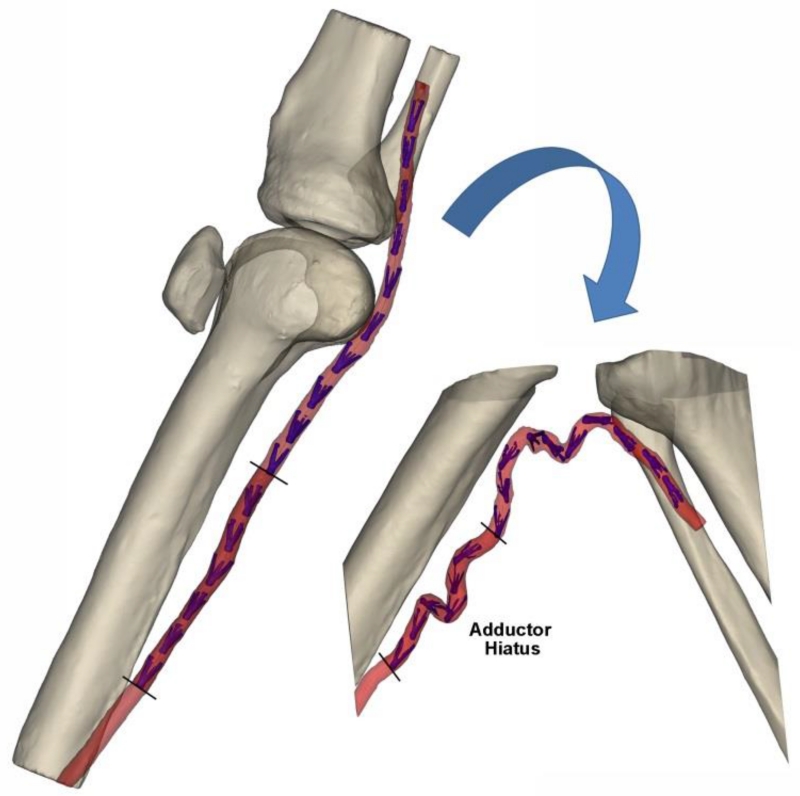
Finite Element (FE) model was created to quantify intramural principal mechanical stresses due to limb flexion-induced FPA deformation. Segment of the artery at the Adductor Hiatus (AH) was chosen for analysis because it is known to experience severe mechanical deformations with limb flexion and extension (Ansari et al. 2013; MacTaggart et al. 2014) (Fig. 1). Python script was written to automate model development and post-processing for all constitutive models and age groups.

Fig. 1.

3D CT reconstruction of the limb in the standing (180°, left) and gardening (60°, right) postures. Segment of the FPA at the Adductor Hiatus (AH) that was used for FE analysis is marked with dark red color. Intra-arterial markers (MacTaggart et al. 2014) are colored blue. Knee cap in the gardening posture was outside of the CT gantry and was not imaged

2.5.1 Geometry

AH segment was modeled as a tube of a 6 mm diameter and 1 mm thickness extruded along the centerline that represented the straight limb position. The centerline length in this position was uniformly scaled down using an inverse of the longitudinal pre-stretch ${\lambda }_z^{\text{in situ}}$ specific to each age group or slightly embalmed FPA.

2.5.2 Boundary conditions

Differences between the FPA centerlines in the straight and flexed limb postures define the arterial deformation field associated with limb flexion. However, the deformed geometry may be different in younger and more compliant arteries with higher longitudinal pre-stretch. To account for this, a set of springs and dashpots were used instead of applying displacement field directly. Springs and dashpots were tuned using the benchmark straight and flexed anatomies of the lightly embalmed FPA, and then used to simulate limb flexion in the non-embalmed age group-specific tissues.

The geometry representing the AH segment was sectioned perpendicular to the centerline at every marker position and midway between each marker pair. These sections were assumed rigid bodies, each governed by its corresponding reference point (RP). Additional spring reference points (RPspr) were created 0.1 mm away from the section RPs. Pairs of linear springs and dashpots were placed between corresponding section RPs and spring RPsprs.

FPA constitutive model with material properties and longitudinal pre-stretch of the lightly embalmed cadaver was used to select spring stiffness. High values of spring stiffness produce similar effect as the application of the displacement field; therefore, the smallest values that describe the deformed shape and stress field while also capturing differences between the four constitutive models were selected. To determine these values, nine spring stiffness constants ranging from 0.1 N/m to 1000 N/m were compared. The sum of spring displacements was used to assess the effects of spring stiffness on the deformed shape of the artery, and mean values of maximum principal stresses through thickness were used to assess the effects on the stress field. Dashpot coefficient was set 1000-fold smaller than the spring stiffness value.

After selecting the appropriate spring stiffness, the artery was loaded quasi-statically by applying displacements to spring reference points using smooth step amplitude. Soft springs allowed the artery to assume different shapes depending on the stiffness and longitudinal pre-stretch of the FPA in each age group. Frictionless contact with no penetration was assumed on all surfaces. Kinetic and internal energies were monitored to ensure that kinetic energy stayed within 5% of the internal energy and the loading remained quasi-static.

2.5.3 Mesh

Four-node linear reduced integration shell elements (S4R) were used to create a FE mesh. Enhanced hourglass control was used to avoid mesh instability due to hourglass modes. Convergence study was performed to determine optimum mesh size.

2.5.4 Endpoints

Constitutive model and age group effects were quantified using two endpoints. Maximum principal stresses through wall thickness were used as an endpoint for the stress field. They were extracted in each element of the model except near the rigid rings where stresses were expected to have artificial values. Sum of all spring displacements was used as an endpoint for differences in the deformed shapes.

3. RESULTS

3.1 Deformations of the FPA with limb flexion

Three-dimensional CT reconstruction of the lightly embalmed FPA in standing (straight) and gardening (acutely bent) postures is demonstrated in Fig. 1. Markers that were used to track spatial position of each arterial segment are colored blue and the region around the AH that was used for FE modeling is colored dark red. Severe deformations of the FPA with limb flexion are observed at the AH and below the knee.

3.2 Constitutive parameters for the FPA

3.2.1 Benchmark lightly embalmed material properties

Material parameters for the lightly embalmed FPA are summarized in Table 1. Coefficient of determination R² is given to demonstrate the quality of fit to the experimental data. As expected, the four-fiber FPA model described experimental data most accurately, whereas a single-parameter Neo-Hookean model demonstrated the worst fit. Surprisingly, the two-parameter Demiray (Delfino) model demonstrated somewhat better fit than the four-parameter two-fiber HGO.

Table 1.

Material properties for the lightly embalmed FPA. Table contains constitutive parameters for each of the four constitutive models: four-fiber FPA, two-fiber HGO, Demiray (Delfino), and Neo-Hookean. Longitudinal pre-stretch ${\lambda }_z^{\text{in situ}}$ = 1.11

Model	C0, kPa	$C_1^{\mathit{el}}$, kPa	$C_2^{\mathit{el}}$	$C_1^{\mathit{smc}}$, kPa	$C_2^{\mathit{smc}}$	$C_1^{\mathit{col}}$, kPa	$C_2^{\mathit{col}}$	γ,°	C10, kPa	a, kPa	b	R 2
Four-fiber FPA	38.05	27.41	26.88	318.07	2.06	31.62	50.97	40.86				0.9832
Two-fiber HGO	89.44					28.84	79.63	45.08				0.8771
Demiray (Delfino)										77.25	26.04	0.9013
Neo-Hookean									61.36			0.8134

3.2.2 Fresh tissue material properties for age groups

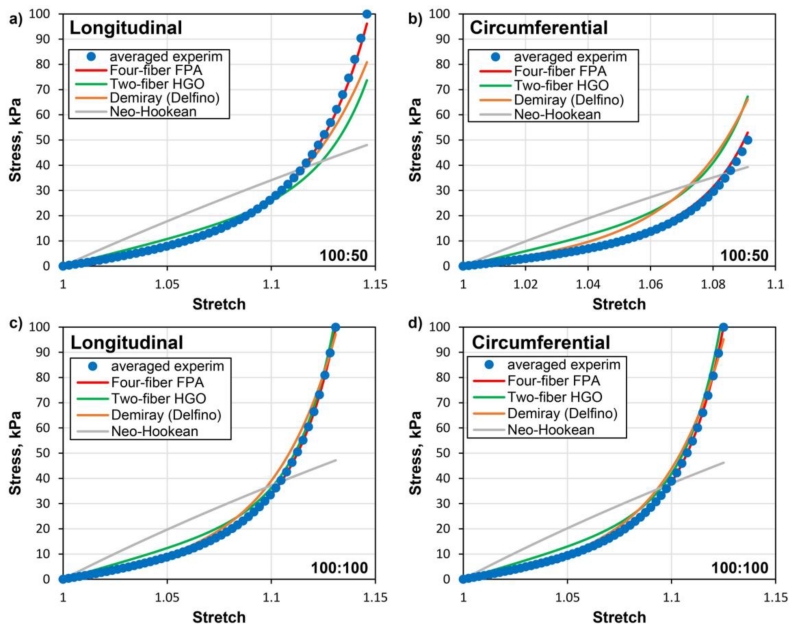
Material properties for the fresh (non-embalmed) FPAs in seven age groups and the associated longitudinal pre-stretch were adopted from our previous study (Kamenskiy et al. 2016b) and are summarized in Table 2 for convenience. Note that arteries in all age groups are longitudinally pre-stretched when measured in the straight limb posture, although the value of pre-stretch is age-dependent. The same experimental dataset was used to derive constitutive parameters for the HGO, Demiray (Delfino) and Neo-Hookean models, and the associated values are provided in Table 3. Representative fits of the experimental data in the longitudinal and circumferential directions for the 70-80 year-old artery are demonstrated in Fig. 2. Note that the quality of fit depends on the loading protocol. The four-fiber FPA model demonstrates the best fit under all 21 planar biaxial loading conditions(Kamenskiy et al. 2016b), while the two-fiber HGO and Demiray (Delfino) models performed best under equibiaxial tests.

Table 2.

Material properties and longitudinal pre-stretch for FPAs in seven age groups. Constitutive parameters are provided for the four-fiber FPA model. Second column (n) signifies the number of specimens in each age group used to derive these constitutive parameters (Kamenskiy et al. 2016b).

Age group, years	n	Mean age, years	${\lambda }_z^{\text{in situ}}$	C0, kPa	$C_1^{\mathit{el}}$, kPa	$C_2^{\mathit{el}}$	$C_1^{\mathit{smc}}$, kPa	$C_2^{\mathit{smc}}$	$C_1^{\mathit{col}}$, kPa	$C_2^{\mathit{col}}$	γ,°
11-20	21	16.7	1.53	10.51	20.92	0.22	2.34	1.76	3.32	2.05	60.84
21-30	15	25.0	1.39	16.81	17.35	0.69	7.72	3.68	3.80	3.28	50.17
31-40	26	35.7	1.36	9.96	17.57	0.99	4.74	2.81	2.45	4.10	55.88
41-50	39	47.2	1.27	13.46	14.54	2.41	8.20	7.29	2.31	9.96	46.84
51-60	106	56.1	1.19	10.69	20.77	3.60	11.58	8.38	3.28	13.19	45.62
61-70	83	64.6	1.15	7.83	24.81	5.73	16.82	12.56	5.24	21.76	46.58
71-80	32	76.1	1.10	7.01	37.03	12.81	36.09	15.96	11.65	36.08	45.02

Table 3.

Material properties for FPAs in seven age groups obtained using two-fiber HGO, Demiray (Delfino) and Neo-Hookean models.

Mean age, years	Two-fiber HGO				Demiray (Delfino)		Neo- Hookean
	C0, kPa	$C_1^{\mathit{col}}$, kPa	$C_2^{\mathit{col}}$	γ,°	a, kPa	b	C10, kPa
16.7	15.12	13.35	0.81	40.84	17.98	1.69	16.40
25.0	26.73	8.73	2.77	43.72	24.62	2.25	20.72
35.7	15.01	11.44	2.35	42.61	15.22	3.10	17.00
47.2	21.88	8.23	7.35	45.18	17.06	5.63	20.53
56.1	21.60	10.60	10.17	44.45	17.11	7.95	22.45
64.6	23.31	12.04	18.20	45.22	17.32	13.10	25.79
76.1	36.24	15.17	37.08	45.81	26.34	21.16	35.66

Fig. 2.

Representative fits of the experimental data in the longitudinal and circumferential directions for the 70-80 year-old artery under non-equibiaxial (100kPa/50kPa) (a,b) and equibiaxial (100kPa/100kPa) (c,d) loads. Experimental data is marked with dots while solid lines represent performance of different constitutive models.

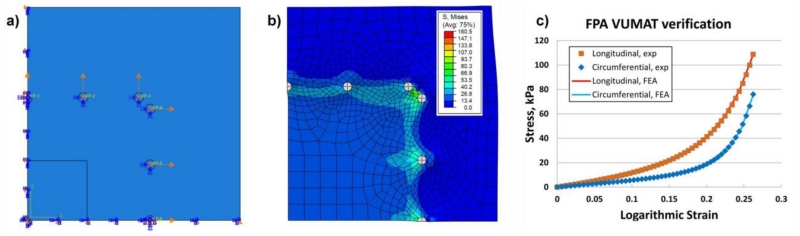
3.3 VUMAT verification

Fig. 3 demonstrates FE VUMAT verification procedure using biaxial experimental data for the equibiaxial stretch protocol. Panels a) and b) show quarter sample loaded by applying displacements to the rigid circles representing specimen attachment points. Panel c) demonstrates Cauchy stress – logarithmic strain obtained from the experiment and calculated for the center of the specimen using four-fiber FPA VUMAT. Graphs demonstrate excellent agreement in both longitudinal and circumferential directions.

Fig. 3.

a) FE model of the quarter sample loaded by applying displacements to the rigid circles representing specimen attachment points; b) Von Mises stress (kPa) distribution in the loaded sample; c) Comparison of experimental and FE calculated Cauchy stress (kPa) - logarithmic strain curves in the longitudinal and circumferential directions. Graphs were obtained for the center of the specimen

3.4 Spring stiffness

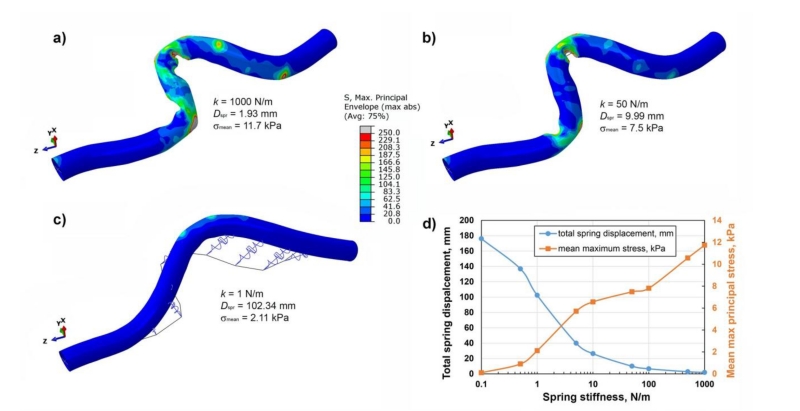
The effect of spring stiffness on FPA deformations is demonstrated in Fig. 4. Solid line represents the target position measured on the CTA of the flexed limb (Fig. 1). Reduction in spring stiffness resulted in smoother wall but larger differences with the target position. Noticeable deviations from the target line started at spring stiffness of 5 N/m. When the softest 0.1 N/m spring was used, practically no arterial bending was observed while the total spring displacement was 180 mm. Fig. 4d) demonstrates the combined effect of spring stiffness on the sum of spring displacements and mean values of the maximum principal stress through wall thickness. Sum of spring displacements changed insignificantly up to k=50 N/m, but started to increase rapidly with softer springs achieving two-fold increase with k=10 N/m. Mean max stress increased with stiffer springs reaching 12 kPa for k=1000 N/m. Based on these results, spring stiffness of k=50 N/m was chosen for the rest of the analysis as the softest spring that did not produce significant perturbations in values for neither total sum of spring displacements nor mean values of stresses.

Fig. 4.

Effect of spring stiffness on the deformed shape of the artery for a) k = 1000 N/m, b) k = 50 N/m, c) k = 1 N/m. Panel d) describes changes in spring displacements (mm) and mean maximum principal stress (kPa) for varying values of spring stiffness

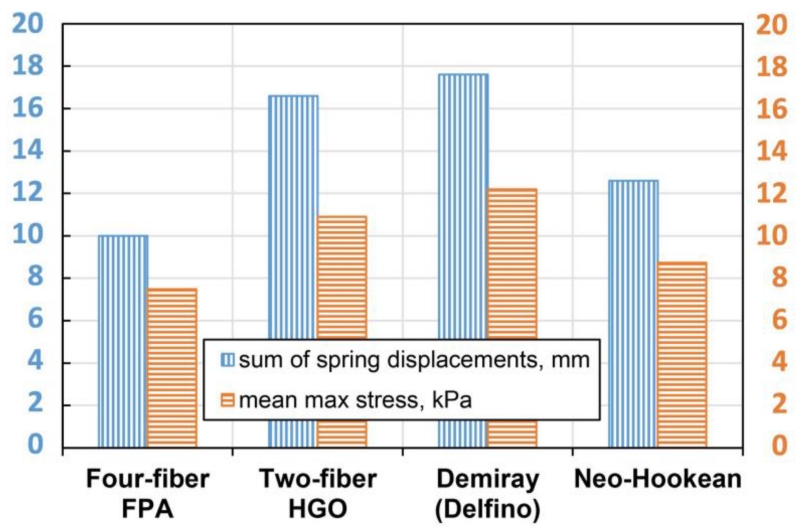
Sensitivity of the model to different constitutive formulations was assessed by using lightly embalmed tissue properties and k=50 N/m spring stiffness. Fig. 5 demonstrates differences between the four considered formulations in terms of the sum of spring displacements and mean maximum stress.

Fig. 5.

Sensitivity of the model to different constitutive formulations assessed by calculating the sum of spring displacements (mm) and mean max stress (kPa) for a benchmark lightly embalmed cadaveric artery using spring stiffness of k = 50 N/m

3.5 Constitutive formulation and deformed shape

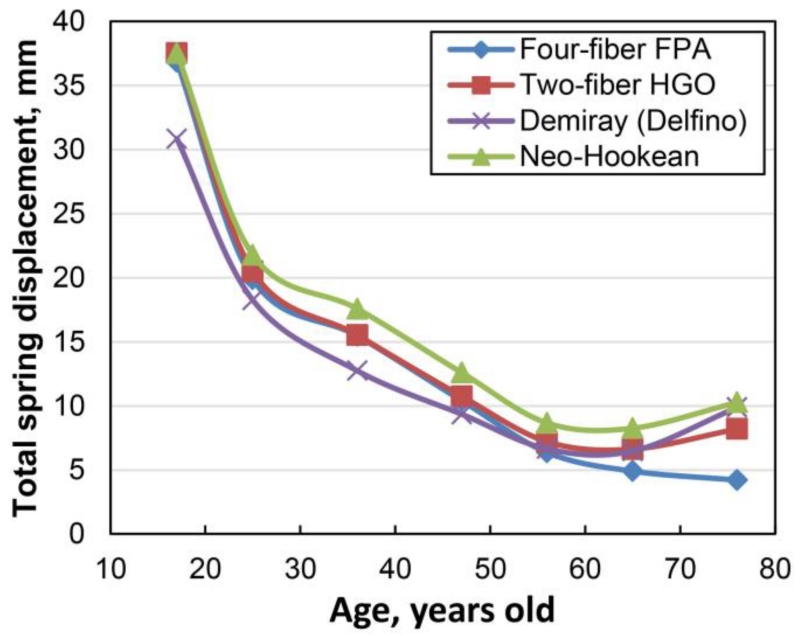
The sum of spring displacements for each material model and age group is demonstrated in Fig. 6. Variation of the total spring displacement for subjects younger than 50 years of age was within 20% of the benchmark four-fiber FPA formulation. Two-fiber HGO model demonstrated the closest match. For subjects older than 50 years of age, differences between the constitutive formulations became more pronounced, approaching 144% of the benchmark for the oldest age group and Neo-Hookean model. For subjects older than 50 years of age, Demiray (Delfino) and classic HGO formulations demonstrated smallest differences with the benchmark.

Fig. 6.

Effects of the FPA constitutive model on the overall shape of the artery judged by the total spring displacement for different age groups

3.6 Constitutive formulation and intramural stresses

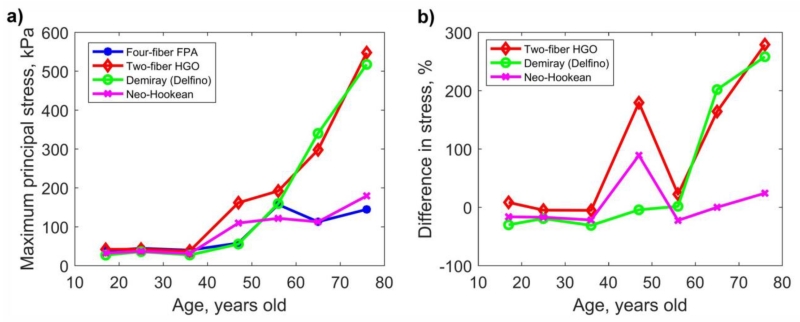
Change in the maximum principal stress with age for all four constitutive models is demonstrated in Fig. 7a. Stresses were relatively constant for ages younger than 40 years fluctuating around 25-50 kPa for all models. After 40 years of age, stresses associated with limb flexion increased dramatically, but the rate of change was model-dependent. HGO and Demiray (Delfino) formulations demonstrated the most rapid increase in maximum principal stress with age, while the four-fiber FPA and Neo-Hookean models were more conservative. The difference in the maximum principal stresses between the benchmark FPA and HGO/Demiray (Delfino) formulations was above 250% for the oldest group (Fig. 7b), while the difference with the Neo-Hookean formulation was only 24%. For all age groups except 41-50 years old, Neo-Hookean model demonstrated closest maximum principal stresses to the FPA model.

Fig. 7.

a) Maximum principal stresses computed with four different constitutive models as a function of age. b) Difference (%) in maximum principal stresses for constitutive models compared with the four-fiber FPA model

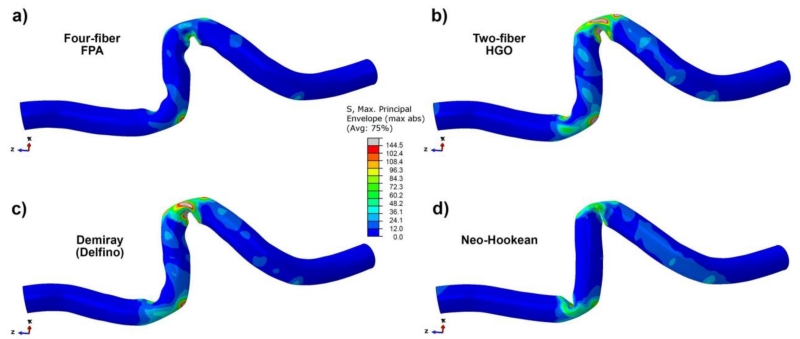
Fig. 8 illustrates differences in the maximum principal stresses plotted for each of the constitutive models using properties from the oldest (71-80 years old) age group. The results demonstrate closest stress values for the FPA and Neo-Hookean models but differences in the deformed shapes.

Fig. 8.

Maximum principal stress (kPa) distribution in the deformed segment of the FPA calculated using four constitutive models and mechanical properties for the oldest (71-80 years old) age group; a) four-fiber FPA, b) two-fiber HGO, c) Demiray (Delfino), d) Neo-Hookean formulations

4. DISCUSSION

The FPA is significantly different from other vascular beds, because it is highly mobile and undergoes large deformations during flexion of the limb. These severe deformations put repair materials and devices through substantial mechanical challenges and expose the artery to the risk of injury when device characteristics are inadequate. Computational modeling is instrumental for analyzing the ability of the device to accommodate limb flexion-induced FPA deformations and the associated stresses, but the models heavily depend on the input parameters, such as the boundary and loading conditions and the mechanical properties. The current study describes a computational approach to simulate limb flexion-induced deformations of the human FPA accounting for age-specific pre-stretch and mechanical properties. In addition, several commonly used constitutive models for arterial tissue were considered and recommendations regarding their use for each age group are provided.

Computational modeling of the FPA is a relatively unexplored area primarily due to lack of information describing limb flexion-induced deformations. One of the first efforts to model FPA deformations with limb flexion was performed by Diehm et al (Diehm et al. 2011). They used patient-specific MRI images to model the below knee popliteal artery represented by the linear elastic material. Ghriallais et al (Ní Ghriallais and Bruzzi 2013) augmented the model by incorporating the effects of surrounding tissues and stenting, with the stent represented by a stiffened segment of the artery (Ní Ghriallais and Bruzzi 2014). Petrini et al (Petrini et al. 2016) incorporated stent geometry explicitly and numerically studied fatigue under axial extension and bending loads in a short idealized arterial segment. Recently Conti et al (Conti et al. 2016) included both the geometry of the stent and the patient-specific anatomy of the FPA to model arterial deformation with limb flexion. They used FEA in combination with a displacement field technique to push the artery and the stent into the deformed configuration.

While significant progress has been achieved using these computational models, they are limited to an a priori defined deformed state of the FPA in the flexed limb posture. Among other characteristics, this deformed state heavily depends on the longitudinal pre-stretch and mechanical properties, both of which change with age (Jani and Rajkumar 2006; Shroff et al. 2009; Lee and Oh 2010; Kamenskiy et al. 2015; Kamenskiy et al. 2016a). To account for these characteristics of the ageing artery, a novel modeling approach using a system of springs was proposed in this work. Springs represented the effects of surrounding tissues that push the artery into the deformed configuration producing different deformed shapes for different age groups. The advantage of this approach is that the model can be developed and tuned using a single set of material parameters and pre-stretch, independent of donor age. It can then be applied to simulate deformed arterial shapes in other age groups that have different mechanical and pre-stretch characteristics.

Constitutive description of arterial wall behavior is an essential part of this computational model. A low number of constitutive parameters is beneficial, but simple constitutive relations may not be sensitive enough to describe the non-linear orthotropic arterial properties. The choice of constitutive relation can be based on the evaluation of fit quality when using bench-top experimental data, but the loading conditions of the FPA in the flexed limb can be different from the bench-top protocols, and a fitting exercise may not be sufficient. In this study we have used limb flexion-induced deformations to evaluate the performance of four constitutive models that are frequently used to describe arterial behavior. Furthermore, we have assessed the performance of each model in seven age groups to determine whether they can adequately capture age-specific deformed shapes and stress fields associated with limb flexion. All four models were invariant-based and had one to eight constitutive parameters. One and two parameter models represented isotropic response, and the four and eight parameter models described anisotropic responses. While the eight-parameter FPA formulation provided the most accurate results, all four constitutive formulations adequately described arterial behavior in subjects younger than 40 years of age. In older subjects, Demiray (Delfino) and classic HGO formulations produced deformed arterial shapes that were closest to the one produced by the FPA formulation, but these two models significantly overestimated the mechanical principal stresses. In terms of stress field, the Neo-Hookean model produced the closest match to the benchmark FPA formulation.

Our results demonstrate that if the deformed shape is known a priori, for example from clinical imaging of straight and flexed limbs, then the Neo-Hookean model can give a reasonable approximation of the associated stresses. If the deformed shape is unknown and the goal is to determine this configuration with computational modeling, then a slightly more complex Demiray (Delfino) model should be used. The Demiray (Delfino) model will reasonably simulate the deformed shape, but it will not give accurate estimation of stresses. Finally, if both the deformed shape and the stress distribution are to be determined with computational analysis, then a four-fiber FPA formulation is more appropriate. The latter case is illustrated in this study when the deformed shape for younger arteries was initially unknown, but was determined with computational modeling along with the associated stress field.

Young FPAs are known to be highly anisotropic with significantly higher longitudinal compliance due to axially oriented elastic fibers (Kamenskiy et al. 2015; Kamenskiy et al. 2016a). Degradation and fragmentation of this elastin, accumulation and crosslinking of collagen, and changes to the smooth muscle with ageing result in reduction of anisotropy as equibiaxial longitudinal and circumferential stress-stretch curves move closer to each other (Kamenskiy et al. 2015; Kamenskiy et al. 2016b). Stiffer and more isotropic responses of older FPAs may be responsible for reasonable prediction of stresses by the Neo-Hookean formulation in older arteries. On the other hand, smaller limb flexion-induced deformations (Cheng et al. 2010) and the associated stresses in the more compliant young arteries likely contributed to similar performance of all constitutive formulations in subjects younger than 40 years of age.

While more studies are required to validate these results, they suggest that stresses associated with known limb flexion-induced FPA deformations can in certain cases be estimated with reasonable accuracy using simple material descriptions and properties obtained from basic experiments, perhaps even from patient-specific in vivo tests. Such tests can include X-ray angiography, Magnetic Resonance Imaging or Duplex Ultrasound to provide in vivo assessment of pressure-diameter relations in human arteries. The small number of constitutive parameters required for these simple constitutive models may eliminate problems with overparameterization and ill-conditioning usually associated with more comprehensive material descriptions (Masson et al. 2011; Liberson et al. 2016), but computational approaches using these formulations may need to rely on a priori determined deformed states.

Results of this study should be viewed in the context of its limitations. While the proposed modeling technique allowed obtaining different deformed configurations for FPAs in different age groups, it assumes that the effects of surrounding tissues that push the artery into its deformed state are not affected by aging. The new age-specific deformed configurations obtained with our model still need to be validated experimentally in younger arteries to assess the validity of this assumption. A second limitation is concerned with the use of rigid rings that were used for spring attachments. Ring rigidity does not allow pressurization of the artery, therefore in vivo FPA shape and stress distribution may be somewhat different from those presented here. Additional studies are required to validate this speculation. Lastly, comparison of constitutive models was performed using only a single FPA, and modeling of other anatomies and postures is currently underway.