Water: A Tale of Two Liquids

Abstract

Water is the most abundant liquid on earth and also the substance with the largest number of anomalies in its properties. It is a prerequisite for life and as such a most important subject of current research in chemical physics and physical chemistry. In spite of its simplicity as a liquid, it has an enormously rich phase diagram where different types of ices, amorphous phases, and anomalies disclose a path that points to unique thermodynamics of its supercooled liquid state that still hides many unraveled secrets. In this review we describe the behavior of water in the regime from ambient conditions to the deeply supercooled region. The review describes simulations and experiments on this anomalous liquid. Several scenarios have been proposed to explain the anomalous properties that become strongly enhanced in the supercooled region. Among those, the second critical-point scenario has been investigated extensively, and at present most experimental evidence point to this scenario. Starting from very low temperatures, a coexistence line between a high-density amorphous phase and a low-density amorphous phase would continue in a coexistence line between a high-density and a low-density liquid phase terminating in a liquid–liquid critical point, LLCP. On approaching this LLCP from the one-phase region, a crossover in thermodynamics and dynamics can be found. This is discussed based on a picture of a temperature-dependent balance between a high-density liquid and a low-density liquid favored by, respectively, entropy and enthalpy, leading to a consistent picture of the thermodynamics of bulk water. Ice nucleation is also discussed, since this is what severely impedes experimental investigation of the vicinity of the proposed LLCP. Experimental investigation of stretched water, i.e., water at negative pressure, gives access to a different regime of the complex water diagram. Different ways to inhibit crystallization through confinement and aqueous solutions are discussed through results from experiments and simulations using the most sophisticated and advanced techniques. These findings represent tiles of a global picture that still needs to be completed. Some of the possible experimental lines of research that are essential to complete this picture are explored.

1. Introduction

Water is the most abundant liquid, exhibits the most anomalous behavior, and is a prerequisite for life on this planet and probably for life elsewhere.¹⁻¹⁰ It shows a density maximum at 4 °C (277 K) under ambient conditions, and the solid phase has a lower density than the liquid (ice floats in the liquid).¹¹⁻¹³ Its thermodynamic response functions, such as specific heat, C_P, compressibility, κ_T, and thermal expansion coefficient, α_P, all of which can be determined by entropy or volume fluctuations, i.e.

1

and

also show anomalous behaviors.^{4−6,13−18}

For example, at atmospheric pressure κ_T increases when T < 46 °C (319 K) but exhibits normal behavior when T > 46 °C. Similarly, at atmospheric pressure C_p increases when T < 35 °C (308 K) and the value of α_P becomes negative, indicating that the volume expands below 4 °C. One characteristic of the three thermodynamic properties shown in eq 1 is that they are related to fluctuations in liquid water that increase upon cooling below a certain temperature instead of decrease as in simple liquids. Figure 1 shows how this anomalous behavior becomes more pronounced in the deeply supercooled region and seems to diverge when T approaches −45 °C (228 K).¹²Figure 2 uses simulations of the TIP4P/2005 water model¹⁹ to show the structurally anomalous regime in water that encloses the region of diffusional anomaly which in turn encloses the region of density anomaly. This nested structure gives rise to the idea of a cascade of anomalies, where progressive enhancement of the degree of structural anomaly gives rise to various transport and thermodynamic anomalies. Comparisons of the cascade structure and the order maps of a number of tetrahedral liquids are now available and indicate the complexity of describing the thermodynamics of these systems.²⁰⁻²²

Figure 1.

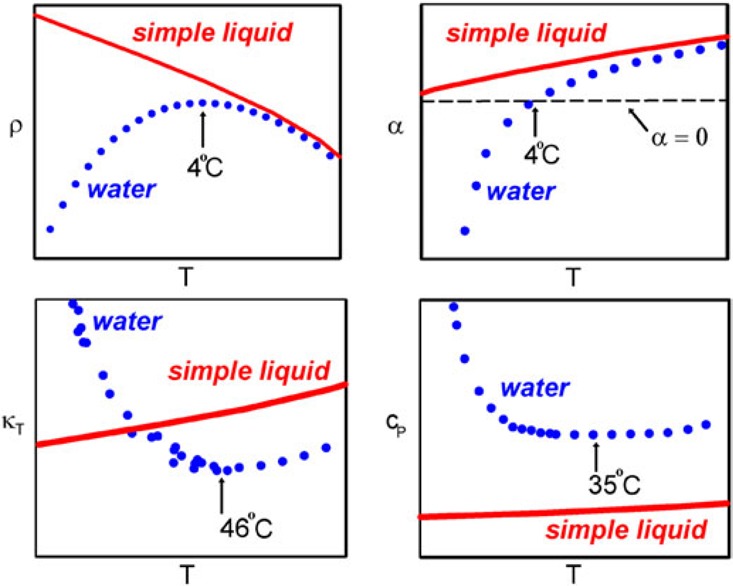
Anomalous thermodynamic properties of water compared to simple liquids. Schematic comparison of the isobaric temperature dependence of the density ρ, thermal expansion coefficient α_P, isothermal compressibility κ_T, and isobaric heat capacity, C_P, for water and a simple liquid. Reproduced with permission from ref (4). Copyright 2003 by IOP Publishing.

Figure 2.

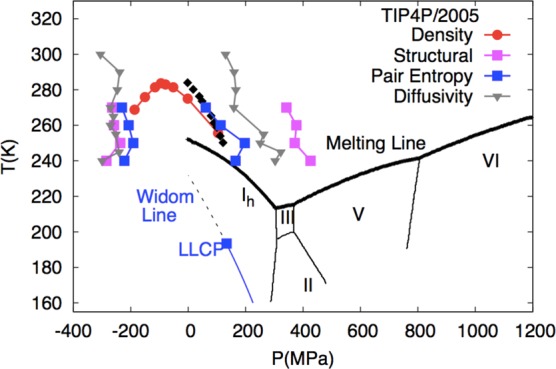
Thermodynamics of the condensed phases of water, illustrated for the TIP4P/2005 rigid-body model of water.¹⁹ Data for the phase boundaries are taken from ref (24). Boundaries of the structural, density, pair-entropy, and diffusivity anomalies are taken from ref (25). The experimental TMD line shown in filled black diamonds is taken from ref (26). The Widom line (see the definition in section 6) is taken from ref (27). Reproduced from ref (21) with permission from the PCCP Owner Societies.

Here, we review the behavior of water in the anomalous regime from ambient conditions to the deeply supercooled region. The regime above 232 K (temperature of homogeneous ice nucleation) and below the crystallization temperature 160 K of amorphous ice (at ambient pressure) has provided the most information since it is more accessible. Among several theoretical scenarios, a liquid–liquid phase transition and an associated critical point (LLCP) are conjectured²³ and are assumed to lie in the regime between 232 and 160 K, the so-called no-man’s land in the phase diagram, so named because ice nucleation occurs too rapidly for conventional measurement techniques. We connect the thermodynamic behavior of liquid water—its restructuring, anomalous behavior, and dynamics in the ambient and moderately supercooled regimes where experimental and simulation data are more accessible—to its behavior in the deeply supercooled region where an LLCP, real or virtual, may be located.

This review is structured as follows: in the next section we describe the scenarios that have been proposed over the years to explain water anomalies in the supercooled state. The following section focuses on the most extensively investigated scenario, the one that foresees the presence of a liquid–liquid transition terminating in a second-order critical point. Section 4 deals with theoretical and experimental results on the competition between the two alternative structures that exist in water, described as a low- and a high-density liquid, and with how two-state thermodynamics can explain “liquid polymorphism”. Section 5 deals with the important phenomenon of nucleation that prevents experiments, at least so far, from accessing the region where the LLCP is supposedly located. Due to these difficulties many alternative routes have been tried to clarify water behavior in the supercooled realm, and these are described in the remaining sections. Section 6 describes the close relation between dynamics and thermodynamics that in recent years was very much explored because of the possibility to locate from a dynamic crossover in water an important precursor of a critical point, the Widom line. The possibility to reach the low-temperature region with stretched water is explored in section 7. Other possible routes are confined water (section 8) and aqueous solutions (section 9). Depending on the kind of confinement and on the solution, supercooling can be easier and the properties of water can remain bulk-like. The last section is devoted to explore possible future directions.

2. Several Scenarios

Over the past years, different scenarios have been proposed to explain the origin of the anomalies briefly described in the preceding section.^23,28−32 The first was in 1982 in a remarkable paper by Robin Speedy,³³ which has become known as the “Speedy stability limit conjecture”. It has the same form of metastable water phase diagram as that yielded by empirical equations of state for water produced by the water and steam engineers. It was followed in 1992 by the famous “second critical-point hypothesis” of Poole, Sciortino, Essmann, and Stanley²³ on the basis of molecular dynamics simulations of the ST2 model. This has been by far the most influential scenario and has been supported, explained, and contested by various authors, e.g., Tanaka,³⁴⁻³⁶ Anisimov,³⁷⁻³⁹ Stanley, and co-workers,^23,40−42 Limmer and Chandler,^43,44 and Nilsson and Pettersson⁴⁵ to name a few. Then, among scenarios that are qualitatively distinct, there is the “critical-point-free” scenario, initially presented in 1994 as one of two cases within a bond-modified van der Waals model of the tetrahedral liquid state by Poole et al.⁴⁶ and recently revisited by one of the present authors.³² This was followed in 1996 by the “singularity-free” scenario of Sastry et al.,³¹ based on lattice model calculations.

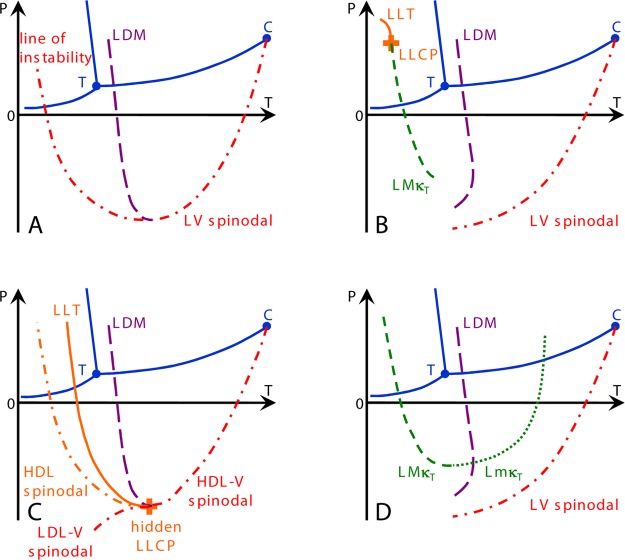
The essential differences between these four scenarios are depicted in the series of phase diagrams of Figure 3, adapted from the recent paper of Pallares et al.,⁴⁷ and may be summarized as follows (see also the figure caption).

Figure 3.

Scenarios that might account for the behavior observed in Figure 1. (A) Speedy’s stability limit conjecture,³³ (B) Poole et al.’s second critical point,²³ (C) Poole et al.’s “weak bond”-modified van der Waals model, now the critical-point-free scenario,⁴⁶ and (D) Sastry et al.’s singularity-free scenario.³¹ Continuous blue curves show the known equilibrium coexistence lines between liquid, solid, and vapor with the triple point marked as T. Liquid–vapor equilibrium terminates at the critical point C. The long-dashed purple line shows the line of density maxima (LDM), and the short-dashed and dotted green lines are the lines of isothermal compressibility maxima (LMκT) and minima (LmκT), respectively. Dash–dotted lines indicate lines of instability. In scenarios A and C, the LDM keeps a negative slope and ends at a line of instability. In scenarios B and D, the LDM reaches a maximum temperature and changes its slope, eventually merging with a line of density minima (not shown for clarity). When the scenario comprises a liquid–liquid transition, it is displayed with a continuous orange line (LLT), and the liquid–liquid critical point is shown as an orange plus. Adapted from ref (47). Copyright 2014 National Academy of Sciences.

In the “stability limit conjecture” scenario, Figure 3A, the boundary of the liquid state at high temperatures (the well-known spinodal limit to the stability of the superheated liquid state that terminates at the liquid–gas critical point) is reversing its temperature dependence where the line of density maxima meets the liquid–vapor spinodal at negative pressure. It then retraces to establish the limit to supercooling of the ambient pressure and low-pressure liquid. Debenedetti⁴ correctly argues that the intersection between a liquid–vapor spinodal and the metastable continuation of the liquid–vapor equilibrium line must be a critical point. However, this is not necessary if the line of instability at positive pressure is not a liquid–vapor spinodal but rather a line of instability toward another phase. The critical-point-free scenario^31,32 (Figure 3C) provides such a line (see below).

Figure 3B shows the second critical-point scenario in its most familiar form, wherein a second critical point exists at positive pressure, where it terminates a line of liquid–liquid transition. From the second critical point emanates a Widom line, the locus of extrema of the correlation length. This scenario also includes other lines of response function maxima, extending to lower and negative pressures. Near the critical point these lines merge with the Widom line.

In Figure 3C is depicted the critical-point-free scenario by which is meant that the liquid–liquid transition exists but the LLCP has moved sufficiently to negative pressures that it meets the liquid–vapor spinodal and the fluctuations characteristic of each merge and lose identity.

Finally, the singularity-free scenario (Figure 3D) is characterized by sharp but nondivergent maxima in the different response functions, occurring at different temperatures but without a liquid–liquid transition and with a critical point only at 0 K.

Only in the first of the above scenarios does the form agree with that of the various multiparameter empirical equations of state, for which the spinodal limit to liquid stability reverses its position in pressure and retraces to positive pressures. Only in the second and third of these scenarios does a liquid–liquid coexistence line exist. Also, only in one of these does a second critical point exist.

3. Liquid–Liquid Transition

Among the scenarios presented in section 2, the second critical-point scenario²³ (Figure 3B) with the possible existence of a liquid–liquid critical point (LLCP) and its associated critical fluctuations, which are considered as the source of water anomalies,^{5,6,28−30,40,48,49} has been investigated extensively both in amorphous glassy water and in deeply supercooled liquid water, see, for example refs (49−52). Although most authors are of the opinion that the critical zone in real water lies fully at positive pressures and that scenario B of section 2 is the appropriate description of real water behavior, the issue is not yet settled. There is a powerful argument by Binder (see ref (53)) to the effect that in a metastable system a true critical point cannot exist because the diverging time scale needed for its ergodic manifestation would cross the finite lifetime for the liquid imposed by crystallization kinetics. This argument, which however only concerns the immediate vicinity of the critical point, leads us to refer to a critical “zone” within which ergodicity in principle cannot be established but on either side of which a liquid–liquid line or a Widom line could exist and could play a role in the physics of the liquid. With this caveat the second critical-point scenario and its associated liquid–liquid phase transition (LLPT) will be the focus of the present review.

In the mid-1980s, Mishima et al.^52,54 amorphized ice I_h at 77 K by compression beyond 1.1 GPa and observed a first-order-like phase transition from high-density amorphous ice (HDA) to low-density amorphous ice (LDA) by heating the pressure-amorphized material at ambient pressure.⁵⁴ LDA and HDA differ in structure and density, where both states consist of fully hydrogen-bonded tetrahedral networks, but in HDA five first neighbors exist where the fifth molecule sits on an interstitial place between the first and the second shell.⁵⁵ The radial distribution functions of LDA and HDA are examined in the article “X-ray and Neutron Scattering of Water”⁵⁶ contained within this issue.

The idea that water is a “mixture” of two different structures dates back to the 19th century^57,58 and was reinvigorated in the late 20th century.⁵⁹⁻⁶¹ In 1992, in a seminal paper,²³ using molecular dynamics simulations on the ST2 model of water, Poole, Sciortino, Essman, and Stanley found a first-order phase transition from low-density liquid (LDL) to high-density liquid (HDL) with an LLCP located at T_C ≈ 235 K and P_C ≈ 200 MPa.²⁸⁻³⁰ In this scenario the LLPT is determined by extending the HDA and LDA first-order phase transition into the higher temperature and lower pressure region of the phase diagram,^{41,54,62−68} see Figure 4. If there is a second critical point as suggested in Figure 3B it may be at either positive or negative pressure. While most simulation work suggests it to be at positive pressure, a couple suggest it to be at negative pressure, as summarized in ref (69). From the experimental side the question of the location of a possible second critical point is still open, especially because its location is presumed to be in no-man’s land, where rapid crystallization takes place and experiments have to probe the liquid very fast.

Figure 4.

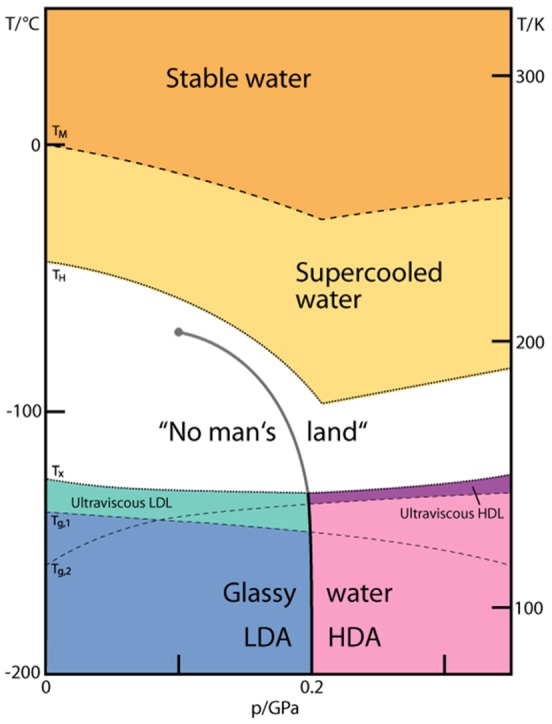
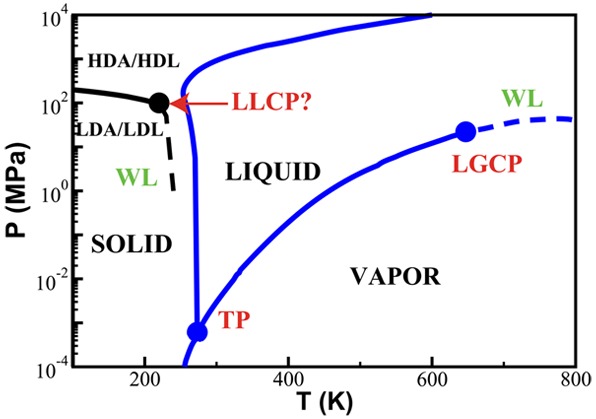
Phase diagram of noncrystalline water (adapted from ref (75), courtesy of Stephan Fuhrmann and Thomas Loerting). No-man’s land indicates the region in which only crystalline ices have been observed so far. It is enclosed by the homogeneous crystallization line T_H from the top and the crystallization line T_X from the bottom. Two ultraviscous liquid domains, low- and high-density liquid water (LDL and HDL), can be found just below T_X. The two corresponding glass transition temperatures T_g,1 and T_g,2 separating the glassy solids LDA and HDA from the ultraviscous liquids LDL and HDL are taken from refs (76) and (77), respectively. Please note the metastable extension of T_g,1 into the stability region of HDA and of T_g,2 into the stability region of LDA/LDL. A first-order liquid–liquid phase transition line (LLPT) ends in the purported liquid–liquid critical point (LLCP).

The most elegant technique to date to study the transition was employed by Mishima,^48,70 who studied decompression- and compression-induced melting of high-pressure ices in the stability domain of hexagonal ice. On the basis of subtle temperature changes in the sample Mishima claims to be able to detect the transition from the high-pressure ice to either HDL or LDL first, which is then immediately followed by crystallization. In order to avoid the direct transition from the metastable high-pressure ice phase to hexagonal ice, skipping over the liquid phase, Mishima used water in oil emulsions. The key finding of this work is a kink in the metastable melting line of ices IV and V but a rather smooth metastable melting line of ice III. The kink is interpreted by Mishima to indicate a transition from melting to LDL rather than HDL. On the basis of the density difference of about 20% between LDL and HDL and the Clausius–Clapeyron equation, the slope of the high-pressure melting line needs to change by about 20% at the LDL–HDL first-order transition line, which is the case for ices IV and V but not for III. On the basis of these findings Mishima locates the first-order liquid–liquid transition line from 0.075 GPa/223 K to 0.10 GPa/215 K for H₂O and very close to that for D₂O.⁷⁰ According to Mishima’s interpretation of the data, there is no kink in the melting line of ice III, which passes through 230 K and 0.01 GPa, i.e., the first-order liquid–liquid transition line and the metastable ice III melting line do not intersect. As a consequence, Mishima is able to locate the second critical point between the melting lines of ice III and IV, i.e., at positive pressures between about 0.02 and 0.07 GPa and between 223 and 230 K.

If Mishima’s interpretation is correct, this settles the discussion and the critical point is at positive pressure. There is, however, some doubt about the method when working very close to ambient pressure, which is necessary to locate the metastable ice III melting line. Thus, the ice III melting line might be smooth or there might be a kink overlooked by Mishima. Furthermore, there is no direct evidence provided by Mishima that the high-pressure ices in emulsions indeed first melt to the liquid rather than directly transform to stable hexagonal ice. For these reasons we consider Mishima’s work to represent the best experimental narrowing down of the location of the second critical point, if it exists at all, but it does not completely rule it out to be at negative pressure.

About a decade later, Mishima again utilized the property of emulsified water to hinder crystallization and mapped the specific volume of supercooled water.⁷¹⁻⁷³ He noted a slightly concave-downward change in the plot of volume against temperature at high pressures, which favors the scenario in Figure 3B over the scenario in Figure 3A. The second critical point is roughly suggested to be located at 0.05 GPa and 223 K, in agreement with his own earlier work on the metastable melting lines of high-pressure ices.

Using neutron diffraction, first Bellissent-Funel⁶⁸ and then Soper and Ricci⁶⁷ verified the structure transformation in liquid water from LDL to HDL with increasing pressure at ambient temperature, see Figure 5. They found that the main difference between LDL and HDL lies in the second shell, i.e., the second shell of LDL sits at approximately the tetrahedral distance, but the second shell of HDL substantially collapses with interstitial molecules and contributions from less specific, bifurcated hydrogen bonds.⁷⁴ Using similar techniques, Bellissent-Funel et al. further demonstrated that the structure of liquid water becomes HDA when cooled at high pressures but changes to LDA when cooled at low pressures. This again indicates a continuation of the LDA–HDA transition line to a LLPT in water^64,65 and is consistent with results obtained using dilatometry and powder X-ray diffraction.^66,67

Figure 5.

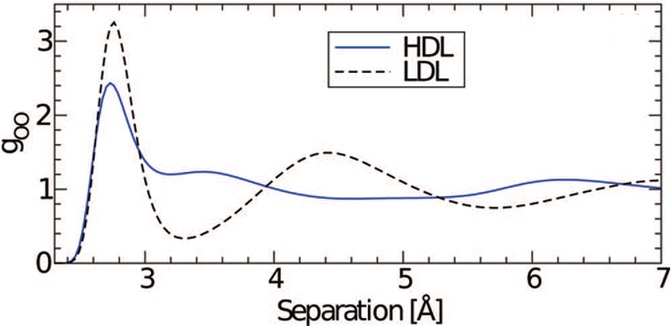
Radial oxygen–oxygen pair-distribution functions for HDL and LDL demonstrating the structural difference between high- and low-density water at ambient temperature. Adapted with permission from ref (67). Copyright 2000 by the American Physical Society.

The phase diagram of noncrystalline water including a postulated location of a liquid–liquid critical point is shown in Figure 4. This diagram is restricted to pressures p < 0.35 GPa because the HDA–LDA and the liquid–liquid transition associated with these glassy ices is most relevant for our understanding of ambient pressure water. The two corresponding glass transition temperatures T_g,1 and T_g,2 separating the glassy solids LDA and HDA from the ultraviscous liquids LDL and HDL are taken from refs (76) and (77), respectively. The two glass transition temperatures are clearly distinct both at ambient pressure⁷⁸ and at high pressure, in particular at the binodal separating HDA and LDA at 0.2 GPa.^76,77 Furthermore, T_g,1 decreases with pressure, whereas T_g,2 increases. Such behavior was found for the ST2 model of water⁷⁶ and in a Jagla-like model.⁷⁹ However, it was not found for the SPC/E model of water.⁷⁶

The phase diagram of noncrystalline water extending to a pressure of about 10 GPa is shown in Figures 3 and 4 of ref (80). Above a pressure p ≈ 0.8 GPa a third form of amorphous ice, called very-high-density amorphous ice (VHDA), becomes the most stable form of amorphous ice. A sudden change in compressibility⁸¹ and in dynamic properties⁸² marks the transition between HDA and VHDA. The possibility of further liquid–liquid critical points was raised in computational work,⁸³⁻⁸⁶ although the methods used in refs (83) and (84) were seriously questioned by the considerations and the results of Liu et al.⁸⁷ Very recent in situ experiments on the dynamics of HDA and VHDA suggest that if there is such a critical point associated with HDA–VHDA, it has to be located at very low temperatures near 0.8 GPa.⁸² A more detailed account of the nature of the relationship between HDA and VHDA can be found in earlier review articles, see refs (80), (88), and (89). In the present review we do not touch further on the question about the relation between HDA and VHDA and the possibility of yet another liquid–liquid transition.

The transition between HDA and LDA under pressure was studied by Mishima and Suzuki,⁹⁰ Klotz et al.,⁹¹ and Yoshimura et al.⁹² Their experiments demonstrate the first-order nature of the transition by revealing phase boundaries between two phases, phase coexistence, and a discontinuous change of structural properties at the transformation. Going beyond these studies, Winkel et al.^93,94 saw evidence of a first-order transition in the ultraviscous liquid domain at ∼140 K and 100 MPa under decompression (i.e., on the downstroke). The location of the ultraviscous liquid domains for HDL and LDL is mapped by several experiments on the glass transition of amorphous ices, see Figure 4 in ref (77) and refs (76) and (95).

A glass transition onset temperature of ∼136 K was detected in LDA by following the change in heat capacity upon heating LDA ice at ambient pressure at a rate of 10 K/min.⁹⁶⁻⁹⁸ Although LDA can be prepared in several ways—by vapor deposition, by hyperquenching, and by the transformation from HDA described above—all studies find a similar increase in heat capacity, ΔC_p of ∼1 J K^–1 mol^–1.⁹⁹ The real nature of this extremely weak signal has been discussed for decades.^32,100 The main point of the controversy concerns the question of whether a liquid nature is reached prior to crystallization¹⁰¹ and the question whether translational motion¹⁰² or rather defect dynamics as in a crystalline system¹⁰³ is observed above T_g. More recently, the interpretation that LDA undergoes a glass–liquid transition at the calorimetric glass transition near 136 K has received considerable support.^80,104,105 In the most recent scenario, the feeble signal is explained by the suspected strong or even superstrong nature of the low-density liquid near the glass transition temperature.^32,100,106 This suspicion found recent confirmation by dielectric measurements, indicating that LDL is actually the strongest of all known liquids.^78,107

The glass transition of high-density amorphous ices was studied by in situ high-pressure methods by Mishima,^108,109 Andersson,^95,110,111 and Loerting et al.^82,112,113 These measurements were recently reviewed in ref (77). All measurements indicate that the glass transition at elevated pressures of p > 200 MPa appears to be at T_g > 140 K. These measurements also indicate that the glass transition in HDA can be observed even at pressures < 200 MPa, where LDA is thermodynamically favored over HDA,¹¹⁴ i.e., metastability alone does not preclude the observation of glass transitions if the time scale of the transformation to the thermodynamically more stable phase is significantly longer than the time scale of equilibration. The transformation time scales can in fact greatly exceed those required for the equilibration of HDA, even at ambient pressure. Thus, measurements of HDA become possible in an extended temperature range and reveal an ambient-pressure heat capacity step and a dielectric relaxation time that indicates a glass transition at 116 K.⁷⁸ This glass transition in HDA is 20 K lower than the glass transition in LDA and thus represents water’s second glass transition. The possibility that two distinct glass transitions occur has been further supported by the simulation results of Xu et al.^115,116 and Giovambattista et al.,⁷⁶ which indicate that the experimental observations are qualitatively consistent with water and water-like models having a LLPT, e.g., the ST2 water model, but not with models lacking two liquid phases, e.g., SPC/E water. Also, a Jagla-like, square-shoulder model liquid has been shown to exhibit two T_g lines,⁷⁹ supporting the view that polymorphic liquids can be expected to have two such (intersecting) T_g lines.

The hypothesized LLCP is located in the deeply supercooled region, the no-man’s land below the temperature of homogeneous nucleation.^{23,28−30,40,48,49} Various potential model studies^{27−30,37,38,87,120−133} have demonstrated the existence of an LLCP, and Table 1 provides the reported location of the LLCP in the various long-range all-atom models.

Table 1. Critical Temperature, T_c, Pressure, P_c, and Density, ρ_c, Reported Using Different Water Potentials^a.

potential	Tc (K)	Pc (MPa)	ρc (g/cm3)
ST2c23	235	200	1
ST2c122	245	180	0.94
ST2a43	−	−	−
ST2b,c44	−	−	−
ST2b87	237 ± 4	167 ± 24	0.99 ± 0.02
ST2c134	247 ± 3	185 ± 15	0.955 ± 0.010
TIP4P133	190	150	1.06
TIP4P/200527	193	135	1.012
TIP4P-EW124	210	310	1.09
TIP5P121	217 ± 3	340 ± 20	1.13 ± 0.04
TIP5P-E123	210	310	1.09

^aST2a, ST2b, and ST2c are variants of ST2 as described in the text.

Some models show a number of water’s anomalies but do not have an LLCP, e.g., the short-range monatomic mW model.^135,136 On the other hand, other short-range monatomic models, e.g., the Jagla model, do show the presence of an LLCP.¹³⁷ The use of the technique of successive umbrella sampling grand canonical Monte Carlo and of finite-size scaling has allowed to prove rigorously that the Jagla LLCP is a second-order critical point that belongs to the Ising universality class and to determine with great precision its location.¹³⁸ Importantly, the estimate of the LLCP position that was previously obtained by molecular dynamics (MD) simulation¹³⁷ is in very good agreement with the true location of the LLCP in the model, as found with the rigorous finite-size scaling approach.¹³⁸ These results prove that the techniques for locating the LLCP at the maximum temperature of the spinodals in MD finite-size simulations are valid and lead to the same result as the rigorous technique.

The liquid–liquid transition phenomenon for a one-component liquid also applies to other network-forming, tetrahedrally coordinated liquids where simulations show the possible existence of an LLCP, see for example refs (139−144.)

The landmark paper by Poole, Sciortino, Essman, and Stanley²³ that first proposed the possibility of an LLPT in a molecular model of water described their molecular dynamics simulations as using the 5-site, rigid ST2 model¹⁴⁵ that includes both Coulombic and van der Waals forces. Long-range interactions for the Coulombic forces were taken into account using the reaction-field method. We label this variant of the model ST2c to distinguish it from the two other variants that we will introduce below. Poole et al. observed that at sufficiently low temperatures the liquid isotherms exhibit behavior consistent with an approach to a critical point, which they proposed would terminate a liquid–liquid coexistence line in the deeply supercooled region of the phase diagram. More recently, Liu et al.¹¹⁸ used grand canonical Monte Carlo to study the ST2 model with an Ewald summation of electrostatic interactions. This approach determines the free energy of the system as a function of density but does not permit precise control of other order parameters.

An Ewald summation of Coulombic interactions requires an assumption about the dielectric properties of the medium surrounding the system at infinite distance. Reference (118) used vacuum boundary conditions (ϵ_∞= 1), which we will refer to as the ST2b model. Limmer and Chandler^43,44 studied different versions of the ST2 model using a hybrid Monte Carlo approach in which both the density ρ and the orientational order parameter Q₆ that discriminates between disordered liquid and crystalline environments can be controlled. They did not find evidence of an LLPT for any model variation and suggested that results pointing to an LLPT were due to insufficient equilibration and sampling. A subsequent study by Liu et al.¹¹⁷ used NPT Monte Carlo sampling and a weighted histogram analysis method to obtain the free energy as a function of ρ, Q₆, and temperature T. The existence of an LLPT for the ST2b (ϵ_∞= 1) model was confirmed (see Figure 6). For the ST2a (ϵ_∞ → ∞) model, rapid crystallization to an unphysical high-density (ρ ≈ 1.5–1.7 g/cm³) dipolar-ordered ice phase was observed. A phase diagram similar to that shown in Figure 6 (shifted to slightly higher temperatures and pressures) was obtained by Cuthbertson and Poole¹³⁴ and Poole et al.¹⁴⁶ for the ST2c (reaction field) model using molecular dynamics and umbrella sampling Monte Carlo, respectively. The most comprehensive study to date of an LLPT in a molecular model of water was reported recently by Palmer et al.,¹¹⁹ who focused on the ST2b (ϵ_∞= 1) model. Six different computational protocols were used to obtain the free energy as a function of ρ, Q₆, and temperature T, and all three basins (HDL, LDL, and crystal) were sampled reversibly (see Figure 7). The free-energy barrier between HDL and LDL was obtained as a function of system size and found to be consistent with the N^2/3 scaling law expected for a first-order phase transition.

Figure 6.

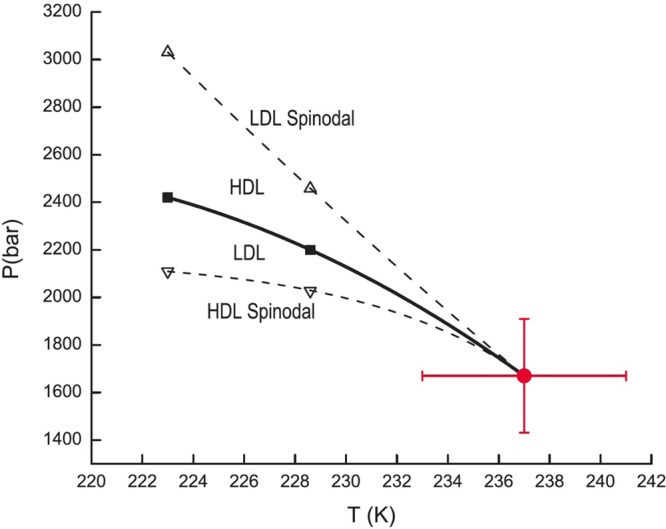
Pressure–temperature projection of the metastable phase behavior of the ST2b model for water from Liu et al.¹¹⁷ showing the liquid–liquid coexistence curve (black squares), the LDL spinodal (up triangles), and the HDL spinodal (down triangles). Solid and dashed lines are a guide to the eye, and the red circle is the critical point from ref (118). Reproduced with permission from ref (117). Copyright 2012 American Institute of Physics.

Figure 7.

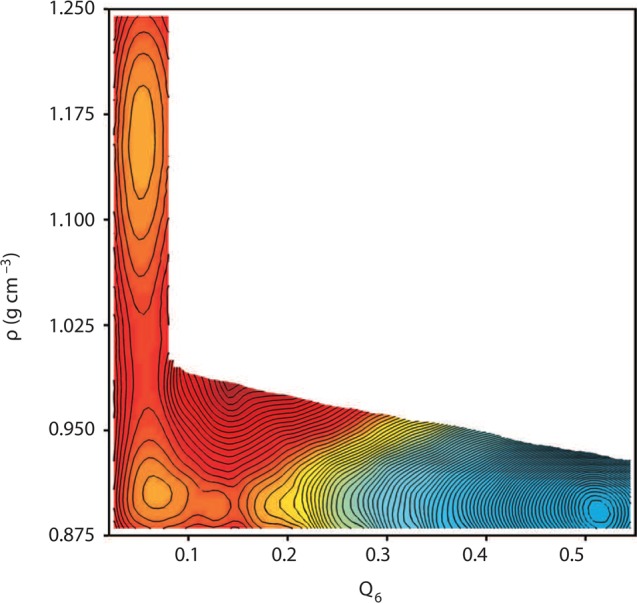
Free-energy surface of the ST2 model with vacuum boundary conditions at 228.6 K and 2.4 bar from Palmer et al.¹¹⁹ These conditions correspond to liquid–liquid equilibrium. Contours are spaced 1 k_BT apart. Reproduced with permission from ref (119). Copyright 2014 Macmillan Publishers Limited.

At LLPT conditions, both liquids are metastable with respect to crystallization, and if the time is sufficiently long and the system size sufficiently large, crystallization will eventually occur. Unlike the mW model,¹⁴⁷ crystallization time scales for the ST2 model of water are longer than the time scales for equilibration of the liquid. For example, in a study of the ST2c (reaction field) model using an N = 4000 molecule system, Yagasaki et al.¹⁴⁸ observed liquid–liquid coexistence at T = 235 K for approximately 800 ns, followed by ice nucleation and crystal growth. In that study a rectangular simulation box was used to minimize the interfacial energy and allow liquid–liquid coexistence to develop. These results were later criticized by Overduin and Patey,¹⁴⁹ who found that the density differences that are observed for TIP4P/2005 and TIP5P water using smaller simulation cells disappear when larger cells (N = 32 000) are considered.

Using the same force-field model as Yagasaki et al., Kesselring et al.^150,151 performed many 1 μs simulations of systems ranging in size from 216 to 729 molecules and found LDL to be stable with respect to the crystal in over 98% of their runs. Small crystal nuclei (“crystallites”) are easily detected using the bond order parameter d₃ introduced by Ghiringhelli et al.¹⁵² This parameter characterizes the bond between two molecules and is designed to distinguish between a fluid and a diamond structure. A molecule is typically considered part of a crystal if three of its four bonds exhibit d₃ < 0.87. In the simulations done by Kesselring et al., tiny crystallites grew and then melted within 1 μs. On the basis of the few crystallization events that occurred, they estimated that the critical size of a crystallite is approximately 70 ± 10 molecules before spontaneous crystallization occurs.

Two recent studies by Sciortino and co-workers rigorously examine the LLPT for a general model of tetrahedrally coordinated liquids¹⁴⁰ and for variations of the ST2 model of water.¹⁵³ They show that bond flexibility affects the relative stability of the liquid and crystal phases. On increasing bond flexibility, the liquid–liquid critical point moves to a temperature where the liquid is more stable than ice. Taken together with the work of Palmer et al.,¹¹⁹ these studies conclusively show that the claim of Limmer and Chandler—that the liquid–liquid transition is a misinterpreted crystallization transition in all atomistic models of water—is incorrect in its generality. It is certainly true for the mW model, while for TIP4P/2005 water the situation is unclear.^{27,148,149,154} The origin of the discrepancy between different simulations using the ST2 model has still not been clearly identified, but potential contributions are discussed in ref (155).

We conclude this section by noting that the strong debate about the potential existence of a LLPT in real and simulated supercooled water has driven a rapid development of computational methodologies and led to rigorous sampling of low-temperature properties in several water models. However, to conclusively determine which case describes real water we will need new experimental data that go deeper into no-man’s land.

4. Competition between Two Alternative Structures

The anomalies of supercooled water and the possibility of metastable liquid–liquid separation in water can be explained if water is viewed as a mixture of two interconvertible organizations of hydrogen bonds whose ratio is controlled by thermodynamic equilibrium.^{38,39,156,157} Beginning with the mixture models of Whiting and Röntgen,^57,58 two-scale models^137,158 have often been invoked as possible explanations of the thermodynamic and dynamic anomalies of liquid water. These models posit a separation of the energy states available to water molecules into two distinct groups: one corresponding to low-energy/low-entropy ordered configurations and the other to high-energy/high-entropy configurations. In this picture the complexity of water is thus modeled by a mixture of these two structural motifs.

Conceptually similar but differently formulated approaches have been taken using two-state models. Tanaka^34,36,156 recognizes that in any liquid locally favored structures with low configurational entropy are formed in a sea of random, normal-liquid structures with high configurational entropy. A phenomenological two-state model approximates this picture as a bimodal distribution of possible molecular configurations and sees cold and supercooled liquid water as a “mixture” of two distinct competing states, where the fraction of each state is controlled by pressure and temperature. Anisimov and co-workers^38,39,159 describe a competition between an ideal entropy of mixing and a nonideal part of the Gibbs energy of mixing. The existence of two structures does not necessarily mean that they will phase separate.^39,157,159 If these structures form an ideal solution, the liquid will remain homogeneous at any temperature or pressure, while the competition between the two structures may cause the density maximum and nondiverging anomalies of the response functions.¹⁵⁷ However, if the solution is nonideal, a positive excess Gibbs energy of mixing could lead to phase separation if the nonideality of mixing of these two states is strong enough. If the excess Gibbs energy is primarily associated with a heat of mixing, the separation will be energy driven. If the excess Gibbs energy is primarily associated with excess entropy, the separation will be entropy driven. The entropy-driven nature of this separation means that if the two states were unmixed they would allow more possible statistical configurations and thus a higher entropy.

One example of this is the Woodcock–Angell–Cheeseman (WAC) model¹⁶⁰ modified by Lascaris.¹⁶¹ The original WAC model was for liquid silica (SiO₂), a close relative of water. Both liquids are tetrahedral and consist of large four-coordinated atoms (O in water, Si in silica) surrounded by twice as many smaller atoms (H in water, O in silica), but unlike most water models the WAC model has no explicit bonds and is simply a mixture of Si⁴⁺ and O^2– ions. It was recently found that the WAC model is remarkably close to having a LLCP,¹⁶² and it was subsequently demonstrated that by decreasing the ion charge the model can be tuned such that a LLCP appears, as indicated by the crossing of the isochores and the diverging response function maxima at the state point where the LLCP is located.^42,122 Increasing the charge separates the isochores and greatly reduces the magnitude of the response function maxima. In addition, the response function maxima move to separate state points, indicating that the LLCP has disappeared.¹⁶¹ Changing the ion charge in the WAC model has this effect due to the Gibbs free energy of mixing, ΔG_mix = ΔH_mix – TΔS_mix. Because increasing the charge makes the Si–O bond more attractive, more Si ions are drawn into the first coordination shell. This increases the HDL entropy and thus the ΔS_mix. The result is that ΔG_mix becomes negative at all temperatures and pressures, and no liquid–liquid transition occurs. A decrease in the ion charge reverses this effect. These considerations suggest that the liquid–liquid transition in the modified WAC model may be entropy driven, a scenario that has also been proposed for water.³⁹

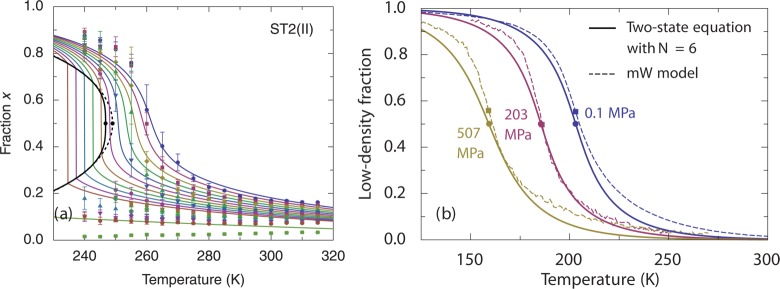
According to Mishima and Stanley,⁴⁰ if the intermolecular potential of a pure fluid exhibits two minima, the interplay between the two indicates that a liquid–liquid separation may be present. Another possibility is a double-step potential caused by hydrogen-bond bending, as shown by Tu et al.¹⁶⁴ A liquid–liquid transition in the two-scale spherically symmetric Jagla ramp model of anomalous liquids has been demonstrated,¹³⁷ and the LLCP has rigorously been proven to be second order and belonging to the Ising universality class.¹³⁸ Ponyatovsky et al.¹⁶⁵ and Moynihan¹⁶⁶ assume that water is a “regular binary solution” of two states, and this implies that the phase separation is driven by energy. Cuthbertson and Poole¹³⁴ and Holten et al.¹⁶³ apply the energy-driven version of the two-state thermodynamics to describe the fraction of molecules in the high-density structure of two versions of the ST2 model of water, which exhibits liquid–liquid separation. Holten et al.¹³⁶ also describe the thermodynamic anomalies of the mW model with the same equation of state as used in ref (39) to correlate thermodynamic anomalies in real supercooled water. Although direct computations of the fraction of molecules involved in the low-density structure in the ST2 and mW models are in agreement with the prediction of the two-state thermodynamics^136,159 (see Figure 8), in the mW model the athermal, entropy-driven nonideality of mixing of the two alternative structures is not sufficiently strong to cause liquid–liquid phase separation. The situation in real water remains less certain, but the recent correlation of available experimental data^39,167 (see Figure 9) favors a nonideality in entropy-driven mixing of the alternative molecular configurations. Thus, from a phenomenological point of view and even without a microscopic understanding of the differences between the alternative configurations, the two-state model clearly yields an equation of state of supercooled water that can be fitted to agree remarkably well with experimental results^{34,39,156,167} (see Figure 9).

Figure 8.

Low-density fraction from simulations of water-like models, and the predictions from the two-state thermodynamics (Reproduced with permission from ref (163). Copyright 2014 AIP Publishing LLC): (a) ST2(II) (denoted ST2b in Table 1), a version of the ST2 model.¹⁶³ Fraction x is the low-density fraction. Symbols are simulation data. Solid curves are theoretical predictions. Dashed curve is a mean-field approximation. (b) mW model. Reproduced with permission from ref (136). Copyright 2013 AIP Publishing LLC. Solid curves are theoretical predictions which include clustering of water molecules with average aggregation number N = 6.

Figure 9.

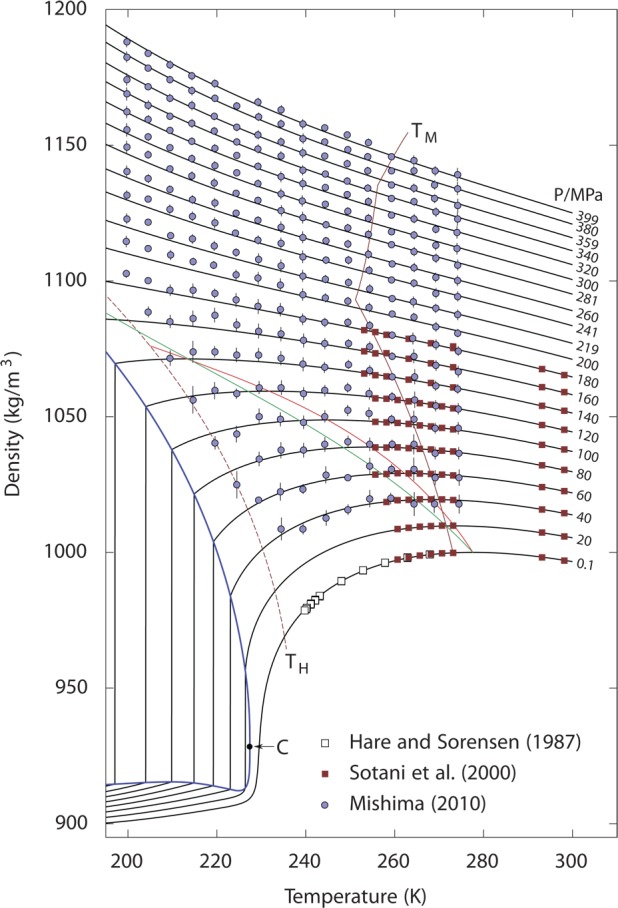
Density of cold and supercooled water as a function of temperature along isobars. Reproduced with permission from ref (39). Copyright 2012 MacMillan Publishers. Symbols represent experimental data.^71,168,169 Black curves are the predictions of the two-state model.³⁹T_M (dark red) indicates the melting temperature, and T_H indicates the homogeneous nucleation temperature. The thick blue line is the predicted liquid–liquid equilibrium curve, with the critical point C. The red line is the line of maximum density, and the green line is the line of a constant LDL fraction of about 0.12.

A difficulty associated with correlating data that are obtained in the experimentally accessible region (above the ice homogeneous nucleation temperature) is accurately locating the liquid–liquid critical point and determining the critical pressure based on these data. Using the optimization shown in Figure 10, any critical pressure value above 100 MPa is excluded and the lower limit is uncertain. This is in contrast to the extensively studied water models, the ST2 model and the TIP4P/2005 model proposed by Abascal and Vega,¹⁷⁰ for which the critical points are located at about 180 and 135 MPa, respectively, see Table 1. However, any attempt to predict the location of a possible LLCP becomes highly uncertain because the anomalous behavior intensifies as it moves into regions of lower temperature and higher pressure where measurements are lacking (see Figure 10). Indeed, we note the uncertainty in the location of a possible LLCP in the TIP4P/2005 model as there have been different proposals,^27,148,154 and the existence of an LLCP in the model has been questioned.^149,171

Figure 10.

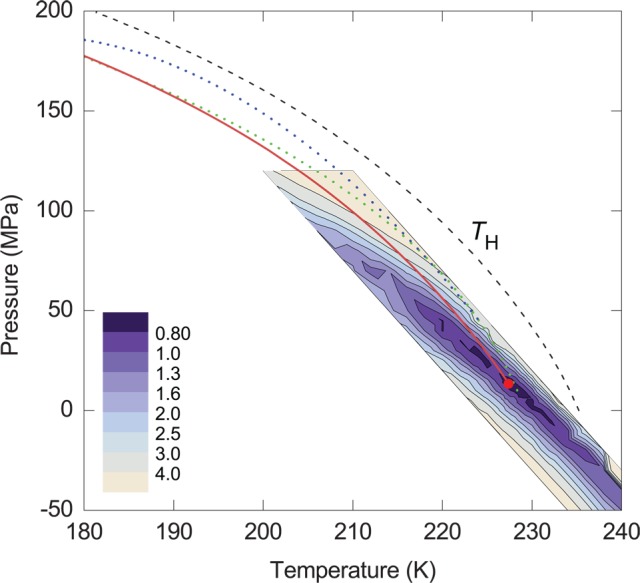
Optimization of the critical-point location (Reproduced with permission from ref (39). Copyright 2012 Macmillan Publishers Limited). For a given location of the critical point and a particular set of the adjustable parameters, the residual for each experimental data point is computed as the difference between the measured value and the computed value of that property. These individual residuals are made dimensionless by an experimental uncertainty and then summed, with the lowest value of the sum of squared residuals that can be achieved for each location of the critical point by varying the adjustable parameters. The solid red line is the hypothesized liquid–liquid transition curve. The dashed curve shows the temperature of homogeneous ice nucleation. The blue dotted curve is the liquid–liquid transition curve suggested by Mishima,⁷¹ and the green dotted curve is the singularity line suggested by Kanno and Angell.¹⁸

4.1. Experimental Structural Results

More generally, two-state thermodynamics can explain “liquid polymorphism”, defined as the existence of a single-component substance in more than one different liquid form.^{72,156,157,172−175} Liquid polymorphism has been experimentally observed or theoretically suggested in molten silicon, liquid phosphorus, triphenyl phosphate, and in some other molecular-network-forming substances.^{21,144,157,172,173} Recent experiments^176−182 suggest the existence of a bimodal distribution of molecular configurations in water. From a molecular point of view, water does not consist of distinct species. It is the nature of the hydrogen-bonding network that implies that fluctuations in density, correlated with local tetrahedral ordering, give rise to structurally distinct regions of local order that in turn give rise to pseudobinary behavior. Indeed, data from small-angle X-ray scattering (SAXS) have been interpreted in terms of density inhomogeneities in the liquid—with an average spatial extent of ∼1 nm at ambient conditions¹⁸³—that grow upon supercooling.¹⁸⁴ Although this interpretation has been criticized,^185−187 it has received support from a purely statistical mechanical perspective.¹⁸⁸

X-ray absorption spectroscopy (XAS) has also indicated the presence of two types of local structure in liquid water: very tetrahedral and very disordered.^179,189,190 The former would correspond to LDL and the latter to HDL. There is general agreement that the pre- (535 eV) and main-edge peaks (537–538 eV) in the XAS of liquid water are fingerprints of distorted H bonds, whereas the postedge (540–541 eV) is associated with strong H bonds and is further enhanced for tetrahedral H-bond structures.^{179,189−193} Interpretations of the spectra in terms of structure either emphasize the ultrafast nature of the X-ray probe and suggest small, instantaneous distortions around a mainly tetrahedral network^193−196 or propose fluctuations that are of a sufficiently long duration and are sufficiently extended that a distinction in terms of local HDL and LDL environments becomes meaningful.^{176,183,185,197}

The most direct evidence of bimodality in terms of local structures is found in X-ray emission spectroscopy (XES) in which the sharp, nonbonding lone-pair peak of gas-phase water becomes broadened and shifted down in energy in crystalline ice (see Figure 11). In water we observe two sharp peaks that interconvert but do not broaden with increasing temperature.^{180,181,183,198−201} The peak close to the peak in tetrahedral ice is assigned to local LDL-like tetrahedral coordination, and the other peak, close to the gas-phase position, is assigned to disordered HDL-like local structures with broken or weakened H bonds. The origin of the split is under debate,^202,203 with one interpretation in terms of differences in final state^198,199 and the other in terms of differences in the initial state.^180,183,204 However, both interpretations require the existence of two different local environments. As further support for a bimodal distribution of structures, we note the recent time-resolved optical Kerr effect (OKE) measurements by Taschin et al.¹⁷⁷ OKE involves low-energy vibrations in the H-bonding network where there are clearly identified signatures of HDL and LDL with the same temperature dependence as in the other spectroscopies.

Figure 11.

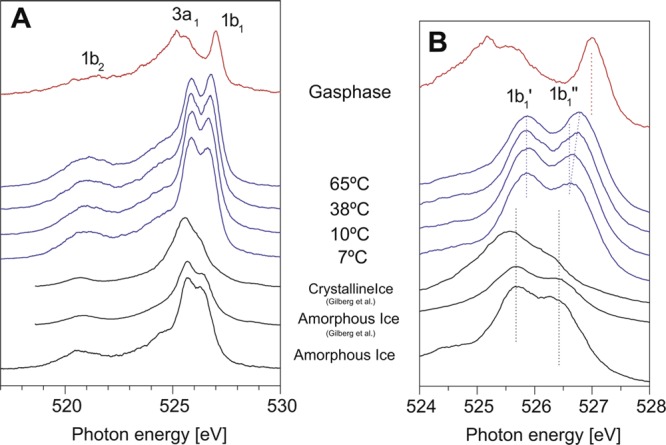
Experimental O 1s soft X-ray emission spectra of gas-phase water, liquid water at different temperatures, and amorphous and crystalline ice, with an energy scale displaying the full spectrum (A) or only the lone-pair, 1b₁ region (B). The excitation energy is 550 eV, well above the ionization threshold. Peak components are labeled based on the molecular orbitals for a water molecule. The highest peak (1b₁) splits into double peaks (1b₁^′ and 1b₁). XES spectra of amorphous (−190 °C (83 K)) and crystalline ice from Gilberg et al.²⁰⁵ are included for comparison. Figure adapted with permission from ref (180). Copyright 2008 by Elsevier.

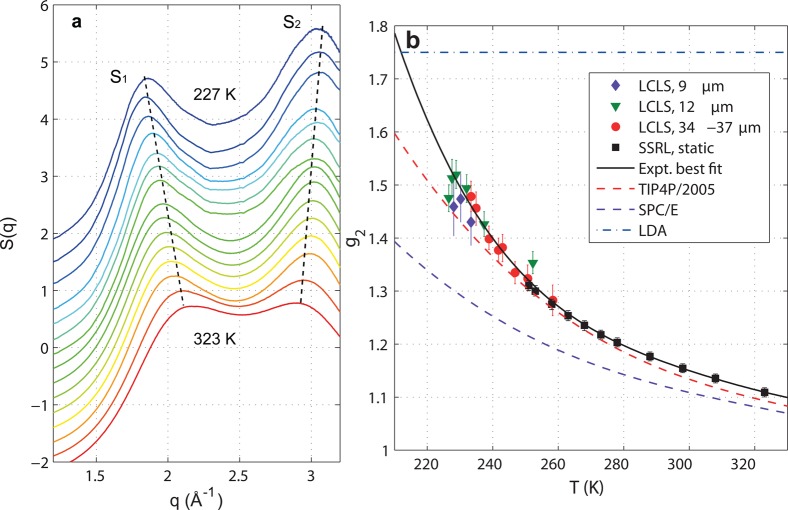
Using an X-ray free-electron laser the transformation of water structure in micrometer-sized water droplets has been observed as they are cooled to below the temperature of homogeneous nucleation¹⁷⁸ (see Figure 12). The droplets are injected into vacuum, where they almost instantly cool through evaporation, and a diffraction pattern is obtained from individual droplets when they are hit by the 50 fs duration, intense X-ray pulses. The temperature of the droplets can be controlled by varying the distance between the nozzle where the droplets are generated and the region where they interact with the X-rays. If the diffraction pattern exhibits Bragg spots the droplets are ice containing, and if it exhibits diffuse rings the droplets are liquid. The lowest temperature at which liquid droplets are still present is 227 K, i.e., 5 K below the previous upper boundary of the no-man’s land. Analysis of the data shows a continuous but accelerated transformation of the structure toward an LDL-dominated liquid.¹⁷⁸ Thus, the structure of water is LDA when it cools through the no-man’s land (to T < 136 K) without crystallization.^99,206−209

Figure 12.

Ultrafast X-ray probing of water structure below the homogeneous ice nucleation using micrometer-sized water droplets falling in vacuum, Reproduced with permission from ref (178). Copyright 2014 Macmillan Publishers Limited. (a) Scattering structure factor, S(q). Data reveal a continuously increasing split of the principal S(q) maximum into two well-separated peaks, S₁ and S₂ (dashed lines). (b) Experimental tetrahedrality (g₂) values, derived from the measured split, Δq, between the two peaks in (a) as calibrated against a fit to molecular dynamics data. g₂ is the height of the second peak in the O–O pair-distribution function. Error bars are estimated from the maximum and minimum Δq values allowed by the uncertainty in the S₁ and S₂ peak positions. Also shown is the fourth-order polynomial least-squares fit to the experimental data (black solid line), where the last (that is, low-T) two data points for the 12 μm diameter droplets and the last data point for the 9 μm diameter droplets are ignored owing to high nonlinearity in the detector response (see ref (178)). For comparison, the temperature dependences of g₂ for the TIP4P/2005 (red dashed line) and SPC/E (purple dashed line) models are depicted along with the characteristic value of g₂ for LDA ice²¹⁰ (blue dash-dotted line).

The transition curve from ref (178) now provides experimental data based on which molecular simulations can be calibrated, but even more importantly it also gives information on the location of a potential LLCP or LLPT.⁴⁵ In Figure 8 we show the temperature- and pressure-dependent fraction of the low-density species in two different models of water. The ST2 model has recently been shown to exhibit liquid–liquid coexistence, and a LLCP and the shape of the low-density fraction curves clearly depend on whether they approach the LLPT or traverse the one-phase region and then the sharpness of the rise depends on the distance in pressure and temperature from the critical point. This was used by Nilsson and Pettersson⁴⁵ to deduce an LLCP, real or virtual, in the range of pressure 500–1500 bar. A virtual LLCP would exhibit instability between HDL and LDL as for a real LLCP but would lead to crystallization before the correlation length can develop a divergence.²¹¹

4.2. Order Parameter

In the present section we will focus on characterizing the local structure related to HDL and LDL based on various order parameters. Since the focus is on the local environment we will here use the terminology locally favored structures to distinguish from the global structure of LDL. We define the locally favored states as states in which a water molecule is hydrogen bonded with four neighbors with a high tetrahedral symmetry and there is no penetration of other water molecules inside the first shell. The other component instead shows significant local disorder with a fifth neighbor at interstitial position.

A two-order parameter model³⁶ provides a framework for understanding the spectroscopic results and the various thermodynamic features in terms of two competing order parameters: a density-dependent order metric that promotes close-packed structures in both the crystal and the liquid and an anisotropic or bond-driven order parameter that promotes open, tetrahedral local order. The local structure of the liquid tends to correspond to that of the underlying crystalline phase, and a triple point is seen, i.e., a point where the low-density crystal, the high-density crystal, and the liquid are in equilibrium.³⁵ Glass-forming tendencies are most pronounced in the neighborhood of the triple point,^212,213 where structural frustration due to competition between the two order metrics is most pronounced.³⁶

The connection between the two-order parameter description of water-like liquids and an atomistic picture of liquid state structure and dynamics was first provided by Errington and Debenedetti using the rigid-body SPC/E water model.²¹⁴ This connection requires that local order metrics be defined in terms of particle positions. A suitable order metric that defines density-driven local order applicable to both simple and complex fluids is the translational- or pair-ordering metric in terms of the atom–atom pair-correlation function g(r).²¹⁵ In the case of H₂O, this order parameter may be defined as

2

where ξ = rρ^1/3 is the distance r between the oxygen atoms of a pair of molecules divided by the mean pair separation ρ^–1/3, where ρ is the number density N/V, and g_OO(ξ) is the oxygen–oxygen pair-correlation function. A convenient measure of local tetrahedrality associated with a given oxygen atom i is given by

3

where ψ_jk is the angle between the bond vectors r_ij and r_ik where j and k in the two summations label the four nearest oxygen atoms. At low densities or temperatures the probability distributions of tetrahedral order P(q_tet) have a peak at high tetrahedrality. At intermediate densities or temperatures P(q_tet) has a bimodal or shoulder structure with a second peak at intermediate tetrahedrality. Order maps displaying the correlation between translational and tetrahedral order provide an interaction-independent summary of the variation of structural order over a wide range of state points. In the case of SPC/E and other rigid-body models of water, one can define a structurally anomalous region in the phase diagram such that all state points in this regime fall on essentially the same curve in the (q_tet, T) plane. This strong correlation between tetrahedral- and pair-order indicates that distortions from local tetrahedrality in the hydrogen-bonded network reduce pair correlations and enhance disorder in the anomalous regime. At high densities, tetrahedral order ceases to be significant and the system behaves as a simple liquid dominated by pair ordering.

The phenomenological order parameter in the two-state model is the extent of the “reaction” between the two alternative structures^39,159,163 (see Figure 8). Thermodynamically, this order parameter belongs to the Ising model universality class and it is a nonconserved dynamic property.¹⁷⁴ However, two-state thermodynamic models cannot microscopically describe the alternative liquid structures in water, thus hindering attempts to build the two-state thermodynamics from purely microscopic information.

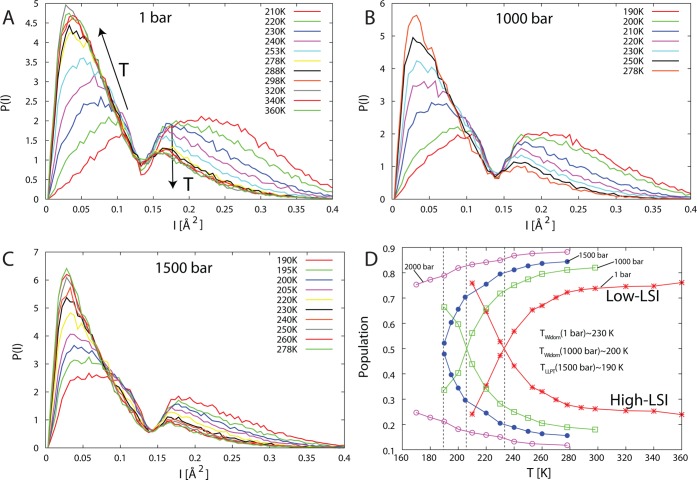
The most popular order parameters used in microscopic two-state models of water are the tetrahedral order parameter q_tet(136,215) (defined in eq 3), g₅(r) (the average density of fifth-nearest neighbor),¹³⁴ ζ (the distance between the first and second shell),²¹⁶ and the local structure index (LSI).^217−221

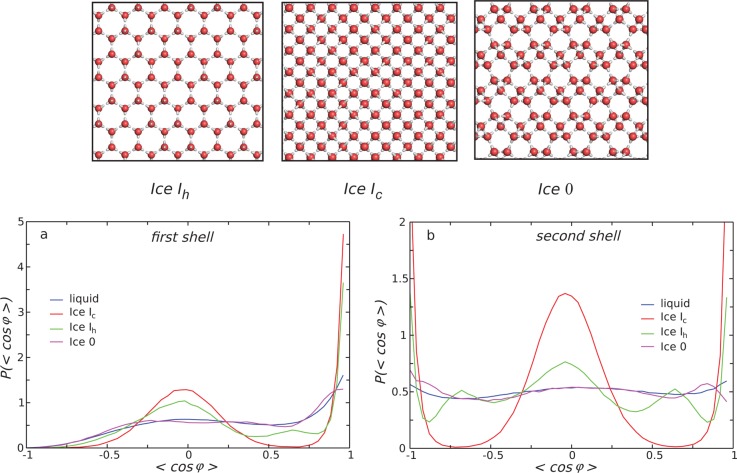
Here we consider several properties of supercooled liquid water that can be defined using the order parameter. In reference to a possible liquid–liquid phase transition in water, evidence has been found that there are two different forms of the liquid that differ in the structure of their second-nearest neighbor shell.⁶⁷ The low-energy/low-entropy state is characterized by an open tetrahedral structure and the high-energy/high-entropy state by a collapsed second-nearest neighbor shell with substantial shell interpenetration.⁴⁰ The microscopic pathway to the crystallization of supercooled water is also relevant in that hydrogen bonding causes water to acquire a high degree of translational order prior to crystallization, i.e., in supercooled water molecules progressively organize themselves in well-defined shells. In contrast, simple liquids such as hard-sphere fluids have a high degree of orientational order prior to crystallization and acquire translational order only after a liquid-to-solid transition.²²² Thus, to detect locally favored states in water, the order parameter must take into account the structure up to the second-nearest neighbor shell, defined in terms of the network of hydrogen bonds, and be based on translational order rather than orientational order. Thus, tetrahedral order only takes into account the first coordination shell and is obtained from bond angles rather than bond distances, and g₅(r) ignores the underlying hydrogen-bond network.

We thus next consider the order parameter ζ,²¹⁶ which measures the distance between the shells of the second and first nearest neighbors. This is obtained by reconstructing the network of hydrogen bonds and then computing for each water molecule the difference between the radial distance of the closest oxygen in the second shell and that of the farthest oxygen atom in the first shell. Locally favored states (S) are represented by a Gaussian population centered around a finite value of ζ, and the disordered state is characterized by a Gaussian population centered around a null value of ζ, with substantial shell interpenetration (ζ < 0).

Figure 13a shows that by decomposing the two populations for many state points it is possible to extract the fraction s of locally favored states, where s is the order parameter that indicates the degree of structural order. This fraction can then be fitted with a two-state model (see the lines in Figure 13a), which is obtained solely from microscopic information. Note that the isobars become mechanically unstable at high pressure and low temperature, indicating the presence of a liquid–liquid critical point (full symbol).

Figure 13.

Two-state model for TIP4P/2005 water. (a) Values of the fraction of the locally favored S state (s) as a function of temperature for all simulated pressures. Symbols mark the values obtained by decomposition of the order parameter distribution, P(ζ), at the corresponding state point. Continuous lines are fits according to the two-state model. (b) Temperature dependence of density for several pressures. Continuous lines are simulation results, while symbols are obtained from the two-state model. Reproduced with permission from ref (216). Copyright 2014 Macmillan Publishers Limited.

The structural order parameter estimated using microscopic measurements enables us to predict quantitatively the magnitude of the anomalies and compare them with those obtained in simulations. Figure 13b compares the simulations (symbols) with the two-state model predictions (lines) for the density anomaly of TIP4P/2005. The two-state model agrees with the measured anomalies, indicating that a microscopic two-state description of the phase behavior of water is possible. Reference (216) carries out extended analyses for both the TIP4P/2005 and the TIP5P models of water.

Although it was recently proposed that a liquid–liquid phase separation can only occur on time scales shorter than the equilibration time of the simulated (or real) liquid—and thus only liquid–solid transitions are possible^43,44—results from several water models showing strong fluctuations between high- and low-density liquid indicate the presence of an HDL–LDL transition.^134,138,150 The extensive study by Palmer et al.¹¹⁹ using several different computational protocols verifies a metastable liquid–liquid coexistence for the ST2 model. For other simulation models, such as TIP4P/2005, the situation is less clear (see discussion in section 3). The studies above were performed in the deeply supercooled and pressurized region of the phase diagram, while water anomalies set in already under ambient conditions. As already discussed, these anomalies find a simple description in a two-state model, and evidence of a bimodal distribution of local, instantaneous structures has been found in ambient real water both from X-ray spectroscopies^{179−181,183} and from measurements of the optical Kerr effect.¹⁷⁷ However, no molecular dynamics simulation has so far shown a bimodal structural distribution under ambient conditions.

On the other hand, Sciortino and co-workers^219,221 applied the local-structure index (LSI) of Shiratani and Sasai^217,218 to the inherent structure of SPC/E water and found that the resulting distribution of this order parameter was bimodal in terms of HDL and LDL at all investigated temperatures. The inherent structure²²³ is obtained by removing thermal disorder, i.e., quenching the instantaneous structure to the nearest local minimum through minimizing the energy in an optimization of the geometry.

The LSI for each molecule i is acquired by putting the distances of the nearest neighbors j from the reference molecule i in increasing order, i.e., r₁ < r₂ < r₃ < ··· < r_n(i) < 3.7 Å < r_n(i)+1, where n(i) is the number of molecules within 3.7 Å from molecule i (using the positions of the oxygen atoms). The LSI distinguishes molecules with well-separated first and second coordination shells from molecules in a disordered environment, containing molecules in interstitial positions, using the parameter I(i) defined by

4

Here, Δ(j;i) = r_j+1 – r_j and Δ_mean(i) is the average of Δ(j;i) over all neighbors j of molecule i within the cutoff. The LSI measures the degree of order in the pair-correlation function out to the second shell for a given oxygen; a high value indicates a highly structured, locally favored tetrahedral or LDL-like, local environment, while a low value indicates a highly disordered, more close-packed or HDL-like structure.^217,218 A connection between the inherent structure of the more realistic TIP4P/2005 water model and the phase diagram of water was made by Wikfeldt et al.²²⁰ They found a perfectly bimodal distribution of structures separated at the same LSI value for all temperatures and pressures (Figure 14A–C). The fraction in each distribution is plotted in Figure 14D, where a weak dependence on temperature is seen in the ambient regime, but as the temperature is decreased into the supercooled regime, an accelerated conversion of low-LSI (HDL) species into high-LSI (LDL) is observed fully consistent with recent measurements on micrometer-sized water droplets where a continuous but accelerated transformation to a highly tetrahedral liquid was observed down to 227 K.¹⁷⁸ Interestingly, the 3:1 ratio between HDL- and LDL-like local environments in the inherent structure at ambient conditions is very close to what has been concluded from spectroscopic measurements.^{177,179−181,183}

Figure 14.

Analysis of the inherent structure in simulations of TIP4P/2005 water. (A–C) Plot of the temperature-dependent distributions of LSI values at (A) 1, (B) 1000, and (C) 1500 bar. (D) Fraction of molecules in each distribution as a function of temperature and pressure. The Widom line (see the definition in section 6) at each pressure is indicated by a vertical line and corresponds to the crossing point between the high- and low-LSI distributions. Figure adapted with permission from ref (220). Copyright 2011 Royal Society of Chemistry.

A direct connection with thermodynamics is found for the crossing point, i.e., where the populations in the two distributions are equal. At each investigated pressure the crossing point coincides with the Widom line (see the definition in section 6) in the model where fluctuations are maximal. A further observation regarding the inherent structure can be made from the temperature dependence within each distribution where with increasing temperature the low-LSI (HDL-like) species exhibit increasing disorder (shift to lower LSI values) while the maximum of the high-LSI (LDL-like) distribution remains at fixed LSI value while the magnitude decreases. This is consistent with the temperature dependence of the two lone-pair peaks in X-ray emission spectroscopy^180,181,183 as well as the temperature evolution of X-ray absorption spectra of water.¹⁹⁰ However, in simulations of ambient water published so far the bimodality of the inherent structure becomes smeared out and more of an average is observed.

5. Nucleation of Ice from Supercooled Water

Ice crystallization creates a severe obstacle to experimentally determining whether there actually exists a liquid–liquid coexistence line and LLCP. Thus, nucleation of ice from the liquid and, in particular, the nucleation rate become essential to determine when designing experiments that aim to study water in no-man’s land. Below the melting point, water is metastable and will eventually freeze into its thermodynamically stable phase (ice). The transformation involves overcoming a free energy barrier so that the freezing is an activated process. Often the transformation into ice occurs on the surface of solid impurities (heterogeneous nucleation). Some solid compounds, such as AgI²²⁴ or feldspar,²²⁵ are quite efficient in reducing the free energy barrier for nucleation. Dust particles of the Sahara desert thus play a key role in the freezing of water in the upper atmosphere.²²⁵ In the absence of impurities, metastable liquid water can survive even at temperatures well below the melting point until a critical nucleus of ice appears in the bulk (homogeneous nucleation). By condensing micrometer-sized water droplets (microdroplets) from saturated vapor in expansion cloud chambers, it has been possible to prepare metastable liquid water at temperatures down to 232 K.^226−228 Below this temperature (known as the homogeneous nucleation temperature T_H) water freezes too quickly for traditional measurement techniques. Note that this is different from the micrometer-sized droplets of Figure 12, which were generated directly as liquid droplets.¹⁷⁸

From the fraction of droplets containing ice as a function of time at a given temperature it is possible to experimentally determine the nucleation rate, J, i.e., the number of critical ice clusters per unit of volume and time. Classical nucleation theory (CNT) has often been used to describe the experimental results. According to CNT, J is given by^229−231J = K* exp(−ΔG*/(k_BT)), where K* is a kinetic prefactor related to the time required for a particle of the fluid to be incorporated into a solid cluster and ΔG* is the free energy barrier. In CNT ΔG* is related to the interfacial free energy γ_sl between the two phases, ice I_h and liquid, and to their chemical potential difference Δμ and is given by the relation ΔG* ∝ (γ_sl)³/(Δμ)². Δμ is well known from experiments and increases as the temperature decreases (thus reducing the free energy barrier), but the experimental value of γ_sl for the ice I_h–water interface is not so well known (values between 25 and 35 mN/m have been reported^232,233). By inserting solid clusters of ice I_h (seeds) in simulations of supercooled water and using CNT to interpret the results it has been possible to estimate J from computer simulations^234,235 in a range of temperatures larger than previous studies.^236−242

Various experimental techniques to determine J are compared in Figure 15. Above T_H, 232 K, microdroplets have been produced in (water-in-oil) emulsions using microfluidic devices by Stan et al.²⁴³ and Riechers et al.,²⁴⁴ whereas Stöckel et al.²⁴⁵ levitated single water droplets in an electrodynamic balance and Murray et al.²⁴⁶ determined the nucleation rate from microdroplets supported on a hydrophobic substrate. All these techniques agree within the error bars of the experiments²⁴⁶ and have determined J within an order of magnitude between 235 and 244 K to 7 × 10⁸ and 5 × 10^–10 cm^–3 s^–1, respectively.^{243−246,255} If CNT is applied to the experimental data in this temperature regime, the fit closely resembles that of a “fragile” liquid. Below 232 K, however, nonconventional techniques that cool water rapidly and simultaneously detect ice nucleation have to be applied to overcome the homogeneous nucleation temperature, which has resulted in that various measurements do not agree. Hagen et al.²⁴⁷ used an expansion cloud chamber to nucleate microdroplets between 228 and 233 K and obtained J of 2 × 10¹⁷ and 2 × 10¹² cm^–3 s^–1, respectively. Hagen et al. relied on using a droplet growth model²⁴⁷ that may introduce large uncertainties in the estimation of the temperature and droplet size.²⁴⁶ Very recently, Sellberg et al.¹⁷⁸ exploited the intense 50 fs X-ray pulses from the Linac Coherent Light Source (LCLS) free-electron X-ray laser to measure the structure of water in microdroplets evaporatively cooled in vacuum to a range of temperatures down to 227 K, i.e., 5 K below T_H. On the basis of these data Laksmono et al.²⁴⁸ analyzed the ice fraction and obtained J ranging from 2 × 10¹¹ to 4 × 10¹² cm^–3 s^–1 as the temperature decreased from 232 to 227 K.²⁴⁸ Sellberg et al. and Laksmono et al. determined the droplet diameters through ex situ optical microscopy and scanning electron microscopy but were forced to rely on Knudsen theory of evaporation, which was calibrated toward reference data above 250 K, to determine the droplet temperature as well as to MD simulations of droplet cooling to verify the Knudsen model.¹⁷⁸

Figure 15.

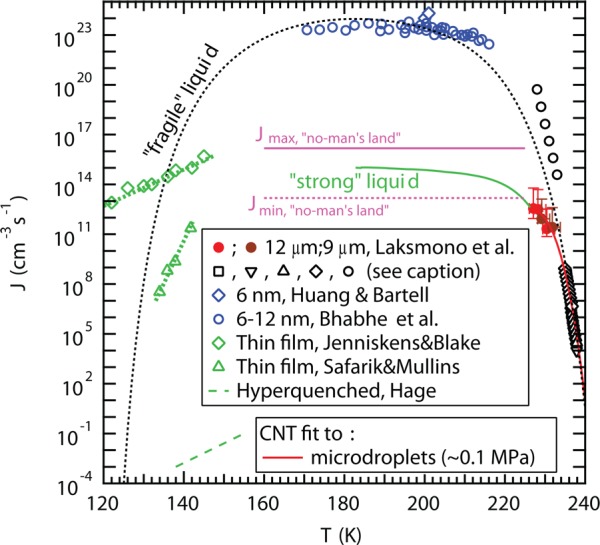
Comparison of experimentally determined nucleation rates J of water using microdroplets (black hollow markers^243−247 and red and brown filled dots²⁴⁸), nanodroplets (blue hollow markers^249,250), thin films (green open diamonds and triangles,^251,252 and hyperquenched water.^253,254 Data of microdroplets (red solid line) and nanodroplets (blue symbols) follow different trajectories where the nanodroplet data might be affected by the large surface area to volume ratio and elevated internal pressure. An upper limit for the nucleation rate maximum within no-man’s land J_max (pink solid line) and a corresponding lower limit J_min (pink dashed line) were calculated from hyperquenching experiments on microdroplets.^99,206−209 The expected CNT behavior for a “fragile” (black dotted line) and a “strong” (green solid line) liquid are included as guides to the eye. We follow Jenniskens and Blake²⁵¹ to obtain the “fragile liquid” CNT curve and also include an expected extension of the nucleation rate into no-man’s land (green curve) based on the requirement to lie between the upper and the lower limits from hyperquenched microdroplets. Figure adapted from ref (248). Copyright 2005 American Chemical Society.

Huang and Bartell,²⁴⁹ Manka et al.,²⁵⁶ and Babhe et al.²⁵⁰ used a different approach and condensed water vapor in a supersonic flow, which reduced the droplets to nanometer-sized dimensions (nanodroplets). This reduces the probability of nucleation but also increases the surface-to-volume ratio and internal Laplace pressure and therefore may not be representable of bulk water at ambient pressure.²⁴⁸ These measurements have yielded J of ∼10²³ cm^–3 s^–1 between 170 and 215 K with nearly no temperature dependence,^249,250,256 which would be the expected behavior if water behaves as a “fragile” liquid in this temperature regime. However, additional information obtained from hyperquenching experiments using micrometer-sized water droplets can be used to place upper and lower limits on the maximum nucleation rate^99,206−209 at temperatures further into no-man’s land. These limits can be defined based on the observation that essentially all droplets crystallize in huge ensembles of droplets of 3 μm in diameter, when they are cooled at 10⁴ K/s, whereas crystallization was not detected when cooled at 10⁷ K/s through the 70 K broad no-man’s land.^99,206−209 These limits are included in Figure 15.

Finally, the crystallization rate has also been measured in the temperature range between 122 and 143 K using thin films of amorphous ice created by vapor deposition. Jenniskens and Blake²⁵¹ obtained J ranging from 4 × 10¹² to 7 × 10¹⁴ cm^–3 s^–1 between 122 and 140 K, respectively, in support of water behaving as a “strong” liquid around the glass transition temperature of 136 K^96,98,258 and in agreement with dielectric relaxation and calorimetric measurements.⁷⁸ In contrast, Safarik and Mullins²⁵² obtained much lower values of J ranging from 3 × 10⁷ to 2 × 10¹¹ cm^–3 s^–1 between 134 and 142 K. These measurements are clearly inconsistent with each other and may be affected by the growth rate that limits the crystallization rate at these temperatures and therefore renders it difficult to obtain J. The nucleation rate in hyperquenched microdroplets as extracted from the data of Hage et al.^253,254 is even more than 10 orders of magnitude smaller than the rates extracted from the thin film measurements. Thus, it remains a challenge to distinguish between crystal growth in preseeded amorphous ice from nucleation in seed-free amorphous ice.

Results for the TIP4P/2005 model of water are shown in Figure 16. The agreement with experiment is good. From the computer simulation, it has been estimated that K* is of the order of 10³¹ cm^–3 s^–1 at 235 K and γ_sl of about 29 mN/m at the melting point (decreasing with temperature). At moderate supercooling, the growth rate of ice, u, is fast, so that the limiting step for crystallizing a certain fraction of the sample ϕ into ice is the time, τ_ν, required for the formation of a critical cluster. However, at low T, u is small²⁵⁹ and the time τ_x required to crystallize a certain fraction ϕ of the sample provides an important measure. According to Avrami’s equation^2,260 this time depends on J and u as τ_x ∝ (Ju³)^−1/4. Since J increases while u decreases as the temperature becomes lower, the time scale τ_x has a minimum. The existence of this minimum has been obtained from brute force simulations for the mW model of water.¹³⁵ It has also been estimated for the TIP4P/2005 model for which results are presented in Figure 17. For this model τ_x reaches a value of about 10 μs at the minimum. To avoid crystallization one must cross the 50 K region around this minimum at least 10 times faster, which means that the cooling rate must be about 50 K/(1 μs) = 5 × 10⁷ K/s. This estimate is in reasonable agreement with the experimental finding that to form water in the glassy state (thus avoiding crystallization) the liquid phase must be cooled at rates higher than 10⁶–10⁷ K/s⁹⁹ and is also consistent with the maximum J in no-man’s land discussed in connection with Figure 15.

Figure 16.

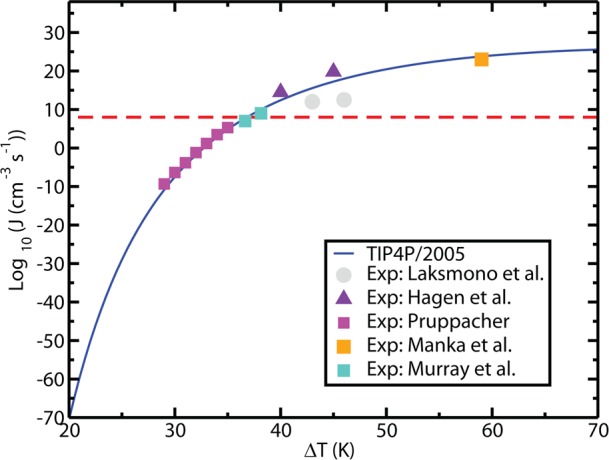
Nucleation rate J as determined for the TIP4P/2005 model (blue solid line) compared to experiments (filled squares) of Pruppacher,²⁵⁵ Murray et al.,²⁴⁶ and Manka et al.²⁵⁶ Experimental results from Laksmono et al.²⁴⁸ (filled circles) and Hagen et al.²⁴⁷ (filled triangles) were also included. The horizontal line corresponds to log₁₀J (cm^–3 s^–1) = 8, which is the approximate value of J at the homogeneous nucleation temperature in experiments (i.e., about 38 K below the melting point). Figure adapted with permission from ref (235). Copyright 2014 American Institute of Physics.

Figure 17.

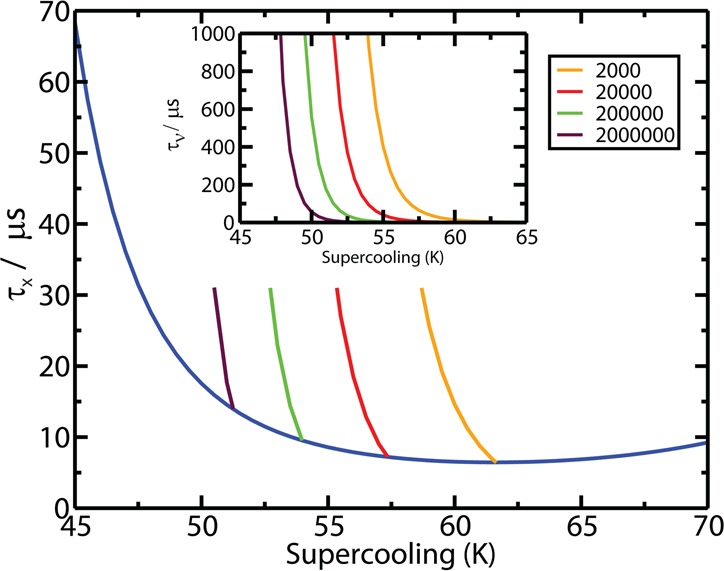
τ_x for ϕ = 0.7 for the TIP4P/2005 model as a function of the supercooling. τ_x is the time necessary to crystallize 70% of the system in an infinitely large system (blue line). (Inset) Plot of the nucleation time, τ_ν, versus the supercooling for systems having different numbers, N, of molecules of water. Figure reproduced with permission from ref (235). Copyright 2014 American Institute of Physics.

Obviously, water is not an easy glass former as one requires high cooling rates to form the glass (i.e., amorphous water). In computer simulations it has been found that certain response functions (as compressibility, heat capacity) reach a maximum when the liquid is cooled at constant pressure. For TIP4P/2005 (at 1 bar) a maximum in the isothermal compressibility has been found^{27,257,261,262} at 232 K, indicating crossing of the Widom line (see the definition and discussion about the Widom line in water in section 6). Results for this maximum are given in Figure 18, where it is shown that the results of several groups are in agreement. As discussed above, for this model Wikfeldt et al.²²⁰ evaluated the amount of HDL and LDL as a function of T at room pressure with assignment based on the inherent structure. At 232 K, the populations of the two species cross. An issue with simulations at low temperatures is equilibration, and it has been suggested that this maximum may be due to transient ice coarsening.⁴⁴ However, as can be seen in Figure 16, the value of J at 232 K and 1 bar (where the maximum in compressibility occurs and 20 K below the melting point of the model) is terribly small (i.e., 10^–70 cm^–3s^–1) so that no ice formation is observed in the simulations; see also the discussion in section 3. In fact, a key question concerning the possible existence of a liquid–liquid critical point in supercooled water^23,117,119 (and/or the existence of a Widom line in response functions) is if the liquid can be equilibrated before it freezes. Limmer and Chandler⁴³ pointed out that a relevant magnitude is the ratio between τ_x and τ_e (i.e., the time required to equilibrate the system). If this ratio is large/small, the system can/cannot be equilibrated before it freezes. It is also important to point out that both τ_x and τ_e may depend on the system size.²⁶³ For the mW model the maximum in the compressibility at ambient pressure cannot be reached since water freezes first. This is a clear case where the ratio of τ_x to τ_e is close to one and one cannot observe some of the water anomalies because water simply freezes first. However, for TIP4P/2005 water at room pressure this seems not to be the case, and the maximum in compressibility occurs without any indication of ice formation. It would be of interest to analyze this ratio at higher pressures. The fact that two different water models behave differently means that “chemistry matters” and one cannot expect universal behavior for all water models. Thus, it is difficult to establish definite conclusions. Further studies both from experiment and from simulations determining both equilibration and nucleation times in droplets between the nanometer and the micrometer scale would be very useful to clarify the value of the ratio between τ_x and τ_e in real water.

Figure 18.

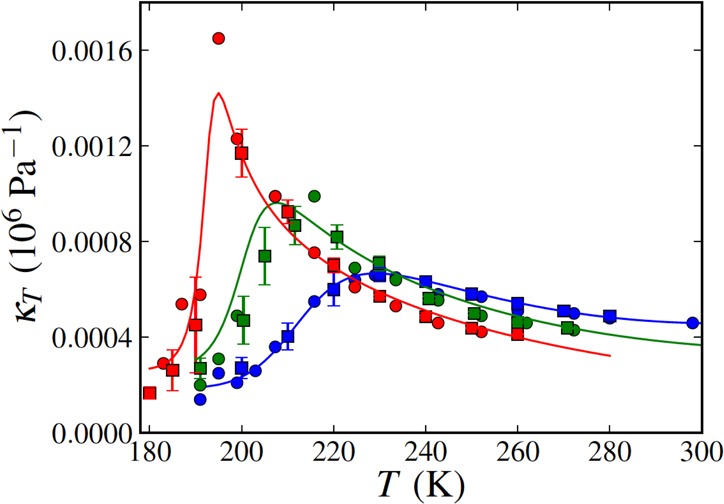
Isothermal compressibility of TIP4P/2005 water at 1 (blue), 70 (green), and 1200 bar (red) as a function of temperature. Symbols indicate the simulated values: squares (with error bars) obtained by Bresme et al.²⁵⁷ and circles (without error bars) obtained previously by Abascal and Vega.²⁷ Curves represent values calculated from the two-structure equation of state. Figure reproduced with permission from ref (257). Copyright 2014 American Institute of Physics.

5.1. Local Structural Ordering in Water Has an Impact on Ice Nucleation

Structural ordering in water involves both translational and orientational ordering, reflecting the nature of hydrogen bonding that selects not only distance but also orientation. It has been proposed that the local structural ordering in water controls not only water’s anomalies but also ice nucleation and that this feature may be generic to so-called water-type liquids.^35,36

An analysis of locally favored structures in simulated water reveals that a large fraction of second-nearest neighbors participates in five-membered rings of hydrogen-bonded molecules and that this fraction increases with decreasing temperature and pressure. These five-membered rings, being absent in the stable crystalline phases of ice (the cubic and hexagonal polytypes), have been proposed to be responsible for the long lifetime of the locally favored states^36,157 and to act as a source of frustration against crystallization to ice I.^216,242 As the temperature decreases, the lifetime of hydrogen bonds increases and the opening of five-membered rings to form six-membered rings becomes increasingly rare. This can partly explain why water has such a large metastability gap, in which, in the absence of impurities, it can persist in its liquid form down to 40 degrees (°C or K) below the melting temperature.

Work by Molinero and collaborators has shown that homogeneous crystal nucleation starts from tetrahedrally ordered regions inside the liquid phase.¹³⁵ In the language of two-state models, crystallization should thus be initiated from locally favored structures, which already have the full translational symmetry of the crystal up to the second shell. These locally favored structures have long lifetimes at supercooled conditions due to the inclusion of five-membered rings of hydrogen-bonded molecules, which severely constrains the orientational degrees of freedom of the involved water molecules and thus stops the development of the orientational order necessary to trigger the liquid-to-ice I transition. The differences in local structure between the supercooled liquid phase and the ice I phase can be measured with quantities such as the dipole–dipole spatial correlation or the topology of hydrogen-bond loops (see Figure 19).

Figure 19.

(Top) Crystal planes for the stable phases and ice 0. (Bottom left) Distribution of the average angle ⟨cos θ⟩ between the dipole moment of a molecule and its hydrogen-bonded neighbors for TIP4P/2005 water at T = 200 K and P = 1 bar in the liquid phase and the ice I_c, I_h, and ice 0 phases. (Bottom right) The same as in the left panel but for second-nearest neighbors. Adapted from ref (242). Copyright 2014 Macmillan Publishers Limited.

To overcome frustration effects, the pathway to crystallization can occur through intermediate steps, in line with Ostwald’s empirical step rule of phases²⁶⁴ (see, e.g., ref (265) for a theoretical basis in terms of minimum entropy production). In fact, in many molecular and soft-matter systems, crystallization does not occur directly into the stable crystalline phase but instead involves one or more intermediate steps where the melt crystallizes first in metastable phases.²⁶⁴ These metastable crystals are structurally more similar to the melt than to the stable phase. This structural similarity leads to a significant reduction of the interfacial energy, although the bulk free energy of metastable states is only intermediate between the one of the melt and that of the stable phase.

The idea of two-step water crystallization involving a metastable phase was recently put forward in ref (242). The authors identified a novel metastable phase, called ice 0, with a tetragonal unit cell with 12 molecules, the thermodynamic and structural properties of which are intermediate between the melt and the solid crystalline phase. This is shown in Figure 19, where the average dipole–dipole orientation is computed between molecules which are first neighbors (bottom left) and second-nearest neighbors (bottom right). The angle distribution is very similar between the supercooled phase and ice 0, in contrast with the distributions of both the hexagonal and the cubic ice forms. Moreover, ice 0 is rich in five-membered rings, which are also very common within the locally favored structures where crystallization first originates.

The structural similarity between supercooled water and the metastable ice 0 form plays an important role in homogeneous ice nucleation. According to Ostwald’s step rule of phases, first a small nucleus of the metastable phase should form, which later converts to the stable ice I form. It is thus natural to expect that close to the homogeneous nucleation line, where the size of the critical nucleus is negligible, the rate of ice nucleation should be controlled by the thermodynamic properties of ice 0. Reference (242) has indeed shown that the homogeneous nucleation line for the mW model of water coincides with a line of constant thermodynamic driving force with respect to ice 0 (i.e., the homogeneous nucleation line is the locus of constant chemical potential difference between the melt and ice 0). This scenario was confirmed both by direct simulations and by computation of the nucleation rates of ice.

In Figure 20 the phase diagram of mW water is reported, with dots representing the locus of homogeneous nucleation and the dashed line that of constant driving force with respect to ice 0. This suggests that it is possible to derive the homogeneous nucleation line from purely thermodynamic arguments. Furthermore, by adopting translational order of the second shell as the order parameter, it is possible to describe the phase behavior of liquid water to a good approximation from purely microscopic information.

Figure 20.

(Top) Snapshot of two configurations with the birth of a small crystalline nucleus (left) and a section of a nucleus of critical size (right). The color code is yellow for ice I_c, green for ice I_h, and magenta for ice 0. (Bottom) P–T phase diagram of mW water. Continuous lines indicate coexistence between the liquid phase and different crystal structures: ice I_h/I_c (blue), ice 0 (red), and clathrate CS-II (green). Dashed lines indicate constant chemical potential differences between the liquid and ice I_h/I_c (βΔμ = −0.721, in blue) and the liquid and ice 0 (βΔμ = −0.365, in red). The green dashed-dotted line is the I_c/CS-II coexistence line. Red open circles indicate state points where homogeneous nucleation is observed in simulations. Adapted from ref (242). Copyright 2014 Macmillan Publishers Limited.

Locally favored states are stabilized by five-membered rings of hydrogen-bonded molecules, which act as a source of frustration against crystallization to ice I. This dynamical pathway reflects in the crystallization transition, in which the metastable crystalline phase can play an important role. In particular, there is evidence that a novel metastable phase, ice 0, being structurally similar to the supercooled melt, can act as an intermediate step during crystallization. Water would first transform into small nuclei of this phase that then grow into the stable crystalline phases. According to this scenario, the homogeneous nucleation line would then be controlled by the thermodynamic properties of ice 0.

6. Relation between Dynamics and Thermodynamics

The dynamical behavior of bulk water simulated upon supercooling^266,267 fits in the framework of the idealized version of mode coupling theory (MCT).²⁶⁸ The normal diffusive behavior of a liquid is Brownian. When we start to follow the motion of a particle (at t = 0) the single particle has an initial ballistic diffusion and then switches to a Brownian (random) regime. When a simple liquid is cooled below the melting line the dynamics starts to be dominated by the “cage effect”, which means that after the initial ballistic behavior the particle is trapped by the transient caging by its first neighbors and rattles in this cage until the cage relaxes and the particle is free to diffuse away and restore the Brownian regime. Upon supercooling the relaxation time of the cages becomes longer and longer and relaxation times of the liquid stretch by orders of magnitude. The ideal version of the theory predicts that at the MCT crossover temperature T_C all cages are frozen. If structural relaxations were the only relaxation channels for having an ergodic liquid then T_C would be the glass transition temperature. When the relaxation time of the cage is stretched enough, already slightly above T_C, hopping processes start and the liquid does not lose ergodicity even below T_C, where cages are frozen and these activated processes become the only source of diffusion.

Glass-former liquids which are described by MCT show relaxation times with a super-Arrhenius behavior. This behavior can be phenomenologically fitted either with the Vogel–Fulcher–Tamman (VFT) relation²⁶⁹

5

or with the MCT power law²⁶⁸

6

and this behavior is termed “fragile”. Below T_C, according to the idealized version of MCT, the system is frozen, but since in real structural glasses hopping processes restore ergodicity, around T_C the liquid turns its behavior to that of a strong liquid.^268,270 The relaxation time of strong liquids increases upon decreasing temperature with an Arrhenius behavior²⁷¹

7

The crossover from non-Arrhenius to Arrhenius behavior is referred to as a fragile-to-strong (FTS) crossover, and it is a feature of many glass formers, see for example refs (272) and (273). MCT provides therefore an explanation to the fragile–strong crossover without requiring the existence of a LLPT.

In the case of water however the MCT crossover temperature, which always falls close to the FTS transition temperature, is very close to the singular temperature T_S,^266,267 which is the temperature where thermodynamic and dynamic quantities show power law divergences.^1,12 This finding points to a connection between the glassy dynamics and the thermodynamics in water.

Experimental observations have demonstrated that bulk water behaves as a fragile liquid.^4,274,275 The translational region of Raman spectra of water has been interpreted in terms of scaling behavior predicted by MCT with a T_C close to T_S.²⁷⁶ Relaxation times from time-resolved spectroscopy follow MCT predictions²⁷⁷ and show a T_C close to T_S in agreement with simulations.^266,267 On the basis of two-dimensional infrared spectroscopy of water from 293 K down to supercooled (260 K), Perakis and Hamm²⁷⁸ used a power-law fit to deduce an exponent γ = 2.2 and a singularity temperature T_S = 221 K. We note that very recently Dehaoui et al.²⁷⁵ found that viscosity and diffusivity are not coupled in water while viscosity remains coupled to rotations. MCT predicts that diffusivity is coupled only to translational viscosity as it does not take into account contributions to viscosity coming from rotations. The finding by Dehaoui et al.²⁷⁵ is due to the fact that when a molecular glass-former liquid is supercooled the translational diffusion coefficient gets fractionally decoupled from viscosity, while rotational diffusion remains coupled to viscosity.²⁷⁹ This result for water further supports the idea that water behaves as a true glass former.

It is important to stress that in water, a network-forming liquid, the caging phenomenon is due to the breaking and reforming of the hydrogen-bond local network.²⁸⁰

The change in behavior from fragile to strong in water was experimentally discussed,²⁸¹ also pointing out that the FTS crossover in water is connected to the presence of a thermodynamic event. An FTS crossover in water was also observed in computer simulations for SPC/E water.²⁸²

Though simulation studies and experimental results approaching the no-man’s land region of bulk water have shown evidence supporting the existence of LLPT, advanced experimental techniques are still needed to reach this no-man’s land region^178,283 in order to establish whether an LLPT exists in deeply supercooled water. Experiments on water in confinement have shown that a fragile-to-strong (FTS) transition line as a function of pressure was pointing to where the LLCP is supposedly located.²⁸³ On the basis of a simulation study on the two-scale Jagla model with an accessible LLCP, Xu et al. proposed an alternative way to detect the LLCP from the one-phase region above the LLCP at higher temperature and lower pressure.^{42,122,137,284} Generally speaking, in a fluid, when moving away from a critical point into the single-phase region, the correlation length keeps a maximum reminiscent of the critical divergence. On approaching the critical point from this region, thermodynamic quantities such as the specific heat and the isothermal compressibility show maxima that are expected to merge on a pseudocritical single line terminating at the critical point. The maxima of those response functions collapse on the same line on approaching the critical point because they become proportional to power laws of the correlation length. This line, called the Widom line,^42,137 is defined as the loci of maxima extending from the critical point into the single-phase region. Moving away from the critical point into the single-phase region, the maxima are progressively smeared out and their values decrease.²⁸⁵ If a second critical point exists in water, the system undergoes a continuous transition from HDL-like to LDL-like liquid upon cooling at constant pressure in the one-phase region.^{42,122,137,284} Thermodynamic response functions, such as the isobaric heat capacity, C_P, isothermal compressibility, κ_T, and thermal expansion coefficient, α_P, show extrema in this region, the loci of which asymptotically approach one another and converge to the Widom line in the vicinity of the LLCP. This phenomenon has been clearly detected in numerous water simulation studies: the Widom line pointing to the LLCP has been found for the ST2 and Jagla potentials,^{42,122,137,284} for the TIP4P potential,^133,286 and for the TIP4P/2005 potential.²⁷ It has also been found in simulations of aqueous solutions^133,286,287 as will be discussed in section 9. In experiments on supercooled water, the Widom line is of particular interest since it can be used to trace the hypothesized LLCP from the one-phase region, thus avoiding the two-phase region where crystallization occurs easily. Across the Widom line not only the structural response functions but also the dynamic properties change and a unified picture of slow dynamics and thermodynamics emerges where a FTS dynamic crossover happens for water upon crossing the Widom line as explicitly found in bulk water for the ST2 and Jagla potentials,^42,137,284 the TIP4P potential,²⁸⁸ and more recently for the TIP4P/2005 potential.²⁸⁹ A recent study of the van Hove self-correlation function for TIP4P/2005 water explicitly connects the freezing of the structural relaxations and the start of activated processes to the FTS transition.²⁸⁹ This coincidence between the FTS and the Widom line also persists in solutions^290,291 (see discussion in section 9). We note here that these findings clarify the connections between glassy dynamics and thermodynamics that are peculiar to water and that were hypothesized from the past studies discussed in connection with MCT above.

Xu et al.²⁹² and later Wikfeldt et al.²²⁰ showed that the populations of LDL-like and HDL-like structures in simulated water change upon crossing the Widom line, and due to these structural changes the system shows the dynamic crossover from non-Arrhenius (fragile) behavior at higher temperature to Arrhenius (strong) behavior at lower temperature.^{42,122,137,284,288,290,291}

The structural change is observed experimentally by infrared (IR), nuclear magnetic resonance (NMR), and quasi-elastic neutron scattering (QENS) experiments on confined water and by X-ray scattering measurements in bulk water¹⁷⁸ at ambient pressure. This is consistent with the results of model studies upon crossing the Widom line from the one-phase region in water. Using QENS and NMR on water confined in MCM-41, Liu et al. observed a cusp-like dynamic transition,²⁸³ from non-Arrhenius (fragile) behavior at high T to Arrhenius (strong) behavior at low temperature. This transition was linked to the FTS transition upon crossing the Widom line in the vicinity of the LLCP with the high- and low-temperature liquids corresponding to the HDL and LDL, respectively. The picture of water confined in MCM-41 undergoing a FTS was reproduced, linked to bulk water and framed in the MCT context by a simulation study^293−295 (see also the section on confined water). Fourier transform infrared (FTIR) experiments on confined water also showed that an HDL-like to LDL-like continuous transition occurs upon crossing the Widom line (see Figure 21).²⁹² According to these experiments, we should be able to trace the LLCP—if it exists—as the terminal point of the dynamic crossover in the one-phase region, located at P_c = 1600 ± 400 bar and T_c = 200 ± 10 K. However, it must be noted that the cited pressure is that applied to water using a fluid outside the pores. The actual pressure in water might be different and even negative due to the Laplace pressure effect.^296,297

Figure 21.

Experimental IR results for structural change of confined water upon crossing the Widom line (Adapted with permission from ref (292). Copyright 2009 Macmillan Publishers Limited.). (a) Relative population of HDA-like and LDA-like water species as a function of temperature. (b) Derivative of the relative population for HDA-like and LDA-like water species. The maximal change occurs at the temperature T_max, where the Widom line is crossed.

Connecting entropy with structure-based order parameters for fluids, particularly in the context of biomolecular simulations, has been an active area of research.^298−304 A useful route in the context of simple and anomalous liquids is provided by the multiparticle correlation expansion of the entropy. S_e = S₂ + S₃ + ..., where S_n denotes the entropy contribution due to n-particle correlations.^305−309 Since the thermodynamic excess entropy can be obtained from simulations or from calorimetric data, the multiparticle expansion serves to highlight the role of pair-, triplet-, and higher-order correlations in determining the liquid entropy. The behavior of simple liquids is dominated by pair correlations, which contribute 85–90% of S_e. For multiatomic systems, the pair-entropy term can be generalized in terms of atom–atom pair-distribution functions accessible from simulations, X-ray, or neutron scattering. For tetrahedral liquids such as water, however, the three-body or triplet correlations can be significant since they are associated with the locally anisotropic nature of the liquid-state network.

A convenient conceptual bridge connecting thermodynamic and dynamic properties of dense fluids is also provided by excess entropy scaling relationships for transport properties; the excess entropy, s_e, is defined as the difference between the entropy of the fluid and that of the ideal gas.³¹⁰ In dense fluids, diffusion proceeds by a combination of binary collisions and cage relaxations. Transport properties can be conveniently reduced to dimensionless form using reduction factors based on kinetic theory. Rosenfeld and others^310−325 showed that for a wide range of simple liquids the following semiempirical scaling relationship was valid: X* = A exp(αS_e), where X* are dimensionless transport properties, including diffusivity, viscosity, and thermal conductivity. The scaling parameters A and α depend on both the nature of the interactions and the transport property.

For example, for simple liquids, the scaled diffusivity, D_R^* = Dr^1/3/(k_BT/m)^1/2, obeys excess entropy scaling with quasiuniversal values of A and α. Rosenfeld-type exponential scaling relationships between transport properties and excess entropies hold for a much wider variety of dense liquids in the stable and supercritical regimes than was originally assumed, including liquid metals, molecular fluids, ionic melts, core-softened model fluids, chain fluids, room-temperature ionic liquids, and colloidal fluids, even though the exact scaling parameters may vary substantially. Deviations from Rosenfeld-scaling behavior arise as a consequence of cooperative effects, but for a large number of fluids, transport properties from a wide range of state points scale with the excess entropy.

Stanley and co-workers³²⁶ used the TIP5P water model to investigate the relationship between the excess entropy and anomalies of water. They report that the two-body excess entropy reliably predicts the regions of structural, dynamic, and thermodynamic anomalies of the model as well as the location of the Widom line. Given the idea behind Rosenfeld scaling, Gallo and co-workers^327,328 have shown in a recent study on TIP4P water that if s_e is approximated with s₂, i.e., the two-body term of the excess entropy, the same FTS transition of the diffusion coefficient is found for s₂. The two-body approximation for s_e might not be valid in all contexts of interest but the aforementioned simulation studies indicate that the two-body term shows the FTS crossover and therefore captures the features of water behavior also in the high-density side. It would be very important to test this result from experimentally measured radial distribution functions of water upon supercooling. The relation between s₂ and the radial distribution function is in fact straightforward, and for a one-component fluid it is

8

where g(r) for water is the oxygen–oxygen g(r).

Stillinger–Weber liquids with a variable tetrahedrality parameter can be used to model molten phases of Group 14 elements (C, Si, Ge, Sn, Pb) as well as provide a coarse-grained, monatomic (mW) model for water.^{135,147,329−332} As a function of increasing tetrahedrality, the triplet contribution to the excess entropy is significantly higher than the pair-entropy contribution.³³³ Transformation to a triplet-dominated fluid strongly favors the formation of a tetrahedral crystal as well as the existence of a heat capacity anomaly, and the local order within the first neighbor shell is a critical factor in determining the behavior upon supercooling. The characteristic rise in heat capacity on the isobaric cooling of tetrahedral liquids is closely tracked by the pair and triplet contributions to the entropy (see Figure 22) and thus provides a direct connection between structural correlations and thermodynamics. Preliminary results for triplet O–O–O correlations in pair-additive, rigid-body, atomistic models of water strongly resemble the mW water model.³³⁴

Figure 22.

Multiparticle correlation. Contributions to the entropy and the heat capacity anomaly. The total (C_P), pair (C₂), and triplet (C₃) contributions as a function of temperature (T) for the monatomic water (mW) model at 1 atm pressure. Reproduced with permission from ref (333). Copyright 2014 American Institute of Physics.

We note that the phenomenon of the Widom line is of interest also in the supercritical state, i.e., in the one-phase region above the well-known liquid–gas critical point both in water³³⁵ and in other liquids.^144,336,337 In supercritical water the Widom line is clearly found both in experiments and in simulations.^335,338 A dynamic crossover passing through the Widom line has also been shown to exist in the supercritical state of water where changes in trends in diffusion coefficient and viscosity have been observed upon crossing this line on isobaric paths.^335,338 Similarly, Simeoni and co-workers³³⁶ studied supercritical argon and found a dynamical crossover associated with the Widom line which divided the single-phase region beyond the critical point into liquid-like and gas-like in terms of the dynamical properties.

Finally, we note that there is yet another approach to make a link between structure and dynamics on the basis of a two-order-parameter model.^36,339 In this approach, it is assumed that locally favored structures have a higher activation energy than the normal liquid structures. Then the total activation energy is given by their average. In this way, the dynamic anomaly can be described by the same order parameter used for explaining the thermodynamic anomaly.

We will discuss further the fragile to strong transition in water and the connection between dynamics and thermodynamics in sections 8 and 9.

7. Stretched Water

Because ice nucleation prevents conventional techniques from reaching the low-temperature region where a liquid–liquid transition or its signature might be observed, researchers have attempted to follow other routes. These attempts will be discussed in the following sections: bulk water at negative pressure (this section), confined water (section 8), and aqueous solutions (section 9).

Water, like any liquid, can resist mechanical traction and become metastable with respect to its vapor.² We will not be able to claim that we understand the “most anomalous liquid” properly until we have learned to measure and understand the properties of water and its solutions accurately also in the negative-pressure domain. In particular, the behavior of the line of density maxima (LDM) at negative pressure can help discriminate between the proposed theoretical scenarios, depending on whether when the pressure decreases the LDM reaches a maximum temperature or its temperature keeps increasing (see Figure 3). Moreover, a region exists, at negative pressure and temperatures below the melting point of ice, where water is doubly metastable with respect to both ice and vapor. Is it possible to observe the Widom line (or one of the lines of maxima in a thermodynamic response function) in the doubly metastable region? A comparison between the experimental line of homogeneous nucleation of ice and simulations with the TIP4P/2005 potential (Figure 23) suggests that it might be possible.^47,297

Figure 23.

Pressure–temperature phase diagram of water. Reproduced with permission from ref (297). Copyright 2015 Elsevier. Colored areas are used to identify the different possible states for liquid water. The melting line of ice I_h is shown at positive pressure by a solid blue curve and its extrapolation to negative pressure by a dashed blue curve. Black crossed white squares show the experimental supercooling limit.³⁴⁰ They define the homogeneous nucleation line based on conventional experimental techniques (solid black curve), which is extrapolated here to negative pressure (dashed black curve). Recent experiments using fast cooling techniques can shift the nucleation line to lower temperatures (new border, purple curves); they are displayed as white triangles²⁵⁶ and circle.¹⁷⁸ Isochores of TIP4P/2005 water for the two densities used in a recent experiment⁴⁷ are shown by the thick red and black curves. Simulations of TIP4P/2005 water are performed to find the maximum of κ_T along several isobars (brown diamonds), defining the line of maxima in κ_T (brown curve), that might emanate from an LLCP (white plus symbol). Because the predictions of TIP4P/2005 are in satisfactory agreement with the reported experimental results in the supercooled region,²⁶¹ this figure seems to indicate that the line of maxima in κ_T (and other extrema in the response functions) is not accessible to conventional experiments at positive pressure but might become accessible to fast cooling techniques at positive pressure or to conventional techniques but in the doubly metastable region at negative pressure.

Before describing experiments on water at negative pressure, we discuss the pressure of the LLCP found in simulations: could it actually be located at negative pressure? This possibility was first suggested by Hideki Tanaka. Simulating the TIP4P model along the 0.1 MPa isobar, he found a large change in density and potential energy around 213 K,³⁴¹ which he interpreted as the signature of a first-order transition between two liquid phases. The large changes were confirmed by simulations at +200 MPa, whereas they disappeared at −200 MPa,³⁴² from which it was concluded that the LLCP pressure should be between −200 and 0.1 MPa. However, Sciortino et al.³⁰ later found this interpretation to be incorrect. They noted that a first-order transition should manifest itself as a van der Waals loop in a simulated P–V isotherm, which is not seen down to 200 K with the TIP4P model. The large changes mentioned above are rather due to a Widom line. Locating the line of compressibility maxima along isobars for TIP4P, Sciortino et al. concluded that if a LLCP exists for TIP4P, it should be at T < 200 K and P > 70 MPa. The location of the LLCP was later refined to 190 K and 150 MPa.¹³³ Other reports of LLCP at negative pressure were made by Brovchenko et al., who performed restricted ensemble Monte Carlo simulations of the isotherms of homogenized systems and phase equilibria simulations in the Gibbs ensemble. Using simple truncation of electrostatic interactions, they found three liquid–liquid transitions in ST2⁸³ and two transitions in the TIP4P, TIP5P, and SPCE models.⁸⁴ Among these transitions, one was at negative pressure for ST2, TIP4P, and SPCE. When the long-range Coulombic forces were treated with reaction field, two transitions at positive pressure were found in ST2.⁸⁴ These studies were however seriously questioned by Liu et al.⁸⁷ All the technical details mentioned here have their importance, as only one liquid–liquid transition was found by Liu et al.⁸⁷ for ST2 using histogram-reweighting Monte Carlo simulations in the grand-canonical ensemble with Ewald summation treatment of long-range electrostatic interactions. Table 1 also shows how the location of the LLCP depends on the technical details of the simulations. Still there is now consensus that for all realistic models of water there is no more than one LLCP at positive pressure. What about real water? At present there is no direct experimental evidence for a LLCP. However, under the assumption that it exists, it is interesting to investigate where the available data for real water would locate the LLCP. This is the logic followed by Holten and Anisimov.³⁹ In their two-state model (see section 4) they treated the LLCP coordinates as a fitting parameter to be optimized to reduce the deviation between model and experiment. They found that this deviation changes only slightly in a narrow band in the P–T plane, which crosses zero pressure (see Figure 10). This prevents reaching a firm conclusion about the sign of the critical pressure and calls for more measurements on metastable water, including at negative pressure.

Whereas negative pressures are routinely accessible in simulations, experiments are notoriously difficult because a small perturbation can trigger the rupture of the liquid by nucleation of a bubble (cavitation). The most documented quantity is the largest negative pressure that could be reached. For water, all experimental techniques but one are limited to −30 MPa.^297,343,344 Negative-pressure studies seem to come into focus about every 20 years. In 1950 Briggs³⁴⁵ reached −25 MPa for water (compared with −50 MPa for mercury), while Winnick and Cho³⁴⁶ developed a clever centrifugal force method in 1971 but were still unable to get beyond Briggs’ limit. Henderson and Speedy’s outstanding works of 1987 were slightly ahead of the pattern. They reported the line of density maxima to −20.3 MPa³⁴⁷ and the melting temperature of ice to −24 MPa.³⁴⁸ They both lie on a natural extension of the positive-pressure data, but cavitation prevented following these properties to larger negative pressure.

The 20 year cycle for negative pressure studies was restored in 1991 by Green et al.³⁴⁹ and Zheng et al.,^350,351 who broke new ground. They showed that with a microscopic version of the original (1850) Berthelot tube approach unprecedented tensions, in the vicinity of −150 MPa, could be reached before their water-filled ≃5 by 15 μm dimension vesicles in quartz crystals, cavitated. Since these tensions are close to the values predicted for the same temperature 40–47 °C by classical nucleation theory nearly 70 years ago³⁵² and quantitatively supported by more recent theory,^131,353 it appeared that a major barrier had been crossed.

What was of high significance in these studies was the finding of a tension maximum, identified by the erratic behavior at 40–47 °C of the vesicles in a preparation of density 0.91 g/cm³, and the failure to cavitate at any temperature for inclusions of higher densities. Different vesicles in the same sample which, at other densities would all behave in the same manner, would sometimes cavitate during cooling but at different temperatures in the range 40–47 °C and sometimes not at all. Any inclusion that survived cavitation to 40 °C would never cavitate, making it clear that a tension maximum, very close to the limiting tension for that sample, had been traversed. This suggested the existence of a density maximum at this low density. However, since the cavitation probability depends on a combination of negative pressure and surface tension, a more refined analysis is needed, see below. In the measurements of the 1990s era were also the first direct measurements of a physical property in the new high-tension range made available by the micro-Berthelot tube. Alvarenga et al.³⁵⁴ showed it was possible, using micro-Brillouin scattering methods, to obtain the isochoric velocity of sound and hence the adiabatic compressibility along the isochore.

After a further two decade lapse, a new set of experiments has emerged since 2010 from the Caupin laboratory. Using an acoustic wave to stretch water, an experimental equation of state was measured at ambient temperature to −26 MPa.³⁵⁵ It agrees with the extrapolation of the recommended formulation of the equation of state measured at positive pressure.^356,357 Later, using the same autoclaving method established by geochemists³⁵⁸ and used by Zheng et al.³⁵⁰ and Schmulovich et al.,³⁵⁹ El Mekki et al.³⁶⁰ obtained a perfectly formed vesicle with which they were able to study the statistics of cavitation in a single vesicle as a function of temperature and thereby to estimate the temperature of the minimum energy barrier for cavitation, around 320 K. This must, however, be corrected for the variation of surface tension with temperature in order to locate the temperature of the tension maximum for the isochore of the studied density, 0.922 g/cm³. The correction depends on the model chosen to express the energy barrier for cavitation. Using classical nucleation theory with a Tolman length correction to the surface tension, the results are not inconsistent with the extrapolation of the positive pressure equation of state,^356,357 which is a temperature of density maximum near 296 K at 0.922 g/cm³. Obviously more direct measurements would be useful.

Another line of research uses the fact that some of the water inclusions are able to survive cooling without any bubble nucleation,^47,350 which gives access to the doubly metastable region. Revisiting the work of Alvarenga et al.,³⁵⁴ Pallares et al. recently measured the sound velocity in two doubly metastable samples.⁴⁷ An estimate of the path followed in the phase diagram is given in Figure 23. This study suggests that (i) the experimental equation of state deviates from the extrapolation of positive pressure data at low temperature, (ii) the adiabatic compressibility passes through a maximum when the temperature varies at constant density, and (iii) the sound velocity vs density at constant temperature becomes nonmonotonic at low temperature.

These features are consistent both with the liquid–liquid critical-point scenario²³ and with the singularity-free interpretation.³¹ It has also been suggested that the experiments might have found the liquid–liquid transition;³⁶¹ although not impossible, this does not seem likely.⁴⁷ The sound velocity measurements were recently analyzed³⁶² to provide an experimental equation of state at large negative pressure. In particular, as the pressure becomes more negative, the temperature of line of density maxima is found to increase monotonically to 17.8 C at −116 MPa. Although the slope becomes more vertical in the pressure–temperature plane, the sample studied did not allow one to decide whether the LDM reaches a turning point as in the second critical point scenario (Figure 3B) or singularity-free scenarios (Figure 3D) or remains monotonic as in the stability limit (Figure 3A) or critical-point-free (Figure 3C) scenarios. More measurements on water in the doubly metastable region would certainly help to shed light on the origin of its anomalies.

8. Thermodynamics and Dynamics of Confined Water

The dynamical properties of water in restricted geometries and at interfaces have been studied intensely because of the important effects in systems of interest to biology, chemistry, and geophysics, the behavior of which depends on how the pore size and structure influence the diffusion of water. Those properties are particularly relevant for understanding phenomena like the mobility of water in biological channels or the dynamics of hydrated proteins⁸⁻¹⁰ also in connection with cryopreservation, see, for example, ref (363). Of all this vast field we will here focus only on the relation between dynamics and thermodynamics in confinement and in particular on to what extent confinement can be of help to shed light on the thermodynamics of bulk water in the supercooled region.

Confined water is generally speaking different from bulk water, but since water has a strong tendency to form a network, several studies in hydrophilic confinement have proven that a bulk-like behavior can be recovered also in restricted geometries provided that a proper numerical analysis and/or suitable experimental probes are used. Molecular dynamics microscopic studies on water confined in hydrophilic silica porous glasses like Vycor^364,365 and MCM-41^293−295 upon supercooling have in fact evidentiated that for this kind of pores and hydrophilic surfaces the dynamics of water can be split in two ranges: (i) the dynamics of the bound water, close to the surface of the pores that is very slow already at ambient temperature, and (ii) the dynamics of the inner water, often called free water, which is bulk-like. The dynamics of the bulk-like inner part follows the MCT in the region of mild supercooling and upon further supercooling shows a FTS crossover. The MCT temperature and exponents and the FTS crossover obtained analyzing the translational relaxation times of the free water, in the confined hydrophilic pores, do not differ so much from those of bulk water.^{293−295,364,365}

Experiments show that it is easier to avoid crystallization of water in confinement than in bulk. In particular, by confining water in nanopores of mesoporous silica MCM-41-S with cylindrical pores of 14 Å diameter it was possible to study its dynamical behavior in a temperature range down to 160 K, without crystallization.^283,366 Quasielastic neutron scattering (QENS) is the most suitable technique to study translational dynamics as its cross section is directly related to the (Q, ω) Fourier transform of the density–density correlation function. Care must instead be taken when analyzing relaxation times with techniques that probe orientational degrees of freedom as the FTS transition is only translational in nature. Besides QENS experiments are sensitive only to the more mobile water contained in the inner part of the pores as the sluggish water close to the surface of the strongly hydrophilic pores gives a signal which is buried in the resolution of the instrument. The QENS experiments performed on supercooled water in confinement found evidence of a FTS dynamic crossover^283,366 already hypothesized in bulk water and in analogy with other network-forming liquids.²⁷⁰

Most important is that it was found that the FTS line, as a function of pressure, points to the zone where the LLCP is supposed to exist.^42,283,367 After that the FTS transition line was identified to coincide with the Widom line in simulations of bulk water;⁴² Gallo et al. simulated water in MCM-41 and obtained the same results as in the experiments, see Figure 24, further finding that the FTS crossover coincides with a peak in the specific heat that identifies the Widom line^293,295 and thus bridging the gap between experiments in confinement^283,366 and MD results in the bulk.⁴² This link between Widom line and FTS crossover described in these last two sections shows that for water the Widom line appears to also be a switching line for hopping, favored on the side where water is less dense.

Figure 24.

Molecular dynamics simulations of water in MCM-41. In the picture we can see the difference between bound and free water which show distinct dynamical behavior and the behavior of the relaxation time of free water that shows the FTS transition that coincides with the Widom line (not shown). Reproduced with permission from ref (293). Copyright 2010 American Chemical Society.

Another typical feature of glass-forming materials that has recently been related to the crossing of the Widom line and consequent stiffening of the hydrogen-bond network³⁶⁸ is the appearance of the Boson peak, which is an excess of intensity in the low-frequency range of the vibrational spectrum.

Since water inside Vycor and MCM-41 pores does not have a uniform behavior it is however important to stress again that experimentally many probes are not suited for extracting this kind of information.

9. Thermodynamics and Dynamics of Aqueous Solutions

In this section we will discuss how and to what extent aqueous solutions can be used as a route to reach no-man’s land. Similar to confinement, many aqueous solutions have the invaluable advantage that they can be supercooled more than the neat bulk.^369−371 Besides, in the natural environment water is almost always found as solvent in a mixture of two or more components.

Archer and Carter showed that in NaCl(aq) solution the heat capacity and the density anomalies are still present in dilute solutions,^372,373 while at higher concentration of NaCl the heat capacity anomaly disappears, as seen in Figure 25. This fact does not contradict the possibility of a liquid–liquid transition in supercooled aqueous solutions of NaCl, stemming from the liquid–liquid transition in pure water. Moreover, suppression of the heat capacity anomaly measured at constant composition is predicted by thermodynamics and, as seen in Figure 25, well described by the two-state model.¹⁵⁹

Figure 25.

Suppression of the anomaly of the heat capacity in aqueous solutions of sodium chloride (Reproduced with permission from ref (159). Copyright 2014 AIP Publishing LLC). Symbols: experimental data of Archer and Carter.^372,373 Solid curves: predictions based on two-state thermodynamics.¹⁵⁹ Dashed curve shows the positions of the melting temperatures. Dashed-dotted curve shows the temperatures of homogeneous ice formation.

Suzuki and Mishima³⁷⁴ measured Raman spectra of glassy alkalichloride solutions (LiCl, NaCl, and KCl) which had been vitrified using liquid hyperquenching.²⁰⁹ They observed two distinctly different OH stretch modes in the glasses and concluded that this is consistent with there being two distinct glassy states in dilute solutions. Later Mishima performed experiments on LiCl aqueous solutions where the observed decompression-induced volumetric change of dilute LiCl aqueous solution can be interpreted by the polyamorphic viewpoint about the solvent water and can be regarded as the expected polyamorphic phase separation.^375,376 This finding is supported by later experiments³⁷⁷ and by simulations.^378,379 Kobayashi and Tanaka^212,213 studied the glass-forming ability of LiCl–water mixtures and found that it is maximized near the eutectic point. Furthermore, it was demonstrated that the dependence of the viscosity and the Raman spectra on salt concentration can be explained by a simple two-state model.

Chatterjee and Debenedetti studied the thermodynamics of solvophobic aqueous-like solutions. In the presence of an LLCP for the aqueous-like component, critical lines will stem from the LLCP of the pure substance upon increasing the solute content.^380,381

Given this evidence, if an LLCP in water exists then it could be found with a properly tuned aqueous solution. Indeed, a LLCP was claimed for the glycerol–water system by Suzuki and Mishima at 0.12–0.15 mole fraction, 150 K, and 30–50 MPa.³⁸² Murata and Tanaka also reported the observation of a liquid–liquid transition in supercooled aqueous solutions of glycerol³⁸³ and also in many other aqueous organic solutions.³⁸⁴ The Murata/Tanaka interpretation has, however, been questioned for water–glycerol mixtures and ice formation instead suggested as the origin.^382,385,386 However, in a very recent 2D-IR study two liquid phases were reported as well as the ice phase and a liquid–liquid transition was suggested that was immediately followed by formation of small ice crystals.³⁸⁷

Corradini et al. studied with MD simulations NaCl dissolved in TIP4P water with concentrations ranging from c = 0.67 to 2.10 mol/kg.^133,286 The liquid–liquid critical point is present both in the bulk and in solutions, and its position in the thermodynamic plane shifts to higher temperature and lower pressure upon adding salt. Comparison with available experimental data allowed producing the phase diagrams of both bulk water and the aqueous solution as should be measurable in experiments as shown in Figure 26. Given the position of the liquid–liquid critical point in solution as obtained in these simulations, experimental determination of the hypothesized liquid–liquid critical point of water in aqueous solutions of salts appears possible. For the experimental c = 0.67 mol/kg NaCl(aq) the LLCP is predicted to be at around T_c = 230 K and P_c = −120 MPa. In NaCl(aq) with concentration c = 0.8 mol/kg experiments have shown that rupture occurs at P = −140 MPa.³⁴⁹ More recently, a series of aqueous solutions was studied³⁵⁹ and cavitation pressures beyond −100 MPa were also observed. From refs (340) and (370) the homogeneous nucleation temperature position can be estimated to be slightly below that of the LLCP of c = 0.67 mol/kg.

Figure 26.

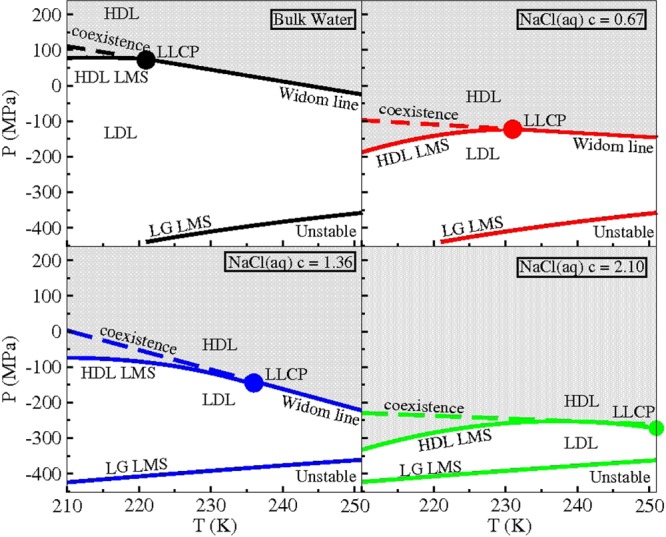
Phase diagram of NaCl aqueous solutions of supercooled water as obtained from molecular dynamics simulations properly matched to the experimental data. Upon increasing salt content the LDL region shrinks and the LLCP is shifted to lower pressures and higher temperatures. Reproduced from ref (286). Copyright 2011 American Chemical Society.

Upon further adding salt (Figure 26) the LDL region shrinks more and more as ions are more favorably solvated by the high-density liquid.^379,388

To complete the picture of low-concentration solutions of NaCl in water an MCT behavior and a FTS transition were found upon supercooling and the FTS transition happens on crossing the Widom line, see Figure 27, confirming also for these electrolyte solutions at low concentrations the link between dynamics and thermodynamics found in the bulk.^288,291 The excess entropy, approximated by the two-body terms extracted from MD simulations of NaCl(aq), shows the same FTS transition as the diffusion coefficient,³²⁷ and this means that from a direct experimental measurement of the g(r) the FTS transition should be measurable also in solutions.

Figure 27.

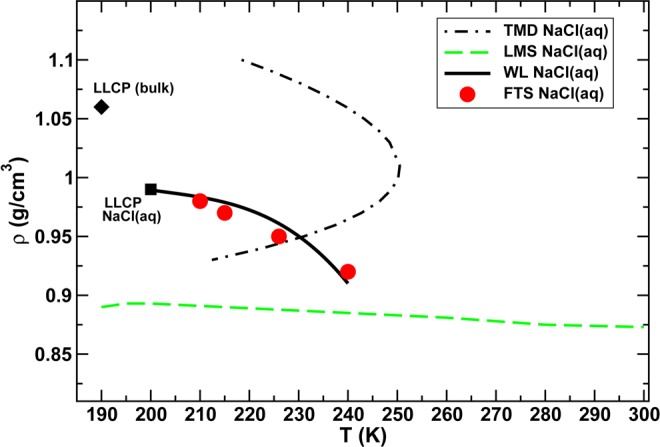
FTS transition points (circles) and Widom line (continuous line) in a NaCl aqueous solution as obtained from molecular dynamics simulations. The nose-shaped line is the TMD, and the dashed line is the liquid–gas limit of mechanical stability. Reproduced with permission from ref (291). Copyright 2013 American Institute of Physics.

Small angle X-ray scattering experiments of NaCl aqueous solutions also demonstrate the persistence of the anomalous behavior in solution since they show that the correlation length can be fit with a power law, similar to the bulk, upon cooling.³⁸⁹

Biddle et al.¹⁵⁹analyzed the thermodynamics of aqueous solutions. If the liquid–liquid transition exists and if it is terminated by a critical point, the addition of a solute should generate a line of liquid–liquid critical points emanating from the critical point of pure metastable water. Unlike liquid–liquid phase separation in binary solutions caused by nonideality of mixing between two species the liquid–liquid transition in pure water is driven by the nonideality of mixing between two alternative structures of water. Biddle et al.¹⁵⁹ compared their equation of state for solutions based on the ideas described in section 4 with the MD results of NaCl(aq) of Corradini et al.^133,286 and found agreement.

Recent experiments on melting of precipitated ice IV in supercooled LiCl–H₂O solution by Mishima^390,391 can be explained presuming the existence of polymorphism in water and by the simple assumption that LiCl is dissolved mainly in high-density liquid water as also found in simulation studies on NaCl(aq).³⁸⁸ The melting of ice IV was detected from the temperature change of the emulsified sample during the decompression. A sudden change in the slope of the ice IV melting curve in the pressure–temperature diagram was found. At the high-pressure and high-temperature side of the change, the solute-induced freezing point depression was observed. At the low-pressure and low-temperature side, ice IV transformed into ice I_h on the decompression and the transition was almost unrelated to the concentration of LiCl.

A similar picture to that of electrolyte solutions was also found for the phase diagram of the small amphiphilic methanol molecule. The phase diagram is shifted down in pressure, but no shift in temperature is detected at variance with electrolyte solutions. The LLCP is still found to exist for low concentrations.³⁹² A FTS dynamical crossover was also measured in methanol solutions at low concentrations,³⁹³ within this framework the FTS dynamical crossover should mark the crossing of the Widom line.

Studies on a model potential, the Jagla potential, show upon addition of a solvophobic solute the same phenomenology described so far. In particular, solutions of Jagla water upon insertion of hard spheres show a shift of the LLCP to higher pressures and lower temperatures that becomes more and more marked upon increasing the hard spheres concentration. Also, in this kind of solution it is possible to detect the Widom line as a dynamic crossover in the diffusion coefficient which is found exactly upon crossing the Widom line.^287,290

Experiments, theory, and simulations on supercooled aqueous solutions thus indicate that they provide a viable route to solve the mysteries of supercooled water both allowing easier access to the supercooled state of this anomalous liquid and possibly shifting the LLCP, if it exists, to more accessible zones of the phase diagram.

10. Future Directions

The foregoing review makes clear that despite many, often highly sophisticated, experimental and computational efforts to obtain a full understanding of the complex behavior of water, there remain many gaps in our knowledge and understanding of this most anomalous liquid. In this section we seek to identify the most serious of these gaps and to explore how they might be dealt with. The biggest problem faced is that of the “crystallization curtain” that has until recently blocked our knowledge of behavior below the homogeneous nucleation temperature. How best to capitalize on the success of Nilsson and co-workers¹⁷⁸ in penetrating this barrier by means of microdroplet streams and pulsed X-ray laser interrogation is obviously one line of study to be explored, and this is the first issue that will be considered below.

However, there are other possibilities for circumventing the crystallization problem to be considered. Each has its own set of difficulties and uncertainties but also promise. There is, for instance, the approach outlined by Koop and co-workers³⁹⁴ to effectively mimic the raising of pressure on water by introduction of second components. Although this usually results in the wiping out of the anomalies at the same time as it removes the crystallization event (Figures 25 and 26), it now seems it is possible to decouple the two effects by using the right kind of solute. This approach should be worthy of detailed study since it is basically simple.

Then there is the prospect raised by recent studies of water under high tension,^47,297 which have suggested that the anomalous domain can be elevated above the fast crystallization domain, perhaps due to competition between ice I_h and various empty clathrate structures that frustrate the generation of critical nuclei of any one crystal form. The negative-pressure domain is the only remaining unexplored region of metastable water’s existence, and although the challenges in sample production and in exploring anything other than isochoric behavior are many, the rewards might be great. It has been argued^297,395 that it is in this domain that the observations needed to distinguish between the different scenarios of section 2 will need to be made.

Also, of course, there are developments and refinements in the field of computer simulations that are much needed for the understanding of deeply supercooled water. The need is illustrated by a comparison of laboratory data for the fundamental thermodynamic properties, isothermal compressibility and constant pressure heat capacity, with those determined by calculations with one of the best pair potential currently available. The comparison of ambient pressure compressibility obtained with the pair potential given most attention in this review, viz. TIP4P/2005 is shown in Figure 28. The agreement is quite good for the first 20 °C of supercooling but then becomes rapidly poorer at lower temperatures where the simulations go through a mild maximum and the experimental quantity shows a strong tendency to diverge at about the same temperature. The power law behavior is seen not only for the compressibility but also for the heat capacity (Figure 1) and even more clearly for various transport properties such as viscosity, dielectric relaxation, spin–lattice relaxation, and the related reorientation relaxation time, all measured by different authors, so is probably a reliable representation of the observable data. The divergence temperature, which has not been confirmed because it lies in no-man’s land, falls in the range 223–228 K, depending on the range of data fitted and nature of background corrections. We now consider each of these routes in sequence.

Figure 28.

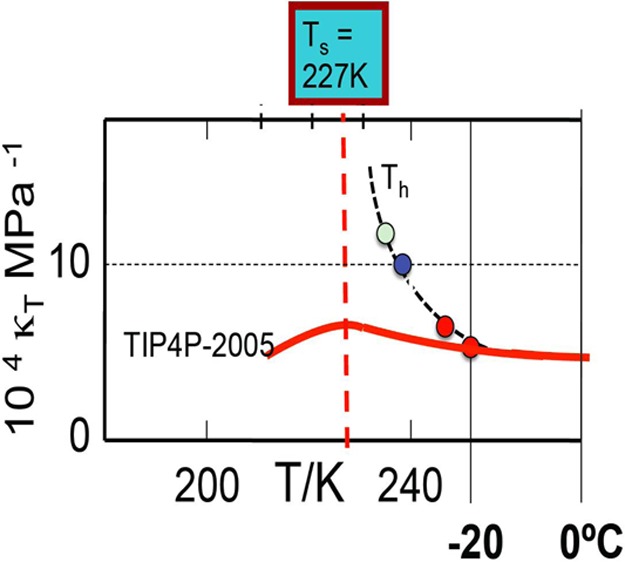
Comparison of the compressibility vs temperature relation at 0.1 MPa obtained with the TIP4P/2005 pair potential (heavy red curve) with the experimental findings and their extensions with decreasing temperature as follows: (first red point) −20 °C (253 K), combination of SAXS data (Huang et al.¹⁸⁴) and direct p–V data (Speedy and Angell¹²) that are in close agreement; (second red point) −24 °C (249 K), lowest temperature direct measurement of Speedy and Angell;¹² (dark green point) 239 K, limit of Holten and Anisimov extrapolation³⁹ of ambient pressure fitted data; (light green point) 235 K, based on low-T limit of heat capacity measurements that follow the power law with divergence temperature of 226 K,¹⁵ essentially the same as for the compressibility.

10.1. Ultrafast Probing

As described in section 4 there has been a development in terms of a general method for studying liquid structures below T_H based on fast cooling and ultrafast probing using femtosecond short X-ray pulses by exploiting the unique capabilities of the X-ray laser LCLS.^178,248 This needs to be further developed to allow other types of measurements both at ambient pressure and eventually at elevated pressures. It will be essential to measure the thermodynamic response functions, such as C_P and κ_T, on small water droplets into no-man’s land and also the correlation length (ξ). If direct temperature measurements on the droplets can be developed and a heat source introduced to induce a temperature rise then potentially C_P could be determined.

SAXS is the most direct probe of density variations or fluctuations on different length scales in a liquid, and from such measurements both κ_T and ξ could be determined using X-ray lasers. There is a thermodynamic relationship that relates κ_T to the structure factor at q = 0 as S(0) = nk_BTκ_T, where k_B is the Boltzmann constant, T is the absolute temperature, and n is the molecular number density.³⁹⁶ We can then test the hypothesis that neither ξ, C_P, nor κ_T will diverge to infinity but will reach a maximum at T_s, i.e., within the LLCP hypothesis, at the Widom line. Depending on how flat the temperature-dependent region around T_s is, this could provide further insight into the validity of the various scenarios and if there exists an LLCP. It will also be essential to follow ξ and κ_T to lower temperature below T_s. Furthermore, it would be valuable to conduct the experiment using D₂O in order to probe isotope effects as well as use NaCl solution, since the latter has an effect similar to pressure^389,397 as discussed in section 9. It could also be possible to determine the density variation from wide-angle X-ray scattering (WAXS) at very high q. The scattering intensity will have weak q dependence and become proportional to the density of the liquid. From such measurements it could also be possible to derive the thermal expansivity α_P. Here, it will be essential to observe if there is a minimum in α_P close to the Widom line. Eventually all these classes of experiments should be developed to also involve higher pressures. This will become a major experimental challenge, but it is essential that an effort will be devoted to this since it could provide a final answer as to which of the various scenarios best describes real water.

Another essential question to address is the proposed scenario that there is only a liquid to solid transition and that an LDL liquid crystallizes faster than the relaxation time of the liquid.^43,135 Could we then observe at which temperature the time scale of liquid equilibration becomes longer than the time scale for ice crystallization? By directly comparing these time scales we could establish if and at which temperature the liquid could no longer equilibrate relative to fast ice nucleation. We would expect that the structural fluctuations significantly slow down entering into the supercooled regime and maybe in the no-man’s land region could become on the order of 10 or 100 ps. This could also be related to the much discussed fragile to strong transition in the temperature dependence of the viscosity of water both above and below no-man’s land.^{32,277,281,292,398} It has been suggested that there is a dynamic transition at 228 K that would coincide with the temperature of the T_s or Widom line.²⁸¹

10.2. Second-Component Studies

Koop et al.³⁹⁴ showed that ice nucleation commences at a temperature determined by the water activity irrespective of whether the water activity is reduced by an increase of pressure or by addition of a second component that dissolves in the water. The more hydrophilic the solute the less of it is required to reduce the nucleation temperature to a target value or alternatively to remove the possibility of crystallization altogether. Hydrophilic solutes like LiCl or MgCl₂ lower the nucleation temperature rapidly, leading to noncrystallizing solutions. On computational time scales, NaCl behaves the same way.²⁸⁶ The general consequence of high hydrophilicity is that the structures responsible for the interesting anomalies of water are quickly dismantled (or at least are pushed out of sight to negative pressures, see Figure 26 and ref (286)). There are other solutes, however, which do not lower the activity of water very rapidly, that in fact lead to demonstrably ideal solution behavior according to melting point depression criteria, and it is found that in these cases the low-temperature behavior retains the anomalies of water, indeed in enhanced form.³⁹⁹ This behavior is only recently recognized and not yet much exploited. It might provide a convincing demonstration of how water would behave during cooling in the absence of crystallization. Its relation to the studies of Murata and Tanaka³⁸⁴ needs to be clarified in future work. However, because second-component incorporation is a proxy for increasing pressure, neither provides clear answers to the burning question of pure water behavior at ambient pressure in the absence of crystallization. This may be more easily approached from the other end of the pressure scale, namely, at high states of tension or negative pressure.

10.3. Studies at Negative Pressure

Studies of water at large negative pressures have been sparse because of the difficulty of preparing the microscopic samples of water in mineral matrices needed to evaluate the behavior of water in this exotic state and the difficulty of studying them once successfully formed. Regrettably the fluid inclusion strategy seems to offer the only feasible way of obtaining samples suitable for evaluating the behavior of water in this interesting domain. The constraint to constant volume over the temperature range of study is another problem. Nevertheless, the difficulties have been mastered by different groups, and Caupin and co-workers,^47,297 in particular, have given evidence that the anomalous behavior can emerge from and be studied outside of the fast crystallization zone (no-man’s land), see section 7. Clearly this provides a challenge to future workers to perform measurements additional to the velocity of sound studies that have so far been performed and to design sampling procedures that permit more variable pVT conditions.

The arguments given by Speedy for an essentially continuous line of compressibility infinities from a negative pressure extreme to strong positive pressures and the similarity to the engineering equations of state coupled with the lack of any isochore crossing point for the available isochores from the IAPWS-95 equation of state in the positive pressure range (such as that seen so clearly for ST2 water¹²²) leaves the situation with real water in some doubt. While this can be rationalized by locating the critical point very close to ambient pressure, as fitted by Holten and Anisimov,³⁹ the fact that the “most likely” second critical-point pressure has moved steadily to lower pressures with passing time over some two decades keeps the final location of the critical point and liquid–liquid line or HDL spinodal vs Widom line at ambient pressure, a matter for continuing debate and future work. An important part of this debate concerns the behavior of the line of density maxima (LDM), which itself passes through a maximum at negative pressures according to all pair-potential models but does the opposite in the case of the empirical equations of state and the scenario C of section 2. A positive identification of the behavior of the LDM is badly needed as the TMD claimed in the original study of Zheng et al.³⁵⁰ is now subject to adjustment by a surface tension argument given earlier in section 7. Two possibilities are identified here for future work.

First, the existence of a density maximum can be identified directly from the Brillouin light scattering measurement by the vanishing of the central line intensity since the Landau–Placzek ratio must go to zero at a density maximum. The Landau–Placzek ratio connects the intensities of the Brillouin peaks, I_B, and of the elastic peak, I_R, in light scattering with the specific heat at constant volume and that at constant pressure according to the following equation

9

However, in the quartz inclusion milieu presently used, the stray light is far too intense for this observation to be a possibility. Further developments of stray light canceling strategies or ways of producing a single perfect vesicle in a perfect quartz crystal may eventually permit this simple measurement to generate an unambiguous line of density maxima that will end the debate one way or another.

Second, and more immediately, introduction of small dye molecules that are sensitive to pressure and thus can “report” the pressure in the experiment offer the possibility of direct spectroscopic determination of a density maximum. For instance, there is the water-soluble dyestuff molecules of the type recently used for analyzing friction patterns on sliding surfaces.⁴⁰⁰ These studies depended on the sensitivity of the fluorescence spectrum to pressure or viscosity or both.⁴⁰¹

The fluorescence intensity of molecule 1 of Figure 29A is depicted in Figure 29B. The sensitivity to pressure is seen to be quite high, and although the isochoric nature of the projected experiment will possibly complicate the interpretation, the likelihood of a null result at the tension maximum seems small. In any case, this is not the only pressure-sensitive dyestuff that is available. If the pressure sensitivity is due to a pressure-dependent viscosity, so much the better since the diffusivity of water is known to decrease with great rapidity as pressure decreases in the direction of the tensile domain.⁴⁰²

Figure 29.

(A) Fluorescent molecules whose intensities I_f have high sensitivity to pressure or viscosity. (B) Pressure dependence of the fluorescence intensity of molecule 1 in 1 M solution in acetone. Reproduced from ref (401) with permission. Copyright 2015 WILEY-VCH Verlag GmbH & Co.

Of course, the molecule must first survive the autoclaving procedure used to produce the samples, but there is precedence for this in the successful introduction of a water-insoluble polyphenyl, orthoterphenyl, into the vesicles prepared by Zheng (and only reported in ref (403)). We expect that a water-soluble version of the molecule seen in Figure 29 will likewise survive as it need only be present in very low concentrations.

If the temperature of maximum density detected by such fluorescence intensity studies confirms the reversal of the TMD trajectory in pressure the existence of the second critical point at zero pressure or thereabouts will find strong support.

However, what will it imply if such a study confirms the high values of the TMD reported from the original inclusion measurements or their successor studies? First, it will confirm the great sensitivity of the equation of state parameters to the choice of L–L coexistence data which was pointed out by the authors of ref (39), and second, it will support the qualitative validity of engineering equations of state for water, which to date have been given little credence by the metastable water community.

The origin of the sensitivity can be found in the way the TMD is approaching the liquid–gas spinodal limit. This can be seen from the work of Vashist et al.¹⁴² on liquid Si in the Stillinger–Weber (S–W) model where the point of reversal of the TMD with increasing tension is extremely close to the spinodal limit for the liquid state. Since the latter cannot be penetrated, the said reversal must suddenly switch in the opposite direction if the λ parameter of the S–W model is made any larger. Indeed, if it is raised to the value 23 used by Molinero and Moore¹⁴⁷ in their successful adaptation of the S–W form of potential to the description of water then the isochore minima, which determine the TMD, no longer reverse their direction with increasing temperature but rather behave in the manner given by, for instance, the HGK, or IAPWS-95 equations of state for water. This is demonstrated by current assessments of the isochores of the tuned S–W model seen in Figure 30 (LH panel), which no longer cross at a critical point as they do for values of λ of 21 and lower.⁴⁰⁴

Figure 30.

(Left) Behavior of the isochores and the TMD with isochore density in the tuned S–W model with λ parameter = 23. The TMD does not reverse as it does for the silicon potential λ = 21. Flattened segments at lower temperatures correspond to broken ergodicity states (glasses on the simulation time scale). (Right) Isochores and density maxima behavior of the HGK equation of state for water.

More importantly, it might also require recognition that not only have the critical-point-related anomalies emerged from no-man’s land (as suggested by the negative pressure studies of Caupin and coauthors^47,297) but also the critical point itself has disappeared into the liquid–gas spinodal and become a virtual phenomenon. It would mean that the Widom line does not exist but rather that the anomalies of water are provoked by close approach to a line of spinodal instabilities of the high-density liquid that lies just a few Kelvin on the low-temperature side of a line of liquid–liquid transitions that itself lies close to but below the line of homogeneous nucleation temperatures. This is now called the “critical-point-free” scenario³² (diagram C in Figure 3). Thus, in light of Figure 1 above and the latter challenges, there seems to be a need for more work on water models that will provide better agreement with experiment in these extreme conditions.

Why have pair-potential models not yet acquired the ability to show the above sequence of possibilities? According to the X-ray laser data shown in Figure 12, the TIP4P/2005 model is not “going tetrahedral” quickly enough with decreasing temperature. Perhaps, as in mW water,¹³⁵ they need the additional drive to tetrahedrality that is provided by potentials of the S–W form, in which a departure from tetrahedrality is penalized by a repulsive energy component that opposes the pairwise additive attraction component of the total potential. In water this would act on the O–O–O alignments which need to be tetrahedral in an LDA-like structure. While such possibilities as the above remain uninvestigated, water is likely to maintain its mystique as the most anomalous and least understood liquid.

Biographies

Paola Gallo is Professor of Theoretical Condensed Matter Physics at the University Roma Tre, Rome, Italy. She graduated in Physics at the University of Rome “La Sapienza” in Italy and received her Ph.D. degree in Condensed Matter Physics from the University of L’Aquila, Italy. From 1994 to 1996 she worked in the United States at the Massachusetts Institute of Technology with Prof. Sow-Hsin Chen. Since then her research has been focused on simulations of supercooled liquids and metastable water. Over her career she has contributed to characterizing the glassy behavior of supercooled water and the dynamics of water in confinement and in solutions. Currently, her research group focuses on the structure, dynamics, and thermodynamics of solutions for cryopreservation, of doped ice, and of water under extreme conditions: supercooled, superheated, in hydrophilic and hydrophobic confinement and in electrolyte and amphiphilic solutions.

Katrin Amann-Winkel studied physics at the Technical University Darmstadt. She completed her Ph.D. degree under the supervision of Erwin Mayer and Thomas Loerting on amorphous ices in 2009 at the University of Innsbruck. She continued her studies on the glass transition of amorphous ices in Innsbruck until 2014 and then moved to Stockholm University, working now in the group of Anders Nilsson.

Austen Angell is a Regents’ Professor in the recently formed School of Molecular Sciences at Arizona State University (ASU). He has published some 510 papers, more than 70 of which have been cited over 100 times (recently averaging 72 citations per paper). He has been the awardee (internationally contested) of four different technical societies (ACS 2004, MRS (2006), ACERS-1991, ECS-2010), most notably the Hildebrand Award of the ACS, 2004 (for liquids studies), and the David Turnbull Lecture Award of the MRS (2006) (for glasses), and has been the elected chairman of three different Gordon Research Conferences dealing with liquids (Molten Salts and Metals (1977), Water and Aqueous Solutions (1980), and Physics and Chemistry of Liquids (1997). He has always been fascinated by the behavior of laboratory water in the supercooled and stretched states and by its role as a Rosetta stone in the study of glass-forming liquids in general and has written a number of papers and reviews on these aspects of the water anomalies.

Mikhail A. Anisimov is a Russian and American interdisciplinary scientist. He received his Ph.D. degree (Physical Chemistry, 1969) from Moscow State University and a Doctor of Science degree (Molecular and Thermal Physics, 1976) from the Kurchatov Institute of Atomic Energy in Moscow. Since 1994 he has been working in the United States. Currently, he is a professor in the Department of Chemical and Biomolecular Engineering and in the Institute for Physical Science and Technology at the University of Maryland, College Park. His field of research has been thermodynamics of fluids and fluid mixtures, liquid crystals, polymers, and other soft-matter materials. His research group at the University of Maryland is one of the leading authorities, nationally and internationally, in the field of critical phenomena and phase transitions.

Frédéric Caupin was born on October 20, 1976, in Douai, France. He received his Ph.D. degree from the Université Pierre et Marie Curie in Paris under the direction of Sébastien Balibar in 2001. He spent 9 years as an assistant professor at Ecole Normale Supérieure, Paris. After studying the condensed phases of helium 3 and 4, his research interests evolved toward the properties of water. In 2010 he became Professor at the University Claude Bernard Lyon 1 to lead the European Research Council Starting Grant project “Water anomalies in the stretched and supercooled regions”.

Charusita Chakravarty (1964–2016) received her B.Sc. degree in Chemistry from the University of Delhi and then went on to graduate with her B.A. degree (Natural Sciences Tripos) from the University of Cambridge. Her doctoral work was with Prof. David C. Clary FRS on quantum scattering and spectroscopy of van der Waals dimers. During her postdoctoral work with Prof. Horia Metiu at the University of California, Santa Barbara, her research interests shifted to quantum and classical simulations of molecular systems. After a year as a Junior Research Fellow in Churchill College, Cambridge, she joined the Department of Chemistry, Indian Institute of Technology Delhi, in 1994 where she became Professor. Her research interests were in the structure and dynamics of simple and anomalous liquids, biomolecular hydration, phase transitions, and nanoscale self-assembly.

Erik Lascaris was born on July 16, 1981, in Amsterdam, The Netherlands. After receiving his engineering degree in Applied Physics from the University of Twente in 2006, he continued his studies at Boston University, where he was awarded the Chair’s Book Award for Excellence in Teaching. In 2014 he received his Ph.D. degree in Physics for work on liquid–liquid phase transitions. He is currently a Postdoctoral Associate at Boston University, studying the effects of radiation and high temperatures on Fe–Cr alloys using molecular dynamics and phase field methods.

Thomas Loerting was born in 1973, studied chemistry at the University of Innsbruck in Austria, and obtained his Ph.D. degree in Theoretical Chemistry under the supervision of Prof. Klaus R. Liedl in 2000. As a postdoctoral fellow he changed from theory to experiments and worked with Prof. Erwin Mayer in Innsbruck and Nobel Laureate Prof. Mario J. Molina at the Massachussetts Institute of Technology. After his Habilitation in Physical Chemistry in 2008 he became Associate Professor and speaker of the Research Platform “Material- and Nanosciences” at the University of Innsbruck and member of the Austrian Academy of Sciences (“Junge Kurie”). His group’s research on cryochemistry, supercooled water, amorphous and crystalline ices, and clathrate hydrates was honored with a dozen awards, including the Starting Grant of the European Research Council (ERC), the START-Preis of the Austrian Federal Ministry of Research and Sciences, the Bodenstein award of the German Bunsen Society, and the Bessel award of the Alexander von Humboldt foundation. Recently, he was Visiting Scientist at TU Dortmund University, collaborating with Prof. Roland Böhmer.

Athanassios Z. Panagiotopoulos received his undergraduate degree from the National Technical University of Athens and Ph.D. degree from MIT, both in Chemical Engineering. After a postdoctoral stay in Physical Chemistry at the University of Oxford, he has held faculty positions at Cornell and the University of Maryland; he is currently the Susan Dod Brown Professor of Chemical and Biological Engineering at Princeton University. He is a member of the U.S. National Academy of Engineering and the American Academy of Arts and Sciences. His research focuses on development and application of theoretical and computer simulation techniques for the study of properties of fluids and materials.

John Russo received his Ph.D. degree in Physics in 2010 from the University of Rome La Sapienza. He then joined the University of Tokyo to work at the Institute of Industrial Science. He is presently a Royal Society University Research Fellow and Lecturer in Applied Mathematics at the School of Maths, the University of Bristol. His research interests include both equilibrium and nonequilibrium properties of colloidal systems, patchy particles, and complex fluids such as water.

Jonas A. Sellberg was born on July 30, 1985, in Stockholm, Sweden. After completing his M.Sc. studies in Chemistry and Chemical Engineering at the KTH Royal Institute of Technology in 2009, with internships at Princeton University and University of Tokyo, he received his Ph.D. degree in Physics from Stockholm University in 2014, with honors. Jonas continued his scientific career as Postdoctoral Fellow at Uppsala University (2014−2015) and returned recently to KTH Royal Institute of Technology, where he is currently an Assistant Professor in Applied Physics. His expertise lies within X-ray scattering and spectroscopy of water and ice, ultrafast pump−probe X-ray spectroscopy of surface adsorbates, and coherent diffractive imaging of live viruses and cells.

Eugene H. Stanley works in collaboration with students and colleagues attempting to understand puzzles of interdisciplinary science. He has been elected to the U.S. National Academy of Sciences (NAS) and received the 2004 IUPAP Boltzmann Medal. His main current focus is understanding the anomalous behavior of liquid water in bulk, nanoconfined, and biological environments. He has also worked on a range of other topics in complex systems, such as quantifying correlations among the constituents of the Alzheimer brain and quantifying fluctuations in noncoding and coding DNA sequences, and interbeat intervals of the healthy and diseased heart. His publications—all available online at http://polymer.bu.edu/hes/—have received more than 80 000 ISI Web of Science citations and more than 120 000 citations in Google Scholar. His ISI Hirsch index is currently h = 128.

Hajime Tanaka received his Ph.D. degree in Applied Physics (1982) from the University of Tokyo. He is currently Professor at the Institute of Industrial Science, the University of Tokyo. He has worked on a wide range of problems related to soft matter physics and liquid matter physics both experimentally and theoretically. He has been intrigued by the general behavior of a system having spatiotemporally hierarchical structures and the commonality between soft matter and liquid matter in that respect. More specifically, he has been interested in pattern formation and nonlinear rheology of soft matter, physics of water, liquid–liquid transition, glass transition, and crystallization. He has published some 260 papers in refereed journals. Awards for research have included the Award of the Society of Polymer Science, Japan (1997), Humboldt Research Award (Alexander von Humboldt Foundation, Germany) (2006), and The Liquid Crystal Society, Top Paper Award (2010). He became a Fellow of the Institute of Physics in 2007.

Carlos Vega was born in 1964 in Madrid. In 1991 he finished his Ph.D. degree at Complutense University under the direction of Prof. Santiago Lago. For 18 months he was a postdoctoral Fulbright Fellow in Amherst, Massachusetts, supervised by Prof. Peter Monson. Since 2005 he has been Full Professor of Physical Chemistry at Universidad Complutense de Madrid. His research interest is focused on computer simulations of water, with special emphasis on the evaluation of the phase diagram for simple potential models. In 2005, along with Prof. Abascal, he proposed the TIP4P/2005 model of water.

Limei Xu received her Ph.D. degree from the Department of Physics, Boston University in 2007. After that she was a postdoctoral fellow in the Chemistry Department, University of Utah. In 2008 she joined the Advanced Institute of Materials Research (WPI-AIMR) at Tohoku University as an assistant professor. In 2011 she took the tenure-track associate professor position in the International Center for Quantum Materials (ICQM) at Peking University and was promoted to a tenured professor in 2015. She was selected as the Junior 1000 Talents by the Recruitment Program of Global Experts of China in 2011 and was awarded the National Science Fund for Distinguished Young Scholars in 2015. Her current research interests include critical and supercritical phenomena, properties of water in confinement and on surfaces, and nonequilibrium statistical physics.

Lars G. M. Pettersson was born in Norrköping, Sweden, in 1951 and received his B.Sc. degree in Physics (1976) and Ph.D. degree in Theoretical Physics (1984) from Stockholm University, Sweden, where he focused on highly accurate quantum chemical calculations as well as developing approximate modeling techniques. He did postdoctoral studies (1984–1986) in California at IBM, San Jose, and NASA Ames Research Center. He returned to Stockholm University, where he is currently Professor in theoretical chemical physics. His research focus lies on quantum chemical modeling of processes at surfaces and theoretical treatment and application of inner-shell spectroscopies, but the main effort is currently devoted to understanding the structure and dynamics of water and aqueous solutions.

The authors declare no competing financial interest.

Dedication

During the final preparation of this review, we became saddened by the news that Prof. Charusita Chakravarty had succumbed to cancer. She was a deeply warm individual, who touched the lives of many of us. Among her many scientific achievements, she has greatly contributed to our understanding of the properties of water. Her death leaves a big emptiness in our hearts and in our research field.