Distribution and cluster analysis of predicted intrinsically disordered protein Pfam domains

Abstract

The Pfam database groups regions of proteins by how well hidden Markov models (HMMs) can be trained to recognize similarities among them. Conservation pressure is probably in play here. The Pfam seed training set includes sequence and structure information, being drawn largely from the PDB. A long standing hypothesis among intrinsically disordered protein (IDP) investigators has held that conservation pressures are also at play in the evolution of different kinds of intrinsic disorder, but we find that predicted intrinsic disorder (PID) is not always conserved across Pfam domains. Here we analyze distributions and clusters of PID regions in 193024 members of the version 23.0 Pfam seed database. To include the maximum information available for proteins that remain unfolded in solution, we employ the 10 linearly independent Kidera factors^1–3 for the amino acids, combined with PONDR⁴ predictions of disorder tendency, to transform the sequences of these Pfam members into an 11 column matrix where the number of rows is the length of each Pfam region. Cluster analyses of the set of all regions, including those that are folded, show 6 groupings of domains. Cluster analyses of domains with mean VSL2b scores greater than 0.5 (half predicted disorder or more) show at least 3 separated groups. It is hypothesized that grouping sets into shorter sequences with more uniform length will reveal more information about intrinsic disorder and lead to more finely structured and perhaps more accurate predictions. HMMs could be trained to include this information.

Table 10. Members from 618 unique mammalian Pfam 23.0 domains^a that are 100% PID.

a0pjt4_mouse_378–569	dvl1l_human_144–215	ldlr_rat_107–143	q3unq1_mouse_16–227
a2ad83_mouse_289–336	dvl3_human_142–213	ldlr_rat_196–232	q3unv7_mouse_27–199
a2ahf9_mouse_351–552	e41l1_human_493–544	ldlr_rat_66–104	q3zc44_bovin_1–71
a2ar56_mouse_308–354	e41la_mouse_310–355	lipb2_human_192–256	q4kln1_rat_423–459
a2bhy4_human_702–736	edf1_mouse_4–73	lmx1b_human_197–253	q4qrk6_human_9–99
a6qnu2_bovin_1–68	enpp2_rat_54–98	lphn1_rat_1151–1515	q5dtp7_mouse_1310–1374
a6qqj3_bovin_11–94	ep300_human_1990–2106	ls14b_human_310–351	q5f2c2_mouse_1–183
ada10_human_466–549	erbb4_human_1159–1167	ltbp1_rat_185–212	q5h8v1_human_16–46
ada15_human_430–506	ezri_bovin_338–581	lzts2_human_439–637	q5j8k6_mouse_150–911
ada15_mouse_431–507	fa10_bovin_45–86	ma7d1_human_576–735	q5m9m1_mouse_2–84
ada17_human_484–561	fa10_mouse_45–86	ma7d2_human_377–567	q5spl1_human_1165–1204
ada19_mouse_426–501	fa10_rabit_45–86	mad1_human_57–109	q5u1v4_human_366–465
ada32_mouse_396–477	fa10_rat_45–86	mad3_rat_58–110	q61213_mouse_783–827
adam7_mouse_410–485	fa12_human_98–130	mad4_human_54–106	q61769_mouse_1108–1211
adam8_human_417–492	fa5_bovin_1065–1073	maml1_mouse_14–73	q61769_mouse_1578–1686
adam8_mouse_412–487	fa5_bovin_1197–1205	maml3_human_67–127	q61769_mouse_1697–1807
adm1b_mouse_415–488	fa5_bovin_1206–1214	man1_mouse_8–50	q61769_mouse_2056–2167
agrin_rat_311–356	fa5_bovin_1215–1223	map2_human_1660–1691	q61769_mouse_2178–2287
agrin_rat_515–559	fa5_bovin_1404–1412	map2_human_1692–1722	q61769_mouse_2402–2510
agrin_rat_91–137	fa5_bovin_1422–1430	map2_human_1723–1754	q61769_mouse_2521–2633
aka7a_human_44–104	fa7_bovin_45–86	map2_rat_1695–1725	q61769_mouse_994–1103
akap7_mouse_21–81	farp1_human_328–374	map2_rat_86–103	q62287_mouse_404–482
akt1_bovin_428–478	fbln1_mouse_36–69	map7_human_456–625	q62700_rat_129–211
anfb_bovin_18–97	fila_human_1228–1279	marcs_human_2–329	q66h25_rat_5–91
anfb_human_46–128	fila_human_3173–3224	marcs_mouse_2–309	q6pi41_human_89–124
apc_human_1369–1394	fila_human_3292–3346	matn2_human_908–954	q7tmh0_mouse_332–390
apc_human_1568–1589	finc_bovin_2130–2167	mbd1_mouse_235–280	q7tpu6_mouse_30–90
apc_human_1840–1866	finc_bovin_21–56	mbp_bovin_14–168	q7z3e9_human_731–799
apc_human_1948–1973	fmn2_mouse_955–1102	mefv_human_370–412	q80yd0_mouse_355–396
apc_human_2006–2031	frat1_mouse_1–234	mmp9_bovin_477–512	q811y3_rat_332–389
apc_human_2220–2579	fst_human_270–316	mmp9_human_472–507	q8c0x4_mouse_1–280
apc_human_2670–2843	fstl3_mouse_118–165	mmp9_rabit_472–507	q8c2z6_mouse_1–212
apoc1_human_27–83	fst_pig_266–316	mmp9_rat_475–510	q8c6x4_mouse_144–196
apoe_rabit_74–292	fxl17_mouse_80–128	moes_human_338–577	q8cbm5_mouse_322–379
arhg5_human_313–424	gagd3_human_1–111	moti_horse_2–29	q8cgr8_mouse_5–93
atf1_human_211–270	gagd4_human_1–111	moti_rabit_62–120	q8ix62_human_17–83
atf1_human_43–83	gagd5_human_1–108	mpdz_rat_6–63	q8ix62_human_186–252
atf4_human_276–339	gas6_mouse_50–91	mrcka_rat_881–941	q8k3v0_rat_27–186
atp4a_mouse_2–41	gbg11_rat_12–66	mrckb_rat_878–939	q8nhd2_human_57–86
atp4a_pig_2–42	gbg1_human_12–66	mrckg_human_744–801	q8tbz7_human_408–483
atp4a_rabit_2–43	gbgt2_human_8–62	msre_human_276–335	q8vdw8_mouse_1–229
atp4a_rat_2–41	gemi_human_1–190	mt2c_rabit_1–62	q8wnq3_pig_276–565
atty_human_1–40	gemi_mouse_1–187	mt3_bovin_1–68	q95mn0_rabit_332–391
atx2_mouse_378–446	gfap_human_5–67	mtcpa_human_4–68	q99053_rat_218–273
atx2_mouse_880–897	grm1_mouse_1149–1199	mtss1_human_727–744	q99m65_rat_332–389
axn1_human_464–496	grm5_human_1162–1212	mybb_human_451–626	q9bx99_human_386–420
baalc_mouse_1–53	grn_human_377–418	myf5_bovin_1–83	q9cy05_mouse_1–178
baalc_pig_1–53	grn_rat_374–415	myh6_human_1070–1928	q9d4a3_mouse_5–93
bad_human_1–168	hcls1_human_119–155	myh7_human_34–75	q9d5i5_mouse_16–227
bad_rat_43–205	hcls1_human_156–192	n4bp3_mouse_359–520	q9d5i7_mouse_42–173
bat2_human_1–192	hcls1_human_82–118	nab1_human_322–487	q9d5q6_mouse_49–129
bat4_mouse_271–315	hes6_mouse_28–78	nbpf3_human_236–298	q9d6s9_mouse_1–169
baz2a_human_1377–1389	hirp3_human_484–520	nbpf3_human_394–460	q9d9p1_mouse_14–175
baz2a_human_622–634	hmgn1_bovin_2–97	nbpff_human_180–242	q9da45_mouse_1–212
baz2b_human_543–617	hnf1a_mouse_282–539	ncf1_bovin_332–392	q9dam8_mouse_1–212
bbx_human_191–323	hnf1a_rat_282–539	ncf1_human_331–390	q9eq53_mouse_427–466
bex3_human_1–111	hnf1b_pig_315–553	ncf1_mouse_332–390	q9eq53_mouse_470–511
bex5_bovin_1–112	hnrpk_rabit_1–43	ncoa1_human_1149–1199	q9eq55_mouse_197–236
bex5_human_1–111	hsbp1_human_9–62	ncoa1_human_1212–1268	q9eq55_mouse_285–322
bptf_human_101–161	hsp1_bovin_2–50	ncoa1_mouse_1218–1274	q9eq55_mouse_326–367
brca2_mouse_1623–1656	hsp1_horse_2–48	ncoa1_mouse_629–712	q9eq55_mouse_371–410
brca2_mouse_1924–1958	hsp1_pig_2–49	ncoa2_human_1281–1338	q9eq56_mouse_141–182
brca2_rat_1405–1439	hsp1_rabit_2–49	ncoa2_human_636–709	q9eqn8_mouse_3–142
cabin_rat_2118–2152	hxb9_mouse_1–171	ncoa2_mouse_1279–1336	q9gkn1_rabit_3–142
calca_horse_80–121	hxc13_human_261–317	ncoa2_rat_1281–1338	q9gkn2_rabit_3–142
cald1_human_1–793	ibp1_bovin_32–91	ncoa3_human_1291–1348	q9gkn3_bovin_3–142
casc3_rat_138–246	ibp2_human_45–119	ncoa3_mouse_1265–1322	q9jlp2_mouse_359–411
cc124_mouse_95–209	ibp3_bovin_40–101	ncoa3_mouse_609–697	q9jmb2_rat_533–581
ccd12_mouse_9–160	ibp6_human_29–89	ncoa3_rat_949–1006	q9jmb2_rat_843–956
ccd49_mouse_11–47	ibp6_rat_30–81	nfkb2_human_776–851	q9nxy1_human_591–651
ccd55_mouse_55–180	ical_bovin_212–346	nhrf2_human_297–337	q9tun3_rabit_593–624
cd97_human_160–207	ical_bovin_357–489	nol10_mouse_482–511	q9uge8_human_22–124
cdc26_human_1–85	ical__bovin500–626	notc2_mouse_1825–1872	q9umz1_human_2–101
cdx1_mouse_13–147	ical_bovin_77–204	notc3_human_1382–1418	q9z1i2_rat_18–62
cdx4_human_13–171	ical_human_512–638	notc3_mouse_1789–1837	radi_human_338–583
cdx4_mouse_13–169	ical_pig_372–502	notc4_mouse_1628–1660	rbm6_human_1051–1095
cebpa_bovin_276–329	ical_pig_513–638	notc4_mouse_1661–1694	recq5_human_625–829
cebpd_bovin_177–230	ical_pig_99–225	nrbf2_mouse_45–287	roaa_human_1–70
cenpf_human_1–288	ical_rabit_232–361	nrl_human_130–224	rock1_human_948–1014
cenpf_human_2227–2366	ical_rabit_372–505	nrl_human_67–102	rock1_rabit_458–542
cenpf_human_2409–2548	ical_rat_270–395	nu153_human_113–634	rock1_rabit_948–1014
cenpf_human_3061–3109	ical_rat_406–506	nu153_human_793–822	rock2_human_475–559
cf057_mouse_47–104	ical_rat_517–641	nu153_human_851–880	rock2_human_978–1046
chch3_human_14–175	ictl_pig_1–67	nupr1_human_19–77	s12a6_human_1018–1047
chch6_human_16–189	ikbe_human_119–153	o02714_pig_99–139	sc6a4_human_23–64
chch6_mouse_16–227	ikbe_human_154–186	o08769_rat_30–80	sc6a4_mouse_23–64
chd8_human_363–425	ikbe_human_187–219	o14549_human_185–219	serf1_human_1–59
chd8_human_445–499	ima1_human_2–96	o35265_rat_200–254	serf2_mouse_1–59
ci094_human_434–466	ima5_human_2–94	o46422_pig_35–76	sftpd_rat_223–268
co1a1_human_1019–1078	invo_mouse_1–67	o60424_human_497–596	shox2_human_308–328
co1a1_human_1079–1138	invo_mouse_208–248	o70148_rat_1–188	shrm2_human_639–806
co1a1_human_236–295	invo_mouse_252–292	o70192_mouse_52–105	shrm3_mouse_881–1060
co1a1_human_296–355	invo_mouse_294–335	o70419_rat_120–156	sim2_mouse_358–651
co1a1_human_356–415	invo_pig_1–69	o70419_rat_194–230	smca2_human_584–629
co1a1_human_416–475	invo_pig_80–123	o70419_rat_83–119	sp.r1a_human_1–87
co1a1_human_476–535	invo_rat_152–192	o70420_rat_231–267	sp.r1a_mouse_1–142
co1a1_human_536–595	invo_rat_220–261	o75370_human_111–162	sp.rl1_rat_403–424
co1a1_human_596–655	invo_rat_265–306	o75370_human_230–284	sp.rr3_human_1–167
co1a1_human_656–715	invo_rat_316–355	o77779_bovin_448–522	sp.rr3_mouse_1–236
co1a1_human_716–775	invo_rat_359–400	o88205_rat_189–243	sp.rr3_rabit_1–231
co1a1_human_779–838	invo_rat_417–456	o88311_rat_1–75	sp.tb2_human_1592–1696
co1a1_human_839–898	ipkb_mouse_23–92	o88527_rat_377–424	src8_human_157–193
co1a1_human_899–958	isk5_human_160–214	o97671_rabit_18–74	src8_mouse_268–304
co1a1_human_959–1018	isk5_human_224–279	odp2_rat_339–377	srcap_human_2936–2948
co3a1_human_1017–1076	isk5_human_436–491	odpx_human_180–218	ssrp1_human_547–615
co3a1_human_1077–1136	isk5_human_495–556	pairb_human_189–314	st18_rat_797–828
co3a1_human_1137–1196	isk5_human_631–686	parp1_mouse_385–463	syep_human_832–886
co3a1_human_168–227	isk5_human_706–760	pde8b_human_1–52	tcf7_human_1–211
co3a1_human_234–293	isk5_human_773–828	pkn1_mouse_37–110	tcfl5_human_353–406
co3a1_human_294–353	isk5_human_848–903	pkn2_human_47–119	tcrg1_human_727–776
co3a1_human_354–413	itb5_human_555–585	pkn3_human_105–182	tcrg1_human_794–843
co3a1_human_414–473	itb6_bovin_583–614	pkn3_human_18–90	tcrg1_human_898–949
co3a1_human_474–533	kad2_mouse_142–177	pkn3_mouse_15–87	tcrg1_human_956–1007
co3a1_human_534–593	kcna4_rat_1–75	plcb1_rat_997–1189	tf3b_mouse_453–546
co3a1_human_594–653	ki67_human_1002–1113	plcb2_rat_974–1154	thyg_bovin_1149–1210
co3a1_human_654–713	ki67_human_1124–1235	plcb3_mouse_1023–1216	thyg_mouse_1464–1509
co3a1_human_714–773	ki67_human_1368–1478	plmn_bovin_192–269	ticn2_mouse_135–180
co3a1_human_777–836	ki67_human_1610–1721	plmn_bovin_282–359	titin_human_10239–10266
co3a1_human_837–896	ki67_human_1732–1843	pp14a_pig_1–147	titin_human_10531–10558
co3a1_human_897–956	ki67_human_1854–1965	pp1rb_human_29–82	titin_human_10587–10614
co3a1_human_957–1016	ki67_human_1976–2087	ppr1a_human_1–171	titin_human_10762–10788
co4b_mouse_700–734	ki67_human_2459–2570	ppr1a_rabit_1–166	titin_human_10793–10818
co6_human_138–173	ki67_human_2581–2690	pr40a_human_142–171	titin_human_11241–11265
co9_human_99–134	ki67_human_2701–2811	pr40a_human_183–212	titin_human_11698–11725
co9_mouse_97–132	ki67_human_2820–2929	prm2_mouse_1–91	titin_human_11762–11787
cobl_human_1109–1129	kr151_mouse_1–145	prm2_pig_1–91	tlr7_human_597–624
cobl_human_1149–1169	kra11_human_1–177	proc_bovin_44–85	tlr7_human_676–695
cox17_mouse_2–63	kra13_human_1–177	prp6_human_13–169	tnap3_human_759–784
cox19_mouse_23–64	lama1_human_1403–1449	ptma_rat_2–112	tnr6c_mouse_825–891
crem_human_284–343	lama1_human_397–451	q01212_human_194–245	tnr6_mouse_125–161
crem_mouse_97–137	lama1_human_951–995	q01212_human_520–571	tnr6_mouse_44–78
crim1_human_469–498	lamb1_mouse_1084–1129	q05331_human_258–306	tnr6_mouse_81–123
crim1_mouse_567–592	lamb2_rat_1041–1095	q05331_human_374–428	top2a_human_1435–1523
cspg5_human_31–277	lamb2_rat_1098–1143	q12771_human_1–77	top2a_mouse_1431–1519
ctro_mouse_377–424	lamb2_rat_413–470	q155p7_mouse_2313–2449	top2a_pig_1437–1525
dbnd1_human_14–153	lamb2_rat_473–522	q1lz73_bovin_1–288	top2b_human_1508–1611
def1_mouse_64–92	lamb2_rat_786–831	q1lzm4_mouse_106–174	trbm_bovin_180–213
def2_rabit_3–32	lamb2_rat_880–927	q1rml0_bovin_452–492	tsp1_human_383–428
def5_human_65–93	lamb2_rat_989–1038	q28659_rabit_451–524	ubf1_human_112–180
diap1_human_574–743	lamc1_mouse_340–393	q28707_rabit_1–126	v1ar_rat_378–424
diap1_mouse_1180–1194	lamc1_mouse_396–440	q2tle4_human_1–178	vldlr_rabit_111–149
diap1_mouse_589–747	lamc1_mouse_722–768	q2vxs9_human_1–98	vldlr_rabit_152–188
diap2_human_1054–1068	lamc1_mouse_882–930	q2vyc3_bovin_98–125	vldlr_rabit_191–229
dip2c_human_7–120	lamc1_mouse_933–978	q3mui2_rat_285–371	vldlr_rabit_237–273
dkk2_human_77–129	lap2a_human_110–152	q3syz0_bovin_1–168	vldlr_rabit_276–312
dkk3_mouse_146–197	lats2_mouse_950–1004	q3tgg2_mouse_176–245	vldlr_rabit_70–108
dkk4_human_40–92	ldlr_human_195–231	q3tjs8_mouse_16–227	vps4b_human_380–441
dmpk_mouse_472–532	ldlr_human_66–104	q3tk27_mouse_16–93	wwp1_human_351–380
dnjc1_mouse_492–541	ldlr_mouse_235–271	q3tnj4_mouse_1–281	zan_mouse_1555–1608
dnjc7_mouse_381–448	ldlr_rabit_133–171	q3u106_mouse_19–49	zan_mouse_1941–1995
dnmt1_mouse_16–106	ldlr_rabit_182–218	q3u9y3_mouse_332–390	zan_mouse_4504–4562
dnmt1_mouse_648–694	ldlr_rabit_261–300	q3ua02_mouse_293–351	zbt24_human_159–171
dss1_mouse_3–63	ldlr_rabit_53–91	q3ubi5_mouse_345–404	zbt48_human_319–342
dux1_human_95–151	ldlr_rabit_94–130	q3ue58_mouse_332–390	zfp60_mouse_484–506

^a Pfam members are listed here by protein name rather than Pfam number because disorder in the version 23.0 domains and families was not always completely conserved here. A discussion of this is found in the context of Figures 7 and 8.

Introduction

Intrinsically disordered proteins (IDPs) and regions (IDRs) have biological activities that, at least for part of the time, require the absence of stable 3-dimensional or secondary structure under physiological conditions.^5-17 Numbers estimating the amount of intrinsic disorder in proteins are stunning; about 43% of known mammalian protein sequence is in predicted intrinsic disorder (PID).^18-21 Between 35 and 51% of eukaryotic proteins have been predicted to contain IDRs that span 40 or more residues.²² Between 25 and 30% of eukaryotic proteins have been predicted to be half intrinsically disordered or more.²³ More than 70% of signaling proteins, and most of the cancer-associated proteins have been predicted to contain long disordered regions.²⁴

Disprot^25,26 is the repository for experimentally verified and annotated IDP data. Sequence/structure information in Disprot has been used by members of the IDP community to build more than 50 different methods for predicting regions of intrinsic disorder in proteins,^27-31 and to estimate statistics for the accuracy of these methods. Nine of these predictors, along with predictions for 10,429,761 sequences in 1,765 proteomes from 1,256 distinct species, are available on the D²P² site.³²

Direct experimental evidence for the existence of IDPs and IDRs comes primarily from the protein data bank (PDB)⁵³ where NMR solution structures show conformational ensembles that clearly indicate dynamic disorder. Many PDB entries contain segments of protein sequence that are completely missing from X-ray and neutron diffraction crystal structures, but as is well-known by crystallographers, these segments can correspond to structured regions that are unobserved for a variety of technical reasons. For this reason, intrinsic disorder cannot be assigned to residues in crystallized proteins solely because they are not located.

Nevertheless, 7% of the crystal structures in the PDB, which is highly selective for ordered proteins, have been assigned to IDRs longer than 10 residues.^54,55 IDPs and proteins with significant IDRs continue to resist crystallization, a situation that is unlikely to change.^56,57 With few exceptions, crystal structures of largely disordered proteins have been obtained only from relatively small isolated sections of biologically active IDPs, many of them co-crystallized with, or covalently bound to, much larger structured molecular complexes. Even under these conditions many residues in the IDRs cannot be located in the electron density, and the crystallized complex may not represent the interaction in solution.⁵⁸

Solution NMR data from a variety of chemical shift, relaxation, and heteronuclear NOE measurements yield unique information about the spectrum of conformational disorder and dynamics in proteins that is less specific but more accurate than that obtained from diffraction measurements.⁵⁹ Taken together, and supported by circular dichroism, vibrational spectroscopy, chromatography, and small angle scattering methods, these measurements provide certainty about the extent of static and dynamic disorder in IDPs and IDRs,^59,60 and this information is recorded in the Disprot database.²⁵ There are many biophysical techniques that can be used to characterize dynamic structure of IDPs, and many of these methods have been the subjects of focused reviews and books.^61-67

The p53 and 14–3-3 proteins provide 2 particularly striking examples of the biological activity of intrinsically disordered proteins.¹³ The p53 protein has several different IDRs that bind to different partners, and some IDRs that each bind in different conformations to several different partners, an association termed “one-to-many.” 14-3-3 on the other hand is a structured protein that binds many different intrinsically disordered partners in associations termed “many-to-one”¹³.

The Pfam-A database⁶⁸ is a curated collection of biologically conserved, and for many—functional, regions in proteins. Pfam sequences are grouped in large part by function and used to train hidden Markov models (HMMs) that are used to find similar regions in proteins where there is no protein based evidence of biological activity. The training set of sequences, Pfam-A.seed, contains regions from proteins that have been experimentally validated. It is this set that has been used in the present study to relate biological function with intrinsic disorder.

There have been 2 previous studies of IDRs in Pfam domains. Recent work,⁶⁹ looked at 71,974 version 22.0 Pfam-A seed members of 6,857 unique domains, limited to those that included GO annotations or had at least one literature citation. 12.14% of the domains had greater than 50% predicted disorder, and 4.15% were fully (95–100%) disordered. The high percentage of fully disordered domains was attributed to the uneven length distribution of domains, with somewhat shorter domains dominating at high percentage of disorder.⁶⁹ Earlier, 40% of Pfam domains were shown to contain conserved protein fragments that were predicted to be disordered (conserved disorder predictions, CDPs).⁷⁰ These CDPs were found in proteins from all domains/kingdoms of life, including viruses, with eukaryota having one order of magnitude more proteins containing long disordered regions than did archaea and bacteria. Functional analyses revealed that CDP regions frequently participate in signaling, regulation, and interaction with DNA/RNA and other proteins, common in ribosomal proteins.⁷¹ In the present work these findings reported earlier are reexamined in detail with some new results.

Here we analyze the distribution of intrinsic disorder in Pfam domain sequences using the 10 dimensional space provided by the Kidera factors for the 20 naturally occurring amino acids^1-3,72-76 combined with PONDR⁴ predictions of intrinsic disorder. The Kidera factors have been developed expressly to describe properties of the amino acid residues that may be related to protein folding with a minimum number of parameters. They are derived from a multivariate statistical analysis beginning with 188 quantitative measurements of the amino acids available in 1985. Because this set of factors contains most of the measurable information relating the amino acids, it is possible to estimate the numerical values for amino acids where measurements may be missing.

Four of the Kidera factors, helix/bend preference, side-chain size, extended structure preference, and hydrophobicity are essentially pure factors (Table 1). Each one has been derived from a cluster of measurements of the same property. For example, the cluster for hydrophobicity contains only the relatively large set of measurements related to amino acid solubility.

Table 1. Labels and abbreviations used here for the Kidera factors¹.

abbreviation	factor	abbreviation	factor
1. hel	Helix/bend preference	6. fle	Flat extended preference
2. siz	Side-chain size	7. psb	Partial specific volume
3. ext	Extended structure preference	8. alp	Occurrence in α region
4. hph	Hydrophobicity	9. pkc	pK-C
5. dbe	Double-bend preference	10. sur	Surrounding hydrophobicity

¹ These factors are principle components of a large set of experimental measurements, scaled from −1 to 1.3 The first 4: hel, siz, ext, and hph, are close to being pure physical properties. The remaining 6 labels describe the primary characteristic of the factor. Kidera factors, being orthonormal, contain 10 times the information contained in the sequence alone. An analysis of short range interactions in sequences benefits when these factors are included, potentially increasing the information available to an HMM analysis many fold.

The remaining 6 factors consist of weighted linear combinations of different measurements, labeled for convenience by the name of the most heavily weighted component.³ Where factors appear to have names related to similar properties, the similarity is in name only. For example, the vectors composed of the 10 factors for extended structure preference (ext) and flat extended preference (fle) for each of the 20 amino acids are themselves orthonormal. Likewise, the similarly named pairs hel/alp and siz/psb are also orthonormal (Table 1); there is no correlation between these factors.

As indicated by the authors, the Kidera factors are orthonormal by design to avoid problems arising from incompleteness and correlation (they are normalized and their inner product is zero.) They do not contain information about interactions as may arise from an analysis of a length of sequence for periodicity or interactions.

Information about interactions can be derived from a sliding window analysis of any of the 10 factors. As we show here, an average over sets of orthonormal factors can yield correlated results with reduced information content. However, an analysis of periodicity in sliding windows can also increase information content.

Some of the factors included in the original Kidera data set have been included in the set used to train the PONDR predictors used to make predictions here. These include the hydrophobicity scales from Kyte and Doolittle³⁵ and from Rose (for predicting turns in globular proteins),⁷⁷ and side chain volume.⁷⁸ Also included in PONDR training were charge (K+RD-E), aromatic count (W + F + Y), and coordination number,⁷⁹ which correlate strongly with hydrophobicity and side chain volume. Side chain volume, related to the convenience named partial specific volume Kidera factor, does not come close to being a pure physical property (Table 1 and ref. 3) and by itself is incomplete. Other factors included in PONDR training depend on the Kidera information in lengths of sequence and include a flexibility index calculated from a sliding window,⁸⁰ the hydrophobic periodicity moments from Eisenberg, Weiss, and Terwilliger,^81,82 codon number,⁸³ and alphabet size.⁸⁴ These scales are derived from a small part of the information contained in the Kidera data.

The PONDR predictors continue to be among the most accurate available,^85,86 suggesting that hydrophobicity, may be among the principle physical properties of the amino acids determining the tendency of proteins to evolve with functions in intrinsically disordered states. However, we show here that all 10 of the Kidera factors contribute to a clustering of different types of predicted intrinsic disorder in Pfam domains, and that plots of PONDR VSL2b predictor scores against hydrophobicity have a spread and appearance that is similar to that seen in plots of the VSL2b scores against any of the other Kidera factors. The inclusion of the Kidera factors in the training of disorder predictors could hypothetically increase the information content available to an analysis of intrinsic protein disorder by several fold.

Results and Discussion

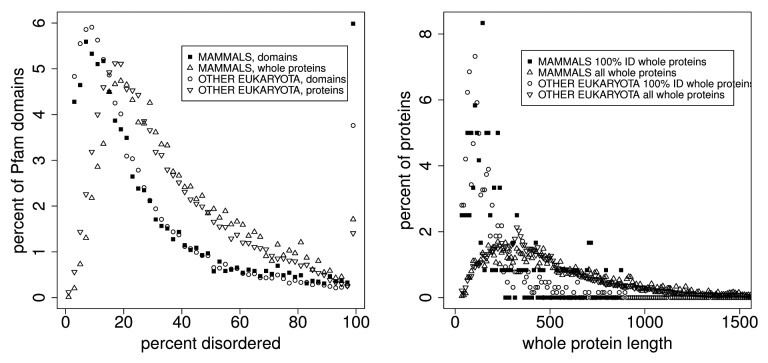
The results are shown and annotated in the figures and tables. Note that while Figure 1 includes the 15‒20% of Pfam members that contained no PID, subsequent figures exclude members with 0% PID by simply excluding data below 2% from the plot.

Figure 1. End effects do not contribute significantly to disorder distributions, as is shown here and in Table 2 in a comparison of the distribution of percent predicted disorder, as a function of the percentage of predicted disorder in 2% wide bins, in all Pfam seed proteins where domain members start or end within 19, 29, and 39 residues of the whole seed protein ends. All predictions in this work were performed on whole proteins, not on isolated domains, so sequence end prediction artifacts are restricted to Pfam domains at the N or C-terminus of proteins. When all proteins where end effects may affect prediction are removed, the prevalence of 100% predicted disordered domain members, shown here at 100% and in previous work,³³ does not significantly decrease (Table 2). The inset shows the distribution of lengths for 100% predicted intrinsically disordered (PID) Pfam sequences. Table 5 shows the quantiles. The mean length of 100% PID Pfam sequences is 82 residues. The mean length for PID regions in whole mammalian proteins in the Pfam seed set is 16 residues (Table 7).

The 10 Kidera factors are listed in Table 1. Testing the hypothesis that intrinsic protein disorder preference, like helix preference, is a fundamental physical property of the amino acids that was not included when the Kidera factors were calculated, a singular value decomposition of the 20 by 11 matrix composed of the Kidera factors and the frequencies of occurrence of the amino acids in IDPs yielded only 10 non-zero eigenvalues; the disorder preferences of the amino acids are linear combinations of the Kidera factors.

Of the 618 100% PID members of Pfam domains, 176 start at residues 1 through 19 of the parent protein. The VSL2b predictor is biased to assign disordered structure to the first 20 residues of a protein or isolated segment. We tested the hypothesis that about 176 members may be incorrectly predicted to be 100% disordered and that this error biased our calculations. The results, shown in Figure 1 and Table 2, indicate that end effects do not contribute significantly to the 100% PID group.

Table 2. Comparison of distributions for percent predicted disorder¹ in mammalian Pfam seed members that are more than 19 or 29 residues from the N and C protein termini (Fig. 1).

Pfam set	25%	med	mean	75%	N	compare2	99% conf int2	p-value	shift
Mam3	6.6	16.7	27.2	37.4	10654	Mam-19N	4.7e−5→2.8	1.4e−6	0.7
Mam	..	..	..	..	..	Mam-19CN	1.1→2.8	1.4e−15	2.0
Mam	..	..	..	..	..	Mam-29N	2.6e−5→1.5	1.2e−6	0.7
Mam-19N	5.9	15.2	25.4	33.3	8700	Mam-29N	−1.9e−5→6.0e−2	0.9	1.9e−6
Mam-29N	5.8	15.1	25.5	33.3	7964	Mam-29CN	3.9e−5→1.7	2.7e−5	0.7
Mam-19CN	4.8	14.1	23.7	31.5	4667	Mam-29CN	−2.1e−5→0.4	0.5	6.9e−5
Mam-29CN	4.3	13.8	23.8	31.7	3900	Mam	−3.0 → −1.3	3.0e−16	−2.2

¹ We test the Null hypothesis that the distribution for (1) the object under “Pfam set” differs from that for (2) the object under “diff” by a location shift of zero. The alternative is that they differ by some other 1- or 2-sided location shift. Percent disorder statistics are given as the quartiles of the distribution of PID calculated with R from a table where each row lists a domain or protein followed by the % disorder in that domain or protein. ²Compared with: this test, and the 99.9% confidence interval, are calculated using the R Wilcoxon rank sum (Mann-Whitney) test with continuity correction. The Mann-Whitney test is appropriate and accurate for comparing the medians of 2 large sample non-paired non-normal distributions, when those distributions are the same. ³All members of the version 23.0 Pfam-A seed database are included. Total numbers of member sequences are listed under “domains.” Mammals include only human, mouse, rat, bovine, rabbit, pig, and horse.

The sequence length mean of 100% PID Pfam sequences is 82, the median is just below 50, and includes many above 150. This broad and skewed distribution distorts the cluster analysis performed here to some extent where averages of Kidera factors taken over long sequences tend toward their central value of zero, while in shorter sequences there is a greater chance that a particular type of intrinsic disorder may be isolated, in a way that is analogous to searching for segments of helix, β-strand, or turn in folded structures. Earlier work finding 3 distinct albeit overlapping flavors of disorder⁵² evaluated amino acid composition in windows 41 residues long. The effects of our use of a homogeneous distribution of lengths here are discussed below where we evaluate the high dimensional analysis of our data.

Figure 2 and Table 3 show the distributions of PID in several proteomes compared with that in Human Pfam seed proteins. There are more long PID regions in the proteome than in the Pfam seeds for Humans. About 4% of the chimp, mouse, and human proteome whole proteins are 100% PID. Lower phylogenetic domains have smaller proportions of 100% disordered Pfam domains, and of disorder overall, in the following order: mammals > other eukaryota > viruses > bacteria > archaea. The median length of disordered regions in this 100% disordered group is 59 residues. Distributions of disorder in each of the 5 phylogenetic domains have positions that differ at the 0.999 level with p values less than 1 × 10⁻¹⁰ .

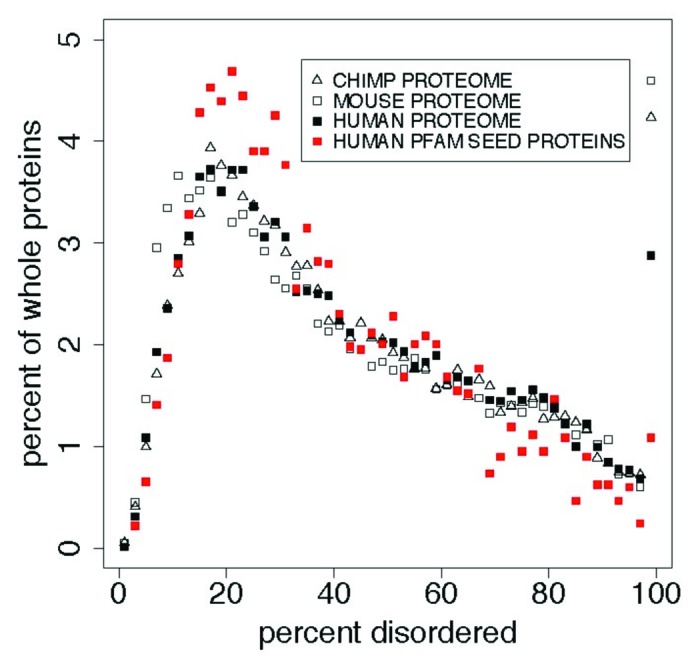
Figure 2. In whole proteins there appears to be a predominance of 100% PID over what is found in the Pfam seed database for humans, with more (here) in mouse and chimp than in human proteins. This cannot be attributed to an uneven distribution of Pfam domain or PID lengths, and suggests that the Pfam seed database excludes some IDPs. This is shown here in comparisons of the distribution of percent predicted disorder in the human proteome with the PanTroglodytes chimpanzee and MusMusculus mouse proteomes, and with human proteins chosen as sources for Pfam seed members (red). Table 3 shows statistics for these distributions. Proteins with 0% disorder are not plotted here. We note that the distribution for mouse is shifted 1% to the left of that for chimp and human proteomes while 100% PID is highest for the mouse.

Table 3. Comparison of distributions for percent disorder¹ in the proteomes for human, PanTroglodytes chimpanzee, and MusMusculus mouse (Fig. 2).

Proteomes	25%	med	mean	75%	N	compare	conf int1	p-value	shift
Human2	21.4	37.9	43.3	63.0	15859	Mouse	−3.2e−5→ 1.5	0.0014	0.7
Mouse2	19.5	37.0	43.2	64.1	26143	Chimp	−0.4 → −1.9	4.1e−7	−1.1
Chimp2	21.6	37.9	43.9	63.8	19710	Human	−0.3 → 1.2	0.072	0.4
Human Pfam	20.6	33.1	39.2	55.0	3688	Human	−4.5 → −1.7	3.5e−14	−3.1

¹ 99.9%; see footnotes 1 and 3 in Figure 2. ²These figures derive from whole proteins from entire Proteomes, and not Pfam domains. “Human Pfam” here indicates whole proteins in the Pfam seed set.

Overall, 28% of Pfam members with 100% PID are derived from whole proteins that are 100% PID, and Mammalian domains in the Pfam seed database contain 27% PID. This is 13.8% less than in their source proteins and 16% less than in mammalian proteomes. This can be seen, with the additional 3.1%, in Tables 3 and 4. We hypothesize that this is an artifact of low complexity sequence filtering in the selection of Pfam seeds, by accident or design. The null hypothesis, that each distribution does not differ from any other, can be rejected at the 0.999 level.

Table 4. Comparison of distributions for percent disorder¹ in Pfam seed members and whole proteins² (Fig. 3, left) comparing mammals and other eukaryota.

sample	25%	med	mean	75%	N	compare	conf int3	p-value	shift
Mam WP2	20.2	32.5	38.5	53.0	8357	Mam	−14.7 → −12.9	< 2e−16	−13.8
Mam WP	20.2	32.5	38.5	53.0	8357	Euk WP	2.6 → 4.1	< 2e−16	3.3
Euk WP	17.6	28.7	35.0	47.9	52060	Euk	−12.5 → −11.8	< 2e−16	−12.2

¹ Percent disorder statistics are given here as the quartiles of the distribution of intrinsic disorder calculated with R from a table where each row lists a domain or protein followed by the % disorder in that domain or protein. ²All members of the version 23.0 Pfam-A seed database were included. Total numbers of domain members are listed under “domains.” Whole proteins are indicated with “WP.” Mammals included only human, mouse, rat, bovine, rabbit, pig, and horse. Eukaryota here have only these removed.³99.9% confidence interval calculated using the R Wilcoxon rank sum test with continuity correction. The null hypothesis is that the distributions for mammals and the other domains listed here differ by a location shift of zero. The alternative is that they differ by some other one or two sided location shift.

Figure 3, and Tables 4 and 5, show the distributions of PID for Pfam seed members (regions of proteins) and the whole proteins from which seeds are derived.

Figure 3. Left: A comparison of the distribution of percent PID in Pfam seed domain members and Pfam whole proteins for mammals and other eukaryota in 2% wide bins show 2 things. About 1.7% of whole proteins and 6% of Pfam members are predicted to be 100% PID, but whole proteins contain significantly more PID overall. Again, whole proteins contain 28% of the Pfam sequences predicted to be 100% disordered, and do not fall into the category where uneven length distribution of domains accounts for 100% disordered Pfam domains. Also, predicted disorder is estimated to be 13% lower in Pfam domains than in Pfam whole proteins, shown in Table 4, “est dif.” Proteins and domains with 0% disorder are not plotted here. Right: Here, the median length of predicted 100% disordered whole proteins is about 70 residues longer than that of predicted 100% disordered Pfam domains (Table 5), and in Figure 4 the median length of Pfam domains is much larger than the median length of predicted intrinsically disordered regions. Clearly, some 100% PID Pfam sequences derive from whole proteins where PID extends beyond the ends of the Pfam segments as proposed earlier,³³ but there is no obvious reason why this classifies the significant category of predicted entirely disordered Pfam sequences as an artifact.

Table 5. Comparison of quantiles and means for the distributions of length in 100% PID: for Pfam seed members and whole proteins,¹ also shown in Figure 3, right, and Figure 1 inset.

sample	0%	25%	50%	mean	75%	100%	N
Mammal members	9	42	59	82	93	859	616
Mammal whole proteins	34	102	166	220	239	878	120
Eukaryota members	10	42	59	77	89	945	2090
Eukaryota whole proteins	32	87	132	186	222	1921	642

¹ as in Table 4. Statistics are rounded to nearest whole number. All statistics here are for the subset of sequences that are 100% PID.

Figure 4, and Tables 6 and 7, show the distributions for percent disorder in Pfam members, Pfam member length, predicted intrinsic disorder (ID) length in whole proteins, and numbers of ID regions in whole proteins. The inset in each plot shows the quartiles for each phylogenetic domain.

Figure 4. Distributions of Pfam seed sequences for mammals, other eukaryota, viruses, bacteria, and archaea, showing, upper left: the percent of Pfam domains as a function of the percentage of predicted disorder in 2% wide bins, and the spike in the number of domains that are 100% disordered (see also Table 4). Upper right: Pfam domain sequence lengths for mammals are 12 to 40 residues shorter than they are in other eukaryota, viruses, bacteria, and archaea, but the order of domain sequence lengths does not follow the order of 100% PID, as also shown in Table 7 under “shift.” The mean domain length is 145 residues (Table 7). Lower left: Intrinsically disordered region (IDR) lengths (distinct from Pfam domain lengths) for mammals are 1–5 residues longer than in other domains/kingdoms of life, also shown in Table 6, and the order of ID length follows the order of 100% PID. Most predicted intrinsically disordered regions are shorter than 10 residues, much shorter than the median Pfam domain sequence length. Lower right: there are significantly fewer IDRs in mammals than in viruses, and marginally fewer than in other eukaryota. The median is near 2, and some proteins are predicted to have more than 20 IDRs.

Table 6. Comparison of distributions for percent predicted disorder in Pfam seed members¹ (Fig. 4, upper left) comparing Mammals, Eukaryota, Viruses, Bacteria, and Archaea.

sample	25%	med	mean	75%	N	compare	Conf int1	p-value	shift
Mam	6.6	16.7	27.2	37.4	10660	Mam	−0.2→∞	0.5	−9e−07
Euk1	6.4	15.4	24.1	32.1	53395	Mam	0.4→∞	3e−15	1
Vir	6.7	14.2	21.5	28	6361	Mam	1→∞	2e−16	1.9
Bac	5.2	12.3	18.2	23.9	101959	Mam	3.4→∞	< 2e−16	3.9
Arc	4.3	10.9	15.4	20.7	12721	Mam	4.8→∞	< 2e−16	5.4

¹ as in Table 4

Table 7. Comparisons of distributions for Pfam seed member lengths¹ also shown in Figure 4 upper right, for mammals, eukaryota, viruses, bacteria, and archaea, showing that there are small but significant differences, and that the mean length for 100% PID members in mammalian proteins (top row of this table) is 60 residues shorter than that for mammalian Pfam member lengths².

sample	min	25%	med	mean	75%	max	compare	conf int2	p-value	shift
Mam PID lengths2	1	4	7	16.2	14	989	Mam			60
Mam 100%PID3	9	42	59	82.0	93	859	Mam	−∞ → −32	< 2e−16	−39
Mam	9	62	104	145.1	188	1372	Mam	−∞ → 3	0.5	1e−5
Euk1	10	73	121	162.5	218	1532	Mam	−∞ → −10	< 2e−16	−12
Vir	14	91	152	212.2	282	2188	Mam	−∞ → −36	< 2e−16	−41
Bac	12	80	124	157.0	205	1560	Mam	−∞ → −15	< 2e−16	−17
Arc	16	84	128	156.6	198	1462	Mam	−∞ → −17	< 2e−16	−20

¹ As in Table 4. ²Shown here for comparison, this line includes allmMammalian predicted intrinsically disordered region lengths, and not Pfam domains; see Figure 4 lower left. All other samples here are Pfam domain members. ³Domains 100% PID from Table 5 top row.

Most striking is the spike at the right side of Figure 4 top left indicating that there are more Mammalian Pfam members 100% PID than there are in any other 2% wide bin of the data. There are 618 100% PID Mammalian Pfam members in this set. Our initial hypothesis here—that this set of PID sequences was characterized by factors that differed from those in other PID sequences—could not be supported.

Also shown in Figure 4 top right and bottom left, while most PID sequences are shorter than 10 residues, very few Pfam members are this short, and the mean Pfam member length is 145 residues (Table 7).

Table 7 shows that each 100% PID Pfam member clearly derives from a PID region that is longer than the Pfam member. However, there is no compelling evidence here that the presence of entirely disordered Pfam members is an artifact, and does not have a special evolutionary significance, perhaps conferring an advantage to “higher” or “lower” phylogenetic domains. The evidence against artifact is also not especially compelling: the mean length of Pfam domain members, 145 residues, is much longer here than the mean length of PID regions, 16 residues. Pfam member lengths for mammals are 12–40 residues shorter than they are in other eukaryota, viruses, bacteria, and archaea. There appears to be a predominance of 100% PID in the eukaryotic proteome that is also seen in Pfam domain members. The Pfam seed database appears to exclude some IDPs. Predicted disorder is estimated here to be 13% lower in Pfam domains than in Pfam whole proteins. Twenty-eight percent of Pfam members that are 100% PID are derived from whole proteins that are 100% PID. Statistics alone cannot resolve this question.

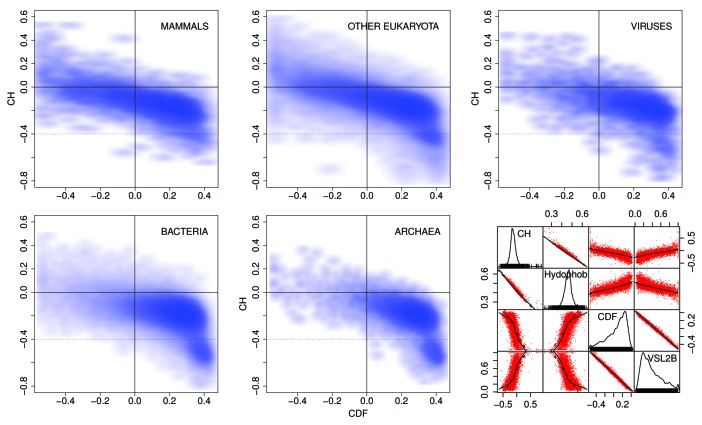
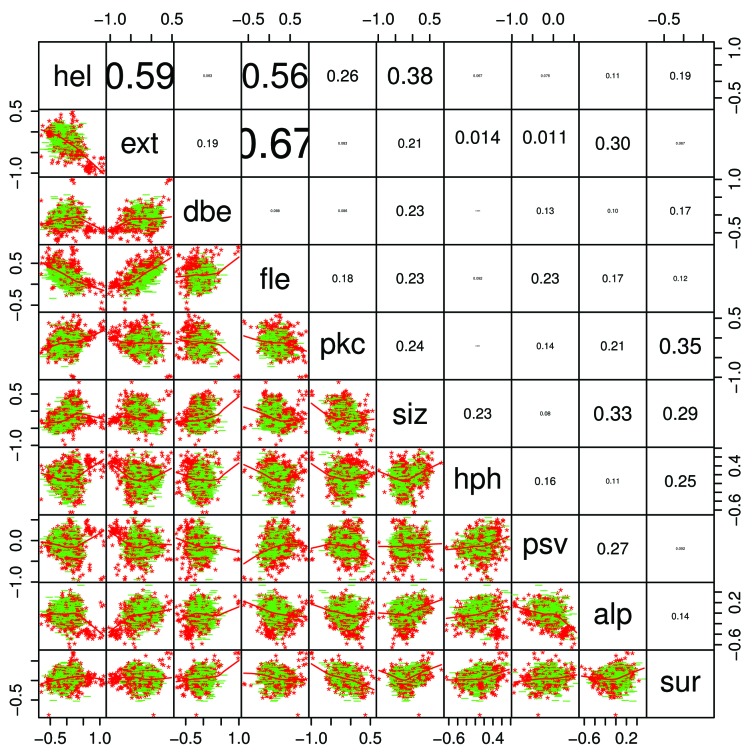
Figure 5 shows CH/CDF scatter plots³⁴ for the distributions of predicted disorder in Pfam-A version 23.0 members in mammals (10,660 Pfam members), other eukaryota (71,765), viruses (6,360), bacteria (101,959), and archaea (12,721). The CH/CDF plot shows, for all practical purposes, the VSL2b disorder prediction score on the x axis and hydropathy on the y axis. This can be seen in the scatter plot matrix in the lower right where CH, hydropathy,³⁵ CDF, and the VSL2b scores for mammals are all plotted against each other. CDF and VSL2b are highly correlated, as are CH and hydropathy.

Figure 5. CH/CDF plots³⁴ for mammals, other eukaryota, viruses, bacteria, and archaea. The scatterplot matrix (bottom right) shows density (number of sequences) as a function of CH, hydrophobicity,³⁵ CDF, and VSL2b,³⁶ while the off-diagonal plots show the correlations between each of these parameters. The off-diagonal plots: (1) corresponding to CH/CDF on the diagonal duplicate the plot for all Pfam seed sequences for Mammals (top left), and (2) corresponding to CH or CDF on the one hand and hydrophobicity or VSL2b on the other, show the high correlation between CH and hydrophobicity, and between CDF and VSL2b. Only 2 or 3 clearly separate clusters are evident here, but the cluster analyses of the Mammalian data, shown in Figures 9‒15 reveal much more information.

The CH/CDF plots are divided into 6 sections. Density in the lower and middle right hand sections of the CH/CDF plots corresponds to mostly ordered Pfam members, while density in the middle and upper left hand sections represents mostly disordered Pfam members. As can be seen, density shifts from the lower right to the upper left as plots progress from archaea, bacteria, viruses, and other eukaryota, to mammals. The grouping in the lower right hand side of the plots for archaea and bacteria in Figure 5, corresponding to proteins with no predicted intrinsic disorder, is not included in the cluster analyses below.

Figure 6 shows more detailed structure than can be seen in the Figure 5. Each plot here contrasts data from all of the phylogenetic domains, and shows the differences between domains more clearly than can be seen in Figure 4. Here the percent of Pfam members is on the Y axis, and the percent of predicted disorder in each region is on the X axis in 5% wide bins. We note that in each sub-plot the lines for all of the domains tend to cross at 1 point, giving the appearance of an isosbestic point, suggesting that there are at least 2 independent states in each of the 5 sections. A cluster analysis of these sections (not shown) indicates 2 components in each section, with the exception of the “spot” representing ordered proteins. Second, in the upper left quadrant, there are more eukaryota Pfam members in the 95–100% disordered group than in any other 5% wide group.

Figure 6. Pfam sequences plotted in each section of Figure 5 are plotted here as a function of percent disorder in each sequence, correlated with but not the same as the VSL2b parameter. We note that the ordering of phylogenetic domains, with respect to increasing PID, is preserved with the exception of the upper right quadrant where the sample size is too small to be significant. The shifts in PID from 1 domain to the next are more quantitative here, and each “quadrant” appears to represent 2 distinct states.

As discussed above, some methods of predicting intrinsically disordered structure are subject to end effects, such that, for VSL2b here, N-and C-terminals are predicted to be disordered when they are possibly not. This problem probably accounts for part of the approximately 20 percent false positive rate observed for some disorder predictors. As can be seen in the top left frame of Figure 6, corresponding to the lower-right spot in Figure 5 bottom center, in that group of proteins that are the least disordered, only 2–4% are predicted to have no disorder at all. End effects, at least here, partly account for this.

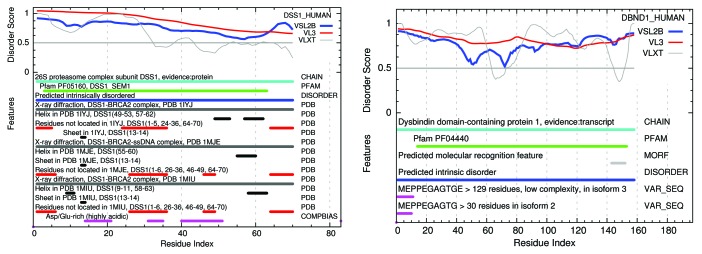
Figures 7 and 8 show structure-function feature maps for 3 examples of the 618 mammalian proteins found here with 100% predicted disordered Pfam members, chosen on the basis of their known involvement in human disease and presented in order of length. The program that generates these figures was written for this work and is now part of the Disprot PONDR predictors available on the Disprot site.⁴⁰

Figure 7. Structure-function maps of 2 100% PID whole proteins, each dominated by 1 Pfam domain, are shown above with Pfam sequences marked in green. Many similar examples exist where parts of these proteins have been crystallized, but in the presence of SDS or in co-crystals with partner molecules, illustrating the induced conformation nature of IDPs. X-ray crystal structure is marked in black. NMR solution structure is marked in gray. PF05160 DSS1 HUMAN has been co-crystallized in complexes: 1iyj,³⁷ 1mje,³⁸ and 1miu³⁹). No pdb evidence of structure yet exists for PF04440 DBND1 HUMAN. These plots of PONDR prediction results are available on the Disprot site.⁴⁰

Figure 8. A structure-function map of APC HUMAN shows an example of a protein with a mix of PID and structure with multiple Pfam domains (green), most predicted to be mostly disordered (blue). X-ray crystal structures (black) also include many residues not observed in these structured segments (red). The longest fragment of APC HUMAN to be obtained in large quantities is seen to be 100% disordered in the NMR solution structure (also red). Many of the X-ray structures for APC HUMAN have been co-crystalized with other molecules, suggesting that these conformations are induced by the binding of an IDP with a structured partner.

Included in each figure are the IDR prediction profiles from the PONDR VSL2b, VL3, and VXLT methods,⁴ markers for: Pfam family and domain members, predicted IDRs based on VSL2b, predicted molecular recognition features based on the VXLT profiles, regions of these proteins represented in the protein data bank by X-ray crystal diffraction and NMR evidence both for order and disorder, sites of phosphorylation and methylation, and for sequence variations related to human disease. These are described below with a comparison to other members of the same Pfam family.

PF05160: DSS1 HUMAN plays a role in ubiquitin-dependent proteolysis, interacts with the C-terminal of BRCA2, and is involved in split hand-split foot malformation.⁸⁷ Other members of this family predicted here to be 100% disordered are DSS1MOUSE-3-63, SEM1-DROME-15-75, and SEM11ARATH-8-70. The following members of the PfamA.seed set predicted to be less disordered are: Q9LIY2ORYSJ-9-97, 86%, SEM1-YEAST-19-84, 67%, and DSS1-SCHPO-2-66, 91%. In a limited sample some non-seed members show even lower amounts of PID, but we cannot say that it is generally true that some family members have widely differing amounts of PID.

PF04440: DBND1 HUMAN-14-153 binds to α- and β-dystrobrevin in muscle and brain, and genetic variation is thought to be associated with Schizophrenia.⁸⁸ Other members of this family in the seed set: DBND1-MOUSE-14-155, 94% PID, and DBND2HUMAN-100-254, 99% PID.

PF05923: APC HUMAN, Found repeated in the mid region of the adenomatous polyposis proteins (APCs), near many cancer-linked SNPs. These repeats bind β-catenin.⁸⁹ Most other V23.0 seed members of this family in human are 100% PID: 13691394, 1840-1866, 2006-2031, and 1948-1973, but 1485-1510 is 85% PID and 1636-1661 is 27% PID.

The Pfam V23.0 seed set appears to be accurate with respect to most of the IDPs we have sampled. However, there are, as with all prediction methods, some inconsistencies, and we note that we are applying a prediction to a prediction here.

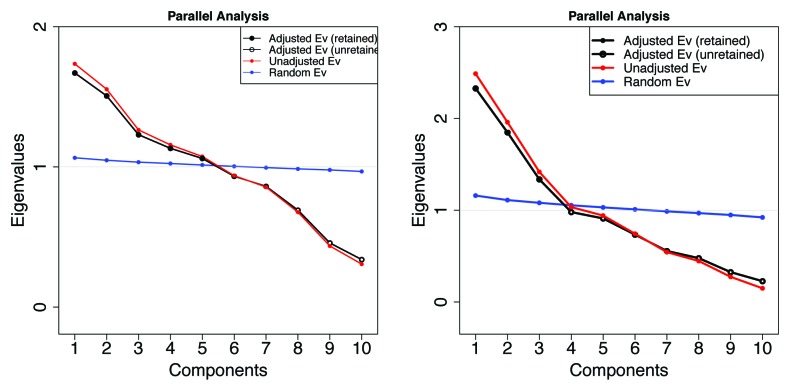
Figure 9 shows, on the right, a parallel analysis plot^41,42 indicating that there are probably 3 independent types of mostly or entirely disordered Pfam members where differences are based only on the averaged physical properties of their amino acids, and VSL2b scores are greater than 0.5. Likewise, on the left, we cannot reject the null hypothesis that there are 5 types of Pfam members in mammals based on the averaged physical characteristics. There are 6 when archaea are included (not shown). These groups are in addition to the HMM classifications.

Figure 9. Retention and rejection in the Glorfeld Principle Component Analysis^41-45 of Pfam sequence information represented by the 10 Kidera factors. Left: 5 components are retained from 10532 mammalian Pfam domains. Six components are retained when archaea are included (not shown). Right: 3 components are retained when the sample is restricted to 1913 members here where the VSL2b parameter is greater than 0.5 (more than half of each member is predicted to be disordered). As can be seen in the figures below, these components form well separated groups with very little overlap.

In an earlier study aimed specifically at finding different flavors of intrinsic protein disorder in the Swissprot database, Vucetic et al.⁵² found 3 groups characterized by their amino acid composition. These groups, composed of predicted intrinsically disordered regions divided into windows 41 residues long, were related to function. It is not possible to compare those groups to the ones seen in this work with respect to physical properties. The question here is: how do the clusters found here relate to Pfam families and function. There is substantial evidence that functional intrinsic disorder, particularly in long sequences, is composed of multiple shorter structural features, such as those found in MoRFs.^90,91 To be meaningful, the mapping of types of disorder to function or Pfam family should include a windowing analysis, similar to that performed earlier, of shorter segments that includes the kind of periodic features used to train PONDR in this respect.

Figure 10 shows a pairs graph⁴⁶ (a scatterplot of all factors against all others) of the mean Kidera factors for Pfam members where the average VSL2b score is greater than 0.5, indicating that the sequence is likely to be more than half disordered. As in Figure 9, red and green delineate 100% PID members from others that are between 50 and 100% PID. Members that are 100% PID show visually distinct clusters. This is where the VSL2b score, the predictor of intrinsic disorder, is highest. The 100% PID members here appear above the correlation line in the ext vs fle plot, and in the lower left of the dbe vs alp plot. However, these are not particularly special cases; there is some degree of separation in the predictions of partly and completely disordered structure by all pairs of factors, indicating again that all factors contribute to this distinction. Also, in the scatterplot matrix figure below, where the VSL2b score is included and the color distinction is made for clusters and not for degrees of disorder, the VSL2b score does not appear to be well correlated with either color mapping or with the overall trend of the scatter. Another way of viewing the clustering, and non-clustering, of 100% PID Pfam members is shown in the dendrogram plots below.

Figure 10. A pairs graph⁴⁶ shows scatterplot, regression lines, and typographically scaled absolute values of the correlation coefficients between the mean Kidera factors for the 1913 members where the mean VSL2b parameters are greater than 0.5 (half disordered or more). Points for domains that are 100% PID are red, while all others are green, showing several visually distinct clusters in each of the 2-dimensional plots in a way that is almost impossible with 2-dimensional projections of high-dimensional objects, and the corresponding dendrogram shown in Figure 13, right, does not reveal the level of structure shown here. Helix/bend (hel) and extended structure preferences (ext and fle) are negatively correlated, and the 2 extended structure preferences are positively correlated, as can be seen also in Figure 11. This is expected, but other correlations are relatively small. The Kidera factors themselves have zero correlation.

Note that although the Kidera factors themselves have zero correlation, some factors averaged over the entire lengths of Pfam sequences do show substantial correlation, albeit with large variance. There is a positive correlation here between average ext (extended) and fle (flat extended) factors, and a negative correlation between these and the average hel (helix) factors for entire Pfam sequences. These correlations appear again in Figure 11.

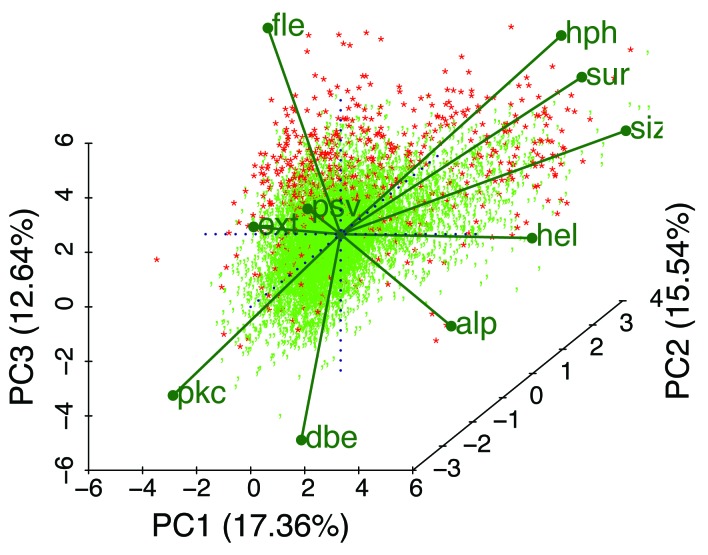
Figure 11. A biplot⁴⁷ of the data calculated from 10572 Pfam sequences and 10 mean Kidera factors shows a 2-dimensional projection of 3 of the 5 principle components, vectors of equal length representing the Kidera factors (Table 1), and 100% PID sequences colored in red. Note that the apparent correlation between hph and sur is caused by the projection into 2 dimensions, and that the actual correlation is 0.25 (Fig. 10). IDPs appear to arise here from a variety of combinations of average factors. These distinctions become even more evident when only shorter Pfam sequences, or windows of uniformly shorter segments, are chosen (not shown). As Pfam sequences become longer, the means of the Kidera factors tend toward the central value, zero, masking the diversity of IDP types in Pfam domains. We anticipate that, for example, a cluster will appear along the hel (helix) or alp (occurrence in α region) axis in an analysis that includes windows of 20 residues each, and that shorter windows may yield a cluster along the dbe (double-bend preference) axis.

Figure 11 shows a PCA biplot of all Pfam members here scored by the principle components of the 10 mean Kidera factors for the members. Each point represents an identifiable member with eigenvalues or coefficients corresponding to how much each component contributes to the variance in the original data. The 10 labeled vectors are projections of the mean Kidera axes onto the 2-dimensional plot shown here, indicating their contributions, however difficult to see in only 2 dimensions, to the 3 principle components represented here. The positively correlated average extended- and flat-extended factors point away from the average helix factor to which they are negatively correlated, and these are somewhat aligned along the PC1 and (for fle) PC3 axes. Note that 100% PID members, in red, are clustered primarily along the fle axis, but that some occupy positions at the far ends of other factors. All of the Kidera factors appear to contribute to the preference for types of order or disorder.

A better visualization of how all 10 factors contribute to the principle components, particularly when there are more than 3 PCs, can be obtained by rotating the PCA biplot in 2- and 3-dimensional projections in real time using the RGgobi and (for Windows only) BiplotGUI R packages.^92,93 Both there, as well as in static plots shown here, individual points can be labeled with their accession numbers to better explore these relationships.

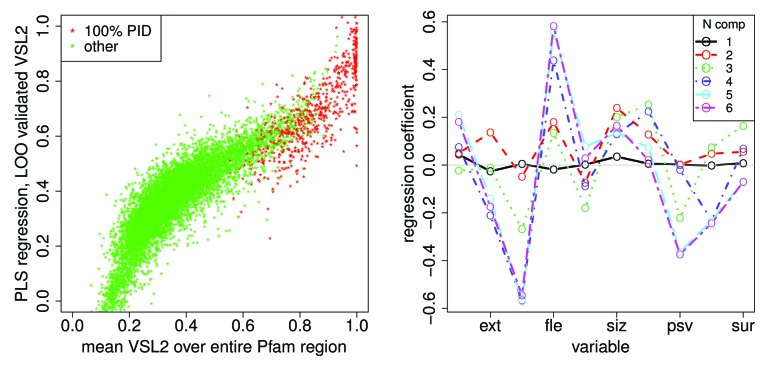
Figure 12 shows a partial least squares and principal component regression⁴⁸ of the mean VSL2b score against the 10 mean Kidera factors for all Pfam members included here. Each point on the left represents a Pfam member scaled by 6 eigenvectors of the PCA decomposition. Plots of the regression coefficients on the right show that only 5 components show noticeable differences, so the regression here is essentially in 5 dimensions. The distribution of lengths in Pfam members here is broad, causing the mean values of the Kidera factors to have a limited value, tending toward zero a central value where lengths are long.

Figure 12. A partial least squares and principal component regression⁴⁸ of the mean VSL2b factor against the 10 mean Kidera factors for 10572 Pfam sequences, left, shows a prediction of the mean VSL2b factor for Pfam sequences using “leave one out” validation, with 100% PID sequences in red. Here the x axis represents mean VSL2b scores calculated directly from the VSL2b predictions for each sequence (these are just mean VSL2b scores) and the y axis represents predictions from the multivariate linear regression on 6 principle components of the Kidera factors (see Methods). We hypothesize that the nonlinearity and spread of the data here is partly due to errors in the VSL2b predictions themselves, that the Kidera factors more accurately represent the tendency to disorder, and that the spread will narrow in an analysis of smaller uniform windows of sequence. Five components yield the same results, consistent with the results shown in Figure 9, and here to the right. The plot on the right shows the regression coefficients for these 6 sets of principle components. Here the sets containing 5 and 6 components have nearly the same coefficients, indicating, as was also shown using a different analysis in Figure 9, that the sixth component contributes little to the information contained in the Kidera factor averages. We hypothesize here that convergence will shift to more coefficients when smaller uniform windows are analyzed.

Figure 13 shows dendrograms⁴⁹ of the mean Kidera and VSL2b factors for the complete 10532 member set, and for the 1913 member set that includes only members with mean VSL2b scores above 0.5. It appears to be clear that 100% PID members are in distinct groups. Depending on where the y axis line is drawn, it is possible to find between 5 and 7 clusters here. However, in the 1,913 member subset, although we know that there are only 3 distinct clusters (Fig. 9, right), it is difficult to distinguish them here. 100% PID members appear to be distributed randomly among several distinct groups.

Figure 13. The dendrogram⁴⁹ on the left shows the mean Kidera and VSL2b factors for 10532 Pfam members, with clustered 100% PID members in red. Five clusters are obtained here by drawing a horizontal line crossing six of the vertical markers near y = 2.1. The marker on the far left is an outlier. Vertical lines at the bottom overlap considerably. The dendrogram on the right shows the same mean factors for 1913 Pfam members where the VSL2b mean is above 0.5 and sequences are half PID or more. Three clusters are obtained here by intersecting 3 vertical markers at y = 2.5. The 100% PID members plotted in red are not well clustered, indicating that here we cannot say they are different from those that are half PID. When sequences are chosen to be on the order of 10 residues, distinct clusters do appear (not shown).

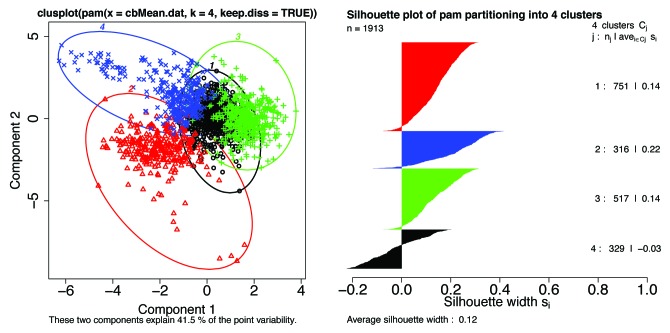
We now turn to a principle component analysis (PCA) of the Kidera factors averaged over entire Pfam sequence lengths, in Figure 14 below where the mean VSL2b scores are excluded, and in Figure 15 where they are included to show an almost complete lack of correlation with any single mean Kidera factor. Figure 14 shows a bivariate cluster plot,⁵⁰ showing only 2 components, of the 1,913 member subset where 4 components are retained to show the tendency of long members to have the same Kidera factor means, reducing the dimensionality available for discriminating between disorder types. The 4 clusters have the same colors in both the cluster and silhouette plots. While values around 0.2 in silhouette plots are low, indicating weak clustering, these values become larger as longer members are excluded.

Figure 14. Left: A bivariate cluster plot⁵⁰ of a Partitioning Around Medoids (PAM)⁵¹ for k = 4 clusters shows 3 clusters with almost no overlap, and 1 cluster with considerable overlap (black). The observations near zero tend to be from long Pfam sequences where means in the distance matrix tend to the central value. This calculation included the mean VSL2b factors and the 10 mean Kidera factors for 1913 Pfam members where the mean VSL2b factor is greater than 0.5. When k is set to 3, the black and blue points are combined into one group. Again, individual Pfam members can be identified here. Right: A silhouette plot of the same PAM object using the same colors also shows 3 mostly non-overlapping groups and one with significant overlap. Silhouette widths: near 1 indicate well clustered groups, near 0 indicates that observations lay between 2 clusters, and negative means that observations overlap or are in the wrong cluster. Colors, but not numbers, correspond to the same groups in each plot. The same observations with the same colors are also plotted in Figure 15. We note that overlap in the previous work⁵² was greater than 70%.

Figure 15. Scatterplot matrix of the mean VSL2b factors and 10 mean Kidera factors for 1913 Pfam members where the mean VSL2b factor is greater than 0.5. Points plotted here have the same colors used in the PAM cluster analysis⁵⁰ plotted in Figure 14. The scatter plot shown here for VSL2b (vsl) and hydrophobicity (hph) is essentially the same plot shown in Figure 5, with the exception that here only the left side of Figure 5 is represented. Note that the cluster identified in red is most prominent where size is plotted against the other parameters, and that it runs parallel to the VSL2b axis, indicating that sequences in this cluster containing large amino acids are present in both ordered and PID Pfam members. The cluster identified in green is most prominent when helix preference is plotted against other parameters, marking sequences with low mean helix preference, and for blue sequences with high mean helix preference.

The distribution of residue lengths has a distorting effect on cluster plots. While residue lengths of most PID sequences are less than 10 (4), the mean length of 100% PID Pfam sequences is 82, the median is less than 50, and many are longer than 150 (Fig. 1). These much longer sequences tend to have mean Kidera factors near zero, even though they may contain regions that vary from this and from each other significantly. Presently not well supported by the statistics, both the blue and red clusters on the left (Fig. 14) can be divided again to form 5 well separated clusters, and we think these will become more significant as a windowing scheme is imposed on the size of cluster members and the members colored in black become redistributed.

Figure 15 shows a scatterplot matrix for the 1913 member set where mean VSL2b factors greater than 0.5. Members plotted here have the same colors used in the PAM cluster analysis⁵⁰ plotted in Figure 14, but no PCA is performed here. Again, these plots take on different characteristics as sequence lengths become more uniform (not shown).

Perhaps the most notable feature of this figure: the cross-plot for vsl and hph, showing the relationship between VSL2b score and hydrophobicity, is essentially the same as is shown in the top left of Figure 5 where CDF is less than zero and CH is between -0.4 and 0.6. Note that the cross plots for vsl against all of the other Kidera factors show a similar spread of data, indicating that hydrophobicity is not the only factor important in predicting intrinsic disorder.

As in Figure 10, a positive correlation can be seen here between extended and flat extended structure, but here there is also a clear separation of clusters (colors) along the axis of the correlation. Also, the negative correlation between the 2 extended factors and helix shows a separation of clusters.

Note in this figure that amino acid size (siz) and partial specific volume (psv) have very different distributions plotted against predicted disorder (vsl). At least from this perspective, size divides both folded and disordered Pfam sequences along the vsl axis in a very clear way, while volume, one of the factors used in PONDR training, does not appear to discriminate. Likewise, hydrophobicity (hph), while showing more of a separation of the three primary clusters, does not show a direct relationship with vsl. The single Kidera factor that appears to be in the most direct relationship with vsl here is pkc where, on the top line of plots, blue predominates in the upper right and green somewhat in the lower left.

The Kidera factors contain most of what is known about the statistically countable and experimentally measurable physical characteristics of the amino acids, effectively increasing the information content of the sequence by 10-fold. Principle component and cluster analyses of the averages of these factors for each Pfam member, included those that are folded, reveal 6 separate groups. In the subset of Pfam members where the VSL2b disorder predictor is greater than 0.5 at least 3 groups are found, despite the homogeneous distribution of Pfam member lengths.

In the earlier study aimed specifically at finding different flavors of intrinsic protein disorder, Vucetic et al.⁵² found three groups characterized by their amino acid composition in windows 41 residues long in predicted intrinsically disordered regions in 80,000 sequences of the Swissprot database. It is not possible to compare those groups to the ones seen in this work with respect to physical properties. However, we can observe that the overlap of clusters in the previous work is considerable, while here in Figure 14 the overlap of 1913 sequences is very small but the clustering is weak in the usual interpretation of the silhouette plot.

Where sequences are long the average of the Kidera factors tend toward zero, limiting the capacity of the analyses to discriminate. It is hypothesized that grouping sequences into smaller subsets with more uniform lengths will reveal more information, and lead to more finely structured and perhaps more accurate predictions of intrinsic disorder. Adding additional information derived from sliding window calculations based on the physical properties, related to interactions such as is provided by hydrophobic moment,⁸¹ and flexibility,^4,80 strengthens predictor training, particularly for features important for molecular recognition.^90,91

Tables 8 and 9 show the percent of non-mammal single and multiple cell Eukaryotes, respectively, with unique Pfam members that are 100% PID. It has been shown previously that the average fractions of disordered residues in unicellular and multicellular Eukaryotes are about the same, with unicellular eukaryotes having more scatter (ref. 21 and Fig. 1). We observe here, in a relatively small sample size, that single cell eukaryotes are predicted to have fewer species with 100% intrinsically disordered Pfam domains than multiple cell eukaryota. This may be an artifact of the selection of Pfam seed sequences in these 2 groups, or it may have some evolutionary significance.

Table 8. Percent of single cell eukaryotaa from unique Pfam domains 100% PID.

weighted mean and variance
name	Ndis	tot	%dis	taxonomyb
Mean 1.5%, variance 0.6				Eukaryota:
TRIVA	4	541	0.7	Parabasalidea Trichomonada TrichomonadidaTrichomonadidae...
GUITH	1	112	0.9	Cryptophyta Pyrenomonadales Geminigeraceae Guillardia
GIALA	2	193	1	Diplomonadida Hexamitidae Giardiinae Giardia
LEIMA	4	330	1.2	Euglenozoa Kinetoplastida Trypanosomatidae Leishmania
TRYCR	6	365	1.6	Euglenozoa Kinetoplastida TrypanosomatidaeTrypanosoma...
PLAF7	10	391	2.6	Alveolata Apicomplexa Aconoidasida Hemosporida Plasmodium...
PLAFA	2	161	1.2	Alveolata Apicomplexa Aconoidasida Hemosporida Plasmodium...
PLAYO	3	231	1.3	Alveolata Apicomplexa Aconoidasida Hemosporida Plasmodium...
THEAN	5	142	3.5	Alveolata Apicomplexa Aconoidasida Piroplasmida Theileriidae...
THEPA	3	208	1.4	Alveolata Apicomplexa Aconoidasida Piroplasmida Theileriidae...
CRYHO	1	105	0.9	Alveolata Apicomplexa Coccidia Eucoccidiorida Eimeriorina...
CRYPV	3	122	2.5	Alveolata Apicomplexa Coccidia Eucoccidiorida Eimeriorina...
Mean 1.1%, variance 0.2				Eukaryota Viridiplantae Chlorophyta:
OSTTA	4	293	1.4	Prasinophyceae Mamiellales Ostreococcus
CHLRE	1	148	0.7	Chlorophyceae Chlamydomonadales Chlamydomonadaceae Chlamydomonas
Mean 2.5%, variance 0.1				Eukaryota Alveolata Ciliophora Intramacronucleata Oligohymenophorea:
TETTH	6	279	2.2	Hymenostomatida Tetrahymenina Tetrahymenidae Tetrahymena
PARTE	13	494	2.6	Peniculida Parameciidae Paramecium
Mean 2.2%, variance 0.5				Eukaryota Fungi Dikarya Ascomycota:
YARLI	19	707	2.7	Saccharomyceta Saccharomycotina Saccharomycetes Saccharomycetales...
ASHGO	14	560	2.5	Saccharomyceta Saccharomycotina Saccharomycetes Saccharomycetales...
CANAL	22	709	3.1	Saccharomyceta Saccharomycotina Saccharomycetes Saccharomycetales...
YEAST	49	2811	1.7	Saccharomyceta Saccharomycotina Saccharomycetes Saccharomycetales...
CANGA	13	561	2.3	Saccharomyceta Saccharomycotina Saccharomycetes Saccharomycetales...
DEBHA	21	558	3.8	Saccharomyceta Saccharomycotina Saccharomycetes Saccharomycetales...
KLULA	15	631	2.4	Saccharomyceta Saccharomycotina Saccharomycetes Saccharomycetales...
SCHPO	30	1970	1.5	Taphrinomycotina Schizosaccharomycetes Schizosaccharomycetales...
27.90% (one sample)			Eukaryota Fungi Dikarya Ascomycota Taphrinomycotina:
PNECA	50	179	27.9	Pneumocystidomycetes Pneumocystidaceae Pneumocystis (pneumonia)
Mean 4.2%, variance 0.5				Eukaryota Fungi Dikarya Basidiomycota:
USTMA	18	488	3.7	Ustilaginomycotina Ustilaginomycetes Ustilaginales Ustilaginaceae Ustilago
CRYNE	26	560	4.6	Agaricomycotina	Tremellomycetes	Tremellales	Tremellaceae	Filobasidiella
0.90% (one sample)			Eukaryota Fungi Microsporidia Unikaryonidae Encephalitozoon:
ENCCU	2	217	0.9
2.50% (one sample)			Eukaryota Amoebozoa Mycetozoa Dictyosteliida Dictyostelium:
DICDI	15	593	2.5

^a Only species represented by 100 or more Pfam domains in the seed database are included. Ndis: number of proteins; 100% PID; tot: total number of proteins analyzed; ^b “...” indicates where not all levels of taxonomy are listed.

Table 9. Percent of non-mammal multiple cell Eukaryota with unique Pfam members^a 100% PID.

weighted mean and variance
name	Ndis	tot	%dis	taxonomyb
mean 3.0%, variance 4.3				Eukaryota Metazoa:
CIOIN	5	111	4.5	Chordata (mostly vertabrates) Urochordata Ascidiacea Enterogona Phlebobranchia...
SCHJA	10	290	3.4	Platyhelminthes (〉atworms) Trematoda Digenea Strigeidida Schistosomatoidea...
STRPU	11	130	8.5	Echinodermata Eleutherozoa Echinozoa Echinoidea Euechinoidea Echinacea...
CAEEL	196	6844	2.9	Nematoda (roundworms) Chromadorea Rhabditida Rhabditoidea Rhabditidae...
mean 5.9%, variance 1.2				Eukaryota Metazoa Chordata Craniata Vertebrata Euteleostomi:
DANRE	77	1244	6.2	Actinopterygii Neopterygii Teleostei Ostariophysi Cypriniformes Cyprinidae...
ONCMY	5	112	4.5	Actinopterygii Neopterygii Teleostei Euteleostei Protacanthopterygii Salmoniformes...
TETNG	53	1029	5.2	Actinopterygii Neopterygii Teleostei Euteleostei Neoteleostei Acanthomorpha...
XENLA	76	1102	6.9	Amphibia Batrachia Anura Mesobatrachia Pipoidea Pipidae Xenopodinae Xenopus
XENTR	10	266	3.8	Amphibia Batrachia Anura Mesobatrachia Pipoidea Pipidae Xenopodinae Xenopus
mean 2.5%, variance 6.4				Eukaryota Viridiplantae Streptophyta Embryophyta Tracheophyta Spermatophyta Magnoliophyta eudicotyledons core eudicotyledons:
ARATH	166	7503	2.2	rosids malvids Brassicales Brassicaceae Arabidopsis (Mouse-ear cress)
SOYBN	19	206	9.2	rosids fabids Fabales Fabaceae Papilionoideae Phaseoleae Glycine (soybean)
PEA	4	156	2.6	rosids fabids Fabales Fabaceae Papilionoideae Fabeae Pisum (garden pea)
VITVI	10	142	7.0	rosids Vitales Vitaceae Vitis (grape)
SOLTU	4	141	2.8	asterids lamiids Solanales Solanaceae Solanoideae Solaneae Solanum (potato)
SOLLC	6	273	2.2	asterids lamiids Solanales Solanaceae Solanoideae Solaneae Solanum... (tomato)
TOBAC	7	188	3.7	asterids lamiids Solanales Solanaceae Nicotianoideae Nicotianeae Nicotiana (tobaco)
mean 4.5%, variance 2.2				Eukaryota Viridiplantae Streptophyta Embryophyta Tracheophyta Spermatophyta Magnoliophyta Liliopsida Poales Poaceae:
ORYSA	13	303	4.3	BEP clade Ehrhartoideae Oryzeae Oryza (rice)
ORYSJ	115	2562	4.5	BEP clade Ehrhartoideae Oryzeae Oryza (rice)
WHEAT	10	106	9.4	BEP clade Pooideae Triticeae Triticum (wheat)
HORVU	4	126	3.2	BEP clade Pooideae Triticeae Hordeum (barley)
MAIZE	10	281	3.6	PACCAD clade Panicoideae Andropogoneae Zea (maize)
mean 4.3%, variance 0.8				Eukaryota Fungi Dikarya Ascomycota Saccharomyceta Pezizomycotina Leotiomyceta:
COCIM	17	340	5.0	Eurotiomycetes Eurotiomycetidae Onygenales mitosporic Onygenales Coccidioides
ASPCL	11	276	4.0	Eurotiomycetes Eurotiomycetidae Eurotiales Trichocomaceae... Aspergillus
ASPFU	9	234	3.8	Eurotiomycetes Eurotiomycetidae Eurotiales Trichocomaceae... Aspergillus
ASPOR	11	374	2.9	Eurotiomycetes Eurotiomycetidae Eurotiales Trichocomaceae... Aspergillus
ASPTN	9	212	4.2	Eurotiomycetes Eurotiomycetidae Eurotiales Trichocomaceae... Aspergillus
EMENI	23	614	3.7	Eurotiomycetes Eurotiomycetidae Eurotiales Trichocomaceae Emericella
NEOFI	12	164	7.3	Eurotiomycetes Eurotiomycetidae Eurotiales Trichocomaceae... (aspergillus
NEUCR	54	1192	4.5	Sordariomyceta Sordariomycetes Sordariomycetidae Sordariales... Neurospora
CHAGB	19	378	5.0	Sordariomyceta Sordariomycetes Sordariomycetidae Sordariales... Chaetomium
PODAN	6	115	5.2	Sordariomyceta Sordariomycetes Sordariomycetidae Sordariales... Podospora
MAGGR	5	166	3.0	Sordariomyceta Sordariomycetes Sordariomycetidae Magnaporthales... Magnaporthe
PHANO	20	441	4.5	Dothideomyceta Dothideomycetes Pleosporomycetidae Pleosporales... Phaeosphaeria
mean 3.4%, variance 0.5				Eukaryota Metazoa Arthropoda Hexapoda Insecta Pterygota Neoptera Endopterygota (insects):
AEDAE	28	692	4.0	Diptera Nematocera Culicoidea Culicidae Culicinae Culicini Aedes (Yellowfever)
ANOGA	25	1019	2.4	Diptera Nematocera Culicoidea Culicidae Anophelinae Anopheles (malaria)
DROME	143	3963	3.6	Diptera Brachycera Muscomorpha Ephydroidea Drosophilidae Drosophila
DROPS	16	512	3.1	Diptera Brachycera Muscomorpha Ephydroidea Drosophilidae Drosophila
BOMMO	4	200	2.0	Lepidoptera Glossata Ditrysia Bombycoidea Bombycidae Bombycinae Bombyx

^a,b as in Table 8

Conclusions

A standing hypothesis among IDP investigators proposes that intrinsically disordered protein (IDP) has evolved into different classes that can be identified by physical characteristics or functions, analogous to those identified by HMMs in the Pfam database. We analyze distributions and clusters of PID in 193024 members of the version 23.0 Pfam seed database, representing 12456 unique domains, families, and repeats. Of these sequences, 616 mammalian members associated with 315 biological functions, and 120 of the parent whole protein set, are 100% PID.

Exploring ways to find the maximum information content in intrinsically disordered proteins independent of sequence information used to train HMMs, we applied the 10 linearly independent Kidera factors¹ containing most of the variance in the physical properties of the amino acids to a transformation and analysis of sequence in Pfam training set members. The hypothesis that intrinsic protein disorder exists in multiple forms with preferences analogous to those for protein secondary structure, as is evidenced in the success of MoRF predictors^90,91 is supported by this analysis. There are 3 principle conclusions:

(1) Each of the 10 orthonormal Kidera factors contributes to intrinsic protein disorder. The PONDR predictors used here, while still among the most accurate, included less than 2 of the Kidera factors in training. The inclusion of all 10 Kidera factors could hypothetically increase the information available to a predictor by more than 5-fold.

(2) We identify 3 clearly separate and non-overlapping clusters of intrinsically disordered Mammalian Pfam sequences where the VSL2b score for disorder is not clearly correlated with cluster parameters, and where HMM training or sliding window calculations are not involved. The distributions of length in these Pfam sequences are broad and skewed, so these 3 clusters are groupings of intrinsically disordered Pfam sequences (or families), and not of types of intrinsic disorder. A sliding window analysis limiting sequence size to uniform lengths characteristic of MoRFs and other features important to IDP function could hypothetically increase the number of non-overlapping clusters several fold and reveal a meaningful correlation between disorder cluster type and function. The next step is to train an intrinsic disorder predictor against the Kidera transformed Disprot Database, with the addition of these other methods for recognizing patterns in sequence.

(3) While mammalian proteins in the Pfam seed database contain 40% PID sequence here, only 27% of the Pfam members in this set contain PID regions, suggesting that the Pfam database is missing functionally important PID protein domains.

Methods

The Kidera factors consist of 10 linearly independent vectors derived from an eigenvalue—eigenvector decomposition of statistically and experimentally determined physical properties of the amino acids. The frequencies of occurrence of each amino acid in experimentally known intrinsic disorder, from the Disprot database, can be added to the Kidera matrix to make 11 columns, but a singular value decomposition of this matrix shows only 10 linearly independent vectors; the preference for intrinsic disorder is contained in the 10 Kidera factors. Our 3 letter abbreviations for these factors are shown in Table 1.

This analysis included 193024 members of the version 23.0 Pfam seed database,⁶⁸ representing 12456 unique domains, families, and repeats. The term “members” here refers to individual Pfam domain member sequences and not to entire Pfam domains. The term “domains” here is used for both Pfam domains and phylogenetic domains, but the distinction is spelled out. The term “regions” here refers to parts of proteins, or parts of Pfam members. The term “sequence” here refers to protein in whole or part, and if in part, whether it is isolated or not is spelled out.

Whole protein sequences represented in the Pfam seed set, and the human, mouse, and chimp proteomes were obtained from Uniprot.¹⁹

Predictions of intrinsic disorder were performed on 193024 whole proteins using predictors VSL2b,³⁶ VL3,⁹⁴ and a method that is predictive of molecular recognition features, VLXT.^90,91,95 The VSL2b predictor used for the statistical results here compares well with other methods, available on the D²P² site.³²

Statistics, cluster, factor, and principle component analyses, were calculated using R core and contributed packages.^{41,46-50,92,96,97} The R implementation of the Wilcoxon rank sum test with continuity correction is used to compare distributions, testing the null hypothesis that the distributions of x and y differ by a location shift of “mu.” The alternative is that they differ by some other 1- or 2-sided location shift. Rejection of a null hypothesis in some cases sampled here may have no practical significance if other larger effects are present, such as the possibility that populations of Pfam domains may contain artifacts of HMM training methods, as it appears to be a factor here with respect to low complexity sequences.

Cluster analyses are notoriously difficult to validate. Clusters can appear at random in nature. Confidence intervals on the results of a singular value or eigenvector–eigenvalue decomposition can be calculated when the standard error in the data noise is known because the scale of the original data are maintained through the transformation and eigenvectors can be compared with noise.^98,99 Again, even if the level of the noise were known here, other larger effects may render it meaningless.

To obtain some statistical confidence in our results, a parallel analysis^41,42 was performed using an eigenvalue-eigenvector decomposition and Glorfelds principle component analysis⁴⁵ of the 10532-Pfam-member by 10-mean-Kidera-factor matrix. Each Pfam family or domain member was represented by a vector of the means of the 10 Kidera factors listed in Table 1 over each entire Pfam region. Paran options included 1000 and 5000 iterations, giving the same results at the 99th percentile. A common factor analysis (not shown) retained seven factors from the 10532 sample set. No real difference was seen in the number of eigenvalues retained when VSL2b scores are added to the Kidera set.

A partial least squares and principal component regression, plsr,⁴⁸ of the mean VSL2b factor against the 10 mean Kidera factors for 10572 Pfam sequences were calculated using the following model: vsl hel + ext + dbe + 〉e + pkc + siz + hph + psv + alp + sur.

Structure and function information extracted from Uniprot database or fasta format files is combined with predictions of intrinsic disorder here to provide graphical representation of the relationships between these features. This program is available on the Disprot database prediction site.¹⁰⁰

Disclosure of Potential Conflicts of Interest

No potential conflicts of interest were disclosed.

Acknowledgments

Supported by Department of Defense High Performance Computing Modernization Program project number ODEFN26263101 and USU project C02928.