Mechanotransduction Dynamics at the Cell-Matrix Interface

Abstract

The ability of cells to sense and respond to mechanical cues from the surrounding environment has been implicated as a key regulator of cell differentiation, migration, and proliferation. The extracellular matrix (ECM) is an oft-overlooked component of the interface between cells and their surroundings. Cells assemble soluble ECM proteins into insoluble fibrils with unique mechanical properties that can alter the mechanical cues a cell receives. In this study, we construct a model that predicts the dynamics of cellular traction force generation and subsequent assembly of fibrils of the ECM protein fibronectin (FN). FN fibrils are the primary component in primordial ECM and, as such, FN assembly is a critical component in the cellular mechanical response. The model consists of a network of Hookean springs, each representing an extensible domain within an assembling FN fibril. As actomyosin forces stretch the spring network, simulations predict the resulting traction force and FN fibril formation. The model accurately predicts FN fibril morphometry and demonstrates a mechanism by which FN fibril assembly regulates traction force dynamics in response to mechanical stimuli and varying surrounding substrate stiffness.

Introduction

Mechanical interactions between cells and their underlying substrate are of great interest and have spawned an entire field of study (reviewed in the literature (1, 2, 3, 4)). Previous studies have demonstrated that the elastic modulus of an underlying surface can modulate cell migration (5, 6, 7, 8), cell differentiation (9, 10, 11, 12, 13), cell spreading (14, 15), and cell survival (16, 17, 18). Clinical studies have shown that tissue stiffness can have profound effects on disease progression: patients bearing malignant tumors with increased elastic modulus present with more severe disease (19, 20); increased elastic modulus in liver tissue is a predictor of cirrhosis (21); and kidney tissue stiffness has been shown to correlate with disease progression in chronic kidney disease (22). Clearly, cells are able to sense the mechanical properties of their surroundings, and subsequent cell fate and function are determined by mechanically transduced signals.

The primary mechanism of mechanotransduction is via transmembrane integrins, which are linked to the actin cytoskeleton via focal adhesion (FA) complexes. Integrins transmit myosin-generated forces that act on the cytoskeleton to the surrounding extracellular substrate. Mechanosensory proteins within the FA complex respond to altered forces and/or strains that result from these interactions, and these forces are altered based on the elastic modulus of the surface to which cells are attached. A previous study from the Odde group elegantly modeled the elements of this system and demonstrated two distinct regimes (23): on rigid surfaces, integrin-substrate rupture events are frequent, so transmitted forces are low (a frictional-slippage regime). On soft surfaces, integrin-substrate rupture events are reduced due to the compliance of the substrate; as such, cells are able to maintain large forces for longer periods of time (a load-and-fail regime). Measured traction forces generated by embryonic chick forebrain neurons support this model (23); however, several experimental studies have indicated contrary data, in which traction forces increase with increasing substrate stiffness (14, 24, 25, 26, 27, 28).

There are several possible explanations for the variable cellular response to substrate stiffness, including cell-dependent manipulation of actomyosin motor and clutch parameters, as was described in a subsequent study by Bangasser et al. (29). We posit another possible explanation: mechanical modulation by the extracellular matrix (ECM). The ECM is a web of proteins that are assembled by cells; several of the major ECM components are proteins assembled into a fibrillar structure, including collagen, fibronectin, fibrillin, and elastin. These assembled fibrils have unique mechanical properties and serve as intermediate elastic elements between a cell and the substrate to which it is attached. We propose that the cellular response to substrates with varied mechanical properties is mediated by ECM fibrils throughout the assembly process. In this study, we develop a model that accounts for the assembly of one such ECM fibrillar protein in response to cell generated forces, fibronectin (FN).

FN fibrils are one of the earliest ECM proteins assembled during embryogenesis and wound healing (reviewed in Schwarzbauer and DeSimone (30) and Mao and Schwarzbauer (31)). Previous studies have indicated that FN fibrils require actomyosin-based force to assemble (32, 33) and are extremely elastic and extensible (34). It is thus reasonable to envision that FN fibril assembly modulates the effective rigidity of an underlying substrate. Previous studies from our group have demonstrated that FN fibrils indeed modify the magnitude of contractile forces generated by cells, regardless of substrate rigidity (14).

We present here a computational model of the actomyosin-FA-FN fibril-substrate unit that simulates the assembly of a single FN fibril and the emergent reciprocal effects of the FN fibril on the effective substrate rigidity and resulting cell-generated contractile force. The model consists of an elastic substrate, represented by a Hookean spring, attached to a series of Hookean springs that represent the extensible domains within a single FN molecule. Integrin binding to FN is represented by a first-order reversible reaction with a force-dependent dissociation rate, and the actomyosin machinery is represented by a pulling force with an inverse force-velocity relationship. When an individual FN domain is stretched beyond a critical threshold, binding of a new FN molecule to the assembling FN fibril is simulated by the addition of a new series of Hookean springs attached in parallel, such that the assembling FN fibril is represented by a large Hookean spring network (Fig. 1). The model accurately reproduces experimental measures of FN fibril morphometry and extensibility. Further, simulations predict that the presence of assembled FN fibrils at the cell-substrate interface creates an intermediate domain between the load-and-fail and frictional-slippage regimes.

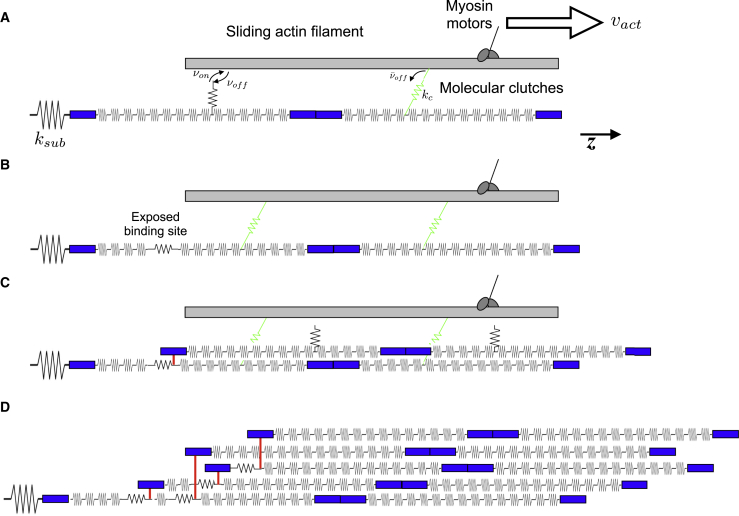
Figure 1.

Schematic illustration of the FN model. (A) Assembly begins with a single FN molecule, represented by 30 springs in series, attached to an elastic substrate, with stiffness k_sub. Myosin motors pull on the sliding actin filament at velocity v_act along the z axis. Molecular clutches reversibly bind the actin filament with rates v_on and v_off. Engaged molecular clutches transmit a force proportional to the clutch stiffness k_c, and disengage with a force-dependent off-rate ${\overline{v}}_{\text{off}}$. Note that engaged clutches are connected in parallel with springs representing FN Type III domains. (B) Actomyosin-driven forces stretch the FN Type III domains, exposing a cryptic FN binding site. (C) A soluble FN molecule in the extracellular space binds to the exposed binding site. (D) Subsequent molecular clutch engagement, FN Type III domain stretching, and FN-FN binding events produce an elastic, insoluble FN fibril. To see this figure in color, go online.

Materials and Methods

A detailed description of the model formulation, equations, implementation, numerical integration, and parameters is provided in the Supporting Material. An abbreviated model description is given below.

Fibronectin as a series of Hookean springs

Fibronectin consists of a series of nominally 29 independently folded domains. These domains are referred to as Type I, Type II, or Type III, depending on their structure (35, 36). While both Type I and Type II domains contain multiple disulfide bonds, which inhibit domain unfolding in response to contractile force, the 15 Type III domains, lacking disulfide bonds, have been shown to unfold in response to contractile force (37, 38, 39). Atomic force microscopy experiments have shown that the magnitudes of force required for domain unfolding are unique for many of the domains (39). As such, we model each Type III domain as a time-varying Hookean spring, with a unique resting stiffness, with values determined from experimental data where available (38, 39) and estimated based on chemical unfolding data when mechanical data was unavailable (T. Ohashi and H. Erickson, personal communication) (Fig. 1 A).

Type I and II domains are present at both the N- and C- terminus of the molecule (nine Type I and two Type II domains at the N-terminus, and three Type I domains at the C-terminus). The lengths of these domains are modeled using available crystal structure data, but because these domains do not unfold, the lengths are merely included as spacing elements with no force-dependent stretch (Fig. 1 A, solid blue regions). Because FN exists as a homodimer in the extracellular space, each FN molecule is represented by 30 springs in series (one spring per each Type III domain, with 15 Type III domains per FN molecule in each of the two FNs that comprise the dimer) with the requisite lengths added for the nondeformable Type I and II regions at the appropriate locations.

The time-dependent domain spring constant $k_i^j\left(t\right)$ and the force $f_i^j\left(t\right)$ for the (i,j)th Type III domain are related to the domain node displacements $u_i^j\left(t\right)$ and $u_{i+1}^j\left(t\right)$ by Hooke’s law,

$$f_i^j=k_i^j\left(u_{i+1}^j-u_i^j\right)=k_i^j{\mathit{ϵ}}_i^j,$$ (1)

where $i\in \left\{1,\cdots ,30\right\}$, $j\in \left\{1,\cdots ,N_{FN}\left(t\right)\right\}$ are Type III domain and FN molecule indices, respectively; N_FN(t) is the total number of FN molecules in the growing FN fibril; $u_i^j$ is the displacement of the (i,j)th Type III domain node from its position equilibrium in the absence of force; and ${\mathit{ϵ}}_i^j=u_{i+1}^j-u_i^j$ is the elongation or stretch of each Type III domain. The time-dependency of the domain spring constant, $k_i^j\left(t\right)$, is described in Modeling Nonlinear Stiffness of FN Domains, below.

The elasticity of the substrate is represented by a Hookean spring, with spring constant k_sub, connected in series with the spring representing FNIII-1 of the first FN molecule at one node (Fig. 1 A). The other node of the substrate spring is fixed, i.e., the displacement equal to 0 is an imposed relationship, or boundary condition. Thus, the elongation or stretch of the substrate is ${\mathit{ϵ}}_{\text{sub}}=u_1^1$, the node displacement for the first domain in the first FN molecule.

Modeling cell-FN binding

Cells bind to FN via transmembrane integrins, specifically binding to an arginine-glycine-asparagine loop in the 10th Type III domain of FN (40). Following the approach by Chan and Odde (23), we represent the cell-FN connection with a single Hookean spring with spring constant k_c and refer to this connection as a “molecular clutch” (Fig. 1 A, green springs). When engaged, clutch springs are connected in parallel with the springs representing FN Type III domains. In our model, integrin binding to the FNIII-10 domain, i.e., clutch engagement/disengagement, is represented as a stochastic first-order reversible reaction,

$$\left(\text{disengaged}\right)\mathcal{D}\begin{array}{c}{\nu }_{\text{on}}\\ \rightleftharpoons \\ {\overline{\nu }}_{m,\text{off}}^j\end{array}\mathcal{E}\left(\text{engaged}\right),$$ (2)

where ν_on and ${\overline{\nu }}_{m,\text{off}}^j$ are rates with units of inverse time; and m ∈ {1,2} is the index of the clutch. Engaged clutches build tension, as the connection via the clutch spring is stretched by actin motion.

Increased traction forces increase the likelihood of rupture events between integrins and the FNIII-10 domain, represented by modeling the dissociation rate as force-dependent according to Bell’s Law (41),

$${\overline{\nu }}_{m,\text{off}}^j={\nu }_{\text{off}}\text{exp}\left(f_{c,m}^j/f_b\right),$$ (3)

where ν_off is the disengagement rate in the absence of clutch displacement; f_b is a break force; and the clutch force $f_{c,m}^j\left(t\right)$ in the (m,j)th clutch is given by

$$f_{c,m}^j=k_c\left(u_{c,m}^j-u_{10m+1}^j\right),$$ (4)

and $u_{c,m}^j\left(t\right)$ is the displacement of the (m,j)th clutch node from its equilibrium position. The displacement $u_{10m+1}^j\left(t\right)$ represents the displacement of the two FNIII-10 domains in the jth FN dimer, with indices 11 and 21, respectively.

Modeling actomyosin force transmission to FN

Actomyosin force transmission is modeled as in the Chan-Odde model (23). Integrins, acting as a molecular clutch, transmit actomyosin forces to the assembling FN fibril. The interaction between actin velocity and transmitted myosin force is governed by an inverse force-velocity relationship that was described in Chan and Odde (23) and Bangasser et al. (29) and which is supported by retrograde actin velocity experiments (42, 43),

$$v_{\text{act}}=v_u\left(1-\frac{f_{\text{sub}}}{f_{\text{stall}}}\right),$$ (5)

where v_act is the actin velocity; v_u is the unloaded actin velocity; f_stall is a stall force dependent on the number of myosin motors; and traction force is f_sub = k_subϵ_sub.

The extension of FNIII-10-bound integrins is calculated from the actin filament velocity (Fig. 1), producing deflections of each individual domain in the assembling FN fibril, such that, assuming a rapid equilibrium, node positions for each domain can be solved by the direct stiffness method, a standard finite element method approach (44). The resulting traction force f_sub, in turn, feeds back on the actin filament velocity. When traction force reaches the stall force, actin filament velocity is zero and assembly terminates.

Modeling FN-FN interactions in an assembling fibril

Previous studies have indicated that FN fibrils only assemble when FN molecules are subjected to cell contractile forces (32, 33), and have suggested that there is a buried cryptic binding site in FN molecules that only is exposed when under tension (32). Based on prior work (45), we assign a threshold value for domain stretch ϵ_t, above which the domain is likely to be able to bind to a soluble FN molecule. FN binding is modeled as a two-step process: binding site exposure, followed by soluble FN binding to the exposed binding site. Binding site exposure is modeled as a stochastic process, with probability ${\pi }_i^j$ predicted by a Hill equation with a half-maximal response when domain stretch is equal to ϵ_t,

$${\pi }_i^j=\frac{{\left({\mathit{ϵ}}_i^j\right)}^{\eta }}{{\left({\mathit{ϵ}}_i^j\right)}^{\eta }+{\mathit{ϵ}}_t^{\eta }},$$ (6)

where η is a scaling factor that determines the threshold steepness. Soluble FN can then bind to an exposed binding site via a stochastic irreversible reaction.

Which domains contain the cryptic FN-FN binding sites? Deletion mutant studies in which each Type III domain of FN is serially deleted have demonstrated that no Type III domain is absolutely required, with the exception of the 10th Type III domain, the site of integrin attachment (46). This suggests that there are multiple FN-FN binding sites. We have previously hypothesized that all 15 Type III domains are capable of facilitating FN-FN binding (14). This is notably only one possible hypothesis for FN assembly at the molecular level. For this study, we utilize this mechanism; however, the model has been formulated to test alternative hypotheses with a smaller subset of FN-FN binding sites. Future studies will explore the effects of specific FN binding locations on the geometry and extensibility of FN fibrils.

Modeling the three-dimensional architecture of the FN fibril

The model simulates FN fibril assembly and extension along a single dimension (i.e., the z axis). While individual domain stretch is directed along the z axis, the model additionally accounts for the three-dimensional (3D) architecture of the assembling FN fibril by defining the location of each FN molecule in the x,y plane, to compare simulation results to experimental measures of FN fibril morphometry. While there is no data indicating the 3D FN fibril architecture, there are likely steric hindrances that limit the addition of new FN molecules to the assembling fibril. As such, we model the growing fibril using a hexagonal packing geometry (Fig. 2 B). Each FN molecule can have at most six neighbors in the x,y plane. When a soluble FN molecule binds to an exposed binding site, the new FN molecule is assigned randomly to an open position around the stretched FN molecule. Once all six positions are occupied, a FN molecule is considered interior and is incapable of binding additional FN molecules. Additionally, integrin attachment (described above) is limited to FNIII-10 domains on perimeter FN molecules; interior FN molecules are considered to be sterically hindered from attaching to the cell surface.

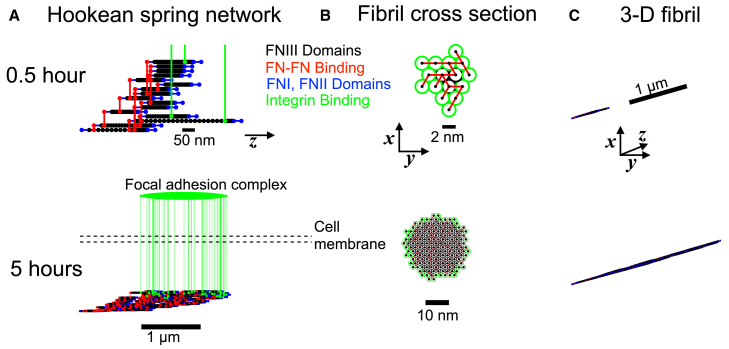
Figure 2.

Structure and architecture of the assembling fibronectin fibril. A representative simulation structure and architecture are shown at 0.5 and 5 h. (A) The Hookean spring network connections along the z axis are shown: elastic FN Type III domains (black), FN-FN binding (red), inelastic FN Type I and II domains (blue), and integrin binding (green) are shown. The FA complex is illustrated in the intracellular space as spanning the range of FN-bound integrins. (B) The FN fibril cross section in the x,y plane is shown, with FN-FN connections (red). Interior and exterior FN molecules are shown in black and green, respectively. (C) The 3D FN fibril architecture is shown. Parameters: k_sub = 1000 pN/nm. To see this figure in color, go online.

Modeling nonlinear stiffness of FN domains

Each Type III domain is modeled as a Hookean spring, such that the spring force is proportional to the elongation of the spring. However, it is not physiologically accurate to represent each domain as a spring with a constant stiffness, because both experimental and computational studies suggest that the domain stiffness changes as the domain unfolds (39, 45, 47). While previous studies have demonstrated that Type III domains have unique mechanical unfolding properties (39), we assume that these unique properties only exist until secondary structures are disrupted, after which point, domains are modeled as unstructured polypeptides that behave as entropic springs. Stiffness in this regime can be modeled using the wormlike chain (WLC) model (48, 49). The WLC model relates the extension and force of a semiflexible polymer that, importantly, accounts for the nonlinearity in the force-extension relationship as the polymer approaches its full contour length. To account for both the domain-specific mechanical properties when domains are folded, and the domain-independent, WLC behavior at larger stretches, we formulated a stretch-dependent stiffness relationship in which the stiffness at rest is determined from published data, and approaches an identical WLC-predicted stiffness as stretch increases (Fig. 3):

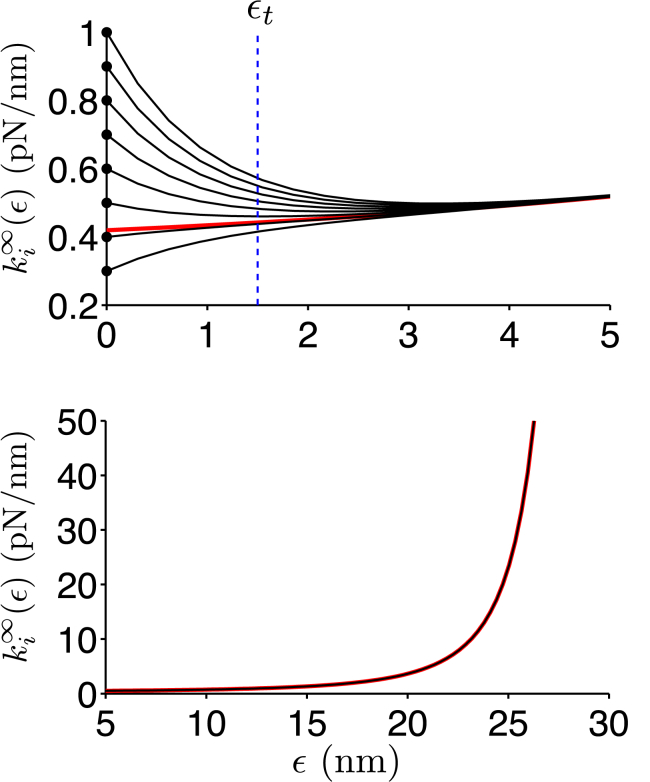
Figure 3.

Nonlinear spring stiffness for FN Type III domains. The steady-state spring stiffness values for the FN Type III domains ($k_i^{\infty }$ in Eq. 7) are shown as a function of the domain stretch ϵ. (Top) In the absence of actomyosin forces and small domain stretch, each FN Type III domain spring constant k is equal to a unique spring constant k_i,0 (Table S2), representing the unique mechanical properties of each FN Type III domain (black lines). (Bottom) In the presence of large actomyosin forces and large domain stretch, domain stiffness values are governed by a WLC model, producing a highly nonlinear increase in domain stiffness. (Red line) Domain binding site exposure threshold ϵ_t. (Dashed vertical blue line, top panel) To see this figure in color, go online.

The steady-state stretch-dependent domain stiffness $k_i^{\infty }\left({\mathit{ϵ}}_i^j\right)$ transitions between the regimes for unique stiffness and the identical WLC-governed stiffness, i.e., $k_i^{\infty }\left(0\right)=k_{i,0}$ (see Table S2), and for large ${\mathit{ϵ}}_i^j$, $k_i^{\infty }$ approaches $k_{\omega }\left({\mathit{ϵ}}_i^j\right)$,

$$k_i^{\infty }\left({\mathit{ϵ}}_i^j\right)=k_{\omega }\left({\mathit{ϵ}}_i^j\right)+\left[k_{i,0}-k_{\omega }\left(0\right)\right]\text{exp}\left(-{\mathit{ϵ}}_i^j/{\lambda }_{\omega }\right),$$ (7)

where λ_ω is a length scale that defines the regime transition; and k_ω is defined below. For large domain stretches, the WLC model relates the molecular force F_ω and stretch or elongation ϵ,

$$F_{\omega }\left(\mathit{ϵ}\right)=\left(\frac{k_{\text{B}}T}{{\chi }_p}\right)\left[\frac{1}{4{\left(1-\mathit{ϵ}/{\chi }_d\right)}^2}-\frac{1}{4}+\frac{\mathit{ϵ}}{{\chi }_d}\right],$$ (8)

where k_B is the Boltzmann’s constant; T is the absolute temperature; χ_p is the domain persistence length; and χ_d is the domain contour length. To relate the WLC model to the spring network that is the basis of our model, we define the spring constant k_ω relating the force F_ω and displacement ϵ of spring from rest as the derivative of F_ω in Eq. 8, respective to ϵ,

$$k_{\omega }\left(\mathit{ϵ}\right)=\frac{d{F}_{\omega }}{d\mathit{ϵ}}=\left(\frac{k_{\text{B}}T}{{\chi }_d{\chi }_p}\right)\left[\frac{1}{2{\left(1-\mathit{ϵ}/{\chi }_d\right)}^3}+1\right].$$ (9)

Accounting for the dynamics of the transition between domain stiffness regimes, the time-varying domain stiffness $k_i^j\left(t\right)$ is governed by a first-order isomerization reaction, with steady-state domain stiffness $k_i^{\infty }\left({\mathit{ϵ}}_i^j\right)$ (Eq. 7) and time constant τ_ω,

$$\frac{d{k}_i^j}{dt}=\frac{k_i^{\infty }\left({\mathit{ϵ}}_i^j\right)-k_i^j}{{\tau }_{\omega }}.$$ (10)

Our approach allows us to define stretch- and time-dependent stiffness relationships, for which we can define unique mechanical properties at rest and characteristic polymer entropic spring properties, including domain persistence and contour length, in the WLC regime, using simple first-order differential equations, without necessitating a significantly more complex system based on viscoelastic materials, e.g., the Maxwell or Kelvin-Voigt models.

FN fibrils assembly simulations

Simulation of FN fibril assembly involves timescales ranging over several orders of magnitude: Molecular clutch engagement/disengagements are stochastic events occurring on the order of milliseconds, while FN fibril assembly occurs on the order of hours to days. To simulate fibril assembly, we utilize a multiscale hybrid stochastic-deterministic integration scheme that enables the use of a relatively large numerical integration time step, while still appropriately accounting for clutch engagement/disengagement stochastic events. Details are provided in the Supporting Material.

Simulations were performed in the software MATLAB (The MathWorks, Natick, MA). Computational time mean ± SD was 66.8 ± 32.7 h using high performance computing nodes with Xeon E5-2670 2.5-GHz v2 processors (Intel, Santa Clara, CA). Summary measurements (see Figs. 5, 6, and 7) are averaged over the final 10 min of simulation time, to account for measurement fluctuations arising due to integrin binding and unbinding events (k_sub = 1000 pN/nm, 500 simulations; all other k_sub values, 100 simulations).

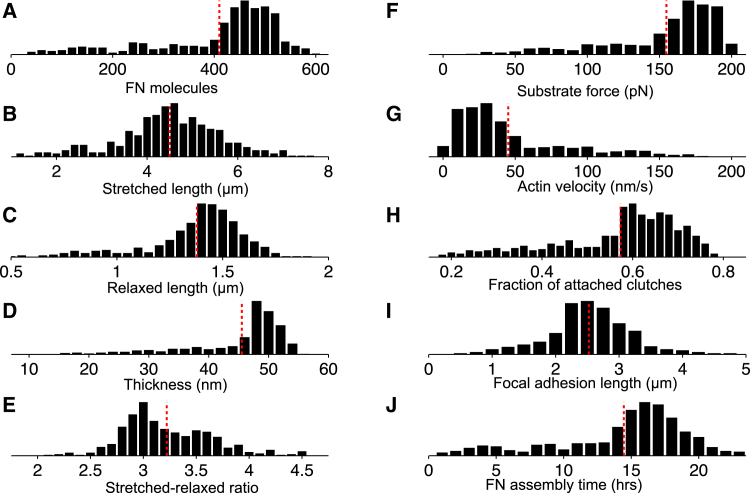
Figure 5.

Summary of morphometrical, mechanical, and biochemical properties of assembled FN fibrils. Histograms for the following measurements and properties are shown for 500 numerical simulations: (A) number of FN molecules, (B) stretched length, (C) relaxed length, (D) thickness, (E) extensibility, given by the stretched-relaxed length ratio, (F) substrate force, (G) actin filament velocity, (H) the fraction of attached molecular clutches, and (I) FA length. (J) Summary data for total assembly time is shown. In all panels, the dashed red line denotes the mean. Parameters: k_sub = 1000 pN/nm. To see this figure in color, go online.

Figure 6.

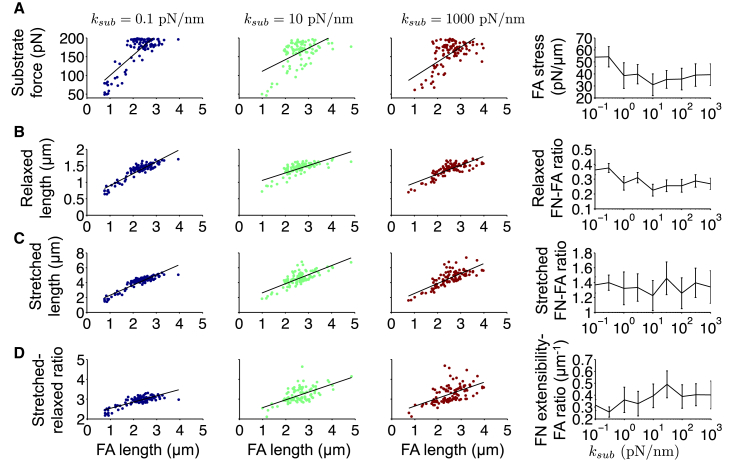
Model predictions for the relationship between FA length and assembled FN fibril morphometrical and mechanical properties. (Left three panels) (A) Substrate force, (B) relaxed FN fibril length, (C) stretched FN fibril length, and (D) fibril extensibility (stretched-relaxed FN length ratio) are plotted as a function of predicted FA length, for different values of substrate stiffness k_sub. Each dot represents a single simulation. (Right panels) (A) FA stress (substrate force-FA length ratio), (B) relaxed FN length-FA length ratio, (C) stretched FN length-FA length ratio, and (D) FN extensibility-FA length ratio, as determined by a linear least squares fit, are shown as a function of k_sub. To see this figure in color, go online.

Figure 7.

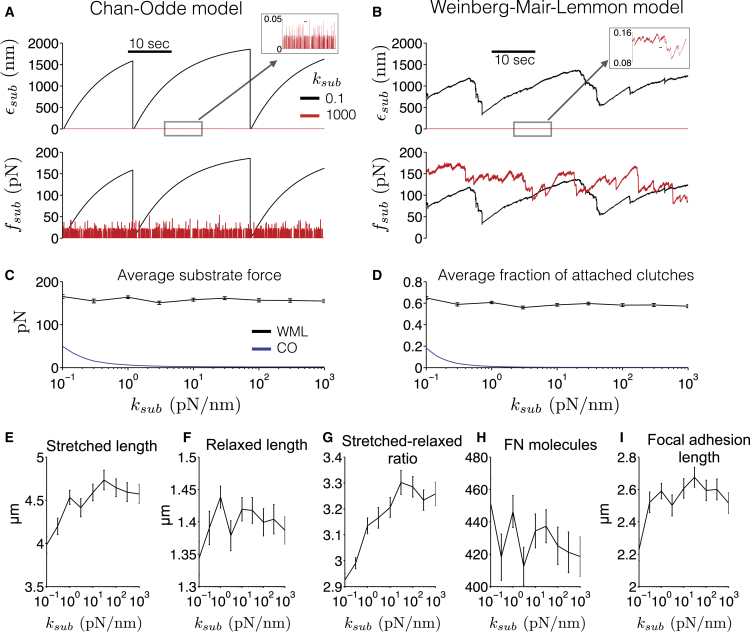
Mechanotransduction model predictions of substrate stiffness dependence. (A) Chan-Odde (CO) model is simulated (23), using model parameters given in Tables S1 and S2. Substrate deflection ϵ_sub (top) and force f_sub (bottom) are shown as a function of time on soft (black lines) and rigid (red lines) substrates, illustrating the load-and-fail and frictional-slippage regimes, respectively. (B) Substrate deflection and force, from simulations of our model (Weinberg-Mair-Lemmon, WML), illustrate an intermediate mechanotransduction regime. WML model mean ± SE, for (C) substrate force and (D) fraction of attached molecular clutches are shown as a function of substrate stiffness k_sub in the CO (blue lines) and WML (black lines) models. Mean ± SE, for (E) stretched length, (F) relaxed length, (G) stretched-relaxed length ratio, (H) number of FN molecules, and (I) FA length are shown as a function of k_sub. Pearson correlation coefficient between the logarithm of k_sub and WML model means (95% confidence interval): (E) 0.779 (0.237,0.951), p = 0.013, (F) 0.290 (−0.463,0.800), p = 0.445, (G) 0.871 (0.490, 0.973), p = 0.0022, (H) −0.467 (−0.863, 0.286), p = 0.205, (I) 0.557 (−0.169, 0.8915), p = 0.119. In (C) and (D), CO model means are computed by time-averaging over a 1-min simulation. In (C)–(I), WML model averages are computed by time-averaging over the minute preceding FN assembly termination, and then averaged over 100 simulations. To see this figure in color, go online.

Experimental quantification of FN fibril geometry

To quantify FN fibril morphometry, 10⁵ WI-38 human embryonic lung fibroblasts (American Type Culture Collection, Manassas, VA) were plated on 12-mm-diameter glass coverslips coated in 40 nM FN. Cells were allowed to assemble fibrils and were fixed at determined intervals ranging from 3 to 72 h. After fixing, cells were immunofluorescently labeled using a polyclonal FN antibody. After acquisition of immunofluorescence images, the properties of individual FN fibrils were analyzed with custom MATLAB code using the image processing toolbox, to quantify individual FN fibril area, length, and total fibril count per image. Each experiment was repeated in triplicate for each time point. Data was acquired for 20 images from each experimental replicate.

To collect FN force measurements, cell-generated traction forces were quantified as previously described in Scott et al. (14). Briefly, 40,000 cells were plated on microfabricated post array detectors (mPADs). Post deflection was measured based on the positions of the tops and bottoms of the posts. For a given deflection, beam bending theory was utilized to calculate force, based on post height, the elastic modulus, and the moment of inertia. Each experiment was repeated in triplicate for each time point. Data was acquired for 20 cells from each experimental replicate.

Results

Model predicts FN fibrils with physiologically accurate architecture, extensibility, and traction forces

Numerical simulations of our model were performed for 30 h of simulation time, or until assembly termination via stalled actin filaments. Spring network architecture and fibril geometry is shown for a representative simulation in Fig. 2. Hookean spring connections are shown among Type III domains (black), connected FN molecules (red), and bound integrins (green), in addition to inelastic Type I and II domains (blue) (Fig. 2 A). While the FA complex is not explicitly represented in simulations, model predictions of the FA complex length can be made based on measures of the length between the most proximal and distal FN-bound integrin connections (green oval). The fibril cross section illustrates the hexagonal packing structure of individual FN molecules (Fig. 2 B), and a 3D view illustrates the size of the assembling FN fibril, with all axes on the same scale (Fig. 2 C). Movie S1 shows the FN fibril spring network and geometry throughout assembly.

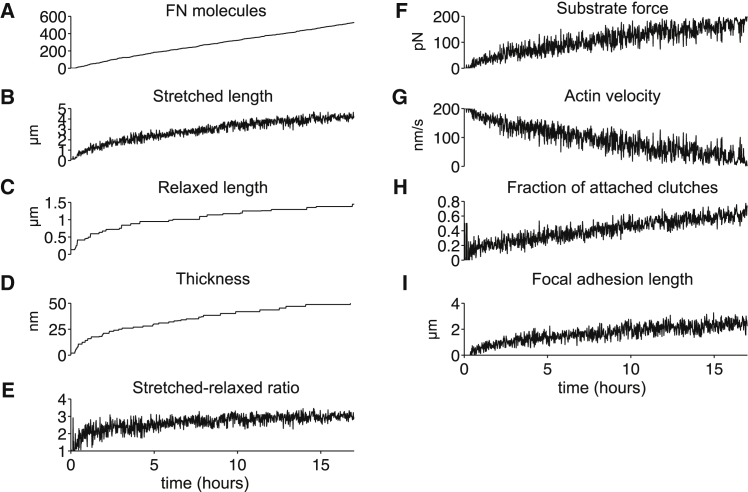
Time-series measurements from the same simulation are shown in Fig. 4. The number of FN molecules per fibril increases approximately linearly with time (Fig. 4 A). Fibril length is represented by two measurements: the stretched length, which represents the total length of the fibril while under tension from the actomyosin-induced forces (Fig. 4 B); and the relaxed length, in which tension is removed (Fig. 4 C). The relaxed length is determined solely based on the Hookean spring network architecture (Fig. 2), assuming that all spring nodes are in their respective equilibrium position. Both stretched and relaxed length increase as a function of time and approach a steady-state value, as does fibril thickness (Fig. 4 D), which is measured as the maximum diameter of fibril cross section.

Figure 4.

Morphometrical, mechanical, and biochemical properties during FN fibril assembly. (A) The number of FN molecules, (B) stretched length, (C) relaxed length, (D) thickness, (E) extensibility, given by the stretched-relaxed length ratio, (F) substrate force, (G) actin filament velocity, (H) the fraction of attached molecular clutches, and (I) the FA length are shown as a function of time for a 16-h simulation of an assembling FN fibril. The fraction of attached molecular clutches is given by total clutches bound to the FN Type III-10 domain, divided by the total number of clutches available for binding (two per exterior FN molecule). Measurements are for the simulation presented in Fig. 2.

Our model predicts that FN fibril extensibility, given by the stretched-relaxed length ratio, approaches a value of ∼4 (Fig. 4 E), in close agreement with previous experimental measures of a maximum of fourfold extensibility in cell-derived FN fibrils (34). Force on the fibril increases as a function of time, (Fig. 4 F), consistent with our prior work (14, 33). In concert with the increase in substrate force, actin velocity decreases while the fraction of attached molecular clutches increases as a function of time. (Fig. 4, G and H). FA length is predicted to gradually increase, following a similar time course as stretched and relaxed FN length and substrate force (Fig. 4 I).

Histograms of terminal FN fibril measurements are shown for a population of 500 simulations in Fig. 5. To account for stochasticity, measurements were averaged over the final 10 min preceding assembly termination for each simulation. In general, the distributions for FN fibril sizes (FN molecule, stretched and relaxed length, and thickness) were left-tailed, i.e., the population mean (red dashed line) is less than the distribution peak (Fig. 5, A–D). Thus, while most FN fibrils exhibited significant assembly, as in the example in Fig. 4, the model also predicts a small population of smaller FN fibrils. Most FN fibrils exhibited extensibility between 2.5 and 4.5 (Fig. 5 E). Just preceding assembly termination, substrate force typically approached the stall force (200 pN), such that actin velocity was typically near zero (Fig. 5, F and G). The distribution of the fraction of attached molecular clutches was also left-tailed, with the largest number of FN fibrils exhibiting greater than half of clutches attached at assembly termination (Fig. 5 H). The predicted FA length distribution was symmetric, with an average of 2.5 μm, with most FA complexes between 1 and 4 μm (Fig. 5 I). The average FN assembly time was ∼14.5 h; however, the distribution of FN assembly time was bimodal, with a small peak at 4 h corresponding to small fibrils and a larger peak at 16 h corresponding with larger fibrils (Fig. 5 J). Interestingly, all FN fibril size measurements are highly correlated with FN assembly time (Pearson correlation coefficient, 95% confidence interval: FN molecules 0.949 (0.940,0.957); stretched length 0.769 (0.730,0.802); relaxed length 0.838 (0.810,0.862); thickness 0.920 (0.905,0.932); all p < 10⁻¹⁰).

FA length and FN fibril morphometrical and mechanical properties are related in a substrate stiffness-dependent manner

The model predicts a similar time course between the FA length and assembled FN fibril morphometrical and mechanical properties (Fig. 4). Further, our model predicts that substrate force, and relaxed and stretched length of the assembled FN fibril are positively correlated with the FA length, independent of substrate stiffness (Fig. 6), consistent with our previously shown experimental results (14).

We next investigated the substrate stiffness dependency of the relationship between FA length and fibril properties. The substrate force-FA length ratio, or FA stress, is predicted to have a U-shaped dependence on substrate stiffness (Fig. 6 A), consistent with 2010 experiments from the Chen lab, showing FA stress increasing with substrate stiffness for more rigid substrates (25).

The relaxed FN fibril length-FA length ratio ranges from ∼0.5 to 0.6 and also generally follows a U-shaped dependence on substrate stiffness (Fig. 6 B), while the stretched FN fibril length-FA length ratio ranges from ∼1.6 to 1.9 and generally increases on more rigid substrates (Fig. 6 C). Thus, the model predicts that, on average, FA length is approximately twice the relaxed fibril length, while approximately half of the stretched fibril length, with moderate substrate stiffness dependence. Finally, the positive correlation between fibril extensibility and FA length demonstrates that longer FAs are associated with greater fibril elasticity (Fig. 6 D). The extensibility-FA length ratio ranges from ∼0.2 to 0.5 and generally increases on more rigid substrates.

FN fibrils create an intermediate regime between frictional slippage and load-and-fail and are only weakly dependent on substrate modulus

Next, we investigated the dependence of substrate stiffness in our model, and compared with the Chan-Odde model, to demonstrate the importance of FN fibril interactions with the cell and substrate (Fig. 7). As was previously observed (23), the Chan-Odde model predicts large substrate deflections and large forces on soft surfaces (black lines) that precipitate periodic catastrophic integrin-substrate rupture events (i.e., load-and-fail regime), resulting in a rapid decrease to zero traction forces, while near-zero deflections and small forces are observed on stiff surfaces (red lines), due to frequent rupture events (i.e., frictional-slippage regime) (Fig. 7 A).

Interestingly, our model predicts an intermediate regime that does not strictly follow the dynamics of either of the two extreme load-and-fail or frictional-slippage regimes, because, critically, rupture event occurrences are intermediate to both the catastrophic and the frequent rupture events observed in the Chan-Odde model for soft and rigid substrates, respectively (Fig. 7 B). On soft surfaces, our model predicts that the maximum substrate deflection and forces are smaller, compared with the Chan-Odde model, while the minimum deflection and forces do not approach zero (black lines). On rigid surfaces, substrate deflection is still small, but also nonzero, while traction forces are much larger, compared with the Chan-Odde model (red lines). As a result of this intermediate regime, overall, substrate forces are similar for both soft and rigid substrates. Physiologically, this suggests that FN fibrils may serve to compensate for detrimental effects of either soft or rigid substrates by inserting an elastic fibril between cell and substrate.

The critical difference between the models can be summarized as follows: In the Chan-Odde model, both traction forces and integrin-substrate binding dynamics evolve at a single location—the cell-substrate interface. However, in our model, traction forces and integrin-fibril binding are distributed throughout the highly elastic assembling fibril, which mitigates both catastrophic and frequent rupture events. As such, the presence of the assembling fibril in our model facilitates, on average, much larger traction forces (Fig. 7 C), due to an increased likelihood of attached molecular clutches, i.e., integrin binding (Fig. 7 D), compared with the Chan-Odde model, for all substrate stiffness values. This is in agreement with a previous study from our group, in which we demonstrated that the presence of FN fibrils was necessary for WI-38 lung embryonic fibroblasts to generate large forces on rigid substrates (14).

Simulation outputs indicate that the degree of FN assembly and the morphology of FN fibrils is similar across a range of physiologically relevant stiffness values (Fig. 7, E–H), in agreement with previously published work from our lab that indicates similar degrees of FN fibril assembly regardless of substrate stiffness (14). Only the stretched-relaxed length ratio and, to a lesser extent, the stretched length show a significant correlation with substrate stiffness.

Further model analysis of fibril morphometric and mechanical properties and substrate stiffness is provided in the Supporting Material, detailing the role of both fibril architecture and Type III domain extension on fibril length and the U-shaped dependence of FA stress on substrate stiffness (Fig. S1). Our model also predicts that increasing unloaded actin velocity (v_u; see Eq. 5) greatly truncates the fibril assembly process, due to frequent integrin binding rupture events comparable to frictional-slippage dynamics (Fig. S2).

Experiments and simulations predict stable FN fibril size

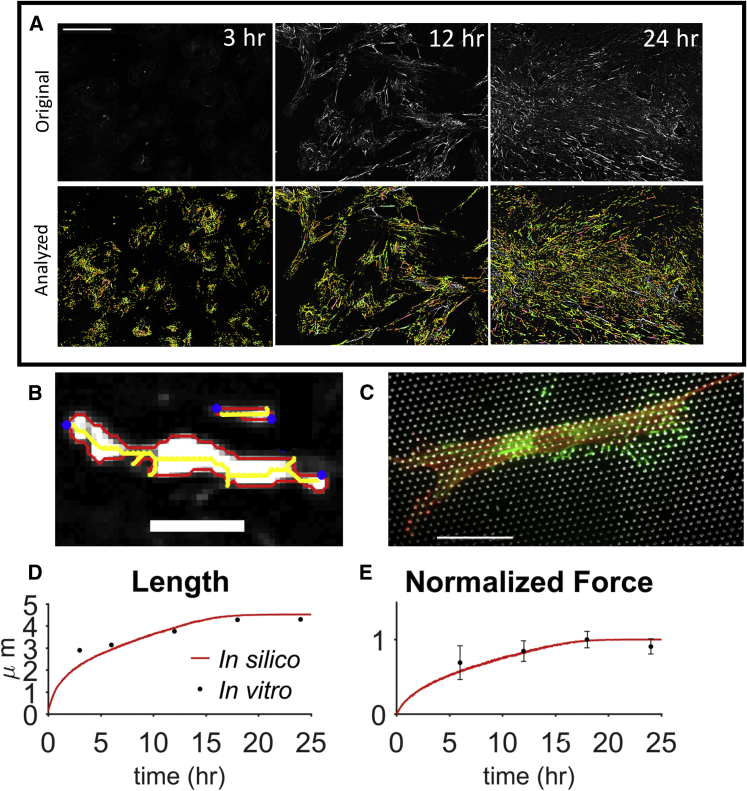
To evaluate the efficacy of the model, we quantified FN fibril morphometry and forces as a function of time in WI-38 human lung embryonic fibroblasts, cells representative of a stereotypical fibroblast morphology (50). Representative images of FN fibrils are shown at 3, 12, and 24 (Fig. 8 A), with custom image processing identifying individual fibrils and quantifying fibril length (Fig. 8 B). A representative composite image of a cell and mPADs is shown, used to measure cell-generated forces (Fig. 8 C).

Figure 8.

FN fibril in vitro morphometrical and force measurements. (A) Raw (top) and analyzed (bottom) FN fibril images at different time points. Scale bars, 100 μm. (B) Two analyzed FN fibrils, in which custom image processing measures fibril image outline (red), skeleton (yellow), and end points (blue). Fibril length is quantified as the maximum end-to-end distance of the image skeleton. Scale bars, 5 μm. (C) Composite image of a cell on mPADs, used to quantify cell-generated traction forces. (Red) Actin; (white) mPAD posts; (green) FN. Scale bars, 50 μm. (D) Comparison of in silico (red) and in vitro (black) FN fibril length. Standard error bars too small to be visible. (E) Comparison of in silico and in vitro normalized force data. In silico and in vitro measurements normalized to a maximum of 155.7 and 6.2 pN, respectively. In (D) and (E), error bars denote the standard error. To see this figure in color, go online.

Summary analysis shows that individual FN fibril length increases as a function of time, with fibrils reaching steady-state values at ∼18 h, comparable to the duration of FN assembly predicted by the model (Fig. 8 D). Importantly, model predictions of FN fibril length, as both a function of time and at a steady state, closely match experimental measurements, with some deviation at early time points when fibril counts are low. We next measured the time-dependence of traction forces to compare with the model, normalizing force values due to in vitro FN fibrils often spanning multiple posts, distributing forces and thus reducing force magnitude. Importantly, simulations accurately reproduce the time-dependent increase in cell-generated traction force, also reaching a steady state at ∼18 h (Fig. 8 E).

Discussion

Previous models of cell-substrate mechanical interactions fail to account for the extracellular matrix, an intermediate element between the cell and the substrate. In this study we develop, to our knowledge, a novel model of cell-matrix-substrate interactions which reproduces the assembly of fibrils of the ECM protein FN. Simulations predict FN fibrils with physiologically accurate architecture and mechanical properties. Our model, which predicts FN fibril assembly starting from a first-principles, molecule-by-molecule approach, is, to our knowledge, the first of its kind and can lead to great insights into how the ECM modulates mechanical signals to cells. Importantly, our model reproduces experimental measurements of key morphometrical FN fibril properties, including length and fourfold extensibility in the presence of actomyosin forces, and the duration of FN fibril assembly.

Previous studies have demonstrated that cell differentiation is a function of both tissue stiffness and soluble ligand presentation (11, 51), suggesting that cells are integrating mechanical and soluble signals to determine differentiation fate. However, it is still unclear how these signals are integrated. It is possible that the ECM, assembled by cell-generated forces, acts as a critical point of integration. One could hypothesize that because FN assembly is force-dependent, and forces are larger on stiffer surfaces, that FN assembly is more prevalent on stiffer surfaces; however, neither simulations presented here, nor our previously published work (14) support this hypothesis. In contrast, both simulations and experiments show relatively constant FN fibril assembly across a range of elastic moduli, with a slight peak at intermediate modulus values, highlighting that robust ECM assembly is a critical component of cellular mechanical signaling.

The model does, however, demonstrate an important aspect of cell-ECM mechanotransduction dynamics: assembly of FN fibrils allows cells to modify a stiff surface (which would typically be dominated by a frictional slippage regime in which large forces cannot be generated) to seem more like a soft surface, in which elastic elements allow cells to generate larger forces, by inserting highly elastic fibrils between the cell and substrate. Higher forces have been implicated as a critical component in several pathologies, including differentiation and activation on myofibroblasts in fibrotic disease (52, 53, 54) and transformation to a malignant phenotype in cancer (17, 24, 55). The assembly of FN fibrils may play a key role in facilitating these larger forces, and thus could prove an effective target in blocking increased contractile forces in these disease states.

Assembly of FN fibrils has been studied over the last 40 years. Despite significant work, the fundamental mechanism underlying FN fibrillogenesis is still not understood. Critically, our model facilitates an investigation of the effects of molecular-level binding events on the macroscopic morphometry of FN fibrils and traction forces. As discussed above, the site(s) of FN-FN interactions have been debated. Several of the Type III domains have been implicated as sites of FN-FN binding (reviewed in Schwarzbauer and DeSimone (30)). However, deletion studies have shown that only domain III-10, which contains the arginine-glycine-asparagine integrin binding sequence, is essential for FN assembly (46), which suggests that there are multiple FN-FN binding sites. Our model readily allows us to simulate competing hypotheses for FN-FN interactions, and future studies will determine whether the location and number of FN-FN binding sites dictates changes in the fibril morphometry.

Another area of active debate in FN biology is the mechanism of FN fibril elasticity. Studies have posited that this could be attributed to the unfolding of individual Type III domains (56) and/or the transition of FN from a compact conformation that is observed in solution (57) to an extended conformation (58). In our model, we only represent individual domain opening and neglect any transition from a compact to extended conformation. However, our model clearly demonstrates a maximal fourfold elasticity of fibrils, which is consistent with experimental observations (34). Previous work by the senior author quantified the force needed to open a single Type III domain and argued that the force needed to stretch each domain fourfold is greater than physiologically relevant forces (59). However, this calculation only examined a single FN molecule and did not consider an entire FN fibril, as our current model does. This work demonstrates that by accounting for appropriate FN fibril geometry, in which actomyosin forces are transmitted via multiple integrin binding sites and distributed over a network of FN molecules, we can predict appropriate FN elasticity at physiologically relevant force magnitudes.

The role of the ECM in mediating contractile force transduction to cell surroundings is not well understood. By constructing a computational model of the interface among substrate, ECM components, and the cell contractile machinery, we gain significant insight into how these mechanical events are coregulated. As such, our model represents a significant step toward integrating molecular-level ECM assembly events and macroscale mechanobiology that will dramatically improve our understanding of mechanical signaling in cells.

Author Contributions

S.H.W. and C.A.L. conceptualized the model formulation; S.H.W. implemented the model code; D.B.M. collected and analyzed all experimental data; and C.A.L. oversaw model development and experimental data collection.

Editor: Celeste Nelson.

Supporting Citations

References (60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72) appear in the Supporting Material.

Supporting Material

Movie S1. Simulation of FN Fibril Assembly, Shown in Figs. 2 and 4

(Top) The Hookean spring network and position along the z axis is shown as a function of time. Elastic FN Type III domains (black), FN-FN binding (red), inelastic FN Type I and II domains (blue), and integrin binding (green). (Bottom, left) The FN fibril cross section in the x,y plane, with FN-FN connections (red). (Bottom, right) The 3D FN fibril architecture. The first hour is shown with 1-min time increments, and the subsequent 16 h are shown in 15-min time increments.