Competing Pathways and Multiple Folding Nuclei in a Large Multidomain Protein, Luciferase

Abstract

Proteins obtain their final functional configuration through incremental folding with many intermediate steps in the folding pathway. If known, these intermediate steps could be valuable new targets for designing therapeutics and the sequence of events could elucidate the mechanism of refolding. However, determining these intermediate steps is hardly an easy feat, and has been elusive for most proteins, especially large, multidomain proteins. Here, we effectively map part of the folding pathway for the model large multidomain protein, Luciferase, by combining single-molecule force-spectroscopy experiments and coarse-grained simulation. Single-molecule refolding experiments reveal the initial nucleation of folding while simulations corroborate these stable core structures of Luciferase, and indicate the relative propensities for each to propagate to the final folded native state. Both experimental refolding and Monte Carlo simulations of Markov state models generated from simulation reveal that Luciferase most often folds along a pathway originating from the nucleation of the N-terminal domain, and that this pathway is the least likely to form nonnative structures. We then engineer truncated variants of Luciferase whose sequences corresponded to the putative structure from simulation and we use atomic force spectroscopy to determine their unfolding and stability. These experimental results corroborate the structures predicted from the folding simulation and strongly suggest that they are intermediates along the folding pathway. Taken together, our results suggest that initial Luciferase refolding occurs along a vectorial pathway and also suggest a mechanism that chaperones may exploit to prevent misfolding.

Introduction

An understanding of how proteins incrementally obtain their structure through folding is crucial for the prevention of diseases and development of new therapeutics (1, 2, 3, 4). The previous 50 years of protein folding research (see reviews (5, 6, 7, 8, 9, 10)) have produced excellent theoretical frameworks for understanding protein folding of single-domain proteins, but most proteins are multidomain as they comprise >70% of the proteomes in all kingdoms of life (11). Multidomain protein folding behavior is not well understood, and recent experiments have shown that the simple smooth energy landscape theories typically do not apply to multidomain proteins, which often display non-Anfinsen mechanisms like kinetic partitioning (12), cotranslational folding (13, 14, 15, 16, 17, 18), coexisting intersecting folding pathways (19), or confinement by chaperonins (20, 21).

Here we make use of the model multidomain protein, Firefly Luciferase (Photinus pyralis, denoted as “Luciferase” hereafter), which effectively cannot refold (refolding takes up to 72 h (22, 23)), and only folds due to the involvement of molecular chaperones, or the ribosome (23, 24, 25, 26). In this study, we ask the following: is the structural topology of Luciferase inherently predisposed to inhibit spontaneous refolding while promoting cotranslational or vectorial folding? To answer this question, we use a combination of experiment and simulation. We first use single-molecule refolding experiments to identify initial steps in refolding, and then we use coarse-grain simulation to identify autonomously folded core substructures (27, 28). Finally, we use systematic truncation and single-molecule force spectroscopy to experimentally test the selected Luciferase substructures (29, 30, 31, 32, 33, 34, 35).

In contrast to previous truncation studies that use traditional spectroscopic techniques to evaluate stability (36, 37), we experimentally test the structure and stability of the simulation-predicted structures using single-molecule force spectroscopy (SMFS, reviewed in (38, 39, 40, 41, 42, 43, 44)). Our method of truncation has three distinct advantages over traditional truncation studies, as follows. First, SMFS takes advantage of the observation that mechanically stable structures produce distinct and consistent force peaks while unstructured polypeptides lack any discernible force peaks and follow a simple wormlike chain polymer elasticity (45). Second, using polyproteins as flanking handles eliminates the introduction of the C-terminal carboxyl charge or N-terminal amino charge at the sites of truncation, which should not be present in the true protein and may introduce anomalous charge interactions. Third, single-molecule experiments unfold proteins in isolation, which can minimize their tendency to aggregate.

Whereas SMFS can relay information about the stability through the unfolding force peak, the extension of the polypeptide chain after the unfolding event (contour-length increment) directly measures the number of amino acids initially present in the stable folded structure (46). Thus the results from SMFS can be directly compared to steered-molecular dynamic simulations to infer whether the measured contour-length increment is consistent with the structure identified in the simulations. This powerful combination of simulation and experiment reveals that Luciferase has the greatest propensity to fold correct without misfolding when the process occurs vectorially, from N-terminal domain to the C-terminal, as it does proceed cotranslationally.

Materials and Methods

Protein purification

Plasmids containing I91₃-Luciferase-I91₄ construct and the I91₉ were used to purify protein as described in the literature (47, 48). Truncated versions of Luciferase were generated at the DNA level through mutagenesis or gene synthesis from GenScript (Piscataway, NJ) at the residues specified in the main text. Plasmids were transformed and overexpressed in C41(DE3)pLysS cells (Lucigen; www.lucigen.com) and then purified using NiNTA columns (Qiagen, Hilden, Germany). The resulting purified protein was dialyzed into a buffer containing either 1× or 2× PBS pH 7.6 at a concentration of 1–10 mg/mL and used for atomic force microscopy (AFM) measurements.

Atomic force spectroscopy

Atomic force spectroscopy (AFS) experiments were performed using custom-built instruments (49). Proteins were diluted to 150 μg/mL in a 2× PBS buffer and loaded onto a freshly evaporated gold substrate for 1 h. The substrate was then washed once and used for pulling experiments. We used either OBL cantilevers (spring constant ∼6 pN/nm) or MLCT cantilevers (spring constant ∼16 pN/nm) (Bruker, Billerica, MA). The spring constant of each cantilever was calibrated using the energy equipartition approach (49). During unfolding experiments, the AFM cantilever was pressed against the sample at a contact force of 100–500 pN to nonspecifically bind to the protein. The presence of at least five I91 domains (ΔLc ∼28 nm and unfolding force ∼200 pN) allowed for the unequivocal determination of the unfolding pattern of the protein. During refolding experiments, the AFM cantilever tip was first moved toward the sample, relaxing the protein and then was retracted away from the sample to determine the force extension data of the refolded polypeptide; this procedure minimized unwanted tip-surface interactions. All data was analyzed using the software MATLAB 7.10 (The MathWorks, Natick, MA). The Gaussian mixture model fitting for three was done using an Expectation maximization algorithm.

Steered molecular dynamics

Simulations were conducted using the software GROMACS 4.5.7 (www.gromacs.org) (50) using a coarse-grain Cα model of Luciferase generated using the software SMOG (Software Modeling Group; http://smog.iem.pw.edu.pl/) (51, 52) from the apo-conformation crystal structure of Luciferase (53). Truncated variants of Luciferase were generated by truncating contacts from the original Luciferase coarse-grain Cα model. Simulations were conducted using a temperature of 150 temperature units. This temperature is near the heat capacity for this particular coarse-grain Cα model of Luciferase, as shown previously (47). All simulations were performed at a speed of 1 nm/s using a spring constant of 6 pN/nm, by pulling from the N-terminus and fixing the C-terminus. Similar results were obtained when pulling from the C-terminus and fixing the N-terminus (data not shown).

Molecular dynamics of luciferase folding

Simulations were conducted using the software GROMACS 5.0.6 (54) using a coarse-grain Cα model of the apo-conformation of Luciferase (53) generated using the software SMOG (51, 52). Simulations were first initialized by heating the Luciferase model to 300 temperature units, which immediately denatures the coarse-grain model of the protein. We then conducted 407 coarse-grain simulations starting from a randomly selected heat denatured state and quenched the temperature to 150 temperature units. This temperature is near the heat capacity for this particular coarse-grain Cα model of Luciferase, as shown previously, and allows the coarse-grain model to refold (47). Simulations were done for 1,000,000,000 steps, with step size of 0.0005. Every 1,000,000 steps were saved to an output file and used for analysis.

Markov state models

Markov state models (MSMs) are useful for determining a complete description of kinetic and thermodynamic properties from many simulations (55, 56, 57). The MSMs in this study were determined by clustering trajectories into a series of metastable states, and then determining the transition matrix that corresponds to the exchange between these states.

First, simulations were analyzed and clustered using the software Python 2.7.6 (https://www.python.org/download/releases/2.7.6/; accessed January 22, 2015) with packages from SciPy, NumPy, and Scikit-learn (58, 59). Each frame from the resulting trajectory was analyzed for whether any of the 1956 contacts of Luciferase were present to create a contact vector. Frames with <20% of the total contacts were automatically clustered as “unfolded” whereas frames containing >90% of the total contacts were automatically clustered as “folded”. A matrix containing the contact vector for every other frame was then used for clustering via K-means or DBSCAN algorithms. Similar results were obtained for both clustering methods, and different size of clusters as shown in Fig. S1.

The transition matrix for the MSM was generated by identifying transitions between metastable states in each individual simulation and then tallying into a single matrix showing the probability between any two given states in all the simulations, P (60). The MSMs were visualized using the software Graphviz (Graph Visualization Software; graphviz.org) (61). These visualizations (Fig. S2) omit the self-transitions and transitions below a minimum threshold of 0.001%. Kinetics were determined using an initialization vector for relative occupancy, v(0), and then determining the subsequent relative occupancy through matrix multiplication, as follows:

$$v\left(t\right)=v\left(0\right)\times P^t,$$ (1)

where P is the normalized transition probability matrix for the Markov chain, and t is the step. Results from kinetic calculations were also similar irrespective of cluster size or method.

For the scope of this work we will limit the discussion to the results from clustering of Luciferase into 14 states, shown in Fig. S3, which are related by their transition probabilities shown in Fig. S2. The results of all other clustering is shown in Figs. S4–S7, which all give similar conclusions.

Monte Carlo simulations

The percentage of pathways that are able to reach the native state, as shown in Fig. 4, was determined using a Monte Carlo simulation of the MSM for the 14-state cluster shown in Fig. S3. We simulated 10,000 trajectories that start in the unfolded state and progress to the folded state via the probabilities outlined in the MSM transition matrix. Trajectories that regressed back to the unfolded state were ignored. The probabilities in Fig. 4 represent the number of these trajectories that pass through that particular state.

Figure 4.

Representation of the main folding routes from coarse-grain simulations (back arrows representing unfolding not shown; for complete Markov state model, see Fig. S2). The numbers above each state represent that state number for the 14-state clustering (reference in Fig. S3), while the percentage is the probability of obtaining that structure during any given folding pathway (see Materials and Methods). The arrow thickness qualitatively represents the relative flux through the pair of states. Structures with a star indicate that they were evaluated experimentally by SMFS. To see this figure in color, go online.

Results

Luciferase is a 550-amino-acid monomeric protein that uses ATP to catalyze oxidation of D-(-)-Luciferin (Luciferin) to produce a photon of light in Firefly insects (62, 63, 64). The structural conformation of Luciferase has high homology with other AMP-forming ligases like acyl-CoA ligases (65) and nonribosomal peptide synthetases (66). Most structural studies indicate that there are three structural domains in Luciferase, as follows: an N-terminal, a middle, and a C-terminal domain, but the precise structural boundaries are difficult to ascertain and the boundary definitions depend highly on the method of characterization, as shown in Fig. S8 (colored bars). A recent method by Porter and Rose (67) used a thermodynamic metric of protein domains and observed that Luciferase has four domains, as follows: residues 15–266, 267–337, 338–433, and 434–522. Protein Domain Parser (68) determined that there are three domains, as follows: residues 18–218, 219–437, and 438–542. Conti et al. (69) determined a structure for Luciferase and observed that there are four structural domains. Previous results in our lab show that experimental and simulated mechanical unfolding occurs in three domains composed of residues 1–248, 249–443, and 444–550 (47), but their contribution to the folding pathway is unknown and it is unclear how the structure of the domain is obtained incrementally through folding.

Luciferase initiates refolding through folding nuclei

Luciferase does not readily refold and requires the use of chaperones to accelerate its refolding (22, 23, 25, 47, 70). This may be due to Luciferase’s propensity to aggregate after unfolding (23), while chaperones may be able to avert this process by acting as an unfoldase to relieve nonnative protein-protein interactions before allowing the protein to refold (71, 72, 73, 74, 75, 76). Thus, we sought to use an atomic force microscope as the ultimate unfoldase, to perform single-molecule refolding on Luciferase by first prestretching the molecule to a high force (≈100 pN) before attempting to refold.

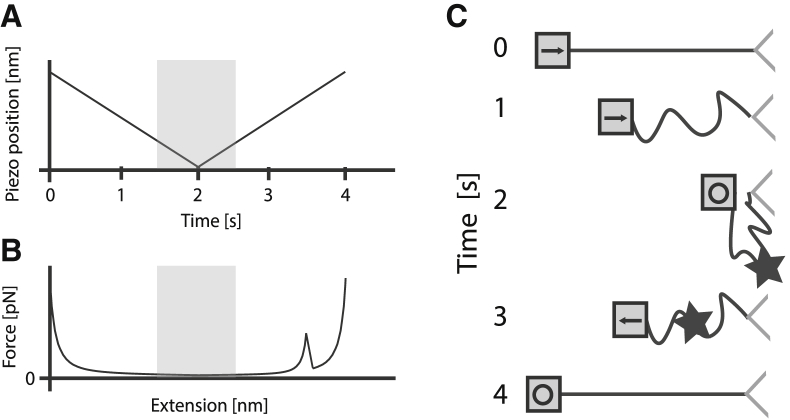
In our refolding experiment (schematic in Fig. 1), each attempt begins with the molecule prestretched. A refolding attempt is initiated when the substrate is moved at constant velocity toward a set point, after which it immediately retracts at constant velocity. During each refolding attempt the protein experiences a force related to the entropic elasticity of the polypeptide chain, which is well approximated by a wormlike chain (77). A polypeptide approximated by a wormlike chain with a persistence length of 0.4 nm, moving at constant velocity, will spend 27% of the time under a force of 5 pN. This force of 5 pN is the observed isometric unfolding force for many molecules (i.e., the force at which the molecule will spend 50% folded/unfolded), and forces below will favor refolding over unfolding (78, 79, 80, 81). Thus, a refolding attempt spanning 4 s will allow ≈1 s where the force on the molecule is below the typical isometric force so refolding can occur. Successful refolding is detected during the retraction, where the folded domain may be forcefully unfolded under the increasing force, resulting in a peak of the force-extension curve (denoted an “unfolding event”). We hypothesized that this method of refolding would allow us to observe refolding events of Luciferase.

Figure 1.

Schematic of the refolding experiments for I91₃-Luciferase-I91₄ construct and I91₉. The distance between the substrate and the tip is modulated by the piezo, which executes a constant velocity ramp as shown in (A). The force on the molecule as determined by the extension, closely approximated by a wormlike chain, is shown in (B). The shaded region in (A) and (B) is where the molecule experiences a force that is below the typical isometric unfolding force (5 pN). The physical schematic of the experiment is shown in (C), where the piezo moves toward the cantilever, at which a protein can fold (denoted by the star), which is determined by the subsequent unfolding that results in a force peak.

We first performed 765 refolding attempts on >50 single molecules of the polyprotein I91₉, without Luciferase, as a control experiment. Most of the refolding attempts yielded fully folded I91 and/or fully unfolded I91 (unstructured polypeptide chain), but there was a small fraction that contained events that have neither the characteristic unfolding contour-length increment of 28 nm nor the unfolding force of 200 pN, as shown in Figs. S9 and S10. The vast majority of these peaks are <120 pN, which we use as the cutoff threshold for non-I91 unfolding events (Fig. S9). We observe that 11% of refolding attempts yield non-I91 unfolding events. Previous literature has detected similar types of events, which were determined to be misfolded I91 (82, 83, 84, 85).

We then performed 849 refolding attempts on >50 single molecules of I91-flanked Luciferase construct (I91₃-Luciferase-I91₄). The presence of flanking I91 domains serves as a positive control for the single-molecule under extension and as a handle for manipulation of the molecule of interest (86). The refolding pattern contained a single non-I91 event in 37.4 ± 0.3% of recordings, as shown in Fig. 3 (bottom) with representative examples in Fig. 2. When the pulling speed is decreased to allow up to 10 s of time in which the molecule experiences a force <5 pN, the refolding pattern contains a single non-I91 event in 36.9 ± 0.8% of recordings. Thus, we cannot detect a difference in the propensity of refolding with the time range that our AFM can probe. The origin of this event could be from the misfolding of I91 or the misfolding/refolding of Luciferase. However, several observations point to the conclusion that the majority of these events are from Luciferase and not I91. First, the presence of non-I91 events occurs approximately three times more often with Luciferase (31% with I91₃-Luciferase-I91₄ and 11% with I91₉), despite having fewer domains and similar experimental times. Second, the contour length to the first I91 domain for the Luciferase refolding events is consistent with the size of Luciferase (which should provide ∼200 nm of contour-length, Fig. S11). Third, the distribution of contour-length increments of the non-I91 events of Luciferase do not match the distribution from I91 alone (Fig. 3).

Figure 3.

Distributions of the contour-length increments for non-I91 peaks in refolding recordings (peaks with force <120 pN; see Fig. S9 for all peaks). Top shows the distribution for refolding of I91₉. Bottom shows the distribution for the refolding of I91₃-Luciferase-I91₄, which has events not present in I91₉ and match previous results for the unfolding of full Luciferase. To see this figure in color, go online.

Figure 2.

Four examples of successive refolding attempts on a single molecule of I91₃-Luciferase-I91₄. The order of recordings goes from bottom to top for each set. As can be seen, the I91 molecules (200 pN unfolding force) are able to refold successfully upon each attempt. A single non-I91 peak appears a fraction of the time, and a wormlike chain (dashed line) shows a contour-length increments that match previously reported contour-length increments for individual domains of Luciferase.

The distribution of the contour-length increments for the non-I91 events also indicate that Luciferase may be refolding and not misfolding. There are three distributions (R3, R4, and R5) unique only to Luciferase, centered at 49.1, 70.1, and 84.5 nm. These distributions and forces (shown in Table 1) are consistent with the previous results for the contour-length increments for the unfolding of the natively folded truncated N-terminal domain (54.3 nm; Fig. S12), middle domain (71.9 nm; Fig. S13), and the N-terminal domain of Luciferase (87.4 nm; Fig. S14), respectively (47). Thus, these results indicate that Luciferase is able to, in most cases, initially refold to the native state of one of its domains. The first two distributions, R1 and R2, may be indicative of refolding of the smaller C-terminal domain of Luciferase (Fig. S15) or partial structures of the other two domains; however, we are currently unable to rule out events similar to I91 events, as shown in Figs. S16 and S17. We note that none of these refolding attempts yielded a fully folded Luciferase, which may indicate a still difficult barrier to the full refolding of Luciferase.

Table 1.

Results for the Contour-Length Increment and Unfolding Force for Non-I91 Events from Refolding of Luciferase

Unfolding Event	ΔLc [nm]	Fu [pN]
R1	22.0 ± 4.0	58 ± 29
R2	31.2 ± 4.3	55 ± 28
R3	49.1 ± 5.2	45 ± 22
R4	70.1 ± 2.9	45 ± 25
R5	84.5 ± 3.7	46 ± 26

Unfolding events are labeled according to clusters in Fig. 3.

Folding simulations reveal three independent folding nuclei

We sought to understand the domains that correspond to the initial and subsequent refolding events for Luciferase using molecular dynamic simulations of structure-based models. These models explicitly encode the native state but are well suited for determining the degree of topological frustration that exists in a protein acquiring its native fold. We simulated 407 model-dependent folding trajectories where each started from the unfolded state. These trajectories were then used to generate a Markov state model (MSM), which can provide a complete description of the thermodynamic and kinetic properties of the combined simulations (more details in Materials and Methods) (57, 87, 88, 89).

The prominent states determined from the folding simulations are shown in Fig. 4. The transition probabilities (Fig. S2) predict that only three states are accessible to Luciferase, from the unfolded ensemble. These three states have the same contact maps and transition probabilities, regardless of clustering method or number of clusters as shown in Fig. S1. Although the clustering results are similar across number of clusters and method (Fig. S1), this article will focus on the 14-state clustering of the coarse-grained folding trajectory of Luciferase, whose MSM is shown in Fig. S2.

The states that are first occupied by Luciferase after being unfolded are states 11 (C-terminal domain), 1 (core of middle domain), and 3 (core of N-terminal domain), whose structural representations are shown in Fig. 4 and contact maps in Fig. S3. The transitions between the unfolded ensemble and these three states (and self-transitions) account for 99.998% captured in the simulation, and offer three distinct pathways for folding.

The most frequent pathway, which goes through state 1, is composed of the core of the second middle half of Luciferase, namely residues 332–440 (Fig. 4, orange structure). The unfolded ensemble transitions to state 1 with a probability of 0.70% during each step of the simulation. While it is the most frequent state originating from the unfolded ensemble, this state only results in reaching the final folded state 36% of the time. State 1 is also moderately unstable, as it regresses back to the unfolded ensemble 3.3% of the time and only transits further down the folding pathway 2.2% of the time (whereas the rest of the time it transitions back to itself), as shown in the full MSM in Fig. S2.

The second most frequent pathway passes through state 3, which has a probability of 0.26% for transitioning from the unfolded ensemble during each step in the simulation. This state is the core of the Luciferase N-terminal domain, composed of residues 46–180, as shown in Fig. 4 as the blue structure. The N-terminal core is the most proficient at reaching the final folded state, as 52% of the folding pathways originate from it. In contrast to a state corresponding to the middle domain of Luciferase, the N-terminal core is much more stable. Although it transitions back to the unfolded ensemble 0.9% of the time, it will transit further down the folding pathway 9.7% percent of the time.

The third and final most frequented pathway from the unfolded ensemble is state 11, which corresponds to the C-terminal domain of Luciferase (Fig. 4 as the red structure). The C-terminal domain is the least likely to be the origin for the final folded state, as it is present in only 4% of all folding pathways, and because the unfolded ensemble transitions to the C-terminal domain with a low probability of 0.13% at each step of the simulation. This state is moderately unstable—similar to the middle domain of Luciferase—as it unfolds 3.7% of the time and only continues along the folding pathway 1.5% of the time.

Nonnative states predicted from simulation

As can be seen in the kinetics from the Monte Carlo simulations of the Markov states (Fig. S18), there are four states—2, 4, 7, and 10—that have nonzero occupancy with the folded state when the simulation converges. With the exception of state 2, which represents the natively folded Luciferase without the C-terminal domain (Fig. 4; Fig. S2), these states represent a nonnative topology.

All of the nonnative states from our simulations involve an incorrect threading of the N-terminal residues (Fig. 5). In the first case, state 7, a β-hairpin at residues 36–52, is interrupted by residues 261–278. Normally residues 268–278 would form a helix; however, because of the threading, there are too many steric clashes for a helix to form, so those contacts cannot be acquired. The structure is stable, though, because the surrounding contacts can still form natively. This state is most often obtained from state 5, which is along the pathway of nucleating from the C-terminal or middle domain (where the N-terminal domain remains unfolded).

Figure 5.

Representative structures of the topologically misfolded states obtained during folding of Luciferase, with the state labeled in bold (referring to 14-state clustering in Fig. S2). The structures are colored from red (N-terminal residues) to blue (C-terminal residues). The right side shows a template molecule of the correctly folded form of Luciferase. To see this figure in color, go online.

In the second case of nonnative topology, state 10, the linker residues 104–110 enter the loop formed by the helix-turn-strand residues 73–95, instead of going around. Because of this, the helix between residues 109 and 121 cannot form properly, although the rest of the native contacts are formed normally. This state transitions from the fully folded state (although this could be mislabeling, as the number of contacts are very similar), but it also transitions often from state 8, which is a case where the N-terminal folds and the C-terminal part of the middle domain folds—but the interface is not yet set.

In the third case of nonnative topology, state 4, the first helix, residues 19–34, are not natively formed because the most N-terminal residues are caught between a helix composed of residues 82–95 and hairpin-helix composed of residues 36–67. The N-terminal residues 1–15 normally form contacts with the middle domain of Luciferase (data not shown) and the rest of the contacts are enough to stabilize this fold. The states 5 and 9 can transition to this state, and are both along the pathway leading to state 11.

The transition probabilities from the 14-state cluster (Materials and Methods) can be used to determine which pathway is the most frequent origin for misfolding. Using a Monte Carlo approach, we started simulations in the unfolded ensemble and progressed the state until either a nonnative state or a fully folded state was reached. The simulations that folded from the C-terminal domain (state 11) obtained one of the nonnative states 88% of the time. The simulations that folded from the middle domain (state 1 or 12) obtained a nonnative state in 37% of its trajectories. The N-terminal (state 3 or 6) had the best avoidance of nonnative states, as trajectories starting from these states only obtained a misfolded state in 16% of its trajectories.

Experimental stability of conformations predicted from simulation

Folding nuclei are experimentally stable

The three states determined from coarse-grained simulations, 11, 1, and 3, represent the folding nuclei of the C-terminal, middle, and N-terminal domains of Luciferase, respectively (Fig. 4). To determine whether these folding nuclei are stable, we engineered the truncated variants of the proteins corresponding to the three states and examined their force-extension profiles using force spectroscopy. If they are stable structures, probing by force spectroscopy will produce distinct and consistent force peaks, whereas no discernible force peaks will be produced if the truncated variants are unstable or unfolded, as these would simply follow wormlike chain polymer elasticity.

Before experimentally perturbing with force, we first simulated the mechanical force experiment using the prospective structures from states 3, 1, and 11 with coarse-grained steered molecular dynamics (Materials and Methods) to determine whether their elasticity follows a simple wormlike chain or reveals unfolding force peaks that produce contour-length increments that could be later compared to the experimental observations. The simulated structures were generated by double-truncation of the full model of Luciferase at the residues specified from the three states. All three of these steered molecular dynamic simulations yielded a single rupture event with a contour-length increment (dLc) that matched the experimental contour-length increment (see Fig. 7; Table 2). We would expect that experimental measurements of the contour-length increment should yield a similar result, if the domain is folded as predicted.

Figure 7.

Experimental SMFS results of the contour-length increment (left) and unfolding force (right) for Luciferase truncations. Previous results on the full Luciferase (47) are shown at the top for comparison, which shows unfolding of C-terminal domain (light shading), middle domain (dark shading), and N-terminal domain (solid). The dashed bar shows the result for the contour-length increment calculated from SMD simulations.

Table 2.

Results for the Contour-Length Increment and Unfolding Force for Unfolding of Full Luciferase and Luciferase Truncations

Unfolding event	ΔLc [nm] (Simulations)	ΔLc [nm] (Experiments)	Fu [pN]
Luciferase, Peak 1	35.0	38.7 ± 6.6	24 ± 12
Luciferase, Peak 2	68.0	71.9 ± 5.7	38 ± 14
Luciferase, Peak 3	91.3	87.4 ± 5.2	54 ± 18
Luc1-203	59.5	51.1 ± 10.5	53 ± 29
Luc1-268	83.2	79.6 ± 8.1	81 ± 37
Luc1-450-Peak1	67.5	72.8 ± 7.3	39 ± 16
Luc1-450-Peak2	90.5	84.1 ± 6.8	54 ± 15
Luc332-440	33.7	26.0 ± 5.7	51 ± 21
Luc46-180	47.0	36.2 ± 8.7	78 ± 39
Luc433-550	36.1	33.5 ± 6.4	29 ± 15

Distributions of results are shown in Fig. 7. Representative results are shown in Fig. 6. The Simulations column corresponds to the contour-length increment measured from steered-molecular dynamic coarse-grain simulations of the respective molecule.

We made protein constructs representing the three states by engineering at the DNA level their sequence and then flanking by I91 domains as for native Luciferase (47). These proteins were produced and purified and then subjected to mechanical force (see Materials and Methods). Representative results of the force-extension curves are shown in Fig. 6 and the distributions of contour-length increment and unfolding force are shown in Fig. 7. All three states, state 11 (C-terminal domain), state 1 (core middle domain, Luc332-440), and state 3 (core of N-terminal domain, Luc46-180) showed distributions of contour lengths that peaked very close to the simulated contour-length increment determined from SMD calculations, indicating that these truncated variants are all stable and have structures near the predicted model structure. The contour-length increment and the unfolding forces of state 11 (C-terminal domain, Luc433-550) were very similar to the distributions of the full Luciferase unfolding for Peak 1 (determined earlier to be the C-terminal domain by Scholl et al. (47)), tested using the Kolmogorov-Smirnov test and corrected for the multiple hypothesis testing. However, contour-length increments for state 1 and state 3 determined from force-spectroscopy measurements on truncated variants were shorter than the contour-length increments corresponding to Peaks 2 and 3, respectively, in full-length Luciferase. This is understandable, as both these states are truncations of the larger domains whose unfolding give rise to Peaks 2 and 3.

Figure 6.

Three representative examples of experimental force-spectroscopy recordings obtained for each construct in this study. All the vertical scale bars represent 100 pN and the horizontal scale bars all represent 50 nm. Arrows indicate the force rupture event used in analysis.

The contour-length increments determined from refolding experiments (Table 1) and truncation unfolding experiments (Table 2) indicate that the refolding may populate these truncations. The contour-length increments for R2 (〈ΔLc〉 = 31.2 nm) could contain contributions from Luc46–180 (〈ΔLc〉 = 36.2 nm) and Luc433–50 (〈ΔLc〉 = 33.5 nm). Similarly, the contour-length increment distribution for R1 (〈ΔLc〉 = 22.0 nm) could contain contributions from folded Luc332–433 (〈ΔLc〉 = 26.0 nm). However, both R1 and R2 also exist in the refolding of only I91₉ (Fig. 3), so these could also have contributions from I91 (for example, Figs. S16 and S17). The contribution from I91 for R2 is less than R1, however, because the percentage of R2 (29%) is higher than R1 (16%) in Luciferase refolding, but not I91₉ refolding. We plan on refolding these truncations individually to more accurately determine their contributions to the total refolding of Luciferase.

Predominant folding transitions are experimentally stable

After forming the initial core of Luciferase (states 11, 1, or 3), there are several predominant states along the folding pathway of Luciferase. The Monte Carlo simulations of folding (Fig. 4) and the kinetics (Fig. S18) indicate that the states 2, 6, and 12 are frequently observed along the folding pathway to the native state (>30% of all pathways). States 2 and 6 are expansions of the N-terminal core, containing residues 1–450 and 1–268, respectively, as shown in Figs. 4 and S3. State 12 is an expansion on state 1 (Fig. S3), which we chose not to further investigate experimentally in this study, as it lies on the less predominant pathway folding from state 1.

Following our approach for states 1, 3, and 11, we engineered truncated variants for state 2 and state 6 and examined their structure and stability by SMD and by AFM. In the following discussion we also include earlier results obtained on a truncation from residues 1–203, which is similar to state 6, only slightly smaller (47). Representative experimental force-extension curves are shown in Fig. 6 and the results from the experimental force-spectroscopy measurements are shown in Fig. 7.

The simulated contour-length increments calculated from SMD simulations corresponds well with the experimentally measured contour-length increments, indicating that all the original models appropriately represent the N-C extension of the folded state of the Luciferase truncation. Also, as expected, the truncation encompassing residues 1–450 from state 2 results in two separate peaks. These two peaks match Peaks 2 and 3 of the full Luciferase unfolding as their contour-length increment distributions and their rupture force distributions are not statistically significantly different (as tested using the Kolmogorov-Smirnov test). This is in line with previous results positing that Peak 1 from the full Luciferase unfolding originates from the unfolding of the C-terminal domain of Luciferase and that Peaks 2 and 3 correspond to the unfolding of the middle domain of Luciferase and the N-terminal domain, respectively. These experiments indicate that these structures are all likely configured in a similar structure as predicted by simulation.

As suggested by full Luciferase, the truncations may also be present in the refolding experiments as determined by examining similarities in contour-length increment refolding experiments (Table 1) and truncation experiments (Table 2). The contour length increment distribution for R3 (〈ΔLc〉 = 49.1 nm) closely matches Luc1–203 (N-terminal core, 〈ΔLc〉 = 51.1 nm). Similarly, the contour-length distribution for R4 (〈ΔLc〉 = 70.1 nm) is similar to Luc1–450 Peak 1 (middle domain of Luciferase, 〈ΔLc〉 = 72.8 nm). Also, the contour-length increment distribution of R5 (〈ΔLc〉 = 84.5 nm) matches Luc1–450 peak 2 (N-terminal domain, 〈ΔLc〉 = 84.1 nm). This further supports our view that the refolding experiments detect events that originate from natively folded Luciferase.

Discussion

Here we use AFM-based SMFS and simulation to identify the folding nuclei that initialize refolding of Luciferase. Previous experiments found that Luciferase was unable to refold in an appreciable amount of time (22, 23) and that Luciferase must either acquire its native fold through the one-time event of cotranslational folding (25, 26) or through interaction with chaperones (24, 47). We find that the refolding of Luciferase can begin under certain conditions, in the absence of chaperones, and that the folding complexity is mainly due to competing substructures. There were four major conclusions from our experiments and simulations, as follows.

First, we observe that the presence of an unfoldase-like (71, 72, 73) interaction helps to initialize refolding of Luciferase. Previous single-molecule attempts to refold Luciferase often encountered misfolding or nonspecific interactions (47, 70), unless chaperones were provided. Here, we use AFM as the ultimate unfoldase from which we observe force-extension curves that are either absent of refolding, or that contain an event that matches what would be expected for the refolding of one of the domains of Luciferase (Fig. 3). This seems to support the idea that some chaperone proteins may affect refolding positively by binding and prestretching the molecule to alleviate nonspecific interactions (74, 75, 76). We never observed complete refolding of Luciferase, although our timespan for refolding was only extended up to 10 s, while in principle Luciferase may take hours to refold (22, 23). This is currently beyond the temporal stability of our AFM, though we plan to implement new techniques to considerably improve this stability (90) for performing longer timespans in the future.

Second, we find that Luciferase initially refolds through competing pathways that involve either the N-terminal domain or the middle domain. Simulations of the folding pathway predict that the majority of successful refolding occurs through the N-terminal domain, as these were obtained 52% of the time in Monte Carlo simulations from Markov state models of refolding (Fig. 4). Refolding experiments also detected a distribution of contour-length increments that closely matched the correct unfolding of N-terminal domain residues 1–203 or residues 1–268, which were obtained 41% of the time in experiments (R3 and R5; Fig. 3). The middle domain of Luciferase, residues 268–440, was also identified as the secondmost common starting point for refolding: it occurred in 35% of pathways in simulation (Fig. 4). The middle domain of Luciferase was also definitively identified in refolding experiments (R4; Fig. 3), which was observed to account for at least 14% of refolding events. Thus, both simulations and experiments are in agreement with a vectorial folding of Luciferase, which predisposes Luciferase to optimal cotranslational folding.

Third, we find that the topology of Luciferase allows for several viable substructures. Folding simulations revealed distinct and consistent states where Luciferase incrementally acquires its native fold (Fig. 4). All tested substructures were found to be mechanically stable and have a contour-length increment expected from the hypothetical structure (Fig. 7). This implies that Luciferase is capable of forming native interactions incrementally, and the pathway from the unfolded to folded state may only transition through a finite number of consistent substructures. We note that although these substructures are mechanically stable, their atomic structure may deviate from prediction and require further biophysical characterization to understand their role in the folding pathway. We plan to carry out these characterizations on truncated mutants, without flanking domains, in future work.

Fourth, our simulations of folding lend insight into the type of nonnative interactions that can occur in Luciferase (Fig. 5). All examples of these nonnative structures were caused by folding into an incorrect topology in the loops between N-terminal helices. Monte Carlo simulations using the MSM transition matrix indicate that the nonnative interactions originated from the C-terminal domain, middle domain, and N-terminal domain with probabilities 88, 36 and 17%, respectively. These observations suggest, due to the topology of Luciferase, that nonnative interactions can be avoided by initializing folding from the N-terminal domain, which is the predominant initialization of refolding that we observed experimentally. These observations also suggest that, under denaturing conditions such as heat-shock, the unfolded C-terminal domain may contribute to the progeny of misfolding and guide the protein to a nonnative structure. We plan to test these hypotheses in future work.

Conclusions

Whereas much is known about protein folding in general, the folding of large, multidomain proteins is still a difficult problem that has not been solved. Here we make use of coarse-grained simulation and SMFS to broach several steps in the folding of Luciferase, a model multidomain protein. Our results indicate that Luciferase initializes its folding from competing pathways, either from a core N-terminal domain or through the middle domain. This is similar to what has been expected to occur under cotranslational conditions and our results likely represent key components of the intermediate structures along this pathway. Our observation that folding from the C-terminal domain leads to nonnative structures suggests a mechanism for chaperones to prevent misfolding by eliminating this pathway.

Author Contributions

Z.N.S., W.Y., and P.E.M. designed research and wrote the paper. Z.N.S. performed research and analyzed data.

Editor: Daniel Muller.