Nuclear Positioning and Its Translational Dynamics Are Regulated by Cell Geometry

Abstract

The collective activity of several molecular motors and other active processes generate large forces for directional motion within the cell, which is vital for a multitude of cellular functions such as migration, division, contraction, transport, and positioning of various organelles. These processes also generate a background of fluctuating forces, which influence intracellular dynamics and thereby create unique biophysical signatures, which are altered in many diseases. In this study, we have used the nucleus as a probe particle to understand the microrheological properties of altered intracellular environments by using micropatterning to confine cells in two structurally and functionally extreme geometries. We find that nuclear positional dynamics is sensitive to the cytoskeletal organization by studying the effect of actin polymerization and nuclear rigidity on the diffusive behavior of the nucleus. Taken together, our results suggest that mapping nuclear positional dynamics provides important insights into biophysical properties of the active cytoplasmic medium. These biophysical signatures have the potential to be used as an ultrasensitive single-cell assay for early disease diagnostics.

Introduction

The dynamic and complex environment of the cytoplasm arises due to the activity of molecular motors, along with many active processes involving the reorganization of the cytoskeletal filaments. Together, these mechanisms have crucial effects on the positioning and dynamics of various organelles in the cell. There have been significant advances in experimental techniques and theory on the use of optically trapped or injected beads to probe the mechanical properties of cells and the intracellular dynamics (1, 2, 3, 4, 5). In a number of microrheological studies of living cells that used microinjected particles as probes (6), the large-scale properties of the cytoplasm were estimated using multiparticle correlation studies due to the difficulty of introducing large particles into the cell. Alternatively, one can use the cellular organelles themselves as probe particles instead of introducing foreign particles, although this approach has not been well explored.

The nucleus is the largest cellular organelle. Within the complex cytoplasmic environment, it is subjected to active forces that generate directional transport as well as an incoherent background of fluctuating forces contributing to a complex motion (1). The positioning of the nucleus in cells has been shown to depend on cell type, stage of the cell cycle, migratory state, and differentiation status (7). In addition, the nucleus also exhibits different kinds of movements, i.e., continuous and unidirectional motion as well as bidirectional movements with short pauses (8). This diversity of nuclear movements indicates the presence of multiple mechanisms involved in nuclear positioning depending on different cellular contexts (8, 9, 10, 11). Numerous diseases resulting from genetic alterations in the proteins involved in nuclear movement confirm the significance of proper nuclear positioning (12, 13). Cellular geometry has been shown to impinge on gene expression and nuclear morphology, orientation, rotational dynamics, and deformability (14, 15, 16, 17) in studies utilizing micropatterned cells of defined shapes and spread area. However, in well-defined boundary conditions that mimic tissue environments, nuclear positioning and its translational dynamics in single cells has not been studied.

In this article, we study the role of cell geometry on nuclear positioning and use the nucleus as a dynamic probe of the active cytoplasmic medium. Toward this end, NIH3T3 cells were cultured on micropatterned substrates to control their geometry. We show that the nuclear centroid positions are sensitive to geometric constraints and are modulated by the actin cytoskeleton. The translation dynamics of the nucleus, mapped using live cell imaging, reveal that the nucleus exhibits confined diffusion at short timescales crossing over to superdiffusion in elongated cells. In contrast, the reduction in cell matrix constraints results in the loss of confined diffusion. In addition, loss of nuclear lamina enhances the diffusion timescales while maintaining the similar diffusion characteristics in both cellular geometries. More importantly, we show that the nuclear diffusion characteristics are very sensitive to cytokines that modulate the actin cytoskeleton. Fitting the experimental observations to a two-timescale corralled diffusion model reveals a characteristic cytoskeletal mesh size of ∼250 nm. Collectively, our observations present, to our knowledge, a novel approach to detect small changes in the cytoplasmic rheology.

Materials and Methods

Micropatterning

Polydimethylsiloxane (PDMS) elastomer (SYL-GARD 184; Dow Corning, Midland, MI) was prepared at a 1:10 ratio of curative to precursor according to the manufacturer’s protocol. The PDMS was then poured onto microfabricated silicon wafers containing an array of microwells of the desired geometry and cured at 80°C for 2 h. The solidified PDMS was subsequently peeled off the silicon mold and used as stamps to transfer fibronectin to culture dishes by microcontact printing, as explained below.

The surface of the PDMS stamps (containing protrusions with the desired geometry) was treated with high power oxygen plasma (Plasma Cleaner Cat. No. PDC-002; Harrick Scientific Products, Pleasantville, NY) for 5 min and fibronectin solution (50 μg/mL) was allowed to adsorb onto the surface. The fibronectin-containing surface was then brought into contact with the culture dish, thereby depositing islands of fibronectin on the dish with the desired geometry. Once used, the PDMS stamps were carefully removed and discarded.

This resulted in an array of fibronectin islands of a defined geometry on the culture dish. The remaining area of the dish was passivated with 2 mg/mL Pluronic F-127 (Sigma-Aldrich, St. Louis, MO) to ensure that the cells do not migrate out of the two-dimensional (2D) fibronectin islands. The pluronic acid treatment was carried out for 10 min and the excess solution was properly washed away with PBS before cells were seen on the dish.

Cell culture, drug treatment, and plasmid transfection

NIH 3T3 mouse embryonic fibroblasts (wild-type or stably expressing H2B-EGFP) were cultured in DMEM (Life Technologies/Thermo Fisher Scientific, Carlsbad, CA) supplemented with 10% (v/v) FBS (GIBCO/Life Technologies/Thermo Fisher Scientific) and 1% (v/v) Antibiotic-Antimycotic (Life Technologies/Thermo Fisher Scientific), at 37°C in 5% CO₂. Before seeding the cells on the patterned substrate, Pluronic F-127 (Sigma-Aldrich) was removed and dishes were rinsed twice with 1× PBS, then the cells were seeded for 10 min. Unadhered cells were removed and the remaining cells were washed once with 1× PBS and incubated in 2 mL of media for 3 h. Cytoskeletal filaments were depolymerized with 1 μM Cytochalasin D (CytoD; Sigma-Aldrich) and 0.5 μg/mL Nocodazole (NOC; Sigma-Aldrich) for 30 min. In addition to H2B, transient transfection of TRF1-DsRed was also used to track the nucleus. Transfection was carried out using jetPRIME (Polyplus Transfection, Illkirch, France) as per manufacturer’s protocol.

Fluorescent staining

The cells were rinsed twice with 1× PBS, followed by fixation using 4% paraformaldehyde (Sigma-Aldrich) in 1× PBS for 15 min. Cells were washed and stained using Wheat Germ Agglutinin (5 μg/mL; Life Technologies) for 10 min and permeabilized with 0.25% Triton-X (Sigma-Aldrich) in 1× PBS for 15 min. DNA and F-actin were then stained using Hoechst-33342 (1 mg/mL) and rhodamine phalloidin (1 mg/mL) for 15 min. For immunostaining, α-tubulin antibody (1:200; Abcam, Cambridge, UK) was used according to manufacturer’s instructions.

Imaging and analysis

Images of fully adhered single cells were taken using a model No. A1R microscope (Nikon, Melville, NY) with a 100×, 1.4 NA oil objective. Imaging conditions were kept similar in all of the experiments. Images for the static measurements were captured using a 1.4 NA objective, with a pixel size of 0.1 μm (open pinhole). To capture the nuclear dynamics, the acquired 2D confocal images were analyzed by selecting the central region of the cell. Single cells were imaged sequentially. The image analysis was carried out in the software ImageJ (National Institutes of Health, Bethesda, MD) and the statistical analysis was carried out in R and MATLAB (The MathWorks, Natick, MA).

Results

Nuclear positioning is sensitive to cell geometry

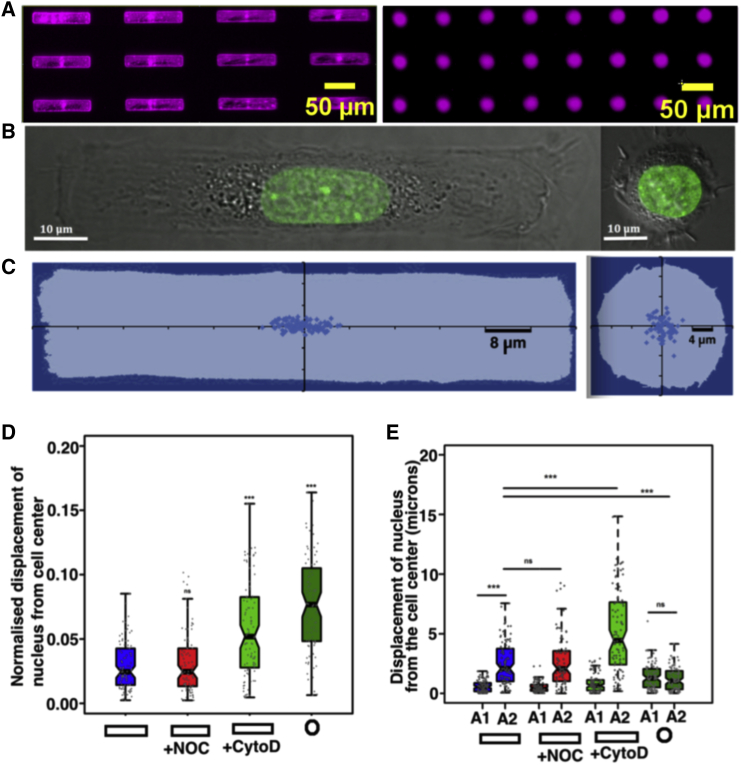
To test whether cellular geometry controls the nuclear positioning, NIH3T3 cells were cultured on fibronectin-coated micropatterns of two geometries, a rectangle with an area of 1800 μm² that had an aspect ratio of 1:5, and a circle with an area of 500 μm². The fibronectin islands where cells were constrained are shown in Fig. 1 A. To estimate the distance explored by the nucleus in the two geometries, the displacement of the nuclear centroid from the cell centroid was measured from a population of cells Fig. S1.2). The cell boundary was marked using Wheat Germ Agglutinin and the nucleus was labeled using Hoechst-33342. Cells grown on rectangular patterns had an average length of 95 μm and a width of 19 μm, while the diameter of the cells on circular patterns was ∼25 μm (Fig. S2.1). We found that the nucleus was displaced from the cell center by an average of ∼2 μm in both of the geometries (Fig. S2.2). However, when this displacement is normalized to the largest dimension of the object (Fig. 1 D), we find that the nucleus explores a larger space in the small isotropic circular geometry when compared to the large anisotropic rectangular geometry. Interestingly, we found that this exploration of the nucleus is anisotropic on the large polar rectangular pattern. On the anisotropic rectangular geometries the nucleus is displaced more along the long axis of the cell, while on isotropic circular geometries, the nuclear displacement is more isotropic (Fig. 1 E).

Figure 1.

Nuclear positioning is sensitive to cell geometry. (A) Shown here are rectangular and circular fibronectin patterns on imaging dishes visualized using Alexa Fluor 647 dye. (B) Shown here are NIH 3T3 cells expressing H2B-EGFP constrained on rectangular and circular geometries. (C) Distribution of nuclear centroid from the cell centroid (the origin) in constrained geometries is given. (D) Here, we show normalized displacement of nucleus in rectangles and circles, and rectangles treated with CytoD and NOC. (E) Displacement of nuclear centroid along the short (A1) and long (A2) axis of the cell under geometric constraints and cytoskeletal perturbations is shown. For circular geometry, we have the axis A1 = axis A2. N = 101 rectangular cells, N = 87 rectangular cells treated with CytoD, N = 97 rectangular cells treated NOC, and N = 100 circular cells. Statistical comparisons were carried out using Student’s t test, ^∗∗∗p value < 0.001.

To test the sensitivity of nuclear position to cytoskeletal structure, we disrupted actin using CytoD and microtubules using NOC in cells on rectangular geometries, and measured the displacement of the nucleus from the cell center (Fig. 1 D). The dimensions of the cells did not vary significantly with the treatments (Fig. S2.1). We found that whereas loss of microtubules did not cause significant nuclear displacement, the loss of actin contractility caused a significant dislocation of the nucleus from the cell center. In addition, the disruption of actin caused the nucleus to displace along the long axis of the cell (Fig. 1 E). This suggests that in static elongated cells, actin filaments play a greater role than microtubules in restricting the nuclear displacement from the cell center. To ascertain the importance of cell shape in nuclear positioning, we performed the same experiment with cells grown on 1800 μm² circle and triangle patterns in addition to the 1800 μm² rectangle (Fig. S1.1). We found that the shape alone could change the nuclear positioning (Fig. S2.2). To probe how these changes in cytoskeletal environments induced by changes in geometry is reflected in nuclear motion, we subsequently performed time-lapse live imaging of these geometrically confined cells.

Translational dynamics of the nucleus is dependent on cell geometry

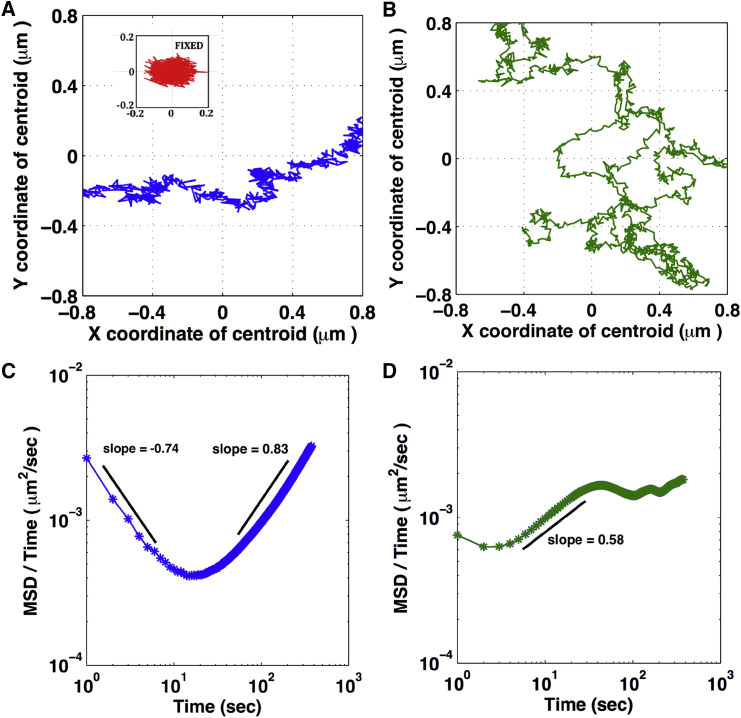
NIH3T3 cells stably expressing H2B-EGFP were used to probe the translational dynamics of the nucleus. 2D confocal images of the nucleus were acquired at 1 frame/s to capture its diffusional characteristics. This frame rate used for acquisition was estimated using a diffusion constant of a nuclear-sized particle (10⁻³ μm²/s) in a viscoelastic liquid medium that had a viscosity comparable to cytoplasm (10⁻² Pas). From the recorded image series we obtained the coordinates of the nuclear centroid and plotted the mean shifted trajectories of the nuclear centroid in a region with dimensions of 1.6 × 1.6 μm to visualize the small scale features (Fig. 2, A and B). Over a typical duration of 1500 s, nuclear displacement in live cells was ∼3 μm, whereas in a fixed cell nuclear displacement was ∼300 nm over the same duration of time (inset, Fig. 2 A). The nuclear trajectories have a distinct behavior depending on the different geometries. In rectangular cells, the nucleus shows directional movement along the long axis, while in circular cells the nucleus exhibits isotropic displacements.

Figure 2.

Translational dynamics of the nucleus is dependent on cytoskeletal organization. (A and B) The mean shifted trajectory of the nuclear centroid in rectangular geometry (A) and circular geometry (B) is shown. The two panels show part of the trajectories from movies of 1500 s that would fit in a 1.6 × 1.6 μm spatial window. The inset in (A) shows the mean shifted nuclear centroid trajectory of a fixed cell on the rectangular geometry over a duration of 1500 s. (C and D) Plots of 〈r²(τ)〉/τ as a function of τ for the rectangular (C) and circular (D) geometry are given. Number of cells measured: 19 rectangles and 17 circles.

To estimate quantitative changes in nuclear motion brought by the geometrical constraints, the mean square displacement (MSD) is calculated for the centroid of each nucleus by finding the average displacement between two time points with a time interval τ = nΔt, where n takes integer values, as follows:

$$\langle {\mathit{r}}^2\left(\mathit{\tau }\right)\rangle =\frac{1}{\mathit{N}-\mathit{n}}\sum _{\mathit{k}=1}^{\mathit{N}-\mathit{n}}{\left[\mathit{r}\left(\left(\mathit{k}-1\right)\Delta \mathit{t}+\mathit{n}\Delta \mathit{t}\right)-\mathit{r}\left(\left(\mathit{k}-1\right)\Delta \mathit{t}\right)\right]}^2.$$ (1)

Here r is the position vector of the particle at each time point and N is the total number of measured points. For normal diffusion, the MSD will linearly depend on τ, 〈r² (τ)〉 = 2dDτ, where d is the spatial dimension and D is the diffusion coefficient.

We find distinct dynamics of the nucleus between the two geometric constraints, both of which deviate significantly from normal diffusion. For anomalous diffusion, the MSD can be expressed as 〈r² (τ)〉 = Aτ^α with values of α deviating from unity. A time-dependent diffusion coefficient D(τ) can be defined as D(τ) = 〈r² (τ)〉/τ = Aτ^α−1 and it is convenient to realize the diffusive behavior by plotting 〈r² (τ)〉/τ as a function of τ in a log-log scale (18, 19). In this plot, α − 1 represents the slope of the graph, and a negative or positive slope corresponds to a subdiffusive regime (α < 1) or superdiffusive regime (α > 1), respectively. A horizontal region represents a normal diffusive regime (α = 1).

In Fig. 2, C and D, we plot 〈r² (τ)〉/τ as a function of τ for cells grown on the two geometries. For the rectangular geometry, the curve shows two distinct regimes, one with slope = −0.74 and the other with slope = 0.83 corresponding to the subdiffusive and superdiffusive regimes, and a crossover from one regime to the other occurs at ∼τ = 18 s. For the circular geometry, only superdiffusive behavior (slope = 0.58) was observed for nuclear motion over much shorter timescales of τ = 2 s, and at ∼τ = 36 s a transition to normal diffusion is observed as indicated by the nearly horizontal region in the plot. The exponents and the time at which the crossover between the diffusive regimes take place, as indicated by the slopes, have been quantified for several cells and the results are shown in Table 1, where A₁(τ) and A₂(τ) are the time-dependent diffusion constants in subdiffusive and superdiffusive regions and α₁ and α₂ are the corresponding exponents.

Table 1.

Diffusion Characteristics of the Nucleus in Cells of Different Geometries

Geometry	Condition	Region 1: A1(τ) μm2/s	α1	Region 1: A2(τ) μm2/s	α2	τ Crossover (s)	n
Rectangle	control	1.5 × 10−3 to 2.6 × 10−4	0.26 ± 0.17	2.6 × 10−4 to 2.1 × 10−3	1.66 ± 0.17	18.6 ± 14.6	19
Rectangle	control x component	1.22 × 10−3 to 2.2 × 10−4	0.27 ± 0.18	2.2 × 10−4 to 1.98 × 10−3	1.66 ± 0.26	18.4 ± 16.1	18
Rectangle	control y component	3.14 × 10−4 to 4.25 × 10−5	0.24 ± 0.17	4.25 × 10−4 to 1.5 × 10−4	1.48 ± 0.35	24.6 ± 14.8	18
Circle	control	—	—	6.4 × 10−4 to 2.2 × 10−3	1.54 ± 0.12	2.0 ± 1.1	17
Circle	control x component	—	—	3.2 × 10−4 to 1.9 × 10−3	1.55 ± 0.10	2.1 ± 1.2	17
Circle	control y component	—	—	3.2 × 10−4 to 1.25 × 10−3	1.55 ± 0.10	1.8 ± 0.9	17
Rectangle	lamin A−/C− component	8.0 × 10−3 to 1.8 × 10−3	0.24 ± 0.09	1.8 × 10−3 to 7.7 × 10−3	1.45 ± 0.32	10.6 ± 3.6	5
Rectangle	lamin A−/C−x component	6.9 × 10−3 to 1.6 × 10−3	0.25 ± 0.10	1.6 × 10−3 to 7.6 × 10−3	1.46 ± 0.32	10.2 ± 2.8	5
Rectangle	lamin A−/C−y component	9.6 × 10−4 to 1.7 × 10−4	0.19 ± 0.06	1.7 × 10−4 to 4.3 × 10−4	1.29 ± 0.25	20.8 ± 16.7	5
Circle	lamin A−/C−	—	—	2.6 × 10−3 to 1.0 × 10−2	1.43 ± 0.05	3.25 ± 1.89	4
Circle	lamin A−/C−x component	—	—	1.3 × 10−3 to 6.0 × 10−3	1.43 ± 0.14	3.5 ± 3.0	4
Circle	lamin A−/C−y component	—	—	1.2 × 10−3 to 3.7 × 10−3	1.37 ± 0.11	3.25 ± 2.2	4

Because nuclear positioning was found to be anisotropic in the rectangular condition, we also studied the diffusive properties of the nucleus along the major and minor axes separately. We found that the translation dynamics was enhanced along the major axis of the rectangular cells, while in the circular cells, there was no major difference between the x and y components. In the rectangular case, the crossover times were found to be ∼18 s and 24 s along the x and y directions, respectively, and the same was found to be ∼2 s along both the x and the y directions of the circular cells. The 〈r² (τ)〉/τ versus τ plots are shown in Fig. S3 and the result summary has been tabulated in Table 1.

We next probed the importance of the major nuclear lamina components, lamin A/C, in nuclear diffusion, because the cytoskeleton is physically linked to the nucleus via the nuclear lamina (20).

Loss of lamin A/C amplifies diffusive motion while preserving the diffusion characteristics of the cell geometry

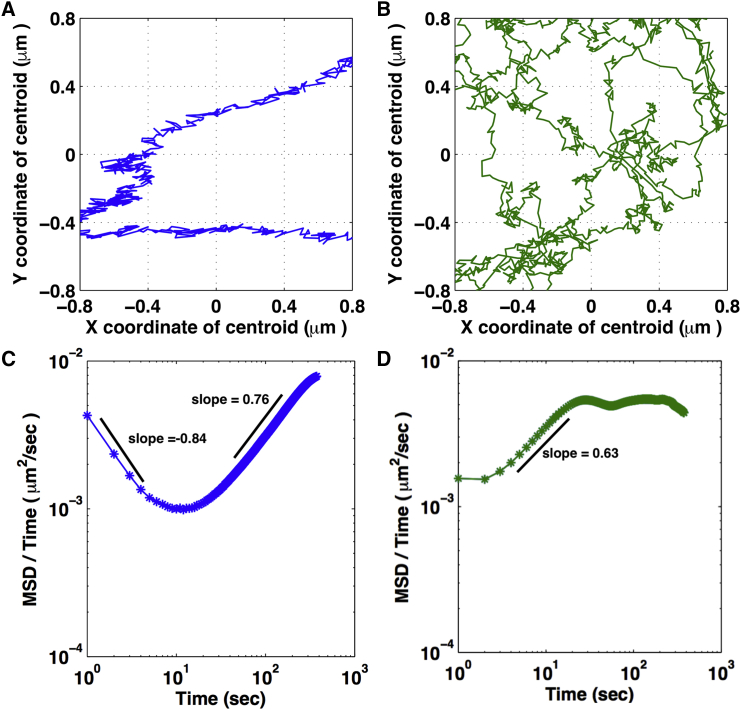
NIH3T3 Lamin A/C deficient cells were transiently transfected with H2B-EGFP to mark the nucleus and cultured on the rectangular or circular geometries. 2D confocal images of these nuclei were acquired under the aforementioned imaging conditions and the diffusion characteristics were measured. On both geometries, the nucleus underwent significant deformations in the absence of lamin proteins. Remarkably, we found that the nuclear trajectories and dynamics in lamin-deficient cells were similar to those observed in wild-type cells on corresponding geometry (Fig. 3, A and B), although the lamin-deficient nuclei explored larger regions.

Figure 3.

Role of Lamin A/C in nuclear diffusion. (A and B) Mean shifted nuclear trajectories for Lamin A/C deficient cells constrained in rectangular (A) and circular (B) geometries are given. The two panels show part of the trajectories from movies of 1500 s that would fit in a 1.6 × 1.6 μm spatial window. (C and D) 〈r²(τ)〉/τ as a function of τ for the centroid of the nucleus in the Lamin A/C-deficient cells in the rectangular (C) and circular (D) geometry is given. Number of cells measured: five rectangles and four circles.

For the rectangular geometry, the time-dependent diffusion constant curve shows two distinct regimes, one with a slope = −0.84 and the other with a slope = 0.76 corresponding to subdiffusive and superdiffusive behavior, respectively, with a crossover occurring at ∼τ = 10 s. For the circular geometry, a superdiffusive behavior (slope = 0.63) was observed for nuclear motion over much shorter timescales (τ = 3.5 s), and at ∼τ = 33 s a transition to normal diffusion is observed as indicated by the nearly horizontal region in the plot (Fig. 3, C and D). The ranges of time-dependent diffusion coefficients for nuclei were larger for lamin-deficient cells compared to control cells in rectangular geometry (Table 1). The cells on the circular geometry have been shown to have low lamin A/C (17) and the knock-down of lamin A/C did not show significant changes in the nuclear diffusion characteristics. We again observed amplified diffusion characteristics along the x axis of the rectangular cells compared to their y axis, while no such difference was visible in the circular cells (Fig. S4; Table 1).

To test the reproducibility of this observation, we measured the nuclear displacement from the cell centroid for a population (n = ∼50) of fixed cells and found that the trend remains the same (Fig. S2.2). These observations suggest that cellular geometry, which is dictated by the cytoskeleton, has a dominant role in the translational dynamics, compared to lamins that determine nuclear rigidity. Because two different regimes of diffusions were observed, in the next section we fitted the data to a moving corral (MC) model to get further insights on the diffusive behavior of the nucleus.

Analysis of microrheological properties of the cytoplasm using nuclear trajectories

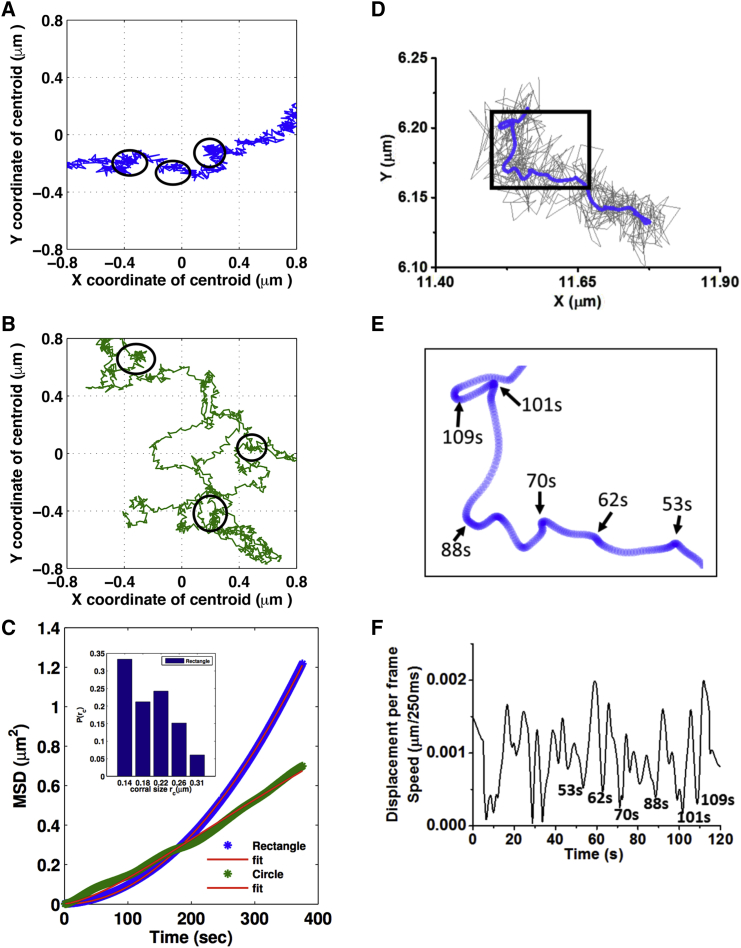
Nuclear trajectories in rectangular cells show spatial clustering, or corrals with an approximate size of 217 ± 52 nm, which is sparingly present in circles (Fig. 4, A and B). Therefore, we applied the MC model, which considers diffusion at two timescales. At short timescales the model considers diffusive motion of the centroid within these clusters and at longer timescales it assumes the clusters themselves to be diffusing corresponding to two different diffusion constants (21). From this model the MSD, 〈r² (τ)〉 = 2dDτ, is given by the following:

$$\langle {\mathit{r}}^2\left(\mathit{\tau }\right)\rangle =\langle {\mathit{r}}_{\mathit{c}}^2\rangle \times \left(1+\frac{4{\mathit{D}}_{\mathit{c}}\mathit{\tau }}{\langle {\mathit{r}}_{\mathit{c}}^2\rangle }\right)\left[1-\exp \left(\frac{-4{\mathit{D}}_{\mathit{b}}\mathit{\tau }}{\langle {\mathit{r}}_{\mathit{c}}^2\rangle }\right)\right],$$ (2)

where D_b refers to the diffusion constant within the corral, D_c refers to the diffusion constant of the corral, and r_c is the size of the corral. The MSD obtained from the MC model fits well with our observed MSD data of the nuclear trajectories (Fig. S5, A–D). The typical values of D_b and D_c for the nuclear motion in rectangular cells are 2.92 × 10⁻⁵ and 2.73 × 10⁻⁴ μm²/s, respectively. In circular cells, because the corrals were not prominent, we used the estimated r_c value from the rectangular cells and determined the values of D_b and D_c to be 4.05 × 10⁻⁴ and 4.61 × 10⁻⁴ μm²/s, respectively. The diffusion constant D_b for the rectangular geometry is much smaller than D_c, whereas for the circular geometry both diffusion constants were of the same order of magnitude. D_b and D_c values for lamin-deficient rectangles are 3.39 × 10⁻⁴ ± 2.49 × 10⁻⁴ μm²/s and 1.2 × 10⁻³ ± 1.4 × 10⁻³ μm²/s, respectively, and for lamin-deficient circles are 6.67 × 10⁻⁴ ± 3.58 × 10⁻⁴ μm²/s and 1.5 × 10⁻³ ± 8.9 × 10⁻³ μm²/s, respectively. The parameters obtained from this model are tabulated in Table 2.

Figure 4.

MC diffusion model. (A and B) Mean shifted nuclear centroid trajectories show defined corralled structures in rectangular geometry (A) compared to circular geometry (B). (C) The MC model was fitted (red) to MSD curves for nuclei in rectangular (blue) and circular geometry (green). (Inset) Distribution of the approximate corral sizes r_c, estimated from the trajectories of nucleus in rectangular geometry, is shown. (D) (Gray) Nuclear trajectory of a cell seeded on rectangular pattern imaged at 4 frame/s is given. (Blue) Robust Lowess smoothened trajectory with a window of 10 s is shown. (E) Here, we show a zoomed-in view of a section from (A). (F) Instantaneous speed of the nucleus as a function of time is shown.

Table 2.

Diffusion Characteristics Obtained from the MC Model

Geometry	Condition	Db (μm2/s)	Dc (μm2/s)	rc (μm)	n
Rectangle	control	2.92 × 10−5 ± 2.11 × 10−5	2.73 × 10−4 ± 1.79 × 10−4	0.22	12
Circle	control	4.05 × 10−4 ± 2.52 × 10−4	4.61 × 10−4 ± 2.78 × 10−4	0.22	12
Rectangle	lamin A−/C−	4.05 × 10−4 ± 2.52 × 10−4	1.2 × 10−3 ± 1.4 × 10−3	0.22	3
Circle	lamin A−/C−	4.05 × 10−4 ± 2.52 × 10−4	1.5 × 10−3 ± 8.9 × 10−4	0.26	3

The above corralled diffusion model suggested that the typical corral size is ∼200 nm with a timescale <10 s. To visualize these transient pinning sites (corrals), the nuclear trajectories were recorded at four frame/s from cells seeded on the rectangular geometry. After smoothening the data, such corrals were clearly visible from the nuclear x-y trajectory (Fig. 4, D and E). The nucleus was found to spend <10 s within each corral and these corrals were separated by ∼10 s. Furthermore, the instantaneous speed of the nucleus was plotted against time (Fig. 4 F) whereby the pinning sites are clearly visible by dips in speed.

Because the cytoskeletal organization can influence the correlation in direction of forces exerted on the nucleus, we next computed the autocorrelation function of the nuclear trajectories in the two geometries. The autocorrelation function was defined as the following:

$$\langle {\mathit{C}}_{\left(\mathit{\tau }\right)}\rangle =\frac{\langle \left(\mathit{R}\left(\mathit{t}\right)-\overline{\mathit{R}}\right)\times \left(\mathit{R}\left(\mathit{t}+\mathit{\tau }\right)-\overline{\mathit{R}}\right)\rangle }{\langle {\left(\mathit{R}\left(\mathit{t}\right)-\overline{\mathit{R}}\right)}^2\rangle },$$ (3)

where R(t) and R(t + τ) are position vectors of the centroid of the nucleus at times t and t+τ, respectively, and $\overline{\mathit{R}}$ is the time-averaged position of the nuclear centroid. The function was normalized to have values between +1 and −1 (Fig. S6, A and B). The correlation times were obtained by fitting a single exponential function to the curve, and we calculated that the correlation time for rectangular geometry is 236 ± 103 s, whereas for circular geometry, the time was 125 ± 62 s. This indicates that the forces are much more correlated when the cells are elongated.

To understand the effect of the fluctuating component of the forces present in the cytoplasm, the power spectral analysis of the detrended time series of the trajectories was then carried out and the spectral power was plotted against the frequency in logarithmic scale (Fig. S6, C and D). In rectangular and circular geometry the slopes of the curves are measured between 20 and 50 mHz and the mean slope of the plot is −2.23 ± 1.11 and −3.25 ± 1.67, respectively. At further higher frequencies, a near horizontal power spectrum is obtained indicating uncorrelated fluctuations. The difference in slopes of the power spectral plot in the two geometries again shows that active fluctuations are more correlated in rectangular geometry. This could be a reflection on its more oriented cytoskeletal network.

Discussion

Studies have shown that matrix-constrained cells in defined geometries have differential cytoskeletal organization particularly in the case of apical actin stress fibers (ASF), which impinge on nuclear morphology and orientation (17). In this article, we have shown the sensitivity of nuclear positioning in such model systems with a combination of static and dynamic measurements. In contrast to migrating cells (7), we show that in these immobilized cells, the actin cytoskeletal filaments (CSK) are more critical than microtubules in positioning the nucleus. The differential CSK organization in the two cellular geometries indicates the presence of different rheological microenvironments. Because this would affect the way the nucleus samples the cytosol, we followed the translational movement of the nucleus over time and discovered that the dynamics profile is distinct and sensitive to geometry.

From measuring the MSDs of the nucleus we were able to observe different regimes of nuclear diffusion. In rectangular geometry, the corralled nature of trajectories (size ∼217 nm) contributes to the subdiffusive regime, and typically after a timescale of 18 s a crossover to superdiffusive behavior was observed. Using the MC model, we calculated a D_c/D_b value of ∼14.7 (Table 2), which further supports the strong, corralled nature of nuclear trajectories in rectangular cells. Importantly, high speed imaging of the nuclear dynamics in rectangular cells confirmed the presence of these transient pinning sites (corrals). In contrast, in the isotropic geometry the subdiffusive regime is significantly reduced, and the crossover to superdiffusive motion occurs after ∼2 s, which subsequently changes over to diffusive motion after ∼36 s. The calculated D_c/D_b value was ∼1.87, indicating that the trajectories do not have a prominent subdiffusive regime or maintain a corralled structure. Taken together, this demonstrates that the nucleus in cells on small circular geometry is highly dynamic compared to the nucleus in large elongated cells over all timescales.

These measurements were shown to be sensitive to the internal cytoskeletal organization as well as the structural integrity of the nucleus. In lamin A/C-deficient cells, the corralled nature was not as prominent as in control cells (D_c/D_b ∼19.17 for lamin A⁻/C⁻ rectangles). The magnitudes of diffusion constants (D_c, D_b) were also larger compared to control cells (D_b ∼ 11.6, D_c ∼ 5.2 times larger). The range of anomalous diffusion constants for the nucleus is one order-of-magnitude larger in lamin-deficient cells than in control cells (Fig. S5 E). This is consistent with the results obtained from earlier microrheological experiments with incorporated nanoparticles (22). The significant drop in viscosity of the cytoplasmic environment is reflected in the larger diffusion constants when cells are lamin deficient.

At longer timescales, the nuclear movement is diffusive in the small circular cells whereas it is superdiffusive in rectangular cells. Additionally, rectangular cells have perinuclear ASFs aligned parallel to the long axis of the cell and the nucleus is anisotropically displaced along this axis. In contrast, circular cells have basal actin fibers but lack perinuclear ASFs and the nucleus is isotropically displaced. Further, both the autocorrelation and power spectral analysis show that the forces that act on the nucleus are more correlated in rectangular cells. These observations indicate the presence of ordered perinuclear CSK structures can direct nuclear motion. Previous studies that have shown that actin (de)polymerization dynamics can exert forces on the nucleus and the chromatin: depolymerized actin-myosin-formin nodes act as force-generating units in circular cells and the perinuclear ASFs can exert compressive forces on the nucleus in rectangular cells (15, 17). Based on these results, we propound that molecular links between perinuclear ASFs and nuclear envelope act as cables that direct the mobility of nucleus in rectangular cells and the lateral actin network confines the nucleus at shorter timescales. When the molecular links between the CSF and nuclear envelope are disturbed by knocking out lamin A/C in rectangular cells, there is loss of friction that previously restricted the nuclear dynamics leading to nuclei having higher diffusion constants. Whereas in circular cells, lower actin polymerization states and lower levels of lamin A/C (17) lead to a highly dynamic nucleus. Additionally, the absence of perinuclear actin cables leads to an isotropic distribution of forces resulting in isotropic displacement of nucleus from the cell center in these cells.

Conclusions

Precise nuclear positioning is important for many cellular functions. In adherent immobile fibroblast cells, the central positioning of the nucleus evinces the presence of an intact mechanical homeostasis. Many diseases are characterized by alterations in elements of nuclear lamina and cytoskeleton (12, 13, 23, 24), leading to destabilization of this mechanical homeostasis. In this context, our results show that nuclear positioning dynamics is very sensitive to both the internal and external microenvironment of the cell. Importantly, these results provide sensitive biophysical signatures for detecting cellular abnormalities using the nucleus as a probe particle.

Author Contributions

A.V.R., S.V., and G.V.S. designed the project. A.V.R., D.S.J., and S.V. carried out the experiments. A.V.R., D.S.J., S.V., and G.V.S. analyzed the data and wrote the manuscript.

Editor: Alexander Dunn.