Abstract
The intracellular environment is composed of a filamentous network that exhibits dynamic turnover of cytoskeletal components and internal force generation from molecular motors. Particle tracking microrheology enables a means to probe the internal mechanics and dynamics. Here, we develop an analytical model to capture the basic features of the active intracellular mechanical environment, including both thermal and motor-driven effects, and show consistency with a diverse range of experimental microrheology data. We further perform microrheology experiments, integrated with Brownian dynamics simulations of the active cytoskeleton, on metastatic breast cancer cells embedded in a three-dimensional collagen matrix with and without the presence of epidermal growth factor to probe the intracellular mechanical response in a physiologically mimicking scenario. Our results demonstrate that EGF stimulation can alter intracellular stiffness and power output from molecular motor-driven fluctuations in cells overexpressing an invasive isoform of the actin-associated protein Mena.
Introduction
The cytoskeleton, the intracellular mechanical structure, consists of a cross-linked, filamentous network driven by molecular motors and confers upon cells physical form and functionality. During cancer invasion, this machinery is engaged to promote drastic cell morphology changes and persistent migration across confining physiological barriers, including the dense extracellular matrix of the tumor stroma, endothelial junctions, basement membranes, small vessels, and interstitial tracks (1). The intrinsic nature of different cell types and extrinsic environmental factors can result in altered mechanical phenotypes. Highly invasive cancer cells tend to generate larger contractile forces and have altered deformability (2, 3, 4, 5), and physical properties of the microenvironment, such as stiffness, topography, and dimensionality, can influence cell contractility, migratory behavior, multicellular morphologies, and intracellular transport and fluctuations (5, 6, 7, 8, 9, 10, 11). Various techniques have been developed to directly measure the basic mechanical properties of cells, including local active rheometry via atomic force microscopy or magnetic or optical tweezers (12), microfluidics-based micropipette arrays (13) and hydrodynamic stretching (14), noncontact Brillouin microscopy (15), and particle-tracking microrheology (16). However, it is currently not well understood how intracellular mechanics is modulated under realistic pathophysiological conditions, which entail three-dimensional (3D) environments and growth factor stimulation.
Many molecular factors contribute to the intracellular mechanical state, including the turnover rate of molecular components such as actin filaments and actin binding proteins, the walking rate of myosin motors, and the concentrations and mechanical properties of these cytoskeletal components (17, 18). Although it is difficult to directly measure the motions of individual cytoskeletal proteins or the material properties of the cytoskeleton, particularly of cells embedded inside 3D physiologically mimicking environments, it is feasible to image the trajectories of visible tracer particles, such as injected microbeads and nanotubes or endogenous organelles. Passive particle tracking microrheology, based on relating particle motions to viscoelastic properties of the surrounding medium via the fluctuation-dissipation theorem (FDT), has been applied to measure the complex shear moduli of reconstituted cytoskeletal protein networks and other complex fluids as well as living cells (19, 20, 21). However, the FDT breaks down for systems not in thermodynamic equilibrium. In particular, the intracellular environment is active with ATP-dependent processes driving additional motions beyond thermal fluctuations (22, 23). As a result, a modified relation is required to relate internal motions to material properties. Here we derive an analytical relation that captures the heterogeneous trends observed in typical experimental timescales and provides fundamental physical interpretations of displacement fluctuation data inside living cells. We measure the internal fluctuations of highly metastatic breast cancer cells embedded in a 3D collagen matrix and demonstrate the impact of epidermal growth factor (EGF) stimulation, which promotes directed cancer invasion (24, 25, 26), on intracellular mechanical properties. To uncover insights toward the fundamental mechanical mechanisms that can drive physical changes in cells under EGF stimulation, we perform Brownian dynamics computational simulations of the active actin cytoskeleton that incorporate the complex network dynamics of large numbers of interacting kinetic and mechanical cytoskeletal components.
Materials and Methods
MDA-MB-231 cells with and without MenaINV overexpression were obtained from the Gertler and Lauffenburger labs at the Massachusetts Institute of Technology. Both MenaINV and non-MenaINV overexpressing MDA-MB-231 cells were cultured at 37°C, 5% CO2 in DMEM with 10% fetal bovine serum and 1% penicillin-streptomycin. In experiments, cells were embedded in a 3D 2 mg/mL rat tail collagen I matrix and incubated for at least 12 h in serum-free media (DMEM only) before experiments. Microrheology experiments were performed under serum-free conditions with or without 5 nM EGF added for at least 1 h before measurements. Mitochondria, which were used as tracer particles for the microrheology experiments, were labeled with Mitotracker Red (Life Technologies, Carlsbad, CA) 1 h before the start of measurements. Fluorescence imaging was performed on a spinning disk confocal microscope with a 63× oil immersion objective, and images were taken at 50 ms per frame for at least 50 s. Practical limitations, including bulk cell motions, photobleaching, and tracers moving out of plane, hinder longer term particle-tracking microrheology experiments here. As a result, mean squared displacement (MSD) data of individual tracers at longer time intervals are inherently less reliable due to reduced sampling from videos of finite duration. The software IMARIS (Bitplane; www.bitplane.com/) was used to trace mitochondria trajectories, and custom MATLAB programs (The MathWorks, Natick, MA) were used to process the data. Net displacements of tracers were subtracted to correct for drift and directed motions. In data fits, mitochondria are assumed to have an average effective radius of 70 nm based on MSD scaling compared to injected microbeads (9). The logarithmic slope β is calculated from a locally smoothened MSD (20). Note that mitochondria are convenient probes for tracking intracellular fluctuations, particularly for cells embedded in complex environments, because they are endogenous and abundant. They and other endogenous granules have been used in particle tracking microrheology experiments and their MSD trends are also comparable to those of exogenously injected beads (9, 22, 27, 28). A key limitation is their nonhomogeneous nature, including diverse shapes and sizes. Thus mitochondria-based microrheology studies may be best suited for comparing between relative changes in the ensemble average of MSDs in response to experimental conditions. Higher resolution imaging that can resolve the shape and size of individual tracers can help overcome this limitation.
Results and Discussion
The Nature of Intracellular Fluctuations
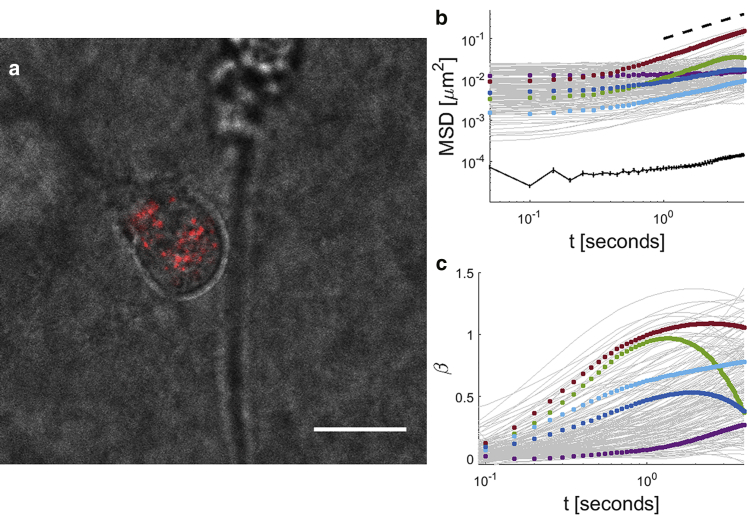
We track the fluctuations of mitochondria, which act as tracer particles of the intracellular environment. Previously it was shown that the motions of mitochondria and injected microbeads are comparable, indicating that comparable basic internal machinery controls their behaviors (9, 27). We perform these experiments on MDA-MB-231 metastatic breast cancer cells embedded in a 3D collagen matrix, as shown in Fig. 1 a. The experimental mean-squared displacements, MSD , and , are shown in Fig. 1, b and c. β is an important parameter that indicates the nature of anomalous diffusion. Typically, β < 1 for confined motions such as Brownian motion in a viscoelastic medium; β = 1 for diffusive or diffusivelike motions such as Brownian motion in a Newtonian fluid; and β > 1 for superdiffusive or persistent motions such as the ballistic regime of Brownian motion at very short timescales. Intracellular motions display a heterogeneous quality, in that different tracers appear to exhibit fundamentally distinct trends, including some that appear completely flat and others with two or three temporal regimes (Fig. 1).
Figure 1.
Intracellular fluctuations of cell in a 3D matrix. (a) An MDA-MB-231 cell, with labeled mitochondria (red), is embedded inside a 2 mg/mL collagen matrix. (b) Profiles of in-plane MSD versus time interval t of intracellular fluctuations from mitochondria tracers (gray curves) display heterogeneity. Different colored dots highlight typical MSDs with distinct characteristics. Dashed line is proportional to t. Note that the average MSD of stuck fluorescent beads on glass is ∼10−4μm2, as shown by the lower black curve. Error bars are mean ± SE (n = 40). (c) Profiles display the logarithmic derivatives, beta's, of the MSD’s shown in (b), with corresponding colors. Scale bars represent 20 μm.
Previous experiments that measure the rheological properties of cells using active methods, such as magnetic or optical tweezers, show that cells are relatively elastic, with a very weak power-law dependence of the shear modulus on frequency (22, 29). Under these conditions, Brownian motion should result in a relatively flat MSD with no time interval dependence. Recent work has shown that nonthermal forces generated by molecular motors, particularly myosin II, add an altered spectrum of fluctuations, resulting in MSDs proportional to t at relatively long timescales >∼0.1 s (22, 23). The diverse trends exhibited by intracellular MSDs therefore reflect both passive properties of the cytoskeleton and the complex nature of motor-driven activities. We next derive a fundamental relation that accounts for the range of observed trends.
Fluctuation Dissipation with Active Forces
We assume that intracellular tracer particles or organelles are surrounded by the cytoskeleton, with a smaller mesh size, which acts as a linear viscoelastic continuum. The motions of these tracers can then be described by a generalized Langevin equation with both thermal forces fth and molecular motor-driven forces fmot, as:
| (1) |
where m is the mass of the tracer, is the time derivative of the tracer velocity v, and ζ is the memory function (purely elastic media have perfect memory (constant) and purely viscous media have no memory (δ-function)) (16). In the Laplace frequency domain, v can be expressed as follows:
| (2) |
where denotes the Laplace transform of a given function F, v0 is the velocity at time zero, and s is the Laplace frequency. The Laplace transform of the velocity autocorrelation can then be calculated as follows:
| (3) |
where 〈〉 denotes ensemble average. By identity, we have:
| (4) |
where is the Laplace transform of the mean-squared displacement MSD = 〈Δx2(t)〉. Because the motor-generated forces are not simply δ-correlated noise but rather have some characteristic persistence, there should be correlation to some extent between motor-generated forces and the velocity of the tracer. Previously, it is assumed that motors generate forces in the form of square pulses (kicks) and each pulse has a characteristic duration (30). Within the characteristic duration, the force is constant. Here, we take into consideration that myosin II motors inside living cells, to be processive, are in the form of thick polarized filaments that consist of many myosin II motors chained together (i.e., many myosin heads connected to a backbone) (31, 32). Each motor that constitutes the thick filament can bind and unbind to actin and generate forces when bound, and we assume that the filament will generate a net directed force. Here, we consider that after a motor filament binds, there is an unbinding rate for each motor in the filament and the unbinding rate is independent for each motor such that the number of bound motors over time τ follows:
| (5) |
where Nmot is the number of bound motors and ku is the unbinding rate for each motor. The solution gives the number of bound motors over time, which we assume to be proportional to the net force generated by the motor filament, as follows:
| (6) |
where N0 is the number of bound motors at some time τ = 0 when the motor filament binds. Once all of the motors of any particular motor filament unbinds, the filament has walked or diffused away and the subsequent rebinding of the filament or binding of another motor filament will result in forces uncorrelated with the previous. The velocity-active force correlation is then in the form (for time interval t ≥ 0), as follows:
| (7) |
where s0 = ku, and A is the average instantaneous power that the motors generate onto the tracer. Here, we assume that the instantaneous power is related to the ATP consumption rate by the motors and independent of material properties of the surrounding medium. However, later we will revisit this assumption for possible implications on medium-dependent power output. The power spectral density of the active forces can also be calculated by taking the bilateral Fourier transform of 〈fmot(0)fmot(t)〉, which is a Lorentzian in frequency space assuming exponential force pulses in time. Note that in the physiological case in a live cell, the motion of tracer particles can be the result of advection from cytoskeletal fluctuations due to molecular motor activity, particularly from myosin II filaments with numerous myosin heads that bind to actin filaments. The motor-induced forces on the cytoskeleton appear random but have some persistence time as each myosin II filament walks along multiple actin filaments in a directed manner toward the barbed ends, which could result in force dipoles, and generates correlated forces during that motion. The correlation decays as the motor filament walks away via binding and unbinding of motor heads. As new motor filaments, which are assumed not to be coordinated with previous motors, walk into the vicinity of a tracer, new forces are exhibited that are uncorrelated with previous force pulses. In our model, for a purely viscous material, highly persistent motors can lead to directed forces and therefore directed transport of tracers. However, for a purely elastic material, a persistent or constant force would not lead to directed transport. In this scenario, directed transport may arise from tracers moving through pores within the elastic material and not experiencing restoring forces from the cytoskeletal network. This mode is not accounted for in our model.
At relatively high frequencies or short timescales, it has been demonstrated that the fluctuation-dissipation theorem is accurate for molecular motor-driven gels and living cells, as validated by comparing active and passive microrheology measurements in addition to modulating ATP-driven activities (22, 23). Therefore, the total kinetic energy of the system should be dominated by thermal energy, resulting in the following:
| (8) |
where N is dimensionality and inertia is neglected. The memory function is related to the frequency-dependent viscosity and shear modulus by (33), as follows:
| (9) |
| (10) |
Cells have been shown to exhibit power-law frequency scaling of the shear modulus (22, 29), which takes the following form:
| (11) |
where 0 ≤ α ≤ 1 (zero for purely elastic and one for purely viscous) and B is a constant. The Laplace transform pair of the MSD can now be represented as the following:
| (12) |
| (13) |
where Γ is the γ-function. At short timescales smaller than 1/s0 (but above inertial timescales), we have the following:
| (14) |
For a Newtonian fluid, the MSD reduces to the following:
| (15) |
and for relatively short timescales smaller than 1/s0 to the following:
| (16) |
This is consistent for an active persistent force in a Newtonian fluid (above inertial timescales), leading to 〈Δx2(t)〉 ∝ t2 at timescales above thermal domination.
For a purely linear elastic medium, the MSD becomes the following:
| (17) |
which for relatively short timescales, smaller than 1/s0, leads to the following:
| (18) |
This accurately predicts that below the characteristic persistence time due to molecular motor activity and above the short timescale regime dominated by thermal forces, 〈Δx2(t)〉 ∝ t inside living cells, which are relatively elastic (22).
Note here that at times above the thermal regime and below 1/s0, (12), (13), (14) indicate that 〈Δx2(t)〉 ∝ t1+α. However, if the power generated by molecular motors is dependent on the material properties of the medium such that in the frequency domain, then 〈Δx2(t)〉 ∝ t1+2α. Moreover, in this scenario, 〈Δx2(t)〉 ∝ t/G2 for linear elastic media. This form is similar to previous theory (22, 28, 30), but it is not clear currently whether motor-generated power should be dependent on the mechanical properties of the local environment. Our theory derived here thus provides a framework for testing this fundamental property in future studies. In this work, we consider cells that are relatively elastic at the timescales of interest (22) and thus α ≈ 0, so A is not dependent on time or frequency.
This current derivation is consistent with both empirical data for intracellular measurements and the classical limit of persistent forces acting on an object in a Newtonian fluid. These equations ((1), (2), (3), (4), (5), (6), (7), (8), (9), (10), (11), (12), (13), (14), (15), (16), (17), (18)) provide a quantitative and physical relation between the experimental observable—the MSD—and the underlying intracellular material properties and motor-driven activity over a continuous range that spans thermal and active regimes. They provide, to our knowledge, a novel, direct means to calculate the power generated by molecular motor activity, which is of particular importance because this is fundamentally related to the rate of consumption of chemical energy (ATP) required to drive active intracellular activities. Moreover, the theory accounts for the molecular picture of myosin II motors that form thick filaments and exhibit binding kinetics to substrates. Interestingly, the phosphorylation of myosin II via Rho kinase (34, 35), which enables the motors to unbind and walk along actin filaments, occurs at the timescale in the order of 10 s, which should be related to 1/s0 based on our theory. Intracellular MSDs are observed to plateau on that timescale (22).
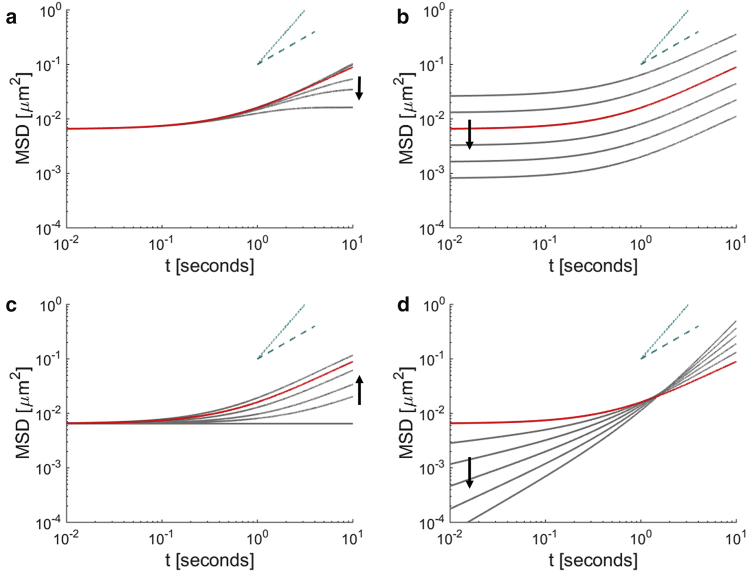
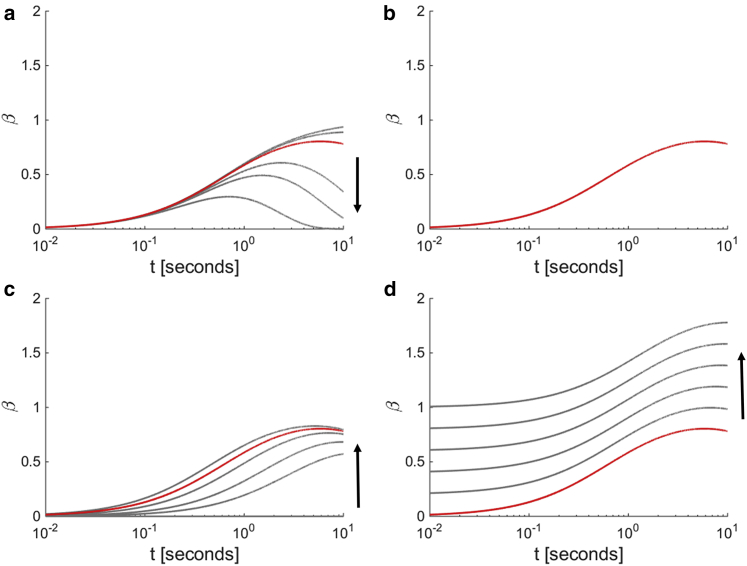
Figs. 2 and 3 demonstrate the nature of the MSD and β, respectively, as calculated by Eq. 13, when different physical, internal characteristics are modulated, and the diverse experimental trends shown in Fig. 1, b and c are qualitatively captured. (12), (13), (14), (15), (16), (17), (18) represent, to our knowledge, a novel framework that extends beyond the thermal equilibrium assumption of the FDT, which was previously applied to measure the shear modulus of soft materials and does not account for active behaviors. Our framework enables key fundamental parameters of the intracellular environment—the shear modulus (magnitude and power-law scaling exponent, B and α), persistence time of nonequilibrium effects 1/s0, and the instantaneous power of motor-driven activity and molecular level energetics A—to now all be interpretable and computable.
Figure 2.
MSD versus active parameters. (a) Altering s0 leads to a modulation in the onset of the plateau at long timescales. (b) Altering B shifts the magnitude of the MSD. (c) Altering A modulates the onset of the high slope regime at long timescales. (d) Altering α modulates the logarithmic slope at both the short and long timescales. The arrow indicates the direction of increasing the parameter of interest. The red curve is a common reference curve for (a–d) and has parameter values of A = 1.5 kBT [s−1], B = 2 [Pa s−α], α = 0, s0 = 1/30 Hz, dimensions = 2, T = 310 K, rtracer = 70 nm. The dashed blue line scales as t and the dotted blue line scales as t2.
Figure 3.
β versus active parameters. (a–d) These panels correspond to (a–d) in Fig. 2. (a) Increasing s0 shortens the timescale when β at long timescales returns to the value of β at short timescales. (b) Increasing B does not alter β. (c) Altering A modulates how quickly β increases at long timescales. (d) Altering α shifts the magnitude of β. The arrow indicates the direction of increasing the parameter of interest, and the red curve indicates the identical reference for (a–d) with parameter values indicated in the caption of Fig. 2.
A number of previous studies have generated data that are captured and unified within our theoretical framework, with four fundamental parameters characterizing the mechanical properties of live, active cells. The internal fluctuations of Amoeba cells have been shown to display two temporal regimes (36), as consistent with thermal and motor-driven regimes. Interestingly, for these cells, the MSDs at short time intervals scale close to t, suggesting a fluidlike rather than elastic intracellular environment, whereas the MSDs at longer time intervals scale close to t2. This is consistent with our theoretical model that MSDs in the motor-driven regime (before 1/s0) scale as t1+α rather than t1+2α, as shown in Fig. 2 d. Furthermore, it has been shown in fibroblasts that the MSDs in the perinuclear region are shifted vertically compared to the MSDs in the lamella (37), which is consistent with a change in the shear modulus coefficient B, as shown in Fig. 2 b. Finally, suppressing motor activity via blebbistatin or ATP depletion results in a delay (or abolishment) in the onset of the enhanced power-law regime (22), consistent with a reduction in motor power generation A, as shown in Fig. 2 c.
We note here that there are limitations and key assumptions in our theoretical framework. The theory requires the usual assumptions of passive particle tracking microrheology (16) (with the exception of thermal equilibrium), particularly that the material being probed can be modeled as a linear viscoelastic continuum. The shear modulus of the material also needs to scale as a power law with frequency, which has been shown in different cell types as well as in cross-linked actin gels (22, 29, 38, 39). Additionally, motor-driven activity starts to dominate at longer timescales, typically >∼0.1 s (i.e., <10 Hz), consistent with observations in active biological gels and live cells (22, 23). This effectively enables the MSD at short time intervals to be used for interpreting passive cell material properties and at long time intervals for interpreting active behaviors. Conditions that deviate from these requirements will not be properly captured in our derived model. For instance, the cytoskeleton can undergo phase transition through molecular disruption (17) or during embryo morphogenesis (40, 41). In these cases, the cytoskeleton becomes a multiphased material with regions of high and low actin density that are heterogeneous. Our model may not be able to capture the detailed properties of these complex cytoskeletal forms. As another example, if a condition changes cell properties from a purely elastic to a Maxwell material, our model will not be accurate as the nature of the long time behavior of the MSD will be incorrectly attributed to motor activity rather than creep in the material. However, if the nature of the shear modulus is known, i.e., the form and frequency response, and the nature of forces from molecular motors is consistent with previous experimental measurements (22, 23, 28), then it is possible to solve for the relationship between the MSD profile of the tracer probes and the passive and active mechanical properties of the cell, as guided by our derivation in (1), (2), (3), (4), (5), (6), (7), (8), (9), (10), (11), (12), (13), (14), (15), (16), (17), (18). Additionally, our theoretical model can be impacted by conditions that alter the properties of the tracer, such as the effective radius, shape, and any boundary effects between the tracer and the cytoskeleton (16, 42), which can confound the interpretation of intracellular mechanical properties from tracer MSD data.
Microrheology of Metastatic Breast Cancer Cells Inside a 3D Matrix
Here we investigate intracellular mechanics and dynamics under pathophysiologically mimicking conditions. We perform particle tracking microrheology experiments on MDA-MB-231 metastatic breast adenocarcinoma cells, with and without overexpression of MenaINV, embedded in a 3D collagen matrix. A 3D fibrillar microenvironment, compared to a two-dimensional (2D) planar substrate, embodies a closer semblance to connective tissues and the tumor stromal matrix (43) and induces fundamentally different mechanical characteristics in cells, from migratory strategies to morphologies and internal organization and dynamics (43, 44). MenaINV is an isoform of an actin-binding protein Mena that promotes invasion in an epidermal growth factor EGF-dependent manner (25) and is induced to be overexpressed by the tumor microenvironment in vivo (45).
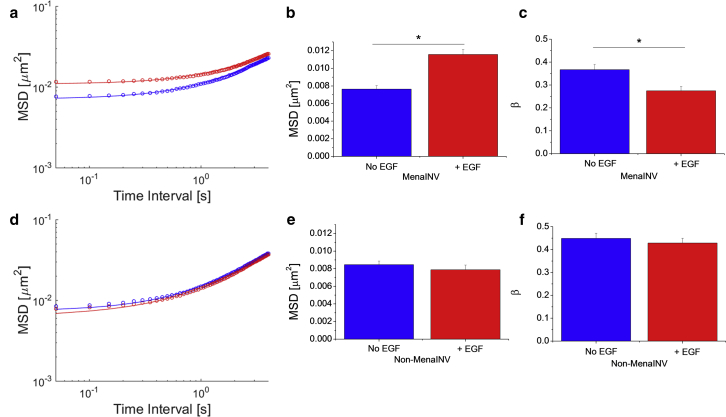
As shown in Fig. 4, a–c, for MenaINV cells, EGF-stimulation leads to an increase in MSDs at short times and a decrease in β at longer times. The average 2D MSDs data shown in Fig. 4, a and d, fit well to Eq. 14, as the plateau region is not observed on average, and the key parameters A, B, and α can be extracted from each condition. Recall that A is the instantaneous power output generated by molecular motors, B is the coefficient of the shear modulus with a power-law frequency scaling, and α is the power-law exponent of the shear modulus. For MenaINV cells, , with EGF stimulation, and without EGF stimulation, indicating that EGF reduces intracellular stiffness and instantaneous power from motor activities. Without MenaINV overexpression, the EGF-dependent internal mechanical response is not observed, as shown in Fig. 4, d–f. These results represent, to our knowledge, novel physical characterizations, including both passive and active properties, of metastatic breast cancer cells under relevant pathological and physiological conditions. To avoid introducing extra error due to curve fitting, we only performed statistical analyses on MSDs and β-values. Additionally, there is substantial heterogeneity in the data, as shown in Fig. S1, a–d. This could be the result of factors such as local regions of different stiffness, enzymatic activity, or concentration of cytoskeletal proteins, which can give rise to qualitatively distinct MSD profiles (39, 46). We also performed statistical analyses on log(MSD) as shown in Fig. S1, e and f. MSD data with error bars are shown in Fig. S2. We further measured the size and shape of the tracers (mitochondria) under the different experimental conditions, which could lead to similar effects on the MSDs as modulating B according to our theory. As shown in Fig. S3, mitochondria sizes and shapes do not appear to be modulated substantially enough to explain our experimental results.
Figure 4.
Impact of EGF stimulation on MDA-MB-231 breast cancer cells with (a–c) and without (d–f) overexpression of MenaINV. (a) Average 2D MSD of MenaINV overexpressing cells without EGF (blue) and with 5 nM EGF (red). Circles are data and curves are fits to Eq. 14. The R2 values for the fits are 0.9986 for without EGF and 0.9956 for with EGF. (b) MSDs at t = 0.05 s without EGF (blue) (0.0076 ± 0.0004 μm2, n = 157) and with EGF (red) (0.0116 ± 0.0005 μm2, n = 162). (c) β at t = 1 s without EGF (blue) (0.37 ± 0.02, n = 157) and with EGF (red) (0.27 ± 0.02, n = 162). (d) Average 2D MSD of non-MenaINV overexpressing cells without EGF (blue) and with 5 nM EGF (red). Circles are data and curves are fits to Eq. 14. The R2 values for the fits are 0.9994 for without EGF and 0.9992 for with EGF. (e) MSDs at t = 0.05 s without EGF (blue) (0.0085 ± 0.0004 μm2, n =148) and with EGF (red) (0.0079 ± 0.0004 μm2, n = 169). (f) β at t = 1 s without EGF (blue) (0.45 × 0.02, n =148) and with EGF (red) (0.43 ± 0.02, n = 169). Asterisk indicates p < 0.01, n is the number of particles tracked in each case, and error bars and values indicate mean ± SE.
Mena is a multifunctional actin binding protein. It serves as an anticapping protein for actin filaments, thus promoting polymerization, and can also bundle actin (47). Upon EGF stimulation, Mena is recruited to the leading edge of cells and helps coordinate Arp2/3 activity and actin polymerization (25). The invasive isoform MenaINV sensitizes cell protrusion dynamics to EGF-stimulation, enhances chemotaxis toward an EGF source, and is correlated to increased metastases in vivo (25, 48). Enhanced EGF sensitivity promoted by MenaINV may be due to altered signaling dynamics in which the tyrosine phosphatase PTP1B, which localizes to and attenuates EGF receptors upon EGF stimulation, is impaired (49). Here, our results demonstrate that in a 3D environment, MenaINV overexpressing cells soften under EGF stimulation, and interestingly, enhanced deformability appears to be characteristic of more invasive cancer cells (2, 3). These results implicate that physiologically relevant conditions exhibited by cancer cells—specifically growth factor stimulation and altered expression of cytoskeletal modifying proteins—can substantially impact fundamental intracellular mechanical properties, which may complement alterations in biochemical signaling dynamics toward driving metastasis.
Computational Simulations of Active Cytoskeletal Networks
Through Brownian dynamics simulations of the active actin cytoskeleton, we investigate the fundamental mechanical mechanisms driving physical differences in cells in response to EGF treatment. The computational model was previously developed and validated to accurately capture realistic mechanical properties of the active actin cytoskeleton. Extensive benchmarking and testing of the model and detailed parameter values can be found in our previous work (17, 50, 51, 52). Briefly, the model consists of actin filaments, actin cross-linking proteins (ACPs), and molecular motors that all act as mechanical springs with bending and extensional stiffnesses. They are also active and kinetic—actin filaments can nucleate, polymerize, and depolymerize; ACPs connect actin filaments and can bind and unbind in response to force; and motors behave like thick myosin II filaments that can bind to multiple sites on actin filaments and walk along them generating internal stress in the network. This computational model captures the basic mechanical and chemical features of cytoskeletal components and simulates the resulting network behavior with many of these components interacting dynamically with each other. The resulting stresses and fluctuations in the global cytoskeletal network are presumed to be the drivers of motions of tracers in microrheology experiments (9, 23, 28). Reaction kinetics of cytoskeletal components, such as actin polymerization and nucleation rates, can be precisely tuned to simulate the mechanical effects of chemical stimulation. Previously, we demonstrated that, in addition to motor activity, actin turnover dynamics can modulate the forces and morphologies of the cytoskeleton. Here, we analyze the potential role of EGF in cytoskeletal mechanics.
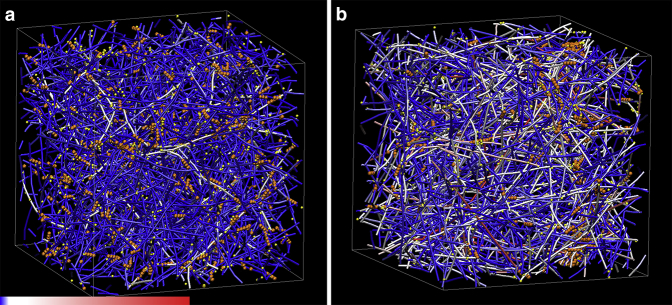
EGF treatment has been demonstrated to induce increased actin filament nucleation (53, 54). Representative simulations are shown in Fig. 5 for relatively high and low actin nucleation rates. Lower nucleation rates lead to larger average internal stresses (Figs. 5 and 6, a and c). Cytoskeletal stiffness has been shown to increase with increasing prestress in these simulated cross-linked actin networks (52), as consistent with experimental data from rheometry measurements of prestressed and cross-linked actin networks (38) and from magnetic cytometry in live cells stimulated with histamine to enhance contractility (55). Enhanced nucleation also leads to shorter average filament lengths (Fig. 6 c, inset), which can reduce the connectivity of the network required for generating global internal stress. Furthermore, stress fluctuations—undulations in stress levels over time—that drive intracellular motions are diminished with increasing nucleation rates (Fig. 6, b and c). These results indicate that increasing nucleation rates via EGF can lead to cytoskeletal softening and reduction in motor-generated intracellular motions, as consistent with our experimental microrheology results in Fig. 4, a–c. Note that EGF is implicated in a multitude of signaling pathways involved in cell motility and proliferation (56). Further studies will be required to explore the full spectrum of the impact of EGF on cytoskeletal network mechanics and dynamics.
Figure 5.
Brownian dynamics simulations of active actin networks in 3D. Networks with actin nucleation rates of (a) 0.1 and (b) 0.01 μM−1 s−1. All simulated networks have 25 M actin, 1% ACPs to actin, and 1% myosin II motors to actin in a 3 × 3 × 3 μm3 domain with periodic boundary conditions. The actin turnover (treadmilling) rate is set to 300 s−1, which is sufficient to maintain homogeneous rather than clustered networks in these simulations. Orange represents motors, yellow represents ACPs, and fibers represent actin filaments. The color scale applies to the actin filaments and represents a tensile force range from 0 (blue) to 100 pN (red).
Figure 6.
The impact of actin nucleation rates on actin network mechanics and dynamics. (a) Stress profiles over time for cross-linked actomyosin networks with varying nucleation rates. All simulated networks have 25 μM actin, 1% ACPs to actin, and 1% myosin motors to actin. The actin turnover rate is set to 300 s−1. Stresses are calculated by averaging the sum of the normal tensile forces per unit area across eight 3 × 3 μm2 cross sections along each dimension of the domain. (b) Normalized distributions of stress fluctuations from the mean over 1 s time intervals from the data shown in (a). Open circles are from computational data and solid curves are Gaussian fits with corresponding means and SDs. (c) Average stress versus nucleation rate. Upper and lower bounds represent the stress fluctuations from the mean over 1 s as calculated from the SD of each of the stress fluctuation distributions in (b). Inset shows average filament length versus nucleation rate. (d) Normalized stress autocorrelation. Open squares are simulation data points and solid curves are fits to exponential decays with time constants between 3 and 5 s. In (a), (b), and (d), blue, red, yellow, and purple correspond to nucleation rates of 0.01, 0.05, 0.1, and 0.2 μM−1 s−1, respectively.
Additionally, we considered the normalized stress autocorrelation function:
where 〈〉 indicates average and S is the difference between the stress and mean stress. As shown in Fig. 6 d, the stress autocorrelation from our computational data fits well to an exponential decay, which supports our theoretical model (Eq. 7) that provides insight toward the fundamental temporal and spectral nature of intracellular motor-generated forces. These stress fluctuations play critical roles in the active redistribution of molecules inside cells (22), which is a crowded environment (57, 58) where important molecules such as ATP are potentially compartmentalized (59, 60).
Conclusions
The intracellular environment is driven by molecular motors that agitate the cytoskeletal network. The nature of particle motions inside the cell provides a readout of internal mechanical characteristics, including medium viscoelasticity and power output and temporal coherence of molecular motor activity. Our mathematical derivations provide a means to interpret tracer fluctuations and account for nonequilibrium features, enabling rich information content to be extracted from cells in more complex, physiologically mimicking 3D environments. We performed microrheology experiments and applied our theory toward studying breast cancer cell mechanics under pathological conditions and found that growth factor stimulation can profoundly alter intracellular mechanical behavior in cells with pathologically relevant altered isoforms of cytoskeletal modifying proteins such as Mena. Finally, our computational simulations indicate that enhanced actin nucleation due to EGF can lead to a reduction in intracellular prestress and diminished stress fluctuations due to molecular motors, consistent with our experimental data. The integrated theoretical, experimental, and computational platform demonstrated here provides a basis for elucidating fundamental intracellular mechanical properties of cells under physical-chemical modulation.
Author Contributions
M.M., M.H.Z., and R.D.K. designed the research. M.M. developed the theoretical model and performed the computational simulations. M.M., S.A., M.C.M., J.E.K., and A.B.-C. performed the experiments. M.M., F.S., M.H.Z., and R.D.K. analyzed the results. M.M., M.H.Z., and R.D.K. wrote the paper.
Acknowledgments
We acknowledge support from the National Cancer Institute under grant No. 5U01CA177799. M.M. is supported by National Cancer Institute of the National Institutes of Health National Research Service Award No. F32CA196149. A.B.-C. is supported by the Cancer Research Institute Irvington Postdoctoral Fellowship.
Editor: Paul Wiseman.
Footnotes
Three figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(17)30378-8.
Contributor Information
Michael Mak, Email: michael.mak@yale.edu.
Muhammad H. Zaman, Email: zaman@bu.edu.
Roger D. Kamm, Email: rdkamm@mit.edu.
Supporting Material
References
- 1.Kumar S., Weaver V.M. Mechanics, malignancy, and metastasis: the force journey of a tumor cell. Cancer Metastasis Rev. 2009;28:113–127. doi: 10.1007/s10555-008-9173-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Guck J., Schinkinger S., Bilby C. Optical deformability as an inherent cell marker for testing malignant transformation and metastatic competence. Biophys. J. 2005;88:3689–3698. doi: 10.1529/biophysj.104.045476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Swaminathan V., Mythreye K., Superfine R. Mechanical stiffness grades metastatic potential in patient tumor cells and in cancer cell lines. Cancer Res. 2011;71:5075–5080. doi: 10.1158/0008-5472.CAN-11-0247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kraning-Rush C.M., Califano J.P., Reinhart-King C.A. Cellular traction stresses increase with increasing metastatic potential. PLoS One. 2012;7:e32572. doi: 10.1371/journal.pone.0032572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Paszek M.J., Zahir N., Weaver V.M. Tensional homeostasis and the malignant phenotype. Cancer Cell. 2005;8:241–254. doi: 10.1016/j.ccr.2005.08.010. [DOI] [PubMed] [Google Scholar]
- 6.Lo C.-M., Wang H.-B., Wang Y.L. Cell movement is guided by the rigidity of the substrate. Biophys. J. 2000;79:144–152. doi: 10.1016/S0006-3495(00)76279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mak M., Reinhart-King C.A., Erickson D. Elucidating mechanical transition effects of invading cancer cells with a subnucleus-scaled microfluidic serial dimensional modulation device. Lab Chip. 2013;13:340–348. doi: 10.1039/c2lc41117b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mak M., Erickson D. Mechanical decision trees for investigating and modulating single-cell cancer invasion dynamics. Lab Chip. 2014;14:964–971. doi: 10.1039/c3lc51173a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mak M., Kamm R.D., Zaman M.H. Impact of dimensionality and network disruption on microrheology of cancer cells in 3D environments. PLOS Comput. Biol. 2014;10:e1003959. doi: 10.1371/journal.pcbi.1003959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Oakes P.W., Banerjee S., Gardel M.L. Geometry regulates traction stresses in adherent cells. Biophys. J. 2014;107:825–833. doi: 10.1016/j.bpj.2014.06.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yeung T., Georges P.C., Janmey P.A. Effects of substrate stiffness on cell morphology, cytoskeletal structure, and adhesion. Cell Motil. Cytoskeleton. 2005;60:24–34. doi: 10.1002/cm.20041. [DOI] [PubMed] [Google Scholar]
- 12.Bao G., Suresh S. Cell and molecular mechanics of biological materials. Nat. Mater. 2003;2:715–725. doi: 10.1038/nmat1001. [DOI] [PubMed] [Google Scholar]
- 13.Mak M., Erickson D. A serial micropipette microfluidic device with applications to cancer cell repeated deformation studies. Integr. Biol. 2013;5:1374–1384. doi: 10.1039/c3ib40128f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gossett D.R., Tse H.T.K., Di Carlo D. Hydrodynamic stretching of single cells for large population mechanical phenotyping. Proc. Natl. Acad. Sci. USA. 2012;109:7630–7635. doi: 10.1073/pnas.1200107109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Scarcelli G., Polacheck W.J., Yun S.H. Noncontact three-dimensional mapping of intracellular hydromechanical properties by Brillouin microscopy. Nat. Methods. 2015;12:1132–1134. doi: 10.1038/nmeth.3616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Squires T.M., Mason T.G. Fluid mechanics of microrheology. Annu. Rev. Fluid Mech. 2010;42:413–438. [Google Scholar]
- 17.Mak M., Zaman M.H., Kim T. Interplay of active processes modulates tension and drives phase transition in self-renewing, motor-driven cytoskeletal networks. Nat. Commun. 2016;7:10323. doi: 10.1038/ncomms10323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Fletcher D.A., Mullins R.D. Cell mechanics and the cytoskeleton. Nature. 2010;463:485–492. doi: 10.1038/nature08908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Crocker J.C., Valentine M.T., Weitz D.A. Two-point microrheology of inhomogeneous soft materials. Phys. Rev. Lett. 2000;85:888–891. doi: 10.1103/PhysRevLett.85.888. [DOI] [PubMed] [Google Scholar]
- 20.Dasgupta B.R., Tee S.-Y., Weitz D.A. Microrheology of polyethylene oxide using diffusing wave spectroscopy and single scattering. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2002;65:051505. doi: 10.1103/PhysRevE.65.051505. [DOI] [PubMed] [Google Scholar]
- 21.Baker E.L., Bonnecaze R.T., Zaman M.H. Extracellular matrix stiffness and architecture govern intracellular rheology in cancer. Biophys. J. 2009;97:1013–1021. doi: 10.1016/j.bpj.2009.05.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Guo M., Ehrlicher A.J., Weitz D.A. Probing the stochastic, motor-driven properties of the cytoplasm using force spectrum microscopy. Cell. 2014;158:822–832. doi: 10.1016/j.cell.2014.06.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mizuno D., Tardin C., Mackintosh F.C. Nonequilibrium mechanics of active cytoskeletal networks. Science. 2007;315:370–373. doi: 10.1126/science.1134404. [DOI] [PubMed] [Google Scholar]
- 24.Roussos E.T., Condeelis J.S., Patsialou A. Chemotaxis in cancer. Nat. Rev. Cancer. 2011;11:573–587. doi: 10.1038/nrc3078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Philippar U., Roussos E.T., Gertler F.B. A Mena invasion isoform potentiates EGF-induced carcinoma cell invasion and metastasis. Dev. Cell. 2008;15:813–828. doi: 10.1016/j.devcel.2008.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Wells A., Kassis J., Lauffenburger D.A. Growth factor-induced cell motility in tumor invasion. Acta Oncol. 2002;41:124–130. doi: 10.1080/028418602753669481. [DOI] [PubMed] [Google Scholar]
- 27.del Álamo J.C., Norwich G.N., Chien S. Anisotropic rheology and directional mechanotransduction in vascular endothelial cells. Proc. Natl. Acad. Sci. USA. 2008;105:15411–15416. doi: 10.1073/pnas.0804573105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lau A.W.C., Hoffman B.D., Lubensky T.C. Microrheology, stress fluctuations, and active behavior of living cells. Phys. Rev. Lett. 2003;91:198101. doi: 10.1103/PhysRevLett.91.198101. [DOI] [PubMed] [Google Scholar]
- 29.Fabry B., Maksym G.N., Fredberg J.J. Scaling the microrheology of living cells. Phys. Rev. Lett. 2001;87:148102. doi: 10.1103/PhysRevLett.87.148102. [DOI] [PubMed] [Google Scholar]
- 30.Levine A.J., MacKintosh F.C. The mechanics and fluctuation spectrum of active gels. J. Phys. Chem. B. 2009;113:3820–3830. doi: 10.1021/jp808192w. [DOI] [PubMed] [Google Scholar]
- 31.Vicente-Manzanares M., Ma X., Horwitz A.R. Non-muscle myosin II takes centre stage in cell adhesion and migration. Nat. Rev. Mol. Cell Biol. 2009;10:778–790. doi: 10.1038/nrm2786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tonino P., Simon M., Craig R. Mass determination of native smooth muscle myosin filaments by scanning transmission electron microscopy. J. Mol. Biol. 2002;318:999–1007. doi: 10.1016/S0022-2836(02)00191-2. [DOI] [PubMed] [Google Scholar]
- 33.Mason T.G., Weitz D.A. Optical measurements of frequency-dependent linear viscoelastic moduli of complex fluids. Phys. Rev. Lett. 1995;74:1250–1253. doi: 10.1103/PhysRevLett.74.1250. [DOI] [PubMed] [Google Scholar]
- 34.Amano M., Ito M., Kaibuchi K. Phosphorylation and activation of myosin by Rho-associated kinase (Rho-kinase) J. Biol. Chem. 1996;271:20246–20249. doi: 10.1074/jbc.271.34.20246. [DOI] [PubMed] [Google Scholar]
- 35.Bresnick A.R. Molecular mechanisms of nonmuscle myosin-II regulation. Curr. Opin. Cell Biol. 1999;11:26–33. doi: 10.1016/s0955-0674(99)80004-0. [DOI] [PubMed] [Google Scholar]
- 36.Rogers S.S., Waigh T.A., Lu J.R. Intracellular microrheology of motile Amoeba proteus. Biophys. J. 2008;94:3313–3322. doi: 10.1529/biophysj.107.123851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kole T.P., Tseng Y., Wirtz D. Intracellular mechanics of migrating fibroblasts. Mol. Biol. Cell. 2005;16:328–338. doi: 10.1091/mbc.E04-06-0485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gardel M.L., Nakamura F., Weitz D.A. Prestressed F-actin networks cross-linked by hinged filamins replicate mechanical properties of cells. Proc. Natl. Acad. Sci. USA. 2006;103:1762–1767. doi: 10.1073/pnas.0504777103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hoffman B.D., Massiera G., Crocker J.C. The consensus mechanics of cultured mammalian cells. Proc. Natl. Acad. Sci. USA. 2006;103:10259–10264. doi: 10.1073/pnas.0510348103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Martin A.C., Kaschube M., Wieschaus E.F. Pulsed contractions of an actin-myosin network drive apical constriction. Nature. 2009;457:495–499. doi: 10.1038/nature07522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Munro E., Nance J., Priess J.R. Cortical flows powered by asymmetrical contraction transport PAR proteins to establish and maintain anterior-posterior polarity in the early C. elegans embryo. Dev. Cell. 2004;7:413–424. doi: 10.1016/j.devcel.2004.08.001. [DOI] [PubMed] [Google Scholar]
- 42.Van Citters K.M., Hoffman B.D., Crocker J.C. The role of F-actin and myosin in epithelial cell rheology. Biophys. J. 2006;91:3946–3956. doi: 10.1529/biophysj.106.091264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Friedl P., Alexander S. Cancer invasion and the microenvironment: plasticity and reciprocity. Cell. 2011;147:992–1009. doi: 10.1016/j.cell.2011.11.016. [DOI] [PubMed] [Google Scholar]
- 44.Mak M., Spill F., Zaman M.H. Single-cell migration in complex microenvironments: mechanics and signaling dynamics. J. Biomech. Eng. 2016;138:021004. doi: 10.1115/1.4032188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Roussos E.T., Goswami S., Oktay M.H. Mena invasive (Mena(INV)) and Mena11a isoforms play distinct roles in breast cancer cell cohesion and association with TMEM. Clin. Exp. Metastasis. 2011;28:515–527. doi: 10.1007/s10585-011-9388-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Girard K.D., Kuo S.C., Robinson D.N. Dictyostelium myosin II mechanochemistry promotes active behavior of the cortex on long time scales. Proc. Natl. Acad. Sci. USA. 2006;103:2103–2108. doi: 10.1073/pnas.0508819103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Gertler F., Condeelis J. Metastasis: tumor cells becoming MENAcing. Trends Cell Biol. 2011;21:81–90. doi: 10.1016/j.tcb.2010.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Roussos E.T., Balsamo M., Condeelis J.S. Mena invasive (MenaINV) promotes multicellular streaming motility and transendothelial migration in a mouse model of breast cancer. J. Cell Sci. 2011;124:2120–2131. doi: 10.1242/jcs.086231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Hughes S.K., Oudin M.J., Gertler F.B. PTP1B-dependent regulation of receptor tyrosine kinase signaling by the actin-binding protein Mena. Mol. Biol. Cell. 2015;26:3867–3878. doi: 10.1091/mbc.E15-06-0442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kim T. Determinants of contractile forces generated in disorganized actomyosin bundles. Biomech. Model. Mechanobiol. 2014;14:345–355. doi: 10.1007/s10237-014-0608-2. [DOI] [PubMed] [Google Scholar]
- 51.Kim T., Hwang W., Kamm R.D. Computational analysis of a cross-linked actin-like network. Exp. Mech. 2009;49:91–104. [Google Scholar]
- 52.Kim T., Hwang W., Kamm R.D. Computational analysis of viscoelastic properties of crosslinked actin networks. PLoS Comput. Biol. 2009;5:e1000439. doi: 10.1371/journal.pcbi.1000439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Chan A.Y., Raft S., Condeelis J.S. EGF stimulates an increase in actin nucleation and filament number at the leading edge of the lamellipod in mammary adenocarcinoma cells. J. Cell Sci. 1998;111:199–211. doi: 10.1242/jcs.111.2.199. [DOI] [PubMed] [Google Scholar]
- 54.Chan A.Y., Bailly M., Condeelis J.S. Role of cofilin in epidermal growth factor-stimulated actin polymerization and lamellipod protrusion. J. Cell Biol. 2000;148:531–542. doi: 10.1083/jcb.148.3.531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Wang N., Tolić-Nørrelykke I.M., Stamenović D. Cell prestress. I. Stiffness and prestress are closely associated in adherent contractile cells. Am. J. Physiol. Cell Physiol. 2002;282:C606–C616. doi: 10.1152/ajpcell.00269.2001. [DOI] [PubMed] [Google Scholar]
- 56.Jorissen R.N., Walker F., Burgess A.W. Epidermal growth factor receptor: mechanisms of activation and signalling. Exp. Cell Res. 2003;284:31–53. doi: 10.1016/s0014-4827(02)00098-8. [DOI] [PubMed] [Google Scholar]
- 57.Dix J.A., Verkman A.S. Crowding effects on diffusion in solutions and cells. Annu. Rev. Biophys. 2008;37:247–263. doi: 10.1146/annurev.biophys.37.032807.125824. [DOI] [PubMed] [Google Scholar]
- 58.Ellis R.J. Macromolecular crowding: obvious but underappreciated. Trends Biochem. Sci. 2001;26:597–604. doi: 10.1016/s0968-0004(01)01938-7. [DOI] [PubMed] [Google Scholar]
- 59.Wallimann T., Wyss M., Eppenberger H.M. Intracellular compartmentation, structure and function of creatine kinase isoenzymes in tissues with high and fluctuating energy demands: the ‘phosphocreatine circuit’ for cellular energy homeostasis. Biochem. J. 1992;281:21–40. doi: 10.1042/bj2810021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Ovádi J., Saks V. On the origin of intracellular compartmentation and organized metabolic systems. Mol. Cell. Biochem. 2004;256–257:5–12. doi: 10.1023/b:mcbi.0000009855.14648.2c. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.