Protein sorting and membrane-mediated interactions

Abstract

Sorting of membrane proteins is of vital importance for living cells. Indeed, roughly one-third of a eukaryotic cell’s proteome consists of peripheral and transmembrane proteins. These need to be properly distributed and dynamically maintained at distinct locations in the compartmentalized cell, and one may wonder how proteins determine where, when, and how to travel to reach a specific organelle. While specific binary interactions between proteins have been invoked in explaining the trafficking and sorting processes, a more active role of lipids in this context has become visible in recent years. In particular, membrane-mediated interactions have been suggested to serve as a robust physicochemical mechanism to facilitate protein sorting. Here, we will review some recent insights into these aspects.

Introduction

Membranes are a universal feature of living systems. Not only do they form the outer envelope of cells, but they also structure the interior of eukaryotes into organelles (Alberts 2008). This compartmentalization allows for chemically distinct reaction vessels that exchange material (and information) only via well-regulated mechanisms. A prototypical mode of exchange between membrane-bound organelles is the formation of transport vesicles that emerge at a donor compartment and eventually fuse with an acceptor membrane, e.g., another organelle, to deliver transported cargo proteins (Alberts 2008).

Vesicle formation is typically mediated by peripheral membrane proteins that adsorb and dissociate to and from donor membranes. The most prominent coat proteins that promote formation of vesicles are clathrin, COPI, and COPII proteins (Kirchhausen 2000). These act at different instances of the secretory pathway (Fig. 1) and are believed to be specific for anterograde or retrograde modes of transport. In all cases, a small GTPase serves as a docking factor that recruits additional coat components after being firmly bound to the membrane of a specific organelle. For illustration, we consider the (dis)assembly of the COPII coat that is responsible for the formation of 50-nm vesicles at exit sites of the endoplasmic reticulum (ER) (Kirchhausen 2000): After nucleotide exchange, GTP-loaded Sar1p (Barlowe 1995) undergoes a conformational change that mediates a firm association with ER membranes via amphipathic structures. In its membrane-bound form, Sar1p recruits two heterodimeric coat complexes, Sec23/24p and Sec13/31p, that are responsible for interacting with cargo proteins and for bending the membrane during vesicle formation (Mancias and Goldberg 2005). Both complexes, however, also stimulate GTP hydrolysis by Sar1p and a subsequent dissociation of the COPII coat, hence rendering the whole coat unstable. Indeed, COPII proteins show a rapid turnover with only a few seconds of residence time on ER membranes (Forster et al. 2006). For COPI coat molecules, the residence time is somewhat longer (Elsner et al. 2003).

Fig. 1.

Nascent membrane proteins translocate into the endoplasmic reticulum (ER) after translation at ER-attached ribosomes. Upon diffusing within the ER and clearing the quality control for proper folding, proteins may enter the region of ER exit sites (ERES, indicated as dashed line). Here, COPII proteins form small vesicles that mediate anterograde transport towards the Golgi apparatus (via the ER-to-Golgi intermediate compartment, ERGIC). Proper loading with proteins increases the residence time of COPII proteins on ER membranes and therefore facilitates budding (cf. dissociation of the coat at the “empty” bud). Proteins arriving at the so-called cis-face of the Golgi will be sorted into populations that are also allowed to enter medial and trans cisternae of the Golgi (dark gray proteins). In contrast, another population (black) is destined for retrograde transport to the ER via COPI-coated vesicles. Eventually, proteins may enter the trans-Golgi network (TGN) from which they are finally sent to their final destination via clathrin-coated transport intermediates. Gray-shaded distributions below the organelles indicate nonuniform steady-state distributions of proteins that localize dynamically along the pathway. See also main text for more details

Concomitant to the emergence of a transport vesicle, cargo proteins, e.g., transmembrane enzymes and receptors or membrane-associated morphogens, need to be sorted into a pool that can/must enter the transport intermediate and a pool of proteins that are not allowed to leave the donor organelle. While for quite some time the making of a vesicle has been studied as a separate event from its loading with cargo, several studies have shown that the two are indeed coupled (Lanoix et al. 1999, 2001; Aridor and Traub 2002; Weiss and Nilsson 2003; Forster et al. 2006).

Given that about 30% of the eukaryotic proteome is composed of membrane proteins, sorting of membrane-resident cargo proteins during the formation of transport carriers is a formidable task. Lacking a cellular mastermind, all sorting events need to be based on fairly robust physicochemical principles that allow for a differential discrimination of the transport behavior of protein families in different organelles. Failure in protein sorting and transport often is linked to severe diseases, e.g., cystic fibrosis, or aberrations in embryonal development. At this point it is also worth noting that the cell’s endoplasmic reticulum is the only place in the cell where a consistent quality control for proper folding of membrane proteins is performed, e.g., within the calnexin/calreticulin cycle (Ellgaard and Helenius 2003). Hence, there is an immediate need for proper sorting right after translation of proteins and their concomitant translocation into the ER.

Here, we will review some basic physicochemical mechanisms that provide a robust and fundamental means for the sorting of membrane proteins. In particular, we will focus on collective phenomena that go beyond a simple specific interaction between a cargo protein and a coat molecule.

Fundamental structural and dynamic aspects of (bio)membranes

Some basic facts about membranes

Placing amphiphiles, e.g., lipids, into an aqueous solution perturbs the hydrogen bond network of water molecules. In an attempt to decrease the overall free energy of the system, amphiphiles aggregate into larger structures with a hydrophobic core and a hydrophilic surface if the concentration of amphiphiles is sufficiently high. Hydrophobic groups therefore are spatially separated from water. The associated loss in mixing entropy of the amphiphiles is over-compensated by the gain in entropy of water molecules, hence driving the system into a thermodynamically more favorable state. The emerging structure depends on the shape of the amphiphile (Boal 2002). Phospholipids form bilayers, for example, due to their almost cylindrical shape. Here, the lipids’ fatty acid chains are buried in the core of the bilayer while polar headgroups face the aqueous environment (cf. also Fig. 2).

Fig. 2.

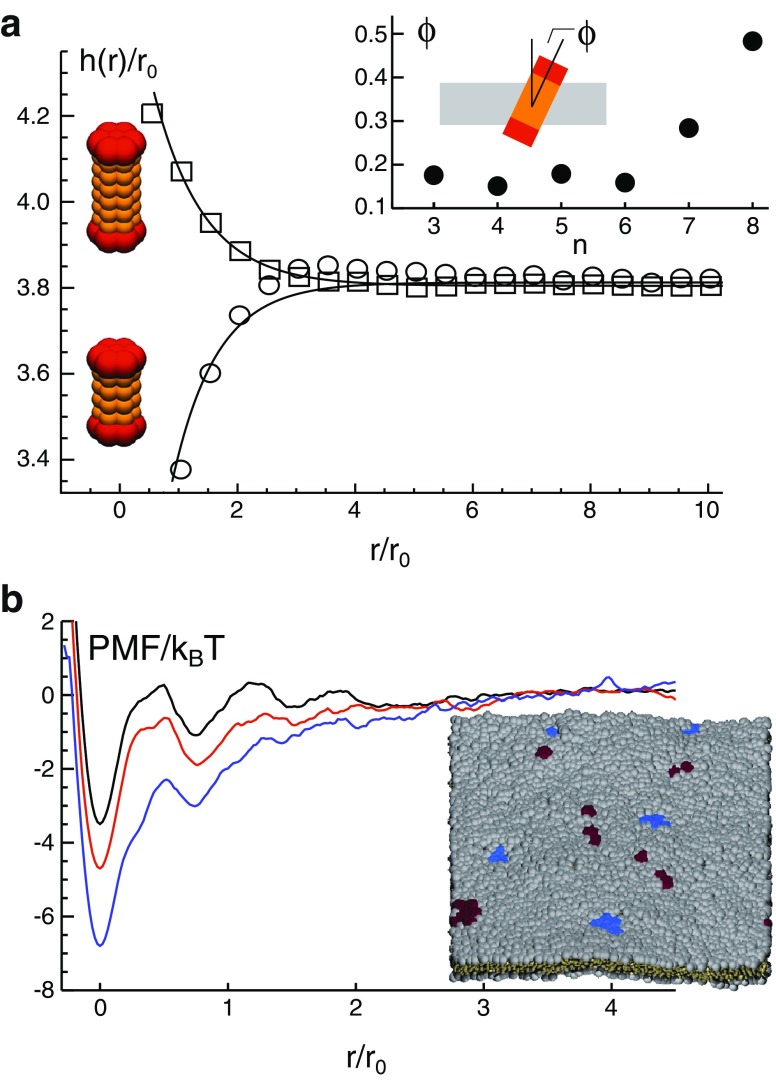
a A transmembrane protein will alter the thickness, h(r), in its vicinity. A thickening is observed for proteins with a positive mismatch, whereas a negative mismatch leads to a local thinning. For large distances, r, from the protein no perturbations are seen. Inset Protein tilting is observed when the length of the transmembrane domain, n, exceeds the maximum bilayer thickness that lipids can support in a fully stretched configuration. b The potential of mean force (PMF) between two embedded proteins shows a local minimum, hence indicating a bound state. With increasing mismatch, the minimum in the PMF becomes deeper (black to red to blue). For large distances, proteins do not interact, and the PMF is flat. Inset Snapshot of a simulated membrane (gray) with two protein species (red and blue) with grossly differing hydrophobic mismatches. Figure adapted from Schmidt et al. 2008, 2010

Typical lipid bilayers have a thickness of only 3–4 nm, and the thickness changes linearly with the length of the lipids’ acyl chains (Lewis and Engelman 1983). Albeit very thin, bilayers can extend as sheet-like structures over several hundred micrometers. Consequently, they can be viewed in a first approach as an infinitely thin two-dimensional plate that is characterized by a bending energy in the range of some 10k _B T (Mouritsen 2005). Hence, thermally driven undulations on several length scales are an important and observable feature of membranes (Nielsen et al. 2000). Another elastic constant, the area compression modulus, describes how much one can separate lipids in the bilayer from their neighbors without rupturing the sheet; typical values are in the range of 0.1 N/m (Mouritsen 2005).

Going beyond the mere elastic properties, phase transitions of lipids are also of fundamental importance for an understanding of membranes. Being situated in a bilayer, lipids can show several thermodynamic phases. A periodical order of lipids within the bilayer with all fatty acid chains being straight is typically observed for low temperatures (e.g., for DMPC below 24°C); the bilayer is then in the gel phase. For higher temperatures, the configuration of fatty acids and the lattice-like arrangement of lipids within the bilayer vanish, and the membrane is said to be in the fluid state. Here, the bilayer can indeed be regarded as a two-dimensional fluid and all lipids can freely diffuse with a fairly high mobility. Notably, lipid phases are characterized by a difference in their bilayer thickness that is defined, for example, via the average distance of opposing lipid headgroups: due to their higher ordering, gel phases are somewhat thicker and, more strikingly, the diffusive mobility of lipids is about two orders of magnitude lower than in the fluid phase.

Phases and domains on membranes

While lipid bilayers with a single lipid species provide a homogeneous two-dimensional fluid, using a mixture of different lipids can yield phase coexistence on a single membrane. A binary mixture of a low-melting and a high-melting lipid species can yield, for example, a coexistence of a gel and a fluid phase in a temperature range between the melting temperatures of the individual lipids. Hence, the membrane shows one or more gel domains that float in a “sea” of fluid lipids. Going beyond earlier indications for this coexistence that have been derived with NMR and differential scanning calorimetry, this coexistence has been visualized more recently by fluorescence microscopy (Fidorra et al. 2009).

When both lipids are in the fluid (liquid-disordered) phase, binary mixtures yield a homogeneous and uniformly fluorescent bilayer. Phase separation into a darker and brighter domain occurs below the gel (solid ordered)-fluid transition of the higher melting species. The brightness level of a particular domain depends on the fluorescent probe as well as the lipid mixture and therefore cannot be used to distinguish gel-like and fluid-like domains in general (Bagatolli et al. 1999; Bagatolli and Gratton 2000a, b). Gel-like domains can be identified, for example, with Prodan, a fluorescent probe whose partition coefficient into the gel phase is 35 times lower as compared to the fluid phase (Krasnowska et al. 1998). In contrast, Laurdan partitions uniformly into gel and fluid phases, but its emission is more red-shifted in the fluid phase. A major advantage of fluorescence microscopy on domain coexistence is the possibility to determine domain shapes that are determined by the interplay of line tension, lateral tension, bending stiffness, and curvature (Bagatolli and Gratton 2000b; Gordon et al. 2006). Gel domains in a surrounding fluid phase can be hexagonal, rhombic, six-cornered star, dumbbell, dendritic, and striped (Gordon et al. 2006). In all cases, gel domains move around in the fluid phases. Movement slows down with decreasing temperature and stops almost completely when the mixture enters the gel-gel coexistence regime.

Introducing a third component alters the fluidity of the existing domains without changing their shape (Korlach et al. 1999; Bagatolli et al. 1999), or it may even induce a new set of phases (Veatch and Keller 2005). Most ternary mixtures are a combination of a low melting lipid, a high melting lipid, and cholesterol. The low melting component is usually an unsaturated or a short chain saturated phosphatidylcholine (PC). The high melting component can be a long chain saturated PC, sphingomyelin, cerebroside, or ceramide (Longo and Blanchette 2010).

Phase behavior of ternary mixtures with cholesterol depends on the difference in melting transition temperatures of the high and low melting components. Liquid ordered–liquid disordered phase coexistence is observed for large differences in melting temperatures and liquid ordered–solid ordered coexistence for small differences (Korlach et al. 1999). In the latter case, addition of cholesterol gradually solidifies the liquid disordered phase into a liquid ordered one, which is evidenced by ever slower diffusion. Liquid-ordered phases appear dark with most fluorescent probes, and their circular shape is determined by minimizing the line tension along the boundary. Liquid-ordered domains diffuse rapidly and may eventually coalesce upon contact, into a single dark domain, except when being stabilized by curvature (Baumgart et al. 2003; Semrau et al. 2009).

The liquid-ordered phase is strongly enriched in the high-melting lipid and slightly enriched in cholesterol, whereas the liquid-disordered phase is enriched in the low-melting lipid. Even a small percentage of the low melting component is sufficient to induce liquid immiscibility (Veatch and Keller 2005). Similarly, small amounts of impurities in ternary mixtures, such as proteins or other lipids, can move the miscibility transition by several Kelvin. Impurities that partition equally into both liquid phases will lower the transition temperature while impurities that prefer one of the liquid phases will increase it (Veatch and Keller 2005).

Biological relevance was given to these artificial systems when coexistence of two liquid phases was observed on giant unilamellar vesicles (GUVs) made from pulmonary surfactant extracts (Bernardino de la Serna et al. 2009) and in giant plasma membrane vesicles (Veatch et al. 2008). For the latter example, it was shown that the line tension, which is responsible for the circular domain shape, vanishes at the critical point, and circular domains break up into critical fluctuations (Veatch et al. 2006). Even in the absence of macroscopic phase separation, a segregation into nanodomains may be observed (Heberle et al. 2010). The latter result is of particular importance in the cell-biological context, where domains of lipids and proteins (“rafts”) have been postulated (Simons and Ikonen 1997) on the basis of detergent-insoluble membrane fractions. So far, however, a more quantitative assessment with biophysical methods, e.g., with light nanoscopy (Eggeling et al. 2009), has revealed that these domains are well below the diffraction limit. In other words, despite being “more mosaic than fluid” (Engelman 2005), the membrane is a dynamically changing, inhomogeneous bilayer without stable entities. Thus, even though artificial systems clearly show macroscopic domain formation, a clear and unambiguous proof of the existence of (meta-)stable “rafts” in vivo is still missing.

Diffusion and reactions in membranes

Exploring an inhomogeneous membrane requires a protein to diffuse in a two-dimensional fluid. In fact, diffusion in a lipid bilayer is somewhat different from its counterpart in bulk solution. In three dimensions, the famous Einstein-Stokes equation, D = kB T/(6πηR), yields a simple expression for the diffusion coefficient D of a spherical particle (radius R) in a fluid of viscosity η. The situation is, however, much more complicated on membranes due to the Stokes paradox in two-dimensional hydrodynamics. Derivation of a closed expression of the drag coefficient therefore is impossible. A way out was devised by Saffman and Delbruck (Saffman and Delbruck 1975). Considering the fluid adjacent to the membrane (i.e., above and below the bilayer), one obtains via perturbation theory for small radii:

1

Here, h is the thickness of the membrane, R is the in-plane radius of the diffusing protein, γ ≈ 0.5772 is Euler’s constant, and η _m, η _c are the effective viscosities of the membrane and the adjacent fluid, respectively. The viscosities are effective only since the derivation of Eq. (1) relies on a cylindrical inclusion in a structureless two dimensional fluid, i.e., the protein is assumed to have a circular transmembrane shape, and no residues that reach out of the plane of the bilayer are considered. This is clearly an over-simplification for real world data, yet all corrections (e.g., a finite penetration depth into the bilayer as well as the friction of soluble parts of the protein imposed by other proteins) can be mapped into the parameters η _m and η _c.

For radii beyond a critical value, R _c > hη _m/η _c ≈ 100 nm, the perturbative expression in Eq. (1) breaks down, and additional terms have to be taken into account (Hughes et al. 1981). Only in the limit of very large radii, where the particle mimics an edgewise motion of a thin disk, is a simple scaling, D ∼ 1/R, obtained.

Another particularity of two-dimensional systems, e.g., membranes, is the failure of standard assumptions of kinetic reactions, e.g., the law of mass action. While in three dimensions, reaction constants, including the diffusion constant, can be derived easily, this approach fails in two dimensions as the trajectory of Brownian motion represents a compact random walk. In general, the kinetics of a diffusion-limited reaction can be classified as either classical or geometry-controlled (Benichou et al. 2010). The distinction between these two regimes is given by the sampling behavior of the reactants’ diffusion process: if the fractal dimension of the particle trajectories is lower than the fractal dimension of the support, the exploration is non-compact. This is fulfilled for Brownian motion in three but not in two dimensions. Indeed, compact random walks have been shown to lead to time-dependent reaction coefficients and reactant segregation (Kopelman 1988; Hellmann et al. 2011). Hence, diffusion-limited reactions on membranes may already yield a patterning by a mere effect of dimensionality.

Protein sorting and membrane-mediated interactions

If protein distributions are inspected along the secretory pathway (cf. Fig. 1), many resident proteins show dynamically stabilized, nonuniform steady-state patterns (Nilsson et al. 1993a; Rabouille et al. 1995; Rottger et al. 1998). Some proteins, e.g., the p24 family, cycle between the ER and the cis-face of the Golgi apparatus, whereas Golgi resident enzymes such as MannII and GalT show peaked distributions in the medial and trans cisternae, respectively. Maintaining these distributions while passing a high number of proteins that are destined for locations beyond the Golgi apparatus is a complex logistical problem.

Traditionally, protein sorting was linked to the interaction of transmembrane proteins with specific coat molecules that are responsible for the formation of transport intermediates (cf. the “Introduction” section). In particular, two cytoplasmic motifs of transmembrane proteins have been identified that give rise to an (in)direct interaction with the COPI coat. The first is the famous KDEL motif (Munro and Pelham 1987) that leads to retrieval of proteins via the transmembrane KDEL receptor. The second, more differential retrieval signal is a cytoplasmic di-lysine motif (KKXX) that also mediates retrograde transport of proteins via direct interactions with COPI (Nilsson et al. 1989).

However, several proteins, e.g., members of the p24 family, have been shown to be retrieved although they lack any known motif (Fullekrug et al. 1999). To explain such findings, two models have been hypothesized: Bretscher and Munro formulated the “membrane thickness” hypothesis, which links the length of the transmembrane domain to a (putative) gradient of membrane thickness along the secretory pathway (Bretscher and Munro 1993). Indeed, recent data have supported the idea of a thickness gradient (Mitra et al. 2004) and a direct link of the transmembrane length with localization properties (Sharpe et al. 2010). An alternative model, the “kin recognition hypothesis,” was formulated by Nilsson et al. at about the same time (Nilsson et al. 1993b). This model is capable of also capturing retrieval without sorting motifs due to a transient oligomerization of proteins of the same “kin” where only some members may carry a retrieval motif. The “kin” is hence defined via a common localization property. Indeed, both models imply a sorting effect due to properties of the transmembrane domain, and both have been supported by experimental data (Munro 1995).

Beyond a pairwise attractive or repulsive interaction of proteins, one may also think about collective phenomena that drive sorting events. A hydrophobic mismatching of membrane proteins with their surrounding bilayer, for instance, is a possible and relevant driving force for such collective phenomena. A protein is said to have a positive/negative mismatch with the surrounding bilayer if the hydrophilic transmembrane domain is longer/shorter than the unperturbed thickness of the lipid bilayer. With a hydrophobic mismatch, a protein certainly can “read” out thickness variations in a continuous membrane, e.g., within the ER. Driven by diffusion, the protein will seek that part of the membrane that provides the least mismatch. This feature basically underlies the above-mentioned “membrane thickness model” (Bretscher and Munro 1993).

Yet, proteins do not only explore a given membrane environment, they also actively perturb it. Several simulation studies (Venturoli et al. 2005; de Meyer et al. 2008; Schmidt et al. 2008) have quantified local bilayer deformations due to embedded transmembrane proteins. Around the protein a local increase (or decrease, depending on the type of mismatch) of the bilayer thickness is observed (Fig. 2a) that is accompanied by an ordering of lipids. If a positive mismatch grows too strong to be balanced by an altered configuration of lipids, the protein shows a strong tilt with respect to the bilayer normal. Hence, proteins induce a lipid ordering at their surface that reduces the system’s entropy. Similarly to the formation of micelles by lipids in water, one may expect here that the overall entropy of the system increases if the interface between proteins and lipids is minimized.

Indeed, the entropy-driven formation of clusters has been observed, i.e., attractive membrane-mediated interactions can promote an oligomerization of proteins (Schmidt et al. 2008). The interaction between two proteins can be quantified via the potential of mean force (PMF). The PMF is given by the negative logarithm of the proteins’ distance distribution and can hence report not only on conservative pairwise attractive forces but also on collective phenomena, e.g., depletion forces. The PMFs obtained for proteins with hydrophobic mismatching show a deep minimum at short inter-protein distances that indicates a bound state (Fig. 2b). For large distances the potential becomes flat and featureless, i.e., proteins do not interact any more. The depth of the PMF minimum strongly depends on the strength of the mismatch. Therefore, binding energies ΔE = min(PMF) − PMF(r→ ∞) in the range of some 10k _B T can emerge. The stability of the bound state can be extracted via the mean first passage time, τ, from the PMF’s minimum to a distance with no interaction. It scales in lowest order with the Boltzmann factor of the binding energy, i.e., τ ∼ exp(ΔE/k _B T). Thus, mismatch-induced protein clusters can be very long-lived entities.

Interestingly, proteins with a very different mismatch segregate into homo-oligomers (Fig. 2b), i.e., a basic sorting scheme according to the type of mismatching is observed (Schmidt et al. 2010). In contrast, proteins with a similar mismatch form hetero-oligomers. It is tempting to relate this phenomenon to the above-mentioned kin recognition hypothesis (see also next section). The mismatch alone, however, is only a very rough sorting mechanism. An improvement can be achieved when considering that a number of transmembrane proteins are also acylated. An additional lipid anchor at a transmembrane protein sounds odd at first, since palmitoylations and similar modifications are usually used to facilitate a membrane association of soluble proteins. It was shown by simulations, however, that acylated transmembrane proteins display a different tilting with respect to the bilayer normal as well as an altered partitioning behavior that also affects the ability to form mismatch-induced clusters (Morozova and Weiss 2010). These simulation results compare favorably to experimental observations on the trafficking of the transmembrane protein LRP6 (Abrami et al. 2008): While the native protein travels along the secretory pathway, mutants that had a shorter transmembrane domain or lacked the palmitoylation were retained in the ER. In contrast, mutants with a shortened transmembrane domain and a lack of palmitoylation trafficked normally. Hence, sorting by hydrophobic mismatching can be fine-tuned by exploiting a reversible acylation, e.g., a palmitoylation.

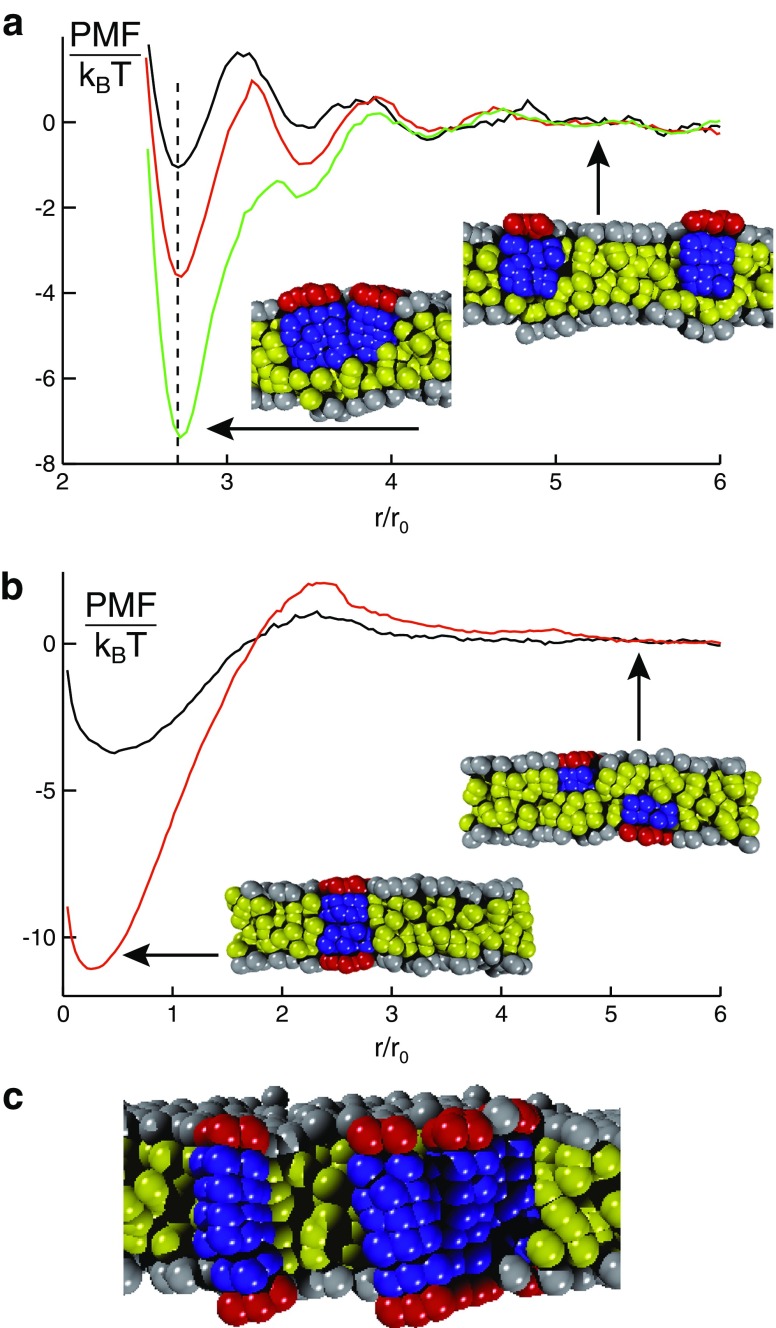
Given that peripheral membrane proteins also travel along the secretory pathway, one may ask whether these membrane proteins can also benefit from membrane-mediated interactions. Similarly to transmembrane proteins, peripheral proteins also perturb the lipid bilayer, which induces membrane-mediated interactions (Morozova et al. 2011). Due to the reduced penetration depth, it is mainly the host leaflet of the bilayer that is affected, but also the opposing leaflet may be perturbed. As a consequence of these perturbations, again an entropy-driven attractive net interaction emerges that leads to an in-plane oligomerization within the host leaflet (Fig. 3a) or even to a cross-leaflet dimerization (Fig. 3b). The associated binding energies are again in the range of some 10k _B T or even more, depending on the radius and penetration depth of the involved proteins. Interestingly, cross-leaflet dimers, i.e., transient effective transmembrane proteins, can also form larger assemblies (Fig. 3c). This observation challenges the common view that transmembrane proteins are mandatory for signal transduction across a membrane. Indeed, one may envisage a scenario in which a peripheral membrane protein undergoes a conformational change upon binding a ligand. This event promotes, via altering the protein’s effective radius, the formation of a cross-leaflet dimer with an appropriate peripheral protein in the opposing leaflet. These effective transmembrane proteins can now act in very much the same way as “normal” transmembrane proteins in typical signaling cascades. While being an attractive model, this scenario is so far only a prediction that requires solid experimental tests.

Fig. 3.

a PMF for two peripheral membrane proteins in the same leaflet of a homogeneous lipid bilayer. While proteins do not interact at large distances, a minimum in the PMF emerges for small separations, hence indicating a bound state. b PMF for peripheral membrane proteins that reside in opposing leaflets of a homogeneous lipid bilayer. Proteins can form cross-leaflet dimers with a configuration and binding energy that depends on the penetration depths and radii of the involved proteins. c Snapshot of a transient oligomer of cross-leaflet dimers that mimics an assembly of transmembrane proteins. Figure adapted from Morozova et al. 2011

A model for traffic along the secretory pathway

Following up on the above-mentioned hypotheses on protein sorting in the secretory pathway (membrane thickness and kin recognition), one may wonder if and to what extent cells can utilize membrane-mediated interactions and (transient) oligomerization events for regulating protein traffic along the secretory pathway. A challenge is here that not only a diffusive partitioning within a continuous membrane is needed, but a coupling of vesicle-mediated transport and membrane probing is required.

Let us assume, for simplicity, that a nascent transmembrane protein experiences a positive mismatch in the ER after having passed the quality control for proper folding (Fig. 4). Diffusing in the ER, it may localize to a subdomain of the membrane from which it cannot be exported (Ronchi et al. 2008). Alternatively, it will enter, at least transiently, an exit site of the ER from which it may be exported via an emerging COPII vesicle (Fig. 1). Indeed, ER exit sites are frequent 300-nm functional domains in the ER that assume a quasi-crystalline arrangement (Heinzer et al. 2008), i.e., proteins will enter these regions with a high probability unless hindered from doing so. Owing to the mismatch, the protein will have oligomerized (which does not affect the diffusional mobility too much, cf. discussion on the Saffman-Delbruck result above) and now it can down-modulate the local turnover rate of COPII proteins (Forster et al. 2006). Being longer on the membrane, COPII proteins will hence form a vesicle at the locus of the protein cluster that wants to be transported (Fig. 4).

Fig. 4.

A membrane protein that experiences a positive mismatch (lower panel), e.g., in the ER, will oligomerize and down-modulate the respective coat machinery, e.g., COPII. The emerging vesicle transports the protein cluster to a new compartment (middle), e.g., the cis-cisterna of the Golgi apparatus. Here, a slightly thicker membrane may extinguish cluster formation due to a lack of hydrophobic mismatching. As a consequence, proteins rarely leave this compartment (indicated by thinner arrows). If the protein experiences a positive mismatch (e.g., during cisternal maturation or after having left the best-matching bilayer by mistake), the protein will again start to form clusters that will stabilize coat molecules at this locus (e.g., COPI at this time). This facilitates a retrieval to the better matching bilayer

After pinch-off, the vesicle will carry the protein cluster to another membrane, e.g., the cis-cisterna of the Golgi apparatus. Here, the protein cluster dissolves as the membrane environment may provide a vanishing mismatch. Hence, the protein will retain only a very low ability for traveling away. As a function of time, the membrane may grow thicker due to the massive lipid metabolism at the Golgi apparatus. Alternatively, the protein may escape by erroneously entering another vesicle. In any case, it may end up in a compartment in which it experiences a negative mismatch, say in a medial cisterna of the Golgi apparatus. As before, oligomerization sets in and by down-modulating the turnover of, say, COPI proteins, the protein cluster will again promote the formation of a vesicle at its location. This vesicle may now return the protein to the better matching (sub)organelle. Analogously to a diffusive partitioning on inhomogeneous membranes, this search process is also dynamic and stochastic, leading to an increased residence time in the compartment with the best-matching membrane due to modulation of the transport rates (cf. arrows of different thickness in Fig. 4).

The outlined trafficking scenario represents a synthesis of the two earlier models (bilayer thickness and kin recognition) in that membrane thickness is the important driving force for the localization, yet with a transient oligomerization of proteins with similar transmembrane domains. Since both models have found experimental support, there is quite some evidence that the combined hypothesis is a realistic scenario to describe the basic physicochemical mechanism of protein sorting in the early secretory pathway.