Abstract
Upon biological self-assembly, the number of accessible translational configurations of water in the system increases considerably, leading to a large gain in water entropy. It is important to calculate the solvation entropy of a biomolecule with a prescribed structure by accounting for the change in water–water correlations caused by solute insertion. Modeling water as a dielectric continuum is not capable of capturing the physical essence of the water entropy effect. As a reliable tool, we propose a hybrid of the angle-dependent integral equation theory combined with a multipolar water model and a morphometric approach. Using our methods wherein the water entropy effect is treated as the key factor, we can elucidate a variety of processes such as protein folding, cold, pressure, and heat denaturating of a protein, molecular recognition, ordered association of proteins such as amyloid fibril formation, and functioning of ATP-driven proteins.
Keywords: Solvation entropy, Biological self-assembly, Protein folding, Protein denaturation, Molecular recognition, ATP-driven protein, Integral equation theory, Morphometric approach
Introduction
The structures formed by biological self-assembly are collapsed by the application of high pressures (Yoshidome et al. 2009). Typical examples are denaturation of a protein, dissociation of filamentous actin (F-actin) into actin monomers, and destruction of amyloid fibril. At low temperatures, the power of forming the structures becomes considerably weaker (Yoshidome and Kinoshita 2012). For example, a protein is unfolded and the binding of myosin to F-actin is weakened. This weakening is also relevant to the following: upon temperature lowering, the solubility of methane increases, the critical micelle concentration becomes higher, and the average size of micelles for nonionic amphiphilic molecules becomes smaller. These phenomena are suggestive that there are common features of biological self-assembly, and a certain physical factor universally plays a dominant role as the driving force. What is this physical factor?
It is often claimed that the formation of intramolecular or intermolecular hydrogen bonds by biomolecules derive biological self-assembly. However, they accompany the break of biomolecule–water hydrogen bonds. The energy decrease and increase arising from the formation and break, respectively, are somewhat compensating. The electrostatic attractive interaction between oppositely charged groups of a biomolecule or biomolecules is also considered to be important. Though it is quite strong and long ranged in vacuum, it becomes orders of magnitude weaker and shorter ranged in aqueous solution (∼0.15 M-NaCl solution in biological systems) due to the screening effects by water molecules and counter-ions (Kinoshita and Harano 2005).
In the present article, we review the results of our studies and point out that the physical factor mentioned above is the entropic effect originating from the translational displacement of water molecules which coexist with biomolecules in the system (Kinoshita 2009a). In particular, the gain in the translational entropy of water due to the biomolecule–water–water triplet and higher order correlations (i.e., the reduction in water crowding) is the most important. The principal topic is protein folding and unfolding, but the qualitative aspects of the conclusions are also applicable to such processes as molecular recognition and association of proteins. The water entropy effect plays imperative roles even in the functioning of ATP-driven proteins such as unidirectional movement of myosin along F-actin (Amano et al. 2010) and protein flux through a chaperonin system (Amano et al. 2011). As an important example, we revisit our rotational mechanism for the γ-subunit in F1-ATPase.
Protein folding in aqueous solution under physiological condition
Protein folding occurs with the system pressure and volume kept almost unchanged (Yoshidome et al. 2008). Hence, we consider the constant volume condition. Let ΔA (A is a thermodynamic quantity) be “A of the native state” minus “A of the unfolded state”. The free energy change for the system upon protein folding ΔF can be expressed as
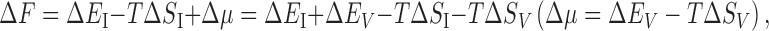 |
1 |
where E I and S I denote the protein intramolecular energy and entropy, respectively, and E V, S V, and μ denote the solvation energy, entropy, and free energy, respectively, and T is the absolute temperature (μ = E V −TS V). Δμ takes a large, positive value: In this sense, water destabilizes the native state. This is because ΔE V is positive and very large. Conversely, ΔE I is negative and very large. ΔE V and ΔE I are somewhat compensating, but “ΔE V + ΔE I” takes a positive value. It is apparent that ΔS I is negative because the folding accompanies a conformational entropy loss. For ΔF to become negative, a factor surpassing “ΔE I + ΔE V−TΔS I” is required: this is ΔS V which takes a large, positive value. Protein folding is driven by a large water entropy gain. Many of the donors and acceptors for intramolecular hydrogen bonds (e.g., N and O, respectively) are buried in the interior due to the water entropy effect after the break of hydrogen bonds with water molecules (e.g., CO–W and NH–W; W denotes a water molecule). There is no problem if intramolecular hydrogen bonds (e.g., CO–HN) are formed. However, such formation is not always realized, giving rise to a positive value of “ΔE V + ΔE I”.
The validity of the above picture of protein folding has been supported by the novel experiment by Terazima et al. in which apoplastocyanin (apoPC) is made to fold at 298 K (Yoshidome et al. 2008). The folding accompanies the significantly large increase in enthalpy (corresponding to “ΔE V + ΔE I”), ∼870 kJ/mol. In conventional experiments, a protein is denatured at a high temperature and the changes in enthalpy and specific heat upon thermal denaturation are measured. Assuming that the specific heat change is constant against T, they estimate the changes in enthalpy and entropy upon protein folding of the system at 298 K, ΔH 298 and ΔS 298, using the thermodynamic equations. However, the specific heat change upon the denaturation, which is positive, increases to a considerably large extent as T becomes lower. The conventional assumption tends to estimate that both ΔH 298 and ΔS 298 are negative (Kinoshita 2009b). The experiment by Terazima et al. is free from this type of problem.
Entropic excluded-volume effect
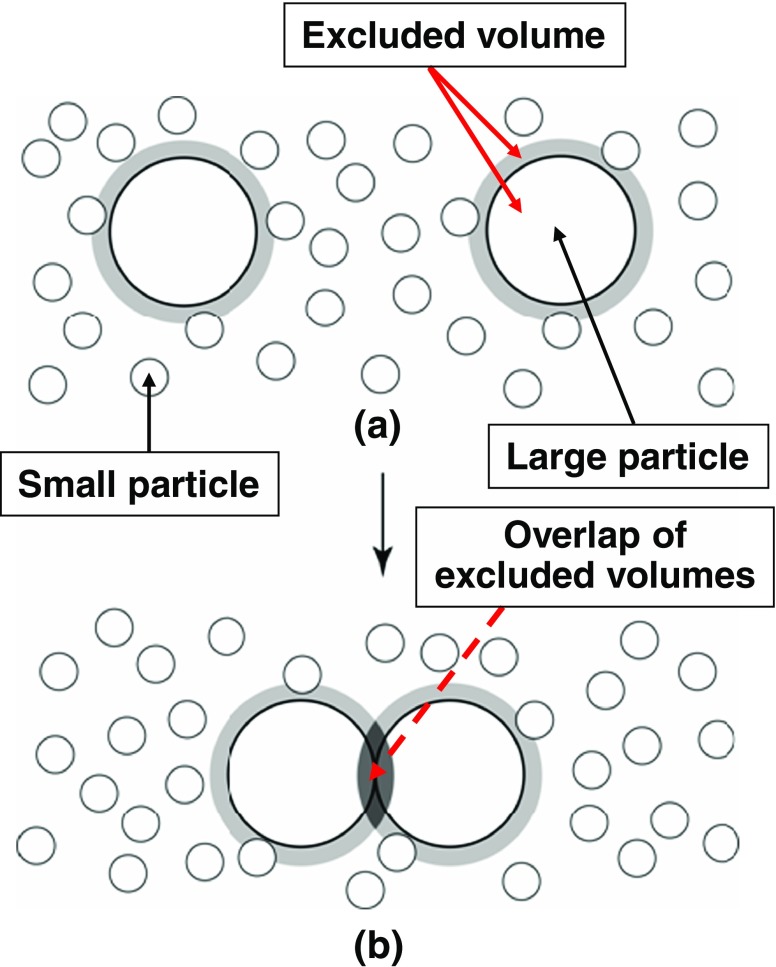
Why does a large gain in water entropy occur upon protein folding? To answer this question, we explain the excluded-volume effect (Kinoshita 2009a) using simplified geometries. As shown in Fig. 1a, the presence of a large particle, a solute molecule, in small particles forming the solvent generates a space from which the centers of small particles are excluded. Upon the contact of a pair of large particles illustrated in Fig. 1b, the two excluded spaces overlap, and the total volume available to the translational displacement of small particles increases by the volume of this overlapped space. A denser layer of small particles is formed near a large particle (see “Importance of solute–solvent many-body correlations”). Upon contact, part of the small particles within the dense layers is released to the bulk, with the result that the system pressure remains roughly unchanged. The contact leads to an increase in the number of accessible translational configurations of small particles and to a resultant gain of the translational entropy of small particles. The large particles are driven to contact each other. Since this effect is induced even when all of the particles are hard bodies with no soft interaction potentials (all of the allowed system configurations share the same energy and the system behavior becomes purely entropic in origin), it is called the “entropic excluded-volume effect”. This effect is dependent not only on the excluded volume but also on the area and curvature of the surface that is accessible to the centers of small particles. It is also influenced by the structure of small particles confined by large particles. An elaborate statistical–mechanical theory (e.g., an integral equation theory) shows that an interaction, which reaches several times the diameter of small particles, is entropically induced between large particles (Kinoshita 2009a).
Fig. 1.
Contact of a pair of large particles in small particles. When the small particles are spheres with diameter d S and the large particle is a sphere with diameter d L, the excluded space (the space occupied by the large sphere itself plus the space shown in gray) is a sphere with diameter “d S + d L”. Upon the contact, the two excluded spaces overlap (the overlapped space is marked in black)
The entropic excluded-volume effect plays important roles in a colloidal suspension (Kinoshita 2006). When colloidal particles with highly charged surfaces (e.g., polystyrene microspheres) are immersed in salt solution with appropriately low salt concentration (e.g., ∼0.01 M NaCl), due to the screening of the surface charges, the interaction between colloidal particles can be described by nearly hard-sphere potential in a sea of salt solution; water molecules need not explicitly be treated. The hard-sphere diameter is roughly equal to the diameter of the particle itself plus the Debye length, that is much larger than several times the molecular diameter of water. For a colloidal suspension containing these particles of significantly different sizes, where the number density of larger particles is much lower than that of smaller particles, we can take the view that the larger particles generate excluded volumes for the smaller particles. The salt solution can be regarded as an inert background. In biological systems, however, this simple treatment is no longer acceptable for the following reason. A biomolecule such as a protein is characterized by the heterogeneity that it comprises nonpolar groups as well as positively and negatively charged groups. Moreover, the charges are screened by water molecules and counter-ions. The concentration of NaCl is ∼0.15 M, which is over an order of magnitude higher than ∼0.01 M. Consequently, biomolecules or their portions can approach each other up to a separation that is smaller than several times the diameter of water molecules. They can even contact each other. The presence of water molecules must explicitly be taken into account. Water molecules and biomolecules as solutes correspond to “small particles” and “large particles”, respectively. In fact, we have shown that the water entropy effect is usually dominant in biological systems (Kinoshita 2009a).
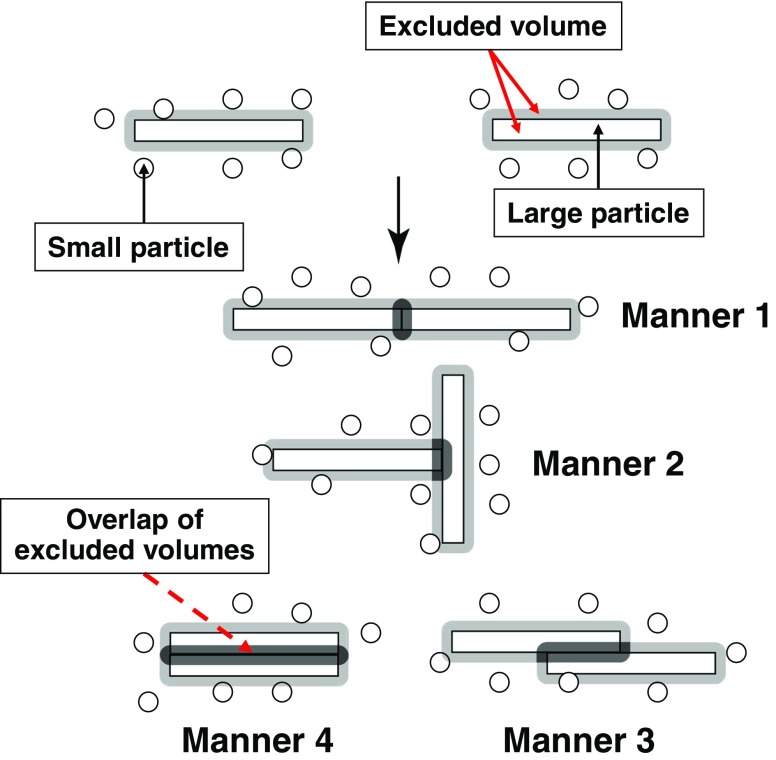
When the shape of solutes is highly aspherical (e.g., long cylinders, thin discs, etc.), the entropic excluded-volume effect exhibits very interesting behavior. For example, among the four contact manners of solutes shown in Fig. 2, manner 4 maximizes the volume of the overlapped space and the entropic gain of solvent molecules. Hence, the solvent forces the solutes to contact each other in manner 4. Thus, regular or orderly contacts or association of solutes in specific manners are driven by the solvent entropy effect (Kinoshita 2004). The translational displacement of solutes, which is also important, favors the dispersion of solutes. This is the effect of entropy of mixing which competes with the excluded-volume effect. If the solute concentration is low, the former dominates. If it becomes sufficiently high, the latter becomes substantially larger.
Fig. 2.
Four contact manners of large particles, solutes, with high asphericity (e.g., long cylinders, thin discs, etc.) immersed in small particles forming the solvent. Manner 4 maximizes the volume of the overlapped space (the space marked in black)
Thermodynamics of apoplastocyanin folding
The formation of a helical structure by a portion of the backbone occurs in the α-helix (Fig. 3a) and a lateral contact of portions of the backbone occurs in the β-sheet (Fig. 3b), leading to a significantly large decrease in the total excluded volume for water molecules. At the same time, the intramolecular hydrogen bonds, which compensate for the break of hydrogen bonds with water molecules, can also be assured. Thus, these two secondary structures are very advantageous units. When side chains are closely packed (Fig. 3c), the decrease in the total excluded volume is quite large. Protein folding can be characterized by the formation of as much α-helix and β-sheet as possible and the close packing of the backbone and side chains with a variety of geometric features (Yasuda et al. 2010). Using a tube model mimicking the backbone or its portion, some other groups (Snir and Kamien 2007; Hansen-Goos et al. 2007; Poletto et al. 2008) have examined which of the α-helix and the β-sheet is more stabilized when the density and molecular diameter of the solvent are varied as important parameters. The solvent entropy effect is treated as the key factor. However, the effect of the side-chain packing specific to their geometric features cannot be argued with the tube model. The adoption of the polyatomic structure is crucial in the argument.
Fig. 3.

Crucial importance of water entropy effect in protein folding. a Formation of a helical structure by a portion of the backbone occurring in the α-helix. b Lateral contact of portions of the backbone occurring in the β-sheet. c Close packing of side chains
The experimental study by Terazima et al. for apoPC (with 99 residues) folding and our theoretical analysis have shown that the water entropy gain upon folding reaches ∼670k B (k B is the Boltzmann constant). The analysis for apoPC folding has been performed using the hybrid of an integral equation theory and the morphometric approach which is described in the next section. The water entropy gain upon protein folding is given by “S V of the native state” minus “S V of the unfolded state”. The results obtained can be summarized as follows (Yoshidome et al. 2008): the large gain in water entropy is ascribed primarily to the reduction in the excluded volume generated by the protein; the water entropy gain, which is attributable to the change in the surface properties (e.g., the ASA), makes no essential contributions to the net gain; and the rotational entropy gain of water is only ∼5 % of the net gain. The large gain in water entropy cannot be elucidated by the classical picture that the amount of water structuring near nonpolar groups decreases upon protein folding.
In the original Asakura–Oosawa (AO) theory (Asakura and Oosawa 1958), “large particles” and “small particles” corresponded to colloidal particles and macromolecules, respectively, and the solvent was regarded as inert background (Ellis and Minton 2003 also treat the solvent as inert background). We can apply the AO theory to protein folding by considering water molecules to be the small particles. Since the AO theory considers only the excluded-volume term of the protein–water pair correlation component (see “Importance of solute–solvent many-body correlations”), the water entropy gain is simply given by k B ρ S|ΔV ex| where ρ S is the number density of bulk water and ΔV ex (<0) is the change in the excluded volume generated by the protein. According to this equation, the water entropy gain upon apoPC folding is only ∼180k B, indicating an unacceptable underestimation. (The AO mechanism has been rederived by Vrij 1976 using a different approach.)
Hybrid of integral equation theory and morphometric approach
The solvation entropy S V (<0), a loss of solvent entropy upon solute insertion, is an essential quantity in elucidating the biological self-assembly. Any theory in which water is regarded as a dielectric continuum is not capable of accounting for the entropic excluded-volume effect. It is critical to treat water as a system consisting of “particles with finite sizes”. In physical analyses focused on the effect of the translational displacement of water molecules, water can often be modeled as hard spheres (Harano and Kinoshita 2005; Kinoshita 2009a). However, when the temperature dependence of the effect is crucial as in the case of cold denaturation of a protein (Yoshidome and Kinoshita 2012) or when a number of rather compact structures are compared in terms of the stability in aqueous solution (Yasuda et al. 2011, 2012), a suitable molecular model must be employed for water. A problem in such cases is that the calculation of S V for a large, polyatomic solute like a protein is a formidable task. We have solved this problem by combining an integral equation theory with the morphometric approach (MA). S V is fairly insensitive to the solute–water interaction potential while E V and μ are not (Yoshidome et al. 2008, 2012). Therefore, a protein can be modeled as a set of fused hard spheres just for calculating its S V.
The idea of the MA is to express S V by the linear combination of only four geometric measures of a solute molecule (Roth et al. 2006):
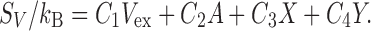 |
2 |
Here, Eq. (2) is referred to as the morphometric form, V ex is the excluded volume, A is the solvent-accessible surface area, and X and Y are the integrated mean and Gaussian curvatures of the accessible surface, respectively. The solvent-accessible surface is the surface that is accessible to the centers of solvent molecules. S V is influenced not only by V ex but also by the other three geometric measures. In the MA, the solute shape enters S V only via the four geometric measures. Therefore, the four coefficients (C 1−C 4) can be determined in simple geometries. They are calculated from the values of S V for hard-sphere solutes with various diameters immersed in the solvent. (The morphometric form can also be applied to μ/(k B T) of a solute in hard-sphere solvent and μ/(k B T) of a nonpolar solute in water.)
The procedure of calculating S V of a protein with a prescribed structure comprises the following four steps (Mishima et al. 2012).
S V of a hard-sphere solute with diameter d U is calculated. The values of S V are prepared for sufficiently many different values of d U (e.g., 0 ≤ d U ≤ 30d S; d S is the diameter of solvent molecules). In principle, any statistical–mechanical theory or computer simulation can be employed for this calculation. We use the radial-symmetric integral equation theory and the angle-dependent integral equation theory (ADIET) for simple-fluid solvent (e.g., hard-sphere solvent) and for water with a molecular model, respectively. It is important to include sufficiently small values of d U especially for water (Yoshidome and Kinoshita 2012).
The four coefficients are determined by the least square fitting applied to the following equation for hard-sphere solutes (i.e., Eq. (2) applied to hard-sphere solutes):
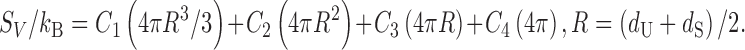 |
3 |
-
(3)
The four geometric measures of a protein (V ex, A, X, and Y) with a prescribed structure are calculated. The x-y-z coordinates of the protein atoms are used as part of the input data to account for the polyatomic structure at the atomic level. The diameter of each atom is set at the sigma value of the Lennard-Jones potential parameters.
-
(4)
S V of a protein with a prescribed structure is obtained from Eq. (2) in which the four coefficients determined in step (2) are used. The computation time required in steps (3) and (4) is shorter than 1 s on our workstation even for a very large protein.
The ADIET is a statistical–mechanical theory for molecular liquids (Kusalik and Patey 1988a; Kinoshita 2008). In this theory, a multipolar model is employed for water. For example, a water molecule is modeled as a hard sphere with diameter d S = 0.28 nm in which a point dipole and a point quadrupole of tetrahedral symmetry are embedded. The effect of the molecular polarizability is taken into account using the self-consistent mean field (SCMF) theory. At the SCMF level the water–water many-body-induced interactions are reduced to pairwise additive potentials involving an effective dipole moment. We have shown that the ADIET (Kinoshita 2008) predominates over the reference interaction site model (RISM) and related theories (Hirata and Rossky 1981; Perkyns and Pettitt 1992) in the elucidation of hydrophobic hydration. Although the integral equation theory implemented by Lado et al. (Giacometti et al. 2010) is angle-dependent, its details are somewhat different from the version which has been used by Patey et al. (Kusalik and Patey 1988b) and our group. The rotational-invariant expansion which is considerably more convenient is not employed in Lado’s version.
The four coefficients calculated are dependent on the solvent species, thermodynamic state (e.g., temperature and pressure) of the solvent, and the method employed in step (1). When the solvent is a simple fluid, S V of a protein can directly be calculated using the three-dimensional integral equation theory. Even in such cases, the hybrid of the radial-symmetric integral equation theory and the MA gives the results with errors smaller than ±1 % and computation time that is four orders of magnitude shorter (Roth et al. 2006).
The high reliability of our hybrid method in calculating S V has been demonstrated in the following examples: quantitative reproduction of the experimentally measured changes in thermodynamic quantities upon apoPC folding; elucidation of the molecular mechanisms of pressure (Harano et al. 2008; Yoshidome et al. 2009) and cold (Oshima et al. 2009; Yoshidome and Kinoshita 2012) denaturating of proteins; proposal of a reliable measure of the thermal stability of proteins (Oda et al. 2011); structural stability of membrane proteins (Yasuda et al. 2012); development of a free-energy function capturing the features of the native fold for discriminating it from a number of misfolded decoys (Yasuda et al. 2011); development of a reliable method of characterizing the native-structure models of a protein determined through the X-ray crystallography and NMR experiments combined with structure calculations (Mishima et al. 2012); and prediction of the so-called hot spots (i.e., residues accounting for the majority of the protein-protein binding free energy despite that they comprise only a small fraction of the protein–protein interface) in protein–protein complexes (Oshima et al. 2011).
We have recently extended the MA to a multi-component solvent (Kodama et al. 2011). The extended version will be useful for analyses on the salt (e.g., NaCl) and cosolvent (e.g., sugar) effects. We note that the solvent entropy effect is influenced by cosolvents. For example, the solubility of hydrophobic solutes exhibits a significant decrease upon salt addition to water, and the native state of a protein is more stabilized by addition of sugars such as sucrose and glucose.
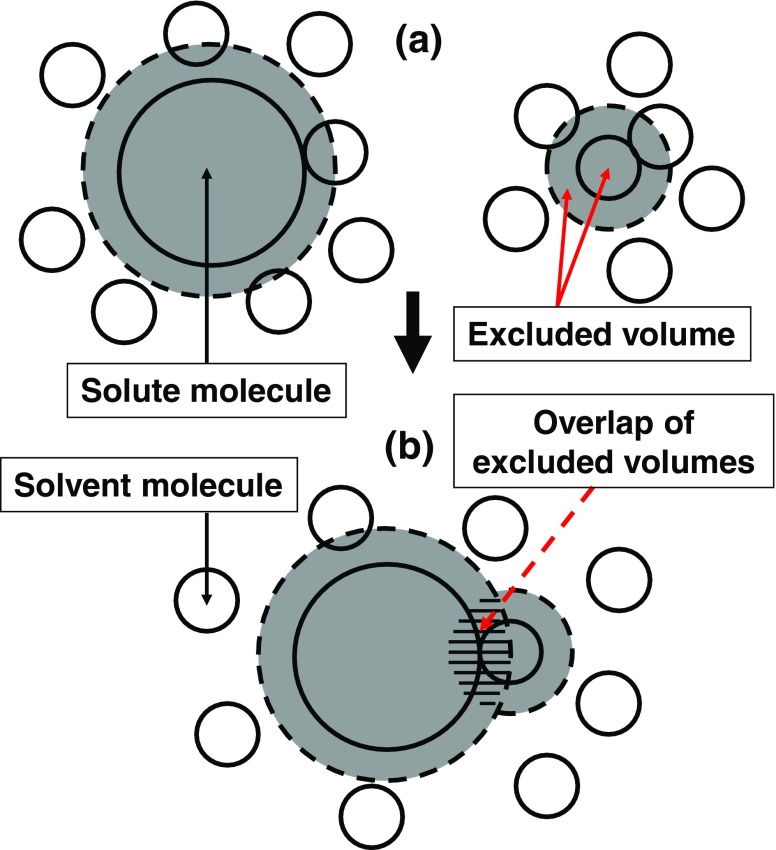
Importance of solute–solvent many-body correlations
S V comprises the solute–solvent pair correlation component and solute–solvent–solvent triplet and higher-order (solute–solvent many-body) correlation component. Each solvent molecule generates an excluded volume for the other solvent molecules (see Fig. 4a), giving rise to the entropic correlations among solvent molecules (i.e., solvent crowding). This is the origin of the many-body correlations. Changes in the translational freedom of each individual solvent molecule and in solvent crowding occur upon solute insertion. A difference between the pair and many-body correlations is as follows. When a solvent molecule contacts the solute as illustrated in Fig. 4b, an overlap of the excluded volumes generated by the solvent molecule and the solute occurs. The total volume available to the other solvent molecules increases by the overlapped volume. The translational freedom of the solvent molecule in contact with the solute is restricted (effect 1), but that of the other solvent molecules is increased (effect 2). Effect 1 originates from the pair correlation while effect 2 is ascribed to the many-body correlations. Due to effect 2, sufficiently many solvent molecules are driven to contact the solute, leading to the formation of a denser layer of solvent molecules near the solute. The structure of the layer is determined by the interplay of these two opposing effects. At low pressures, solvent crowding is not serious and effect 2 is not very important, with the result that the number of solvent molecules in contact with the solute is not large. At high pressures, by contrast, effect 2 becomes essential due to the severe solvent crowding, and considerably more solvent molecules are driven to contact the solute. When the solute possesses a flexible, polyatomic structure as in the case of a protein, its structure is changed to the one with a much larger solvent-accessible surface area and an excluded volume kept sufficiently small: i.e., the pressure-denatured structure (Yoshidome et al. 2009).
Fig. 4.
Illustration of a difference between the solute–solvent pair correlation and solute–solvent–solvent triplet and higher-order (solute–solvent many-body) correlations
Using an integral equation theory, we can decompose S V into the pair correlation and many-body correlation components (Yoshidome et al. 2009). Each of the pair correlation and many-body correlation components can further be decomposed into the excluded-volume term (term 1) and the solvent-accessible-surface term (term 2; dependent on A, X, and Y) using Eq. (2). The solvent molecules near the solute contribute to term 2 while those in the bulk contribute to term 1. There are the four constituents of S V: terms 1 and 2 of the pair correlation component and terms 1 and 2 of the many-body correlation component. Term 1 of the pair correlation component represents a decrease in the total volume available to each solvent molecule in the bulk. Term 1 of the many-body correlation component represents an increase in solvent crowding in the bulk. Term 2 of the pair correlation component is related to an increase in translational and orientational restrictions for each solvent molecule near the solute. Term 2 of the many-body correlation component is discussed in the next paragraph.
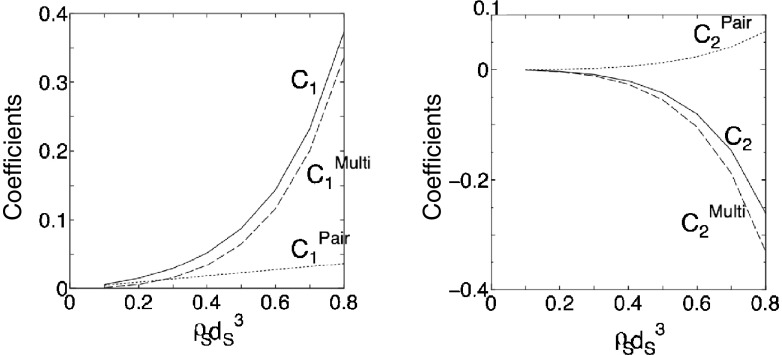
The coefficients in the morphometric forms for the pair correlation and many-body correlation components of −S V/k B (note the minus sign) are dependent on the reduced number density of the bulk solvent, ρ S d S 3 (d S is the diameter of solvent molecules). The dependence of the first and second coefficients on ρ S d S 3 for hard-sphere solvent (μ/(k B T) = −S V/k B) is shown in Fig. 5. (The value of ρ S d S 3 for water at ambient temperature and pressure is 0.7317.) For both term 1 and term 2, the many-body correlation component is far larger than the pair correlation component. Moreover, it is much more strongly dependent on ρ S d S 3, which is a reflection of the strong dependence of solvent crowding on ρ S d S 3. Term 2 of the many-body correlation component is attributable to the following two factors: the structuring of solvent molecules near the solute (factor 1), and reduction in solvent crowding originating from “an increase in translational restriction for each solvent molecule near the solute” and from “the translational structuring of solvent molecules near the solute” (factor 2). It is interesting to note that factor 2 makes a positive contribution to S V. Its physical interpretation is the following: as the solvent-accessible surface increases, the number of solvent molecules in contact with the solute becomes larger, leading to a positive value of term 2 of the many-body correlation component as well as a negative value of term 2 of the pair correlation component (see Fig. 4). C 2 Multi is negative because factor 2 is larger than factor 1 making a negative contribution to S V. If the AO theory is applied to the present system, all of C 1 Multi, C 2 Pair, and C 2 Multi are set at zero.
Fig. 5.
Dependence of C 1 Pair, C 1 Multi, C 2 Pair, and C 2 Multi on ρ S d S 3 for hard-sphere solvent. C 1 Pair = C 1 for the pair correlation component of −S V/k B (C 1 Pair = ρ S), C 1 Multi = C 1 for the many-body correlation component of −S V/k B, C 2 Pair = C 2 for the pair correlation component of −S V/k B, and C 2 Multi = C 2 for the many-body correlation component of −S V/k B. C 1 = C 1 Pair + C 1 Multi and C 2 = C 2 Pair + C 2 Multi. C 1 and C 2 are the first and second principal coefficients in the morphometric forms. S V, k B, ρ S, and d S are the solvation entropy, Boltzmann constant, number density of bulk solvent, and diameter of solvent molecules, respectively. If the Asakura–Oosawa theory is applied to the present system, C 1 Pair = ρ S, C 1 Multi = 0, C 2 Pair = 0, and C 2 Multi = 0
When the hard-sphere solvent is replaced by water, the behavior of C 1 Multi, C 2 Pair, and C 2 Multi becomes quantitatively different but qualitatively similar at ambient temperature. The change in the rotational freedom of water molecules upon solute insertion is also included in S V. However, this change does not possess the excluded-volume term. The insertion reduces the translational and rotational freedoms of water molecules, causing losses of translational and rotational entropies of water, respectively. Only the water molecules near the solute undergo the rotational reduction, while the translational reduction also reaches the water molecules far from the solute. The loss of the translational entropy is substantially larger than that of the rotational entropy.
Comparison with other methods for biomolecular solvation
Biomolecular solvation has also been investigated by some other groups at the atomic level. For example, the RISM and related theories are useful in analyses of the water entropy effect. However, even their three-dimensional versions (Beglov and Roux 1997; Yoshida et al. 2009; Palmer et al. 2010), which have been shown to be far superior to the one-dimensional versions, are incapable of reproducing the pressure and temperature dependences of the effect. They fail to elucidate cold and pressure denaturating of proteins: A protein is not denatured at low temperatures and the pressure-denatured structure is more stable than the native structure even at low pressures. Moreover, they considerably underestimate the entropic gain of water upon protein folding (Imai et al. 2007). The molecular dynamics (MD) simulation combined with a new solution theory in the energy representation developed by Matubayasi et al. (Karino and Matubayasi 2011) is far more efficient than the standard MD simulation and potentially a reliable tool in studies on biomolecular solvation. However, it is still much more laborious than the integral equation theories. The great advantages of our hybrid method, which distinguishes it from these methods, are as follows: (1) the computation time required is orders of magnitude shorter; and (2) the solvation entropy can be decomposed into physically insightful constituents using the morphometric approach and the physical origin of any result can be clarified.
Rotational mechanism for γ-subunit in F1-ATPase
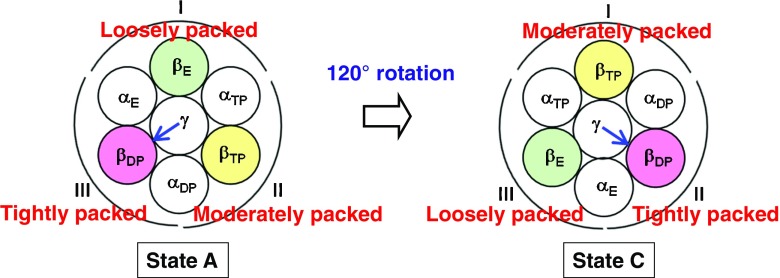
The γ subunit in the α3β3γ complex taken from F1-ATPase has been shown to exhibit a rotation. During one hydrolysis cycle of ATP comprising the three processes, ATP binding, hydrolysis of ATP into ADP and Pi, and dissociation of ADP and Pi, the γ subunit rotates by 120° (see Fig. 6). It is desired for a protein or a complex of proteins that the backbones and side chains be tightly packed to maximize the water entropy. However, this is not always possible. Even in cases where the overall tight packing is not achievable, there are certainly portions that can be tightly packed. It is important to pack such portions preferentially. In our view, such inhomogeneity of the packing structure plays essential roles in the rotation mechanism for the γ subunit.
Fig. 6.
States A and C of the α3β3γ complex. State C: after the 120° rotation of the γ subunit
We consider state A shown in Fig. 6 where ATP is bound to the β subunit named βTP, ATP that is ready to be hydrolyzed into ADP and Pi is bound to the β subunit named βDP, and nothing is bound to the β subunit named βE (only Pi remains within βE). The three α subunits are named αTP, αDP, and αE, respectively. βTP and βDP are in closed conformations while βE takes an open conformation. We define the following three groups, “group I: γ, βE, αE, and αTP”, “group II: γ, βTP, αTP, and αDP”, and “group III: γ, βDP, αDP, and αE” (see state A in Fig. 6). The structures of the α3β3γ complex before and after the 120° rotation of the γ subunit are the same. We emphasize that the groups are defined in terms of their positions. For example, after the γ subunit rotates by 120°, the arrangement changes into state C in Fig. 6 and group III now comprises γ, βE, αE, and αTP.
We have analyzed the solvation entropies of the three groups using the hybrid of the ADIET and MA (Yoshidome et al. 2011, 2012). In what follows, we summarize the physical picture of the rotational mechanism obtained. When a local, tight packing of βDP, αDP, αE, and the γ subunit with a particular orientation is preferentially achieved, the water entropy is maximized. The other two groups are packed moderately and loosely, respectively (see state A in Fig. 6). When the receptor has higher affinity with ATP than with ADP and the ATP and ADP concentrations are sufficiently high and low, respectively, any of the three processes in the hydrolysis cycle mentioned above leads to the lowering of the system free energy and unavoidably occurs. In the case of the α3β3γ complex, Pi is released from βE, ATP is hydrolyzed within βDP, ATP binds to βE, and ADP is released from βDP, with the result that βE, βDP, and βTP change to βTP, βE, and βDP, respectively: The γ subunit rotates by 120° to recover the local, tight packing with βDP, αDP, and αE (see state C in Fig. 6). The system free energy of state C is lower than that of state A by the free energy decrease upon the ATP hydrolysis in aqueous solution, F H (<0).
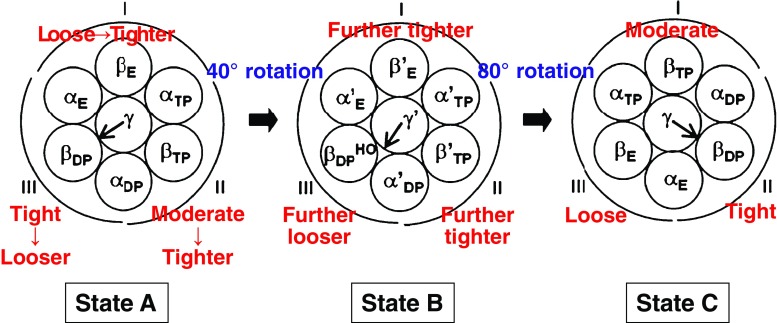
It is experimentally known that the conformation of βDP becomes half-open upon the release of Pi from βE and hydrolysis of ATP within βDP. Namely, the most tightly packed group becomes looser. Instead, the moderately packed and loosely packed groups are made tighter to recover the water entropy, inducing the 40° rotation of the γ subunit: state A→state B in Fig. 7. The ATP binding to βE’ and release of ADP from βDP HO give rise to further promotion of these changes in the packing structures of the three groups, inducing the 80° rotation of the γ subunit: state B→state C in Fig. 7. Thus, three portions which are different from one another in the degree of packing are always formed, and they are cyclically exchanged. The γ subunit simply follows this cyclic exchange arising from the interplay of water entropy and hydrolysis cycle of ATP. This picture is consistent with the initially surprising experimental observation (Uchihashi et al. 2011) that the inhomogeneous packing structure rotates even without the γ subunit.
Fig. 7.
States A, B, and C of the α3β3γ complex. State B: after the 40° rotation of the γ subunit. The release of Pi from βE and hydrolysis of ATP within βDP induces the 40° rotation. The ATP binding to βE’ and release of ADP from βDP HO (half-open conformation of βDP) induces the 80° rotation. Prime represents that the packing structure has more or less changed
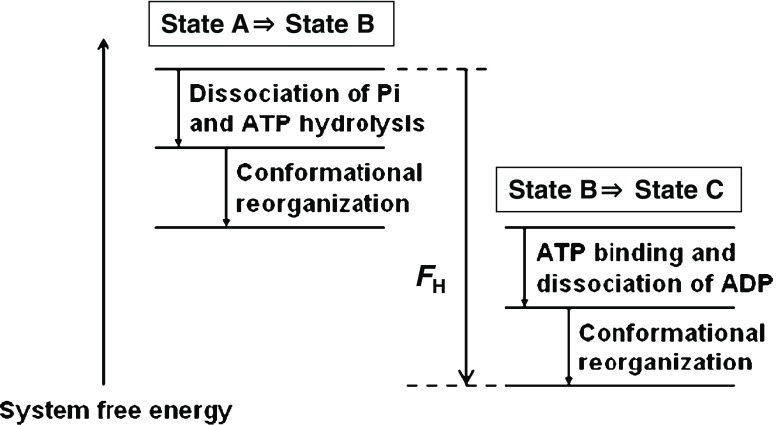
The change in the system free energy during the 120° rotation of the γ subunit is explained in Fig. 8. The sum of the free energy decreases arising from the following events is equal to F H: Pi release and ATP hydrolysis, reorganization of the packing structure of the α3β3γ complex accompanying the 40° rotation of the γ subunit, ATP binding and release of ADP, and reorganization of the packing structure of the complex accompanying the 80° rotation of the γ subunit. The reorganization is driven by the water entropy effect.
Fig. 8.
Change in the system free energy during the 120° rotation of the γ subunit. F H (<0) denotes the free energy decrease upon the ATP hydrolysis in aqueous solution
Protein folding occurs so that the system free energy can be lowered. The native state is visually different from the unfolded state. In the α3β3γ complex, however, state C appears to be the same as state A (see Fig. 6). Actually, they are different: one ATP molecule is hydrolyzed, and the system free energy in state C is lower by F H. Without the three processes in the hydrolysis cycle, state A does not exhibit any change once it is stabilized. The three processes drive the rotation in the complex so that the system free energy can be lowered. The ATP hydrolysis into ADP and Pi is required just for recovering the original state by releasing ADP and Pi. The recovery allows the complex to repeat the rotational function. Water executes the rotation, and the ATP action provides a switch initiating the state change. We believe that all the ATP-driven proteins share the same physical essence.
Concluding remarks
The entropic excluded-volume effect becomes stronger as the molecular size of the solvent decreases and/or the solvent number density increases. Thanks to the hydrogen bonding, water can exist in liquid state at ambient temperature and pressure despite its exceptionally small molecular size. The effect, which stems from the translational displacement of solvent molecules, is the largest for water among ordinary liquids in nature. This is an answer to the question: why is water indispensable to life?
The physical factor driving the biological self-assembly referred to in the “Introduction” is a gain in the translational entropy of water brought by the reduction in water crowding in the system, i.e., the water entropy effect arising from the biomolecule–water many-body correlations. We have shown that this effect is the true physical origin of hydrophobicity (Yoshidome and Kinoshita 2012). The water entropy effect becomes considerably less powerful at low temperatures, giving rise to the collapse of the self-assembled structures (e.g., cold denaturation of a protein).
Acknowledgments
The author thanks all the collaborators. Sincere appreciation should be expressed to Prof. Kuniaki Nagayama for his continuous encouragement. This work was supported mainly by Grants-in-Aid for Scientific Research on Innovative Areas (No. 20118004) from the Ministry of Education, Culture, Sports, Science and Technology of Japan.
Conflict of interest
None.
References
- Amano K, Yoshidome T, Iwaki M, Suzuki M, Kinoshita M. Entropic potential field formed for a linear-motor protein near a filament: statistical-mechanical analyses using simple models. J Chem Phys. 2010;133:045103. doi: 10.1063/1.3462279. [DOI] [PubMed] [Google Scholar]
- Amano K, Oshima H, Kinoshita M. Potential of mean force between a large solute and a biomolecular complex: a model analysis on protein flux through chaperonin system. J Chem Phys. 2011;135:185101. doi: 10.1063/1.3657856. [DOI] [PubMed] [Google Scholar]
- Asakura S, Oosawa F. Interaction between particles suspended in solutions of macromolecules. J Polymer Sci. 1958;33:183–192. doi: 10.1002/pol.1958.1203312618. [DOI] [Google Scholar]
- Beglov D, Roux B. An integral equation to describe the solvation of polar molecules in liquid water. J Phys Chem B. 1997;101:7821–7826. doi: 10.1021/jp971083h. [DOI] [Google Scholar]
- Ellis RJ, Minton AP. Cell biology: join the crowd. Nature. 2003;425:27–28. doi: 10.1038/425027a. [DOI] [PubMed] [Google Scholar]
- Giacometti A, Lado F, Largo J, Pastore G, Sciortino F. Effects of patch size and number within a simple model of patchy colloids. J Chem Phys. 2010;132:174110. doi: 10.1063/1.3415490. [DOI] [PubMed] [Google Scholar]
- Hansen-Goos H, Roth R, Mecke K, Dietrich S. Solvation of proteins: linking thermodynamics to geometry. Phys Rev Lett. 2007;99:128101. doi: 10.1103/PhysRevLett.99.128101. [DOI] [PubMed] [Google Scholar]
- Harano Y, Kinoshita M. Translational-entropy gain of solvent upon protein folding. Biophys J. 2005;89:2701–2710. doi: 10.1529/biophysj.104.057604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harano Y, Yoshidome T, Kinoshita M. Molecular mechanism of pressure denaturation of proteins. J Chem Phys. 2008;129:145103. doi: 10.1063/1.2991176. [DOI] [PubMed] [Google Scholar]
- Hirata F, Rossky PJ. An extended RISM equation for molecular polar fluids. Chem Phys Lett. 1981;83:329–334. doi: 10.1016/0009-2614(81)85474-7. [DOI] [Google Scholar]
- Imai T, Harano Y, Kinoshita M, Kovalenko A, Hirata F. A theoretical analysis on changes in thermodynamic quantities upon protein folding: essential roles of hydration. J Chem Phys. 2007;126:225102. doi: 10.1063/1.2743962. [DOI] [PubMed] [Google Scholar]
- Karino Y, Matubayasi N. Free-energy analysis of hydration effect on protein with explicit solvent: equilibrium fluctuation of cytochrome c. J Chem Phys. 2011;134:041105. doi: 10.1063/1.3535560. [DOI] [PubMed] [Google Scholar]
- Kinoshita M. Ordered aggregation of big bodies with high asphericity in small spheres: a possible mechanism of the amyloid fibril formation. Chem Phys Lett. 2004;387:54–60. doi: 10.1016/j.cplett.2004.01.112. [DOI] [Google Scholar]
- Kinoshita M. Roles of entropic excluded-volume effects in colloidal and biological systems: analyses using the three-dimensional integral equation theory. Chem Eng Sci. 2006;61:2150–2160. doi: 10.1016/j.ces.2004.02.023. [DOI] [Google Scholar]
- Kinoshita M. Molecular origin of the hydrophobic effect: analysis using the angle-dependent integral equation theory. J Chem Phys. 2008;128:024507. doi: 10.1063/1.2823733. [DOI] [PubMed] [Google Scholar]
- Kinoshita M. Roles of translational motion of water molecules in sustaining life. Front Biosci. 2009;14:3419–3454. doi: 10.2741/3463. [DOI] [PubMed] [Google Scholar]
- Kinoshita M. Importance of translational entropy of water in biological self-assembly processes like protein folding. Int J Mol Sci. 2009;10:1064–1080. doi: 10.3390/ijms10031064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinoshita M, Harano Y. Potential of mean force between solute atoms in salt solution: effects due to salt species and relevance to conformational transition of biomolecules. Bull Chem Soc Jpn. 2005;78:1431–1441. doi: 10.1246/bcsj.78.1431. [DOI] [Google Scholar]
- Kodama R, Roth R, Harano Y, Kinoshita M. Morphometric approach to thermodynamic quantities of solvation of complex molecules: extension to multicomponent solvent. J Chem Phys. 2011;135:045103. doi: 10.1063/1.3617247. [DOI] [PubMed] [Google Scholar]
- Kusalik PG, Patey GN. The solution of the reference hypernetted-chain approximation for water-like models. Mol Phys. 1988;65:1105–1119. doi: 10.1080/00268978800101631. [DOI] [Google Scholar]
- Kusalik PG, Patey GN. On the molecular theory of aqueous electrolyte solutions. I. The solution of the RHNC approximation for models at finite concentration. J Chem Phys. 1988;88:7715–7738. doi: 10.1063/1.454286. [DOI] [Google Scholar]
- Mishima H, Yasuda S, Yoshidome T, Oshima H, Harano Y, Ikeguchi M, Kinoshita M. Characterization of experimentally determined native-structure models of a protein using energetic and entropic components of free-energy function. J Phys Chem B. 2012;116:7776–7786. doi: 10.1021/jp301541z. [DOI] [PubMed] [Google Scholar]
- Oda K, Kodama R, Yoshidome T, Yamanaka M, Sambongi Y, Kinoshita M. Effects of heme on the thermal stability of mesophilic and thermophilic cytochromes c: comparison between experimental and theoretical results. J Chem Phys. 2011;134:025101. doi: 10.1063/1.3519814. [DOI] [PubMed] [Google Scholar]
- Oshima H, Yoshidome T, Amano K, Kinoshita M. A theoretical analysis on characteristics of protein structures induced by cold denaturation. J Chem Phys. 2009;131:205102. doi: 10.1063/1.3265985. [DOI] [PubMed] [Google Scholar]
- Oshima H, Yasuda S, Yoshidome T, Ikeguchi M, Kinoshita M. Crucial importance of water-entropy effect for predicting hot spots in protein-protein complexes. Phys Chem Chem Phys. 2011;13:16236–16246. doi: 10.1039/c1cp21597c. [DOI] [PubMed] [Google Scholar]
- Palmer DS, Sergiievskyi VP, Jensen F, Fedorov MV. Accurate calculations of the hydration free energies of druglike molecules using the reference interaction site model. J Chem Phys. 2010;133:044104. doi: 10.1063/1.3458798. [DOI] [PubMed] [Google Scholar]
- Perkyns JS, Pettitt BM. A site-site theory for finite concentration saline solutions. J Chem Phys. 1992;97:7656–7666. doi: 10.1063/1.463485. [DOI] [Google Scholar]
- Poletto C, Giacometti A, Trovato A, Banavar JR, Maritan A. Emergence of secondary motifs in tubelike polymers in a solvent. Phys Rev E. 2008;77:61804. doi: 10.1103/PhysRevE.77.061804. [DOI] [PubMed] [Google Scholar]
- Roth R, Harano Y, Kinoshita M. Morphometric approach to the solvation free energy of complex molecules. Phys Rev Lett. 2006;97:078101. doi: 10.1103/PhysRevLett.97.078101. [DOI] [PubMed] [Google Scholar]
- Snir Y, Kamien RD. Helical tubes in crowded environments. Phys Rev E. 2007;75:051114. doi: 10.1103/PhysRevE.75.051114. [DOI] [PubMed] [Google Scholar]
- Uchihashi T, Iino R, Ando T, Noji H. Science. 2011;333:755–758. doi: 10.1126/science.1205510. [DOI] [PubMed] [Google Scholar]
- Vrij A. Polymers at interfaces and the interactions in colloidal suspensions. Pure Appl Chem. 1976;48:471–483. doi: 10.1351/pac197648040471. [DOI] [Google Scholar]
- Yasuda S, Yoshidome T, Oshima H, Kodama R, Harano Y, Kinoshita M. Effects of side-chain packing on the formation of secondary structures in protein folding. J Chem Phys. 2010;132:065105. doi: 10.1063/1.3319509. [DOI] [PubMed] [Google Scholar]
- Yasuda S, Yoshidome T, Harano Y, Roth R, Oshima H, Oda K, Sugita Y, Ikeguchi M, Kinoshita M. Free-energy function for discriminating the native fold of a protein from misfolded decoys. Proteins. 2011;79:2161–2171. doi: 10.1002/prot.23036. [DOI] [PubMed] [Google Scholar]
- Yasuda S, Oshima H, Kinoshita M. Structural stability of proteins in aqueous and nonpolar environments. J Chem Phys. 2012;137:135103. doi: 10.1063/1.4755755. [DOI] [PubMed] [Google Scholar]
- Yoshida N, Imai T, Phongphanphanee S, Kovalenko A, Hirata F. Molecular recognition studied by statistical-mechanical integral-equation theory of liquids. J Phys Chem B. 2009;113:873–886. doi: 10.1021/jp807068k. [DOI] [PubMed] [Google Scholar]
- Yoshidome T, Kinoshita M. Physical origin of hydrophobicity studied in terms of cold denaturation of proteins: comparison between water and simple fluids. Phys Chem Chem Phys. 2012;14:14554–14566. doi: 10.1039/c2cp41738c. [DOI] [PubMed] [Google Scholar]
- Yoshidome T, Kinoshita M, Hirota S, Baden N, Terazima M. Thermodynamics of apoplastocyanin folding: comparison between experimental and theoretical results. J Chem Phys. 2008;128:225104. doi: 10.1063/1.2929836. [DOI] [PubMed] [Google Scholar]
- Yoshidome T, Harano Y, Kinoshita M. Pressure effects on structures formed by the entropically driven self-assembly: illustration for denaturation of proteins. Phys Rev E. 2009;79:011912. doi: 10.1103/PhysRevE.79.011912. [DOI] [PubMed] [Google Scholar]
- Yoshidome T, Ito Y, Ikeguchi M, Kinoshita M. Rotation mechanism of F1-ATPase: crucial importance of the water-entropy effect. J Am Chem Soc. 2011;133:4030–4039. doi: 10.1021/ja109594y. [DOI] [PubMed] [Google Scholar]
- Yoshidome T, Ito Y, Matubayasi N, Ikeguchi M, Kinoshita M. Structural characteristics of yeast F1-ATPase before and after 16° rotation of the γ subunit: theoretical analysis focused on the water-entropy effect. J Chem Phys. 2012;137:035102. doi: 10.1063/1.4734298. [DOI] [PubMed] [Google Scholar]