Skip to main content
NCBI home page
Biophysical Reviews logoLink to Biophysical Reviews
. 2014 Jan 14;6(1):63–74. doi: 10.1007/s12551-013-0129-8

Electric dipole moments of the fluorescent probes Prodan and Laurdan: experimental and theoretical evaluations

Cíntia C Vequi-Suplicy 1, Kaline Coutinho 1, M Teresa Lamy 1,✉
PMCID: PMC5425710  PMID: 28509963

Abstract

Several experimental and theoretical approaches can be used for a comprehensive understanding of solvent effects on the electronic structure of solutes. In this review, we revisit the influence of solvents on the electronic structure of the fluorescent probes Prodan and Laurdan, focusing on their electric dipole moments. These biologically used probes were synthesized to be sensitive to the environment polarity. However, their solvent-dependent electronic structures are still a matter of discussion in the literature. The absorption and emission spectra of Prodan and Laurdan in different solvents indicate that the two probes have very similar electronic structures in both the ground and excited states. Theoretical calculations confirm that their electronic ground states are very much alike. In this review, we discuss the electric dipole moments of the ground and excited states calculated using the widely applied Lippert–Mataga equation, using both spherical and spheroid prolate cavities for the solute. The dimensions of the cavity were found to be crucial for the calculated dipole moments. These values are compared to those obtained by quantum mechanics calculations, considering Prodan in vacuum, in a polarizable continuum solvent, and using a hybrid quantum mechanics–molecular mechanics methodology. Based on the theoretical approaches it is evident that the Prodan dipole moment can change even in the absence of solute–solvent-specific interactions, which is not taken into consideration with the experimental Lippert–Mataga method. Moreover, in water, for electric dipole moment calculations, it is fundamental to consider hydrogen-bonded molecules.

Keywords: Prodan, Laurdan, Optical absorption and fluorescence, Electric dipole moment, Lippert–Mataga equation, Quantum mechanics calculations

Introduction

The solvent effect on electronic properties of molecules is a topic of great interest, both in the experimental (Reichardt 2004; Lippert 1955; Mataga et al. 1956) and theoretical (Tomasi 2004; Tomasi et al. 2005; Miertus et al. 1981; Field et al. 1990; Coutinho and Canuto 1997) areas. Solvents can produce significant changes in molecular properties, such as absorption and emission spectra, reactivity, electrochemistry, solubility, among others (Reichardt 2004). Several experimental and theoretical approaches can be used for a comprehensive understanding of solvent effects. In this review, we revisit the influence of solvents on the electronic structure of the fluorescent probes Prodan and Laurdan, focusing on the electric dipole moments of these fluorophores.

Prodan and Laurdan (Fig. 1) are largely used in biological relevant systems. They were synthesized to be sensitive to the environment polarity, so their emission spectra shift about 120 nm from cyclohexane to water (Weber and Farris 1979; Parasassi et al. 1986; Catalan et al. 1991; Lakowicz 2006). When inserted into membranes, their emission spectra are extremely dependent on the lipid bilayer phase (gel or fluid) (Zeng and Chong 1991; Rottenberg 1992; Ferretti et al. 1993; Ambrosini et al. 1994, 2001; Alleva et al. 1995; Bell et al. 1996; Bagatolli et al. 1997; De Vequi-Suplicy et al. 2006; Moyano et al. 2008; Lucio et al. 2010; Vequi-Suplicy et al. 2013).

Fig. 1.

Fig. 1

Open in a new tab

Prodan (top) and Laurdan (bottom) structures and atom numbers used in the text

However, the mechanism that makes Prodan and Laurdan so sensitive to polarity changes, and to lipid gel–fluid phase transition, is still under discussion. A number of polemic points are presented in the literature on the structure and electronic distribution of the fluorophores in different solvents, both in the ground and excited states (Balter et al. 1988; Bunker et al. 1993; Mennucci et al. 2008). For example, one very controversial point is the structure and electronic distribution of the excited state. At least two emission bands are present in the emission spectra of Prodan or Laurdan. These have been attributed to two excited electronic states: a locally excited state (LE), and an internal charge transfer (ICT) or a twisted ICT state (TICT) (Rollinson and Drickamer 1980; Nowak et al. 1986; Ilich and Prendergast 1989; Parusel et al. 1997, 1998, 2001; Viard et al. 1997; Parusel 1998; Kozyra et al. 2003; Tomin et al. 2003; Tomin 2006; Tomin and Hubisz 2006; Novaira et al. 2007, 2008; Adhikary et al. 2009; Morozova et al. 2009; Everett et al. 2010; ). In the latter state, the dimethylamine and the propanoyl groups would be rotated out of the naphthalene ring due to the high charge separation. However, several authors do not agree with the above explanation (Balter et al. 1988; Catalan et al. 1991; Bunker et al. 1993; Samanta and Fessenden 2000; Lobo and Abelt 2003; Mennucci et al. 2008; Rowe et al. 2008).

Another discussion in the literature concerns the dipole moment values of Prodan and Laurdan (Weber and Farris 1979; Nowak et al. 1986; Balter et al. 1988; Balter et al. 1988; Ilich and Prendergast 1989; Catalan et al. 1991; Bunker et al. 1993; Sun et al. 1997; Parusel et al. 1997, 1998, 2001; Parusel 1998; Kawski et al. 2000; Frisch et al. 2004; Huang et al. 2006), and this is the focus of the present review. Here we consider the evaluation of electric dipole moments for Prodan and Laurdan using two different approaches. The experimental approach is based on the largely used solvatochromic shift method, with the Lippert–Mataga equation (Lippert 1955; Mataga et al. 1956), and on a modification of this equation, considering a different geometry for the solute cavity (Scholte 1949). This methodology assumes that the fluorophore electric dipole moments, both for the ground and the excited states, are independent of the solvent. Conversely, theoretical calculations of the ground state electric dipole moment will be discussed, considering both the polarizable continuum model (PCM) (Miertus et al. 1981; Tomasi et al. 2005) and a more complex discrete model, with quantum mechanics/molecular mechanics hybrid calculations (S-QM/MM) (Coutinho and Canuto 1997; Canuto et al. 2000; Georg et al. 2006).

Comparing the optical absorption and emission spectra of Prodan and Laurdan

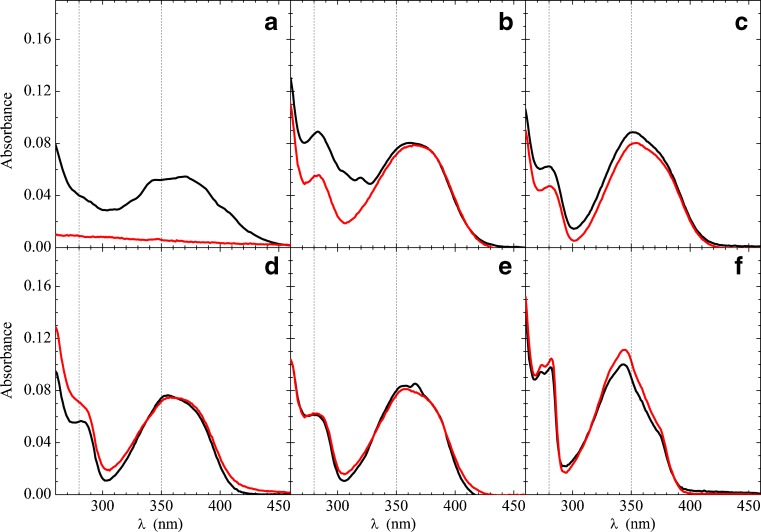
To understand the electric structure of Prodan and Laurdan, it is fundamental to analyze the optical absorption and emission spectra of the fluorophores in different solvents. Figure 2 shows the absorption spectra of Prodan (black) and Laurdan (red) in solvents with different polarities: cyclohexane, chloroform, dichloromethane, acetonitrile, methanol and water1. Considering that the word “polarity” is used in a very wide way (Reichardt 2004), Table 1 shows the different parameters for the solvents cited above, developed to assess the sample polarity: refraction index (n), electric dipole moment (μ), dielectric constant (ε), and the polarity scales, Δf (Lippert 1955; Mataga et al. 1956) and E T N (Reichardt 1994).

Fig. 2.

Fig. 2

Open in a new tab

Comparing Prodan (black line) and Laurdan (red line) absorption spectra in water (a), methanol (b), acetonitrile (c), dichloromethane (d), chloroform (e) and cyclohexane (f). [Prodan] = [Laurdan] = 4 μM. Dashed lines at 280 and 350 nm are for guiding the eyes only

Table 1.

Polarity parameters for the solvents used in this review

Solvent ε a μ (D)a n a Δf b E T Nc
Cyclohexane 2.0 ∼0 1.43 0.00 0.006
Chloroform 4.8 1.0 1.45 0.15 0.259
Dichloromethane 8.9 1.6 1.42 0.22 0.309
Acenonitrile 36.6 3.9 1.34 0.30 0.460
Methanol 33.0 1.7 1.33 0.31 0.762
Water 78.9 2.7 1.00 0.32 1.000
Open in a new tab

ε, Dielectric constant; μ, electric dipole moment, n, refractive index, Δf, E T N, polarity scales. Temperature was approx.  25 °C

aLide et al. (2002)

b Δf=ε−12ε+1−n2−12n2−1

cNormalized polarity scale ET (Reichardt 1994)

In all solvents used, Prodan and Laurdan can be seen to display very similar optical absorption spectra (Fig. 2), apart from water, where Laurdan is not soluble. This is a strong indication that the two probes have very similar ground state energies and geometries. Although that was expected, it needed to be confirmed. For instance, the Laurdan hydrocarbon chain could induce steric repulsion on solvent molecules, changing its optical absorption spectrum. Spectra were found to be temperature independent in the range 25–40 °C. The lower energy band, around 362 nm, seems to be more solvent dependent than the other two bands at higher energies (lower wavelengths), around 250 nm and 280 nm (Fig. 2).

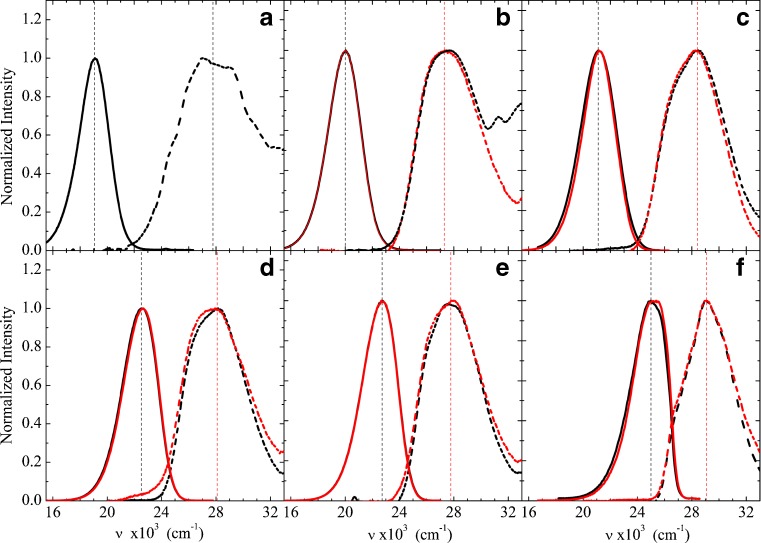
As it is well-known (Weber and Farris 1979; Catalan et al. 1991; Sun et al. 1997; Kawski 1999; Kawski et al. 2000; Rowe et al. 2008), Prodan and Laurdan fluorescence spectra are extremely dependent on the polarity of the solvent. Figure 3 shows the fluorescence spectra of the two probes in the solvents mentioned above, together with their lower energy (higher wavelength) absorption band (the latter also shown in Fig. 2): from cyclohexane to water, there is a shift of 125 nm (approx. 6.0 × 10−3 cm−1), as the Prodan emission spectrum (maximum intensity) goes from approximately 395 nm in cyclohexane to 525 nm in water (Fig. 3). Similar to the absorption spectra, the emission spectra of the two probes are very much alike, except in water, where Laurdan is not soluble. Therefore, it can be concluded that their ground and excited state energies are very close, indicating that the two fluorophores have very similar electronic structures and that the different molecular groups bound to the C6 atom have negligible influence.

Fig. 3.

Fig. 3

Open in a new tab

Prodan (black) and Laurdan (red) emission spectra (solid line) and absorption spectra (dashed line) in water (a), methanol (b), acetonitrile (c), dichloromethane (d), chloroform (e), and cyclohexane (f). Dotted lines assign the positions considered as the maximum band intensities, as presented in Table 2. For each solvent, λexc is that of maximum absorption intensity (assigned)

Experimental approaches for electric dipole moment calculation

The Lippert–Mataga equation (Lippert 1955; Mataga et al. 1956) has been largely used to calculate the ground (μ G) and excited (μ E) states of the electric dipole moments of fluorophores (Seliskar and Brand 1971; Simon and Thompson 1990; Suppan 1990; Ghoneim and Suppan 1995; Siddlingeshwar and Hanagodimath 2010; Dwivedi et al. 2011). This approach is also called the solvatochromic shift methodology, where the fluorophore is supposed to occupy a spherical cavity in a continuous, homogeneous solvent, no specific solute–solvent interaction is considered, and hence the electric dipole moment of the solute is assumed to be independent of the solvent. The organization of the solvent around the solute is only dependent on the solvent refractive index n (fast, electronic reorganization) and on the solvent dielectric constant ε (slow, electronic and molecular reorganization). Accordingly, the relationships between the absorption (ν ab) and emission (ν em) wavenumbers of a fluorophore in a specific solvent can be shown to be (Lippert 1955; Balter et al. 1988; Lakowicz 2006):

νab−νem=gfε−fnhcμE−μG2+const 1
νab+νem=−gfε+fnhcμE2−μG2+const 2

where g is a geometrical factor, g = 2/a 3, a is the cavity radius, and

fn=n2−12n2+1andfε=ε−12ε+1 3

The usual experimental procedure is to measure the optical absorption and emission spectra of the solute in different solvents with no specific interactions and then plot (ν ab − ν em) and (ν ab + ν em) as a function of [f(ε) − f(n)] and [f(ε) + f(n)], respectively. This method allows the graphical assessment of (μ E − μ G)2 and (μ 2E −  μ 2G) (angular coefficients of the linear fittings of Eqs. 1 and 2) and, thereby, the calculation of the ground (μ G) and excited (μ E) state electric dipole moments of the fluorophore.

As mentioned above, Eqs. 1 and 2 consider the solute in a spherical cavity in the solvent. However, considering that the fluorophore structure of Prodan or Laurdan is closer to a spheroid prolate than to a sphere, the equations developed by (Scholte 1949) will be also considered here. Scholte showed that for a spheroide prolate cavity, in a continuous solvent medium, one could arrive at equations similar to Eqs. 1 and 2, but with g = 3/abd, where a, b, and d are the prolate dimensions, a > b = d, and

fn=A11−A1n2−1n2+1−n2A1andfε=A11−A1ε−1ε+1−εA1 4
A1=−1p2−1+pp2−13lnp+p2−1andp=a/b. 5

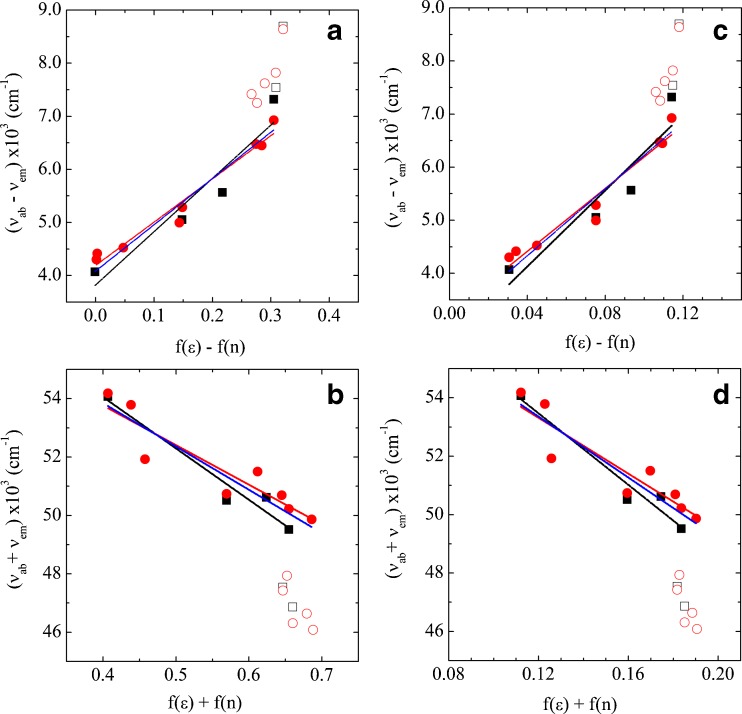
The experimental data and linear fittings for Prodan are presented in Fig. 4. The black symbols are data obtained from spectra shown in Fig. 3 (positions of ν ab and ν em are listed in Table 2), and the red symbols are data obtained from Weber and Farris (1979)2. Open symbols represent protic solvents, where hydrogen bonds are present; so, as discussed above, they are not expected to follow the Lippert–Mataga equation and were not considered in the fittings. In Fig. 4a, b, data were fitted with Eqs. 1 and 2 for solute spherical cavity, and in Fig. 4c, d, a solute spheroid prolate cavity was considered, as discussed above.

Fig. 4.

Fig. 4

Open in a new tab

Plots for Prodan data, following Eqs. 1 and 2. ν ab, ν em are the absorption and emission wavenumbers, respectively, of Prodan in different solvents, as listed in Table 2. f(ε) and f(n) were calculated using a spherical cavity, according to Eq. 3 (a, b), and for a spheroid prolate cavity according to Eqs. 4 and 5 (c, d). Black symbols (open and closed squares) are data obtained from spectra shown in Fig. 3, red symbols (open and closed circles) are data obtained from Weber and Farris (1979). Open symbols represent protic solvents and were not considered in the fittings. Black lines correspond to the best linear fittings considering our data only, red lines are those obtained considering data from Weber and Farris (1979), blue lines correspond to the best fittings considering all data

Table 2.

Absorption (ν ab) and emission (ν em) maxima used to calculate the difference (ν ab − ν em) and the sum (ν ab  + ν em) for Prodan and Laurdan in several solvents

Solvent Prodan Laurdan
ν ab (×10 3 cm −1 ) ν em (×10 3 cm −1 ) ν ab (×10 3 cm −1 ) ν em (×10 3 cm −1 )
Water 27.8 (360) 19.1 (524) - -
Methanol 27.5 (363) 20.0 (500) 27.4 (365) 20.0 (500)
Acetonitrile 28.4 (352) 21.1 (474) 28.2 (355) 21.2 (471)
Dichloromethane 28.1 (356) 22.5 (444) 27.8 (360) 22.6 (442)
Chloroform 27.8 (360) 22.7 (440) 27.8 (360) 22.7 (440)
Cyclohexane 29.1 (344) 25.0 (400) 29.1 (344) 25.2 (397)
Open in a new tab

These values were used in Fig. 4. The values in wavelength (nm) are presented in parentheses

In each graph of Fig. 4 (a–d), three different sets of data were considered for the fitting: black lines correspond to the best linear fittings considering our data only, red lines are those obtained considering data from Weber and Farris (1979), and blue lines correspond to the best fittings considering all data shown in Fig. 4 (apart from those relative to protic solvents, open symbols). Similar plots were performed for Laurdan, but using data presented here only (Table 2).

To calculate the ground (μ G) and excited (μ E) state electric dipole moments of the fluorophores, it is necessary to estimate the dimensions of the cavity occupied by the molecule in the solvent; this can be either a spherical cavity, with radius a, or a spheroid prolate cavity, with dimensions a > b = d.

To our knowledge, Prodan has always been considered in a spherical cavity, the radius of which has been mostly assumed to be 4.2 Å, half the distance between the atoms O5 and N26 in the molecule (Fig. 1). Values obtained by the different fittings in Fig. 4a, b are listed in Table 3. It can be observed that values yielded by the different fittings, for a spherical cavity of radius 4.2 Å, are rather similar. However, 3.0 D seems to be a low electric dipole moment value for the ground state of Prodan in view of the expected molecule charge separation (Weber and Farris 1979; Parusel et al. 1997). Considering the dimensions of Prodan (12.5 × 5.6 × 1.8 Å, obtained from the geometry optimized with quantum mechanics), larger cavity radii were considered here, namely, 5.6 and 6.3 Å (half of the larger dimension), yielding larger ground and excited state dipole moments (Table 3). Hence, this methodology is extremely dependent on the assumed radius for the fluorophore cavity. As expected, due to the very similar optical absorption and emission spectra (Fig. 3), the electric dipole moments of Prodan and Laurdan were found to be very much alike (Table 3).

Table 3.

Calculated electric dipole moments for Prodan and Laurdana for different cavity dimensions and shapes, using Eqs. 1–5 and data and fittings from Fig. 4

Dimensions:b a or a, b, d (Å) This work Weber and Farris (1979) All
μ G (D) μ E (D) μ G (D) μ E (D) μ G (D) μ E (D)
Spherical
   4.2 3.0 (3.2) 10.9 (11.4) 2.4 9.5 2.6 10.0
   5.6 4.6 (5.0) 14.6 (15.2) 3.7 14.6 4.0 15.4
   6.3 5.5 (5.9) 20.0 (20.9) 4.4 17.5 4.8 18.3
Spheroid prolate
   6.3, 2.8, 2.8 3.6 (4.8) 13.5 (14.4) 2.3 11.8 3.1 12.4
Open in a new tab

μ G, μ E, Ground and excited states of the electric dipole moments of fluorophores

aCalculated electric dipole moments for Laurdan are given in parenthesis

bSpherical cavity, with radius a, or a spheroid prolate cavity, with dimensions a > b = d.

Considering the above discussion on the relevance of the cavity dimensions for dipole moment calculations, and since Prodan and Laurdan molecules are closer to a spheroid prolate geometry than a spherical one, a prolate cavity was also considered. Cavity dimensions were assumed to be half of the largest dimensions of Prodan (6.3 and 2.8 Å, for a and b = d, respectively, in Eqs. 1, 2, 4 and 5). It is interesting to observe that the values obtained for μ G and μ E are similar to those yielded considering de fluorophores in a spherical cavity of radius 4.2 Å (Table 3). So, this apparently more appropriate cavity geometry does not strongly influence the dipole moment already calculated considering a spherical cavity.

Table 4 presents the electric dipole moments reported for Prodan using experimental approaches. For the molecule in the ground state, the values vary from 2.1 to 7 D, and for the excited state, from 6.4 to 20.0 D. As discussed above, part of this discrepancy can be attributed to the broadness of the absorption and emission bands; hence, the uncertainty about ν ab and ν em values and the choice of the appropriate shape and dimensions for the fluorophore cavity in the solvent. However, it is important to keep in mind that the largely used solvatochromic shift methodology assumes that the fluorophore electric dipole moment is independent of the solvent, and this assumption might not be correct, as discussed below.

Table 4.

Prodan electric dipole moments obtained with different experimental methodologies

Reference Methodology a (Å) μ G (D) μ E (D)
Weber and Farris (1979) Solvatochromic shift 4.2 5-7 -
Balter et al. (1988) Solvatochromic shift 4.2 2.9 10.9
Catalan et al. (1991) Solvatochromic shift 4.7 4.7 11.7
Bunker et al. (1993) Solvatochromic shift 4.2 2.85 9.8
Kawski (1999) Solvent perturbation 4.2/4.6 2.1/2.5 6.4/7.4
Kawski et al. (2000) Solvatochromic shift 4.2/4.6 2.14/2.46 6.46/7.37
Kawski et al. (2000) Thermochromic shift 4.2/4.6 2.45/2.80 6.65/7.60
Samanta and Fessenden (2000) Microwave absorption - 5.2 10.2
This work Solvatochromic Shift 6.3 5.5 20.0
Open in a new tab

Theoretical approaches for the ground state electric dipole moment

In vacuum: electronic distributions and dipole moments

In the last three decades, the electric dipole moment for the ground state of Prodan in vacuum has been calculated by different authors who have used both quantum mechanics with semi-empirical (MNDO, CNDO and AM1) and ab initio methods such as Hartree-Fock (HF), density functional theory (B3LYP), and second-order Møller–Plesset perturbation theory (MP2). These values are presented in Table 5 in chronological order. For all calculations, the Prodan optimized geometry is almost the same (planar conformation), and the major difference is the theoretical method used to calculate the charge distribution and the dipole moment. Considering the calculation level, the most reliable values are those obtained with B3LYP (Mennucci et al. 2008) and MP2 (this work), particularly those with larger basis functions (6-311 + G** and aug-cc-pVDZ, respectively). Therefore, the best theoretical values for the Prodan ground state dipole moment in vacuum are in the range of 5.8–6.1 D. Hence, when these values are compared with the experimental estimation values presented in Tables 3 and 4, it is clear that the cavity radius current used for Prodan (4.2 Å) is underestimated. The best comparison between the theoretical calculations (5.8–6.1 D) and experimental estimation (5.5 D) for the dipole moment is obtained with a cavity radius of 6.3 Å.

Table 5.

Dipole moments for Prodan ground state in vacuum

Article Methodology μ G (D)
Nowak et al. (1986) MNDO 6.7
Balter et al. (1988) CNDO/2 3.8
Parusel et al. (1997) HF/D95** 5.6
HF/3-21 + G* 5.7
Parusel et al. (1998) AM1-DFT 5.0-5.7
Parusel (1998) AM1 (CISD = 10) 6.0
AM1 5.2
Parusel et al. (2001) AM1 4.5
Huang et al. (2006) TD-B3LYP/6-31 + G* 6.0
Mennucci et al. (2008) TD-B3LYP/6-311 + G** 6.1
This worka MP2/aug-cc-pVDZ 5.8
This worka MP2/cc-pVDZ 5.5
Open in a new tab

aProgram Gaussian03 was used

To compare the fluorophore structure in the two molecules (Fig. 1), theoretical calculations were performed with isolated Prodan and Laurdan in vacuum. The geometries were obtained with density functional theory, B3LYP/6-31G* (Becke 1988; Lee et al. 1988; Stephens et al. 1994; Hertwig and Koch 1997), and dipole moments and atomic charges were calculated using second order perturbation theory (MP2/cc-pVDZ; Moller and Plesset 1934). Electronic transitions and molecular orbitals were calculated using semiempirical method with spectroscopic parameterization (INDO/S), which uses the configuration interaction method with single excitation (CIS) (Ridley and Zerner 1973; Bacon and Zerner 1979; Canuto et al. 2000), as implemented in ZINDO program (Zerner 2000). Table 6 shows the obtained electric dipole moments and electronic transition wavelengths and wavenumbers. Values obtained for Prodan and Laurdan were found to be very similar. Interestingly, calculated dipole moments in vacuum (Table 6) are comparable to experimental values obtained using the Lippert–Mataga equations, but considering a large spherical cavity of 6.3 Å radius (Table 3), suggesting that the cavity radii used in the literature to date (Table 4) are too small, leading to an underestimated dipole moment. The electronic transition values are very similar to the maximum of the lower energy absorption band measured for Prodan and Laurdan in cyclohexane (Fig. 2; Table 2).

Table 6.

Calculated values for the ground state electric dipole moment using second order perturbation theory (MP2/cc-pVDZ)a and HOMO–LUMO transition parametersb

Molecule μ G (D) Wavelength (nm) Wavenumber (×103 cm−1)
Prodan 5.5 344 29.1
Laurdan 5.6 341 29.3
Open in a new tab

aCalculated with Gaussian03

bHOMO, Highest occupied molecular orbital); LUMO, lowest unoccupied molecular orbital states. Calculated using semiempirical method with spectroscopic parametrization (INDO/S) with program ZINDO

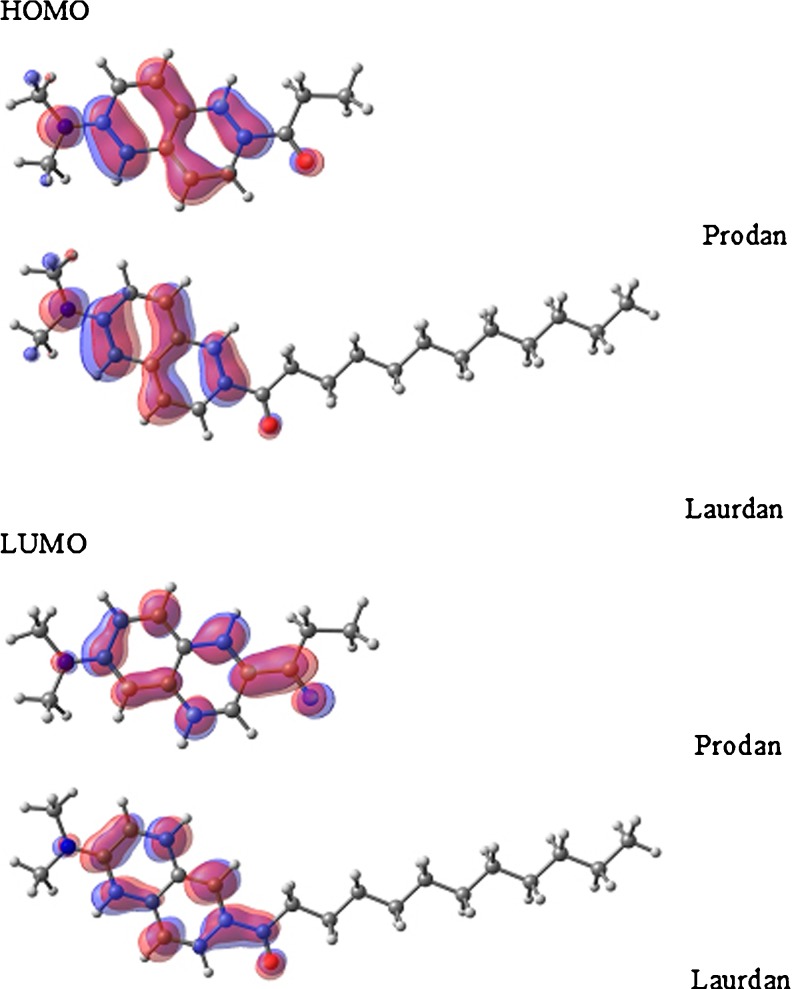
In Fig. 5, we show the calculated molecular orbitals for Prodan and Laurdan: HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital) states. It is possible to identify a small displacement of the orbitals (HOMO–LUMO) from N → O. Therefore, this result is in accord with those reported by authors who assigned the HOMO–LUMO transition for Prodan as a charge transfer transition between the O5 and N26 atoms (Parusel et al. 1997; Viard et al. 1997; Parusel 1998). The orbital symmetry related to the aromatic rings shows that HOMO is a π orbital and LUMO is a π*. So the electronic transition can be characterized as a π–π* transition, with a small charge transfer. The data in Table 6 and Fig. 5 reinforce the fact that the ground state of Prodan and Laurdan are very much alike, as discussed above (Fig. 3).

Fig. 5.

Fig. 5

Open in a new tab

Comparing the molecular orbitals HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital) for Prodan and Laurdan, calculated with the ZINDO program (Zerner 2000)

In solvents: electronic distributions and dipole moments

The electronic polarization of the solute, due to the presence of the solvent environment, is an important effect that emerges from the solute–solvent interaction. Therefore, solvents with different polarities can induce different polarizations on the solute, thereby changing the electric dipole moment of the solute.

A simple way to estimate the induced dipole moment with quantum mechanics calculations is to use the PCM (Miertus et al. 1981; Tomasi 2004; Tomasi et al. 2005) where the solvent is considered as a dielectric and continuum medium, and includes a self-consistent polarization process.

A more detailed and realistic model of the solvent can also be used. The sequential quantum mechanics (QM) and molecular mechanics (MM) methodology (S-QM/MM) was developed to describe the electronic properties of molecules in solution (Coutinho and Canuto 1997; Canuto et al. 2000; Georg et al. 2006). To calculate the induced dipole moment of a solute in the presence of the solvent, this methodology can be applied iteratively, starting with the charge distribution of the solute in vacuum and concluding with a charge distribution of the solute in the presence of the solvent (Georg et al. 2006). In this procedure, it is possible to follow the charge redistribution of the solute due to the presence of the solvent in each iterative step, through the evaluation of the induced dipole moment up to its convergence (see Fig. 6).

Fig. 6.

Fig. 6

Open in a new tab

Convergence of Prodan ground state electric dipole moment during the polarization process in several solvents (sequential quantum mechanics and molecular mechanics methodology): Filled green diamond Cyclohexane, filled blue triangle dichloromethane, filled red circle acetonitrile, filled black square water. Horizontal line is the dipole moment in vacuum

For Prodan, MM simulations were performed using the standard Monte Carlo (MC) method, with the Metropolis sampling technique in the NpT ensemble at standard conditions (T = 298 K, p = 1 atm), in a parallelogram box. The system consisted of one Prodan and 1,000 water molecules or 500 molecules for the other solvents (cyclohexane, dichloromethane, acetonitrile)3. The intermolecular interactions were described by the Lennard–Jones plus Coulomb potential, with three parameters for each atom I (ε i, σ i, and q i).4

All MC simulations were performed with the program DICE (Coutinho and Canuto 2009), consisting of a thermalization process of 1.2 × 108 MC steps, followed by 1.2 × 108 MC steps to obtain the average values and configurations. In all solvents, 75 statistically uncorrelated configurations were selected. Using these 75 configurations, it was possible to generate one electrostatic average configuration (ASEC), as described by Coutinho and co-workers (Coutinho et al. 2007). This ASEC configuration was used in the polarization process of Prodan in solution.

The polarization process was started with the atomic charges calculated for Prodan in vacuum (5.8 D). Figure 6 presents the evolution of the induced dipole moment value as a function of the number of iterations in the polarization process. In cyclohexane, the final induced dipole moment was achieved in the first iteration, 6.1 D, and an increase of only 5 % compared to the value obtained in vacuum is observed. In dichloromethane, it took three iterations to achieve the final induced dipole, 7.7 D, with an increase of 33 %. For acetonitrile, eight iterations were necessary to achieve a dipole stabilization in 8.0 D, with an increase of 38 %. Finally, for Prodan in aqueous solution, the stabilization was confirmed after nine iterations, with a dipole moment of 10.2 D, which is 76 % larger than the dipole in vacuum. The final values for the Prodan induced electric dipole moments (μ QM/MM) in the four solvents are presented in Table 7.

Table 7.

Prodan ground state induced electric dipole moment (D) in several solventsa

Prodan ground state-induced electric dipole moment Cyclohexane Dichloromethane Acetonitrile Water
This work
    μ QM/MM 6.1 7.7 8.0 10.2
    μ PCM 6.2 7.6 7.9 8.2
Mennucci et al. (2008)
    μ PCM 7.7 - 9.3 9.4
    μ vacuum b - - - 9.8
    μ PCM c - - - 13.2
Open in a new tab

For comparison, results from Mennucci et al. (2008) are included (see text)

aCalculated using the sequential quantum mechanics (QM) and molecular mechanics (MM) methodology (S-QM/MM; μ QM/MM) procedure and the polarizable continuum model (μ PCM), both with MP2/aug-ccpVDZ/CHELPG (see Fig. 6 and text)

bIn this calculation, the water environment was modeled as two hydrogen-bonded water molecules only.

cIn this calculation, the water environment was modeled as two hydrogen-bonded water molecules plus PCM model

For comparison, electronic dipole moments were also calculated using PCM with MP2/aug-ccpVDZ/CHELPG (μ PCM, Table 7). It is interesting to note that only in water is there a significant difference between the PCM calculated dipole, μ PCM, and the iterative S-QM/MM calculated dipole, μ QM/MM. In this solvent, with PCM, the dipole moment increases only by 41 % when compared with the vacuum dipole, but with iterative S-QM/MM, it increases by 76 %. Hence, specific interactions, as hydrogen bonds, which are included in the S-QM/MM methodology but not in PCM, are extremely important for Prodan polarization in water.

Prodan electric dipole moments calculated by Mennucci et al. (2008), using a modified PCM model, are also presented in Table 7. In vaccum (Table 5), acetonitrile, and cyclohexane, these dipole moment values are greater than those obtained by us using S-QM-MM calculations, probably due to the difference in the QM level of calculation. In their paper, these authors also calculated the dipole for an optimized cluster: a Prodan with two water molecules hydrogen-bonded to the O5 atom. They calculated the dipole moment of this cluster in the absence (μ vacuum *) and in the presence of the PCM (μ PCM *) (see Table 7). Interestingly, in vacuum, with the two hydrogen bonds only, the value obtained by Mennucci et al. (2008), 9.8 D, is very similar to that obtained by us with the iterative S-QM-MM methodology, showing that the specific interaction between Prodan and these two water molecules is fundamental to describing Prodan–water interactions. The optimized geometry (Mennucci et al. 2008) probably overestimates the solute–water interactions, as it is able to reach the μ QM/MM value, which takes into account both hydrogen bonds and bulk interactions. When the two hydrogen bonds were considered in the PCM model (Mennucci et al. 2008), the obtained dipole moment is overestimated (13.21 D) compared with the μ QM/MM value (10.2 D). Using the S-QM-MM method, after the polarization process, the number of water molecules hydrogen-bonded to the O5 was found to be 2.7 per configuration, on average. This value is compatible with the two water molecules used by Mennucci et al. (2008). However, in the optimized cluster used by these authors, hydrogen-bond interactions are stronger because the model neglects the remaining water–water interactions, which are considered in the S-QM-MM simulation.

The final calculated atomic charges of Prodan in the iterative S-QM/MM procedure are presented in Table 8. Surprisingly, no expected charge separation between O5 and N26 was observed in the ground state, as proposed by Weber and Farris (1979), which is in agreement with the results of Nitschke et al. (2012). As the solvent polarity increases, from cyclohexane to water, the O5 atom becomes more negative, but the negative charge is not coming from the N26 atom, but mostly from the C4 atom, which is bonded to O5 (see Fig. 1), showing a local charge separation between the two atoms. It is possible to observe that the carbon atoms in the naphthalene ring (C2, C3, C6-C25) also have their charge modified in order to favor the charge separation between C4 and O5. Therefore, this collective effect results in the increase of Prodan dipole moment in water.

Table 8.

Atomic charges calculated after the polarization process with iterative S-QM/MM

Atom Vacuum Cyclohexane Dichloromethane Acetonitrile Water
C2 −0.193 −0.121 −0.096 −0.092 −0.056
C3 0.014 −0.065 −0.093 −0.089 −0.157
C4 0.364 0.456 0.495 0.474 0.601
O5 −0.444 −0.537 −0.604 −0.590 −0.761
C6 0.123 0.118 0.134 0.145 0.141
C9 −0.062 −0.052 −0.052 −0.057 −0.040
C13 0.024 0.100 0.102 0.090 0.116
C15 −0.089 −0.183 −0.193 −0.190 −0.193
C17 0.133 0.294 0.297 0.303 0.322
C18 −0.202 −0.319 −0.337 −0.342 −0.363
C20 0.274 0.395 0.415 0.426 0.430
C21 −0.019 −0.116 −0.110 −0.114 −0.103
C23 −0.143 −0.058 −0.050 −0.051 −0.041
C25 0.235 0.127 0.117 0.118 0.105
N26 −0.275 −0.284 −0.307 −0.328 −0.291
C27 0.125 0.123 0.140 0.151 0.144
C31 0.135 0.123 0.142 0.146 0.146
Open in a new tab

In bold, the most relevant data discussed in the text

Conclusions

We confirm the assignment of the Prodan and Laurdan electronic transition as a π–π* transition (HOMO–LUMO), with a small charge transfer (N → O). The HOMO and LUMO of both fluorophores are localized in the region between the amine and carbonyl groups and show a negligible influence of the hydrophobic tail of Laurdan in the orbitals involved in the electronic transition. Therefore, the calculated HOMO and LUMO for Prodan and Laurdan indicate almost identical electronic structures for both molecules and explain the similarity between the experimental absorption spectra of Prodan and Laurdan in different solvents. The very similar emission spectra of Prodan and Laurdan indicate the similarity of the excited state structures of the two probes.

Values of the ground and excited state electric dipole moments, μ G and μ E, of Prodan and Laurdan are shown, as obtained using the Lippert–Mataga equation and the QM calculation of the isolated molecules in vacuum. Although the values obtained with the Lippert–Mataga equation depend on cavity shape and dimensions, comparing both methodologies, we suggest that the best estimate values are μ G = 5.5 D and μ E = 20.0 D for Prodan, and μ G = 5.9 D and μ E = 20.9 D for Laurdan. This value for the Prodan ground state is in good agreement with the most reliable theoretical values presented in literature (6.1 D) and in this work (5.8 D). Additionally, using an iterative and sequential hybrid method with QM and MM, it is shown that the Prodan ground state electric dipole moment is very dependent on the medium, even for non-protic solvents. In vacuum, its calculated dipole moment is around 5.5 D and increases to 6.1 D in cyclohexane, 7.7 D in dichloromethane, 8.0 D in acetonitrile, and 10.2 D in water. Here, we identify that the Prodan polarization, induced by the presence of the solvent, is responsible for local charge separation in the C = O bond of Prodan. This is different from what could be initially expected, considering that the chemical structure of Prodan presents an electron donor group, N(CH3)2, and an electron acceptor group, C=O.

For comparison, the solvent as PCM was also used to calculate the induced electric dipole moment of Prodan in solution. Although PCM is a simple solvent model, it was able to well describe the polarization of Prodan in solution except for water, where it was found important to include at least two water molecules hydrogen-bonded to Prodan.

Acknowledgments

This work was supported by FAPESP, CNPq, CAPES, NAP-FCx, INCT-FCx, and nBioNet. Additionally, CCV-S acknowledges a fellowship from FAPESP and MTL and KC research fellowships from CNPq.

This article does not contain any studies with human or animal subjects performed by any of the authors.

Conflict of interest

None.

Footnotes

1

Several papers mention the wavelengths of the maximum absorption of the lower energy band of Prodan in different solvents (Weber and Farris 1979; Heisel et al. 1987; Balter et al. 1988; Catalan et al. 1991; Kawski 1999; Moyano et al. 2006). Possibly due to the broad absorption band, the cited positions of the maximum absorption of the lower energy band vary from 354.9 to 361 nm in chloroform, and from 356.8 to 364 nm in water. In some solvents, the Prodan optical absorption spectrum has been published (Bunker et al. 1993; Parusel et al. 1998; Artukhov et al. 2007; Sun et al. 1997). To our knowledge, this is the first time that absorption spectra of Laurdan are published and compared with Prodan in different solvents.

2

Different values of ν ab and ν em obtained by different groups could possibly be attributed to the very broad band of Prodan and Laurdan, mainly the absorption spectra, as mentioned before (see Fig. 3 and Table 2).

3

Solvents average density: water 1.022 ± 0.008 g/cm3, cyclohexane 0.770 ± 0.006 g/cm3, dichloromethane 1.19 ± 0.01 g/cm3, acetonitrile 0.834 ± 0.009 g/cm3.

4

For Prodan, the ε i and σ i were obtained from OPLS force field (Jorgensen et al. 1996), and the atomic charges were calculated with quantum mechanics (MP2/aug-cc-pVDZ), using the fitting of the electrostatic potential, the CHELPG procedure (Breneman and Wiberg 1990). The geometry and the parameters for the four solvents used were: single point charge model (SPC/E; Berendsen et al. 1987) for water, the Madden model (Bohm et al. 1983) for acetonitrile, and OPLS-AA for dichloromethane and cyclohexane, the latter in chair conformation (Jorgensen et al. 1996). The geometry for Prodan was obtained using the QM calculation, with density functional theory (B3LYP/6-31G*), starting from a X-ray geometry (Ilich and Prendergast 1989).

Special Issue Advances in Biophysics in Latin America

References

  1. Adhikary R, Barnes CA, Petrich JW. Solvation dynamics of the fluorescent probe PRODAN in heterogeneous environments: contributions from the locally excited and charge-transferred states. J Phys Chem B. 2009;113(35):11999–12004. doi: 10.1021/jp905139n. [DOI] [PubMed] [Google Scholar]
  2. Alleva R, Ferretti G, Borghi B, Pignotti E, Bassi A, Curatola G. Physicochemical properties of membranes of recovered erythrocytes in blood autologous transfusion–a study using fluorescence technique. Transfus Sci. 1995;16(3):291–297. doi: 10.1016/0955-3886(95)00033-T. [DOI] [PubMed] [Google Scholar]
  3. Ambrosini A, Bertoli E, Tanfani F, Wozniak M, Zolese G. The effect of N-Acyl ethanolamines on phosphatidylethanolamine phase-transitions Studied by laurdan generalized polarization. Chem Phys Lipids. 1994;72(2):127–134. doi: 10.1016/0009-3084(94)90096-5. [DOI] [PubMed] [Google Scholar]
  4. Ambrosini A, Zolese G, Balercia G, Bertoli E, Arnaldi G, Mantero F. Laurdan* fluorescence: a simple method to evaluate sperm plasma membrane alterations. Fertil Steril. 2001;76(3):501–505. doi: 10.1016/S0015-0282(01)01970-7. [DOI] [PubMed] [Google Scholar]
  5. Artukhov VY, Zharkova OM, Morozova JP. Features of absorption and fluorescence spectra of prodan. Spectrochim Acta A. 2007;68(1):36–42. doi: 10.1016/j.saa.2006.10.048. [DOI] [PubMed] [Google Scholar]
  6. Bacon AD, Zerner MC. Intermediate neglect of differential overlap theory for transition-metal complexes—Fe, Co and Cu chlorides. Theor Chim Acta. 1979;53(1):21–54. doi: 10.1007/BF00547605. [DOI] [Google Scholar]
  7. Bagatolli LA, Maggio B, Aguilar F, Sotomayor CP, Fidelio GD. Laurdan properties in glycosphingolipid-phospholipid mixtures: a comparative fluorescence and calorimetric study. Biochim Biophys Acta Biomembr. 1997;1325(1):80–90. doi: 10.1016/S0005-2736(96)00246-5. [DOI] [PubMed] [Google Scholar]
  8. Balter A, Nowak W, Pawelkiewicz W, Kowalczyk A. Some remarks on the interpretation of the spectral properties of Prodan. Chem Phys Lett. 1988;143(6):565–570. doi: 10.1016/0009-2614(88)87067-2. [DOI] [Google Scholar]
  9. Becke AD. Density-functional exchange-energy approximation with correct asymptotic-behavior. Phys Rev A. 1988;38(6):3098–3100. doi: 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
  10. Bell JD, Burnside M, Owen JA, Royall ML, Baker ML. Relationships between bilayer structure and phospholipase A(2) activity: interactions among temperature, diacylglycerol, lysolecithin, palmitic acid, and dipalmitoylphosphatidylcholine. Biochemistry. 1996;35(15):4945–4955. doi: 10.1021/bi952274i. [DOI] [PubMed] [Google Scholar]
  11. Berendsen HJC, Grigera JR, Straatsma TP. The missing term in effective pair potentials. J Phys Chem. 1987;91(24):6269–6271. doi: 10.1021/j100308a038. [DOI] [Google Scholar]
  12. Bohm HJ, Mcdonald IR, Madden PA. An effective pair potential for liquid acetonitrile. Mol Phys. 1983;49(2):347–360. doi: 10.1080/00268978300101211. [DOI] [Google Scholar]
  13. Breneman CM, Wiberg KB. Determining atom-centered monopoles from molecular electrostatic potentials—the need for high sampling density in formamide conformational-analysis. J Comput Chem. 1990;11(3):361–373. doi: 10.1002/jcc.540110311. [DOI] [Google Scholar]
  14. Bunker CE, Bowen TL, Sun YP. A photophysical study of solvatochromic Probe 6-Propionyl-2-(N, N-Dimethylamino)Naphthalene (Prodan) in solution. Photochem Photobiol. 1993;58(4):499–505. doi: 10.1111/j.1751-1097.1993.tb04921.x. [DOI] [Google Scholar]
  15. Canuto S, Coutinho K, Zerner MC. Including dispersion in configuration interaction-singles calculations for the spectroscopy of chromophores in solution. J Chem Phys. 2000;112(17):7293–7299. doi: 10.1063/1.481332. [DOI] [Google Scholar]
  16. Catalan J, Perez P, Laynez J, Blanco FG. Analysis of the solvent effect on the photophysics properties of 6-Propionyl-2-(dimethylamino)naphthalene (PRODAN) J Fluoresc. 1991;1(4):215–223. doi: 10.1007/BF00865246. [DOI] [PubMed] [Google Scholar]
  17. Coutinho K, Canuto S. Solvent effects from a sequential Monte Carlo–Quantum mechanical approach. Adv Quantum Chem. 1997;28:89–105. [Google Scholar]
  18. Coutinho K, Canuto S (2009) DICE: a Monte Carlo program for molecular liquid simulation, version 2.9. University of São Paulo, São Paulo, Brazil
  19. Coutinho K, Georg HC, Fonseca TL, Ludwig V, Canuto S. An efficient statistically converged average configuration for solvent effects. Chem Phys Lett. 2007;437(1–3):148–152. doi: 10.1016/j.cplett.2007.02.012. [DOI] [Google Scholar]
  20. De Vequi-Suplicy CC, Benatti CR, Lamy MT. Laurdan in fluid bilayers: position and structural sensitivity. J Fluoresc. 2006;16(3):431–439. doi: 10.1007/s10895-005-0059-3. [DOI] [PubMed] [Google Scholar]
  21. Dwivedi Y, Kant S, Rai SB, Rai RN. Synthesis, physicochemical and optical characterization of novel fluorescing complex: o-Phenylenediamine-Benzoin. J Fluoresc. 2011;21(3):1255–1263. doi: 10.1007/s10895-010-0808-9. [DOI] [PubMed] [Google Scholar]
  22. Everett RK, Nguyen AA, Abelt CJ. Does PRODAN possess an O-TICTexcited state? Synthesis and properties of two constrained derivatives. J Phys Chem A. 2010;114(14):4946–4950. doi: 10.1021/jp1002808. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Ferretti G, Taus M, Dousset N, Solera ML, Valdiguie P, Curatola G. Physicochemical properties of copper-oxidized high-density-lipoprotein—a fluorescence study. Biochem Mol Biol Int. 1993;30(4):713–719. [PubMed] [Google Scholar]
  24. Field MJ, Bash PA, Karplus M. A combined quantum-mechanical and molecular mechanical potential for molecular-dynamics simulations. J Comput Chem. 1990;11(6):700–733. doi: 10.1002/jcc.540110605. [DOI] [Google Scholar]
  25. Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JA TV, Jr, Kudin KN, Burant JC, Millam JM, Iyengar SS, Tomasi J, Barone V, Mennucci B, Cossi M, Scalmani G, Rega N, Petersson GA, Nakatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Klene M, Li X, Knox JE, Hratchian HP, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Ayala PY, Morokuma K, Voth GA, Salvador P, Dannenberg JJ, Zakrzewski VG, Dapprich S, Daniels AD, Strain MC, Farkas O, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Ortiz JV, Cui Q, Baboul AG, Clifford S, Cioslowski J, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin RL, Fox DJ, Keith T, Al-Laham MA, Peng CY, Nanayakkara A, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Gonzalez C, Pople JA. GAUSSIAN. Wallingford: Gaussian, Inc; 2004. [Google Scholar]
  26. Georg HC, Coutinho K, Canuto S. Converged electronic polarization of acetone in liquid water and the role in the n-pi* transition. Chem Phys Lett. 2006;429(1–3):119–123. doi: 10.1016/j.cplett.2006.08.047. [DOI] [Google Scholar]
  27. Ghoneim N, Suppan P. Solvatochromic shifts of nondipolar molecules in polar-solvents. Spectrochim Acta A. 1995;51(6):1043–1050. doi: 10.1016/0584-8539(94)00196-I. [DOI] [Google Scholar]
  28. Heisel F, Miehe JA, Szemik AW. Experimental-evidence of an intramolecular reaction in excited Prodan solution. Chem Phys Lett. 1987;138(4):321–326. doi: 10.1016/0009-2614(87)80391-3. [DOI] [Google Scholar]
  29. Hertwig RH, Koch W. On the parameterization of the local correlation functional. What is Becke-3-LYP? Chem Phys Lett. 1997;268(5–6):345–351. doi: 10.1016/S0009-2614(97)00207-8. [DOI] [Google Scholar]
  30. Huang Y, Li XY, Fu KX, Zhu Q. New formulation for non-equilibrium solvation: Spectral shifts and cavity radii of 6-propanoyl-2(N, N-dimethylamino) naphthalene and 4-(N, N-dimethylamino) benzonitrile. J Chem Theory Comput. 2006;5:355–374. doi: 10.1142/S0219633606002313. [DOI] [Google Scholar]
  31. Ilich P, Prendergast FG. Singlet adiabatic states of solvated PRODAN: a semiempirical molecular orbital study. J Phys Chem. 1989;93:4441–4447. doi: 10.1021/j100348a014. [DOI] [Google Scholar]
  32. Jorgensen WL, Maxwell DS, TiradoRives J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J Am Chem Soc. 1996;118(45):11225–11236. doi: 10.1021/ja9621760. [DOI] [Google Scholar]
  33. Kawski A. Ground- and excited-state dipole moments of 6-propionyl-2-(dimethylamino)naphthalene determined from solvatochromic shifts. Z Naturforsch A J Phys Sci. 1999;54(6–7):379–381. [Google Scholar]
  34. Kawski A, Kuklinski B, Bojarski P. Thermochromic shifts of absorption and fluorescence spectra and excited state dipole moment of PRODAN. Z Naturforsch A Phys Sci. 2000;55(5):550–554. [Google Scholar]
  35. Kozyra KA, Heldt JR, Heldt J, Engelke M, Diehl HA. Concentration and temperature dependence of Laurdan fluorescence in glycerol. Z Naturforsch A Phys Sci. 2003;58(9–10):581–588. [Google Scholar]
  36. Lakowicz JR. Principles of fluorescence spectroscopy. 3. New York: Plenum; 2006. [Google Scholar]
  37. Lee CT, Yang WT, Parr RG. Development of the colle-salvetti correlation-energy formula into a functional of the electron-density. Phys Rev B. 1988;37(2):785–789. doi: 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  38. Lide DR, Weast RC, Chemical Rubber Company . CRC Handbook of chemistry and physics: a ready reference book of chemical and physical data. 83. Boca Raton: CRC Press; 2002. [Google Scholar]
  39. Lippert E. Dipolmoment Und Elektronenstruktur Von Angeregten Molekulen. Z Naturforsch A Astrophys Phys Physikalisch Chem. 1955;10(7):541–545. [Google Scholar]
  40. Lobo BC, Abelt CJ. Does PRODAN possess a planar or twisted charge-transfer excited state? Photophysical properties of two PRODAN derivatives. J Phys Chem A. 2003;107(50):10938–10943. doi: 10.1021/jp036013r. [DOI] [Google Scholar]
  41. Lucio AD, Vequi-Suplicy CC, Fernandez RM, Lamy MT. Laurdan spectrum decomposition as a tool for the analysis of surface bilayer structure and polarity: a study with DMPG, peptides and cholesterol. J Fluoresc. 2010;20(2):473–482. doi: 10.1007/s10895-009-0569-5. [DOI] [PubMed] [Google Scholar]
  42. Mataga N, Kaifu Y, Koizumi M. Solvent effects upon fluorescence spectra and the dipolemoments of excited molecules. Bull Chem Soc Jpn. 1956;29(4):465–470. doi: 10.1246/bcsj.29.465. [DOI] [Google Scholar]
  43. Mennucci B, Caricato M, Ingrosso F, Cappelli C, Cammi R, Tomasi J, Scalmani G, Frisch MJ. How the environment controls absorption and fluorescence spectra of PRODAN: a quantum-mechanical study in homogeneous and heterogeneous media. J Phys Chem B. 2008;112(2):414–423. doi: 10.1021/jp076138m. [DOI] [PubMed] [Google Scholar]
  44. Miertus S, Scrocco E, Tomasi J. Electrostatic interaction of a solute with a continuum—a direct utilization of abinitio molecular potentials for the prevision of solvent effects. Chem Phys. 1981;55(1):117–129. doi: 10.1016/0301-0104(81)85090-2. [DOI] [Google Scholar]
  45. Moller C, Plesset MS. Note on an approximation treatment for many-electron systems. Phys Rev. 1934;46(7):0618–0622. doi: 10.1103/PhysRev.46.618. [DOI] [Google Scholar]
  46. Morozova YP, Zharkova OM, Balakina TY, Artyukhov VY. Effect of proton-donor solvent and structural flexibility of prodan and laurdan molecules on their spectral-luminescent properties. J Appl Spectrosc. 2009;76(3):312–318. doi: 10.1007/s10812-009-9193-z. [DOI] [Google Scholar]
  47. Moyano F, Biasutti MA, Silber JJ, Correa NM. New insights on the behavior of PRODAN in homogeneous media and in large unilamellar vesicles. J Phys Chem B. 2006;110(24):11838–11846. doi: 10.1021/jp057208x. [DOI] [PubMed] [Google Scholar]
  48. Moyano F, Silber JJ, Correa NM. On the investigation of the bilayer functionalities of 1,2-di-oleoyl-sn-glycero-3-phosphatidylcholine (DOPC) large unilamellar vesicles using cationic hemicyanines as optical probes: A wavelength-selective fluorescence approach. J Colloid Interface Sci. 2008;317(1):332–345. doi: 10.1016/j.jcis.2007.09.051. [DOI] [PubMed] [Google Scholar]
  49. Nitschke WK, Vequi-Suplicy CC, Coutinho K, Stassen H. Molecular dynamics investigations of PRODAN in a DLPC bilayer. J Phys Chem B. 2012;116(9):2713–2721. doi: 10.1021/jp2085582. [DOI] [PubMed] [Google Scholar]
  50. Novaira M, Biasutti MA, Silber JJ, Correa NM. New insights on the photophysical behavior of PRODAN in anionic and cationic reverse micelles: From which state or states does it emit? J Phys Chem B. 2007;111(4):748–759. doi: 10.1021/jp065528q. [DOI] [PubMed] [Google Scholar]
  51. Novaira M, Moyano F, Biasutti MA, Silber JJ, Correa NM. An example of how to use AOT reverse micelle interfaces to control a photoinduced intramolecular charge-transfer process. Langmuir. 2008;24(9):4637–4646. doi: 10.1021/la704004m. [DOI] [PubMed] [Google Scholar]
  52. Nowak W, Adamczak P, Balter A, Sygula A. On the possibility of fluorescence from twisted intramolecular charge-transfer states of 2-dimethylamino-6-acylnaphthalenes—a quantum-chemical study. Theochem J Mol Struct. 1986;139(1–2):13–23. doi: 10.1016/0166-1280(86)80103-8. [DOI] [Google Scholar]
  53. Parasassi T, Conti F, Gratton E. Time-resolved fluorescence emission-spectra of laurdan in phospholipid-vesicles by multifrequency phase and modulation fluorometry. Cell Mol Biol. 1986;32(1):103–108. [PubMed] [Google Scholar]
  54. Parusel A. Semiempirical studies of solvent effects on the intramolecular charge transfer of the fluorescence probe PRODAN. J Chem Soc-Faraday Trans. 1998;94(19):2923–2927. doi: 10.1039/a804841j. [DOI] [Google Scholar]
  55. Parusel ABJ, Schneider FW, Kohler G. An ab initio study on excited and ground state properties of the organic fluorescence probe PRODAN. Theochem J Mol Struct. 1997;398:341–346. doi: 10.1016/S0166-1280(96)05002-6. [DOI] [Google Scholar]
  56. Parusel ABJ, Nowak W, Grimme S, Kohler G. Comparative theoretical study on charge-transfer fluorescence probes: 6-propanoyl-2-(N, N-dimethylamino)naphthalene and derivatives. J Phys Chem A. 1998;102(36):7149–7156. doi: 10.1021/jp981540+. [DOI] [Google Scholar]
  57. Parusel ABJ, Schamschule R, Kohler G. Nonlinear optics. A semiempirical study of organic chromophores. J Mol Struct Theochem. 2001;544:253–261. doi: 10.1016/S0166-1280(01)00384-0. [DOI] [Google Scholar]
  58. Reichardt C. Solvatochromic dyes as solvent polarity indicators. Chem Rev. 1994;94(8):2319–2358. doi: 10.1021/cr00032a005. [DOI] [Google Scholar]
  59. Reichardt C. Solvents and solvent effects in organic chemistry. 3. Weinheim: Wiley-VCH; 2004. [Google Scholar]
  60. Ridley J, Zerner M. Intermediate neglect of differential overlap technique for spectroscopy—pyrrole and azines. Theor Chim Acta. 1973;32(2):111–134. doi: 10.1007/BF00528484. [DOI] [Google Scholar]
  61. Rollinson AM, Drickamer HG. High-pressure study of luminescence from intramolecular Ct compounds. J Chem Phys. 1980;73(12):5981–5996. doi: 10.1063/1.440132. [DOI] [Google Scholar]
  62. Rottenberg H. Probing the interactions of alcohols with biological-membranes with the fluorescent-probe prodan. Biochemistry. 1992;31(39):9473–9481. doi: 10.1021/bi00154a021. [DOI] [PubMed] [Google Scholar]
  63. Rowe BA, Roach CA, Lin J, Asiago V, Dmitrenko O, Neal SL. Spectral heterogeneity of PRODAN fluorescence in isotropic solvents revealed by multivariate photokinetic analysis. J Phys Chem A. 2008;112(51):13402–13412. doi: 10.1021/jp802260y. [DOI] [PubMed] [Google Scholar]
  64. Samanta A, Fessenden RW. Excited state dipole moment of PRODAN as determined from transient dielectric loss measurements. J Phys Chem A. 2000;104(39):8972–8975. doi: 10.1021/jp0009960. [DOI] [Google Scholar]
  65. Scholte TG. A contribution to the theory of the dielectric constant of polar liquids. Physica. 1949;15(5–6):437–449. doi: 10.1016/0031-8914(49)90088-9. [DOI] [Google Scholar]
  66. Seliskar CJ, Brand L. Electronic spectra of 2-aminonaphthalene-6-sulfonate and related molecules. General properties and excited-state reactions. J Am Chem Soc. 1971;93(21):5405. doi: 10.1021/ja00750a016. [DOI] [Google Scholar]
  67. Siddlingeshwar B, Hanagodimath SM. Estimation of the ground and the first excited singlet-state dipole moments of 1,4-disubstituted anthraquinone dyes by the solvatochromic method. Spectrochim Acta A Mol Biomol Spectrosc. 2010;75(4):1203–1210. doi: 10.1016/j.saa.2009.12.007. [DOI] [PubMed] [Google Scholar]
  68. Simon JD, Thompson PA. Spectroscopy and rotational-dynamics of oxazine-725 in alcohols—a test of dielectric friction theories. J Chem Phys. 1990;92(5):2891–2896. doi: 10.1063/1.457936. [DOI] [Google Scholar]
  69. Stephens PJ, Devlin FJ, Chabalowski CF, Frisch MJ. Ab-initio calculation of vibrational absorption and circular-dichroism spectra using density-functional force-fields. J Phys Chem. 1994;98(45):11623–11627. doi: 10.1021/j100096a001. [DOI] [Google Scholar]
  70. Sun SY, Heitz MP, Perez SA, Colon LA, Bruckenstein S, Bright FV. 6-Propionyl-2-(N, N-dimethylamino)naphthalene(PRODAN) revisited. Appl Spectrosc. 1997;51(9):1316–1322. doi: 10.1366/0003702971941980. [DOI] [Google Scholar]
  71. Suppan P. Solvatochromic shifts - the influence of the medium on the energy of electronic states. J Photochem Photobiol A Chem. 1990;50(3):293–330. doi: 10.1016/1010-6030(90)87021-3. [DOI] [Google Scholar]
  72. Tomasi J. Thirty years of continuum solvation chemistry: a review, and prospects for the near future. Theor Chem Accounts. 2004;112(4):184–203. doi: 10.1007/s00214-004-0582-3. [DOI] [Google Scholar]
  73. Tomasi J, Mennucci B, Cammi R. Quantum mechanical continuum solvation models. Chem Rev. 2005;105(8):2999–3093. doi: 10.1021/cr9904009. [DOI] [PubMed] [Google Scholar]
  74. Tomin VI. Nonradiative energy transfer in a concentrated solution of prodan. Opt Spectrosc. 2006;101(4):563–567. doi: 10.1134/S0030400X06100109. [DOI] [Google Scholar]
  75. Tomin VI, Hubisz K. Inhomogeneous spectral broadening and the decay kinetics of the luminescence spectra of prodan. Opt Spectrosc. 2006;101(1):98–104. doi: 10.1134/S0030400X06070174. [DOI] [Google Scholar]
  76. Tomin VI, Brozis M, Heldt J. The red-edge effects in laurdan solutions. Z Naturforsch A J Phys Sci. 2003;58(2–3):109–117. [Google Scholar]
  77. Vequi-Suplicy CC, Lamy MT, Marquezin CA. The new fluorescent membrane probe Ahba: a comparative study with the largely used Laurdan. J Fluoresc. 2013;23(3):479–486. doi: 10.1007/s10895-013-1172-3. [DOI] [PubMed] [Google Scholar]
  78. Viard M, Gallay J, Vincent M, Meyer O, Robert B, Paternostre M. Laurdan solvatochromism: Solvent dielectric relaxation and intramolecular excited-state reaction. Biophys J. 1997;73(4):2221–2234. doi: 10.1016/S0006-3495(97)78253-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  79. Weber G, Farris FJ. Synthesis and spectral properties of a hydrophobic fluorescent-probe—6-propionyl-2-(dimethylamino)naphthalene. Biochemistry. 1979;18(14):3075–3078. doi: 10.1021/bi00581a025. [DOI] [PubMed] [Google Scholar]
  80. Zeng JW, Chong PLG. Interactions between pressure and ethanol on the formation of interdigitated Dppc liposomes - a study with prodan fluorescence. Biochemistry. 1991;30(39):9485–9491. doi: 10.1021/bi00103a014. [DOI] [PubMed] [Google Scholar]
  81. Zerner MC (2000) INDO/UF: A semi-empirical package. University of Florida, Gainesville

Articles from Biophysical Reviews are provided here courtesy of Springer

RESOURCES