A historical perspective of the biophysics of the thrombin–heparin system: an example of nonspecific binding and the consequent parking problem in action

Abstract

Difficulties are encountered in the thermodynamic characterization of interactions between a protein ligand and a linear acceptor, such as a polynucleotide or a polysaccharide, because of the involvement of more than one unit of the polymer chain in each attachment of a protein molecule. Complications arise from the fact that random attachment of ligand to the polymer chain, each unit of which is a potential binding site, initially leads to suboptimal location of protein molecules along the polymer chain—a situation that has to be rectified before the attainment of thermodynamic equilibrium can be realized. Kinetic as well as thermodynamic consequences of such nonspecific binding, termed the parking problem, therefore need to be considered in any quantitative characterization of the interaction between a large ligand and a linear polymer acceptor chain. Results for the thrombin–heparin interaction have been used to illustrate a thermodynamic characterization of nonspecific binding that takes into account these consequences of the parking problem.

Introduction

Discovery of the anticoagulant activity of heparin has led not only to its widespread clinical use but also to the search for other highly-sulfated polysaccharides as heparin substitutes/supplanters—a search that is ongoing (Chen et al. 2012; Fernández et al. 2013) despite concurrent emphasis on direct thrombin inhibitors (Coppens et al. 2012; Marson et al. 2012). Heparin, a sulfated glycosaminoglycan in which the repeat unit is a disaccharide comprising α-L-iduronic acid-2-sulfate linked β-1,4 to N-sulfurylglucosamine-6-sulfate, exerts its therapeutic effect by catalyzing the antithrombin-mediated inhibition of various coagulation proteases (Björk and Lindahl 1982; Björk et al. 1989). For thrombin, this inactivation of blood clotting entails the formation of a ternary complex in which enzyme and antithrombin are both bound to heparin (Olson and Shore 1981; Olson 1988). Physicochemical characterization of the interaction between antithrombin and the polysaccharide proved to be relatively straightforward in that the reaction involves binding of the enzyme to a unique pentasaccharide sequence of heparin (Rosenberg and Damus 1973; Laurent et al. 1978; Olson 1988). On the other hand, the initial enthusiasm for quantitative characterization of the corresponding interaction between thrombin and heparin (Nesheim et al. 1986; Evington et al. 1986) seems to have been quashed by the realization (Olson et al. 1991) that heparin does not possess a specific binding site for thrombin, which merely binds electrostatically to the highly charged polyanion. Since then, the only experimental studies have entailed molecular mapping to identify the basic residues of thrombin involved in the interaction (Gan et al. 1994; Sheehan and Sadler 1994), and the determination of the crystal structure for thrombin bound to a heparin octasaccharide (Carter et al. 2005). Further biophysical characterization of complex formation between thrombin and heparin has been confined to reinterpretation (Munro et al. 1998, 2000) of the published experimental data (Nesheim et al. 1986; Olson et al. 1991), in terms of binding theory developed mainly by Epstein (1978, 1979a, b) for the interaction of a multivalent ligand with linear segments of a polymeric acceptor in which any unit is a potential starting point of the linear acceptor sequence to which ligand binds.

The invitation to prepare this contribution on the biophysics of the thrombin–heparin interaction has afforded an opportunity to review the characterization of nonspecific binding, a phenomenon considered initially in the context of protein–polynucleotide interactions (Latt and Sober 1967; McGhee and von Hippel 1974)—systems for which the length of the polymeric acceptor chain could be regarded as infinite. Use of the thrombin–heparin interaction as the model system requires account to be taken of additional thermodynamic and kinetic complexities that arise in ligand binding to segments of a polymeric acceptor with finite chainlength (Epstein 1978, 1979a, b; Munro et al. 1998, 2000). Provided that experimental studies of the biophysics of the thrombin–heparin are in a state of dormancy rather than demise, this review should serve not only as a historical record of research from a bygone era but also as a summary of factors requiring attention in any future attempted characterization of this system, or, indeed, of any other interaction involving the nonspecific binding of a protein to linear segments of a polymeric acceptor.

Nonspecific binding

The binding of proteins to polymer chains comprising identical or very similar units sometimes entails interaction of the protein (ligand) with a linear sequence of units on the polymer (acceptor) chain. Examples include the binding of proteins to polynucleotides (Latt and Sober 1967; McGhee and von Hippel 1974), to polysaccharides (Olson et al. 1991), and to a protein polymer chain such as the actin filament (Greene and Eisenberg 1980). Thermodynamic characterization of such systems is complicated because the similarity of repeat units in the polymer chain creates a situation wherein any residue sequence of appropriate length is a potential binding site. An absence of specific acceptor sites for ligand (protein) has led to the description of the protein–polymer interactions as nonspecific binding, even in instances where the same intrinsic association constant (Klotz 1946) applies to all interactions. Unfortunately, the same term has also been used in another context to describe much weaker acceptor–ligand binding than the high-affinity interaction of particular interest. Because the random attachment of protein to linear segments of the polymer chain leads to suboptimal alignment of ligand molecules on the acceptor chain, additional dissociation and reassociation events are required to achieve the ultimate arrangement that reflects the attainment of thermodynamic equilibrium. This complicating factor has been designated as the parking problem (Hill 1978; Hill et al. 1980).

The conclusion that nonspecific binding of a protein to linear segments of a one-dimensional polymer lattice results in binding curves that deviate in negatively cooperative fashion from the classical rectangular hyperbolic dependence upon ligand concentration predicted for specific binding to equivalent and independent acceptor sites (Klotz 1946; Scatchard 1949) was reached long ago (McGhee and von Hippel 1974; Epstein 1978; Hill 1978). However, subsequent quantitative kinetic considerations (Epstein 1979a, b; Munro et al. 1998, 2000) have revealed potential difficulties in establishing the reaction stoichiometry (integer value of the number of polymer units in the one-dimensional lattice divided by the length of the linear segment to which protein binds), because a rapidly attained transient (pseudoequilibrium) state precedes a much slower progression towards thermodynamic equilibrium. Although attainment of the pseudoequilibrium state may occur within seconds, the subsequent dissociation and reassociation events required to achieve true equilibrium take much longer. In an experimental study entailing spectral monitoring of the approach to equilibrium, there is clearly a potential for misidentification of the pseudoequilibrium response as the equilibrium value. Inasmuch as the difference in time-scales for the two events (initial random attachment and ligand rearrangement to achieve optimal ligand binding) increases dramatically with the extent of acceptor-site occupancy, the definition of the reaction stoichiometry by extrapolation of the binding data at high levels of acceptor saturation becomes susceptible to underestimation.

The parking problem

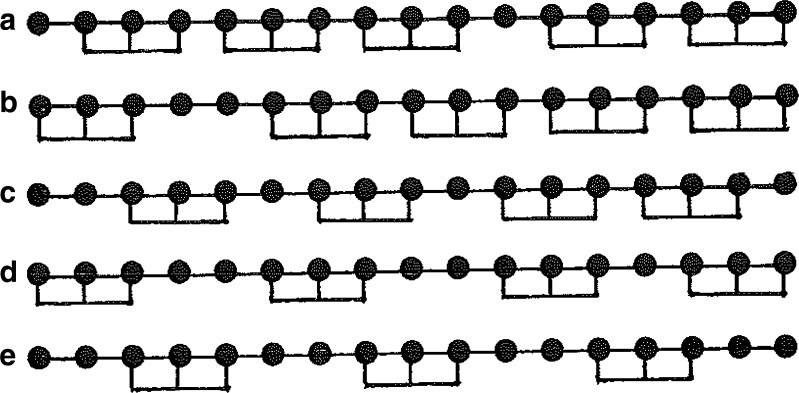
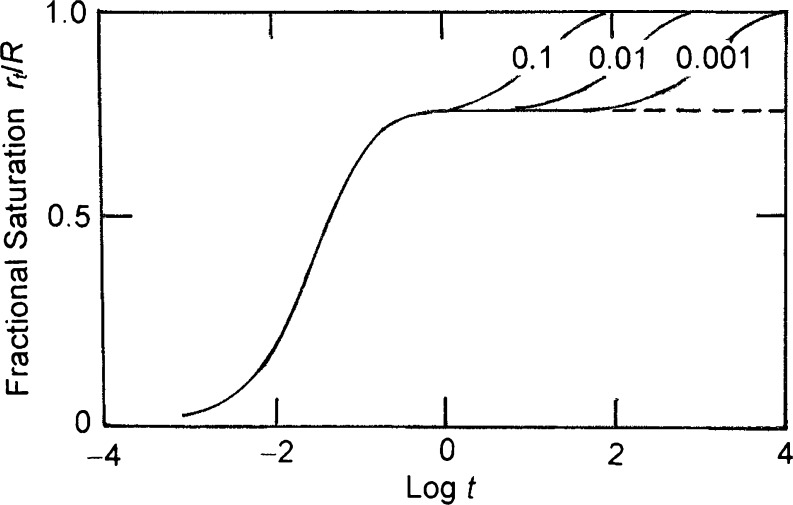
The parking problem is illustrated by considering the binding of a large ligand to three-residue linear sequences on a 17-unit one-dimensional lattice. Random attachment of ligand molecules can lead to the existence on the acceptor lattice of spaces containing too few unoccupied residues to accommodate an additional ligand molecule. Although the maximum number of ligand molecules that can attach to the acceptor chain is five (e.g., Fig. 1a, b), situations can arise in which the acceptor lattice is effectively saturated with only four (e.g., Fig. 1c, d) or even three (Fig. 1e) ligand molecules attached. From a thermodynamic viewpoint, the last three examples do not represent equilibrium situations: instead, they merely represent transient (pseudoequilibrium) states en route to lattice saturation with five ligand molecules attached. However, the life-time of those transient states can be considerable, because the attainment of acceptor saturation is conditional upon prior dissociation events, which can be slow for a high-affinity ligand–acceptor interaction (Epstein 1979a; Munro et al. 1998). Relative stability of the transient state is evident from Fig. 2, which summarizes the results of kinetic simulations (described later) with total acceptor and ligand concentrations of 1 μM and 100 μM, respectively, for systems in which the binding of ligand to three-residue sequences of a six-residue acceptor lattice is governed by an association rate constant of 0.1 μM⁻¹ s⁻¹ and dissociation constants ranging between 0.1 and 0.001 s⁻¹. These systems with intrinsic association constants (Klotz 1946) of 10⁶ to10⁸ M⁻¹ attain a pseudoequilibrium state within a second, and, for the weakest-affinity system, equilibrium is attained within 2 min. Although the parking problem should therefore be of little concern in quantifying the equilibrium response for this system, considerably more patience would be required on the part of an experimenter to avoid misidentification of the transient plateau as the equilibrium response for the highest-affinity system, which is only attained after almost 3 h.

Fig. 1.

Schematic representation of five “saturated” complexes formed during the early stages of random ligand attachment to three-unit segments of a 17-unit acceptor lattice. Whereas the first two examples (a, b) satisfy the thermodynamic requirement that five ligand molecules are required to saturate the lattice, the others demonstrate transient states in which initial saturation can involve the attachment of only four (c, d) or even three (e) ligand molecules

Fig. 2.

Logarithmic time dependence (t in s) of the approach to equilibrium predicted by simulations of nonspecific binding between ligand (S) and three-unit sequences of a six-unit acceptor lattice (A) in situations with [A _tot] = 1 μM, [S _tot] = 100 μM, k _f = 0.1 μM⁻¹ s⁻¹ and the indicated magnitudes (s⁻¹) for the dissociation rate constant (k _r): the broken line is obtained for irreversible binding (i.e., k _r = 0)

Thermodynamic consequences of nonspecific binding

Consider the situation in which a large ligand (S) binds to a linear sequence of n but occupies m units of a uni-dimensional lattice (A) containing N units. The interaction is governed by intrinsic association constant K, which can be multiplied by a factor ω to accommodate cooperativity (positive or negative). The thermodynamic characterization of nonspecific binding has been treated in greatest detail by Epstein (1978), who considered not only the question of cooperativity but also that of acceptor chainlength—an important consideration in the analysis of data for the thrombin–heparin interaction (Olson et al. 1991) because of its use of a relatively short acceptor (N = 13).

Non-cooperative binding

For non-cooperative binding to a sequence of n units of an acceptor lattice comprising N such units, the general form of the binding equation for r, the molar ratio of bound ligand to total acceptor, is (Klotz 1946)

1

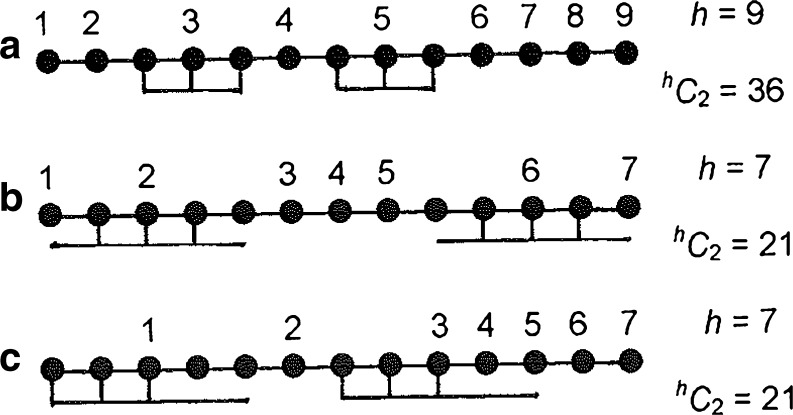
where [S] is the free ligand concentration, R the integer value of N/n, and where ^h C _i = h!/{i!(h − i)!} is the number of possible arrangements of the h items (bound ligand and unoccupied units) available for distribution in the lattice. In the attachment of the i-th ligand molecule to an N-unit acceptor lattice the number of items to be arranged is h = N − ni + i (Fig. 3a, where N = 13), whereupon (Latt and Sober 1967)

2

Fig. 3.

Schematic representation of the binding of a ligand to three-unit sequences of a 13-unit acceptor lattice illustrating the number of items (h) to be arranged in determination of the number of possible arrangements thereof, ^h Ci [Eqs. (2) and (3)]. a m = n = 3; b m = 5, m = 3 with symmetrical overlap of lattice units; c m = 5, m = 3 with asymmetrical overlap of lattice units

Extension of this combinatorial approach to include the possibility of the ligand occupying m units while only binding to n is accommodated (Kelly et al. 1976; Epstein 1978) by substituting [m(i − 1) + n] for ni in Eq. (2) to give

3

In that regard, it is immaterial whether the overlap is symmetrical or asymmetrical provided that the same specific asymmetry holds for all ligand attachments (Fig. 3b, c).

Cooperative binding

In order to incorporate the concept of cooperative binding, the intrinsic binding constant is multiplied by the factor ω whenever ligand attachment occurs adjacent to another bound ligand molecule on the acceptor lattice (Kelly et al. 1976; Epstein 1978). Because two adjacencies are encountered when the incoming ligand molecule occupies the entire space between two bound ligand molecules, the cooperativity factor becomes ω ². Consequently, the salient factor in the consideration of cooperative binding is the number of attachments to adjacent segments (j) possible in a particular arrangement of ligands on a linear lattice. For the situation with i ligands bound, the various possible arrangements contain a maximum of (i − 1) adjacencies, whereupon the ^h C _i coefficients now need to be expressed in terms of the number of ways of attaching i ligands with j adjacencies, ^h C _i(j), and the cooperativity parameter (ω) raised to the appropriate power (the number of adjacencies, j). Thus

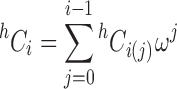4

where (Munro et al. 2000)

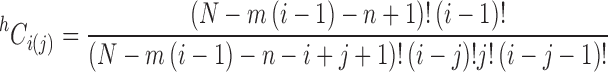5

As required, this expression simplifies to the corresponding expression reported by Epstein (1978) for the situation in which there is no overlap (m = n).

Kinetic consequences of the parking problem

The time course of equilibrium attainment can be determined either by Monte Carlo simulation or by solving numerically the set of ordinary differential equations for the binding of ligand to n-unit sequences on the N-unit acceptor lattice (Epstein 1978, 1979a, b). In that regard, the necessity to fix the free ligand concentration in order to effect numerical solution of those equations at that time no longer applies (Munro et al. 1998) because of advances in computer technology that now also allow [S] to be a variable, and hence allow exact numerical solutions to be obtained by either procedure. Although Monte Carlo procedures provide the simpler method for following the time course of equilibrium attainment, they require much greater amounts of computer time and capacity. On the other hand, numerical solution of the set of ordinary differential equations places demands on the experimenter to write the correct set of differential equations to be solved.

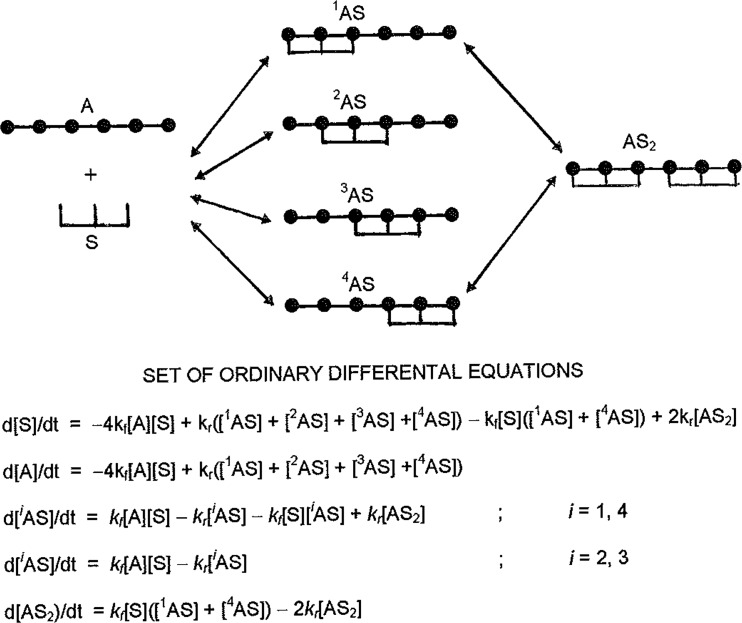
The method of constructing that set of differential equations is illustrated by considering the interactions of ligand with three consecutive units of a six-unit acceptor lattice. From the schematic representation of the system in the upper part of Fig. 4, there are four positions available for attachment of the first ligand molecule, all of which are equally probable. As well as these four 1:1 complexes (¹AS to ⁴AS), there is an AS₂ complex which can be generated by two pathways. The next step entails establishment of the differential equation for formation and loss of each species (lower part of Fig. 4).

Fig. 4.

Schematic representation of the various acceptor–ligand complexes formed in the nonspecific binding of a ligand (S) to three-unit sequences of an acceptor lattice (A) comprising six units: arrows indicate the interconversion of various acceptor–ligand species resulting from the attachment or removal of ligand. Also included are the set of ordinary differential equations that need to be solved for description of the time-course of equilibrium attainment

Numerical simulations of the kinetics of ligand binding have been used (Munro et al. 1998) to deduce the conditions under which the parking problem is likely to preclude the experimental measurement of equilibrium binding data. Specifically, time courses of equilibrium attainment (summarized in fig. 5b of Munro et al. 1998) were simulated for the intermediate situation shown in Fig. 2—a system in which the binding of ligand to three-unit sequences on a six-unit acceptor lattice ([A_tot] = 1 μM) is governed by k _f = 0.1 μM⁻¹ s⁻¹ and k _r = 0.01 s⁻¹ (i.e., by an intrinsic association constant of 10⁷ M⁻¹). Equilibrium was attained within 30 s at a low ligand concentration ([S_tot] = 0.1 μM), a situation commensurate with minimal (<5 %) saturation of the acceptor lattice. Although an increase in [S_tot] to 1 μM (leading to 46 % lattice saturation) sufficed to render detectable the consequences of the parking problem, a satisfactory estimate of the binding function would still have been obtained within 3 min. At a higher level of acceptor saturation ([S_tot] = 10 μM, 98 % lattice saturation), equilibrium attainment would have taken about 3 h. Reference to the reaction scheme for this system in Fig. 4 shows that formation of the saturated complex from either ¹AS or ⁴AS merely entails addition of the extra ligand molecule, whereas saturation of lattices with ²AS or ³AS as the initial complex requires dissociation of the currently bound ligand molecule (a relatively slow process) to allow the formation of either ¹AS or ⁴AS in the next attempt to saturate the lattice. At low levels of acceptor saturation, there are many potential arrangements of ligand on the lattice that meet the equilibrium requirement, and hence there is relatively little need for dissociation of non-saturable species. However, at the other end of the binding curve, this dissociation process becomes the dominating factor in the rate of attainment of thermodynamic equilibrium.

The results of those simulations serve as a warning of the need to ascertain whether a seemingly stable binding response reflects equilibrium attainment or merely the onset of the slow phase of a progress curve—a factor emphasized by plotting the progress curve on a logarithmic time scale (Fig. 2, which refers to time courses for essentially stoichiometric interaction). Although the restriction of ligand binding measurements to low levels of acceptor saturation should suffice to produce reasonably accurate estimates of the binding function r in experiments where r is measured directly, difficulties arise in situations where the parameter being monitored is the fractional saturation (as in spectral studies): the maximal response is not the appropriate parameter for acceptor-saturation at equilibrium. As shown later, this problem can be obviated by considering the maximal response in terms irreversible binding—the capacity prior to elimination of suboptimal ligand alignment. Support for that contention is provided by exact correspondence between the transient plateau observed in simulated time dependences of equilibrium attainment and the limiting value (R _i/R) for irreversible binding. In that regard an even more convincing example than Fig. 2 is presented in Fig. 5, which compares progress curve results (on a logarithmic time scale) obtained (Epstein 1979a) by Monte Carlo simulations () for the reversible binding of ligand to three-unit sequences on a 15-unit acceptor lattice with the corresponding dependence for irreversible binding (^_____). A procedure for calculating the value of R _i (Munro et al. 1998) now follows as a necessary prerequisite for quantifying nonspecific binding from spectral data on the basis of the response associated with seeming acceptor saturation.

Fig. 5.

Time-course of equilibrium attainment () for the reversible binding of ligand to three-unit sequences of a 15-unit acceptor lattice under conditions conducive to lattice saturation: [A _tot] = 20 μM, [S _tot] = 1 mM, k _f = 10⁹ M⁻¹ s⁻¹, k _r = 10³ s⁻¹ (K = 10⁶ M⁻¹). The solid line is the corresponding time-course for irreversible binding (k _r = 0). (Data taken from Epstein 1979a)

Nonspecific binding with an irreversible parking problem

The preceding section has demonstrated the existence of an impediment to direct experimental determination of the reaction stoichiometry for the nonspecific binding of a large ligand to linear segments of a one-dimensional acceptor lattice. On the grounds that stoichiometric titrations almost certainly yield the “irreversible” endpoint (the endpoint prior to dissociation of nonsaturable complexes to achieve optimal alignment), procedures have been devised to deduce the reaction stoichiometry on the basis of the irreversible capacity (Epstein 1978; Munro et al. 1998, 2000). Whereas the earlier procedure (Epstein 1978) calculates the average irreversible binding capacity from the average number of unoccupied acceptor sites on the N-unit acceptor lattice, the latter method (Munro et al. 1998, 2000) employs exactly the same recursive arguments to derive the average irreversible capacity directly. Although this more direct procedure has also been developed for situations involving cooperative as well as noncooperative binding (Munro et al. 1998, 2000), only the latter needs to be considered at this stage.

For each point of first attachment, the lattice has the potential to bind that ligand molecule plus the capacities of the sublattices on either side of that position (Epstein 1978). The total number of attached ligands, calculated by considering all points of initial attachment plus the consequent sublattice capacities, is then averaged over the number of points of initial attachment to give the irreversible capacity. The recursive relationship for the irreversible capacity, (R _i)_N, of an N-unit lattice for ligand binding to n consecutive units is

6

where (R _i)_L is the irreversible capacity of a sublattice with L units. Initial terms are determined by considering that the lattice (or sublattice) must be at least as large as n; and that lattices with a length less than twice that span (2n) can only bind one ligand molecule. A specific example is used to illustrate the rationale behind the recursive relationship.

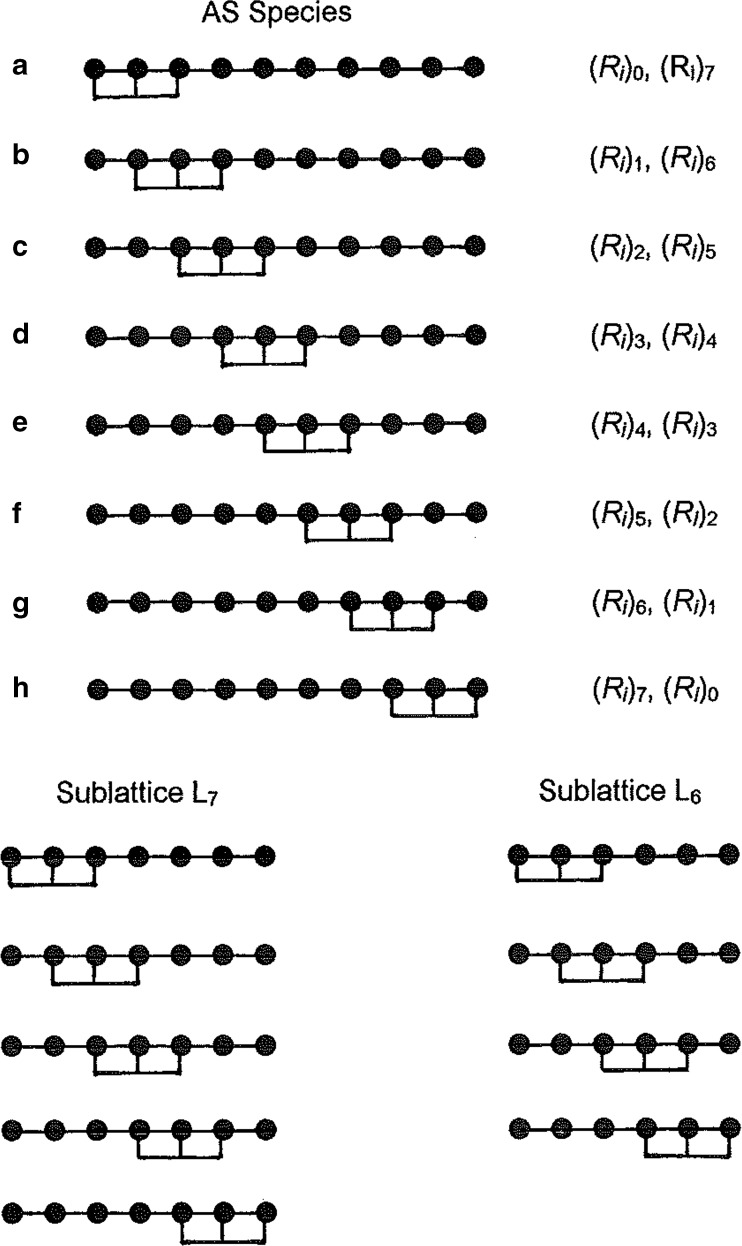
Consider the attachment of the first ligand molecule to a 3-unit sequence of a 10-unit lattice (Fig. 6). For ligand attachment commencing at any of the first three units (species A, B, C), there are insufficient units in the left-hand sublattice for further ligand attachments, but there are sublattices with ligand-binding potential to the right of the attached ligand molecule. This situation is reversed when the first attachment occurs at any of the last three acceptor units (species F, G and H), in that the sublattices with further ligand-binding potential are on the left. Only for species D and E are there two sublattices created with potential for further ligand binding—one with three units and the other with four.

Fig. 6.

Schematic representation of possible ligand attachments in the irreversible binding of ligand to three-unit segments (n = 3) of a ten-unit acceptor lattice (n = 10) showing the sublattice formation from which the capacity is deduced by recursive logic on the basis of Eq. (6)

On the grounds that (R _i)₀ = (R _i)₁ = (R _i)₂ = 0 and (R _i)₃ = (R _i)₄ = (R _i)₅ = 1, the only irreversible capacities still to be evaluated are those for the sublattices comprising six and seven units (L ₆, L ₇). Inspection of the seven-unit sublattice (Fig. 6) shows that only one of the five possible AS species is incapable of binding a second ligand, whereupon (R _i)₇ = 1.8. On the grounds that two of the four possible AS species for a six-unit acceptor sublattice are unsaturable, (R _i)₆ = 1.5. The irreversible capacity of the ten-unit lattice, (R _i)₁₀, thus becomes

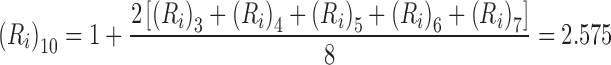7

which signifies the irreversible capacity is 85.8 % of its reversible counterpart (R = 3) for the binding of ligand to three-unit sequences of this ten-unit acceptor lattice. Values of (R _i)_N obtained by the application of Eq. (6) are summarized in table 2 of Munro et al. (1998) for nonspecific ligand binding to two- to eight-unit sequences of acceptors up to 40 units in length.

Provided that the overlap is symmetrical, the counterpart of Eq. (6) for the situation in which ligand binds to an n-unit sequence but occupies m units is (Munro et al. 1998)

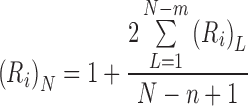8

Because the only difference between Eqs. (6) and (8) is the upper limit of the summation, the irreversible binding capacity is identical with that for the binding of ligand to a m-unit sequence of an acceptor lattice comprising N + (m − n) units.

Allowance for cooperativity

To incorporate the consequences of cooperativity into the recursive argument allowance needs to be made for the modified probability of binding that occurs at positions adjacent to another bound ligand molecule (Epstein 1978). A weighting factor ω _f applies when there is only one adjacency involved, but becomes in the event that the additional ligand molecule occupies the entire intervening space between two bound ligand molecules. Inasmuch as ω _f is the kinetic cooperativity factor associated with the forward rate constant k _f, it is related to the thermodynamic cooperativity parameter (ω) already discussed by the relationship ω _f = ωω _r, where ω _r is the weighting factor for k _r, the dissociation rate constant (zero in the present instance because of presumed irreversibility of binding).

The recursive argument follows the same general pathway as that outlined in relation to Fig. 5 for the noncooperative binding situation except that there is now a need to distinguish between sublattices that are singly-bordered by a bound ligand molecule (L′) and those (L″) with a bound ligand at each end; these sublattices then become the lattices to which a further ligand molecule can attach and thereby generate further sublattices. General recursive relationships are therefore required for the irreversible capacity of an N-unit naked lattice, (R _i)_N, as well as of its singly-bordered, (R _i)_N′, and doubly-bordered, (R _i)_N″, counterparts. Those irreversible capacities are as follows (Munro et al. 2000).

9a

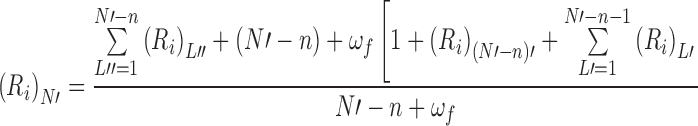9b

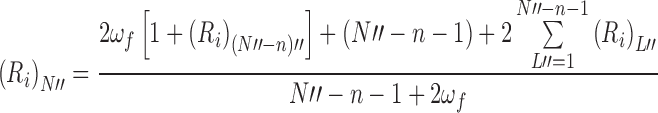9c

In that regard, Eq. (9a) is necessarily identical with Eq. (6) for the naked lattice except for the indication that the lattices generated are singly bordered.

Despite being a non-thermodynamic parameter, the irreversible capacity of a one-dimensional acceptor lattice for a protein ligand can guide selection of the model of nonspecific binding to be used for the interpretation of equilibrium binding data on the same system. Such identification of n, or of n and m for a system with unit overlap greater than the actual binding segment, defines the magnitude of the thermodynamic capacity R as the integer value of N/n or (N + m − n)/m to be used for the analysis of equilibrium binding data. Advantage is now taken of this additional information to characterize the thrombin–heparin interaction.

Biophysics of the thrombin–heparin interaction

Although initial attempts to characterize the interaction between thrombin and heparin (Nesheim et al. 1986; Evington et al. 1986) were in terms of classical binding theory (Klotz 1946), the concept of a specific site for thrombin had already been effectively precluded by the failure to fractionate heparin by affinity chromatography on immobilized thrombin (Nordenman and Björk 1980), as well as by the observation of a correlation between the stoichiometry of thrombin binding and heparin chainlength (Nesheim et al. 1986; Evington et al. 1986). The possibility that thrombin merely binds electrostatically to the highly charged polyanion was therefore investigated by Olson et al. (1991), who interpreted spectrofluorometric binding data in terms of nonspecific interaction between the enzyme and three-disaccharide segments of the heparin chain. Subsequent molecular mapping studies to identify the basic amino acid residues involved in the interaction (Gan et al. 1994; Sheehan and Sadler 1994) has narrowed the heparin segment to two disaccharide units (Gan et al. 1994). Although studies of the crystal structure of thrombin bound to heparin were interpreted as confirming enzyme interaction with a hexasaccharidic heparin sequence (Carter et al. 2005), a comparison of their Fig. 2a with fig. 3c of Gan et al. (1994) shows the strongest binding to be restricted to a tetrasaccharidic sequence (units 3–6 of the octasaccharide present in the crystal). That the enforced juxtaposition of potentially reactive groups within the crystal can foster additional weaker interactions between thrombin and heparin is evident from the deduced X-ray structure, which comprises two enzyme molecules attached to the same heparin oligosaccharide. Such a situation contrasts markedly with the 1:1 reaction stoichiometry that is signified by equilibrium binding and molecular weight measurements on comparable thrombin–heparin mixtures in solution (Nesheim et al. 1986; Olson et al. 1991).

An important point to note in the above studies is the lack of any consideration being given to the notion that thrombin could be blocking access to disaccharide units additional to those actually involved in the binding process—a situation favored by reinterpretation of the binding data (Munro et al. 1998, 2000). Indeed, that possibility (m > n) has received subsequent support from the published X-ray crystal structure (fig. 1 of Carter et al. 2005), where the octasaccharide clearly does not span the entire thrombin molecule: a model with n = 2 and m > 4 is thereby implicated.

Stoichiometry of the thrombin–heparin interaction

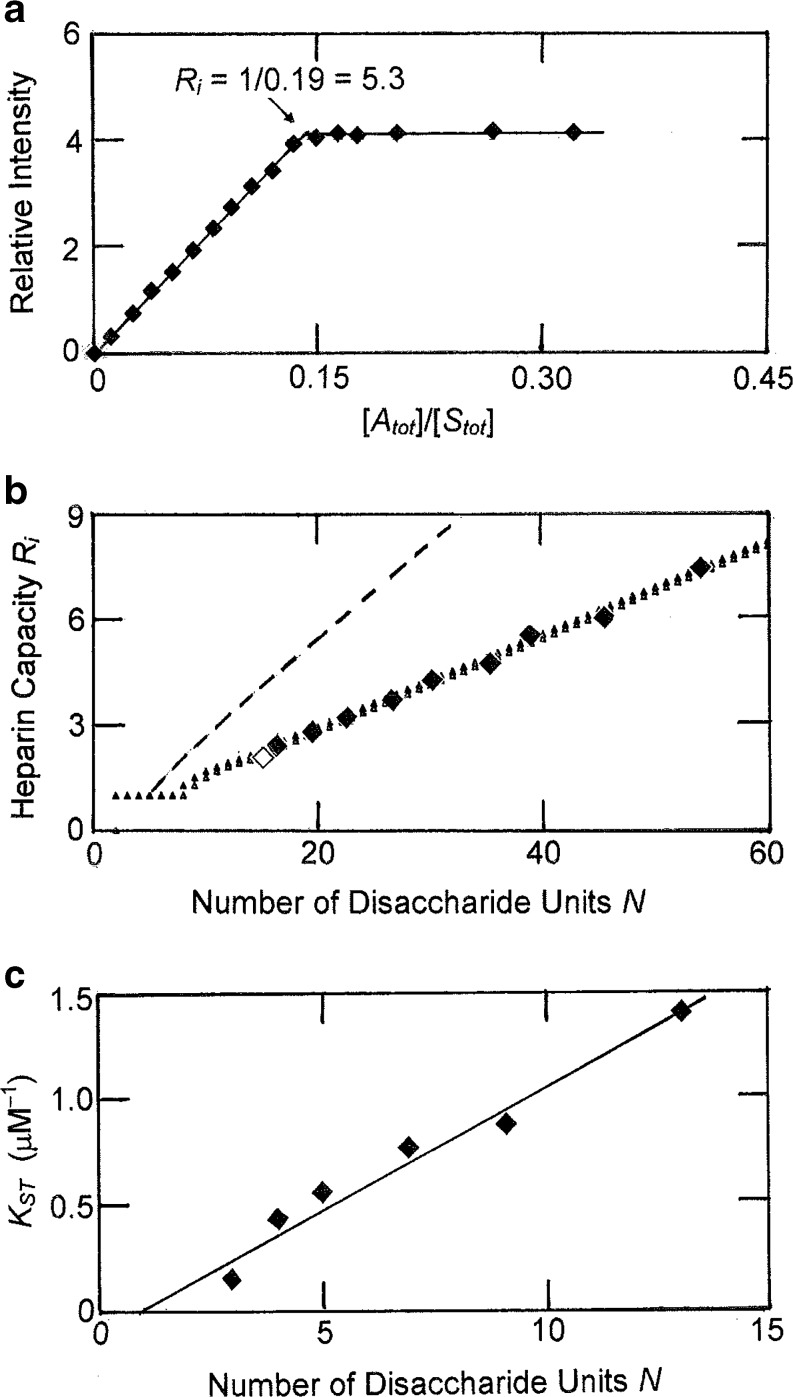
The most extensive investigation of reaction stoichiometry for the thrombin–heparin interaction is a spectrofluorimetric study by Nesheim et al. (1986), whose main approach to the problem entailed the titration of heparin with a fixed amount (1.5 mL, 0.68 μM) of dansylated thrombin (Fig. 7a). At that time, results were being interpreted in terms of specific binding, and the endpoint of the titration was taken to signify the presence of 5.3 such sites on the 27,400-Da heparin chain. Those measurements of the dependence of heparin capacity upon polysaccharide chainlength are summarized () in Fig. 7b, where the abscissa is expressed in terms of disaccharide content (N = M _A/615, the ratio of heparin molecular mass to that of the disaccharide repeat unit). A few experiments involving the titration of thrombin into dansylated heparin were also conducted (Nesheim et al. 1986), and a capacity of 2.1 thrombin molecules per molecule of 9,400-Da heparin (, Fig. 7b) was presented as evidence for independence of the titration endpoint upon its method of measurement.

Fig. 7.

Stoichiometry of the nonspecific interaction between thrombin and heparin. a Spectrofluorimetric titration of dansylated thrombin with a heparin sample characterized by a molecular mass of 27,400 (n = 45). b Comparison of experimental results (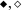) with the predicted chainlength dependence [Eq. (6)] of heparin capacity (− − −) for irreversible binding of enzyme to three-disaccharide units of the polysaccharide (n = 3), the originally postulated nonspecific binding model (Olson et al. 1991). Also shown are the predicted dependencies for overlap models in which thrombin occupies six disaccharide units (m = 6) whilst binding to either three (n = 3, lower points ) or two (n = 2, upper points ) units. c Evaluation of the size of the binding segment (n) from quantitative affinity chromatographic estimates of the stoichiometric binding constant under conditions where binding is restricted to 1:1 interaction; the abscissa intercept defines the magnitude of (n − 1). (Data in (a) and (b) taken from Nesheim et al. 1986, and those in (c) from Olson et al. 1991)

Those attempts to employ spectrofluorimetric measurements for the estimation of reaction stoichiometry were frequently complicated by the onset of precipitation in thrombin–heparin mixtures being studied at low ionic strength (Evington et al. 1986) or at high thrombin concentrations (Nesheim et al. 1986; Olson et al. 1991). On the grounds that analyses of the thrombin and heparin contents of those precipitates yielded molar ratios comparable with the capacities shown in Fig. 8b (Nesheim et al. 1986; Evington et al. 1986), the weaker interaction responsible for the precipitation is evidently self-association of the thrombin–heparin complex rather than interaction of a second enzyme molecule with the 1:1 complex (Carter et al. 2005).

Fig. 8.

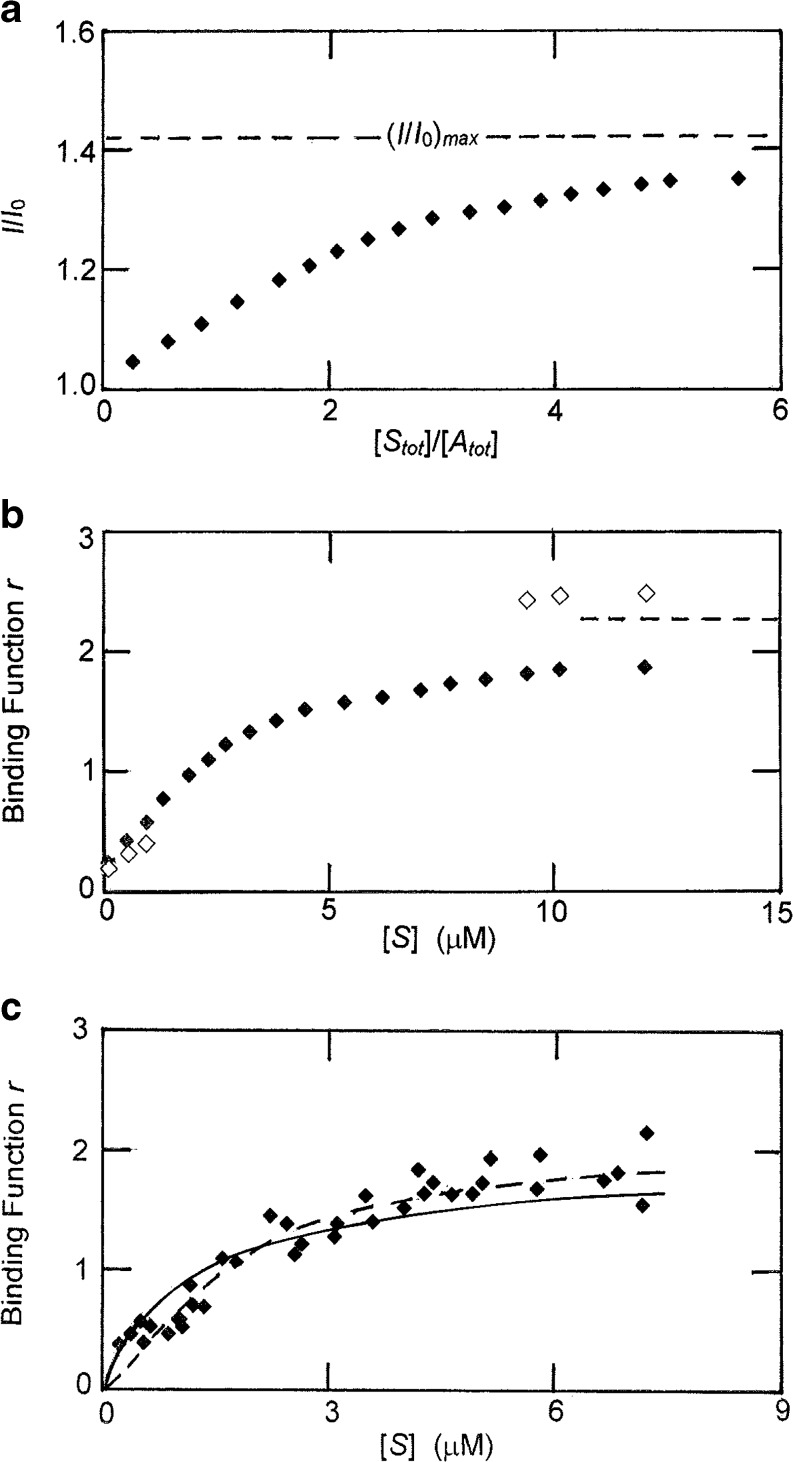
Analysis of binding data for the thombin–heparin interaction on the basis of the overlap model involving nonspecific binding of enzyme to two but occupancy of six disaccharide units. a Spectrofluorimetric measurement of the binding of thrombin to a dansylated heparin (3.2 μM) comprising 15 disaccharide units; the broken line signifies the maximal fluorescence enhancement obtained from the semi-reciprocal plot (I/I ₀ upon [A _tot]/[S _tot]). b Binding curve () obtained by equating (I/I ₀)_max with maximal heparin capacity; open symbols are illustrative estimates of the binding function based on a value of 3.00 (the thermodynamic capacity) rather than 2.26 (the irreversible capacity). c Spectrofluorimetric binding data for the interaction of thrombin (7.6 μM) with a 13-dissacharide heparin sample, a system for which the above ambiguity of interpretation is eliminated because of identity of the reversible and irreversible capacities; the solid line is the best-fit description in terms of noncooperative binding [Eq. (11)], whereas the broken line is its best-fit counterpart for cooperative binding [Eq. (12)]. (Data in (a) and (c) taken from Nesheim et al. 1986 and Olson et al. 1991, respectively)

The first decision to be made is whether the heparin capacities reported in Fig. 7b reflect equilibrium or pseudoequilibrium (irreversible) endpoints of the stoichiometric titrations. Of relevance to that issue is the statement (Nesheim et al. 1986) that subsequent addition of unlabelled thrombin failed to affect the extent of quenching already measured for a titrated mixture of heparin and dansylated thrombin. Although the authors were at a loss to account for this result so out of keeping with their expectation, a plausible explanation is that a slow dissociation rate constant effectively precluded any dissociation of unsaturated acceptor–ligand complexes in the relatively short time (order of 1 min) allowed for re-equilibration. The heparin capacity data are therefore considered in terms of titrations that reflect the irreversible endpoints prior to elimination of the parking problem.

The initial attempt to rationalize binding data for the thrombin–heparin interaction was in terms of enzyme attachment to linear three-disaccharide segments of the polysaccharide lattice (Olson et al. 1991). However, reference to Fig. 7b reveals incompatibility of the predicted dependence (Eq. 6) of heparin capacity upon polymer chainlength (− − −) with the experimental data obtained by stoichiometric titration. As noted subsequently (Munro et al. 1998), a much better fit of those titration data in terms of irreversible binding is obtained by invoking an overlap model in which thrombin occupies three extra sites as well as the three to which it actually binds (, Fig. 7b). An equally satisfactory fit also applies to the situation in which enzyme binds to two but occupies six disaccharide units (▲, Fig. 7b)—a model rendered relevant by the conclusion that the chemical interaction between thrombin and heparin is restricted to two disaccharide units (Gan et al. 1994).

Additional evidence favoring the smaller value of n can be gleaned from measurements of the stoichiometric binding constant for 1:1 interaction (K _ST) by quantitative affinity chromatography of thrombin on immobilized heparin under conditions where the concentration of competing polysaccharide ensures a value less than unity for the binding function (Olson et al. 1991). On the grounds that the stoichiometric binding constant for 1:1 interaction is related to its intrinsic counterpart (K) by the expression

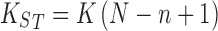10

a value of n may be inferred from the magnitude of the abscissa intercept, (n − 1), of the dependence of K _ST upon heparin chainlength (N). Experimental results taken from fig. 5 of Olson et al. (1991) are certainly consistent with an estimate of unity for this intercept (Fig. 7c). The following equilibrium binding studies will therefore be considered in terms of thrombin occupancy of six but interaction with two disaccharide segments of heparin.

Equilibrium binding studies

Most attempts to characterize the interaction between thrombin and heparin have entailed measurements of either the enhancement or the quenching of fluorescence accompanying complex formation. For example, Fig. 8a summarizes the increase in fluorescence that accompanied the addition of thrombin to a 3.2 μM solution of dansylated heparin (M _A = 9,400 Da, N = 15) in a study performed by Nesheim et al. (1986). Calculation of a binding curve on the bases that [S _bound] = [S _tot](I/I ₀ − 1)/{(I/I ₀)_max − 1} and [S] = [S_tot] − [S _bound] yields the results () shown in Fig. 8b. Noteworthy is the limiting magnitude of 2.26 for the binding function, which is the value of (R _i)_N predicted by Eq. (6) for the present system with N = 15, m = 6 and n = 2, rather than the thermodynamic (equilibrium) capacity (R) of 3.00—an observation which clearly throws into question the validity of the binding data. For small extents of complex formation (i.e., low [S]) the rapid attainment of thermodynamic equilibrium would have ensured a valid estimate of the fluorescence enhancement (I/I ₀), but the experimental estimate of r is based on a heparin capacity of 2.26 instead of 3.00: the thermodynamic estimate of r () is therefore smaller in this region of the binding curve. On the other hand, the experimental estimates of r at the other end of the binding curve are underestimates because of their proximity to the irreversible capacity of the heparin chain. Although the quantitative correctness of the open symbols in this region (based on an unverifiable assumption that a correction factor of 3.00/2.26 applies) is open to question, the direction of the shift is unequivocal. In any event, the important point to emerge from Fig. 8b is the inability of the spectrofluorimetric study of this system to provide a sufficiently accurate binding curve for quantitative characterization of the nonspecific interaction between thrombin and this heparin sample with N = 15.

In the only experimental study to involve analysis of results on the basis of nonspecific binding (Olson et al. 1991) advantage was taken of the decreased fluorescence exhibited by a thrombin-bound probe, p-aminobenzamidine, that accompanies complex formation between heparin and the labelled enzyme. Fortunately, the acceptor in this investigation was a heparin sample (M _A = 7,900 Da) comprising 13 disaccharide units, whereupon the identity of reversible and irreversible acceptor capacities (R _i = R = 2.00) for N = 13 means that equilibrium binding data can be inferred from the extent of fluorescence quenching associated with the addition of this heparin to a thrombin solution supplemented with 200 μM p-aminobenzamidine to ensure probe-saturation of the enzyme active site. Binding data obtained from the spectrofluorimetric titration of a 7.6 μM thrombin solution with this heparin (Olson et al. 1991; Munro et al. 2000) are shown () in Fig. 8c.

The substitution of values of 13 for N, 6 for m and 2 for n into Eq. (3) leads to respective magnitudes of 12 and 21 for ^h C ₁ and ^h C ₂, whereupon the general expression for noncooperative binding [Eq. (1)] becomes

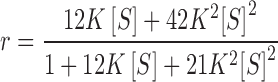11

for this system with R = 2. Nonlinear least-squares curve-fitting of the experimental results to this expression gives rise to an intrinsic association constant (±2 SD) of 0.16 (±0.03) μM⁻¹ and the theoretical r − [S] dependence (^_____) shown in Fig. 8c. This value of the intrinsic binding constant finds parallel in the K of 0.12 (±0.02) μM⁻¹ that emanates from the slope of Fig. 7c—a value rendered dependent only on the value of n (rather than of m and n) by the choice of reactant concentrations that restricted complex formation to 1:1 interaction. On the grounds that better conformity with the experimental results should, in principle, be achievable by invoking positive cooperativity of binding (Epstein 1978), the results have also been analyzed according to the relationship

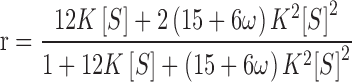12

which is obtained by incorporating a value of unity for j in Eq. (5), the expression for ^h C _i(j), on the grounds that only a single adjacency is possible for a system with R = 2. Although the resulting best-fit description (− − −, Fig. 8c) exhibits closer adherence to the trend of the experimental data, the analysis [K = 0.03 (±0.02) μM⁻¹, ω = 57 (±73)] is inconclusive in that no statistical significance can be attached to the magnitude of the cooperativity factor at the 95 % confidence level.

The fact that these deliberations on the biophysics of the thrombin–heparin interaction have finished on an inconclusive note is rather disappointing. However, that state of affairs must be viewed in the light that the characterization of nonspecific binding is in its relative infancy, despite the passage of more than three decades since attention was drawn to existence of the parking problem (Hill 1978). Furthermore, 20 years then elapsed before the first attempt (Munro et al. 1998, 2000) to incorporate considerations of its kinetic consequences (Epstein 1979a, b).

Concluding remarks

The first purpose of this review has been to draw attention to the considerations that provide a theoretical basis for the characterization of nonspecific binding of a ligand to linear segments of a one-dimensional acceptor lattice. Despite the publication of those theoretical contributions over three decades ago (Epstein 1978, 1979a, b), their application some 20 years later to biophysical characterization of the thrombin–heparin interaction (Munro et al. 1998, 2000) represents the first occasion on which the full ramifications of those quantitative considerations have been exposed. Furthermore, those analyses of results for the thrombin–heparin system have merely served to illustrate the extreme difficulty of obtaining an unequivocal characterization of nonspecific binding. Although the analyses discussed above have provided reasonable justification for describing the reaction stoichiometry in terms of thrombin occupancy of a six-disaccharide segment, but with chemical interaction confined to only two of those units (Fig. 7a–c), the results presented in Fig. 8a–c show that much more work is required in the way of experimental design before the goal of unequivocal characterization of the interaction can be achieved. In that regard, the major obstacle is the ever-present potential for mistaken use of a transient (pseudoequilibrium) acceptor capacity (R _i) for its thermodynamic counterpart (R). Although that consequence of the parking problem in Fig. 8a was exposed in Fig. 8b by calculating the binding function in order to demonstrate attainment of the irreversible binding capacity instead of its thermodynamic counterpart, it must be emphasized that the current practice of employing direct global analysis of spectral data would almost certainly have failed to detect the invalidity of applying equilibrium theory to the spectrofluorimetric results, because consideration of [(I/I ₀)_max − 1] as a direct measure of the thermodynamic acceptor capacity is embedded in those global analysis programs. The fact that the later spectrofluorimetric study (Olson et al. 1991) did prove to be amenable to thermodynamic analysis merely reflected a fortuitous situation in which the irreversible and thermodynamic capacities were identical for the 13-disaccharide heparin chosen as the acceptor lattice.

An obvious outcome of these deliberations is the conclusion that nonspecific binding is more amenable to characterization by methods such as frontal size exclusion chromatography (Nichol and Winzor 1964; Hogg and Winzor 1985; Cann and Winzor 1987) under conditions where the extent of ligand binding can be measured directly as the difference between free and total ligand concentrations. Ironically, virtually all attempts to characterize the thrombin–heparin interaction have entailed spectral procedures for indirect determination of the extent of complex formation from the ratio of equilibrium response to the maximal response (as in Fig. 8a, b).

In summary, this review has highlighted the pitfalls that have been encountered in attempts thus far to quantify the nonspecific binding of a ligand to a sequence of units on a polymer lattice. It therefore provides guidelines for future research aimed at obtaining an unequivocal quantitative characterization of the thrombin–heparin system, or, indeed, of any other interaction involving the nonspecific binding of a protein to linear segments of a polymeric acceptor.