Stochastic chemical kinetics

Abstract

A review of the physical principles that are the ground of the stochastic formulation of chemical kinetics is presented along with a survey of the algorithms currently used to simulate it. This review covers the main literature of the last decade and focuses on the mathematical models describing the characteristics and the behavior of systems of chemical reactions at the nano- and micro-scale. Advantages and limitations of the models are also discussed in the light of the more and more frequent use of these models and algorithms in modeling and simulating biochemical and even biological processes.

Electronic supplementary material

The online version of this article (doi:10.1007/s12551-013-0122-2) contains supplementary material, which is available to authorized users.

Introduction

Stochastic chemical kinetics describes the time evolution of a chemically reacting system in a way that takes into account the fact that molecules come in whole numbers and their collisions are random events. The stochasticity of reaction events becomes significant when a small number of reactant species are involved in the system.

The theoretical foundations of stochastic chemical kinetics and its simulation date back to more than 30 years ago when a mathematical probabilistic formalization of the physical processes underlying molecular collisions was given by Gillespie [1–6], and McQuarry [7]. At the end of the 1970s, Gillespie paved the way for the development of algorithms able to numerically simulate the time evolution of systems of coupled chemical reactions, and, several years later, in 1992, 2001, and 2007, he returned to this topic [8–10], as the scientific community of modelers and chemists showed a renewed interest in the numerical simulation of the time behavior of a chemical system. Especially in the last decade, researchers are increasingly using a stochastic approach to chemical kinetics in the analysis of cellular systems in biology, where the small molecular populations of only a few reactant species can lead to deviations from the predictions of the deterministic differential equations of classical chemical kinetics. Nowadays, a plethora of algorithms and tools are at the disposal of the researchers who want to simulate the kinetics of chemical and biochemical systems. In spite of the large number of available software tools, the mathematical models and the derived algorithms for the stochastic chemical kinetics belong principally to four classes: (1) the exact methods, (2) the approximate methods, that simulate only the waiting time of reaction and the sequence of reaction events without taking into account the spatial location of interacting molecules, the homogeneity of the reaction medium, and the eventuality of ldiffusion-driven reactions, (3) the spatio-temporal algorithms that simulate the chemical kinetics in 3D space, and (4) the hybrid algorithms that simulate fast dynamics subsystems by either ordinary differential equations or stochastic differential equations and the slow dynamics subsystem by stochastic simulation algorithms.

This paper reviews the mathematical models rather than the existent software tools currently implemented to simulate them. This review exposes—in a detailed and critical way—the physical foundations, the assumptions, and the extents of validity of different mathematical “pictures” of a stochastic chemical reacting system. The main purpose of this review effort is to guide researchers, practitioners, but also chemists and biochemists to adopt the appropriate mathematical framework for a specific problem.

This review does not focus on the technical features and the performances of the software tools implementing the models. This kind of review can be found in many other recent works mainly devoted to the presentation of new tools and to the comparison with their efficiency with the efficiency of the existent ones. Some good reviews of the state-of-the-art tools can be found [11–15]. The motivation of our focus is to provide a theoretical background to enable researchers, but also students in the field, to make them aware of the uses, abuses, and misuses of models. We are confident that this can help researchers, practitioners, and students to make a rational choice among the models before choosing from among the tools.

The paper is organized as follows: the next section introduces the Markov processes and chemical master equation, which are preliminary to the understanding of the mathematical formalization of the stochastic molecular approach to chemical kinetics (described in section Molecular approach to chemical kinetics section ). Fundamental hypothesis of stochastic chemical kinetics section describes the physics of the reactive collision between molecules, explaining the meaning of important concepts as reaction orders and reaction rate constant. Then, The reaction probability density function section introduces the concept of reaction probability density function which—in the stochastic framework—replaces the deterministic reaction rate equation and is necessary to understand the mathematical formalization of stochastic chemical kinetics proposed by Gillespie. The next section—The stochastic simulation algorithms section—reviews the exact stochastic simulation algorithms, while Time-dependent extension of the First Reaction Method section reviews a recent extension of theGillespie exact stochastic simulation algorithm. Approximate stochastic simulation algorithms section switches to the approximate stochastic simulation algorithm and Advantages and drawbacks of Gillespie algorithm section discusses the advantages and the limitations of Gillespie’s stochastic simulation algorithms. Finally, Spatio-temporal algorithms sections, The Langevin equation section, and Conclusions section present the responses to the limitation of stochastic simulation algorithms: the spatio-temporal stochastic algorithm, the Langevin equation, and the hybrid deterministic/stochastic algorithms, respectively.

The master equation

The story of the master equation usually begins with Markov processes. A Markov process is a special case of a stochastic process. Stochastic processes are often used in physics, biology, and economy to model randomness. In particular, Markov processes are often used to model randomness, since it is much more tractable than a general stochastic process. A general stochastic process is a random function f(X; t), where X is a stochastic variable and t is time. The definition of a stochastic variable consists in specifying

• a set of possible values (called “set of states“ or “sample space”)

• a probability distribution over this set

The set of states may be discrete, e.g., the number of molecules of a certain component in a reacting mixture. Or the set may be continuous in a given interval, e.g., one velocity component of a Brownian particle and the kinetic energy of that particle. Finally, the set may be partly discrete and partly continuous, e.g., the energy of an electron in the presence of binding centers. Moreover, the set of states may be multidimensional; in this case, tX is written as a vector X, for example, X may stand for the three velocity components of a Brownian particle or for the collection of all numbers of molecules of the various components in a reacting mixture.

The probability distribution, in the case of a continuous one-dimensional range, is given by a function P(x) that is non-negative

$$P\left(x\right)\ge 0$$

and normalized in the sense

$$\int P\left(x\right)\mathit{dx}=1$$

where the integral extends over the whole range. The probability that X has a value between x and x + dx is

$$P\left(x\right)\mathit{dx}$$

Often in physical and biological sciences, a probability distribution is visualized by an “ensemble”. From this point of view, a fictitious set of an arbitrary large number N of quantities, all having different values in the given range, is introduced in such a way the number of these quantities having a value between x and x + dx is NP(x ) dx. Thus, the probability distribution is replaced with a density distribution of a large number of “samples”. This does not affect any simulation result, since it is merely a convenience in talking about probabilities, and in this work, we will use this language. It may be added that it can happen that a biochemical system does consist of a large number of identical replica, which to a certain extent constitute a physical realization of an ensemble. For instance, the molecules of an ideal gas may serve as an ensemble representing the Maxwell probability distribution for the velocity. The use of an ensemble is not limited to such cases, nor based on them, but serves as a more concrete visualization of a probability distribution.

Finally, we remark that in a continuous range it is possible for P(x) to involve delta functions,

$$P\left(x\right)={\displaystyle \sum _n{p}_n\delta \left(x-x_n\right)+\tilde{P}\left(x\right),}$$

Where $\tilde{P}$ is finite or at least integrable and non-negative, P _n > 0, and

$${\displaystyle \sum _n{p}_n+{\displaystyle \int \tilde{P}\left(x\right)\mathit{dx}=1}}$$

Physically, this may be visualized as a set of discrete states x _n with probability p _n embedded in a continuous range. If P(x) consists of δ functions alone i. e. P ( x ) = 0, then it can also be considered asa probability distribution p _n on the discrete set of states x _n.

A general way to specify a stochastic process is to define the joint probability densities for values x₁, x₂, x₃,… at times t₁, t₂, t₃,… respectively

$$p\left(x_1,t_1;x_2,t_2;x_3,t_3;\dots \right)$$ 1

If all such probabilities are known, the stochastic process is fully specified, (but, in general, it is not an easy task to find all such distributions). Using (1) the conditional probabilities can be defined as usual

$$p\left(\left.x_1,t_1;x_2,t_2;\dots \right|y_1,{\tau }_1;y_2,{\tau }_2;\dots \right)=\frac{p\left(\left.x_1,t_1;x_2,t_2;\dots \right|y_1,{\tau }_1;y_2,{\tau }_2;\dots \right)}{p\left(y_1,{\tau }_1;y_2,{\tau }_2;\dots \right)}$$

Where x ₁, x ₂,… and y ₁, y ₂,… are values at times t ₁ ≥ t ₂ ≥ ⋯ ≥ τ ₁ ≥ τ ₂ ≥ …. This is where a Markov process has a very attractive property. It has no memory. For a Markov process

$$p\left(\left.x_1,t_1;x_2,t_2;\dots \right|y_1,\tau 1;y_2,{\tau }_2;\dots \right)=p\left(\left.x_1,t_1;x_2,t_2;\dots \right|y_1,{\tau }_1\right)$$

the probability to reach a state x ₁ at time t ₁ and state x ₂ at time t ₁, if the state is y ₁ at time τ ₁, is independent of any previous state, with times ordered as before. This property makes it possible to construct any of the probabilities (1) by a transition probability p _→(x,t|y, τ), (t ≥ τ), and an initial probability distribution p (x _n , t _n ):

$$\begin{array}{l}p\left(x_1,t_1;x_2,t_2;\dots x_n,t_n\right)=\hfill \\ p_{\to }\left(\left.x_1,t_1\right|x_2,t_2\right)p_{\to }\left(\left.x_2,t_2\right|x_3,t_3\right)\dots p_{\to }\left(\left.x_{n-1}{t}_{n-1}\right|x_n,t_n\right)p\left(x_n,t_n\right)\hfill \end{array}$$ 2

A consequence of the Markov property is the Chapman–Kolmogorov equation

$$p_{\to }\left(\left.x_1,t_1\right|x_3,t_3\right)={\displaystyle \int p_{\to }\left(\left.x_1,t_1\right|x_2,t_2\right)p_{\to }\left(\left.x_2,t_2\right|x_3,t_3\right)d{x}_2}$$ 3

The master equation is a differential form of the Chapman–Kolmogorov Eq. 3. The terminology differs between different authors. Sometimes, the term “master equation” is used only for jump processes. Jump processes are characterized by discontinuous motion, that is there is a bounded and non-vanishing transition probability per unit time

$$w\left(\left.x\right|y,t\right)=\underset{\mathit{\Delta t}\to 0}{lim}\frac{p_{\to }\left(\left.x,t+\mathit{\Delta t}\right|y,t\right)}{\mathit{\Delta t}}$$

for some y such that |x − y| > ∈. Here, the function w(x|y; t) = w(x|y).

The master equation for jump processes can be written

$$\frac{\partial p\left(x,t\right)}{\partial t}={\displaystyle \int \left(w\left(\left|x\right|x\prime \right)p\left(x\prime ,t\right)-w\left(\left.x\prime \right|x\right)p\left(x,t\right)\right)\mathit{dx}\prime }$$ 4

The master equation has a very intuitive interpretation. The first part of the integral is the gain of probability from the state x’ and the second part is the loss of probability to x’. The solution is a probability distribution for the state space. Analytical solutions of the master equation are possible to calculate only for simple special cases.

The chemical master equation

A reaction R is defined as a jump to the state X from a state X_R, where X, X _R ∈ Z ^N₊. The propensity $w\left({\mathbf{X}}_R\right)=\tilde{v}\left(\mathbf{X}\right)$ is the probability for transition from X_R to X per unit time. A reaction can be written as

$${\mathbf{X}}_{\mathbf{R}}\stackrel{w\left({\mathbf{X}}_{\mathbf{R}}\right)}{\to }\mathbf{X}$$

The difference in molecule numbers n_R = X _R − X is used to write the master Eq. 4 for a system with M reactions

$$\frac{\mathit{dp}\left(\mathbf{X},t\right)}{\mathit{dt}}={\displaystyle \sum _{i=1}^{M}w\left(\mathbf{X}+n\right)p\left(\mathbf{X}+{\mathrm{n}}_R,t\right)-{\displaystyle \sum _{i=1}^{M}w\left(\mathbf{X}\right)p\left(\mathbf{X},t\right)}}$$ 5

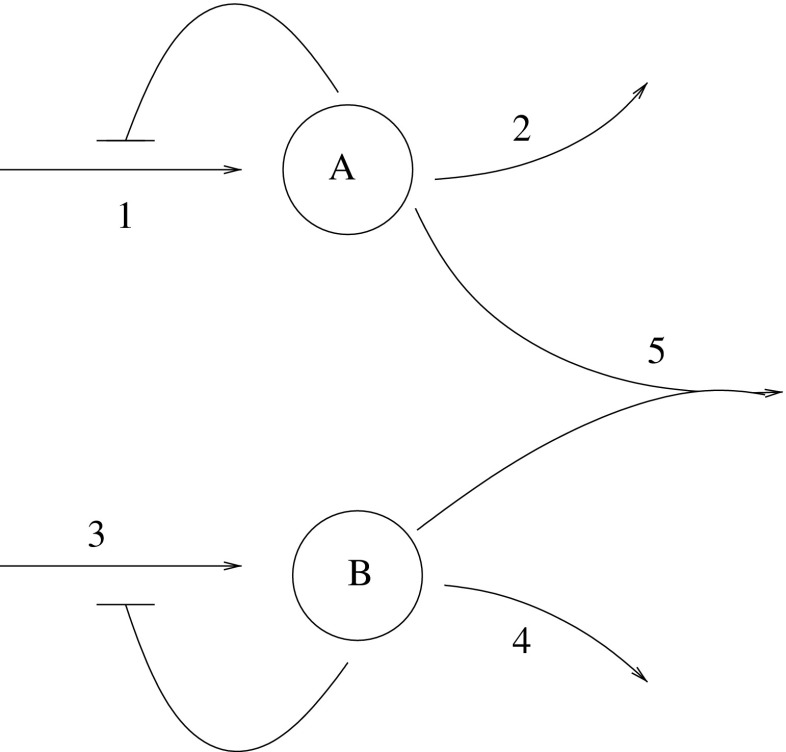
This special case of master equations is called the chemical master equation (CME) [7, 16]. It is fairly easy to write; however, solving it is quite another matter. The number of problems for which the CME can besolved analytically is even fewer than the number of problems for which the deterministic reaction-rate equations can be solved analytically. Attempts to use the master equation to construct tractable time-evolution equations are also usually unsuccessful, unless all the reactions in the system are simple monomolecular reactions [5]. Consider, for instance, a deterministic model of two metabolites coupled by a bimolecular reaction, as shown in Fig. 1. The set of differential equation describing the dynamic of this model is given in Table 1, where the [A] and [B] are the concentrations of metabolite A and metabolite B, while k, K, and μ determine the maximal rate of synthesis, the strength of the feedback, and the rate of degradation, respectively.

Fig. 1.

Two metabolites A and B coupled by a bimolecular reaction. Adapted from [17]

Table 1.

Reactions of the chemical model displayed in Fig. 1; No. corresponds to the number in the figure

No.	Reaction	Rate equation	Type
1	$\varphi \stackrel{v_1\left(\left[A\right]\right)}{\to }A$	$v_1\left(\left[A\right]\right)=\frac{k_1}{1+\left[A\right]K_1}$	Synthesis
2	$A\stackrel{v_2\left(A\right)}{\to }\varphi$	v 2([A]) = μ[A]	Degradation
3	$\varphi \stackrel{v_3\left(\left[B\right]\right)}{\leftarrow }B$	$v_3\left(\left[B\right]\right)=\frac{k_2}{1+\left[B\right]/K_2}$	Synthesis
4	$B\stackrel{v_4\left(\left[B\right]\right)}{\to }\varphi$	v 4([B]) = μ[B]	Degradation
5	$A+B\stackrel{v_5\left(\left[A\right]\right),\left(\left[B\right]\right)}{\to }\varphi$	v 5([A],[B]) = k 3[A][B]	Bimolecular reaction

In the formalism of the Markov process, the reactions in Table 1 are written as in Table 2. The CME equation for the system of two metabolites of Fig. 1 looks fairly complex as in Table 3.

Table 2.

Reactions of the chemical model depicted in Fig. 1, their propensity and corresponding “jump” of state vector n ^T_R; V is the volume in which the reactions occur

No.	Reaction	w (X)	n TR
1	$\varphi \stackrel{w_1\left(a\right)}{\to }A$	w 1(a) = Vk 1/(1 + a/VK 1))	(−1, 0)
2	$A\stackrel{w_2\left(a\right)}{\to }\varphi$	w 2(a) = μa	(1, 0)
3	$\varphi \stackrel{w_3\left(a\right)}{\to }B$	w 3(b) = VK 2/(1 + b/VK 2))	(0,−1)
4	$B\stackrel{w_4\left(b\right)}{\to }\varphi$	w 4(b) = μb	(0, 1)
5	$A+B\stackrel{w_5\left(a,b\right)}{\to }\varphi$	w 5(a,b) = k 2 ab/V	(1, 1)

Table 3.

Set of chemical master equations describing the metabolites interaction showed in Fig. 1

$\frac{\partial \left(0,0,t\right)}{\partial t}=\mathit{\mu p}\left(1,0,t\right)+\mathit{\mu p}\left(0,1,t\right)+\frac{k_3}{V}p\left(1,1,t\right)-V\left(k_1+k_2\right)p\left(0,0,t\right)$

$\begin{array}{c}\hfill \frac{\partial \left(0,b,t\right)}{\partial t}=V\frac{k_2}{1+\frac{b-1}{V{K}_2}}p\left(0,b-1,t\right)\hfill \\ \hfill +\mathit{\mu p}\left(1,b,t\right)+\mu \left(b+t\right)p\left(0,b+1,t\right)+\frac{k_3}{V}\left(b+1\right)p\left(1,b+1,t\right)-\hfill \\ \hfill -\left(V\left(k_1+\frac{k_2}{1+\frac{b}{V{K}_2}}\right)+\mathit{\mu b}\right)p\left(0,b,t\right)\hfill \end{array}$

$\begin{array}{c}\hfill \frac{\partial p\left(a,0,t\right)}{\partial t}=V\frac{k_1}{1+\frac{a-1}{V{K}_1}}p\left(a-1,0,t\right)+\hfill \\ \hfill +\mu \left(a+1\right)p\left(a+1,0,t\right)+\mathit{\mu p}\left(a,1,t\right)+\hfill \\ \hfill +\frac{k_3}{V}\left(a+1\right)p\left(a+1,1,t\right)-\hfill \\ \hfill -\left(V\left(\frac{k_1}{1+\frac{a}{V{K}_1}}\right)+\mathit{\mu a}\right)p\left(a,0,t\right)\hfill \end{array}$

$\begin{array}{c}\hfill \frac{\partial p\left(a,b,t\right)}{\partial t}=V\frac{k_1}{1+\frac{a-1}{V{K}_1}}p\left(a-1,b,t\right)+V\frac{k_2}{1+\frac{b-1}{V{K}_2}}p\left(a,b-1,t\right)+\hfill \\ \hfill +\mu \left(a+1\right)p\left(a+1,b,t\right)+\mu \left(b+1\right)p\left(a,b+1,t\right)+\hfill \\ \hfill +\frac{k_3}{V}\left(a+1\right)\left(b+1\right)p\left(a+1,b+1,t\right)-\hfill \\ \hfill -\left(V\left(\frac{k_1}{1+\frac{a}{V{K}_1}}+\frac{k_2}{1+\frac{b}{V{K}_2}}\right)+\mu \left(a+b\right)+\frac{k_3}{V}\mathit{ab}\right)p\left(a,b,t\right)\hfill \end{array}$

Molecular approach to chemical kinetics

To understand how chemical kinetics can be modeled in a stochastic way, first we need to address the difference between the deterministic and the stochastic approach in the representation of the amount of molecular species. In the stochastic model, this is an integer representing the number of molecules of the species, but in the deterministic model, it is a concentration, measured in M (mol per liter). Then, for a concentration of X of [X] M in a volume of V liters, there are [X]V mol of X and hence N _A[X]V molecules, where n _A ≃ 6.023 × 10²³ is the Avogadro’s constant (the number of molecules in 1 mol). The second issue that needs to be addressed is the rate constant conversion. Much of the literature on biochemical reaction is dominated by a continuous deterministic view of kinetics. Consequently, where rate constants are documented, they are usually deterministic constants k. In the following, we review the expression of the reaction propensity and the formulae that convert the deterministic rate constants into stochastic rate constants.

Reactions are collisions

For a reaction to take place, molecules must collide with sufficient energy to create a transition state. Ludwig Boltzmann developed a very general idea about how energy was distributed among systems consisting of many particles. He said that the number of particles with energy E would be proportional to the value exp[−E/k _B T]. The Boltzmann distribution predicts the distribution function for the fractional number of particles N _i/N occupying a set of states i which each have energy E _i:

$$\frac{N_i}{N}=\frac{g_i{e}^{-E_i/k_{B}T}}{Z\left(T\right)}$$

where k _B is the Boltzmann constant, T is temperature (assumed to be a sharply well-defined quantity), g _i is the degeneracy, or number of states having energy E _i, N is the total number of particles:

$$N={\displaystyle \sum _i{N}_i,}$$

and Z(T) is called the partition function

$$Z\left(T\right)={\displaystyle \sum _i{g}_i{e}^{-E_i/k_{B}T}}$$

Alternatively, for a single system at a well-defined temperature, it gives the probability that the system is in the specified state. The Boltzmann distribution applies only to particles at a high enough temperature and low enough density that quantum effects can be ignored.

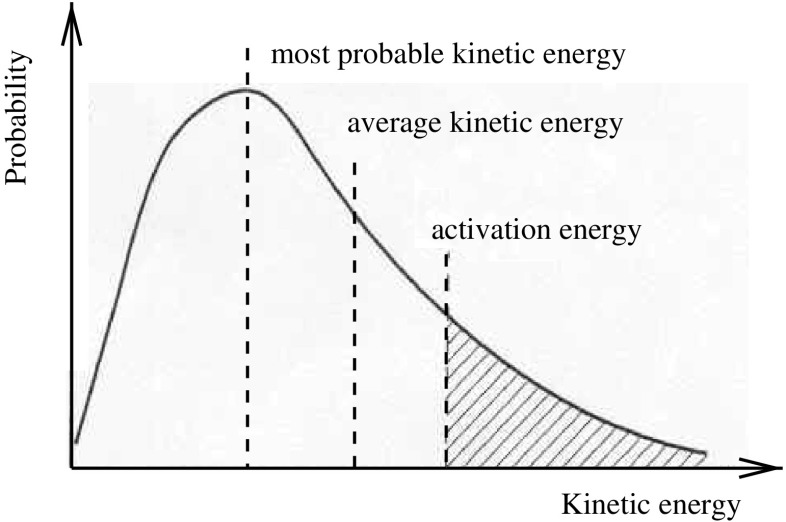
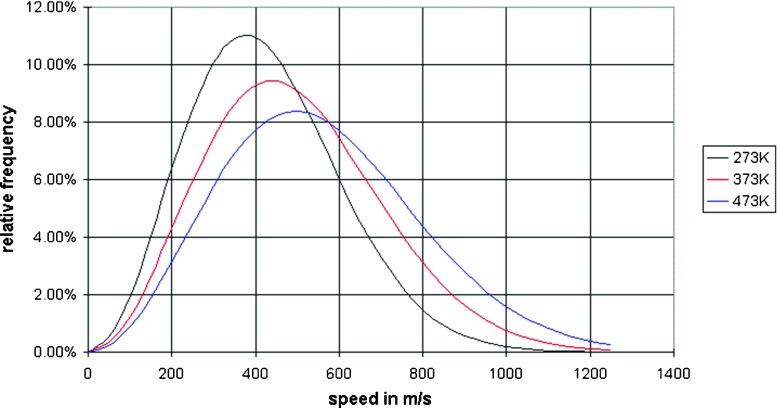
James Clerk Maxwell used Boltzmann’s ideas and applied them to the particles of an ideal gas to produce the distribution bearing both men’s names (the Maxwell–Boltzmann distribution). Maxwell also used, for the energy E, the formula for kinetic energy E = (1/2)mv ², where v is the velocity of the particle. The distribution is best shown as a graph which shows how many particles have a particular speed in the gas. It may also be shown with energy rather than speed along the x axis. Two graphs are shown in Figs. 2 and 3.

Fig. 2.

Since the curve shape is not symmetric, the average kinetic energy will always be greater than the most probable. For the reaction to occur, the particles involved need a minimum amount of energy—the activation energy

Fig. 3.

Maxwell–Boltzmann speed distributions at different temperatures. As the temperature increases, the curve will spread to the right and the value of the most probable kinetic energy will decrease. At temperature increases the probability of finding molecules at higher energy increases. Note also that the area under the curve is constant since total probability must be one

Consider a bi-molecular reaction of the form

$$S_1+S_2\to \dots$$ 6

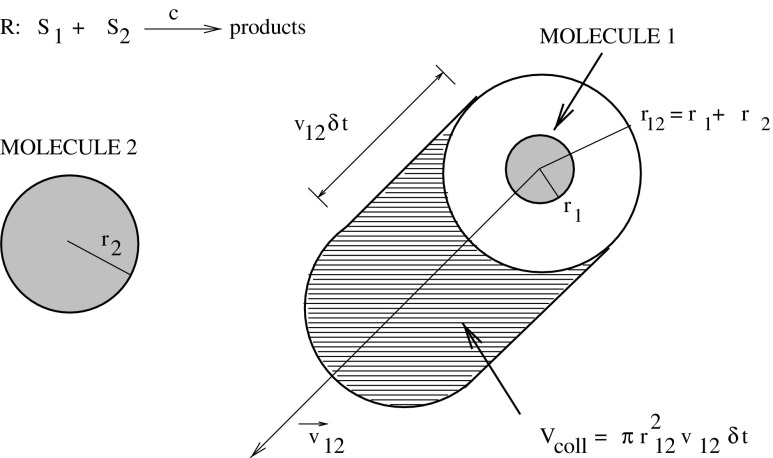
the right-hand side is not important. This reaction means that a molecule of S ₁ is able to react with a molecule of S ₂ if the pair happen to collide with one another with sufficient energy, while moving around randomly, driven by Brownian motion. Consider a single pair of such molecules in a closed volume V. It is possible to use statistical mechanics arguments to understand the physical meaning of the propensity (i.e. hazard) of molecules colliding. Under the assumptions that the volume is not too large or well stirred, and in thermal equilibrium, it can be rigorously demonstrated that the collision propensity (also called collision hazard, hazard function or reaction hazard) is constant, provided that the volume is fixed and the temperature is constant. Since the molecules are uniformly distributed throughout the volume and this distribution does not depend on time, then the probabilitythat the molecules are within reaction distance is also independent of time. A comprehensive treatment of this issue is given in Gillespie [5, 8]. Here, we briefly review it by highlighting the physical basis of the stochastic formulation of chemical kinetics. Consider now that the system is composed of a mixture of the two molecular species, S ₁ and S ₂ in gas-phase and in thermal, but not necessarily chemical equilibrium inside the volume V. Assume that the S ₁ and S ₂ molecules are hard spheres of radii r ₁ and r ₂, respectively. A collision will occur whenever the center-to-center distance between an S ₁ molecule and an S ₂ molecule is less than r ₁₂ = r ₁ + r ₂ (Fig. 4). To calculate the molecular collision rate, pick an arbitrary 1–2 molecular pair, and denote by v ₁₂ the speed of molecule 1 relative to molecule 2. Then, in the next small time interval δt, molecule 1 will sweep out, relative to molecule 2, a collision volume

$$\mathit{\delta }{\mathit{V}}_{\mathit{coll}}=\pi r_{12}^2{v}_{12}\mathit{\delta t}$$

Fig. 4.

The collision volume δV _coll which molecule 1 will sweep out relative to molecule 2 in the next small time interval δt (adapted from [1]).

i.e. if the center of molecule 2 happens to lie inside δV _coll at time t, then the two molecules will collide in the time interval (t, t + δt) (Table 4). Now, the classical procedure would estimate the number of S ₂ molecules whose centers lie inside δV _coll, divide the number by δt, and then take the limit δ → 0 to obtain the rate at which the S ₁ molecule is colliding with S ₂ molecules. However, this procedure suffers from the following difficulty: as δV _coll → 0, the number of S ₂ molecules whose centers lie inside δV _coll will be either 1 or 0, with the latter possibility become more and more likely as the limiting process proceeds. Then, in the limit of vanishingly small δt, it is physically meaningless to talk about “the number of molecules whose center lie inside δV _coll”.

To override this difficulty, we can exploit the assumption of thermal equilibrium. Since the system is in thermal equilibrium, the molecules will at all times be distributed randomly and uniformly throughout the containing volume V. Therefore, the probability that the center of an arbitrary S ₂ molecule will be found inside δV _coll at time t will be given by the ratio δV _coll/V; note that this is true even in the limit of vanishingly small δV _coll. If we now average this ratio over the velocity distributions of S ₁ and S ₂ molecules, we may conclude that the average probability that a particular 1–2 molecular pair will collide in the next vanishingly small time interval δt is

$$\overline{\delta V_{\mathit{coll}}/V}=\frac{\pi r_{12}^2\overline{v_{12}}\mathit{\delta t}}{V}$$ 7

For Maxwellian velocity distributions, the average relative speed $\overline{v_{12}}$ is

$$\overline{v_{12}}={\left(\frac{8\mathit{kT}}{\pi m_{12}}\right)}^{\frac{1}{2}}$$

where k is the Boltzmann’s constant, T the absolute temperature, and m ₁₂ the reduced mass m ₁ m ₂/(m ₁ + m ₂). If we are given that at time t there are X ₁ molecules of the species S ₁ and X ₂ molecules of the species S ₂, making a total of X ₁ X ₂ distinct 1–2 molecular pairs, then it follows from (7) that the probability that a 1–2 collision will occur somewhere inside V in the next infinitesimal time interval (t, t + dt) is

$$\frac{X_1{X}_2\mathrm{\pi }{r}_{12}^2\overline{v_{12}}\mathit{dt}}{V}$$ 8

Although we cannot rigorously calculate the number of 1–2 collisions occurring in V in any infinitesimal interval, we can rigorously calculate the probability of a 1–2 collision occurring in V in any infinitesimal time interval. Consequently, we really ought to characterize a system of thermally equilibrated molecules by a collision probability per unit time, namely the coefficient of dt in (8) instead of a collision rate. This is why these collisions constitute a stochastic Markov process instead of a deterministic rate process.

Then, we can conclude that, for a bimolecular reaction of the form (6), the probability that a randomly chosen A–B pair will react according to R in next dt is

$$\begin{array}{c}\hfill P_{\mathit{react}}=\left\{\left(\frac{\left(\overline{v_{12}}\mathit{dt}\right)\left(\mathrm{\pi }{r}_{12}^2\right)}{V}\right)\times exp\left[-E/\left(k_{B}T\right)\right]\right\}\times X_1{X}_2\hfill \\ \hfill =\left\{\left(\frac{\overline{v_{12}}\left(\mathrm{\pi }{r}_{12}^2\right)}{V}exp\left(-E/\left(k_{B}T\right)\right.\right.\right\}{X}_1{X}_2\mathit{dt}\hfill \end{array}$$ 9

Reaction rates

The reaction rate for a reactant or product in a particular reaction is defined as the amount of the chemical that is formed or removed (in mol or mass units) per unit time per unit volume. The main factors that influence the reaction rate include: the physical state of the reactants, the volume in which the reaction occurs, the temperature at which the reaction occurs, and whether or not any catalysts are present in the reaction.

Physical state

The physical state (solid, liquid, gas, plasma) of a reactant is also an important factor of the rate of change. When reactants are in the same phase, as in aqueous solution, thermal motion brings them into contact. However, when they are in different phases, the reaction is limited to the interface between the reactants. Reaction can only occur at their area of contact, in the case of a liquid and a gas, and at the surface of the liquid. Vigorous shaking and stirring may be needed to bring the reaction to completion. This means that the more finely divided a solid or liquid reactant, the greater its surface area per unit volume, and the more contact it makes with the other reactant, thus the faster the reaction.

Volume

The reaction propensity is inversely proportional to the volume. We can explain this fact in the following way. Consider two molecules, Molecule 1 and Molecule 2. Let the molecules positions in space be denoted by p ₁ and p ₂, respectively. If p ₁ and p ₂ are uniformly and independently distributed over the volume V, for a sub-region of space D with volume V’, the probability that a molecule is inside D is

$$\mathrm{Pr}\left(p_i\in D\right)=\frac{V\prime }{V}i=1,2$$

If we are interested in the probability that Molecule 1 and Molecule 2 are within a reacting distance r of one another at any given instant in time (assuming that r is much smaller than the dimensions of the container, sothat boundary effects can be ignored), this probability can be calculated as

$$\mathrm{Pr}\left(\left|p_1-p_2\right|<r\right)=E\left(\mathrm{Pr}\left(\left|p_1-p_2\right|<\left.r\right|p_2\right)\right)$$

but the conditional probability will be the same for any p ₂ away from the boundary, so that the expectation in redundant, and we can state that

$$E\left(\mathrm{Pr}\left(\left|p_1-p_2\right|<\left.r\right|p_2\right)\right)=\mathrm{Pr}\left(\left|p_1-p_2\right|<r\right)=\mathrm{Pr}\left(p_i\in D\right)=\frac{4\mathrm{\pi }{r}^3}{3V}$$

This probability is inverse proportional to V.

Arrhenius equation

Temperature usually has a major effect on the speed of a reaction. Since a molecule has more energy when it is heated, then the more energy it has, the more chances it has to collide with other reactants. Thus, at a higher temperature, more collisions occur. More importantly, however, is the fact that heating a molecule affects its kinetic energy, and therefore the “energy” of the collision.

The reaction rate coefficient k has a temperature dependency, which is usually given by the empirical Arrhenius law:

$$k=Aexp\left[-\frac{E_a}{\mathit{RT}}\right]$$ 10

E _a is the activation energy and R is the gas constant. Since at temperature T the molecules have energies given by a Boltzmann distribution, one can expect the number of collisions with energy greater than E _a to be proportional to exp[−E _a/RT]. A is the frequency factor. This factor indicates how many collisions between reactants have the correct orientation to lead to the products. The values for A and E _a are dependent on the reaction.

It can be seen that either increasing the temperature or decreasing the activation energy (for example, through the use of catalysts) will result in an increase in the rate of reaction.

While remarkably accurate in a wide range of circumstances, the Arrhenius equation is not exact, and various other expressions are sometimes found to be more useful in particular situations. One example comes from the “collision theory” of chemical reactions, developed by Max Trautz and William Lewis in the years 1916–1918. In this theory, molecules react if they collide with a relative kinetic energy along their line-of-centers that exceeds E _a This leads to an expression very similar to the Arrhenius equation, with the difference that the pre-exponential factor “A” is not constant but instead is proportional to the square root of temperature. This reflects the fact that the overall rate of all collisions, reactive or not, is proportional to the average molecular speed which in turn is proportional to $\sqrt{T}$. In practice, the square root temperature dependence of the pre-exponential factor is usually very slow compared to the exponential dependence associated with E _a.

Another Arrhenius-like expression appears in the Transition State Theory of chemical reactions, formulated by Wigner, Eyring, Polanyi, and Evans in the 1930s. This takes various forms, but one of the most common is:

$$k=\frac{k_{B}T}{h}exp\left[-\frac{\mathit{\Delta G}}{\mathit{RT}}\right]$$

where ∆G is the Gibbs free energy of activation, k _B is Boltzmann’s constant, and h is Planck’s constant. At first sight, this looks like an exponential multiplied by a factor that is linear in temperature. However, one must remember that free energy is itself a temperature-dependent quantity. The free energy of activation includes an entropy term as well as an enthalpy term, both of which depend on temperature, and when all of the details are worked out one ends up with an expression that again takes the form of an Arrhenius exponential multiplied by a slowly varying function of T. The precise form of the temperature dependence depends upon the reaction, and can be calculated using formulae from statistical mechanics (it involves the partition functions of the reactants and of the activated complex).

Catalysts

A catalyst is a substance that accelerates the rate of a chemical reaction but remains unchanged afterward. The catalyst increases the rate reaction by providing a different reaction mechanism to occur with a lower activation energy. In autocatalysis, a reaction product is itself a catalyst for that reaction possibly leading to a chain reaction. Proteins that act as catalysts in biochemical reactions are called enzymes.

The formulation of stochastic chemical kinetics of Gillespie assumes that temperature and volume do not change in time. We will see later in this paper how these hypothesis can be relaxed and the mathematical framework of chemical kinetics can be reformulated to take into account temperature and volume variations occurring in a reaction chamber.

The reaction rate constant in the stochastic formulation of chemical kinetics

Switching from a deterministic framework to a stochastic one imposes the conversion of the measurement units from concentration units to numbers of molecules units. In the following, we review the conversion formulas in the case of zero-th, first, second and higher order of reaction.

Zeroth-order reactions

These reactions have the following form

$$R_{\mu }:\varphi \stackrel{c_{\mu }}{\to }\mathit{X}$$ 11

Although in practice things are not created from nothing, it is sometimes useful to mode a constant rate of production of a chemical species (or influx from another compartment) via a zeroth-order reaction. In this case, c _μ is the propensity of a reaction of this type occurring, and so

$$a_{\mu }\left(Y,c_{\mu }\right)=c_{\mu }$$ 12

For a reaction of this nature, the deterministic rate law is k Ms ⁻¹, and thus for a volume V, X is produced at a rate n _A Vk _μ molecules per second, where k _μ is the deterministic rate constant for the reaction R _μ. As the stochastic rate law is just c _μ molecules per second, we have

$$c_{\mu }=n_{A}V{k}_{\mu }$$ 13

First-order reactions

Consider the first-order reaction

$$R_{\mu }:X_i\stackrel{c_{\mu }}{\to }\dots$$ 14

Here, c _μ represents the propensity that a particular molecule of X _i will undergo the reaction. However, if there are x _i molecules of of X _i, each of which having a propensity of c _μ of reacting, the combined propensity for a reaction of this type is

$$a_{\mu }\left(Y,c_{\mu }\right)=c_{\mu }{x}_i$$ 15

First-order reactions of this nature represent the spontaneous change of a molecule into one or more other molecules or the spontaneous dissociation of a complex molecule into simpler molecules. They are not intended to model the conversionof one molecule into another in the presence of a catalysts, as this is really a second-order reaction. However, in the presence of a large pool of catalyst that can be considered not to vary in concentration during the time evolution of the reaction network, a first-order reaction provides a good approximation. For a first-order reaction, the deterministic rate law is k _μ[X] M s ⁻¹, and so for a volume V, a concentration [X] corresponds to x = n _A[X]V molecules. Since [X] decreases at rate n _A k _μ[X]V = k _μ x molecules per second, and since the stochastic rate law is c _μ x molecules per second, we have

$$c_{\mu }=k_{\mu }$$ 16

i.e. for first-order reactions, the stochastic and the deterministic rate constants are equal.

Second-order reactions

The form of the second-order reaction is the following

$$R_{\mu }:X_i+X_k\stackrel{c_{\mu }}{\to }\dots$$ 17

Here, c _μ represents the propensity that a particular pair of molecules X _i and X _k will react. But, if there are x _i molecule of X _i and x _k molecules of X _k, there are x _i x _k different pairs of molecules of this type, and so this gives the combined propensity of

$$a_{\mu }\left(Y,c_{\mu }\right)=c_{\mu }{x}_i{x}_k$$ 18

There is another type of second-order reaction, called the homodimerization reaction, which needs to be considered:

$$R_{\mu }:2X_i\stackrel{c_{\mu }}{\to }\dots$$ 19

Again, c _μ is the propensity of a particular pair of molecules reacting, but here there are only x _i(x _i − 1)/2 pairs of molecules of species X _i, and so

$$a_{\mu }\left(Y,c_{\mu }\right)=c_{\mu }\frac{x_i\left(x_i-1\right)}{2}$$ 20

For second-order reactions, the deterministic rate law is k _μ[X _i][X _k] M s ⁻¹. Here, for a volume V, the reaction proceeds at a rate of n _A k _μ[X _i][X _k]V = k _μ x _i x _k/(n _A V) molecules per second. Since the stochastic rate law is c _μ x _i x _k molecules per second, we have

$$c_{\mu }=\frac{k_{\mu }}{n_{A}V}$$ 21

For the homodimerization reaction, the deterministic law is k _μ[X _i]², so the concentration of X _i decreases at rate n _A4k _μ[X _i]² V = 2k _μ x ²_i/(n _A V) molecules per second. The stochastic rate law is c _μ x _i(x _i − 1)/2 so that molecules X _i are consumed at a rate of c _μ x _i(x _i-1) molecules per second. These two laws do not match, but for large x _i, x _i(x _i-1) can be approximated by x ²_i, and so, to the extent that the kinetics match, we have

$$c_{\mu }=\frac{2k_{\mu }}{n_{A}V}$$ 22

Note the additional factor of two in this case.

By combining Eq. 21 with Eq. 9, we obtain the following expression for the deterministic rate of a second-order reaction of type (17)

$$k_{\mu }=n_A\overline{v_{12}}\mathrm{\pi }{r}_{12}^{2}exp\left[\frac{E_{\mu }}{k_{B}T}\right]$$ 23

while for a second-order reaction of type (19), the deterministic rate constant is

$$k_{\mu }=\frac{1}{2}{n}_A\overline{v_{12}}\mathrm{\pi }{r}_{12}^{2}exp\left[\frac{E_{\mu }}{k_{B}T}\right]$$ 24

Higher-order reactions

Most (although not all) reactions that are normally written as a single reaction of order higher than two, in fact represent the combined effect of two or more reactions of order one or two. In these cases, it is usually recommended to model the reactions in detail rather than via high-order stochastic kinetics. Consider, for example, the following trimerization reaction

$$c_{\mu }:3X\stackrel{c_{\mu }}{\to }{X}_3$$

The rate constant c _μ represents the propensity of triples of molecules of X coming together simultaneously and reacting, leading to a combined propensity of the form

$$a_{\mu }\left(Y,c_{\mu }\right)=c_{\mu }\left({}_3^x\right)=c_{\mu }\frac{x\left(x-1\right)\left(x-2\right)}{6}$$ 25

However, in most cases, it is likely to be more realistic to model the process as the pair of second-order reactions

$$\begin{array}{r}\hfill 2X\to X_2\\ \hfill X_2+X\to X_3\end{array}$$

and this system will have a quite different dynamics to the corresponding third-order system.

In the next section, we will review the derivation of the general conversion formula of the rate constant given by Wolkenhauer et al. in [18].

Fundamental hypothesis of stochastic chemical kinetics

Let us now generalize, using a more rigorous approach, the concepts exposed in the previous section. If we apply the foregoing arguments specifically to reactive collisions (i.e. to those collisions which result in an alteration of the state vector), the chemical reactions are more properly characterized by a reaction probability per unit time instead of a reaction rate. Thus, suppose that S ₁ and S ₂ molecules can undergo the reactions

$$R_1:S_1+S_2\to \dots$$ 26

Then, in analogy with Eq. 7, we may assert the existence of a constant c ₁, which depends only on the physical properties of the two molecules and the temperature of the system, such that

$$\begin{array}{c}\hfill c_1\mathit{dt}=\mathrm{average}\mathrm{probability}\mathrm{that}\mathrm{a}\mathrm{particular}1–2\hfill \\ \hfill \mathrm{molecular}\mathrm{pair}\mathrm{will}\mathrm{react}\mathrm{according}\mathrm{to}\mathit{R}1\hfill \\ \hfill \mathrm{in}\mathrm{the}\mathrm{next}\mathrm{innitesimal}\mathrm{time}\mathrm{interval}\mathit{dt}\hfill \end{array}$$ 27

More generally, if, under the assumption of spatial homogeneity (or thermal equilibrium), the volume V contains a mixture of X _i molecules of chemical species S _i, (i = 1, 2,…,N), and these N species can interact through M specified chemical reaction channels c _μ ($\mathit{\mu }$=1, 2,…,M), we may assert the existence of M constants c _μ, depending only on the physical properties of the molecules and the temperature of the system. Formally, we assert that

$$\begin{array}{c}\hfill c_{\mu }=\mathrm{average}\mathrm{probability}\mathrm{that}\mathrm{a}\mathrm{particular}\mathrm{combination}\hfill \\ \hfill \mathrm{of}{\mathit{c}}_{\mathit{\mu }}\mathrm{reactant}\mathrm{molecules}\mathrm{will}\mathrm{react}\mathrm{accordingly}\mathrm{to}\hfill \\ \hfill {\mathit{c}}_{\mathit{\mu }}\mathrm{in}\mathrm{the}\mathrm{next}\mathrm{innitesimal}\mathrm{time}\mathrm{interval}\mathit{dt}.\hfill \end{array}$$ 28

This equation is regarded both as the definition of the stochastic reaction constant c _μ, and also as the fundamental hypothesis of the stochastic formulation of chemical kinetics. This hypothesis is valid for any molecular system that is kept “well mixed”, either by direct stirring or else by simply requiring that non-reactive collisions occur much more frequently than reactive molecular collisions.

Finally, the reaction propensity a _μ per unit time in the following is defined as follows:

$$\begin{array}{c}\hfill a_{\mu }\mathit{dt}\equiv c_{\mu }\times \left\{\mathrm{number}\mathrm{of}\mathrm{distinct}\mathrm{molecular}\mathrm{combinations}\mathrm{in}\mathrm{the}\mathrm{state}\mathrm{X}\right\}\hfill \\ \hfill =\mathrm{probability}\mathrm{that}\mathrm{an}{\mathit{c}}_{\mu }\mathrm{reaction}\mathrm{will}\mathrm{occur}\mathrm{in}\mathrm{V}\mathrm{in}\left(t=\mathit{dt}\right),\hfill \\ \hfill \mathit{given}\mathrm{that}\mathrm{the}\mathrm{system}\mathrm{is}\mathrm{in}\mathrm{the}\mathrm{state}\left(X_1,X_2,\dots ,X_N\right)\mathrm{at}\mathrm{time}\mathit{t}.\hfill \end{array}$$ 29

In the next subsection, we will use these concepts to explain the derivation of a general formula converting the rate constants of chemical reactions from their deterministic expression into the stochastic one.

General derivation of the rate constant in the stochastic framework

The general derivation for c _μ, which we are going to present in this section, has been developed by Wolkenhauer et. al. [18]. We report the main passages of this derivation and then we will compare it with the derivationof Gillespie. Let consider a reaction pathway involving N molecular species s _i. A network, which may include reversible reactions, is decomposed into M unidirectional basic reaction channels R _μ

$$R_{\mu }:l_{\mu 1}{S}_{p\left(\mu ,1\right)}+l_{\mu 2}{S}_{p\left(\mu ,2\right)}+\dots +l_{\mu L_{\mu }}{S}_{p\left(\mu ,L_{\mu }\right)}\stackrel{k_{\mu }}{\to }\dots$$

where L _μ is the number of reactant species in channel R _μ, l _μj is the stoichiometric coefficient of reactant species S _{p(μ, j)}, and the index p(μ, j) selects those S _i participating in R _μ. k _μ is the rate constant. Assuming a constant temperature and a homogeneous mixture of reactant molecules, the generalized mass action models (GMA) consist of N differential rate equations

$$\frac{d}{\mathit{dt}}\left[S_i\right]={\displaystyle \sum _{\mu =1}^M{v}_{\mathit{\mu i}}{k}_{\mu }{\mathit{\Pi }}_{j=1}^{L_{\mu }}}{\left[S_{p\left(\mu ,j\right)}\right]}^{l_{\mathit{\mu j}}}$$ 30

where v _μ denotes the change in molecules of S _i resulting from a single reaction R _μ. We write, for concentrations and count of molecules, respectively

$$\left[S\right]=\frac{〈S〉}{V}$$ 31

and

$$\#S=S{N}_A$$ 32

where N _A is the Avogadro’s number. The units of [S] are mol per liter, M = mol/liter. In this context, S is the number of moles and #S is the count of molecules.

Let use the following example for a chemical reaction

$$S_1+\alpha S_2\stackrel{k_1}{\to }\beta S_3\stackrel{k_2}{\to }\alpha S_2+\mathrm{\gamma }{S}_4$$

which for the purpose of a stochastic simulation is split into two reaction channels

$$\begin{array}{l}{R}_1:S_1+\alpha S_2\stackrel{k_1}{\to }\beta S_3\hfill \\ R_2:\beta S_3\stackrel{k_2}{\to }\alpha S_2+\mathrm{\gamma }{S}_4\hfill \end{array}.$$ 33

The GMA representation of these reactions is given by the following rate equations

$$\begin{array}{c}\hfill \frac{d\left[S_1\right]}{\mathit{dt}}=-k_1\left[S_1\right]{\left[S_2\right]}^{\mathrm{\alpha }}\hfill \\ \hfill \frac{d\left[S_2\right]}{\mathit{dt}}=\alpha k_1\left[S_1\right]{\left[S_2\right]}^{\mathrm{\alpha }}+\mathrm{\alpha }{k}_2{\left[S_3\right]}^{\beta }\hfill \\ \hfill \frac{d\left[S_3\right]}{\mathit{dt}}=\beta k_1\left[S_1\right]{\left[S_2\right]}^{\mathrm{\alpha }}-\beta k_2{\left[S_3\right]}^{\beta }\hfill \\ \hfill \frac{d\left[S4\right]}{\mathit{dt}}=\mathrm{\gamma }{k}_2{\left[S_3\right]}^{\beta }\hfill \end{array}$$ 34

Substituting (31) and (32) in (30) gives

$$\frac{d}{\mathit{dt}}〈\#S_i〉={\displaystyle \sum _{\mathit{\mu }=1}^M\frac{v_{\mathit{\mu i}}{k}_{\mu }}{{\left(N_{A}V\right)}^{K_{\mu }-1}}}{\mathit{\Pi }}_{j=1}^{L_{\mu }}{〈\#S_{p\left(\mu ,j\right)}〉}^{l_{\mathit{\mu j}}}$$ 35

where

$$K_{\mathit{\mu }}={\displaystyle \sum _{j=1}^{L_{\mu }}{l}_{\mathit{\mu j}}}$$

denotes the molecularity of the reaction channel R _μ. The differential operator is justified only with the assumption of large numbers of molecules involved, such that near continuous changes are observed.

Now, the “particle-O.D.E.” for the temporal evolution of <#S _i> is

$$\frac{d}{\mathit{dt}}〈\#S_i〉={\displaystyle \sum _{\mu =1}^M{v}_{\mathit{\mu i}}{k}_{\mu }^{\prime }}{\mathit{\Pi }}_{j=1}^{L_{\mu }}{〈\#S_{p\left(\mu ,j\right)}〉}^{l_{\mathit{\mu j}}}$$ 36

Comparing (35) with (36), we find

$$k_{\mathit{\mu }}^{\prime }=\frac{k_{\mu }}{{\left(N_{A}V\right)}^{K_{\mu }-1}}$$ 37

This equation then describes the interpretation of the rate constant, dependent on whether we consider concentrations or counts of molecules.

Let us now arrive at a general expression for the propensity a _μ. Note that, from (36), the average number of reactions R _μ occurring in (t, t + dt) is

$$〈R_{\mathit{\mu }}〉=k_{\mathit{\mu }}^{\prime }{\mathit{\Pi }}_{j=1}^{L_{\mathit{\mu }}}{〈\#S_{p\left(\mathit{\mu },j\right)}〉}^{l_{\mathit{\mu j}}}\mathit{dt}$$ 38

Let #R _μ be the number of reactions R _μ. If we consider #R _μ a discrete random variable with probability distribution function $p_{r_{\mu }}=\mathit{Prob}\left\{\#R_{\mu }=r_{\mu }\right\}$, where r _μ is the value assumed by the random variable #R _μ, the expectation value 〈 # R _μ〉 is given by

$$〈\#R_{\mu }〉={\displaystyle \sum _{r_{\mu }}{r}_{\mu }〈p{r}_{\mu }〉r_{\mu }=0,1,2,\dots }$$ 39

where

$$p{r}_{\mu }=\left\{\begin{array}{cc}\hfill a_{\mu }\mathit{dt}+o\left(\mathit{dt}\right)\hfill & \hfill \mathrm{if}{r}_{\mu }=1\hfill \\ \hfill 1-a_{\mu }\mathit{dt}+o\left(\mathit{dt}\right)\hfill & \hfill \mathrm{if}{r}_{\mu }=0\hfill \\ \hfill o\left(\mathit{dt}\right)\hfill & \hfill \mathrm{if}{r}_{\mu }>0\hfill \end{array}\right.$$ 40

where o(dt) is a negligible probability for more than one R _μ reaction to occur during dt. Since pr _μ is randomly varying and then the average 〈pr _μ〉 over the ensemble is in (39), and Eq. 39 becomes

$$〈\#R_{\mu }〉=0\cdot p_0+1\cdot p_1+{\displaystyle \sum _{r_{\mu }}{r}_{\mu }}〈p_{r_{\mu }}〉$$

From (39) and (40), we then have

$$〈\#R_{\mu }〉=〈a_{\mu }\mathit{dt}〉+o\left(\mathit{dt}\right)$$ 41

where, from (38) and (41), the propensity of R _μ reaction to occur in dt is given as

$$〈a_{\mu }〉=k_{\mu }^{\prime }{\Pi }_{j=1}^{L_{\mu }}{〈\#S_{p\left(\mu ,j\right)}〉}^{l_{\mathit{\mu j}}}$$ 42

As already seen in the previous section, the propensity a _μ for a reaction R _μ is expressed as the product of the stochastic rate constant c _μ and the number h _μ of distinct combinations of reactant molecules of R _μ

$$a_{\mu }=c_{\mu }\cdot h_{\mu }$$ 43

In the literature, h _μ is known as the redundancy function. This function varies over time in the following way

$$h_{\mu }\left(n\right)\left\{\begin{array}{ll}{\displaystyle \prod {}_{j=1}^{L_{\mu }}\left({}_{l_{\mathit{\mu j}}}^{n_p\left(\mu ,j\right)}\right)}\hfill & \mathrm{for}{n}_{p\left(\mu ,j\right)}>0\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$ 44

If n _p(μ,j) is large and l _μj > 1, terms like (n _p(μ,j) − 1),…, (n _p(μ,j) − l _μj + 1) are not much different from n _p(μ,j), and we may write

$$h_{\mu }\approxeq {\displaystyle \prod {}_{j=1}^{L_{\mu }}\frac{{\left(n_{p\left(\mu ,j\right)}\right)}^{l_{\mathit{\mu j}}}}{l_{\mathit{\mu j}}!}=\frac{{\displaystyle \prod {}_{j=1}^{L_{\mu }}{\left(n_{p\left(\mu ,j\right)}\right)}^{l_{\mathit{\mu j}}}}}{{\displaystyle \prod {}_{j=1}^{L_{\mu }}{l}_{\mathit{\mu j}}!}}}$$ 45

We can write an alternative expression for a _μ by substituting (45) into (43) and considering the average

$$〈a_{\mu }〉=c_{\mu }\cdot 〈\frac{{\displaystyle \prod {}_{j=1}^{L_{\mu }}{\left(\#S_{p\left(\mu ,j\right)}\right)}^{l_{\mathit{\mu j}}}}}{{\displaystyle \prod {}_{j=1}^{L_{\mu }}{l}_{\mathit{\mu j}}!}}〉$$ 46

where #S _p(μ,i) is the random variable whose value is n _p(μ,j). Comparing (42) with (46), we obtain

$$k_{\mu }^{\prime }{\displaystyle \prod {}_{j=1}^{L_{\mu }}{〈\#S_{p\left(\mu ,j\right)}〉}^{l_{\mathit{\mu j}}}}=\frac{c_{\mu }〈{\displaystyle \prod {}_{j=1}^{L_{\mu }}{〈\#S_{p\left(\mu ,j\right)}〉}^{l_{\mathit{\mu j}}}}〉}{{\displaystyle \prod {}_{j=1}^{L_{\mu }}{l}_{\mathit{\mu j}}!}}$$

Making the assumption of zero covariance (i. e. 〈#S_i#S_j〉 = 〈#S_i〉 〈#S_j〉 means for i  ≠ j nullifying correlation, and for i = j nullifying random fluctuations) gives

$$k_{\mu }^{\prime }=\frac{c_{\mu }}{{\displaystyle \prod {}_{j=1}^{L_{\mu }}{l}_{\mathit{\mu j}}!}}$$ 47

which can be turned into an expression for c _μ

$$c_{\mu }=k_{\mu }^{\prime }\cdot {\displaystyle \prod {}_{j=1}^{L_{\mu }}{l}_{\mathit{\mu j}}!}$$ 48

Inserting (37) for k ^′_μ, we arrive at

$$c_{\mu }=\left(\frac{k_{\mu }}{{\left(N_{A}V\right)}^{K_{\mu }-1}}\right)\cdot {\displaystyle \prod {}_{j=1}^{L_{\mu }}{l}_{\mathit{\mu j}}!}$$ 49

Equation 49 is the law of conversion of the deterministic rate constant k _μ into the stochastic rate constant c _μ and is used in most implementations of Gillespie-like stochastic simulation algorithms. Note that if, above, we substitute 〈S〉/V in (30) for [S] instead of 〈 # S〉/(N _A V), the only difference to (37) and (49) is that NA would not appear in these equations.

This derivation is different from the one given by Gillespie in [6]. The difference is that Wolkenhauer et al. introduced the average number of reactions (Eq. 38) to move from the general GMA representation (30), which is independent of particular examples, to an expression that allows to derive parameter c _μ of the stochastic simulation (49) without referring to the temporal evolution of moments of CME. This makes the derivation more compact. Moreover, in [6], the temporal evolution of the mean is derived for examples of bi- and tri-molecular reactions only.

Finally, we add some comments to this derivation and its implications in a simulation algorithm. First, using the approximation (45) for h _m u is valid for large numbers of molecules with l_μj >1. In the simulations presented in this paper, this does not lead to significant differences. More important, however, is the fact that the derivation (49) relies on the rate constant of the GMA model. Nevertheless, this does not mean that the CME approach relies on the GMA model, since, to derive rather than postulate a rate equation, one must first postulate a stochastic mechanism from which the GMA arises as a limit.

The existence of a relationship between deterministic and stochastic models assumes the existence of a way to compare these two approaches. In principle, we can assert that the GMA model (30) has the following advantage with respect to the CME model: its terms and parameters are the direct translation of the biochemical reaction diagrams that capture the biochemical relationships of the molecules involved. On the contrary, rate equations are in virtually all cases simpler than CME. However, for any realistic pathway model, a formal analysis is not always feasible and a numerical solution (simulation) is the only way to compare two models. In this case, the Gillespie algorithm, which will be presented in the following sections, provides an efficient implementation to generate the realization of the CME (i.e. it is a realization of a time-continuous Markov process).

The reaction probability density function

In this section, we introduce the foundation of the stochastic simulation algorithm of Gillespie. If we are given that the system is in the state X = X ₁,…,X _N at time t, computing its stochastic evolution means “moving the system forward in time”. In order to do that, we need to answer two questions.

1. When will the next reaction occur?

2. What kind of reaction will it be?

Because of the essentially random nature of chemical interactions, these two questions are answerable only in a probabilistic way.

Let us introduce the function P (τ, μ) defined as the probability that, given the state X at time t, the next reaction in the volume V will occur in the infinitesimal time interval (t + τ, t + τ + dτ), and will be an R _μ reaction. P (τ, μ) is called the reaction probability density function, because it is a joint probability density function on the space of the continuous variable τ (0 ≤ τ < ∞) and the discrete variable μ (μ = 1, 2, …, M).

The values of the variables τ and μ will give us answer to the two questions mentioned above. Gillespie showed that, from the fundamental hypothesis of stochastic chemical kinetics (see Section 4), it is possible to derive an analytical expression for P (τ, μ), and then use it to extract the values for τ and μ. Gillespie showed how to derive from the fundamental hypothesis and from an analytical expression of P (τ, μ). First of all, P (τ, μ) can be written as the product of P ₀(τ), the probability that given the state X at time t, no reaction will occur in the time interval (t, t + dt), times a _μ dτ, the probability that an R _μ reaction will occur in the time interval (t + τ, t + τ + dτ)

$$P\left(\mu ,\tau \right)\mathit{d\tau }=P_0\left(\tau \right)a_{\mu }\mathit{dt}$$ 50

In turn, P ₀ (τ) is given by

$$P_0\left(\tau \prime +\mathit{d\tau }\prime \right)=P_0\left(\tau \prime \right)\left[1-{\displaystyle \sum _{i=1}^M{a}_i\mathit{d\tau }\prime }\right]$$ 51

where [1 − ∑ ^M_i = 1 a _i dτ ′] is the probability that no reaction will occur in time dτ′ from the state X. Therefore,

$${\P }_0\left(\tau \right)=exp\left[-{\displaystyle \sum _{i=1}^M{a}_i\mathit{\tau }}\right]$$ 52

Inserting (51) into (50), we find the following expression for the reaction probability density function

$$P\left(\mu ,\tau \right)=\left\{\begin{array}{ll}{a}_{\mu }exp\left(-a_0\tau \right)\hfill & \mathrm{if}0\le \tau <\mathit{infty}\hfill \\ 0\hfill & \mathit{otherwise}\hfill \end{array}\right.$$ 53

where a _μ is given by (43) and

$$a_0\equiv {\displaystyle \sum _{i=1}^M{a}_i\equiv {\displaystyle \sum _{i=1}^M{h}_i{c}_i}}$$ 54

The expression for P (μ, τ) in (53) is, like the master equation in (5), a rigorous mathematical consequence of the fundamental hypothesis (28). Notice finally that P (τ, μ) depends on all the reaction constants (not just on c _μ) and on the current numbers of all reactant species (not just on the R _μ reactants).

The stochastic simulation algorithms

In this section, we review the three formulations of stochastic simulation variants of Gillespie algorithm: Direct, First Reaction, and Next Reaction Method.

Direct method

On each step, the Direct Method generates two random numbers, r ₁ and r ₂, from a set of uniformly distributed random numbers in the interval (0, 1). The time for the next reaction to occur is given by t + τ, where τ is given by

$$\tau =\frac{1}{a_0}ln\left(\frac{1}{r_1}\right)$$ 55

The index μ of the occurring reaction is given by the smallest integer satisfying

$${\displaystyle \sum _{j=1}^{\mu }{a}_j>r_2{a}_0}$$ 56

The system states are updated by X(t + τ) = X(t) + v _μ, then the simulation proceeds to the next occurring time.

Algorithm

1. Initialization: set the initial numbers of molecules for each chemical species; input the desired values for the M reaction constants c ₁, c ₂,…,c _M. Set the simulation time variable t to zero and the duration T of the simulation.

2. Calculate and store the propensity functions a ₁ for all the reaction channels (i = 1,…,M), and a ₀.

3. Generate two random numbers r ₁ and r ₂ in Unif (0, 1).

4. Calculate τ according to (55)

5. Search for μ as the smallest integer satisfying (56).

6. Update the states of the species to reflect the execution of μ (e. g. if R _μ : S _i + S ₂ → 2S ₁, and there are X ₁ molecules of the species S ₁ and X ₂ molecules of the species S ₂, then increase X ₁ by 1 and decrease X ₂ by 1). Set t ← t + τ.

7. If t < T then go to step 2, otherwise terminate.

Note that the random pair (τ, μ), where τ is given by (55) and μ by (56), is generated according to the probability density function in (53). A rigorous proof of this fact may be found in [1]. Suffice here to say that (55) generates a random number τ according to the probability density function

$$P_1\left(\tau \right)=a_{0}exp\left(-a_0\tau \right)$$ 57

while (56) generates an integer μ according to the probability density function

$$P_2\left(\mu \right)=\frac{a_{\mu }}{a_0}$$ 58

and the stated result follows because

$$P\left(\tau ,\mu \right)=P_1\left(\tau \right)\cdot P_2\left(\mu \right)$$

Note finally that, to generate random numbers between 0 and 1, we can do as follows. Let F _X(x) be a distribution function of an exponentially distributed variable X and let U ∼ Unif[0,1) denote an uniformly distributed random variable U on the interval (0, 1).

$$F_X\left(x\right)=\left\{\begin{array}{ll}1-e^{-\mathit{ax}}\hfill & \mathrm{if}\mathit{x}\ge 0\hfill \\ 0\hfill & \mathrm{if}\mathit{x}<0\hfill \end{array}\right.$$ 59

F _x (x) is a continuous non-decreasing function and this implies that it has an inverse F ^− 1_X. Now, let X(U) = F ^− 1_X(U) and we get the following

$$P\left(X\left(U\right)\le x\right)=P\left(F_X^{-1}\left(U\right)\le x\right)$$ 60

$$\begin{array}{l}=P\left(U\le F_X\left(x\right)\right.\hfill \\ =F_X\left(x\right)\hfill \end{array}$$ 61

It follows that

$$F_X^{-1}\left(U\right)=-\frac{ln\left(1-U\right)}{a}\sim \mathit{Exp}\left(a\right)$$ 62

In returning to step 1 from step 7, it is necessary to re-calculate only those quantities a _i, corresponding to the reactions R _i whose reactant population levels were altered in step 6; also, a ₀ must be re-calculated simply by adding to it the difference between each newly changed a _i value and its corresponding old value. This algorithm uses M random numbers per iteration, takes time proportional to M to update the a _is, and takes time proportional to M to identify the smallest putative time.

First reaction method

The First Reaction Method generates a τ _k for each reaction channel R _μ according to

$${\tau }_i=\frac{1}{a_i}ln\left(\frac{1}{r_i}\right)$$ 63

where r ₁, r ₂,…,r _M are M statistically independent samplings of Unif (0, 1). Then, τ and μ are chosen as

$$\tau =min\left\{{\tau }_1,{\tau }_2,\dots ,{\tau }_M\right\}$$ 64

and

$$\mu =\mathrm{the}\mathrm{index}\mathrm{of}min\left\{{\tau }_1,{\tau }_2,\dots {\tau }_M\right\}.$$ 65

Algorithm

1. Initialization: set the initial numbers of molecules for each chemical species; input the desired values for the M reaction constants c ₁, c ₂,…,c _M. Set the simulation time variable t to zero and the duration T of the simulation.

2. Calculate and store the propensity functions a ₁ for all the reaction channels (i = 1, dots.M), and a ₀.

3. Generate M independent random numbers from Unif (0, 10).

4. Generate the times τ _i, (i = 1, 2,…,M) according to (63).

5. Find τ and μ according to (64) and (65), respectively.

6. Update the states of the species to reflect the execution of reaction μ. Set t ← t + τ.

7. If t < T then go to step 2, otherwise terminate.

The Direct and the First Reaction methods are fully equivalent to each other [1, 5]. The random pairs (τ, μ) generated by both methods follow the same distribution.

Next reaction method

Gibson and Bruck [19] transformed the First Reaction Method into an equivalent but more efficient new scheme. The Next Reaction Method is more efficient than the Direct method when the system involves many species and loosely coupled reaction channels. This method can be viewed as an extension of the First Reaction Method in which the unused M-1 reaction times (64) are suitably modified for reuse. Clever data storage structures are employed to efficiently find τ and μ.

Algorithm

1. Initialize:

   • set the initial numbers of molecules, set the simulation time variable t to zero, generate a dependency graph G;
   • calculate the propensity functions α _i, for all i
   • for each i, (i = 1,2,…,M), generate a putative time τ _i, according to an exponential distribution with parameter a _i
   • store the τ _i values in an indexed priority queue P.

2. Let μ be the reaction whose putative time τ _μ stored in P, is least. Set τ ← τ _μ.

3. Update the states of the species to reflect the execution of the reaction μ. Set τ ← τ _μ.

4. For each edge (μ, α) in the dependency graph G

   • update a ₀
   • if α ≠ μ, set

     $${\tau }_{\alpha }\leftarrow \frac{a_{\alpha ,\mathit{old}}}{a_{\alpha ,\mathit{new}}}\left({\tau }_{\alpha }-t\right)+t$$ 66
   • if α = μ, generate a random number r and compute τ _α according to the following equation

     $${\tau }_{\alpha }=\frac{1}{a_{\alpha }\left(t\right)}ln\left(\frac{1}{r}\right)+t$$ 67
   • replace the old τ _α value in P with the new value

5. Go to step 2.

   Two data structures are used in this method:

   • The dependency graph G is a data structure that tells precisely which a _i should change when a given reaction is executed. Each reaction channel is denoted as a node in the graph. A direct edge connects R _i to R _j if and only if the execution of R _i affects the reactants in R _j. The dependency graph can be used to recalculate only the minimal number of propensity functions in step 4.
   • The indexed priority queue consists of a tree structure of ordered pairs of the form (i, τ _i), where i is a reaction channel index and τ _i is the corresponding time when the next R _i reaction is expected to occur, and an index structure whose ith element points to the position in the tree which contains (i, τ _i). In the tree, each parent has a smaller τ than either of its children. The minimum τ always stays on the top of the node and the order is only vertical. In each step, the update changes the value of the node and then bubbles it up or down according to its value to obtain the new priority queue. Theoretically, this procedure takes at most 1n (M) operations. In practice, usually there are a few reactions that occur much more frequently. Thus, the actual update takes less than 1n (M) operations.

The Next Reaction Method takes some CPU time to maintain the two data structures. For a small system, this cost dominates the simulation. For a large system, the cost of maintaining the data structures may be relatively smaller compared to the savings. The argument for the advantage of the Next Reaction Method over the Direct Method is based on two observations: first, in each step, the Next Reaction Method generates only one uniform random number, while the Direct Method requires two. Second, the search for the index μ of the next reaction channel takes O(M) time for the Direct Method, while the corresponding cost for the Next Reaction Method is on the update of the indexed priority queue which is O(ln(M))

Time-dependent extension of the First Reaction Method

The Gillespie algorithm has been used on numerous occasions to simulate biochemical kinetics and even complex biological systems. Its success is due to its proved equivalence with Master Equation and its efficiency and precision: no time is wasted on simulation iterations in which no reactions occur, and the treatment of the time as a continuum allows the generation of exact series of τ values based on rigorously derived probability density functions. However, all the formulations of the algorithm are grounded on the fundamental hypothesis of stochastic chemical kinetics and do not consider the effects on the rate constant of eventual temporal changes of volumes and temperature of the reaction chamber, the activation energy, and the presence of catalyst concentration. In this section, we review an extension of First Reaction Method to the case of time-depending rates. This extension has been developed by Lecca [20, 21] and is inspired by [22]. It focuses on the time dependency of the kinetic rates on volume and temperature deterministic changes. This re-formulation has been adapted to be incorporated in the framework of stochastic π-calculus and its implementation has been applied to a sample simulation in biology: the passive glucose cellular transport [20, 21].

Assume that the volume V _s (t) contains a mixture of chemical species, X _i (i = 1,…,N) which may interact through the reaction channels R _μ, μ = 1,…,M. Let suppose furthermore that a subset of these channels is characterized by the time-dependent propensities

$$a_s\left(t\right)=a_s^{\prime }/V\left(t\right),s=1,\dots ,S$$ 68

and another sub-set is characterized by the time-dependent propensities

$$a_q\left(t\right)=a_q^{\prime }/V\left(t\right),q=S+1,\dots ,M$$ 69

Where a ^′_s and (a ^′_q) are the time-independent propensities, that have to be computed using Eqs. 12, 15 and 18, according to the type of reaction.

Following the Gillespie approach, let introduce these probabilities:

1. P(τ,μ|Y, t)dτ: probability that, given the state Y = (X ₁, …,X _N) at time t, the next reaction will occur in the infinitesimal time interval (t + τ, t + τ + dτ), at it will be reaction R _μ

2. a _μ (t) dt: probability that, given the state Y = (X ₁, …,X _N) at time t, reaction R _μ will occur within the interval (t, t + dt).

P(τ,μ|Y, t)dτ is computed as a product of the probabilities that no reaction will occur within (t, t + τ) times the probability that R _μ will occur within the subsequent interval (t + τ, t + τ + dτ)

$$P\left(\left.\tau ,\mu \right|Y,t\right)\mathit{d\tau }=P_0\left(\left.\tau \right|Y,t\right)\cdot a_{\mu }\left(\tau +t\right)\mathit{d\tau }$$ 70

where, summing over all reaction channels μ = 1,…,M and splitting the sum in the two terms over s and q

$$P_0\left(\left.\tau +\mathit{d\tau }\right|Y,t\right)=P_0\left(\left.\tau \right|Y,t\right)\left[1-\mathit{d\tau }{\displaystyle \sum _{s=1}^S{a}_s\left(t+\tau \right)-\mathit{d\tau }{\displaystyle \sum _{q=S+1}^M{a}_q\left(t+\tau \right)}}\right]$$ 71

With the initial condition P ₀(τ = 0|Y, t) = 1, the solution of this differential equation is

$$P_0\left(\left.\tau \right|Y,t\right)=exp\left[-{\displaystyle \sum _s{\displaystyle {\int }_t^{t+\tau }{a}_s\left(t+\tau \prime \right)\mathit{d\tau }\prime -{\displaystyle \sum _q{\displaystyle {\int }_t^{t+\tau }{a}_q\left(t+\tau \prime \right)\mathit{d\tau }\prime }}}}\right]$$ 72

Now, by combining Eq. 70 with Eq. 72, we obtain

$$\begin{array}{l}P\left(\left.\tau ,\mu \right|,Y,y\right)=\hfill \\ \begin{array}{l}{a}_{\mu }\left(t+\tau \right)\cdot exp\left[-{\displaystyle \sum _s{\displaystyle {\int }_t^{t+\tau }{a}_s\left(t+\tau \prime \right)-{\displaystyle \sum _q{\displaystyle {\int }_t^{t+\tau }{a}_q\left(t+\tau \prime \right)\mathit{d\tau }\prime }}}}\right]\\ \end{array}\hfill \end{array}$$ 73

By introducing two functions f _s (τ) and f _q (τ) describing the variation of volume in time, the time-dependence of the volumes can be described by these expressions:

$$V_s\left(t+\tau \right)=V_s\left(t\right)f_s\left(\tau \right)\mathrm{and}{V}_q\left(t+\tau \right)=V_q\left(t\right)f_q\left(\tau \right).$$

Consequently, the propensities are

$$a_s\left(t+\tau \right)=a_s\left(t\right)/f_s\left(\tau \right)\mathrm{and}{a}_q\left(t+\tau \right)=a_q\left(t\right)/f_q\left(\tau \right).$$

Substituting these expressions in Eq. 73, and introducing, for convenience

$$\begin{array}{rrr}\hfill A_s\equiv {\displaystyle \sum _s{a}_s\left(t\right)}& \hfill \mathrm{and}& \hfill A_q\equiv {\displaystyle \sum _q{a}_q\left(t\right)}\\ \hfill F_s\left(\tau \right)\equiv {\displaystyle {\int }_t^{t+\tau }\frac{1}{f_s\left(\tau \prime \right)}\mathit{d\tau }\prime }& \hfill \mathrm{and}& \hfill F_q\left(\tau \right)={\displaystyle {\int }_t^{t+\tau }\frac{1}{f_q\left(\tau \prime \right)}\mathit{d\tau }\prime }\end{array}$$

so that Eq. 73 can be re-written as

$$P\left(\left.\tau ,\mu \right|Y,t\right)=\left\{\begin{array}{l}\frac{a_s\left(t\right)}{f_s\left(\tau \right)}\cdot exp\left[-A_s{F}_s\left(\tau \right)-A_q{F}_q\left(\tau \right)\right]\hfill \\ \frac{a_q\left(t\right)}{f_q\left(\tau \right)}\cdot exp\left[-A_s{F}_s\left(\tau \right)-A_q{F}_q\left(\tau \right)\right]\hfill \end{array}\right.$$ 74

Finally, the probability of any reaction occurring between time t and the time t + t′, is obtained by integrating Eq. 74 over time and summing over all channels:

$${\displaystyle {\int }_0^{\prime }{\displaystyle \sum _{\mu }P\left(\left.\tau ,\mu \right|Y,t\right)\mathit{d\tau }=\left\{\begin{array}{l}{\displaystyle {\int }_0^{t\prime }{\displaystyle {\sum }_{s\prime =1}^S\frac{a_{s\prime \left(t\right)}}{f_s\left(\tau \right)}}}\cdot exp\left[-A_s{F}_s\left(\tau \right)-A_q{F}_q\left(\tau \right)\right]\mathit{d\tau }\hfill \\ {\displaystyle {\int }_0^{t\prime }{\displaystyle {\sum }_{q\prime =S+1}^M\frac{a_{q\prime \left(t\right)}}{f_q\left(\tau \right)}}}\cdot exp\left[-A_s{F}_s\left(\tau \right)-A_q{F}_q\left(\tau \right)\right]\mathit{d\tau }\hfill \end{array}\right.}}$$ 75

Generalizing, in systems where the physical reaction space is divided into n sub-spaces whose volumes change in time, the probability density function of reaction is split into n exponential terms multiplied by theratio between reaction propensity and volume of the sub-space. The volume of each sub-space can follow a different temporal behavior. Consequently, a different reaction probability and a different expression of reaction time are obtained for each sub-regions of the space.

Approximate stochastic simulation algorithms

The stochastic simulation algorithm is exact in the sense that it is rigorously based on the same microphysical premise that underlies the chemical master equation; thus, a history or “realisation” of the systems produced by the stochastic simulation algorithm (SSA) gives a more realistic representation of the system’s evolution than would a history inferred from the conventional deterministic reaction rate equation. However, the huge computational effort needed for exact stochastic simulation entailed a lively search for approximate simulation methods that sacrifice an acceptable amount of accuracy in order to speed up the simulation. A good review of the approximated stochastic simulation algorithm is a recent paper of Pahle [23].

The proposed methods often involve a grouping of reaction events, i.e. they permit more than one reaction event per step. Namely, the time axis is divided into small discrete chunks, and the underlying kinetics are approximated so that advancement of the state from the start of one chunk to another can be made in one go. Most of the methods work on the assumption that the time intervals have been chosen to be sufficiently small that the reaction hazards can be assumed constant over the interval.

Poisson timestep method

A point process with constant hazard is a (homogeneous) Poisson process. Based on the definition of the Poisson process, we assume that the number of reactions (of a given type) occurring in a short time interval has a Poisson distribution (independently of other reaction types).

For a fixed small time step ∆t, we can use an approximate simulation algorithm as follows.

1. Initialize the system with time t ← 0, rate constants c, state X, and stoichiometry. Set the simulation time T.

2. Calculate the propensities a _i (X _i, c _i) and simulate the u-dimensional reaction vector r, with i-th entry a Po(a _i(X_i,c _i)Δt) random quantity

3. Update the state according to X ← X + Sr.

4. Update t ← t + Δt

5. If t < T return to step 2.

The Poisson method is a precursor of the τ-leap method originally developed by Gillespie in 2001 [9].

The τ-leap method

The τ-leap method [9] and its recent variants [3, 24–28] are an adaptation of the Poisson timestep method to allow stepping ahead in time by a variable amount τ, whereeach time step τ is chosen in an appropriate way in order to ensure a sensible trade-off between accuracy and algorithmic speed. This is achieved by making τ as large as possible but still satisfying some constraint designed to ensure accuracy. In this context accuracy is determined by the extent to which the assumption of constant hazard over the time interval is appropriate.

Let us suppose that the history of the system is to be recorded by marking on a time axis the successive instants t ₁, t ₂, t ₃,… at which the first, second, third, …, reaction events occur, and also appending to those points the indices j ₁, j ₂, j ₃,… of the respective reaction channels R _j, that “fire” at those instants. This “history axis” completely describes a realization of X (t); this can be constructed by monitoring the τ, i-generating procedure of the stochastic simulation algorithm as it dutifully steps us from each t _n to t _n+1. This “stepping” among the history axis is both a point of strength and point of weakness. It is a point of strength because the precise construction of every individual reaction event gives a complete and detailed history of X (t). It is a weakness because that construction is a time-consuming task for chemical/biochemical system of realistic size.

The system history axis can be divided into a set of contiguous subintervals is such a way that, if we could only determine how many times each reaction channel fired in each subinterval, we could forego knowing the precise instants at which those firings took place. Such a circumstance would allow us to leap along the system’s history axis from one subinterval to the next, instead of stepping along from one reaction event to the next. If enough of the subintervals contained many individual reaction events, the gain in simulation speed could be substantial (provided that each subinterval leap could be done expeditiously).

Now, let us go deep into the mathematical formulation of the τ-leap method. Consider the probability function

$$Q\left(\tau ,\mathrm{X},t\right)$$

which is the probability, given X(t) = x, that in the time interval (t, t + τ) exactly k _j firings of reaction channel R _j will occur for each j = 1,…M. (M is number of reactions).

Q is the joint probability density function of the M integer variables

$$K_j\left(\tau ,x,t\right)$$

giving the number of times, given X(t) = x, that reaction channel R _j will fire in the time interval (t, t + τ). (j = 1,…M).

To determine Q(τ,X,t) for an arbitrary τ is fairly hard, but we can get a simple approximate form for Q(τ,X,t) if we impose the following condition on τ. It is known as the Leap Condition and requires μ to be small enough that the change in the state during (t, t + τ) is so slight that no propensity function suffers a macroscopical change in its value.

If the Leap Condition is satisfied, during the time interval (t, t + τ), the propensity function for each reaction channel R _j will remain constant at the value a _j (x). This means that a _j (x) dt is the probability that reaction channel R _j fires during any infinitesimal interval dt inside (t, t + τ), regardless of what the other reaction channels are doing. In that case, K _j (τ, x, t) will be a Poisson random variable

$$\begin{array}{ll}{K}_j\left(\tau ,x,t\right)=\mathit{Po}\left(a_j\left(x,\tau \right)\right)\hfill & j=1,\dots ,M\hfill \end{array}$$

and since these M random variables K ₁(τ,x,t), …, K _M(τ,x,t) are statistically independent, the joint density function is the product of the density functions of the individual Poisson random variables

$$Q\left(\tau ,\mathrm{X},t\right)={\mathit{\Pi }}_{j=1}^M{P}_{p_o}\left(k_j;a_j\left(x,\tau \right)\right)$$ 76

where P _Po (k;at) denotes the probability that Po(a,t) = k.

It is easy to show that

$$\mathit{Po}\left(0,a,t\right)=exp\left(-\mathit{at}\right)$$

and by the laws of probability, we have for any integer k ≥ 1,

$$P_{P_o}\left(k,\mathit{a},t\right)={\displaystyle {\int }_{t\prime }^t{P}_{P_o}\left(k-1,a,t\prime \right)\times \mathit{adt}\prime \times P_{\mathit{po}}\left(0,a,t-t\prime \right)}$$

Using this recursion relationship, we can establish by induction that

$$\begin{array}{ll}{P}_{P_o}\left(k,a,t\right)=\frac{e^{-\mathit{at}}{\left(\mathit{at}\right)}^k}{k!}\hfill & \left(k=0,1,2,\dots \right)\hfill \end{array}$$

We can show from this result that the mean and the variance of P _Po (k;at) are both equal to at:

$$E\left(P_{P_o}\left(k;a,t\right)\right)=\mathrm{Var}\left(P_{P_o}\left(k:a,t\right)\right)=\mathit{at}$$ 77

The Eq. 77 is the basis for the following well-known rule-of-thumb:

"for random events occurring at a rate ‘a’, i.e. with mean time per event a − 1, the number of events expected in a time t is

$$\mathit{at}\pm \sqrt{\mathit{at}}$$

Note that the Poisson random variable Po (a,t) is defined to be the number of reaction events that occur in a time t, given that a·dt is the probability for an event to occur in any next infinitesimal time interval dt. The parameters a and t can be any positive real numbers; however, the random variable Po (a,t) itself in a non-negative integer.

If the Leap Condition is satisfied, we can leap down the history axis of the system by the amount τ from state x at time t by proceeding as follows.

• For each reaction channel R _j generates, a sample value k _j of the Poisson random variable Po(a _j(x), τ).

  k _j will be the number of times reaction channel R _j fires in (t,t + τ). Since each firing of R _j changes the S _i population by v _ji molecules, the net change in the state of the system in (t,t + τ) will be

  $$\lambda ={\displaystyle \sum _{j=1}^M{k}_j{v}_{\mathrm{j}}}$$ 78

  where v _j is the state-change vector, whose i-th, v _ji, is the number of S _i molecules produced by one R _j reaction (j = 1,…,M and i = 1,…,N).

Algorithm

1. Choose a value of τ that satisfies the Leap Condition; i. e. a temporal leap τ resulting in a state change λ which is such that, for every reaction channel R _j

   $$\left|a_j\left(x+v\right)-a_j\left(x\right)\right|$$

   is “effectively infinitesimal”.

2. Generate for each j = 1,…,M a sample value k _j of the Poisson random variable Po(a _j(x,τ)) and compute λ as in formula (78).

3. Effect the leap by replacing t with t + τ and x by x + λ

The accuracy of the τ-leap algorithm depends upon how well the Leap Condition is satisfied.

In trivial case, none of the propensity functions depend on x. In this case the Leap Condition is satisfied for any τ, and the τ leaping will be exact. In a realistic case, most commonly, the propensity functions depend linearly or quadratically on the molecular populations, and τ-leaping will not be exact. Since each reaction event changes the reactant population by no more than one or two molecules, then if the reactant molecule populations are very large, the algorithm will need to perform a very large number of reaction events to change the propensity functions noticeably.

So, if we have large molecular populations, in order to make the τ-leap algorithm efficient we have to be able to satisfy the Leap Condition with a choice of τ that allows many reaction events to occur in (t,t + τ); that will result in a “leap” on the history axis of the system that is much longer than the single reaction “step” of the exact stochastic simulation algorithm. On the other hand, in order to satisfy the Leap Condition, τ must be so small that only a very few reactions are leaped over. Therefore, it would be faster to forego leaping and use the exact stochastic simulation algorithm!

For example, if we take

$$\tau =\frac{1}{a_0}$$ 79

where a ₀ = ∑ ^M_j = 1 a _j. Consequently, the resultant leap would be the expected size of the next time step in exact SSA (see Gillespie Direct Method), and very likely one of the generated k _j’s would be 1 and all the others would be 0. Still, a choice of smaller τ would result in leaps in which all the k _j’s would likely be 0. This situation would gain us nothing!

To use τ-leap method when $\tau \le \frac{1}{a_0\left(\mathrm{x}\right)}$ is inefficient, but not incorrect. What we expect is that as τ decreases to $\frac{1}{a_0\left(\mathrm{x}\right)}$ or less, the results produced by the τ-leap algorithm will follow smoothly the results that would be produced by the exact SSA.

In order to successfully employ the τ-leap algorithm in practical situations, we need to determine the largest value of τ that is compatible with the Leap Condition.

A procedure for determining τ may be the following. Since the mean (or expected value) of k _j is

$$E\left(\mathit{Po}\left(a_j\left(x,\tau \right)\right)\right)=a_j\left(\mathrm{x}\right)\tau$$

then the expected net change in state in the interval (t,t + τ) will be

$$E\left(\mathrm{\lambda }\left(\mathrm{x},\tau \right)\right)={\displaystyle \sum _{j=1}^M{\mathrm{v}}_j{a}_j\left(\mathrm{x}\right)}\tau =\mathit{\tau \xi }\left(\mathrm{x}\right)$$ 80

where

$$\xi \left(\mathrm{x}\right)\equiv {\displaystyle \sum _{j=1}^M{a}_j\left(\mathrm{x}\right)v_j}$$ 81

ξ (x) is the mean or expected state change in a unit of time.

Now, assume that the expected changes in the propensity functions in time τ is bounded by some specified 0 < ∈ < 1 of the sum of all the propensity functions:

$$\begin{array}{ll}\left|a_j\left(\mathrm{x}+E\left(\mathit{\lambda }\right)\right)-a_j\left(\mathrm{x}\right)\right|\le \in a_0\left(\mathrm{x}\right)\hfill & j=1,\dots ,M\hfill \end{array}$$ 82

We can estimate the difference on the left side of Eq. 82, by a first-order Taylor expansion

$$a_j\left(\mathrm{x}+E\left(\lambda \right)\right)-\left.a_j\left(\mathrm{x}\right)\approx E\left(\lambda \right)\right|\cdot \nabla a_j\left(\mathrm{x}\right)={\displaystyle \sum _{i=1}^N\mathit{\tau \xi i}\left(\mathrm{x}\right)}\frac{\partial }{\partial x_i}{a}_j\left(\mathrm{x}\right)$$

So, defining

$$\begin{array}{lll}{b}_{\mathit{ji}}\left(x\right)=\frac{\partial a_j\left(x\right)}{\partial x_i}\hfill & j-1,\dots ,M\hfill & i=1,\dots ,N\hfill \end{array}$$ 83

where M is the number of reactions and N is the number of chemical species, Eq. 82 becomes

$$\tau \left|{\displaystyle \sum _{i=1}^N{\xi }_i\left(x\right)b_{\mathit{ji}}\left(x\right)}\right|\le \in a_0\left(x\right)$$ 84

The largest value of τ that is consistent with this condition is

$$\tau =\underset{j\in \left[1,M\right]}{min}\left\{\frac{\in a_o\left(\mathrm{x}\right)}{\left|{\displaystyle {\sum }_{i=1}^N{\xi }_i\left(\mathrm{x}\right)b_{\mathit{ji}}\left(\mathrm{x}\right)}\right|}\right\}$$ 85

StochSim algorithm

In 1998, Morton-Firth [29] developed the StochSim algorithm. The algorithm treats the biological components, for example, enzymes and proteins, as individual objects interacting according to probability distribution derived from experimental data. In every iteration, a pair of molecules is tested for reaction. Due to the probabilistic treatment of the interactions between the molecules, Stochsim is capable of reproducing realistic stochastic phenomena in the biological system. Both the Gillespie algorithm and the Stochsim algorithm are based on identical assumptions [29, 30]. A detailed proof of the equivalence of physical assumptions in the Gillespie and StochSim algorithms can be found in [31].

The main diferences that distinguish the StochSim algorithm from the Gillespie approach are the following: (1) the reaction system is composed of two sets: the “real” molecules and the “pseudo-molecules”; (2) the time is quantized into a series of discrete, independent time-slices, the sizes of which [are] determined by the most rapid reaction in the system; and (3) reaction probabilities are precomputed and stored in a look-up table, so that they need not to be calculated during the execution of each time slice.

In each time slice, StochSim selects one molecule at random from the population of “real” molecules, and then makes another selection from the entire population including the “pseudo-molecules”. If two molecules are selected, they are tested for all possible bimolecular reactions, retrieved from the look-up table for the particular reactant combination. If one “real” molecule and one “pseudo-molecule” are selected, the “real” molecule is tested for all possible unimolecular reactions it can undergo. StochSim iterates through the reactions and their probabilities and computes the cumulative probabilities for each of them. The set of cumulative probabilities can then be compared with a single random number to choose the reaction, if any occurs. If a reaction does occur, the system is updated accordingly and the next time slice begins with another pair of molecules being chosen.

The probabilities stirred in the look-up table for uni- and bi-molecular reactions (P ₁ and P ₂, respectively) are

$$p_1=\frac{k_{1}n\left(n+n_0\right)\mathit{\Delta t}}{n_0}$$ 86

$$p_2=\frac{k_{2}n\left(n+n_0\right)\mathit{\Delta t}}{2N_{A}V}$$ 87

where k ₁ and k ₂ are the deterministic rate constants for uni- and bi-molecular reaction, respectively, Δt is the size of the time slice, n is the total number of molecules in the system, n ₀ is the number of pseudo-molecules, and V the volume of the system

Advantages and drawbacks of Gillespie algorithm

The Gillespie algorithm makes time steps of variable length, based on the reaction rate constants and population size of each chemical species. Both the time of the next reaction τ, and the time of the next reaction μ, are determined by the rate constants of all reactions and the current numbers of their substrate molecules. Unlike the common simulation strategies of discretizing time into finite intervals, as in the StochSim procedure, the Gillespie algorithm benefits from both efficiency and precision, i.e. no time is wasted on simulation iterations in which no reactions occur, and the treatment of time as continuum allows the generation of an “exact” series of τ values based on rigorously derived probability density functions. However, the precision of the Gillespie approach is guaranteed only for spatially homogeneous, thermodynamically equilibrated systems in which non-reactive molecular collisions occur much more frequently than reactive ones. Therefore, the algorithm cannot be easily adapted to simulate diffusion, localization, and spatial heterogeneity. A second limitation of the Gillespie algorithm is that it results in computational infeasibility when the species contain multi-state molecules. For example, a protein which has ten binding sites will have a total of 210 states and it requires the same number of reaction channels to simulate this multi-state protein in the Gillespie algorithms. Since the Gillespie algorithm scales with the number of reaction channels, it is impossible to conduct such a simulation [32] The StochSim algorithm can be modified to overcome this problem by associating the states to the molecules without introducing many computational difficulties.

Although the Gillespie algorithm solves the master equation exactly, it requires substantial efforts to simulate a complex system. Three situations cause an increase of the computational effort. These conditions decrease the time step of each iteration, thus forcing the algorithm to run for a larger number of iterations to simulate a given environment. The conditions are the following:

• increase in the number of reaction channels

• increase in the number of molecules of the species

• faster reactions rate of the reaction channels.

However, under special circumstances when the number of reactions is small and the number of molecules is large, the Gillespie algorithm is more efficient than the Stochsim algorithm.

Spatio-temporal algorithms

Previous sections have covered the stochastic algorithms for modeling biological pathways with no spatial information. However, the real biological world consists of components which interact in a 3D space. Within a cell compartment, the intracellular material is not distributed homogeneously in space and molecular localization plays an important role, e.g., diffusion of ions and molecules across membranes and propagation of an action potential along a nerve fiber’s axon. Thus, basic assumption of spatial homogeneity and large concentration diffusion is no longer valid in realistic biological systems [33]. In this context, stochastic spatio-temporal simulation of biological systems is required.

The enhancement on the performance of Gillespie algorithms has made the spatio-temporal simulation tractable. Stundzia and Lumsden [34] and Elf et al. [33] extended the Gillespie algorithms to model intracellular diffusion. They formalized the reaction–diffusion master equation and the diffusion probability density functions. The entire volume of a model was divided into multiple subvolumes and, by treating diffusion processes as chemical reactions, the Gillespie algorithm was applied without much modification. Stundzia has showcased the application of the algorithm on calcium wave propagation within living cells and has observed regional fluctuations and spatial correlations in the small particles limit. However, this approach requires detailed knowledge about the diffusion processes that are available, in order to estimate the probability density function for diffusion. Furthermore, the algorithms have only been applied to small systems with finite numbers of molecular species but requires large amounts of computational power.

Shimizu [32] also extended the Stochsim algorithm to include spatial effects of the system. In his approach, spatial information was added to the attributes of each molecular species and a simple two-dimensional lattice was formed to enable interaction between neighboring nodes. The algorithm was applied to study the action of a complex of signaling proteins associated with the chemotactic receptors of coliform bacteria. He showed that the interactions among receptors could contribute to high sensitivity and wide dynamic range in the bacterial chemotaxis pathway.

Another way of simulating stochastic diffusion is to directly approximate the Brownian movements of the individual molecules (MCell; [35]). In this case, the motion and direction of the molecules are determined by using random numbers during the simulation. Similarly, collisions with potential binding sites and surfaces are detected and handled by using only random numbers with a computed binding probability. MCell is capable of treating stochastic and a 3D biological model that involves a discrete number of molecules. Though MCell incorporates 3D spatial partitioning and parallel computing to increase algorithmic efficiency, the simulation is limited to the microphysiological processes such as synaptic transmission due to high computational requirement.

Recently, Redi (Reaction–diffusion simulator) has been developed by Lecca et al. [36]. Redi implements a generalization of Fick’s law in which the diffusion coefficients depends of the local concentration, frictional force,s and local temperature. This diffusion model has been incorporated in a Gillespie-like simulation framework and used to simulate complex biochemical systems, such as the growth of non-small lung cancer tumor cells chemo-therapically treated [37] and the diffusion of bicoid morphogen in Drosophila melanogaster [36].

Apart from the enhancements on various algorithms, the simulation of a spatio-stochastic biological system is still infeasible. Regardless of the fact that the knowledge is incomplete, it is still unclear how to extract diffusion coefficients from experimental results and to track 3D shapes or structural changes in the cells.

The Langevin equation

While internal fluctuations are self-generated in the system, and they can also occur in closed and open systems, external fluctuations are determined by the environment of the system. We have seen that a characteristic property of internal fluctuations is that they scale with the system size and tend to vanish in the thermodynamics limit. External noise has a crucial role in the formation of ordered biological structures. External noise-induced ordering was introduced to model the ontogenetic development and plastic behavior of certain neural structures [38]. Moreover, it has been demonstrated that noise can support the transition of a system from a stable state to another stable state. Since stochastic models might exhibit qualitatively different behavior than their deterministic counterpart, external noise can support transitions to states which are not available (or even do not exist) in a deterministic framework [39].

In the case of extrinsic stochasticity, the stochasticity is introduced by incorporating multiplicative or additive stochastic terms into the governing reaction equations [88]. These terms, normally viewed as random perturbations to the deterministic system, are also known as stochastic differential equations. The general equation is:

$$\frac{\mathit{dx}}{\mathit{dt}}=f\left(x\right)+{\xi }_x\left(t\right)$$ 88

The definition of the additional term ξ _x differs according to the formalism adopted. In Langevin equations [9], ξ _x is represented by Eq. 89. Other studies [40] adopt a different definition where ξ _i (t) is a rapidly fluctuating term with zero mean {[ξ _i(t)] = 0}. The statistics of i (t) are such that {[ξ _i(t)ξ _i(t ′)]  = 0} = Dδ _ij(t − t ′) to maintain independence of random fluctuations between different species (D is proportional to the strength of the fluctuation).

$${\xi }_x\left(t\right)={\displaystyle \sum _{j=1}^M{V}_{\mathit{ij}}\sqrt{{\alpha }_j}X\left(t\right)N_j\left(t\right)}$$ 89

where V _ij is the change in number of molecules of species i brought by one reaction j and N _j are statistically independent normal random variables with mean 0 and variance 1.

Use and abuse of Langevin equation

The way in which Langevin introduced fluctuations into the equation of molecular population level evolution does not carry over nonlinear systems. This section briefly sketches the difficulties to which such a generalization leads. External noise denotes fluctuations created in an otherwise deterministic system by the application of a random force, whose stochastic properties are supposed to be known. Internal noise is due to the fact that the system itself consists of dicrete particles. It is inherent in the mechanism by which the state of the system evolves and cannot be divorced from its evolution equation. A Brownian particle, with its surrounding fluid, is a closed physical system with internal noise. Langevin, however, treated the particle as a mechanical system subject to the force exerted by the fluid. This force he subdivided in a deterministic damped force and a random force, which he treated as external, i.e. its properties as a function of time were supposed to be known. For the physical pictures, these properties will not be altered if an additional force on the particle is introduced.

In more recent years, however, Eq. 88 has also been used in modeling the evolution of biochemical systems, although the noise source in a chemical reacting network is internal and no physical basis is available for a separation into a mechanical part and a random term with known properties. The strategy used in the application of the Langevin equation in modeling the evolution of a system of chemical reacting particles is the following. Suppose there is a system whose evolution is described phenomenologically by a deterministic differential equation

$$\frac{\mathit{dx}}{\mathit{dt}}=\left.f\right|\left(x\right)$$ 90

where x stands for a finite set of macroscopic variables, but for simplicity in the presernt discussion we take the case that x is a single variable. Let us suppose to know that for some reason there must also be fluctuations about these macroscopic values. Therefore, we supplement (90) with a Langevin term

$$\frac{\mathit{dx}}{\mathit{dt}}=f\left(x\right)+L\left(t\right)$$ 91

Note now that, on averaging (91), one does not find that <x> obeys the phenomenological Eq. 90, rather than

$${\partial }_t〈x〉=〈f\left(x\right)〉=f\left(〈x〉\right)+\frac{1}{2}〈{\left(x-〈x〉\right)}^2〉{\partial }_t^2\left(〈x〉\right)+\dots$$

It follows that 〈x〉 does not obey any differential equation at all. This reveals the basic flaw in the application of the Langevin approach to the internal noise of systems whose phenomenological law is nonlinear. The phenomenological Eq. 90 holds only in the approximation in which fluctuations are neglected. That implies that f(x) is determined phenomenologically with an inherent margin of uncertainty of the order of fluctuations. If we deduce a certain form of f(x) from a theory or experiment in which fluctuations are ignored, there is no justification for postulating that f(x) is to be used in (91). There may be a mismatch between both of the same size as the fluctuations that would not show up in macroscopic results, but cannot of course be neglected in the equation of the fluctuations themselves.

Hybrid algorithms

Biological systems are stiff by nature in the sense that processes with very different time scales are coupled. Some molecules are quickly synthesized and degenerated (typically metabolites) and take a long time to run over (typically macromolecules). Some biochemical reactions involve a chain of many steps, while other reactions just involve a single association or dissociation event. This difference in time scales can be exploited by assuming quasi-equilibrium and using the equilibrium constant to eliminate some components from the model, and thus to reduce its complexity.

Stochastic algorithms suffer from the same “stiffness” problems as those of deterministic algorithms. In order to capture the fast dynamics of the system, the entire simulation is slowed down significantly. Hence, the basic idea of hybrid algorithms aims to exploit the advantages of other algorithms to offset the disadvantages of the stochastic algorithms.

Several attempts have been made to illustrate the relevance and feasibility of hybrid algorithms. Bundschuh et al. [41], Haseltine and Rawlings [42], and Puchalka and Kierzek [43] have used a similar approach to integrate ODE/Langevin with Gillespie algorithms. In both cases, the modeler has to identify methods and criteria to partition the system into fast dynamics and slow dynamics sub-systems. The fast dynamics subsystem can be handled by either ODE or Langevin equations while the slow dynamics subsystem can be handled by Gillespie algorithms. In addition, numerical treatment such as the “slow variables” in [41], and the “probability of no reaction” in [42], is required to maintain the accuracy of the solutions. The algorithms show promising results and the results are consistent with those from Gillespie algorithms. Haseltine and Rawlings in [42] showed the applicability of hybrid algorithms by simulating the effect of stochasticity to the bi-modality of an intracellular viral infection model using the algorithm. Kiehl et al. [44] also tested the algorithms on the λ phage model.

The relevance of hybrid algorithms has been pointed out in several papers ([45–47]). Bockmayr and Courtois used hybrid constraint programming methods to model an alternative splicing regulation model. This implementation is very useful under circumstances where detailed knowledge about the model is unavailable. Meanwhile, Alur et al. used CHARON, a formal description language of hybrid system which combines ODE with “mode switching” mechanism to model the quorum sensing phenomenon in Vibrio fischeri, a marine bacterium that involves the Lux regulon. A Hybrid Petri Net [46] approach has been employed to model a hybrid system using ODEs and discrete events. This method has been used to model the growth pathway control of λ phage.

Hybrid algorithms aim to close the gap between macroscopic and mesoscopic scales of the system. In particular, the relevance of hybrid modeling has been proved necessary to capture the behavior of a real biological system. Moreover, hybrid algorithms have substantially cut down the computational cost of large-scale modeling and simulation. One major drawback here is that, by introducing additional numerical treatment to the algorithms, more parameters have to be defined and the accuracy of the solutions is dependent on the accuracy of parameters. Mostly, the simulations result in solutions of highly tuned parameters. Although these hybrid approaches show significant improvements in the computational cost, there are still lots of computational issues to be resolved before they can be applied to a realistic problem. Some of the issues are:

• accuracy of results,

• consistency of system parameters between different levels of abstraction,

• highly non-linear system,

• methodology to separate the systems into different subsystems, dynamic switching between different mathematical formalisms.

Conclusions

This paper provides a detailed critical review of stochastic modeling approaches relevant to chemistry and biochemistry. Modeling is an attempt to describe, in a mathematical formalism, our understanding of the components of a system of interest, their states, and their interactions. The model should be sufficiently detailed so that it can be used to simulate the behavior of the system on a computer, but it should not even be too complex to avoid difficulties in changing, integrating its specification and in understanding its outcomes. Therefore, the first question to address when embarking in a modelling project is to decide which features to include in the model, and in particular, the level of details that the model is intended to capture (see Table 4 for a summary about the complexity of different stochastic simulation approaches). The use of the mathematical formalisms to describe the physical processes is familiar to the physicists almost since the birth of physics. The use of mathematical formalisms in biochemistry and in biology is more recent and is based on the physical model of molecular collisions. The recent and closer and closer convergence of biology, physics, mathematics, and computer science has lead to a intense use of computer simulation of mathematical models of biochemical systems of several molecules and several reactions at the level of detail required by a stochastic molecular approach. Many software tools have been developed in these last years with the intention to allow the simulation of the kinetics of complex and large systems of molecules. It is timely to provide a critical review of the models implemented by the majority of the tools to make users aware of the level of abstraction of which a model, and consequently a tool, is capable. At the same time, this review highlights that none of the existing models fits all problems and warns the user about the advantages and limitations of each of the presented methods.

Table 4.

Summary of the complexity of the approaches to stochastic simulation algorithms reviewed in this paper

Algorithm	Complexity
Direct method	It takes time proportional to the number of reactions M to update the propensities (a i s): it takes time proportional to the number of reactions to calculate Σ j a j and to generate a random number according to p(μ) = a μ/a 0
First reaction method	The algorithm uses M random numbers per iteration (where M is the number of reactions): it takes time proportional to M to update the a i s; (ii) it takes time proportional to M to calculate the smallest waiting time of reaction.
Next reaction method	The complexity is O (ln M), where M is the number of reactions.
Approximate simulation algorithms	Performances strongly dependent on ∆t. When ∆t is sufficiently small, the performances are similar to those of the exact simulation algorithms [48].
Spatial algorithms	The performances depend (1) on the complexity of models of diffusion-driven reaction systems in terms both of number of reactant species and interactions, and (2) on the stochastic simulation algorithm incorporated in the modeling and simulation framework. See [48, 50] for state of the art.
Hybrid algorithms	The performances depend on (1) the complexity of models in terms both of number of reactant species and interactions, and (2) the stochastic simulation algorithm adopted. See [49–52] for state of the art.

This review ends by indicating two promising directions: the spatio-temporal models and algorithms, and the hybrid methods. The first deal with the problem of diffusion-driven reactions simulation and the second deals with the important problem of stiffness, which is often present in (bio)chemical models. Both models appear to be flexible enough to allow for general stochastic solvers in the future even for very big and heterogeneous models. However, an established type of partitioning (reaction-wise and/or species-wise, space-wise and/or time-wise) are still missing. Hybrid algorithms are the most challenging methods to implement. Most of them also still need much user supervision. These are open questions to be addressed in the near future.

Electronic supplementary material

Below is the link to the electronic supplementary material.