Enhanced sampling simulations to construct free-energy landscape of protein–partner substrate interaction

Abstract

Molecular dynamics (MD) simulations using all-atom and explicit solvent models provide valuable information on the detailed behavior of protein–partner substrate binding at the atomic level. As the power of computational resources increase, MD simulations are being used more widely and easily. However, it is still difficult to investigate the thermodynamic properties of protein–partner substrate binding and protein folding with conventional MD simulations. Enhanced sampling methods have been developed to sample conformations that reflect equilibrium conditions in a more efficient manner than conventional MD simulations, thereby allowing the construction of accurate free-energy landscapes. In this review, we discuss these enhanced sampling methods using a series of case-by-case examples. In particular, we review enhanced sampling methods conforming to trivial trajectory parallelization, virtual-system coupled multicanonical MD, and adaptive lambda square dynamics. These methods have been recently developed based on the existing method of multicanonical MD simulation. Their applications are reviewed with an emphasis on describing their practical implementation. In our concluding remarks we explore extensions of the enhanced sampling methods that may allow for even more efficient sampling.

Introduction

Interactions between biomolecules (such as that between a receptor and a ligand) are crucial and fundamental events in biological activity because a biomolecule, such as a protein, must bind to and recognize its target molecule for signal transduction, catalytic action, storage, among others. Therefore, the determining factors which regulate the strength of such interactions are pertinent research questions to be studied and answered. The interaction strength is characterized by the binding affinity between the receptor and the ligand, which is quantified by the free-energy difference between the isolated (i.e., free) and bound states. When the bound state is more stable than the isolated state at a given concentration of the receptor and ligand, then the free energy of the bound state is lower than that of the isolated state. Physical factors that stabilize the bound state originate from hydrogen bonding, salt bridges, van der Waals interactions, and hydrophobic interactions. The dominant factors among these have been identified by investigating the specific receptor–ligand complex structures using structural biology methods. Structurally ambiguous regions in some complex structures have been shown to contribute to binding due to the fact that the affinity of the complex is altered when the ambiguous region is removed. Along the same line, complexes, which are less stable than the most stable complex structure, may be formed in the ligand–receptor interaction process and may play an important role in exerting their biological functions. Those complexes possessing potentially important structural ambiguity or multiple complex forms have been referred to as “fuzzy complexes” (Tompa and Fuxreiter 2008). In addition, such structural ambiguity/multiple complex forms may be related to each other, although uncovering such relations by experimental means is difficult. Molecular simulation is an extremely powerful tool for investigating the microscopic conformations involved in the binding process. Recently, efficient computational sampling methods have been applied to the study of free-energy and conformational profiles associated with the conversion from free to bound states.

Molecular simulation provides microscopic conformations as snapshots at an atomic resolution. Under exhaustive sampling conditions, the free energy is estimated from the ensemble of the snapshots. In such cases, the calculation of the binding affinity can be turned into a counting problem through enumeration of the number of snapshots in both the bound and isolated states. From knowledge of the density of states, the free-energy profile along the binding process can be then obtained. The free-energy profile, defined in relation to a specific reaction coordinate, is referred to as the free-energy landscape (FEL). One facile example of a reaction coordinate is the separation distance between the receptor and the ligand. In this case, the FEL is expressed as a function of the separation distance. Not only the bound state but also intermediate states or encounter complexes may be identified in the FEL, with a knowledge of all species helping to provide an understanding of the binding mechanism. A more rigorous means to describe the FEL is to use two structural parameters, such as the separation distance and the relative molecular orientation between the receptor and the ligand. In this case, the FEL is expressed two-dimensionally, which gives it a higher resolution than one-dimensional FELs and thereby allows easier identification of the intermediate or encounter complexes. Here, we note that the reliability of the FEL strongly depends on the quality of the simulation data. Typically, there are two practical problems in generating FELs: imperfect force fields and limited sampling times. The former results from the difficulty in determining physical parameters to calculate the potential energy. For example, the torsion energy for the protein backbone affects the secondary structure contents of the snapshots (Ikebe et al. 2007; Kamiya et al. 2005). Tuning of the torsion-energy parameters is still an extremely active research topic in this field (Maier et al. 2015; Sakae and Okamoto 2014). The second problem, which is related to the statistical accuracy of the resultant FEL, is the focus of this review. In the following sections we explain sampling techniques aimed at improving statistical accuracy and introduce the novel methodology we have developed.

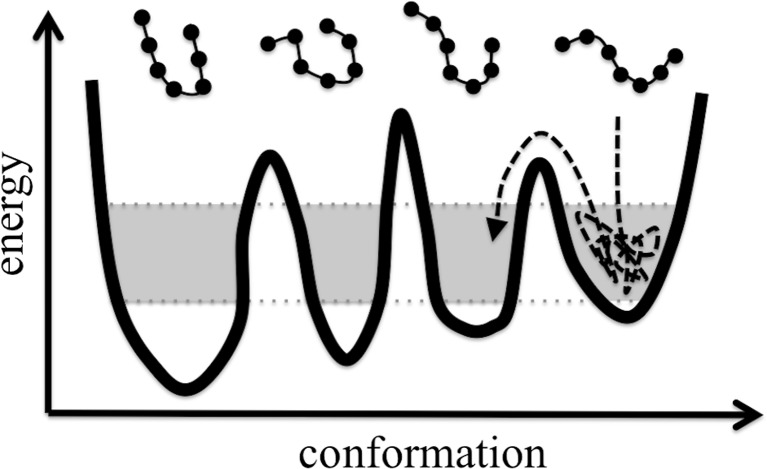
We first consider the limitation of sampling time. With respect to biological molecules, the simulation of the equilibrium state at temperatures near that of room temperature is of primary concern. Conventional molecular dynamics (MD) simulations (i.e., canonical MD) at constant temperature and constant volume yield a conformational ensemble (ensemble of snapshots) that will only cover part of the entire ensemble of conformations at equilibrium. In the ideal case in which simulation proceeds with exhaustive sampling, this entire ensemble is called the canonical ensemble. In reality, however, although conventional MD simulation using an all-atom model is a powerful and precise tool for producing biomolecular conformations, the simulation time is limited up to micro- or milliseconds, even with use of state-of-the-art computers. Given these time constraints, the conventional method is insufficient to sample the entire ensemble at room temperature to complete the FEL of the biomolecular system (Fig. 1). In general, there are many energy minima (or energy basins) in a space that express the conformation of the biomolecule(s). This space, called the “conformational space”, is characterized by a series of energy basins separated by energy barriers (Fig. 1). In a completely general manner we may suppose that our simulated system is in an energy basin. In order to access the surrounding conformational space the system must overcome an energy barrier, i.e., make it to the next energy basin. When the energy barrier is high, the system is trapped in the energy basin, and the system cannot escape from the basin quickly. Successful barrier crossing corresponds to a “rare event”. To search various conformations, barrier crossing should be facilitated (Fig. 1), as it is these time-consuming events which limit efficient sampling within the contraints of simulation time. Enhanced sampling methods have been developed to avoid such non-productive trapping. These representative enhanced sampling methods are discussed in the next section.

Fig. 1.

Schematic view of the ragged free-energy landscape (FEL) of a biomolecule. There are three energy barriers and four basins. The four representative conformations at each of the four basins are shown as chains of filled circles. The shaded regions of each basin correspond to the respective conformation with high probability at room temperature. Within the constraint of simulation time for conventional molecular dynamics (MD), the MD trajectory (dashed curved line) spends most of the time in one basin, ultimately surpassing an energy barrier but unable to search all of the basins for the highlighted regions

Enhanced conformational sampling methods

There are a number of enhanced sampling methods (Bernardi et al. 2015; Christen and van Gunsteren 2008; Mitsutake et al. 2001). Here we only discuss those methods which produce the equilibrium ensemble at room temperature from the stock of snapshots without any additional simulation. Two such methods deserving particular attention are umbrella sampling and parallel tempering.

Umbrella sampling

The umbrella sampling method (Chandler 1987; Deng and Roux 2009) facilitates sampling by introducing bias potential functions (so-called umbrella potential). During a simulation, the system is guided by the bias potential functions so that the system fluctuates in regions where the bias is low. Each umbrella potential is usually designed as a convex-downward harmonic potential, and the minima of these umbrella potential functions are typically set at points reflecting the high-free energy barriers. After umbrella sampling, the probability calculated from the sampled snapshots is, of course, affected by the umbrella potential functions. The probability independent of the umbrella potential can be estimated using the weighted histogram analysis method (WHAM; Kumar et al. 1992), and the FEL is reconstructed for the correct unbiased probability. Here, it is worth pointing out a practical aspect—that the choice of the variable (reaction coordinate) and the weight for the umbrella potential determine the sampling efficiency and that this choice is highly system-dependant.

Parallel tempering

The parallel tempering method is a widely used enhanced sampling method (Earl and Deem 2005) and is also known as the temperature replica exchange method (tREM) (Sugita and Okamoto 1999). In tREM, a set of different temperatures is utilized that range from a lower temperature (i.e., room temperature) to a significantly higher temperature. Multiple conventional canonical MD runs are started simultaneously at these different temperatures such that each simulation has a different temperature. Each run is named a replica. During tREM, the temperature of a replica is exchanged with the temperature of one of its two neighboring replicas when the principle of detailed balance is satisfied to keep equilibrium. The temperature of a trajectory then fluctuates over a wide temperature range. At a higher temperature, the system can escape readily from a trapped state. As a practical check, when performing tREM, one might monitor how frequently exchange occurs. If no exchange occurs, the sampling is not enhanced because the run is simply a conventional canonical simulation. For the case of tREM, the fewer the transitions, the less effective is the sampling. Such situations generally occur when the difference in temperature between replicas is relatively large, as well as the system (i.e., many, many atoms). Very recently, the replica-permutation method (RPM) (Itoh and Okumura 2013b) and “heat bath like criteria” (HLC) method (Kondo and Taiji 2013) have been proposed. These methods uses the Suwa–Todo algorithm (Suwa and Todo 2010) to obtain an equilibrium ensemble without imposing the detailed balance criterion, which increases the exchange ratio between the different temperatures among the replicas. With such developments the RPM and HLC may ultimately prove to be more efficient than tREM.

There are also other types of enhanced sampling methods which modify the potential energy directly to lower the energy barrier. Examples of this approach include an extended tREM, accelerated MD (aMD) (Doshi and Hamelberg 2015; Hamelberg et al. 2004), metadynamics (Laio and Parrinello 2002), and multicanonical MD methods. In the extended tREM, the replicas have different physical parameters [van der Waals radius (Itoh et al. 2010); coulomb potentials (Itoh and Okumura 2013a), model resolution (Lyman et al. 2006), and umbrella potentials (Okumura and Itoh 2013)] instead of different temperatures. Exchange between replicas involves transition between the different simulation runs under the detailed-balance condition. These extended methods of tREM could be generalized as the replica exchange umbrella sampling method (Sugita et al. 2000) and Hamiltonian replica exchange method (Fukunishi et al. 2002). In aMD, a particular potential energy is scaled by a user-defined factor, and the scaled energy is used throughout the simulation. After the aMD simulation, the probability with the genuine energy is reconstructed. In metadynamics, the bottom level of an energy basin along a reaction coordinate is raised gradually during simulation. Raising the bottom level pushes the conformation out of the energy basin where it is trapped and, consequently, the system can travel widely along the reaction coordinate. In the multicanonical method, the potential energy travels randomly and continuously in a wide potential energy range. How to achieve such sampling by the multicanonical method is described in the next section.

The basics of the multicanonical method were developed Berg and Neuhaus (1992) and are based on the Monte Carlo scheme and applied to the simple statistical mechanical Potts model. Hansmann and Okamoto (1993) applied the multicanonical method for searching the lowest energy conformation of the 5-residue peptide, Met-enkephalin. The multicanonical method was then incorporated into a MD scheme (Hansmann et al. 1996; Nakajima et al. 1997). The multicanonical MD (McMD) simulation has been improved and applied to larger protein systems with an all-atom model in an explicit solvent. The McMD method has been used to obtain the FELs for a chameleon sequence (Ikeda and Higo 2003), the binding between lysozyme and a saccharide (Kamiya et al. 2008), and domain-size protein folding (Ikebe et al. 2011a). In the following section, we provide a concise description of McMD. In subsequent sections, we introduce the theory and application of more efficient enhanced sampling methods, namely trivial trajectory parallelization (TTP) (Ikebe et al. 2011b), virtual-system coupled McMD (V-McMD) (Higo et al. 2013), and adaptive lambda square dynamics (ALSD) (Ikebe et al. 2014).

McMD simulation

To construct an accurate FEL, a well-equilibrated conformational ensemble must be obtained. McMD (Hansmann et al. 1996; Nakajima et al. 1997) provides a way to overcome energy barriers in the conformational space by scaling the potential energy, thereby allowing markedly faster sampling of the ensemble than is possible using conventional canonical MD. Here we briefly explain McMD simulation.

McMD is an MD simulation at constant temperature T ₀ with a modified potential energy E _mc,

$$E_{mc}={\lambda }_{mc}\left(E,T_0\right)E=\left(1+\frac{R{T}_{0}ln{P}_c\left(E,T_0\right)}{E}\right)E=E+R{T}_{0}ln{P}_c\left(E,T_0\right)\text{,}$$ 1

instead of the original potential energy, E. In this case, the forces acting on atoms are derived from derivatives of E _mc rather than E. We represent E _mc with three equivalent expressions in Eq. 1. The first expression means that McMD modulates E by a scaling factor λ_mc. When 0 < λ_mc < 1, the potential energy is scaled down and, consequently, the forces are also scaled down. This scaling enhances conformational change of the simulated system because it weakens interaction energy to stabilize the conformations. As a result, the system explores a greater conformational space than canonical MD. The second expression provides details on λ_mc, where R is a gas constant and P _c(E,T ₀) is a probability distribution function of energy for a well-equilibrated canonical ensemble (canonical probability distribution) at T ₀ on the E axis, although the functional form of P _c(E,T ₀) is unknown a priori. The factor λ_mc is designed to realize a random walk of the system on the E axis [for more details on the derivation, the reader is referred to the review of Higo et al. (2012)]. The random walk efficiently facilitates the overcoming of energy barriers and the search for various energy minima in the conformational space. In a practical McMD procedure, a canonical MD simulation run is first performed to approximate the unknown function P _c(E,T ₀), followed by gradual refinement of P _c(E,T ₀) by iterative McMD runs. After these iterative runs, a productive McMD simulation run using the refined P _c(E,T ₀) is performed to sample the ensemble. The productive run provides an ensemble (i.e., multicanonical conformational ensemble) which realizes a flat multicanonical probability distribution P _mc(E,T ₀) on the E axis due to the random walk. The third expression explains how the McMD formalism can be regarded as a type of complex umbrella sampling MD (Chandler 1987; Deng and Roux 2009) with an umbrella potential RT ₀lnP _c(E,T ₀). A canonical ensemble at an arbitrary temperature T can be reconstructed from the multicanonical conformational ensemble with a reweighting scheme (Higo et al. 2012) as

$$P_{\mathrm{c}}\left(E,T\right)=P_{\mathrm{m}\mathrm{c}}\left(E,T_0\right)W_{\mathrm{m}\mathrm{c}}\left(E,T_0,T\right)=P_{\mathrm{m}\mathrm{c}}\left(E,T_0\right)exp\left\{{\lambda }_{mc}\left(E,T_0\right)E/R{T}_0\right\}exp\left(-E/RT\right)\mathrm{C}$$ 2

where W _mc is a reweighting factor for McMD and C is a normalization constant. Assigning a probability P _c(E,T) to each snapshot, whose real energy is E in the multicanonical conformational ensemble, the canonical conformational ensemble at T is constructed, and through mapping of these re-weighted snapshots to a conformational space, a FEL can be generated.

Trivial trajectory parallelization of McMD

Although McMD allows for more efficient conformational sampling than canonical MD it still requires long simulation times for large systems in order to generate statistically reliable data. Parallel computing of MD simulation is a commonly used technique to speed up conformational sampling. Parallel computing with MPI (Message Passing Interface Standard) and/or OpenMP (Open Multi-Processing) is generally implemented in MD simulation programs with multiple central processing units (CPUs). The MD technique with a general-purpose graphics processing unit (GPGPU) (Götz et al. 2012; Mashimo et al. 2013; Pall et al. 2014; Salomon-Ferrer et al. 2013) is growing in importance due to multiple processors being less expensive than CPUs. Hardware architectures specialized for MD, such as Anton (Shaw et al. 2009) and MD-GRAPE (Narumi et al. 2006), have enabled extremely long-time scale MD simulations (Kikugawa et al. 2009; Lindorff-Larsen et al. 2011; Shaw et al. 2010). These specialized architectures speed up a single MD simulation run and provide an increased number of conformations from the long MD trajectory. Combining these architectures and McMD would further enhance efficient generation of FELs.

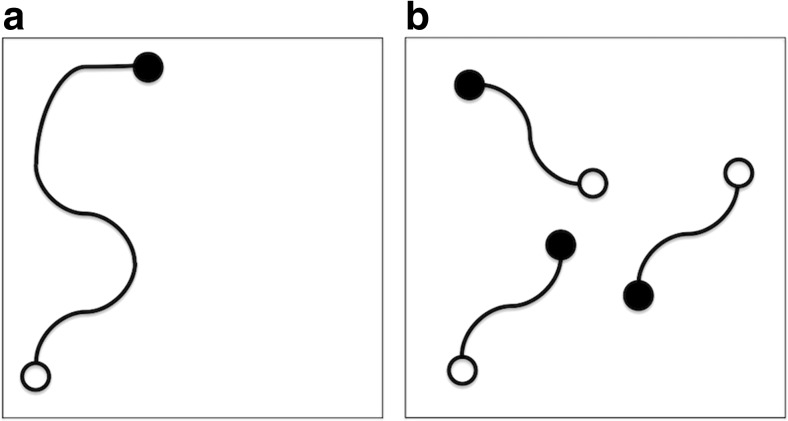
Another form of parallel computing is to perform multiple MD runs. The benefit of this type of parallelization is that no additional device need be implemented in the MD code and no costly machine is required. The method provides an increased number of conformations, not from a single long trajectory, but from independent multiple trajectories, each of which may be short. The parallel computing method with multiple McMD runs, trivial trajectory parallelization of McMD (TTP-McMD) (Higo et al. 2009; Ikebe et al. 2011b), provides a conformational ensemble where the multiple McMD runs use a common E _mc and are started from different initial conformations that are widely distributed in conformational space (Fig. 2). Our group has empirically examined the efficiency of TTP-McMD for a short peptide system (Higo et al. 2009) and have provided a theoretical framework for its interpretation (Ikebe et al. 2011b). The latter study demonstrated that TTP-McMD with N runs generates a more accurate FEL than a single McMD run N-times longer than each TTP-McMD run. In the iterative simulations of TTP-McMD, the final snapshot of each trajectory is used as the initial one for each following iterative run. This treatment is of essential importance for efficient sampling (Ikebe et al. 2011b). As mentioned above, this method requires neither special hardware nor highly adjusted software to improve sampling efficiency. Furthermore, its parallelization efficiency is always 100 %. The TTP procedure enables McMD to search FELs of complex systems, such as proteins and their substrates. Moreover, TTP is readily applicable to other sampling methods, such as V-McMD and ALSD (to be discussed later in this review).

Fig. 2.

Schematic figures showing sampling with multicanonical MD (McMD; a) and trivial trajectory parallelization-McMD (McMD; b). Boxes represent conformational spaces, curved lines capped at each end by circles show McMD simulation trajectories. Open and filled circles at the termini of the trajectories Initial and final snapshots of the McMD trajectories, respectively. McMD explores conformational space using of a single long trajectory. In contrast, TTP-McMD explores conformational space that by N-independent trajectories that are widely distributed in the conformational space. TTP-McMD with N runs generally constructs a more accurate FEL than a McMD run which is N-times longer than a single TTP-McMD run

Applications of TTP-McMD to interactions between intrinsically disordered proteins and its partner protein

In this section, we describe the application of TTP-McMD to systems of intrinsically disordered proteins (IDPs) (Uversky 2013; Wright and Dyson 2015), which are involved in cellular signaling and transcriptional machinery (Dunker et al. 2002). In general, an ordinary protein folds into a specific and stable conformation (i.e., a specific tertiary structure) under physiological conditions, and the ordered conformation determines its unique function. We designate this specific structural conformation as C_ss in this review. In contrast, IDPs have no specific conformation and interconvert among semi-stable conformations in the free state (unbound state). When the IDP interacts with its partner protein, it often folds into the C_ss form and the complex structure is formed. This folding mechanism of IDP accompanied by binding to the partner is referred to as the “coupled folding and binding” mechanism. Two representative schemes have been suggested to explain this mechanism, namely, population shift (Bosshard 2001; James and Tawfik 2003; Monod et al. 1965) and induced fit (Koshland 1960). In the former scheme, C_ss is intrinsically included even in the conformational ensemble of the unbound single-chain IDP, even though its population for C_ss may be small. The partner protein then selects C_ss when the complex is formed. In the latter scheme, IDP first binds to the partner with conformations different from C_ss, and then C_ss is induced. At the present time it is still unclear which scheme is appropriate. The detailed binding mechanisms have been investigation in two experimental settings where TTP-McMD was applied to two IDPs: the N-terminal repressor domain of neural restrictive silencer factor (NRSF) (Higo et al. 2011) and the phosphorylated kinase-inducible domain (pKID) of the cyclic-AMP response element binding protein (CREB) (Umezawa et al. 2012).

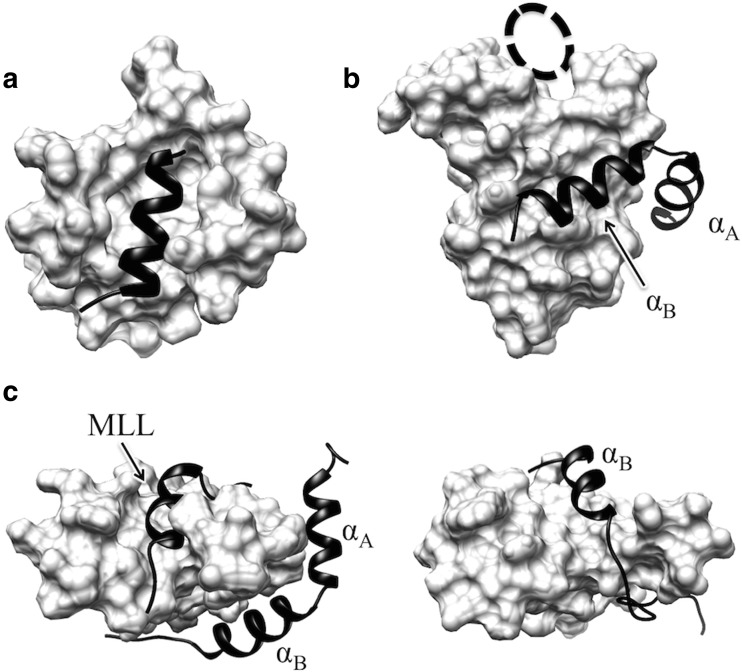
The complex structure of NRSF and its partner protein, the paired amphipathic helix (PAH) domain of mSin3 (Nomura et al. 2005), has been determined experimentally (Fig. 3a). For simplicity, we refer here to the molecule as mSin3. To obtain the conformational ensembles of NRSF, TTP-McMD of NRSF was conducted in the absence and presence of mSin3 with these two systems denoted as single-chain NRSF and the NRSF-mSin3 system, respectively. To initiate either simulation, the NRSF conformation was randomized. In the NRSF-mSin3 system, the two proteins were separated from each other. The proteins were also immersed in an explicit solvent for both systems. No artificial restraint to movement was placed on NRSF while the conformation of mSin3 was weakly restrained to the experimental structure throughout the simulation (discussed later in this review). From the TTP-McMD simulations, FELs of NRSF were constructed for both systems. The FEL of the NRSF-mSin3 system could be clustered into a number of states. Importantly, the largest cluster (i.e., thermodynamically most stable cluster or the lowest free-energy cluster) corresponded to the native-like complex structure. Three super clusters were apparent, one of which involved the largest cluster, and free-energy barriers existed among the super clusters. The existence of the super clusters led to the proposal of the following scenario for complex formation: once an encounter complex, which is involved in a cluster other than the main (and largest) cluster is formed, NRSF should change in conformation to overcome the free-energy barriers among the clusters to reach the native-complex structure.

Fig. 3.

Folded structures of target intrinsically disordered proteins (IDPs) [N-terminal repressor domain of neural restrictive silencer factor (NRSF) and phosphorylated kinase-inducible domain (pKID) of CREB] in the complex with their partner proteins. a Native complex structure of NRSF is shown as black ribbon on the mSin3 surface (PDB ID: 2CZY). NRSF is bound to the cleft of mSin3. b Black ribbon represents the native structure of pKID on the KIX surface (PDB ID: 1KDX). The two helices (αA, αB) are attached in the shallow concave on the surface of KIX. Dashed-line circle MLL binding site. c Left panel Native structure of MLL in the triple complex with KIX and pKID (PDB ID: 2LXT), corresponding to the top view of b. The MLL and pKID structures are represented as black ribbons and the KIX as its surface. Right panel Conformation of pKID binding to the MLL-binding site of KIX, which was taken from the TTP-McMD ensemble of the pKID-KIX system. The viewing angle at right is the same as that of the left. The shapes of the KIX surfaces are different between the left and the right views because KIX has dynamic side chains and its C-terminus is flexible in the simulation

The single-chain NRSF system produced a conformational ensemble consisting of various conformational clusters characterized by α-helix and β-strand secondary structural elements as well as other structural elements. Interestingly, a majority of those NRSF conformations were found in the ensemble of the NRSF–mSin3 coexisting system. Therefore, the population shift paradigm may readily incorporate the existence of various encounter complexes. However, the conformation of the encounter complex should undergo sufficient change to reach the native complex, as mentioned above. In this context, the induced fit takes place and folding and binding in the NRSF-mSin3 system proceeds in a way that the conformational shift and induced fit are coupled.

The other application of TTP-McMD targeted pKID. pKID in complex with its partner, the KIX domain of CREB binding protein (CBP), adopts a specific conformation composed of N- and C-terminal helices (these regions are denoted as αA and αB, respectively, even when the segments do not adopt helical conformation in a simulation snapshot) and a loop region spacing these helices (Radhakrishnan et al. 1997) (Fig. 3b). Using the same procedure as for the NRSF systems, we conducted TTP-McMD of two systems of pKID in the absence and presence of the KIX domain, denoted as the single-chain pKID and pKID-KIX systems, respectively. The FEL of the single-chain pKID system showed that the helical propensity for the αB region is considerably smaller than that of the αA region, which is in agreement with experimental results (Radhakrishnan et al. 1998). In the pKID-KIX coexisting system, FEL illustrated a number of semi-stable bound forms, including the native-like complex conformation. Subsequent analyses determined that the coupled folding and binding mechanism of the αA and the αB regions are different. The αA region bound with KIX exhibited large fluctuations, and therefore discernment of the appropriate mechanism for the αA region could not be concluded. When categorized, the binding of the αA region could be seen to follow the population shift mechanism. To the contrary, the αB region follows the induced fit mechanism. The αB region folds into a helix when it binds to either one of two distinct hydrophobic sites on the KIX domain: the native binding site (genuine binding site) in the native structure and another binding site, whose location is far from the native binding site (Fig. 3b, c). Interestingly, the latter corresponds to the binding site for another KIX-binding transcription factor, the mixed-lineage leukemia protein (MLL) (Fig. 3b, c), where a segment of MLL adopts a helical conformation (Brüschweiler et al. 2013; De Guzman et al. 2006) (PDB IDs: 2AGH, 2LXS, 2LXT). Experimental results suggest that pKID also binds to the MLL-binding site (Sugase et al. 2007), although a detailed structure of the complex has not been determined. A benefit of molecular simulation is that the simulation can provide atomistic information for the molecular structure. Such simulations suggested a conformation of pKID on the MLL-binding site that was helical and overlapped well with the bound form of the MLL segment (Fig. 3c). Thus, TTP-McMD yielded pictures that furthers our understanding of the binding mechanism and conformational characteristics of IDPs; such information cannot be obtained from experiments.

However, we should add a note of caution regarding the technical treatment of the partner proteins in both the NRSF-mSin3 and pKID-KIX coexisting systems. The partner molecules, mSim3 and KIX, respectively, are ordered proteins. Since the McMD simulation scales the whole energy of the systems (i.e., the whole energy is elevated to a high temperature during the simulation), the partner proteins may undergo unfolding. Therefore, the conformation of the ordered partner proteins is restrained weakly around the native structure to avoid such undesired sampling for the unfolded state of the partner, while the targeted IDP is not restrained. Herein, our cautionary note is that very strong structural restraints on the partner can yield artificial outputs. In the native NRSF-mSin3 complex, the natively bound NRSF is buried in the closed crevice of the mSin3 surface. Thus, if the structural restraints are so strong as to freeze the open/close fluctuations of the crevice, NRSF might not reach the natively bound form in the simulation. Also in the pKID-KIX system, the strong restraint seems to be inadequate if the research is focused on an allosteric mechanism of the KIX domain (Law et al. 2014). Therefore, a method free from the application of structural restraints is useful to remove any artificial effects induced within the sampling. Such a restraint-free method is described in the section Adaptive Lambda Square Dynamics of this review.

Theory of virtual-system coupled McMD

Enhanced sampling methods, such as McMD, provide a flat probability distribution over a wide range of energy or reaction coordinates, meaning that the system walks randomly over a wide range. In McMD, the system can search low-energy conformations by overcoming the energy barriers. If we imagine that the McMD simulation starts from a non-equilibrated conformation in a low-energy region, then the energy of the system transitions to a high-energy region when climbing an energy barrier, and to a low energy region when the barrier is overcome. Since the McMD simulation is a method to obtain an equilibrated ensemble at an arbitrarily temperature, these up-and-down motions of energy lead the system to a relaxed conformation in the low-energy range. Thus, traffic between the low- and high-energy regions is very important for the system to rapidly reach a well-equilibrated conformational ensemble. However, some systems may have an energy surface where the low-energy regions and high-energy regions are connected by a very narrow pathway. In such cases simple McMD sampling may not sufficiently improve the sampling efficiency (Higo et al. 2012; Higo and Nakamura 2012).

To achieve the efficient traffic in multicanonical sampling, a variant of McMD, named “virtual-system coupled multicanonical molecular dynamics” (V-McMD), was developed (Higo et al. 2013). First, a brief introduction of the virtual system: imagine an abstract degree of freedom (i.e., virtual degree of freedom) v, which expresses a system (virtual system). Because v does not actually exist, we need not define a specific system for the virtual system. It is assumed that v varies discretely (v = v ₁,v ₂,…), and the discrete values are termed “virtual states”. The number and the energy of the virtual states are denoted as Nv and $E_{V_i}$ (i = 1, 2, 3, …, Nv), respectively.

Note that the entire system (the molecular system + the virtual system) is specified by the potential energy, E, of the molecular system and the virtual state, v _i. If there are no direct interactions between the molecular system and the virtual system, E is apparently expressed only by the coordinates of the molecular system. We then design the energy of the entire system as

$$E_{V_i}\left(E\right)=E+R{T}_0\mathit{ln}\left\{\frac{P_c\left(E\right)}{g_i\left(E\right)}\right\}=R{T}_0\mathit{ln}\left\{\frac{n\left(E\right)}{g_i\left(E\right)}\right\}\text{,}$$ 3

where P _c(E) is the canonical probability distribution function of E and g _i(E) is a arbitrary function of E under the condition that the virtual system is in the i-th virtual state. Note that g _i(E) is defined by both E and the virtual state number i, which means that $E_{V_i}$ involves interference between the molecular and virtual systems despite E not involving v _i. The resulting probability distribution of E in the i-th virtual state, is given as:

$$P_{V_i}\left(E\right)\propto n\left(E\right)exp\left(-\frac{E_{V_i}}{R{T}_0}\right)\propto g_i\left(E\right)\text{.}$$ 4

When g _i(E) is a constant, a flat energy distribution results, similar to that for the conventional McMD simulation.

Up to this point, the method for time development of the system has not been given. In V-McMD, the time development for the molecular system is performed by integrating the Newtonian equations as usually done for MD. However, the time development for the virtual system is done with the Monte Carlo scheme, with the transition probability from the i-th to j-th virtual states set so that the transition satisfies the detailed balance, as per Eq. 5.

$$P_{V_i\to V_j}\left(E\right)=min\left[1,exp\left(-\frac{E_{V_j}-E_{V_i}}{R{T}_0}\right)\right]=min\left[1,\frac{g_j\left(E\right)}{g_i\left(E\right)}\right]\cdot$$ 5

In actual sampling, the molecular system moves according to the multicanonical MD scheme for a time interval of τ, during which the virtual system is kept in a virtual state. Then, at the end of the interval, the transition among virtual states is attempted according to the Monte Carlo scheme, at which point the molecular system is then fixed at the current conformation. After the trial, the molecular system time-develops for another interval of τ, and so on. What is important is that we can set the function shape for g _i arbitrarily because the virtual system is literally a virtual object. g _i(E) and g _i + 1(E) are designed as

$$g_i\left(E\right)=\left\{\begin{array}{c}\hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \end{array}\begin{array}{c}\hfill \left(E_{V_i}^{\mathit{Max}}<E\right)\hfill \\ \hfill \left(E_{V_i}^{Min}\le E\le E_{V_i}^{\mathit{Max}}\right)\hfill \\ \hfill \left(E<E_{V_i}^{Min}\right)\hfill \end{array}\right.\mathrm{and}{g}_i+1\left(E\right)=\left\{\begin{array}{c}\hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \end{array}\begin{array}{c}\hfill \left(E_{V_{i+1}}^{\mathit{Max}}<E\right)\hfill \\ \hfill \left(E_{V_{i+1}}^{Min}\le E\le E_{V_{i+1}}^{\mathit{Max}}\right)\hfill \\ \hfill \left(E<E_{V_{i+1}}^{Min}\right)\hfill \end{array}\right.\text{,}$$ 6

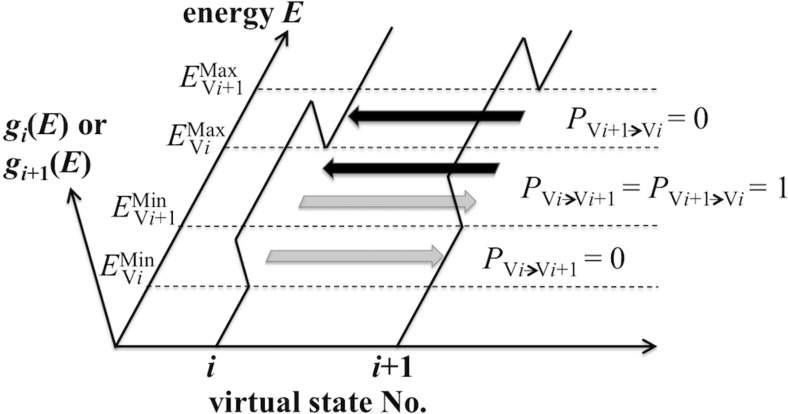
respectively, where the boundary parameters are aligned as $E_{V_i}^{Min}<E_{V_{i+1}}^{Min}<E_{V_i}^{\mathit{Max}}<E_{V_{i+1}}^{\mathit{Max}}$. We call the overlapping range $\left[E_{V_{i+1}}^{Min},E_{V_i}^{\mathit{Max}}\right]$ between non-zero ranges of g _i(E) and g _i + 1(E) as the “zone”, then the transition probability from the i-th to j-th virtual states is 1 in the zone, and 0 outside the zone (illustrated in Fig. 4). Thus, the multicanonical distributions at the i-th and j-th virtual states are connected, thereby maintaining the detailed balance criterion. Here, the key point of V-McMD is that the connection is achieved with the probability of 1 so that the traffic is driven with keeping the equilibrium condition (for details, see Higo et al. 2013).

Fig. 4.

The transition probabilities between the i -th and (i + 1)-th virtual states in virtual-system coupled McMD (V-McMD). For definition of the symbols, see text in section Theory of virtual-system coupled McMD. Functions g _i(E) and g _i + 1(E) are defined in Eq. 6. Dashed lines denote the energy boundaries for the two virtual states: $E_{V_i}^{Min}$ and $E_{V_i}^{\mathit{Max}}$ for g _i(E), and $E_{V_{i+1}}^{Min}$ and $E_{V_{i+1}}^{\mathit{Max}}$ for g _i + 1(E). When the system with energy E attempts to transfer from the i -th to (i + 1)-th state (gray arrow), the transition probability $P_{V_i\to V_{i+1}}\left(E\right)$ equals 1 in the zone ($E_{V_{i+1}}^{Min}\le E\le E_{V_i}^{\mathit{Max}}$) and 0 outside the zone. On the other hand, from the (i + 1) -th to i -th state (black arrow), the transition probability $P_{V_{i+1}\to V_i}\left(E\right)$ equals 1 in the zone and 0 outside the zone. Thus, the transition between the two states succeeds undoubtedly in the zone. If three virtual states exist (Nv = 3), there are zones between the first and second states and between the second and third states. The system can then travel from the first/third to the third/first states via two sequential transitions as from the first/third to the second and from the second to the third/first

In practical terms, multiple runs (i.e., TTP procedure) can be applied to V-McMD in a straightforward manner—a process referred to as “TTP-V-McMD”. One trajectory taken from the multiple V-McMD runs migrates to another trajectory, where the migration occurs unconditionally. Therefore, it should be once again noted that this migration facilitates the traffic (the low-to-high and the opposite transition of the energy) during simulation, and it yields more rapid equilibration than conventional MD simulations. The equilibration speed is discussed in the following section.

Applications of virtual-system coupled methods for a peptide homodimer

In the study of Hoh et al. (2004), the target for TTP-V-McMD was a bioactive peptide, Endothelin-1 derivative (KR-CSH-ET1), which forms a stable antisymmetric homodimer (Fig. 5a). The dimerization of KR-CSH-ET1 was investigated by Higo et al. (2013) to test the equilibration speed of TTP-V-McMD as compared with TTP-McMD. Two molecules of KR-CSH-ET1 were separated from each other and immersed in an explicit solvent for the initial conformation of TTP-V-McMD, and both TTP-V-McMD and TTP-McMD were performed with the same number of multiple runs. The protocol is described in detail in Higo et al. (2013). Although both TTP-V-McMD and TTP-McMD produced the native-like dimer for the most thermodynamically stable conformation, the convergence speed of TTP-V-McMD was faster than that of TTP-McMD.

Fig. 5.

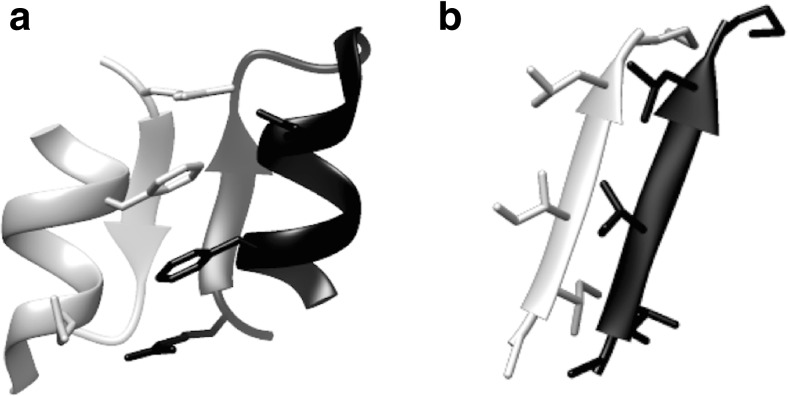
Native structures of target homodimers of the Endothelin-1 variant (KR-CSH-ET1). a The X-ray crystal structure of KR-CSH-ET1 (PDB ID: 1T7H), with one chain shown in gray and the other in black. The inter-molecular hydrophobic interaction of phenylalanine and the salt bridge between glutamate and arginine stabilizes the homodimer. Their side chains are displayed as the stick model. The inter-molecular main-chain interaction with the anti-parallel β-sheet also contributes to the stability. b The two segments of Amyloid-β peptide (sequence: ALA-ILE-ILE-GLY-LEU-MET) shown in gray and black, respectively, as taken from amyloid fibril structure (PDB ID: 2Y3J)

The virtual-system and trajectory-parallelization procedures are extendable to other enhanced sampling methods. Here we describe the method for adaptive umbrella sampling (AUS), which is abbreviated as TTP-V-AUS (Higo et al. 2015). The TTP-AUS (i.e., trajectory-parallelization of the conventional AUS) yields a random walk over a wide range of reaction coordinates. In TTP-V-AUS, the range of the reaction coordinate is divided into the virtual states, as done for the energy axis in TTP-V-McMD, and the transitions among the virtual states are defined as the same way as for TTP-V-McMD (for details, see Higo et al. 2015). The traffic was compared between TTP-V-AUS and the conventional TTP-AUS with sampling association/dissociation of two Amyloid-β peptides in an explicit solvent, where the separation distance between the two peptides was adopted as the variable for the sampling enhancement. This peptide is known to form an amyloid fibril (Fig. 5b). The free-energy landscape shows that various complex forms, such as the antiparallel β sheet, parallel β sheets, α-helix, and other complex forms, are distributed in a conformational space. In comparison between TTP-V-McMD and TTP-McMD, TTP-V-AUS realized quicker convergence than TTP-AUS. Thus, it would appear that the virtual-system method improves the traffic along the reaction coordinate in comparison to methods without the virtual system (Higo et al. 2015).

Adaptive lambda square dynamics simulations

Adaptive lambda square dynamics (Ikebe et al. 2014) has been developed from two free energy calculation methods, namely, adaptive umbrella sampling (Mezei 1987) and λ dynamics (Kong and Brooks CL III 1996), and is an effective method for sampling the ensemble of a complex system that is not dependent upon the application of structural restraints. As previously described, the imposition of strong restraints may cause artifacts. ALSD enhances sampling only for a part of the system. For this purpose, the potential energy E is divided into a number of terms, and these terms are differently scaled. The division of E is accomplished through two stages, energy term division (ETD) and spatial energy division (SED), which are sequentially processed.

A potential energy is decomposed usually as

$$E=E_{\mathrm{bond}}+E_{\mathrm{angle}}+E_{\mathrm{tors}}+E_{\mathrm{imp}}+E_{\mathrm{e}\mathrm{l}\mathrm{e}}+E_{\mathrm{v}\mathrm{d}\mathrm{W}}\text{,}$$ 7

where the subscripts “bond”, “angle”, “tors”, “imp”, “ele”, and “vdW” stand for the bond length, bond angle, torsion angle, improper torsion angle, electrostatic, and van der Waals potential energies, respectively. In the ETD stage, the terms are classified into two groups: interesting terms (E _{int_term}) and others (E _{rest_term}). In the original article on ALSD (Ikebe et al. 2014), three terms, namely, E _tors, E _ele, and E _vdW, were selected for E _{int_term} because these three terms may affect the global conformation of the system more than the other terms do: E _{int_term} = E _tors + E _ele + E _vdW. E is then expressed as:

$$E=E_{\mathrm{i}\mathrm{n}\mathrm{t}\_\mathrm{term}}+E_{\mathrm{rest}\_\mathrm{term}}\text{,}$$ 8

In SED, the system is divided spatially into an interesting region (region A) and the other region (region B) in order to selectively enhance the sampling of region A. For a complex system, it would be reasonable that the substrate (ligand) and the other components (receptor protein, ions, and solvent molecules) are set as region A and B, respectively (Fig. 6a). According to this spatial division, each interaction term in E _{int_term} is assigned to “intra-A”, “inter-A–B”, or “rest”. For a pairwise interaction between two atoms, the interaction is assigned to intra-A or rest, when both atoms are in region A or B. When the atoms belong to different regions, the interaction is done to inter-A–B. To assign a torsion angle interaction that is specified by a straight chain of four atoms, A–B–C–D, bound with covalent bonds, atoms A and D are considered to interact. All interactions in E _{rest_term} are assigned to rest. As a result, E is decomposed into three terms:

$$E=E_{\mathrm{intAA}}+E_{\mathrm{intAB}}+E_{\mathrm{rest}}\text{,}$$ 9

where the subscripts “intAA”,“intAB”, and “rest” denote intra-A , inter-A–B, and rest, respectively.

Fig. 6.

Examples of spatial energy division (SED) in adaptive lambda square dynamics (ALSD). ALSD enhances conformational sampling of region A while maintaining the conformation of region B in thermal fluctuations at the simulation temperature. a An example of SED for a complex system consisting of receptor protein (region B) and the ligand (region A). McMD tends to enhance conformational changes not only for the ligand but also for the protein. Thus, in McMD for such complex system, weak restraint forces are applied to the protein to maintain the conformation. On the other hand, ALSD can maintain the protein conformation without the restraint forces. b SED for an H3 histone tail on a nucleosome system. The histone tail and the nucleosome core particle (NCP) were assigned as region A and B, respectively. This system is highly polarized: negatively charged DNA covers the surface of the NCP, and the histone tail includes a many positively charged lysine and arginine residues. McMD could not sufficiently sample conformations of the histone tail because the histone tail is stuck to DNA by strong electrostatic interactions. To the contrary, SED in ALSD realized dissociation of the histone tail from DNA and sampled the various conformations. See Section Adaptive lambda square dynamics simulations for details. c SED in ALSD, as originally described in Ikebe et al. (2014). ALSD was originally developed as a more efficient conformational sampling method than McMD. In the original article, ALSD was applied to a short peptide (poly-lysine decapeptide, region A) system in explicit solvent (region B) to compare its sampling efficiency with that by McMD. To sample various conformations of the peptide, McMD must explore a wide potential energy range of the whole system, composed of the peptide and many water molecules. To the contrary, ALSD selectively enhances the conformational sampling of the peptide by exploration only in a narrower potential energy range with respect to the peptide. This focused sampling reduces the conformational space to be sampled for the solvent and concomitantly increases the sampling efficiency for the peptide. This system was also used in this review for ALSD simulations to investigate the efficient operation procedure of energy term division (ETD) on the sampling efficiency

ALSD is an MD simulation on an extended coordinate space (r, λ) at constant temperature T ₀ with a modified Hamiltonian:

$$H_{\mathrm{ALSD}}\left(\mathit{r},\stackrel{.}{\mathit{r}},\lambda ,\stackrel{.}{\lambda }\right)={\lambda }^2{E}_{\mathrm{intAA}}\left(\mathit{r}\right)+\lambda E_{\mathrm{intAB}}\left(\mathit{r}\right)+E_{\mathrm{rest}}\left(\mathit{r}\right)+K\left(\stackrel{.}{\mathit{r}}\right)+\frac{1}{2}{m}_{\mathrm{\lambda }}{\stackrel{.}{\lambda }}^2+R{T}_0\mathit{ln}{P}_{\mathrm{ex}}\left(\lambda ,T_0\right)\text{,}$$ 10

where r and $\stackrel{.}{\mathit{r}}$ are sets of atomic coordinates and their velocities, respectively, λ is a scaling factor for ALSD as an extra dynamic variable with the fictitious mass m _λ, K is the kinetic energy of the system, $\stackrel{.}{\lambda }$ is the velocity of λ, and P _ex(λ, T ₀) is a canonical probability distribution on the λ axis obtained from a well-equilibrated canonical MD simulation with the scaled potential energy E _ex (= λ ² E _intAA + λE _intAB + E _rest) in the (r, λ) space. During an ALSD simulation, the scaling factor λ moves as a variable obeying H _ALSD and scales only the potential energy terms with respect to region A (i.e., E_intAA and E_intAB). When 0 < λ < 1, E _intAA and E _intAB are scaled down and only the conformational changes of region A are enhanced. Meanwhile, the conformation of region B is maintained in thermal fluctuations at T ₀ without structural restraint forces. As with McMD, H _ALSD is designed to realize a random walk on the λ axis. Iterative ALSD runs are required to estimate a priori the unknown P _ex(λ,T ₀). A canonical ensemble at λ = 1 is reconstructed by a reweighting scheme. The reader is referred to the original article by Ikebe et al. (2014) for more details.

An application of ALSD to a highly polarized system

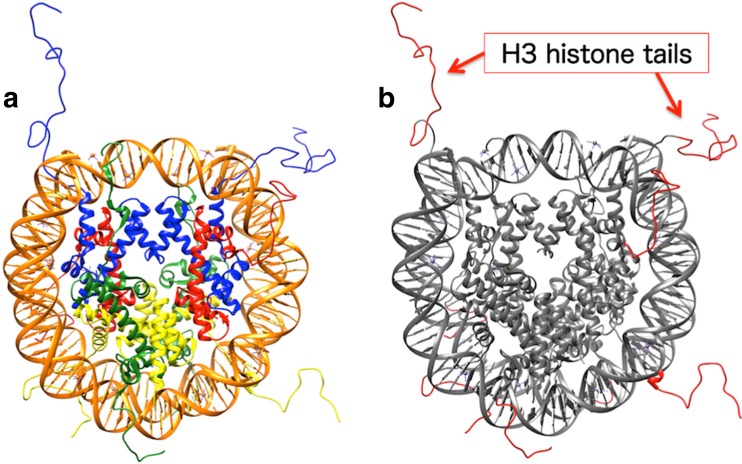
Ikebe et al. (2015) applied ALSD to conformational sampling of the histone tails on a nucleosome system (Fig. 7). The nucleosome is a fundamental conformational unit of DNA in a eucaryotic nucleus and is composed of DNA wrapped around histone proteins. Although the structures of the core region of the nucleosome have been determined by X-ray crystallography, the flexible N-terminal regions of the histone proteins, referred to as histone tails, have no specific stable conformation. It is known that chemical modifications on the histone tails induce conformational changes of the histone tail itself, DNA, and nucleosome. These conformational changes concomitantly regulate biologically important DNA functions, such as transcription, duplication, splicing, and DNA repair (Jenuwein and Allis 2001; Sidoli et al. 2012; Strahl and Allis 2000). To elucidate the mechanism of the conformational changes by the chemical modifications, it is necessary to obtain the conformational ensemble of the histone tails on a nucleosome.

Fig. 7.

a An X-ray crystal structure of a nucleosome (PDB ID: 1KX5). The nucleosome is composed of 147 base pairs of DNA (orange) wrapped around a histone octamer, which is composed of two copies of H3 (blue), H4 (red), H2A (green), and H2B (yellow) histone proteins. b Locations of histone tails in the nucleosome. Although crystal structures of the nucleosome core region (gray) have already been determined, the N-terminal regions (histone tails, red) of the histone proteins have not yet been determined due to their inate structural flexibility. The histone tail conformations in 1KX5 are modeled ones. In the applied research of ALSD, conformational sampling of an H3 histone tail was performed

However, it had been difficult to sample the ensemble because the system is highly polarized compared to general protein–substrate complex systems: negatively charged DNA covers the surface of the nucleosome, and the histone tails include a lot of positively charged lysine and arginine residues. The attractive electrostatic interactions between them make the histone tails stick to DNA and constrain the conformational changes of the histone tails. To realize efficient conformational sampling, it is important to dissociate the histone tails from the DNA during the simulation. An McMD simulation of a histone tail (H3 histone tail) on the nucleosome system could not sufficiently sample a variety of conformations of the histone tail (data not shown). The H3 histone tail has 13 positively and no negatively charged amino acids in the N-terminal 40 residues. To dissociate the histone tail from the DNA, the histone tail must break all electrostatic contacts with DNA simultaneously. Although the McMD equally scaled down all interactions, including electrostatic interactions between DNA and the histone tail, when λ_mc < 1, the scaling was not sufficient to dissociate them even when the λ_mc was quite small (=0.5).

To the contrary, ALSD, which sets the histone tail to region A (Fig. 6b) and E _{int_term} = E, was able to dissociate them and sampled a variety of conformations of the H3 histone tail. Although the ALSD scaled down interactions of DNA with the histone tail when λ < 1, it did not scale down those with ions and solvent, unlike McMD: in ALSD, DNA preferentially interacted with positive ions and positively polarized hydrogen atoms of solvent water rather than the histone tail, which allowed the histone tail to dissociate from DNA. This result showsn that ALSD is a promising method for highly polarized systems, which pose difficulties to sampling by other methods, such as McMD.

Efficient operation procedures for ALSD

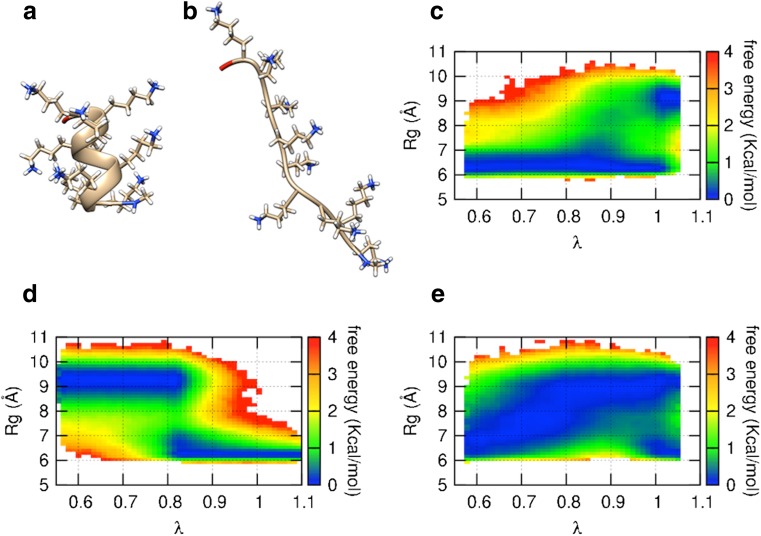
Here we note efficient operation procedures for ALSD. Although E _{int_term} can be set arbitrarily in theory, E _ele and E _vdW should not be individually treated in the ETD stage. To present the problem, we performed three ALSD simulations of a short peptide (poly-lysine decapeptide), which is the same one as that studied in the original ALSD article (Ikebe et al. 2014), at different settings of ETD: E _{int_term} = E _ele (referred to as “ALSD_ele”), E _{int_term} = E _vdW (“ALSD_vdW”), and E _{int_term} = E _ele + E _vdW (“ALSD_both”). In these simulations, the peptide and the solvent were selected as region A and B, respectively (Fig. 6c). These simulations were performed under the same simulation condition: seven iterative runs to refine P _ex(λ, T ₀) and the productive run to sample the ensemble with TTP (10 ns × 64 trajectories). Note that the total simulation time for each simulation was shorter than that in the original ALSD article (30 ns × 72 trajectories). In theory, these ALSD simulations provide the equivalent canonical ensembles at λ = 1 if the simulation times are sufficiently long. However, the different setting of ETD affects the sampling efficiency when the simulation times are insufficient.

The correlations between λ and the radius of gyration (Rg) of the peptide are shown as FESs in Fig. 8. The free energy was calculated as −RT ₀lnP(λ, Rg) and normalized for each λ where T ₀ was 300 K and P(λ, Rg) was a probability distribution function at (λ, Rg). The peptide is known to have two stable conformations: a compact α-helix and an elongated polyproline II helix-like conformation (JiJi et al. 2006; Tiffany and Krimm 1968) corresponding to an Rg  of approximately 6.5 and 9 Å, respectively (Fig. 8a, b). Although ALSD_ele sampled these two stable conformations at λ = 1, the peptide was compact at small λ (Fig. 8c). Scaling-down of E _ele corresponds to scaling-down of point charge parameters for region A. For more detail, the reader is referred to the original article (Ikebe et al. 2014). Thus, the scaling-down of E _ele without the scaling-down of E _vdW makes the peptide more hydrophobic and concomitantly compact. In contrast, ALSD_vdW sampled elongated conformations for small λ (Fig. 8d). It should be remembered that the conformational ensemble at 300 K is the same as that at λ = 1. The scaling-down of E _vdW weakens the collision energy of atoms in region A, and exposure of the peptide to the solvent induces a decrease of the potential energy. Thus, the scaling-down of E _vdW without any scaling-down of E _ele makes the peptide elongate with decreasing λ. The authors of the original ALSD article (Ikebe et al. 2014) have suggested that such unbalanced sampling at λ < 1 provides a worse sampling efficiency. However, ALSD_both sampled various conformations of the peptide in a wide range of Rg with decreasing λ in (Fig. 8e) because the compaction by scaling-down of E _ele and the elongation by that of E _vdW offset each other. The ALSD method extends the potential surface by including λ. The force field parameters for E _ele and E _vdW work in a complementary manner, with the result that the extended potential surface is simple to sample. We strongly recommend that E _ele and E _vdW should be scaled together for efficient sampling.

Fig. 8.

Representative structures showing compact α-helix (a) and elongated polyproline II helix-like conformations of poly-lysine decapeptide (b) obtained from ALSD_both at an λ of 1. It is known that the peptide adopts these two conformations as the thermodynamically stable ones in the canonical ensemble. The terminal regions colored in red are the N-termini of the peptide. c–e Free energy landscapes on a space composed of λ and the radius of gyration (Rg) of the peptide obtained from ALSD_ele (c), ALSD_vdW (d), and ALSD_both (e). See text in section Efficient operation procedures for ALSD for explanation of terms

Of course, the SED procedure also affects the sampling efficiency. An arbitrary setting of region A does not necessarily realize efficient sampling. For an extreme example, we consider an ALSD simulation of a complex system at a temperature that is sufficienty low to freeze the solvent. When the substrate is set as region A, the substrate is not sampled sufficiently because the frozen solvent suppresses the conformational motions of the substrate. Note that ALSD presupposes that conformational fluctuations in region B are sufficiently large to allow efficient sampling for region A.

For a practical case of protein–ligand binding, another precaution may be useful: a protein is relatively rigid and the conformational changes are slow. As such, a long simulation time is required to realize binding and dissociation of the ligand during a simulation. It may therefore be useful to set region A not only to the ligand but also to the prospective binding sites on the protein.

Future perspective of enhanced sampling methods

We have described enhanced sampling methods in general, as well as our specific enhanced methods to sample the equilibrium ensemble with all-atom models in an explicit solvent. Despite the limitations of simulation time, these methods could provide the reliable conformational ensembles to construct the accurate and fine-grained FELs. In this final section, we introduce studies that have gone beyond the fine-grained model and which possibly represent new strategies for further development of enhanced sampling methods.

The MD simulation evolves the system at each small time-step. The size of the time-step is set to safely simulate the fastest motion (i.e., avoid numerical violation). An atom with a light mass usually moves rapidly, and the vibrational motions of a chemical bond are rapid. The gold standard method of the SHAKE algorithm maintains the length of the covalent bonds with hydrogen atoms so that the time-step elongates by approximately 2 fs, which is the time-step elongation that we used in the studies described in the preceding sections of this review. If we could take a larger time-step, however, the MD simulation would concomitantly be generated over a longer time-scale for the same computational output. To achieve this, early researchers simply increased the masses of all atoms (or alternatively only hydrogens) to slow these rapid motions, resulting in an increase in the total mass of the system. An unwanted side-effect of the increase in total mass, however, was the scale down of the whole motion of the system (not only the fast, but also the meaningful dynamics). Subsequent studies led to the exploration of the repartitioning of masses (Feenstra et al. 1999), such that a heavier mass was assigned to hydrogen atoms and smaller masses were assigned to heavy atoms, with the result being that the total mass was kept constant. The long-time MD simulation with the hydrogen-mass repartitioning (HMR) method (Hopkins et al. 2015) reported that a 4-fs time-step provided a numerically safe result and did not influence thermodynamic properties. Furthermore, reducing the solvent viscosity by rescaling the mass of water molecules was effective (Gee and van Gunsteren 2006; Lin and Tuckerman 2010). Under low-viscosity conditions, the biomolecule moves smoothly. Another method for a larger time-step is the reversible multiple time-scale algorithm (RESPA) (Tuckerman et al. 1992), which enables a larger time-step of about 4 fs for the long-distant interaction terms because the long-distant interactions vary slowly. Combining such longer time-step methods with the enhanced sampling method may realize less computational cost to obtain the conformational ensemble.

The energy and the forces on atoms are calculated in MD simulations. Rapid calculation methods have been developed by approximating long-distance interactions, with the particle mesh Ewald (PME) (Darden et al. 1993) for periodic boundary condition and multipole method (Ding et al. 1992) for spherical solvent boundary (droplet) being frequently used examples. Cutoff methods, where the interactions over a threshold distance are neglected or approximated, are also used. A zero-dipole method (Fukuda et al. 2011) (or zero-multipole method generally) (Fukuda 2013) for the periodic boundary condition has recently been developed as an extension of the cutoff method. The zero-dipole method is implemented to take advantage of massively parallelized computational resource rather than PME because it needs less communication for parallelization. Importantly, the electrostatic accuracy of the zero-dipole method is compatible with that of the PME method.

Computational costs can be lowered by using alternate methods. Most of the computational cost of such studies results from including the interaction terms for the solvent molecules. When solvation effects are treated approximately using the pair-wise function among solute atoms, the computational cost can be smaller. In such treatments, the system does not contain solvent atoms explicitly, rather it exhibits the solvation effect and is thus described as implicit solvent. In the implicit solvent, solute atoms move smoothly because collisions between solute and solvent atoms vanish. There are several implicit solvent models based on the continuum solvent model, namely, the EEF (effective energy function) 1 model (Lazaridis and Karplus 1999), the generalized-born (GB) model (Still et al. 1990), and their variants (Kleinjung and Fraternali 2014). A distance-dependent dielectric treatment had been used for many years as a convenient approximation. However, it is a crude approximation for the all-atom model of biomolecules as the solvent effect is of critical importance in determining the stability of the peptide conformation and FEL (Mitomo et al. 2006; Shell et al. 2008; Zhou and Berne 2002). As such implicit solvent models should be employed carefully. Rigorous methods for the solvation free energy have been developed by the three-dimensional reference-interaction-site-model (3D-RISM) theory (Kovalenko and Hirata 2000a; Kovalenko and Hirata 2000b) and the morphometric approach (Roth et al. 2006), which are based on statistical physics. Although the more rigorous methods require computational cost, they are especially powerful for distinguishing the native structure outside of the pools, including decoy (close but not native) conformations (Yasuda et al. 2011). The combination of conventional McMD and the RISM theory was attempted to calculate the ensemble of Met-enkephalin (Mitsutake et al. 2000).

Restriction on the translational space of substrate is also useful when the aim is to compute the binding free energy. Without the restriction, the substrate tends to travel through all space of the system volume. When the substrate is significantly far from the receptor, the potential of mean force should be homogeneous. Then, confining the substrate to a spherical or cone-shaped space by the restriction can reduce the computation cost for the homogeneous part. This confinement method has been combined with metadynamics to obtain the binding/unbinding kinetics as well as the binding free energy (Limongelli et al. 2013; Tiwary et al. 2015). It should be noted that this confinement space should be designed so that its center locates at the determinate binding site. If the binding site is known in advance, this method can therefore be selected. Similar to reducing sampling space, there is a method to sample the conformations and FEL along a certain binding pathway: the filling potential method (Fukunishi et al. 2003). Application of the confinement method without any knowledge of the binding site has also been reported with the use of the replica exchange method (Anselmi and Pisabarro 2015), where the ligand resides inside a receptor-shaped closed surface larger than the receptor surface. This procedure can be useful for finding the binding mode and binding affinity at the same time.

Coarse-grained (CG) models for biomolecules (Saunders and Voth 2013; Takada 2012; Tozzini 2005) have been used to investigate the behavior of large biomolecules. In the CG models, the biomolecule is modeled with a particle that represents a sum of several atoms. For example, one particle represents one amino acid residue of protein, and the chain of the particles depicts the protein. The time-step for the CG model can be larger than that for the all-atom model. The energy function for the CG model may involve the solvation effect implicitly. A type of CG model uses a specific structure (such as the experimental structure or native structure) of biomolecule to determine the bottom of the energy funnel with this approach, also known as a Go-like model or native structure-based model (Clementi et al. 2000; Karanicolas and Brooks 2003). Studies with the Go-like model have revealed a protein folding mechanism (Onuchic and Wolynes 2004), and a binding mechanism of biomolecular interaction has been proposed (Levy et al. 2007). Energy functions for the CG model that do not require the specific structure have been developed and used for prediction of protein folding (Gront et al. 2008). Such energy functions are referred to as physics-based or sequence-dependent potentials. The energy functions of these models are defined in various ways, with physics-based potentials using physical relations specified between atoms (or coarser united atom representations) while statistical potentials infer relations from the examination of a large number of structures gathered in a structural database. Statistics-based energy functions are also referred to as knowledge-based (Sippl 1995). A combination of physics-based models and native structure-based models have been used to investigate protein–protein (Ganguly et al. 2012; Kim and Hummer 2008; Okazaki et al. 2012), protein–DNA (Terakawa et al. 2012; Vuzman et al. 2010), and protein receptor–small compound association/dissociation mechanisms (Negami et al. 2014). The inter-molecular interactions were treated by the physics-based model, while the intra-molecular interactions were treated with native structure-based model. Research into the use of CG models is focused on the kinetic behaviors of binding/unbinding as well as thermodynamics. The tREM and McMD methods have been used to sample the conformational ensemble by the CG models (Li et al. 2012; Nanias et al. 2006). The improved sampling methods introduced in this review may contribute to even more rapid simulation procedures based on the use of CG models.

The multicanonical algorithm is specific for the flat distribution method. The interested reader may realize that the iteration procedure is crucial to both the refinement of the canonical distribution function in Eq. 1 and equilibration of the conformational ensemble. Although V-McMD requires fewer iterations, it still takes time. However, if no iteration technique is available, it is the generally more useful method. There are two types of non-iteration techniques: on-the-fly and one-time. The former technique, also known as the Wang–Landau method (Shimoyama et al. 2011; Wang and Landau 2001), involves updating the estimation of the canonical probability at every step of the simulation. When the probability function converges, the Wang–Landau simulation is finished. After that, the conventional McMD with the converged probability is performed to obtain an equilibrated conformational ensemble. The one-time technique was proposed by Terada et al. (2003). The canonical probability distribution function in a wide energy range is estimated only once from multiple canonical runs at different temperatures. Such techniques can be useful for small systems. However, when the system is large and complex, the techniques are less efficient, especially for the low-energy range because of shortage of covering conformational space. We use the one-time technique in V-McMD and ALSD to produce the first guess of the probability distribution function with subsequent iterative improvement. The estimation of correct canonical probability is inextricably associated with an efficient search for the conformational space. The rapid conformational search method (Harada et al. 2015; Klvana et al. 2009; Lüdemann et al. 2000) can then be useful for generating initial widespread conformations although their conformations are non-equilibrated.

Summary

Molecular dynamics simulations using all-atom models in explicit solvent can provide meaningful biomolecular conformations that can be hard/impossible to determine experimentally. However, it is still difficult to correctly sample the conformational ensemble, with the result that errors are introduced into all estimates of the FEL of biomolecular interactions. These difficulties are due to the problem of overcoming numerous time-consuming energy barriers in the entire conformational space. This has led to the development of enhanced sampling method to achieve efficient sampling of the total conformational space. It is these methods which we have reviewed in this article. We also introduced the theory and application of three improved enhanced sampling methods, namely, TTP-McMD, V-McMD, and ALSD. In the final section, we introduced computational techniques, such as larger time-step and implicit solvent, which can be combined with the enhanced sampling methods. These enhanced sampling methods can be extrapolated from the all-atom model to the CG models for larger biomolecules. Such enhanced sampling methods are important applications to determine the thermodynamic properties of biomolecules by computational methods.

Compliance with ethical standards

Conflict of interest

Jinzen Ikebe, Koji Umezawa, and Junichi Higo declare that they have no conflict of interest.

Ethical approval

This article does not contain any studies with human or animal subjects performed by any of the authors.