Relaxation dispersion NMR spectroscopy for the study of protein allostery

Abstract

Allosteric transmission of information between distant sites in biological macromolecules often involves collective transitions between active and inactive conformations. Nuclear magnetic resonance (NMR) spectroscopy can yield detailed information on these dynamics. In particular, relaxation dispersion techniques provide structural, dynamic, and mechanistic information on conformational transitions occurring on the millisecond to microsecond timescales. In this review, we provide an overview of the theory and analysis of Carr-Purcell-Meiboom-Gill (CPMG) relaxation dispersion NMR experiments and briefly describe their application to the study of allosteric dynamics in the homeodomain from the PBX transcription factor (PBX-HD). CPMG NMR data show that local folding (helix/coil) transitions in one part of PBX-HD help to communicate information between two distant binding sites. Furthermore, the combination of CPMG and other spin relaxation data show that this region can also undergo local misfolding, reminiscent of conformational ensemble models of allostery.

Introduction

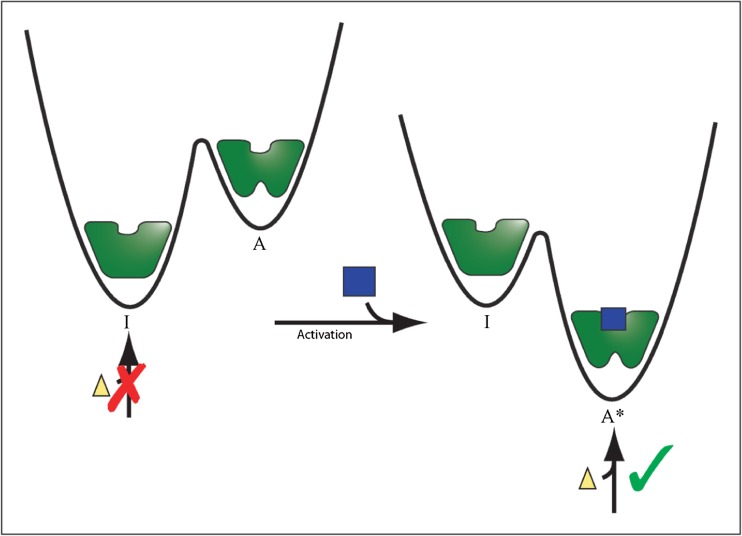
Allostery is a biological phenomenon in which ligand binding (Koshland et al. 1966; Monod et al. 1965), conformational rearrangements (Farber and Mittermaier 2011; Volkman et al. 2001), post-translational modifications (Nussinov et al. 2012; Volkman et al. 2001), or changes in dynamics (Popovych et al. 2006) in one region of a protein produce a change in the structure, dynamics, or activity at a distal site (Fig. 1). This often manifests as switching between an active and inactive form, which is essential for many biological processes including cell signaling and transcriptional control (Lefstin and Yamamoto 1998; Nussinov et al. 2013; Smock and Gierasch 2009). For example, the binding of cAMP in one domain of the catabolite activator protein (CAP) allosterically activates DNA binding in the DNA binding domain, more than 20 Å away (Tzeng and Kalodimos 2009). Phosphorylation of the bacterial nitrogen regulatory protein C (NtrC) leads to a large conformational change, oligomerization, and transcriptional activation (Volkman et al. 2001). The KIX domain from the CREB-binding protein cooperatively interacts with the activation domain from the mixed-lineage leukemia transcription factor (MLL), and causes a second binding site to transiently adopt its “bound” configuration, even in the absence of the second ligand (Bruschweiler et al. 2009). A disorder-to-helix conformational change in the C-terminal region of the PBX homeodomain results in a five-fold increase in its affinity for DNA although this region does not directly contact the DNA (Green et al. 1998).

Fig. 1.

Schematic representation of an allosterically activated enzyme. The molecule can populate both an inactive (I) conformer with low affinity for an allosteric activator (blue square) and an active conformer (A) with high affinity for the activator. Initially, the equilibrium favors the (I) state and the enzyme is inactive. Upon binding to the allosteric activator, the population shifts to the (A*) form and the enzyme is active and able to bind to the substrate (yellow triangle)

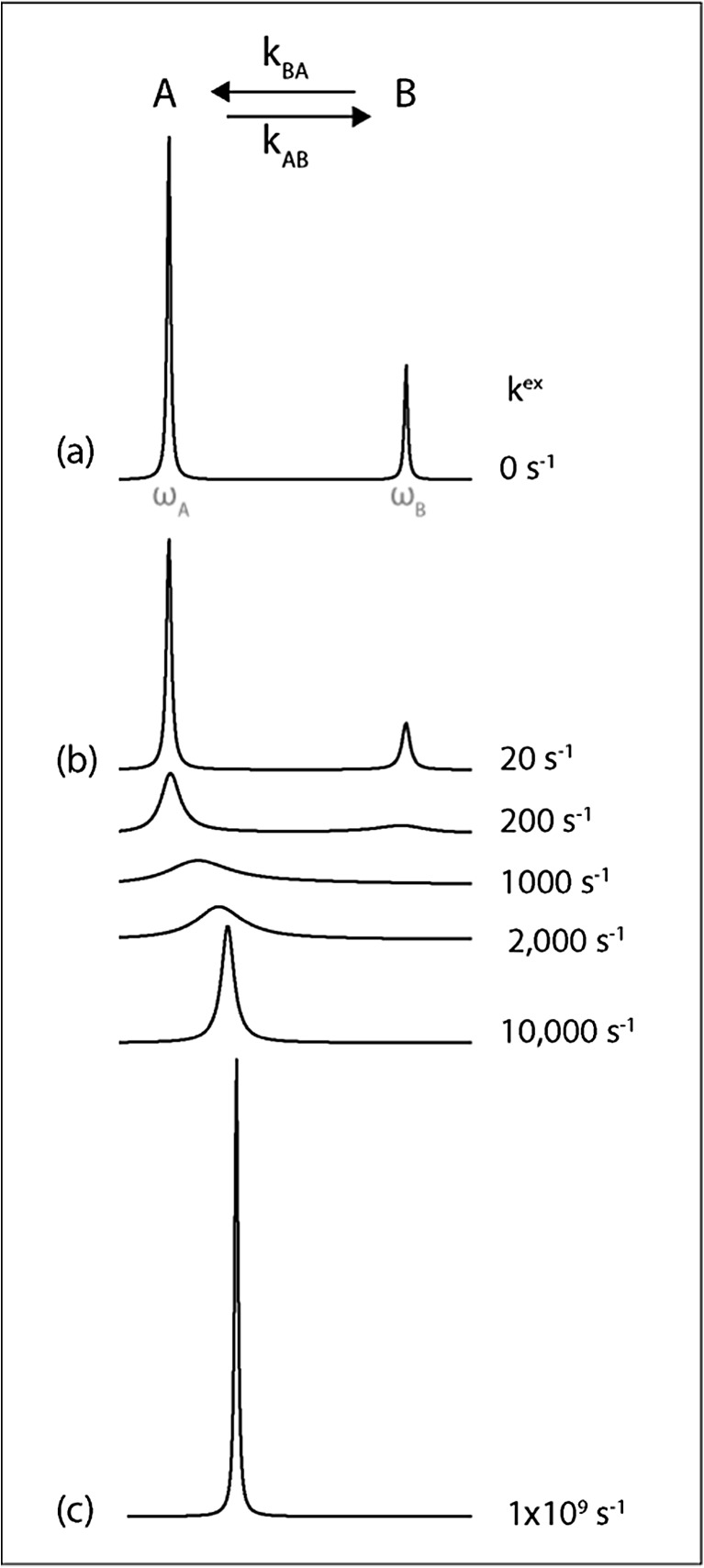
Solution nuclear magnetic resonance (NMR) spectroscopy can provide detailed structural and dynamic information on allosteric transitions, such as between active and inactive forms. There exists an array of NMR experimental techniques that can be used to characterize protein motions occurring on timescales between microseconds and seconds, including R_1ρ (microseconds) (Palmer and Massi 2006), Carr-Purcell-Meiboom-Gill (CPMG) relaxation dispersion (ms) (Hansen et al. 2008a; Loria et al. 1999), chemical exchange saturation transfer (CEST) (≤s) (Vallurupalli et al. 2012), and ZZ-exchange (s) (Farrow et al. 1994). In all the examples above (i.e. CAP, NtrC, KIX, and PBX), NMR dynamics experiments have shown that active and inactive forms exist in dynamic equilibria (Bruschweiler et al. 2009; Farber et al. 2012; Tzeng and Kalodimos 2013; Volkman et al. 2001). The sensitivity of NMR signals to molecular dynamics is illustrated in Fig. 2 in which a probe (nucleus) in a molecule of interest reports on conformational exchange between two states. The NMR resonance frequency (chemical shift) of a probe depends on its molecular environment. In this example, the number, width, and position of peaks in NMR spectra depend on the exchange rate between the states. At slow exchange rates, a pair of peaks derived from the individual states is observed in NMR spectra, whereas the signals shift, broaden and finally merge into a single sharp peak as the rate increases. The increase in the line width of the peak (broadening) at intermediate rates is a rich source of information on the exchange process. This review focuses on different ways of extracting information from NMR line broadening and their application to allosteric dynamics in the homeodomain from the PBX transcription factor.

Fig. 2.

Simulated one-dimensional NMR spectra for nuclei exchanging between two distinct chemical environments. a When the rate of exchange is much slower than the difference in chemical shift, separate peaks are observed for the two states. b Exchange broadening is caused by stochastic variations in chemical shift, which cause the NMR signal to decay more rapidly, leading to broader, weaker signals. c When exchange is far more rapid than the difference in chemical shift, a single sharp peak is obtained at the population weighted average chemical shift

Relaxation dispersion NMR

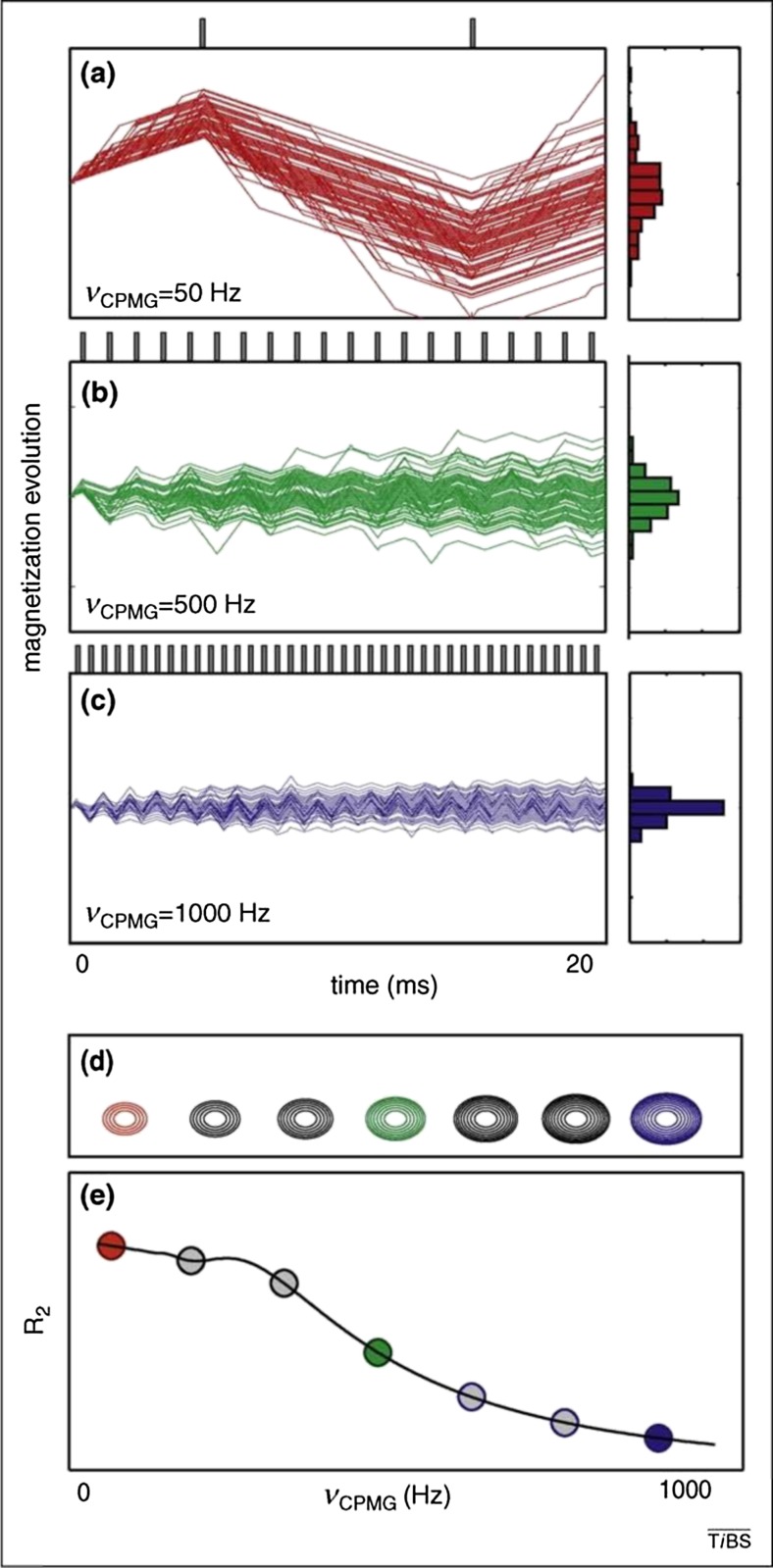
Peak broadening due to conformational exchange can be analyzed by relaxation dispersion NMR techniques, including rotating-frame (R _1ρ) relaxation and CPMG experiments. These provide thermodynamic, kinetic, structural, and mechanistic information on systems that undergo conformational exchange on the millisecond to microsecond time scales. They are sensitive to low-lying excited states with populations down to about 1 % (Loria et al. 1999; Luz and Meiboom 1963; Palmer et al. 2001). Conformational exchange on the millisecond time scale can lead to fluctuations in chemical shift that cause dephasing of the NMR signal, peak broadening, and the elevation of R ₂ (transverse) relaxation rates by an amount R _ex such that R ₂ ^observed = R ₂ ⁰ + R _ex, where R ₂ ⁰ is the intrinsic (exchange-free) relaxation rate. The application of variable spin-lock irradiation (R _1ρ) or trains of refocusing pulses (CPMG) quenches the relaxation due to exchange (Fig. 3). Sets of transverse relaxation rates collected as a function of spin-lock strength and frequency (R _1ρ) or refocusing pulse repetition rate (CPMG) vary between (R ₂ ⁰ + R _ex) at low spin-lock fields or pulse repetition rates and asymptotically approach R ₂ ⁰ at large fields or repetition rates. These dispersion profiles can be fitted to dynamical models consisting of two (Carver and Richards 1972) or more (Korzhnev et al. 2004) exchanging states, as described below. The fits yield thermodynamic and kinetic data in the form of populations and rates of exchange, as well as structural information in form of chemical shift differences between the exchanging states. Relaxation dispersion experiments performed over a range of temperatures can provide information on enthalpy differences and activation energies between exchanging states. Furthermore, comparisons of data extracted at different sites within the molecule can help to establish whether conformational transitions are cooperative (Farber et al. 2010), and identify intermediates along the reaction pathway (Korzhnev et al. 2004; Sugase et al. 2007).

Fig. 3.

CPMG relaxation dispersion experiments. a–c Simulated signal trajectories for an ensemble of nuclei exchanging stochastically between two environments with different chemical shifts during a 20 ms relaxation delay. Vertical bars at the top of each panel represent refocusing pulses applied during the relaxation delay. d Simulated peak that increases in intensity at higher pulse repetition rates. e Calculated transverse relaxation rates (R ₂) plotted as a function of ν_CPMG = 1/(2τ), where τ is the delay between successive refocusing pulses. Reprinted from Mittermaier and Kay, Observing biological dynamics at atomic resolution using NMR. Trends in Biochemical Science, 34/12, , 601–611, Copyright 2009, with permission from Elsevier

Two site exchange

Consider an exchange between two states, A and B, associated with spin precession frequencies of ω_A and ω_B, and first order rate constants k_AB and k_BA:

$${\omega }_A\underset{k_{\mathit{BA}}}{\overset{k_{\mathit{AB}}}{\rightleftarrows }}{\omega }_B\text{.}$$ 1

In this case, a CPMG relaxation dispersion profile can be parameterized in terms of the exchange rate, k_ex = k_AB + k_BA, the population of the minor (B) state, p_B = k_AB/k_ex, and the squared difference in precession frequency (or chemical shift) between the two states, Δω_AB ² = (ω_B – ω_A)². In the fast timescale regime, where k_ex> > |Δω_AB|, the transverse relaxation rate is given by the following analytical expression (Palmer et al. 2001):

$$R_2=p_A{R}_{2A}^0+p_B{R}_{2B}^0+\frac{{\Phi }_{ex}}{k_{ex}}(1-\frac{4v_{CPMG}}{k_{ex}}\tanh \left(\frac{k_{ex}}{4v_{CPMG}}\right))$$ 2

Φ_ex = p_Ap_BΔω_AB ², while R _2A ⁰ and R _2B ⁰ are the intrinsic (exchange-free) transverse relaxation rates in states A and B, and ν_CPMG = 1/(2τ_cp), where τ_cp is the delay between successive refocusing pulses in the CPMG pulse train. In the intermediate timescale regime, where k_ex ≈ |Δω_AB|, the transverse relaxation rate is given by the Carver-Richards expression (Palmer et al. 2001):

$$\begin{array}{l}{R}_2\left(v_{CPMG}\right)=\frac{1}{2}(R_{2A}^0+R_{2B}^0+k_{ex}-2v_{CPMG}{\cosh }^{-1}(D_{+}\cosh \left({\eta }_{+}\right)-D-\cosh \left({\eta }_{-}\right)))\\ D_{+}=\frac{1}{2}(\pm 1+\frac{2\Delta {\omega }_{AB}^2}{\sqrt{{\text{ψ}}^2+{\xi }^2}})\\ {\eta }_{\pm }=\frac{\sqrt{2}}{4v_{CPMG}}\sqrt{\pm \text{ψ}+\sqrt{{\text{ψ}}^2+{\xi }^2}}\\ \text{ψ}={(R_{2A}^0-R_{2B}^0+p_B{k}_{ex}-p_A{k}_{ex})}^2-\Delta {\omega }_{AB}^2+4p_A{p}_B{k}_{ex}^2\\ \xi =2\Delta {\omega }_{AB}(R_{2A}^0-R_{2B}^0+p_B{k}_{ex}-p_A{k}_{ex})\end{array}$$ 3

For CPMG experiments in which magnetization remains in-phase during the entire relaxation component (Hansen et al. 2008b), an exact solution for R ₂(ν_CPMG) has been derived. This can be expressed as Eq. (2) with a linear correction (Baldwin 2014).

It should be noted that relaxation dispersion profiles are usually fitted assuming R _2A ⁰ = R _2B ⁰ (as we have done in the examples below) even when the two intrinsic relaxation rates differ. In the fast exchange limit (Eq. (2)), this assumption does not affect the fitted kinetic parameters. However in the case of intermediate exchange, this can lead to systematic errors in the extracted values of k_ex and p_B, according to (Ishima and Torchia 2006):

$$\begin{array}{c}\hfill k_{\mathit{ex}}^{\mathit{app}}=k_{\mathit{ex}}\left(1-\frac{\Delta p\Delta R_2^0}{k_{\mathit{ex}}}\right)\hfill \\ \hfill p_B^{\mathit{app}}=p_B\frac{k_{\mathit{ex}}+\Delta R_2^0}{k_{\mathit{ex}}-\Delta p\Delta R_2^0}\hfill \end{array}$$ 4

where k_ex ^app and p_B ^app are the apparent exchange rate and population of the minor state, k_ex and p_B are the true values, Δp = p_A–p_B, and ΔR ₂ ⁰ = ΔR _2A ⁰–ΔR _2B ⁰. In the example below, we estimate that this could introduce errors in the fitted parameters on the order of 2-6 %.

Three state exchange

If CPMG relaxation dispersion data cannot be adequately fit to a two-state exchange model, it can often be due to the presence of more than two exchanging states. The analysis of CPMG data becomes increasingly complex with increasing numbers of exchanging states, and often requires additional information in order to extract accurate rates and populations (Neudecker et al. 2006). The simplest multi-state system involves linear three state exchange:

$$C\underset{k_{-2}}{\overset{k_2}{\rightleftarrows }}A\underset{k_{-1}}{\overset{k_1}{\rightleftarrows }}B$$ 5

In the fast exchange limit, the corresponding relaxation dispersion profiles are given by the expressions (Grey et al. 2003):

$$\begin{array}{l}{R}_2=R_2^0+\frac{{\varphi }_{\mathit{fast}}}{{\kappa }_{\mathit{fast}}}\left(1-\frac{4{\nu }_{\mathit{CPMG}}}{{\kappa }_{\mathit{fast}}}tanh\left[\frac{{\kappa }_{\mathit{fast}}}{4{\nu }_{\mathit{CPMG}}}\right]\right)+\frac{{\varphi }_{\mathit{slow}}}{{\kappa }_{\mathit{slow}}}\left(1-\frac{4{\nu }_{\mathit{CPMG}}}{{\kappa }_{\mathit{slow}}}tanh\left[\frac{{\kappa }_{\mathit{slow}}}{4{\nu }_{\mathit{CPMG}}}\right]\right),\hfill \\ {\varphi }_{\mathit{fast}}=\left(-{\kappa }_{\mathit{slow}}{\alpha }_1+{\alpha }_2\right)/Z,\hfill \\ {\varphi }_{\mathit{slow}}=\left({\kappa }_{\mathit{fast}}{\alpha }_1-{\alpha }_2\right)/Z,\hfill \\ {\kappa }_{\mathit{fast}}=\left(k_{\mathrm{ex}}+Z\right)/2,\hfill \\ {\kappa }_{\mathit{slow}}=\left(k_{\mathrm{ex}}-Z\right)/2,\hfill \\ k_{\mathrm{ex}}=k_1+k_{-1}+k_2+k_{-2}\hfill \\ Z={\left({k_{\mathrm{ex}}}^2-4B\right)}^{1/2}\hfill \\ B=k_{-1}{k}_{-2}+k_1{k}_{-2}+k_{-1}{k}_2\hfill \\ {\alpha }_1=p_A{p}_B\Delta {{\omega }_{\mathit{AB}}}^2+p_B{p}_C\Delta {{\omega }_{BC}}^2+p_A{p}_C\Delta {{\omega }_{\mathit{AC}}}^2\hfill \\ {\alpha }_2=p_A\left(k_1\Delta {{\omega }_{\mathit{AB}}}^2+k_2\Delta {{\omega }_{\mathit{AC}}}^2\right)\hfill \\ p_A=k_{-1}{k}_{-2}/B\hfill \\ p_B=k_1{k}_{-2}/B\hfill \\ p_C=k_{-1}{k}_2/B\hfill \end{array}$$ 6

where p _A, p _B, and p _C are the relative populations of states A, B, and C, and Δω_XY is the difference between ¹⁵N resonance frequencies in states X and Y. Equations for three-site exchange in the intermediate timescale are far more complicated, consequently explicit numerical modeling of the Bloch-McConnell equations (McConnell 1958) is typically performed (https://github.com/gbouvignies/chemex/releases; Korzhnev et al. 2004; Vallurupalli et al. 2012).

Global fitting

In general, an NMR analysis of millisecond-microsecond timescale protein dynamics begins with individual fits of relaxation data obtained for each broadened peak in NMR spectra. In this step, a separate set of motional parameters (eg. k_ex, p_B, Δω², and R ₂ ⁰) are obtained for each residue undergoing exchange. If data for many residues throughout a protein yield similar dynamical parameters, this can indicate that different regions of the molecule participate in concerted motions. In this case, analyzing the data for multiple residues simultaneously yields a more accurate description of the exchange process. Fits are performed assuming that the parameters describing the shared characteristics of the concerted motion (e.g., k_ex and p_B) are identical for every residue, while the local parameters (e.g., Δω², R ₂ ⁰) are optimized separately for each residue. The goodness of fit is evaluated using the standard residual χ ² parameter,

$${\chi }^2={\displaystyle \sum \frac{{\left(R_2^{\text{exp}}-R_2^{\mathit{calc}}\right)}^2}{{\sigma }_{R2}^2}}\text{,}$$ 7

where R ₂ ^exp and R ₂ ^calc are experimental and calculated transverse relaxation rates, respectively, σ_R2 is the experimental uncertainty, and the sum runs over all data for a given residue. A comparison of values obtained in individual fits (χ ² _individual) with those of global fits where exchange parameters are shared among all residues (χ ² _global) can identify residues experiencing dynamics distinct from the collective process. Global fitting is repeated, excluding in each iteration data for the residue with the largest χ ² _global/χ ² _individual ratio. This procedure is then repeated until the largest χ ² _global/χ ² _individual drops below a certain threshold (we have found a threshold of 2 yields satisfactory results) (Mulder et al. 2001).

In the fast timescale regime for global exchange between states, the concerted process is described by a single shared parameter that gives the kinetics of the process, k_ex ^global. In addition, each residue is associated with an individual parameter, Φ_ex = p_Ap_BΔω², that varies depending on the magnitude of the difference in chemical shift between the two states. Values can be calculated using a two-step protocol (Farber et al. 2010, 2012; Farber and Mittermaier 2011). In the first step, k_ex is fixed at closely-spaced intervals between a lower and upper bound (e.g., 100 and 10,000 s^-1). For each value of k_ex, all individual parameters are adjusted to minimize the χ ² function

$${\chi }^2\left(k_{\mathit{ex}}\right)={\displaystyle \sum \frac{{\left(R_2^{\text{exp}}-R_2^{\mathit{calc}}\left(k_{\mathit{ex}}\right)\right)}^2}{{\sigma }_{R2}^2}}\text{,}$$ 8

where R ₂ ^calc(k_ex) is computed using Eq. (2) and the sum runs over all R ₂ data points for a single residue. Aggregate χ ² versus k_ex profiles can then be calculated according to

$${\chi }_{\mathit{total}}^2\left(k_{\mathit{ex}}\right)={\displaystyle \sum {\chi }^2\left(k_{\mathit{ex}}\right)}\text{,}$$ 9

where the sum runs over data for all residues. The global value of k_ex is then selected such that

$${\chi }_{\mathit{total}}^2\left(k_{\mathit{ex}}^{\mathit{global}}\right)=min\left({\chi }_{\mathit{total}}^2\left(k_{\mathit{ex}}\right)\right)\text{.}$$ 10

In the second step, values of Φ_ex are obtained for all residues by minimizing Eq. (8), fixing k_ex = k_ex ^global. Populations and chemical shift differences of the major and minor states can be obtained from Φ_ex only if the populations or differences in chemical shifts for the two states are known.

In the fast timescale regime for global linear interconversion between three states, the concerted process is described by two shared parameters that are related to the kinetics of exchange, κ_fast ^global and κ_slow ^global. In addition, each residue is associated with individual parameters, φ _fast and φ _slow, that vary depending on the magnitudes of the differences in chemical shift between the three states. Similarly to fast-timescale two-state exchange, a grid-search approach can be used to determine the dynamical parameters for fast-timescale three state exchange (Farber et al. 2012). In the first step, κ_fast and κ_slow are arrayed over appropriate ranges of values (κ_fast > κ_slow). Values of φ_fast, φ_slow, and R₂ ⁰ values are then adjusted on a per-residue basis to minimize the χ ² function

$${\chi }^2\left({\kappa }_{\mathit{fast}},{\kappa }_{\mathit{slow}}\right)={\displaystyle \sum \frac{{\left(R_2^{\text{exp}}-R_2^{\mathit{calc}}\left({\kappa }_{\mathit{fast}},{\kappa }_{\mathit{slow}}\right)\right)}^2}{{\sigma }_{R_2}^2}}\text{.}$$ 11

R ₂ ^calc is computed using Eq. (6), and the sum runs over all R ₂ data points for a single residue at at least two magnetic field strengths. Aggregate χ ² surfaces are then calculated according to

$${\chi }_{\mathit{total}}^2\left({\kappa }_{\mathit{fast}},{\kappa }_{\mathit{slow}}\right)={\displaystyle \sum {\chi }^2\left({\kappa }_{\mathit{fast}},{\kappa }_{\mathit{slow}}\right)}\text{,}$$ 12

where the sum runs over data for all selected residues. Globally-optimized values for κ_fast and κ_slow are selected such that

$${\chi }_{\mathit{total}}^2\left({\kappa }_{\mathit{fast}}^{\mathit{global}},{\kappa }_{\mathit{slow}}^{\mathit{global}}\right)=min\left({\chi }_{\mathit{total}}^2\left({\kappa }_{\mathit{fast}},{\kappa }_{\mathit{slow}}\right)\right)\text{.}$$ 13

In the second step, values of φ _fast and φ _slow are obtained for all residues by minimizing Eq. (11), fixing κ_fast = κ_fast ^global and κ_slow = κ_slow ^global.

Experimental determination of R₂⁰ – LOMSQ experiments

Instrumental considerations limit the maximum values of ν_CPMG (CPMG) or spin-lock field strengths (R _1ρ) that are experimentally accessible. As a consequence, these measurements may not fully quench exchange contributions to R ₂ (R _ex) when exchange is extremely rapid (k_ex > ≈ 10⁴ s^-1). In this situation it can be challenging to determine the exchange-free transverse relaxation rate, R ₂ ⁰ or conversely, R _ex. Kay and co-workers (Hansen et al. 2007) have designed an elegant suite of four relaxation experiments that provides exchange-free measures of dipole–dipole ¹⁵N transverse relaxation. In what follows, these will be referred to as LOSMQ (longitudinal order, single and multiple quantum) experiments. These experiments can be combined with spectral density mapping (Farrow et al. 1995) in order to obtain close estimates of R ₂ ⁰. Measurements of single quantum longitudinal relaxation rates in the presence of either ¹H or ¹⁵N spin-lock fields, R _1ρ(2H'_zN_z) and R _1ρ(2H_zN'_z), are combined with multiple quantum ¹H-¹⁵N relaxation rates, R _1ρ ² (2H'_zN'_z), where both ¹H and ¹⁵N spin-locks are applied and two spin order relaxation rates, R ₁(2H_zN_z), to isolate only contributions from ¹H-¹⁵N dipolar relaxation (Hansen et al. 2007). Exchange-free transverse dipole-dipole relaxation rates, R _dd, can then be obtained from the linear combination of the four relaxation rates. R ₂ ⁰ and R _dd values differ since the former, but not the latter, contain contributions from the chemical shift anisotropy relaxation mechanism. In order to obtain R ₂ ⁰ estimates, longitudinal ¹⁵N relaxation rates, R₁, and ¹H-¹⁵N steady-state NOE values can be combined with R _dd values to determine values of the spectral density function, J(ω), at ω = 0, ω_N and 0.87ω_H, where ω_N and ω_H are the ¹⁵N and ¹H Larmor frequencies, respectively (Farber et al. 2012; Farrow et al. 1994, 1995; Hansen et al. 2007). Exchange-free ¹⁵N R ₂ ⁰ relaxation rates can then be back-calculated using the values of the spectral density function extracted above, according to the expression:

$$R_2^0=\left(d^2/8\right)\left[4J\left(0\right)+3J\left({\omega }_N\right)+13J\left(0.870{\omega }_H\right)\right]+\left(c^2/6\right)\left[4J\left(0\right)+3J\left({\omega }_N\right)\right]\text{,}$$ 14

where d = [μ ₀ hγ _H γ _N/8π ²]〈r ^− 3_NH〉, $c=\left({\omega }_N/\sqrt{3}\right)\left({\sigma }_{\parallel }-{\sigma }_{\perp }\right)$, μ₀ is the permeability of free space, γ_H and γ_N are the respective gyromagnetic ratios, h is Planck’s constant, r _NH is the length of the amide bond, and σ_|| and σ_⊥ are the parallel and perpendicular components, respectively, of the axially symmetric ¹⁵N chemical shift tensor (Cornilescu and Bax 2000). These R ₂ ⁰ estimates can be used to constrain fits of CPMG or R _1ρ relaxation dispersion data, significantly improving the accuracy of the analysis. An important caveat is that this comparison is only quantitative when CPMG pulse sequences that measure in-phase ¹⁵N transverse relaxation rates, such as rczz (Wang et al. 2001) or ¹H-decoupled (Hansen et al. 2008a) schemes are used. In contrast, relaxation rates obtained using traditional relaxation-compensated CPMG schemes (Loria et al. 1999) are a mixture of in-phase and anti-phase ¹⁵ N transverse relaxation rates and cannot be compared directly to LOSMQ-derived values. Also note that alternative methods can be used to obtain independent R ₂ ⁰ estimates, such as the ¹H-¹⁵ N dipole/¹⁵N CSA relaxation interference approach developed by Palmer and co-workers (Kroenke et al. 1998).

Application to the PBX1 homeodomain

Allostery mediated by a helix/coil transition

The PBX1 homeodomain (PBX-HD) is an 81-residue protein consisting of 3 alpha helices that adopt a consensus homeodomain structure and an unstructured 18-residue C-terminal extension. PBX-HD cooperatively binds DNA with Hox transcription factors and plays an important role in anterior-posterior patterning in vertebrate development (Chang et al. 1995). Allosteric interactions are important for the formation of this ternary complex. DNA binding at one surface of PBX-HD enhances interactions with Hox proteins at another interface. Additionally, upon binding DNA, the C-terminal extension of PBX-HD undergoes a disorder-to-helix folding transition, although this region of the protein does not directly contact DNA. Removal of the C-terminal extension decreases the binding affinity of PBX-HD for DNA by 5-fold and reduces cooperative interactions between PBX-HD and Hox proteins when they bind DNA (Chang et al. 1995; Green et al. 1998). Thus, the C-terminal extension is implicated in mediating allosteric communication between the DNA- and Hox-binding regions of the PBX-HD. We recently studied the nature of this allosteric coupling using NMR CPMG dynamics experiments (Farber and Mittermaier 2011; Farber et al. 2012).

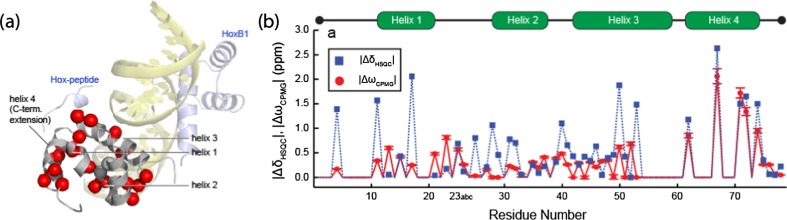
NMR ¹⁵N/¹H cross-peaks for residues throughout PBX-HD produced large-amplitude CPMG relaxation dispersion profiles, indicative of millisecond timescale conformational exchange. In particular, many signals from the C-terminal extension were broadened beyond detection, and the remaining signals produced the largest relaxation dispersion profiles (Fig. 4). Individual analyses of relaxation dispersion profiles for C-terminal residues yielded similar rates and populations. Thus fitting was repeated assuming a global two-site exchange process. Relaxation dispersion experiments were recorded over a range of termperatures and k_ex, p_B, and Δω² values were obtained at each temperature, yielding populations of the minor state of 5–10 % and exchange rates of 1500–2500 s⁻¹. The population of the minor state, p_B, was found to decrease with increasing temperature, while k_ex increased. A van ‘t Hoff plot yielded a large negative enthalpy change of ΔH_AB = –9.5 kcal mol⁻¹, and an entropy change of ΔS_AB = –38 cal mol⁻¹ K⁻¹. These values are about one-third of those obtained for the entire folding reaction of a truncated three-helix version of PBX-HD at 20 °C (ΔH = –30 kcal mol⁻¹, ΔS = –91 cal mol⁻¹ K⁻¹) (Farber et al. 2010). Thus the transition to the minor state is consistent with the folding of an unstructured region into an alpha helix. Furthermore, Δω² values obtained from relaxation dispersion data agree with chemical shift changes produced by DNA binding, suggesting that the C-terminal extension adopts similar (folded) conformations in the bound state and the weakly-populated “B” conformation in the free state (Fig. 4b).

Fig. 4.

Allostery in PBX-HD. a Red spheres identify residues whose dispersion data agree with the global exchange process involving folding of the C-terminal extension. Structures of DNA (light yellow) and HoxB1 homeodomain (light blue) were taken from the X-ray crystal structure of the ternay complex formed by the human isoforms of the proteins (1B72; Piper et al. 1999). The Hox-peptide is connected to the remainder of the HoxB1 homeodomain by 20 disordered residues. b Differences in ¹⁵N chemical shift between the two exchanging forms of unbound PBX-HD extracted from CPMG dynamics data (Δω_CPMG) and ¹⁵N chemical shift changes produced by DNA binding (Δδ_HSQC) for all residues with detectable signals in PBX-HD. Reprinted (adapted) from Farber and Mittermaier, Concerted dynamics link allosteric sites in the PBX Homeodomain, Journal of Molecular Biology, 405/3, 819–830, Copyright 2011, with permission from Elsevier

Relaxation dispersion data in the consensus homeodomain region were consistent with the exchange dynamics found for the C-terminal extension. This strongly suggested that PBX-HD exchanges between a ground state in which the C-terminal extension is disordered and a state in which the C-terminal extension is ordered and the rest of the homeodomain experiences some conformational rearrangement. Notably, these concerted motions included residues in the Hox binding site and in helix 3, which binds in the major groove of DNA (Fig. 4). Thus, concerted motions occur in three regions of the protein known to communicate allosterically, reinforcing the idea that these regions are energetically linked. These dynamics suggested a simple physical model based on classical Monod-Wyman-Changeux (MWC) theory (Monod et al. 1965) to explain the allostery observed for PBX-HD. In this model, the major (A) conformer of PBX-HD has little or no affinity for either DNA or the Hox-peptide, while the minor (B) conformer has much greater affinity for both ligands. When PBX-HD binds to DNA, it becomes locked in the minor (high affinity) conformation, in which the C-terminal extension is ordered and the Hox binding surface is remodelled. This is consistent with DNA-induced folding of the C-terminal extension, as has been observed experimentally. Further, binding of either DNA or the Hox-peptide to PBX-HD locks the unoccupied site in the high-affinity configuration. According to this mechanism, binding of the first ligand could enhance the affinity for the second ligand by as much as a factor of (1-p_B)/p_B, which corresponds to about a factor of 34 at 37 °C. This helps to explain why DNA binding is promoted by addition of the Hox-peptide (Knoepfler and Kamps 1995), and why the PBX/Hox-peptide interaction has not been detected in the absence of DNA, since it is fairly weak even in the presence of DNA (Sprules et al. 2003).

PBX-HD transient local misfolding

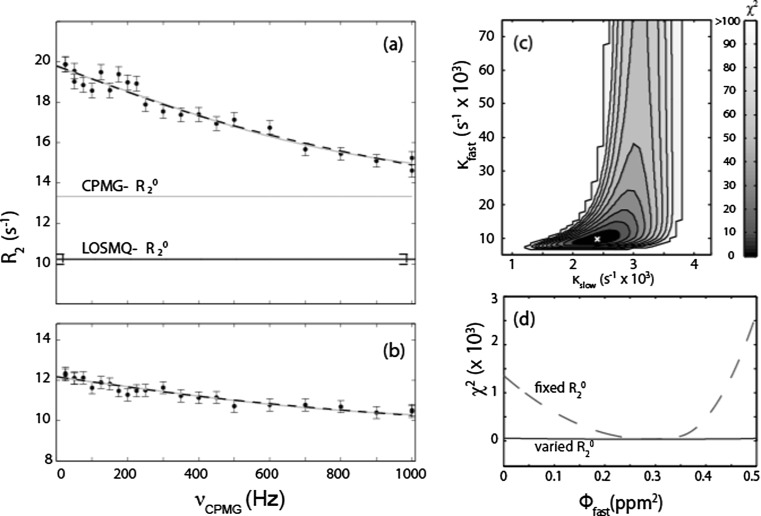
We subsequently used LOSMQ spin relaxation experiments to estimate exchange-free ¹⁵N transverse relaxation rates, R ₂ ⁰, in PBX-HD. Notably, in many cases, the LOSMQ-R ₂ ⁰ were much greater than those extracted from an analysis of CPMG data assuming two-state exchange (Fig. 5a, b). This implied that PBX-HD undergoes millisecond/microsecond exchange among more than two conformational states. We therefore performed a global linear three-state exchange analysis of the CPMG data, fixing R ₂ ⁰ (i.e. the asymptotes of the dispersion curves) equal to the LOSMQ-derived R ₂ ⁰ values. This fit gave the global values κ_fast = 9500 s⁻¹ and κ_slow = 2400 s⁻¹, which relate to the overall timescale of exchange. As well, it yielded as values of φ_fast and φ_slow on a per residue basis. These relate to chemical shift differences among the three states (Fig. 5c). Fixing the LOSMQ-R ₂ ⁰ was necessary for the analysis; fits with fixed R ₂ ⁰ yielded definite values of φ_fast, while these parameters were completely undefined when R ₂ ⁰ was allowed to vary in the fits (Fig. 5d).

Fig. 5.

Three-state fitting of PBX-HD: ¹⁵N CPMG relaxation dispersion NMR data for N23c, located in the Hox binding site, of PBX-HD measured at (a) 18.8 T and (b) 11.7 T. The horizontal gray lines (CPMG-R ₂ ⁰) correspond to the asymptotic values of R ₂ (ν_CPMG = ∞), extracted as adjustable parameters from global fits of CPMG data using a two-state exchange model, Eq. (1). The horizontal black lines (LOSMQ-R ₂ ⁰) correspond to exchange-free ¹⁵N R ₂ values obtained from LOSMQ relaxation data using Eq. (14). Gray curves correspond to global fits of CPMG data using a two-state model, Eq. (1). Black dashed curves correspond to global fits using a linear three-state exchange model, Eq. (5), with the asymptotic R ₂ ⁰(18.8 T) fixed equal to LOSMQ-R ₂ ⁰. c Residual χ ² surface for global fits of a linear three-state exchange model (Eq. 6) to CPMG data, employing a two-dimensional grid search in κ_fast and κ_slow. The surface was normalized relative to the minimum χ ² value (indicated white x) which was assigned a value of zero. d χ ² profile for fits of a linear three-state exchange model to CPMG data for N23c, the third residue of a three amino acid loop extension occurring after homeodomain consensus residue 23, employing a one-dimensional search in φ _fast with fixed values of κ_fast = 9500 s⁻¹ and κ_slow = 2400 s⁻¹, and R ₂ ⁰(18.8 T) either fixed equal to LOSMQ-R ₂ ⁰ (dashed curve), or varied as an adjustable parameter in the fit (solid black curve). Reprinted (adapted) with permission from (Farber et al. 2012). Copyright 2012 American Chemical Society

The extracted parameters did not, in themselves, yield much physical insight into the nature of the exchange process. There is a clear distinction between the CPMG-derived macroscopic model, which is described by the parameters κ _slow, κ _fast, φ _slow, and φ _fast, and “microscopic models” which are described by the rate constants k ₁, k ₋₁, k ₂, k ₋₂, as well as the chemical shift differences Δω _AB, Δω _AC, and Δω _BC. In general, a microscopic model is of more value, as it provides an explicit description of the conformational dynamics. The challenge lies in the fact that a great many different microscopic models can be consistent with the same macroscopic exchange parameters. In order to resolve this degeneracy, we noted that a strong correlation (r = 0.99) existed between values of φ _slow and squared differences in ¹⁵N chemical shift between the free and DNA-bound forms of PBX-HD, Δδ². Using this information in a grid-search selection procedure, we showed that the populations of linear three-state exchange are heavily skewed towards the middle state, A, which is populated to more than 90 % (Farber et al. 2012), and in which the C-terminal extension is unfolded. State A undergoes exchange on the order of 2000 s⁻¹ with a DNA bound-like state (2 %) in which the C-terminal extension forms an α helix, and ultrafast exchange on the order of 9000 s⁻¹ with a state (5 %) in which the C-terminal extension adopts an alternate conformation. This conformation represents a locally misfolded form of the C-terminal extension, which must unfold to re-form the major conformation before it can proceed to the α helical form.

This has implications for the nature of allostery in PBX-HD. In classical paradigms, protein molecules exist in two conformations, often referred to as the “tense” and “relaxed” states (Koshland et al. 1966; Monod et al. 1965). This implies a tightly-controlled energy landscape with a small number energy minima corresponding to discrete functional states. More recently, allostery has been recast in terms of folding and binding energy funnels (Boehr et al. 2009; Kumar et al. 2000). These descriptions invoke the breadth of the protein conformational ensemble: “proteins are inherently dynamic and sample a vast ensemble of conformations” (Boehr et al. 2009), that represent “the repertoire of molecules available for the binding event.” (Kumar et al. 2000) The behavior exhibited by PBX-HD is reminiscent of both the old and new paradigms. The free protein exchanges among three conformational states separated by significant energy barriers. One of the states resembles the ligand-bound form. Thus, classical theory involving transitions among discrete states provides a useful explanation for allostery in this molecule. Yet, the existence of the “locally misfolded” state is best understood within the framework of folding and binding funnels, in accordance with the new ensemble view of allostery.

Conclusions

CPMG relaxation dispersion NMR experiments can provide detailed atomic resolution information on millisecond timescale dynamics underlying allostery. In the case of exchange between two distinct conformations, such as that between active and inactive forms, CPMG data yield the populations, exchange rate, and chemical shift differences for the two states. When exchange involves more than two states, combining CPMG relaxation dispersion and LOSMQ spin relaxation data is a powerful approach for characterizing the dynamics. The parameters extracted from a three-state fit of CPMG NMR data can be directly related to the physical parameters describing the exchange process only if additional chemical shift, kinetic, or thermodynamic information is available. By applying CPMG and LOSMQ methods to PBX-HD, we found that in the absence of binding partners, the protein exchanges among three states: a highly populated one in which the C-terminal extension is unfolded, a second in which the C-terminal extension forms an alpha helix and likely mediates activation of DNA- and Hox-binding surfaces, and a third in which the C-terminal extension is misfolded. This combination of exchange between high and low binding affinity forms with additional conformational equilibria represents a hybrid of traditional and more recent conformational ensemble views of allostery.