Abstract
Protein–DNA interactions are central to the control of gene expression across all forms of life. The development of approaches to rigorously model such interactions has often been hindered both by a lack of quantitative binding data and by the difficulty in accounting for parameters relevant to the intracellular situation, such as DNA looping and thermodynamic non-ideality. Here, we review these considerations by developing a thermodynamically based mathematical model that attempts to simulate the functioning of an Escherichia coli expression system incorporating two of the best characterised prokaryotic DNA binding proteins, Lac repressor and lambda CI repressor. The key aim was to reproduce experimentally observed reporter gene activities arising from the expression of either wild-type CI repressor or one of three positive-control CI mutants. The model considers the role of several potentially important, but sometimes neglected, biochemical features, including DNA looping, macromolecular crowding and non-specific binding, and allowed us to obtain association constants for the binding of CI and its variants to a specific operator sequence.
Electronic supplementary material
The online version of this article (doi:10.1007/s12551-016-0231-9) contains supplementary material, which is available to authorized users.
Keywords: Synthetic biology, Mathematical model, lac repressor, Lambda CI repressor, Escherichia coli expression system
Introduction
With recent developments in synthetic biology and CRISPR/Cas9 methodology facilitating the design and manipulation of almost any DNA sequence within the cells of both prokaryotes and eukaryotes (Jinek et al. 2012; Kim 2016), it seems timely to review the feasibility of developing a full mathematical description of the workings of a synthetic construct in vivo. To that end, this review utilises quantitative studies, published over the last 40 years, to model the workings of a synthetic construct incorporating both LacI and CI, the two best studied regulators of transcription in Escherichia coli.
Gene expression in prokaryotes is commonly controlled at the transcription initiation stage by proteins dedicated to that purpose. Such proteins function either by repression of transcription initiation (negative control) or activation (positive control) or both (Jacob and Monod 1961). Throughout the history of molecular biology, the lac repressor (LacI) from E. coli and CI from phage λ have played central roles: LacI is the control protein that enables E. coli to respond to lactose in its environment (Müller-Hill 1996), while CI is utilised by the phage λ virus in maintaining a lysogenic (quiescent) state of infection of E. coli (Ptashne 2004).
Both systems have provided a wealth of quantitative experimental data amenable to thermodynamic modelling. The somewhat simpler Lac system, which involves DNA binding and looping between three separated LacI binding sites, has been extensively modelled; the studies of Mossing and Record (1986), Garcia and Phillips (2011), Lewis (2013) and Priest et al. (2014) provide some examples. The lambda regulatory system has proven to be more complex and, like the Lac system, has led to the discovery of several fundamental principles of gene control (Ptashne 2004). In a landmark study, Shea and Ackers (1985) succeeded in using a statistical mechanical approach to simulate the detailed features of CI control of the alternative states of growth of phage λ in E. coli. This model was later extended (Dodd et al. 2004; Cui et al. 2013) following the discovery (Révet et al. 1999) that the CI protein can also mediate DNA looping between distant CI operators. The model of CI control of gene expression has since been shown to hold under a number of experimental conditions, including in vitro single DNA molecule approaches (Zurla et al. 2009) and in vitro transcription assays (Lewis et al. 2011), as well as in vivo at the level of individual cells (Hensel et al. 2012; Sepúlveda et al. 2016).
Kolkhof and Müller-Hill (1994) designed an E. coli expression/reporter system incorporating coupled LacI and CI control of the β-galactosidase reporter gene, lacZ. Their study focused on three CI mutants, each deficient in wild-type CI’s ability to activate transcription, as revealed in altered patterns of reporter gene expression. Their extensive in vivo observations beckoned computer simulation. Previous successful modelling attempts instilled confidence that a thermodynamically based simulation study, incorporating both LacI and CI control, was feasible. Utilising results from numerous in vitro studies of LacI and CI control, the present model accurately simulates the in vivo observations of Kolkhof and Müller-Hill for both their wild-type CI system and three mutant CI systems, but also points to the difficulties which arise when attempting to develop biochemically rigorous models of ever more complex circuits.
Model
Kolkhof and Müller-Hill expression system
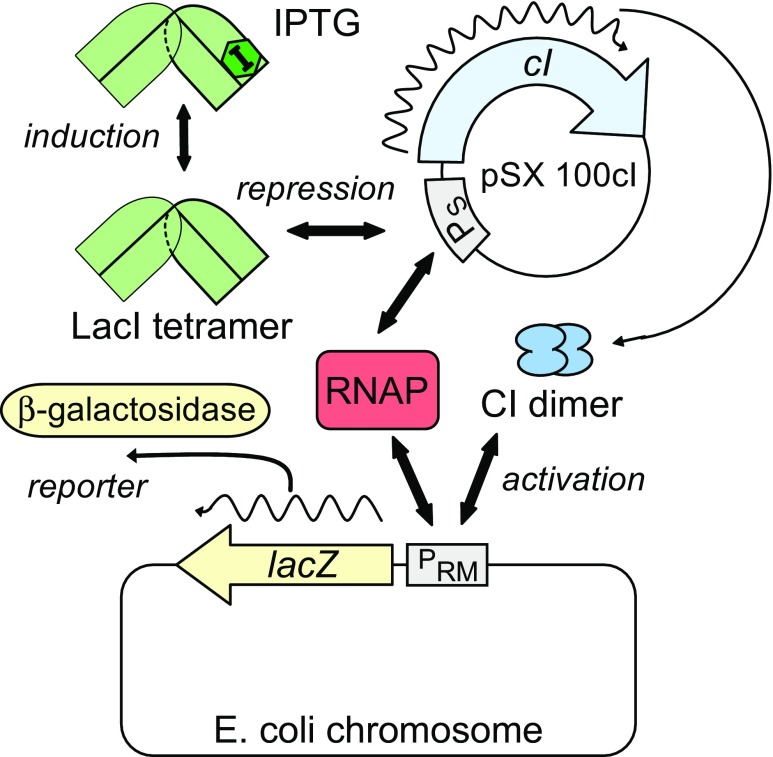
Kolkhof and Müller-Hill constructed an E. coli expression system combining LacI and CI control mechanisms. In their system, as illustrated in Fig. 1, LacI represses expression of the cI gene, while the addition of isopropyl β-D-1-thiogalactopyranoside (IPTG) relieves that repression. The resultant CI protein activates expression of the β-galactosidase gene, lacZ.
Fig. 1.
The Escherichia coli expression/reporter system constructed by Kolkhof and Müller-Hill (1994). Expression of the cI gene on plasmid pSX 100cI occurs upon binding by RNA polymerase (RNAP) to promoter PS. LacI represses expression of the cI gene by binding to operators adjacent to PS; isopropyl β-D-1-thiogalactopyranoside (IPTG) induces cI expression by binding to LacI, greatly reducing LacI’s affinity for its operators (see Fig. 3). Expression of lacZ, the gene for the reporter enzyme β-galactosidase, occurs upon binding by RNAP to promoter PRM on the E. coli chromosome. CI activates expression of lacZ when bound immediately adjacent to PRM-bound RNAP (see Fig. 4)
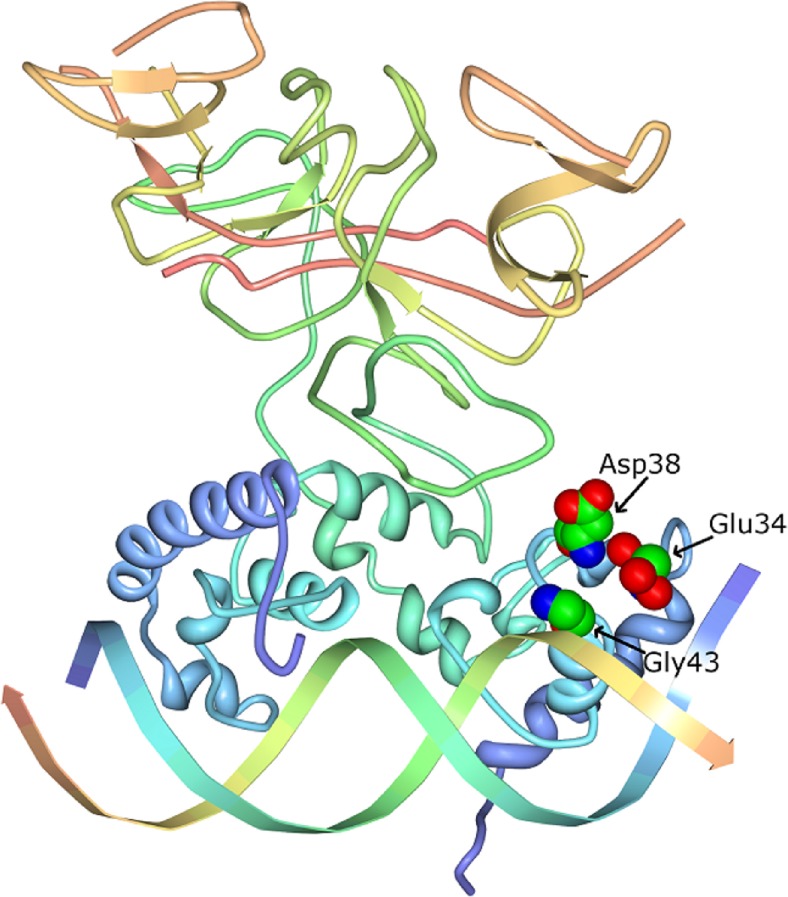
In their study, Kolkhof and Müller-Hill investigated three CI positive-control mutants, designated pc-1 (G43R), pc-2 (D38N) and pc-3 (E34K), each lacking wild-type CI’s ability to activate mRNA transcription. Those three mutations are positioned in the helix–turn–helix region involved in operator DNA binding (Fig. 2). All three residues mutated are exposed on the protein surface and are generally considered to interact directly with adjacently bound RNA polymerase (RNAP) (Li et al. 1997). Details of the LacI and CI control mechanisms follow.
Fig. 2.
CI wild-type dimer bound to operator DNA [PDB ID: 3bdn (Stayrook et al. 2008)]. The positive-control (pc) mutants in the Kolkhof and Müller-Hill study (1994) arise from separate changes in three residues in the helix–turn–helix region of CI, namely: pc-1: G43R, pc-2: D38N and pc-3: E34K. Image of PDB ID: 3bdn (Stayrook et al. 2008) created with Protein Workshop (Moreland et al. 2005), http://www.pdb.org
LacI control of transcription from promoter PS
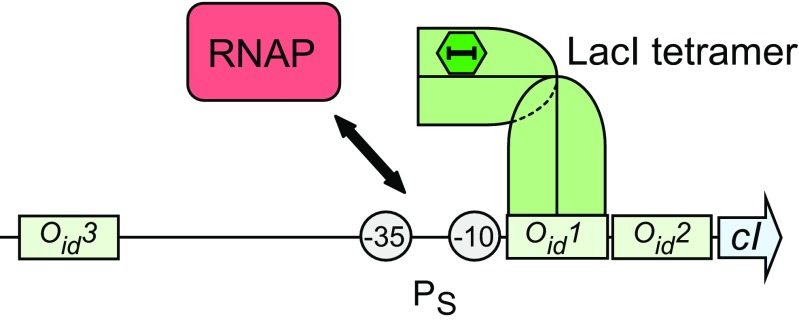
The synthetic promoter PS is the site of transcription initiation for the cI gene on plasmid pSX 100cI (Fig. 3). Repression of transcription from PS is achieved by the appropriate placement of three identical ideal (palindromic) LacI operators, Oid1, Oid2 and Oid3. A constant level of LacI (100 to 200 molecules) is present in the system from a separate plasmid. Two positions of LacI are important: bound to Oid1, LacI sterically hinders RNAP from binding to PS (Schlax et al. 1995); or bound to Oid2, too distant to sterically hinder RNAP from binding to PS, LacI, instead, increases the frequency of abortive initiation from PS (Lopez et al. 1998; Hao et al. 2014). A further repression mechanism is the formation of looped DNA complexes, whereby LacI simultaneously occupies Oid3 and either Oid1 or Oid2, thereby excluding RNAP from PS (Law et al. 1993; Müller et al. 1996).
Fig. 3.
LacI repression of transcription from synthetic promoter PS. Our modelling was based on the following proposed operation of the PS control region: LacI, bound to operator Oid1 by its IPTG-free dimeric-half, sterically hinders RNAP from binding to PS, and vice versa. LacI, bound to Oid2, reduces the initiation rate constant of RNAP by destabilising the elongating RNAP. LacI can form looped complexes by simultaneously binding to Oid3 and either Oid1 or Oid2, inhibiting RNAP from binding to the promoter. IPTG induces CI expression by binding LacI and effecting an allosteric transition that greatly reduces the ability of LacI to bind its operators. The midpoint of Oid3 is 83 base pairs upstream of the midpoint of Oid1, while Oid1 and Oid2 are separated by 24 bp, centre to centre
The addition of IPTG to the bacterial culture induces cI expression by binding to LacI, effecting an allosteric transition that greatly reduces LacI’s affinity for wild-type operator (O’Gorman et al. 1980; Lewis et al. 1996) and also, it is assumed, for ideal operator, Oid. Consequently, as the amount of IPTG in the culture medium is increased, repression by LacI is reduced, and precise increases in CI expression are achieved.
Because of the structure of the LacI tetramer—two distinct dimeric-halves joined by a four helical coil structure (Lewis et al. 1996)—it was reasoned that an IPTG molecule would only incapacitate that dimeric-half of the LacI tetramer to which it was directly bound. It follows that a second IPTG molecule, bound to the same dimeric-half, would not affect the molecule further; however, if it were bound to the other dimeric-half, it would complete the incapacitation of the LacI tetramer. This mechanism fits the observation that approximately two molecules of IPTG per LacI tetramer are required to inactivate LacI’s ability to bind to operator DNA (O’Gorman et al. 1980).
Kolkhof and Müller-Hill used an E. coli strain with the wild-type lac operon deleted. Consequent absence of the lac permease gene prevented intracellular accumulation of IPTG, providing assurance that the intracellular IPTG concentration equalled the concentration in the culture medium.
CI control of transcription from promoter PRM
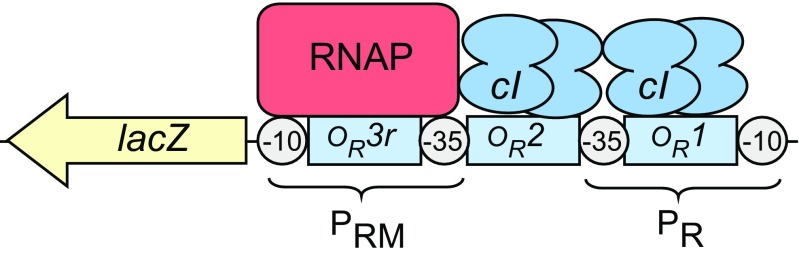
The promoter for repressor maintenance, PRM, is the site of transcription initiation for the β-galactosidase reporter gene, lacZ, inserted in the E. coli chromosome (Fig. 4). CI dimer has the dual ability to both activate and repress transcription from PRM: bound at OR2, immediately adjacent to PRM-bound RNAP, it activates transcription; bound at OR3, positioned between the -10 and -35 PRM regions, it represses transcription. Here, OR3 (renamed OR3r) bears the double mutation (r3r1), with the aim of reducing CI binding to this operator (Kolkhof and Müller-Hill 1994). The degree of this reduction was investigated in the present study, assuming that the positive cooperativity between CI dimer binding at OR2 and OR3r remained unchanged. The focus of the Kolkhof and Müller-Hill study was to qualitatively characterise the three positive-control CI mutants (pc-1, pc-2 and pc-3) in terms of their changed activation and repression abilities.
Fig. 4.
CI control of transcription from promoter PRM. Our modelling was based on the standard alternate pairwise mechanism of CI binding to the PRM control region (Shea and Ackers 1985; Ptashne 2004), where CI dimers are bound cooperatively at operators OR1 and OR2, and a CI dimer bound at OR2 activates transcription from PRM. CI bound to OR3 excludes RNAP from PRM and vice versa. Note that, in the Kolkhof and Muller-Hill system, the LacZ reporter gene has been placed downstream of PRM and that OR3 (here named OR3r) has two mutated base pairs (r3r1) which reduce CI binding (Kolkhof and Müller-Hill 1994)
To measure the β-galactosidase output of their E. coli cells, Kolkhof and Müller-Hill used the assay from Miller (1972), where exponential growth occurs in aerated minimal media consisting principally of glucose and inorganic salts (see Model variables below for the exact composition), with the pH adjusted to 7.0 and the temperature maintained at 37 °C. The basis of reproducibility for the β-galactosidase assay is the maintenance of exponential growth conditions, allowing all cellular expression to be considered to be at steady state. This greatly facilitates modelling: the differential equations describing gene expression can be simply converted to the algebraic counterparts that pertain under steady-state conditions, as explained in the following section.
Mathematical model of the expression system
The computer simulations of the Kolkhof and Müller-Hill expression system were carried out with freely available JSim software (NSR Physiome Project, RRID:SCR_007379, http://www.physiome.org/jsim/). For the purposes of the exploratory modelling described here, fitting of simulated curves to observed data by manual changes of parameters was sufficient. Below is a description of the model variables and parameters, and a complete derivation of the model equations, grouped into two divisions based on the transcription control regions PS and PRM.
Preliminaries
β-Galactosidase assay
In order to utilise the Kolkhof and Müller-Hill data, it was necessary to convert the reported β-galactosidase production from specific activity units to concentration. For this, the estimate of 13.3 monomers of β-galactosidase per specific activity unit (Kolkhof and Müller-Hill 1994) was used. Now, the dimensions of the average E. coli cell (1 μm wide by 2 μm in length) (Neidhardt et al. 1990) are such that the number of intracellular molecules directly equates with nanomolar concentration. Thus, an observed specific activity of 80 units of β-galactosidase equals 80 times 13.3; that is, 1064 monomers per cell of β-galactosidase, which is 1.064 μM. Similarly, protein concentrations were directly converted from average numbers in a cell to nM concentration; thus, 95 molecules was 95 nM. However, as will be discussed shortly, in the case of large molecules such as proteins, allowances have to be made not only for self-assembly into larger molecules, but also for crowding effects that reduce the internal volume of the cell that is accessible to the large molecules.
In the absence of an observed doubling time under the β-galactosidase assay conditions in the Kolkhof and Müller-Hill report, a value of 40 min was assumed. (The validity of this assumption was examined. See Product of parameters.) This and similar decisions were made with reference to the literature (Richey et al. 1987; Neidhardt et al. 1990; Cayley et al. 1991; Bremer and Dennis 1996). No explicit allowances for differences between E. coli strains B/r and K-12 have been made.
Model variables
The input variable in the model is the total concentration of IPTG, and the output variable is the total concentration of β-galactosidase, as per Kolkhof and Müller-Hill’s data (Kolkhof and Müller-Hill 1994). Initially, the free concentration of IPTG was used as the input variable in the model, with bound and total IPTG subsequently calculated. However, as there proved to be no significant difference between free and total IPTG, the latter has been utilised as the input variable, a situation more convenient for plotting the fit between simulated and observed data. Interim variables in the model were the free concentrations of RNAP, LacI and CI.
RNAP, the central molecule in transcription, has an estimated population of about 3000 viable molecules in the average cell, with only 1 % free in solution, and the other 99 % either engaged in transcription or bound non-specifically (McClure 1983, 1985). The effective concentration of RNAP, [P]eff, is the product of the free concentration, [P], and the activity parameter, γP, due to macromolecular crowding. Cayley et al. (1991) have determined theoretical values for the activity coefficient of RNAP as a function of the total concentration of protein plus RNA within the cell, a concentration that they experimentally demonstrated to be a function of the osmolarity of the culture medium (i.e. the total concentration of dissociated species). The major species in the β-galactosidase assay medium are 22 mM glucose {1}, 60 mM K2HPO4 {3}, 33 mM KH2PO4 {2} and 7.6 mM (NH4)2SO4 {3} (Miller 1972, 1992), where the numbers in curly brackets represent the number of species into which the compound dissociates. Of these species, K2HPO4 has the most significant deviation from ideality: at 60 mM, K2HPO4 has a non-ideal osmolarity of 140 mOsM (Wolf and Brown 1966). Assuming that this complex mixture behaves as the sum of its components, the total osmolarity is approximately 250 mOsM. At this osmolarity, the crowded intracellular environment of 275 mg/ml protein plus RNA, in an average aggregation state of 2.5, has been estimated to give RNAP an activity coefficient (γP) of 100 (Cayley et al. 1991).
That activity coefficient of 100 is the number pertinent to the simulations. Thus, the effective concentration of RNAP, [P]eff, is 100 times 30 nM, i.e. 3000 nM. Note that the two effects, DNA binding and molecular crowding, have, here, compensated for each other exactly.
A constant total level of LacI (100 to 200 molecules, modelled as 150 molecules) was present in the Kolkhof and Müller-Hill system from a separate plasmid. A major effort was made to calculate the free concentration of LacI, resolved below as the solution of a cubic equation. This resolution was only possible because a number of simplifications could be made for LacI. Given its high tetramerisation constant (∼1011 M−1) (Levandoski et al. 1996), all LacI monomers were considered to be assembled into tetramers. Also, it has been calculated for LacI tetramers that the increased activity due to macromolecular crowding is sufficient to compensate for the dilution of free molecules due to non-specific binding (Law et al. 1993): non-specific binding reduces the free concentration to approximately 10 % of the total concentration, while macromolecular crowding results in activity coefficients ranging from 8 to 35, to produce an effective free concentration approximately equal to the total concentration. While being aware that this range for the activity coefficients was calculated for an 0.1 OsM culture medium, it was considered that the slight (5 %) decrease in cell volume given a 0.25 OsM medium (Cayley et al. 1991) would not significantly affect this range. Again this produces the situation, in this case for LacI, where non-specific binding and crowding have exactly compensatory effects.
Because CI dimer has to reach a reasonable concentration before it can successfully compete with RNAP for the OR2::PR::OR1 region (Fig. 4), the approximations were made that, first, the processes of dimerisation, non-operator binding and macromolecular crowding could be considered separately from operator binding, and, second, the effective concentration of CI dimer, determined to exist free from non-operator binding, equalled the effective free concentration relevant to operator binding. In these calculations, the activity parameter for the CI dimer was taken as 8, the low end of the scale just mentioned for the larger LacI tetramer (Law et al. 1993).
Model parameters
The complete set of parameters used in the model is listed in Tables 1 and 2. Some parameters have determined error limits; some are better described as best guesses. While acknowledging the difficulty of recreating the intracellular environment in vitro (Record et al. 1998), this study focused on parameters collected under conditions commonly assumed to mimic the in vivo situation: 200 mM KCl, 2.5 mM MgCl2, 100 μg/mL BSA, pH 7.0 and 37 °C (Koblan and Ackers 1992). Of course, particular experimental demands may have dictated the inclusion of components at concentrations not found in the cytoplasm: for example, quantitative DNase footprint titrations require the addition of 1.0 mM CaCl2 for nuclease activity (Koblan and Ackers 1992). Whether this affects the equilibrium binding of CI to operator is unresolved.
Table 1.
Model parameters for the expression system incorporating wild-type CI
| Parameter | Definition | Valuea | Sensitivityb (σ) | Comments and sources |
|---|---|---|---|---|
| A. Fitted | ||||
| K IL | IPTG-LacI association constant | 0.48 × 10−3 nM−1 | Close to 20 °C value of 0.67 × 10−3 nM−1(Chen et al. 1994) | |
| K 3r | CI-OR3r association constant | 0.001–0.005 nM−1 | plat. | Compare with K 3 below |
| K PS | RNAP-PS association constant | 0.05 nM−1 | 1.0 | Weak promoter (McClure 1983) |
| B. PS control region | ||||
| (i) General parameters | ||||
| [X]tot | pSX 100cI total concentration | 20 nM | 1.1 | (Miller 1992) |
| F | β-Galactosidase conversion factor | 13.3 monomers (spec. activity unit)−1 | 1.5 | (Kolkhof and Müller-Hill 1994) |
| (ii) RNAP parameters | ||||
| γR | RNAP activity coefficient | 100 | 0.8 | (Cayley et al. 1991) |
| [P] | RNAP free concentration | 30 nM | 0.8 | (McClure 1983, 1985) |
| (iii) LacI parameters | ||||
| α LacI | LacI transcriptional activation param. | 0.0064 | 1.1 | Sect. Kinetic cooperativity parameter, αLacI |
| ΛLO | LacI looping param. | 103 | 1.0 | (Müller et al. 1996) |
| K LO | LacI-Oid association constant | 100 nM−1 | 0.7 | (Frank et al. 1997) |
| [L] tot | LacI total concentration | 150 nM | 0.55 | (Kolkhof and Müller-Hill 1994) |
| C. PRM control region | ||||
| (i) RNAP parameters | ||||
| K PRM | RNAP-PRM association constant | 0.013 nM−1 | 1.0 plat. | (McClure 1983; Li et al. 1997) |
| K PR | RNAP-PR association constant | 0.65 nM−1 | 0.8 | (McClure 1983; Shea and Ackers 1985) |
| (ii) CI parametersc | ||||
| α CI | CI transcriptional activation param. | 5.3 | n.a. | Sect. Kinetic cooperativity factor, αCI |
| γ CI | CI activity param. | 8 | 1.05 | Sect. Model variables |
| ω 12 | CI-OR1::CI-OR2 cooperativity param. | 80 ± 30 | 1.25 plat. | (Koblan and Ackers 1992) |
| ω 23 | CI-OR2::CI-OR3 cooperativity param. | 110 ± 50 | 1.05 | (Koblan and Ackers 1992) |
| ω 123 | CI-OR1::CI-OR2::CI-OR3 coop. param. | 80 ± 30 | 1.0 plat. | (Koblan and Ackers 1992) |
| K 1 | CI-OR1 association constant | 0.65 ± 0.30 nM−1 | 1.2 | (Koblan and Ackers 1992) |
| K 2 | CI-OR2 association constant | 0.025 ± 0.009 nM−1 | 1.2 | (Koblan and Ackers 1992) |
| K 3 | CI-OR3 association constant | 0.005 ± 0.003 nM−1 | n. a. | (Koblan and Ackers 1992) |
| K dim | CI dimerisation constant | 0.057 ± 0.02 nM−1 | 1.01 | (Koblan and Ackers 1991) |
aFor management of computational rounding errors, all association constants have been expressed in nM−1 (i.e. 109 M−1). See Model parameters for a comment on the solution conditions. Conversion factors used: one molecule per cell = 1nM and K = exp(−ΔG/(RT)), where RT = 0.616 kcal mol−1 at 37 °C. Error limits, if shown, are 67 % confidence intervals
bFactor by which the best-fit K IL is modified upon halving the given parameter: for example, if K LO is halved to 50 nM−1, then K IL had to be changed to 0.39 × 10−3 nM−1 to restore the data fit. plat., affects upper plateau region of curve. n.a., not applicable
cFor parameters relating to CI-non-operator binding, see Concentration of free CI dimer
Table 2.
Fitted association constants for positive-control mutants binding to OR3ra
| PC | Mutation | K3r |
|---|---|---|
| pc-1 | G43R | 0.075 nM−1 |
| pc-2 | D38N | 0.005 nM−1 |
| pc-3 | E34K | 2.5 nM−1 |
aαCI set equal to 1, other parameters from Table 1 assumed constant
In the following mathematical description of the model, it is shown that the required products of a number of parameters are incorporated in the asymptotes of the Kolkhof and Müller-Hill data curves. That analysis notes that allowance for background transcription is achieved by relatively small shifts in data points. Finally, we employ a simple procedure for testing parameter sensitivity, namely simulating the effect on the data fit of halving the value of any given parameter.
General equation for gene expression
The differential equation for the total concentration of protein monomers, [protein]tot, produced by a gene can be stated in general terms as:
| 1 |
Here, k in and k deg are the rate constants for transcription initiation and protein degradation, respectively, in E. coli cells expanding with a rate constant of k vol. There are A viable protein monomers translated per mRNA. Implicit in this equation is the assumption that transcription initiation is much slower than detachment of the RNAP from the promoter (Hawley and Mcclure 1982), whereupon the concentration of RNAP bound to promoter, [P prom], is at equilibrium.
The β-galactosidase assay (Miller 1972) used by Kolkhof and Müller-Hill is a standard procedure undertaken with a population of E. coli cells in an exponential growth phase, thereby producing proteins at a steady-state (subscript ss) level; that is, for any protein in the cell, d[protein]tot,ss/dt = 0. Thus, Eq. (1) becomes:
| 2 |
establishing the important point that protein concentration is directly proportional to the concentration of promoter-bound RNAP, [P prom].
Model equations and parameters for the PS control region
Equation for CI production
Expression of the cI gene follows upon the binding of RNAP to promoter PS, with the level of expression controlled by LacI binding to its three ideal operator sites, Oid1, Oid2 and Oid3 (Fig. 3; Supplementary Material Equation Set 1.2). In the form of Eq. (2), we have:
| 3 |
where the fractional saturation of PS by RNAP takes two forms: 〈P PS〉1, with no LacI bound adjacently on Oid2, and 〈P PS〉2, with LacI bound adjacently on Oid2, reducing the initiation rate constant k PS by a kinetic cooperativity factor α LacI, via the mechanism of destabilisation of RNAP processivity (Lopez et al. 1998; Hao et al. 2014); [X]tot is the total number of pSX 100cI plasmids; and A cI is the total number of active CI monomers translated per mRNA.
Product of parameters
To determine the parameters required in Eq. (3), results from Kolkhof and Müller-Hill pertaining to an interim plasmid constructed to test the expression range of the pSX-type plasmid were used. That interim plasmid had a β-galactosidase gene where the cI gene was later inserted. With 10−2 M IPTG present in the culture, a concentration sufficient to inactivate all LacI (present at a constant concentration, i q, of 100 nM), the interim plasmid produced 300 units of specific β-galactosidase activity. With all LacI inactivated, RNAP saturates PS (given an association constant KPS > 10−2 nM−1, see Table 1), i.e. <PPS>1 = 1 and <PPS>2 = 0. Substituting these values in Eq. (3) gives as the product of the various parameters:
| 4 |
Here, a conversion factor F converts total monomers of β-galactosidase into specific activity: Kolkhof and Müller-Hill give this factor as 13.3 monomers per specific activity unit. There is an implicit assumption that all active β-galactosidase monomers are assembled into active tetramers, a reasonable assumption given the obviously high tetramerisation constant (Craven et al. 1965). The further assumption has been made that the number of active CI monomers and active β-galactosidase monomers translated per respective mRNA are equal, i.e. A cI = A βgal.
Equation (4) can be tested by inserting some common values for these parameters: k PS = 2 × 10−3 (mRNA) s−1 plasmid−1 (McClure 1983, 1985); k deg << k vol (assumed); k vol = ln 2/(2400 s) = 2.9 × 10−4 s−1 (for a doubling time of 40 min); [X]tot = 20 plasmids cell−1 (for plasmids derived from pBR322 (Miller 1992)); and Aβgal = 30 (βgal monomers) (mRNA)−1 (Neidhardt et al. 1990). With these estimates, Eq. (4) produces a β-galactosidase value of about 300 units of specific activity, understood as being per cell (Miller 1972, 1992), validating the use of 40 min for the doubling time. Importantly, Eq. (4) implicitly incorporates such factors, giving a value for the coupled total of the parameters required for Eq. (3), thus negating the need for an exact value for each parameter.
Kinetic cooperativity parameter, αLacI
The value of the kinetic cooperativity parameter, αLacI, was determined from the observed 125-fold increase (J) in transcription for the interim plasmid with 10−2 M IPTG present in the culture media compared to the situation with no IPTG present (Kolkhof and Müller-Hill 1994). Repeating, that with 10−2 M IPTG present, it is expected that all LacI will be inactivated, giving <PPS>1,βmax = 1 and <PPS>2,βmax = 0. By comparison, with no IPTG present, all RNAP at PS is expected to have a LacI tetramer positioned adjacently at Oid2; that is, <PPS>1,βmin = 0 and <PPS>2,βmin = 1. Note that using the binding constants and effective cellular concentrations for RNAP and LacI given in Table 1, and the binding model given in Supplementary Material Equation Set 1.2, it follows that: (i) RNAP can effectively compete with LacI for the overlapping PS::Oid1 region and (ii) the strong operators Oid2 and Oid3 are saturated with separate LacI tetramers, rather than looped structures.
Inserting these two sets of values in Eq. (3), and taking the ratio, demonstrates that αLacI equals the inverse of J: a simple determination of this critical kinetic cooperativity parameter, Kolkhof and Müller-Hill’s report of J as 125-fold (Kolkhof and Müller-Hill 1994), changes to a higher value if allowance is made for background transcription (Whipple et al. 1997). Positing a value of 0.5 units for this (c.f. the value of 3 for the chromosomal PRM region) adjusts the β-galactosidase range for the interim plasmid to become 1.9 to 299.5 units; hence, the ratio, J, changes to 160.
Concentration of free LacI tetramer
Determining the free concentration of the control protein LacI required consideration of the various complexes that form between IPTG (I), LacI (L), RNA polymerase (P) and plasmid pSX 100cI (X). The mass balance equations relevant to these complexes are:
| 5a |
| 5b |
| 5c |
| 5d |
The total concentration of each species is shown as the sum of its free concentration (written as square brackets with no subscript) and the concentration complexed with other species (bold and underlined to indicate multiple species).
The four mass balance equations to be solved can be reduced to two, by making the simplifications that the free concentration of RNAP, [P], is constant and that the free IPTG concentration, [I], equals the total IPTG concentration, [I]tot. The equations remaining to be solved are Eqs. (5b) and (5d), the equations for [L]tot and [X]tot, respectively. These can be combined into a single cubic equation as shown below.
Equations Sets 1.1 to 1.4 (Supplementary Material) give the expansions for each of the terms in Eqs. (5b) and (5d), as well as the factors contributing to the numerical statistical coefficients. Note that in the cartoons, the id subscripts have been dropped from the operator abbreviations for economy of space.
Consider the equation for [L]tot, Eq. (5b). From Equation Set 1.1 (Supplementary Material), we have:
| 6a |
where:
| 6b |
K IL is the equilibrium constant for the binding of IPTG to LacI. Here, succinctness reflects binding symmetry: ΨIL is the partition function describing the binding of IPTG to the four available sites on LacI, given that they are equal and independent (O’Gorman et al. 1980), and expansion gives the statistical terms (4, 6, 4 and 1) corresponding to the number of different ways of attaching from one to four IPTG molecules.
Next, consider the remaining terms in Eq. (5b). Using Equation Sets 1.2, 1.3 and 1.4 (Supplementary Material), we obtain:
| 7a |
| 7b |
| 7c |
| 7d |
Here, K LO is the equilibrium constant describing the binding of LacI to operator Oid; ΛLO is the cooperativity parameter for the looped complex; and K PS is the equilibrium constant describing the binding of RNAP to PS.
By substituting these equations into Eq. (5b) and further collection of terms, we obtain a substantial simplification, namely:
| 8a |
where:
| 8b |
| 8c |
In using Eqs. (8b) and (8c) in the computer simulations, [P] was replaced by [P]eff, the effective concentration due to molecular crowding.
Similarly, we determine that Eq. (5d) becomes:
| 9a |
where:
| 9b |
and b and c are as given in Eqs. (8b) and (8c), respectively. Rearranging, we have:
| 10 |
Substituting Eq. (10) into Eq. (8a), the system to be solved reduces from two equations in terms of [L] and [X] to a single cubic equation in terms of [L]:
| 11a |
with:
| 11b |
| 11c |
| 11d |
Of the three possible solutions to this cubic equation, the appropriate solution (checked by simulation) is (Wang 1995):
| 12a |
using:
| 12b |
| 12c |
| 12d |
| 12e |
Hence, we have determined the concentration of free LacI, [L], as a function of [IPTG]tot, [X]tot, [L]tot and the appropriate binding parameters (Table 1).
Concentration of species formed on the PS control region
Knowledge of [L] allows the determination of 〈PPS〉, the fractional saturation of promoter PS by RNAP with attendant complexes, as required in Eq. (3). For situation 1, no LacI present on Oid2, we have:
| 13a |
where from Equation Set 1.2 (Supplementary Material):
| 13b |
and from Equation Sets 1.2 and 1.4 (Supplementary Material):
| 13c |
The factor 0.5 arises because we are concerned with species where LacI is bound at Oid3, with Oid2 vacant. Others attempting to replicate these simulations may argue that this consideration of the LacI species bound at Oid3 merely introduces terms in the numerator and denominator of Eq. (13a) that subsequently cancel. The present thesis is that that would be the case but for the existence of the looped DNA species: because the model incorporates species whereby LacI simultaneously occupied Oid3 and either Oid1 or Oid2 ( in Equation Set 1.2; Supplementary Material), it was necessary to consider all possible LacI species bound at Oid3.
For situation 2, LacI present on Oid2, resulting in abortive initiations, the pertinent expression is:
| 14a |
where:
| 14b |
The G term arises because now we are concerned with species where LacI is bound at Oid2, but not at Oid3. All of the terms in H are detailed in Equation Sets 1.2 and 1.4 (Supplementary Material). The main convenience of using fractional saturation of promoter is evident from substituting Eq. (9) for [X]tot in Eqs. (13a) and (14a): the [X] term cancels.
The values for the fractional saturation of promoter PS, namely <P PS>1 and <P PS>2, that we have here calculated, when substituted in Eq. (3), determine the amount of CI produced by plasmid pSX 100cI. In turn, CI controls expression from the promoter PRM inserted in the E. coli chromosome, as mathematically detailed in the next section.
Model equations and parameters for the PRM control region
Expression of the β-galactosidase reporter gene, lacZ, follows upon binding of RNAP to PRM, with activation of expression occurring when CI dimer is bound adjacently at OR2. Because the dimeric form of CI is the form active in OR binding, calculation of CI’s monomer–dimer distribution was required. Also, in order to investigate the postulate that the pc-3 mutant exhibits greatly increased non-operator binding (Nelson and Sauer 1985; Whipple et al. 1997), the model incorporates equations describing both binding by CI dimers to non-specific DNA and compensatory crowding of CI dimers by the cell’s macromolecular population.
β-Galactosidase production
In the form of Eq. (2), the equation for β-galactosidase production, [βgal]tot, is (Shea and Ackers 1985):
| 15 |
Here, k PRM is the kinetic rate constant for transcription initiation from PRM. The <P PRM>1 term represents the fractional saturation of PRM by RNAP with CI bound adjacently at OR2 (Fig. 4), resulting in the activation of transcription by the kinetic cooperativity factor, α CI. Non-activated transcription is represented as <PPRM>2. [D]tot is the total concentration of PRM control regions, taken as being equal to 2.13, the number of chromosomes in the average cell, given a doubling time of 40 min (Bremer and Dennis 1996). The factor F interconverts β-galactosidase monomers and activity units: each unit of special activity is equivalent to 13.3 monomers of β-galactosidase per bacterial cell (Kolkhof and Müller-Hill 1994).
Coupled parameters
Kolkhof and Müller-Hill provided results from a control expression system where the cI gene had been removed (ΔcI) (Kolkhof and Müller-Hill 1994). In this case with <PPRM>1 = 0 and <PPRM>2 = 1, the coupled parameters in Eq. (15) are determined as:
| 16 |
For this system, β-galactosidase expression, [β-gal]ΔcI, remained relatively constant at 21 units of specific activity per cell, across the complete range of IPTG concentrations. Taking the chromosomal background transcription as 3 (the lower asymptotic limit for pc-3 in Fig. 7c) gives us a corrected value of [β-gal]ΔcI as 18, the value used in the simulations.
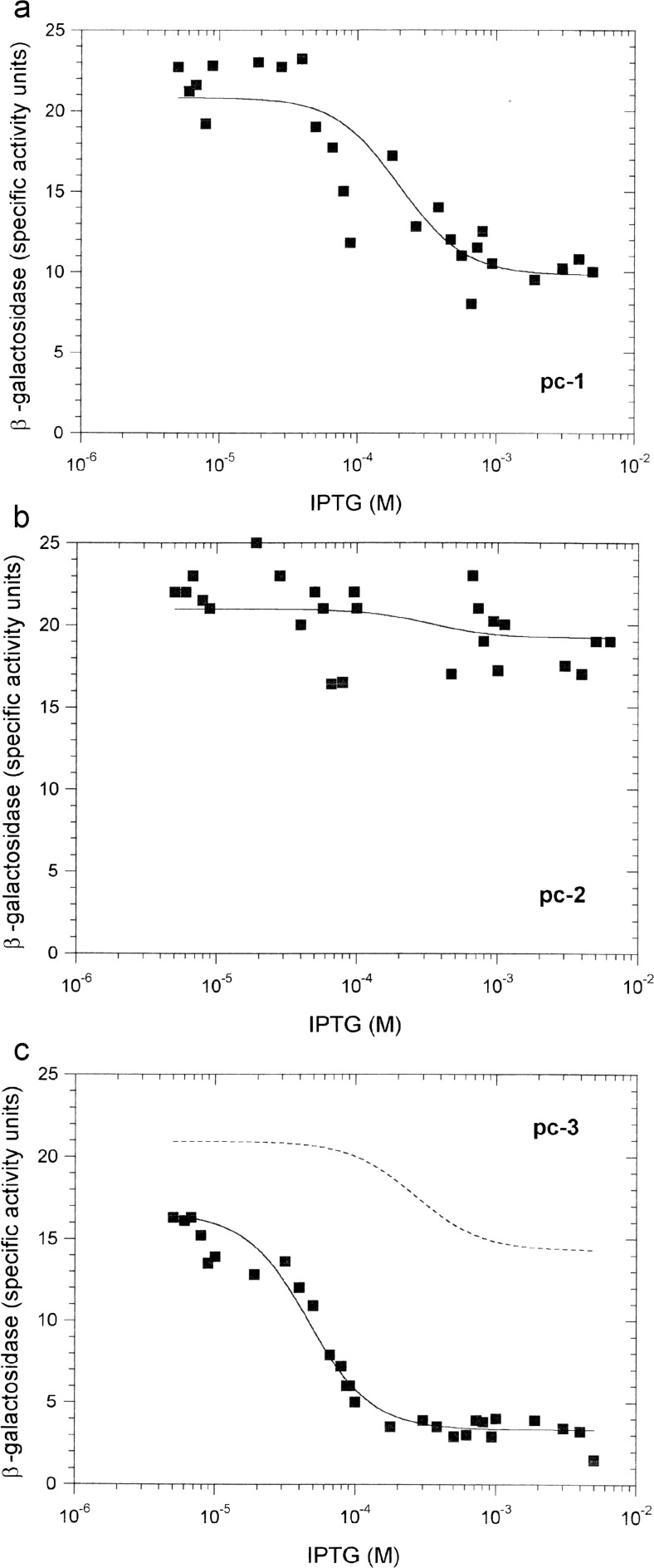
Fig. 7.
Fit of the effect of increasing amounts of the CI pc mutants on PRM-lacZ activity. Note the change in scale of the ordinate axis here compared to Figs. 5 and 6. a CI pc-1. The solid line was obtained by setting αCI = 1 and K 3r = 75 μM−1. b CI pc-2. The solid line was obtained by setting αCI = 1 and K 3r = 5.0 μM−1. c CI pc-3. The solid line was obtained by setting αCI = 1 and K 3r = 2.5 nM−1. The dashed line illustrates the effect of also increasing K ns, the CI-non-specific DNA binding constant, 100-fold. In a–c, other parameters were as given in Table 1
This product can be checked by inserting in Eq. (16) the parameter values given in Product of parameters for the PS promoter, with the following changes: k PRM varies from 0.7 × 10−3 (Hawley and Mcclure 1982) to 5 × 10−3 mRNA s−1 chromosome−1 (with potassium glutamate in the medium) (Li et al. 1997) and [D]tot = 2.13 chromosomes (given a 40-min doubling time) (Neidhardt et al. 1990; Bremer and Dennis 1996). These values result in a range for [β-gal]ΔcI of 12 to 83, so 18 is at the lower end of that range. Equation (16), by providing the product of the parameters in Eq. (15), avoids the need to ascertain individual values for each of those parameters.
Kinetic cooperativity factor, αCI
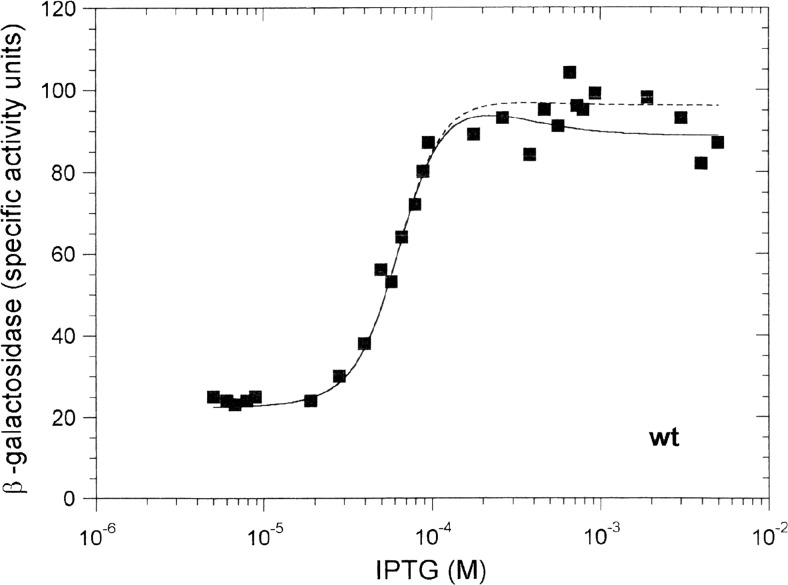
The asymptotic expression levels for the wild-type cI system, observed in Fig. 5, can be used to determine the value of αCI. There, allowing for background transcription of 3 units (the lower asymptotic limit in Fig. 7c), the ratio of maximal to minimal expression is (100 − 3)/(24 − 3), equalling 4.6. Maximal lacZ expression is observed when CI saturates OR2, at which point simulation demonstrates that <PPRM>1 ≈ 0.88 and <PPRM>2 ≈ 0; minimal lacZ expression is observed when cI expression from pSX 100cI is repressed, at which point <PPRM>1 ≈ 0 and < PPRM>2 ≈ 0.98, using K PRM = 0.013 nM−1 (Table 1). Inserting these two sets of values for fractional saturation in Eq. (15) and taking the ratio gives αCI equal to 5.3.
Fig. 5.
Fit of the effect of increasing amounts of wild-type CI on PRM-lacZ activity. The solid line was obtained by setting K IL = 0.48 μM−1, and K 3r = 5.0 μM−1, equal to K 3. The dashed line was obtained by setting K IL = 0.48 μM−1 and K 3r = 1.0 μM−1. Other parameters were as given in Table 1. The data points here and in subsequent figures are taken from Kolkhof and Müller-Hill (1994)
Concentration of free CI dimer
CI dimer (R) binds to both operator and non-operator sites. Even though non-operator binding is orders of magnitude weaker than operator binding, it achieves significance because of the large number of such sites. CI dimer binds to 20 base pairs of non-operator DNA with a binding constant of about 105 M−1 at 20 °C (Pray et al. 1998), which, following the trend observed for operator binding (Record et al. 1998), is expected to decrease to about 104 M−1 at 37 °C.
The number of non-specific DNA binding sites in a cell has be estimated in various ways. In the protein–nucleic acid interaction field, this number is often estimated on the assumption that every nucleotide on both strands can be the first nucleotide of a non-specific site, such that one E. coli chromosome has around 9 million non-specific sites, regardless of the length of the specific site. Some non-specific sites will be more operator-like than others, and so giving a range of possible ‘non-specific’ binding constants, anywhere from 102 M−1 to 106 M−1. On this basis, it can be calculated that, at any instant, all CI is non-specifically bound and must find its specific operator by transient dissociation and reassociation elsewhere. Hence, an attempt to estimate non-specific binding gives rise to an ‘effective’ value, reflecting a redefined ‘concentration’ of the mobile fraction of the protein of interest.
Here, we explicitly consider an extra factor, non-specific competition between CI and the high concentration of other proteins present in the cell. The average E. coli cell, growing in glucose minimal media with a division time of 40 min, has 2.1 chromosomes, each of which are 4.6 × 106 base pairs in length (Neidhardt et al. 1990; Bremer and Dennis 1996). At saturation, we take the average site size as 20 base pairs, giving 4.2 × 105 non-specific sites. In binding to these non-specific sites, CI dimer has to compete with the cellular population of 1.2 × 106 proteins (in dimer units) (Neidhardt et al. 1990), which, given a binding constant of between 102 to 103 M−1, and an activity parameter of 5 due to crowding considerations, would occupy from 20 to 70 % of the non-specific sites. Taking this figure as 50 % leaves approximately 2.1 × 105 non-specific sites available for CI dimer binding, [nsDNA]avail.
The two processes of assembly and non-specific (ns) binding occur simultaneously, in accordance with the reactions:
| 17a |
| 17b |
where R is CI dimer and R ns is CI dimer complexed with non-specific DNA.
Here, the respective equilibrium constants are:
| 18a |
| 18b |
where γ CI is the CI dimer’s activity parameter due to macromolecular crowding. The crowding parameters for non-specific DNA sites, with and without CI dimer bound, have been taken as being equal and, therefore, cancelled. Also, non-specific binding and macromolecular crowding have been assumed to be not significant at the CI monomer level.
The mass balance equations for assembly and non-specific binding are:
| 19a |
| 19b |
where [nsDNA]avail is the available concentration of non-specific DNA sites (≈2.5 × 105 nM, see above). Substitution of Eqs. (18a), (18b) and (19b) into Eq. (19a) gives the following quadratic equation in terms of [CI mon]:
| 20a |
where:
| 20b |
The solution of this quadratic equation gives:
| 21 |
allowing calculation of the free concentration of CI dimers, [R], as:
| 22 |
The appropriate concentration used in the simulations was the effective concentration, [R]eff, equal to γCI [R]. The CI dimer crowding parameter, γCI, was set equal to 8, the bottom of the range estimated for the LacI tetramer (Law et al. 1993).
Concentration of complexes formed in the PRM control region
Having calculated [R]eff, the concentration of complexes that form in the PRM control region can be determined. The fractional saturation of PRM by RNAP, with CI bound adjacently, is:
| 23 |
Here, K PRM is the equilibrium constant describing RNAP binding to promoter PRM; K 1 and K 2 are the equilibrium constants for CI dimer binding to OR1 and OR2, respectively; and ω 12 is the cooperativity parameter describing the changed probability of CI dimer binding to OR2, given that OR1 is already occupied by CI dimer, and vice versa. The total acceptor concentration in Eq. (23) is determined as:
| 24 |
using the terms given in Equation Set 2 (Supplementary Material). Note that the [D] term cancels upon substitution of Eq. (24) into Eq. (23).
The non-activated fraction in Eq. (15) is:
| 25 |
In summary, the total concentration of β-galactosidase, [βgal]tot, produced according to Eq. (15) is a function of the fractional saturation of promoter PRM by RNAP, as calculated using Eqs. (23) and (25).
Overview of model equations
The independent variable of the model is the total concentration of IPTG. The two chief equations of the model, Eqs. (3) and (15), describe CI production and β-galactosidase production, respectively. For both equations, a good estimate of the product of their coupled parameters is given by Eqs. (4) and (16), respectively. Solving Eqs. (3) and (15) involved calculation of the concentrations of the complexes that RNAP forms, in combination with the LacI and CI control proteins, in the PS and PRM control regions, respectively. This required prior calculation of free LacI tetramer concentration, using the cubic formula to solve Eq. (9), and free CI dimer concentration, using the quadratic formula to solve Eq. (20). In summary, the model equations were used to simulate the level of β-galactosidase expected for a given amount of IPTG added and the results are reviewed in the following section.
Simulations using the model equations
The basic approach used to fit the Kolkhof and Müller-Hill data was, first, to simulate the data describing the wild-type CI system, and, then, to vary the minimal number of parameters required to fit the data describing the mutant systems. As illustrated by the error limits for the Koblan and Ackers data (Koblan and Ackers 1991, 1992) in Table 1, given no systematic errors, the highest level of experimental accuracy presently possible is 50 % relative error, using the 67 % confidence interval as the error limits. Consequently, the predictions made below for missing parameters cannot have a greater accuracy: realistically, they should be regarded as order of magnitude predictions.
Fitting of wild-type data
Fitting the wild-type data (Fig. 5) required the determination of three unknown equilibrium constants, K IL, K PS and K 3r. Of these, the value of K IL, the IPTG-LacI equilibrium constant, was found to be of greatest significance, affecting the fit in the steeply rising part of the simulation curve. K IL was fitted as 0.48 μM−1, close to the room temperature value of 0.67 μM−1 (Chen et al. 1994). K PS, the RNAP-PS equilibrium constant, was fitted as 0.05 nM−1, which is at the lower end of the 100-fold range proposed for RNAP operator binding (Bremer and Dennis 1996). The wild-type data fit was found to be insensitive to a 2-fold variation in this value. K 3r, the constant describing CI binding to the mutant operator OR3r, affected the upper plateau region of the curve. A reasonable fit was obtained with values up to 5.0 μM−1 (Fig. 5), compared with 5.0 μM−1 for K 3, the wild-type CI-OR3 binding constant (Koblan and Ackers 1992). However, the value of K 3r is poorly resolved, simply because there is little or no repression of PRM activity at higher CI concentrations (Fig. 5). Indeed, even with the wild-type OR3 operator sequence, PRM is poorly repressed by CI in the absence of looping to the OL region (Dodd et al. 2004; Cui et al. 2013).
Parameter sensitivity
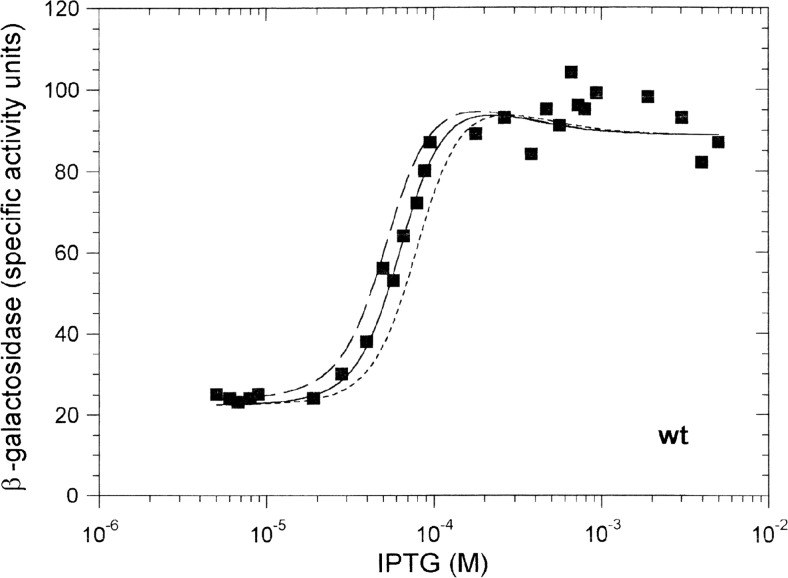
To determine confidence in the predicted value for K IL, a parameter sensitivity test was conducted whereby other parameters were reduced individually to one-half the value listed in Table 1. Then the new value of K IL, required to return the simulated curve to the position of best-fit, was determined. This new value for KIL is shown as some fraction, σ, of the original K IL (σ = new K IL/original K IL, Table 1). An example of this sensitivity procedure is illustrated in Fig. 6, where the effect of halving the value of K PR, the RNAP-PR association constant, is seen to be reversed by reducing K IL from 0.48 to 0.38 μM−1 (i.e. σ = 0.8). As shown in Table 1, the shift away from the best data fit, due a 50 % reduction in any single parameter, could be remedied by a 20 %, or less, change in K IL,, highlighting the central importance of this parameter.
Fig. 6.
Parameter sensitivity in fitting of wild-type CI data. The long dashed line shows the effect of halving K PR (i.e. reduced from 0.65 to 0.325 nM−1). The short dashed line shows the effect of reduction in K IL from 0.48 to 0.38 μM−1. The solid line is the original simulation, shown as coincident with the combined effect of halving K PR and reducing K IL from 0.48 to 0.38 μM−1. Other parameters were as given in Table 1
A number of other points can be made about the sensitivity values (σ) in Table 1. The value of K IL, the IPTG-LacI binding constant, was found to be most sensitive to the value of F, the factor for converting β-galactosidase activity units into the total number of monomers. Also, it was found that the expression system would not be useful for determining K PS, the RNAP-PS binding constant, as the data fit is insensitive to changes in its value. Given well-determined values for K IL and F, the expression system could be used to determine control protein parameters, as illustrated by the following predictions for the CI positive-control mutants.
Simulating mutant data
The CI positive-control (pc) mutants were each characterised in terms of their changed transcription-activation parameter, αCI, and changed pc-OR3r association constant, K 3r (in comparison with the CI-OR3 association constant, K 3). The simplest solution (Table 2) to fitting the CI pc data was, assuming all other parameters being unchanged, first, to set αCI equal to 1 for all mutants and, second, to set K 3r equal to 0.075 nM−1 for the pc-1 system (Fig. 7a), equal to 0.005 nM−1 for the pc-2 system (Fig. 7b) and equal to 2.5 nM−1 for the pc-3 system (Fig. 7c). In good agreement with model predictions, Li et al. (1997) observed that pc-2 has no effect on the basal transcription-initiation rate constant (i.e. αCI = 1 for pc-2), and Nelson and Sauer (1985) found that CI pc-3 binds 600 times more tightly to OR3 than wild-type CI. A further interpretation of Nelson and Sauer (1985) that pc-3 binds 100-fold more tightly to non-operator DNA than wild-type CI, while certainly plausible given the charge change (E to K), could not be substantiated by the model’s simulations; it was found that an increase of this magnitude resulted in a loss of fit to the data (Fig. 7c).
Conclusions and future directions
Here, we have explored the nature of the information needed to develop a comprehensive and biochemically realistic thermodynamic model of a prokaryotic gene expression system. To this end, equations describing LacI control of promoter PS were added to the elements of the pioneering Shea and Ackers’ quantitative model (Shea and Ackers 1985) describing CI control of promoter PRM.
The equations describing the control of PS and PRM are strikingly similar; there are examples of steric hindrance in both regions, and cooperativity terms are used to describe both repression by LacI (negative cooperativity) and activation by CI (positive cooperativity). With LacI, the additional control mechanism requiring mathematical description was the operation of looped DNA structures between widely separated operator sites (Mossing and Record 1986; Schlax et al. 1995; Priest et al. 2014). In the specific system of Kolkhof and Müller-Hill examined here, the distant OL operators required for lambda CI-mediated looping were absent, allowing us to neglect the effect of looping on CI regulation. Their inclusion would have added considerable complexity; Cui et al. developed a statistical mechanical model simulating the influence of CI and RNAP on the lambda OR-OL region, which needed to account for 192 possible species (Cui et al. 2013).
In modelling the action of proteins in the intracellular environment, it is necessary to consider non-specific binding and macromolecular crowding, and make decisions regarding their relative significance. In the case of LacI, non-specific binding and crowding were considered to be approximately compensatory (Law et al. 1993) and, therefore, equations for neither were included, whereas in the case of CI, these two mechanisms were explicitly modelled in order to test the postulate of Nelson and Sauer (1985) that pc-3 exhibits increased non-specific binding in comparison to wild-type CI. Simulations, based on our treatment of non-specific binding, did not support this postulate. It remains possible, however, that with other definitions of K ns, even a 100-fold increase in non-specific affinity may make little difference to the ‘effective’ or ‘mobile’ concentration of CI.
A key aim of any model is to calculate parameters that had not previously been determined. Here, the system incorporating wild-type CI was first simulated in order to determine K IL, the association constant describing binding by IPTG to LacI at 37 °C. It was found to be approximately equal to the value determined at room temperature (presumably 20 °C) (Chen et al. 1994). Note that the equation set includes the notion that LacI bound at an operator, an appropriate distance downstream from the promoter, destabilises the processivity of E. coli RNAP (σ70) enzyme (Schlax et al. 1995; Hao et al. 2014). A simpler model, incorporating only steric exclusion, resulted in a fitted K IL an order of magnitude reduced from the value obtained using the present model.
Second, the systems incorporating positive-control mutants were simulated. The simplest interpretation providing a satisfactory fit to the data is that all positive-control mutants have lost the ability to activate transcription (αCI = 1). This is consistent with the value of PRM activity in the presence of each mutant CI being very similar to basal PRM activities in the absence of CI. Having set that parameter, the association constants for mutated CIs binding to OR3r were adjusted in order to fit their data points. In comparison with the association constant for wild-type CI binding to OR3r, the association constants for the CI pc mutants were determined as being increased for pc-1 and pc-3, and unchanged for pc-2. Structurally, these findings seem reasonable, in that the pc-1 (G43R) and pc-3 (E34K) mutations result in a change to a positively charged amino acid, and their positions (Fig. 2) may allow interaction with the negatively charged DNA backbone. On the other hand, the pc-2 mutation (D38N) results in substitution of an uncharged amino acid such that new electrostatic interactions with the DNA backbone are not possible.
Of course a thermodynamically based mathematical model does not unequivocally allow one to determine if the simplifying assumptions are truly justified, or to exclude alternative mechanistic explanations. However, the benefit of a sufficiently detailed model is that it can generate specific predictions which can then be tested by experiments. For example, the observed repression of PRM activity seen at higher concentrations of CI-pc3 (Fig. 7c) was proposed by (Li et al. 1997) to arise from an unfavourable interaction of CI-pc3 with RNAP, rather than increased affinity of CI-pc3 for the operator DNA. In vitro binding experiments would be required to resolve these alternative mechanistic interpretations.
Our attempt at developing a rigorous, thermodynamically based model described here, while able to satisfactorily describe carefully measured, quantitative in vivo data, also demonstrates the complexities and limitations of this approach. Drawing on perhaps the two most well-characterised systems in prokaryotic biology, and modelling a synthetic expression construct with just four protein (LacI, CI, RNAP and β-galactosidase) and two DNA regulatory (Lac and lambda) components (Fig. 1), it is clear that the equilibria and the equations describing their interaction quickly become complex. Additional factors likely to be present in other systems, such as non-equilibrium (irreversible) events or the presence of multiple transcription factors acting at, for example, a eukaryotic promoter would substantially add to model complexity. Complementary experimental approaches, such as single-cell and single-molecule studies (reviewed by Golding 2016) are proving critical to capturing the stochastic nature of the many cellular interactions which occur at low numbers of molecules. Combined with stochastic (e.g. Hao et al. 2016) and dynamic (e.g. Chen et al. 2014) simulations, these and other tools are essential to provide an ever more complete description of cellular events. Recent developments in synthetic biology, such as automated circuit design (Nielsen et al. 2016), also promise the accelerated development of ever more complex synthetic circuits.
Electronic supplementary material
Equation sets 1 and 2 are given in the Supplementary Material.
Videos showing how to use JSim to run the simulations are available on YouTube: https://goo.gl/KcBIm3.
Equation and data files for the JSim simulations are available in DropBox: https://goo.gl/VQWWgL.
(PDF 324 kb)
Acknowledgements
PDM and KES wish to dedicate this paper to Professor Donald J. Winzor, whose postgraduate supervision gave us the ability to pursue the research presented here. PDM also wishes to acknowledge his gratitude to Gary K. Ackers (deceased), in whose laboratory the majority of this work was undertaken, and to thank Allen P. Minton for the helpful discussions. Initial funding support came from the National Institutes of Health grants GM-39343 and R37GM-24486 to GKA. The work was also supported in part by an Australian Research Council grant (DP160101450) to KES.
Compliance with ethical standards
Conflict of interest
Peter D. Munro declares that he has no conflict of interest. Gary K. Ackers declares that he has no conflict of interest. Keith E. Shearwin declares that he has no conflict of interest.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Footnotes
Gary K. Ackers died May 20, 2011.
This article is part of a Special Issue on ‘Analytical Quantitative Relations in Biochemistry’ edited by Damien Hall and Stephen Harding.
Electronic supplementary material
The online version of this article (doi:10.1007/s12551-016-0231-9) contains supplementary material, which is available to authorized users.
Contributor Information
Peter D. Munro, Phone: +61 7 3255 3515, Email: munro_brisbane@hotmail.com
Keith E. Shearwin, Phone: +61 8 83135361, Email: keith.shearwin@adelaide.edu.au
References
- Bremer H, Dennis PP (1996) Modulation of chemical composition and other parameters of the cell by growth rate. In: Neidhardt FC, Curtiss R, Ingraham JL et al (eds) Escherichia coli and Salmonella: cellular and molecular biology. ASM Press, Washington, DC, pp 1553–1569
- Cayley S, Lewis BA, Guttman HJ, Record MT. Characterization of the cytoplasm of Escherichia coli K-12 as a function of external osmolarity: implications for protein–DNA interactions in vivo. J Mol Biol. 1991;222:281–300. doi: 10.1016/0022-2836(91)90212-O. [DOI] [PubMed] [Google Scholar]
- Chen J, Alberti S, Matthews KS. Wild-type operator binding and altered cooperativity for inducer binding of lac repressor dimer mutant R3. J Biol Chem. 1994;269:12482–12487. [PubMed] [Google Scholar]
- Chen Y-J, Johnson S, Mulligan P, Spakowitz AJ, Phillips R. Modulation of DNA loop lifetimes by the free energy of loop formation. Proc Natl Acad Sci U S A. 2014;111:17396–17401. doi: 10.1073/pnas.1415685111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Craven GR, Steers E, Anfinsen CB. Purification, composition, and molecular weight of the beta-galactosidase of Escherichia Coli K12. J Biol Chem. 1965;240:2468–2477. [PubMed] [Google Scholar]
- Cui L, Murchland I, Shearwin KE, Dodd IB. Enhancer-like long-range transcriptional activation by lambda CI-mediated DNA looping. Proc Natl Acad Sci U S A. 2013;110:2922–2927. doi: 10.1073/pnas.1221322110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dodd IB, Shearwin KE, Perkins AJ, Burr T, Hochschild A, Egan JB. Cooperativity in long-range gene regulation by the lambda CI repressor. Genes Dev. 2004;18:344–354. doi: 10.1101/gad.1167904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank DE, Saecker RM, Bond JP, et al. Thermodynamics of the interactions of Lac repressor with variants of the symmetric Lac operator: effects of converting a consensus site to a non-specific site. J Mol Biol. 1997;267:1186–1206. doi: 10.1006/jmbi.1997.0920. [DOI] [PubMed] [Google Scholar]
- Garcia HG, Phillips R. Quantitative dissection of the simple repression input–output function. Proc Natl Acad Sci U S A. 2011;108:12173–12178. doi: 10.1073/pnas.1015616108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golding I. Single-cell studies of phage λ: hidden treasures under Occam’s rug. Annu Rev Virol. 2016 doi: 10.1146/annurev-virology-110615-042127. [DOI] [PubMed] [Google Scholar]
- Hao N, Krishna S, Ahlgren-Berg A, Cutts EE, Shearwin KE, Dodd IB. Road rules for traffic on DNA—systematic analysis of transcriptional roadblocking in vivo. Nucleic Acids Res. 2014;42:8861–8872. doi: 10.1093/nar/gku627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hao N, Palmer AC, Ahlgren-Berg A, Shearwin KE, Dodd IB. The role of repressor kinetics in relief of transcriptional interference between convergent promoters. Nucleic Acids Res. 2016;44:6625–6638. doi: 10.1093/nar/gkw600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hawley DK, Mcclure WR. Mechanism of activation of transcription initiation from the lambda PRM promoter. J Mol Biol. 1982;157:493–525. doi: 10.1016/0022-2836(82)90473-9. [DOI] [PubMed] [Google Scholar]
- Hensel Z, Feng H, Han B, Hatem C, Wang J, Xiao J. Stochastic expression dynamics of a transcription factor revealed by single-molecule noise analysis. Nat Struct Mol Biol. 2012;19:797–802. doi: 10.1038/nsmb.2336. [DOI] [PubMed] [Google Scholar]
- Jacob F, Monod J. Genetic regulatory mechanisms in the synthesis of proteins. J Mol Biol. 1961;3:318–356. doi: 10.1016/S0022-2836(61)80072-7. [DOI] [PubMed] [Google Scholar]
- Jinek M, Chylinski K, Fonfara I, Hauer M, Doudna JA, Charpentier E. A programmable dual-RNA-guided DNA endonuclease in adaptive bacterial immunity. Science. 2012;337:816–821. doi: 10.1126/science.1225829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J-S. Genome editing comes of age. Nat Protoc. 2016;11:1573–1578. doi: 10.1038/nprot.2016.104. [DOI] [PubMed] [Google Scholar]
- Koblan KS, Ackers GK. Energetics of subunit dimerization in bacteriophage lambda cI repressor: linkage to protons, temperature, and KCl. Biochemistry. 1991;30:7817–7821. doi: 10.1021/bi00245a022. [DOI] [PubMed] [Google Scholar]
- Koblan KS, Ackers GK. Site-specific enthalpic regulation of DNA transcription at bacteriophage lambda OR. Biochemistry. 1992;31:57–65. doi: 10.1021/bi00116a010. [DOI] [PubMed] [Google Scholar]
- Kolkhof P, Müller-Hill B. Lambda cI repressor mutants altered in transcriptional activation. J Mol Biol. 1994;242:23–36. doi: 10.1006/jmbi.1994.1554. [DOI] [PubMed] [Google Scholar]
- Law SM, Bellomy GR, Schlax PJ, Record MT. In vivo thermodynamic analysis of repression with and without looping in lac constructs: estimates of free and local lac repressor concentrations and of physical properties of a region of supercoiled plasmid DNA in vivo. J Mol Biol. 1993;230:161–173. doi: 10.1006/jmbi.1993.1133. [DOI] [PubMed] [Google Scholar]
- Levandoski MM, Tsodikov OV, Frank DE, Melcher SE, Saecker RM, Record TM., Jr Cooperative and anticooperative effects in binding of the first and second plasmid Osym operators to a LacI tetramer: evidence for contributions of non-operator DNA binding by wrapping and looping. J Mol Biol. 1996;260:697–717. doi: 10.1006/jmbi.1996.0431. [DOI] [PubMed] [Google Scholar]
- Lewis M. Allostery and the lac operon. J Mol Biol. 2013;425:2309–2316. doi: 10.1016/j.jmb.2013.03.003. [DOI] [PubMed] [Google Scholar]
- Lewis M, Chang G, Horton NC, Kercher MA. Crystal structure of the lactose operon repressor and its complexes with DNA and inducer. Science. 1996;271:1247–1254. doi: 10.1126/science.271.5253.1247. [DOI] [PubMed] [Google Scholar]
- Lewis D, Le P, Zurla C, Finzi L, Adhya S. Multilevel autoregulation of λ repressor protein CI by DNA looping in vitro. Proc Natl Acad Sci U S A. 2011;108:14807–14812. doi: 10.1073/pnas.1111221108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M, McClure WR, Susskind MM. Changing the mechanism of transcriptional activation by phage lambda repressor. Proc Natl Acad Sci U S A. 1997;94:3691–3696. doi: 10.1073/pnas.94.8.3691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopez PJ, Guillerez J, Sousa R, Dreyfus M. On the mechanism of inhibition of phage T7 RNA polymerase by lac repressor. J Mol Biol. 1998;276:861–875. doi: 10.1006/jmbi.1997.1576. [DOI] [PubMed] [Google Scholar]
- McClure WR. A biochemical analysis of the effect of RNA polymerase concentration on the in vivo control of RNA chain initiation frequency. In: Lennon DLF, Stratman FW, Zahlten RN, editors. Biochemistry of metabolic processes. New York: Elsevier Biomedical; 1983. pp. 207–217. [Google Scholar]
- McClure WR. Mechanism and control of transcription initiation in prokaryotes. Annu Rev Biochem. 1985;54:171–204. doi: 10.1146/annurev.bi.54.070185.001131. [DOI] [PubMed] [Google Scholar]
- Miller JH. Experiments in molecular genetics. Cold Spring Harbor: Cold Spring Harbor Laboratory Press; 1972. [Google Scholar]
- Miller JH. A short course in bacterial genetics. Cold Spring Harbor: Cold Spring Harbor Laboratory Press; 1992. [Google Scholar]
- Moreland JL, Gramada A, Buzko OV, Zhang Q, Bourne PE. The Molecular Biology Toolkit (MBT): a modular platform for developing molecular visualization applications. BMC Bioinf. 2005;6:21. doi: 10.1186/1471-2105-6-21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mossing MC, Record MT. Upstream operators enhance repression of the lac promoter. Science. 1986;233:889–892. doi: 10.1126/science.3090685. [DOI] [PubMed] [Google Scholar]
- Müller J, Oehler S, Müller-Hill B. Repression of lac promoter as a function of distance, phase and quality of an auxiliary lac operator. J Mol Biol. 1996;257:21–29. doi: 10.1006/jmbi.1996.0143. [DOI] [PubMed] [Google Scholar]
- Müller-Hill B (1996) The lac operon: a short history of a genetic paradigm. Walter de Gruyter, Berlin
- Neidhardt FC, Ingraham JL, Schaechter M (1990) Physiology of the bacterial cell. Sinauer Associates, Sunderland
- Nelson HCM, Sauer RT. Lambda repressor mutations that increase the affinity and specificity of operator binding. Cell. 1985;42:549–558. doi: 10.1016/0092-8674(85)90112-6. [DOI] [PubMed] [Google Scholar]
- Nielsen AAK, Der BS, Shin J, et al. Genetic circuit design automation. Science. 2016;352:aac7341. doi: 10.1126/science.aac7341. [DOI] [PubMed] [Google Scholar]
- O’Gorman RB, Rosenberg JM, Kallai OB, et al. Equilibrium binding of inducer to lac repressor.operator DNA complex. J Biol Chem. 1980;255:10107–10114. [PubMed] [Google Scholar]
- Pray TR, Burz DS, Ackers GK. Cooperative non-specific DNA binding by octamerizing lambda cI repressors: a site-specific thermodynamic analysis. J Mol Biol. 1998;282:947–958. doi: 10.1006/jmbi.1998.2056. [DOI] [PubMed] [Google Scholar]
- Priest DG, Cui L, Kumar S, Dunlap DD, Dodd IB, Shearwin KE. Quantitation of the DNA tethering effect in long-range DNA looping in vivo and in vitro using the Lac and λ repressors. Proc Natl Acad Sci U S A. 2014;111:349–354. doi: 10.1073/pnas.1317817111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ptashne M. A genetic switch: phage lambda revisited. Cold Spring Harbor: Cold Spring Harbor Laboratory Press; 2004. [Google Scholar]
- Record MT, Courtenay ES, Cayley S, Guttman HJ. Biophysical compensation mechanisms buffering E. coli protein–nucleic acid interactions against changing environments. Trends Biochem Sci. 1998;23:190–194. doi: 10.1016/S0968-0004(98)01207-9. [DOI] [PubMed] [Google Scholar]
- Révet B, Von Wilcken-Bergmann B, Bessert H, Barker A, Müller-Hill B. Four dimers of λ repressor bound to two suitably spaced pairs of λ operators form octamers and DNA loops over large distances. Curr Biol. 1999;9:151–154. doi: 10.1016/S0960-9822(99)80069-4. [DOI] [PubMed] [Google Scholar]
- Richey B, Cayley DS, Mossing MC, et al. Variability of the intracellular ionic environment of Escherichia coli. Differences between in vitro and in vivo effects of ion concentrations on protein–DNA interactions and gene expression. J Biol Chem. 1987;262:7157–7164. [PubMed] [Google Scholar]
- Schlax PJ, Capp MW, Record MT., Jr Inhibition of transcription initiation by lac repressor. J Mol Biol. 1995;245:331–350. doi: 10.1006/jmbi.1994.0028. [DOI] [PubMed] [Google Scholar]
- Sepúlveda LA, Xu H, Zhang J, Wang M, Golding I. Measurement of gene regulation in individual cells reveals rapid switching between promoter states. Science. 2016;351:1218–1222. doi: 10.1126/science.aad0635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shea MA, Ackers GK. The OR control system of bacteriophage lambda: a physical–chemical model for gene regulation. J Mol Biol. 1985;181:211–230. doi: 10.1016/0022-2836(85)90086-5. [DOI] [PubMed] [Google Scholar]
- Stayrook S, Jaru-Ampornpan P, Ni J, Hochschild A, Lewis M. Crystal structure of the lambda repressor and a model for pairwise cooperative operator binding. Nature. 2008;452:1022–1025. doi: 10.1038/nature06831. [DOI] [PubMed] [Google Scholar]
- Wang Z-X. An exact mathematical expression for describing competitive binding of two different ligands to a protein molecule. FEBS Lett. 1995;360:111–114. doi: 10.1016/0014-5793(95)00062-E. [DOI] [PubMed] [Google Scholar]
- Whipple FW, Ptashne M, Hochschild A. The activation defect of a lambda cI positive control mutant. J Mol Biol. 1997;265:261–265. doi: 10.1006/jmbi.1996.0735. [DOI] [PubMed] [Google Scholar]
- Wolf AV, Brown MG. Concentrative properties of aqueous solutions: conversion tables. In: Weast RC, editor. CRC handbook of physics and chemistry. Cleveland, OH: Chemical Rubber Company; 1966. [Google Scholar]
- Zurla C, Manzo C, Dunlap D, et al. Direct demonstration and quantification of long-range DNA looping by the lambda bacteriophage repressor. Nucleic Acids Res. 2009;37:2789–2795. doi: 10.1093/nar/gkp134. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(PDF 324 kb)