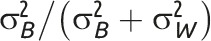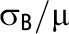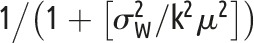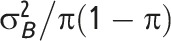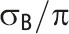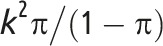Abstract
In 2004, Murray et al. reviewed methodological developments in the design and analysis of group-randomized trials (GRTs). We have highlighted the developments of the past 13 years in design with a companion article to focus on developments in analysis. As a pair, these articles update the 2004 review.
We have discussed developments in the topics of the earlier review (e.g., clustering, matching, and individually randomized group-treatment trials) and in new topics, including constrained randomization and a range of randomized designs that are alternatives to the standard parallel-arm GRT.
These include the stepped-wedge GRT, the pseudocluster randomized trial, and the network-randomized GRT, which, like the parallel-arm GRT, require clustering to be accounted for in both their design and analysis.
A group-randomized trial (GRT) is a randomized controlled trial in which the unit of randomization is a group, and outcome measurements are obtained for members of the group.1 Also called a cluster-randomized trial or community trial,2–5 a GRT is the best comparative design available if the intervention operates at a group level, manipulates the physical or social environment, cannot be delivered to individual members of the group without substantial risk of contamination across study arms, or if there are other circumstances that warrant the design, such as a desire for herd immunity or a need to estimate both the direct and indirect intervention effects in studies of infectious diseases.1–5
In GRTs, outcomes on members of the same group are likely to be more similar to each other than to outcomes on members from other groups.1 Such clustering must be accounted for in the design of GRTs to avoid underpowering the study, and it must be accounted for in the analysis to avoid underestimated SEs and inflated type I error for the intervention effect.1–5
In 2004, Murray et al.6 published a review of methodological developments in the design and analysis of GRTs. In the 13 years since, there have been many developments in both areas. We highlight developments in both areas in a 2-part series of articles. In this article (part 1), we focus on developments in design. In the second article (part 2), we focus on developments in analysis.7 (The glossary of terms is available as a supplement to the online version of this article at http://www.ajph.org.) As a pair, these articles update the 2004 review. With both articles, we provide a broad and comprehensive review to guide readers to seek out appropriate materials for their own circumstances.
DEVELOPMENTS IN FUNDAMENTALS OF DESIGN
Clustering and the choice between a cohort and a cross-sectional GRT design are fundamental to both the design and analysis of GRTs.
Clustering
In its most basic form, a GRT has a hierarchical structure with groups nested within study arms and members nested within groups. Additional levels of nesting may arise through repeated measures over time or from more complex group structures (e.g., children nested in classrooms nested in schools). When designing and analyzing a GRT, it is necessary to account for the clustering associated with the nested design.1–5
The intraclass correlation coefficient (ICC), or intracluster correlation coefficient, is the clustering measure most commonly used in power calculations and most commonly reported in published studies.8 Eldridge et al.9 provide a comprehensive review of ICC definitions and measures in general clustered data for both continuous and binary outcomes, the most commonly reported outcomes in GRTs.10,11 Although the ICC for continuous outcome measures is well defined and generally well understood,1–4 Eldridge et al.9 highlight some of the challenges for binary outcomes and provide several definitions (Table 1 displays the form most commonly presented in GRT texts).2,4,5,9 Others compare methods to estimate the ICC of a binary outcome.12–17 The ICC is not easily defined for rates on the basis of person–time data.2,4 Recent publications have defined ICC for time-to-event data.18,19
TABLE 1—
Two Common Measures of Clustering for General Clustered Data for Two Common Types of Outcome
Note. CV = coefficient of variation; GRT = group-randomized trial; ICC = intraclass correlation coefficient. μ is the overall mean for continuous outcome data; π is the overall proportion for binary outcome data; 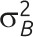 is the between-group variance;
is the between-group variance; 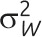 is the within-group variance (i.e., residual error variance). As is common practice, the 2 clustering measures are for general clustered data and do not focus on the GRT design in which the intervention effect is of primary interest (chapter 2 of Hayes and Moulton,2 e.g., provides more detail). The intervention parameter of interest in GRTs is typically the following: difference of means for continuous outcomes; difference of proportions; ratio of proportions or odds ratio for binary outcomes; or rate difference or rate ratio for event outcomes.
is the within-group variance (i.e., residual error variance). As is common practice, the 2 clustering measures are for general clustered data and do not focus on the GRT design in which the intervention effect is of primary interest (chapter 2 of Hayes and Moulton,2 e.g., provides more detail). The intervention parameter of interest in GRTs is typically the following: difference of means for continuous outcomes; difference of proportions; ratio of proportions or odds ratio for binary outcomes; or rate difference or rate ratio for event outcomes.
There are multiple definitions of the ICC for binary outcomes.12–17 The specific formulation we have provided is 1 of the simplest and most commonly used (e.g., Equation 2.4 of Hayes and Moulton2 and Equation 8 of Eldridge et al.9).
Note that whereas the relationship for binary outcomes is only a function of k and the distributional parameter of interest, π, the relationship for continuous outcomes is a function of both the distributional parameter of interest, μ, and 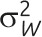 .
.
The coefficient of variation (CV) is a measure of clustering that is defined for general clustered data when the distributional parameter of interest is a mean, proportion, or rate.3,17 The CV and ICC for continuous and binary outcomes are associated by a mathematical relationship as a function of the distributional parameter of interest (i.e., mean or proportion) and, for continuous outcomes, of the within-group variance, 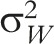 (Table 1).2,4 Hayes and Moulton2 advocate the CV generally in power calculations; Donner and Klar agree for event data analyzed as rates.3
(Table 1).2,4 Hayes and Moulton2 advocate the CV generally in power calculations; Donner and Klar agree for event data analyzed as rates.3
Because of the central role of clustering in planning GRTs, imprecision in the estimated level of clustering can lead to an underpowered trial. Multiple authors address imprecision, and all focus on the ICC.20–26 Simultaneously, increasingly more publications are reporting ICCs (e.g., Moerbeek and Teerenstra27 provide a comprehensive list of such articles) to aid the planning of future studies, consistent with the CONSORT (Consolidated Standards of Reporting Trials) statement on GRTs.28
Cohort vs Cross-Sectional Designs
The choice between a cohort and a cross-sectional GRT design (or their combination) is driven by the nature of the research question.1 The cross-sectional design is preferred when the question is about change in a population1 or when the time to the outcome is so short as to make a cohort study impractical (e.g., studies involving acute conditions).2 For example, to observe enough participants with malaria at 6-month follow-up time points and to be able to draw conclusions about population-level behavior related to malaria treatment choices, Laktabai et al.29 chose a cross-sectional design in which they obtained different population samples at each follow-up time point.
By contrast, when interested in change in specific individuals, or in mediation, the most natural choice is the cohort design, in which a cohort of individuals is enrolled and followed over time.1 For example, Turner et al.30 chose such a design to study child outcomes in mothers with prenatal depression.
Similarly, the cohort design is usually required to generate event data in individuals.2 A combination design could be used whereby the cross-sectional design is augmented by subsampling a cohort of individuals who are followed over time, such as in the COMMIT (Clopidogrel and Metoprolol in Myocardial Infarction Trial) study.31 A recent review indicated that the cohort design is the most common GRT design (67% of 75 GRTs).32
DESIGN OF PARALLEL-ARM GRTS
As for individually randomized controlled trials, the goal of randomization in GRTs is to achieve balance of baseline covariates. In contrast to individually randomized controlled trials, another form of baseline balance applies to GRTs, namely, baseline balance of group sample size. Both forms of balance play a role in the sample size and power calculations that are required to design GRTs.
Baseline Imbalance of Group Sample Size
An imbalance of group sample size means that group sizes are different across the groups randomized in the study, which has implications for statistical efficiency. Donner discussed variation in group size for GRTs for a design stratified by group size.33 Guittet et al.34 and Carter35 studied the impact on power using simulations, which showed the greatest reduction in power with few groups, high ICC, or both.
Several authors have offered adjustments to the standard sample size formula for a GRT to correct for variability in group size on the basis of the mean and variance of the group size or the actual size of each group.36–39 Others have offered adjustments on the basis of relative efficiency.40–43
Candel et al.40,41 reported that relative efficiency ranged from 1.0 to 0.8 across a variety of distributions for group size, with lower values for higher ICCs and greater variability in group size; the minimum relative efficiency was usually no worse than 0.9 for continuous outcomes. They recommended dividing the result from standard formulas for balanced designs by the relative efficiency for the expected group size distribution, which is a function of the ICC and the mean and variance of the group size.40 For binary outcomes, they suggested an additional correction factor on the basis of the estimation method planned for the analysis.41
You et al.42 defined relative efficiency in terms of noncentrality parameters; their measure of relative efficiency was a function of the ICC, the mean and variance of the group size, and the number of groups per study arm. Candel and Van Breukelen43 considered variability not only in group size but also between arms in error variance and the number of groups per arm. They recommended increasing the number of groups in each arm by the inverse of the relative efficiency minus 1. Their estimate of the relative efficiency was a function of the number of groups per study arm, the ICC in each study arm, the ratio of the variances in the 2 study arms, and the mean and variance of the group size.
Consistent across these studies was the recommendation that expectations for variation in group sample size be considered during both the planning stages and the analysis stage. Failure in planning can result in an underpowered study,40–43 and failure in analysis can result in type I error rate inflation.44
Baseline Imbalance of Covariates
Imbalance of covariates at baseline threatens the internal validity of the trial. Yet GRTs often randomize a limited number of groups that are heterogeneous in baseline covariates and in baseline outcome measurements. As a result, there is a good chance of baseline covariate imbalance.6,45 Restricted randomization strategies such as stratification, matching or constrained randomization can be implemented in the design phase to address this issue.
However, stratification may have limited use in GRTs if there are more than a handful of covariates to balance, because of the small number of groups in most trials.46 Pair matching also comes with several disadvantages,46 because it affects the proper calculation of ICC47 and complicates the significance testing of individual-level risk factors.48 More recently, Imai et al. presented a design-based estimator,49 which led them to advocate the use of pair matching on the basis of the unbiasedness and efficiency of their estimator. Several others highlighted features of this work,50–52 including the authors’ power calculation that does not depend on the ICC, thus avoiding the known ICC problem.53
Despite the efficiency gains of pair matching over stratification, a simulation study conducted by Imbens led him to conclude that stratified randomization would generally be preferred to pair matching.54 We note that strata of size 4 provide virtually all the advantages of pair matching while avoiding the disadvantages, and may be preferred over pair matching for that reason.
To overcome challenges when trying to balance on multiple, possibly continuous, covariates, Raab and Butcher55 proposed constrained randomization. It is on the basis of a balancing criterion calculated by a weighted sum of squared differences between the study arm means on any group-level or individual-level covariate and seeks to offer better internal validity than both pair matching and stratification. The approach randomly selects 1 allocation scheme from a subset of schemes that achieve acceptable balance, identified on the basis of having the smallest values of the balancing criterion.
Carter and Hood56 extended this work to randomize multiple blocks of groups and provided an efficient computer program for public use. de Hoop et al. proposed the “best balance” score to measure imbalance of group-level factors under constrained randomization.57 In simulations with 4 to 20 groups, constrained randomization with the best balance score was shown to optimally reduce quadratic imbalances compared with simple randomization, matching, and minimization.
Li et al.58 systematically studied the design parameters of constrained randomization for continuous outcomes, including choice of balancing criterion, candidate set size, and number of covariates to balance. With extensive simulations, they demonstrated that constrained randomization with a balanced candidate subset could improve study power while maintaining the nominal type I error rate, both for a model-based analysis and for a permutation test, as long as the analysis adjusted for potential confounding.
Moulton59 proposed to check for overly constrained designs by counting the number of times each pair of groups received the same study arm allocation. He revealed the risk of inflated type I error in overly constrained designs using a simulation example with 10 groups per study arm. Li et al. further noticed the limitation of overly constrained designs in that they may fail to support a permutation test with a fixed size.58 In practice, if covariate imbalance is present even after using 1 of the design strategies described, such imbalance can be accounted for by using adjusted analysis that is either preplanned in the protocol or through post hoc sensitivity analysis.7 In summary, constrained randomization seeks to provide both internal validity and efficiency.
Methods and Software for Sample Size
If the ICC is positive, not accounting for it in the analysis will inflate the type I error rate, and the power of the trial will be unknown. If the ICC is estimated as negative, as it can be when the true value is close to zero and sampling error leads to a negative estimate or when there is competition within groups,1–4,9,60 not accounting for it will reduce the type I error rate so that the test is more conservative, and the power of the trial will be lower than planned.61 Thus, a good estimate of the ICC is essential for sample size calculation for all GRTs.
One of the simplest power analysis methods often offered for a standard parallel-arm GRT with a single follow-up measurement is to compute the power for an individually randomized trial using the standard formula and to then inflate this by the design effect,62 given by 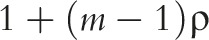 . In this formula,
. In this formula, 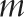 is the number of subjects per group and ρ is the ICC.
is the number of subjects per group and ρ is the ICC.
Unfortunately, this approach addresses only the first of the 2 penalties associated with group randomization that were identified by Cornfield almost 40 years ago63: extra variation and limited degrees of freedom for the test of the intervention effect. To accurately estimate sample size and power for a GRT, it is necessary to also account for the limited degrees of freedom that can arise because of having few groups to randomize. This can be achieved by using appropriate methods detailed in one of the GRT texts rather than using the naïve approach of simply inflating the individually randomized trial sample size by the design effect.1–5,61
In general, appropriate methods calculate sample size using a variance estimate inflated on the basis of the expected ICC and use a t test rather than a z test to reflect the desired power and type I error rate, with degrees of freedom determined on the basis of the number of groups to be randomized.
In practice, both cross-sectional and cohort GRTs are commonly powered on the basis of a comparison between study arms at a single point in time. Then, for GRTs with cohort designs, the analysis section of the study protocol may state that power will be gained by accounting for the repeated measures design in the analysis. However, methods exist for directly computing power in the case of repeated measures in the context of both cross-sectional and cohort designs.1,27
Authors have noted that regression adjustment for covariates often reduces both the ICC and the residual variance, thereby improving power.1,64 Heo et al.65 and Murray et al.66 provide methods that use data from across the entire course of the study, rather than just comparing 2 means at the end of the study. In practice, the user would require estimates of the variance reduction expected from repeated measures or from regression adjustment for covariates, which could be obtained from previous studies or pilot data.
Methods exist to power GRTs with additional layers of clustering, whether from additional structural hierarchies1,67–69 or from the repeated measures in the cohort design.1,27,64,66,70–73 Konstantopoulos describes how to incorporate cost into the power calculation for 3-level GRTs.74 Hemming et al. discuss approaches to take when the number of groups is fixed ahead of time.75 Two recent articles focus specifically on binary outcome variables.13,76 Candel and Van Breukelen examine the effects of varying group sizes in the context of a 2-arm GRT.77 Durán Pacheco et al. focus on power methods for overdispersed counts.78
Rutterford et al. and Gao et al. summarize a wide array of methods for sample size calculations in GRTs,79,80 including for GRT designs involving 1 to 2 measurements per member or per group and for designs involving 3 or more measurements per member or per group. A new textbook on power analysis for studies with multilevel data also provides a thorough treatment.27 Previous textbooks on the design and analysis of GRTs devoted at least a chapter to methods for power and sample size.1–5 A range of software and procedures are available to implement power and sample size calculations for GRTs (Table 2).
TABLE 2—
Software for Sample Size Calculations in Parallel-Arm GRTs
| Software | Functionality |
| PASSa | Sample size calculations for GRTs comparing 2 means (noninferiority, equivalence, or superiority), 2 proportions (noninferiority, equivalence, or superiority), 2 Poisson rates, and a log-rank test |
| nQueryb | Comparison of 2 means, proportions, and rates |
| Statac | User-provided command clustersampsi; can compute sample size for continuous, binary, and rate outcomes for 2-sided tests in equal-sized arms |
| Rd | Package CRTSize for comparing 2 means or 2 binary proportions |
| SASe | No built-in functionality at this time |
| Calculator | For some simple designs, parameter values can be plugged into formulas provided in textbooks |
Note. GRT = group-randomized trial; PASS = Power and Analysis Software.
Version 15 (NCSS Statistical Software, Kaysville, UT).
Version 7 (Statsols, Boston, MA).
Version 14 (StataCorp LP, College Station, TX).
Version 3.3.2 (R Foundation for Statistical Computing, Vienna, Austria).
Version 9.4 (SAS Institute, Cary, NC).
DEVELOPMENTS IN THE DESIGN OF ALTERNATIVES
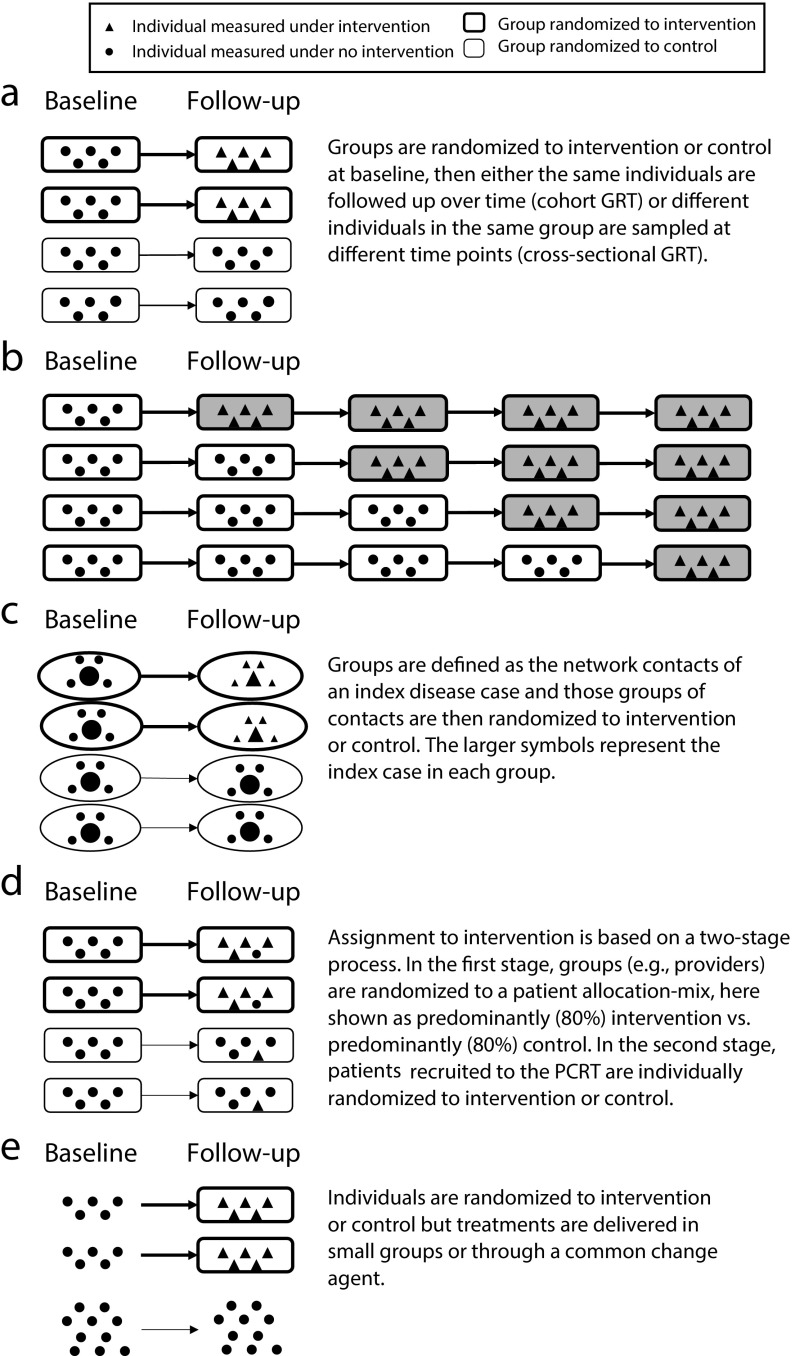
Many alternative designs can be used in place of a traditional parallel-arm GRT (Figure 1a). We consider four alternative designs, all of which involve randomization and some form of clustering that must be appropriately accounted for in both the design and analysis (Figure 1, Table 3). Thus, they share key features of the standard parallel-arm GRT, yet all have distinct and different features that are important to understand. In practice, some of these designs are still poorly understood.
FIGURE 1—
Pictorial Representation of Designs for (a) Parallel-Arm GRT, (b) Stepped-Wedge GRT, (c) Network-Randomized GRT, (d) Pseudocluster Randomized Trial (PCRT), and (e) Individually Randomized Group-Treatment (IRGT) Trial
Note. GRT = group-randomized trial. Each pictorial representation is an example of the specific design in which baseline measurements are taken. Other versions of each design exist. All examples show 5 individuals per group. The stepped-wedge GRT is a 1-directional crossover GRT in which time is divided into intervals and all groups eventually receive the intervention, indicated by the shading of the boxes. The design is an example of a “complete design,” that is, every group is measured at every time point. Like parallel-arm GRTs, stepped-wedge GRTs can be either cross-sectional or cohort. In the pseudocluster randomized trial, a group randomized to “intervention” is a group that contains a larger proportion of group members receiving the intervention than does a group randomized to “control”.
TABLE 3—
Characteristics of the Parallel-Arm Group Randomized Trial and of Alternative Group Designs
| One-Stage Randomization |
Type of Follow-Up Possible |
||||
| Design (Abbreviation) | By Group | By Individual | Two-Stage Randomization | Cross-Sectional | Cohort |
| Parallel-arm group-randomized trial (GRT) | ✓ | . . . | . . . | ✓ | ✓ |
| Stepped-wedge group-randomized trial (SW-GRT) | ✓ | . . . | . . . | ✓ | ✓ |
| Network-randomized group-randomized trial (NR-GRT) | ✓ | . . . | . . . | . . . | ✓a |
| Pseudocluster randomized trial (PCRT) | . . . | . . . | ✓ | . . . | ✓b |
| Individually randomized group-treatment trial (IRGT trial) | . . . | ✓ | . . . | . . . | ✓c |
In the NR-GRT, the index case and its network are usually defined at baseline, and therefore the design is expected to use a cohort design and not allow a cross-sectional design.
In the PCRT, because randomization is undertaken in 2 stages with individuals randomized to intervention or control in the second stage, the design requires that a cohort of individuals be enrolled at study baseline to be followed over time.
In the IRGT trial, individual randomization is performed, and therefore, like the pseudocluster randomized trial, a cohort of individuals is enrolled and followed over time.
Stepped-Wedge GRTs
The stepped-wedge GRT (SW-GRT) is a 1-directional crossover GRT in which time is divided into intervals and all groups eventually receive the intervention (Figure 1b).81 Systematic reviews indicate increasing popularity.82–84 Trials recently published a special issue (2015, issue 16) on the design and analysis of SW-GRTs, and many issues of the Journal of Clinical Epidemiology have featured multiple SW-GRT articles (e.g., 2012, 65[12] and 2013, 66[9]).
The rationale for this alternative is primarily logistical: it may not be possible to roll out the intervention in all groups simultaneously,85–88 although a staggered parallel-arm GRT design could alternatively be used in which blocks of groups are randomized to intervention or control instead of all groups eventually receiving the intervention as in the SW-GRT.89–91 Others propose a SW-GRT for ethical and acceptability reasons because all groups eventually receive the intervention.82 This second argument has been discounted because the intervention could be delivered to all control groups at the end of a parallel-arm GRT design,88,92 often earlier than would be the case in a SW-GRT.93 When SW-GRTs are conducted in low-incidence settings, Hayes et al. emphasized that the order and period of intervention allocation is crucial.94
For the parallel-arm GRT, design choices include cross-sectional82 versus cohort,95 with most SW-GRT methodological literature focused on cross-sectional designs, although most published SW-GRTs are cohort designs.96 An additional variation is that of complete versus incomplete SW-GRTs defined according to whether each group is measured at every time point.90 Regardless of the specifics of the SW-GRT design, it is important to consider the possible confounding and moderating effects of time in the analysis.85,90,97–99 Failure to account for both, if they exist, will threaten the internal validity of the study.
Cross-sectional SW-GRT sample size formulas are available for complete and incomplete designs.90,100–103 Hemming et al. provide a unified approach for the design of both parallel-arm and SW-GRTs and allow multiple layers of clustering.90 Cohort SW-GRT sample size calculation relies on simulation.97,104 Recent work on optimal designs shows that, for large studies, the optimal design is a mixture of a stepped-wedge trial embedded in a parallel-arm trial.105,106 Moerbeek and Teerenstra devote a chapter to sample size methods for SW-GRTs.27
Network-Randomized GRTs
GRTs have historically been used to minimize the contamination between study arms; such contamination is also called “interference.”107 This contamination may give rise to a network of connections between individuals both within and between study arms. The latter is of particular relevance to GRT design because it leads to reduced power, although sample size methods exist to preserve power and efficiency.108
The network-randomized GRT is a novel design that uses network information to address the challenge of potential contamination in GRTs of infectious diseases.109–111 In such a design, groups are defined as the network contacts of a disease (index) case, and those groups are randomized to study arms. Examples include the snowball trial and the ring trial, each with a distinct way to deliver the intervention. In the snowball trial, only the index case directly receives the intervention; the index is then encouraged to share the intervention with her or his contacts (e.g., see Latkin et al.109 for such a trial of HIV prevention in injection drug users). In the ring trial, “rings” of contacts of the index case are randomized to receive the intervention (Figure 1c). This design has been used to study foot-and-mouth disease,112 smallpox,113 and Ebola.114 For the same sample size, ring trials are more powerful than are classical GRTs when the incidence of the infection is low.115
Pseudocluster Randomized Trials
In GRTs where all members of the selected groups are recruited to the study, study participants are expected to be representative of the underlying population and, as a result, selection bias is expected to be minimal. By contrast, GRTs with unblinded recruitment after randomization are at risk for selection bias. For example, consider a GRT used to evaluate the effect of a behavioral intervention delivered by providers in the primary care setting. If a provider is first randomized to a study arm and then prospectively recruits participants, she or he may differentially select participants depending on whether she or he is randomized to the intervention or control arm.116
To reduce the risk of such selection bias, Borm et al. introduced the pseudocluster randomized trial (PCRT) to allocate intervention to participants in a 2-stage process.117 In the first stage, providers are randomized to a patient allocation mix (e.g., patients predominantly randomized to intervention vs patients predominantly randomized to control). In the second stage, patients recruited to the PCRT are individually randomized to intervention or control according to the allocation probability of their provider (e.g., 80% to intervention vs 20% to intervention; Figure 1d).
An obvious threat to a PCRT design is that the same providers are asked to implement both the intervention and the control arms, depending on which patient they are seeing. Concerns about contamination are a common reason to randomize providers (i.e., group randomization) so that they deliver either the intervention or the control but not both. The PCRT design would not be appropriate if there are concerns about contamination and if they exceed concerns about selection bias.
In 2 published cases, providers were blinded to the 2-stage form of randomization and instead assumed that patients were individually randomized to the intervention arm with equal probability.118,119 Later publications indicate that the PCRT design did well at balancing contamination and selection bias in both studies.120–122
Borm et al. provide sample size calculations for continuous outcomes.117 The clustering by provider (or unit of first-stage randomization) must be accounted for in both the design and analysis. No explicit sample size methods are known to be available for noncontinuous outcomes. Moerbeek and Teerenstra devote a chapter to sample size methods for PCRTs.27
Individually Randomized Group-Treatment Trials
Pals et al.123 identified studies that randomize individuals to study arms but deliver interventions in small groups or through a common change agent as individually randomized group-treatment (IRGT) trials, also called “partially clustered or partially nested designs” (Figure 1e).72,124 Examples include studies of psychotherapy,125 weight loss,126 and reduction in sun exposure.127 Clustering associated with these small groups or change agents must be accounted for in the analysis to avoid type I error rate inflation.72,123,124,128,129 Even so, this accounting appears to be rare in practice.123,130–133
Recent articles have reported sample size formulas for IRGT trials with clustering in only 1 study arm, both for balanced72,123,128,134 and unbalanced designs.77,128 Moerbeek and Teerenstra devote a chapter to sample size methods for IRGT trials focused on methods with clustering in either 1 or both arms.27 Roberts addresses sample size methods for IRGT trials in which members belong to more than 1 small group at the same time or change small groups over the course of the study.135 Both features have been shown to increase the type I error rate if ignored in the analysis.135,136
CONCLUSIONS
We have summarized many of the most important advances in the design of GRTs during the 13 years since the publication of the earlier review by Murray et al.6 Many of these developments have focused on alternatives to the standard parallel-arm GRT design as well as those related to the nature of clustering and its features in all the designs presented. Space limitations have prevented us from including recent developments involving pilot and feasibility GRTs; designs to improve efficiency, such as factorial and crossover GRTs; and group designs, such as cutoff designs and regression discontinuity applied to groups. Interested readers are directed to the recently launched peer-reviewed journal Pilot and Feasibility Studies and related references 4,137; to a recent methodological review of efficiency improvements for GRTs by Crespi,138 including factorial and crossover GRTs; to additional developments in crossover GRTs,139,140 including a recent review by Arnup et al.141; to additional reflections on the factorial GRT by Mdege et al.142; and to cutoff design references by Pennell et al.143 and by Schochet.144
With this review, we have sought to ensure that the reader is reminded of the value of good design and gains knowledge in the fundamental principles of a range of recent and potentially beneficial design strategies. Pairing this knowledge with our companion review of developments in the analysis of GRTs,7 we hope that our work leads to continued improvements in the design and analysis of GRTs.
ACKNOWLEDGMENTS
This work was partly funded by the National Institutes of Health (grants R01 HD075875, R37 AI51164, R01 AI110478 and K01 MH104310).
We would like to thank Indrani Saran and Ryan Simmons, for their valuable input on Figure 1, and the 2 anonymous reviewers, whose comments greatly helped improve the final version of this article.
Note. The content is solely the responsibility of the authors and does not necessarily represent the official views of National Institutes of Health. The study sponsors had no influence on the study design; data collection, analysis or interpretation; content of the article; nor the authors' decision to submit this article. The researchers operated independently from the funders in these matters.
HUMAN PARTICIPANT PROTECTION
No protocol approval was needed for this project because no human participants were involved.
Footnotes
See also Vaughan, p. 830.
REFERENCES
- 1.Murray DM. Design and Analysis of Group-Randomized Trials. New York, NY: Oxford University Press; 1998. [Google Scholar]
- 2.Hayes RJ, Moulton LH. Cluster Randomised Trials. Boca Raton, FL: CRC Press; 2009. [Google Scholar]
- 3.Donner A, Klar N. Design and Analysis of Cluster Randomization Trials in Health Research. London, England: Arnold; 2000. [Google Scholar]
- 4.Eldridge S, Kerry S. A Practical Guide to Cluster Randomised Trials in Health Services Research. Chichester, UK: Wiley; 2012. [Google Scholar]
- 5.Campbell MJ, Walters SJ. How to Design, Analyse and Report Cluster Randomised Trials in Medicine and Health Related Research. Chichester, UK: Wiley; 2014. [Google Scholar]
- 6.Murray DM, Varnell SP, Blitstein JL. Design and analysis of group-randomized trials: a review of recent methodological developments. Am J Public Health. 2004;94(3):423–432. doi: 10.2105/ajph.94.3.423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Turner EL, Prague M, Gallis JA, Li F, Murray DM. Review of recent methodological developments in group-randomized trials: part 2—analysis. Am J Public Health. 2017 doi: 10.2105/AJPH.2017.303706. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Campbell MK, Fayers PM, Grimshaw JM. Determinants of the intracluster correlation coefficient in cluster randomized trials: the case of implementation research. Clin Trials. 2005;2(2):99–107. doi: 10.1191/1740774505cn071oa. [DOI] [PubMed] [Google Scholar]
- 9.Eldridge SM, Ukoumunne OC, Carlin JB. The intra-cluster correlation coefficient in cluster randomized trials: a review of definitions. Int Stat Rev. 2009;77(3):378–394. [Google Scholar]
- 10.Fiero MH, Huang S, Oren E, Bell ML. Statistical analysis and handling of missing data in cluster randomized trials: a systematic review. Trials. 2016;17:72. doi: 10.1186/s13063-016-1201-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rutterford C, Taljaard M, Dixon S, Copas A, Eldridge S. Reporting and methodological quality of sample size calculations in cluster randomized trials could be improved: a review. J Clin Epidemiol. 2015;68(6):716–723. doi: 10.1016/j.jclinepi.2014.10.006. [DOI] [PubMed] [Google Scholar]
- 12.Ridout MS, Demétrio CG, Firth D. Estimating intraclass correlation for binary data. Biometrics. 1999;55(1):137–148. doi: 10.1111/j.0006-341x.1999.00137.x. [DOI] [PubMed] [Google Scholar]
- 13.Chakraborty H, Moore J, Hartwell TD. Intracluster correlation adjustments to maintain power in cluster trials for binary outcomes. Contemp Clin Trials. 2009;30(5):473–480. doi: 10.1016/j.cct.2009.04.005. [DOI] [PubMed] [Google Scholar]
- 14.Thomson A, Hayes R, Cousens S. Measures of between-cluster variability in cluster randomized trials with binary outcomes. Stat Med. 2009;28(12):1739–1751. doi: 10.1002/sim.3582. [DOI] [PubMed] [Google Scholar]
- 15.Yelland LN, Salter AB, Ryan P. Performance of the modified Poisson regression approach for estimating relative risks from clustered prospective data. Am J Epidemiol. 2011;174(8):984–992. doi: 10.1093/aje/kwr183. [DOI] [PubMed] [Google Scholar]
- 16.Crespi CM, Wong WK, Wu S. A new dependence parameter approach to improve the design of cluster randomized trials with binary outcomes. Clin Trials. 2011;8(6):687–698. doi: 10.1177/1740774511423851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wu S, Crespi CM, Wong WK. Comparison of methods for estimating the intraclass correlation coefficient for binary responses in cancer prevention cluster randomized trials. Contemp Clin Trials. 2012;33(5):869–880. doi: 10.1016/j.cct.2012.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Jahn-Eimermacher A, Ingel K, Schneider A. Sample size in cluster-randomized trials with time to event as the primary endpoint. Stat Med. 2013;32(5):739–751. doi: 10.1002/sim.5548. [DOI] [PubMed] [Google Scholar]
- 19.Oliveira IR, Molenberghs G, Demétrio CG, Dias CT, Giolo SR, Andrade MC. Quantifying intraclass correlations for count and time-to-event data. Biom J. 2016;58(4):852–867. doi: 10.1002/bimj.201500093. [DOI] [PubMed] [Google Scholar]
- 20.Ukoumunne OC, Davison AC, Gulliford MC, Chinn S. Non-parametric bootstrap confidence intervals for the intraclass correlation coefficient. Stat Med. 2003;22(24):3805–3821. doi: 10.1002/sim.1643. [DOI] [PubMed] [Google Scholar]
- 21.Zou G, Donner A. Confidence interval estimation of the intraclass correlation coefficient for binary outcome data. Biometrics. 2004;60(3):807–811. doi: 10.1111/j.0006-341X.2004.00232.x. [DOI] [PubMed] [Google Scholar]
- 22.Turner RM, Toby Prevost A, Thompson SG. Allowing for imprecision of the intracluster correlation coefficient in the design of cluster randomized trials. Stat Med. 2004;23(8):1195–1214. doi: 10.1002/sim.1721. [DOI] [PubMed] [Google Scholar]
- 23.Turner RM, Thompson SG, Spiegelhalter DJ. Prior distributions for the intracluster correlation coefficient, based on multiple previous estimates, and their application in cluster randomized trials. Clin Trials. 2005;2(2):108–118. doi: 10.1191/1740774505cn072oa. [DOI] [PubMed] [Google Scholar]
- 24.Turner RM, Omar RZ, Thompson SG. Constructing intervals for the intracluster correlation coefficient using Bayesian modelling, and application in cluster randomized trials. Stat Med. 2006;25(9):1443–1456. doi: 10.1002/sim.2304. [DOI] [PubMed] [Google Scholar]
- 25.Braschel MC, Svec I, Darlington GA, Donner A. A comparison of confidence interval methods for the intraclass correlation coefficient in community-based cluster randomization trials with a binary outcome. Clin Trials. 2016;13(2):180–187. doi: 10.1177/1740774515606377. [DOI] [PubMed] [Google Scholar]
- 26.Shoukri MM, Donner A, El-Dali A. Covariate-adjusted confidence interval for the intraclass correlation coefficient. Contemp Clin Trials. 2013;36(1):244–253. doi: 10.1016/j.cct.2013.07.003. [DOI] [PubMed] [Google Scholar]
- 27.Moerbeek M, Teerenstra S. Power Analysis of Trials With Multilevel Data. Boca Raton, FL: CRC Press; 2016. [Google Scholar]
- 28.Campbell MK, Elbourne DR, Altman DG. CONSORT statement: extension to cluster randomised trials. BMJ. 2004;328(7441):702–708. doi: 10.1136/bmj.328.7441.702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Laktabai J, Lesser A, Platt A et al. Innovative public–private partnership to target subsidized antimalarials: a study protocol for a cluster randomised controlled trial to evaluate a community intervention in Western Kenya. BMJ Open. 2017;7(3):e013972. doi: 10.1136/bmjopen-2016-013972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Turner EL, Sikander S, Bangash O et al. The effectiveness of the peer delivered Thinking Healthy Plus (THPP+) Programme for maternal depression and child socio-emotional development in Pakistan: study protocol for a three-year cluster randomized controlled trial. Trials. 2016;17(1):442. doi: 10.1186/s13063-016-1530-y. [Erratum in: The effectiveness of the peer delivered Thinking Healthy Plus (THPP+) Programme for maternal depression and child socio-emotional development in Pakistan: study protocol for A three-year cluster randomized controlled trial. Trials. 2017] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.COMMIT Research Group. Community Intervention Trial for Smoking Cessation (COMMIT): summary of design and intervention. J Natl Cancer Inst. 1991;83(22):1620–1628. doi: 10.1093/jnci/83.22.1620. [DOI] [PubMed] [Google Scholar]
- 32.Murray DM, Pals SP, Blitstein JL, Alfano CM, Lehman J. Design and analysis of group-randomized trials in cancer: a review of current practices. J Natl Cancer Inst. 2008;100(7):483–491. doi: 10.1093/jnci/djn066. [DOI] [PubMed] [Google Scholar]
- 33.Donner A. Sample size requirements for stratified cluster randomization designs. Stat Med. 1992;11(6):743–750. doi: 10.1002/sim.4780110605. [DOI] [PubMed] [Google Scholar]
- 34.Guittet L, Ravaud P, Giraudeau B. Planning a cluster randomized trial with unequal cluster sizes: practical issues involving continuous outcomes. BMC Med Res Methodol. 2006;6:17. doi: 10.1186/1471-2288-6-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Carter B. Cluster size variability and imbalance in cluster randomized controlled trials. Stat Med. 2010;29(29):2984–2993. doi: 10.1002/sim.4050. [DOI] [PubMed] [Google Scholar]
- 36.Lake S, Kaumann E, Klar N, Betensky R. Sample size re-estimation in cluster randomization trials. Stat Med. 2002;21(10):1337–1350. doi: 10.1002/sim.1121. [DOI] [PubMed] [Google Scholar]
- 37.Manatunga AK, Hudgens MG, Chen SD. Sample size estimation in cluster randomized studies with varying cluster size. Biom J. 2001;43(1):75–86. [Google Scholar]
- 38.Kerry SM, Bland JM. Unequal cluster sizes for trials in English and Welsh general practice: implications for sample size calculations. Stat Med. 2001;20(3):377–390. doi: 10.1002/1097-0258(20010215)20:3<377::aid-sim799>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
- 39.Eldridge SM, Ashby D, Kerry S. Sample size for cluster randomized trials: effect of coefficient of variation of cluster size and analysis method. Int J Epidemiol. 2006;35(5):1292–1300. doi: 10.1093/ije/dyl129. [DOI] [PubMed] [Google Scholar]
- 40.van Breukelen GJ, Candel MJ, Berger MP. Relative efficiency of unequal versus equal cluster sizes in cluster randomized and multicentre trials. Stat Med. 2007;26(13):2589–2603. doi: 10.1002/sim.2740. [DOI] [PubMed] [Google Scholar]
- 41.Candel MJ, Van Breukelen GJ. Sample size adjustments for varying cluster sizes in cluster randomized trials with binary outcomes analyzed with second-order PQL mixed logistic regression. Stat Med. 2010;29(14):1488–1501. doi: 10.1002/sim.3857. [DOI] [PubMed] [Google Scholar]
- 42.You Z, Williams OD, Aban I, Kabagambe EK, Tiwari HK, Cutter G. Relative efficiency and sample size for cluster randomized trials with variable cluster sizes. Clin Trials. 2011;8(1):27–36. doi: 10.1177/1740774510391492. [DOI] [PubMed] [Google Scholar]
- 43.Candel MJ, Van Breukelen GJ. Repairing the efficiency loss due to varying cluster sizes in two-level two-armed randomized trials with heterogeneous clustering. Stat Med. 2016;35(12):2000–2015. doi: 10.1002/sim.6851. [DOI] [PubMed] [Google Scholar]
- 44.Johnson JL, Kreidler SM, Catellier DJ, Murray DM, Muller KE, Glueck DH. Recommendations for choosing an analysis method that controls type I error for unbalanced cluster sample designs with Gaussian outcomes. Stat Med. 2015;34(27):3531–3545. doi: 10.1002/sim.6565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Wright N, Ivers N, Eldridge S, Taljaard M, Bremner S. A review of the use of covariates in cluster randomized trials uncovers marked discrepancies between guidance and practice. J Clin Epidemiol. 2015;68(6):603–609. doi: 10.1016/j.jclinepi.2014.12.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Ivers NM, Halperin IJ, Barnsley J et al. Allocation techniques for balance at baseline in cluster randomized trials: a methodological review. Trials. 2012;13:120. doi: 10.1186/1745-6215-13-120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Donner A, Klar N. Pitfalls of and controversies in cluster randomized trials. Am J Public Health. 2004;94(3):416–422. doi: 10.2105/ajph.94.3.416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Donner A, Taljaard M, Klar N. The merits of breaking the matches: a cautionary tale. Stat Med. 2007;26(9):2036–2051. doi: 10.1002/sim.2662. [DOI] [PubMed] [Google Scholar]
- 49.Imai K, King G, Nall C. The essential role of pair matching in cluster-randomized experiments, with application to the Mexican universal health insurance evaluation. Stat Sci. 2009;24(1):29–53. [Google Scholar]
- 50.Hill J, Scott M. Comment: the essential role of pair matching. Stat Sci. 2009;24(1):54–58. [Google Scholar]
- 51.Zhang K, Small DS. Comment: the essential role of pair matching in cluster-randomized experiments, with application to the Mexican Universal Health Insurance Evaluation. Stat Sci. 2009;24(1):59–64. [Google Scholar]
- 52.Imai K, King G, Nall C. Rejoinder: matched pairs and the future of cluster-randomized experiments. Stat Sci. 2009;24(1):65–72. [Google Scholar]
- 53.Klar N, Donner A. The merits of matching in community intervention trials: a cautionary tale. Stat Med. 1997;16(15):1753–1764. doi: 10.1002/(sici)1097-0258(19970815)16:15<1753::aid-sim597>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- 54. Imbens GW. Experimental design for unit and cluster randomized trials. Paper presented at: Initiative for Impact Evaluation. Cuernavaca, Mexico; June 15–17, 2011.
- 55.Raab GM, Butcher I. Balance in cluster randomized trials. Stat Med. 2001;20(3):351–365. doi: 10.1002/1097-0258(20010215)20:3<351::aid-sim797>3.0.co;2-c. [DOI] [PubMed] [Google Scholar]
- 56.Carter BR, Hood K. Balance algorithm for cluster randomized trials. BMC Med Res Methodol. 2008;8:65. doi: 10.1186/1471-2288-8-65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.de Hoop E, Teerenstra S, van Gaal BG, Moerbeek M, Borm GF. The “best balance” allocation led to optimal balance in cluster-controlled trials. J Clin Epidemiol. 2012;65(2):132–137. doi: 10.1016/j.jclinepi.2011.05.006. [DOI] [PubMed] [Google Scholar]
- 58.Li F, Lokhnygina Y, Murray DM, Heagerty PJ, DeLong ER. An evaluation of constrained randomization for the design and analysis of group-randomized trials. Stat Med. 2016;35(10):1565–1579. doi: 10.1002/sim.6813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Moulton LH. Covariate-based constrained randomization of group-randomized trials. Clin Trials. 2004;1(3):297–305. doi: 10.1191/1740774504cn024oa. [DOI] [PubMed] [Google Scholar]
- 60.Snedecor GW, Cochran WG. Statistical Methods. 8th ed. Ames: Iowa State University Press; 1989. [Google Scholar]
- 61.Murray DM, Hannan PJ, Baker WL. A Monte Carlo study of alternative responses to intraclass correlation in community trials. Is it ever possible to avoid Cornfield’s penalties? Eval Rev. 1996;20(3):313–337. doi: 10.1177/0193841X9602000305. [DOI] [PubMed] [Google Scholar]
- 62.Donner A, Birkett N, Buck C. Randomization by cluster sample size requirements and analysis. Am J Epidemiol. 1981;114(6):906–914. doi: 10.1093/oxfordjournals.aje.a113261. [DOI] [PubMed] [Google Scholar]
- 63.Cornfield J. Randomization by group: a formal analysis. Am J Epidemiol. 1978;108(2):100–102. doi: 10.1093/oxfordjournals.aje.a112592. [DOI] [PubMed] [Google Scholar]
- 64.Teerenstra S, Eldridge S, Graff M, Hoop E, Borm GF. A simple sample size formula for analysis of covariance in cluster randomized trials. Stat Med. 2012;31(20):2169–2178. doi: 10.1002/sim.5352. [DOI] [PubMed] [Google Scholar]
- 65.Heo M, Kim Y, Xue X, Kim MY. Sample size requirement to detect an intervention effect at the end of follow-up in a longitudinal cluster randomized trial. Stat Med. 2010;29(3):382–390. doi: 10.1002/sim.3806. [DOI] [PubMed] [Google Scholar]
- 66.Murray DM, Blitstein JL, Hannan PJ, Baker WL, Lytle LA. Sizing a trial to alter the trajectory of health behaviours: methods, parameter estimates, and their application. Stat Med. 2007;26(11):2297–2316. doi: 10.1002/sim.2714. [DOI] [PubMed] [Google Scholar]
- 67.Teerenstra S, Lu B, Preisser JS, van Achterberg T, Borm GF. Sample size considerations for GEE analyses of three-level cluster randomized trials. Biometrics. 2010;66(4):1230–1237. doi: 10.1111/j.1541-0420.2009.01374.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Heo M, Leon AC. Statistical power and sample size requirements for three level hierarchical cluster randomized trials. Biometrics. 2008;64(4):1256–1262. doi: 10.1111/j.1541-0420.2008.00993.x. [DOI] [PubMed] [Google Scholar]
- 69.Teerenstra S, Moerbeek M, van Achterberg T, Pelzer BJ, Borm GF. Sample size calculations for 3-level cluster randomized trials. Clin Trials. 2008;5(5):486–495. doi: 10.1177/1740774508096476. [DOI] [PubMed] [Google Scholar]
- 70.Heo M. Impact of subject attrition on sample size determinations for longitudinal cluster randomized clinical trials. J Biopharm Stat. 2014;24(3):507–522. doi: 10.1080/10543406.2014.888442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Heo M, Leon AC. Sample size requirements to detect an intervention by time interaction in longitudinal cluster randomized clinical trials. Stat Med. 2009;28(6):1017–1027. doi: 10.1002/sim.3527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Heo M, Litwin AH, Blackstock O, Kim N, Arnsten JH. Sample size determinations for group-based randomized clinical trials with different levels of data hierarchy between experimental and control arms. Stat Methods Med Res. 2014;26(1):399–413. doi: 10.1177/0962280214547381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Heo M, Xue X, Kim MY. Sample size requirements to detect an intervention by time interaction in longitudinal cluster randomized clinical trials with random slopes. Comput Stat Data Anal. 2013;60:169–178. doi: 10.1016/j.csda.2012.11.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Konstantopoulos S. Incorporating cost in power analysis for three-level cluster-randomized designs. Eval Rev. 2009;33(4):335–357. doi: 10.1177/0193841X09337991. [DOI] [PubMed] [Google Scholar]
- 75.Hemming K, Girling AJ, Sitch AJ, Marsh J, Lilford RJ. Sample size calculations for cluster randomised controlled trials with a fixed number of clusters. BMC Med Res Methodol. 2011;11:102. doi: 10.1186/1471-2288-11-102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Ahn C, Hu F, Skinner CS, Ahn D. Effect of imbalance and intracluster correlation coefficient in cluster randomization trials with binary outcomes when the available number of clusters is fixed in advance. Contemp Clin Trials. 2009;30(4):317–320. doi: 10.1016/j.cct.2009.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Candel MJ, Van Breukelen GJ. Varying cluster sizes in trials with clusters in one treatment arm: sample size adjustments when testing treatment effects with linear mixed models. Stat Med. 2009;28(18):2307–2324. doi: 10.1002/sim.3620. [DOI] [PubMed] [Google Scholar]
- 78.Durán Pacheco G, Hattendorf J, Colford JM, Jr, Mäusezahl D, Smith T. Performance of analytical methods for overdispersed counts in cluster randomized trials: sample size, degree of clustering and imbalance. Stat Med. 2009;28(24):2989–3011. doi: 10.1002/sim.3681. [DOI] [PubMed] [Google Scholar]
- 79.Rutterford C, Copas A, Eldridge S. Methods for sample size determination in cluster randomized trials. Int J Epidemiol. 2015;44(3):1051–1067. doi: 10.1093/ije/dyv113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Gao F, Earnest A, Matchar DB, Campbell MJ, Machin D. Sample size calculations for the design of cluster randomized trials: a summary of methodology. Contemp Clin Trials. 2015;42:41–50. doi: 10.1016/j.cct.2015.02.011. [DOI] [PubMed] [Google Scholar]
- 81.Spiegelman D. Evaluating public health interventions: 2. Stepping up to routine public health evaluation with the stepped wedge design. Am J Public Health. 2016;106(3):453–457. doi: 10.2105/AJPH.2016.303068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Brown CA, Lilford RJ. The stepped wedge trial design: a systematic review. BMC Med Res Methodol. 2006;6:54. doi: 10.1186/1471-2288-6-54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Mdege ND, Man MS. Taylor Nee Brown CA, Torgerson DJ. Systematic review of stepped wedge cluster randomized trials shows that design is particularly used to evaluate interventions during routine implementation. J Clin Epidemiol. 2011;64(9):936–948. doi: 10.1016/j.jclinepi.2010.12.003. [DOI] [PubMed] [Google Scholar]
- 84.Beard E, Lewis JJ, Copas A et al. Stepped wedge randomised controlled trials: systematic review of studies published between 2010 and 2014. Trials. 2015;16:353. doi: 10.1186/s13063-015-0839-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Hussey MA, Hughes JP. Design and analysis of stepped wedge cluster randomized trials. Contemp Clin Trials. 2007;28(2):182–191. doi: 10.1016/j.cct.2006.05.007. [DOI] [PubMed] [Google Scholar]
- 86.Hargreaves JR, Copas AJ, Beard E et al. Five questions to consider before conducting a stepped wedge trial. Trials. 2015;16:350. doi: 10.1186/s13063-015-0841-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Moulton LH, Golub JE, Durovni B et al. Statistical design of THRio: a phased implementation clinic-randomized study of a tuberculosis preventive therapy intervention. Clin Trials. 2007;4(2):190–199. doi: 10.1177/1740774507076937. [DOI] [PubMed] [Google Scholar]
- 88.Prost A, Binik A, Abubakar I et al. Logistic, ethical, and political dimensions of stepped wedge trials: critical review and case studies. Trials. 2015;16:351. doi: 10.1186/s13063-015-0837-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Shah More N, Das S, Bapat U et al. Community resource centres to improve the health of women and children in Mumbai slums: study protocol for a cluster randomized controlled trial. Trials. 2013;14:132. doi: 10.1186/1745-6215-14-132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Hemming K, Lilford R, Girling AJ. Stepped-wedge cluster randomised controlled trials: a generic framework including parallel and multiple-level designs. Stat Med. 2015;34(2):181–196. doi: 10.1002/sim.6325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Kotz D, Spigt M, Arts IC, Crutzen R, Viechtbauer W. Use of the stepped wedge design cannot be recommended: a critical appraisal and comparison with the classic cluster randomized controlled trial design. J Clin Epidemiol. 2012;65(12):1249–1252. doi: 10.1016/j.jclinepi.2012.06.004. [DOI] [PubMed] [Google Scholar]
- 92.Kotz D, Spigt M, Arts IC, Crutzen R, Viechtbauer W. Researchers should convince policy makers to perform a classic cluster randomized controlled trial instead of a stepped wedge design when an intervention is rolled out. J Clin Epidemiol. 2012;65(12):1255–1256. doi: 10.1016/j.jclinepi.2012.06.016. [DOI] [PubMed] [Google Scholar]
- 93.Murray DM, Pennell M, Rhoda D, Hade EM, Paskett ED. Designing studies that would address the multilayered nature of health care. J Natl Cancer Inst Monogr. 2010;2010(40):90–96. doi: 10.1093/jncimonographs/lgq014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Hayes RJ, Alexander ND, Bennett S, Cousens SN. Design and analysis issues in cluster-randomized trials of interventions against infectious diseases. Stat Methods Med Res. 2000;9(2):95–116. doi: 10.1177/096228020000900203. [DOI] [PubMed] [Google Scholar]
- 95.Copas AJ, Lewis JJ, Thompson JA, Davey C, Baio G, Hargreaves JR. Designing a stepped wedge trial: three main designs, carry-over effects and randomisation approaches. Trials. 2015;16:352. doi: 10.1186/s13063-015-0842-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Hemming K, Haines TP, Chilton PJ, Girling AJ, Lilford RJ. The stepped wedge cluster randomised trial: rationale, design, analysis, and reporting. BMJ. 2015;350:h391. doi: 10.1136/bmj.h391. [DOI] [PubMed] [Google Scholar]
- 97.Baio G, Copas A, Ambler G, Hargreaves J, Beard E, Omar RZ. Sample size calculation for a stepped wedge trial. Trials. 2015;16:354. doi: 10.1186/s13063-015-0840-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Handley MA, Schillinger D, Shiboski S. Quasi-experimental designs in practice-based research settings: design and implementation considerations. J Am Board Fam Med. 2011;24(5):589–596. doi: 10.3122/jabfm.2011.05.110067. [DOI] [PubMed] [Google Scholar]
- 99. Liao X, Zhou X, Spiegelman D. A note on “Design and analysis of stepped wedge cluster randomized trials.” Contemp Clin Trials. 2015;45(pt B):338–339. [Comment on: Design and analysis of stepped wedge cluster randomized trials. Contemp Clin Trials. 2007]. [DOI] [PMC free article] [PubMed]
- 100.Hemming K, Taljaard M. Sample size calculations for stepped wedge and cluster randomised trials: a unified approach. J Clin Epidemiol. 2016;69:137–146. doi: 10.1016/j.jclinepi.2015.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Hemming K, Girling A. A menu-driven facility for power and detectable-difference calculations in stepped-wedge cluster-randomized trials. Stata J. 2014;14(2):363–380. [Google Scholar]
- 102.Hughes J. Calculation of power for stepped wedge design. Available at: http://tinyurl.com/hwp5dgr. Accessed January 12, 2017.
- 103.Hughes J. Calculation of power for stepped wedge design (means) Available at: http://tinyurl.com/jvcr5bu. Accessed January 12, 2017.
- 104.Baio G. SWSamp: simulation-based sample size calculations for a stepped wedge trial (and more) 2016. Available at: https://sites.google.com/a/statistica.it/gianluca/swsamp. Accessed January 25, 2017.
- 105.Lawrie J, Carlin JB, Forbes AB. Optimal stepped wedge designs. Stat Probab Lett. 2015;99:210–214. [Google Scholar]
- 106.Girling AJ, Hemming K. Statistical efficiency and optimal design for stepped cluster studies under linear mixed effects models. Stat Med. 2016;35(13):2149–2166. doi: 10.1002/sim.6850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Hudgens MG, Halloran ME. Toward causal inference with interference. J Am Stat Assoc. 2008;103(482):832–842. doi: 10.1198/016214508000000292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Wang R, Goyal R, Lei Q, Essex M, De Gruttola V. Sample size considerations in the design of cluster randomized trials of combination HIV prevention. Clin Trials. 2014;11(3):309–318. doi: 10.1177/1740774514523351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Latkin C, Donnell D, Liu TY, Davey-Rothwell M, Celentano D, Metzger D. The dynamic relationship between social norms and behaviors: the results of an HIV prevention network intervention for injection drug users. Addiction. 2013;108(5):934–943. doi: 10.1111/add.12095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Staples PC, Ogburn EL, Onnela JP. Incorporating contact network structure in cluster randomized trials. Sci Rep. 2015;5:17581. doi: 10.1038/srep17581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Harling G, Wang R, Onnela JP, De Gruttola V. Leveraging contact network structure in the design of cluster randomized trials. Clin Trials. 2017;14(1):37–47. doi: 10.1177/1740774516673355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Keeling MJ, Woolhouse ME, May RM, Davies G, Grenfell B. Modelling vaccination strategies against foot-and-mouth disease. Nature. 2003;421(6919):136–142. doi: 10.1038/nature01343. [DOI] [PubMed] [Google Scholar]
- 113.Kretzschmar M, Van den Hof S, Wallinga J, Van Wijngaarden J. Ring vaccination and smallpox control. Emerg Infect Dis. 2004;10(5):832–841. doi: 10.3201/eid1005.030419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Enserink M. The Ebola epidemic. High hopes for Guinean vaccine trial. Science. 2015;347(6219):219–220. doi: 10.1126/science.347.6219.219. [DOI] [PubMed] [Google Scholar]
- 115.Ebola Ça Suffit Ring Vaccination Trial Consortium. The ring vaccination trial: a novel cluster randomised controlled trial design to evaluate vaccine efficacy and effectiveness during outbreaks, with special reference to Ebola. BMJ. 2015;351:h3740. doi: 10.1136/bmj.h3740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Farrin A, Russell I, Torgerson D, Underwood M. UK Beam Trial Team. Differential recruitment in a cluster randomized trial in primary care: the experience of the UK back pain, exercise, active management and manipulation (UK BEAM) feasibility study. Clin Trials. 2005;2(2):119–124. doi: 10.1191/1740774505cn073oa. [DOI] [PubMed] [Google Scholar]
- 117.Borm GF, Melis RJ, Teerenstra S, Peer PG. Pseudo cluster randomization: a treatment allocation method to minimize contamination and selection bias. Stat Med. 2005;24(23):3535–3547. doi: 10.1002/sim.2200. [DOI] [PubMed] [Google Scholar]
- 118.Melis RJ, van Eijken MI, Borm GF et al. The design of the Dutch EASYcare study: a randomised controlled trial on the effectiveness of a problem-based community intervention model for frail elderly people. BMC Health Serv Res. 2005;5:65. doi: 10.1186/1472-6963-5-65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Pence BW, Gaynes BN, Thielman NM et al. Balancing contamination and referral bias in a randomized clinical trial: an application of pseudocluster randomization. Am J Epidemiol. 2015;182(12):1039–1046. doi: 10.1093/aje/kwv132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Melis RJ, Teerenstra S, Rikkert MG, Borm GF. Pseudo cluster randomization performed well when used in practice. J Clin Epidemiol. 2008;61(11):1169–1175. doi: 10.1016/j.jclinepi.2007.12.001. [DOI] [PubMed] [Google Scholar]
- 121.Pence BW, Gaynes BN, Adams JL et al. The effect of antidepressant treatment on HIV and depression outcomes: results from a randomized trial. AIDS. 2015;29(15):1975–1986. doi: 10.1097/QAD.0000000000000797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Teerenstra S, Melis RJ, Peer PG, Borm GF. Pseudo cluster randomization dealt with selection bias and contamination in clinical trials. J Clin Epidemiol. 2006;59(4):381–386. doi: 10.1016/j.jclinepi.2005.10.003. [DOI] [PubMed] [Google Scholar]
- 123.Pals SL, Murray DM, Alfano CM, Shadish WR, Hannan PJ, Baker WL. Individually randomized group treatment trials: a critical appraisal of frequently used design and analytic approaches. Am J Public Health. 2008;98(8):1418–1424. doi: 10.2105/AJPH.2007.127027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Baldwin SA, Bauer DJ, Stice E, Rohde P. Evaluating models for partially clustered designs. Psychol Methods. 2011;16(2):149–165. doi: 10.1037/a0023464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Carlbring P, Bohman S, Brunt S et al. Remote treatment of panic disorder: a randomized trial of Internet-based cognitive behavior therapy supplemented with telephone calls. Am J Psychiatry. 2006;163(12):2119–2125. doi: 10.1176/ajp.2006.163.12.2119. [DOI] [PubMed] [Google Scholar]
- 126.Jeffery RW, Linde JA, Finch EA, Rothman AJ, King CM. A satisfaction enhancement intervention for long-term weight loss. Obesity (Silver Spring) 2006;14(5):863–869. doi: 10.1038/oby.2006.100. [DOI] [PubMed] [Google Scholar]
- 127.Jackson KM, Aiken LS. Evaluation of a multicomponent appearance-based sun-protective intervention for young women: uncovering the mechanisms of program efficacy. Health Psychol. 2006;25(1):34–46. doi: 10.1037/0278-6133.25.1.34. [DOI] [PubMed] [Google Scholar]
- 128.Roberts C, Roberts SA. Design and analysis of clinical trials with clustering effects due to treatment. Clin Trials. 2005;2(2):152–162. doi: 10.1191/1740774505cn076oa. [DOI] [PubMed] [Google Scholar]
- 129.Kahan BC, Morris TP. Assessing potential sources of clustering in individually randomised trials. BMC Med Res Methodol. 2013;13:58. doi: 10.1186/1471-2288-13-58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Pals SL, Wiegand RE, Murray DM. Ignoring the group in group-level HIV/AIDS intervention trials: a review of reported design and analytic methods. AIDS. 2011;25(7):989–996. doi: 10.1097/QAD.0b013e3283467198. [DOI] [PubMed] [Google Scholar]
- 131.Lee KJ, Thompson SG. Clustering by health professional in individually randomised trials. BMJ. 2005;330(7483):142–144. doi: 10.1136/bmj.330.7483.142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Biau DJ, Porcher R, Boutron I. The account for provider and center effects in multicenter interventional and surgical randomized controlled trials is in need of improvement: a review. J Clin Epidemiol. 2008;61(5):435–439. doi: 10.1016/j.jclinepi.2007.10.018. [DOI] [PubMed] [Google Scholar]
- 133.Oltean H, Gagnier JJ. Use of clustering analysis in randomized controlled trials in orthopaedic surgery. BMC Med Res Methodol. 2015;15:17. doi: 10.1186/s12874-015-0006-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.Moerbeek M, Wong WK. Sample size formulae for trials comparing group and individual treatments in a multilevel model. Stat Med. 2008;27(15):2850–2864. doi: 10.1002/sim.3115. [DOI] [PubMed] [Google Scholar]
- 135.Roberts C, Walwyn R. Design and analysis of non-pharmacological treatment trials with multiple therapists per patient. Stat Med. 2013;32(1):81–98. doi: 10.1002/sim.5521. [DOI] [PubMed] [Google Scholar]
- 136.Andridge RR, Shoben AB, Muller KE, Murray DM. Analytic methods for individually randomized group treatment trials and group-randomized trials when subjects belong to multiple groups. Stat Med. 2014;33(13):2178–2190. doi: 10.1002/sim.6083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Eldridge SM, Costelloe CE, Kahan BC, Lancaster GA, Kerry SM. How big should the pilot study for my cluster randomised trial be? Stat Methods Med Res. 2016;25(3):1039–1056. doi: 10.1177/0962280215588242. [DOI] [PubMed] [Google Scholar]
- 138.Crespi CM. Improved designs for cluster randomized trials. Annu. Rev. Public Health. 2016;37:1–16. doi: 10.1146/annurev-publhealth-032315-021702. [DOI] [PubMed] [Google Scholar]
- 139.Rietbergen C, Moerbeek M. The design of cluster randomized crossover trials. J Educ Behav Stat. 2011;36(4):472–490. [Google Scholar]
- 140.Giraudeau B, Ravaud P, Donner A. Sample size calculation for cluster randomized cross-over trials. Stat Med. 2008;27(27):5578–5585. doi: 10.1002/sim.3383. [DOI] [PubMed] [Google Scholar]
- 141.Arnup SJ, Forbes AB, Kahan BC, Morgan KE, McKenzie JE. The quality of reporting in cluster randomised crossover trials: proposal for reporting items and an assessment of reporting quality. Trials. 2016;17(1):575. doi: 10.1186/s13063-016-1685-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.Mdege ND, Brabyn S, Hewitt C, Richardson R, Torgerson DJ. The 2 × 2 cluster randomized controlled factorial trial design is mainly used for efficiency and to explore intervention interactions: a systematic review. J Clin Epid. 2014;67(10):1083–1092. doi: 10.1016/j.jclinepi.2014.06.004. [DOI] [PubMed] [Google Scholar]
- 143.Pennell ML, Hade EM, Murray DM, Rhoda DA. Cutoff designs for community-based intervention studies. Stat Med. 2011;30(15):1865–1882. doi: 10.1002/sim.4237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144.Schochet PZ. Statistical power for regression discontinuity designs in education evaluations. J Educ Behav Stat. 2009;34(2):238–266. [Google Scholar]