Low-Frequency Cortical Oscillations Entrain to Subthreshold Rhythmic Auditory Stimuli

Abstract

Many environmental stimuli contain temporal regularities, a feature that can help predict forthcoming input. Phase locking (entrainment) of ongoing low-frequency neuronal oscillations to rhythmic stimuli is proposed as a potential mechanism for enhancing neuronal responses and perceptual sensitivity, by aligning high-excitability phases to events within a stimulus stream. Previous experiments show that rhythmic structure has a behavioral benefit even when the rhythm itself is below perceptual detection thresholds (ten Oever et al., 2014). It is not known whether this “inaudible” rhythmic sound stream also induces entrainment. Here we tested this hypothesis using magnetoencephalography and electrocorticography in humans to record changes in neuronal activity as subthreshold rhythmic stimuli gradually became audible. We found that significant phase locking to the rhythmic sounds preceded participants' detection of them. Moreover, no significant auditory-evoked responses accompanied this prethreshold entrainment. These auditory-evoked responses, distinguished by robust, broad-band increases in intertrial coherence, only appeared after sounds were reported as audible. Taken together with the reduced perceptual thresholds observed for rhythmic sequences, these findings support the proposition that entrainment of low-frequency oscillations serves a mechanistic role in enhancing perceptual sensitivity for temporally predictive sounds. This framework has broad implications for understanding the neural mechanisms involved in generating temporal predictions and their relevance for perception, attention, and awareness.

SIGNIFICANCE STATEMENT The environment is full of rhythmically structured signals that the nervous system can exploit for information processing. Thus, it is important to understand how the brain processes such temporally structured, regular features of external stimuli. Here we report the alignment of slowly fluctuating oscillatory brain activity to external rhythmic structure before its behavioral detection. These results indicate that phase alignment is a general mechanism of the brain to process rhythmic structure and can occur without the perceptual detection of this temporal structure.

Introduction

Entrainment of neural activity to temporal regularities in the environment enhances neuronal processing by aligning depolarization (high-excitability) phases of ongoing oscillations to the arrival time of expected task-relevant events (Lakatos et al., 2008; Schroeder and Lakatos, 2009; Besle et al., 2011). Since these phases correspond to periods of high neuronal excitability, weaker inputs can elicit action potentials and thus this mechanism can facilitate downstream information processing (Buzsáki, 2004). It has been reported repeatedly that perceptual sensitivity varies systematically as a function of low-frequency phase (Henry and Obleser, 2012; Fiebelkorn et al., 2013; Arnal et al., 2015; ten Oever et al., 2015), and that rhythmic temporal regularities within a stimulus carry behavioral benefits (Cravo et al., 2013; Arnal et al., 2015).

In a previous study, we presented participants with sequences of auditory tones, which were either rhythmic or random. The tones were initially below perceptual detection threshold. Over the course of the trial the intensity increased gradually and participants indicated when they started to hear the sounds. It was shown that rhythm has a beneficial effect on perception even when the sound stream conveying the rhythm itself is presented below perceptual threshold (ten Oever et al., 2014). This suggests that temporal information is extracted and exploited even when a stream is not perceptible. However, it is an open question whether this “inaudible” rhythmic sound pattern also elicits neuronal entrainment. This is a key question, as it dissects the mechanistic connection between overt perception and entrainment. On one hand, it may be that a stream must be perceptible for the auditory system to entrain to it (Lakatos et al., 2013; Zion Golumbic et al., 2013; Henry et al., 2014; Doelling and Poeppel, 2015; Zoefel and VanRullen, 2016). On the other hand, it is possible that auditory streams that have appropriate rhythmic characteristics are inherently salient, independent of whether or not they are perceptible. If the latter is true, the overt perception of a rhythmic structure is not a prerequisite for entrainment.

To answer this question, we performed an analogous behavioral study while collecting data from two experiments using magnetoencephalography (MEG) and electrocorticography (ECoG). This enabled us to compare neuronal responses to rhythmic and random sounds sequences when stimuli were either above or below perceptual detection thresholds. Besides our main goal of examining the presence of entrainment to inaudible rhythmic sequences, investigating entrainment for stimuli below perceptual detection levels grants another advantage that is also critical from a mechanistic perspective. Typically, when presenting rhythmic stimuli at suprathreshold levels, strong intertrial coherence (ITC) is observed at the stimulation rate compared to random stimulus sequences (Will and Berg, 2007; Notbohm et al., 2016). However, resulting rhythmic patterns of neural activity are dominated by large evoked responses, which obscure the ability to detect smaller underlying fluctuations in oscillatory activity (Keitel et al., 2014; Notbohm et al., 2016). Consequently, it is difficult to determine whether these ITC effects are driven purely by the evoked responses or are also influenced by the alignment of ongoing oscillations to the input structure (but see Luo et al., 2013). Low-intensity stimuli below perceptual detection thresholds produce little or no evoked response (Elberling et al., 1981; Lütkenhöner and Klein, 2007). If these low-intensity sounds show strong ITC at the repetition rate without detectable evoked responses, neural entrainment of ongoing oscillations might be decoupled from direct evoked responses. Moreover, observing substantial ITC for rhythmic sounds even when sound intensities are below perceptual detection thresholds would suggest that rhythms in the environment entrain neural oscillations by default, by virtue of their temporal structure, and that this is not a consequence of their overt perception. Thus, this experimental approach has the potential to shed light on the neuronal mechanism involved in representing and processing temporal regularities in our environment.

Materials and Methods

Participants

Sixteen participants completed the MEG experiment (range, 23–37; mean age 27; 7 male). All had normal or corrected-to-normal vision and gave written informed consent. Participants received monetary compensation. The study was approved by the New York University Committee on Activities Involving Human Subjects. The data from one participant were excluded from the data analyses since he did not follow the instructions of the behavioral task.

Additionally, one participant (male, age 30) undergoing intracranial electrocorticographic recordings (North Shore University Hospital, Manhasset, NY) for intractable epilepsy participated in the study. (We also recorded from a second patient, but this patient was excluded since he had high epileptiform activity in the regions of interest.) The placement of intracranial electrodes was based solely on the clinical needs of the participant, without any reference to the present study. Ethical approval was provided by the Institutional Review Board of the Feinstein Institute for Medical Research. Informed consent was obtained before the experiment.

Stimulus material

Auditory stimuli were sinusoidal 1 kHz beeps, lasting 50 ms (with a linear rise and fall time of 5 ms) embedded in continuous white noise (53 dB). The software Presentation was used for stimulus delivery (Neurobehavioral Systems). The signal-to-noise (SNR) changes are described below.

Procedure

Auditory localizer.

Before the main experiment, participants in the MEG experiment underwent an auditory localizer procedure. This localizer consistent of a total of 200 sinusoidal tones (400 ms duration) of which half were high frequency (1000 Hz) and the other half a low frequency (250 Hz). Two tones were chosen to minimize the habituation to one sound. Stimulus-onset asynchrony (SOA) was varied between 1.2, 1.3, and 1.4 s. SOA and stimulus frequency were randomized. The task lasted ∼5 min and participants had to fixate on the screen.

Main experiment.

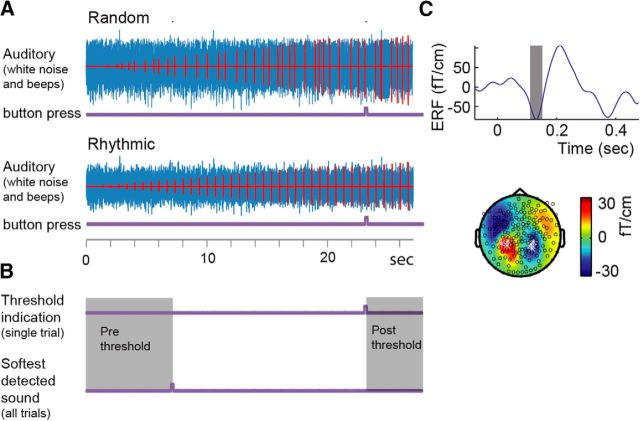
The main experiment was similar to our previous study (ten Oever et al., 2014). Participants listened to a stream of auditory beeps embedded in continuous white noise. The SNR of the beeps was initially below threshold, and the intensity of the beeps increased monotonically over the trial (Fig. 1A). Participants were asked to indicate via button press when the beeps were first detected. The starting SNR was 7% (tone at 34 dB). Over the trial, SNR increased incrementally in steps of 0.25, 0.5, or 0.75%. The different incremental steps were randomized to ensure that the sequence of sounds and length of the trials were not predictable across trials. Stimuli were presented until an SNR of 17.5% (tone at 40 dB), independent of the participant's response. After the participant indicated that they had heard a sound, the fixation cross changed color from gray to green and stayed green for five consecutive sounds before turning back to gray. In the Rhythmic condition, there was a constant interstimulus interval (ISI) of 667 ms between the beeps, whereas for the Random condition the ISI was randomized at 21 evenly spaced time points between 333 and 1000 ms, maintaining an average ISI of 667 ms.

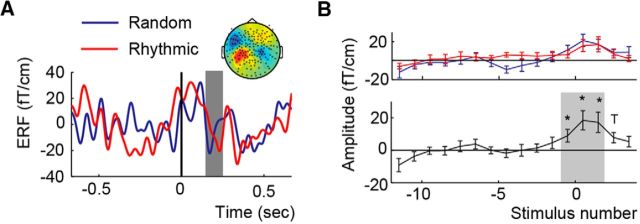
Figure 1.

Illustration of the trial structure and auditory localizer. A, Beeps (red) were embedded in white noise (blue), with their intensity increasing monotonically over the trial. Participants indicated the moment that they perceived the sounds for the first time via button press (purple lines). B, Prethreshold and postthreshold epoch selection. All sounds at intensities below the softest detected sound, across all trials, are classified as prethreshold. All sounds at intensities above indication of detection in that specific trial are classified as postthreshold. C, Example for the determination of peak amplitude, latency, and electrodes of the M100 for one participant in an independent auditory localizer. The ERF of the average of the six highlighted channels is displayed (multiplying the left channels by −1; this will be the convention in the following figures). The topography reflects the average of the gray shaded area in the time course.

Participants were explicitly instructed to maintain fixation on a gray cross in the middle of the screen. Trials were randomized across conditions (20 trials per condition) and the experiment was divided in four blocks of approximately eleven minutes each. After every block participants were encouraged to take a break. A trial was defined as the whole period from the onset of the white noise until the last sound was presented.

Behavioral analysis

At different SNR bins (ranging from 0–2.5% to 17.5–20% in steps of 2.5%), we calculated for each participant and condition the percentage of detected sounds. Per condition outlier trials were removed (trials further than ±1.5 * IQR (interquartile range) from the median; on average, 1.3 trials were removed; SD, 1.1). We fitted a psychometric function to the data using the toolbox Modelfree, version 1.1. (Zchaluk and Foster, 2009; fitting a logit function with guessing and lapsing rate at 0). From this psychometric function, we calculated for each participant the SNR at which 75% of the sounds were detected. These individual SNR values were compared for the random and rhythmic condition using (one-sided) paired samples t test.

MEG recordings and data preprocessing

A 160-channel axial gradiometer (157 data and 3 reference channels), whole-head MEG system (KIT) was used for data acquisition. Head position was monitored via five electromagnetic coils attached to the participant's head located in respect to the nasion and both preauricular points using 3D digitizer software (Source Signal Imaging) and digitizing hardware (Polhemus). The sampling rate was 1000 Hz with online filtering of DC-200Hz. Initial noise reduction was using the CALM algorithm (Adachi et al., 2001) implemented in the MEG160 software (KIT). Other analyses were performed using the Fieldtrip toolbox (Oostenveld et al., 2011) implemented in MATLAB (MathWorks). First, data were downsampled to 256 Hz (using a shape-preserving piecewise cubic interpolation), and bad channels were replaced by the average of the neighboring channels. Then, independent component analyses [ICAs; using the logistic infomax ICA algorithm (Bell and Sejnowski, 1995) extracting 75 independent components; on average, 10.9 components were removed; SD, 3.0] was performed to remove artifacts related eye blinks, eye movements, and heartbeat. Trials with remaining artifacts were removed via visual inspection (average amount of trials per condition, Random, 20; SD, 2.5; Rhythmic, 20; SD, 3.4; these trials reflect the full length of one trial until the button press, thus with multiple sounds included).

MEG analyses

We used the independent auditory localizer to identify channels with the strongest M100 response (collapsed over all tones). We selected the three channels with the strongest (absolute) posterior response on the left and on the right hemispheres, and the averages of these channels were used for all subsequent analyses. The locations of the identified channels conform to classic auditory topography of the M100 (Fig. 1C).

ITC estimation.

First we epoched the data around each sound onset (−1 to 1 s) and baseline corrected to the 200 ms before trial onset (similar for all upcoming analyses unless specified). Then, we sorted the epochs either as prethreshold or postthreshold. Prethreshold epochs included those centered around stimuli with intensities at least 0.75 SNR lower than the minimal detection-threshold value ever indicated (across all trials and conditions). This ensured that we included only intervals in which the stimulus intensity was never detected (Fig. 1B). Postthreshold epochs included those occurring after indication of detection in that specific trial.

We performed a frequency analysis of each epoch using Hanning tapers, extracted the mean phase of the complex Fourier spectrum at different frequencies (0.5 until 5 Hz in 0.5 Hz steps) and calculated the intertrial coherence (Matlab Circular Statistics toolbox; Berens, 2009) to estimate the consistency of phase distribution across epochs. The numbers of trials included in ITC estimation in the Random and Rhythmic conditions were equated, separately for the prethreshold and postthreshold periods. Statistical testing of the entrainment effect at the repetition rate of 1.5 Hz was performed using repeated measures ANOVA with the factors Condition (Random or Rhythmic) and Perception (Prethreshold or Postthreshold).

To evaluate the development of the ITC throughout the trial, we relabeled the epochs to reflect their position in the stimulus-sequence relative to the first sound detected (−1 indicates the first sound before detection etc.). Given the length of the trials in the current design (∼30 s), we had a limited number of trials (20 per condition). Thus, to increase the statistical power of this analysis, we used a moving window approach in which two sequential epochs were used to estimate the ITC at 16 positions ranging from −12 to 4. However, since each position included phase estimations from two adjacent epochs, we have labeled them with half numbers, between −11.5 and +3.5. We tested the ITC effect at 1.5 Hz statistically using repeated measures ANOVA with factors Condition and Stimulus Position. We used the Huyn–Feldt method to correct for violations for sphericity (in all following analyses). Simple effects analyses were performed for significant interactions using the false discovery rate (FDR) to correct for multiple comparisons (Benjamin and Hochberg, 1995).

Power estimation.

We repeated the same analyses described above, except using the square of the absolute value of the complex Fourier spectra to estimate the power in each epoch. The power spectra for the prethreshold versus postthreshold analysis were normalized, to make power value more comparable over participants, by subtracting the average over both conditions and perception intervals (Prethreshold and Postthreshold) from the individual power values and dividing by this average. Power spectra for the second analysis, in which we evaluated the development of power throughout the trial, were normalized by subtracting the power of the −11.5 stimulus. Trials with extreme power values were removed. (These were also excluded from the ITC analyses.)

Time-frequency analysis.

To detect phase locking of neural responses across a broad range of frequency bands in the prethreshold period, we performed a full time-frequency analysis of ITC and power in two different intervals: (1) a subset of the prethreshold trials, including only trials in the two consecutive stimulus positions where 1.5 Hz ITC became significantly higher in the Rhythmic versus Random condition (see above in the section ITC estimation), and (2) Postthreshold trials as defined above. We used wavelets ranging from 0.5–70 Hz (in 30 logarithmically spaced steps; with a width of 3.5 at 0.5 Hz increasing to 10 at 70 Hz; epoching the data from −2.5–2.5 around sound onset), with a time range of −0.15–0.7 s in steps of 0.01 s. Time-frequency power spectra were normalized by calculating the relative change of the power spectra with a time-frequency decomposition of the interval before the white noise onset [(original power-baseline power)/baseline power]. We compared the Random condition with the Rhythmic condition in both intervals using nonparametric bootstrap statistics of the difference (in Fieldtrip, the “nonparametric_individual” option; n = 1000), correcting for multiple comparisons using the cluster statistics as implemented in Fieldtrip (alpha and cluster-alpha, one-sided, 0.05; cluster statistics, “maxsum”; Maris and Oostenveld, 2007). Moreover, to estimate evoked responses, we compared for each individual condition whether its response after sound onset was significantly stronger than before stimulus onset (the average of the −0.15–0 s interval).

M100.

The same epochs as in the analyses of the development of the entrainment were used to evaluate whether the delta-band ITC effects can be explained by the development of an evoked M100 response throughout the trial. To this end, we bandpass filtered the data between 3 and 20 Hz using a second-order Butterworth filter. Then, for each epoch, we extracted the mean amplitude in a 50 ms wide window around the “M100 latency” (as determined in the independent localizer task). Here, we extracted the latency of the peak amplitude in a window between 80 and 150 ms, which had a matching M100 topography (Fig. 1B). This latency was used in the following analysis to extract the M100 amplitude calculating the average of all data points around a 50-ms-wide interval. Initially, the analysis did not show any results; however, it is known that stimuli with a low intensity have a significantly later M100 latency compared to high intensity stimuli (Elberling et al., 1981; Stufflebeam et al., 1998; Lütkenhöner and Klein, 2007), which were used in the localizer. Therefore, we added 50 ms to our M100 latency in the current analysis.

Since M100 responses in the right and left hemispheres have opposite polarities, we multiplied all the left hemispheric values with −1 before averaging over hemispheres. For statistical comparisons, we first performed a 2 * 16 repeated measures ANOVAs with factors Condition (Random and Rhythmic) and Stimulus Position (ranging from −11.5 to +3.5). As a post hoc analysis, we performed pairwise comparisons investigating whether the amplitude of the −11.5 stimulus was significantly different from all the other time points (corrected for multiple comparisons using FDR).

ECoG analysis

ECoG data acquisition and preprocessing.

We recorded ECoG from one participant implanted with clinical subdural and depths electrodes. These electrodes consist of platinum disks with a round, 2.3-mm-diameter exposed surface and 1 cm spacing between electrodes (total of 127 electrodes on the right hemisphere including an 6 × 8 electrode grid providing a dense sampling from the lateral frontal, temporal, and parietal lobes; in addition, electrode strips and depth electrodes sampled other regions more sparsely; see Fig. 6). Data were recorded using a clinical video-EEG system (XLTEK EMU128FS; 500 Hz sampling rate; 0.1–200 Hz analog bandpass filter before 16 bit digitization; Natus Medical). Reference and ground electrodes were inserted subdermally at the vertex.

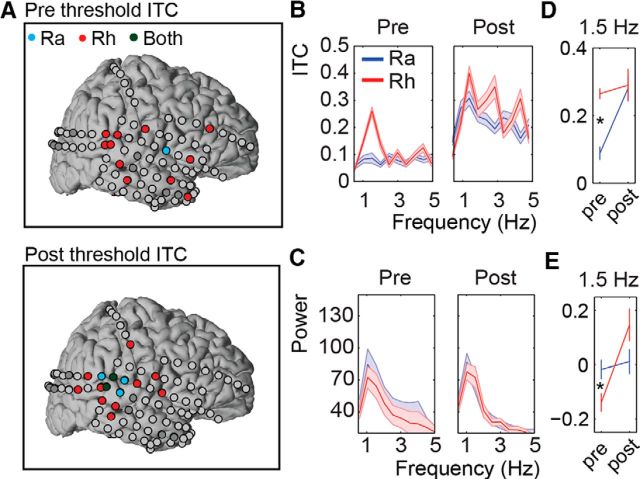
Figure 6.

ECoG Results. A, Red, blue, and dark green circles indicate significant ITC for the Rhythmic, Random, or both conditions, respectively. Dark gray electrodes show the electrodes of the seizure onset zone, which were removed from the analysis. Both the prethreshold (left) and postthreshold (right) intervals are shown. B, ITC for the significant ITC channels in the prethreshold (left) and postthreshold intervals (right). C, Power for the significant ITC channels in the prethreshold (left) and postthreshold intervals (right). Shaded areas indicate the SEM over all the significant electrodes. D, ITC at 1.5 Hz. Note that all values are based on the significant ITC prethreshold channels. E, Power at 1.5 Hz for the significant ITC prethreshold channels. Power reflects the relative change to the average of the two conditions and two perception intervals. Asterisks indicate significance at the 0.05 level.

Intracranial electrode localization.

The procedure for localizing intracranial electrodes is described by Groppe et al., (2017). Briefly, a postimplant 3D CT scan was coregistered to a preimplant 3D T1 3-Tesla MRI scan via a postimplant 3D T1 1.5-Tesla MRI scan using rigid affine transformations derived from FSL's FLIRT algorithm (Jenkinson and Smith, 2001).

The locations of the electrodes in the CT scan were manually identified using BioimageSuite (http://www.bioimagesuite.org). To correct for postimplant brain shift, electrodes were projected to the nearest point on the preimplant dural surface (Dykstra et al., 2012). The dural surface was derived automatically via FreeSurfer (http://freesurfer.net). The locations of the penetrating depth electrodes were not corrected for postimplant brain shifts.

ECoG signal processing.

All data were epoched from −10 s to +2.5 s relative to the first detected sound. These epochs were bandpass filtered to 0.5–30 Hz (second-order Butterworth filter). We epoched the data in smaller segments around the onset of each individual sound (−1 to +1 relative to sound onset). Trials with extreme variance were removed. Furthermore, all electrodes clinically identified as the seizure onset zones and electrodes with high epileptiform activity were excluded from further analysis. First, we extracted ITC and average power for the prethreshold and postthreshold intervals in the same manner as for the MEG analysis (using FFT). We estimated whether there was significant 1.5 Hz ITC for each electrode using the Rayleigh test, separately for the Rhythmic and Random conditions, and for prethreshold and postthreshold intervals. We corrected for multiple comparisons with FDR. For the power analysis we contrasted the absolute power of the Rhythmic and Random conditions for all channels that had a significant ITC with an independent samples t test (again correcting for multiple comparisons with FDR).

We then performed the same repeated measures ANOVA used in the MEG analysis with the factors Condition (Rhythmic and Random) and Perception (Prethreshold and Postthreshold) both for ITC and power using as units the channels significant in the Rayleigh test in the prethresholdthreshold interval. We normalized the power estimation by subtracting the average over both conditions and perception intervals (Prethreshold and Postthreshold) from the individual power values and dividing by this average.

Next, we investigated the development of the 1.5 Hz ITC and power for all electrodes significant in the Rayleigh test. We extracted the 1.5 Hz ITC and power for three consecutive sound intervals (three consecutive sounds instead of two due to even fewer trials in the ECoG analysis compared to the MEG) ranging from stimulus position −10 to 1 relative to sound detection. We normalized the power by the mean power of the −10 stimulus position. We performed a repeated measures ANOVA with the factors Condition (Random and Rhythmic) and Stimulus Position (ranging from −10 to 1 for ITC and −9 to 1 for power). We calculated the average time-frequency response of all the electrodes significant in the Rayleight test of the prethreshold interval. The analysis was identical to the MEG analysis except that the frequency ranged from 0.5–150 Hz (in 50 logarithmically spaced steps). Moreover, since the ITC of the Rhythmic condition was already significantly stronger than the Random condition early in the development (see Results) we included all trials earlier labeled as prethreshold for the first interval. Trials were reepoched from −2.5–2.5 s relative to sound onset and not filtered.

Results

Behavioral results

A paired samples t test showed that participants detected 75% of the sounds at lower intensities for the Rhythmic compared to the Random condition (Random, mean SNR, 12.9; Rhythmic, mean SNR, 12.5; t₍₁₄₎ = 1.8103, p < 0.05), replicating the behavioral effect reported previously (ten Oever et al., 2014).

MEG results

Prethreshold and postthreshold ITC

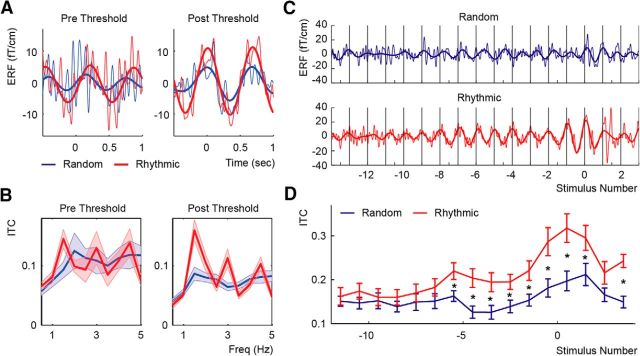
Figure 2A shows the event related fields (ERFs) for Prethreshold and Postthreshold intervals filtered at 1–2 and 1–20 Hz. The MEG channels included for this analysis reflect the channels significant in an independent auditory localizer (see Materials and Methods). A 1.5 Hz modulation can be observed in the Rhythmic condition, even in the Prethreshold epochs. Calculation of the intertrial coherence shows clear peaks at 1.5 Hz and its harmonics for the Rhythmic but not for the Random condition, in both the predetection and postdetection intervals (Fig. 2B). A repeated measures ANOVA for ITC at 1.5 Hz with the factors Condition (Random vs Rhythmic) and Perception (Prethreshold vs Postthreshold) indicated that the Rhythmic condition had a significantly stronger ITC than the Random condition (F_(1,14) = 19.103, p < 0.001; partial η squared = 0.54). No other effects were significant, although there was a trend for Condition * Perception (F_(1,14) = 3.48, p = 0.083).

Figure 2.

ITC analysis. A, ERFs for the predetection and postdetection epochs for both conditions for data bandpass filtered from 1–20 Hz (thin traces) and from 1–2 Hz (thick traces). B, Average ITC over participants of all the predetection and postdetection threshold epochs for both the Random (blue) and Rhythmic (red) conditions. Clear peaks at 1.5 Hz and their harmonics are visible in the rhythmic condition. C, ERF traces of the full trial, locked to the last stimulus before detection (t = 0) for data filtered between 1–20 Hz (thin traces) and 1–2 Hz (thick traces). Vertical black lines indicate the times of sound presentation in the rhythmic condition. D, ITC over the course of the trial. Error bars and shaded areas indicate the SEM. Asterisks indicate significant differences between the Random and Rhythmic conditions (p < 0.05, FDR corrected). For the ERFs in A and C, the data from the left hemisphere were multiplied by −1.

Development of the 1.5 Hz ITC

To better characterize the development of this phase locking over the course of a trial, we sorted the individual epochs based on their relative distance from indication of sound detection (stimulus position 0 indicating the sound that was first detected). Figure 2C shows that in the Rhythmic, condition the phase of the averaged MEG signal around the onset of each sound becomes stable relatively early in the trial and well before indication of detection. To test the consistency of this phase locking, we calculated the 1.5 Hz ITC at each of 16 positions ranging from −11.5 to 3.5 (half numbers representing the use of a moving window approach for calculating the ITC; for details, see Materials and Methods; Fig. 2D). A repeated measures ANOVA with the factors Condition (Random and Rhythmic) and Stimulus Position revealed an interaction between Condition and Stimulus Position (F_(15,210) = 2.248, p < 0.05, partial η squared = 0.138). Additionally, we found a main effect for Stimulus Position (F_(15,210) = 7.195, p < 0.001, partial η squared = 0.339) and Condition (F_(1,14) = 21.909, p < 0.001, partial η squared = 0.610). Simple effects analysis comparing the Random and Rhythmic conditions at each stimulus position showed that the ITC in the Rhythmic condition was significantly higher than in the Random condition starting from stimulus position −5.5 (5–2.33 s before detection) and that this difference was consistently significant throughout the rest of the trial (excluding stimulus position 2.5; FDR corrected for multiple comparisons).

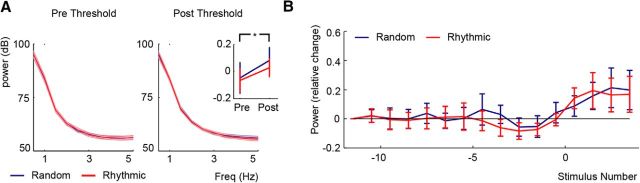
Prethreshold and postthreshold power

Next, we investigated whether the increase in ITC was accompanied by an increase in 1.5 Hz power. In Figure 3A, the nonnormalized overall power is shown for both the Prethreshold and Postdetection intervals. In both spectra a clear 1/f distribution is visible, typical of any EEG/MEG response (Pritchard, 1992; Miller et al., 2009). The ANOVA for difference in 1.5 Hz power [with the factors Condition (Random and Rhythmic) and Perception (Prethreshold and Postthreshold)] showed significantly higher 1.5 Hz power for the Postthreshold trials compared to the Prethreshold trials (Figure 3A, inset; F_(1,14) = 6.029, p < 0.05, partial η squared = 0.301). The main effect of Condition was not significant (F_(1,14) = 0.327, p = 0.576, partial η squared = 0.023; 95% confidence interval, −0.05 to 0.09), and the interaction was not significant (F_(1,14) = 0.333, p = 0.573, partial η squared = 0.023).

Figure 3.

Power analysis. A, Average power over participants for the predetection and postdetection epochs in the Random (blue) and Rhythmic (red) conditions. The MEG shows a typical 1/f distribution, but no peaks at 1.5 Hz are present. The inset on the right indicates a significant increase in 1.5 Hz power between the predetection and postdetection epochs, but no difference between rhythmic and random conditions. *p < 0.05. B, The 1.5 Hz power over the course of the trial. The relative change in power is presented for both conditions (compared to stimulus position, −11.5). Error bars and shaded areas indicate the SEM.

Development of the 1.5 Hz power

1.5 Hz power did not increase before sound detection, but seemed to develop only after detection (Fig. 3B). The ANOVA for the development of 1.5 Hz power showed a significant effect of stimulus Position (F_(14,196) = 3.035, p < 0.05, partial η squared = 0.178). Though there appears to be a drop in power accompanying the increased ITC in the predetection epoch in the rhythmic condition, this effect was not significant here or in the subsequent time-frequency analysis (below). To verify the apparent increase in power after sound detection we compared the power values at each stimulus position with zero. However, none of these contrasts survived the correction for multiple comparisons. Neither the main effect of Condition nor the interaction effect were significant (F_(1,14) = 0.062, p = 0.807; 95% confidence interval, −0.07 to 0.17; F_(14,196) = 0.285, p = 0.949, partial squared η = 0.020).

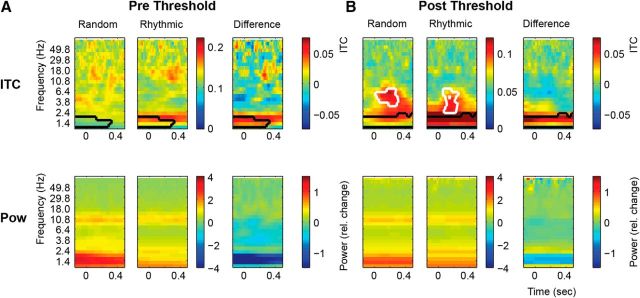
Time-frequency analysis

To fully characterize the response frequency domain profile before and after sound detection, we calculated the time-frequency representation for power and ITC for a subset of Prethreshold trials (using only the trials in the −6 to −4 positions where the Rhythmic condition began showing significantly higher 1.5 Hz ITC relative to the Random condition) and the Postthreshold interval. As expected, results show a stronger 1.5 Hz ITC for the Rhythmic condition in the Prethreshold and Postthreshold intervals (Prethreshold, cluster statistics, 7.76; p < 0.01; Postthreshold, cluster statistics, 14.17; p < 0.05; Fig. 4). Moreover, broadband ITC responses were only present in the Postthreshold interval, but not in the Prethreshold interval, suggesting they reflect sensory evoked responses (Random, cluster statistics, 3.06; p < 0.01; Rhythmic, cluster statistics, 2.43; p < 0.001).

Figure 4.

Time-frequency analysis. A, Prethreshold (trials −6 to −4 before detection) time-frequency analysis displaying the ITC (top row) and power (bottom row) for the Random (left column) and Rhythmic conditions (middle column) and their difference (right column). B, Postthreshold time-frequency analysis. Conventions are the same as in A. Black contours indicate significant clusters for differences between the Random and Rhythmic condition as detected with the cluster analysis. White contours indicate significant clusters for differences between the time frequency response and the average response in the −0.15–0 s interval.

The time-frequency analysis for power did not reveal any significant effects, either for the Random versus Rhythmic condition [strongest cluster in the prethreshold interval (overlaying alpha activity); cluster statistics, −6.43; p = 0.366) or the analysis comparing activation prior and after sound onset. Although some 1.5 Hz power appeared to be present in both intervals and higher in the Random condition, this did not reach significance and was highly influenced by one participant who had high 1.5 Hz power in the random condition.

M100

Finally, we investigated modulation of the evoked responses in the time domain as measured with M100. To estimate the M100 responses to each auditory stimulus in the rhythmic condition, we extracted the amplitude at the M100 latency in each of the 16 positions described above in the section Development of the 1.5 Hz ITC. This M100 latency was individually determined via an independent localizer (Fig. 1C), and then shifted by 50 ms to account for the low sound intensity (see Materials and Methods). A shifted M100 (around 180 ms) is evident in the grand average ERF locked to the first detected sound (Fig. 5A,B). We entered the shifted M100 amplitude into a Repeated Measures ANOVA with factors Condition and Stimulus Position. This analysis revealed a significant effect of Stimulus Position (F_(15,210) = 5.339, p < 0.001, partial η squared = 0.276) and a trend for an interaction between Stimulus Position and Condition (F_(15,210) = 2.008, p = 0.052; partial η squared = 0.125). Follow up t tests comparing the M100 amplitude at each position with M100 amplitude of the first stimulus (position −11.5) shows a significant M100 response only in positions −0.5 to 3.5, suggesting that evoked responses were identifiable only at intensities above the perceptual detection threshold (Fig. 5C). The main effect of Condition was not significant (F_(1,14) = 0.226, p = 0.642; partial η squared = 0.016). It is important to note that the amplitudes of the M100 for stimuli in positions 0.5 and 1.5 were also likely influenced by visual evoked responses, as the fixation cross changed from gray to green after participants pressed the button.

Figure 5.

ERF and M100 effects. A, ERF average over the different hemispheres using only the epochs of the first detected sound (filtered between 0.5 and 20 Hz). The gray area indicates the location of the M100. The inset reflects the topographies of the M100 using the individual peak timing per participant. B, Development of the M100 over the course of the trial for the Random (blue) and Rhythmic (red) conditions and their average (black). Error bars indicate the SEM. Asterisks indicate where the M100 is significantly stronger than the earliest stimulus.

ECoG results

Prethreshold and postthreshold ITC and power

We repeated the same experiment in one participant undergoing intracranial monitoring for surgical treatment of refractory epilepsy. The ITC at 1.5 Hz for each electrode in the Prethreshold and Postthreshold intervals in both conditions was calculated using the same procedure as for the MEG data. Significance of each electrode was investigated using the Rayleigh test and corrected for multiple comparisons with FDR. We found electrodes with significant 1.5 Hz ITC in the Rhythmic condition (red) in both the Prethreshold and Postthreshold intervals (Prethreshold, 13 electrodes; Postthreshold, 16 electrodes; Fig. 6A,B). We also found one electrode with significant prethreshold ITC in the Random condition (blue; and seven significant postthreshold). The electrodes with significant Prethreshold ITC were primarily located in the temporal lobe (posterior and anterior), but also included some frontal electrodes. Subsequently, we investigated whether the significant ITC was accompanied by any power changes. We contrasted the 1.5 Hz power in the Random and Rhythmic conditions for all the electrodes with significant predetection or postdetection ITC; however, none of the electrodes locations showed a significant power difference between the conditions (Prethreshold, highest t value, t₍₂₃₇₎ = 1.038, p = 0.782; Fig. 6C). In contrast, we found one electrode that had a significantly stronger 1.5 Hz power for the random compared to the rhythmic condition (t₍₂₃₇₎ = −3.4960, p < 0.05).

A repeated measures ANOVA for 1.5 Hz ITC [with the factors Condition (Random and Rhythmic) and Perception (Prethreshold and Postthreshold)] showed a significant Condition * Perception interaction (F_(1,13) = 7.71, p < 0.05; Fig. 6D) and main effect for Condition (F_(1,13) = 12.58, p < 0.005) as well as Perception (F_(1,13) = 11.48, p < 0.005). Follow-up t tests showed a significantly higher ITC for the Rhythmic compared to the Random condition in the Prethreshold (t₍₁₃₎ = 5.65, p < 0.001) but not in Postthreshold interval (t₍₁₃₎ = 0.20, p = 0.84). The same analysis for the normalized power also showed a significant Condition * Perception interaction (F_(1,13) = 5.74, p < 0.05; Fig. 6E) and a main effect for Perception (F_(1,13) = 10.63, p < 0.01) but no significant main Condition effect (F_(1,13) = 0.018, p = 1). Interestingly, follow-up t tests revealed a significantly higher power for the Random condition compared to the Rhythmic condition in the Prethreshold interval (t₍₁₃₎ = −2.55, p < 0.05). This difference was absent in the Postthreshold interval (t₍₁₃₎ = 1.45, p = 0.342).

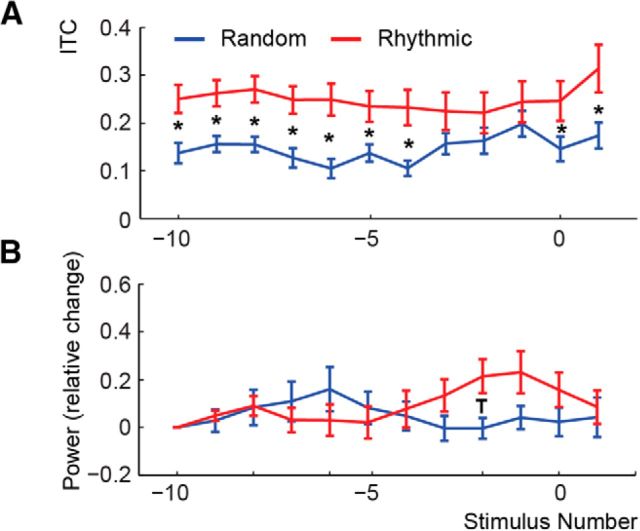
Development of 1.5 Hz ITC and power

We performed a repeated measures ANOVA on the 1.5 Hz ITC and power (averaged across all electrodes showing significant prethreshold phase locking) with the factors Condition and Stimulus Position. This analysis yielded a main effect of ITC for Condition (F_(1,13) = 15.714, p < 0.01, partial η squared = 0.547), indicating overall stronger ITC for the Rhythmic condition compared to the Random condition over the entire course of the trial (Fig. 7A). No other effects were significant (Stimulus Position, F_(11,143) = 1.337, p = 0.266; Condition * Stimulus Position, F_(11,143) = 1.027, p = 0.416). The ANOVA on 1.5 Hz power did not yield any significant main effects (Stimulus Position, F_(10,130) = 0.614, p = 0.588; Condition, F_(1,13) = 0.459, p = 0.510). We did find a significant interaction between Condition and Stimulus Position (F_(10,130) = 2.952, p < 0.05, partial η squared = 0.185; Figure 7B); however, a simple effect analysis comparing the Random and Rhythmic conditions for each stimulus position did not reveal any significant result (without correcting for multiple comparisons, only stimulus position 2 was significant, t₍₁₃₎ = 2.4251, p < 0.05).

Figure 7.

1.5 Hz ITC and power development for the ECoG data. A, B, The 1.5 Hz ITC (A) and power (B) over the course of the trial. Error bars indicate the SEM (over electrodes). Asterisks indicate significant differences between the Rhythmic and Random condition at the 0.05 level. The “T” indicates a trend at the 0.10 level.

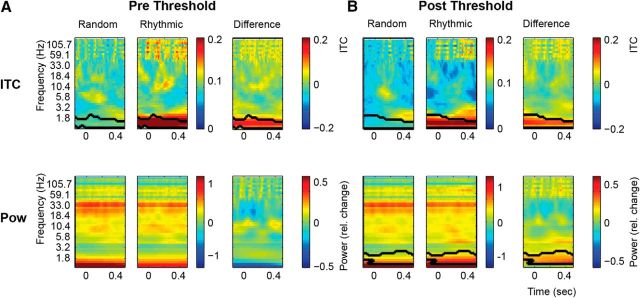
Time-frequency analysis

Next, we calculated the ITC and power for the interval −0.15–0.5 s for frequencies ranging from 0.6 to 150 Hz for the average of all significant channels. As expected, we found significantly stronger 1.5 Hz ITC for the Rhythmic compared to the Random condition both for the Prethreshold (cluster statistics, 93.37; p < 0.001; Fig. 8A) and Postthreshold conditions (cluster statistics, 80.04; p < 0.01; Fig. 8B). Regarding the power measures, though there appears to be a reduction in prethreshold power in the Rhythmic versus the Random condition, this effect did not reach significance. The only statistically significant effect in this arena was significantly higher 1.5 Hz power in the Postthreshold interval (cluster statistics, 741.55, p < 0.05). Neither ITC nor power was significant in any other frequency band.

Figure 8.

Time-frequency analysis for the ECoG data. A, Prethreshold (trials −6 to −4 before detection) time-frequency analysis displaying the ITC (top row) and power (bottom row) for the Random (left column) and Rhythmic conditions (middle column) and their difference (right column). B, Postthreshold time-frequency analysis. The conventions are the same as in A. Black contours indicate significant clusters as detected with the cluster analysis.

Discussion

We investigated the effects of stimulus rhythmicity on neural responses to subthreshold auditory stimuli that gradually increased in intensity to become audible during the course of each trial. We show significant phase locking of low-frequency neural activity to rhythmic sounds before their detection, but no significant phase locking for arrhythmic subthreshold sounds. Moreover, no apparent sensory evoked responses accompanied this entrainment, as sensory evoked responses appeared only at stimulus intensities that participants perceived overtly. These neurophysiological data, coupled with our behavioral findings of reduced perceptual thresholds for rhythmic sounds (ten Oever et al., 2014), suggest that despite being below detection threshold, the rhythmic structure of these low-intensity stimuli is sufficient to entrain low-frequency oscillations.

Entrainment boosts sensitivity

Neuronal oscillations are intrinsically generated and are widespread through the brain (Buzsáki, 2004; Lakatos et al., 2007). The alignment of oscillatory phases within and across brain regions has been shown to improve neuronal processing (Singer, 2009; Singer and Gray, 1995; Fries, 2005; Fell and Axmacher, 2011). Specifically, when their excitable phases are aligned, neurons fire at similar time points, leading, by hypothesis, to increased reciprocal communication. While these patterns emerge intrinsically, they can be influenced by external input. Rhythmic stimuli in particular can “entrain” intrinsic oscillations, locking oscillatory phases to an external input (Lakatos et al., 2008; Schroeder and Lakatos, 2009). It has been proposed that when stimuli are attended, high-excitability phases align to the onsets of incoming stimuli (Lakatos et al., 2008; Besle et al., 2011), thereby increasing processing efficiency and reducing detection thresholds.

Our results are consistent with this “neural entrainment hypothesis” (Schroeder et al., 2008; Schroeder and Lakatos, 2009). Using two complementary measures—MEG and ECoG—we show that indeed neuronal entrainment occurs robustly for rhythmic stimuli, remarkably even for those rhythmic stimuli below perceptual detection. Previous studies have reported that entrainment can improve perceptual sensitivity (Henry and Obleser, 2012; Fiebelkorn et al., 2013; Arnal et al., 2015; ten Oever et al., 2015). However, our study adds a new dimension by showing that entrainment occurs without explicit perceptual awareness of this rhythmic structure. Furthermore, the low-intensity rhythmic sound patterns did not result in any measurable evoked responses, as indexed by broadband ITC and power increase; if anything, there is a drop in low frequency power accompanying prethreshold entrainment. Altogether this pattern of results indicates a decoupling of low-frequency phase locking from sensory evoked responses. Sensory evoked responses often complicate the interpretation of entrainment patterns (Keitel et al., 2014; Notbohm et al., 2016). Our findings suggest that environmental rhythmic information can be used by the brain even before we can explicitly report on this stimulation (ten Oever et al., 2014).

The environment is rich in rhythmic structures that are important for human behavior, such as music, biological motion, or speech (Coull and Nobre, 1998). Considering that at rest, brain activity seems to be dominated by complex oscillatory patterns of rhythmically varying membrane potentials rather than purely random fluctuations (Berger, 1929; Buzsáki, 2004), its machinery seems especially fit for aligning to rhythmic inputs. Subthreshold inputs have been shown to align the phases of slow fluctuations of groups of neurons, even when the number of spikes does not increase (Pike et al., 2000; Buzsáki and Draguhn, 2004; Buzsáki, 2004). Here, we show that rhythmic input from the environment can act upon this machinery by influencing the phase of these ongoing oscillations even when clear evoked responses are absent.

Absence of evoked responses

Our measure of evoked responses focused on power analysis across frequencies, activity in the expected time window of the M100 response, and broadband ITC responses. None of these measures, in either MEG and ECoG recordings, showed any differentiation between the random and rhythmic conditions, except at intensity levels where participants could detect the sound stream. These separate complementary measures suggest that evoked responses are not driving the observed prethreshold effects. Naturally, the absence of evidence does not constitute evidence of absence. However, at minimum, our results show that prethreshold effects are clearly and strongly driven by phase alignment, as only this measure identified differences between the random and rhythmic conditions.

Rate specificity of subthreshold entrainment

In the current study, we found a significant ITC difference between the rhythmic and random condition ∼2.3 s before its perceptual detection in the MEG. One intriguing questions is how this prethreshold entrainment would manifest for other presentation rates. Here, we chose to focus on a rate of 1.5 Hz, as it is commonly found to be a comfortable tapping rate for most individuals (for review, see Repp, 2003), and it is known that entrainment is stronger at rates that match natural oscillators in the brain/motor system (Hoppensteadt and Izhikevich, 1998; Schroeder and Lakatos, 2009; Ali et al., 2013; Lowet et al., 2015). However, whether the emergence of subthreshold entrainment and/or perceptual threshold levels varies with presentation rate remains an open question. Previous studies have failed to show an influence of repetition rates on detection thresholds (Fay and Coombs, 1983; Heil and Neubauer, 2003); however, future studies are still necessary to investigate the effect of repetition rate on predetection entrainment.

Conclusion

Many natural stimuli contain temporal regularities, and the brain is tuned to process the natural statistics of the environment (Bonte et al., 2005; Schroeder et al., 2008). Our study has implications for understanding the neural mechanisms involved in exploiting these temporal regularities in the aid of perceptual and cognitive processing. We show that even when rhythmic sounds are not consciously detected, they can proactively enhance subsequent processing. Specifically, we extend the evidence supporting the “entrainment hypothesis,” which posits that alignment of neuronal excitable phases to the temporal structure of incoming stimuli enhances sensory processing. Our data also support the argument that it is the phase alignment, and not sensory evoked responses, that largely drives entrainment. Such a mechanism has broad implications for understanding the neural bases of perception and attention (Large and Jones, 1999; Schroeder et al., 2008; Zion Golumbic et al., 2013), as it emphasizes the predisposition of the system to identify and use temporal statistics in the environment to form predictions and ultimately facilitate neural processing.