When we try to compare proportions of a categorical outcome according to different independent groups, we can consider several statistical tests such as chi-squared test, Fisher's exact test, or z-test. The chi-squared test and Fisher's exact test can assess for independence between two variables when the comparing groups are independent and not correlated. The chi-squared test applies an approximation assuming the sample is large, while the Fisher's exact test runs an exact procedure especially for small-sized samples.
Chi-squared test
1. Independency test
The chi-squared test is used to compare the distribution of a categorical variable in a sample or a group with the distribution in another one. If the distribution of the categorical variable is not much different over different groups, we can conclude the distribution of the categorical variable is not related to the variable of groups. Or we can say the categorical variable and groups are independent. For example, if men have a specific condition more than women, there is bigger chance to find a person with the condition among men than among women. We don't think gender is independent from the condition. If there is equal chance of having the condition among men and women, we will find the chance of observing the condition is the same regardless of gender and can conclude their relationship as independent. Examples 1 and 2 in Table 1 show perfect independent relationship between condition (A and B) and gender (male and female), while example 3 represents a strong association between them. In example 3, women had a greater chance to have the condition A (p = 0.7) compared to men (p = 0.3).
Table 1. Contingency tables and procedure for Chi-squared test.
| Observed frequency (O) | Expected frequency (E) | O − E | (O − E)2 / E | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Example 1 | A | B | Total | A | B | Total | A | B | Total | A | B | Total | |
| Male | 50 | 50 | 100 | 50 | 50 | 100 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Female | 50 | 50 | 100 | 50 | 50 | 100 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Total | 100 | 100 | 200 | 100 | 100 | 200 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Example 2 | A | B | Total | A | B | Total | A | B | Total | A | B | Total | |
| Male | 30 | 70 | 100 | 30 | 70 | 100 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Female | 30 | 70 | 100 | 30 | 70 | 100 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Total | 60 | 140 | 200 | 60 | 140 | 200 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Example 3 | A | B | Total | A | B | Total | A | B | Total | A | B | Total | |
| Male | 30 | 70 | 100 | 50 | 50 | 100 | −20 | 20 | 0 | 8 | 8 | 16 | |
| Female | 70 | 30 | 100 | 50 | 50 | 100 | 20 | −20 | 0 | 8 | 8 | 16 | |
| Total | 100 | 100 | 200 | 100 | 100 | 200 | 0 | 0 | 0 | 16 | 16 | 32 | |
The chi-squared test performs an independency test under following null and alternative hypotheses, H0 and H1, respectively.
H0: Independent (no association)
H1: Not independent (association)
The test statistic of chi-squared test: with degrees of freedom (r - 1)(c - 1), Where O and E represent observed and expected frequency, and r and c is the number of rows and columns of the contingency table.
The first step of the chi-squared test is calculation of expected frequencies (E). E is calculated under the assumption of independent relation or, in other words, no association. Under independent relationship, the cell frequencies are determined only by marginal proportions, i.e., proportion of A (60/200 = 0.3) and B (1400/200 = 0.7) in example 2. In example 2, the expected frequency of the male and A cell is calculated as 30 that is the proportion of 0.3 (proportion of A) in 100 Males. Similarly, the expected frequency of the male and A cell is 50 that is the proportion of 0.5 (proportion of A = 100/200 = 0.5) in 100 Males in example 3 (Table 1).
The second step is obtaining (O - E)2/E for each cell and summing up the values over each cell. The final summed value follows chi-squared distribution. For the ‘male and A’ cell in example 3, (O - E)2/E = (30 - 50)2/50 = 8. in example 3. For examples 1 and 2, the chi-squared statistics equal zero. A big difference between observed value and expected value or a large chi-squared statistic implies that the assumption of independency applied in calculation of expected value is irrelevant to the observed data that is being tested. The degrees of freedom is one as the data has two rows and two columns: (r - 1) * (c - 1) = (2 - 1) * (2 - 1) = 1.
The final step is making conclusion referring to the chi-squared distribution. We reject the null hypothesis of independence if the calculated chi-squared statistic is larger than the critical value from the chi-squared distribution. In the chi-squared distribution, the critical values are 3.84, 5.99, 7.82, and 9.49, with corresponding degrees of freedom of 1, 2, 3, and 4, respectively, at an alpha level of 0.5. Larger chi-square statistics than these critical values of specific corresponding degrees of freedom lead to the rejection of null hypothesis of independence. In examples 1 and 2, the chi-squared statistic is zero which is smaller than the critical value of 3.84, concluding independent relationship between gender and condition. However, data in example 3 have a large chi-squared statistic of 32 which is larger than 3.84; it is large enough to reject the null hypothesis of independence, concluding a significant association between two variables.
The chi-squared test needs an adequate large sample size because it is based on an approximation approach. The result is relevant only when no more than 20% of cells with expected frequencies < 5 and no cell have expected frequency < 1.1
2. Effect size
As the significant test does not tell us the degree of effect, displaying effect size is helpful to show the magnitude of effect. There are three different measures of effect size for chi-squared test, Phi (φ), Cramer's V (V), and odds ratio (OR). Among them φ and OR can be used as the effect size only in 2 × 2 contingency tables, but not for bigger tables.
, where n is total number of observation, and df is degrees of freedom calculated by (r - 1) * (c - 1). Here, r and c are the numbers of rows and columns of the contingency table.
In example 3, we can calculate them as , , and . Referring to Table 2, the effect size V = 0.4 is interpreted medium to large. If number of rows and/or columns are larger than 2, only Cramer's V is available.
Table 2. Effect size for chi-squared test, Cramer's V and its interpretation2.
| Degree of freedom | Small | Medium | Large |
|---|---|---|---|
| 1 | 0.10 | 0.30 | 0.50 |
| 2 | 0.07 | 0.21 | 0.35 |
| 3 | 0.06 | 0.17 | 0.29 |
| 4 | 0.05 | 0.15 | 0.25 |
| 5 | 0.04 | 0.13 | 0.22 |
3. Post-hoc pairwise comparison of chi-squared test
The chi-squared test assesses a global question whether relation between two variables is independent or associated. If there are three or more levels in either variable, a post-hoc pairwise comparison is required to compare the levels of each other. Let's say that there are three comparative groups like control, experiment 1, and experiment 2 and we try to compare the prevalence of a certain disease. If the chi-squared test concludes that there is significant association, we may want to know if there is any significant difference in three compared pairs, between control and experiment 1, between control and experiment 2, and between experiment 1 and experiment 2. We can reduce the table into multiple 2 × 2 contingency tables and perform the chi-squared test with applying the Bonferroni corrected alpha level (corrected α = 0.05/3 compared pairs = 0.017).
Fisher's exact test
Fisher's exact test is practically applied only in analysis of small samples but actually it is valid for all sample sizes. While the chi-squared test relies on an approximation, Fisher's exact test is one of exact tests. Especially when more than 20% of cells have expected frequencies < 5, we need to use Fisher's exact test because applying approximation method is inadequate. Fisher's exact test assesses the null hypothesis of independence applying hypergeometric distribution of the numbers in the cells of the table. Many packages provide the results of Fisher's exact test for 2 × 2 contingency tables but not for bigger contingency tables with more rows or columns. For example, the SPSS statistical package automatically provides an analytical result of Fisher's exact test as well as chi-squared test only for 2 × 2 contingency tables. For Fisher's exact test of bigger contingency tables, we can use web pages providing such analyses. For example, the web page ‘Social Science Statistics’ (http://www.socscistatistics.com/tests/chisquare2/Default2.aspx) permits performance of Fisher exact test for up to 5 × 5 contingency tables.
The procedure of chi-squared test and Fisher's exact test using IBM SPSS Statistics for Windows Version 23.0 (IBM Corp., Armonk, NY, USA) is as follows: 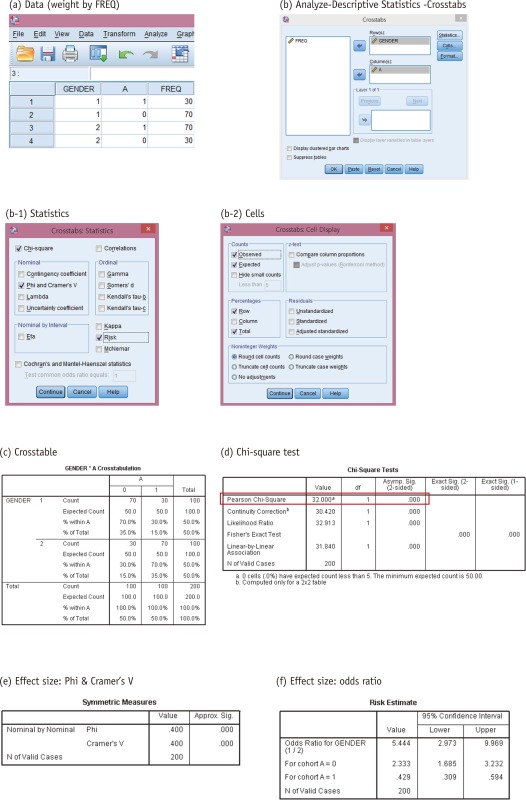
References
- 1.Bewick V, Cheek L, Ball J. Statistics review 8: qualitative data - tests of association. Crit Care. 2004;8:46–53. doi: 10.1186/cc2428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cohen J. Statistical power and analysis for the behavioral sciences. 2nd ed. Hisdale, NJ: Lawrence Erlbaum Associates; 1988. pp. 79–80. [Google Scholar]


