Testing Differential Networks with Applications to Detecting Gene-by-Gene Interactions

Summary

Model organisms and human studies have led to increasing empirical evidence that interactions among genes contribute broadly to genetic variation of complex traits. In the presence of gene-by-gene interactions, the dimensionality of the feature space becomes extremely high relative to the sample size. This imposes a significant methodological challenge in identifying gene-by-gene interactions. In the present paper, through a Gaussian graphical model framework, we translate the problem of identifying gene-by-gene interactions associated with a binary trait D into an inference problem on the difference of two high-dimensional precision matrices, which summarize the conditional dependence network structures of the genes. We propose a procedure for testing the differential network globally that is particularly powerful against sparse alternatives. In addition, a multiple testing procedure with false discovery rate control is developed to infer the specific structure of the differential network. Theoretical justification is provided to ensure the validity of the proposed tests and optimality results are derived under sparsity assumptions. A simulation study demonstrates that the proposed tests maintain the desired error rates under the null and have good power under the alternative. The methods are applied to a breast cancer gene expression study.

1. INTRODUCTION

High throughput technologies, enabling comprehensive monitoring of a biological system, have fundamentally transformed biomedical research. Studies using such technologies have led to successful molecular classifications of diseases into clinically relevant subtypes and genetic signatures predictive of disease progression and treatment response (van’t Veer et al., 2002; Gregg et al., 2008; Hu et al., 2009, e.g.). Irrespective of the technology used, analysis of high-throughput data typically considers one marker at a time and yields a list of differentially expressed genes or proteins. On the other hand, epistasis, or interactions between genes, has long been recognized as crucial to understanding the genetic architecture of disease phenotypes (Phillips, 2008; Eichler et al., 2010). Increasing empirical evidence from model organisms and human studies suggests that gene-by-gene interactions may make an important contribution to total genetic variation of complex traits (Zerba et al., 2000; Marchini et al., 2005). In this paper, we are specifically interested in gene-by-gene interactions with respect to the interactive effects of two genes on a binary disease trait D.

In the presence of gene-by-gene interactions, the dimensionality of the feature space becomes extremely high relative to the sample size. This, together with the variability of the data, imposes a significant methodological challenge in identifying gene-by-gene interactions using currently available studies, which typically have limited sample sizes and power. Recent development in interaction modeling has led to several useful methods including multi-factor dimensionality reduction (Ritchie et al., 2001; Moore, 2004), polymorphism interaction analysis (Mechanic et al., 2008), random forests (Breiman, 2001), various variations of logistic regression with interactive effects (Chatterjee et al., 2006; Chapman & Clayton, 2007; Kooperberg & Ruczinski, 2005; Kooperberg & LeBlanc, 2008) and sure independence screening (Fan & Lv, 2008). However, to overcome the high dimensionality, a majority of these methods use multistage procedures and marginal assessments of the effects of a gene pair without simultaneously accounting for the effects of other genes. Multistage procedures may have limited power in detecting genes that affect the outcome through interactions with other genes without strong main effects. The interactive effects detected through models that only consider one pair of genes at a time without conditioning on other genes may also result in false identification of interactions due to the discrepancy between conditional and unconditional effects. Furthermore, none of the existing methods provide false discovery rate control in the presence of interactions. Due to the large number of tests, the power of multiple testing procedures using the standard Bonferroni or naive false discovery rate corrections can dissipate quickly.

In this paper, through a Gaussian graphical model framework, we translate the problem of identifying gene-by-gene interactions associated with a binary trait D into the comparison of two high-dimensional precision matrices. Let G denote a p × 1 vector of genomic markers and assume that, conditional on D = d, G ~ N(μ_d, Σ_d), for d = 1, 2. Then the posterior risk given G is

$$\text{pr}(D=1|G)=g\{\text{constant}-\frac{1}{2}{G}^{\mathrm{T}}({\mathrm{\Omega }}_1-{\mathrm{\Omega }}_2)G+G^{\mathrm{T}}({\mathrm{\Omega }}_1{\mu }_1-{\mathrm{\Omega }}_2{\mu }_2)\}$$

where g(x) = e^x/(1 + e^x) and ${\mathrm{\Omega }}_d=({\omega }_{i,j,d})={\displaystyle {\sum }_d^{-1}}$ is the precision matrix for G conditional on D = d. Hence, an interaction between the gene pair (i, j) affects the disease risk if and only if δ_i,j= ω_i,j,1 − ω_i,j,2 = 0. The difference between the two precision matrices, denoted by Δ = (δ_i,j) = Ω₁ – Ω₂, is called the differential network. This type of model for a differential network has been used in Li et al. (2007) and Danaher et al. (2014). We thus propose to test for gene-by-gene interactions both by testing the global hypotheses

$$H_0:\mathrm{\Delta }=0\text{versus}{H}_1:\mathrm{\Delta }\ne 0,$$ (1)

and by simultaneously testing the hypotheses

$$H_{0,i,j}:{\delta }_{i,j}=0\text{versus}{H}_{1,i,j}:{\delta }_{i,j}\ne 0,1\le i<j\le p,$$

while controlling for the overall false discovery rate at a pre-specified level.

Few authors have considered testing the equality of two precision matrices in the high-dimensional setting. The global null hypothesis Δ = 0, or equivalently Ω₁ = Ω₂, corresponds to the hypothesis that none of the gene pairs have interactive effects on D. The equality of two precision matrices is equivalent to the equality of two covariance matrices, and the latter has been studied under various alternatives. Under the dense alternative, where Σ₁ and Σ₂ differ in a large number of entries, various sum-of-square type testing procedures have been proposed (Schott, 2007; Srivastava & Yanagihara, 2010; Li & Chen, 2012). Under the sparse alternative with Σ₁ and Σ₂ differing only in a small number of entries, Cai et al. (2013) introduced a particularly powerful test. However, in the gene-by-gene interaction setting, the goal is to identify the structure of the differential network. In such cases, it is often reasonable to assume that Δ is sparse, while Σ₁ – Σ₂ is not. Hence, testing procedures that can leverage information on the sparsity of Δ may improve power. Furthermore, due to the fundamental difference between conditional and unconditional dependences, the various procedures for testing the covariance matrices may not be well adapted to testing specific entries of the precision matrices.

The first goal of this paper is to develop a global test for H₀ : Δ = 0 that is powerful against sparse alternatives. We then develop a multiple testing procedure for simultaneously testing the hypotheses {H_0,i,j : 1 ≤ i < j ≤ p} with false discovery rate control to infer the structure of the differential network. In the high-dimensional setting, there is no sample precision matrix that one can use to approximate Ω_d. We propose to infer Ω_d by relating its elements to the coefficients of a set of regression models for G conditional on D = d. We then construct test statistics based on the covariances between the residuals from the fitted regression models. The testing procedures are easy to implement. A Matlab implementation is available in the Supplementary Material.

2. Global Testing of Differential Networks

2.1. Notation and Definitions

In this section we consider testing the global hypothesis (1). We begin with notation and definitions that will be used in the rest of the paper. Let X_k ε ℝ^p and Y_k ε ℝ^p denote G given D = 1 and D = 2, respectively, X_k ~ N(μ₁,Σ₁) for k = 1,…, n₁, Y_k ~ N(μ₁,Σ₂) for k = 1,…, n₂, where Σ_d = (σ_i,j,d) for d = 1, 2, and {X_k : k = 1,…, n₁} and {Y_k : k = 1,…, n₂} are independent observations from the two populations. Let X = (X₁,…, X_n1)^T and Y = (Y₁,…, Y_n2)^T denote the data matrices. Let ${\mathrm{\Omega }}_d=({\omega }_{i,j,d})={\displaystyle {\sum }_d^{-1}}$, for d = 1,2.

For subscripts, we use the convention that i stands for the i^th entry of a vector and (i,j) for the entry in the i^th row and j^th column of a matrix, k represents the k^th sample and d indexes the binary trait. Let β_i,₁ = (β_1,i,1,…,β_p−1,i,1)^T denote the regression coefficients of X_k,i regressed on the rest of the entries of X_k and let β_i,2 = (β₁,_i,2,…,β_p−1,i,2)^T denote the regression coefficients of Y_k,i regressed on the rest of the entries of Y_k.

For any vector μ_d with dimension p × 1, let μ_−i,d denote the (p – 1) × 1 vector by removing the i^th entry from μ_d. For a symmetric matrix A, let λ_max(A) and λ_min(A) denote the largest and smallest eigenvalues of A. For any p × q matrix A, A_i,_−j denotes the i^th row of A with its j^th entry removed and A_−i,j denotes the j^th column of A with its i^th entry removed. The matrix A_−i,_−j denotes a (p – 1) × (q – 1) matrix obtained by removing the i^th row and j^th column of A. For an n × p data matrix U = (U₁,…, U_n)^T, let $U{.}_{,-i}={(U_{1,-i}^{\mathrm{T}},\dots ,U_{n,-i}^{\mathrm{T}})}^{\mathrm{T}}$ with dimension $n\times (p-1),\overline{U}{.}_{,-i}=n^{-1}{\displaystyle {\sum }_{k=1}^n{U}_{k,-i}}$ with dimension 1 × (p − 1), U_(i) = (U₁,_i,…, U_n,i)^T with dimension $n\times 1,{\overline{U}}_{(i)}={({\overline{U}}_i,\dots ,{\overline{U}}_i)}^{\mathrm{T}}$ with dimension n × 1, where ${\overline{U}}_i=n^{-1}{\displaystyle {\sum }_{k=1}^n{U}_{k,i}}$, and ${\overline{U}}_{(\cdot ,-i)}={({\overline{U}}_{\cdot ,-i}^{\mathrm{T}},\dots ,{\overline{U}}_{\cdot ,-i}^{\mathrm{T}})}^{\mathrm{T}}$ with dimension n × (p − 1). For tuning parameters λ, let ${\lambda }_{n_d,i,d}$ represent the i^th tuning parameter for binary trait d, which depends on the sample size n_d.

For a vector β = (β₁,…,β_p)^T ε ℝ^p, define the ℓ_q norm by $|\beta {|}_q={({\displaystyle {\sum }_{i=1}^p|{\beta }_i{|}^q})}^{1/q}$ for 1 ≤ q ≤ ∞. A vector β is called k-sparse if it has at most k nonzero entries. For a matrix Ω = (ω_i,j)_p×p, the matrix 1-norm is the maximum absolute column sum, $\Vert \mathrm{\Omega }{\Vert }_{L_1}={max}_{1\le i,j\le p}{\displaystyle {\sum }_{i=1}^p|{\omega }_{i,j}|}$, the matrix elementwise infinity norm is defined to be ||Ω||_∞ = max_1≤i,j≤p |ω_i,j| and the elementwise ℓ₁ norm is $\Vert \mathrm{\Omega }{\Vert }_1={{\displaystyle {\sum }_{i=1}^p{\displaystyle {\sum }_{j=1}^p|\omega }}}_{i,j}|$. For a matrix Ω, we say Ω is k-sparse if each row/column has at most k nonzero entries. For a set ℋ, denote by |ℋ| the cardinality of ℋ. For two sequences of real numbers {a_n} and {b_n}, write a_n = O(b_n) if there exists a constant C such that |a_n| ≤ C|b_n| holds for all n, write a_n = o(b_n) if lim_n→∞ a_n/b_n = 0, and write a_n ≍ b_n if there are positive constants c and C such that c ≤ a_n/b_n ≤ C for all n.

2 2. Testing Procedure

It is well known (e.g., Anderson, 2003, Section 2.5), that in the Gaussian setting the precision matrix can be described in terms of regression models. Specifically, we may write

$$X_{k,i}={\alpha }_{i,1}+X_{k,-i}{\beta }_{i,1}+{\epsilon }_{k,i,1},(i=1,\dots ,p;k=1,\dots ,n_1),$$ (2)

$$Y_{k,i}={\alpha }_{i,2}+Y_{k,-i}{\beta }_{i,2}+{\epsilon }_{k,i,2},(i=1,\dots ,p;k=1,\dots ,n_2),$$ (3)

where ${\epsilon }_{k,i,d}\sim N(0,{\sigma }_{i,i,d}-{\displaystyle {\sum }_{i,-i,d}{\displaystyle {\sum }_{-i,-i,d}^{-1}{\displaystyle {\sum }_{-i,i,d}}}})(d=1,2)$, are independent of X_k,−i and Y_k,−i respectively, and ${\alpha }_{i,d}={\mu }_{i,d}-{\displaystyle {\sum }_{i,-i,d}{\displaystyle {\sum }_{-i,-i,d}^{-1}{\mu }_{-i,d}}}$. The regression coefficient vectors β_i,d and the error terms ε_k,i,d satisfy

$${\beta }_{i,d}=-{\omega }_{i,i,d}^{-1}{\mathrm{\Omega }}_{-i,i,d},r_{i,j,d}=\mathrm{cov}({\epsilon }_{k,i,d},{\epsilon }_{k,j,d})=\frac{{\omega }_{i,j,d}}{{\omega }_{i,i,d}{\omega }_{j,j,d}},$$

where cov(·,·) denotes the population covariance. Since the null hypothesis H₀ : Δ = 0 is equivalent to the hypothesis

$$H_0:\underset{1\le i\le j\le p}{max}|{\omega }_{i,j,1}-{\omega }_{i,j,2}|=0,$$

a natural approach to test H₀ is to first construct estimators of ω_i,j,d, and then base the test on the maximum standardized differences. We first construct estimators of r_i,j,d

Let ${\widehat{\beta }}_{i,d}={({\widehat{\beta }}_{1,i,d},\dots ,{\widehat{\beta }}_{p-1,i,d})}^{\mathrm{T}}$ be estimators of β_i,d satisfying

$$\underset{1\le i\le p}{max}|{\widehat{\beta }}_{i,d}-{\beta }_{i,d}|1=o_{\mathit{p}}\{{(\log p)}^{-1}\},$$ (4)

$$\underset{1\le i\le p}{max}|{\widehat{\beta }}_{i,d}-{\beta }_{i,d}|2=o_{\mathit{p}}\{{(n_d\log p)}^{-1/4}\}.$$ (5)

Estimators ${\widehat{\beta }}_{i,d}$ that satisfy (4) and (5) can be obtained easily via methods such as the lasso and Dantzig selector. See Section 2.3 for details. Define the residuals by

$${\widehat{\epsilon }}_{k,i,1}=X_{k,i}-{\overline{X}}_i-(X_{k,-i}-\overline{X}{.}_{,-i}){\widehat{\beta }}_{i,1},{\widehat{\epsilon }}_{k,i,2}=Y_{k,i}-{\overline{Y}}_i-(Y_{k,-i}-\overline{Y}{.}_{,-i}){\widehat{\beta }}_{i,2}.$$

A natural estimator of r_i,j,d is the sample covariance between the residuals,

$${\stackrel{\sim }{r}}_{i,j,d}=\frac{1}{n_d}{\displaystyle \sum _{k=1}^{n_d}{\widehat{\epsilon }}_{k,i,d}}{\widehat{\epsilon }}_{k,j,d}.$$ (6)

However, when $i\ne j,{\stackrel{\sim }{r}}_{i,j,d}$ tends to be biased due to the correlation induced by the estimated parameters and it is desirable to construct a bias-corrected estimator. Lemma 2 shows that

$${\stackrel{\sim }{r}}_{i,j,d}={\stackrel{\sim }{R}}_{i,j,d}-{\stackrel{\sim }{r}}_{i,i,d}({\widehat{\beta }}_{i,j,d}-{\beta }_{i,j,d})-{\stackrel{\sim }{r}}_{j,j,d}({\widehat{\beta }}_{j-1,i,d}-{\beta }_{j-1,i,d})+o_{\mathrm{p}}\{{(n_d\log p)}^{-\frac{1}{2}}\}$$

where ${\stackrel{\sim }{R}}_{i,j,d}$ is the empirical covariance between {ε_k,i,d: k = 1,… ,n_d} and {ε_k,j,d : k = 1,…,n_d}. For 1 ≤ i ≤ j ≤ p, β_i,j,d = − ω_i,j,d/ω_j,j,d and β_j−1,i,d = −ω_i,j,d/ω_i,i,d Thus, we propose a bias-corrected estimator of r_i,j,d as

$${\widehat{r}}_{i,j,d}=-({\stackrel{\sim }{r}}_{i,j,d}+{\stackrel{\sim }{r}}_{i,i,d}{\widehat{\beta }}_{i,j,d}+{\stackrel{\sim }{r}}_{j,j,d}{\widehat{\beta }}_{j-1,i,d}),1\le i<j\le p.$$ (7)

The bias of ${\widehat{r}}_{i,j,d}$ is of order max{r_i,j,d(log p/n_d)^1/2,(n_dlog p)^−1/2}.

For i = j, note that r_i,i,d = 1/u_i,_i,_d. We show in Lemma 2 that

$$\underset{1\le i\le p}{max}|{\stackrel{\sim }{r}}_{i,i,d}-r_{i,i,d}|=O_{\mathrm{p}}\{{(\log p/n_d)}^{1/2}\},$$

which implies that ${\widehat{r}}_{i,i,d}={\stackrel{\sim }{r}}_{i,i,d}$ is a nearly unbiased estimator of r_i,i,d. A natural estimator of ω_i,j,d can then be defined by

$${\mathrm{T}}_{i,j,d}=\frac{{\widehat{r}}_{i,j,d}}{{\widehat{r}}_{i,i,d}{\widehat{r}}_{j,j,d}},1\le i\le j\le p$$ (8)

We test H₀ : Δ = 0 based on the estimators $\mathcal{T}=\{{\mathrm{T}}_{i,j,1}-{\mathrm{T}}_{i,j,2}:1\le i\le j\le p\}$

The estimators T_i,j,1 − T_i,j,2 in $\mathcal{T}$ are heteroscedastic and possibly have a wide range of variability. We first standardize T_i,j,1 − T_i,j,2 before combining information from all entries in $\mathcal{T}$. Let $U_{i,j,d}=(1/n_d){\displaystyle {\sum }_{k=1}^{n_d}\{{\epsilon }_{k,i,d}{\epsilon }_{k,j,d}-E({\epsilon }_{k,i,d}{\epsilon }_{k,j,d})\}}$ and ${\stackrel{\sim }{U}}_{i,j,d}=(r_{i,j,d}-U_{i,j,d})/(r_{i,i,d}{r}_{j,j,d})$. It will be shown in Lemma 2 that, uniformly in 1 ≤ i ≤ j ≤ p,

$$|{\mathrm{T}}_{i,j,d}-{\stackrel{\sim }{U}}_{i,j,d}|=O_{\mathrm{p}}\{{(\log p/n_d)}^{\frac{1}{2}}\}{r}_{i,j,d}+o_{\mathrm{p}}\{{(n_d\log p)}^{-\frac{1}{2}}\}.$$

Let ${\theta }_{i,j,d}=\mathrm{var}({\stackrel{\sim }{U}}_{i,j,d})$. Note that

$${\theta }_{i,j,d}=\mathrm{var}\{{\epsilon }_{k,i,d}{\epsilon }_{k,j,d}/(r_{i,i,d}{r}_{j,j,d})\}/n_d=(1+{\rho }_{i,j,d}^2)/(n_d{r}_{i,i,d}{r}_{j,j,d}),$$

where ${\rho }_{i,j,d}^2={\beta }_{i,j,d}^2{r}_{i,i,d}/r_{j,j,d}$. We then estimate θ_i,j,d by

$${\widehat{\theta }}_{i,j,d}=(1+{\widehat{\beta }}_{i,j,d}^2{\widehat{r}}_{i,i,d}/{\widehat{r}}_{j,j,d})/(n_d{\widehat{r}}_{i,i,d}{\widehat{r}}_{j,j,d}).$$

Define the standardized statistics

$$W_{i,j}=\frac{{\mathrm{T}}_{i,j,1}-{\mathrm{T}}_{i,j,2}}{{({\widehat{\theta }}_{i,j,1}+{\widehat{\theta }}_{i,j,2})}^{1/2}},1\le i\le j\le p.$$ (9)

Finally, we propose the following test statistic for testing the global null hypothesis H₀,

$$M_n=\underset{1\le i\le j\le p}{max}{W}_{i,j}^2=\underset{1\le i\le j\le p}{max}\frac{{({\mathrm{T}}_{i,j,1}-{\mathrm{T}}_{i,j,2})}^2}{{\widehat{\theta }}_{i,j,1}+{\widehat{\theta }}_{i,j,2}}.$$ (10)

The asymptotic properties of M_n will be studied in detail in Section 3. Intuitively, {W_i,j} are approximately standard normal variables under the null H₀ and they are only weakly dependent under suitable conditions. Thus M_n is the maximum of the squares of p(p + 1)/2 such random variables, so its value should be close to 2 log{p(p + 1)/2} ≈ 4 log p under H₀. We show in Section 3 that, under certain regularity conditions, M_n − 4 log p − log log p converges to a type I extreme value distribution under H₀ : Δ = 0.

Based on the limiting null distribution of M_n, which will be developed in Section 3.1, we define the test ψ_α by

$${\mathrm{\Psi }}_{\alpha }=I(M_n\ge q_{\alpha }+4\log p-\log \log p)$$ (11)

where q_α is the 1 − α quantile of the type I extreme value distribution with the cumulative distribution function exp{(8π)^−1/2e^−t/2}, i.e.,

$$q_{\alpha }=-\log (8\pi )-2\log \log {(1-\alpha )}^{-1}.$$ (12)

The hypothesis H₀ is rejected whenever ψ_α = 1.

2.3. Data-driven estimation of regression coefficients

The testing procedure requires the estimation of regression coefficients β_i,d, for i = 1,…,p and d = 1, 2. Various estimators have been studied in the literature, including the lasso and Dantizg selector. Here, we use the lasso by solving the optimization problem,

$${\widehat{\beta }}_{i,1}=D_{i,1}^{-1/2}\underset{u\in {ℝ}^{p-1}}{\arg min}\{{(2n_1)}^{-1}|(X{.}_{,-i}-{\overline{X}}_{(\cdot ,-i)})D_{i,1}^{-1/2}u-(X_{(i)}-{\overline{X}}_{(i)}){|}_2^2+{\lambda }_{n_1,i,1}|u|1\},$$ (13)

$${\widehat{\beta }}_{i,2}=D_{i,2}^{-1/2}\underset{v\in {ℝ}^{p-1}}{\arg min}\{{(2n_2)}^{-1}|(Y{.}_{,-i}-{\overline{Y}}_{(\cdot ,-i)})D_{i,2}^{-1/2}v-(Y_{(i)}-{\overline{Y}}_{(i)}){|}_2^2+{\lambda }_{n_2,i,2}|v|1\},$$ (14)

where $D_{i,d}=\text{diag}({\widehat{\sum }}_{-i,-i,d})$ and ${\lambda }_{n_d,i,d}={\kappa }_d{({\widehat{\sigma }}_{i,i,d}\log p/n_d)}^{1/2}$ , d = 1,2. Then by Proposition 4.2 of Liu (2013), under Condition (C1) given in Section 3 and a mild condition on the sparsity of β_i,d (i = 1,…, p, d = 1,2), the convergence rates in (4) and (5) can be guaranteed by using any κ_d > 2. The result is formally stated in Corollary 1. In practice, κ_d = 2 works well for global testing of H₀ : Δ = 0, and for the multiple testing procedure with false discovery rate control, a data-driven algorithm is proposed in Section 5 to select κ_d adaptively.

2.4. Discussion

The global test ψ_α given in (11) is based on estimators of ω_i,j,₁ − ω_i,j,₂ Here we estimate ω_i,j,d by first constructing estimators for r_i,j,d = ω_i,j,d/(ω_i,i,dω_j,j,d), and then estimating r_i,j,d through bias correction of the residuals ${\widehat{r}}_{i,j,d}$ defined in (7).

Liu (2013) considered multiple testing of entries of a single precision matrix Ω = (ω_i,j). In the one-sample case, ω_i,j = 0 is equivalent to r_i,j= ω_i,j/(ω_i,iω_j,j) = 0 under the null and r_i,j is easier to estimate. The procedure in Liu (2013) is based on the estimation of r_i,j instead of ω_i,j. However, in Section 4 we will also consider multiple testing between two groups, and ω_i,j,₁= ω_i,j,2 is not equivalent to r_i,j,₁= r_i,j,2. Thus, it is necessary to construct testing procedures based directly on estimators of ω_i,j,₁ − ω_i,j,₂.

Testing the global hypothesis H₀ : Ω₁ = Ω₂ is equivalent to testing H₀ : Σ₁ = Σ₂, which has been well studied (Schott, 2007; Srivastava & Yanagihara, 2010; Li & Chen, 2012; Cai et al., 2013). In particular, Cai et al. (2013) constructed a global test for H₀ : Σ₁ = Σ₂ that is powerful against the alternative where Σ₁ − Σ₂ is sparse. However, in many applications, the goal is to learn the structure of the differential network, and we are interested in both testing the global hypothesis H₀ : Ω₁ = Ω₂ and multiple testing of the entrywise hypotheses H_0,i,j : ω_i,j,₁ = ω_i,j,2. In such cases, it is often reasonable to assume that Δ = Ω₁ − Ω₂ is sparse, but Σ₁ − Σ₂ is not. Hence, testing procedures for H₀ : Σ₁ = Σ₂ cannot leverage information on the sparsity of Δ and more importantly do not naturally lead to a multiple testing procedure for simultaneously testing the entrywise hypotheses H_0,i,j : ω_i,j,₁ = ω_i,j,2.

3. Theoretical Results for the Global Test

3 1. Asymptotic Null Distribution of M_n

In this section, we analyze the properties of the new test for testing the global null hypothesis H₀ : Δ = 0, including the null distribution of the test statistic M_n, the asymptotic size and power. We are particularly interested in the power of the new test under the alternative with Δ sparse. We further show that the power is minimax rate optimal.

Under assumptions (C1) and (C2), Theorem 1 indicates that under H₀, M_n − 4 log p + log log p converges weakly to a Gumbel random variable with distribution function exp{−(8π)^−1/2e^−t/2}.

• (C1)Assume that log p = o(n^1/5), n₁ ≍ n₂, and for some constant $C_0>0,C_0^{-1}\le {\lambda }_{min}({\mathrm{\Omega }}_d)\le {\lambda }_{max}({\mathrm{\Omega }}_d)\le C_0$, for d = 1,2. There exists some τ > 0 such that | A_τ| = o(p^1/16) where A_τ = {(i,j) : |ω_i,j,d| ≥ (log p)^−2−τ, 1 ≤ i<j ≤ p, for d = 1 or 2}.
• (C2)Let D_d be the diagonal of Ω_d and let $({\eta }_{i,j,d})=R_d=D_d^{-1/2}{\mathrm{\Omega }}_d{D}_d^{-1/2}$, for d = 1,2. Assume that max_{1≤i≤j≤p} |η_i,j,d| ≤ η_d ≤ 1 for some constant 0 < η_d < 1.

Condition (C1) on the eigenvalues is a common assumption in the high-dimensional setting and implies that most of the variables are not highly correlated with each other. Condition (C2) is also mild. For example, if max_{1≤i≤j≤p} |η_i,j,d| = 1, then Ω_d is singular. The following theorem states the asymptotic null distribution for M_n.

Theorem 1

Suppose that (C1), (C2), (4) and (5) hold. Then under H₀, for any t ε ℝ,

$$\text{pr}(M_n-4\log p+\log \log p\le t)\to \exp \{-{(8\pi )}^{-1/2}\exp (-t/2)\},as{n}_1,n_2,p\to \infty ,$$ (15)

where M_n is defined in equation (10). Under H₀, the convergence in (15) is uniform for all {X_k : k = 1,…, n₁} and {Y_k : k = 1,…, n₂} satisfying (C1), (C2), (4) and (5).

Equations (4) and (5) are mild conditions on the estimator of β_i,d in order to obtain the limiting distribution in Theorem 1. As discussed in Section 2 3, these conditions can be guaranteed by the lasso estimator for example.

Corollary 1

Suppose that (C1) and (C2) hold and max_1≤i≤p |β_i,_d|₀ = o{n^1/2 / (log p)^3/2}. Then under H₀, for any κ_d > 2 in (13) and (14), and for any t ε ℝ,

$$\text{pr}(M_n-4\log p+\log \log p\le t)\to \exp \{-{(8\pi )}^{-1/2}\exp (-t/2)\},n_1,n_2,p\to \infty ,$$ (16)

where M_n is defined in (10).

3 2. Power Analysis

We now turn to an analysis of the power of the test ψ_α given in (11). We shall define the following class of precision matrices:

$$\mathcal{U}(c)=\left\{({\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2):\underset{1\le i\le j\le p}{max}\frac{|{\omega }_{i,j,1}-{\omega }_{i,j,2}|}{{({\theta }_{i,j,1}+{\theta }_{i,j,2})}^{1/2}}\ge c{(\log p)}^{1/2}\right\}.$$ (17)

The next theorem shows that the null parameter set in which Ω₁ = Ω₂ is asymptotically distinguishable from $\mathcal{U}$(4) by the test ψ_α. That is, H₀ is rejected by the test ψ_α with overwhelming probability if $({\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2)\in \mathcal{U}(4)$.

Theorem 2

Let the test ψ_α be given as in (11). Suppose that (C1), (4) and (5) hold. Then

$$\underset{({\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2)\in \mathcal{U}(4)}{\inf }\text{pr}({\mathrm{\Psi }}_{\alpha }=1)\to 1,n,p\to \infty .$$

The following result shows that this lower bound is rate-optimal. Let ${\mathcal{T}}_{\alpha }$ be the set of all α-level tests, i.e., pr(T_α = 1) ≤ α under H₀ for all ${\mathrm{T}}_{\alpha }\in {\mathcal{T}}_{\alpha }$.

Theorem 3

Suppose that log p = o(n). Let α, β > 0 and α + β < 1. Then there exists a constant c₀ > 0 such that for all sufficiently large n and p,

$$\underset{({\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2)\in \mathcal{U}(c_0)}{\inf }\underset{{\mathrm{T}}_{\alpha }\in {\mathcal{T}}_{\alpha }}{\sup }\text{pr}({\mathrm{T}}_{\alpha }=1)\le 1-\beta .$$

Theorem 3 shows that, if c₀ is sufficiently small, then any α level test is unable to reject the null hypothesis correctly uniformly over $({\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2)\in \mathcal{U}(c_0)$ with probability tending to one. So the order (logp)^1/2 in the lower bound of max_{1≤i≤j≤p}{|ω_i,j,₁ − ω_i,j,2/(θ_i,j,₁ + θ_i,j,₂)^1/2} in (17) cannot be improved.

4. Multiple Testing with False Discovery Rate Control

If the global null hypothesis is rejected, it is often of interest to investigate the structure of the differential network Δ. A natural approach is to carry out simultaneous testing on the elements of Δ. In this section, we introduce a multiple testing procedure with false discovery rate control for testing (p² − p) /2 hypotheses

$$H_{0,i,j}:{\delta }_{i,j}=0\text{versus}{H}_{1,i,j}:{\delta }_{i,j}\ne 0,1\le i<j\le p.$$ (18)

The standardized differences of T_i,j,₁ and T_i,j,₂ are defined by the test statistics $W_{i,j}=({\mathrm{T}}_{i,j,1}-{\mathrm{T}}_{i,j,2})/{({\widehat{\theta }}_{i,j,1}+{\widehat{\theta }}_{i,j,2})}^{1/2}$ as in (9). Let t be the threshold level such that H_0,i,j is rejected if |W_i,j |≥ t. Let ℋ₀ = {(i, j) : δ_i,j = 0,1 ≤ i < j ≤ p} be the set of true nulls. Denote by $R_0(t)={\displaystyle {\sum }_{(i,j)\in {\mathscr{H}}_0}I(|W_{i,j}|\ge t)}$ the total number of false positives, and by R(t) = Σ_1≤i<j≤p I(|W_i,j|≥ t) the total number of rejections. The false discovery proportion and false discovery rate are defined as

$$\text{FDP}(t)=\frac{R_0(t)}{R(t)\vee 1},\text{FDR}(t)=E\{\text{FDP}(t)\}.$$

An ideal choice of t would reject as many true positives as possible while controlling the false discovery rate and false discovery proportion at the pre-specified level α. That is, we select

$$t_0=\inf \left\{0\le t\le 2{(\log p)}^{1/2}:\text{FDP}(t)\le \alpha \right\}.$$

Since ℋ₀ is unknown, we can estimate ${\displaystyle {\sum }_{(i,j)\in {\mathscr{H}}_0}I\{|W_{i,j}|\ge t\}}$ by $2\{1-\mathrm{\Phi }(t)\}|{\mathscr{H}}_0|$ as in Liu (2013), where ϕ(t) is the standard normal cumulative distribution function. Note that $|{\mathscr{H}}_0|$ can be estimated by (p² − p)/2 due to the sparsity of Δ. This leads to the following multiple testing procedure.

1. Calculate the test statistics W_i,j.

2. For given 0 ≥ α ≥ 1, calculate

   $$\widehat{t}=\inf \left\{0\le t\le 2{(\log p)}^{1/2}:\frac{2\{1-\mathrm{\Phi }(t)\}(p^2-p)/2}{R(t)\vee 1}\le \alpha \right\}.$$

   If $\widehat{t}$ does not exists, set $\widehat{t}=2{(\log p)}^{1/2}$.

3. For 1 ≤ i < j ≤ p, reject H₀,_i,i,. if and only if $|W_{i,j}|\ge \widehat{t}$.

The following theorem shows that, under regularity conditions, the above procedure controls the false discovery proportion and false discovery rate at the pre-specified level α asymptotically.

Theorem 4

Let

$${\mathcal{S}}_{\rho }=\left\{(i,j):1\le i<j\le p,\frac{|{\omega }_{i,j,1}-{\omega }_{i,j,2}|}{{({\theta }_{i,j,1}+{\theta }_{i,j,2})}^{1/2}}\ge {(\log p)}^{1/2+\rho }\right\}.$$

Suppose for some ρ > 0 and some δ > 0, $|{\mathcal{S}}_{\rho }|\ge [1/\{{(8\pi )}^{1/2}\alpha \}+\delta ]{(\log \log p)}^{1/2}$. Suppose that $|A_{\mathcal{T}}\cap {\mathscr{H}}_0|=o(p^{\nu })$ for any ν > 0, where $A_{\tau }$ is given in Condition (C1). Assume that $q_0=|{\mathscr{H}}_0|\ge c{p}^2$ for some c > 0, and (4) and (5) hold. Let q = (p² − p)/2. Then under (C1) with p ≤ cn^r for some c > 0 and r > 0, we have

$$\underset{(n,p)\to \infty }{\lim }\frac{\text{FDR}(\widehat{t})}{\alpha q_0/q}=1,\frac{\text{FDP}(\widehat{t})}{\alpha q_0/q}\to 1$$

in probability, as (n, p) → ∞.

The condition $|{\mathcal{S}}_{\rho }|\ge [1/\{{(8\pi )}^{1/2}\alpha \}+\delta ]{(\log \log p)}^{1/2}$ in Theorem 4 is mild, since there are (p² − p)/2 hypotheses in total and this condition only requires a few entries with the standardized difference having magnitude exceeding {(log p)^1/2+ρ/n}^1/2 for some constant ρ > 0. The technical condition $|A_{\mathcal{T}}\cap {\mathscr{H}}_0|=o(p^{\nu })$ for any ν > 0 is to ensure that most of the regression residuals are not highly correlated with each other under the null hypotheses H_0,i,j : δ_i,j = 0.

The basic idea for the proof of Theorem 4 is similar to that in Liu (2013). However, the setting here is more complicated as ω_i,j,₁ and ω_i,j,2 are not necessarily zero under H_0,i,j : δ_i,j = 0. So the coordinates of the regression residuals in (2) and (3) can be correlated with each other. Thus slightly stronger conditions are needed and the proof is more involved.

5. Simulation Study

The proposed testing procedures are easy to implement, and the Matlab code is available in the Supplementary Material. We carry out a simulation study to investigate the numerical performance, including the size and power, of the global test Ψ_α and the false discovery rate controlled multiple testing procedure.

We first introduce the matrix models used in the simulations. Let D = (D_i,j) be a diagonal matrix with D_i,i = Unif(0.5, 2.5) for i = 1,…,p. The following four models under the null, ${\mathrm{\Omega }}_1={\mathrm{\Omega }}_2={\mathrm{\Omega }}^{(m)}=({\omega }_{i,j}^{(m)})(m=1,\dots ,4)$, are used to study the size of the tests.

• Model 1: ${\mathrm{\Omega }}^{\ast (1)}=({\omega }_{i,j}^{\ast (1)})$ where ${\omega }_{i,i}^{\ast (1)}=1$, ${\omega }_{i,i+1}^{\ast (1)}={\omega }_{i+1,i}^{\ast (1)}=0.6$, ${\omega }_{i,i+2}^{\ast (1)}={\omega }_{i+2,i}^{\ast (1)}=0.3$ and ${\omega }_{i,j}^{\ast (1)}=0$ otherwise. Ω⁽¹⁾ = D^1/2Ω^*(1)D^1/2.

• Model 2: ${\mathrm{\Omega }}^{\ast (2)}=({\omega }_{i,j}^{\ast (2)})$ where ${\omega }_{i,j}^{\ast (2)}={\omega }_{j,i}^{\ast (2)}=0.5$ for i = 10(k − 1) + 1 and 10(k − 1) + 2 ≤ j ≤ 10(k − 1) + 10, 1 ≤ k ≤ p/10. ${\omega }_{i,j}^{\ast (2)}=0$ otherwise. Ω⁽²⁾ = D^1/2(Ω ^*(2) + δI)/(1 + δ)D^1/2 with δ = |λ_min(Ω^*(2))| + 0.05.

• Model 3: ${\mathrm{\Omega }}^{\ast (3)}=({\omega }_{i,j}^{\ast (3)})$ where ${\omega }_{i,i}^{\ast (3)}=1$, ${\omega }_{i,j}^{\ast (3)}=0.8\times \text{Bernoulli}(1,0.05)$ for i < j and ${\omega }_{j,i}^{\ast (3)}={\omega }_{i,j}^{\ast (3)}$. Ω⁽³⁾ = D^1/2(Ω^*(3)+ δI)/(1 + δ)D^1/2 with δ = |λ_min(Ω^*(3))| + 0.05.

• Model 4: ${\sum }^{\ast (4)}=({\sigma }_{i,j}^{\ast (4)})$ where ${\sigma }_{i,i}^{\ast (4)}=1$, ${\sigma }_{i,j}^{\ast (4)}=0.5$ for 2(k − 1) + 1 ≤ i ≠ j ≤ 2k, where k = 1,…, [p/2] and ${\sigma }_{i,j}^{\ast (4)}=0$ otherwise. Ω⁽⁴⁾ = d^1/2{(Σ^*(4) + δI)/(1 + δ)}⁻¹ D^1/2 with δ = |λ_min(Σ^*(4))| + 0.05.

For global testing of H₀ : Δ = 0, the sample sizes are taken to be n₁ = n₂ = 100, while the dimension p varies over the values 50, 100, 200 and 400. For each model, data are generated from multivariate normal distributions with mean zero and covariance matrices ${\sum }_1={\mathrm{\Omega }}_1^{-1}$ and ${\sum }_2={\mathrm{\Omega }}_2^{-1}$ The nominal significance level for all the tests is set at α₁ − 0.05.

To evaluate the power of the proposed tests, let U = (u_i,j) be a matrix with eight random nonzero entries. The locations of four nonzero entries are selected randomly from the upper triangle of U, each with a magnitude generated randomly and uniformly from the set [−2ω(log p/n)^1/2, −ω(log p/n)^1/2] ∪ [ω(log p/n)^1/2,2 ω(log p/n)^1/2], where $\omega ={max}_{1\le i\le p}{\omega }_{i,i}^{(m)}$. The other four nonzero entries in the lower triangle are determined by symmetry. We use the following four pairs of precision matrices $({\mathrm{\Omega }}_1^{(m)},{\mathrm{\Omega }}_2^{(m)})(m=1,\dots ,4)$, to show the power of the test, where ${\mathrm{\Omega }}_1^{(m)}={\mathrm{\Omega }}^{(m)}+\delta I$ and ${\mathrm{\Omega }}_2^{(m)}={\mathrm{\Omega }}^{(m)}+U+\delta I$, with δ = |min{λ_min(Ω^(m) + U), λ_min(Ω^(m))}| + 0.05. The actual sizes and powers in percentage for the four models, reported in Table 1, are estimated from 1000 replications.

Table 1.

Empirical sizes and powers (%) for global testing with α₁ = 0.05, n₁ = n₂ = 100, and 1000 replications.

p	Model 1	Model 2	Model 3	Model 4
	Size
50	3.8	3.9	5.4	4.4
100	3.6	4.4	4.1	3.8
200	3.4	3.6	3.7	3.9
400	3.5	3.7	3.6	3.5
	Power
50	100	98.7	95.6	81.6
100	99.7	96.6	95.1	77.8
200	93.1	88.2	93.6	72.1
400	86.3	73.1	77.7	70.7

Table 1 shows that the sizes of the global test ${\mathrm{\Psi }}_{{\alpha }_1}$ are close to the nominal level in all cases. This reflects the fact that the null distribution of the test statistic M_n is well approximated by its asymptotic distribution. The empirical sizes are slightly below the nominal level in some models, due to the correlation among the variables. Similar phenomena have also been observed in Cai et al. (2013) and are theoretically justified by their Proposition 1. Table 1 shows that the proposed test is powerful in all settings, although the two precision matrices differ only in eight entries with the magnitude of the difference of the order (log p/n)^1/2.

In addition, we consider nearer alternatives by generating the nonzero entries randomly and uniformly from the set [−ω(2 log p/n)^1/2, ω(2 log p/n)^1/2]. The power results are summarized in Table 2. Under the nearer alternatives, the magnitude of the standardized difference of Ω₁ − Ω₂ is smaller and as a result the power is lower.

Table 2.

Empirical power (%) for global testing under nearer alternatives.

p	Model 1	Model 2	Model 3	Model 4
	Power under nearer alternative
50	90.3	71.6	58.9	20.6
100	89.4	70.3	60.8	22.8
200	81.9	55.2	54.2	21.7
400	73.5	54.7	57.7	17.5

More extensive simulation results are presented in the Supplementary Material. The proposed test significantly outperforms both that of Cai et al. (2013), which is powerful when Σ₁ − Σ₂ is sparse under the alternative, and that of Li & Chen (2012), which is powerful when Σ₁ − Σ₂ is dense under the alternative.

For simultaneous testing of the individual entries of the differential network Δ with false discovery rate control, we select ${\lambda }_{n_d,i,d}$ in (13) and (14) adaptively with the principle of making ${\sum }_{(i,j)\in {\mathscr{H}}_0}I(|W_{i,j}|\ge t)$ and $\{2-2\mathrm{\Phi }(t)\}|{\mathscr{H}}_0|$ as close as possible. The algorithm is as follows.

1. For any given i ∈{1,…,p}, let ${\lambda }_{n_1,i,1}=(s/20){({\widehat{\sum }}_{i,i,1}\log p/n_1)}^{1/2}$ and ${\lambda }_{n_2,i,2}=(s/20){({\widehat{\sum }}_{i,i,2}\log p/n_2)}^{1/2}$ for s = 1,…, 40. For each s, calculate ${\widehat{\beta }}_{i,d}^{(s)}(i=1,\dots ,p)$ and d = 1,2. Based on the estimated regression coefficients, construct the corresponding standardized difference $W_{i,j}^{(s)}$ for each s.

2. Choose

   $$\widehat{s}=\arg min{\displaystyle \sum _{l=1}^{10}{\left(\frac{{\sum }_{1\le i\le j\le p}I\{|W_{i,j}^{(s)}|\ge {\mathrm{\Phi }}^{-1}(1-l[1-\mathrm{\Phi }\{{(\log p)}^{1/2}\}]/10)\}}{lp(p-1)[1-\mathrm{\Phi }\{{(\log p)}^{1/2}\}]/10}-1\right)}^2.}$$

The tuning parameters are chosen to be ${\lambda }_{n_1,i,1}=\widehat{s}/20{({\widehat{\sum }}_{i,i,1}\log p/n_1)}^{1/2}$ and ${\lambda }_{n_2,i,2}=\widehat{s}/20{({\widehat{\sum }}_{i,i,2}\log p/n_2)}^{1/2}$.

Pairwise comparisons among these four models are considered. The sample sizes are n₁ = n₂ = 100, while the dimension p = 50, 100, and 200. The false discovery rate level is set at α₂ = 0.1, and the empirical false discovery rate and the power of false discovery rate control in percentage, summarized in Table 3, are estimated from 100 replications. We examine the power based on the average powers for 100 replications as follows

$$\frac{1}{100}{\displaystyle \sum _{l=1}^{100}\frac{{\sum }_{(i,j)\in {\mathscr{H}}_1}I(|W_{i,j,l}|\ge \widehat{t})}{|{\mathscr{H}}_1|},}$$

where W_i,j,l denotes standardized difference for the l^th replication and ${\mathscr{H}}_1$ denotes the nonzero locations. For all six cases, the false discovery rates are close to α across all dimensions. For empirical power, the procedure is powerful when the dimension p is low, and retains high power for the comparisons between Model 1 and Models 2 and 4. However, for the comparison between Model 2 and Model 3, the power is low when dimension is high and this is because all of | ω_i,j,1 − ω_i,j,2|/(θ_i,j,1n₁ + θ_i,j,2n₂)^1/2 is smaller than 0.25 when p = 200 and D = I. Similarly, most nonzero entries of the standardized difference for Model 2 and 4 are smaller than 0.24. Thus it is difficult to detect nonzero locations. Furthermore, under the same scenario, ω_i,j/⁽θ_i,j^n)1/2 is always smaller than 0.16 for Model 3, and thus the detection becomes harder when we compare Model 3 with other models. Thus, the power results are not good when Model 3 is included in the comparison.

Table 3.

Empirical false discovery rate and power (%) with α₂ = 0.1, n₁ = n₂ = 100, and 100 replications.

p	Models 1, 2	Models 1, 3	Models 2, 3	Models 1, 4	Models 2, 4	Models 3, 4
	Empirical False Discovery Rate
50	10.5	11.0	12.6	12.2	11.5	10.2
100	9.5	10.0	12.1	11.8	11.4	9.5
200	9.7	10.4	11.2	11.7	11.6	10.3
	Power
50	67.9	65.6	35.7	55.0	30.2	26.1
100	64.2	38.3	19.3	51.4	25.1	18.2
200	61.1	20.6	17.1	46.1	21.7	11.3

6. Real Data Analysis

The high throughput technology and massively parallel measurement of mRNA expression catalyzed a new area of genomic biomarkers. A number of prominent genomic markers have been identified to assist in predicting breast cancer patient survival in clinical practice, and increasingly, pharmacogenomic endpoints are being incorporated into the design of clinical trials (Olopade et al., 2008). Molecular pathways of pathogenesis for breast cancer have also been increasingly discovered and curated (Nathanson et al., 2001). However, the role of gene-by-gene interactions, within and across pathways, in breast cancer survival remain unclear. Here, we apply our procedures to identify gene-by-gene interactions important for breast cancer survival.

For illustration, we consider 32 pathways from the molecular signature database that are related to breast cancer survival. Examples include the MAPK/ERK, WNT, TGF-β, P13k-AKT-mTOR and ATRBRCA pathways. Existing literature has indicated that a defect in the MAPK pathway may lead to uncontrolled growth, which is a step necessary for the development of all cancers (Santen et al., 2002; Downward, 2003). Mutations or deregulated expression of genes in the Wnt pathway can induce cancer (Klaus & Birchmeier, 2008). The TGF-β signaling pathway is critical to a plethora of cellular processes including cell proliferation, apoptosis and differentiation (Shi & Massagué, 2003). An increase in the TGF-β2 expression is associated with response to tamoxifen for breast cancer patients (Buck & Knabbe, 2006). The ATRBRCA pathway describes the role of BRCA1, BRCA2 and ATR in cancer susceptibility (Venkitaraman, 2002). BRCA1 and BRCA2 are the best-known genes linked to breast cancer risk. Hence, these pathways may play critical roles in breast cancer progression. To examine the interactions between genes in these pathways, we applied our procedure to a recent breast cancer gene expression study of 295 patients with primary breast carcinomas from the Netherlands Cancer Institute (van de Vijver et al., 2002). Out of the 32 pathways, there are a total of p = 754 genes with available data in this study. The two populations we consider are the short term survivors, defined as those 78 patients who died within 5 years; and the long term survivors, defined as those 69 patients who survived more than 10 years. We are particularly interested in identifying gene pairs with interactive effects on the binary cancer survival trait using the proposed procedures. In this setting, the sparsity assumption about β_i,k’s is reasonable as it is generally believed that transcriptional regulation of a single gene is generally defined by a small set of regulatory elements (Segal et al., 2003; Dobra et al., 2004).

Based on our proposed procedures, we identified nine pairs of gene-by-gene interactions as significant at a false discovery rate level of 0.1. An interaction here does not simply indicate a co-expression between a pair of genes, but instead represents a difference between the co-expression patterns among the long terms survivors and among the short term survivors. As shown in Figure 1, the majority of the genes involved in these interactions belong to five major pathways, the MAPK, WNT, TGF-β, Apoptosis, and ATRBRCA pathways, although many of these genes belong to multiple pathways. One pair of the identified interactions represent gene-by-gene interactions within pathways and the remaining eight pairs represent cross-talk between these pathways, some of which are previously documented. A total of five interactions are between the MAPK signaling pathway and the WNT and TGF-β, Apoptosis, ATRBRCA and MTA3 pathways. These cross-talks are not surprising since MAPK modulates a wide range of processes including gene expression, mitosis, proliferation, metabolism and apoptosis (Wada & Penninger, 2004). Several recent studies suggest extensive crosstalk between WNT and MAPK signaling pathways in cancer. For example, hyper-activation of MAPK signaling results in down-regulation of the WNT signal transduction pathway in melanoma, suggesting a negative crosstalk between the two pathways; while in colorectal cancer, stimulating the WNT pathway leads to activation of the MAPK pathway through Ras stabilization, representing a positive crosstalk (Guardavaccaro & Clevers, 2012). The observed interactive effect between the WNT and MAPK pathways suggests that the cross-talk between these two pathways may play an important role in breast cancer survival. The interaction between the tumor suppressor gene BRCA2 and the MAPK pathway has been documented in experiments with prostate cancer cells with upregulation of BRCA2 linked to an increase in MAPK activity (Moro et al., 2007). In the WNT pathway, the WNT1 gene promotes cell survival in various cell types and it has been experimentally shown that blocking WNT1 signaling can induce apoptotic cell death (You et al., 2004). Thus the interaction between WNT1 gene and the PRKACB gene in the Apoptosis pathway may also be crucial for breast cancer.

Fig. 1.

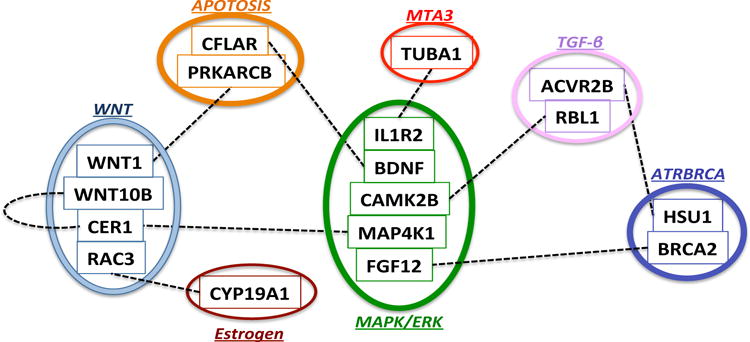
Identified gene-by-gene interactions for the breast cancer example. The dashed lines between gene-paris represent detected interactions. Genes inside each circle belong to the same pathway whose name is also shown.

A. Appendix: Proofs

A·1. Technical Lemmas

We prove the main results in this section. We begin by collecting technical lemmas proved in the supplementary material. The first lemma is the classical Bonferroni inequality.

Lemma A1 (Bonferroni inequality)

Let $B={\cup }_{t=1}^p{B}_t$. For any k < [p/2], we have

$${\displaystyle \sum _{t=1}^{2k}{(-1)}^{t-1}{F}_t\le \text{pr}(B)}\le {\displaystyle \sum _{t=1}^{2k-1}{(-1)}^{t-1}{F}_t,}$$

where $F_t={\sum }_{1\le i_1<\cdots <i_t\le p}\text{pr}(B_{i_1}\cap \cdots \cap B_{i_t})$.

For d = 1, 2, let $U_{i,j,d}=n_d^{-1}{\sum }_{k=1}^{n_d}({\epsilon }_{k,i,d}{\epsilon }_{k,j,d}-E{\epsilon }_{k,i,d}{\epsilon }_{k,j,d})$, and define ${\stackrel{\sim }{U}}_{i,j,d}=(r_{i,j,d}-U_{i,j,d})/(r_{i,i,d}{r}_{j,j,d})$ for 1 ≤ i < j ≤ p and ${\stackrel{\sim }{U}}_{i,i,d}=(r_{i,i,d}+U_{i,i,d})/(r_{i,i,d}{r}_{i,i,d})$.

Lemma A2

Suppose that Conditions (C1), (4) and (5) hold. Then

$$\underset{1\le i\le p}{max}|{\stackrel{\sim }{r}}_{i,i,d}-r_{i,i,d}|=O_{\mathrm{p}}\{{(\log p/n_d)}^{1/2}\},$$

and

$${\stackrel{\sim }{r}}_{i,j,d}={\stackrel{\sim }{R}}_{i,j,d}-{\stackrel{\sim }{r}}_{i,i,d}({\widehat{\beta }}_{i,j,d}-{\beta }_{i,j,d})-{\stackrel{\sim }{r}}_{j,j,d}({\widehat{\beta }}_{j-1,i,d}-{\beta }_{j-1,i,d})+o_{\mathrm{p}}\{{(n_d\log p)}^{-1/2}\},$$

for 1 ≤ i < j ≤ p, where ${\stackrel{\sim }{R}}_{i,j,d}$ is the empirical covariance between {ε_k,i,d : k = 1, …, n_d} and {ε_k,j,d : k = 1, …, n_d}. Consequently, uniformly in 1 ≤ i < j ≤ p,

$$\begin{array}{l}{\widehat{r}}_{i,j,d}-({\omega }_{i,i,d}{\widehat{\sigma }}_{i,i,d,\epsilon }+{\omega }_{j,j,d}{\widehat{\sigma }}_{j,j,d,\epsilon }-1)r_{i,j,d}=-U_{i,j,d}+o_{\mathrm{p}}\{{(n_d\log p)}^{-1/2}\},\\ |{\mathrm{T}}_{i,j,d}-{\stackrel{\sim }{U}}_{i,j,d}|=O_{\mathrm{p}}\{{(\log p/n_d)}^{\frac{1}{2}}\}{r}_{i,j,d}+o_{\mathrm{p}}\{n_d{(\log p)}^{-1/2}\},\end{array}$$

and uniformly in 1 ≤ i ≤ p,

$$|{\mathrm{T}}_{i,i,d}-{\stackrel{\sim }{U}}_{i,i,d}|=o_{\mathrm{p}}\{{(n_d\log p)}^{-1/2}\},$$

where ${\widehat{r}}_{i,j,d}$ is defined in (7), $({\widehat{\sigma }}_{i,j,d,\epsilon })=(1/n_d){\sum }_{k=1}^{n_d}({\epsilon }_{k,d}-{\overline{\epsilon }}_d){({\epsilon }_{k,d}-{\overline{\epsilon }}_d)}^{\mathrm{T}},{\epsilon }_{k,d}=({\epsilon }_{k,1,d},\dots ,{\epsilon }_{k,p,d})$ and ${\overline{\epsilon }}_d=n_d^{-1}{\sum }_{k=1}^{n_d}{\epsilon }_{k,d}$.

Lemma A3

Let X_k ~ N(μ₁, Σ₁) for k = 1, …, n₁ and Y_k ~ N(μ₂, Σ₂) for k = 1, …, n₂. Define

$${\sum ^{\sim }}_1={({\stackrel{\sim }{\sigma }}_{i,j,1})}_{p\times p}=\frac{1}{n_1}{\displaystyle \sum _{k=1}^{n_1}(X-{\mu }_1){(X-{\mu }_1)}^{\mathrm{T}},{\sum ^{\sim }}_2={({\stackrel{\sim }{\sigma }}_{i,j,2})}_{p\times p}=\frac{1}{n_2}{\displaystyle \sum _{k=1}^{n_2}(Y-{\mu }_2){(Y-{\mu }_2)}^{\mathrm{T}}.}}$$

Then, for some constant C > 0, ${\stackrel{\sim }{\sigma }}_{i,j,1}-{\stackrel{\sim }{\sigma }}_{i,j,2}$ satisfies the large deviation bound

$$\begin{array}{l}\text{pr}\left[\underset{(i,j)\in \mathcal{S}}{max}\frac{{({\stackrel{\sim }{\sigma }}_{i,j,1}-{\stackrel{\sim }{\sigma }}_{i,j,2}-{\sigma }_{i,j,1}+{\sigma }_{i,j,2})}^2}{\mathrm{var}\{(X_{k,i}-{\mu }_{1,i})(X_{k,j}-{\mu }_{1,j})\}/n_1+\mathrm{var}\{(Y_{k,i}-{\mu }_{2,i})(Y_{k,j}-{\mu }_{2,j})\}/n_2}\ge x^2\right]\\ \le C|\mathcal{S}|\{1-\mathrm{\Phi }(x)\}+O(p^{-1})\end{array}$$

uniformly for 0 ≤ x ≤ (8 log p)^1/2 and any subset $\mathcal{S}\subseteq \{(i,j):1\le i\le j\le p\}$.

The following lemma is needed for false discovery rate control in Theorem 4.

Lemma A4

Let V_i,j = (U_i,_j,2−U_i,j,1){var(ε_k,i,1ε_k,j,1)/n₁ + var(ε_k,i,2ε_k,j,2)/n₂}^−1/2. Under the same conditions as in Theorem 4, we have for any ε > 0 that,

$$\begin{array}{l}{\displaystyle \sum _{0\le t\le t_p}\text{pr}}\left[\left|\frac{{\sum }_{(i,j)\in {\mathscr{H}}_0\backslash A_{\tau }}\{I(|V_{i,j}|\ge t)-\text{pr}(|V_{i,j}|\ge t)\}}{2q_0\{1-\mathrm{\Phi }(t)\}}\right|\ge \epsilon \right]=o(1),\\ {\displaystyle {\int }_0^{t_p}\text{pr}}\left[\left|\frac{{\sum }_{(i,j)\in {\mathscr{H}}_0\backslash A_{\tau }}\{I(|V_{i,j}|\ge t)-\text{pr}(|V_{i,j}|\ge t)\}}{2q_0\{1-\mathrm{\Phi }(t)\}}\right|\ge \epsilon \right]dt=o(v_p),\end{array}$$

where t_p = (4 log p − log₂ p – log₃ p)^1/2 and v_p = 1/{log p(log₄ p)²}^1/2.

A·2. Proof of Theorem 1

Without loss of generality, throughout this section, we assume that ω_i,i,d = 1 for d = 1, 2 and i = 1,…, p. Let A = {(i, j) : 1 ≤ i ≤ j ≤ p}. (C1) implies |A_τ|=o(p^1/16). To prove Theorem 1, we first show that the terms in A_τ are negligible. Then we use Lemma 1, together with the Gaussian approximation technique, to show that $\text{pr}({max}_{(i,j)\in A\backslash A_{\tau }}{W}_{i,j}^2-4\log p+\log \log p\le t)\to \exp \{-{(8\pi )}^{-1/2}\exp (-t/2)\}$, where W_i,j is defined in equation (9).

For d = 1, 2, let V_i,j = (U_i,j,₂ − U_i,j,₁)/{var(ε_k,i,₁ε_k,j,₁)/n₁ + var(ε_k,i,d ε_k,j,d)/n₂}^1/2, where $\mathrm{var}({\epsilon }_{k,i,d}{\epsilon }_{k,j,d})=r_{i,i,d}{r}_{j,j,d}(1+{\rho }_{i,j,d}^2)$ with ${\rho }_{i,j,d}^2={\beta }_{i,j,d}^2{r}_{i,i,d}/r_{j,j,d}$. The proof of Lemma 2 yields

$$\underset{1\le i\le p}{max}|{\widehat{r}}_{i,i,d}-r_{i,i,d}|=O_{\mathrm{p}}\{{(\log p/n)}^{\frac{1}{2}}\},$$ (A1)

and ${max}_{1\le i\le p}|{\widehat{r}}_{i,i,d}-{\stackrel{\sim }{R}}_{i,i,d}|=o_{\mathrm{p}}\{{(n_d\log p)}^{-1/2}\}$, where n = max{n₁, n₂}. Note that

$$\underset{1\le i\le j\le p}{max}|{\widehat{\beta }}_{i,j,d}^2{\widehat{r}}_{i,i,d}/{\widehat{r}}_{j,j,d}-{\rho }_{i,j,d}^2)=o_{\mathrm{p}}(1/\log p),$$ (A2)

and ${max}_{1\le i\le j\le p}|{\omega }_{i,i,d}{\widehat{\sigma }}_{i,i,d,\epsilon } +{\omega }_{j,j,d}{\widehat{\sigma }}_{j,j,d,\epsilon } -2|=O_{\mathrm{p}}\{{(\log p/n)}^{1/2}\}.$ Also note that for (i, j) ∈ A\A_τ, we have |ω_i,j,d| = o{(log p)⁻¹}. Then by Lemma 2, it is easy to see that, under conditions (C1), (4) and (5), we have, for (i, j) ∈ A\A_τ, ${max}_{(i,j)\in A\backslash A_{\tau }}\Vert W_{i,j}|-|V_{i,j}\Vert =o_{\mathrm{p}}\{{(\log p)}^{-1/2}\}$. For (i,j) ∈ A_τ as a result of Lemma 2, we have W_i,j = V_i,j + b_i,j + o_p 1og p^–1/2), where $b_{i,j}=2\{{\omega }_{i,j}({\widehat{\sigma }}_{i,i,1,\epsilon }-{\widehat{\sigma }}_{i,i,2,\epsilon })+{\omega }_{i,j}({\widehat{\sigma }}_{j,j,1,\epsilon }-{\sigma }_{j,j,2,\epsilon })\}/{({\widehat{\theta }}_{i,j,1}+{\widehat{\theta }}_{i,j,2})}^{1/2}$, $({\widehat{\sigma }}_{i,j,d,\epsilon })=n_d^{-1}{\sum }_{k=1}^{n_d}({\epsilon }_{k,d}-{\overline{\epsilon }}_d){({\epsilon }_{k,d}-{\overline{\epsilon }}_d)}^{\mathrm{T}}$, ${\epsilon }_{k,d}=({\epsilon }_{k,1,d,\dots }{\epsilon }_{k,p,d})$ and ${\overline{\epsilon }}_d=(1/n_d){\sum }_{k=1}^{n_d}{\epsilon }_{k,d}$. Note that

$$|b_{i,j}|\le 2{\left(\frac{2{\rho }_{i,j}^2}{1+{\rho }_{i,j}^2}\right)}^{\frac{1}{2}}\left[\frac{|{\stackrel{\sim }{\sigma }}_{i,i,1,\epsilon }-{\stackrel{\sim }{\sigma }}_{i,i,2,\epsilon }|}{{\{\mathrm{var}({\epsilon }_{k,i,1}^2)/n_1+\mathrm{var}({\epsilon }_{k,i,2}^2)/n_2\}}^{\frac{1}{2}}}+\frac{|{\stackrel{\sim }{\sigma }}_{j,j,1,\epsilon }-{\stackrel{\sim }{\sigma }}_{j,j,2,\epsilon }|}{{\{\mathrm{var}({\epsilon }_{k,j,1}^2)/n_1+\mathrm{var}({\epsilon }_{k,j,2}^2)/n_2\}}^{\frac{1}{2}}}\right]+o\{{(\log p)}^{-1/2}\},$$

where ${\stackrel{\sim }{\sigma }}_{i,i,d,\epsilon }=n_d^{-1}{\sum }_{k=1}^{n_d}{\epsilon }_{k,i,d}^2$. Thus, we have

$$\text{pr}(\underset{(i,j)\in A_{\tau }}{max}{W}_{i,j}^2\ge 4\log p-\log \log p+t)\le \text{Card}(A_{\tau })\{\text{pr}(V_{i,j}^2\ge \log p/8)+\text{pr}(b_{i,j}^2\ge 2\log p)\}=o(1),$$

where the last equality is a direct result of Lemma 3. Thus it suffices to prove that

$$\text{pr}(\underset{(i,j)\in A\backslash A_{\tau }}{max}{V}_{i,j}^2-4\log p+\log \log p\le t)\to \exp \{-{(8\pi )}^{-1/2}\exp (-t/2)\}.$$

We arrange the indices {(i, j) : (i, j) ∈ A\A_τ} in any ordering and set them as {(i_m, j_m) : m = 1, …, q} with q =Card(A\A_τ). Let n₁/n₂ ≤ K with K ≥ 1, ${\theta }_{m,d}=\mathrm{var}({\epsilon }_{i_m,d}{\epsilon }_{j_m,d})$, for d = 1, 2 and define $Z_{k,m}=(n_1/n_2)\{{\epsilon }_{k,i_m,2}{\epsilon }_{k,j_m,2}-E({\epsilon }_{k,i_m,2}{\epsilon }_{k,j_m,2})\}$ for 1 ≤ k ≤ n₂, $Z_{k,m}=-\{{\epsilon }_{k,i_m,1}{\epsilon }_{k,j_m,1}-E({\epsilon }_{k,i_m,1}{\epsilon }_{k,j_m,1})\}$ for n₂ + 1 ≤ k ≤ n₁ + n₂, $V_m={(n_1^2{\theta }_{m,2}/n_2+n_1{\theta }_{m,1})}^{-1/2}{\sum }_{k=1}^{n_1+n_2}{Z}_{k,m}$ and ${\widehat{V}}_m={(n_1^2{\theta }_{m,2}/n_2+n_1{\theta }_{m,1})}^{-1/2}{\sum }_{k=1}^{n_1+n_2}{\widehat{Z}}_{k,m}$, where ${\widehat{Z}}_{k,m}=Z_{k,m}I(|Z_{k,m}|\le {\tau }_n)-E\{Z_{k,m}I(|Z_{k,m}|\le {\tau }_n)\}$, and τ_n = 32K₁ log(p + n). Note that ${max}_{(i,j)\in A\backslash A_{\tau }}{V}_{i,j}^2={max}_{1\le m\le q}{V}_m^2$, and that

$$\begin{array}{l}\underset{1\le m\le q}{max}{n}^{-1/2}{\displaystyle \sum _{k=1}^{n_1+n_2}E[|Z_{k,m}|I\{|Z_{k,m}|\ge 32K_1\log (p+n)\}]}\\ \le C{n}^{1/2}\underset{1\le k\le n_1+n_2}{max}\underset{1\le m\le q}{max}E[|Z_{k,m}|I\{|Z_{k,m}|\ge 32K_1\log (p+n)\}]\\ \le C{n}^{1/2}{(p+n)}^{-4}\underset{1\le k\le n_1+n_2}{max}\underset{1\le m\le q}{max}E[|Z_{k,m}|\exp \{|Z_{k,m}|/(8K_1)\}]\\ \le C{n}^{1/2}{(p+n)}^{-4}.\end{array}$$

Hence, $\text{pr}\{{max}_{1\le m\le q}|V_m-{\widehat{V}}_m|\ge {(\log p)}^{-1}\}\le \text{pr}({max}_{1\le m\le q}{max}_{1\le k\le n_1+n_2}|Z_{k,m}|\ge {\tau }_n)=O(p^{-1})$. By the fact that $\left|{max}_{1\le m\le q}{V}_m^2-{max}_{1\le m\le q}{\widehat{V}}_m^2\right|\le 2{max}_{1\le m\le q}|{\widehat{V}}_m|{max}_{1\le m\le q}|V_m-{\widehat{V}}_m|+{max}_{1\le m\le q}{|V_m-{\widehat{V}}_m|}^2$, it suffices to prove that for any t ∈ ℝ, as n, p → ∞,

$$\text{pr}\left(\underset{1\le m\le q}{max}{\widehat{V}}_m^2-4\log p+\log \log p\le t\right)\to \exp \left\{-{(8\pi )}^{1/2}\exp (-t/2)\right\}.$$ (A3)

By Lemma 1, for any integer l with 0 < l < q/2,

$$\begin{array}{l}{\displaystyle \sum _{d=1}^{2l}{(-1)}^{d-1}{\displaystyle \sum _{1\le m_1<\cdots <m_d\le q}\text{pr}\left({\displaystyle \underset{j=1}{\overset{d}{\cap }}{F}_{m_j}}\right)}}\le \text{pr}\left(\underset{1\le m\le q}{max}{\widehat{V}}_m^2\ge y_p\right)\\ \le {\displaystyle \sum _{d=1}^{2l-1}{(-1)}^{d-1}{\displaystyle \sum _{1\le m_1<\cdots <m_d\le q}\text{pr}\left({\displaystyle \underset{j=1}{\overset{d}{\cap }}{F}_{m_j}}\right),}}\end{array}$$ (A4)

where y_p = 4 log p − log log p + t and $F_{m_j}=({\widehat{V}}_{m_j}^2\ge y_p)$. Let ${\stackrel{\sim }{Z}}_{k,m}={\widehat{Z}}_{k,m}/{(n_1{\theta }_{m,2}/n_2+{\theta }_{m,1})}^{1/2}$ for m = 1, …, q and $W_k=({\stackrel{\sim }{Z}}_{k,m_1},\dots {\stackrel{\sim }{Z}}_{k,m_d})$, for 1 ≤ k ≤ n₁ + n₂. Define ${|a|}_{min}={min}_{1\le i\le d}|a_i|$ for any vector a ∈ R^d. Then we have

$$\text{pr}\left({\displaystyle \underset{j=1}{\overset{d}{\cap }}{F}_{m_j}}\right)=\text{pr}\left({\left|{n_2}^{-\frac{1}{2}}{\displaystyle \sum _{k=1}^{n_1+n_2}{W}_k}\right|}_{min}\ge y_p^{\frac{1}{2}}\right).$$

Then it follows from Theorem 1 in Zaïtsev (1987) that

$$\begin{array}{l}\text{pr}({\left|{n_2}^{-1/2}{\displaystyle \sum _{k=1}^{n_1+n_2}{W}_k}\right|}_{min}\ge y_p^{1/2})\le \text{pr}\left\{{|N_d|}_{min}\ge y_p^{1/2}-{\epsilon }_n{(\log p)}^{-1/2}\right\}\\ +c_1{d}^{\frac{5}{2}}\exp \left\{-\frac{n^{1/2}{\epsilon }_n}{c_2{d}^3{\tau }_n{(\log p)}^{1/2}}\right\},\end{array}$$ (A5)

where c₁ > 0 and c₂ > 0 are constants, ε_n → 0 which will be specified later and $N_d=(N_{m_1},\dots N_{m_d})$ is a normal random vector with E(N_d) = 0 and $\mathrm{cov}(N_d)=n_2/n_1\mathrm{cov}(W_1)+\mathrm{cov}(W_{n_2+1})$. Recall that d is a fixed integer which does not depend on n, p. Because $\log p=o(n^{1/5})$, we can let ε_n → 0 sufficiently slowly that, for any large M > 0

$$c_1{d}^{5/2}\exp \left\{-\frac{n^{1/2}{\epsilon }_n}{c_2{d}^3{\tau }_n{(\log p)}^{1/2}}\right\}=O(p^{-M}).$$ (A6)

Combining (A4), (A5) and (A6) we have

$$\text{pr}\left(\underset{1\le m\le q}{max}{\widehat{V}}_m^2\ge y_p\right)\le {\displaystyle \sum _{d=1}^{2l-1}{(-1)}^{d-1}}{\displaystyle \sum _{1\le m_1<\cdots <m_d\le q}\text{pr}\left\{{|N_d|}_{min}\ge y_p^{1/2}-{\epsilon }_n{(\log p)}^{-1/2}\right\}+o^{(1)}.}$$ (A7)

Similarly, using Theorem 1 in Zaïtsev (1987) again, we can get

$$\text{pr}\left(\underset{1\le m\le q}{max}{\widehat{V}}_m^2\ge y_p\right)\ge {\displaystyle \sum _{d=1}^{2l}{(-1)}^{d-1}}{\displaystyle \sum _{1\le m_1<\cdots <m_d\le q}\text{pr}\left\{{|N_d|}_{min}\ge y_p^{1/2}+{\epsilon }_n{(\log p)}^{-1/2}\right\}-o(1)}.$$ (A8)

We recall the following lemma, which is shown in the supplementary material of Cai et al. (2013).

Lemma A5

For any fixed integer d ≥ 1 and real number t ∈ ℝ,

$${\displaystyle \sum _{1\le m_1<\cdots <m_d\le q}\text{pr}\left\{{|N_d|}_{min}\ge y_p^{1/2}\pm {\epsilon }_n{(\log p)}^{-1/2}\right\}=\frac{1}{d!}{\{{(8\pi )}^{-1/2}\exp (-t/2)\}}^d\{1+o(1)\}}.$$ (A9)

It then follows from Lemma 5, (A7) and (A8) that

$$\begin{array}{l}\underset{n,p\to \infty }{\lim \sup }\text{pr}\left(\underset{1\le m\le q}{max}{\widehat{V}}_m^2\ge y_p\right)\le {\displaystyle \sum _{d=1}^{2l}{(-1)}^{d-1}\frac{1}{d!}{\{{(8\pi )}^{-1/2}\exp (-t/2)\}}^d}\\ \underset{n,p\to \infty }{\lim \inf }\text{pr}\left(\underset{1\le m\le q}{max}{\widehat{V}}_m^2\ge y_p\right)\ge {\displaystyle \sum _{d=1}^{2l}{(-1)}^{d-1}\frac{1}{d!}{\{{(8\pi )}^{-1/2}\exp (-t/2)\}}^d}\end{array}$$

for any positive integer l. By letting l → ∞, we obtain (A3) and Theorem 1 is proved.

A·3. Proof of Theorem 2

Let $M_n^1={max}_{1\le i\le j\le p}{\{{\mathrm{T}}_{i,j,1}-{\mathrm{T}}_{i,j,2}-({\omega }_{i,j,1}-{\omega }_{i,j,2})\}}^2/({\widehat{\theta }}_{i,j,1}+{\widehat{\theta }}_{i,j,2})$. It follows from the proof of Theorem 1 that $\mathrm{pr}(M_n^1\le 4\log p-2^{-1}\log \log p)\to 1$, as n, p → ∞. By (A1), (A2) and the inequalities ${max}_{1\le i\le j\le p}{({\omega }_{i,j,1}-{\omega }_{i,j,2})}^2/({\widehat{\theta }}_{i,j,1}+{\widehat{\theta }}_{i,j,2})\le 2M_n^1+2M_n$, and ${max}_{1\le i\le j\le p}({\omega }_{i,j,1}-{\omega }_{i,j,2}|{({\widehat{\theta }}_{i,j,1}+{\widehat{\theta }}_{i,j,2})}^{1/2}\ge 4{(\log p)}^{1/2}$, we have pr(M_n ≥ q_α + 4 log p − log log p) → 1 as n, p → ∞.

A·4. Proof of Theorem 3

To prove the lower bound result, we first construct the worst case scenario to test between Ω₁ and Ω₂, and then apply the arguments as shown in Baraud (2002).

Let ℳ denote the set of all subsets of {1,…, p} with cardinality p^r, for r < 1/2. Let $\widehat{m}$ be a random subset of {1,…, p}, which is uniformly distributed on ℳ. We construct a class of Ω₁, $\mathcal{N}=\{{\mathrm{\Omega }}_{\widehat{m}},\widehat{m}\in ℳ\}$, such that ω_i,j = 0 for i ≠ j and $1/{\omega }_{i,i}-1=\rho 1_{i\in \widehat{m}}$, for i, j = 1,…, p and ρ = c(log p/n)^1/2, where c > 0 will be specified later. Let Ω₂ = I and Ω₁ be uniformly distributed on $\mathcal{N}$. Let μ_ρ be the distribution of Ω₁ − I. Note that μ_ρ is a probability measure on $\{\mathrm{\Delta }\in \mathcal{S}(p^r):\Vert \mathrm{\Delta }{\Vert }_F^2=p^r{\rho }^2\}$, where $\mathcal{S}(p^r)$ is the class of matrices with p^r nonzero entries. Let dpr₁({X_n, Y_n}) and dpr₂({X_n, Y_n}) be the functions with precision matrices Ω₁ and Ω₂ respectively, likelihood then we have

$$L_{{\mu }_{\rho }}=L_{{\mu }_{\rho }}(\{X_n,Y_n\})=E_{{\mu }_{\rho }}\left\{\frac{d{\text{pr}}_1(\{X_n,Y_n\})}{d{\text{pr}}_2(\{X_n,Y_n\})}\right\},$$

where $E_{{\mu }_{\rho }}(\cdot )$ is the expectation on Ω₁. By the arguments in Baraud (2002), it suffices to show that $E(L_{{\mu }_{\rho }}^2)\le 1+o(1)$. It is easy to check that

$$L_{{\mu }_{\rho }}=E_{\widehat{m}}\left[{\displaystyle \prod _{i=1}^n\frac{1}{|{\sum }_{\widehat{m}}{|}^{1/2}}\exp \left\{-\frac{1}{2}{Z}_i^{\mathrm{T}}({\mathrm{\Omega }}_{\widehat{m}}-I)Z_i\right\}}\right],$$

where ${\sum }_{\widehat{m}}={\mathrm{\Omega }}_{\widehat{m}}^{-1}$ and $Z_1,\dots ,Z_n\stackrel{i,i,d.}{~}N(0,I)$. Thus, we have

$$\begin{array}{l}E(L_{{\mu }_{\rho }}^2)=E{\left({\left(\begin{array}{l}p\\ k_p\end{array}\right)}^{-1}{\displaystyle \sum _{m\in ℳ}\left[{\displaystyle \prod _{i=1}^n\frac{1}{|{\sum }_m{|}^{1/2}}\exp \{-Z_i^{\mathrm{T}}({\mathrm{\Omega }}_m-I)Z_i/2\}}\right]}\right)}^2\\ ={\left(\begin{array}{l}p\\ k_p\end{array}\right)}^{-2}{\displaystyle \sum _{m,m^{\prime }\in ℳ}E\left[{\displaystyle \prod _{i=1}^n\frac{1}{|{\sum }_m{|}^{1/2}}\frac{1}{|{\sum }_{m^{\prime }}{|}^{1/2}}\exp \{-Z_i^{\mathrm{T}}({\mathrm{\Omega }}_m+{\mathrm{\Omega }}_{m^{\prime }}-2I)Z_i/2\}}\right]}\end{array}$$

Set Ω_m + Ω_m′ − 2I = (a_i,j). It is easy to show that a_i,j = 0 for i ≠ j, a_j,j = 0 if j ε (m ∪ m′)^c, a_j,j = 2(1/(1 + ρ)−1) if j ε m ∩ m′ and a_j,j = 1/(1 + ρ) −1 if j ε m \ m′ \ m. Let t = | m ∩ m′|. Then

$$\begin{array}{l}E(L_{{\mu }_{\rho }}^2)={\left(\begin{array}{l}p\\ k_p\end{array}\right)}^{-1}{\displaystyle \sum _{t=0}^{k_p}\left(\begin{array}{l}{k}_p\\ t\end{array}\right)\left(\begin{array}{l}p-k_p\\ k_p-t\end{array}\right)\frac{1}{{(1+\rho )}^{k_{p}n}}{(1+\rho )}^{(k_p-t)n}{\left(\frac{1+\rho }{1-\rho }\right)}^{tn/2}}\\ \le p^{k_p}(p-k_p)!/p!{\displaystyle \sum _{t=0}^{k_p}\left(\begin{array}{l}{k}_p\\ t\end{array}\right){\left(\frac{k_p}{p}\right)}^t{\left(\frac{1}{{1-\rho }^2}\right)}^{tn/2}={\left\{1+\frac{k_p}{p{(1-\rho )}^{n/2}}\right\}}^{k_p}(1+o(1))},\end{array}$$

for r < 1/2. Thus, by letting c be sufficiently small, we have

$$E(L_{{\mu }_{\rho }}^2)\le \exp \{k_p\log (1+k_p{p}^{c^2-1})\}(1+o(1))\le \exp (k_p^2{p}^{c^2-1})(1+o(1))=1+o(1).$$

A·5. Proof of Theorem 4

We first show that $\widehat{t}$, as defined in Section 4, is obtained in the range (0, 2(log p)^1/2). Then we illustrate that R₀(t), defined in Section 4, is close to 2 {1 − Φ(t)}|ℋ₀| by first showing the terms in A_τ are negligible. We then focus on the set ℋ₀ \ A_τ and prove the result based on Lemma 4.

Under the condition of Theorem 4, we have Σ_1≤i<j≤p I{|W_i,j| ≥ 2(log p)^1/2} ≥ [1/{(8π)^1/2 α} + δ](log₂ p)^1/2, with probability going to one. Hence we have with probability going to one,

$$\frac{(p^2-p)/2}{max\{{\sum }_{1\le i<j\le p}I\{|W_{i,j}|\ge 2{(\log p)}^{1/2}\},1\}}\le \frac{p^2-p}{2}{\left\{\frac{1}{{(8\pi )}^{1/2}\alpha }+\delta \right\}}^{-1}{({\log }_{2}p)}^{-1/2}.$$

Let t_p = (4 log p − log₂ p − log₃ p)^1/2. Because $1-\mathrm{\Phi }(t_p)\sim 1/\{{(2\pi )}^{1/2}{t}_p\}\exp (-t_p^2/2)$, we have $\text{pr}(1\le \widehat{t}\le t_p)\to 1$ according to the definition of $\widehat{t}$ in the false discovery rate control algorithm in Section 4. Note that, for $0\le \widehat{t}\le t_p$, we have

$$\frac{2\{1-\mathrm{\Phi }(\widehat{t})\}(p^2-p)/2}{max\{{\sum }_{1\le i<j\le p}I\{|W_{i,j}|\ge 2{(\log p)}^{1/2}\},1\}}=\alpha .$$

Thus to prove Theorem 4, it suffices to prove that $|{\sum }_{(i,j)\in {\mathscr{H}}_0}\{I(|W_{i,j}|\ge t)-G(t)\}|/\{q_{0}G(t)\}\to 0$ in probability, for 0 ≤ t ≤ {4 log p + o(log p)}^1/2, where G(t) = 2{1 − Φ(t)}. Now we consider two cases.

1. If t = {4 log p + o(log p)}^1/2, the proof of Theorem 1 yields that $\text{pr(}{max}_{(i,j)\in A_{\tau }}{\mathrm{W}}_{i,j}^2\ge t^2\text{)}=o(1)$. Thus, it suffices to prove that $|{\sum }_{(i,j)\in {\mathscr{H}}_0}\{I(|W_{i,j}|\ge t)-G(t)\}|/\{q_{0}G(t)\}\to 0$ probability. For (i, j) ∊ ℋ₀ \ A_τ, we have from the proof of Theorem 1 that max_1≤i<j≤p | W_i,j − V_i,j | = o_p {(log p)^−1/2}. Thus, it suffices to show that

   $$\left|\frac{{\sum }_{(i,j)\in {\mathscr{H}}_0\backslash A_{\tau }}{\epsilon }_{i,j}(t)}{q_{0}G(t)}\right|\to 0$$ (A10)

   in probability, where ε_i,j(t) = I(|V_i,j |≥ t) − G(t).
2. If t ≤ (C log p)^1/2 with C < 4, we have

   $$\left|\frac{{\sum }_{(i,j)\in A_{\tau }\cap {\mathscr{H}}_0}\{I(|W_{i,j}|\ge t)-I(|V_{i,j}|\ge t)\}}{q_{0}G(t)}\right|\le \frac{2|A_{\tau }\cap {\mathscr{H}}_0|}{O(p^{2-C/2})}\to 0$$

   in probability. Thus, it is again enough to show that

   $$\left|\frac{{\sum }_{(i,j)\in {\mathscr{H}}_0\backslash A_{\tau }}{\epsilon }_{i,j}(t)}{q_{0}G(t)}\right|\to 0$$ (A11)

   in probability. Define ${\stackrel{\sim }{\mathscr{H}}}_0={\mathscr{H}}_0\backslash A_{\tau }$. Let 0 ≤ t₀ < ⋯ < t_m = t_p such that t_l − t_l−1 = v_p for l = 1,…, m − 1 and t_m − t_m−1 ≤ v_p. Thus we have m·~ t_p/v_p. For any t such that t_l−1 ≤ t ≤ t_l, we have

   $$\frac{{\sum }_{(i,j)\in {\stackrel{\sim }{\mathscr{H}}}_0}I(|V_{i,j}|\ge t_l)}{q_{0}G(t_l)}\frac{G(t_l)}{G(t_{l-1})}\le \frac{{\sum }_{(i,j)\in {\stackrel{\sim }{\mathscr{H}}}_0}I(|V_{i,j}|\ge t_l)}{q_{0}G(t)}\le \frac{{\sum }_{(i,j)\in {\stackrel{\sim }{\mathscr{H}}}_0}I(|V_{i,j}|\ge t_{l-1})}{q_{0}G(t_{l-1})}\frac{G(t_{l-1})}{G(t_l)}.$$

   Thus it suffices to prove ${max}_{0\le l\le m}|{\sum }_{(i,j)\in {\stackrel{\sim }{\mathscr{H}}}_0}{\epsilon }_{i,j}(t_l)|/\{q_{0}G(t_l)\}\to 0$ in probability. Note that

   $$\begin{array}{l}\text{pr}\left\{\underset{0\le l\le m}{max}\right|\frac{{\sum }_{(i,j)\in {\stackrel{\sim }{\mathscr{H}}}_0}{\epsilon }_{i,j}(t_l)}{q_{0}G(t_l)}|\ge \epsilon \}\le {\displaystyle \sum _{l=1}^m\text{pr}\left\{\right|\frac{{\sum }_{(i,j)\in {\stackrel{\sim }{\mathscr{H}}}_0}{\epsilon }_{i,j}(t_l)}{q_{0}G(t_l)}|\ge \epsilon \}}\\ \le \frac{1}{v_p}{\displaystyle {\int }_0^{t_p}\text{pr}\left\{\right|\frac{{\sum }_{(i,j)\in {\stackrel{\sim }{\mathscr{H}}}_0}{\epsilon }_{i,j}(t_l)}{q_{0}G(t)}|\ge \epsilon \}dt+{\displaystyle \sum _{l=m-1}^m\text{pr}\left\{\right|\frac{{\sum }_{(i,j)\in {\stackrel{\sim }{\mathscr{H}}}_0}{\epsilon }_{i,j}(t_l)}{q_{0}G(t_l)}|\ge \epsilon \}}}.\end{array}$$

Thus by (A5) with d = 1 and Lemma 4, Theorem 4 is proved.