Can we predict subject‐specific dynamic cortical thickness maps during infancy from birth?

Abstract

Understanding the early dynamic development of the human cerebral cortex remains a challenging problem. Cortical thickness, as one of the most important morphological attributes of the cerebral cortex, is a sensitive indicator for both normal neurodevelopment and neuropsychiatric disorders, but its early postnatal development remains largely unexplored. In this study, we investigate a key question in neurodevelopmental science: can we predict the future dynamic development of cortical thickness map in an individual infant based on its available MRI data at birth? If this is possible, we might be able to better model and understand the early brain development and also early detect abnormal brain development during infancy. To this end, we develop a novel learning‐based method, called Dynamically‐Assembled Regression Forest (DARF), to predict the development of the cortical thickness map during the first postnatal year, based on neonatal MRI features. We applied our method to 15 healthy infants and predicted their cortical thickness maps at 3, 6, 9, and 12 months of age, with respectively mean absolute errors of 0.209 mm, 0.332 mm, 0.340 mm, and 0.321 mm. Moreover, we found that the prediction precision is region‐specific, with high precision in the unimodal cortex and relatively low precision in the high‐order association cortex, which may be associated with their differential developmental patterns. Additional experiments also suggest that using more early time points for prediction can further significantly improve the prediction accuracy. Hum Brain Mapp 38:2865–2874, 2017. © 2017 Wiley Periodicals, Inc.

INTRODUCTION

The development of the infant cerebral cortex is extremely complex and dynamic, but remains poorly understood [Casey et al., 2005; Dubois et al., 2014; Giedd and Rapoport, 2010; Walhovd et al., 2014], due to the critical lack of computational tools for analyzing infant MRIs, typically with extremely poor imaging quality. Cortical thickness, a key morphological attribute of the cortex, is a sensitive indicator of normal brain structural and functional development [Schnack et al., 2015; Shaw et al., 2006, 2008; Sowell et al., 2004], and is also closely related with many neurodevelopmental disorders, e.g., Williams syndrome [Thompson et al., 2005], attention‐deficit/hyperactivity disorder [Shaw et al., 2007], autism [Zielinski et al., 2014], and bipolar disorder [Rimol et al., 2010]. These observations propelled the investigation of the dynamic aspect of cortical thickness development, thereby resulting in several recent studies that looked into cortical thickness development from birth until the second postnatal year, by leveraging recent advance of infant‐dedicated computational tools [Geng et al., 2016; Li et al., 2015a; Lyall et al., 2015]. For the first time, these studies show that cortical thickness increases dramatically (around 40%) in the first year and then slightly changes during the second year [Li et al., 2015a; Lyall et al., 2015].

However, the majority of existing works on cortical thickness studied the developmental trajectories on a group level [Brown et al., 2012; Li et al., 2015a; Lyall et al., 2015; Shaw et al., 2008; Storsve et al., 2014; Wierenga et al., 2014]. On the other hand, predicting the subject‐specific cortical development is of great importance, because it can potentially be used as early biomarkers for identifying infants at risk for neurodevelopmental disorders [Ecker et al., 2014; Querbes et al., 2009; Singh et al., 2008]. Recently, several methods for predicting/modeling early brain development have been proposed, e.g., the computational growth model, non‐linear mixed effect model, and varifold‐based/current‐based shape morphing‐learning method [Budday et al., 2014; Nie et al., 2012; Rekik et al., 2015a, 2015b, 2016; Sadeghi et al., 2012]. However, none of these methods can predict the development of morphological attributes of the cortex, e.g., cortical thickness, directly from the baseline MRI.

In this article, we aim to address an important question in neuroscience: can we predict the future dynamic development of cortical thickness maps in each individual infant based on its available MRI data at birth? If this is possible, we might be able to better model and understand the mysterious dynamic early brain development and also early detect abnormal brain development during infancy, based on the predicted cortical thickness. To this end, we create a novel generic machine learning‐based framework for accurate prediction of subject‐specific dynamic development of the vertex‐wise cortical thickness map in the first postnatal year, solely based on the MRI features at birth. Of note, developing such a method is challenged by the extremely dynamic and regionally‐heterogeneous growth of the infant cortex, as well as by the considerable inter‐subject variability of cortical morphology and developmental patterns [Li et al., 2015a]. Technically, we propose Dynamically‐Assembled Regression Forest (DARF) to ensure the accuracy and the spatial smoothness of the predicted cortical thickness map and also boost the computational efficiency. We have tested our method on a longitudinal MRI dataset of 15 infants, each with 5 serial scans at around 1, 3, 6, 9, and 12 months of age during the first postnatal year. The experiments show that our method can accurately predict the dynamic development of cortical thickness maps, with prediction errors of 0.209 mm at 3 months, 0.332 mm at 6 months, 0.340 mm at 9 months, and 0.321 mm at 12 months, respectively. Additionally, using multiple time points for prediction, the error is further reduced to 0.313 mm at 6 months, 0.260 mm at 9 months, and 0.219 mm at 12 months. Notably, the prediction results have higher accuracy in the unimodal cortex than the high‐order association cortex. Our method can be easily generalized to predict other cortical attributes, e.g., surface area, sulcal depth, and cortical folding.

MATERIALS AND METHODS

Subjects and MR Image Acquisition

This study was approved by the Institutional Review Board of the University of North Carolina (UNC) School of Medicine. UNC hospitals recruited healthy pregnant mothers during the second trimester for the study. There was no abnormal fetal ultrasound, congenital anomaly, metabolic disease, or focal lesion in the infants in the study cohort. For each infant, informed consents were obtained from both parents. All infants were scanned during natural sleep with no sedation used. During each scan, a physician or a nurse used a pulse oximeter to monitor the heart rate and oxygen saturation of the infant.

In this study, we used MR images from 15 healthy full‐term born infants (10 males/5 females). The demographic information at birth is reported in Table 1. Each infant was scanned at five time points, i.e., around 1, 3, 6, 9, and 12 months of age. At each scan, T1‐, T2‐, and diffusion‐weighted MR images were acquired by a Siemens 3T head‐only MRI scanner with a 32 channel head coil. T1‐weighted images (144 sagittal slices) were acquired with the imaging parameters: repetition time (TR) = 1,900 ms, echo time (TE) = 4.38 ms, flip angle = 7, acquisition matrix = 256 × 192, and voxel size = 1 × 1 × 1 mm³. T2‐weighted images (64 axial slices) were acquired with the imaging parameters: TR/TE = 7,380/119 ms, flip angle = 150, acquisition matrix = 256 × 128, and voxel size = 1.25 × 1.25 × 1.95 mm³. Diffusion‐weighted images (DWI) (60 axial slices) were acquired with the parameters: TR/TE = 7,680/82 ms, acquisition matrix = 128 × 96, voxel size = 2 × 2 × 2 mm³, 42 non‐collinear diffusion gradients, and diffusion weighting b = 1000 s/mm². More information on image acquisition can be found in other publications [Li et al., 2014a; Nie et al., 2012; Wang et al., 2012].

Table 1.

Demographic information at birth

Subjects	Gestational age at birth (days)	Birth weight (g)
All (15)	276 ± 6	3545 ± 422
Male (10)	277 ± 5	3517 ± 241
Female (5)	275 ± 7	3601 ± 678

Image Processing and Cortical Surface Construction

All infant MR images were processed using an infant‐specific computational pipeline for cortical surface‐based analysis, which has been extensively validated on >1,000 infant MRI scans [Li et al., 2013, 2015b, 2016; Lyall et al., 2015; Meng et al., 2014, 2016]. For image preprocessing, each subject's fractional anisotropy (FA) image derived from the diffusion‐weighted images (DWI) and T2‐weighted image was first aligned onto the corresponding T1 image and then resampled to 1 × 1 × 1 mm³ using FLIRT in FSL [Smith et al., 2004]. Second, for each set of aligned T1, T2, and FA images, skull stripping was performed using a learning‐based method [Shi et al., 2012], and then brain stem and cerebellum were removed by propagating their masks from the atlas images to the subject image by using HAMMER registration method [Shen and Davatzikos, 2002]. Third, intensity inhomogeneity was corrected by N3 method [Sled et al., 1998]. Fourth, all longitudinal images of the same infant were rigidly aligned. Fifth, an infant‐specific 4D level‐set method [Wang et al., 2011, 2012, 2014] was used to segment brain tissues. Finally, non‐cortical structures were masked and filled, and each brain image was separated into left and right hemispheres.

A topology‐preserving deformable surface method was used to reconstruct topologically correct and geometrically accurate cortical surfaces for each hemisphere [Li et al., 2012, 2014a]. Specifically, for the white matter, topology correction was first performed [Hao et al., 2016]. Then, the topology‐corrected white matter was tessellated as a triangulated surface mesh. Finally, a deformable surface method was applied to deform the shape of surface mesh, while preserving its initial topology and imposing spatially‐adaptive smoothness, to reconstruct the inner and outer cortical surfaces. To prevent surface meshes from self‐intersection, in each step of the surface deformation, a fast triangle–triangle intersection detection was performed at each vertex. Specifically, if two triangles were intersected, the deformation was reduced to a location without such intersection [Li et al., 2014a]. Cortical thickness of each vertex was computed as the mean of the minimum distance from the inner to outer surfaces and that from the outer to inner surfaces [Li et al., 2015b]. Sulcal depth of each vertex was defined as the shortest distance from the vertex to the cerebral hull surface, and was computed using the method from the work by Li et al. [2014b].

For cortical surface registration and analysis, the inner cortical surfaces were mapped onto a spherical surface [Fischl, 2012]. The intra‐subject registration was first performed to unbiasedly align all longitudinal cortical surfaces of the same infant, using a group‐wise Spherical Demons registration method [Yeo et al., 2010]. The inter‐subject registration was then performed to groupwisely align the mean cortical folding of different infants, using Spherical Demons. Thus, the vertex‐wise correspondence of all surfaces across different infants was established, and each cortical surface was then resampled to the same mesh tessellation. More details on both intra‐subject and inter‐subject surface registrations can be found in the work by Li et al. [2014c].

Cortical Thickness Prediction Method

We adopt DARF as our core regression tool to predict cortical thickness at each vertex on the cortical surface. In the following, we first briefly introduce the concept of regression forest, and then detail both training and testing stages using DARF.

Regression forest

A regression forest consists of a number of binary decision trees that are trained independently. Each binary decision tree can recursively split the data into different subgroups according to predefined split functions, and at the end a regression value is computed for each subgroup. Each tree represents a “weak learner” with a limited ability of regression, but a linear combination of many “weak learners” as a forest yields an accurate regression result [Criminisi et al., 2012]. Note that the regression forest is extremely useful, when it is difficult to find an explicit mathematical expression for modeling the complex relationship between the input and output data manifolds, such as our problem of modeling the vertex‐wise nonlinear developing trajectories of cortical thickness. However, since cortical thickness and its development are highly regionally heterogeneous, a single regression forest cannot precisely model vertex‐wise cortical thickness development. Thus, we propose to use DARF, which locally assembles a number of regression forests, to predict subject‐specific dynamic cortical thickness maps.

Cortical thickness prediction using DARF

Our learning‐based method contains a training stage and a testing stage. Specifically, in the training stage, one individual binary decision tree is trained at each vertex on the cortical surface. As shown in Figure 1a, for a given vertex on the spherical cortical surface (mapped from the original cortical surface), one individual tree is trained using the nearby vertices within a fixed neighborhood (i.e., the region enclosed by the red circle). Each training sample can be denoted as a pair of features and a regression target (x_i ∈ ${ℝ}^d$, y_i ∈ $ℝ$). Herein, x_i is a vector of features encoding both cortical morphological information and postnatal age at MRI scan at the baseline time point (around the 1st month), and y_i, the regression target, is the cortical thickness value at a target time point (i.e., 3rd, 6th, 9th, or 12th month). Specifically, the feature vector x_i includes (1) the accurate postnatal age at MRI scan (in days), (2) the cortical thickness and sulcal depth of vertex i at the baseline time point, and (3) the Haar‐like features extracted from both the local cortical thickness map and sulcal depth map at the baseline time point, which will be detailed later. The reason for using the accurate postnatal age as a feature is because that the infant cortical thickness development is highly related to the age. Furthermore, the purpose of including sulcal depth information in the features is to make use of the correlation between sulcal depth and cortical thickness [Fischl and Dale, 2000; Li et al., 2015a]. Finally, the advantage of using Haar‐like features is that they can provide rich neighboring information, such as mean values and regional differences, as introduced next.

Figure 1.

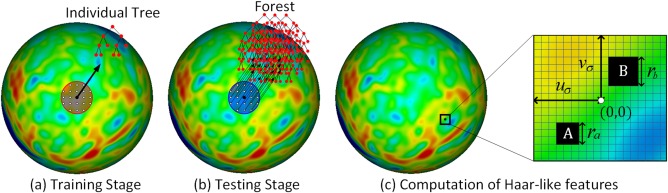
Predicting cortical thickness development using DARF on the spherical cortical surface. The red region in (a) represents a neighborhood, in which all vertices are used as training samples. The blue region in (b) represents a fixed neighborhood, in which all the individual trees are combined together to form a forest in the testing stage. In (c), the rectangular blocks A and B are the two randomly selected regions for computing Haar‐like features. [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 1c illustrates how to compute Haar‐like features from local cortical thickness map for a vertex i on the resampled spherical surface. Specifically, first, the local cortical thickness map around the vertex i is projected onto the tangential plane, where a local 2D coordinate system is built at the center of the vertex i. Two blocks A and B are then randomly selected in the neighborhood $[\pm u_{\sigma },\hspace{0.17em}\pm v_{\sigma }]$, with their sizes r_a and r_b chosen randomly within the interval [r ₁, r ₂], where u_σ, v_σ, r ₁, and r ₂ are the user‐defined parameters. Let Q_A denote the set of all the vertices in block A and also Q_B denote the set of all the vertices in block B, and then the Haar‐like feature at vertex i can be defined as:

$$f(i)=\frac{1}{|{\mathit{Q}}_{\mathit{A}}|}{\displaystyle {\sum }_{(u,v)\in {\mathit{Q}}_{\mathit{A}}}T(u,v)-\delta \frac{1}{|{\mathit{Q}}_{\mathit{B}}|}}{\displaystyle {\sum }_{(u,v)\in {\mathit{Q}}_{\mathit{B}}}T(u,v)}$$ (1)

where T(u,v) is the value of cortical thickness or sulcal depth at position (u,v), and δ is a random coefficient that takes either 0 or 1.

In the testing stage, to predict cortical thickness of a given vertex at a target time point, as shown in Figure 1b, all nearby individual trees within a fixed neighborhood (i.e., the blue region) are grouped together to form a forest. The feature vector of the given vertex is computed and then fed into each individual tree of the formed forest. The prediction result is finally computed as the average of regression outputs from all trees of the formed forest.

Note that, the method above only used the data at 1 month to predict the cortical thickness maps at all future time points. However, since this method is very general, if a subject has data at multiple time points, all these data can be aggregated for the cortical thickness prediction. Indeed, as shown in the next section, using all available data at multiple time points together produce more accurate prediction results than only using the data at 1 month.

Quantitative evaluation

To quantitatively evaluate the prediction results, we used the mean absolute error (MAE) and the mean relative error (MRE). These metrics are respectively computed as follows:

$$\text{MAE}=\frac{1}{N}{\displaystyle {\sum }_{i=1}^N|y_i^{\prime }-y_i|}$$ (2)

$$\text{MRE}=\frac{1}{N}{\displaystyle {\sum }_{i=1}^N|\frac{y_i^{\prime }-y_i}{y_i}|}$$ (3)

where y_i and $y_i^{\prime }$ are respectively the ground truth and estimated result, and N is the total number of vertices.

RESULTS

To evaluate our method, we used two nested leave‐one‐out cross‐validation loops on 15 infants, each with longitudinal MRI scans at 1, 3, 6, 9, and 12 months of age. Herein, the inner loop was used to tune the parameters of DARF, while the outer loop was used to evaluate the prediction results. Specifically, in each fold of the outer cross‐validation, we used 14 infants as training subjects and the remaining one as the testing subject. We first inspected the quality of our prediction results on an individual level, then on a group level, and finally on each cortical region, as detailed below.

Individual‐level Inspection

For each individual, we compared the predicted cortical thickness map with its ground truth, which we obtained using the method in Section “Image Processing and Cortical Surface Construction,” and then computed the prediction error map. Figure 2 provides an example of the predicted cortical thickness maps based on its data at 1 month of age, for a randomly selected subject. It is clear that the predicted map is generally quite similar to the ground truth.

Figure 2.

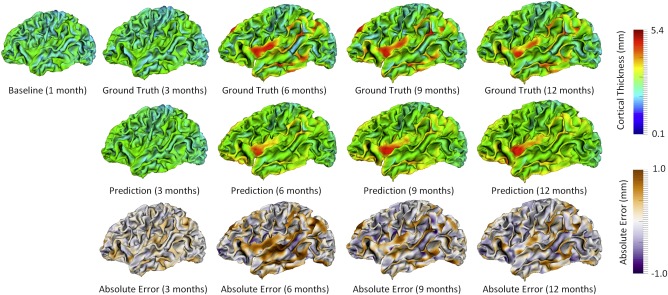
Prediction of the cortical thickness maps for a randomly selected subject. [Color figure can be viewed at http://wileyonlinelibrary.com]

Group‐level Evaluation

For each individual at each time point, we computed the mean value of the predicted cortical thickness over the whole cortical surface, and then explored the longitudinal distribution of the predicted mean cortical thickness. Figure 3 shows a comparison between the longitudinal distributions of ground‐truth mean cortical thickness and its corresponding prediction for 15 subjects. As shown, the distribution of the predicted cortical thickness is generally similar to the distribution of ground‐truth cortical thickness.

Figure 3.

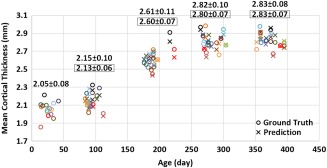
Longitudinal distribution of ground‐truth mean cortical thickness and its corresponding prediction (over the whole cortical surface) for 15 subjects. Different subjects are distinguished by different colors. For each time point, the average ground‐truth mean cortical thickness over all 15 subjects and standard deviation are provided on the top of data distribution, and the values within each black rectangle denote the average and standard deviation of the corresponding prediction results. [Color figure can be viewed at http://wileyonlinelibrary.com]

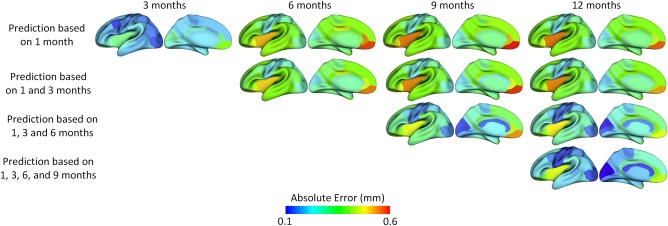
Furthermore, we examined whether adding more early time points could better predict cortical thickness at future time points. To do this, we gradually included more time points in the training data, and compared the respective prediction results. Specifically, we first used the baseline data (i.e., at 1 month of age) as inputs to predict cortical thickness maps at 3, 6, 9, and 12 months of age, and then combined the data at 1 and 3 months of age and used them together as inputs to predict cortical thickness maps at 6, 9, and 12 months of age. We gradually added more time points into the inputs, i.e., up to combination of data at 1, 3, 6, and 9 months of age to predict the cortical thickness map at 12 months of age. Figure 4 shows that using more time points for prediction generally led to better results. Additionally, we found that the error map at each time point is highly correlated with the corresponding standard deviation map of cortical thickness across individuals, with the averaged correlation coefficient of 0.8 ± 0.05. Another observation based on Figure 4 is that the standard deviations at 6th and 9th months are relatively larger than those at other time points, and accordingly the prediction errors at 6th and 9th months are also larger compared with other time points. Of note, the large standard deviation of cortical thickness estimation errors at 6th and 9th months might be caused by the extremely low tissue contrast of infant MRI at these ages, which makes both cortical surface construction and measurement more challenging and less accurate [Li et al., 2014a; Wang et al., 2015]. In Figure 4, we can also observe that the prediction accuracy peaks in the unimodal cortex, e.g., precentral gyrus (primary sensory cortex), postcentral gyrus (primary motor cortex), and occipital cortex (visual cortex), while the prediction accuracy drops in the high‐order association cortex, e.g., prefrontal cortex, temporal cortex, insula cortex, and inferior parietal cortex.

Figure 4.

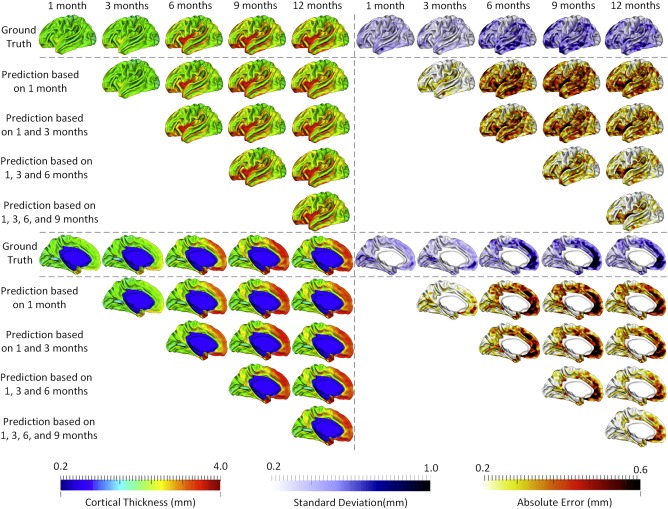
The prediction results from multiple available time points, averaged across 15 subjects. The 1st row and the 6th row show, respectively, the averaged cortical thickness maps (left half columns) and corresponding standard deviation maps (right half columns) at all five time points. The 2nd to 5th rows and 7th to 10th rows show the predicted cortical thickness maps (left half columns) and the corresponding error maps (right half columns). [Color figure can be viewed at http://wileyonlinelibrary.com]

Tables 2 and 3 report the quantitative evaluations for using data at different available time points to predict cortical thickness maps at future time points. When predicting cortical thickness maps from a single time point at 1 month, the prediction error at 3 months of age was the smallest, followed by the large error at 12 months of age, with the prediction errors at 6 and 9 months of age relatively larger. This is consistent with the observations in Figure 4. From these tables, we can also conclude that integrating more time points into the prediction framework generally induces higher accuracy.

Table 2.

Quantitative measures of cortical thickness prediction using mean absolute errors (MAE)

MAE (mm)	Target time point
Adopted Time Point(s)	3rd month	6th month	9th month	12th month
1st month	0.209 ± 0.026	0.332 ± 0.037	0.340 ± 0.030	0.321 ± 0.028
1st, 3rd months	—	0.313 ± 0.036	0.321 ± 0.025	0.301 ± 0.025
1st, 3rd, 6th months	—	—	0.026 ± 0.023	0.247 ± 0.022
1st, 3rd, 6th, 9th months	—	—	—	0.219 ± 0.020

Table 3.

Quantitative measures of cortical thickness prediction using mean relative errors (MRE)

MRE (%)	Target time point
Adopted Time Point(s)	3rd month	6th month	9th month	12th month
1st month	9.9 ± 1.1	13.1 ± 0.9	12.4 ± 0.8	11.7 ± 0.9
1st, 3rd months	—	12.3 ± 0.8	11.7 ± 0.7	11.0 ± 0.7
1st, 3rd, 6th months	—	—	9.5 ± 0.8	9.0 ± 0.7
1st, 3rd, 6th, 9th months	—	—	—	7.9 ± 0.6

To demonstrate the advantage of our method, we have compared our method with the vertex‐wise linear regression model, especially in predicting cortical thickness maps at 3, 6, 9, and 12 months based on the cortical thickness map at birth. The results are reported in Table 4, showing that our method outperforms the linear regression model.

Table 4.

Quantitative comparison between our method and linear regression model using mean absolute errors (MAE) and mean relative errors (MRE)

	Target time point
	3rd month	6th month	9th month	12th month
Our Method (MAE) (mm)	0.209 ± 0.026	0.332 ± 0.037	0.340 ± 0.030	0.321 ± 0.028
Linear Regression (MAE) (mm)	0.244 ± 0.025	0.370 ± 0.041	0.388 ± 0.033	0.362 ± 0.035
Our Method (MRE) (%)	9.9 ± 1.1	13.1 ± 0.9	12.4 ± 0.8	11.7 ± 0.9
Linear Regression (MRE) (%)	11.3 ± 1.0	14.6 ± 1.1	14.4 ± 0.9	13.2 ± 1.1

Region‐based Evaluation

In this section, we parcellated each cortical surface into 35 regions using the method developed by Li et al. [2014c], and then computed the average prediction error in each region. As shown in Figure 5, the regions with smaller errors generally included the unimodal cortex, such as sensorimotor region (in precentral gyrus and postcentral gyrus) and visual area (including cuneus cortex, pericalcarine cortex, lingual gyrus, and lateral occipital cortex), while the regions with larger prediction errors represented high‐order association cortex, such as the prefrontal, lateral temporal, cingulate, and insula cortices.

Figure 5.

The average prediction errors (mm) in 35 cortical regions of interest for 15 infants. [Color figure can be viewed at http://wileyonlinelibrary.com]

DISCUSSION

Cortical thickness is a rich attribute that has the potential to help identify early postnatal neurodevelopmental disorders [Ecker et al., 2014; Querbes et al., 2009; Singh et al., 2008]. To overcome the need of additional MRI scans later on for individual assessment of cortical thickness changes, we proposed a generic prediction framework for any cortical attributes from single or multiple time point(s). Notably, as cortical thickness develops dramatically and regionally heterogeneously in the first postnatal year, the prediction task is extremely difficult. To address this, we developed a novel machine learning‐based method to accurately predict subject‐specific dynamic cortical thickness maps during early postnatal brain development. Specifically, we used a bundle of informative features computed from cortical thickness map and sulcal depth map at the available time points as the inputs to our regression model, for predicting the future cortical thickness maps at 3, 6, 9, and 12 months of age, respectively. Our method was validated based on 15 healthy infants, each with longitudinal MRI scans at five different time points during the first postnatal year using a level‐one‐out cross‐validation. The results show that, leveraging our method, we can accurately predict the vertex‐wise, dynamic cortical thickness maps during infancy, thus capturing the cortical thickness developmental trajectories on both individual and population levels.

The prediction accuracy is affected by many factors, such as the size of the training samples, the quality of cortical surface reconstruction, and the cortical thickness variability across subjects. For example, leveraging more time points for prediction could achieve more accurate results, as shown in Figure 4 and Tables 1 and 2. The main reason might be that the cortical thickness map at each time point has some age‐specific characteristics, and when using such characteristics at multiple time points together, longitudinal information will be encoded, which is very helpful for guiding the regression model. Another important observation is that the prediction accuracy does not strictly rely on the time span between the baseline and the target time point. As shown in Tables 1 and 2, even though the time gap between the 1st and the 12th month is larger than that between the 1st and the 6th month, the prediction accuracy at 12th month is still higher than that at 6th month, when solely using the baseline time point for prediction. This relatively low prediction accuracy of cortical thickness map at 6th month can be explained by the extremely low tissue contrast of MRI at this age [Wang et al., 2015], which affects the accuracy of cortical surface reconstruction and in turn cortical thickness measurement. To address this issue, we have leveraged a longitudinal segmentation approach to jointly segment all longitudinal images with the guidance from the MR images with relatively good contrast, thus obtaining more accurate and longitudinally consistent segmentation results and subsequent cortical surface reconstruction results. It is worth indicating that this longitudinal guidance was applied only to the regions with inconsistent segmentations, thus minimizing the potential bias in the longitudinal segmentations. Of note, cortical thickness was measured based on the inner and outer cortical surfaces, which were reconstructed for each image independently, thus not involving any bias.

We also noted that the prediction accuracy was regionally quite variable. Specifically, high‐accuracy predictions were found in the precentral gyrus, postcentral gyrus, and occipital cortex, corresponding to the unimodal cortex. While low‐accuracy predictions were mainly found in the prefrontal, insula, lateral temporal, and inferior parietal regions, largely corresponding to the high‐order association cortex. One potential explanation is that at birth the unimodal cortex is more mature, compared to the high‐order association cortex. For example, in the first postnatal year, cortical thickness exhibits low growth in the unimodal cortex, but high growth in the high‐order association cortex [Nie et al., 2014; Li et al., 2015a]. Hence, the development of cortical thickness in the unimodal cortex is less influenced by the complex and variable postnatal environments, and thus can be predicted more accurately than the high‐order association cortex, as it is more plastic and easily affected by the postnatal environments [Lenroot et al., 2009]. Another possible explanation is that the unimodal cortex has less variable cortical thickness patterns across individuals than the high‐order association cortex during infancy, as shown in Figure 4. Moreover, the unimodal cortex is marked by a lower inter‐subject variability of functional connectivity than the high‐order association cortex in infants [Gao et al., 2014] as in adults [Mueller et al., 2013]. Hence, our proposed prediction framework can better capture cortical developmental patterns of the unimodal cortex than those of the high‐order association cortex (as marked by a highly heterogeneous growth), thus leading to more accurate predictions in the unimodal cortex. Besides, we speculate that including more training subjects as well as the socioeconomic status of each recruited infant, which likely affect early brain development [Brito and Noble, 2014; Hackman and Farah, 2009; Hackman et al., 2010], could further improve the prediction performance, especially for the high‐order association cortex.

One limitation in our current study is that we only used MRI data from healthy infants to train our prediction method. In the future, we will include subjects with possible abnormal early brain development to test our prediction model, given that many neurodevelopmental disorders are related to the abnormal cortical thickness development during infancy. If our prediction results are of great accuracy, they can potentially help detect early abnormal brain developmental during infancy.

In conclusion, we presented the first learning‐based method for predicting dynamic changes of cortical thickness maps during early brain development, using cortical attributes derived from early MRI scan(s). Our results demonstrated that the prediction accuracy is regionally variable, with higher accuracy in the unimodal cortex than the high‐order association cortex. In our future work, we will add more information from large‐scale training datasets to further improve the overall performance. Importantly, increasing the cortical thickness prediction accuracy may help better model and understand early brain development and also early detect potential abnormalities in early brain development.