Abstract
The bidomain equations are considered to be one of the most complete descriptions of the electrical activity in cardiac tissue, but large scale simulations, as resulting from discretization of an entire heart, remain a computational challenge due to the elliptic portion of the problem, the part associated with solving the extracellular potential. In such cases, the use of iterative solvers and parallel computing environments are mandatory to make parameter studies feasible. The preconditioned conjugate gradient (PCG) method is a standard choice for this problem. Although robust, its efficiency greatly depends on the choice of preconditioner. On structured grids, it has been demonstrated that a geometric multigrid preconditioner performs significantly better than an incomplete LU (ILU) preconditioner. However, unstructured grids are often preferred to better represent organ boundaries and allow for coarser discretization in the bath far from cardiac surfaces. Under these circumstances, algebraic multigrid (AMG) methods are advantageous since they compute coarser levels directly from the system matrix itself, thus avoiding the complexity of explicitly generating coarser, geometric grids. In this paper, the performance of an AMG preconditioner (BoomerAMG) is compared with that of the standard ILU preconditioner and a direct solver. BoomerAMG is used in two different ways, as a preconditioner and as a standalone solver. Two 3-D simulation examples modeling the induction of arrhythmias in rabbit ventricles were used to measure performance in both sequential and parallel simulations. It is shown that the AMG preconditioner is very well suited for the solution of the bidomain equation, being clearly superior to ILU preconditioning in all regards, with speedups by factors in the range 5.9–7.7.
Index Terms: Bidomain equations, computational efficiency, numerical simulation, operator splitting, parallel computing, unstructured grids, whole heart models
I. Introduction
The bidomain equations [1] are considered as one of the most complete descriptions to model the spread of excitation in cardiac tissue. Particularly when bath loading effects, extracellular stimulation or the magnetic field are to be modeled accurately, using a bidomain approach is the only choice [2], [3]. Although the bidomain equations are solved straight-forwardly on current desktop computers up to some hundreds of thousands of unknowns, models of entire hearts at reasonably fine discretizations (< 250μm) lead to systems with millions of unknowns. The solution of these equations still poses a tremendous computational challenge. Efficient numerical methods and the application of parallel computing techniques are mandatory.
Typically, the numerical efficiency is improved by applying operator splitting techniques which avoid the solution of a large nonlinear system at every time step [4]–[7]. The solution process is broken down into a three step scheme involving the solutions of a parabolic partial differential equation (PDE), an elliptic PDE, and a nonlinear system of ordinary differential equations (ODEs). The parabolic PDE is solved efficiently in parallel environments using a forward Euler method (matrix-vector product only and no linear system) or the implicit Crank-Nicholson method (strongly diagonally dominant linear system solved efficiently with cheap, iterative methods). Further, the ODEs, although time consuming with sequential codes, parallelize with linear scaling since the state variables do not diffuse and, thus, no communication is needed (an embarrassingly parallel problem). With bidomain simulations, computation is clearly dominated by the algebraic system associated with the elliptic part [4].
An efficient way of solving the large linear algebraic system that arises from the discretization of the bidomain equations has been a topic of research since 1994 [8]. For large scale problems, the preconditioned conjugate gradient (PCG) method has become the standard choice for an iterative solver. Although the PCG method is very robust (with respect to convergence), it is not necessarily efficient with respect to speed, depending strongly on the choice of a proper preconditioner. The most efficient preconditioner reported so far is a geometric multigrid (GMG) preconditioner which typically performed 2–3 times better than ILU when simulating electrical activity on regular structured grids [9].
Quite often, the use of unstructured grids is preferred. The reasons are twofold. First, unstructured grids allow a better geometric representation of organ boundaries and avoid problems with artifactual currents, as evoked by jagged boundaries on structured grids when defibrillation strength shocks are studied [10], [11]. Second, the spatial discretization of a mesh can be reduced with distance from the cardiac surfaces which leads to significantly fewer unknowns without any negative impact on numerical accuracy. Unfortunately, with unstructured grids, the construction of a proper GMG preconditioner is nontrivial. The explicit generation of coarser grids, along with the creation of prolongation and restriction operators that transfer the information between different grid levels, become complex tasks. In this case, another class of multilevel methods, referred to as algebraic multigrid (AMG), are an appealing alternative. For AMG methods the coarser grids and associated transfer operators are generated directly from the system matrix itself [12].
In this work, we focus on the solution of the linear system associated with the elliptic portion of the bidomain equations using the BoomerAMG code [13] as a preconditioner for the iterative conjugate gradient (CG) solver and as a standalone solver. Two realistic simulation scenarios were considered as benchmarks for both sequential and parallel runs. In the sequential case, induction of an anatomical reentry in a 3-D slice (111 589 unknowns) of rabbit ventricles was simulated. A larger setup, the induction of an arrhythmia in a full 3-D rabbit ventricular model (862 515 unknowns) with two plate electrodes, was chosen to benchmark the parallel performance of the methods. Performance obtained with the AMG preconditioner was compared against a standard preconditioner based on incomplete LU factorization (ILU). Additionally, sequential performance was compared against a sparse direct solver [14] which is known to perform well for small scale problems.
II. Methods
A. Bidomain and Operator Splitting
The bidomain equations were decoupled by operator splitting [15], [16]
| (1) |
| (2) |
| (3) |
where ϕe and Vm are the extracellular potential and transmembrane voltage, respectively; represents the ionic current variables; and are conductivity tensors of intracellular and extracellular spaces, respectively; σb is the isotropic conductivity of the fluid in which the heart is immersed (bath and cavities); Cm is the capacitance per unit area and β is surface to volume ratio; iion and g model ionic currents and specify the cell membrane model.
At the tissue-bath interface, continuity of the normal component of the extracellular current and continuity of ϕe were enforced. The normal component of the intracellular current vanished at all tissue boundaries whereas the normal component of the extracellular current vanished at the boundaries of the bath. A grounding electrode was modelled by enforcing Dirichlet boundary conditions at one lateral face of the bath.
Numerically, a three step scheme was applied involving the solution of a parabolic PDE, an elliptic PDE and a nonlinear system of ODEs at each time step. Both the parabolic PDE and the nonlinear ODE systems were solved via the explicit forward-Euler scheme [4]
| (4) |
| (5) |
| (6) |
| (7) |
where Aξ is the discretized operator; Δt is the time step; Vk, and are the temporal discretizations of Vm, ϕe, and , respectively, for time equal to kΔt. The system of equations was solved using the finite element method, employing linear elements and lumped mass matrices.
B. Benchmark Setups
Based on published geometric data [17], a rabbit ventricular geometry model with smooth epicardial and endocardial surfaces and anatomically realistic fiber orientation (RCV) was discretized using an unstructured grid with an average discretization of 250 μm. The bidomain equations were discretized on this nonuniform grid using linear tetrahedral elements with time steps between 8 μs and 20 μs. Simulations were carried out with Cm = 1 μF/cm2 and β = 1400 cm−1. Initially, conductivity along the fibers was set to σil = 1.74 mS/cm and σel = 6.25 mS/cm, and transverse to the fibers to σit = 0.19 mS/cm and σet = 2.36 mS/cm, in the intracellular and interstitial domain, respectively [18]. The conductivity of the surrounding fluid was set to σb = 1.0 mS/cm.
1). Sequential Benchmark
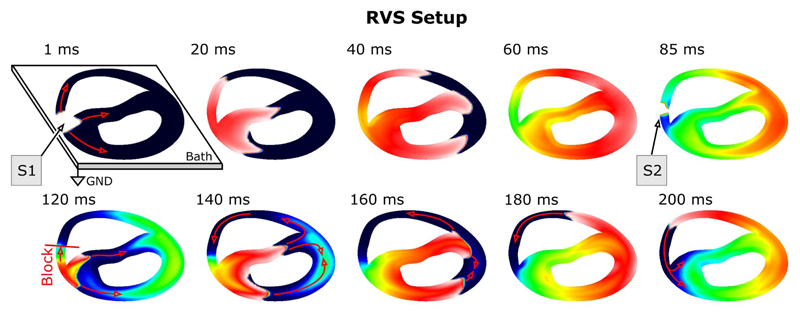
A FEM mesh of a slice through the rabbit ventricle (RVS) of 0.5 mm thickness was generated, resulting in 111 589 and 59 292 degrees of freedom for the elliptic and the parabolic problems, respectively. The computational workload posed by the elliptic problem, Lseq = Nυ × Nt, was 2.78 × 109 with Nυ= 111 589 and Nt = 25 × 103 (500 ms integrated at a time step of 20 μs). An extracellular current stimulus was applied to induce action potential propagation. The entire face of bath next to the left ventricular free wall was grounded (Fig. 1). At 85 ms, another stimulus was applied at a slightly shifted location at the critical recovery isoline, leading to unidirectional block. An anatomical reentry ensued and was sustained over the entire observation period of 500 ms (Fig. 1). The active membrane behavior was described by the Beeler-Reuter Drouhard-Roberge ionic model as modified by Skouibine et al. [19].
Fig. 1.
Setup used to benchmark sequential simulation runs: a sustained anatomical reentry was induced with an S1–S2 pacing protocol. Shown are polarization patterns of Vm for selected instants. Red arrows indicate the conduction pathways of the activation wavefronts. Due to the presence of a bath, the degrees of freedom associated with the elliptic problem are higher than with the parabolic problem. The left upper panel shows the bath geometry and the location of the reference electrode.
2). Parallel Benchmark
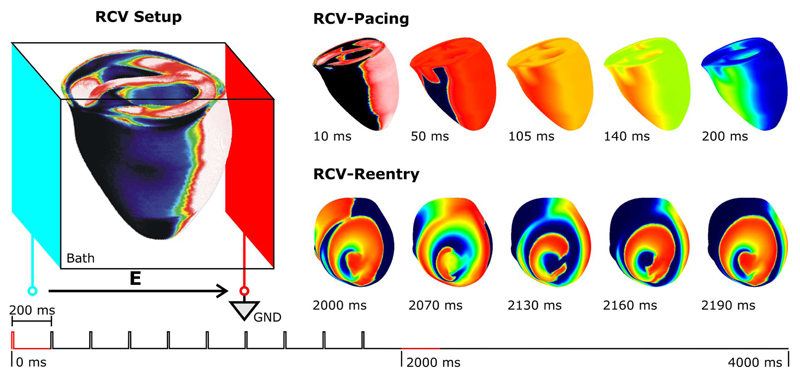
Parallel performance was benchmarked using the RCV model. The elliptic and parabolic problems were associated with 862 515 and 547 680 degrees of freedom, respectively. The computational workload associated with the elliptic problem, was Lpar = 2.2 × 1010 with Nυ = 862515 and Nt = 25 × 103 (200 ms integrated at a time step of 8 μs).
The active membrane behavior was described by the rabbit ventricular Puglisi model [20] incorporating an electroporation current [21] and a hypothetical Ia current [22]. Two plate electrodes, a stimulation electrode and a grounding electrode, were used to stimulate the ventricles by delivering a train of ten pulses. Subsequently, electric activity was simulated for another 2 s.
To determine suitable parameters which lead to a reentry under the given protocol, the basic cycle length (BCL) of the pulses and the wave length of the tissue, λ, given by
| (8) |
were varied. The wavelength was varied by multiplying all conductivities with the square of the desired reduction in wave-length. To speed up this time-consuming procedure, depending on the availability at the NGS and HPCx supercomputing facilities provided by the Integrative Biology Project [23], between 32 and 128 processors were employed. From the series of simulations, a standard was chosen with a BCL of 200 ms and λ reduced to 0.66 of the nominal λ, as computed with the default conductivity settings, leading to a sustained figure of eight reentry circulating around the apex [Fig. 2 (bottom panels)].
Fig. 2.
Setup for the parallel benchmark: A train of 10 pacing stimuli with a basic cycle length of 200 ms was delivered to the RCV via two plate electrodes (left panel, RCV-Setup). A figure-of-eight reentry ensued and was sustained until the end of the simulation run at 4000 ms.
After analyzing the number of iterations per time step, Ns, of the selected simulation run as a function of the right-hand side (RHS), b, where b corresponds to the terms on the RHS of (1), two representative 200-ms sequences were chosen for benchmarking: 1) a 200-ms sequence starting at the onset of the first pacing pulse and ending before the onset of the subsequent pulse (Fig. 2, RCV-Pacing); 2) a 200-ms figure-of-eight reentry sequence following immediately after the last pacing pulse (Fig. 2, RCV-Reentry).
C. Elliptic Solvers
The iterative CG [24] method was used to solve the linear system
| (9) |
associated with the elliptic equation (1). Preconditioning techniques speed up the convergence of the CG by solving a better conditioned equivalent system B−1 AB−T(BTx) = B−1b, where M = BBT is the preconditioner associated with. The more similar M is to A, the faster the convergence is. On the other hand, preconditioning involves the solution of a linear system
| (10) |
for every iteration i, where pi relates to the Krylov space construction [24] and ri is the preconditioned residual. A more complex preconditioner means fewer iterations are necessary to achieve convergence but at a higher computational cost for each iteration.
For the sequential test case, we compared the performance of three different methods: BoomerAMG (BAMG) [13] as a preconditioner for CG; the traditional ILU-CG method; and the sparse direct SuperLU solver [14]. For the parallel benchmarks, only BAMG-CG and ILU-CG were considered. Finally, to examine whether further performance gains can be achieved by setting up the BoomerAMG method as a solver (BAMG-S), both sequential and parallel benchmarks were carried out with this configuration.
1). Incomplete LU Factorization
To solve the elliptic PDE, ILU factorization is widely used as a preconditioner for the CG method and can be considered as the standard method [4]. During parallel runs, the ILU preconditioner was based upon block Jacobi, i.e., ILU was applied to the main diagonal block of the local matrix A, thus avoiding extra communication.
2). BoomerAMG Preconditioner
AMG consists of two parts. First, the setup builds a hierarchy of coarser grids and operators from the fine grid operator. The goal is to generate an operator hierarchy similar to GMG. Second, a normal multigrid cycle uses this automatically generated hierarchy in an iteration or in a preconditioner.
The crucial point in the setup is the coarsening, i.e., the reduction of fine level information onto the next coarser level. To select the coarse grid points in AMG, we seek those unknowns xi which can be used to represent the values of nearby unknowns, xj. This is done via the concepts of dependence and influence. We say that the point i depends on the point j or j influences i, if the value of the unknown xj is important in determining the value of xi from the ith equation, i.e., j influences i if, for i ≠ j, we have −aij ≥ θ maxk≠i {−aik} for 0 ≤ θ ≤ 1 where θ is a scalar between 0 and 1. A coarse grid will be made of points which strongly influence many other points in the fine grid.
BAMG uses the parallel Falgout-coarsening strategy which is a combination of the classical Ruge-Stüben coarsening [25] and CLJP coarsening [13]. First, each processor domain is coarsened using the classical algorithm. Then, the coarse grid points in the interior of each processor domain are taken as the first independent set for the CLJP algorithm which proceeds until all points have been assigned. This way, the interior of a domain is coarsened as in the classical method, while the boundaries are coarsened CLJP-like. A Hybrid Gauss–Seidel/Jacobi method was used for relaxation on all grids but the coarsest, where Gaussian elimination was used [26].
3). BoomerAMG as a Standalone Solver
Further performance gains can be expected from using AMG directly as a solver. If the AMG setup produces high quality coarse meshes and operators such that the condition number of the preconditioned system (10) is close to unity then the AMG preconditioner may perform well when applied as a solver itself. This could save some arithmetic work per iteration compared with the preconditioned CG and, therefore, may result in a further speedup of the solver.
4). Sparse Direct Solver SuperLU
Direct solvers are known to be the fastest solver for the elliptic portion of the bidomain equations [4] in the case of small-scale discretizations (up to some hundred of thousands unknowns), like the sequential test case in this paper. SuperLU [14] was chosen as a sparse direct solver since it integrates seamlessly with the underlying mathematical library [27] upon which our simulator is based [28].
D. Parameter Tuning
Both the RVS and the RCV were used to carry out short simulations consisting of a 5-ms pacing pulse delivered via two plate electrodes and 5 ms of ensuing activity. Parameters of each preconditioner were tuned to minimize the execution time of this sequence using a single processor.
BAMG
First, the algorithm parameters which had major impact on the performance were identified. With BAMG-CG, performance depended mainly on the strong threshold parameter θ, which has to be chosen in a range between 0 and 1. Weak connections of a fine grid node i, that is, matrix entries which satisfy −ai,j < θ maxk≠i {−ai,k} are usually ignored when determining the next coarser level. Increasing θ leads to smaller coarse grids, but worsen convergence rates [29]. To determine the optimal setting, θ was varied between 0 and 1 in steps of 0.1. Further, the effects of reducing the number of grid sweeps, i.e., the number of relaxations per level, on the fine grid and on both up and down cycle on the solver performance was examined.
ILU
The performance of ILU can be improved during sequential runs by increasing the allowed level of fill-in. With increasing fill-in, ILU approaches the full LU decomposition which is the perfect preconditioner, and known to perform best on such small-scale problems. However, since the goal was good parallel performance for large scale problems, we refrained from doing so and kept the fill-in level at zero to preserve the sparsity pattern. Based on experiences gathered in previous studies [9], increasing the fill-in level is not efficient when going parallel, since the preconditioner is applied to the main diagonal block which leads to a decrease in quality of the preconditioner. This can be compensated by using overlapping preconditioning for the entire system (instead of using the nonoverlapping Block Jacobi preconditioner), but at the price of a significant increase in communication which again, depending on the network infrastructure, may hurt parallel performance.
E. Examination of Convergence Behavior
The convergence behavior of all iterative methods under study was analyzed by comparing the decrease of the unpreconditioned L2 norm of the residual at iteration i, ||ri|| = ||Axi − b||. The second time step (the first time step where a nonzero initial guess was available) of the sequential RVS test case was chosen for this purpose.
F. Memory Usage
The memory overhead introduced by a preconditioner or a solver was measured during sequential runs for both the RVS and the RCV setup. Setting up the preconditioner or factorization of the system matrix happened during the first solver step when all other data were loaded into memory already. Hence, the memory overhead of a particular method could be determined by measuring the difference in memory usage immediately before and after the first solver step.
G. Performance Metrics
BAMG-CG, ILU-CG, BAMG-S, and SuperLU [14] were used to solve the sequential test case. The parallel test cases were solved with BAMG-CG, BAMG-S, and ILU-CG only. The BAMG preconditioner was set up with the optimized settings which were determined by the parameter tuning procedure previously described. To compare the performance of the respective methods, the following parameters were considered: Ns, the number of iterations per time step; Ts, the execution time required per time step; Nt, the total number of iterations; Tt, the total execution time; and Tit, the execution time per iteration.
For all iterative methods under study, the solution of the previous time step was used as the initial guess. For the CG algorithm, the stop criterion ||ri|| < δ was used where δ was chosen to be 10−6 for the sequential test case. Since the chosen criterion depends on the problem size, the δ for the parallel test case was scaled by where Nυ,par, and Nυ,seq relate to the respective problem sizes. The BAMG-S method differed from all other methods since the BAMG implementation uses a relative tolerance as its stop criterion. Nevertheless, to allow performance comparisons with all other methods where absolute tolerances were specified, we have chosen a relative tolerance such that the L2-norm of the final residual of all solver steps was smaller than the respective absolute tolerances.
Parallel runs were carried out either at the Kepler Cluster of the Karl Franzens University Graz or at the Oxford Linux Clusters provided by the UK National Grid Service (NGS). Runs using between 4 and 16 processors were carried out on the Kepler cluster, a 16 node dual AMD Opteron 248, 2-GHz system with 4 GB RAM per node running a 64-bit Linux Kernel, and interconnected with a low latency Infiniband interconnect (Infiniband Mellanox MTS 2400, Mellanox Technologies Inc., Santa Clara, CA). Only one processor per node was used to avoid a mixed mode with different latencies depending on whether communication occurred over the Infiniband interconnect or via shared memory.
Further, a subset of the benchmarks was carried out at the Linux clusters provided by the UK National Grid Service to examine parallel performance using a higher number of processors between 16 and 64. At the Oxford NGS cluster, 64 nodes equipped with dual Intel Xeon 3.06-GHz CPUs and 2 GB RAM with a Myrinet high-speed message passing interconnect were available. Benchmarks were carried out in a mixed mode using shared memory for message passing within a single node, and the Myrinet interconnect between the nodes.
H. Implementation
Benchmarks were carried out with the CARP simulator [28] linked against the MPI [30] based PETSc C library v2.2.1 [27], the SuperLU library [14], and the Hypre library v1.9.0b [29] to access the BAMG preconditioner.
III. Results
A. Parameter Tuning
1). Boomer AMG
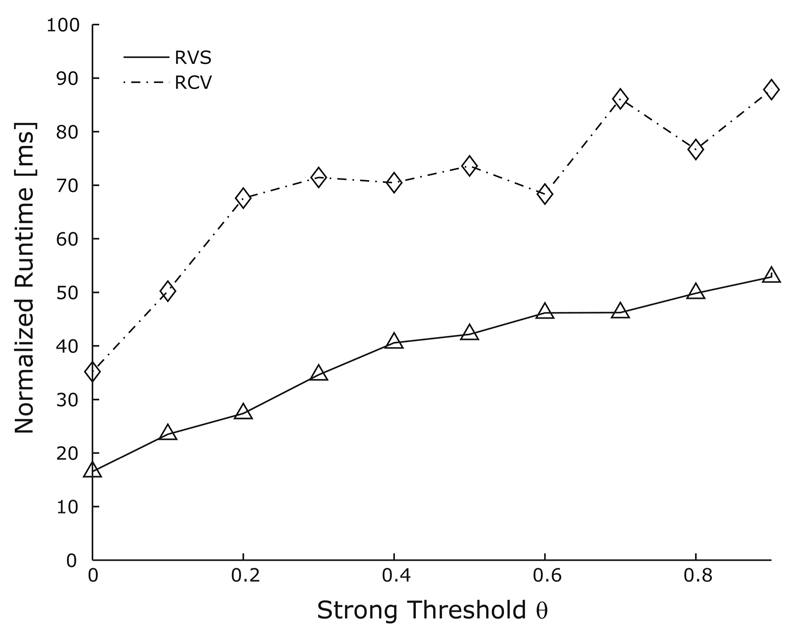
Short 10-ms simulation sequences of both RVS and RCV test cases were carried out on a single processor. Default parameter settings were chosen for the BAMG algorithm; only θ was tuned to optimize performance. Setting θ = 0.0 led to the fastest execution times for both setups (Fig. 3) whereas with θ = 1.0 the execution time increased dramatically. With θ = 0.0, it was also tested whether the reduction of grid sweeps could further improve the performance. Reducing the number of partial sweeps to one on the fine grid and on both up and down cycle (default setting is two) reduced the execution time per iteration, but increased the number of iterations for convergence. In some cases, this led to even better performance, while in other cases a slight decrease in performance was observed. With the setup θ = 0.0 which led to the fastest execution, BAMG used seven and six coarsening levels for the RVS and the RCV test case, respectively, as computed by the Falgout-CLJP coarsening method.
Fig. 3.
BoomerAMG tuning: Effect of varying the strong threshold parameter, θ, for two test cases of varying complexity. Runtime is normalized with respect to the computational workload, Nv×NT. The relative performance of the larger RCV test case was worse compared to the RVS test case, but the overall trend was similar, indicating that θ = 0 is the optimal choice. For θ = 1 (not shown) the runtime increased dramatically.
B. Convergence Behavior
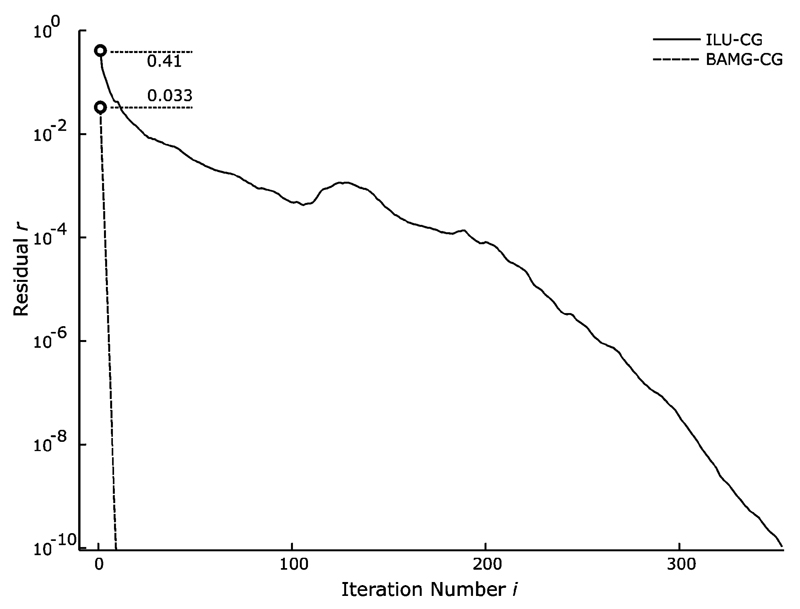
With BAMG the residual decreased at a rate of approximately one order of magnitude per iteration step (the average rate of decrease, measured as the ratio between subsequent residuals, ri+1/ri, was 11.5) whereas with ILU-CG, the rate of decrease was much smaller and nonmonotonic (Fig. 4). After the initial iteration, the residual r0 with BAMG was more than one order of magnitude smaller than with ILU (0.033 versus 0.41).
Fig. 4.
Convergence history of BAMG-CG versus ILU-CG: The residuals ri are plotted semilogarithmically as a function of the iteration number i. Residuals after the first iteration are marked with a circle. In contrast to the ILU-CG method, the relative rate of decrease was exponential and monotonic for BAMG-CG. The average rate of decrease was significantly larger for BAMG which led to much faster convergence.
C. Memory Usage
The memory overhead caused by the preconditioning was measured for ILU-CG, BAMG-CG, BAMG-S, and SuperLU. As expected, ILU-CG is the most efficient in this regard, introducing the least memory overhead. No noticeable differences were measured between BAMG-CG and BAMG-S. Memory usage of the direct SuperLU is excessive limiting its usage to small scale applications like the RVS setup. The RCV setup could not be factorized with SuperLU, not even when 8 GB of memory were available. Results are summarized in Table I.
Table I.
Memory Overhead in MByte
| Method | ILU | BAMG | BAMG-S | SuperLU |
|---|---|---|---|---|
| RVS | 24 | 65 | 63 | 814 |
| RCV | 212 | 741 | 734 | - |
D. Sequential Benchmark
The RVS problem was solved sequentially using ILU-CG, BAMG-CG, BAMG-S, and SuperLU. BAMG-CG turned out to be the fastest iterative method under study being 7.7 times faster than ILU-CG. Although with BAMG-CG the cost per iteration was larger and the average time per solver step, T̄s, was longer (Table II), the average number of iterations, N̄s, was lower than with ILU-CG, which led to an overall faster execution. As expected for this small scale problem, the direct SuperLU solver was the fastest method with an average solution time of 0.55 s, being about 2.9 times faster than BAMG-CG. A slight performance gain of about 7% over BAMG-CG could be achieved by applying BAMG as a standalone solver.
Table II.
Minimum, Mean and Maximum Values of Number of Iterations per Time Step (Ns), Average Execution Time per Time Step (T̄s), Total Number of Iterations Nt, Total Execution Time Tt, and Time per Iteration Tit for Solving Sequential RVS
| Method | Ns |
T̄s s |
Nt 1000’s |
Tt h |
T̄it ms |
|---|---|---|---|---|---|
| ILU-CG | 119/213/237 | 12.3 | 5310 | 85.6 | 58 |
| BAMG-CG | 3/ 4.84/ 5 | 1.61 | 120.6 | 11.12 | 333 |
| SuperLU | 1.00 | 0.55 | 25.0 | 3.58 | 545 |
| BAMG-S | 1.00 | 1.51 | 25.0 | 10.6 | 1508 |
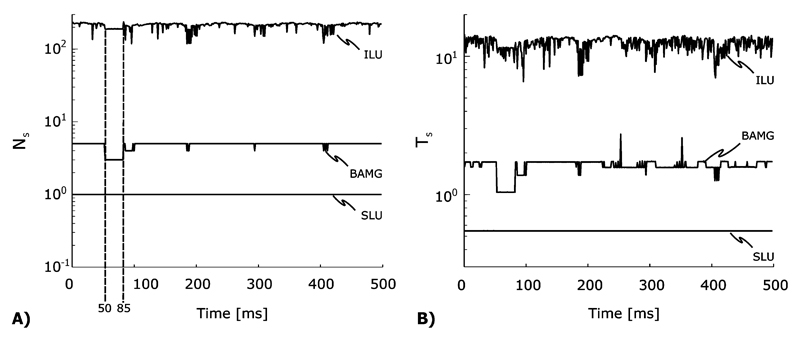
BAMG-CG depended only weakly on the RHS b. Both Ns and Ts were almost constant over the entire simulation sequence, whereas with ILU-CG, a strong dependency on b associated with a large variation of Ns and Ts around the average values N̄s and T̄s was observed [Fig. 5(A) and (B) and Table II].
Fig. 5.
(A) The number of iterations per time step, Ns and (B), the required solver time per time step, Ts, measured during the RVS sequential benchmarks are plotted as a functions of time. Both Ns and Ts dropped noticeably when the entire tissue was depolarized around 50 ms (Fig. 1, panels 40–60 ms), but returned to the same average level as before when reentry was induced by a second stimulus at 85 ms (Fig. 1, panel 85 ms).
E. Parallel Benchmark
Two simulation sequences, RCV-Pacing and RCV-Reentry, were solved in parallel to compare the performance of ILU-CG with BAMG-CG. Running on the Kepler cluster with Np between 4 and 16, BAMG-CG clearly outperformed ILU-CG being 5.9 to 6.9 times faster. To examine possible performance benefits with a larger Np, a subset of the benchmarks (RCV-Reentry) was carried out on the NGS clusters using between 16 and 64 CPUs. In this case, the performance gains with BAMG were slightly smaller, between 3.3- and 4.7-fold, than those measured at the Kepler cluster with a smaller Np. A detailed overview is given in Table III.
Table III.
Minimum, Mean and Maximum Values of Number of Iterations per Time Step (Ns), Average Execution Time per Time Step (T̄s), Total Number of Iterations (Nt), Total Execution Time (Tt) and Time per Iteration (Tit) for Parallel RCV.
| Sequence | Method | Np | Ns |
T̄s s |
Nt 1000’s |
Tt h |
Tit ms |
|---|---|---|---|---|---|---|---|
| Pacing | ILU-CG | 4 | 76 / 179 / 479 | 21.9 | 4478 | 152.1 | 122 |
| 8 | 76 / 179 / 489 | 11.8 | 4468 | 81.9 | 66 | ||
| 16 | 79 / 191 / 523 | 6.6 | 4782 | 46.1 | 35 | ||
| BAMG-CG | 4 | 2 / 3.2 / 11 | 3.4 | 80.5 | 23.4 | 1048 | |
| 8 | 2 / 3.3 / 11 | 2.0 | 81.6 | 13.6 | 601 | ||
| 16 | 2 / 3.4 / 11 | 1.1 | 83.9 | 7.7 | 332 | ||
| Reentry | ILU-CG | 4 | 137 / 201.3 / 377 | 27.4 | 5041.6 | 190.4 | 136 |
| 8 | 138 / 203.4 / 384 | 15.1 | 5092.6 | 105.2 | 74 | ||
| 16 | 150 / 216.1 / 412 | 7.2 | 5410.1 | 60.6 | 33 | ||
| ILU-CG† | 16 | 150 / 216 / 412 | 9.2 | 5410 | 63.9 | 42 | |
| 32 | 154 / 220.2 / 422 | 4.5 | 5513 | 31.4 | 20 | ||
| 64 | 167 / 238.4 / 449 | 3.1 | 5970 | 21.2 | 13 | ||
| BAMG-CG | 4 | 4 / 4.0 / 7 | 4.3 | 100.0 | 29.5 | 1064 | |
| 8 | 4 / 4.0 / 7 | 2.4 | 100.0 | 17.0 | 611 | ||
| 16 | 4 / 4.0 / 7 | 1.3 | 100.0 | 8.8 | 315 | ||
| BAMG-CG† | 16 | 4 / 4.0 / 7 | 2.0 | 100.0 | 13.7 | 492 | |
| 32 | 4 / 4.6 / 8 | 1.4 | 115.7 | 9.5 | 294 | ||
| 64 | 4 / 4.2 / 9 | 0.9 | 105.0 | 6.4 | 221 | ||
| BAMG-S | 4 | 1.0 | 4.2 | 25.0 | 29.5 | 4244 | |
| 8 | 1.0 | 2.3 | 25.0 | 15.3 | 2200 | ||
| 16 | 1.0 | 1.5 | 25.0 | 9.1 | 1311 | ||
Measured at the NGS.
1). Parallel Scaling With Np ≤ 16
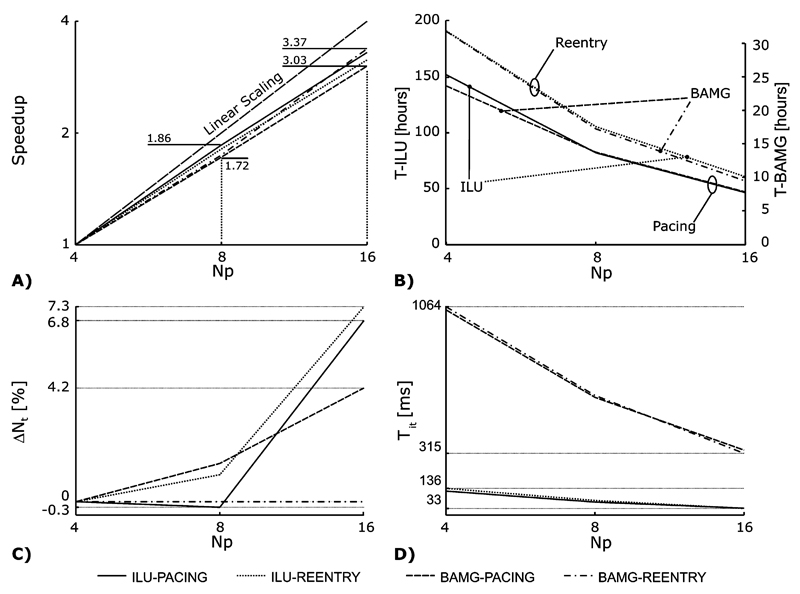
The solution of the elliptic PDE scaled well with both methods, independently of which sequence, pacing or reentry, was simulated (Fig. 6). Scaling efficiency was slightly better with 4–8 processors (between 86% and 93%) than with 8 to 16 (between 76% and 84%). Differences in parallel scaling between the methods were almost negligible.
Fig. 6.
Comparison of the parallel solver performance between ILU-CG and BAMG-CG for the both test sequences. (A) The parallel speedup relative to the case Np = 4 is shown. (B) Shown are the total elliptic solver times. Note that the left ordinate refers to ILU-CG and the right ordinate to BAMG-CG. Although the parallel scaling is similar for both methods, BAMG-CG is about 6 times faster than ILU-CG. (C) Increase in the number of iterations per time step (Ns) relative to the Np = 4 case as a function of Np. (D) Shown is the decrease of Tit with Np.
Simulating the reentrant activation sequence took slightly longer than the pacing sequence [Fig. 6(B)]. With ILU-CG, when increasing the number of processors, Np, from 4 to 16, the total solution time reduced from 152.3 and 190.7 h down to 46.2 and 60.6 h for the pacing and the reentry sequence, respectively. With BAMG-CG both sequences could be computed significantly faster. Execution times decreased from 23.7 and 29.8 h with Np = 4 down to 7.8 and 8.8 h Np = 16 for the pacing and the reentry sequence, respectively, being between 5.9 and 6.9 times faster than ILU-CG. Moreover, BAMG-CG with Np = 4 easily outperformed ILU-CG with Np = 16 by a factor of ≈2 [Fig. 6(B)]. Since the parallel scaling behavior of both methods was very similar [Fig. 6(A) and (B)], the performance ratios between the methods were basically independent of Np.
Further, the total number of iterations, Nt, and the time per iteration, Tit, depended on both Np and the type of activity. That is, an increase of Nt with Np indicates that the quality of a preconditioner suffers from parallelization. Ideally, Tit should decrease with Np in a linear fashion. A decrease of Tit less than linear is caused by communication.
With ILU-CG, an increase in the number of iterations, ΔNt, as a function of Np was observed. With Np = 16, the increase relative to the case with Np = 4 turned out to be 7.3% and 6.8% for the reentry and the pacing sequence, respectively [Fig. 6(C)]. During the reentry sequence when BAMG-CG was used, Nt did not depend on Np at all, but during the pacing sequence a linear relationship was observed leading to an increase ΔNt of 4.2%.
The time for a single iteration, Tit, decreased with Np. With ILU-CG, Tit decreased from 122 and 136 ms to 35 and 33 ms for the pacing and the reentry sequence when Np was increased from 4 to 16 whereas with BAMG-CG, Tit dropped from 1048 and 1064 ms to 332 and 315 ms. Parallel scaling of Tit was always slightly better with ILU than with BAMG. Further, increasing Np from 8 to 16 always scaled better compared to increasing from 4 to 8. As expected, Tit did not depend on the simulated activity [Fig. 6(D)].
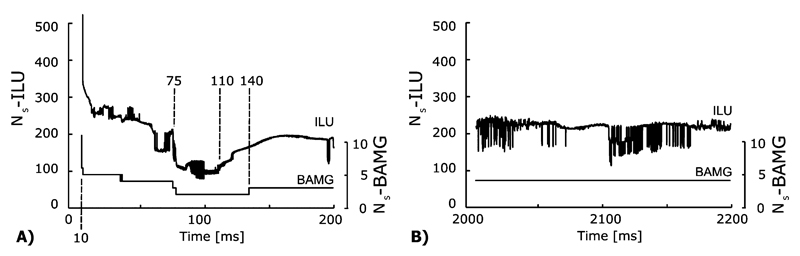
Major differences in the relationship of Ns and b were observed. During the pacing sequence, all methods depended on b, but to a different degree. Ns was highest during the stimulation period, but decreased subsequently starting at 10 ms [Fig. 7(A)]. A minimum in Ns was reached when the entire ventricles were depolarized up to the plateau level around 100 ms followed by a small increase around 140 ms [Figs. 7(A) and Fig. 2], coinciding approximately with the onset of repolarization. In general, the dependency of the BAMG method on b was very weak. In fact, during the reentry sequence there was virtually no dependency with Ns being constant (4 iterations) for all time steps [Fig. 7(B) and bottom of Table III, column Ns], except for the first time step where 7 iterations were needed since no initial guess was available.
Fig. 7.
The dependency of Ns on the RHS b for the parallel solution (Np = 16) of (A) the RCV-Pacing and (B) the RCV-Reentry setup using ILU and BAMG preconditioning.
2). Parallel Scaling With Np ≥ 16
With larger Np between 16 and 64, performance gains with BAMG-CG over ILU-CG were slightly smaller, between 3.3- and 4.7-fold, and depended on Np. ILU scaled better than BAMG when Np was increased from 16 to 32 processors (2.03 versus 1.45). When going from 32 to 64 both methods scaled identically (1.48), but at a level of low efficiency. This is an indication that the problem size, Nυ, is too small for such a large Np, leading to an unfavorable ratio between workload per node and communication. For further details see Table III.
IV. Discussion
A parallel AMG method was applied for the first time as a preconditioner for the iterative CG method to solve the elliptic PDE associated with the bidomain equations. Several 3-D test cases of varying degree of complexity were chosen to benchmark the preconditioner performance, covering a wide range of standard applications of a bidomain model. Benchmark results clearly demonstrate that the AMG preconditioner for the CG iterative solver is very well suited for this particular problem, giving significant performance benefits over the traditional ILU-CG method. The AMG method was superior to ILU-CG in almost all regards, independently of whether small scale sequential runs were carried out, or larger setups were simulated using up to 64 processors of a Linux cluster.
A. Parameter Tuning
BAMG is a sophisticated method with a multitude of parameters which can be adjusted to optimize performance. In this paper, we refrained from exploring the entire parameter space and investigated only the effect of θ and the number of sweeps on BAMG. The focus of this study was to examine whether AMG preconditioning has the potential to speed up the solution of the elliptic problem significantly compared to the standard method, and not to find the optimal setting for this particular setup.
It is worth noting that the optimal θ = 0 found in this paper is quite different from those values recommended by the developers of BoomerAMG [29]. For 2-D and 3-D cases, 0.25 and 0.5 are recommended, respectively,. This discrepancy may be attributed to the fact that the recommended values refer to the solution of steady-state problems whereas in this paper a time-dependent problem was solved. When solving the time-dependent bidomain equations, the costs for the setup phase are negligible compared to the overall execution time. For instance, the 50-ms RCV pacing sequence with Np = 16 executed in 8.8 h where only ≈20 secs were contributed by the setup phase.
B. Convergence Behavior and Error Tolerance δ
Clearly, the convergence history shown in Fig. 4 suggests that the chosen error tolerance δ has a major impact on the performance data reported in this paper. It can be expected that choosing a smaller δ will favor the AMG method, whereas, allowing a larger δ would favor ILU. In [4], it was shown that with the δ of 10−6 chosen in this study, the extracellular solution ϕe is basically indiscernible from the solution obtained by solving the coupled bidomain equations using a direct method. Solving the sequential benchmark and varying δ between 10−2 and 10−9 revealed that the performance gains with BAMG increase only moderately from 6.0 to 6.5 when δ was decreased from 10−6 down to 10−9. Increasing δ showed that even with a large δ 10−3 of, BAMG is still twice as fast as ILU. δ had to be further increased up to 10−2 to make ILU as fast as BAMG. With such a large tolerances, however, major deviations from the true solution will inevitably occur. This suggests that BAMG is always to be preferred in all situations of practical relevance.
C. Performance Comparison
The AMG preconditioner was clearly superior to the ILU method in almost every regard. The residual decreased much faster, showing convergence at a rate of one order of magnitude per iteration (see Fig. 4). Independent of parallelization, although a single iteration takes longer with an AMG method compared to ILU, Ns is always significantly smaller [see Figs. 5 and 7(A) and (B)] which compensates the extra computational expenses and, thus, leads to a much shorter execution time. Further, measured data clearly support the notion that AMG is more robust than ILU. This becomes evident in Fig. 4. These differences in convergence behavior are manifested in the dependency of Ns on the RHS (see Fig. 5). With AMG, Ns was almost independent on b, showing only very modest variations in Ns and Ts, whereas with ILU, the strong dependency resulted in large variation of Ns and Ts. These data clearly confirm that AMG-CG is both more robust (independent of b) and more efficient (much faster execution times, faster convergence).
For the sequential benchmark the direct SuperLU solver was the fastest method. However, this method is only a competitive option for a moderate number of unknowns, like for the RVS in this study. For the RCV problem with SuperLU, the system matrix could not be factorized, not even on a desktop computer equipped with 8 GB RAM, whereas, with ILU or AMG, this setup can be solved on a standard desktop computer with 2GB RAM. Setting up BAMG as a standalone solver showed robust convergence in this configuration since the multigrid error contraction was very good and, thus, the Krylov accelerator is not needed. The performance gains, however, were very moderate (<7%) which was within the uncertainty of the measurements. In a parallel context, BAMG has to be considered as the method of choice due to its fast and robust convergence and the maturity of the implementation which has proven to scale in other large scale application with Np much larger than used in this paper [13].
D. Parallel Scaling
1). Scaling With Np ≤ 16
The parallel scaling behavior of both methods AMG and ILU was almost identical for moderate Np ≤ 16 with scaling efficiencies between 76% and 93%. Since scaling was so similar, the performance ratio between the methods remained almost constant with varying Np, with a significant performance benefit of BAMG being roughly 6 times faster than ILU. For instance, with Np = 16 the simulation of 200-ms reentrant activity in the RCV setup executed in only 8.8 h with BAMG while the same simulation lasted for 60.6 h with ILU. The fact that BAMG running with Np = 4 finished execution two times faster than ILU running with Np = 16 (29.8 h versus 60.6 h) has to be considered as a significant performance improvement, which highlights the advantages of the presented method.
Speedups found in this study using AMG are comparable with those found in a previous study [9] where a GMG method was applied. Although, in general, GMG is considered as being more efficient than AMG, results obtained in this study suggest that AMG can be as efficient as GMG. With the GMG method applied to a 3-D test case in [9], a scaling efficiency of 79% was achieved when increasing Np from 8 to 16. In this study, AMG scaled comparably during RCV-Pacing (77%), but scaled significantly better during RCV-Reentry (94%). However, when comparing these studies, it has to be kept in mind that the computing environments were different. The environment used in this study (Opteron Linux Cluster with Inifiniband Interconnect) is clearly superior to the environment used in the GMG study (Itanium and Gigabit Ethernet), with low latency interconnects making a major difference. This could also explain why differences in performance gains between ILU and AMG were more striking in this study (6 versus 3).
2). Scaling With Np ≥ 16
Data measured at the Kepler cluster with Np ≤ 16 suggest that with ILU-CG, Nt will increase significantly with a higher Np, since the quality of the preconditioner will suffer more and more from the nonoverlapping block Jacobi preconditioner. This will gradually lead to a loss of entries in the ILU subblock preconditioner associated with an increase in Nt. On the other hand, with AMG methods, Nt was almost unaffected by Np; however, a slight decrease in parallel efficiency was observed. Most likely, this can be attributed to an increase in communication, but also the sequential solver step at the coarsest grid might have played a role (Fig. 6). The system to be solved at the coarsest grid was only 11 × 11, though. This was only partly confirmed by benchmarks carried out on the NGS cluster with Np ≥ 16. As expected, the overall number of iteration Nt for ILU increased with Np, with a particularly prominent increase seen between 32 and 64 processors. On the other hand, unlike with Np ≤ 16, Nt started to increase with BAMG as well where Np = 32 turned out to be a particularly adverse constellation (increase of 15.7% over Np = 16). A further increase to Np = 64 led to a decrease in Nt again. However, the overall picture for Np ≥ 16 was the same as for Np ≤ 16. With BAMG significant performance benefits over ILU could be achieved, the difference between the methods was smaller, though. Increasing Np from 16 to 64, the ILU/BAMG performance ratio decreased from 4.5 to 3.2, whereas this ratio was typically around 6 on the Kepler cluster, independent of Np.
It should be further noted that the given RCV problem size is too small to achieve good parallel scaling with large Np. This notion is supported by performance data acquired during the parabolic and the ODE solves (data not presented). The parabolic problem scaled very well when going from 16 to 32 CPUs; however, when going from 32 to 64, the parabolic solver time increased whereas the ODE solve continued to scale linearly. That is, the parabolic solve, which is only a matrix-vector product with the forward Euler method, stopped scaling with Np > 32, unlike the ODE solve, where no communication is required. This behavior suggests that the benchmark problem is not large enough to scale well with Np > 32 since the local computational workload assigned to each node is too small, and the communication overhead starts to dominate. With 64 CPUs, the local problem sizes were only 13477 and 8558 nodes for the elliptic and the parabolic problem, respectively.
E. Hardware-Related Issues
Performance differences measured in this paper can be primarily attributed to the applied algorithms. To a minor extent, however, implementation details and hardware-related optimization issues may have influenced the results as well. In a previous study [9], we compared a GMG method with ILU-CG. The performance gain of GMG-CG over ILU-CG during parallel runs was around 3 which is about the half we observed with AMG-CG. Theoretically, GMG-CG should perform better than AMG-CG; however, the hardware used in our previous work (Itanium system with standard Gigabit ethernet interconnect) was clearly inferior to the hardware used in this paper. Particularly the lack of a low-latency interconnect in our previous study may have led to this significant difference in parallel solver performance.
In this paper, two different platforms were used: The Kepler cluster (Opteron cluster with Infiniband interconnect) for runs with Np ≤ 16 and the Oxford NGS cluster (Xeon cluster with Myrinet interconnect) for runs with Np ≥ 16. Comparing the runs with Np = 16, which were carried out on both platforms, showed noticeable differences in ILU/BAMG performance with a ratio of 6 on the Kepler cluster and of 4.5 only at the NGS cluster. This difference can be attributed to several reasons: the NGS clusters are a shared resource, while at Kepler, exclusive memory and cache access was guaranteed during the course of this study; the 64-bit CARP executable performed better on the Opteron system than the 32-bit executable on the Xeon system; finally, the Infiniband interconnect led to better AMG parallel performance compared to the Myrinet interconnect used at the NGS clusters.
Clearly, performance could be further improved by using different compilers or compiler options to take further advantages of the hardware, although we refrained from doing so. On both platforms, the standard GNU C compiler gcc was used with the optimization flag set to −O3. More sophisticated optimization flags resulted only in marginal improvements if ever.
F. Related and Future Work
Multilevel methods are among the fastest methods for solving elliptic PDEs [31]. A brief overview of the application to bioelectrical field problems and the advantages of a multilevel approach to solve the elliptic portion of the bidomain equations has been presented in a previous work [9]. In contrast to [9], where a GMG preconditioner was applied, more generally applicable AMG methods were studied which do not suffer from any restrictions regarding the structure of the underlying computational grid.
Besides the AMG implementation used in this study, there are other implementations of various AMG flavours like Pebbles [32], [33] and Stüben’s parallel AMG code [34] available which may perform even better than BoomerAMG. Preliminary results suggest that during sequential runs, Pebbles AMG solves the RVS problem almost 2 times faster than BAMG (about 15 times faster than ILU-CG). The performance of Pebbles came very close to the direct method (62%), but did not suffer from the same memory constraints for a larger number of unknowns. Further, parallel test runs with Pebbles suggest that similar performance benefits can be expected. However, to seamlessly integrate this method with our CARP simulator, the development of a PETSc interface for Pebbles is essential. The development of such an interface is a nontrivial task, requiring significant engineering efforts to succeed. However, the expected performance benefits clearly justify this effort and, thus, we will work towards the implementation of such an interface in a future project.
The presented algorithm will be tested running on supercomputing environments provided by the Integrative Biology Project. It will be investigated how well AMG methods are suited for large scale parallel applications. Clearly, the parallel test cases presented in this paper were too small to get good parallel performance with a high Np. In the future, larger test cases associated with linear systems of between 10 and 100 million unknowns, such as a bidomain simulation of an entire human ventricle including a torso, will be used to measure the relative performance of the AMG methods presented in this paper.
G. Conclusions
In this work, we have presented a very efficient method for the solution of the linear system associated with the elliptic portion of the bidomain equations. An AMG preconditioning method was compared against the traditional ILU preconditioner for bidomain simulations of different complexities for both sequential and parallel simulation runs. Results demonstrate that AMG-CG methods are extremely efficient in solving the system under both conditions. AMG methods do not suffer from any restrictions regarding the structure of the underlying computational grid allowing the use of unstructured mesh generation methods for a more concise and realistic representation of the cardiac geometry. The application of AMG preconditioners is a major step forward making large scale bidomain simulations up to some tens of millions of unknowns feasible. Preliminary results carried out at the HPCx supercomputing facilities indicate that bidomain simulations of an entire human heart including a torso have become feasible.
Acknowledgment
The authors wish to thank other members of the Integrative Biology consortium for their input into, and comments on, the work described in this paper, in particular the role of the scientific collaborators in determining the requirements for this project. They would also like to thank Dr. U. Winkler for her support in setting up and adjusting the parallel environment at the Kepler Cluster for the needs of this study.
This work was supported in part by the Integrative Biology project (funded by the EPSRC under Grant GR/S72023/01 and by IBM. The work of G. Plank was supported by the Austrian Science Fund (FWF) under Grant R21-N04. The work of M. Liebmann and G. Haase was supported in part by the Federal Ministry for Education, Science and Culture, Austria, through the Austrian Grid Project. The work of R. Weber dos Santos was supported in part by the Universidade Federal de Juiz de Fora (UFJF-Enxoval) and in part by the Brazilian Ministry of Science and Technology, CNPq (process 473852/2004-7). The work of E. Vigmond was supported in part by a grant from the Natural Sciences and Engineering Research Council of Canada.
Biographies
 Gernot Plank received the M.Sc. and Ph.D. degrees in electrical engineering from the Institute of Biomedical Engineering, the Technical University of Graz, Graz, Austria, in 1996 and 2000, respectively.
Gernot Plank received the M.Sc. and Ph.D. degrees in electrical engineering from the Institute of Biomedical Engineering, the Technical University of Graz, Graz, Austria, in 1996 and 2000, respectively.
He was a Postdoctoral Fellow with the Technical University of Valencia, Valencia, Spain, from 2000 through 2002 and the University of Calgary, Calgary, AB, Canada in 2003. Currently, he is a Postdoctoral Fellow with the Institute of Biophysics, Medical University of Graz. His research interests include computational modeling of cardiac bioelectric activity, microscopic mapping of the cardiac electric field, and defibrillation.
 Manfred Liebmann received the diploma degree in theoretical physics in 2005, from the University of Graz, Graz, Austria. He is working towards the Ph.D. degree at the Max Planck Institute for Mathematics in the Sciences, Leipzig, Germany.
Manfred Liebmann received the diploma degree in theoretical physics in 2005, from the University of Graz, Graz, Austria. He is working towards the Ph.D. degree at the Max Planck Institute for Mathematics in the Sciences, Leipzig, Germany.
He was an Assistant Researcher at the Institute of Computational Mathematics at the University of Linz, Linz, Austria, from 2005–2006. His research interests include large scale numerical simulations, parallel numerical algorithms, object-oriented software development, computer graphics, quantum computation, and the foundations of quantum physics.
 Rodrigo Weber dos Santos received the B.Sc. degree in electrical engineering from the Federal University of Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil, in 1995. He received the M.Sc. and D.Sc. degree from UFRJ, COPPE Systems Engineering and Computer Science Department, in 1998 and from UFRJ, Mathematics Department, in 2002, respectively.
Rodrigo Weber dos Santos received the B.Sc. degree in electrical engineering from the Federal University of Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil, in 1995. He received the M.Sc. and D.Sc. degree from UFRJ, COPPE Systems Engineering and Computer Science Department, in 1998 and from UFRJ, Mathematics Department, in 2002, respectively.
He was a Research Fellow with the Department of Biosignals, Physikalisch-Technische Bundesanstalt, Berlin, Germany, from 2002 through 2004; and a Research Fellow with the European Organization for Nuclear Research (CERN), Geneva, Switzerland, from 1995 through 1996. Currently, he is an Associate Professor with the Department of Computer Science, Universidade Federal de Juiz de Fora (UFJF), Brazil, where he is also the Vice-Coordinator of the Graduate Program in Computational Modeling. His research interests include parallel computing, numerical methods for partial differential equations, and mathematical and computational modeling of the heart.
 Edward J. Vigmond (S’96–M’97) received the B.A.Sc. in electrical and computer engineering from the University of Toronto, Toronto, ON, Canada, in 1988. He received the M.A.Sc. and Ph.D. degrees from the Institute of Biomedical Engineering, University of Toronto, in 1991 and 1996, respectively.
Edward J. Vigmond (S’96–M’97) received the B.A.Sc. in electrical and computer engineering from the University of Toronto, Toronto, ON, Canada, in 1988. He received the M.A.Sc. and Ph.D. degrees from the Institute of Biomedical Engineering, University of Toronto, in 1991 and 1996, respectively.
He was a Postdoctoral Fellow with the University of Montreal, Montreal, QC, Canada, from 1997 through 1999 and Tulane University, from 1999 through 2001. He is currently an Associate Professor with the Department of Electrical and Computer Engineering, University of Calgary, Calgary, AB, Canada, where he is modeling biological electrical activity. His research interests include numerical computation of electrical fields, biomedical signal processing, and modeling of nonlinear biosystems.
 Gundolf Haase received diploma and Ph.D. degrees in computational mathematics from the Institute of Mathematics, Technical University of Chemnitz, Chemnitz, Germany, in 1991 and 1993, respectively.
Gundolf Haase received diploma and Ph.D. degrees in computational mathematics from the Institute of Mathematics, Technical University of Chemnitz, Chemnitz, Germany, in 1991 and 1993, respectively.
He completed the habilitation on parallel numerical algorithms in 2001 at the Institute of Computational Mathematics at the University of Linz, Linz, Austria, where he worked for 11 years as Assistance/Associate Professor until he became a full Professor for Algorithmical Computational Mathematics at the Institute for Mathematics and Computational Sciences, University of Graz, Graz, Austria, in 2004. His research interests include fast algebraic multigrid solvers for large systems of linear equations, parallel algorithms, cache-aware algorithms, and the application of mathematical techniques in applications.
Contributor Information
Gernot Plank, Institute of Biophysics, Center for Physiological Medicine, Medical University Graz, Harrachgasse 21, A-8010 Graz, Austria.
Manfred Liebmann, Institute for Mathematics and Scientific Computing, Karl-Franzens Universität Graz, A-8010 Graz, Austria.
Rodrigo Weber dos Santos, Department of Computer Science and the Graduate Program in Computational Modeling, Universidade Federal de Juiz de Fora, 36036-330 Juiz de Fora, Brazil.
Edward J. Vigmond, Department of Electrical and Computer Engineering, University of Calgary, Calgary, AB T2N 4N1, Canada.
Gundolf Haase, Institute for Mathematics and Scientific Computing, Karl-Franzens Universität Graz, A-8010 Graz, Austria.
References
- [1].Sepulveda NG, Roth BJ, Wikswo JP., Jr Current injection into a two-dimensional anistropic bidomain. Biophysical J. 1989;55:987–999. doi: 10.1016/S0006-3495(89)82897-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Weber dos Santos R, Dickstein F, Marchesin D. Transversal versus longitudinal current propagation on a cardiac tissue and its relation to MCG. Biomedizinische Technik. 2003;47(1):249–252. doi: 10.1515/bmte.2002.47.s1a.249. [DOI] [PubMed] [Google Scholar]
- [3].Weber dos Santos R, Dickstein F. On the influence of a volume conductor on the orientation of currents in a thin cardiac tissue. In: Magnin I, Montagnat J, Clarysse P, Nenonen J, Katila T, editors. Lecture Notes in Computer Science. Berlin, Germany: Springer; 2003. pp. 111–121. [Google Scholar]
- [4].Vigmond E, Aguel F, Trayanova N. Computational techniques for solving the bidomain equations in three dimensions. IEEE Trans Biomed Eng. 2002 Nov;49(11):1260–1269. doi: 10.1109/TBME.2002.804597. [DOI] [PubMed] [Google Scholar]
- [5].Sundnes J, Lines G, Tveito A. Efficient solution of ordinary differential equations modeling electrical activity in cardiac cells. Math Biosci. 2001;172(2):55–72. doi: 10.1016/s0025-5564(01)00069-4. [DOI] [PubMed] [Google Scholar]
- [6].Keener J, Bogar K. A numerical method for the solution of the bidomain equations in cardiac tissue. Chaos. 1998;8(1):234–241. doi: 10.1063/1.166300. [DOI] [PubMed] [Google Scholar]
- [7].Weber dos Santos R. Modelling cardiac electrophysiology. Ph.D. dissertation, Department of Mathematics, Federal University of Rio de Janeiro; Rio de Janeiro, Brazil: 2002. [Google Scholar]
- [8].Hooke N, Henriquez C, Lanzkron P, Rose D. Linear algebraic transformations of the bidomain equations: implications for numerical methods. Math Biosci. 1994;120(2):127–145. doi: 10.1016/0025-5564(94)90049-3. [DOI] [PubMed] [Google Scholar]
- [9].Weber dos Santos R, Plank G, Bauer S, Vigmond E. Parallel multigrid preconditioner for the cardiac bidomain model. IEEE Trans Biomed Eng. 2004 Nov;51(11):1960–1968. doi: 10.1109/TBME.2004.834275. [DOI] [PubMed] [Google Scholar]
- [10].Roth B. Mechanism for polarisation of cardiac tissue at a sealed boundary. Med Biol Eng Comput. 1999;37(4):523–525. doi: 10.1007/BF02513340. [DOI] [PubMed] [Google Scholar]
- [11].Prassl AJ, Plank G. Development of a 3-D computer model for defibrillation studies based on histological rabbit data. presented at the EMBEC 2005—3rd Eur. Medical and Biological Engineering Conf; Prague, Czech Republic. Nov. 20, 2005. [Google Scholar]
- [12].Stüben K. A review of algebraic multigrid. J Comput Appl Math. 2001;128(1–2):281–309. [Google Scholar]
- [13].Henson V, Yang U. BoomerAMG: a parallel algebraic multigrid solver and preconditioner. Appl Numerical Math. 2002;41:155–177. [Google Scholar]
- [14].Li S, Demmel J, Gilber J. SuperLU [Google Scholar]
- [15].Keener J, Sneyd J. Mathematical Physiology. New York: Springer; 1998. [Google Scholar]
- [16].Strang G. On the construction and comparision of difference scheme. SIAM J Numerical Anal. 1968;5:506–517. [Google Scholar]
- [17].Vetter F, McCulloch A. Three-dimensional analysis of regional cardiac function: a model of rabbit ventricular anatomy. Prog Biophys Mol Biol. 1998;69(2–3):157–183. doi: 10.1016/s0079-6107(98)00006-6. [DOI] [PubMed] [Google Scholar]
- [18].Clerc L. Directional differences of impulse spread in trabecular muscle from mammalian heart. J Physiol. 1976;255:335–346. doi: 10.1113/jphysiol.1976.sp011283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Skouibine K, Trayanova NA, Moore PK. Anode/cathode make and break phenomena in a model of defibrillation. IEEE Trans Biomed Eng. 1999 Jul;46(7):769–777. doi: 10.1109/10.771186. [DOI] [PubMed] [Google Scholar]
- [20].Puglisi J, Bers D. LabHEART: an interactive computer model of rabbit ventricular myocyte ion channels and Ca transport. Am J Physiol Cell Physiol. 2001;281(6):C2049–C2060. doi: 10.1152/ajpcell.2001.281.6.C2049. [DOI] [PubMed] [Google Scholar]
- [21].DeBruin K, Krassowska W. Electroporation and shock-induced transmembrane potential in a cardiac fiber during defibrillation strength shocks. Ann Biomed Eng. 1998;26(4):584–596. doi: 10.1114/1.101. [DOI] [PubMed] [Google Scholar]
- [22].Cheng D, Tung L, Sobie E. Nonuniform responses of transmembrane potential during electric field stimulation of single cardiac cells. Am J Physiol. 1999;277(1, pt 2):H351–H362. doi: 10.1152/ajpheart.1999.277.1.H351. [DOI] [PubMed] [Google Scholar]
- [23].Biology Project. [Online]. Available: http://www.integrativebiology.ac.ukIntegrative.
- [24].Saad Y. Iterative Methods for Sparse Linear Systems. Boston, MA: PWS; 1996. [Google Scholar]
- [25].Ruge JW, Stüben K. Algebraic multigrid (AMG) In: McCormick S, editor. Multigrid Methods, ser. Frontiers in Applied Mathematics. Vol. 5. Philadelphia: SIAM; 1986. pp. 73–130. [Google Scholar]
- [26].Yung UM. On the use of relaxation parameters in hybrid smoothers. Numerical Linear Algebra With Appl. 2004;11(2–3):155–172. [Google Scholar]
- [27].Balay S, Buschelman K, Gropp WD, Kaushik D, Knepley M, McInnes LC, Smith BF, Zhang H. PETSc Users Manual Argonne National Laboratory. Tech Rep. 2002 ANL-95/11-Revision 2.1.5. [Google Scholar]
- [28].Vigmond E, Hughes M, Plank G, Leon L. Computational tools for modeling electrical activity in cardiac tissue. J Electrocardiol. 2003 doi: 10.1016/j.jelectrocard.2003.09.017. in press. [DOI] [PubMed] [Google Scholar]
- [29].Hypre. Tech Rep. Software Version: 1.6.0. Lawrence Livermore National Laboratory; 2001. Jul 27, High Performance Preconditioners User’s Manual Center for Applied Scientific Computing. [Online]. Available: http://www.llnl.gov/casc/hypre/hypre-1.6.0/HYPRE_usr_manual.ps. [Google Scholar]
- [30].Message Passing Interface Forum. MPI, a message-passing interface standard. Int J Supercomput. 1994;8:159–416. [Google Scholar]
- [31].Briggs W, Henson V, McCormick S. A Multigrid Tutorial. SIAM; Philadelphia, PA: 2000. Tech. Rep. [Google Scholar]
- [32].Haase G, Reitzinger S. Cache issues of algebraic multigrid methods for linear systems with multiple right-hand sides. SIAM J Sci Comput. 2005;27(1):1–18. [Google Scholar]
- [33].Haase G, Kuhn M, Reitzinger S. Parallel AMG on distributed memory computers. SIAM J Sci Comput. 2002;24(2):410–427. [Google Scholar]
- [34].Krechel A, Stüben K. Parallel algebraic multigrid based on subdomain blocking. Parallel Computing. 2001;27:1009–1031. [Google Scholar]