A big data approach to development of mixed-effects models for seizure count data

Abstract

OBJECTIVE

Our objective was to develop a generalized linear mixed model for predicting seizure count that is useful in the design and analysis of clinical trials. This model also may benefit the design and interpretation of seizure recording paradigms. Most existing seizure count models do not include children and there is currently no consensus regarding the most suitable model that can be applied to children and adults. Therefore, an additional objective was to develop a model that accounts for both adult and pediatric epilepsy.

METHODS

Using data from SeizureTracker.com, a patient-reported seizure diary tool with over 1.2 million recorded seizures across 8 years, we evaluated the appropriateness of Poisson, negative binomial, zero inflated negative binomial, and modified negative binomial models for seizure count data based on minimization of the Bayesian Information Criteria. Generalized linear mixed-effects models were used to account for demographic and etiological covariates and for autocorrelation structure. Hold-out cross-validation was used to evaluate predictive accuracy in simulating seizure frequencies.

RESULTS

For both adults and children, we found that a negative binomial model with autocorrelation over one day was optimal. Using hold-out cross validation, the proposed model was found to provide accurate simulation of seizure counts for patients with up to 4 seizures per day.

SIGNIFICANCE

The optimal model can be used to generate more realistic simulated patient data with very few input parameters. The availability of a parsimonious, realistic virtual patient model can be of great utility in simulations of phase II/III clinical trials, epilepsy monitoring units, outpatient biosensors, and mobile Health (mHealth) applications.

Introduction

Statistical seizure count models can provide insight into epilepsy burden and treatment, and are useful for phase II/III clinical trial design and analysis^1,2. Such models can assist studies in epilepsy monitoring units, by predicting time to epileptic seizures^3,4. Evaluation of newer mobile health (mHealth) tools and outpatient biosensors^5–8 will require accurate models of seizure count. A large proportion of clinical trial placebo effect may be due to natural seizure count fluctuations⁹. Accounting for natural fluctuations when planning future trials would improve modeling of both intervention and placebo arms¹⁰. Many existing seizure count models (Table 1), developed using small datasets, show limited ability to assess covariate effects^11,12. Other models, unsuited to clinical trial simulators, do not allow generation of simulated data^13,14.

Table 1.

Literature search for models currently used to model seizure frequency data. The column “Model” does not include pharmacokinetic models developed in the paper. One number of patients is listed per model developed. PS: Poisson. NB: Negative binomial. PCB: Placebo

First Author, Year (Reference)	Model	Separates children and adults?	Number of patients	Minimum Age in years (mean if reported)
Ahn, 2012 (1)	NB with nonlinear covariate based on number of seizures on previous day	No	1053	12 (mean 38.2)
Albert, 1991 (13)	PS with two-state Markov adjustment	No	13	21
Albert, 2000 (20)	PS with dropout and treatment/pcb term	No	40	14
Alosh, 2009 (21)	PS with Bernoulli thinning	No	59	18
Balish, 1991 (14)	Quasi-likelihood regression	No	13	21
Delattre, 2012 (22)	Hidden mixed Markov	No	788	None reported (mean 33)
Deng, 2016 (23)	Dynamic Inter-Occasion Variability	No	551	8 (mean 33)
Hougaard, 1997 (11)	Generalized Poisson mixture	No	59	18
Molenberghs, 2007 (17)	NB with treatment/pcb term	No	89	18
Nielsen, 2015 (2)	NB with nonlinear covariate based on number of seizures on previous day	Yes	265 children 356 adults	3 18
Thall, 1990 (24)	Quasi-likelihood regression	No	59	18
Troconiz, 2009 (18)	NB with two-state Markov adjustment	No	551	8 (mean 33)

Most existing models have been developed using adult data (Table 1). Most others exclude younger children, developing only one model for childhood and adult epilepsy. However, differences between childhood and adult epilepsies should be considered in model construction^15,16.

We evaluated several new mixed-effects models for seizure count data in large datasets of children and adults, respectively. In predicting seizure count, we evaluated the effect of previous seizure history, as well as demographic and etiological covariates. We assessed the utility of the proposed model for simulating clinical trial seizure count data through hold-out cross-validation.

Methods

Preprocessing

Data was taken from SeizureTracker.com, a free online seizure diary tool⁹. In addition to seizure occurrences, demographic information and self-reported etiologies were available (Figure 1a). Additional demographic data have been published⁹. Data were de-identified and unlinked, as required by the Office of Human Research Protection, OHSR #12301.

Figure 1.

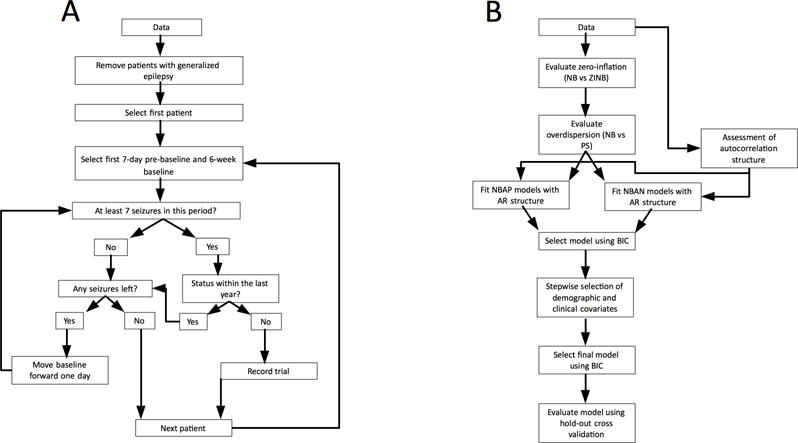
(a) Data selection procedure. Data was recorded from patients meeting common clinical trial eligibility criteria. One 18-week “trial” was recorded from each eligible patient, along with 1 week of “pre-baseline” data. (b) Model selection and analysis procedure. Models were fitted to the data and model fit compared based on the Bayesian Information Criterion (BIC). Models were evaluated sequentially, with more complex models built around the optimal model determined by the previous step. NB = negative binomial. ZINB = zero inflated negative binomial. PS = Poisson. NBAP = negative binomial with autocorrelation on presence/absence of prior day seizures. NBAN = negative binomial with autocorrelation on number of prior day seizures. AR = autoregressive.

For each eligible patient, a seven-day “pre-baseline” period, a six-week “baseline” period, and a 12-week “intervention” period were selected for analysis, representing the temporal relationship typically employed in clinical trials; no actual intervention was performed, though changes in medication might have occurred. Similar time periods are used in many clinical trials for anti-epileptic drugs^17–20. Inclusion criteria were similar to many clinical trials: patients were required to have at least seven seizures over the 49-day period including seven-day “pre-baseline” and six-week “baseline”²¹. Exclusion criteria included: patient diaries suggesting generalized epilepsy (see⁹ for details), status epilepticus within the 49-day eligibility period, no reported seizures after the 12 week intervention period, and no reporting of age or gender. Status epilepticus was defined as any seizure lasting more than five minutes, overlapping seizures with total duration over five minutes, or a set of non-overlapping seizures separated by less than five minutes, with a combined duration of over five minutes²². Erroneous data entry, such as seizures reported as occurring past the date of data export were ignored. The recording of one seizure after the 12-week trial period was required to eliminate patients who ceased using SeizureTracker.com during that period.

For each patient, the first 49-day period in which eligibility criteria were met and the following 12-weeks were used for analysis. Only one trial-sized excerpt was selected from each seizure diary. Allowing more excerpts would have overrepresented patients with longer seizure diaries.

Models

Models described in this paper belong to a class known as “mixed-effects models,” where the probability of Y seizures occurring during a given day is a function of mean number of seizures, $\mu$. The natural log of $\mu$ ( $i.e.\text{ln}\mu$) is the sum of (1) a constant $\beta$_0, describing the population as a whole, (2) a constant b, differing across individuals, and (3) other variables $\beta$₁…_n, which may vary with time.

The models are built from the Poisson (PS) distribution, commonly used to model count data²³ assuming the mean number of seizures equals the variance. However, seizure count data is often overdispersed, such that the variance in seizure counts exceeds the mean¹¹. Our PS model describes the probability of Y seizures occurring on a given day as a function only of $\mu$, the mean number of events. Formally,

$$P\left(Y_{i,j}= n ∊ (\mathbb{N}{{\displaystyle \cup }}^{}0)|\mu \right)= \frac{e^{-\mu }\ast {\mu }^n}{n!}$$

where $\text{ln}(\mu )={\beta }_0+b$. ${\beta }_0$ is the intercept term and b is the subject specific, normally-distributed random effects term, with standard deviation $\sigma$.

The negative binomial (NB) distribution is an extension of the PS distribution frequently used for overdispersed count data¹¹. As in our PS model, $\mu$ is composed of population- and subject-specific constants. The NB differs from the PS model in that the probability of Y seizures occurring in a day is a function of $\mu$ and an additional parameter, $\theta$, which determines overdispersion. Formally,

$$P\left(Y_{i,j}=n ∊ (\mathbb{N}{{\displaystyle \cup }}^{}0)|\mu ,\theta \right)=\frac{\Gamma \left(n+\theta \right)}{\Gamma \left(\theta \right)n!}\ast \frac{{\mu }^n{\theta }^{\theta }}{{\left(\mu +\theta \right)}^{\theta +n}}$$

NB models for seizure count data are limited, assuming independently distributed seizure counts. Several groups have reported clustered seizure counts, finding models with memory (where past results affect probability of future results) perform better than those without^13,14,24. Improvements over the NB model include an NB generalized linear mixed model (GLMM), with effect of treatment or placebo as covariates in the linear predictor.¹² A zero-inflated NB model (ZINB) accounted for Markovian patterns with two sets of mean and overdispersion parameters, one corresponding to days following days without reported seizures, and one corresponding to days following days with reported seizures.²⁴ Similar models have used modified autocorrelation terms¹. We extend these models to account for patient-level demographic and etiological covariates, effects unexplored in the literature^{1,2,11,12,24–30}.

Our ZINB model is similar to our NB model, but for a certain percentage of days, denoted by p, seizure number is set to zero regardless of probabilities given by the NB formula. Formally,

$$P\left(Y_{i,j}= 0|p,\mu ,\theta \right)=p+\left(1-p\right)\ast NB(Y=0|\mu ,\theta )$$

$$P\left(Y_{i,j}=\left(n ∊ \mathbb{N}\right)|p,\mu ,\theta \right)=\left(1-p\right)\ast NB(Y=n|\mu , \theta )$$

$NB(Y=x|\mu ,\theta )$ is the probability of x seizures occurring, according to the NB model.

The negative binomial with autocorrelation number (NBAN) model is identical to the NB model, except that mean seizure frequency is a function of the number of seizures on the previous day, as well as of the population constant and the subject-specific constant. Formally, $\text{ln}\left(\mu \right)= {\beta }_0+{\beta }_N{Y}_{j-1}+b$. $Y_{j-1}$ is the number of seizures on the previous day. ${\beta }_N$ is the corresponding coefficient.

The negative binomial with autocorrelation presence (NBAP) model is similar to the NBAN model, but the binary presence/absence of seizures on the previous day is used instead of seizure count. Formally, $\text{ln}\left(\mu \right)= {\beta }_0+{\beta }_P{P}_{j-1}+b$. $P_{j-1}$ is the binary presence/absence of seizures on the previous day. ${\beta }_P$ is the corresponding coefficient.

The negative binomial with autocorrelation and covariates (NBAC) models add several $\beta$ terms to the formula for $\mu$ in the negative binomial autocorrelation model. Each additional variable corresponds to the binary presence/absence of a certain etiological factor, or to patient age.

Model Fitting/selection

Data for adults and children were analyzed separately. Models were fitted to seizure counts from six-week baseline period and 12-week trial periods only; the seven-day pre-baseline period was used so values for autoregressive terms would be available for the first seven baseline days, as described below. Because parsimony was valued, models were compared using Bayesian Information Criteria (BIC), rewarding better fit and penalizing addition of each covariate^31,32.

Model fitting, selection, and evaluation were conducted as shown (Figure 1b). The appropriateness of a zero-inflated model was assessed by comparing model fit of a zero-inflated negative binomial (ZINB) to a negative binomial (NB) model based on the Bayesian information criterion (BIC); the need to account for overdispersion was assessed by comparing the model with better fit (ZINB vs. NB) to either the zero-inflated Poisson (ZIP) or the Poisson (PS) model, respectively.

In order to model effects of prior seizure history on current seizure count, seizure count stationarity was evaluated through the empirical autocorrelation function. A negative binomial autoregressive model based on the number of seizures on previous days (NBAN) was first fit. The maximum autoregressive order considered was seven days, determined by evaluation of inter-seizure interval (ISI) distribution (Supplemental Figure S-4). Lag order was selected based on the BIC and empirical partial autocorrelation functions (PACF) for individual patients. We used residual analysis and the empirical autocorrelation function of fitted residuals to check that autoregressive processes adequately modeled seizure count time-series. In order to account for the relative reliability of self-reported seizure count⁸, a second model with autoregressive structure based on the presence/absence of seizures on previous days (NBAP) was fitted, with lag order selected based on BIC.

The results of this analysis were used to identify which demographic and etiological covariates further improved model fit (Table 2). Forward selection with backward elimination (FSBE) of these covariates was performed. Variable selection was carried out using “forward.lmer”³³ with lag terms identified above as the initial model in the stepwise search and using an improvement in BIC of at least 1% as a threshold for addition or deletion of covariates. Since the FSBE algorithm has deficiencies, including the possibility of reaching local rather than global extrema, a backwards elimination algorithm starting with all covariates, followed by sequential removal of terms improving BIC by less than 1%, was employed to verify results.

Table 2.

Demographic and etiological covariates evaluated in NBC and NBAC models. All covariates reported by at least 9 children and 9 adults (approximately 1% of each sample) were evaluated. Number of patients reporting each covariate is shown.

Covariate	Adults reporting covariate	Children reporting covariate
Demographic covariates
Age	682 (100%)	844 (100%)
Gender	682 (100%)	844 (100%)
Etiology
Tuberous Sclerosis (TS)	9 (1.3%)	79 (9.3%)
Brain Trauma	90 (13%)	45 (5.3%)
Hematoma	26 (3.8%)	15 (1.8%)
Infectious Disease	58 (8.5%)	33 (3.9%)
Stroke	15 (2.2%)	26 (3.1%)
Genetic Abnormalities	15 (2.2%)	25 (3.0%)
Lack of oxygen at birth	20 (2.9%)	28 (3.3%)
Fever, Metabolic Disorder, or Electrolyte disturbance	13 (1.9%)	15 (1.8%)
Brain malformation or injury during fetal development	48 (7.0%)	73 (8.6%)
Brain tumor or surgery	119 (17%)	58 (6.9%)
Maternal drug use or unspecified congenital disorder	49 (7.2%)	95 (11%)

To assess the potential utility of the identified model to serve as a clinical trial simulator of seizure count data, hold-out cross validation was used to evaluate predictive performance. The data were separated into two subsets: a training set, consisting of the first interval in which each patient met eligibility criteria, and a testing set, consisting of the second interval in which each patient met eligibility criteria. The model fitting and selection procedure was performed on patients in the training set, and used to predict seizure counts for patients in the testing set. To assess predictive performance, the mean squared prediction error (MSE) and quantile-quantile (QQ) plots were used to compare the distribution of the predicted to observed seizure counts in the testing set. To provide a baseline for comparison, we compared our model to a negative binomial model with no autocorrelation using the mean squared prediction error.

MATLAB v. 2015b was used for preprocessing, and R³⁴ v3.2.2 was used for model fitting. Computation was performed on the NIH HPC Biowulf computer cluster.

Results

Adult data (age ≥ 18 years) were separated into training (30,022 seizures from 682 patients) and testing (15,602 seizures from 354 patients) sets. Pediatric data (age < 18 years) were separated into a training set of 52,596 seizures (844 patients) and a testing set of 20,297 seizures (334 patients). Parameter estimates and BIC values for all models are listed (Table 3).

Table 3.

Models and parameter estimates for adult and pediatric patients. ZINB: zero-inflated negative binomial. NB: negative binomial. PS: Poisson. NBAN: negative binomial with autocorrelation based on number of seizures. NBAP: negative binomial with autocorrelation based on presence/absence of seizures. MSE: mea squared error $\mu$: Mean seizure frequency. $\text{ln}(\mu )$: the natural log of $\mu$. ${\beta }_0$: Intercept. ${\beta }_N$: Coefficient for autocorrelation based on number. ${\beta }_P$: Coefficient for autocorrelation based on presence/absence. $\theta$: Overdispersion parameter. b: subject-specific random effect, defined as a normal distribution with standard deviation $\sigma$. p: For the ZINB model, the zero-inflation parameter indicating proportion of zeros. BIC: Bayesian Information Criterion. $Y_{j-1}$: indicates number of seizures on the previous day. $P_{j-1}$: indicates the binary presence or absence of seizures on the previous day.

Age ≥18	Model	$\text{ln}(\mu )$	$p$	$\theta$	${\beta }_0$ (standard error)	${\beta }_N$ (standard error)	${\beta }_P$ (standard error)	$\sigma$	$\text{BIC}$	MSE		Average residual
										Training Set	Testing Set	Training set	Testing Set
	ZINB	${\beta }_o+b$	~10−6	1.021	−1.775	—	—	0.953	99888	1.933159	2.800001	0.004855725	0.06144511
	NB	${\beta }_o+b$	—	0.979	−1.766 (.03744)	—	—	0.938	99982	0.4052321	2.791609	0.002265776	0.06062727
	PS	${\beta }_o+b$	—	—	−1.767 (.03744)	—	—	0.943	106860	0.4051007	2.795019	0.0001609842	0.0587986
	NBAN	${\beta }_o+{\beta }_{N}Y+b$	—	0.93	−1.812 (.035102)	0.144 (.007801)	—	0.872	99427	0.9674286	2.798199	0.009915936	0.06344967
	NBAP*	${\beta }_o+{\beta }_{P}P+b$	—	1.128	−1.923 (.03288)	—	0.731 (.01850)	0.805	98506	0.3931279	2.801164	0.001657169	0.06086472
Age <18	ZINB	${\beta }_o+b$	~10−6	0.766	−1.627	—	—	1.169	143397	1.348431	2.470375	0.006100566	−0.0462341
	NB	${\beta }_o+b$	—	0.751	−1.621 (.04088)	—	—	1.154	143497	1.348323	2.470016	0.005209735	−0.0470346
	PS	${\beta }_o+b$	—	—	−1.621 (.04088)	—	—	1.159	158421	1.347714	2.506156	0.0001290548	−0.0533295
	NBAN	${\beta }_o+{\beta }_{N}Y+b$	—	0.903	−1.735 (.034883)	0.223 (.004592)	—	0.972	140254	2.190371	6.108528	−0.03648377	−0.1112444
	NBAP*	${\beta }_o+{\beta }_{P}P+b$	—	0.96	−1.88 (.03386)	—	1.101 (.01576)	0.935	139608	1.27116	2.568405	0.005129398	−0.0460737

^*Indicates optimal model.

Although histograms of seizures per patient and the proportion of days without reported seizures suggested zero-inflation (Supplemental Figures S1 and S2), the zero-inflation parameter was estimated as ~10⁻⁶ among both adults and children, suggesting that zero-inflation was not required. As there was only marginal improvement in BIC of the ZINB over the NB model (Table 3), the benefit of accounting for zero-inflation was considered minimal. The NB model was significantly superior to the PS model (p < .001, ANOVA) in both adults and children. In both cases, the overdispersion parameter $\theta$ was greater than 0, implying data were overdispersed (Table 3, Figure S3).

Empirical autocorrelation functions suggested stationarity in seizure counts for both adults and children. Analysis of each patient’s PACF found that for 62% of adults and 52% of children, an AR(0) or AR(1) autoregressive structure would be appropriate. Addition of a second autoregressive term improved BIC by less than 1% for NBAN and NBAP models; a better model fit was obtained for the NBAP than NBAN model (Table 3). Residuals plots and autocorrelation plots of fitted residuals were assessed to confirm appropriateness of model fit.

For adults and children, both FSBE and backwards elimination algorithms showed no demographic or etiological covariate improved BIC by more than 1% over the NBAP model.

While the model tends to under-predict seizure counts when patients have greater than 4 seizures per day, nearly all of the data (>99% from adults, and >97% from children) lies within one unit of the y=x line (Figure 2a and 2b). Moreover, a minority of patients (<20% adults, <25% children) have any days with more than four seizures. Among these, the median number of days per diary with seizure counts greater than four is negligible (adults: 1, children: 2.5, from a total of 133 days/diary) (Table 4). For seizure frequencies of ≤4 seizures per day, QQ plots suggest the proposed model provides accurate seizure count prediction (Figure 2a and 2b).

Figure 2.

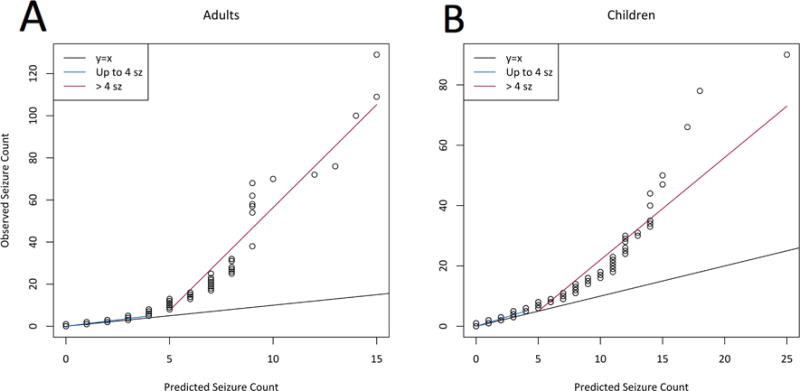
(a) Quantile-quantile (QQ) plot for adult data, comparing distribution of simulated seizure count data from our model to observed seizure count data in the testing set. Two distinct regimes are highlighted: For ≤4 seizures per day, the data closely follows the one-to-one line, indicating that our model is valid for this range; above this point, data is nonlinear. (b) QQ plot for pediatric data. As in the adult data, there are two distinct regimes; the model is adequate for the lower regime.

Table 4.

Percentage of patients who have at least one day with more than four seizures, and the median number of days with more than 4 seizures in those patients.

	Adults	Children
Patients with >4 sz on at least 1 day	18%	24%
Of these, median number of days with >4 sz	1	2.5

For the NBAP model, MSE was calculated by simulating testing set data, with new patient-specific random-effects terms, and was found to be superior to the NB model (Supplemental Table S1). When MSE was calculated using existing random-effects values, the NB model performed slightly better than the NBAP (Table 3).

Discussion

We propose a novel model for daily seizure counts that successfully models complete trial data from 82% of adults and 76% of children. For the remaining patients, the model is generally successful, with seizure rates <= 4 seizures/day (the level for which the model is accurate) in a median of 132.0 of 133.0 days (99.3%) in adults and 130.5 of 133.0 days (98.1%) in children. The models account for system memory, and provide new associations between demographic and etiological covariates with seizure count, and differences between children and adults. Excluding the extreme upper range of seizure count data, the model was validated in a separate data set. Under certain conditions, the NBAP model did not perform better than the NB model; the degree of difference in predictive power suggests that under these conditions, choice of model makes little impact. The NB and NBAP models therefore appear interchangeable under certain conditions, while the NBAP provides larger increases in predictive power under others.

Despite the presence of a large proportion of zeroes in both adult and pediatric seizure count data, zero-inflated models were found to provide minimal improvement over more parsimonious, non-zero-inflated models.

Choice of model

As expected, seizure count data was overdispersed, and the NB model a significantly better fit than the PS model. Other models built on the NB that account for autocorrelation, such as those developed by Ahn et. al.¹ and Troconiz et. al.²⁴, allow for nonlinear autocorrelation structure and a more mechanistic interpretation of autocorrelation, respectively, but are limited by computational inefficiency, as addition of every two Markov elements (i.e. one day of autocorrelation) increases computational time exponentially. Fitting such a model for autocorrelation over a larger number, such as the seven days identified here, is computationally infeasible in larger datasets. Based on the appropriateness of linear autoregressive models from residual analysis and the results of a Brock-Dechert-Scheinkman test, we chose not to investigate nonlinear autocorrelation structure. While such models might be appropriate, they seem unnecessary for most patients.

In our study, we focus on negative binomial models for seizure count data. Other research suggested using mixture models to account for data heterogeneity. Hougaard et. al. found that NB models attain superior performance to the Poisson model, and that a generalized Poisson mixture model attains superior performance to NB model for overdispersed data¹¹. We find NB models accounting for autocorrelation may provide improved model fit compared to NB models as well as standard Poisson modeling. While Poisson mixtures may have been useful in modeling our data, fitting Poisson mixtures requires either specification or estimation of the number of components, with the advantage of flexibility but disadvantage of needing to either fix the number of components a priori or explore transdimensional parameter spaces. Misspecification of either the mixing distribution or the random effects distribution has little impact on parameter estimation³⁵, supporting the selection of the NB as a base model.

Autocorrelation terms

As expected, autocorrelation was useful over only one day because the plurality of patients had median inter-seizure intervals of less than one day. Separation of patients by appropriate autoregressive order may be a useful avenue for future research. Increasing the lag order beyond one day improved BIC by less than 1%. As PACF suggested a lower lag order was appropriate, we decided addition of higher-order autocorrelation terms was not warranted. The superiority of the NBAP model to the NBAN model differs from previous results¹, likely due to the nature of the dataset. Because patients tend not to report all seizures^8,36, it is possible that some diaries are inaccurate.

We found NBAP models for both adults and children provided accurate prediction of seizure counts for the majority of patients. With the exception of a limited subset of patients experiencing >4 seizures per day, our use of hold-out cross-validation shows a similar distribution of seizure counts between simulated and observed seizure data (Figure 2). Even within this limited subset, seizure counts >4 per day occur in only a small fraction of trial days, indicating our model is usually accurate for these patients as well. We do not expect the inability of our model to predict the extreme upper range of seizure count data will have a significant impact on simulation studies utilizing our model. Moreover, as our models were built using data meeting clinical trial eligibility criteria, the simulated patients generated by our model would have relatively high seizure counts. We expect that for most applications, the seizure count required of a simulated patient will be lower than those generated by our model.

Children vs adults

For all models developed in this paper, fit to adult data was much better than to pediatric data in the training data, though the MSE was typically lower for children in the testing set. Variance in the random-effects term was greater for children, and effect of prior seizures was approximately 40% larger in children than adults. This is particularly surprising, given that median inter-seizure interval was lower in children than adults. Possible explanations for this are the differences in seizure patterns between children and adults or a nonlinear effect of age for children. Seizure counts in children might be recorded more accurately, as parents or caregivers kept records rather than children themselves. Conversely, seizures might be undercounted in children when their primary caregiver is not available. We recognize that different results might have been obtained had we used another age cutoff to separate adults and children. As many clinical trials accept only patients aged 18 or older, our cutoff is relevant to clinical trial simulation^17,20,37. Further study of pediatric data is warranted, as our model is one of the few in which childhood seizures are considered separately, and it uses by far one of the largest databases of childhood seizures (Table 1). Separation of pediatric and adult data will allow clinical trial simulation parameters to be changed to reflect different patient populations.

Lack of demographic/etiological covariates

Neither demographic nor etiological covariates were useful in modeling seizure count. Although stepwise variable selection procedures have the benefit of computational speed, particularly important in large datasets, stepwise procedures tend to pick models smaller than desirable for prediction, and may be influenced by the number of candidate variables and algorithm used, and subject to local optima. Although such issues were mitigated by confirming results through multiple stepwise algorithms, inclusion of additional covariates and other variable selection techniques may be useful in future research. Additionally, automated variable selection approaches such as that employed here tend to choose parsimonious models that optimize model fit. This potentially excludes covariates which may have clinical significance but do not improve model fit. An alternative approach which is occasionally employed is to include clinically significant variables regardless of effect on fit. However, this approach may lead to large standard errors of parameter estimates, and numerical instability. Algorithmic variable selection techniques would ideally outperform variable selection based on clinical knowledge in data with a large number of features, as is increasingly common in “Big Data” analyses. This is because clinical knowledge may prevent highly relevant variable inclusion, or may recommend variables that are highly collinear. We therefore relied on algorithmic variable selection techniques.

The absence of demographic/etiological covariates seems to indicate that these covariates have no influence on seizure count. However, conclusions regarding relationships between a particular etiology and seizure count are limited by accuracy of self-reported etiologies, and the low number of patients reporting some etiologies (Table 2). The absence of demographic covariates in the final model does not suggest absent age-related differences in seizure count; there is a clear difference between adults and children. To a first approximation, our results suggest differences in age, gender, and etiology may not have a strong linear contribution to seizure count. Further investigation of contributions of these covariates is warranted.

Limitations

The SeizureTracker.com database represents purely patient reported data; inaccuracies may be present in recorded seizure counts. Our view of this database is one of true signal (true seizure counts), and additional noise (from inaccurate recordings, etc.). The database contains more noise than what might be found in a clinical trial. However, without whole brain cellular-level chronic recordings, inaccurate measures may never be fully mitigated⁸.

Neither epilepsy diagnosis nor self-reported etiologies are physician-verified. Some patients in the database may have psychogenic non-epileptic seizures (PNES). However, mean seizure durations in patients with PNES are over five minutes³⁸, the threshold for our screen for status epilepticus. While patients with PNES may nevertheless be included, and misdiagnosed etiologies are not accounted for at all, misdiagnosis remains an issue in clinical trials as well³⁸.

Our analysis is limited because effects of medication changes were not assessed. Were patients with verifiable medication changes identifiable, noise could have been reduced by excluding them, possibly increasing predictive power. Patients who do get a true intervention will have different final summary statistics (i.e., their overall seizure frequencies would be described by different parameters than otherwise), but those new values would be superimposed upon the natural variability of disease.

Seizure miscounting may affect our results. Miscounting may be compounded in patients with cognitive difficulties, who may not recognize their seizures, and in children, who may be in the care of different individuals throughout the day. Adding physician validation options to Seizure Tracker and related seizure diary systems may allow construction of more reliable models, improving data quality using knowledge of seizures clinical features and mimics, and corroborating diagnostic information. Virtually all clinical trials rely on patient-reported seizure counts, so this limitation is applicable (albeit mitigated by training of clinical trial patients) to prior studies, and relates to all future clinical trials that use patient-reporting for the outcome measure.

Future Directions

Using the optimal models from this study, future investigators will have an opportunity to model a wider range of epilepsy than previously possible. Children and adults can be studied together or independently. For example, when planning a phase II or phase III clinical trial, questions of expected seizure count ranges and expected outcomes can be addressed using these models.

The development of these models is a crucial step towards completion of a full clinical trial simulator. As selection of covariates was performed systematically and with a large number of potential choices, and as the models were developed using one of the largest seizure diary databases in the world, a clinical trial simulator based on these data is expected to be more accurate than those already developed. Including patient population characteristics in the model may improve statistical power predictions for human trials. If early data from phase I trials finds 40% efficacy, one could predict the expected number of patients needed to show effects in phase II and III trials. Virtual trials could allow planners to determine necessary trial length, and optimal inclusion/exclusion criteria; this could save money⁴⁰ and accelerate drug discovery.

In biosensor and mHealth arenas, developers can use optimal models to determine what kinds of operating characteristics to expect from their users. For example, if a wearable device tends to have reduced accuracy after a certain number of events, it would be very valuable to know how many seizures to expect from typical and extreme cases, and likely combinations of seizure frequencies.

A key feature of this model is that it is readily implementable on a personal computer without access to private datasets from drug companies or even Seizure Tracker, and can be used by the widest possible set of investigators.

Conclusions

Our optimized models reveal details on the effects of previous seizures on daily seizure count. They provide new information on relationships among demographics, etiologies and seizure count in children and adults. Models can be used to generate data for trial simulations and novel mHealth and biosensor devices.

Key Points.

• A mixed-effects negative binomial model considering autocorrelation was superior to models without autocorrelation.

• Neither zero-inflation nor demographic/etiological covariates improved model strength.

• In both adults and children, autocorrelation is useful over one day, and presence/absence of seizures is more useful than number of seizures.

• This model can be of use in simulations of clinical trials, epilepsy monitoring units, outpatient biosensors, and mHealth applications.

Abbreviations

mHealth

Mobile health

GLMM

Generalized Linear Mixed Model

PS

Poisson

ZIP

Zero-inflated Poisson

NB

Negative Binomial

ZINB

Zero-inflated Negative Binomial

NBAN

Negative Binomial with autocorrelation (number)

NBAP

Negative binomial with autocorrelation (presence/absence)

NBAC

Negative binomial with autocorrelation and covariates

BIC

Bayesian Information Criteria

ISI

Inter-Seizure Interval

PACF

Partial Autocorrelation Function

FSBE

Forward Selection with Backward Elimination

MSE

Mean Squared Error

QQ

Quantile-quantile

AR

Autoregression

PNES

Psychogenic Non-Epileptic Seizure