Graphical abstract
Abbreviations: 2DC, two-dimensional chart; 3DC, three-dimensional chart; ANOVA, analysis of variance; DFC, dynamic friction coefficient; DIE, dual interaction effect; DMRT, Duncan’s multiple range test; GMD, geometric mean diameter; MRDM, mean relative deviation modulus; MLR, multiple linear regression; RMSE, root mean square error; SFC, static friction coefficient; SE, single effect; TIE, triple interaction effect; MAVET, mean of absolute values of error term
Keywords: Analysis of variance, Duncan’s multiple range test, Moisture content, Sliding velocity, Contact surface
Abstract
This paper deals with studying and modeling static friction coefficient (SFC) and dynamic friction coefficient (DFC) of wheat grain as affected by several treatments. Significance of single effect (SE) and dual interaction effect (DIE) of treatments (moisture content and contact surface) on SFC and, SE, DIE, and triple interaction effect (TIE) of treatments (moisture content, contact surface and sliding velocity) on DFC were determined using statistical analysis methods. Multiple linear regression (MLR) modeling was employed to predict SFC and DFC on different contact surfaces. Predictive ability of developed MLR models was evaluated using some statistical parameters (coefficient of determination (R2), root mean square error (RMSE), and mean relative deviation modulus (MRDM)). Results indicated that significant increasing DIE of treatments on SFC was 3.2 and 3 times greater than significant increasing SE of moisture content and contact surface, respectively. In case of DFC, the significant increasing TIE of treatments was 8.8, 3.7, and 8.9 times greater than SE of moisture content, contact surface, and sliding velocity, respectively. It was also found that the SE of contact surface on SFC was 1.1 times greater than that of moisture content and the SE of contact surface on DFC was 2.4 times greater than that of moisture content or sliding velocity. According to the reasonable average of statistical parameters (R2 = 0.955, RMSE = 0.01788 and MRDM = 3.152%), the SFC and DFC could be successfully predicted by suggested MLR models. Practically, it is recommended to apply the models for direct prediction of SFC and DFC, respective to each contact surface, based on moisture content and sliding velocity.
Nomenclature
- FF
friction force (N)
- FC
friction coefficient
- S
sphericity (%)
- W
width (mm)
- Ww
mass of added distilled water (g)
- Wt
initial mass of sample (g)
- x1
1st MLR model variable
- x2
2nd MLR model variable
- xn
nth MLR model variable
- Ɛ
error term of MLR model
- FCactave
average of actual friction coefficient
- Mf
final moisture content of sample (d. b.%)
- Mi
initial moisture content of sample (d. b.%)
- M
mean of used data
- CV
coefficient of variation (%)
- FCmax
maximum friction coefficient
- C
contribution of variation (%)
- CNU
coefficient of non-uniformity (%)
- NF
normal force (N)
- SSv
sum of square of variation
- FCmin
minimum friction coefficient
- SSt
total sum of square
- SD
standard deviation
- FCact,i
ith actual friction coefficient
- FCpre,i
ith predicted friction coefficient
- N
number of data
- an
nth MLR model coefficient
- a2
2nd MLR model coefficient
- a1
1st MLR model coefficient
- a0
MLR model constant
- Sa
surface area (mm2)
- T
thickness (mm)
- L
length (mm)
- Dg
GMD (mm)
- RMSE
root mean square error
- MRDM
mean relative deviation modulus (%)
Introduction
Wheat is a dominate major crop in human food. The crop is widely cultivated throughout the world. Hence, investigation of different aspects of wheat in planting, harvesting, transporting, storing and processing stage is of great importance in management of its production and preservation.
Physical properties of agricultural products are frequently used for designing of agricultural machinery and equipment of related post-harvest industries [1]. Some physical properties are major dimensions (length, width and thickness), mass, GMD, sphericity and friction coefficients.
Friction coefficients of crops vary on different contact surfaces. Therefore, exact determination of friction coefficients of the crop on different contact surfaces can be useful in performance optimization of mechanical equipment (conveyors, separation, cleaning, drying and storing tools), and consequently, reduction and increment of harmful damages and economic efficiency, respectively [2].
Friction forces perform between two contact surfaces. Required force for initial movement of a motionless object depends on static friction force and the force for continuous movement of an object at a specific velocity relies on dynamic friction force. According to Brubaker and Pos [3], the relation between friction force and friction coefficient can be presented as following equation.
| (1) |
According to Eq. (1), friction coefficient directly affects the friction force value. Therefore, researches about the effect of various conditions and treatments on friction coefficients are needed to gain information for controlling friction forces.
Friction coefficients include SFC and DFC with respect to static and dynamic friction forces, respectively. The SFC and DFC of crop depend on moisture content. Additionally, in case of DFC, the sliding velocity is also an important factor [2].
The frictional forces occur on a vertical plane in storage structures and handling equipment of wheat grain. On walls and floor of storage bins, frictional forces play an important role in discharging process in the plug flow region. The SFC and DFC, and consequently frictional forces, are influenced by the interaction of wheat grain particles and the surface of bin wall [4]. This interaction significantly affects the distribution and magnitude of loads applied on storage structures [5]. However, knowledge about the impact of many treatments on the SFC and DFC is still incomplete. Thus, additional experimental works are needed to determine the exact frictional behavior of wheat grain on different contact surfaces.
A review of published works confirmed that although the SFC of wheat grain has been studied by several previous investigators [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], there is no extended study for the determination of the effect of moisture content and contact surface on SFC of wheat grain. Neither, there are perfect attempts available in literature reporting the effect of moisture content, contact surface or sliding velocity on DFC of wheat grain [24], [25], [26], [27], [28], [29], [30]. Therefore, a comprehensive investigation of SFC and DFC for wheat grain taking several experimental conditions into considerations will be useful for optimization of storage and processing structures, especially grain bins.
In light of the above mentioned deficiencies and the benefits of knowing about SFC and DFC of wheat grain for optimization of related industry structures and equipment, the key scope of the present work on wheat grain was concentrated on following items:
-
(1)
Precise determination of SFC and DFC as effected by moisture content and contact surface, and moisture content, contact surface and sliding velocity, respectively.
-
(2)
To carry out statistical analysis to study the effect of moisture content, sliding velocity, contact surface and their DIE and TIE on DFC, and moisture content, contact surface and their DIE on SFC.
-
(3)
Comparing statistical significance of the effect of different treatment levels on SFC and DFC.
-
(4)
Assessment of predictive ability of MLR model for SFC and DFC based on multiple input variables (moisture content and sliding velocity) for each contact surface.
Material and methods
Grain collection
Shiroudi variety of wheat (Triticum aestivum L.), one of the most commonly used varieties in south region of Iran, was collected from Seed and Plant Breeding Unit, Agricultural Research Center of Fars province. Initially, the grains were cleaned by hand in order to remove undesired materials such as gravel, stone and injured grains. The prepared grains were then transferred to the research laboratory to determine physical properties.
Physical properties
One hundred wheat grains were randomly chosen to determine some physical properties. Three principal dimensions (length, width and thickness) of the grains were then measured with a digital caliper model: 01409A (Neiko, New Jersey, USA). reading to an accuracy of 0.02 (mm). The grains were weighed using a precision electronic balance model: GF-600 (A&D, Tokyo, Japan) with 0.001 (g) accuracy. Besides, some shape indices of the grains (GMD, sphericity and surface area) were calculated based on following equations [2].
| (2) |
| (3) |
| (4) |
Determination of initial moisture content
A ten-gram sample of wheat grains was dried in a convection oven at 130 ± 1 (°C) for 19 (h). The initial moisture content of the grains was then determined as the mass reduction during drying procedure divided by dry mass of the grains [31]. To eliminate measurement error, the tests were completed in triplicate and mean value was used. The initial moisture content of wheat grain was 9.4% (d. b.).
Sample preparation
The grains were moistened to achieve a higher moisture content (13, 17.2, 20.9 and 25% (d. b.)) by attachment of specific quantity of distilled water calculated by following equation [32].
| (5) |
The hydrated samples were packed in separate polyethylene bags and placed in a refrigerator at 5 ± 0.5 (°C) for ten days to allow water be uniformly absorbed into grains [33]. The required quantity of samples was located at ambient condition to warm up to room temperature, almost two hours before starting each frictional experiment [34].
Frictional experiments
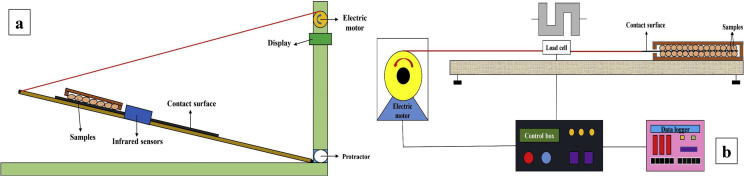
The SFC of samples was precisely measured on five contact surfaces (aluminum, rubber, glass, galvanized steel and plywood) at different levels of moisture content by means of a SFC measuring instrument. The instrument was initially proposed by Singh and Goswami [35] and improved mechanically and electrically by Lorestani et al. [36] and Shafaei et al. [23]. A schematic of the instrument is shown in details in Fig. 1a. Technical specifications and engineering aspects of the instrument are available in the literature.
Fig. 1.
Schematic of the used SFC (a) and DFC (b) measuring instrument.
The DFC of samples was also measured accurately on each type of contact surface at different levels of moisture content and sliding velocities (1, 3.5, 5.75, 9.25, and 12.5 (cm/s)) using a DFC measuring instrument. The higher sliding velocities were ignored in order to avoid probable damages to the samples. The instrument was originally suggested by Clark and Mcfarland [37] and developed and frequently used by other researchers, afterwards [4], [38]. The instrument is schematically illustrated in Fig. 1b. The details of development and engineering considerations of the instrument are fully explained in the literature.
Before starting each experiment, the contact surface was cleaned by means of compressed air to eliminate any remaining matter from previous experiments. Each experiment was accomplished in five replications at constant normal pressure of 22.5 (kPa).
Data analysis
Statistical descriptions
To study changes in measured SFC and DFC of the samples as influenced by applied treatments, the statistical descriptor parameters, namely mean, standard deviation, coefficient of variation and coefficient of non-uniformity were used based on following equations.
| (6) |
| (7) |
| (8) |
| (9) |
Statistical analysis
The collected data (125 and 625 sets for SFC and DFC, respectively) were analyzed for sliding velocity (5 levels), moisture content (5 levels) and contact surface (5 types), each with five replications. For this purpose, the statistical analysis system of SPSS 21 software (SPSS Inc., Chicago, IL, USA) was used. The ANOVA method was applied to determine the effect of moisture content, contact surface and their DIE on SFC and also the effect of sliding velocity, contact surface and moisture content, and their DIE and TIE on DFC. The experiments were performed according to completely randomized factorial design with two and three main treatment factors for SFC and DFC, respectively, at 99% probability level. Contribution of each variation to SFC and DFC was then calculated based on the ANOVA results using Eq. (10). Differences between means of the treatments were also compared using DMRT at 1% significance level.
| (10) |
Development of MLR models
The MLR models, based on Eq. (11), were developed for the means of data (25 and 125 sets for SFC and DFC, respectively) obtained from all five-replication experiments using SPSS 21 software (SPSS Inc., Chicago, IL, USA). The model was fed with one (moisture content) and two (moisture content and sliding velocity) input variables, respectively, for prediction of SFC and DFC on each contact surface. The significance of constants and coefficients of the developed models was also determined at 99% probability level.
| (11) |
In order to assess predictive ability of developed models, statistical parameters (coefficient of determination (R2), RMSE and MRDM) were calculated between modeled and actual SFC or DFC according to following equations.
| (12) |
| (13) |
| (14) |
Results and discussion
Physical properties
The length, width, thickness, mass, GMD, surface area and sphericity of the wheat grain are presented in detail in Table 1.
Table 1.
Some physical properties of wheat grain.
| Physical property | Median | Range | Geometric mean |
|---|---|---|---|
| Length (mm) | 7.546 | 6.513–8.658 | 7.234 |
| Width (mm) | 3.546 | 3.026–3.952 | 3.664 |
| Thickness (mm) | 2.439 | 2.251–2.791 | 2.532 |
| Mass (g) | 0.029 | 0.023–0.048 | 0.036 |
| GMD (mm) | 3.955 | 3.356–4.236 | 4.087 |
| Surface area (mm2) | 48.658 | 47.921–51.650 | 49.126 |
| Sphericity (%) | 65.867 | 57.398–69.425 | 64.345 |
Statistical descriptions
Standard deviation of SFC and DFC for each set of replications obtained in range of 0.004–0.019 and 0.003–0.029, respectively. The limited range of standard deviations verified high accuracy and stability of the measuring instruments.
Statistical descriptor parameters for measured SFC and DFC of wheat grain corresponding to five levels of moisture content and sliding velocity on different contact surfaces are reported in Table 2. According to Table 2, minimum and maximum SFC were obtained in the lowest and highest level of moisture content on glass and rubber, respectively. The inappropriate coefficient of variation and coefficient of non-uniformity for SFC implied that the SFC sharply changed by changing moisture content level or contact surface type.
Table 2.
Statistical description of measured SFC and DFC of wheat grain.
| Type of friction coefficient | Mean | Standard deviation | Minimum | Maximum | CV (%) | CNU (%) |
|---|---|---|---|---|---|---|
| SFC | 0.512 | 0.121 | 0.240 | 0.693 | 23.63 | 88.48 |
| DFC | 0.467 | 0.124 | 0.204 | 0.809 | 26.55 | 129.55 |
Similar to SFC, the lowest and highest DFC were found in minimum and maximum levels of moisture content and sliding velocity on glass and rubber, respectively (Table 2). Improper coefficient of variation and coefficient of non-uniformity for DFC also indicated that the DFC changed sharply as influenced by variation of levels of moisture content, sliding velocity or contact surface type.
Comparison between coefficient of variation and coefficient of non-uniformity for the SFC and DFC in Table 2 demonstrated that the DFC-related values were higher than those of SFC. In case of DFC, three treatments were applied while, two treatments were applied to study SFC behavior. Therefore, the variation of DFC, and consequently the DFC-related values, were higher than those of SFC.
Statistical analysis
Table 3, Table 4, respectively, present ANOVA results for SFC and DFC of wheat grain under different treatments. With reference to the Tables, it can be stated that the effect of treatments and interactions of them (DIE and TIE) on SFC and DFC were significant at 1% probability level (P < 0.01). These effects on SFC and DFC are necessary engineering considerations that should be taken in designing crop handling equipment and storage structures to reach the best operation conditions.
Table 3.
ANOVA results for SFC of wheat grain.
| Source of variation | Degree of freedom | Sum of squares | Mean square | F value |
|---|---|---|---|---|
| Moisture Content (MC) | 4 | 0.771 | 0.193 | 1327.275⁎⁎ |
| Contact Surface (CS) | 4 | 1.037 | 0.259 | 1786.704⁎⁎ |
| MC × CS | 16 | 0.036 | 0.002 | 15.660⁎⁎ |
| Error | 100 | 0.015 | 0.00015 | |
| Total | 124 | 1.859 |
Significant at P < 0.01.
Table 4.
ANOVA results for DFC of wheat grain.
| Source of variation | Degree of freedom | Sum of squares | Mean square | F value |
|---|---|---|---|---|
| Moisture Content (MC) | 4 | 1.418 | 0.355 | 1406.704⁎⁎ |
| Contact surface (CS) | 4 | 6.461 | 1.615 | 6408.071⁎⁎ |
| Sliding velocity (SV) | 4 | 1.362 | 0.341 | 1351.311⁎⁎ |
| MC × CS | 16 | 0.182 | 0.011 | 45.023⁎⁎ |
| MC × SV | 16 | 0.015 | 0.001 | 3.639⁎⁎ |
| CS × SV | 16 | 0.085 | 0.005 | 21.169⁎⁎ |
| MC × CS × SV | 64 | 0.033 | 0.001 | 2.053⁎⁎ |
| Error | 500 | 0.126 | 0.000252 | |
| Total | 624 | 9.682 |
Significant at P < 0.01.
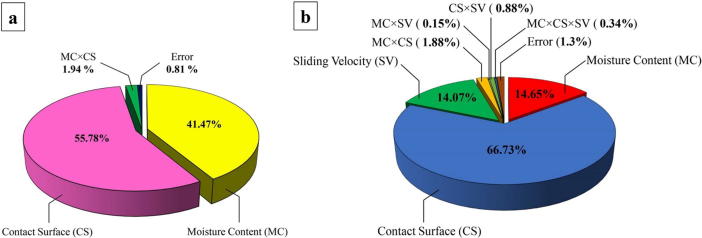
Contribution of each variation to SFC and DFC is displayed in Fig. 2. As it can be seen in Fig. 2a, the contribution of contact surface variation was found to be greater than that of moisture content. This result corresponds to that for DFC (Fig. 2b). Thus, contact surface seems to have had a stronger effect on SFC than moisture content and on DFC than moisture content and sliding velocity.
Fig. 2.
Contribution of variations to SFC (a) and DFC (b) of wheat grain.
Effect of treatments
SE
Moisture content
DMRT results of the effect of moisture content on SFC and DFC of wheat grain are reported in Table 5. It was inferred from the Table that the increment of moisture content from 9.4 to 25% (d. b.) led to SFC and DFC rise of 59 and 33.75%, respectively. As the moisture content increases, the grains become stickier and accordingly, cohesive force between grains and contact surface increases. The higher cohesive forces will result in the higher SFC [39] and DFC [40].
Table 5.
DMRT results for the SE of treatments on SFC and DFC of wheat grain.
| Type of friction coefficient | Treatment | ||||
|---|---|---|---|---|---|
| Moisture content (d. b.%) | |||||
| 9.4 |
13 |
17.2 |
20.9 |
25 |
|
| SFC | 0.387 ± 0.012a⁎ | 0.470 ± 0.010b | 0.521 ± 0.015c | 0.565 ± 0.019d | 0.615 ± 0.009e |
| DFC | 0.400 ± 0.009⁎⁎a | 0.436 ± 0.001b | 0.464 ± 0.001c | 0.501 ± 0.001d | 0.535 ± 0.012e |
| Contact surface | |||||
| Glass |
Aluminum |
Plywood |
Galvanized steel |
Rubber |
|
| SFC | 0.375 ± 0.002a | 0.443 ± 0.014b | 0.527 ± 0.008c | 0.597 ± 0.020d | 0.615 ± 0.011e |
| DFC | 0.374 ± 0.008b | 0.350 ± 0.004a | 0.463 ± 0.005c | 0.517 ± 0.005d | 0.631 ± 0.008e |
| Sliding velocity (cm/s) | |||||
| 1 |
3.5 |
5.75 |
9.25 |
12.5 |
|
| DFC | 0.397 ± 0.001a | 0.437 ± 0.001b | 0.471 ± 0.001c | 0.501 ± 0.011d | 0.530 ± 0.011e |
Different letters show significant differences at probability level of 1%.
Mean ± standard error.
Sliding velocity
Table 5 indicates the increasing trend of DFC of wheat grain with ascending sliding velocity, according to the DMRT results. Based on the Table values, it can be concluded that increment of sliding velocity from 1 to 12.5 (cm/s) led to the notable change of DFC from the lowest to highest value by 33.5%. Higher adhesive force at higher sliding velocity might have resulted in the DFC growth [24].
Contact surface
The DMRT results demonstrated that contact surface significantly affected SFC and DFC of wheat grain (Table 5). The lowest SFC and DFC were found on the glass and aluminum contact surface, respectively. The SFC and DFC changed from lowest to highest value by 64% and 80.29%, respectively. It was due to the coarseness or smoothness of different contact surfaces. Smoother surface resulted in lower adhesion force between the samples and the surface and thereby, the lower SFC and DFC. However, it was expected that the friction coefficients on galvanized steel and aluminum contact surface be similar, the results did not verify this expectation. It might be due to smoother and more polished surface of the aluminum sheet than galvanized steel.
DIE
DMRT results of DIE of moisture content and contact surface on SFC of wheat grain are presented in Table 6. A precise analysis of the results indicated that moisture content increase from 9.4 to 25% (d. b.) along with the change from smooth contact surface to the coarse one (from glass to rubber) resulted in a 189% increment of SFC. In the Table, different letters represent a significant difference among SFCs at probability level of 1%. This significant DIE of moisture content and contact surface on SFC can be interpreted as the grain moisture content could be transferred to the contact surface and the moisturized contact surface acts as a contact surface with different characteristics and accordingly, the SFC vary. Hence, to achieve the same frictional behavior of wheat grain, each treatment combination with identical results on SFC is recommended for controlling SFC regarding available facilities.
Table 6.
DMRT results for the DIE of treatments on SFC of wheat grain.
| Contact surface | Moisture content (d. b.%) |
||||
|---|---|---|---|---|---|
| 9.4 | 13 | 17.2 | 20.9 | 25 | |
| Glass | 0.240 ± 0.019a⁎ | 0.339 ± 0.017bc | 0.356 ± 0.022c | 0.426 ± 0.010de | 0.516 ± 0.011gh |
| Aluminum | 0.320 ± 0.010⁎⁎b | 0.422 ± 0.009de | 0.440 ± 0.012e | 0.496 ± 0.019g | 0.537 ± 0.016hi |
| Plywood | 0.413 ± 0.004d | 0.469 ± 0.004f | 0.518 ± 0.009h | 0.586 ± 0.007j | 0.651 ± 0.007kl |
| Galvanized steel | 0.468 ± 0.017f | 0.548 ± 0.011i | 0.638 ± 0.015k | 0.655 ± 0.011kl | 0.677 ± 0.008mn |
| Rubber | 0.495 ± 0.008g | 0.573 ± 0.009j | 0.651 ± 0.006kl | 0.662 ± 0.009lm | 0.693 ± 0.009n |
Different letters show significant differences at probability level of 1%.
Mean ± standard error.
Table 7 reports the DIE of applied treatments (moisture content, contact surface and sliding velocity) on the DFC of wheat grain on the basis of DMRT results. In the Table, different letters represent a significant difference among DFCs as affected by applied treatments at probability level of 1%. The significant DIE of moisture content and contact surface on DFC can be physically explained in a way similar to that of SFC. The significant DIE of moisture content and sliding velocity could be also related to changes in the temperature of contact surface. As the sliding velocity changes, the frictional energy also changes and releases in the form of heat. The grain moisture content changes as affected by the heat produced, and thereby, the DFC changes. In case of the significant DIE of contact surface and sliding velocity on DFC, it can be stated that the heat which is produced when sliding velocity changes might affect the structure of contact surface and, the DFC changes accordingly.
Table 7.
DMRT results for the DIE of treatments on DFC of wheat grain.
| Treatments | |||||
|---|---|---|---|---|---|
| Contact surface | Moisture content (d. b.%) | ||||
| 9.4 |
13 |
17.2 |
20.9 |
25 |
|
| Glass | 0.290 ± 0.013a⁎ | 0.321 ± 0.013c | 0.370 ± 0.013e | 0.426 ± 0.015h | 0.465 ± 0.014j |
| Aluminum | 0.307 ± 0.007b⁎⁎ | 0.330 ± 0.006c | 0.351 ± 0.005d | 0.373 ± 0.005e | 0.390 ± 0.007f |
| Plywood | 0.409 ± 0.008g | 0.441 ± 0.009i | 0.460 ± 0.010j | 0.490 ± 0.011k | 0.515 ± 0.010l |
| Galvanized steel | 0.463 ± 0.008j | 0.495 ± 0.009k | 0.514 ± 0.010l | 0.544 ± 0.011n | 0.569 ± 0.010o |
| Rubber | 0.529 ± 0.011m | 0.591 ± 0.009p | 0.624 ± 0.009q | 0.673 ± 0.014r | 0.738 ± 0.013s |
| Moisture content (d. b.%) | Sliding velocity (cm/s) | ||||
| 1 |
3.5 |
5.75 |
9.25 |
12.5 |
|
| 9.4 | 0.333 ± 0.019a | 0.368 ± 0.019b | 0.408 ± 0.020c | 0.431 ± 0.020de | 0.458 ± 0.017f |
| 13 | 0.369 ± 0.022b | 0.409 ± 0.022c | 0.443 ± 0.021e | 0.464 ± 0.020fg | 0.494 ± 0.020hi |
| 17.2 | 0.400 ± 0.021c | 0.431 ± 0.021de | 0.470 ± 0.020fg | 0.491 ± 0.020h | 0.527 ± 0.022j |
| 20.9 | 0.426 ± 0.023d | 0.471 ± 0.021g | 0.498 ± 0.022hi | 0.539 ± 0.021j | 0.572 ± 0.023k |
| 25 | 0.458 ± 0.022f | 0.504 ± 0.023i | 0.535 ± 0.024j | 0.580 ± 0.026k | 0.599 ± 0.025l |
| Sliding velocity (cm/s) | Contact surface | ||||
| Glass |
Aluminum |
Plywood |
Galvanized steel |
Rubber |
|
| 1 | 0.278 ± 0.012a | 0.306 ± 0.007b | 0.394 ± 0.006f | 0.448 ± 0.006h | 0.560 ± 0.017m |
| 3.5 | 0.328 ± 0.014c | 0.332 ± 0.006c | 0.436 ± 0.008g | 0.490 ± 0.008j | 0.598 ± 0.014o |
| 5.75 | 0.383 ± 0.014f | 0.353 ± 0.006d | 0.462 ± 0.007i | 0.516 ± 0.007k | 0.639 ± 0.014p |
| 9.25 | 0.424 ± 0.015g | 0.370 ± 0.007e | 0.496 ± 0.009j | 0.550 ± 0.009m | 0.666 ± 0.017q |
| 12.5 | 0.459 ± 0.014hi | 0.389 ± 0.006f | 0.528 ± 0.009l | 0.582 ± 0.009n | 0.692 ± 0.017r |
Different letters show significant differences at probability level of 1%.
Mean ± standard error.
Regarding user point of view, to optimize the performance of corresponding equipment and structures, altering levels of the treatments with insignificant DIE on DFC in Table 7 is suggested.
Analysis of data presented in Table 7 revealed that the DFC increased by 154.48% as a result of concurrent change of contact surface from glass to rubber and moisture content from 9.4 to 25% (d. b.). Besides, DFC increased 79.88% with simultaneous increment of moisture content and sliding velocity from 9.4 to 25% (d. b.) and from 1 to 12.5 (cm/s), respectively. It was also found that the change of contact surface from glass to rubber and sliding velocity from 1 to 12.5 (cm/s) resulted in an increase of DFC by 148.92%.
TIE
Table 8 displays a comparison among mean DFC of wheat grain as affected by triple interaction of the treatments performed by DMRT. According to the Table, a 296.57%. increment of DFC from the poor frictional condition (contact surface: glass, sliding velocity: 1 (cm/s) and moisture content: 9.4% (d. b.)) to the strong frictional condition (contact surface: rubber, sliding velocity: 12.5 (cm/s) and moisture content: 25% (d. b.)) was observed. Different letters in the Table represent significant differences at probability level of 1%. The physical interpretation of this significant TIE on DFC can be mentioned by changes in sliding velocity, the released heat changes the grain moisture content and consequently contact surface structure differs and therefore, the DFC changes.
Table 8.
DMRT results for the TIE of treatments on DFC of wheat grain.
| Contact surface | Moisture content (d. b.%) | Sliding velocity (cm/s) |
||||
|---|---|---|---|---|---|---|
| 1 | 3.5 | 5.75 | 9.25 | 12.5 | ||
| Glass | ||||||
| 9.4 | 0.204 ± 0.003a⁎ | 0.245 ± 0.009bc | 0.294 ± 0.005e-h | 0.328 ± 0.005i-m | 0.379 ± 0.005o-w | |
| 13 | 0.227 ± 0.007ab⁎⁎ | 0.276 ± 0.004de | 0.331 ± 0.006i-m | 0.368 ± 0.005n-r | 0.405 ± 0.007s-A | |
| 17.2 | 0.277 ± 0.005de | 0.316 ± 0.010g-j | 0.397 ± 0.012r-z | 0.421 ± 0.007z-D | 0.440 ± 0.010B-I | |
| 20.9 | 0.319 ± 0.003g-j | 0.388 ± 0.008q-y | 0.414 ± 0.004y-D | 0.482 ± 0.005K-P | 0.528 ± 0.007S-Z | |
| 25 | 0.364 ± 0.008n-q | 0.415 ± 0.003y-D | 0.479 ± 0.006K-P | 0.523 ± 0.007R-Y | 0.542 ± 0.008X-Zαβρ | |
| Aluminum | ||||||
| 9.4 | 0.256 ± 0.005cd | 0.290 ± 0.005e-g | 0.315 ± 0.002g-j | 0.322 ± 0.002h-k | 0.352 ± 0.004l-o | |
| 13 | 0.286 ± 0.003ef | 0.312 ± 0.003f-i | 0.327 ± 0.003i-l | 0.351 ± 0.001k-o | 0.373 ± 0.001n-r | |
| 17.2 | 0.316 ± 0.002g-j | 0.332 ± 0.001i-m | 0.355 ± 0.001l-p | 0.370 ± 0.001n-r | 0.383 ± 0.001p-x | |
| 20.9 | 0.332 ± 0.001i-m | 0.357 ± 0.001m-p | 0.377 ± 0.001o-t | 0.391 ± 0.001q-z | 0.406 ± 0.001t-A | |
| 25 | 0.343 ± 0.001j-n | 0.369 ± 0.001n-r | 0.392 ± 0.001q-z | 0.413 ± 0.006x-C | 0.432 ± 0.001A-G | |
| Plywood | ||||||
| 9.4 | 0.356 ± 0.004l-p | 0.376 ± 0.004o-s | 0.408 ± 0.004w-A | 0.442 ± 0.005C-J | 0.463 ± 0.003I-L | |
| 13 | 0.374 ± 0.003o-r | 0.418 ± 0.005y-D | 0.455 ± 0.002E-K | 0.466 ± 0.002I-M | 0.495 ± 0.002M-R | |
| 17.2 | 0.390 ± 0.004q-z | 0.433 ± 0.003A-H | 0.458 ± 0.004F-L | 0.478 ± 0.003K-O | 0.538 ± 0.005W-Zαβ | |
| 20.9 | 0.408 ± 0.005w-A | 0.459 ± 0.003F-L | 0.484 ± 0.002K-Q | 0.535 ± 0.006W-Zα | 0.565 ± 0.003βρ£ƷØƮ | |
| 25 | 0.441 ± 0.005C-I | 0.494 ± 0.002M-R | 0.504 ± 0.003O-T | 0.557 ± 0.003Zαβρ£Ʒ | 0.578 ± 0.002ƷØƮ | |
| Galvanized steel | ||||||
| 9.4 | 0.410 ± 0.004x-B | 0.430 ± 0.004A-F | 0.462 ± 0.004G-L | 0.496 ± 0.005N-R | 0.517 ± 0.003R-X | |
| 13 | 0.428 ± 0.003A-E | 0.472 ± 0.005J-N | 0.509 ± 0.002P-W | 0.520 ± 0.002R-Y | 0.549 ± 0.002YZαβρ£Ʒ | |
| 17.2 | 0.444 ± 0.004D-J | 0.487 ± 0.003L-Q | 0.512 ± 0.004Q-X | 0.532 ± 0.003T-Zα | 0.592 ± 0.005ƮƐʍ | |
| 20.9 | 0.462 ± 0.005H-L | 0.513 ± 0.003Q-X | 0.538 ± 0.002W-Zαβ | 0.589 ± 0.006ØƮƐ | 0.619 ± 0.003ʍʘµɓ | |
| 25 | 0.495 ± 0.005M-R | 0.548 ± 0.002YZαβρ£ | 0.558 ± 0.003αβρ£Ʒ | 0.611 ± 0.003Ɛʍʘµ | 0.632 ± 0.002ʘµɓɥ | |
| Rubber | ||||||
| 9.4 | 0.441 ± 0.009C-I | 0.499 ± 0.005N-S | 0.561 ± 0.006αβρ£ƷØ | 0.569 ± 0.006ρ£ƷØƮ | 0.577 ± 0.007£ƷØƮ | |
| 13 | 0.532 ± 0.012T-Zα | 0.568 ± 0.005βρ£ƷØƮ | 0.590 ± 0.011ØƮƐʍ | 0.616 ± 0.009Ɛʍʘµ | 0.648 ± 0.010ɥɀ | |
| 17.2 | 0.572 ± 0.005ρ£ƷØƮ | 0.588 ± 0.003ØƮƐ | 0.628 ± 0.010ʘµɓɥ | 0.652 ± 0.014ɥɀ | 0.682 ± 0.005ʇ | |
| 20.9 | 0.610 ± 0.048Ɛʍʘ | 0.639 ± 0.006µɓɥ | 0.675 ± 0.015ɀʇ | 0.697 ± 0.021ʇ | 0.743 ± 0.005ʋ | |
| 25 | 0.646 ± 0.005ɓɥ | 0.697 ± 0.006ʇ | 0.743 ± 0.014ʋ | 0.795 ± 0.004ʊ | 0.809 ± 0.002ʊ | |
Different letters show significant differences at probability level of 1%.
Mean ± standard error.
To attain the best frictional condition based on engineering principles, the applied treatments resulted in the DFC with the same letters in the Table 8 can be considered as alternatives.
Comparison of the positive effect of treatments
SFC
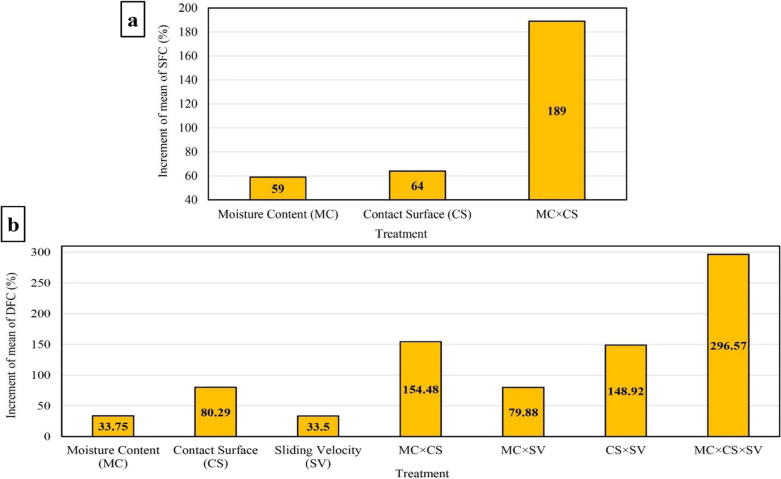
Fig. 3a depicts the increment of SFC of wheat grain obtained from analysis of DMRT results versus applied treatments. It is clearly observed that the variation of SFC as affected by DIE of moisture content and contact surface has been greater (3 and 3.2 times) than that as influenced by SE of contact surface, succeeding by SE of moisture content. The more efficient SE of contact surface than SE of moisture content (1.1 times) was in agreement with the prediction addressed in the Statistical Analysis Section. Therefore, to control the SFC of wheat grain, applying simultaneous changes in moisture content and contact surface rather than individual change of contact surface or moisture content, is suggested as a more effective way.
Fig. 3.
Increment of SFC (a) and DFC (b) of wheat grain as affected by treatments.
DFC
Fig. 3b shows a chart comparing the effect of different treatments on the increment of DFC of wheat grain. As it can be seen in the Fig., TIE of the treatments was more efficient (2, 3.7, and 2 times) than DIE, followed by SE of treatments (8.8, 3.7 and 8.9 times). The greater SE of contact surface (2.4 times) than SE of moisture content or sliding velocity was also predicted by the results of contribution of variation presented in the Statistical Analysis Section. Application of these results is suggested to be considered for decrement or increment of DFC of wheat grain in respective equipment and structures.
Evaluation of developed MLR models
The constants, coefficients and statistical parameters of MLR models developed for prediction of SFC and DFC of wheat grain regarding to each contact surface are listed in Table 9. The acceptable values of coefficient of determination (R2 > 0.9), RMSE and MRDM tabulated in the Table confirmed that the SFC and DFC of wheat grain were appropriately predicted by MLR model in moisture content range of 9.4 to 25% (d. b.) and sliding velocity range of 1 to 12.5 (cm/s) on galvanized steel, glass, aluminum, rubber and plywood contact surfaces. It was also found that the constant and coefficient obtained for each developed MLR model documented in the Table were significant at 99% probability level. Therefore, from the MLR modeling results, it could be clearly indicated that the SFC was function of moisture content and the DFC was function of both moisture content and sliding velocity on contact surfaces. These inferences are similar to those obtained from ANOVA results in the Statistical Analysis Section.
Table 9.
Constants, coefficients and statistical parameters of MLR model fitted to SFC and DFC of wheat grain.
| Contact surface | Type of friction coefficient | a0 | a1 | a2 | R2 | RMSE | MRDM (%) |
|---|---|---|---|---|---|---|---|
| Glass | SFC | 0.0967 | 0.0163 | 0 | 0.959 | 0.02405 | 4.795 |
| DFC | 0.0756 | 0.0116 | 0.0157 | 0.972 | 0.01651 | 3.512 | |
| Aluminum | SFC | 0.2220 | 0.0129 | 0 | 0.939 | 0.02362 | 3.634 |
| DFC | 0.2143 | 0.0053 | 0.0070 | 0.975 | 0.00699 | 1.508 | |
| Plywood | SFC | 0.2682 | 0.0152 | 0 | 0.996 | 0.00717 | 0.842 |
| DFC | 0.2772 | 0.0066 | 0.0113 | 0.966 | 0.01174 | 1.898 | |
| Galvanized steel | SFC | 0.3679 | 0.0134 | 0 | 0.902 | 0.03159 | 3.538 |
| DFC | 0.3312 | 0.0066 | 0.0113 | 0.963 | 0.01174 | 1.696 | |
| Rubber | SFC | 0.4030 | 0.0124 | 0 | 0.911 | 0.02760 | 2.944 |
| DFC | 0.3407 | 0.0128 | 0.0113 | 0.962 | 0.01777 | 2.152 |
Fig. 4 illustrates the distribution of error term values of MLR models developed for SFC and DFC prediction. According to the Fig., it is apparently observed that the error term values randomly happened and no trend was detected. Therefore, error term values of the MLR models were not sensitive to actual data. From the Fig., it was found that the MAVET and its standard deviation were 0.015 and 0.012, respectively, for the SFC. In case of DFC, these values were found as 0.010 and 0.008.
Fig. 4.
Distribution of error term values of the MLR models developed for friction coefficient prediction of wheat grain, SFC (a) and DFC (b) ( glass, ■ aluminum,
glass, ■ aluminum,  plywood,
plywood,  galvanized steel and
galvanized steel and  rubber surface).
rubber surface).
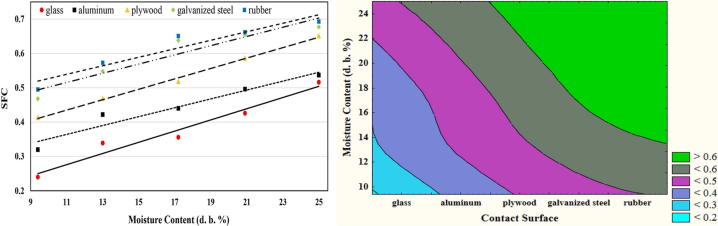
The developed MLR models for SFC prediction of wheat grain are shown in Fig. 5. The 2DC in the Fig. reveals that the SFC linearly has increased with increasing moisture content on each contact surface. The contour plot result of MLR modeling depicted in the Fig. shows the interaction of moisture content and contact surface on SFC. As it can be seen in the plot, moisture content increase from 9.4 to 25% (d. b.) along with the change of contact surface from glass to rubber resulted in integrated increment of SFC from the lowest (<0.2) to the highest bound (>0.6). It corresponds to the results of statistical analysis of DIE of moisture content and contact surface on SFC (DIE Section).
Fig. 5.
MLR modeling of SFC of wheat grain on the used contact surfaces.
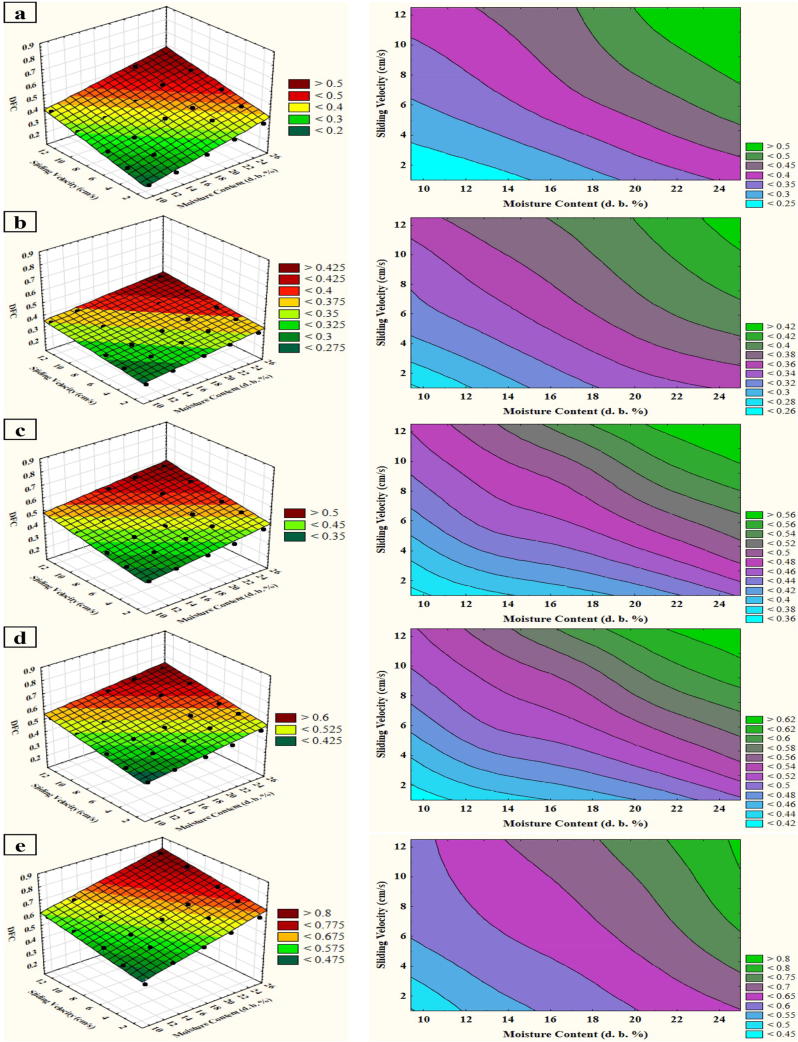
The developed MLR models for DFC prediction of wheat grain with respect to each contact surface are graphically shown in Fig. 6. The 3DCs for DFC prediction clarify the concept of how the model output responds to the input variables. It is apparently seen that the DFC linearly increased with the increase of moisture content and sliding velocity. The contour plot in the Fig. depicts the model output based on the graphical reflection of interaction of the moisture content and sliding velocity. As it can be seen in the plots, the interaction of moisture content and sliding velocity on DFC has been congruent. The DFC increasingly varied as concurrent increase of moisture content and sliding velocity occurred. This modeling result is correspondent to that of statistical analysis of DIE of moisture content and sliding velocity on DFC (DIE Section).
Fig. 6.
MLR modeling of DFC of wheat grain on glass (a), aluminum (b), plywood (c), galvanized steel (d) and rubber surface (e).
To sum up the MLR modeling results, it can be stated that the models are reliable enough for direct determination of friction coefficients of wheat grain in storage and processing conditions with no need for actual measurement of SFC or DFC. Furthermore, the models present an appropriate physical perception of the effect of treatments on SFC and DFC. The physical perception is helpful for proper management and control of SFC and DFC of wheat grain in practical conditions.
Comparison with published data
A condensed summary of comparison of the results obtained in the present study with other published researches is reported in Table 10. According to the Table, measured and predicted data in the study are different from previously published data, especially in case of DFC on galvanized steel, although they are in a similar range. The differences between the results obtained in current study and previous ones could be due to the following factors:
-
(1)
Employment of various SFC measuring instruments based on three methods of pulling force, tilting plate and rotating disk, and different DFC measuring instruments on the basis of two methods of pulling force and rotating disk.
-
(2)
Differences in contact surface characteristics (scratches and roughness) and the wheat variety used.
-
(3)
Applying various investigational levels of treatments (moisture content and sliding velocity) based on the desired experimental conditions.
Table 10.
Comparison of the SFC and DFC of wheat grain results obtained in the present study with other published researches.
| Contact surface | Type of friction coefficient | Measured range | Predicted range by the model | Reported range in literature | Authors |
|---|---|---|---|---|---|
| Glass | SFC | 0.240–0.516 | 0.250–0.504 | 0.279–0.401 | Tabatabaeefar [13] |
| DFC | 0.204–0.542 | 0.200–0.562 | – | – | |
| Aluminum | SFC | 0.320–0.537 | 0.343–0.545 | 0.210–0.260 | Zhang et al. [5] |
| DFC | 0.256–0.432 | 0.271–0.435 | – | – | |
| Plywood | SFC | 0.413–0.651 | 0.411–0.647 | 0.458–0.498 | Zaalouk and Zabady [16] |
| DFC | 0.356–0.578 | 0.351–0.584 | – | – | |
| Galvanized steel | SFC | 0.468–0.677 | 0.494–0.703 | 0.232–0.713 | Kaliniewicz [17] |
| DFC | 0.410–0.632 | 0.405–0.638 | 0.163–0.203 | Molenda et al. [28] | |
| Rubber | SFC | 0.495–0.693 | 0.520–0.713 | 0.496–0.605 | Zaalouk and Zabady [16] |
| DFC | 0.441–0.809 | 0.472–0.801 | 0.510–0.875 | Sharobeem [29] |
Conclusions and recommendations
This work presents some pieces of useful information about SFC and DFC of wheat grain as influenced by several treatments. The following remarkable conclusions can be drawn from the results:
-
(1)
For each experimental condition, the SFC and DFC were unique and changed as moisture content, contact surface or sliding velocity varied.
-
(2)
The SE and DIE, and SE, DIE, and TIE of the treatments, respectively, on SFC and DFC were significant at probability level of 1%.
-
(3)
The DIE of treatments was more effective than SE of contact surface, followed by moisture content, on the SFC. Similarly, in case of DFC, TIE of treatments was stronger than DIE and SE of contact surface, followed by moisture content and sliding velocity.
-
(4)
For all tested contact surfaces, the SFC increased linearly as moisture content increased. The DFC raised linearly as moisture content and sliding velocity raised, too.
-
(5)
The SFC and DFC were successfully modeled by means of MLR modeling technique for each contact surface. Averages of statistical parameters used to evaluate the predictive ability of developed models were R2 = 0.941, RMSE = 0.02281 and MRDM = 3.151% for SFC, and R2 = 0.968, RMSE = 0.01295 and MRDM = 2.153% for DFC. The developed MLR models are powerful tools for direct determination of friction coefficients of wheat grain on studied contact surfaces, with no need for actual measurement of SFC and DFC, on the basis of experimental levels of moisture content and sliding velocity.
The above mentioned conclusions are valuable practical points to optimize storage equipment and processing conditions such as grain bins. The analysis method used in this paper, based on ANOVA and DMRT, is recommended to be applied in investigation of the effect of influential treatments on SFC and DFC of other important major crops.
Conflict of Interest
The authors have declared no conflict of interest.
Compliance with Ethics Requirements
This article does not contain any studies with human or animal subjects.
Footnotes
Peer review under responsibility of Cairo University.
References
- 1.Kashaninejad M., Ahmadi M., Daraei A., Chabra D. Handling and frictional characteristics of soybean as a function of moisture content and variety. Powder Technol. 2008;188(1):1–8. [Google Scholar]
- 2.Mohsenin N.N. Gordon and Breach Science Publisher; New York: 1986. Physical properties of plant and animal materials. [Google Scholar]
- 3.Brubaker J.E., Pos J. Determining static coefficients of friction of grains on structural surfaces. Trans ASAE. 1965;8(1):53–55. [Google Scholar]
- 4.Thompson S.A., Bucklin R.A., Batich C.D., Ross I.J. Variation in the apparent coefficient of friction of wheat on galvanized steel. Trans ASAE. 1988;31(5):1518–1524. [Google Scholar]
- 5.Zhang Q., Puri V.M., Manbeck H.B. Model for frictional behavior of wheat on structural materials. Trans ASAE. 1988;31(3):898–903. [Google Scholar]
- 6.Snyder L.H., Roller W.L., Hall G.E. Coefficients of kinetic friction of wheat on various metal surfaces. Trans ASAE. 1988;10(3):411–413. [Google Scholar]
- 7.Sharan G., Lee J.H.A. Coefficient of friction of wheat grain on grain and steel. Can Agr Eng. 1970;12(1):14–17. [Google Scholar]
- 8.Shemsanga K.H.H., Chuma Y., Uchida S. Internal and material-surface coefficients and repose angle of selected grains and soybeans. J Fac Agric Kyushu Univ. 1983;27(3–4):179–188. [Google Scholar]
- 9.Versavel P.A., Britten M.G. Interaction of bulk wheat with bin wall configuration in model bins. Trans ASAE. 1986;29(2):533–537. [Google Scholar]
- 10.Horabik J., Molenda M. Force and contact area of wheat grain in friction. J Agric Eng Res. 1988;41(1):33–42. [Google Scholar]
- 11.Zhang Q., Britton M.G., Kieper R.J. Interactions between wheat and a corrugated steel surface. Trans ASAE. 1994;37(3):951–956. [Google Scholar]
- 12.Molenda M., Horabik J., Ross I.J., Montross M.D. Friction of wheat: grain-on-grain and on corrugated steel. Trans ASAE. 2002;45(2):415–420. [Google Scholar]
- 13.Tabatabaeefar A. Moisture-dependent physical properties of wheat. Int Agrophys. 2003;17(4):207–211. [Google Scholar]
- 14.Kheiralipour K., Karimi M., Tabatabaeefar A., Naderi M., Khoubakht G. Moisture-depend physical properties of wheat (Triticum aestivum L.) J Agric Tech. 2008;4(1):53–64. [Google Scholar]
- 15.Karimi M., Kheiralipour K., Tabatabaeefar A., Khoubakht G.M., Naderi M. The effect of moisture content on physical properties of wheat. Pakistan J Nutr. 2009;8(1):90–95. [Google Scholar]
- 16.Zaalouk A.K., Zabady F.I. Effect of moisture content on angle of repose and friction coefficient of wheat grain. Misr J Ag Eng. 2009;26(1):418–427. [Google Scholar]
- 17.Kaliniewicz Z. Analysis of frictional properties of cereal seeds. Afr J Agric Res. 2013;8(45):5611–5621. [Google Scholar]
- 18.Moya M., Aguado P.J., Ayuga F. Mechanical properties of some granular agricultural materials used in silo design. Int Agrophys. 2013;27(2):181–193. [Google Scholar]
- 19.Markowski M., Zuk-Gołaszewska K., Kwiatkowski D. Influence of variety on selected physical and mechanical properties of wheat. Ind Crops Prod. 2013;47(1):113–117. [Google Scholar]
- 20.Warechowska M., Warechowski J., Markowska A. Interrelations between selected physical and technological properties of wheat grain. Tech Sci. 2013;16(4):281–290. [Google Scholar]
- 21.Mahjoub M., Movahhed S., Chenarbon H.A. Effective parameters on angle of repose, internal and external friction coefficient in two wheat varieties (Behrang and Shirudi) Int J Biosci. 2014;5(9):117–124. [Google Scholar]
- 22.Urbanska-Gizinska R., Konopka S. Comparison of external friction coefficients for single seeds in the stabilised system. Agr Eng. 2014;18(2):201–208. [Google Scholar]
- 23.Shafaei S.M., Heydari A.R., Masoumi A.A., Sadeghi M. Determining and modeling of static friction coefficient of some agricultural seeds. Jordan J Agr Sci. 2015;11(4):1007–1019. [Google Scholar]
- 24.Thompson S.A., Ross I.J. Compressibility and frictional coefficients of wheat. Trans ASAE. 1983;26(4):1171–1176. [Google Scholar]
- 25.Moore D.W., White G.M., Ross I.J. Friction of wheat on corrugated metal surfaces. Trans ASAE. 1974;27(6):1842–1847. [Google Scholar]
- 26.Irvine D.A., Jayas D.S., Britton M.G., White N.D.G. Dynamic friction characteristics of bulk seeds against flat vertical surfaces. Trans ASAE. 1992;35(2):665–669. [Google Scholar]
- 27.Bucklin R.A., Molenda M., Bridges T.C., Ross I.J. Slip-stick frictional behavior of wheat on galvanized steel. Trans ASAE. 1996;39(2):649–653. [Google Scholar]
- 28.Molenda M., Thompson S.A., Ross I.J. Friction of wheat on corrugated and smooth galvanized steel surfaces. J Agric Eng Res. 2000;77(2):209–219. [Google Scholar]
- 29.Sharobeem Y.F. Apparent dynamic friction coefficients for grain crops. Misr J Ag Eng. 2007;24(3):557–574. [Google Scholar]
- 30.Ibrahim M.M. Determination of dynamic coefficient of friction for some materials for feed pellet under different values of pressure and temperature. Misr J Ag Eng. 2008;25(4):1389–1409. [Google Scholar]
- 31.ASABE, ASABE standards. ASAE S352.2 FEB03, Moisture Measurement-Unground Grain and Seeds. ASABE, 2950 Niles Road, St. Joseph, MI 49085–9659, USA; 2006.
- 32.Balasubramanian D. Physical properties of raw cashew nut. J Agric Eng Res. 2001;78(3):291–297. [Google Scholar]
- 33.Nimkar P.M., Mandwe D.S., Dudhe R.M. Physical properties of moth gram. Biosyst Eng. 2005;91(2):183–189. [Google Scholar]
- 34.Abalone R., Cassinera A., Gaston A., Lara M.A. Some physical properties of amaranth seeds. Biosyst Eng. 2004;89(1):109–117. [Google Scholar]
- 35.Singh K.K., Goswami T.K. Physical properties of cumin seed. J Agric Eng Res. 1996;64(2):93–98. [Google Scholar]
- 36.Lorestani A.N., Rabani R.H., Khazaei Y. Design and construction of an automatic coefficient of friction measuring device. Agric Eng Int: CIGR J. 2012;14(1):120–124. [Google Scholar]
- 37.Clark R.L., McFarland H.A. Granular materials friction apparatus. Trans ASAE. 1973;16(6):1198–1199. [Google Scholar]
- 38.Locurto G.J., Bucklin R.A., Thompson S.A., Abdel-Hadi A.I., Walton O.R. Soybean coefficients of friction for aluminum, glass, and acrylic surfaces. Appl Eng Agric. 2014;30(2):285–289. [Google Scholar]
- 39.Konak M., Carman K.C., Aydin C. Physical properties of chick pea seeds. Biosyst Eng. 2002;82(1):73–78. [Google Scholar]
- 40.Kalkan F., Kara M. Handling, frictional and technological properties of wheat as affected by moisture content and cultivar. Powder Technol. 2011;213(1–3):116–122. [Google Scholar]