Abstract
Key points
The intracellular concentration of free calcium ions ([Ca2+]i) in a nerve terminal controls both transmitter release and synaptic plasticity.
The rapid triggering of transmitter release depends on the local micro‐ or nanodomain of highly elevated [Ca2+]i in the vicinity of open voltage‐gated Ca2+ channels, whereas short‐term synaptic plasticity is often controlled by global changes in residual [Ca2+]i, averaged over the whole nerve terminal volume.
Here we describe dynamic changes of such global [Ca2+]i in the calyx of Held – a giant mammalian glutamatergic nerve terminal, which is particularly suited for biophysical studies.
We provide quantitative data on Ca2+ inflow, Ca2+ buffering and Ca2+ clearance.
These data allow us to predict changes in [Ca2+]i in the nerve terminal in response to a wide range of stimulus protocols at high temporal resolution and provide a basis for the modelling of short‐term plasticity of glutamatergic synapses.
Abstract
Many aspects of short‐term synaptic plasticity (STP) are controlled by relatively slow changes in the presynaptic intracellular concentration of free calcium ions ([Ca2+]i) that occur in the time range of a few milliseconds to several seconds. In nerve terminals, [Ca2+]i equilibrates diffusionally during such slow changes, such that the globally measured, residual [Ca2+]i that persists after the collapse of local domains is often the appropriate parameter governing STP. Here, we study activity‐dependent dynamic changes in global [Ca2+]i at the rat calyx of Held nerve terminal in acute brainstem slices using patch‐clamp and microfluorimetry. We use low concentrations of a low‐affinity Ca2+ indicator dye (100 μm Fura‐6F) in order not to overwhelm endogenous Ca2+ buffers. We first study voltage‐clamped terminals, dialysed with pipette solutions containing minimal amounts of Ca2+ buffers, to determine Ca2+ binding properties of endogenous fixed buffers as well as the mechanisms of Ca2+ clearance. Subsequently, we use pipette solutions including 500 μm EGTA to determine the Ca2+ binding kinetics of this chelator. We provide a formalism and parameters that allow us to predict [Ca2+]i changes in calyx nerve terminals in response to a wide range of stimulus protocols. Unexpectedly, the Ca2+ affinity of EGTA under the conditions of our measurements was substantially lower (K D = 543 ± 51 nm) than measured in vitro, mainly as a consequence of a higher than previously assumed dissociation rate constant (2.38 ± 0.20 s−1), which we need to postulate in order to model the measured presynaptic [Ca2+]i transients.
Keywords: calcium buffer, calcium current, Calyx of Held, EGTA, modelling
Key points
The intracellular concentration of free calcium ions ([Ca2+]i) in a nerve terminal controls both transmitter release and synaptic plasticity.
The rapid triggering of transmitter release depends on the local micro‐ or nanodomain of highly elevated [Ca2+]i in the vicinity of open voltage‐gated Ca2+ channels, whereas short‐term synaptic plasticity is often controlled by global changes in residual [Ca2+]i, averaged over the whole nerve terminal volume.
Here we describe dynamic changes of such global [Ca2+]i in the calyx of Held – a giant mammalian glutamatergic nerve terminal, which is particularly suited for biophysical studies.
We provide quantitative data on Ca2+ inflow, Ca2+ buffering and Ca2+ clearance.
These data allow us to predict changes in [Ca2+]i in the nerve terminal in response to a wide range of stimulus protocols at high temporal resolution and provide a basis for the modelling of short‐term plasticity of glutamatergic synapses.
Abbreviations
- [Ca2+]rest
resting intracellular free [Ca2+]
- 4‐AP
4‐aminopyridine
- aCSF
artificial cerebrospinal fluid
- AP
action potential
- APW
action potential‐like waveform
- ICa
voltage activated Ca2+ current
- MNTB
medial nucleus of the trapezoid body
- Na/CaX
Na+/Ca2+ exchanger
- NCKX2
K+‐dependent Na+/Ca2+ exchanger 2
- P
postnatal day
- QCa
charge flow associated with a voltage activated Ca2+ current
- STP
short‐term synaptic plasticity
- Vh
holding potential
- Vm
membrane potential
Introduction
Although the local nano‐ or microdomain intracellular concentration of free calcium ions [Ca2+]i is generally accepted to be the relevant parameter for triggering neurotransmitter release (for review see Eggermann et al. 2012), measuring the spatially averaged, global [Ca2+]i in nerve terminals has often been instrumental for studying Ca2+‐dependent processes, in particular those underlying short‐term synaptic plasticity (Kamiya & Zucker, 1994; Zucker & Regehr, 2002; Müller et al. 2008; Neher & Sakaba, 2008). Measurements of [Ca2+]i, however, are faced with the problem that Ca2+‐sensing probes such as Ca2+ indicator dyes bind Ca2+ ions and thus necessarily are also Ca2+ buffers, which influence the amplitude and time course of [Ca2+]i transients (Neher, 1995; Müller et al. 2007; Matthews & Dietrich, 2015). Quite often the Ca2+ indicator dyes, when added at concentrations required for well‐resolved signals, overwhelm the endogenous Ca2+ buffering capacity and may cause substantial distortions of the intrinsic [Ca2+]i signals occurring in unperturbed cells.
While such signal distortions have sometimes limited the use of indicator dyes for [Ca2+]i measurement, Ca2+ chelators are often applied intentionally to the cytosol (Smetters et al. 1999; Stosiek et al. 2003) to block Ca2+‐mediated effects or to probe their Ca2+ sensitivity. In particular, the comparison of effects of the slow Ca2+ chelator EGTA with those of the fast buffer BAPTA proved to provide valuable insight regarding the spatial coupling between Ca2+ sources and effectors of Ca2+ action (Fedchyshyn & Wang, 2005; Vyleta & Jonas, 2014; Keller et al. 2015; Nakamura et al. 2015).
Last but not least, [Ca2+]i signals are used as optical readouts of activity in neuronal networks. The time resolution of such measurements is limited, however, due to the intrinsic [Ca2+]i dynamics, which are usually in the range 10–100 ms.
Given the multitude of presynaptic regulatory pathways that are controlled by [Ca2+]i, it is important to have reliable estimates at hand for the parameters which define the dynamics of global [Ca2+]i changes during presynaptic action potential (AP) firing. Such parameters are difficult to establish for small nerve terminals. Here we take advantage of the unique properties of a large mammalian glutamatergic nerve terminal – the calyx of Held – to provide a detailed quantitative analysis of Ca2+ buffering and Ca2+ removal mechanisms, as well as an empirical description of Ca2+ currents during AP trains. Our results also reveal differences between Ca2+ dissociation and association rates of EGTA determined in vitro versus those determined in an intracellular environment. Given the role of EGTA as the ‘yardstick’ for estimating the spatial Ca2+ channel–vesicle coupling we would like to draw attention to this result.
Previous estimates of the parameters governing [Ca2+]i dynamics often depended on additional assumptions about the properties of Ca2+ indicator dyes and Ca2+ chelators, which had been obtained under different conditions and with different indicator dyes (Augustine et al. 1991; Neher & Augustine, 1992; Helmchen et al. 1997; Müller et al. 2007; McMahon et al. 2016). In particular, assumptions about the dissociation constant of Ca2+ indicator dyes vary widely in the literature. We therefore made an attempt to provide a set of parameters, which are internally consistent, all based on the Ca2+ indicator dye Fura‐6F, which has been calibrated under exactly the same conditions as used in our experiments (Woehler et al. 2014). The low Ca2+ affinity of Fura‐6F provides for minimum perturbation of the intrinsic [Ca2+]i signals and allows us to faithfully measure [Ca2+]i transients over a wide range of peak amplitudes (up to 30 μm).
Methods
Ethical approval
All experiments complied with the German Protection of Animals Act and with the guidelines for the welfare of experimental animals issued by the European Communities Council Directive. Experiments were performed on brain tissue from Wistar rats housed in the animal facility of the Max Planck Institute for Biophysical Chemistry. Rat pups were lightly anaesthetized using isoflurane (IsoFlo, Ecuphar, Germany) and killed by rapid decapitation.
Slice preparation
Brainstem slices were prepared from Wistar rats of either sex at postnatal days (P) 8–10 (Fig. 1) or P13–15 (Figs 2, 3, 4, 5) as previously described (Lin et al. 2011). Briefly, rat pups were decapitated and the whole brain was quickly immersed into ice‐cold low Ca2+ artificial cerebrospinal fluid (aCSF) containing (in mm): 125 NaCl, 2.5 KCl, 3 MgCl2, 0.1 CaCl2, 10 glucose, 25 NaHCO3, 1.25 NaH2PO4, 0.4 ascorbic acid, 3 myo‐inositol and 2 sodium pyruvate, pH 7.3. The brainstem was glued onto the stage of a VT1000S vibratome (Leica, Nussloch, Germany) and coronal slices (180–200 μm thick) containing the medial nucleus of the trapezoid body (MNTB) were cut. Slices were incubated for ≥30 min at 35°C in an incubation chamber containing normal aCSF and kept at room temperature (22–24°C) and used for experiments for up to 4 h thereafter. The composition of normal aCSF was identical to that of low Ca2+ aCSF except that 1.0 mm MgCl2 and 2.0 mm CaCl2 were used. All solutions were oxygenated by continuous equilibration with carbogen gas (95% O2, 5% CO2).
Figure 1. Evaluation of the Ca2+ binding ratio κs of endogenous fixed Ca2+ buffers.
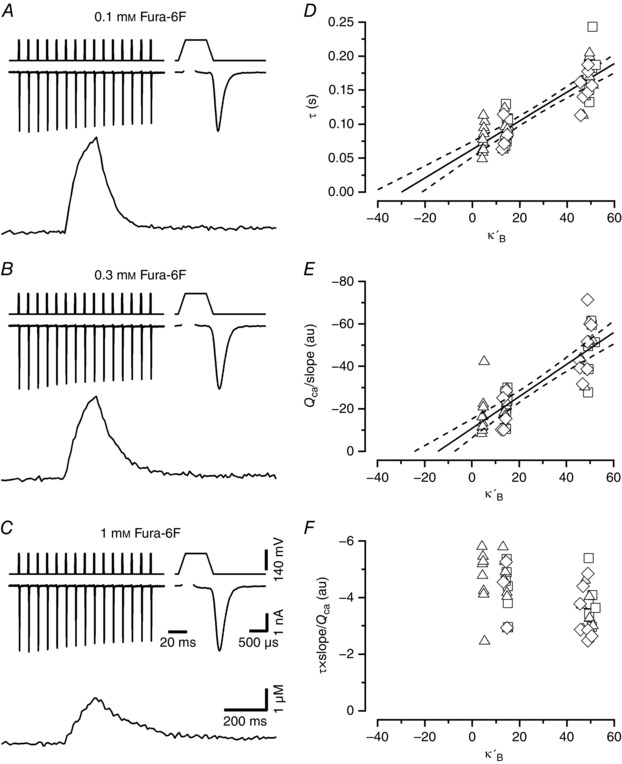
A–C, example traces of presynaptic I Ca (top) together with the corresponding [Ca2+]i transients (bottom) elicited by stimulus trains and recorded in calyx of Held terminals. The first I Ca waveform of the trains is shown at a faster time scale (top right) in the top row of each panel. Voltage‐clamp protocols are shown above I Ca. Stimulus trains consisted of 15 APW depolarizations delivered at a frequency of 100 Hz. APWs consisted of a variable length depolarization to +60 mV (0.2, 0.6 or 1 ms) embedded in two ramps of 0.2 ms duration (from −80 to +60 mV and from +60 to −80 mV). Terminals were loaded with either 0.1 mm (A), 0.3 mm (B) or 1 mm (C) Fura‐6F. For the sample traces shown, peak [Ca2+]i was 4.60 μm (A), 4.02 μm (B) and 2.28 μm (C). Calibration bars in C also apply to A and B. D, decay time constants of the [Ca2+]i transients plotted versus the Ca2+ binding ratios κ′B of Fura‐6F for I Ca evoked by 0.2 ms (squares), 0.6 ms (triangles) and 1 ms (diamonds) APWs. Pooled data obtained from 10 (0.1 mm Fura‐6F), 8 (0.3 mm Fura‐6F) and 7 (1 mm Fura‐6F) calyx terminals. The data are clustered along the x‐axis, with each cluster corresponding to one of the three Fura‐6F concentrations used (0.1 mm left, 0.3 mm middle, 1 mm right). The x‐values within clusters scatter slightly due to differences in peak amplitudes of the respective [Ca2+]i transients. A line fit to the data yields a κs estimate of 29.0 ± 4.9 μm. E, when plotting the ratio Q Ca over initial rate of rise of the [Ca2+]i transients in a similar way as shown in D, the estimated κs amounts to 13.3 ± 4.1 μm. Solid and broken lines in D and E represent regression lines and 95% confidence limits, respectively. Error estimates for κs values were derived from bootstrap analysis using a resampling n of 10,000. F, the ratio of the two quantities shown in D and E is plotted. This ratio should be independent of κ′B, since the influence of the latter is cancelled out. This holds for the comparison of values obtained with 0.1 and 0.3 mm Fura‐6F. However, the mean value for the data obtained with 1 mm Fura‐6F in the pipette (−3.10 ± 0.15×106) is slightly smaller than the mean of the pooled data using 0.1 or 0.3 mm Fura‐6F (−4.29 ± 0.19×106).
Figure 2. Time course of [Ca2+]i transients in the near absence of mobile Ca2+ buffers using either Cs+‐ or K+‐based pipette filling solutions.
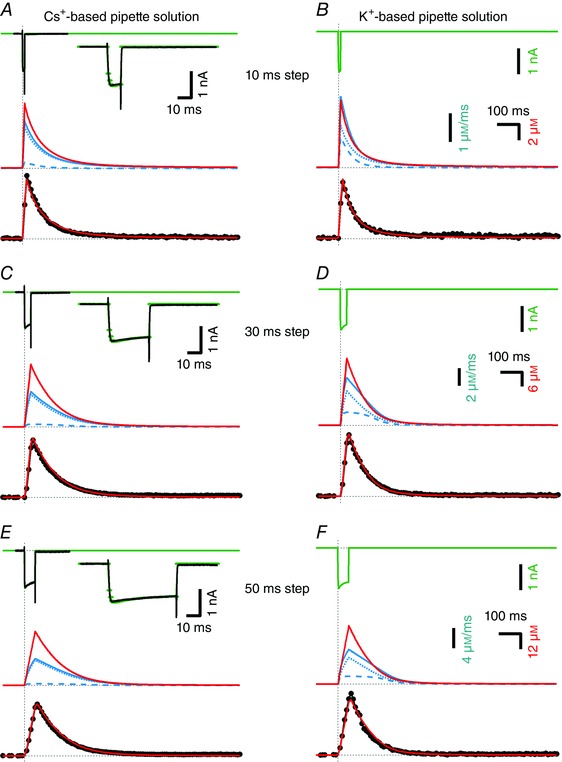
In each panel, measured [Ca2+]i transients (black, bottom) in response to depolarizing voltage‐clamp pulses are compared with the modelled [Ca2+]i (red, middle and bottom). Patch pipettes contained 50 μm EGTA and 100 μm Fura‐6F in all experiments illustrated. A, top, I Ca (black) evoked by a depolarizing voltage step (10 ms to 0 mV) was measured with Cs+‐based pipette solution and is shown superimposed onto the modelled I Ca (green). The inset shows measured and modelled I Ca at a faster time scale. Middle, modelled [Ca2+]i transient (red trace) and Ca2+ extrusion rate j ex (solid blue trace) and its components j ex,Hill (blue broken trace) and j ex,MM (blue dotted trace) are shown at high temporal resolution (Δt = 1 ms). Bottom, modelled (red) and measured (black) [Ca2+]i transients shown superimposed. The modelled [Ca2+]i transient was binned using 10 ms time intervals that were shifted for optimal alignment with the measured trace. C and E, data obtained from the same calyx terminal during similar experiments as shown in A except that the durations of the depolarizing voltage steps were 30 ms (C) and 50 ms (E). The measured peak [Ca2+]i was 8.06 μm (A), 24.4 μm (C) and 40.3 μm (E). B, D and F, similar experiments as illustrated in A, C and E but using K+‐based pipette solution. Since I Ca could not be recorded in isolation under these experimental conditions, only the modelled I Ca (green) is shown. The measured peak [Ca2+]i was 7.16 μm (B), 26.0 μm (D) and 47.7 μm (F). The least‐squares fits to the data shown in A, C and E used 80 data points of the sampled [Ca2+]i transient, starting at onset of the presynaptic depolarization and ending 0.8 s later. The fit to the data shown in B used 37 data points and the fits to the data shown in D and F used 60 data points.
Figure 3. Presynaptic Ca2+ clearance rate as a function of cytosolic [Ca2+]i .
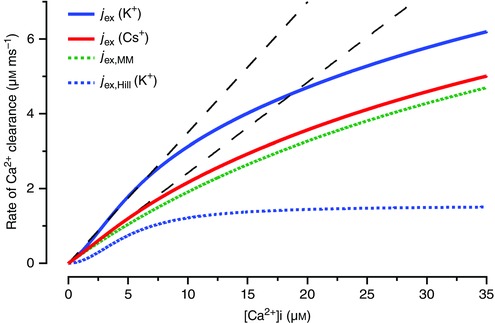
Ca2+ extrusion is modelled as a sum of two mechanisms: (i) a linearly rising, saturable component with Michaelis–Menten‐type characteristics (j ex,MM, green dotted trace) and (ii) a sigmoid mechanism with Hill‐type characteristics (j ex,Hill, blue dotted trace) (Lee et al., 2007b). The two individual components j ex,MM and j ex,Hill are shown here for K+‐based pipette solutions. The solid traces represent the sum of the two components for either K+‐based (blue solid trace) or Cs+‐based (red solid trace) pipette solution. In the former case, j ex,Hill is scaled up by a factor f K = 4.79 relative to its magnitude with Cs+‐based internal solution. Also shown are linear approximations to the total Ca2+ clearance rate under the two recording conditions (black dashed lines) for [Ca2+]i ranging from 0 to 5 μm. These line fits are constrained to pass through the origin. For model parameters describing j ex,MM and j ex,Hill see Table 1 and the Results.
Figure 4. Time course of [Ca2+]i transients in the presence of 500 μm EGTA in the cytosol.
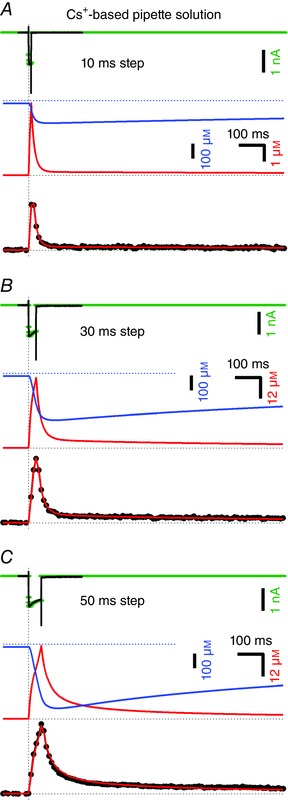
Similar experiment as illustrated in Fig. 2 A, C and E but with a 10‐fold higher EGTA concentration (500 μm), using Cs+‐based pipette solution containing 100 μm Fura‐6F. The durations of the step depolarizations were 10 ms (A), 30 ms (B) and 50 ms (C). All recordings were obtained from the same set of presynaptic terminals (n = 5). Measured I Ca (top) and [Ca2+]i transients (bottom) are shown in black. The simulated I Ca that was used to drive the model is shown in green. The predicted time course of the concentration of free EGTA is shown together with that of [Ca2+]i at high temporal resolution (Δt = 1 ms) in the middle row in blue and red, respectively. The bottom row shows modelled (red) and measured (black) [Ca2+]i transients superimposed. The modelled [Ca2+]i transient was binned using 10 ms time intervals that were shifted for optimal alignment with the measured trace. The measured peak [Ca2+]i was 2.75 μm (A), 6.03 μm (B) and 9.32 μm (C). Model fits used 80 data points of the sampled [Ca2+]i trace starting at the onset of the presynaptic depolarization and ending 0.8 s later.
Figure 5. Time course of [Ca2+]i transients in response to train stimulation in the presence of 500 μm EGTA in the cytosol.
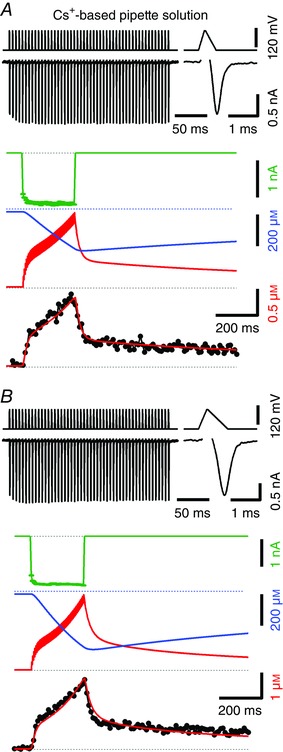
Similar experiment as illustrated in Fig. 4 using Cs+‐based pipette solution containing 100 μm Fura‐6F and 500 μm EGTA but stimulated with 200 Hz trains consisting of 50 AP‐like waveforms (APWs). The shape of the APWs was designed to approximate the time course of the recorded calyceal APs at P7 and P14 shown in Taschenberger & von Gersdorff (2000, their fig. 1A). A, narrow APWs that mimic mature calyceal APs were applied, which generate relatively small I Ca (−1.38 nA for the final I Ca). These APWs consisted of an initial ramp from −80 to +40 mV (200 μs), followed by a plateau at +40 mV (40 μs) and finally a ramp from +40 mV back to −80 mV (360 μs). Measured I Ca is shown in black (top left) together with the voltage‐clamp train protocol. The first I Ca of the train is shown at a faster time scale (top right). The simulated I Ca that was used to drive the model is shown in green (middle). The predicted time courses of the concentration of free EGTA and [Ca2+]i are shown at high temporal resolution (Δt = 1 ms) in blue and red, respectively (middle). [Ca2+]i peaked at ∼1.38 μm at the end of the train while free EGTA dropped to ∼50% of its initial value. The bottom row shows modelled (red) and measured (black) [Ca2+]i transients superimposed. The modelled [Ca2+]i transient was binned using 10 ms time intervals and shifted for optimal alignment with the measured trace. Eighty data points of the sampled [Ca2+]i transient from the start of the stimulus train up to 0.8 s later were included in the model fit. B, similar experiment as shown in A obtained from the same calyx terminals, except that wider APWs mimicking immature calyceal APs were applied which gave rise to a ∼27% larger I Ca (−1.75 nA for the final I Ca). These APWs consisted of an initial ramp from −80 to +40 mV (280 μs), followed by a plateau at +40 mV (40 μs) and finally a ramp from +40 mV back to −80 mV (680 μs). Using this stimulus protocol, [Ca2+]i peaked at ∼2.73 μm at the end of the train while free EGTA dropped to ∼28 % of its initial value. In total, 54 data points from the start of the stimulus train up to 0.54 s later were included in the calculation of least‐squares fits.
Electrophysiology
Patch‐clamp recordings were made from calyx of Held terminals of the MNTB using an EPC‐10 amplifier controlled by Pulse software (HEKA Elektronik, Lambrecht/Pfalz, Germany). Sampling intervals and filter settings were 20 μs and 4.5 kHz, respectively. Cells were visualized by differential interference contrast microscopy through a 60× water‐immersion objective (NA 1.0, Olympus, Hamburg, Germany) using an Axioskop FS microscope (Zeiss, Jena, Germany). All experiments were performed at room temperature.
Patch pipettes were pulled from borosilicate glass (Science Products GmbH, Hofheim, Germany) on a P‐97 micropipette puller (Sutter Instrument, Novato, CA, USA). Pipettes were coated with dental wax to minimize fast capacitive transients during voltage‐clamp experiments and to reduce stray capacitance. Open tip pipette resistance was 4–5 MΩ and access resistance (R s) values were ≤20 MΩ. R s was routinely compensated for by 50–60% during presynaptic voltage‐clamp experiments.
For measuring presynaptic I Ca, pipettes were filled with a solution containing (in mm): 100 caesium gluconate, 30 tetraethylammonium chloride, 30 CsCl, 10 Hepes, 0.5 EGTA, 5 Na2‐phosphocreatine, 4 ATP‐Mg, 0.3 GTP, pH 7.3 with CsOH. We reported previously a Ca2+ contamination of typically 10–15 μm and ∼50 μm for nominally Ca2+‐free K+‐based and caesium gluconate‐based pipette solutions, respectively (Woehler et al. 2014; their table 2). In this study, we supplemented pipette solutions with a minimum of 50 μm EGTA to compensate for any Ca2+ contamination. For numerical simulations (see below), the resting intracellular free [Ca2+] ([Ca2+]rest) was assumed to be 20 or 50 nm for intracellular solutions containing 500 or 50 μm EGTA, respectively. This is consistent with a total Ca2+ contamination in the tens of μm range.
Table 2.
General parameters that were not derived from least‐square fits
| Description | Symbol | Units | Value | Comment |
|---|---|---|---|---|
| General | ||||
| Intracellular free [Mg2+] | [Mg2+]i | m | 5×10−4 | |
| Resting intracellular free [Ca2+] | [Ca2+]rest | m | 5×10−8 | for low [EGTA]i |
| 2×10−8 | for high [EGTA]i | |||
| Calcium current (P13–15) | ||||
| Initial current | I Ca,0 | A | −1.07 ± 0.07×10−9 | mean |
| Duration of current flow | ∂ | s | 1×10−3 | depolarizing steps |
| 3.22×10−4 | mature APW | |||
| 4.83×10−4 | immature APW | |||
| Facilitation parameter y | ||||
| Time constant | τy | s | 0.023 | |
| Maximum value | y max | 1.56 | ||
| Increment | y incr | 0.47 | ||
| Inactivation parameter z | ||||
| Time constant | τz | s | 0.11 | |
| Minimum value | z min | 0.75 | for low [EGTA]i | |
| 0.67 | for high [EGTA]i | |||
| Decrement | z decr | 0.032 | ||
| Fast buffers | ||||
| Total concentration of fixed endogenous | m | 8.44×10−3 | calculated to yield κs = 21.1 at low [Ca2+]i | |
| Dissociation constant of fixed endogenous | K D | m | 4×10−4 | |
| Total concentration of Ca2+ indicator dye | m | 10−4 | ||
| Dissociation constant of Ca2+ indicator dye | K D | m | 1.78×10−5 | Fura‐6F (Woehler et al. 2014) |
The bath solution was supplemented with 1 μm TTX, 1 mm 4‐AP and 40 mm tetraethylammonium chloride to suppress voltage‐gated sodium and potassium currents. The holding potential (V h) was set to −80 mV for all presynaptic voltage‐clamp recordings. No liquid junction potential corrections (<10 mV) were applied.
Presynaptic Ca2+ imaging
Presynaptic [Ca2+]i was monitored using the ratiometric Ca2+ indicator dye Fura‐6F, which was excited at 350 and 380 nm by a monochromator (Polychrome 5, TILL Photonics, Gräfelfing, Germany). Fluorescence images were collected with an interline‐transfer 640×480 pixel 12‐bit monochrome cooled CCD camera (Imago, TILL Photonics) as previously described (Müller et al. 2007; Lin et al. 2012). To allow for brief exposure times, on‐chip pixel binning (8 × 15) was used. The monochromator and CCD camera were controlled by the TILLvisION software (TILL Photonics). Time series images were analysed off‐line.
To increase the time resolution and to minimize photobleaching, single‐wavelength imaging of the Ca2+‐sensitive fluorescence at 380 nm was applied at an acquisition rate of 100 Hz (Müller et al. 2007). Single wavelength images were preceded and followed by 20 images taken with dual excitation at wavelengths of 350 and 380 nm (10 images at each wavelength). These images were used to calculate F sum as a substitute for the fluorescence signal recorded at the isosbestic point. F sum is defined as
| (1) |
where α (= 0.229) is the isocoefficient of Fura‐6F for our setup. The isocoefficient α can be found by searching for a constant that makes the sum of the measured background‐corrected fluorescence F sum independent of [Ca2+]i (Zhou & Neher, 1993). F sum was calculated both from the initial 20 and final 20 images acquired at 350 and 380 nm. Linear interpolation was used to estimate the time course of F sum during single‐wavelength imaging. The background‐corrected fluorescence signals were converted into [Ca2+]i using the following equation (Lee et al. 2000):
| (2) |
where R’ is the ratio F sum/F 380.
The calibration constants R min and R max were obtained from in vitro measurements.
Using K D, R max , R min and α, it is then possible to calculate the effective dissociation constant K eff of the indicator dye according to (Zhou and Neher, 1993):
| (3) |
(note that this equation is given incorrectly in Woehler et al. 2014; their eqn 10).
The K D of Fura‐6F was determined by a titration method using exactly the same solutions as used here for recordings with K+‐based pipette solution (17.8 μm; Woehler et al. 2014). We prefer this latter K D estimate, because it does not rely on another calibration buffer (see Discussion). We therefore used a Fura‐6F K D of 17.8 μm for converting measured fluorescence ratios into [Ca2+]i and in all subsequent evaluations, including calculation of the Ca2+ binding ratio κB of Fura‐6F.
Analysis of electrophysiological and imaging data
All off‐line analysis was done with Igor Pro (WaveMetrics, Lake Oswego, OR, USA). Presynaptic recordings with a leak current > 100 pA were excluded from the analysis. Values are given either as mean ± SEM or else with error estimates, as discussed in the section on modelling.
Modelling of Ca2+ currents and changes in intracellular free Ca2+
Given the thickness of the calyx terminal and the median distance between active zones, which are both about 400 nm (Meinrenken et al. 2002), local [Ca2+]i gradients between active zones after episodes of [Ca2+]i influx dissipate in about 3 ms (using Einstein's equation for mean displacement and an apparent diffusion coefficient of 220 μm2 s–1, divided by κS). To model such global, diffusionally equilibrated [Ca2+]i transients, we follow standard procedures (Neher & Augustine, 1992; Helmchen et al. 1997), assuming that the presynaptic Ca2+‐specific current I Ca injects Ca2+ into a spatially equilibrated accessible volume v. This causes a Ca2+ influx j in of magnitude
| (4) |
where F is the Faraday constant and the flux is in units of mol l−1 s−1. Note that this definition is different from standard use of the symbol j, which often measures flux in mol m−2.
Ca2+ clearance mechanisms (pumps and exchangers, see below) cause a Ca2+ extrusion of magnitude j ex. The balance of total Ca2+ concentration [Ca2+]tot within a short interval Δt is thus:
| (5) |
We consider two fast Ca2+ buffers: (i) a fixed low‐affinity endogenous buffer, characterized by its Ca2+ binding ratio κS, and (ii) the Ca2+ indicator dye, an added buffer with Ca2+ binding ratio κB (Zhou & Neher, 1993). Both buffers are assumed to equilibrate with the free intracellular Ca2+ concentration [Ca2+]i within the time resolution of simulated traces (Δt = 1 ms), such that the change in free [Ca2+]i in the absence of ‘slow’ buffers is given by Neher & Augustine (1992):
| (6) |
κS and κB are calculated according to Zhou & Neher (1993) using two parameters each, namely their total concentrations and dissociation constants (see Table 2).
Furthermore, we consider the Ca2+ chelator EGTA as a slow buffer, which is added at various amounts to the pipette solution. EGTA is assumed to bind Ca2+ at one site in competition with very rapid binding of hydrogen ions. Therefore its kinetic parameters are ‘apparent’ ones, influenced by pH. A pH value of 7.2 is assumed throughout. The binding of EGTA to Ca2+ is characterized by three parameters: the total concentration of binding sites [EGTA]tot, the apparent rate constant k E,Ca+ for Ca2+ binding and the rate constant k E,Ca‐ for Ca2+ dissociation (see Table 1).
Table 1.
Parameters that were derived from or used in the joint least‐square fit
| Description | Symbol | Units | Value | Comment |
|---|---|---|---|---|
| Michaelis–Menten‐type Ca2+ clearance | see eqn (7) | |||
| Low [Ca2+]i slope | γ | s−1 | 230 ± 13 | |
| Half‐maximal [Ca2+]i | K D,MM | m | 4.9 ± 0.62×10−5 | |
| Hill‐type Ca2+ clearance | see eqn (8) | |||
| Maximum flux | j H,max | m s−1 | 3.22 ± 0.82×10−4 | |
| Ca2+ sensitivity | K D,H | m | 5.16 ± 1.3×10−6 | |
| Hill coefficient | n H | 2.0 | fixed (Lee et al. 2007b) | |
| K‐factor | f K | 1 | for Cs+‐based pipette solution (fixed) | |
| 4.79 ± 1.02 | for K+‐based pipette solution (variable) | |||
| Slow buffers | ||||
| Added [EGTA] | [EGTA]T | m | 5×10−5 and 5×10−4 | for 2 sets of experiments, pH 7.2 |
| Apparent Ca2+ binding rate constant | k E,Ca+ | m −1 s−1 | 4.38 ± 0.17×106 | |
| Ca2+ dissociation rate constant | k E,Ca‐ | s−1 | 2.38 ± 0.20 | |
| Dissociation constant | K D | m | 5.43 ± 0.51×10−7 | |
| General | ||||
| Accessible cell volume | v | litres | 3.9 ± 0.48×10−13 | mean ± SEM among synapses |
The same parameter set was used for all traces during the least‐squares fit and allowed to vary jointly. n H and [EGTA]T were constrained to the values given. I ca and v were determined independently by manual fits to I Ca traces.
Presynaptic Ca2+ extrusion j ex is represented in the model by two mechanistically distinct components: (i) a low‐affinity Michaelis–Menten type removal j ex,MM, representing Ca2+ ATPases and possibly contributions by mitochondrial Ca2+ uptake and (ii) a Hill‐type Ca2+ extrusion mechanism j ex,Hill. j ex,MM is characterized by an initial slope γ of its Ca2+ dependence and a half‐maximal concentration K D,MM, according to
| (7) |
At medium [Ca2+]i (>0.5 μm), j ex,Hill, which represents Na+/Ca2+ exchangers (Na/CaX) (Kim et al. 2005), starts to contribute appreciably to Ca2+ extrusion. j ex,Hill is represented in the model by a Hill‐type equation, according to
| (8) |
Here, j H,max is the maximum Ca2+ flux, generated by j ex,Hill, and K D,H together with the Hill coefficient n H (constrained to 2) determine the Ca2+ sensitivity of Na/CaX. A scaling factor f K is included to allow for a variable contribution of j ex,Hill to the Ca2+ clearance, depending on the composition of the ionic milieu inside the presynaptic terminal (see below).
Finally, a constant Ca2+ leak influx j in,leak is assumed to balance Ca2+ extrusion j ex,rest that is operating at resting Ca2+ level ([Ca2+]rest)
| (9) |
With these definitions, the fluxes can be calculated for a given [Ca2+]i and the conservation of total Ca2+ leads to the differential equation
| (10) |
with Σj B representing the sum of ‘fluxes’ due to the binding reactions of slow buffers. We include here the possibility to add further slow buffers for future extensions of the model. For the case of EGTA and the net flux j E associated with it, we use
| (11) |
Here [CaEGTA]i and [EGTA]i are intracellular concentrations of Ca2+‐bound EGTA and free EGTA, and k E,Ca+ and k E,Ca‐ are the Ca2+ binding and unbinding rate constants of EGTA, respectively.
In the absence of slow buffers and for the simplest case of a single linear Ca2+ clearance mechanism with a slope γ, the [Ca2+]i transient after a bout of Ca2+ influx decays exponentially with a time constant τ of (Helmchen et al. 1997):
| (12) |
For the general case, the differential eqn (10) was integrated using a 5th‐order Runge–Kutta–Fehlberg algorithm as provided by Igor Pro (‘IntegrateODE’ routine with step size control set to a maximum relative error of 10−5). Simultaneously, concentrations of Ca2+‐bound and Ca2+‐free slow buffers were integrated. For the case of EGTA the corresponding differential equations are:
| (13) |
| (14) |
Initial values for [EGTA]i and [CaEGTA]i were calculated on the basis of the law of mass action, assuming a [Ca2+]i,rest as specified for the various cases in the Results section.
Dynamic changes in I Ca were modelled at a temporal resolution of 1 ms with two dynamic variables y and z representing facilitation and inactivation, respectively. Although this approach does not allow us to capture the fine kinetic details of I Ca activation and deactivation, its temporal resolution is sufficiently high to describe amplitude changes in Ca2+ influx that occur during either sustained or repetitive depolarizations over a tens of millisecond time window, as required for our [Ca2+]i modelling. The corresponding parameters τy, τz, y max, z min, y inc and z dec are listed in Table 2. Initial values of y and z were set to 1 and I Ca, i corresponding to stimulus i was calculated as the product of the initial current I Ca,0 with the respective time‐dependent values yi and zi:
| (15) |
The latter were integrated simultaneously with the other dynamic variables (see eqns 10, 13, 14) according to
| (16) |
| (17) |
Values for y and z were incremented and decremented, respectively, at the times of AP‐like waveforms with
| (18) |
| (19) |
where ∂ denotes the duration of Ca2+ influx.
Integration according to eqns (10)–(19) was performed piecewise between episodes of presynaptic Ca2+ influx. For AP‐like stimuli, ∂ is the effective duration of an AP, as given in Table 2. ∂ was calculated as the ratio of Ca2+ current integral over I Ca,0.
For longer step depolarizations, parameters y and z were incremented every 1 ms, using the same eqns (18) and (19) with ∂ = 1 ms.
The joint integration of eqns (10)–(19) yielded the time courses of I Ca and of all concentrations involved at a time resolution of 1 ms. Subsequently, we binned the modelled [Ca2+]i time course according to the temporal resolution of the Ca2+ imaging frames (10 or 20 ms), in order to obtain modelled [Ca2+]i transients with the same time resolution as the experimental ones for better comparison. This binning included a small time shift for perfect registry of the two signals.
Procedures for parameter fitting
The overall strategy for determining the parameters of Table 1 is described in the first paragraph of the Results section. More specifically, we started with traces for which I Ca data were available. By comparing experimental and modelled I Ca we first determined the parameters I Ca,0 and those related to variables y and z by trial and error. We arrived at a set of parameters (Table 2), which described all I Ca traces for experiments with Cs+‐based pipette solution (Figs 2 A, C, E, 4 and 5). Parameters describing I Ca were kept constant for the subsequent steps of analysis.
Next we compared experimental [Ca2+]i transients with the binned modelled [Ca2+]i time courses and varied the parameter v, as well as the jointly variable parameters of Table 1 for a visually satisfying fit. Finally, we used a least‐squares fitting routine to refine the fit and to enforce the same values of jointly varying parameters for all traces. A custom‐written stochastic optimization strategy that involved elements of simulated annealing and a genetic algorithm was used to determine a set of those parameters (Table 1), which are expected to be the same for all traces, such as binding and unbinding rate constants of Ca2+ buffers. The optimization algorithm minimized the mean‐square deviation of all modelled [Ca2+]i transients shown in Figs 2, 4 and 5 after normalization with respect to their means. The sections of the modelled and measured [Ca2+]i, considered for the minimization, were typically 0.8 s long starting at the onset of stimulation. In some measured [Ca2+]i transients, in particular when using K+‐based pipette solutions, we noticed small delayed rises in [Ca2+]i, which might be due to reversal of Ca2+ uptake into intracellular stores (Werth & Thayer, 1994). In these cases we reduced the time window for the simulation, as indicated in the respective figure legends. All fits shown used the ‘master set’ of parameters (Tables 1 and 2).
When performing least‐squares fits we noticed that we often encountered closely spaced local minima, which had almost identical least‐squares deviations, but somewhat different subdivision of the Ca2+ clearance between j ex,MM and j ex,Hill. Parameters for Ca2+ buffering by EGTA, on the other hand, were quite robust. To estimate confidence intervals, we determined the Hessian matrix by varying each of the parameters by ± 10% (Monahan, 2001). We used the diagonal elements cii of its inverse and the mean square deviation ε of the fit to calculate a standard error for parameter i as
| (20) |
where N is the number of data points used for the fit. The factor 3 accommodates the finding that data points are not independent, but typically correlated over a mean correlation length of ∼3 (as determined by the half‐point of decay of the auto‐covariance function of residuals). The resulting standard errors are typically larger than variations in parameters between local minima. They are in the range 4–9% for EGTA‐related parameters and for γ, the low [Ca2+]i slope of j ex,MM. For the other fitting parameters they are in the range 15–25%, however (see Table 1).
Results
The aim of this study was to determine a set of internally consistent parameters, which would allow one to model changes in Ca2+ influx and volume‐averaged, global [Ca2+]i at the calyx of Held nerve terminal in response to various stimulation patterns. The time resolution of our experimental measurements was determined by the maximum frame rate (100 s−1) of our imaging device. Ca2+ equilibrates diffusionally across the width of the calyx which is variable but mostly < 1 μm (Sätzler et al. 2002; Dondzillo et al. 2010) and between active zones within 3 ms (see Methods), such that our images report volume‐averaged [Ca2+]i.
As described in the Methods and summarized in Tables 1 and 2, our formalism to model [Ca2+]i transients involves at least 21 parameters [3 general parameters, 7 for describing I Ca, 6 for describing Ca2+ clearance mechanisms and 5 for describing Ca2+ buffers (EGTA and endogenous fixed buffers)]. Some of these parameters were determined by independent measurements (e.g. κs) or were assumed to be known (resting [Ca2+]i and n H), while 16 remaining parameters had to be determined by simulation and curve fitting. Our strategy to handle as many parameters was as follows: we started by determining the Ca2+ binding ratio of fixed endogenous buffers (see next section). These measurements were done after wash‐out of endogenous mobile buffers in the presence of various amounts of Ca2+ indicator dye as the only mobile buffer. They yielded estimates for the Ca2+ binding ratio of fixed endogenous buffers, κS, and for the decay time constant of [Ca2+]i in the absence of any mobile buffer. The two values together allowed us to calculate γ, the initial slope of the relationship between the Ca2+ extrusion rate constant and [Ca2+]i (see eqn 12). In a further analysis, we kept κS fixed and used γ, thus determined, as the starting value for the least‐squares fitting procedure.
Next, we studied [Ca2+]i transients in calyx terminals that were dialysed with a Cs+‐based pipette solution containing 100 μm Fura‐6F and a low concentration of EGTA of 50 μm. This allowed us to measure I Ca and [Ca2+]i simultaneously and to determine parameters related to I Ca and to the Ca2+ extrusion mechanisms by trial and error fitting. At this step, we used a first guess of parameters related to EGTA. Next, we performed similar experiments with the only difference that the concentration of EGTA was increased 10‐fold to 500 μm. This provided refined estimates for EGTA‐related parameters. A few cycles of fits between this data set and the previous one converged onto a set of EGTA parameters, which we consider to be reliable at this stage of analysis. Next, we analysed an additional set of [Ca2+]i measurements that was obtained under whole‐cell conditions with a pipette solution including K+ as the main cation. We added this experimental condition because of the known major contribution of a K+‐sensitive Na/CaX to the Ca2+ extrusion at the calyx of Held (Lee et al. 2007b). To model [Ca2+]i transients that were measured with K+‐based pipette solutions, we kept all parameters determined so far fixed, except for the scaling factor f K which determines the relative contribution of the K+‐sensitive Na/CaX to the total Ca2+ clearance. We found, indeed, that the contribution of Na/CaX increased strongly when using K+‐based pipette solutions.
Up to this point, all fitting was done manually by minimizing deviations between measured and modelled I Ca and/or [Ca2+]i as judged by visual inspection. Next, however, we subjected the whole set of modelled [Ca2+]i transients to a non‐linear, iterative optimization procedure with a jointly variable parameter set (Table 1; see Methods for details). We used the resulting ‘master set’ of parameters from here on. The model parameters are summarized in Tables 1 and 2.
Evaluation of the Ca2+ binding ratio of fixed endogenous buffers, κs
Estimates for the binding ratio κs of P8–10 calyces of Held range between 27 and 71 with an average of ∼40 (Helmchen et al. 1997). Babai et al. (2014) recently reported a somewhat higher value of 46. All these values were derived from [Ca2+]i transients recorded in response to short depolarizations while terminals were loaded with the high‐affinity Ca2+ indicator dye Fura‐2. However, using low‐affinity indicators such as MagFura‐2 and Calcium Orange‐5N, Helmchen et al. (1997) found a κs of ∼20. Estimates for κ obtained during dye loading may contain a contribution of mobile endogenous buffers, which slowly wash out while the indicator dye diffuses into the cell (Matthews & Dietrich, 2015). We therefore re‐evaluated κs by loading calyx terminals with Cs+‐based pipette solutions containing various concentrations of the low‐affinity indicator Fura‐6F (100, 300 and 1000 μm) and evaluating [Ca2+]i transients in response to depolarizations, after dye loading had completed and the concentration of the indicator dye had reached steady state (≥3 min after establishing whole cell configuration). At that time endogenous Ca2+ binding proteins, such as parvalbumin, should be substantially reduced in concentration, although not completely washed out.
We applied 100 Hz trains consisting of 15 action potential‐like waveforms (APWs) of variable durations to elicit short transients of I Ca in the range −2 to −4 nA (Fig. 1 A–C). This caused [Ca2+]i transients with amplitudes of 1.5–3 μm when measured with 1 mm Fura‐6F and between 3 and 5 μm for lower concentrations of the indicator dye. We evaluated the current integrals Q Ca and the [Ca2+]i transients caused by such Ca2+ influx. [Ca2+]i transients rose exponentially during trains and decayed exponentially afterwards (Fig 1 A–C; bottom traces). In Fig. 1 D, the decay time constants τ of the [Ca2+]i transients are plotted as a function of κB, the Ca2+ binding ratio of the indicator dye. The latter was calculated according to eqn (10) of Zhou & Neher (1993). The y‐offset value (63 ± 6 ms) of a regression line to such a scatter plot is an estimate for the time constant of [Ca2+]i decay that would be obtained in the complete absence of indicator dye and any other mobile Ca2+ buffers. The negative x‐axis intercept is an estimate for 1+κs (Neher & Augustine, 1992, their fig. 9). Likewise, another estimate of 1+κs can be obtained from the initial rate of rise s of the [Ca2+]i transients, which is proportional to Q Ca/(1+κs+κB) (Neher & Augustine, 1992; Helmchen et al. 1997). Thus, we also plotted Q Ca/s against κB (Fig. 1 E). Regression lines to both types of plots yielded κs values of 29.0 and 13.3. We used the mean of these two values (21.1) for the simulations described below. This value is lower than those determined previously. However, it is well in line with a consistency argument, put forward by Neher & Taschenberger (2013) and it may be more accurate, as it is based on a low‐affinity Ca2+ indicator, avoiding possible influences of saturation, as well as problems due to incomplete washout of mobile buffers. Yet, the two estimates for κs yield quite different numbers. To explore possible sources for the discrepancy, we plotted the ratio of the two quantities shown in Fig. 1 D and E (Fig. 1 F). In this plot, the influence of buffers should be cancelled out, such that no dependence on κB is expected. However, the values for high κB, corresponding to the experiments with the highest Fura‐6F concentration and lowest [Ca2+]i amplitudes, are significantly lower than the values obtained with lower Fura‐6F concentrations. Possible reasons for these variations are discussed below.
[Ca2+]i dynamics in the near absence of mobile Ca2+ buffers
In the near absence of mobile Ca2+ buffers, assuming that fixed buffers have a low Ca2+ affinity, small changes in [Ca2+]i should be well described by eqn (12), which in the low‐concentration limit relates the decay time constant τ of a [Ca2+]i transient to the Ca2+ binding ratio κs of endogenous fixed buffers and the quantity γ. Given the values for κs and τ as determined in the last section one can calculate γ and thereby arrive at a complete kinetic description of this simplified scenario. It has been shown, however, that Ca2+ clearance mechanisms are quite complex, involving Ca2+ pumps, Na/CaXs and uptake into organelles (Lee et al. 2007b). Such contributions have non‐linear characteristics and set in at [Ca2+]i above 0.5–1 μm. To explore the [Ca2+]i dynamics in the range ≥1 μm, we performed a series of experiments using depolarizing voltage‐clamp steps to a membrane potential yielding large I Ca (V m = 0 mV). These experiments were performed in calyx terminals, which were dialysed with either Cs+‐based or K+‐based pipette solutions. Under the former conditions, we recorded the isolated I Ca together with the volume‐averaged [Ca2+]i transient. In each case, we included low concentrations of EGTA (50 μm) and Ca2+ indicator (100 μm Fura‐6F) in the pipette solution (see Methods for exact composition) and applied depolarizing voltage pulses of 10, 30 and 50 ms duration. At such low concentrations of Ca2+ buffer, the resting [Ca2+]i level is determined by Ca2+ clearance mechanisms and by Ca2+ contamination in the nominal Ca2+‐free pipette solution (∼50 μm; Woehler et al. 2014). Since the low‐affinity indicator dye does not allow accurate measurements of [Ca2+]i in the expected range of values, we assumed a basal [Ca2+]i of 50 nm in this type of experiment and adjusted the baselines for both modelled and measured [Ca2+]i traces accordingly.
Figure 2 shows examples of [Ca2+]i transients (bottom traces) and I Ca (top traces) evoked by step depolarizations of three different durations and recorded with Cs+‐based (Fig. 2 A, C, E) or with K+‐based (Fig. 2 B, D, F) pipette solution. In all cases, the 10 ms binned modelled [Ca2+]i transients obtained with the ‘master set’ of fitting parameters are superimposed. [Ca2+]i model traces (red) and Ca2+ clearance rates (blue) are shown in the middle of panels at full time resolution. Close inspection of the [Ca2+]i transients recorded with K+‐based pipette solutions shows that these decay faster compared to those recorded using Cs+‐based pipette solutions under otherwise identical conditions (compare left vs. right panels in Fig. 2). Exponential fits to the decays of [Ca2+]i transients elicited by 10 ms steps yield time constants of 79.1 ± 1 and 61 ± 2 ms for experiments using Cs+‐based and K+‐based pipette solutions, respectively. Corresponding time constants for 30 ms steps are 102 ± 0.5 and 78.7 ± 0.8 ms, and for 50 ms steps they are 104.9 ± 0.5 and 72.7 ± 1 ms. This result is in line with previous work establishing the K+ dependence of the Ca2+ clearance via Na/CaXs (Lee et al. 2002; Kim et al. 2005). We modelled this situation by assuming a Ca2+ clearance mechanism with two components. The first component was a saturating Michaelis–Menten type mechanism (j ex,MM), representing Ca‐ATPases and possibly some Ca2+ uptake into mitochondria (eqn 7). It was initialized in the fitting procedure to an initial slope of γ at low [Ca2+]i as determined above and an arbitrarily selected maximum contribution. Estimates for these parameters were initially improved by trial‐and‐error fits. The second component was a Hill‐type non‐linear mechanism (j ex,Hill) with a Hill coefficient n H constrained to 2 (Lee et al. 2007b) and with two free parameters determining maximum rate (j max,H) and Ca2+ affinity (K D,H) (eqn 8). To model experimental data obtained with K+‐based pipette solutions, we scaled the latter component with a multiplier f K which was a free fitting parameter. It was, however, constrained to the same value for all [Ca2+]i transients obtained with K+‐based pipette solution. A subsequent least‐squares fitting procedure (see Methods) converged to the parameters listed in Table 1. In particular, it yielded a value of 4.79 ± 1.02 for f K, indicating that j ex,Hill is nearly five‐fold higher when using K+‐based instead of Cs+‐based pipette solution. This is in excellent agreement with Lee et al. (2007a), who found that reverse mode NCKX2 currents were 5 times higher in K+‐based solutions as compared to Cs+‐based ones.
In Fig. 3 the rates for the total Ca2+ extrusion j ex are plotted as functions of [Ca2+]i for both pipette solutions (continuous lines). In addition, the individual components j ex,MM (green dotted line; identical for Cs+‐ and K+‐based pipette solution) and j ex,Hill (blue dotted line; for K+‐based pipette solution) are shown. With Cs+‐based pipette solution, total clearance rates are just marginally higher than those of j ex,MM alone. However, for experiments using K+‐based pipette solutions clearance rises much faster between 1 and 5 μm due to the higher contribution of j ex,Hill. Figure 3 also shows linear approximations for j ex in the low [Ca2+]i range (1 and 5 μm). Line fits are constrained to pass through the origin. For the Cs+‐based pipette solution, the initial slope is 242 s−1, only slightly larger than the parameter γ (= 230 ± 13 s−1), as determined by the least‐squares fit. Deviations between that line and the total Ca2+ clearance (red) are minor for [Ca2+]i ≤10 μm because the sigmoidally increasing j ex,Hill compensates for the beginning saturation of j ex,MM. Thus, for experiments using Cs+‐based pipette solution, a linear clearance mechanism with a slope γ = 242 s−1 is a very good approximation of the total Ca2+ extrusion for [Ca2+]i ≤10 μm, which largely covers the physiologically relevant range of [Ca2+]i.
With K+‐based pipette solutions, the larger contribution of j ex,Hill leads to a steeper slope (349 s−1) for the line fit, although not changing the very initial slope of the model curve. Thus, the Ca2+ extrusion in response to [Ca2+]i elevations with small amplitudes, as generated by single APs (typically 0.3–0.5 μm), has similar kinetics when using either Cs+‐ or K+‐based pipette solution. The Ca2+ extrusion following higher [Ca2+]i elevations as typically observed during high frequency AP trains (in the range 1–5 μm), however, is well approximated by a linear clearance with a rate constant of 349 s−1 (the slope of the line fit) when using K+‐based pipette solution.
The linear approximation discussed here, together with the value of κs as determined above, allows one to predict decay time constants of [Ca2+]i transients after mild stimulation and in the absence of mobile buffers according to eqn (12). For small AP‐evoked signals we predict τ = 22.1/242 s−1 = 91 ms for both Cs+‐ and K+‐based pipette solution, while for [Ca2+]i transients elicited by high frequency trains we expect a value similar to that with Cs+‐based pipette solution, but a faster one (τ = 22.1/349 s−1 = 63 ms) for experiments using K+ as the main internal cation.
Presynaptic voltage‐gated Ca2+ currents
Presynaptic voltage‐activated Ca2+ currents at the calyx of Held have been described to display both facilitation and inactivation depending on the developmental stage and stimulation pattern (Cuttle et al. 1998; Forsythe et al. 1998; Borst & Sakmann, 1998b; Lin et al. 2011). When recording I Ca evoked by 10–30 ms depolarizing voltage pulses with Cs+‐based pipette solutions at P13–15, we observed initial current facilitation (20–25% for AP‐like stimuli at 200 Hz) followed by I Ca inactivation. These changes, although small, markedly influenced the time course of the rising phase of [Ca2+]i, as evident when comparing simulations assuming constant I Ca with those simulating the measured I Ca. During our simulations we fitted I Ca time courses by visual inspection (green traces in Figs 2 A, C, E, 5 and 6), and modelled amplitude changes with two kinetic variables governing facilitation and inactivation (see Methods). The same set of I Ca‐related parameters was used for all model traces (see eqns 15, 16, 17, 18, 19 and Table 2), both for trains of AP‐like stimuli and for step depolarizations, with the exception that two different values were required for low‐ and high‐EGTA traces regarding z min, the lower bound of the inactivation variable (0.75 and 0.67, respectively).
Modelling [Ca2+]i transients yields an estimate of the accessible volume of the presynaptic terminal v (see eqns 4, 5, 6). Using Cs+‐based pipette solutions, we measured the isolated I Ca together with the [Ca2+]i transients elicited by step depolarizations of three different durations (10, 30 and 50 ms). Estimates of v obtained from these experiments yielded 0.30 ± 0.01 and 0.46 ± 0.02 pl for the low‐EGTA and high‐EGTA experiments, respectively. The SEM values given here represent the variation between estimates from the three [Ca2+]i transients, each of which is an average obtained from five terminals. The difference between the v estimates obtained with either low‐EGTA or high‐EGTA pipette solution partially reflects differences in the size of the respective terminals (mean whole‐cell capacitances were 21 and 23 pF) but may also include other influences.
When analysing these data, we first used an endogenous fixed buffer of 2.11 mm total concentration and a dissociation constant of 100 μm (κs = 21.1 at low [Ca2+]i). We noted, however, that v estimates varied systematically when using step depolarizations of different durations, which elicited [Ca2+]i transients of very different amplitudes. For 50 ms long depolarizations ([Ca2+]i peak amplitude = 40 μm), the estimated v was 34% higher than that for 10 ms long depolarizations ([Ca2+]i peak amplitude = 8.06 μm). Such differences are unexpected, since the [Ca2+]i transients were recorded in the same terminals. We therefore hypothesized that the differences might be due to inappropriate assumptions about the affinity of endogenous fixed buffers and reanalysed these [Ca2+]i transients. We found that assuming a much lower Ca2+ affinity of the endogenous buffers (K D = 400 μm) results in similar v estimates for the [Ca2+]i transients obtained with the three different pulse durations. Therefore, we used this K D value together with a total concentration of 8.44 mm (resulting in κs = 21.1 at low [Ca2+]i) for further analysis.
In our presynaptic I Ca recordings we consistently observed small (≤50 pA), but in some cases long‐lasting, inward currents following depolarizations. These slow tail currents tended to increase with the length of the depolarizations (typically −10 and −20 pA for 10 and 30 ms pulses). Although small, relative to the I Ca peak amplitude measured during depolarizations (−1.0 to −1.5 nA), these currents would delay the decay of [Ca2+]i transients after stimulation, if they actually reflected prolonged Ca2+ influx. Yet, an analysis of [Ca2+]i changes in the presence of EGTA argues against their Ca2+ specificity (see below), which led us to disregard the slow tail currents in our simulations.
Presynaptic [Ca2+]i dynamics in the presence of EGTA
The Ca2+ chelator EGTA is often used to manipulate the [Ca2+]i dynamics in nerve terminals. In particular, its slower Ca2+ binding kinetics, as compared to the fast Ca2+ buffer BAPTA, are instrumental in probing the spatial relationships between Ca2+ sources and Ca2+ sensors (for a review see Eggermann et al. 2012). For such inferences, an accurate knowledge of the rate constants for Ca2+ binding and unbinding is essential. However, the literature for such quantitative data is ambiguous, with numbers for the rate constant of Ca2+ binding ranging between 2.7×106 m −1 s−1 (Naraghi & Neher, 1997; for pH = 7.2) and 1.05×107 m −1 s−1 (Nägerl et al. 2000; for pH = 7.3). Therefore, attempted to narrow down the plausible range for these important parameters. To this end, we performed experiments similar to those shown in Fig. 2 A, C and E, except that we increased the concentration of EGTA by a factor of 10, including 500 μm EGTA in the pipette. Figure 4 A–C shows the measured and modelled [Ca2+]i transients. Basal [Ca2+]i is expected to be very low under these conditions (nominally Ca2+‐free pipette solution containing 500 μm EGTA) and cannot be measured accurately with Fura‐6F. We therefore assumed a basal [Ca2+]i of 20 nm and adjusted the baselines accordingly.
There are two obvious differences when comparing [Ca2+]i transients obtained with either 50 or 500 μm EGTA in the pipette solution (Fig. 2 A, C, E): (i) the maximum [Ca2+]i is greatly reduced and (ii) its decay is accelerated at higher [EGTA]i, as expected for the chelating action of EGTA. In addition, there is another, albeit relatively subtle difference: a pedestal of elevated [Ca2+]i which slowly decays over several seconds. This is also expected on the basis of the Ca2+ binding characteristics of a slow chelator, because Ca2+ ions bound to the latter during a transient [Ca2+]i elevation dissociate slowly thereafter, contributing a source of Ca2+ ions, which slowly diminishes, while free Ca2+ is removed from the cytosol. Amplitude and decay kinetics of this pedestal depend critically on the dissociation rate constant of EGTA and therefore provide constraints to that parameter.
We also examined [Ca2+]i transients elicited by 200 Hz trains consisting of APWs. Figure 5 A and B shows average [Ca2+]i transients recorded from the same calyx terminal using two different stimulation strengths. In Fig. 5 A, the APW was designed to simulate the brief presynaptic APs observed in P13–15 calyces (Taschenberger & von Gersdorff, 2000). This resulted in relatively small I Ca with a Q Ca of ∼0.38 pC for the initial APW. The [Ca2+]i transient rose rapidly during the first 5–10 APWs to a level of about 0.6 μm at which the influx of Ca2+ was close to being balanced by Ca2+ extrusion and, more importantly, by Ca2+ binding to EGTA. Subsequently, [Ca2+]i kept rising slowly, while free EGTA decreased. At the end of the stimulus train, free [EGTA]i was reduced to 50% of its initial value (blue dotted trace in Fig. 5 A).
In Fig. 5 B, APWs were designed to simulate the wider APs observed at younger calyces (P8–10). This resulted in larger I Ca corresponding to a QCa of 0.74 pC, in agreement with Borst & Sakmann (1998a). Correspondingly, the rise in [Ca2+]i at the beginning of stimulation was faster, reaching an intermediary plateau level. For these large currents, however, [Ca2+]i kept rising at an accelerating pace. Our simulations indicate that the reason for this late rise is increased depletion of free EGTA, or else ‘escape’ from Ca2+ buffering (blue trace in Fig. 5 B, where minimum [EGTA]i is 28% of the initial value). Following stimulation, [Ca2+]i drops rapidly to the level of the pedestal as observed after step‐depolarization at which Ca2+ clearance is balanced by dissociation of Ca2+ from Ca2+‐bound EGTA.
After strong stimulation, the presynaptic I Ca was sometimes trailed by a small and slow inward tail current reminiscent of the Ca2+‐activated current observed after Ca2+ uncaging via flash photolysis (Wölfel & Schneggenburger, 2003; their fig. 2). We were concerned that this slow tail current might influence the decay of [Ca2+]i, if it reflected small but prolonged influx of Ca2+ ions (see above). However, time courses and amplitudes of the tail currents argue against such contributions. For instance, in the trace for the 10 ms depolarizing pulse displayed in Fig. 4 A, the slow tail current following I Ca with a peak amplitude of −1.38 nA decays from an initial value of ∼12 pA to nearly 0 pA within the first 100 ms after the depolarization. The pedestal [Ca2+]i, however, is maintained over at least 500 ms. The extended small plateau of [Ca2+]i is thus unlikely to be caused by the slow tail current. In the case of the 30 ms pulse the tail current is larger (∼26 pA) and does not decay much during the recording period. We simulated the injection of a Ca2+‐specific current of such magnitude into the terminal and found that this changes the plateau of [Ca2+]i by 30%. This calculation shows that a tail current of such magnitude might contribute to the plateau, if it were Ca2+‐specific. However, we doubt that this is the case, since the plateau for the10 ms trace (during which the tail current vanishes) can be fitted with the same set of parameters as used for fitting the 30 ms trace, in which the tail current persists. We therefore neglected the small tail currents in our simulations and assumed that they were not carried by Ca2+ ions (see also Wölfel & Schneggenburger, 2003).
Discussion
We describe Ca2+ current and [Ca2+]i transient measurements at voltage‐clamped calyx of Held terminals, recorded under three different ionic conditions of intracellular dialysis. We first determine the Ca2+ buffer ratio κs of the endogenous fixed. We go on to use Cs+‐based as well as K+‐based pipette solutions supplemented with a minimal amount of EGTA and 100 μm Fura‐6F. Applying variable length depolarizations to elicit Ca2+ influx, we determine the kinetic parameters and Ca2+ dependence of Ca2+ clearance mechanisms under both ionic conditions, confirming previous results that Ca2+ clearance is faster in the presence of intracellular K+ compared to recordings with Cs+ as the main intracellular cation. Finally, we perform similar experiments with elevated EGTA concentrations (0.5 mm), which allows us to determine the kinetic parameters of Ca2+ binding to and Ca2+ dissociation from this chelator.
Using this set of measurements, we determine the parameters defining Ca2+ influx, Ca2+ clearance and Ca2+ buffering, which will be discussed individually below. The parameters, which we determine by a joint least‐squares fit to the entire data set are summarized in Table 1. Other parameters, in particular parameters resulting from a visual fit to I Ca traces, are given in Table 2.
Parameters related to Ca2+ influx and endogenous buffering
We measured I Ca both during voltage‐step depolarizations of various durations as well as in response to trains of AP‐like short stimuli. To aid [Ca2+]i modelling, we first derived parameters describing changes in I Ca amplitudes during the various stimulus protocols by visual (trial and error) fits for best agreement between modelled and measured I Ca shown in Figs 2, 4 and 5. Subsequently we used these I Ca‐related parameters (Table 2) to drive the [Ca2+]i model. The time constants describing relaxation of I Ca facilitation (23 ms) and recovery from I Ca inactivation (110 ms) are comparable to those derived experimentally for P8–10 calyces (Lin et al. 2012).
Simultaneous measurements of I Ca together with the associated changes in [Ca2+]i allow one to obtain an estimate for the accessible volume v of the presynaptic terminal. Our v estimates (0.30 pl for the set of cells measured under low‐EGTA conditions and 0.46 pl for cells under high‐EGTA conditions) are similar to the previously reported value of 0.4 pl (Helmchen et al. 1997). As expected, they are somewhat less than the estimated total calyx terminal volume (0.48–0.71 pl; Sätzler et al. 2002; Vasileva et al. 2012). It should be pointed out, however, that in the model equations all fluxes are divided by the factor (1+κB+κS). Thus, any error in the latter will lead to an error in the scaling of the fluxes, compensating for the former error. For the case of j in, which for a given I Ca is inversely proportional to v, an underestimate of κS will lead to a concomitant overestimate of v. Also, a false assumption regarding the affinities of the fast buffers will lead to an apparent Ca2+ dependence of v (see also below). Such errors are not included in our error estimates for other fitting parameters, since we assumed a fixed κS for all simulations.
Our estimate for the endogenous fixed buffer ratio κS ( = 21.1; range 13–29) does contain a small contribution of mobile low‐affinity Ca2+ binding species, contained in the pipette filling solution. While the contribution of the indicator dye is eliminated by the procedure of extrapolation to zero indicator dye (Fig. 1 D, E) (Neher & Augustine, 1992), nucleotides and gluconate additionally contribute to the measured value. According to the analysis of Woehler et al. (2014), these contributions amount to 1.8 and 1.75, respectively. Thus, the endogenous fixed buffers contribute only 17.55 to the estimated κS. However, all our measurements were performed with nucleotides and gluconate included in the pipette solution. So, for simplicity we assumed κS = 21.1 for all calculations. The indicator dye was represented in the calculations, as described in the context of eqn (6).
Parameters related to Ca2+ clearance
The parameters given in Table 1 allow a detailed description of two Ca2+ clearance mechanisms as suggested by Lee et al. (2007b). We confirm their finding that a non‐linear component of Ca2+ clearance mediated by a K+‐dependent Na/CaX speeds up Ca2+ clearance in the presence of intracellular K+. However, optimal fitting required a lower affinity of j ex,Hill (K D,H = 5.16 μm) than originally reported by Lee et al. (2007b; K D = 1.7 μm). This discrepancy may well be due to the use of different indicator dyes and discrepant assumptions about their dissociation constants. In particular, the type of analysis on which our K D of Fura‐6F is based yields a corresponding K D for Fura‐2FF of 13.7 μm (Woehler et al. 2014), which is significantly higher than that derived by Lee et al. (2007b; 3.1 μm). Likewise, discrepancies in γ and j H,max between our results and Lee et al. (2007b) are well taken care of by the different assumptions for indicator dye and κS.
Kinetics of Ca2+ binding to EGTA
The Ca2+ dissociation constant of EGTA, calculated from our kinetic parameters (K D = k E,Ca‐/k E,Ca+ = 0.543 μm), is 3.2 times higher than that obtained in vitro, 0.171 μm, as calculated with the software Maxchelator (http://maxchelator.stanford.edu/) for pH 7.2 and an ionic strength of 190 mm. This is largely due to a higher dissociation rate constant of 2.38 s−1. The latter, as calculated as the product of K D and Ca2+ association rate constant, was reported to be 0.5 s−1 (Naraghi 1997) or else 0.74 s−1 (Nägerl et al. 2000). Also our Ca2+ association rate constant is faster than that determined by T‐jump experiments (Naraghi & Neher, 1997) (2.7×106 m −1 s−1), although it is slower than that determined by Nägerl et al. (2000) (1.05×107 m −1 s−1). Part of the latter discrepancy is probably the result of a somewhat higher pH (7.3) and a lower ionic strength (≈ 150 mm) in the measurements of Nägerl et al. (2000). However, we attribute most of the discrepancies to different Ca2+ binding and unbinding rates of EGTA when measured either in vitro as in the previous studies or in situ as described here (see also discussion in Woehler et al. 2014).
A consistent set of parameters for modelling [Ca2+] transients in a presynaptic CNS nerve terminal
To predict [Ca2+ ]i changes in response to voltage‐clamp depolarizations or trains of APWs, a large number of parameters need to be known, as detailed at the beginning of the Results. Estimates for some individual parameters have been reported previously albeit for experiments conducted under a variety of different conditions (temperature, pH, ionic strength, developmental stage and type of nerve terminal). We made an effort to obtain a consistent and comprehensive set of parameters for the recording condition that is commonly used in studies at the calyx of Held. Apart from the determination of κs, which was done using younger calyces (P8–10), all our experiments were performed in P13–15 calyx terminals, at room temperature (20–23°C), and with pipette filling solutions of 190 mm ionic strength and a pH of 7.3. Furthermore, our measurements were all performed with the same Ca2+ indicator dye (Fura‐6F), using a Ca2+ dissociation constant K D = 17.8 μm (Woehler et al. 2014). This value is based exclusively on fluorescence measurements, performed using the same solutions as contained in recording pipettes, and does not rely on another Ca2+ buffer for calibration. Rather it uses a Ca2+ standard for titration. Nevertheless, it remains possible that the Ca2+ affinity of the indicator dye in situ is different from that in vitro (Tsien, 1983; Poenie, 1990) – just like we find for EGTA. Apart from this uncertainty about absolute [Ca2+]i values, our finding that one set of parameters accurately describes [Ca2+]i measurements covering a wide range of amplitudes and obtained using quite different stimulation protocols and ionic conditions, suggests that this set constitutes a sound basis for future studies of endogenous buffers and of the role of [Ca2+]i in synaptic plasticity.
Additional information
Competing interest
The authors declare no competing financial interests.
Author contribution
E.N. designed the study. K.H.L. performed experiments. K.H.L., H.T. and E.N. contributed to collection, analysis and interpretation of experimental data. E.N. performed numerical simulations and wrote the manuscript together with H.T. All authors have approved the final manuscript and agree to be accountable for all aspects of the work. All work was completed in the Department of Membrane Biophysics of the Max Planck Institute for Biophysical Chemistry.
Funding
This work was supported by the Cluster of Excellence and DFG Research Centre Nanoscale Microscopy and Molecular Physiology of the Brain (E.N., H.T.), the European Commission (EUROSPIN, FP7HEALTHF22009241498; E.N.) and the Max Planck Society (E.N.).
Acknowledgements
We thank I. Herfort for excellent technical assistance.
Linked articles This article is highlighted by a Perspective by Petersen. To read this Perspective, visit https://doi.org/10.1113/JP273852.
References
- Augustine GJ, Adler EM & Charlton MP (1991). The calcium signal for transmitter secretion from presynaptic nerve terminals. Ann NY Acad Sci 635, 365–381. [DOI] [PubMed] [Google Scholar]
- Babai N, Kochubey O, Keller D & Schneggenburger R (2014). An alien divalent ion reveals a major role for Ca2+ buffering in controlling slow transmitter release. J Neurosci 34, 12622–12635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borst JG & Sakmann B (1998a). Calcium current during a single action potential in a large presynaptic terminal of the rat brainstem. J Physiol 506, 143–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borst JG & Sakmann B (1998b). Facilitation of presynaptic calcium currents in the rat brainstem. J Physiol 513, 149–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuttle MF, Tsujimoto T, Forsythe ID & Takahashi T (1998). Facilitation of the presynaptic calcium current at an auditory synapse in rat brainstem. J Physiol 512, 723–729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dondzillo A, Satzler K, Horstmann H, Altrock WD, Gundelfinger ED & Kuner T (2010). Targeted three‐dimensional immunohistochemistry reveals localization of presynaptic proteins Bassoon and Piccolo in the rat calyx of Held before and after the onset of hearing. J Comp Neurol 518, 1008–1029. [DOI] [PubMed] [Google Scholar]
- Eggermann E, Bucurenciu I, Goswami SP & Jonas P (2012). Nanodomain coupling between Ca2+ channels and sensors of exocytosis at fast mammalian synapses. Nat Rev Neurosci 13, 7–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fedchyshyn MJ & Wang LY (2005). Developmental transformation of the release modality at the calyx of held synapse. J Neurosci 25, 4131–4140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forsythe ID, Tsujimoto T, Barnes‐Davies M, Cuttle MF & Takahashi T (1998). Inactivation of presynaptic calcium current contributes to synaptic depression at a fast central synapse. Neuron 20, 797–807. [DOI] [PubMed] [Google Scholar]
- Helmchen F, Borst JG & Sakmann B (1997). Calcium dynamics associated with a single action potential in a CNS presynaptic terminal. Biophys J 72, 1458–1471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamiya H & Zucker RS (1994). Residual Ca2+ and short‐term synaptic plasticity. Nature 371, 603–606. [DOI] [PubMed] [Google Scholar]
- Keller D, Babai N, Kochubey O, Han Y, Markram H, Schurmann F & Schneggenburger R (2015). An exclusion zone for Ca2+ channels around docked vesicles explains release control by multiple channels at a CNS synapse. PLoS Comput Biol 11, e1004253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim MH, Korogod N, Schneggenburger R, Ho WK & Lee SH (2005). Interplay between Na+/Ca2+ exchangers and mitochondria in Ca2+ clearance at the calyx of Held. J Neurosci 25, 6057–6065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee JY, Ho WK & Lee SH (2007a). Ionic selectivity of NCKX2, NCKX3, and NCKX4 for monovalent cations at K+‐binding site. Ann NY Acad Sci 1099, 166–170. [DOI] [PubMed] [Google Scholar]
- Lee SH, Kim MH, Lee JY, Lee D, Park KH & Ho WK (2007b). Na+/Ca2+ exchange and Ca2+ homeostasis in axon terminals of mammalian central neurons. Ann N Y Acad Sci 1099, 396–412. [DOI] [PubMed] [Google Scholar]
- Lee SH, Kim MH, Park KH, Earm YE & Ho WK (2002). K+‐dependent Na+/Ca2+ exchange is a major Ca2+ clearance mechanism in axon terminals of rat neurohypophysis. J Neurosci 22, 6891–6899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SH, Rosenmund C, Schwaller B & Neher E (2000). Differences in Ca2+ buffering properties between excitatory and inhibitory hippocampal neurons from the rat. J Physiol 525, 405–418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin KH, Erazo‐Fischer E & Taschenberger H (2012). Similar intracellular Ca2+ requirements for inactivation and facilitation of voltage‐gated Ca2+ channels in a glutamatergic mammalian nerve terminal. J Neurosci 32, 1261–1272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin KH, Oleskevich S & Taschenberger H (2011). Presynaptic Ca2+ influx and vesicle exocytosis at the mouse endbulb of Held: a comparison of two auditory nerve terminals. J Physiol 589, 4301–4320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews EA & Dietrich D (2015). Buffer mobility and the regulation of neuronal calcium domains. Front Cell Neurosci 9, 48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMahon SM, Chang CW & Jackson MB (2016). Multiple cytosolic calcium buffers in posterior pituitary nerve terminals. J Gen Physiol 147, 243–254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meinrenken CJ, Borst JG & Sakmann B (2002). Calcium secretion coupling at calyx of held governed by nonuniform channel‐vesicle topography. J Neurosci 22, 1648–1667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monahan JF (2001). Numerical Methods in Statistics. Cambridge University Press, Cambridge. [Google Scholar]
- Müller M, Felmy F & Schneggenburger R (2008). A limited contribution of Ca2+ current facilitation to paired‐pulse facilitation of transmitter release at the rat calyx of Held. J Physiol 586, 5503–5520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller M, Felmy F, Schwaller B & Schneggenburger R (2007). Parvalbumin is a mobile presynaptic Ca2+ buffer in the calyx of held that accelerates the decay of Ca2+ and short‐term facilitation. J Neurosci 27, 2261–2271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nägerl UV, Novo D, Mody I & Vergara JL (2000). Binding kinetics of calbindin‐D(28k) determined by flash photolysis of caged Ca2+ . Biophys J 79, 3009–3018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakamura Y, Harada H, Kamasawa N, Matsui K, Rothman JS, Shigemoto R, Silver RA, DiGregorio DA & Takahashi T (2015). Nanoscale distribution of presynaptic Ca2+ channels and its impact on vesicular release during development. Neuron 85, 145–158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naraghi M & Neher E (1997). Linearized buffered Ca2+ diffusion in microdomains and its implications for calculation of [Ca2+] at the mouth of a calcium channel. J Neurosci 17, 6961–6973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neher E (1995). The use of fura‐2 for estimating Ca buffers and Ca fluxes. Neuropharmacology 34, 1423–1442. [DOI] [PubMed] [Google Scholar]
- Neher E & Augustine GJ (1992). Calcium gradients and buffers in bovine chromaffin cells. J Physiol 450, 273–301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neher E & Sakaba T (2008). Multiple roles of calcium ions in the regulation of neurotransmitter release. Neuron 59, 861–872. [DOI] [PubMed] [Google Scholar]
- Neher E & Taschenberger H (2013). Transients in global Ca2+ concentration induced by electrical activity in a giant nerve terminal. J Physiol 591, 3189–3195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poenie M (1990). Alteration of intracellular Fura‐2 fluorescence by viscosity: a simple correction. Cell Calcium 11, 85–91. [DOI] [PubMed] [Google Scholar]
- Sätzler K, Sohl LF, Bollmann JH, Borst JG, Frotscher M, Sakmann B & Lübke JH (2002). Three‐dimensional reconstruction of a calyx of Held and its postsynaptic principal neuron in the medial nucleus of the trapezoid body. J Neurosci 22, 10567–10579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smetters D, Majewska A & Yuste R (1999). Detecting action potentials in neuronal populations with calcium imaging. Methods 18, 215–221. [DOI] [PubMed] [Google Scholar]
- Stosiek C, Garaschuk O, Holthoff K & Konnerth A (2003). In vivo two‐photon calcium imaging of neuronal networks. Proc Natl Acad Sci USA 100, 7319–7324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taschenberger H & von Gersdorff H (2000). Fine‐tuning an auditory synapse for speed and fidelity: developmental changes in presynaptic waveform, EPSC kinetics, and synaptic plasticity. J Neurosci 20, 9162–9173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsien RY (1983). Intracellular measurements of ion activities. Annu Rev Biophys Bioeng 12, 91–116. [DOI] [PubMed] [Google Scholar]
- Vasileva M, Horstmann H, Geumann C, Gitler D & Kuner T (2012). Synapsin‐dependent reserve pool of synaptic vesicles supports replenishment of the readily releasable pool under intense synaptic transmission. Eur J Neurosci 36, 3005–3020. [DOI] [PubMed] [Google Scholar]
- Vyleta NP & Jonas P (2014). Loose coupling between Ca2+ channels and release sensors at a plastic hippocampal synapse. Science 343, 665–670. [DOI] [PubMed] [Google Scholar]
- Werth JL & Thayer SA (1994). Mitochondria buffer physiological calcium loads in cultured rat dorsal root ganglion neurons. J Neurosci 14, 348–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woehler A, Lin KH & Neher E (2014). Calcium‐buffering effects of gluconate and nucleotides, as determined by a novel fluorimetric titration method. J Physiol 592, 4863–4875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wölfel M & Schneggenburger R (2003). Presynaptic capacitance measurements and Ca2+ uncaging reveal submillisecond exocytosis kinetics and characterize the Ca2+ sensitivity of vesicle pool depletion at a fast CNS synapse. J Neurosci 23, 7059–7068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou Z & Neher E (1993). Mobile and immobile calcium buffers in bovine adrenal chromaffin cells. J Physiol 469, 245–273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zucker RS & Regehr WG (2002). Short‐term synaptic plasticity. Annu Rev Physiol 64, 355–405. [DOI] [PubMed] [Google Scholar]


