Route searching based on neural networks and heuristic reinforcement learning

Abstract

In this paper, an improved and much stronger RNH-QL method based on RBF network and heuristic Q-learning was put forward for route searching in a larger state space. Firstly, it solves the problem of inefficiency of reinforcement learning if a given problem’s state space is increased and there is a lack of prior information on the environment. Secondly, RBF network as weight updating rule, reward shaping can give an additional feedback to the agent in some intermediate states, which will help to guide the agent towards the goal state in a more controlled fashion. Meanwhile, with the process of Q-learning, it is accessible to the underlying dynamic knowledge, instead of the need of background knowledge of an upper level RBF network. Thirdly, it improves the learning efficiency by incorporating the greedy exploitation strategy to train the neural network, which has been testified by the experimental results.

Introduction

Since the dawn of modern science, scientists have made great efforts to discover and invent feasible methods to construct and develop a machine that can apply intelligent control technologies to replace complex and dangerous human work. Till now, the effort has never subsided, but instead constantly grows with humans’ needs tending to manifest more clearly. For that, robot control technology is an inevitable one. On one hand, traditional reinforcement learning and artificial neural networks show their weaknesses in problem solving in complex situations. On the other hand, with the widespread application in all fields of industrial production and medical and health, robot control technology, along with the modern electronic information technology and intelligent control technology, has become more and more developed.

Reinforcement learning (RL) (see Liu et al. 2013; Ferreira et al. 2014) is a kind of machine learning method. Embedded with reinforcement learning algorithm, an agent could be exploited to study in any unknown environment and display a stronger adaptability. In essence, reinforcement learning makes the mapping from the state of environment to action possible, where the agent’s main task is to get the most reward in the learning process. By sensing and interacting with the environment information continuously, an agent can theoretically study the dynamic optimal strategy in the system through trial and error to adapt to the environment and improve its response. For traditional RL, this is a blind process and will spend much time for an agent to search for a target in a simple unknown region full of obstacles, not to mention a complex situation. So for the sake of improving learning efficiency, people began to explore more alternative ways to ameliorate the learning processes.

Meanwhile, artificial neural network (ANN) (see Duan et al. 2015a, b) is a kind of mathematical algorithm model, which could simulate the characters of animal neural action in terms of theory and carry out the distributed information processing with legible principles. From the analysis taken from nature, neural network is a nonlinear adaptive system, which is composed of abundant simple processing units-neurons in a certain way. The structure and function of each neuron is very simple and the neurons could work together. Thus it has no arithmetic unit, storage and controller. And the information is stored in the nodes between neurons. Research indicates that ANN is similar to human brain which can gain better ability of learning and memory, knowledge generalization and feature information extraction. By adjusting interconnections between the internal nodes, it can realize the given information processed with the help a complicated system. If the hierarchical reinforcement learning model is guided by neural networks, with the aid of neural network’s generation performance, an agent can utilize its learning experience to predict and guide its action in the future.

As a result, an improved and much stronger RNH-QL method based on reinforcement learning and RBF network (see Chen et al. 2015; Cruz et al. 2014) for route searching was put forward in this paper. RNH-QL method adopts a double layer structure with the combination of neural networks and Q-form which is a look-up table and can record Q value (details in “Principle and algorithm” section). The agent’s action is determined by the combined forms of shaping and Q value. Compared with the previous research results, the proposed scheme has the advantage of more adaptability to the environment for an agent by autonomous learning mode in a complex environment. Meanwhile, the agent could handle a large amount of state-action information by utilizing neural network and then enhance the execution efficiency.

The rest of the paper is organized as follows. “Preliminaries” section gives some background information on reinforcement learning and artificial neural network. “Principle and algorithm” section presents the overall architecture and key components of RNH-QL method, and discusses how it will combine the neural networks and reinforcement learning. “Experiment result and analysis” section presents the experimental and comparative results between different learning algorithms. “Conclusion and discussion” section draws a conclusion.

Preliminaries

The terms of “enhanced” and “reinforcement learning” were first put forward by Minsky et al. (1954). According to the time series forecast in the process of reinforcement learning, Sutton and Barto (1998) proposed temporal difference (TD) algorithm. Watkins and Dayan (1992) improved TD algorithm and proposed Q-learning algorithm. For application research, Holroyd and Coles (2002) did the study of nervous system of human error handling. These researches verify that the reinforcement learning is a good method on direct adaptive control.

For an agent, the prior background knowledge could make it stay away from blind search and improve the efficiency. So Ng et al. (1999) introduced the Shaping function to reinforcement learning in the form of prior knowledge and in this way the agent’s inspired value could be added to the return value with effective convergence speed. An inspired accelerated Q-learning algorithm—HAQL was proposed by Bianchi et al. (2008). Grzes and Kudenko (2008) utilized the symbolic knowledge based on the form of Strips for planning and transformed them into potential field function as a high-level guide at the bottom of the reinforcement learning. Chen et al. (2008) proposed a flow algorithm-based reinforcement learning algorithm inspired by the potential energy field. Lin et al. (2008) put forward the model of reinforcement learning based on biased information study.

Previous researches indicate that an agent can gain experience at each round of learning, which can reflect a trend and accelerate the learning process. Thus, it is expected that an agent can automatically inspire the future learning with less prior knowledge or with no knowledge. For that, some scholars have done researches on automatics-inspired reinforcement learning. Chen confirmed that reinforcement learning process can be divided into quantitative layer and qualitative layer in Grzes and Kudenko (2010) and Chen et al. (2011), in which, quantitative layer is in accord with the MDP model and qualitative layer with the SMDP model and the hierarchical control structure constitutes a hybrid model in Gosavi (2014) and Bianchi et al. (2014). Due to the learning ability of qualitative layer, the efficiency and stability of learning can be enhanced significantly. Qian et al. (2013) put forward an algorithm that can speed up the reinforcement learning process from the generated samples with shaping function. Chen et al. (2011) proposed a kind of algorithm with which an agent could apply knowledge to a more complex learning environment. In addition, some more deepgoing introduction about “Cognitive Neurodynamics” could be found in Liu et al. (2010), Gu and Liljenström (2007), Samson et al. (2010), Kozma (2016) and Wang et al. (2013), it will help you to understand this paper more complete and better.

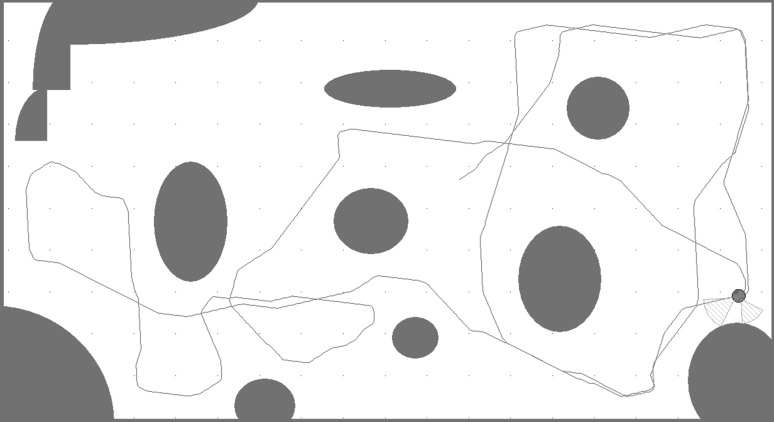
Based on the above research background, some exploratory research has been done by our team. As a member of the team, I finished the part of work about algorithm design and validation. We combined the neural network with Q-Learning, a new algorithm model which was applied in the intelligent control system was presented in Zhong et al. (2013). Furthermore, we have applied to a China National invention patent called “A Q-learning system based on Menristive crossbar array” which was in the public. In these studies, the robot employs the reinforcement learning algorithm based on the mechanism of trial-and-error. The learning process is shown as Fig. 1, which was simulated by MobotSim (an online robot simulation software). This model may enable robots to have the advantage of automatic decision-making capacity. Nevertheless, this is a blind search algorithm. The robot learning from the unknown environment through constant interaction. After a period of time, the robot could shuttle among obstacles freely. In this work, the ability of obstacle avoidance could be achieved based on the algorithm, but it does not has the ability of the optimal route searching. In order to improve the performance of the algorithm, I decided to do more in-depth research, this is my purpose of accomplishing the paper.

Fig. 1.

The learning process of robot

Principle and algorithm

There is important significance of this chapter in the whole paper. For the sake of presenting our modified algorithm and emulation, some basic but considerable theories and algorithms would be introduced. Q-Learning, MDP and RBF network are the cornerstone of other theories, so it is necessary to have detailed description about them. First, a Heuristically Accelerated Q-learning Algorithm (HAQL) makes use of a heuristic function H ( s, a ) in the $\mathrm{\epsilon }\text{-}greedy$ action choice rule, instead of using only the value (or action-value) estimation in the action selection method of an RL algorithm. Second, an updating method of neural networks called RBF network-based Reward Shaping for RL has been applied in updating weights of the neural network. Finally, a complete learning model has been presented to describe the whole process.

Reinforcement learning: Q-learning

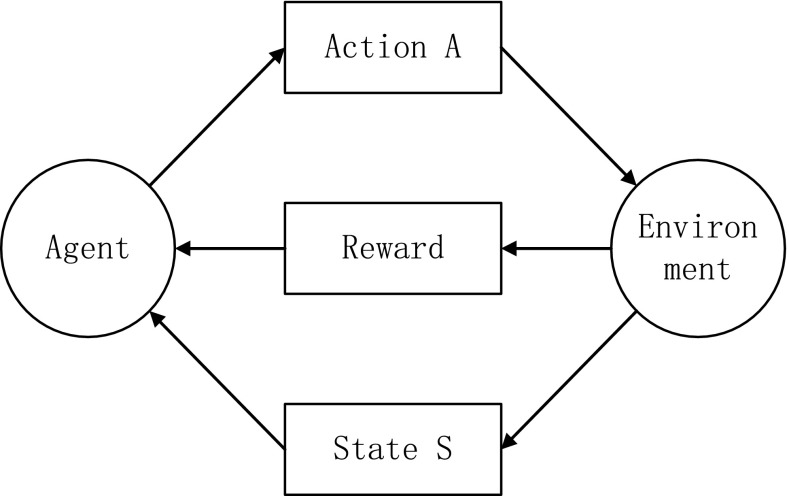
How to make a decision for an agent when interacting with dynamic environment? If an action gets positive reward, then the trend of action strategy will be strengthened. The model of Q-learning is shown in Fig. 2, which treats learning as a process of bonus and where an agent can choose all kinds of actions in the environment. When the environment accepts the changing, it will produce a bonus back to the agent simultaneously. The next action of an agent will depend on the direction in which the agent could acquire the most-positive reward.

Fig. 2.

The process of Q-learning

Q-learning, a stochastic dynamic programming algorithm, which is based on the theory of Markov Decision Process, does not require the interactive model of a machine-environment. By taking action ‘a’ based on state ‘s’, the algorithm evaluates the feedback rewards and updates its Q values from the rewards sequentially. In an acceptable learning period, the Q-learning algorithm performs excellently (see Liu and Zeng 2012; Ni et al. 2012; Millan and Torras 2014).

A Markov Decision Process (MDP) is a tuple of <S, A, T, r> , where $s\in S$ is the state space, $a\in A$ is the action space, $T\left(s,a,s^{\prime }\right)$ is the probability that action a when executed in state s will lead to state $s^{\prime }$, $r\left(\text{s},\text{a},s^{\prime }\right)$ is the immediate reward received when action a taken in state s results in a transition to state $s^{\prime }$ under the state s. The problem of solving an MDP is to find a policy (i.e., a mapping from states to actions) which maximizes the accumulated reward. The MDP based on a discount policy could be described as $M=\left(S,A,T,\mathit{\gamma },r\right)$. where γ is discount factor.

The discount accumulated expectation is defined as $Q^{\mathit{\pi }}\left(s,a\right)$, and its expression is:

$$Q^{\mathit{\pi }}\left(s,a\right)=E\left\{r_t+\mathit{\gamma }{r}_{t+1}+{\mathit{\gamma }}^2{r}_{t+2}+\cdots |s_t=s,a_t=a\right\}$$ 1

where $0<\mathit{\gamma }<1,\mathrm{\pi }$ is the strategy.

$Q^{\ast }\left(s,a\right)$ can be regarded as a Q function when action a has been executed under the state s, and the optimal Q value could be obtained by the following formula:

$$Q^{\ast }\left(s,a\right)=\sum _{s^{\prime }}T\left(s,a,s^{\prime }\right)\left[r\left(s,a,s^{\prime }\right)+\mathit{\gamma }{max}_{a^{\prime }}{Q}^{\ast }\left(s^{\prime },a^{\prime }\right)\right]$$ 2

In practical applications, the environment model and transition probability are usually unpredictable. Aiming at this problem, Q-learning algorithm was presented by Watkins, and its global convergence was proved too. Its iteration formula is expressed as follows:

$$\text{Q}\left(s,a\right)=\text{Q}\left(s,a\right)+\mathit{\alpha }\left[r\left(s,a,s^{\prime }\right)+\mathit{\gamma }maxQ\left(s^{\prime },a^{\prime }\right)-Q\left(s,a\right)\right]$$ 3

Among them, $0<\mathit{\gamma }<1$, $0<\mathit{\alpha }<1$.

The V value is defined under the state s by the following relation:

$$\text{V}\left(\text{s}\right)={max}_{a}Q\left(\text{s},\text{a}\right)$$ 4

The optimal strategy ${\mathit{\pi }}^{\ast }(s)$ defined under the state s is described by:

$${\mathit{\pi }}^{\ast }\left(s\right)=arg{max}_{a}Q\left(s,a\right)$$ 5

For purpose of improving the learning efficiency, additional compensation value should be provided. A suitable heuristic function $\text{F}\left(\text{s},\text{a},s^{\prime }\right)=\mathit{\gamma }\mathit{\phi }\left(s^{\prime }\right)-\mathrm{\phi }\left(\text{s}\right)$ has been set. What’s more, $\mathrm{\phi }\left(\text{s}\right)\text{and}\mathit{\phi }\left(s^{\prime }\right)$ are the potential field functions based on state s and $s^{\prime }$ respectively. The formula (3) could be rewritten by the following form:

$$\text{Q}\left(s,a\right)=\text{Q}\left(s,a\right)+\mathit{\alpha }\left[r\left(s,a,s^{\prime }\right)+\text{F}\left(\text{s},\text{a},s^{\prime }\right)+\mathit{\gamma }{max}_{a^{\prime }}Q\left(s^{\prime },a^{\prime }\right)-Q\left(s,a\right)\right]$$ 6

So the MDP $\text{M}=\left(\text{S},\text{A},\text{T},\mathrm{\gamma },r\right)$ will be converted to a new MDP ${\text{M}}^{\prime }=\left(\text{S},\text{A},\text{T},\mathrm{\gamma },r^{\prime }\right)$ and the optimal strategy can be updated through continuous learning. Furthermore, the new compensation $r^{\prime }\left(s,a,s^{\prime }\right)$ could be defined as: $r^{\prime }\left(s,a,s^{\prime }\right)=r\left(s,a,s^{\prime }\right)+\text{F}\left(\text{s},\text{a},s^{\prime }\right)$.

Theorem: If F is a heuristic function based on the potential field function, and $\text{F}\left(\text{s},\text{a},s^{\prime }\right)=\mathit{\gamma }\mathit{\phi }\left(s^{\prime }\right)-\mathrm{\phi }\left(\text{s}\right)$. only if F is the optimization strategy in ${\text{M}}^{\prime }=\left(\text{S},\text{A},\text{T},\mathrm{\gamma },r^{\prime }\right)$, then it will be true in $\text{M}=\left(\text{S},\text{A},\text{T},\mathrm{\gamma },r\right)$ or F is the optimization strategy in $M=\left(\text{S},\text{A},\text{T},\mathrm{\gamma },r\right)$, then it will be true in ${\text{M}}^{\prime }=\left(\text{S},\text{A},\text{T},\mathrm{\gamma },r^{\prime }\right)$.

RBF network

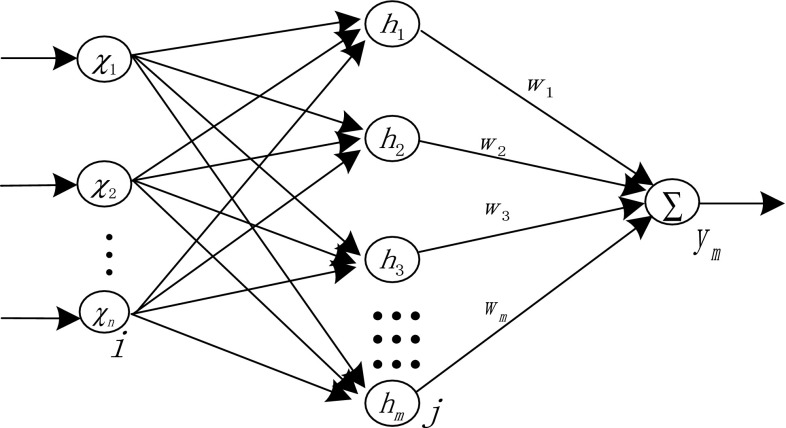
Radial Basis Function (RBF) network is a kind of feed forward network, which possesses good generalization ability and simple network structure. It is a three-layer network, namely the input layer, the output layer and the hidden layer. It is beneficial to function approximation, which can approximate any continuous function with arbitrary precision. For the neurons in the hidden layer, the closer they are, the more accurate it will be. We supposed that RBF network is provided with n input nodes, M hidden layer nodes and one output node. The structure is shown in Fig. 3.

Fig. 3.

The structure of RBF network

Generally we will select the appropriate hidden layer activation function in accordance with the need. Thus Gaussian function is chosen to be used in this paper. By the structure of RBF network, the input vector of the first layer is X = [x1, x2,…, xn]T. The output vector of hidden layer, namely Radial basis vector, is H = [h1, h2,…, hm]T, where ${\text{h}}_j$ is Gaussian function:

$$h_j=exp\left(-\frac{{∥x-C_j∥}^2}{2b_j^2}\right),(j=1,2,\dots ,m)$$ 7

In the above equation, m represents the number of the hidden layer neuron. Cj = [cj1, cj2,…, cji,…, cjn]T, (i = 1, 2,…, n) denotes the center vector of jth neuron. bj denotes the basis width of jth neuron’s RBF, which determines the width of basis function around the center. ||X − Cj|| is the norm of vector X − Cj, denoting the distance between X and Cj.

Assuming that the weight vector of hidden layer to output layer is W = [w1, w2,…, wm]T. Since the mapping from hidden layer to output layer is linear, then the network output is formed by a linearly weighted sum of the number of basic functions in the hidden layer.

$$y_m(k)=W^{T}H=\sum _0^m{w}_i{h}_i$$ 8

Performance index function of RBF neural network is:

$$J=\frac{1}{2}{(y(k)-y_m(k))}^2$$ 9

A heuristically accelerated Q-learning algorithm

A heuristically algorithm which based on the heuristic function. The nature of the algorithm is giving up parts of some universal and generalized concept, only learns from universal rules. When the specific domain knowledge was been added to the algorithm, so the algorithm efficiency will be promoted. Proper learning and control algorithm is the key to guarantee the performance of navigation. In this section, the main idea of HAQL is presented based on the model of MDP. Q-learning algorithm is an offline difference algorithm. The iteration of Q value function and selection strategy are independent for each other (mutual independence). From the formula (3) which shows Q-learning approach’s goal, we can see it is a greedy strategy, and we call it “utilization”. However, greedy algorithm is not only the necessary choice when the agent executes some strategies, and it could choose other sub-optimal policy strategies, so we call it “explore”.

A Heuristically Accelerated Q-learning Algorithm as a way to solve an MDP problem with explicit use of a heuristic function $\mathit{H}:\mathit{S}\times \mathit{A}\to \mathit{R}$ for influencing the choice of actions by the learning agent. The heuristic function is an action policy modifier which does not interfere with the standard bootstrap-like update mechanism of RL algorithms. In the HARL algorithms, instead of using only the value (or action-value) estimation in the action selection method of an RL algorithm. HAQL makes use of a heuristic function H ( s, a ) in the $\mathrm{\epsilon }\text{-}greedy$ action choice rule, that can be written as:

$$\mathrm{\pi }\left(\text{x}\right)=\left\{\begin{array}{c}arg{max}_a\left[\widehat{Q}\left(s,a\right)+\mathit{\xi }H{\left(s,a\right)}^{\mathit{\beta }}\right],\text{normal}\\ a_{random},otherwise\end{array}\right.$$

In this work we propose the new algorithm: the HAQL which extends the QL algorithm by using the same action choice rule as the HAQL.

RBF network-based reward shaping for reinforcement learning

The implementation modality of an agent is designed to update the Q table combined with the process of reinforcement learning at the same time, with the training of high-level neural networks to form a V value gradually. It could be regarded as an online heuristic function to inspire the learning process.

In the process of reinforcement learning, action a will be executed at first, and award r could be got secondly, then the agent will turn into the next state $s^{\prime }$. The V values are stored in the RBF network, receiving the further training from the neural network, which can be regarded as an adaptive algorithm. Even though reward shaping in Ng et al. (1999) has been powerful in many experiments, it quickly turned out to be misleading when used improperly. In our approach, symbolic planning provides additional knowledge to a classical RL agent in a principled way through reward shaping. The reward shaping function based on neural networks is defined as formula (10), F(s, a, s) as the difference of some potential function $V_{NN}$ defined over a source s, a destination state s and an action a.

$$\text{F}\left(\text{s},\text{a},s^{\prime }\right)=\mathit{\gamma }{V}_{NN}\left(s^{\prime }\right)-V_{NN}\left(s\right)$$ 10

The updating method of neural networks

It is an effective method of using greedy exploitation strategy for reinforcement learning, and the learning speed of neural network could be accelerated, meanwhile, the Q-learning based on the form can be inspired more effectively.

The greedy exploitation strategy always attempts to exploit the existing knowledge for responding to the states. With this approach, the action selection mechanism is used to search for a cognitive node that satisfies the vigilance criterion. Therefore, any cognitive node identified to use the action selection mechanism is taken to be suitable for providing an appropriate choice effective to the states.

The Q table’s operation according to the formula (6) and the V value will update according to the formula (4). When the agent performs a non-greedy action, it will not tend to get a larger Q value in the next state. In order to guarantee the effectiveness of learning, Q-learning process will acquire the V value of next state to update the current Q values. A method of V value, according to the greed, is adopted to solve the problems of updating through neural network and qualification of trace at the same time. When a non-greedy action is performed by some agent, the qualification mark will not work any longer, so the qualification mark is assigned with 0 and errors would be blocked to the back. The greedy state-action chain is used as a minimum unit for the update of qualification mark in this paper.

The method of gradient descent is adopted to update the weights of neural networks:

$$\mathrm{\Delta }{w}_i=\mathit{\beta }\left(\left(s_i\right)+\mathit{\gamma }{V}_{NN}\left(s_{t+1}\right)-V_{NN}\left(s_t\right)\right)\times \sum _{k=0}^t{\left(\mathit{\gamma }\mathit{\delta }\right)}^{t-k}\frac{\mathit{\partial }}{\mathit{\partial }w}{V}_{NN}\left(s_k\right)$$ 11

where $\mathrm{\beta }$ is trace rate, $0<\mathit{\beta }<1$; $\mathit{\delta }$ is the qualification coefficient, $0<\mathit{\delta }<1$.

The agent will predict the interpolation of current V value and the next ($\text{r}\left(\text{st}\right)+\mathit{\gamma }{V}_{NN}\left(s_{t+1}\right)-V_{NN}\left(s_t\right)$) to update the weights of neural network through state s. The interpolation of a greedy state-action chain can update V value in the other condition. In the formula (12), defining the qualification and its formula is:

$$e_t=\sum _{k=0}^t\mathit{\gamma }\mathit{\delta }\frac{\mathit{\partial }}{\mathit{\partial }w}{V}_{NN}\left(s_k\right)=\mathit{\gamma }\mathit{\delta }{e}_{t-1}+\frac{\mathit{\partial }}{\mathit{\partial }w}{V}_{NN}\left(s_t\right)$$ 12

The formula (11) is rewritten to a new format:

$$\mathrm{\Delta }{w}_i=\mathit{\beta }\left(r\left(s_t\right)+\mathit{\gamma }{V}_{NN}\left(s_{t+1}\right)-V_{NN}\left(s_t\right)\right)e_t$$ 13

It is easy to modify the weight from RBF network’s hidden layer to the output layer by the weight correction formula (13).

With the agent’s action choice, this paper discusses the problems of the action. In order to solve the problem of exploration-utilization, the method of $\mathrm{\epsilon }\text{-}greedy$ can be used. If the value $\mathrm{\epsilon }$ is smaller, the expectation of greedy state-action chain will get longer; if the value $\mathrm{\epsilon }$ is bigger, the expectation of greedy state-action chain will be shorter.

The reinforcement learning based on Q table will obtain more accurate results with the good ability of generalization and foresight. This algorithm will build an adaptive heuristic reward shaping function with the upper neural network, which combined the structures of two kinds of algorithm and could also improve the operation efficiency and robustness. It is not obvious at the beginning of the learning. With constant learning, the trend information of neural network will be established gradually, and could greatly improve the convergence speed and inspire the Q table as well.

The neural network structure of heuristic reinforcement learning model

Adopting the method of Q-learning based on the form, with the finer form division and decision-making action, the higher strategy precision, the model has given rise to the following two issues: (1) With the increasing of state space, it can make the problem of “dimension disaster” and reduce the learning efficiency greatly; (2) With the decrease of agent’s visual space, it can render the process of searching and become more blind.

In order to improve the efficiency of Q-learning and the foreseeing ability of an agent, it is worthy of exploring how to utilize reinforcement learning without prior knowledge. An agent could form a reward shaping function with neural network in the table space gradually, which has the ability of generalization and foresight. The evolution trend of value function plays a guiding role in the process of learning, which could avoid the agent’s blind action.

In this paper, the Q table and the neural network that we regard as the bottom layer and the upper layer. We utilize the V value which was generated from the implementation process of the RNH-QL algorithm to update the Q table. The heuristic function is gained from training state S through neural network. Learning model is set up as shown in Fig. 4.

Fig. 4.

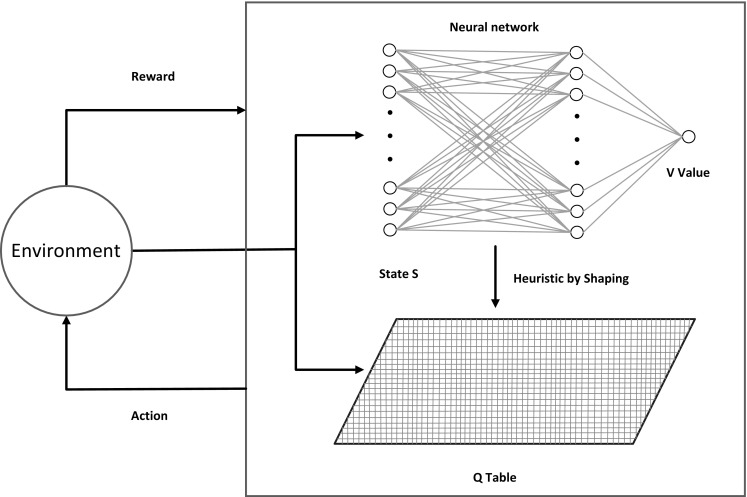
Learning model of RNH-QL

Experiment result and analysis

In this article, I attempt to explain the experiment through the following detailed introduction. Route searching (also known as Pathfinding) strategy often appearing as a pathfinding domain in areas such as robotics and academic research, grid map is a simple yet popular method for representing an environment. As it turns out, grids are draw into academically interesting for the following reason: between any given pair of locations, there are many possible paths usually. Sometimes these paths represent alternative ways of reaching one location from the other but more often they are difficult to make the optimal choice in the sense that the only difference between them is the order in which moves appear. A path (route) in a grid map is an ordered sequence of vectors, where each vector represents a single step from one node on the grid to an adjacent neighbouring node. The RNH-QL algorithm which was proposed in the “Principle and algorithm” section nicely complements existing search-space reduction techniques and also complements most grid-based abstraction methods and memory heuristic approaches. In order to explain the whole process of route searching clearly, so the grid map was been adopted as the simulation environment.

Experiment description

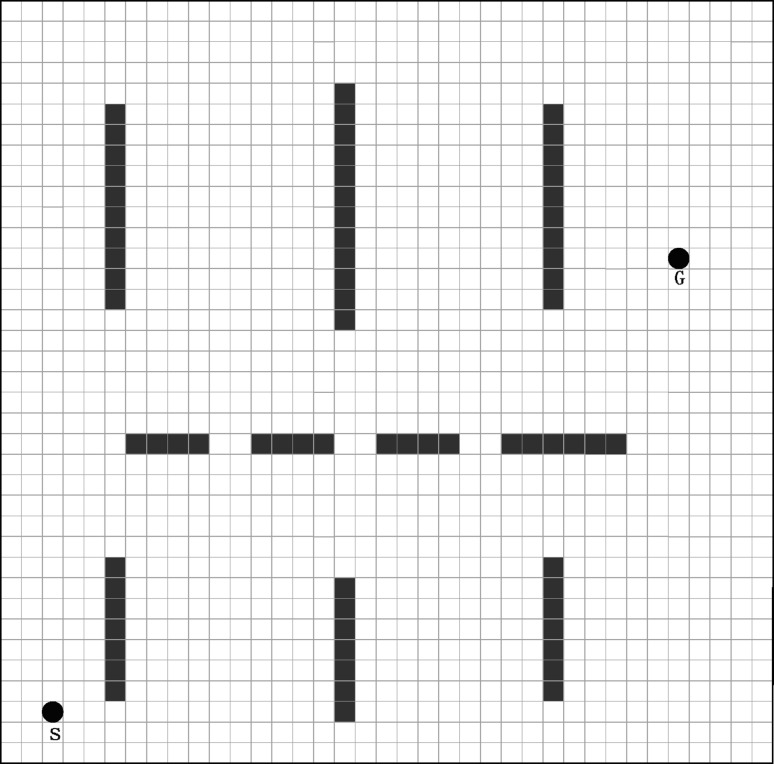
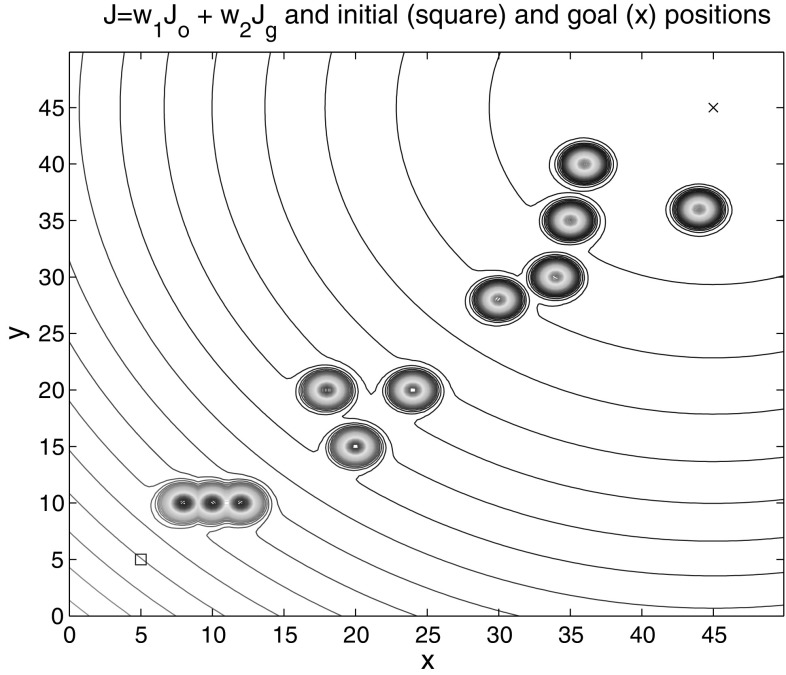
The route searching could verify the effectiveness of RNH-QL algorithm in an unknown environment. As shown in Fig. 5, an M × N = 50 × 50 grid is adopted for experimental domain. The black origin G is the target (the goal position), and each of these grid cells is a square. The hollow squares are the free area for agent, the dark solid squares are the obstacles, and the places around the squares are walls. Naturally, the agent couldn’t get through the walls or the obstacles. Assume that the agent can perceive their own position, but it knows nothing about the environment initially. How an agent finds an optimized way to the point G in any initial position by learning? The action collection of an agent in any state is {up, down, left, right}. The setting compensation value is: if the agent could arrive at the target G, then it would get 100 rewards from the environment; if the agent crashes on the wall in the process of moving and it would go back to the previous state and gain the punishment of −1. In addition, each step of the agent with no touching of obstacles or walls would receive 1 reward. When a round learning (episode) of an agent is completed, the current round’s rewards and punishments would be recorded and summarized, then the next round of learning will start. If the agent found the G in one round of learning and missed the target when getting maximum regulation steps, the round of study is completed. After a certain number of training wheels, the agent is put to the start position S, and it will search the target G with its learning strategy, generated by the route of quality evaluation for the reinforcement learning method’s performance.

Fig. 5.

Experimental environment in Visio

A scenography of route searching is described in Fig. 5. The purpose of this figure is to conduct a detailed description of the searching process and show us how an agent searches the route. The actual simulation is shown in Fig. 6 and the simulation process is completed in MATLAB. The start position in the square is set at the coordinate of (5, 5) and the goal position is in (45, 45). Moreover, there are some random circular obstacles in it. In order to demonstrate these obstacles more clearly, the contour lines are drawn at a point near the barriers and the latitude lines are drawn at the location of barriers. A certain amount of training is executed in the scene before searching the route starts. And the initial point of training process is randomly generated and it can be located anywhere in the free zone.

Fig. 6.

Experimental environment in Matlab

The learning performance of standard Q-learning

The standard Q-learning (standard QL) has been used for testing, the $\mathrm{\epsilon }\text{-}greedy$ method is adopted, and $\mathrm{\epsilon }=0.1$, learning rate $\mathrm{\alpha }=0.1$, the discount factor $\mathrm{\gamma }=0.95$.

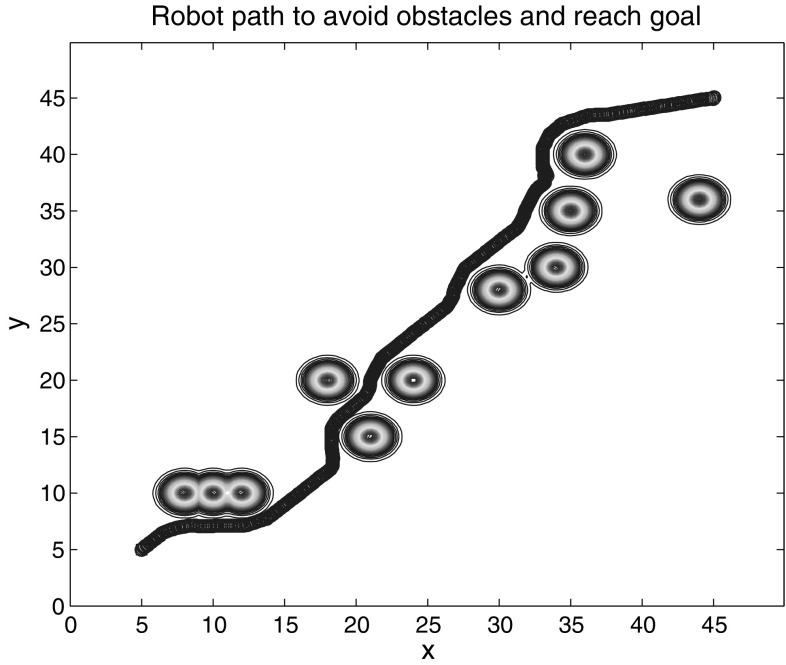
In each round, the limit of learning step is set to be 600. If the agent couldn’t find the target point G, the study would be ended, and then a new search is started. With continuous study, each round of study step is reduced gradually. After 2999 rounds’ study, the agent is put at test point S in the 3000th round, and the search result is shown in Fig. 7. It is a tortuous route. The agent could find the target point from the initial position, but some redundancy is produced in the process of looking for the target, otherwise the route is not optimal. If you want to get the optimal result, the continuous learning and training is necessary.

Fig. 7.

The result of standard Q-learning

The performance of Q-learning based on RBF network

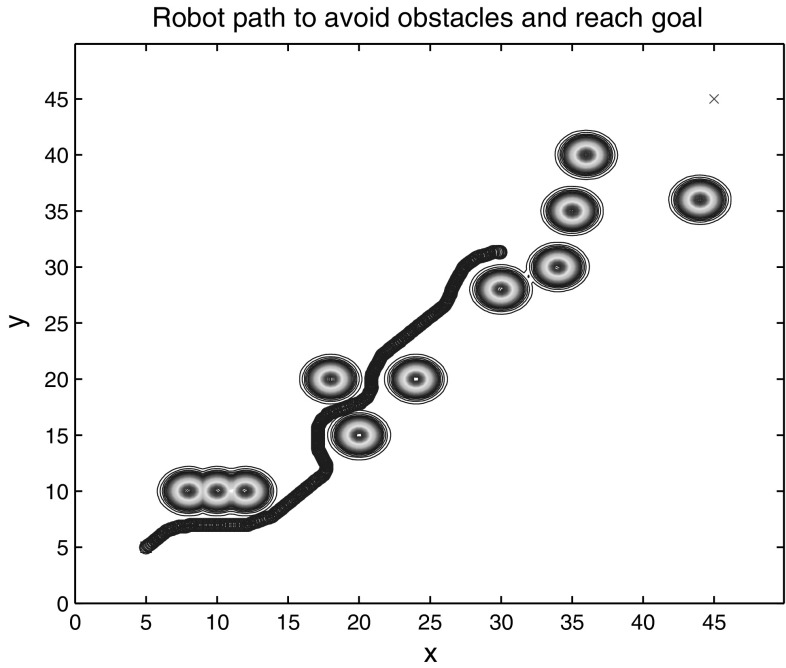
A method of reinforcement learning based on RBF network (RN-QL) is used for route searching in the same experiment. The method of $\mathrm{\epsilon }\text{-}greedy$ is adopted for action selection, and $\mathrm{\epsilon }=0.1$, learning rate $\mathrm{\alpha }=0.1$, the discount factor $\mathrm{\gamma }=0.95$, and the coefficient of qualification mark $\mathrm{\delta }=0.85$. The structure of neural network is 2-10-1. Sigmoid activation function is used for hidden layer nodes, and linear activation function is adopted for output layer nodes. The multi-step updating algorithm based on qualification trace and greedy state-action chain is adopted for neural network’s updating. After enough study, the route search result is shown in Fig. 8 in the 3000th round.

Fig. 8.

The result RN-QL

The trend of an agent’s action could be clearly found by RN-QL method, and the generalized advantage of neural network could be reflected. When approaching to the 2500th round, the average learning steps of each round are 450. In the 3000th round, the initial point is put as the test point. However, the agent did not find the route to the target point, and ran into the “blind area” after 500 steps. What is worse, the agent stopped searching after 600 steps and remained on the temporary point. The searching is terminated in the end. Why such a result will be produced? Because neural networks need to optimize the network’ performance with continuous training and learning, so the learning rounds are deeply increased to 15,000 rounds approximately, and then the agent can be imbedded back to the starting position, which could make it find the relative optimal route to reach the target point.

The learning performance of RNH-QL method

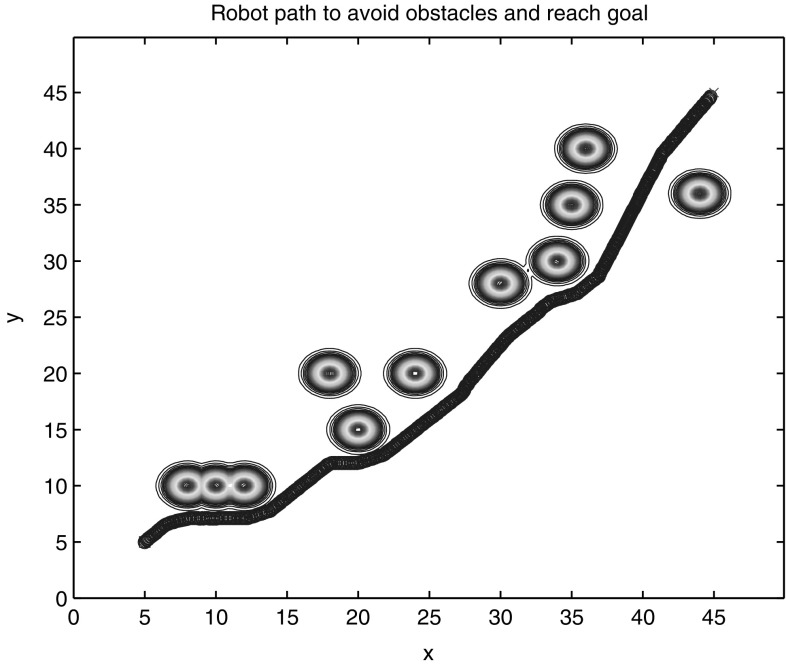
RNH-QL method is adopted for the route searching, which is proposed in this paper. A discrete Q table is used at the lower level, and RBF network is used for the upper, and their parameters are set in accordance with “The learning performance of standard Q-learning” and “The performance of Q-learning based on RBF network” sections.

The learning of RBF network and the Q table started at the same time in the front 300 rounds independently. The reward shaping function isn’t joined into the process because the trend knowledge didn’t form at the beginning of study. After the neural network is fully trained, the neural network would inspire the Q table with shaping function on the 300th round. The average steps of each round would rise with shaping knowledge, because of the process of mutual adaptation and adjustment between the 2 layers. After about 400 rounds, the average steps of each round plummeted suddenly, and after 650 rounds, learning steps became stable, and the optimal results were gotten. The test result of the 3000th round is shown in Fig. 9. By visual inspection, such a route is an ideal result, but whether its search capability is optimal or not, it will be described and compared in the details below.

Fig. 9.

The result of RNH-QL

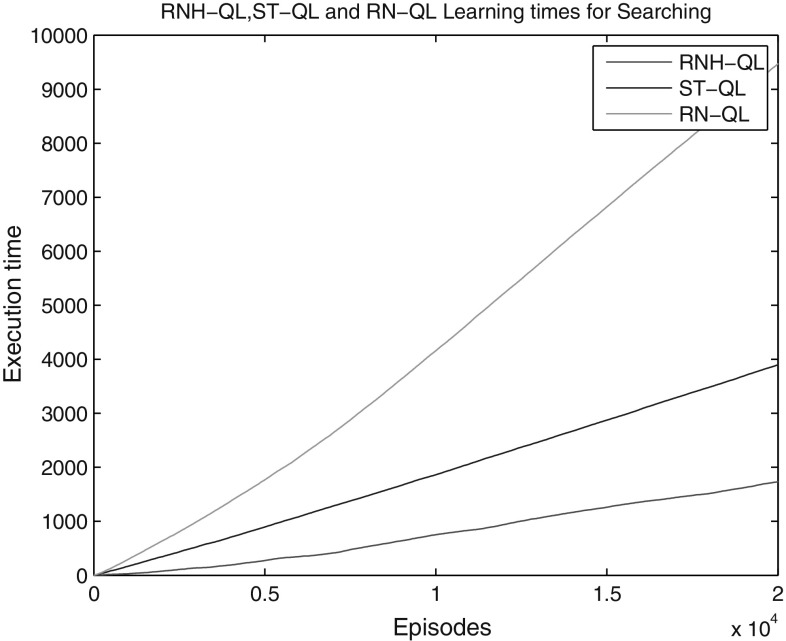
The comparison of three learning methods’ performance is shown in Fig. 10. The unit of execution time is $\mathrm{\mu }\text{s}$ according to the nearby 1000 rounds of mean learning steps for graphics rendering. For completing the same task to gain the goal for route searching, the wheel of time for RNH-QL to learn was minimal (about 1800 $\mathrm{\mu }\text{s}$), followed by ST-QL (about 4000 $\mathrm{\mu }\text{s}$), and RN-QL is the longest (about 9500 $\mathrm{\mu }\text{s}$). RBF network needs to optimize the network’ performance with continuous training and learning, so the execution time of RN-QL will increase. Some redundancy was produced in the process of searching the target, so ST-QL’s continuous learning and training time was increasing.

Fig. 10.

The execution time of three methods

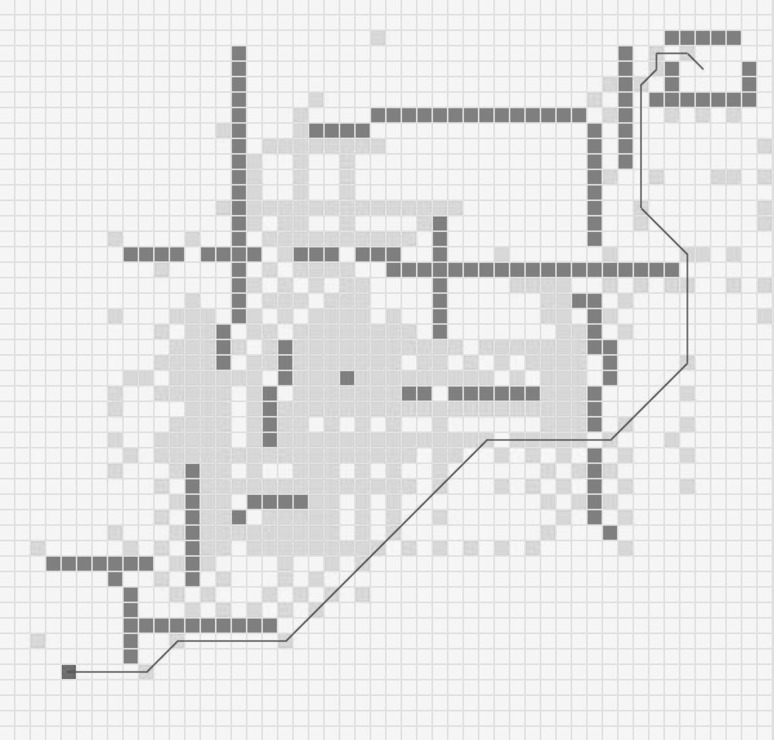
The result of RNH-QL is shown in Fig. 8, it could be regarded as an ideal result. In order to have a detail about the process of simulation, a relatively complex process of route searching is designed in Fig. 11. An object oriented programming method is used in the design of the experiment. Although the experiment looks more complicated, the essence of the algorithm is the same. A 50 × 50 grid map is adopted for experimental domain, the start position is set as a dark green point and the end position is set as a yellow point, the single and sequential gray points are walls (obstacles), the light green points are efficient points that could be arrived in searching. The route is a set of efficient points and we could get a part of route through connecting two efficient points. So, there are many routes in the grid map, therefore, our work is to find a shortest route. The efficient points (including start point and end point) could be put into a collection of tree (a way to store in data structure) and the search algorithm is designed to find the efficient points. In the end, we just starting from the target node (nodes are commonly used in data structure) and traverse along their parent nodes to the end of the beginning, a shortest route could be obtained. The red line is the shortest and optimal route.

Fig. 11.

The result of route searching in grid map

The RNH-QL algorithm is the core of this article. The comparison of three learning methods’ performance has been present in previous paper. Obviously, the result of route searching with RNH-QL algorithm is shortest and optimal. Then, some detailed analysis will be described through the next simulation diagrams. Figure 12 is the statistical analysis of the steps per episode and the average cumulative reward. The blue part is the steps per episode and green part is the average cumulative reward per step in the diagrams. With the increase of the episodes, both of them will tend to be stable. The difference of the four diagrams is the learning rate $\mathrm{\alpha }$. For any finite Markov prediction task, under batch updating, a small $\mathrm{\alpha }$ could be more efficient. So $\mathrm{\alpha }=0.1$ was selected for pervious simulations.

Fig. 12.

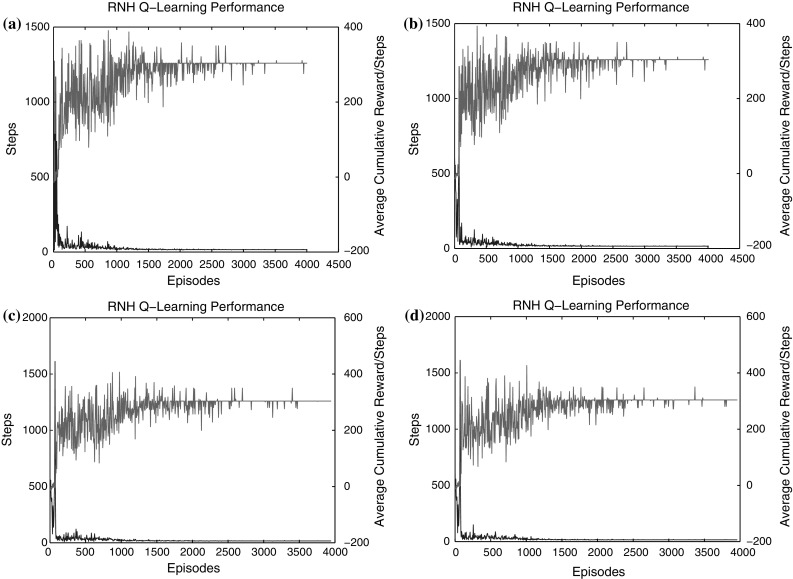
The steps per episode and the average cumulative reward

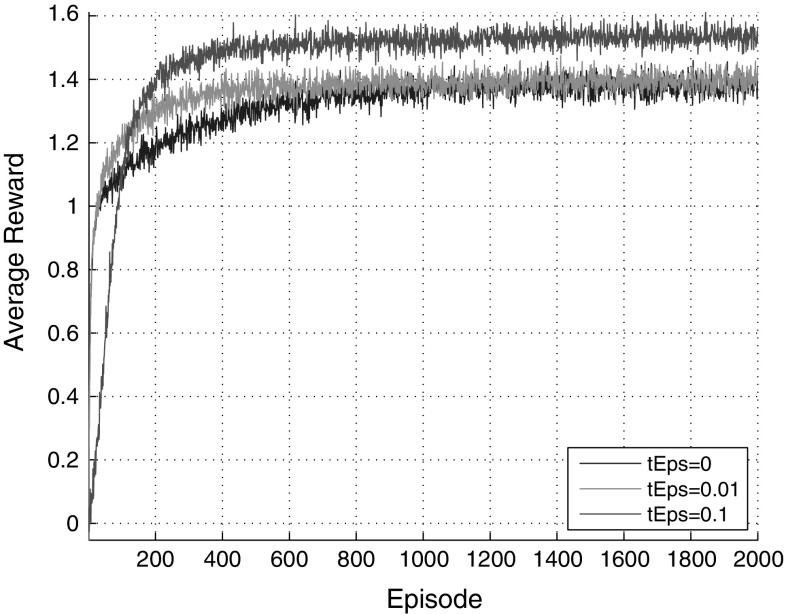
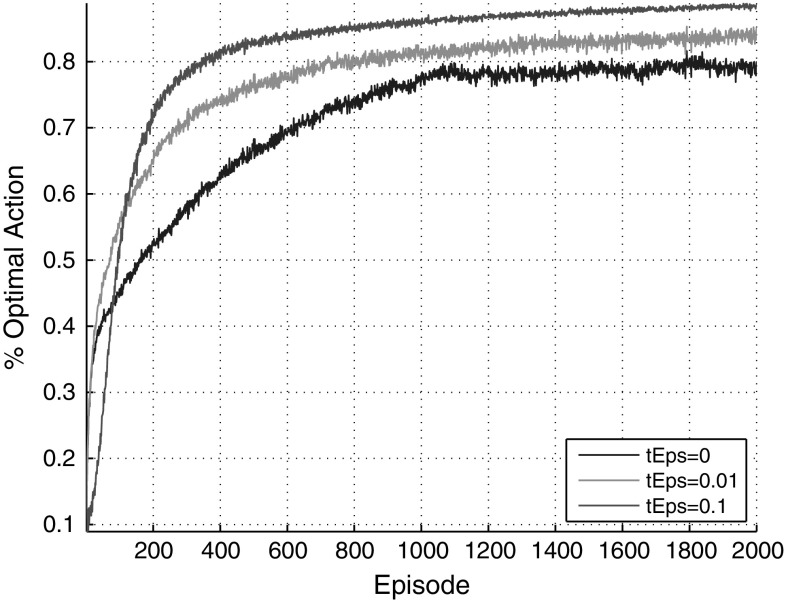
The mechanism of $\mathrm{\epsilon }\text{-}greedy$ action selection is present in Figs. 13 and 14. Each action is chosen randomly from a normal distribution. The whole process of searching has been repeated 2000 times and the average reward is present in figures. The value of $\mathrm{\epsilon }$ is been set to 0, 0.01 and 0.1 respectively. The most average reward per episode will be got and the probability of optimal action will be the highest with the increase of the episodes when $\mathrm{\epsilon }=0.1$. So $\mathrm{\epsilon }=0.1$ was selected for pervious simulations.

Fig. 13.

The average reward per episode

Fig. 14.

The optimal action per episode

The comparison and analysis of different methods

In order to verify the validity of RNH-QL algorithm, different learning methods are used for simulation test based on the same problem in the same environment. The maximum test round is 3000. In each round, if the agent could find the target or perform the steps more than 200th, it would write down the steps of this around, and start a new round to study with a randomized initial position. Clearer graphics could reflect the decreasing trend of learning steps with the rounds increasing continuously.

As shown in Fig. 7, RN-QL learning presents the worst results, because it is hard for the learning methods based on neural network to describe the trend of strategy in the obstacle areas properly and it is easy to mislead the agent’s action. If an ideal result will be expected, both the number of hidden layer nodes of neural network and learning rounds should be increased.

The standard Q-learning method presents the disadvantage of blindness, greater random and more lacking of guidance in large state spaces. Although it is not easy to fall into extreme points, the learning performance is rather poor, and this problem is particularly obvious in the larger state space. The potential function heuristic reinforcement learning (PFH-RL) was put forward by Ng et al. (1999). It is effective to stimulate and study with the better performance at the beginning of learning. However, the heuristic information is static, so it is easy to mislead the whole learning process with some wrong or inappropriate guidance, which could make the learning process unstable. Although it is easy to get the optimized results finally, the time of learning is relatively long. The SARSA-RS method was put forward by Grzes and Kudenko (2008) to avoid the shortcomings of PFH-RL method. It could establish heuristic knowledge with dynamic clustering in the process of learning, thus the learning efficiency would be improved obviously.

The proposed RNH-QL method is a combination of standard Q-learning method based on RBF network’s flexibility, generalization performance and predictability, which can form a trend of neural network in the upper or the lower levels after giving guidance, so as to find the search target quickly. Standard Q-learning’s flexibility can avoid the agent move into extreme value points and generalization ability of neural network can make the agent get the search direction and avoid blind action.

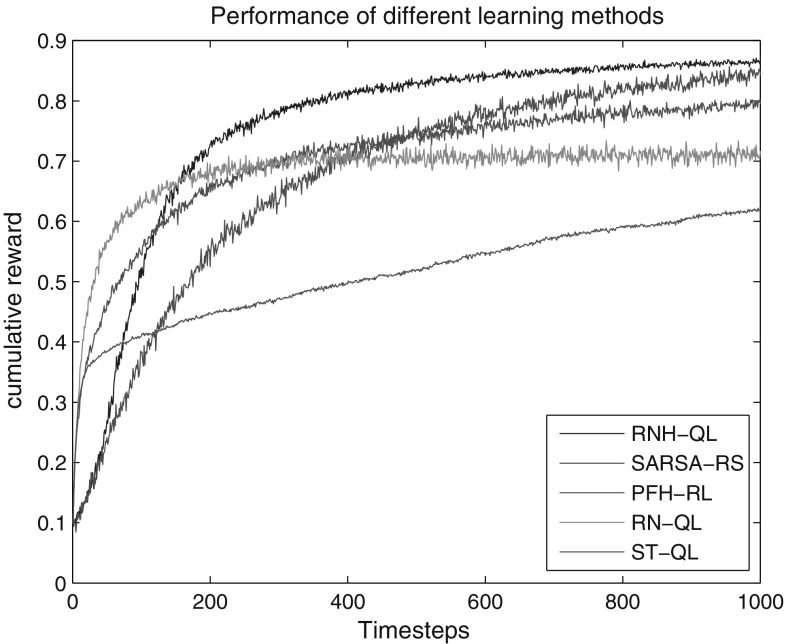
Figure 15 compares the learning performance of various methods. The initial reward is 0.1. The blue line shows the RNH-QL to be the most efficient approach after 1000 steps, the cumulative reward through training iterations is 0.86. Comparison of the same experiment configurations, SARSA-RS (green line) could approach to the RNH-QL in the end, the cumulative reward is 0.85. PFH-RL (red line), RN-QL (light-blue line) and ST-QL (purple line) are growing fast in the early stages, the accumulation speed become slow in the medium with the reward is 0.8, 0.71 and 0.62 respectively in the end. Therefore, the proposed strategies allow RNH-QL method to learn more efficiently and more effectively.

Fig. 15.

Learning performance of five methods’ cumulative reward

The state scale enlarged RNH-QL algorithm performance

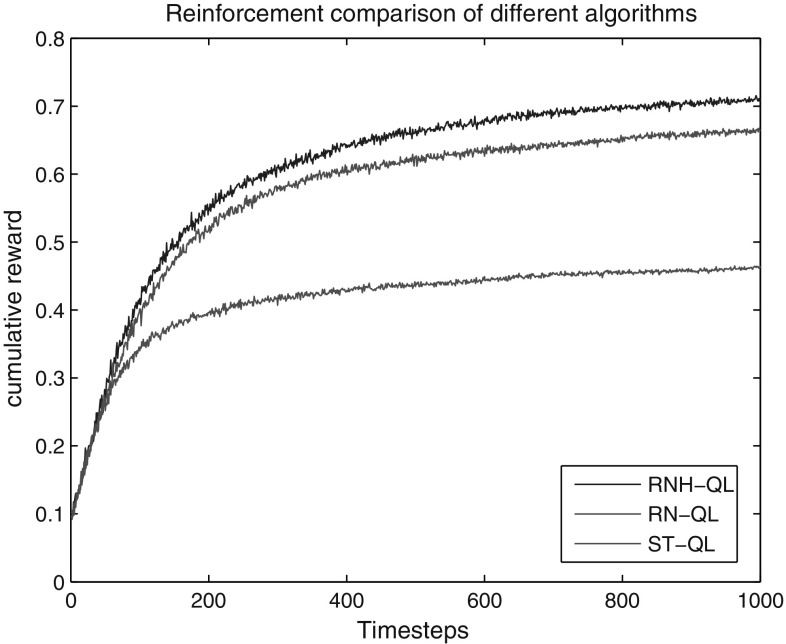
The status space of an agent is size of M × N = 40 × 40 = 1600 in this section and the event space is 4, so the strategy space is size of $4^{1600}$. Then the state space is expanded into M × N = 50 × 50 = 2500 and it keeps the same event space, thus its strategy space becomes $4^{2500}$, therefore, $4^{900}$-fold strategy space has been expanded to the previous. The RNH-QL approach has been adopted to research and other parameters are all set to the same as above. After approximately 300 rounds of learning, the average steps of each round tend to be gradually stabilized, and it can be successful to search the optimal route. The experimental results are shown in Fig. 16.

Fig. 16.

The learning effectiveness of three methods’ average cumulative reward

In a large state space, the RNH-QL method outperforms standard Q-learning method and mere learning method based on RBF network, and the acceleration of algorithm’s performance is more obvious. In order to accomplish the same task of route searching, using the algorithm of RNH-QL with cumulating more rewards.

Conclusion and discussion

This article proposed an improved and much stronger RNH-QL method based on reinforcement learning and RBF network. Previous researches verify that rewarding shaping is a powerful technique to incorporate background knowledge into RL agents. But one problem with this approach is that it’s difficult enough to be represented directly in the form of a shaped reward because of detailed knowledge of states’ potential function is not available and simple heuristic functions were used. For this reason, this paper discusses solutions which will allow the application of potential-based reward shaping when the potential function cannot be defined manually.

On the other hand, the state space scale will be lower with a linear growth, but the strategy space will become complex with the scale of index, so it is difficult for the Q-learning to adapt to large scale problems. By using the adaptive method of RBF network based on the form of Q-learning process with the ideas of potential-based reward shaping, RNH-QL makes the learning efficiency greatly increased.

The experimental results show that the application of RNH-QL algorithm is able to make more favorable decision by itself. And it has the advantage of more adaptability to the environment for an agent in a complex environment. Meanwhile, it can make the agent handle a large amount of state-action information by utilizing neural network and then enhance the execution efficiency. The RNH-QL algorithm is an effective method for route searching, but it couldn’t be regard as a most effective method in grid-world. A* algorithm and Jump Point Search (JPS) algorithm are widely used in route searching and path planning. I will consider utilizing them combined with neural network and reinforcement learning in future study.

An important topic to be investigated in future works is the use of generalization in the value function space to generate the heuristic function and improve the ability of error correction in high-level plan knowledge. Up to this time, the application of plan-based reward shaping to multi-agent learning has been possible in Devlin and Kudenko (2016). Furthermore, the trained neural networks in RNH-QL can be applied as a part of Q-learning for robots to avoid the obstacles and navigate the direction. Our team has thorough research in cell neural networks and memristor (see Li et al. 2015; Wang et al. 2016a, b). Due to the advantage of memristor and the existing results of our related work, the method can be applied to the adaptive control, network routing, intelligent transportation, resource allocation, robot navigation and other fields.