Global asymptotic stability of complex-valued neural networks with additive time-varying delays

Abstract

In this paper, we extensively study the global asymptotic stability problem of complex-valued neural networks with leakage delay and additive time-varying delays. By constructing a suitable Lyapunov–Krasovskii functional and applying newly developed complex valued integral inequalities, sufficient conditions for the global asymptotic stability of proposed neural networks are established in the form of complex-valued linear matrix inequalities. This linear matrix inequalities are efficiently solved by using standard available numerical packages. Finally, three numerical examples are given to demonstrate the effectiveness of the theoretical results.

Introduction

In the past decades, there have been increasing research interests in analyzing the dynamic behaviors of neural networks due to their widespread applications (Guo and Li 2012; Manivannan and Samidurai 2016; Mattia and Sanchez-Vives 2012; Yu et al. 2013), and the references therein. In many applications, complex signals are involved and complex-valued neural network is preferable. In the recent years, the complex-valued neural network is an emerging field of research in both theoretical and practical points of view. The major advantage of complex-valued neural networks is to explore new capabilities and higher performance of the designed network. According to that there has been increasing attention paid to study the dynamical behavior of the complex-valued neural networks and found an applications in different areas, such as pattern classification problems (Nait-Charif 2010), associative memory (Tanaka and Aihara 2009) and optimization problems (Jiang 2008). The equilibrium point of those existing applications are necessary to keep the networks to be stable. Therefore, the stability analysis is the most important dynamical property of complex-valued neural networks.

In real life situation, a time delay often occurs for the reason of the finite switching speed of the amplifiers, and it also appears in the electronic implementation of the neural networks when processing the signal transmission, which may cause the dynamical behaviors of neural networks in the form of instability, bifurcation and oscillation (Alofi et al. 2015; Cao and Li 2017; Hu et al. 2014; Huang et al. 2017). Thus, many authors have taken into account the constant time delays (Hu and Wang 2012; Subramanian and Muthukumar 2016) and time-varying delays (Chen et al. 2017; Gong et al. 2015) in the stability analysis of complex-valued neural networks.

In addition, a time delay in leakage term of the systems, which is called the leakage delay and a considerable factor affecting dynamics for the worse in the systems, is being put to use in the stability analysis of neural networks. The aforesaid results (Bao et al. 2016; Chen et al. 2017; Gong et al. 2015; Hu and Wang 2012; Subramanian and Muthukumar 2016) concerning the dynamical behavior analysis of the complex-valued neural networks with constant time delays or time-varying delays and did not consider the leakage effect. Even though, the leakage delay is extensively studied for real-valued neural networks (Lakshmanan et al. 2013; Li and Cao 2016; Sakthivel et al. 2015; Xie et al. 2016), the complex-valued neural networks with leakage delay has been rarely considered in the literature (Chen and Song 2013; Chen et al. 2016; Gong et al. 2015). As an example, by constructing an appropriate Lyapunov–Krasovskii functionals, the authors Gong et al. (2015) and Chen et al. (2016), respectively, studied the global $\mathit{\mu }$-stability problem for the continuous-time and discrete-time complex-valued neural networks with leakage time delay and unbounded time-varying delays. By employing a combination of fixed point theory, Lyapunov–Krasovskii functional and the free weighting matrix method, the existence, uniqueness and global stability of the equilibrium point of complex-valued neural networks with both leakage delay and time delay on time scales are established in Chen and Song (2013).

Furthermore, the neural networks model with two successive time-varying delays has been introduced in Zhao et al. (2008) and the authors correctly pointed out that since signal transmissions may experience a few segment of networks and the conditions of network transmission may differ for each other, which can possibly produce successive delays with different properties. It is not rational to lump the two time delays into one time delay. Thus, it is more reasonable to model the neural networks with additive time-varying delays. In Shao and Han (2012), the authors discussed the stability and stabilization for continuous-time systems with two additive time-varying input delays arising from networked control systems. The problem of stability criteria of neural networks with two additive time-varying delay components are addressed in Tian and Zhong (2012) by using the both reciprocally convex and convex polyhedron approach. The authors Rakkiyappan et al. (2015) studied the passivity and passification problem for a class of memristor-based recurrent neural networks with additive time-varying delays. From the above, the additive time-varying delays are only presented in the real-valued neural networks in the previous literature.

However, it is worth noting that in those existing results, the time-varying delay considered in the complex-valued neural networks is usually a single. Stability research on complex-valued neural networks with additive time-varying delays has not been considered in the literature, which motivates our research interesting. To the best of authors knowledge, the global asymptotic stability analysis for complex-valued neural networks with leakage delays and additive time-varying delays has not been considered in the literature, and remains as a topic for further investigation.

In this paper, the main contributions are given as follows:

• It is the first time to establish the global asymptotic stability of complex-valued neural networks with leakage delays and additive time-varying delay components.

• A suitable Lyapunov–Krasovskii functional is constructed with the full information of additive time-varying delays and leakage delays.

• A new type of complex-valued triple integral inequality is introduced to estimate the upper bound of the derivative of Lyapunov–Krasovskii functional.

• Based on the model transformation technique, sufficient conditions for the global asymptotic stability of proposed neural networks are obtained in the linear matrix inequality form, which can be checked numerically by using the effective YALMIP toolbox in MATLAB.

• Finally, three illustrative examples are provided to show the effectiveness of the proposed criteria.

The rest of this paper is organized as follows: In “Problem formulation and preliminaries” section, the model of the complex-valued neural networks with leakage delay and additive time-varying delays is presented, and some preliminaries are briefly outlined. In “Main result” section, the sufficient conditions are derived to ascertain the global asymptotic stability of the complex-valued neural networks with leakage delay and additive time-varying delays by Lyapunov–Krasovskii functional method. Three numerical examples are given to show the effectiveness of the acquired conditions in “Numerical example” section. Finally, conclusions are drawn in “Conclusion” section.

Notations

The notation used throughout this paper is fairly standard. ${\mathbb{C}}^n$ and ${\mathbb{C}}^{m\times n}$ denote the set of n-dimensional complex vectors, $m\times n$ complex matrices, respectively. The superscript T and $\ast$ denotes the matrix transposition and complex conjugate transpose, respectively; i denotes the imaginary unit, that is $i=\sqrt{-1}$. For any matrix P, $P>0$ $(P<0)$ means P is positive definite (negative definite) matrix. For complex number $z=x+iy$, the notation $|z|=\sqrt{x^2+y^2}$ stands for the module of z and $\Vert z\Vert =\sqrt{z^{\ast }z}$; $\text{diag}\{·\}$ stands for diagonal of the block- diagonal matrix. If $A\in {\mathbb{C}}^{n\times n}$, denotes by $\Vert A\Vert$ its operator norm, i.e., $\Vert A\Vert =sup\{\Vert Ax\Vert :\Vert x\Vert =1\}=\sqrt{{\mathit{\lambda }}_{max}(A^{\ast }A)}$. The notation $\star$ always denotes the conjugate transpose of block in a Hermitian matrix.

Problem formulation and preliminaries

In this paper, we consider a model of complex-valued neural networks with leakage delay and two additive time-varying delay components, which can be described by

$$\begin{array}{c}\hfill \dot{u}(t)=-Au(t-\mathit{\sigma })+Bg(u(t))+Cg(u(t-{\mathit{\tau }}_1(t)-{\mathit{\tau }}_2(t)))+J,\end{array}$$ 1

where $u(t)={(u_1(t),u_2(t),\dots ,u_n(t))}^T\in {\mathbb{C}}^n$ is the state vector of the neural networks with n neurons at time t, $A=diag\{a_1,a_2,\dots ,a_n\}\in {\mathbb{R}}^{n\times n}$ with $a_j>0(j=1,2,\dots ,n)$ is the self feedback connection weight matrix. $B={(b_{jk})}_{n\times n}\in {\mathbb{C}}^{n\times n}$ and $C={(c_{jk})}_{n\times n}\in {\mathbb{C}}^{n\times n}$ are the connection weight matrix and delayed connection weight matrix, respectively; $g(u(t))={(g_1(u_1(·)),g_2(u_2(·)),\dots ,g_n(u_n(·)))}^T\in {\mathbb{C}}^n$ is the complex-valued neuron activation function; $J={(J_1,J_2,\dots ,J_n)}^T$ is the external input vector; $\mathit{\sigma }$ denotes leakage delay, ${\mathit{\tau }}_1(t)$ and ${\mathit{\tau }}_2(t)$ are two time varying delays satisfies $0\le {\mathit{\tau }}_1(t)\le {\mathit{\tau }}_1$, ${\dot{\mathit{\tau }}}_1(t)\le {\mathit{\mu }}_1$, $0\le {\mathit{\tau }}_2(t)\le {\mathit{\tau }}_2$, ${\dot{\mathit{\tau }}}_2(t)\le {\mathit{\mu }}_2$, $\mathit{\tau }(t)={\mathit{\tau }}_1(t)+{\mathit{\tau }}_2(t)$, $\mathit{\tau }={\mathit{\tau }}_1+{\mathit{\tau }}_2$, $\mathit{\mu }={\mathit{\mu }}_1+{\mathit{\mu }}_2$ and ${\mathit{\mu }}_1,{\mathit{\mu }}_2,\mathit{\mu }$ are less than one. The initial condition associated with the complex-valued neural network (1) is given by

$$\begin{array}{c}\hfill u(s)=\mathit{\varphi }(s),s\in [-\mathit{\rho },0],\text{where}\mathit{\rho }\in max\{\mathit{\sigma },\mathit{\tau }\},\mathit{\varphi }\in C([-\mathit{\rho },0],D).\end{array}$$

It means that u(s) is continuous and satisfies (1). Let $C([-\mathit{\rho },0],D)$ be the space of continuous functions mapping $[-\mathit{\rho },0]$ into $D\in {\mathbb{C}}^n.$

Assumption 2.1

Let $g_j(·)$ satisfies the Lipschitz continuity condition in the complex domain, that is, for all $j=1,2,\dots ,n$, there exists a positive constant ${\widehat{F}}_j$, such that, for $u_1,u_2\in \mathbb{C}$, we have

$$\begin{array}{c}\hfill |g_j(u_1)-g_j(u_2)|\le {\widehat{F}}_j|u_1-u_2|.\end{array}$$

Definition 2.2

The vector $\widehat{u}\in {\mathbb{C}}^n$ is said to be an equilibrium point of complex valued neural networks (1) if it satisfies the following condition

$$\begin{array}{c}\hfill -A\widehat{u}+(B+C)g(\widehat{u})+J=0.\end{array}$$

Theorem 2.3

(Existence of equilibrium point) Under the Assumption  2.1, there exist an equilibrium point $\widehat{u}\in {\mathbb{C}}^n$ for the system (1) if

$$\begin{array}{c}\hfill -A\widehat{u}+(B+C)g(\widehat{u})+J=0.\end{array}$$

Proof

Since the activation function of the system (1) is bounded, there exists a constant $M_i$ such that,

$$\begin{array}{c}\hfill |g_i(u_i)|\le M_i\text{for}\text{any}{u}_i\in \mathbb{C},i=1,2,\dots ,n.\end{array}$$

Let $M=\sum _{i=1}^n{(M_i^2)}^{\frac{1}{2}}$. Then $\Vert g(u)\Vert \le M,$ for $u=(u_1,u_2,\dots ,u_n)\in {\mathbb{C}}^n.$ We denote $\mathcal{A}=\{u\in {\mathbb{C}}^n:\Vert u\Vert \le \Vert A^{-1}\Vert (\Vert B+C\Vert )M+\Vert J\Vert \}$ and let us define the map ${\mathbb{C}}^n\to {\mathbb{C}}^n$ by,

$$\begin{array}{c}\hfill H(u)=A^{-1}(Bg(u)+Cg(u)+J).\end{array}$$

Since, H is a continuous map and using the condition $\Vert g(u)\Vert \le M,$ we obtain that

$$\begin{array}{c}\hfill \Vert H(u)\Vert \le \Vert A^{-1}\Vert (\Vert B+C\Vert M+\Vert J\Vert ).\end{array}$$

Therefore from the definition of $\mathcal{A}$, H maps $\mathcal{A}$ into itself. By Brouwers fixed point theorem, it can be inferred that there exist a fixed point $\widehat{u}$ of H, which satisfies

$$\begin{array}{c}\hfill A^{-1}(Bg(\widehat{u})+Cg(\widehat{u})+J)=\widehat{u}.\end{array}$$

Pre multiplying by the matrix A on both sides, gives

$$\begin{array}{c}\hfill -A\widehat{u}+Bg(\widehat{u})+Cg(\widehat{u})+J=0.\end{array}$$

That is, by Definition 2.2, $\widehat{u}$ is an equilibrium point of (1). Hence, the proof is completed. $\square$

For convenience, we shift the equilibrium point $\widehat{u}$ to the origin by letting $z(t)=u(t)-\widehat{u}.$ Then, the system (1) can be written as

$$\begin{array}{c}\hfill \dot{z}(t)=-Az(t-\mathit{\sigma })+Bf(z(t))+Cf(z(t-{\mathit{\tau }}_1(t)-{\mathit{\tau }}_2(t))).\end{array}$$ 2

where, $f(z(t))=g(z(t)+\widehat{u})-g(\widehat{u}).$ By using the transformation, the system (2) has an equivalent form as follows

$$\begin{array}{c}\hfill \frac{d}{dt}\left[z(t)-A\underset{t-\mathit{\sigma }}{\overset{t}{\int }}z(s)ds\right]=-Az(t)+Bf(z(t))+Cf(z(t-{\mathit{\tau }}_1(t)-{\mathit{\tau }}_2(t))).\end{array}$$ 3

In the following, we introduce relevant assumption and lemmas to facilitate the presentation of main results in the ensuing sections.

Assumption 2.4

Let $f_j(·)$ satisfies the Lipschitz continuity condition in the complex domain, that is, for all $j=1,2,\dots ,n$, there exists a positive constant $F_j$, such that, for $z_1,z_2\in \mathbb{C}$, we have

$$\begin{array}{c}\hfill |f_j(z_1)-f_j(z_2)|\le F_j|z_1-z_2|,\end{array}$$

where $F_j$ is called Lipschitz constant. Moreover, define $\mathrm{\Gamma }=\text{diag}\{F_1^2,F_2^2,\dots ,F_n^2\}.$

Lemma 2.5

Velmurugan et al. (2015)(Schur Complement) A given matrix,

$$\begin{array}{c}\hfill \mathrm{\Omega }=\left(\begin{array}{cc}{\mathrm{\Omega }}_{11}& {\mathrm{\Omega }}_{12}\\ {\mathrm{\Omega }}_{12}^T& {\mathrm{\Omega }}_{22}\end{array}\right)>0,\end{array}$$

where ${\mathrm{\Omega }}_{11}={\mathrm{\Omega }}_{11}^T$, ${\mathrm{\Omega }}_{22}={\mathrm{\Omega }}_{22}^T$ is equivalent to any one of the following conditions

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_{22}>0,{\mathrm{\Omega }}_{11}-{\mathrm{\Omega }}_{12}^T{\mathrm{\Omega }}_{22}^{-1}{\mathrm{\Omega }}_{12}>0,\\ \hfill {\mathrm{\Omega }}_{11}>0,{\mathrm{\Omega }}_{22}-{\mathrm{\Omega }}_{12}{\mathrm{\Omega }}_{11}^{-1}{\mathrm{\Omega }}_{12}^T>0.\end{array}$$

Lemma 2.6

For any constant Hermitian matrix $M\in {\mathbb{C}}^{n\times n}$ and $M>0$, a scalar function $z(s):[a,b]\to {\mathbb{C}}^n$ with scalars $a<b$ such that the following inequalities are satisfied:

• (i) ${\left(\underset{a}{\overset{b}{\int }}z(s)ds\right)}^{\ast }M\left(\underset{a}{\overset{b}{\int }}z(s)ds\right)\le (b-a)\underset{a}{\overset{b}{\int }}{z}^{\ast }(s)Mz(s)ds$
• (ii) ${\left(\underset{a}{\overset{b}{\int }}\underset{s}{\overset{b}{\int }}z(\mathit{\theta })d\mathit{\theta }ds\right)}^{\ast }M\left(\underset{a}{\overset{b}{\int }}\underset{s}{\overset{b}{\int }}z(\mathit{\theta })d\mathit{\theta }ds\right)\le \frac{{(b-a)}^2}{2}\underset{a}{\overset{b}{\int }}\underset{s}{\overset{b}{\int }}{z}^{\ast }(\mathit{\theta })Mz(\mathit{\theta })d\mathit{\theta }ds$
• (iii) ${\left(\underset{a}{\overset{b}{\int }}\underset{s}{\overset{b}{\int }}\underset{\mathit{\theta }}{\overset{b}{\int }}z(\mathit{\gamma })d\mathit{\gamma }d\mathit{\theta }ds\right)}^{\ast }M\left(\underset{a}{\overset{b}{\int }}\underset{s}{\overset{b}{\int }}\underset{\mathit{\theta }}{\overset{b}{\int }}z(\mathit{\gamma })d\mathit{\gamma }d\mathit{\theta }ds\right)\le \frac{{(b-a)}^3}{6}\underset{a}{\overset{b}{\int }}\underset{s}{\overset{b}{\int }}\underset{\mathit{\theta }}{\overset{b}{\int }}{z}^{\ast }(\mathit{\gamma })Mz(\mathit{\gamma })d\mathit{\gamma }d\mathit{\theta }ds.$

Proof

The proof of complex-valued Jensen’s inequality (i) is given in Chen and Song (2013). Therefore, we have to prove (ii) and (iii) as follows:

From (i), the following inequality holds:

$$\begin{array}{c}\hfill {\left(\underset{s}{\overset{b}{\int }}z(\mathit{\theta })d\mathit{\theta }\right)}^{\ast }M\left(\underset{s}{\overset{b}{\int }}z(\mathit{\theta })d\mathit{\theta }\right)\le (b-s)\underset{s}{\overset{b}{\int }}{z}^{\ast }(\mathit{\theta })Mz(\mathit{\theta })d\mathit{\theta }.\end{array}$$

By the Schur complement Lemma (Velmurugan et al. 2015), the above inequality becomes,

$$\begin{array}{c}\hfill \left[\begin{array}{cc}\underset{s}{\overset{b}{\int }}{z}^{\ast }(\mathit{\theta })Mz(\mathit{\theta })d\mathit{\theta }& \underset{s}{\overset{b}{\int }}{z}^{\ast }(\mathit{\theta })d\mathit{\theta }\\ \underset{s}{\overset{b}{\int }}z(\mathit{\theta })d\mathit{\theta }& (b-s)M^{-1}\end{array}\right]\ge 0.\end{array}$$ 4

Integrating (4) from a to b, we have

$$\begin{array}{c}\hfill \left[\begin{array}{cc}\underset{a}{\overset{b}{\int }}\underset{s}{\overset{b}{\int }}{z}^{\ast }(\mathit{\theta })Mz(\mathit{\theta })d\mathit{\theta }ds& {\left(\underset{a}{\overset{b}{\int }}\underset{s}{\overset{b}{\int }}z(\mathit{\theta })d\mathit{\theta }ds\right)}^{\ast }\\ \underset{a}{\overset{b}{\int }}\underset{s}{\overset{b}{\int }}z(\mathit{\theta })d\mathit{\theta }ds& \underset{a}{\overset{b}{\int }}(b-s)M^{-1}ds\end{array}\right]\ge 0,\\ \hfill \left[\begin{array}{cc}\underset{a}{\overset{b}{\int }}\underset{s}{\overset{b}{\int }}{z}^{\ast }(\mathit{\theta })Mz(\mathit{\theta })d\mathit{\theta }ds& {\left(\underset{a}{\overset{b}{\int }}\underset{s}{\overset{b}{\int }}z(\mathit{\theta })d\mathit{\theta }ds\right)}^{\ast }\\ \underset{a}{\overset{b}{\int }}\underset{s}{\overset{b}{\int }}z(\mathit{\theta })d\mathit{\theta }ds& \frac{{(b-a)}^2}{2}{M}^{-1}\end{array}\right]\ge 0.\end{array}$$ 5

By using Schur complement Lemma, the inequality (5) is equivalent to

$$\begin{array}{c}\hfill {\left(\underset{a}{\overset{b}{\int }}\underset{s}{\overset{b}{\int }}z(\mathit{\theta })d\mathit{\theta }ds\right)}^{\ast }M\left(\underset{a}{\overset{b}{\int }}\underset{s}{\overset{b}{\int }}z(\mathit{\theta })d\mathit{\theta }ds\right)\le \frac{{(b-a)}^2}{2}\underset{a}{\overset{b}{\int }}\underset{s}{\overset{b}{\int }}{z}^{\ast }(\mathit{\theta })Mz(\mathit{\theta })d\mathit{\theta }ds.\end{array}$$

This completes the proof of (ii). By applying the same procedure presented in the proof of (ii), the inequality (iii) can be easily derived. Thus, it is omitted. $\square$

Main result

In this section, by utilizing a Lyapunov–Krasovskii functional and integral inequalities, we will present a delay-dependent stability criterion for the complex-valued neural networks with leakage delays and additive time-varying delays (3) via linear matrix inequality.

Theorem 3.1

Under Assumption 2.4, the complex-valued neural networks (3) is globally asymptotically stable, if there exist positive Hermitian matrices J, M, N, O, P, Q, R, S, T, U, V, W, X, Y and positive diagonal matrix G such that the following linear matrix inequality holds:

$$\begin{array}{c}\hfill \mathit{\Theta }=\left[\begin{array}{cccccccccccc}{\mathit{\Theta }}_{1,1}& 0& 0& W& X& 0& PB& PC& {\mathit{\Theta }}_{1,9}& 0& {\mathit{\tau }}_{1}M& {\mathit{\tau }}_{2}N\\ \star & {\mathit{\Theta }}_{2,2}& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ \star & \star & {\mathit{\Theta }}_{3,3}& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ \star & \star & \star & {\mathit{\Theta }}_{4,4}& 0& 0& 0& 0& 0& 0& 0& 0\\ \star & \star & \star & \star & {\mathit{\Theta }}_{5,5}& 0& 0& 0& 0& 0& 0& 0\\ \star & \star & \star & \star & \star & {\mathit{\Theta }}_{6,6}& {\mathit{\Theta }}_{6,7}& {\mathit{\Theta }}_{6,8}& 0& 0& 0& 0\\ \star & \star & \star & \star & \star & \star & {\mathit{\Theta }}_{7,7}& {\mathit{\Theta }}_{7,8}& {\mathit{\Theta }}_{7,9}& 0& 0& 0\\ \star & \star & \star & \star & \star & \star & \star & {\mathit{\Theta }}_{8,8}& {\mathit{\Theta }}_{8,9}& 0& 0& 0\\ \star & \star & \star & \star & \star & \star & \star & \star & {\mathit{\Theta }}_{9,9}& 0& 0& 0\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & {\mathit{\Theta }}_{10,10}& 0& 0\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & {\mathit{\Theta }}_{11,11}& 0\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & {\mathit{\Theta }}_{12,12}\end{array}\right]<0,\end{array}$$ 6

where ${\mathit{\Theta }}_{1,1}=-PA-A^{\ast }P+Q+R+S+T+U+{\mathit{\sigma }}^{2}Y-W-X-{\mathit{\sigma }}^{2}O+\frac{{\mathit{\sigma }}^6}{36}J+G\mathrm{\Gamma }-{\mathit{\tau }}_1^{2}M-{\mathit{\tau }}_2^{2}N$, ${\mathit{\Theta }}_{1,9}=A^{\ast }PA+\mathit{\sigma }O$, ${\mathit{\Theta }}_{2,2}=-(1-{\mathit{\mu }}_1)Q$, ${\mathit{\Theta }}_{3,3}=-(1-{\mathit{\mu }}_2)R$, ${\mathit{\Theta }}_{4,4}=-W-S$, ${\mathit{\Theta }}_{5,5}=-X-T$, ${\mathit{\Theta }}_{6,6}=-U+{\mathit{\tau }}_1^2{A}^{\ast }WA+{\mathit{\tau }}_2^2{A}^{\ast }XA+\frac{{\mathit{\tau }}_1^4}{4}{A}^{\ast }MA+\frac{{\mathit{\tau }}_2^4}{4}{A}^{\ast }NA+\frac{{\mathit{\sigma }}^4}{4}{A}^{\ast }OA$, ${\mathit{\Theta }}_{6,7}=-{\mathit{\tau }}_1^2{A}^{\ast }WB-{\mathit{\tau }}_2^2{A}^{\ast }XB-\frac{{\mathit{\tau }}_1^4}{4}{A}^{\ast }MB-\frac{{\mathit{\tau }}_2^4}{4}{A}^{\ast }NB-\frac{{\mathit{\sigma }}^4}{4}{A}^{\ast }OB$, ${\mathit{\Theta }}_{6,8}=-{\mathit{\tau }}_1^2{A}^{\ast }WC-{\mathit{\tau }}_2^2{A}^{\ast }XC-\frac{{\mathit{\tau }}_1^4}{4}{A}^{\ast }MC-\frac{{\mathit{\tau }}_2^4}{4}{A}^{\ast }NC-\frac{{\mathit{\sigma }}^4}{4}{A}^{\ast }OC$, ${\mathit{\Theta }}_{7,7}={\mathit{\tau }}_1^2{B}^{\ast }WB+{\mathit{\tau }}_2^2{B}^{\ast }XB+\frac{{\mathit{\tau }}_1^4}{4}{B}^{\ast }MB+\frac{{\mathit{\tau }}_2^4}{4}{B}^{\ast }NB+\frac{{\mathit{\sigma }}^4}{4}{B}^{\ast }OB+V-G$, ${\mathit{\Theta }}_{7,8}={\mathit{\tau }}_1^2{B}^{\ast }WC+{\mathit{\tau }}_2^2{B}^{\ast }XC+\frac{{\mathit{\tau }}_1^4}{4}{B}^{\ast }MC+\frac{{\mathit{\tau }}_2^4}{4}{B}^{\ast }NC+\frac{{\mathit{\sigma }}^4}{4}{B}^{\ast }OC$, ${\mathit{\Theta }}_{7,9}=-B^{\ast }PA$, ${\mathit{\Theta }}_{8,8}={\mathit{\tau }}_1^2{C}^{\ast }WC+{\mathit{\tau }}_2^2{C}^{\ast }XC+\frac{{\mathit{\tau }}_1^4}{4}{C}^{\ast }MC+\frac{{\mathit{\tau }}_2^4}{4}{C}^{\ast }NC+\frac{{\mathit{\sigma }}^4}{4}{C}^{\ast }OC-(1-\mathit{\mu })V$, ${\mathit{\Theta }}_{8,9}=-C^{\ast }PA$, ${\mathit{\Theta }}_{9,9}=-Y-O$, ${\mathit{\Theta }}_{10,10}=-J$, ${\mathit{\Theta }}_{11,11}=-M$, ${\mathit{\Theta }}_{12,12}=-N$.

Proof

Consider the following Lyapunov–Krasovskii functional

$$\begin{array}{c}\hfill V(t)=\sum _{j=1}^5{V}_i(t),\end{array}$$ 7

where

$$\begin{array}{cc}\hfill V_1(t)=& {\left[z(t)-\underset{t-\mathit{\sigma }}{\overset{t}{\int }}z(s)ds\right]}^{\ast }P\left[z(t)-\underset{t-\mathit{\sigma }}{\overset{t}{\int }}z(s)ds\right],\hfill \\ \hfill V_2(t)=& \underset{t-{\mathit{\tau }}_1(t)}{\overset{t}{\int }}{z}^{\ast }(s)Qz(s)ds+\underset{t-{\mathit{\tau }}_2(t)}{\overset{t}{\int }}{z}^{\ast }(s)Rz(s)ds+\underset{t-{\mathit{\tau }}_1}{\overset{t}{\int }}{z}^{\ast }(s)Sz(s)ds+\underset{t-{\mathit{\tau }}_2}{\overset{t}{\int }}{z}^{\ast }(s)Tz(s)ds\hfill \\ \hfill & +\underset{t-\mathit{\sigma }}{\overset{t}{\int }}{z}^{\ast }(s)Uz(s)ds+\underset{t-\mathit{\tau }(t)}{\overset{t}{\int }}{f}^{\ast }(z(s))Vf(z(s))ds,\hfill \\ \hfill V_3(t)=& {\mathit{\tau }}_1\underset{-{\mathit{\tau }}_1}{\overset{0}{\int }}\underset{t+\mathit{\theta }}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)W\dot{z}(s)dsd\mathit{\theta }+{\mathit{\tau }}_2\underset{-{\mathit{\tau }}_2}{\overset{0}{\int }}\underset{t+\mathit{\theta }}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)X\dot{z}(s)dsd\mathit{\theta }+\mathit{\sigma }\underset{-\mathit{\sigma }}{\overset{0}{\int }}\underset{t+\mathit{\theta }}{\overset{t}{\int }}{z}^{\ast }(s)Yz(s)dsd\mathit{\theta },\hfill \\ \hfill V_4(t)=& \frac{{\mathit{\tau }}_1^2}{2}\underset{t-{\mathit{\tau }}_1}{\overset{t}{\int }}\underset{\mathit{\theta }}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)M\dot{z}(s)dsd\mathit{\gamma }d\mathit{\theta }+\frac{{\mathit{\tau }}_2^2}{2}\underset{t-{\mathit{\tau }}_2}{\overset{t}{\int }}\underset{\mathit{\theta }}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)N\dot{z}(s)dsd\mathit{\gamma }d\mathit{\theta },\hfill \\ \hfill V_5(t)=& \frac{{\mathit{\sigma }}^2}{2}\underset{t-\mathit{\sigma }}{\overset{t}{\int }}\underset{\mathit{\theta }}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)O\dot{z}(s)dsd\mathit{\gamma }d\mathit{\theta }+\frac{{\mathit{\sigma }}^3}{6}\underset{t-\mathit{\sigma }}{\overset{t}{\int }}\underset{\mathit{\theta }}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}\underset{\mathit{\delta }}{\overset{t}{\int }}{z}^{\ast }(s)Jz(s)dsd\mathit{\delta }d\mathit{\gamma }d\mathit{\theta }.\hfill \end{array}$$

Taking the time derivative of V(t) along the trajectories of system (3), it follows that

$$\begin{array}{cc}\hfill {\dot{V}}_1(t)& =2{\left[z(t)-A\underset{t-\mathit{\sigma }}{\overset{t}{\int }}z(s)ds\right]}^{\ast }P[-Az(t)+Bf(z(t))+Cf(z(t-{\mathit{\tau }}_1(t)-{\mathit{\tau }}_2(t)))],\hfill \\ \hfill & =-2z^{\ast }(t)PAz(t)+2z^{\ast }(t)PBf(z(t))+2z^{\ast }(t)PCf(z(t-{\mathit{\tau }}_1(t)-{\mathit{\tau }}_2(t)))+2\underset{t-\mathit{\sigma }}{\overset{t}{\int }}{z}^{\ast }(s)ds{A}^{\ast }PAz(t)\hfill \\ \hfill & -2\underset{t-\mathit{\sigma }}{\overset{t}{\int }}{z}^{\ast }(s)ds{A}^{\ast }PBf(z(t))-2\underset{t-\mathit{\sigma }}{\overset{t}{\int }}{z}^{\ast }(s)ds{A}^{\ast }PCf(z(t-{\mathit{\tau }}_1(t)-{\mathit{\tau }}_2(t))),\hfill \end{array}$$ 8

$$\begin{array}{cc}\hfill {\dot{V}}_2(t)\le & z^{\ast }(t)[Q+R+S+T+U]z(t)-(1-{\mathit{\mu }}_1)z^{\ast }(t-{\mathit{\tau }}_1(t))Qz(t-{\mathit{\tau }}_1(t))-(1-{\mathit{\mu }}_2)z^{\ast }(t-{\mathit{\tau }}_2(t))R\hfill \\ \hfill & z(t-{\mathit{\tau }}_2(t))-z^{\ast }(t-{\mathit{\tau }}_1)Sz(t-{\mathit{\tau }}_1)-z^{\ast }(t-{\mathit{\tau }}_2)Tz(t-{\mathit{\tau }}_2)-z^{\ast }(t-\mathit{\sigma })Uz(t-\mathit{\sigma })\hfill \\ \hfill & +f^{\ast }(z(t))Vf(z(t))-(1-\mathit{\mu })f^{\ast }(z(t-\mathit{\tau }(t)))Vf(z(t-\mathit{\tau }(t))),\hfill \end{array}$$ 9

$$\begin{array}{cc}\hfill {\dot{V}}_3(t)& ={\dot{z}}^{\ast }(t)({\mathit{\tau }}_1^{2}W+{\mathit{\tau }}_2^{2}X)\dot{z}(t)+{\mathit{\sigma }}^2{z}^{\ast }(t)Yz(t)-{\mathit{\tau }}_1\underset{t-{\mathit{\tau }}_1}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)W\dot{z}(s)ds-{\mathit{\tau }}_2\underset{t-{\mathit{\tau }}_2}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)X\dot{z}(s)ds\hfill \\ \hfill & -\mathit{\sigma }\underset{t-\mathit{\sigma }}{\overset{t}{\int }}{z}^{\ast }(s)Yz(s)ds,\hfill \end{array}$$ 10

$$\begin{array}{cc}\hfill {\dot{V}}_4(t)& =\frac{{\mathit{\tau }}_1^2}{2}\underset{t-{\mathit{\tau }}_1}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}{\dot{z}}^{\ast }(t)M\dot{z}(t)dsd\mathit{\gamma }-\frac{{\mathit{\tau }}_1^2}{2}\underset{t-{\mathit{\tau }}_1}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)M\dot{z}(s)dsd\mathit{\gamma }+\frac{{\mathit{\tau }}_2^2}{2}\underset{t-{\mathit{\tau }}_2}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}{\dot{z}}^{\ast }(t)N\dot{z}(t)dsd\mathit{\gamma }\hfill \\ \hfill & -\frac{{\mathit{\tau }}_2^2}{2}\underset{t-{\mathit{\tau }}_2}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)N\dot{z}(s)dsd\mathit{\gamma },\hfill \\ \hfill & ={\dot{z}}^{\ast }(t)\left(\frac{{\mathit{\tau }}_1^4}{4}M+\frac{{\mathit{\tau }}_2^4}{4}N\right)\dot{z}(t)-\frac{{\mathit{\tau }}_1^2}{2}\underset{t-{\mathit{\tau }}_1}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)M\dot{z}(s)dsd\mathit{\gamma }-\frac{{\mathit{\tau }}_2^2}{2}\underset{t-{\mathit{\tau }}_2}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)N\dot{z}(s)dsd\mathit{\gamma },\hfill \end{array}$$ 11

$$\begin{array}{cc}\hfill {\dot{V}}_5(t)& =\frac{{\mathit{\sigma }}^2}{2}\underset{t-\mathit{\sigma }}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}{\dot{z}}^{\ast }(t)O\dot{z}(t)dsd\mathit{\gamma }-\frac{{\mathit{\sigma }}^2}{2}\underset{t-\mathit{\sigma }}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)O\dot{z}(s)dsd\mathit{\gamma }+\frac{{\mathit{\sigma }}^3}{6}\underset{t-\mathit{\sigma }}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}\underset{\mathit{\delta }}{\overset{t}{\int }}{z}^{\ast }(t)Jz(t)dsd\mathit{\delta }d\mathit{\gamma }\hfill \\ \hfill & -\frac{{\mathit{\sigma }}^3}{6}\underset{t-\mathit{\sigma }}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}\underset{\mathit{\delta }}{\overset{t}{\int }}{z}^{\ast }(s)Jz(s)dsd\mathit{\delta }d\mathit{\gamma },\hfill \\ \hfill & =\frac{{\mathit{\sigma }}^4}{4}{\dot{z}}^{\ast }(t)O\dot{z}(t)+\frac{{\mathit{\sigma }}^6}{36}{z}^{\ast }(t)Jz(t)-\frac{{\mathit{\sigma }}^2}{2}\underset{t-\mathit{\sigma }}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)O\dot{z}(s)dsd\mathit{\gamma }-\frac{{\mathit{\sigma }}^3}{6}\underset{t-\mathit{\sigma }}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}\underset{\mathit{\delta }}{\overset{t}{\int }}{z}^{\ast }(s)Jz(s)dsd\mathit{\delta }d\mathit{\gamma }.\hfill \end{array}$$ 12

Applying Lemma 2.6 (i) to the integral terms of (10) which produces that

$$\begin{array}{cc}\hfill -{\mathit{\tau }}_1\underset{t-{\mathit{\tau }}_1}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)W\dot{z}(s)ds\le & -\underset{t-{\mathit{\tau }}_1}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)dsW\underset{t-{\mathit{\tau }}_1}{\overset{t}{\int }}\dot{z}(s)ds=-{[z(t)-z(t-{\mathit{\tau }}_1)]}^{\ast }W[z(t)-z(t-{\mathit{\tau }}_1)],\hfill \end{array}$$ 13

$$\begin{array}{cc}\hfill -{\mathit{\tau }}_2\underset{t-{\mathit{\tau }}_2}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)X\dot{z}(s)ds\le & -\underset{t-{\mathit{\tau }}_2}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)dsX\underset{t-{\mathit{\tau }}_2}{\overset{t}{\int }}\dot{z}(s)ds=-{[z(t)-z(t-{\mathit{\tau }}_2)]}^{\ast }X[z(t)-z(t-{\mathit{\tau }}_2)],\hfill \end{array}$$ 14

$$\begin{array}{cc}\hfill -\mathit{\sigma }\underset{t-\mathit{\sigma }}{\overset{t}{\int }}{z}^{\ast }(s)Yz(s)ds\le & -\underset{t-\mathit{\sigma }}{\overset{t}{\int }}{z}^{\ast }(s)dsY\underset{t-\mathit{\sigma }}{\overset{t}{\int }}z(s)ds.\hfill \end{array}$$ 15

From (3) and (13)–(15), it follows that

$$\begin{array}{cc}\hfill {\dot{V}}_3(t)\le & z^{\ast }(t-\mathit{\sigma })[{\mathit{\tau }}_1^2{A}^{\ast }WA+{\mathit{\tau }}_2^2{A}^{\ast }XA]z(t-\mathit{\sigma })-z^{\ast }(t-\mathit{\sigma })[{\mathit{\tau }}_1^2{A}^{\ast }WB+{\mathit{\tau }}_2^2{A}^{\ast }XB]f(z(t))-z^{\ast }(t-\mathit{\sigma })\hfill \\ \hfill & [{\mathit{\tau }}_1^2{A}^{\ast }WC+{\mathit{\tau }}_2^2{A}^{\ast }XC]f(z(t-\mathit{\tau }(t)))-f^{\ast }(z(t))[{\mathit{\tau }}_1^2{B}^{\ast }WA+{\mathit{\tau }}_2^2{B}^{\ast }XA]z(t-\mathit{\sigma })+f^{\ast }(z(t))\hfill \\ \hfill & [{\mathit{\tau }}_1^2{B}^{\ast }WB+{\mathit{\tau }}_2^2{B}^{\ast }XB]f(z(t))+f^{\ast }(z(t))[{\mathit{\tau }}_1^2{B}^{\ast }WC+{\mathit{\tau }}_2^2{B}^{\ast }XC]f(z(t-\mathit{\tau }(t)))\hfill \\ \hfill & -f^{\ast }(z(t-\mathit{\tau }(t)))[{\mathit{\tau }}_1^2{C}^{\ast }WA+{\mathit{\tau }}_2^2{C}^{\ast }XA]z(t-\mathit{\sigma })+f^{\ast }(z(t-\mathit{\tau }(t)))[{\mathit{\tau }}_1^2{C}^{\ast }WB+{\mathit{\tau }}_2^2{C}^{\ast }XB]f(z(t))\hfill \\ \hfill & +f^{\ast }(z(t-\mathit{\tau }(t)))[{\mathit{\tau }}_1^2{C}^{\ast }WC+{\mathit{\tau }}_2^2{C}^{\ast }XC]f(z(t-\mathit{\tau }(t)))+z^{\ast }(t)[{\mathit{\sigma }}^{2}Y-W-X]z(t)-z^{\ast }(t-{\mathit{\tau }}_1)\hfill \\ \hfill & \times Wz(t-{\mathit{\tau }}_1)+z^{\ast }(t)Wz(t-{\mathit{\tau }}_1)+z^{\ast }(t-{\mathit{\tau }}_1)Wz(t)-z^{\ast }(t-{\mathit{\tau }}_2)Xz(t-{\mathit{\tau }}_2)+z^{\ast }(t)Xz(t-{\mathit{\tau }}_2)\hfill \\ \hfill & +z^{\ast }(t-{\mathit{\tau }}_2)Xz(t)-\underset{t-\mathit{\sigma }}{\overset{t}{\int }}{z}^{\ast }(s)dsY\underset{t-\mathit{\sigma }}{\overset{t}{\int }}z(s)ds.\hfill \end{array}$$ 16

By using Lemma 2.6 (2), the integral terms in (11) can be estimated as follows:

$$\begin{array}{cc}\hfill -\frac{{\mathit{\tau }}_1^2}{2}\underset{t-{\mathit{\tau }}_1}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)M\dot{z}(s)dsd\mathit{\gamma }\le & -\underset{t-{\mathit{\tau }}_1}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)dsd\mathit{\gamma }M\times \underset{t-{\mathit{\tau }}_1}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}\dot{z}(s)dsd\mathit{\gamma },\hfill \\ \hfill =& -{\left({\mathit{\tau }}_{1}z(t)-\underset{t-{\mathit{\tau }}_1}{\overset{t}{\int }}z(s)ds\right)}^{\ast }\times M\left({\mathit{\tau }}_{1}z(t)-\underset{t-{\mathit{\tau }}_1}{\overset{t}{\int }}z(s)ds\right),\hfill \end{array}$$ 17

$$\begin{array}{cc}\hfill -\frac{{\mathit{\tau }}_2^2}{2}\underset{t-{\mathit{\tau }}_2}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)M\dot{z}(s)dsd\mathit{\gamma }\le & -\underset{t-{\mathit{\tau }}_2}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)dsd\mathit{\gamma }N\underset{t-{\mathit{\tau }}_2}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}\dot{z}(s)dsd\mathit{\gamma },\hfill \\ \hfill =& -{\left({\mathit{\tau }}_{2}z(t)-\underset{t-{\mathit{\tau }}_2}{\overset{t}{\int }}z(s)ds\right)}^{\ast }N\left({\mathit{\tau }}_{2}z(t)-\underset{t-{\mathit{\tau }}_2}{\overset{t}{\int }}z(s)ds\right).\hfill \end{array}$$ 18

Then, substituting (17) and (18) into (11), yields

$$\begin{array}{cc}\hfill {\dot{V}}_4(t)\le & ;z^{\ast }(t-\mathit{\sigma })\left[\frac{{\mathit{\tau }}_1^4}{4}{A}^{\ast }MA+\frac{{\mathit{\tau }}_1^4}{4}{A}^{\ast }NA\right]z(t-\mathit{\sigma })-z^{\ast }(t-\mathit{\sigma })\left[\frac{{\mathit{\tau }}_1^4}{4}{A}^{\ast }MB+\frac{{\mathit{\tau }}_2^4}{4}{A}^{\ast }NB\right]f(z(t))-z^{\ast }(t-\mathit{\sigma })\hfill \\ \hfill & \times \left[\frac{{\mathit{\tau }}_1^4}{4}{A}^{\ast }MC+\frac{{\mathit{\tau }}_2^4}{4}{A}^{\ast }NC\right]f(z(t-\mathit{\tau }(t)))-f^{\ast }(z(t))\left[\frac{{\mathit{\tau }}_2^4}{4}{B}^{\ast }MA+\frac{{\mathit{\tau }}_2^4}{4}{B}^{\ast }NA\right]z(t-\mathit{\sigma })+f^{\ast }(z(t))\hfill \\ \hfill & \times \left[\frac{{\mathit{\tau }}_1^4}{4}{B}^{\ast }MB+\frac{{\mathit{\tau }}_2^4}{4}{B}^{\ast }NB\right]f(z(t))+f^{\ast }(z(t))\left[\frac{{\mathit{\tau }}_1^4}{4}{B}^{\ast }MC+\frac{{\mathit{\tau }}_2^4}{4}{B}^{\ast }NC\right]f(z(t-\mathit{\tau }(t)))\hfill \\ \hfill & -f^{\ast }(z(t-\mathit{\tau }(t)))\left[{\mathit{\tau }}_1^2{C}^{\ast }MA+{\mathit{\tau }}_2^2{C}^{\ast }NA\right]z(t-\mathit{\sigma })+f^{\ast }(z(t-\mathit{\tau }(t)))\left[{\mathit{\tau }}_1^2{C}^{\ast }MB+{\mathit{\tau }}_2^2{C}^{\ast }NB\right]\hfill \\ \hfill & f(z(t))+f^{\ast }(z(t-\mathit{\tau }(t)))\left[\frac{{\mathit{\tau }}_1^4}{4}{C}^{\ast }MC+\frac{{\mathit{\tau }}_2^4}{4}{C}^{\ast }NC\right]f(z(t-\mathit{\tau }(t)))-z^{\ast }(t)[{\mathit{\tau }}_1^{2}M+{\mathit{\tau }}_2^{2}N]z(t)\hfill \\ \hfill & -\underset{t-{\mathit{\tau }}_1}{\overset{t}{\int }}{z}^{\ast }(s)dsM\underset{t-{\mathit{\tau }}_1}{\overset{t}{\int }}z(s)ds+{\mathit{\tau }}_1{z}^{\ast }(t)M\underset{t-{\mathit{\tau }}_1}{\overset{t}{\int }}z(s)ds+{\mathit{\tau }}_1\underset{t-{\mathit{\tau }}_1}{\overset{t}{\int }}{z}^{\ast }(s)dsMz(t)\hfill \\ \hfill & -\underset{t-{\mathit{\tau }}_2}{\overset{t}{\int }}{z}^{\ast }(s)dsN\underset{t-{\mathit{\tau }}_2}{\overset{t}{\int }}z(s)ds+{\mathit{\tau }}_2{z}^{\ast }(t)N\underset{t-{\mathit{\tau }}_2}{\overset{t}{\int }}z(s)ds+{\mathit{\tau }}_2\underset{t-{\mathit{\tau }}_2}{\overset{t}{\int }}{z}^{\ast }(s)dsNz(t).\hfill \end{array}$$ 19

Similarly, by using Lemma 2.6 (ii) and (iii), the integral terms in ${\dot{V}}_5(t)$ can be obtained as follows:

$$\begin{array}{cc}\hfill -\frac{{\mathit{\sigma }}^2}{2}\underset{t-\mathit{\sigma }}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)O\dot{z}(s)dsd\mathit{\gamma }\le & -\underset{t-\mathit{\sigma }}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}{\dot{z}}^{\ast }(s)dsd\mathit{\gamma }O\times \underset{t-\mathit{\sigma }}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}\dot{z}(s)dsd\mathit{\gamma },\hfill \\ \hfill =& -{\left(\mathit{\sigma }z(t)-\underset{t-\mathit{\sigma }}{\overset{t}{\int }}z(s)ds\right)}^{\ast }\times O\left(\mathit{\sigma }z(t)-\underset{t-\mathit{\sigma }}{\overset{t}{\int }}z(s)ds\right),\hfill \end{array}$$ 20

$$\begin{array}{cc}\hfill -\frac{{\mathit{\sigma }}^3}{6}\underset{t-\mathit{\sigma }}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}\underset{\mathit{\delta }}{\overset{t}{\int }}{z}^{\ast }(s)Jz(s)dsd\mathit{\delta }d\mathit{\gamma }\le & -\underset{t-\mathit{\sigma }}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}\underset{\mathit{\delta }}{\overset{t}{\int }}{z}^{\ast }(s)dsd\mathit{\delta }d\mathit{\gamma }J\underset{t-\mathit{\sigma }}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}\underset{\mathit{\delta }}{\overset{t}{\int }}z(s)dsd\mathit{\delta }d\mathit{\gamma }.\hfill \end{array}$$ 21

Therefore, together with (12) and (20), (21), we get

$$\begin{array}{cc}\hfill {\dot{V}}_5(t)\le & z^{\ast }(t-\mathit{\sigma })\left[\frac{{\mathit{\sigma }}^4}{4}{A}^{\ast }OA\right]z(t-\mathit{\sigma })-z^{\ast }(t-\mathit{\sigma })\left[\frac{{\mathit{\sigma }}^4}{4}{A}^{\ast }OB\right]f(z(t))-z^{\ast }(t-\mathit{\sigma })\left[\frac{{\mathit{\sigma }}^4}{4}{A}^{\ast }OC\right]f(z(t-\mathit{\tau }(t)))\hfill \\ \hfill & -f^{\ast }(z(t))\left[\frac{{\mathit{\sigma }}^4}{4}{B}^{\ast }OA\right]z(t-\mathit{\sigma })+f^{\ast }(z(t))\left[\frac{{\mathit{\sigma }}^4}{4}{B}^{\ast }OB\right]f(z(t))+f^{\ast }(z(t))\left[\frac{{\mathit{\sigma }}^4}{4}{B}^{\ast }OC\right]f(z(t-\mathit{\tau }(t)))\hfill \\ \hfill & -f^{\ast }(z(t-\mathit{\tau }(t)))[{\mathit{\sigma }}^2{C}^{\ast }OA]z(t-\mathit{\sigma })+f^{\ast }(z(t-\mathit{\tau }(t)))[{\mathit{\sigma }}^2{C}^{\ast }OB]f(z(t))+f^{\ast }(z(t-\mathit{\tau }(t)))\hfill \\ \hfill & \left[\frac{{\mathit{\sigma }}^4}{4}{C}^{\ast }OC\right]f(z(t-\mathit{\tau }(t)))-z^{\ast }(t)\left[{\mathit{\sigma }}^{2}O+\frac{{\mathit{\sigma }}^6}{36}J\right]z(t)-\underset{t-\mathit{\sigma }}{\overset{t}{\int }}{z}^{\ast }(s)dsO\underset{t-\mathit{\sigma }}{\overset{t}{\int }}z(s)ds\hfill \\ \hfill & +\mathit{\sigma }{z}^{\ast }(t)O\underset{t-\mathit{\sigma }}{\overset{t}{\int }}z(s)ds+\mathit{\sigma }\underset{t-\mathit{\sigma }}{\overset{t}{\int }}{z}^{\ast }(s)dsOz(t)-\underset{t-\mathit{\sigma }}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}\underset{\mathit{\delta }}{\overset{t}{\int }}{z}^{\ast }(s)dsd\mathit{\delta }d\mathit{\gamma }J\underset{t-\mathit{\sigma }}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}\underset{\mathit{\delta }}{\overset{t}{\int }}z(s)dsd\mathit{\delta }d\mathit{\gamma }.\hfill \end{array}$$ 22

Moreover, based on Assumption 2.4, for any $p=1,2,\dots ,n,$ we have

$$\begin{array}{c}\hfill |f_p(z_p(t))|\le F_p|z_p(t)|.\end{array}$$ 23

Let $G=\text{diag}\{s_1,s_2,\dots ,s_n\}>0$. From (23), it can be seen that

$$\begin{array}{c}\hfill s_p{f}_p^{\ast }(z_p(t))f_p(z_p(t))-s_p{F}_p^2{z}_p^{\ast }(t)z_p(t)\le 0,\forall p=1,2,\dots ,n.\end{array}$$

Thus,

$$\begin{array}{c}\hfill f^{\ast }(z(t))Gf(z(t))-z^{\ast }(t)G\mathrm{\Gamma }z(t)\le 0.\end{array}$$ 24

Combining (8), (9), (16), (19), (22) and (24), one can deduce that

$$\begin{array}{c}\hfill \dot{V}(t)\le {\mathit{\zeta }}^{\ast }(t)\mathit{\Theta }\mathit{\zeta }(t),\end{array}$$

where

$$\begin{array}{c}\hfill {\mathit{\zeta }}^{\ast }(t)=\left[z^{\ast }(t)z^{\ast }(t-{\mathit{\tau }}_1(t))z^{\ast }(t-{\mathit{\tau }}_2(t))z^{\ast }(t-{\mathit{\tau }}_1)z^{\ast }(t-{\mathit{\tau }}_2)z^{\ast }(t-\mathit{\sigma })f^{\ast }(z(t))\right.\\ \hfill \left.f^{\ast }(z(t-\mathit{\tau }(t)))\underset{t-\mathit{\sigma }}{\overset{t}{\int }}{z}^{\ast }(s)ds\underset{t-\mathit{\sigma }}{\overset{t}{\int }}\underset{\mathit{\gamma }}{\overset{t}{\int }}\underset{\mathit{\delta }}{\overset{t}{\int }}{z}^{\ast }(s)dsd\mathit{\delta }d\mathit{\gamma }\underset{t-{\mathit{\tau }}_1}{\overset{t}{\int }}{z}^{\ast }(s)ds\underset{t-{\mathit{\tau }}_2}{\overset{t}{\int }}{z}^{\ast }(s)ds\right].\end{array}$$

If (6) holds, then we get

$$\begin{array}{c}\hfill \dot{V}(t)<0.\end{array}$$

Hence, the complex-valued neural networks (3) is globally asymptotically stable. This completes the proof. $\square$

Remark 3.2

In Dey et al. (2010), the problem of asymptotic stability for continuous-time systems with additive time-varying delays is investigated by utilizing the free matrix variables. The authors Wu et al. (2009) addressed the stability problem for a class of uncertain systems with two successive delay components. By using a convex polyhedron method, the delay-dependent stability criteria is established in Shao and Han (2011) for neural networks with two additive time-varying delay components. However, when constructing the Lyapunov–Krasovskii functional, those results are not adequately use the full information about the additive time-varying delays ${\mathit{\tau }}_1(t)$, ${\mathit{\tau }}_2(t)$ and $\mathit{\tau }(t)$, which would be inevitably conservative to some extent. Since, the authors Cheng et al. (2014) utilized the full information about the additive time-varying delays in the constructed Lyapunov–Krasovskii functional and studied the delay-dependent stability of real-valued continuous-time system which gives the less conservative results. Inspired by the above, in the present paper, we also make the full information of additive time-varying delays ${\mathit{\tau }}_1(t)$, ${\mathit{\tau }}_2(t)$ and $\mathit{\tau }(t)$ in the study of stability analysis for complex-valued neural networks.

Remark 3.3

In the existing literature, many researchers studied the stability problem of neural networks and proposed good results, for example see Lakshmanan et al. (2013); Sakthivel et al. (2015); Xie et al. (2016) and references there in. Most of these results are founded on the inequality ${\left(\underset{a}{\overset{b}{\int }}z(s)ds\right)}^{T}M\left(\underset{a}{\overset{b}{\int }}z(s)ds\right)\le (b-a)\underset{a}{\overset{b}{\int }}{z}^T(s)Mz(s)ds.$ Chen and Song (2013) and Velmurugan et al. (2015) studied the stability and passivity analysis of complex-valued neural networks with the help of complex-valued Jensen’s inequality ${\left(\underset{a}{\overset{b}{\int }}z(s)ds\right)}^{\ast }M\left(\underset{a}{\overset{b}{\int }}z(s)ds\right)\le (b-a)\underset{a}{\overset{b}{\int }}{z}^{\ast }(s)Mz(s)ds.$ Based on the above analysis and discussions, in this paper the single integral inequality is handled with the complex-valued Jensen’s inequality. Moreover, in this present paper, we introduce the double integral inequality ${\left(\underset{a}{\overset{b}{\int }}\underset{s}{\overset{b}{\int }}z(\mathit{\theta })d\mathit{\theta }ds\right)}^{\ast }M\left(\underset{a}{\overset{b}{\int }}\underset{s}{\overset{b}{\int }}z(\mathit{\theta })d\mathit{\theta }ds\right)$ $\le \frac{{(b-a)}^2}{2}\underset{a}{\overset{b}{\int }}\underset{s}{\overset{b}{\int }}{z}^{\ast }(\mathit{\theta })Mz(\mathit{\theta })d\mathit{\theta }ds$ and as well as triple integral inequality ${\left(\underset{a}{\overset{b}{\int }}\underset{s}{\overset{b}{\int }}\underset{\mathit{\theta }}{\overset{b}{\int }}z(\mathit{\gamma })d\mathit{\gamma }d\mathit{\theta }ds\right)}^{\ast }M\left(\underset{a}{\overset{b}{\int }}\underset{s}{\overset{b}{\int }}\underset{\mathit{\theta }}{\overset{b}{\int }}z(\mathit{\gamma })d\mathit{\gamma }d\mathit{\theta }ds\right)\le \frac{{(b-a)}^3}{6}\underset{a}{\overset{b}{\int }}\underset{s}{\overset{b}{\int }}\underset{\mathit{\theta }}{\overset{b}{\int }}{z}^{\ast }(\mathit{\gamma })Mz(\mathit{\gamma })d\mathit{\gamma }d\mathit{\theta }ds,$ for calculating the derivative of Lyapunov–Krasovskii functional in the complex-valued neural networks.

Remark 3.4

In the following, we will discuss the global asymptotic stability criteria for complex-valued neural networks with additive time-varying delays, that is, there is no leakage delay $(i.e.,\mathit{\sigma }=0)$ in (3), then the system (3) becomes

$$\begin{array}{cc}\hfill \dot{z}(t)=& -Az(t)+Bf(z(t))+Cf(z(t-{\mathit{\tau }}_1(t)-{\mathit{\tau }}_2(t))),\hfill \\ \hfill z(s)=& \mathit{\varphi }(s),s\in [-\mathit{\tau },0].\hfill \end{array}$$ 25

Then, according to Theorem 3.1, we have the following corollary for the delay-dependent global asymptotic stability of system (25).

Corollary 3.5

Given scalars ${\mathit{\tau }}_1$, ${\mathit{\tau }}_2$, ${\mathit{\mu }}_1$ and ${\mathit{\mu }}_2$, the equilibrium point of complex-valued neural networks (25) with additive time-varying delays is globally asymptotically stable if there exist positive Hermitian matrices M, N, P, Q, R, S, T, V, W, X and positive diagonal matrix G such that the following linear matrix inequality holds:

$$\begin{array}{c}\hfill \tilde{\mathit{\Theta }}=\left[\begin{array}{ccccccccc}{\tilde{\mathit{\Theta }}}_{1,1}& 0& 0& W& X& {\tilde{\mathit{\Theta }}}_{1,6}& {\tilde{\mathit{\Theta }}}_{1,7}& {\mathit{\tau }}_{1}M& {\mathit{\tau }}_{2}N\\ \star & {\tilde{\mathit{\Theta }}}_{2,2}& 0& 0& 0& 0& 0& 0& 0\\ \star & \star & {\tilde{\mathit{\Theta }}}_{3,3}& 0& 0& 0& 0& 0& 0\\ \star & \star & \star & {\tilde{\mathit{\Theta }}}_{4,4}& 0& 0& 0& 0& 0\\ \star & \star & \star & \star & {\tilde{\mathit{\Theta }}}_{5,5}& 0& 0& 0& 0\\ \star & \star & \star & \star & \star & {\tilde{\mathit{\Theta }}}_{6,6}& {\tilde{\mathit{\Theta }}}_{6,7}& 0& 0\\ \star & \star & \star & \star & \star & \star & {\tilde{\mathit{\Theta }}}_{7,7}& 0& 0\\ \star & \star & \star & \star & \star & \star & \star & {\tilde{\mathit{\Theta }}}_{8,8}& 0\\ \star & \star & \star & \star & \star & \star & \star & \star & {\tilde{\mathit{\Theta }}}_{9,9}\end{array}\right]<0,\end{array}$$ 26

where ${\tilde{\mathit{\Theta }}}_{1,1}=-PA-A^{\ast }P+Q+R+S+T-W-X+G\mathrm{\Gamma }-{\mathit{\tau }}_1^{2}M-{\mathit{\tau }}_2^{2}N+{\mathit{\tau }}_1^2{A}^{\ast }WA+{\mathit{\tau }}_2^2{A}^{\ast }XA+\frac{{\mathit{\tau }}_1^4}{4}{A}^{\ast }MA+\frac{{\mathit{\tau }}_2^4}{4}{A}^{\ast }\times NA,$ ${\tilde{\mathit{\Theta }}}_{1,6}=PB-{\mathit{\tau }}_1^2{A}^{\ast }WB-{\mathit{\tau }}_2^2{A}^{\ast }XB-\frac{{\mathit{\tau }}_1^4}{4}{A}^{\ast }MB-\frac{{\mathit{\tau }}_2^4}{4}{A}^{\ast }\times NB,$ ${\tilde{\mathit{\Theta }}}_{1,7}=PC-{\mathit{\tau }}_1^2{A}^{\ast }WC-{\mathit{\tau }}_2^2{A}^{\ast }XC-\frac{{\mathit{\tau }}_1^4}{4}{A}^{\ast }MC-\frac{{\mathit{\tau }}_2^4}{4}{A}^{\ast }\times NC,$ ${\tilde{\mathit{\Theta }}}_{2,2}=-(1-{\mathit{\mu }}_1)Q,$ ${\tilde{\mathit{\Theta }}}_{3,3}=-(1-{\mathit{\mu }}_2)R,$ ${\tilde{\mathit{\Theta }}}_{4,4}=-W-S,$ ${\tilde{\mathit{\Theta }}}_{5,5}=-X-T,$ ${\tilde{\mathit{\Theta }}}_{6,6}={\mathit{\tau }}_1^2{B}^{\ast }WB+{\mathit{\tau }}_2^2{B}^{\ast }XB+\frac{{\mathit{\tau }}_1^4}{4}{B}^{\ast }MB+\frac{{\mathit{\tau }}_2^4}{4}{B}^{\ast }NB+V-G,$ ${\tilde{\mathit{\Theta }}}_{6,7}={\mathit{\tau }}_1^2{B}^{\ast }WC+{\mathit{\tau }}_2^2{B}^{\ast }XC+\frac{{\mathit{\tau }}_1^4}{4}{B}^{\ast }MC+\frac{{\mathit{\tau }}_2^4}{4}{B}^{\ast }NC,$ ${\tilde{\mathit{\Theta }}}_{7,7}={\mathit{\tau }}_1^2{C}^{\ast }WC+{\mathit{\tau }}_2^2{C}^{\ast }XC+\frac{{\mathit{\tau }}_1^4}{4}{C}^{\ast }MC+\frac{{\mathit{\tau }}_2^4}{4}{C}^{\ast }NC-(1-\mathit{\mu })V$, ${\tilde{\mathit{\Theta }}}_{8,8}=-M,$ ${\tilde{\mathit{\Theta }}}_{9,9}=-N.$

Proof

The proof immediately follows from the proof of Theorem 3.1, by setting $\mathit{\sigma }=0$, $U=0,$ $Y=0$, $O=0$ and $J=0,$ hence it is omitted. This completes the proof. $\square$

Remark 3.6

When ${\mathit{\tau }}_1(t)=0$ or ${\mathit{\tau }}_2(t)=0$ complex-valued neural networks with additive time-varying delays (25) reduces to single time-varying delays. Without loss of generality, assume that ${\mathit{\tau }}_2(t)=0$ then (25) becomes

$$\begin{array}{cc}\hfill \dot{z}(t)=& -Az(t)+Bf(z(t))+Cf(z(t-{\mathit{\tau }}_1(t))),\hfill \\ \hfill z(s)=& \mathit{\varphi }(s),s\in [-{\mathit{\tau }}_1,0].\hfill \end{array}$$ 27

By letting ${\mathit{\tau }}_2=0,$ $R=T=X=N=0$ in Corollary 3.5, we can easily obtain the sufficient condition for global asymptotic stability of complex-valued neural networks with time-varying delays (27), which are summarized the following corollary.

Corollary 3.7

Given scalars ${\mathit{\tau }}_1$ and ${\mathit{\mu }}_1$, the equilibrium point of complex-valued neural networks (27) is globally asymptotically stable if there exist positive Hermitian matrices M, P, Q, S, V, W and positive diagonal matrix G such that the following linear matrix inequality holds:

$$\begin{array}{c}\hfill \widehat{\mathit{\Theta }}=\left[\begin{array}{cccccc}{\widehat{\mathit{\Theta }}}_{1,1}& 0& W& {\widehat{\mathit{\Theta }}}_{1,4}& {\widehat{\mathit{\Theta }}}_{1,5}& {\mathit{\tau }}_{1}M\\ \star & -(1-{\mathit{\mu }}_1)Q& 0& 0& 0& 0\\ \star & \star & -W-S& 0& 0& 0\\ \star & \star & \star & {\widehat{\mathit{\Theta }}}_{4,4}& 0& 0\\ \star & \star & \star & \star & {\widehat{\mathit{\Theta }}}_{5,5}& 0\\ \star & \star & \star & \star & \star & -M\end{array}\right]<0,\end{array}$$ 28

where ${\widehat{\mathit{\Theta }}}_{1,1}=-PA-A^{\ast }P+Q+S-W+G\mathrm{\Gamma }-{\mathit{\tau }}_1^{2}M+{\mathit{\tau }}_1^2{A}^{\ast }WA+\frac{{\mathit{\tau }}_1^4}{4}{A}^{\ast }MA$, ${\widehat{\mathit{\Theta }}}_{1,4}=PB-{\mathit{\tau }}_1^2{A}^{\ast }WB-\frac{{\mathit{\tau }}_1^4}{4}{A}^{\ast }MB$, ${\widehat{\mathit{\Theta }}}_{1,5}=PC-{\mathit{\tau }}_1^2{A}^{\ast }WC-\frac{{\mathit{\tau }}_1^4}{4}{A}^{\ast }MC,$ ${\widehat{\mathit{\Theta }}}_{4,4}={\mathit{\tau }}_1^2{B}^{\ast }WB+\frac{{\mathit{\tau }}_1^4}{4}{B}^{\ast }MB+V-G$, ${\widehat{\mathit{\Theta }}}_{4,5}={\mathit{\tau }}_1^2{B}^{\ast }WC+\frac{{\mathit{\tau }}_1^4}{4}{B}^{\ast }MC$, ${\widehat{\mathit{\Theta }}}_{5,5}={\mathit{\tau }}_1^2{C}^{\ast }WC+\frac{{\mathit{\tau }}_1^4}{4}{C}^{\ast }MC-(1-{\mathit{\mu }}_1)V$, ${\widehat{\mathit{\Theta }}}_{6,6}=-M.$

Remark 3.8

In Liu and Chen (2016), the global exponential stability of complex-valued neural networks with asynchronous time delays is established by decomposing the complex-valued networks into its real and imaginary parts and construct an equivalent real-valued system. The authors Xu et al. (2014) derived the exponential stability condition for a class of complex-valued neural networks with time-varying delays and unbounded delays by utilizing the vector Lyapunov–Krasovskii functional method, homeomorphism mapping lemma and the matrix theory. In Liu and Chen (2016) and Xu et al. (2014), the authors addressed the stability results of complex-valued neural networks with constant or time-varying delays by separating their activation function into its real and imaginary parts. However, when the activation functions cannot be expressed by separating their real and imaginary parts, the proposed stability results in Liu and Chen (2016) and Xu et al. (2014) cannot be applied. It should be mentioned that, in this present paper, the proposed stability criterion for complex-valued neural networks is valid regardless of the active functions can be expressed by separating their real and imaginary parts. Thus, the derived delay dependent stability condition in this paper is more general than the existing literature (Liu and Chen 2016; Xu et al. 2014).

Numerical example

In this section, we give three numerical examples to demonstrate the derived main results.

Example 4.1

Consider a two-dimensional complex-valued neural networks (3) with the following parameters:

$$\begin{array}{c}\hfill A=\left[\begin{array}{cc}9& 0\\ 0& 9\end{array}\right],B=\left[\begin{array}{cc}1-i& -1-i\\ 2-i& 2-5i\end{array}\right],C=\left[\begin{array}{cc}1-i& 1-i\\ 1+i& -1-i\end{array}\right],\end{array}$$

The activation functions are chosen as $f(z(t))=\frac{1-e^{-x(t)}}{1+e^{-x(t)}}+i\frac{1}{1+e^{-y(t)}}$. The time-varying delays are considered as ${\mathit{\tau }}_1(t)=0.2sint+0.2$, ${\mathit{\tau }}_2(t)=0.5cost+0.8$, which satisfying ${\mathit{\tau }}_1=0.4,$ ${\mathit{\tau }}_2=1.3,$ ${\mathit{\mu }}_1=0.2$ and ${\mathit{\mu }}_2=0.5.$ Take $\mathrm{\Gamma }=diag\{0.5,0.5\}$ and $\mathit{\sigma }=0.08,$ by using the effective YALMIP toolbox in MATLAB, we can find the feasible solutions to linear matrix inequality in (6) as follows:

$$\begin{array}{cc}& P=\left[\begin{array}{cc}1.5815& -0.1675+0.0342i\\ -0.1675-0.0342i& 1.0867\end{array}\right],Q=\left[\begin{array}{cc}0.2537& -0.1143+0.0229i\\ -0.1143-0.0229i& 0.0772\end{array}\right],\hfill \\ \hfill & R=\left[\begin{array}{cc}0.2538& -0.1144+0.0229i\\ -0.1144-0.0229i& 0.0773\end{array}\right],S=\left[\begin{array}{cc}0.2507& -0.1129+0.0226i\\ -0.1129-0.0226i& 0.0764\end{array}\right],\hfill \\ \hfill & T=\left[\begin{array}{cc}0.2533& -0.1141+0.0229i\\ -0.1141-0.0229i& 0.0771\end{array}\right],U=\left[\begin{array}{cc}0.8848& -0.2728+0.0567i\\ -0.2728-0.0567i& 0.4261\end{array}\right],\hfill \\ \hfill & V=\left[\begin{array}{cc}7.0635& -1.2995+0.8830i\\ -1.2995-0.8830i& 3.1009\end{array}\right],W=\left[\begin{array}{cc}0.0061& -0.0028+0.0006i\\ -0.0028-0.0006i& 0.0017\end{array}\right],\hfill \\ \hfill & J=\left[\begin{array}{cc}87.0921& -0.0011+0.0002i\\ -0.0011-0.0002i& 87.0905\end{array}\right],X={10}^{-03}\times \left[\begin{array}{cc}0.5620& -0.2517+0.0505i\\ -0.2517-0.0505i& 0.1735\end{array}\right],\hfill \\ \hfill & M=\left[\begin{array}{cc}0.2831& -0.1315+0.0264i\\ -0.1315-0.0264i& 0.0802\end{array}\right],Y={10}^{-03}\left[\begin{array}{cc}1.1409& -0.1424+0.0287i\\ -0.1424-0.0287i& 0.7563\end{array}\right],\hfill \\ \hfill & N=\left[\begin{array}{cc}0.0026& -0.0012+0.0002i\\ -0.0012-0.0002i& 0.0007\end{array}\right],O={10}^{-02}\times \left[\begin{array}{cc}0.8791& 0.5352-0.0968i\\ 0.5352+0.0968i& 1.4391\end{array}\right],\hfill \end{array}$$

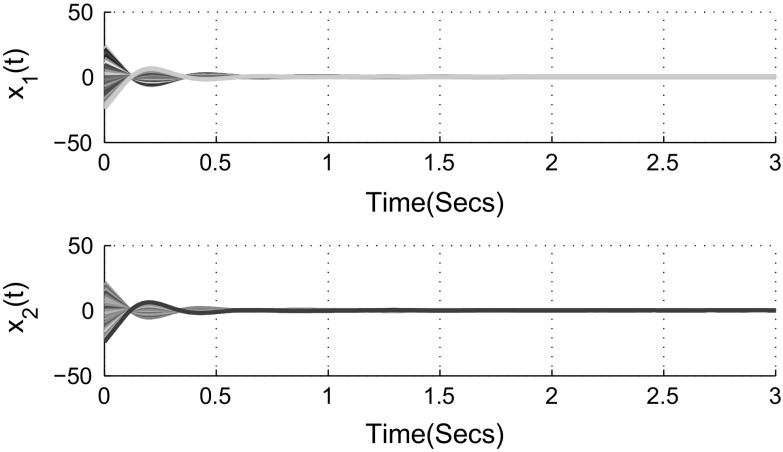
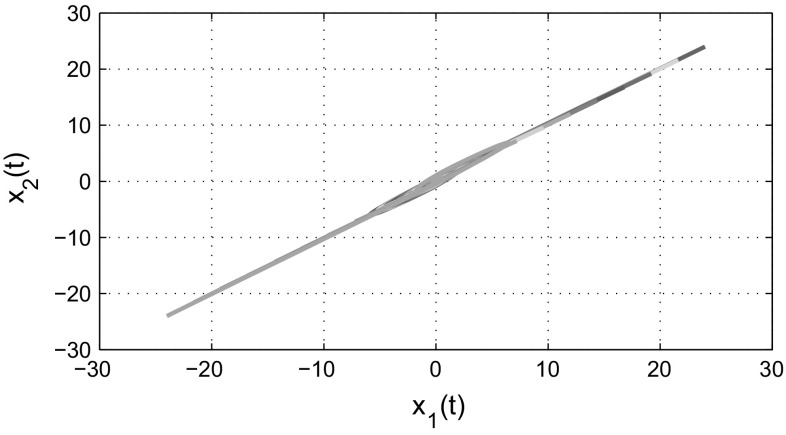
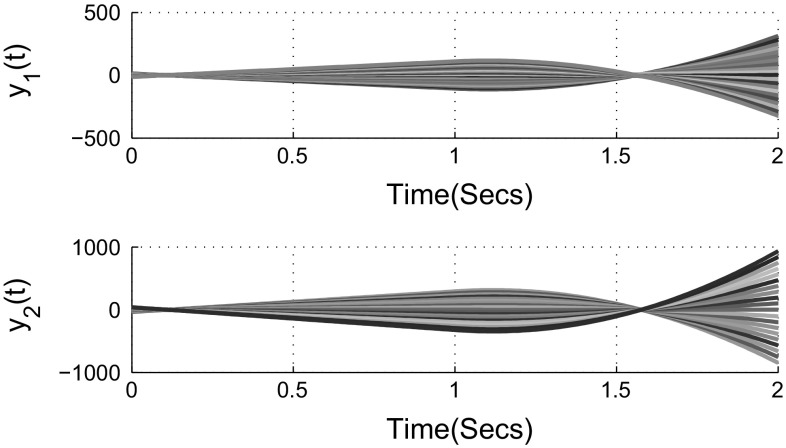
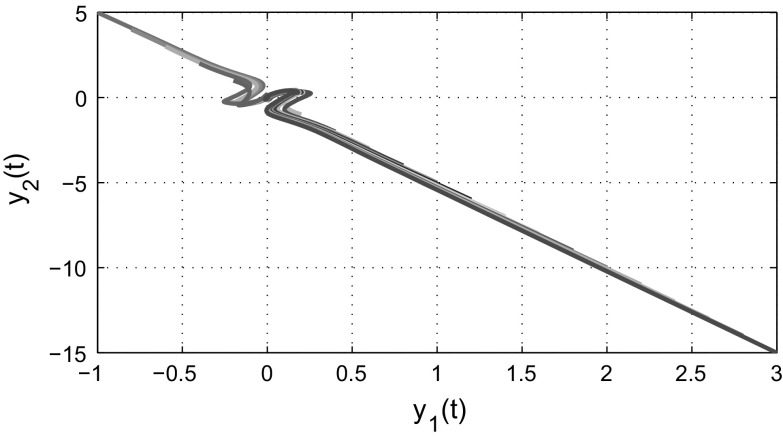
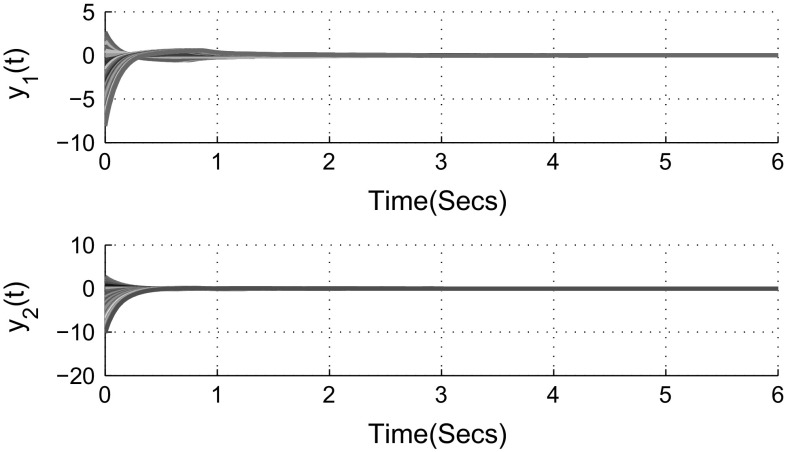
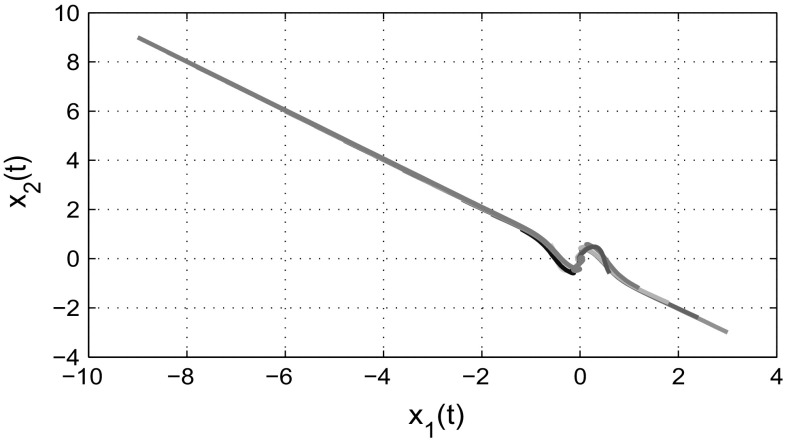
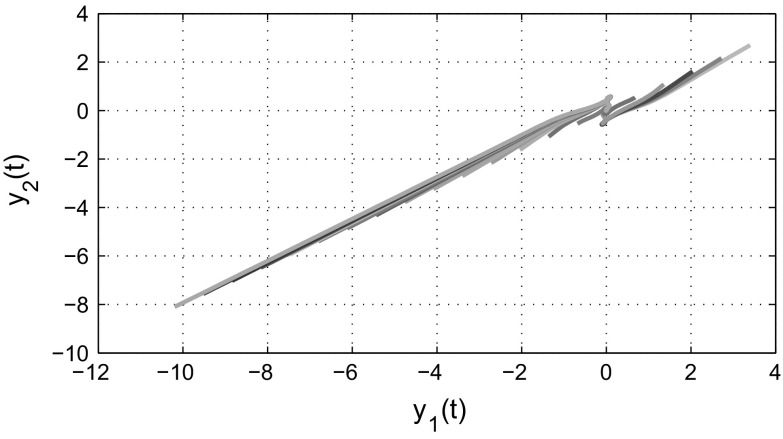
and $G=diag\{9.6363,7.7007\}.$ According to Theorem 3.1, the complex-valued neural networks with leakage delay and additive time-varying delays (3) is globally asymptotically stable. Figures 1 and 2 show that the time responses of the real and imaginary parts of the system (3) with 21 initial conditions, respectively. The phase trajectories of the real parts of the system (3) is given in Fig. 3. Similarly, the phase trajectories for imaginary parts of the system (3) is given in Fig. 4. Also, Figs. 5 and 6 depict the real and imaginary parts of states of the considered complex-valued neural networks (3) with $\mathit{\sigma }=1$ under the same 21 initial conditions. It is easy to check that the unique equilibrium point of the system (3) is unstable, this implies that the delays in leakage term on the dynamics of complex-valued neural networks cannot be ignored when we analyze the stability of complex-valued neural networks.

Fig. 1.

State trajectories of real parts of the system (3) in Example 4.1

Fig. 2.

State trajectories of imaginary parts of the system (3) in Example 4.1

Fig. 3.

State trajectories of neural networks (3) between real subspace $[Re(z_1),Re(z_2)]$

Fig. 4.

State trajectories of neural networks (3) between imaginary subspace $[Im(z_1(t)),Im(z_2(t))]$

Fig. 5.

Time response of real parts of the system (3) when $\mathit{\delta }=1$

Fig. 6.

Time response of imaginary parts of the system (3) when $\mathit{\delta }=1$

Example 4.2

Consider the following two-dimensional complex-valued neural networks (25) with additive time-varying delays:

$$\begin{array}{c}\hfill \dot{z}(t)=-Az(t)+Bf(z(t))+Cf(z(t-{\mathit{\tau }}_1(t)-{\mathit{\tau }}_2(t))),\end{array}$$

where

$$\begin{array}{c}\hfill A=\left[\begin{array}{cc}10& 0\\ 0& 10\end{array}\right],B=\left[\begin{array}{cc}2-i& -1-3i\\ 2-2i& 2-i\end{array}\right],C=\left[\begin{array}{cc}2-i& 1-i\\ 1+i& -3-i\end{array}\right].\end{array}$$

The additive time-varying delays are taken as ${\mathit{\tau }}_1(t)=0.5sin(0.2t)$ and ${\mathit{\tau }}_2(t)=0.4cos(0.6t)$. Choose the nonlinear activation function as $f(z)=tanhz$ with $\mathrm{\Gamma }=\text{diag}\{0.5,0.5\}$, ${\mathit{\tau }}_1=0.5$, ${\mathit{\tau }}_2=0.4$, ${\mathit{\mu }}_1=0.1$, ${\mathit{\mu }}_2=0.24.$ By using the YALMIP toolbox in MATLAB along with the above parameters, the linear matrix inequality (26) is feasible. From Figs. 7 and 8, we have found that the state trajectories of the system with its real and imaginary parts are converge to the zero equilibrium point with different initial conditions, respectively. The phase trajectories of real and imaginary parts of the system (25) are depicted in Figs. 9 and 10, respectively. By Corollary 3.5, we can conclude that the proposed neural networks (25) is globally asymptotically stable.

Fig. 7.

Trajectories of the real parts x(t) of the states z(t) for the neural network (25)

Fig. 8.

Trajectories of the imaginary parts y(t) of the states z(t) for the neural network (25)

Fig. 9.

State trajectories of neural networks (25) between real subspace $[x_1(t),x_2(t)]$

Fig. 10.

State trajectories of neural networks (25) between imaginary subspace $[y_1(t),y_2(t)]$

Example 4.3

Consider the following two-dimensional complex-valued neural networks (27) with time-varying delays:

$$\begin{array}{cc}\hfill \dot{z}(t)=& -Az(t)+Bf(z(t))+Cf(z(t-{\mathit{\tau }}_1(t))),\hfill \end{array}$$

where

$$\begin{array}{c}\hfill A=\left[\begin{array}{cc}8& 0\\ 0& 8\end{array}\right],B=\left[\begin{array}{cc}-1-2i& 1-3i\\ 2-3i& 4-i\end{array}\right],C=\left[\begin{array}{cc}2-2i& 1-i\\ 3+i& 1-i\end{array}\right].\end{array}$$

Choose the nonlinear activation function as $f(z)=tanhz$ with $\mathrm{\Gamma }=\text{diag}\{0.5,0.5\}$. The time-varying delays are chosen as ${\mathit{\tau }}_1(t)=0.1sint+0.6$ which satisfies ${\mathit{\tau }}_1=0.7$, ${\mathit{\mu }}_1=0.1.$ By employing the MATLAB YALMIP Toolbox, we can find the feasible solutions to linear matrix inequalities in (28) as follows, which guarantee the global asymptotic stability of the equilibrium point.

$$\begin{array}{cc}& P=\left[\begin{array}{cc}49.3881& -14.0945+18.3994i\\ -14.0945-18.3994i& 37.0857\end{array}\right],Q=\left[\begin{array}{cc}51.1062& -19.9936+26.6048i\\ -19.9936-26.6048i& 39.9656\end{array}\right],\hfill \\ \hfill & S=\left[\begin{array}{cc}44.6015& -17.1853+23.1041i\\ -17.1853-23.1041i& 34.9374\end{array}\right],V={10}^{02}\times \left[\begin{array}{cc}1.7782& -0.0575-0.4004i\\ -0.0575+0.4004i& 0.7124\end{array}\right],\hfill \\ \hfill & W=\left[\begin{array}{cc}10.7229& -4.4289+5.6768i\\ -4.4289-5.6768i& 7.4946\end{array}\right],M=\left[\begin{array}{cc}38.5826& -8.7800+11.8910i\\ -8.7800-11.8910i& 31.9817\end{array}\right],\hfill \end{array}$$

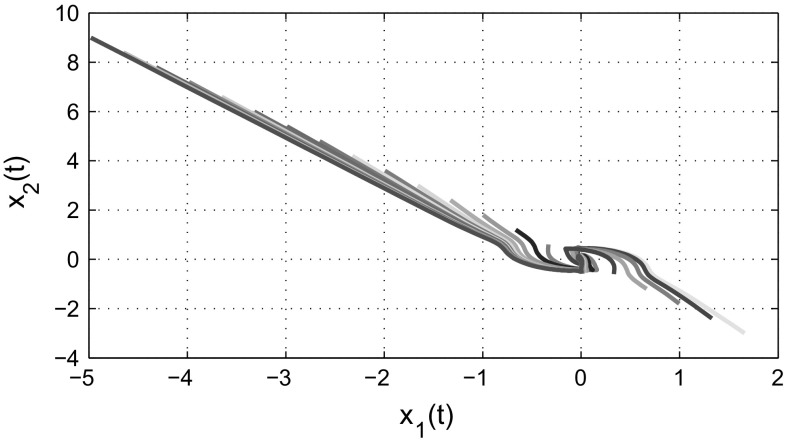
$G=diag\{311.1505,230.5390\}.$ Figures 11 and 12, respectively, displays state trajectories of the complex-valued neural networks (27) with its real and imaginary parts are converge to the origin with 21 randomly selected initial conditions. The phase trajectories of real and imaginary parts of the system (27) are drawn in Figs. 13 and 14, respectively.

Fig. 11.

Time responses of real parts of the system (27) with 21 initial conditions

Fig. 12.

Time responses of imaginary parts of the system (27) with 21 initial conditions

Fig. 13.

Phase trajectories of real parts of the proposed system (27)

Fig. 14.

Phase trajectories of imaginary parts of the proposed system (27)

Conclusion

In this paper, the global asymptotic stability of the complex-valued neural networks with leakage and additive-time varying delays has been studied. The sufficient conditions have been proposed to ascertain the global asymptotic stability of the addressed neural networks based on the appropriate Lyapunov–Krasovskii functional with involving triple integral terms. The complex-valued linear matrix inequalities are used to study the main results which can be easily solved by YALMIP tool in MATLAB. Three numerical examples have been presented to illustrate the effectiveness of theoretical results.