From abstract topology to real thermodynamic brain activity

Abstract

Recent approaches to brain phase spaces reinforce the foremost role of symmetries and energy requirements in the assessment of nervous activity. Changes in thermodynamic parameters and dimensions occur in the brain during symmetry breakings and transitions from one functional state to another. Based on topological results and string-like trajectories into nervous energy landscapes, we provide a novel method for the evaluation of energetic features and constraints in different brain functional activities. We show how abstract approaches, namely the Borsuk–Ulam theorem and its variants, may display real, energetic physical counterparts. When topology meets the physics of the brain, we arrive at a general model of neuronal activity, in terms of multidimensional manifolds and computational geometry, that has the potential to be operationalized.

Introduction

The brain is a complex, non-linear system operating at the edge of chaos, formed by inter-dependent components which exhibit spontaneous self-organization and emergent properties (Tognoli and Kelso 2013; Fraiman and Chialvo 2012; Zare and Grigolini 2013; Xu and Wang 2014). In such a vein, the brain is equipped with phase spaces where particle movements take place (Watanabe et al. 2013; Yan et al. 2013; Kim and Lim 2015; Wang et al. 2017). Such trajectories may display different paths. It has been suggested that the brain is equipped with funnel-like locations in phase space where trajectories converge as time progresses, following the shortest path (Tozzi et al. 2016a; Sengupta et al. 2016). Others proposed that brain function does not exhibit erratic brain dynamics nor attractors, but a stable sequence, the so-called transient heteroclinic channel (Afraimovich et al. 2013) and that a multidimensional functional torus might be displayed during spontaneous brain activity (Tozzi and Peters 2016a). Furthermore, crucial concepts like communication-through-coherence (Deco and Jirsa 2012) and collective movements (Touboul 2012; Tozzi 2015) must be taken into account. In sum, different functional regimes occurring in the brain phase space have been described, both in central nervous systems and in artificial neural networks, and they have been correlated with different brain functions (Tozzi et al. 2016a).

Despite the large number of possible trajectories, the processes governing brain paths may be unified when we take just into account energetic requirements and constraints. Indeed, the second law of thermodynamics states that every process occurring in nature proceeds in the sense in which the sum of the entropies of all bodies taking part in the process is increased (Planck’s formulation). This paper aims to evaluate brain energetic constraints in the framework of algebraic topology, namely the Borsuk–Ulam theorem (BUT) (Borsuk 1933). We will take into account also another important topological ingredient, e.g., the symmetries, widespread at every level of nervous organization. Symmetries may be regarded as the most general feature of biological systems (including the brain), perhaps more general also than energetic requirements, so that giving insights into them might provide a general approach to nervous activities (Tozzi and Peters 2016b). Here we show how BUT and its variants may provide powerful insights into brain functioning, especially if we assess the noteworthy relationships between symmetry breaks, changes of neural dimensions, thermodynamic free-energy and informational entropy.

Abstract topology comes into play

The standard version of the Borsuk–Ulam theorem (BUT)

BUT states that (Dodson 1997):

Every continuous map $f:S^n\to R^n$ must identify a pair of antipodal points (on S ⁿ ).

In other words, if a sphere Sⁿ is mapped continuously into a n-dimensional Euclidean space Rⁿ, there is at least one pair of antipodal points on Sⁿ which map onto the same point of Rⁿ. For further details, see Tozzi and Peters (2016b). Examples of antipodal points are the opposite points along the poles of a sphere (Matoušek 2003). The notation $S^n$ denotes an n-sphere of convex curvature, which is embedded in a n + 1 Euclidean space (Weeks 2002; Marsaglia 1972). The BUT’s ingredients (antipodal points, a versatile use of the exponent n and projections from lower to higher dimensions) can be modified in different guises, in order to achieve a wide range of BUT variants (Tozzi and Peters 2016b; Peters and Tozzi 2016a, b). They provide not just a topological methodology for the evaluation of countless features of brain activity, cast in an empirical fashion that has the potential to be operationalized, but also a quantitative way to give a physical meaning to the otherwise abstract concept of BUT. The next paragraphs will go through recently described BUT variants and their applications to brain activity.

Brain regions instead of points

If we simply evaluate nervous activities instead of points, BUT leads naturally to the possibility of a region-based brain geometry. Indeed, the two opposite points could stand not just for the description of simple topological points (Marsaglia 1972), but also for the signals detected by different neuro-techniques, such as spatial or temporal patterns, vectors, particle trajectories, entropies, free-energies (Peters 2016). Therefore, we can describe brain features as antipodal points on n+1 –dimensional structures. This means that brain signals can be compared, because the two antipodal points can be assessed at higher-dimensional scales of observation, which can be pulled back to single points at lower-dimensional scales (Tozzi and Peters 2016b).

This approach makes it also possible to assess brain functions in the very general terms of particle trajectories taking place on manifolds, if we consider a nervous activity in a given cortical subarea as a geometric structure that has the characteristics of a string. By definition, a string on the surface of an n-sphere is a line that represents the path traced by a moving particle. In a geometric space, a string stands for a region of space with either bounded or unbounded lengths (Goddard and Olive 1985; Olive and Landsberg 1989). In evaluating brain strings, we need to take into account antipodal sets instead of antipodal points (Petty 1971). Indeed, in a point-free geometry (Di Concilio and Gerla 2006; Di Concilio 2013), regions replace points as the primitives. Therefore, in the evaluation of brain activities at every spatio-temporal scale, here we assess antipodal regions instead of antipodal points (Lenzen 1939; Disalle 1995; Peters and Naimpally 2012). There is however a difference between the strings embedded in structures of diverse dimensions. Strings contain more information than their projections in a lower dimensions. Indeed, the higher the dimension, the more the information encompassed in strings, because of the higher number of coordinates. This means that this BUT variant allows us to evaluate systems features in higher dimensions, in order to increase the amount of detectable information. To make an example, you might extract the three-dimensional shape of a cat, just looking at its shadow. Vice versa, dropping down a dimension means that each point in the lower dimensional space is simpler. It must be kept into account that, as BUT dictates, a single feature needs to project to TWO matching features, going one dimension higher. This means that a projection mapping contains multiple mappings in higher levels. Hence, BUT provides a way to evaluate changes of information among different anatomical and functional brain levels in a topological space.

Antipodality

The two points (or regions, or brain activities) do not need necessarily to be antipodal, in order to be described together (Peters 2016). Indeed, the BUT can be generalized not just for the evaluation of antipodal, but also of non-antipodal points on an n-sphere. We can consider regions on an n-sphere that are either adjacent or far apart (Tozzi and Peters 2016b). And this BUT variant applies to the brain, provided there are a pair of regions on the cortex with the same feature value. (Peters 2016). This makes it possible to evaluate matching cortical signals, even if they are not “opposite”, but “near” each other: the antipodal points restriction from the “standard” BUT is no longer needed.

Not just convex structures

The original formulation of BUT describes antipodal points on spatial manifolds in every dimension, provided the n-sphere is a convex structure with positive curvature (i.e., a ball). However, brain functions might occur on manifolds endowed with other types of geometry: for example, Sengupta et al. (2016) described brain functional activity in terms of trajectories taking place on hyperbolic Riemannian n-manifolds of constant sectional curvature −1 and concave shape (i.e., a saddle). BUT can be generalized to symmetries occurring either on flat, or on concave structures (Mitroi-Symeonidis 2015; Tozzi 2016), making it possible for us to look for antipodal points on structures equipped with shapes other than the convex ones. In other words, whether the brain function displays a concave, convex or flat structure, it does not matter: we may always find the points with matching description predicted by BUT.

Not just spatial dimensions

Although BUT was originally described just in case of the term n of Sⁿ being a natural number which expresses a structure embedded in a spatial dimension, nevertheless n can stand for other types of numbers too. Indeed, n can be also cast as an integer, a rational or an irrational number (Tozzi and Peters 2016b). This makes it possible to use the n parameter as a versatile tool for the description of brain features. In particular, this BUT version is useful in describing brain nonlinear dynamics, as we will see in the next chapters.

General BUT

In conclusion, we are allowed to provide a general version of BUT (Gen-BUT), that takes into account all the mentioned BUT variants that can be used in the topological study of the brain in the context of physics. Gen-BUT states that:

Multiple sets of objects with matching descriptions in a d-dimensional manifold M^d are mapped to a single set of objects in M^d−1 and vice versa.

The sets of objects, which can be mathematical, physical or biological features, do not need to be antipodal and their mappings need not to be continuous. The term matching description means the sets of objects display common feature values or symmetries. M stands for a manifold with any kind of curvature, either concave, convex or flat. The notation d stands for a natural, or rational, or irrational number. Note that a force, or a group, an operator, an energetic source, is needed, in order to project from one dimension to another. The process is reversible, depending on energetic constraints.

Systems’ symmetry breaking: changes in brain dimensions

Symmetries are invariances underlining physical and biological systems (Weyl 1982). A symmetry break occurs when the symmetry is present at one level of observation, but “hidden” at another level (Roldán et al. 2014). BUT tells us that we can find, on an n-dimensional sphere, a pair of opposite points that have the same encoding on an n−1 sphere. This means that symmetries can be found when evaluating the system in a proper dimension, while they disappear (are hidden or broken) when we assess the same system in just one dimension lower (Tozzi and Peters 2016b).

There are two different ways to define and assess brain dimensions. Indeed, the term dimension may reflect either functional relationships of brain activities, or anatomical connections between cortical areas. The first approach takes into account the dimensionality of the neural space. Connectivity and complex network analyses of neural signals allow the assessment of the complex dynamics of brain activity, providing a novel insight into the multidimensionality of various neural functions’ representations (Kida et al. 2016). From a dynamical system perspective, one would expect that brain activities are represented as, for example, some scalar quantity measured at different brain locations (say N locations) at different points in time. Then one could describe nervous dynamics as trajectories and/or manifolds in a N-dimensional phase space (Lech et al. 2016). Mazzucato et al. (2016) demonstrated that stimuli reduce the dimensionality of cortical activity. Clustered networks, such as default mode network, have instead a larger dimensionality, because the latter grows with ensemble size: the more neurons are recruited, the more the dimensions (Mazzucato et al. 2016). Apart from giving insights in neural dynamics in the canonical three dimensions (space, time, and frequency), complex network analyses are also able to evaluate other functional dimensions, e.g. categories of neuronal indices such activity magnitude, connectivity, network properties and so on (Kida et al. 2016). It must be taken into account that dimension reduction and symmetry breaking display close relationships, so that symmetries are correlated with changes in functional dimensions in the brain. Indeed, a key feature of dynamical approaches is that the dynamics they predict are characterized by nonequilibrium phase transitions, and therefore breaks of symmetries (Scholz et al. 1987). Many studies emphasized how different levels of behavioral dynamics’ organization take place in neural ensembles. To make some examples, Jirsa et al. (1998), focusing on the cortical left–right symmetry, derived a bimodal description of the brain activity that is connected to behavioral dynamics, while Jirsa et al. (1994) demonstrated that, when an acoustic stimulus frequency is changed systematically, a spontaneous transition in coordination occurs at a critical frequency, in both motor behavior and brain signals.

Concerning the second approach to brain dimensionality, it has been recently suggested that brain trajectories, at least during spontaneous activity, might display four spatial dimensions, instead of three (Tozzi and Peters 2016a). Brain symmetric states display dimensions higher than asymmetric ones, so that, in this case, the space of interest does not refer to dynamical neural spaces, but to detectable physical cortical locations. In such a vein, Stemmler et al. (2015) proposed that animals can navigate by reading out a simple population vector of grid cell activity across multiple spatial scales. Combining population vectors at different microscopic dimensions predicts indeed neural and behavioral correlates of multiscale grid cell readout, that transcend the known link between entorhinal grid cells and hippocampal place cells. While the spatial activity of a single grid cell does not constitute a metric, an ensemble of hierarchically organized grid cells does provide instead a distance measure (Stemmler et al. 2015). In our paper, the mapping of trajectories from high dimensional manifold to lower dimensions refers to both the above described definitions of dimensionality.

In sum, the study of changes in brain dimensions is a promising novel methodology. We need to take into account that, despite neural networks modelling complex systems are known to exhibit rich, lower-order connectivity patterns at the level of individual nodes and edges, however higher-order organization remains largely unknown. Benson et al. (2016) recently developed an algorithmic framework for studying how complex networks are organized by higher-order connectivity patterns, revealing unexpected hubs and geographical elements. In such a vein, Kleinberg et al. (2016) demonstrated that real networks are not just random combinations of single networks, but are instead organized in specific ways dictated by hidden geometric correlation between layers. Such correlations allowed the detection of multidimensional communities, e.g., sets of nodes that are simultaneously similar in multiple layers. Crucial for our topological arguments, such multidimensionality also enables accurate trans-layer link prediction, meaning that connections in one layer can be predicted by observing the hidden geometric space of another layer. For example, when the geometric correlations are sufficiently strong, a multidimensional framework outperforms navigation in the single layers, allowing efficient targeted navigation simply by using local multilayer knowledge (Kleineberg et al. 2016).

Abstract topology meets real physics: brain energetic requirements

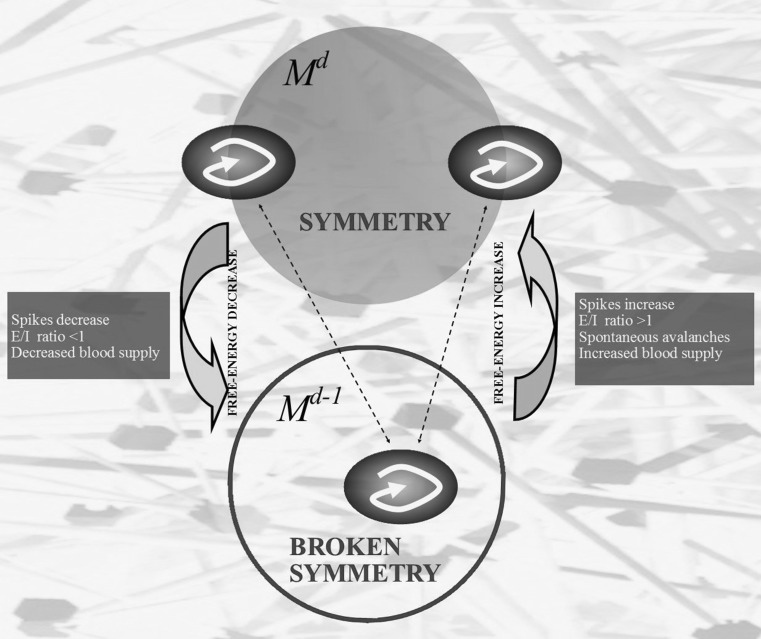
A BUT variant, termed energy-BUT, is particularly useful in our context. There exists a physical link between the abstract concept of BUT and the energetic features of the system formed by two manifolds M ^d and M ^d−1. We start from a manifold M ^d equipped with a pair of antipodal points, standing for a symmetry according to one of the above mentioned BUT variants. When these opposite points map to a n-Euclidean manifold (where M ^d−1lies), a symmetry break/dimensionality reduction occurs, and a single point is achieved (Tozzi and Peters 2016b). However, it is widely recognized that a decrease in symmetry goes together with a decrease in entropy and free-energy, at least in a closed system. This means that the single mapping function on M ^d−1displays energy parameters lower than the two corresponding antipodal functions on M ^d. Therefore, decreases of dimensions give rise to decreases of energy and energy requirements (Fig. 1). In such a way, BUT and its variants yield physical quantities, because we achieve a system in which energetic changes do not depend anymore on thermodynamic parameters, rather on affine connections and homotopies.

Fig. 1.

The manifold M ^d displays two antipodal points with matching description. It this case, according to BUT variants’ dictates, the antipodal points stand for two symmetric functions equipped with the same energetic conformation (black ovals containing curved arrows). When a symmetry break occurs, the manifold M ^d−1 displays just a single function, equipped with an energetic level lower than the sum of the antipodal functions’ ones. Therefore, dimension loss occurs together with a decrease of energy. The lateral dark boxes illustrate some hypothetical but plausible conditions which might cause increase or decrease of energy in the brain. In sum, the system displays a configuration with higher energy in M ^d, and with lower energy when a symmetry break occurs. The background stands for a schematized structure of the brain phase space

It must be taken into account that energy-BUT concerns not just energy, but also information. Indeed, two antipodal points contain more information than their single projection in a lower dimension. Dropping down a dimension means that each point in the lower dimensional space is simpler, because each point has one less coordinate. In sum, energy-BUT provides a way to evaluate decreases in energy and information in topological, other than thermodynamic, terms.

In order to assess the energetic requirements of the brain in a topological fashion, we will provide two examples, the first assuming that the brain is a closed system, and the second that the brain is an open, nonequilibrium biological system.

The brain as a closed system

Here we provide an example in order to calculate the energy requirements of different functional states in the central nervous system. Changing the state of system necessarily entails a modification in thermodynamic free-energy, which is equivalent to the work done on the system, and which can be regarded as the average uncertainty, or the information we have about the system’s microscopic states (Sengupta et al. 2013a). We start from a nervous closed system, shaped in guise of a M ^d−1equipped with a single physical function termed A and characterized, say, by a free-energy = 1 and an entropy = 2. For the gen-BUT, when we project the function to M ^d, we achieve two antipodal functions B and C with matching description, forming a symmetric system. The question here is: which are the values of free-energy and entropy of each one of the two antipodal (symmetric) functions on M ^d? And what happens to enthalpy? This question is crucial, because it calls attention to energy conservation and symmetries. In effect, this question leads to the Noether theorem (Noether 1918), which gives us a physical, testable counterpart to the otherwise algebraic topological BUT. Indeed, if we do not take into account the changes in free energy from A to B and C, there is no possibility to translate the abstract BUT to the physics of brain activity, and we have to use the BUT, as we already did, simply as a useful methodological tool (Peters et al. 2016).

The following scenario can be depicted. The projection (mapping) of the description of a pair of physical points (or regions, or functions) on M ^d into a point in M ^d−1 occurs because we have found a continuous function between the two manifolds. This is a flexible situation, because we can vary the description of the pair physical points (regions, or functions) and achieve a mapping to various Euclidean spaces, depending on the number of features of the antipodes. From the gen-BUT perspective, the entropy of antipodal regions would be part of the description of the antipodes and would be the same for each antipode. This works for regions, since informational entropy is defined in terms of a set of events. Each regional antipode would be the culmination of a set of random events, leading to each antipode. Similarly, the free energy of each antipode would be the same. In sum, if the region A is characterized by free-energy = 1 and an entropy = 2, the regions B and C are both characterized by a free-energy = 1 and an entropy = 2. This means that the total free energy of the system B + C is doubled, compared with A.

The brain as an open, nonequilibrium system

Several authors state that, being the brain an open, nonequilibrium biological system, nonlinear dynamics are of substantial importance in enabling our understanding of neuronal function and in the control of pathological neurological states (Tognoli and Kelso 2013; Fraiman and Chialvo 2012). As thermodynamic entropy measures the dispersion over microstates of a thermodynamic canonical ensemble, informational entropy plays the same role, but over some phase functions or macroscopic variables that change with time (Sengupta et al. 2013a). This means that symmetry breaking in the brain may occur through the widely described phenomena of critical fluctuations and critical slowing (Scholz et al. 1987). Nonlinear dynamics and critical fluctuation can be studied through logistic maps equipped with Hopf bifurcations, where intervals are dictated by the Feigenbaum constants. The BUT variants introduce an approach that offers an explanation of nervous nonlinearity and Hopf bifurcations in terms of algebraic topology (Tozzi and Peters 2016b). Indeed, as reported by Tozzi and Peters (2016b), Hopf bifurcations can be described in terms of antipodal points encompassed in n-spheres. However, in this case, the term n does not stand for a spatial dimension, rather for the Feigenbaum constant’s irrational number (Kim 1997; Schleicher 2007). Therefore, we achieve an abstract sphere made of irrational numbers, where nonlinear dynamics take place in guise of paths and trajectories with matching description. When going one dimension lower, the two antipodal points become just one, that can be described in linear terms. This means that BUT makes it possible for us to evaluate complex nonlinear brain dynamics through much simpler linear techniques.

Brain thermodynamic parameters: when but encompasses a physical quantity

This paragraph correlates thermodynamic and informational parameters with brain dynamical features, in order to analyze and quantify them. The paths described by BUT variants elucidate how the tight energetic coupling among different neural activities gives rise to brains that are in charge of receiving and interpreting signals from other cortical zones, in closely intertwined relationships at every spatio-temporal level. Therefore, topology plus energy becomes one of the central information processing strategies of the nervous system.

Free-energy

The brain represents 2% of the human body mass yet it accounts for about 20% of total energy consumed, a substantial proportion (Attwell and Laughlin 2001). The metabolic brain activity, influenced by a balance between the energy cost incurred by its operation and the benefits realized by energy expenditure, is therefore high and constant over time (Sengupta et al. 2013a). Why does the brain consume such remarkable amounts of energy, despite the fact that evolution is geared toward minimizing very high metabolic costs? Almost 20–60% of the energy allocated for the brain is used to support the metabolic rate of the cortical grey matter and for synapses and action potentials (Sengupta et al. 2013b). For our purposes, we limit our analysis to spike frequency. The free energy roughly corresponds to the electric spike frequency. See Tozzi et al. (2016b) for a technical explanation. It means that the increase in thermodynamic free-energy during brain activity is mostly due to spikes, and that we are allowed to evaluate variations in thermodynamic free-energy during brain activity just in terms of electric spiking. In the context of ongoing fluctuations with complex properties caused by variations in thermodynamic parameters, a foremost issue is the free-energy principle (Friston 2010). A self-organizing system like the brain, at nonequilibrium steady-state with its environment, needs to minimize its free-energy (and associated entropy), in order to resist a tendency towards disorder/entropy. The key thrust is that energy expenditure is balanced by homeostatic mechanisms, in an effort to minimize free-energy, and in an interplay between neuronal structure and activity at many different spatiotemporal scales. A subtle equilibrium takes place among actual sampled sensations, brain’s predictions (e.g., the expected energy), expectation (e.g., the best possible guess), surprise (e.g. an improbable outcome caused by unknown quantities), accuracy (e.g., the surprise about the sensations that are expected) and complexity (e.g., the beliefs before and after observing data through sensory inputs). Such different mechanisms tend towards a main goal: minimising entropy production, which corresponds to minimising the so called variational free-energy. There is a strict correspondence between concepts in Friston’s formalism and that of the thermodynamics. For example, the Gibb’s thermodynamic free-energy stands, in Friston’s framework, for the entropy of recognition density, or in other words, for the above mentioned actual sensation sampled by the brain. Further, because variational and thermodynamic free-energy share a common minimum, we are also allowed to link information processing (e.g., Bayesian belief updating) to metabolic efficiency (Sengupta et al. 2013b), so that the average time of variational free-energy becomes a proxy for entropy.

Temperature

The cortical temperature is not a stable parameter as currently believed. The brain displays instead thermal gradients observed at many spatiotemporal scales (Wang et al. 2014a). Local temperature fluctuations may act as a dynamic variable, modulating presynaptic and postsynaptic events, sensory stimuli, behavioral changes, memory encoding and fine-tune activity-dependent processes (Kalmbach and Waters 2012; Long and Fee 2008). In terms of symmetry breakings achieved during nervous second order phase-transitions, temperature might stand for one of the critical control parameters which dictates how the brain evolves from one coordinated state to another. Therefore, brain temperature can be used as an order parameter to monitor the dynamics of the nervous collective state and deviations from the symmetrical state. Indeed, in terms of informational entropy, cortical temperatures contain information about how large-scale physiological and pathological outcomes arise from the interactions of many small-scale processes, in order that thermal brain variations may lead to different probability outcomes. In sum, non-stationary thermal cortical fluctuations, an underrated general mechanism of nervous function able to modify the energy of the brain and to influence psychophysical characteristics, can be assessed in topological terms.

Entropies

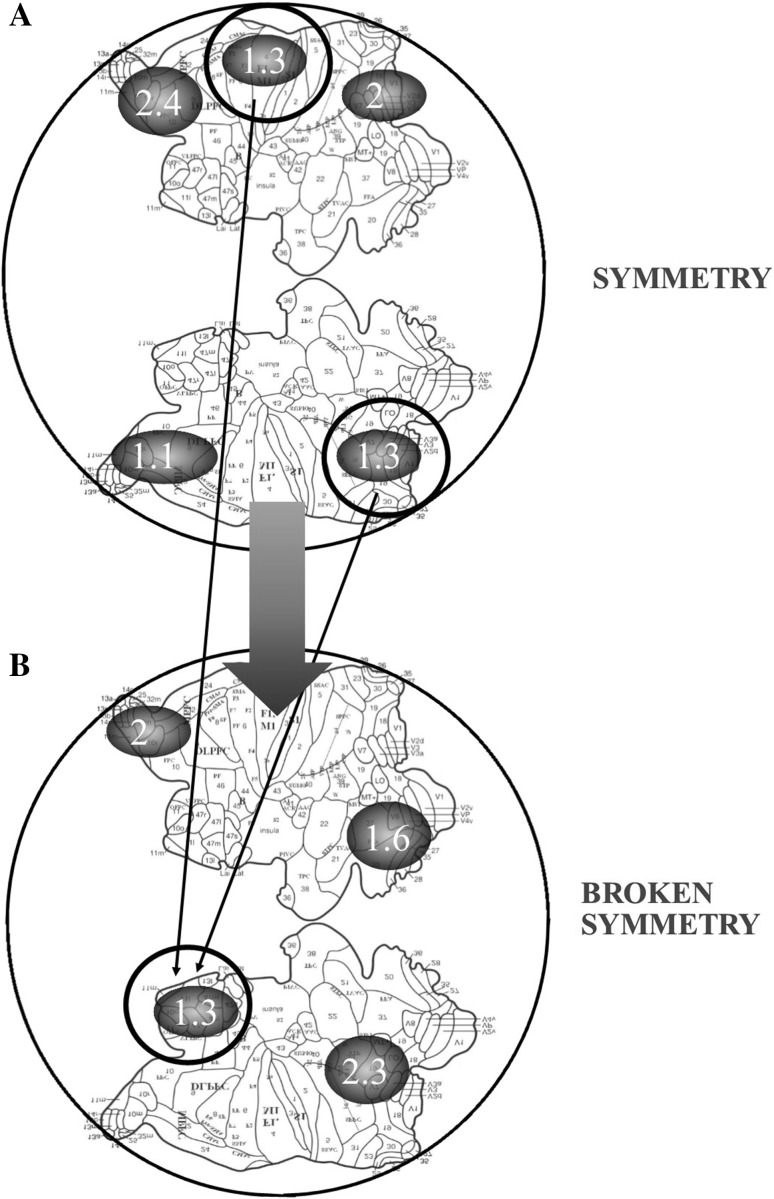
Entropies are evaluated in fMRI functional studies through different techniques, e.g., pairwise entropy (Schneidman et al. 2006; Watanabe et al. 2014; Wang et al. 2014b), Granger causality index, phase slope index, and so on (Kida et al. 2016). Such approaches also make it possible to analyze how the complexity of an adaptive system like the brain is best understood as a dynamic network that aims to decrease its free-energy, for example via entropy transfer. Here we propose a novel topological way to assess, in brain fMRI functional studies, changes in informational entropies. The method, referred here to changes in cortical spatial dimensions, is described in Fig. 2. The Figure shows how, by knowing just the entropy values for each BOLD-activated brain area, we are allowed to correlate two different brain states, e.g., a state with symmetry breaking and a state with preserved symmetries. During a symmetry break or vice versa, the brain may use different mechanisms in order to modify thermodynamic parameters. The possible mechanisms are displayed in Fig. 1. For example, when the system goes from symmetry to symmetry break, the enthalpy must be reduced of the half, via, e.g., a decrease of local blood flow (enthalpy), or a decrease of spike frequency (free-energy). When the system goes from a symmetry break towards a restored symmetry, the brain requires a surplus of external energy to inject into M ^d, and vice versa. Brain spikes, in this framework, could stand for one of the thermodynamic parameters able to give rise to different attractors, and to supply the required enthalpy, in order to proceed from a symmetry to a symmetry breaking and vice versa. There are many good sources of data to test the claim that brain areas are energetically correlated during symmetry breaks. Indeed, unrestricted fMRI data sets are available in web repositories, such as The International Neuroimaging Data-sharing Initiative (INDI), that launched the 1000 Functional Connectomes Project (Biswal et al. 2010), or the Human Connectome Project (Glasser et al. 2016). We will provide an example, in order to demonstrate the feasibility of a combined energetic/topological approach and its aptitude of providing very accurate testable previsions. We have two mental states, one standing for a symmetry, and another for a broken symmetry. Imagine that the brain at rest displays a preserved symmetry, while the brain during a visual task displays a broken symmetry. Our proposed model may predict in fMRI series the energetic values for both the cases. Indeed, according to BUT, a single microarea with symmetry breaking necessarily projects to TWO areas with preserved symmetry. The single area in lower dimensions and the two areas in higher dimensions must to display the same values of entropy. This allows us to recognize which zones of the brain are correlated during symmetry breaks, e.g., during the projective steps from higher to lower levels, and vice versa. Therefore, our framework may predict the following hypothetical results: if we find, during a visual task, say, three microareas with an entropy 1.08, we expect to find, during rest, six or more microareas with entropy = 1.08. In sum, by knowing just the entropy values for each BOLD-activated cortical subarea, we are allowed to correlate two different brain states, e.g., a lower-dimensional state with symmetry breaking and a higher-dimensional state with preserved symmetries.

Fig. 2.

The two brain hemispheres are flattened and displayed in 2D, according to Van Essen (2005). The black circles, depicting hypothetical micro-areas of BOLD signal during fMRI functional studies, contain a number which stands for the corresponding entropy value. a displays a functional state with preserved symmetry (e.g., mind wandering), while b one with symmetry breaking (e.g., a task-related activity). Note that two micro-areas with the same entropy values in a stand for two points with matching description. The latter necessarily project to a single point, in case the brain symmetry is broken, according to the dictates of gen-BUT. This means that in b there must be a micro-area with the same entropy value of the two matching points in a. It allows us to assess which zones of the brain could be correlated during functional symmetry breaks

Conclusions

In this work, we proposed a framework that might be able to achieve, from an abstract topological assessment of brain activity, real thermodynamic parameters, in order to evaluate and correlate different cortical functions. BUT and its novel variants display very useful general features which help us to explain a wide-range of brain phenomena. By satisfying the requirements for BUT, it is possible for us to quantify increases and decreases of free-energy/entropy/enthalpy when going from one functional brain conformation to another, e.g., from the functional 4D sphere of the default mode network during spontaneous brain activity (Tozzi and Peters 2016a), to the lower dimensional 3D manifold during evoked brain activity (Papo 2014). Therefore, the existence of one pair of mappings implies an overall change in thermodynamic and informational parameters. Despite BUT theorem states that it exists at least a pair of antipodal point that maps a dimension lower, nevertheless it does not say that every antipodal pair will be mapped to a single set, nor that all the two sets of objects in higher dimensions display matching descriptions with all the single sets of objects in lower dimensions. It means that we would neither specifically assess if a recorded brain state or a set of trajectories is the image of any antipodes, nor the accurate matching of the mapping from higher-dimension manifolds to lower-dimension ones. However, BUT is still very informative about brain dynamics in practice. Indeed, there exist some trajectories, even if we don’t know which, that are mapped to a lower-dimensional space and imply a predictable energetic change. Because the brain functional micro-zones are countless, the use of BUT is helpful in achieving a drastic reduction and simplification of the areas to investigate. Instead of looking for a needle in a haystack, BUT makes it possible for neuro-researchers to remove the most of the straw and to increase the number of needles. The BUT approach also complements the claim of Simas et al. (2015), who suggested that the algebraic topological approach of embedding a brain network on metric spaces (of different dimensions) may reveal regions that are members of large areas or subsystems, rather than regions with a specific role in information processing. Indeed, Simas’ framework is not restricted to the static aggregation, rather the multilayers assemblies can be seen as temporal brain windows, and their dynamics as a minimization of inter-level energy in an average time window. In sum, contrary to the classical averaging of connectivity matrices, the BUT approach reveals brain areas with a specific role in information processing.

A shift in conceptualizations is evident in a methodological approach based on BUT. That is, the opportunity to treat brain dynamics as topological structures gives us the invaluable chance to describe them through the tools of functional analysis (Dol’nikov 1992). The BUT perspective enunciates a symmetry property located in the physical space (the environment and the brain) to be translated to an abstract space and vice versa, enabling us to achieve maps from one system to another. This approach is in touch with recent proposals, which provide a rigorous way of measuring distance on brain manifolds (Sengupta et al. 2016). We might imagine the brain as a manifold, equipped with a high number of symmetries and with an internal, mathematically structured, holistic generative model of the external world. Depending on external stimuli (Tozzi et al. 2016a) and on individual background, symmetry breaks occur, giving rise to phase spaces equipped with a lower number of dimensions. This takes us into the realm of metric algebraic topology (Willard 1970), where multidimensional manifold describe the structural order of the relationships between nervous anatomical components and their functional paths.