Abstract
Isotopes separation through quantum sieving effect of membranes is quite promising for industrial applications. For the light hydrogen isotopologues (eg. H2, D2), the confinement of potential wells in porous membranes to isotopologues was commonly regarded to be crucial for highly efficient separation ability. Here, we demonstrate from first-principles that a potential barrier is also favorable for efficient hydrogen isotopologues separation. Taking an already-synthesized two-dimensional carbon nitride (C2N-h2D) as an example, we predict that the competition between quantum tunneling and zero-point-energy (ZPE) effects regulated by the tensile strain leads to high selectivity and permeance. Both kinetic quantum sieving and equilibrium quantum sieving effects are considered. The quantum effects revealed in this work offer a prospective strategy for highly efficient hydrogen isotopologues separation.
Introduction
The separation of hydrogen isotopologues, such as H2, D2 and T2, is a crucial and inevitable stage for their applications in the nuclear industry. However, the low productivity and high energy cost of conventional hydrogen isotopologues separation methods hamper the relevant applications1–5. The emerging quantum sieving technology for isotopes separation has seized great attention due to its low energy consumption. Most of the prevalent works focus on the adsorptive capacities or diffusion properties of isotopologues in specific confined systems, such as carbon nanotubes, carbon nanohorns, metal-organic framework, as well as single-atomic membranes6–11. These porous structures impose nano-confinement to the guest molecules, invoking difference in the quantum levels associated with different masses, which can be magnified at low temperature for isotopes separation12. The separation efficiency of these systems significantly depends on the pore size and shape10, 13–16. However, the precise control of the porous structures remains a challenge in experiments.
Previous works using the equilibrium and kinetic quantum sieving approaches indicate that the confinement of potential wells to isotopologues is favorable for H2/D2 separation6, 7, 15–17, whereas potential barriers are regarded to be unsuitable for efficient isotopologues separation due to its low permeance10. However, when a barrier exists on the diffusion path, quantum tunneling effect begins to impact the diffusion behaviors at low temperatures, especially for such light molecule as hydrogen. This phenomenon has been demonstrated to effectively enable the helium isotopes separation by several two-dimensional (2D) membranes at low temperatures, where the lighter isotope (e.g. 3He) is more inclined to transmit through the membranes18–20. In these systems, the interaction between the membrane and the guest isotopes can be tuned by applying tensile strain which modifies the pore size of the membrane, and highly efficient isotopes separation with optimized selectivity and permeance can be obtained21. It is noteworthy that the zero-point-energy (ZPE) of hydrogen in confined systems would affect the energy barrier on the diffusion pathway12. Heavier isotopologues (e.g. D2) experience a lower energy barrier than the light ones (e.g. H2) according to the inversely scale law of the vibrational frequencies versus masses, which favors the transmission of the heavier ones, in contrary to the quantum tunneling effect22. The ZPE effect has been investigated in the cylindrical confinement systems such as carbon nanotubes by using equilibrium quantum sieving approaches6, 15, 16. Additionally, quantum tunneling of hydrogen ions through a graphene sheet or a hexagonal boron nitride membrane offered alternatives for isotopes separation23–25.
In this work, we investigate the quantum tunneling of hydrogen isotopologues through an energy barrier by taking the ZPE correction into account. We employed kinetic quantum sieving and equilibrium quantum sieving approaches within a pseudo-one-dimensional approximation. Using an experimentally available membrane (C2N-h2D) as an example, we demonstrate that the competition between quantum tunneling effect and ZPE effect regulated by the tensile strain leads to high selectivity and permeance of hydrogen isotopologues separation. This provides a promising strategy for efficient D2 harvest for both scientific and industrial applications. In particular, we show that the unique porous structure of C2N-h2D with uniformly distributed pores (as shown in Fig. 1(a)), offers an ideal energy barrier for various gas separation utilization without the needs of additional modification, in contrary to previously proposed porous graphene sheets10, 26.
Figure 1.
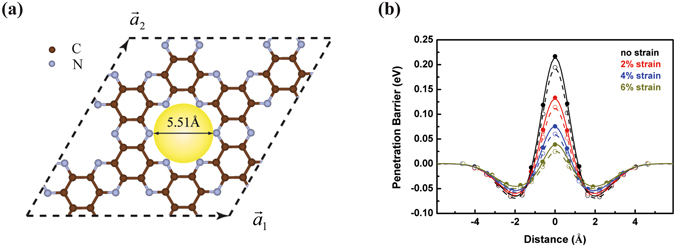
(a) The top view of the optimized (2 × 2) C2N-h2D supercell, where , represent two primitive vectors. The brown and blue balls represent the C and N atoms respectively. The inscribed circle is indicated by the yellow circle. (b) The effective barriers of H2 (solid balls, solid lines), D2 (open balls, dashed lines) passing through C2N-h2D membrane along the perpendicular direction under different tensile strains. Colored points indicate the results obtained by first-principles calculations; while the curves show the numerically interpolated potentials.
Results
Energy profiles with ZPE correction
We firstly optimized the unit cell of C2N-h2D using the density function theory (DFT) implemented in Vienna Ab initio Simulation Package (VASP)27, 28. The lattice is calculated to be 8.33 Å, in good agreement with the experimental data29. Figure 1(a) presents a top view of a fully relaxed (2 × 2) C2N-h2D supercell. The pore size characterized by the diameter of the inscribed circle is 5.51 Å. In order to regulate the energy barrier of a hydrogen molecule passing through the membrane, a series of biaxial tensile strain, defined by the ratio of the deformation Δa to the initial lattice constant a 0, ε = Δa/a 0, were then applied to enlarge the pore of the C2N-h2D membrane. The minimum energy pathway of hydrogen molecule passing through the C2N-h2D membrane under strains (0%, 2%, 4% and 6%) were searched by the climbing image nudged elastic band method (CNEB)30, 31, where the isotropic effect was not involved. Along the diffusion pathway, the displacements of the molecule parallel to the membrane are negligible compared to that perpendicular to the membrane (Fig. S1). We therefore took a pseudo-1D approximation (along the perpendicular direction) to treat the transmission process for simplification. Besides, the quantum effects of the translation, rotation and vibration of the molecule were taken into account through the ZPE correction as discussed below.
The ZPE correction for each image in the CNEB method was calculated on the basis of the density functional perturbation theory implemented in VASP, and then added to the CNEB energy profiles to obtain the effective penetration barriers. Three translational modes, two rotational modes and one vibrational mode were involved in the ZPE correction, among which the vibrational mode dominates. The effective energy barriers for H2 and D2 are well separated due to different ZPE values, as shown in Fig. 1(b). Each energy profile for both isotopologues consists of two wells separated by a wall. The wells correspond to the adsorption of hydrogen isotopologues on the C2N-h2D membrane, while the barriers arise from the pore confinement. The effective barriers for H2 (solid circles, solid lines) and D2 (open circles, dashed lines) through the pore of the membrane decrease with the increase of the tensile strain. Similar to the case in the well confinement7, D2 always experiences a lower barrier compared with H2, due to the smaller ZPE correction values. Additionally, this difference decreases with increasing tensile strain (Fig. S2), indicating that ZPE effect becomes enhanced at high energy barrier conditions.
Kinetic quantum sieving
We utilized the one-dimensional (1D) finite difference method32 to evaluate the quantum tunneling probability t(E) (Fig. 2), the D2 permeance Q(D 2) and the kinetic selectivity S(D 2/H 2)19, 21, 33, 34. Unlike the case of helium isotopes21, 33, the ZPE correction leads to a lower barrier for D2 than that for H2, and thus the larger quantum tunneling probability of D2.
Figure 2.
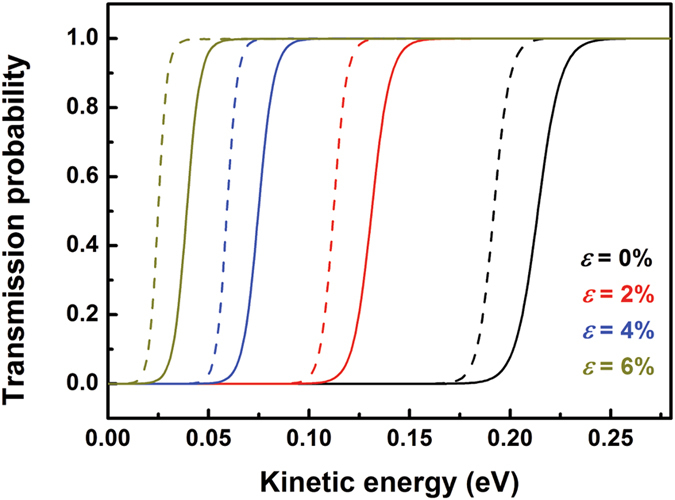
Quantum tunneling probability t(E) of hydrogen passing through the pore of C2N-h2D membrane as a function of kinetic energy under different strains. The solid curves represent the quantum-mechanical transmission of H2 and the dashed curves represents that of D2, respectively.
As only the pore areas contribute to hydrogen transmission, we defined a fractional parameter in the permeance calculations , where Å is the kinetic diameter of H2 or D2 molecule35 and a is the lattice constant of the strained C2N-h2D. Therefore, the D2 permeance is
| 1 |
| 2 |
| 3 |
where p(T) is the thermally-weighted transmission that has to be numerically evaluated via Eq. (2) and both the incoming pressure and the pressure drop are assumed to be 1 bar. Figure 3 depicts the D2 permeance and the kinetic selectivity variation with temperature under different tensile strains. The D2 permeance increases with the increase of the tensile strain, as lower barriers permit more flux. The selectivity varies non-monotonically with the temperature: with the increase of temperature, the D2/H2 kinetic selectivity increases and reaches a maximal value at a critical temperature, above which it drastically decreases with temperature, similar to the results of atomistic molecular dynamics simulations17. The critical temperature shifts towards to a lower value with the increase of tensile strain. These variations indicate the competition between the quantum tunneling and the ZPE: at low temperatures, the quantum tunneling effect is dominating which favors the transmission of the lighter isotope, while as temperature increases the heavier isotopes are more inclined to pass through the membrane since ZPE becomes dominating. Under 4% and 6% strains, the membrane exhibit optimized efficiency on both permeance and selectivity, which are 9.6 and 2.6 × 10−7 mol/s/cm2/bar at 51 K (4% strain), and 13.7 and 2.04 × 10−4 mol/s/cm2/bar at 39 K (6% strain), respectively. It has been demonstrated that the C2N-h2D is stable under strain less than 10%21, the 4~6% strained membrane is thus practical for industrial application.
Figure 3.
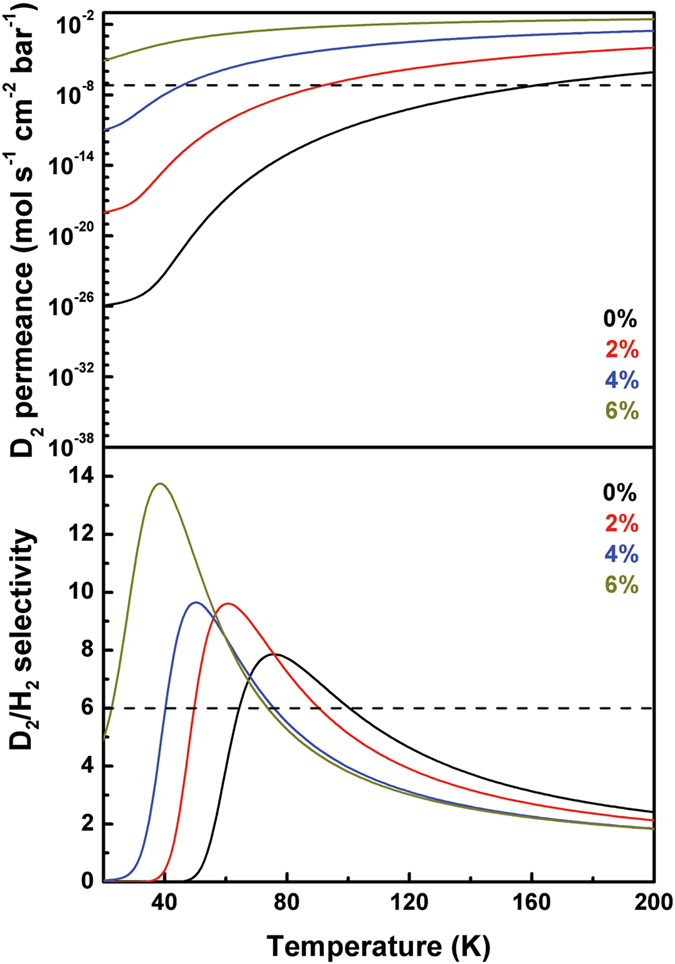
The D2 permeance and the kinetic selectivity under different strains for temperature ranging from 20 to 200 K. Different colors indicate different strains ranging from 0% to 6%. The dashed lines indicate the industrial-acceptable values for permeance (6.7 × 10−8 mol/s/cm2/bar) and selectivity (6), respectively.
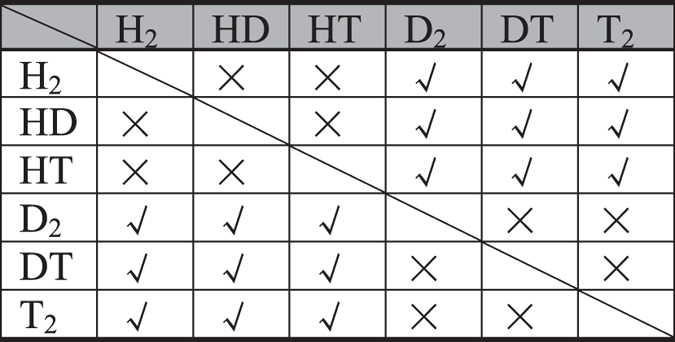
It is noteworthy that there are other hydrogen isotopologues, such as HD, HT, DT, T2. Using the same strategy, we have calculated the ZPE corrected energy barriers for these hydrogen isotopologues (Fig. S3) and evaluated the separation efficiency between all six isotopes (Fig. S4). The separation abilities of C2N-h2D membrane for these hydrogen isotopologues are summarized in Table 1. It can be seen that C2N-h2D membrane is available for separation of H2/D2, H2/DT, H2/T2, HD/D2, HD/DT, HD/T2, HT/D2, HT/DT, HT/T2 with good permeance and selectivity.
Table 1.
The separation abilities of C2N-h2D membrane for hydrogen isotopologues (H2, HD, HT, D2, DT, T2). The tick symbol indicates that the C2N-h2D membrane is able to efficiently separate two isotopologues with industrial acceptable permeance and selectivity, while the cross symbol represents the opposite situation.
Equilibrium quantum sieving
The thermally-driven equilibrium sieving calculations were performed following the Schrier’s approach22, 26, which combines transition state theory (TST) with quantum tunneling effect. This strategy holds for the case where two ideal gases at different temperature (cold reservoir and hot reservoir) are separated by a nanoporous barrier, e.g. C2N-h2D membrane. Here we took the H2/D2 separation as an example to investigate the equilibrium quantum sieving efficiency of the C2N-h2D membrane. As the tunneling barriers for two isotopologues are different in our case, the H2/D2 separation factor is changed accordingly:
| 4 |
where is the thermally-weighted classical barrier transmission probability and V corresponds to the barrier height in Fig. 1(b).
Figure 4 depicts the H2/D2 separation factors obtained for the strained C2N-h2D membrane at thermal reservoir temperatures ranging from 50 K to 300 K. Without strain, the competition between the ZPE and quantum tunneling results in both r TST+Q > 1 and r TST+Q < 1 at different reservoir temperature conditions, which means that by properly choosing the reservoir temperature, either H2 or D2 enrichment can be achieved. However, when strain larger than 2% is imposed to this membrane, only D2 enrichment is obtained regardless of mechanisms. Especially, under strain of 6% (Fig. 4(d)), D2 enrichment with r TST+Q = 0.17 (corresponding to 6:1 isotope enrichment) can be obtained with permeance of 8 × 10−4 mol/s/cm2/bar which meets the requirement of industrial applications.
Figure 4.
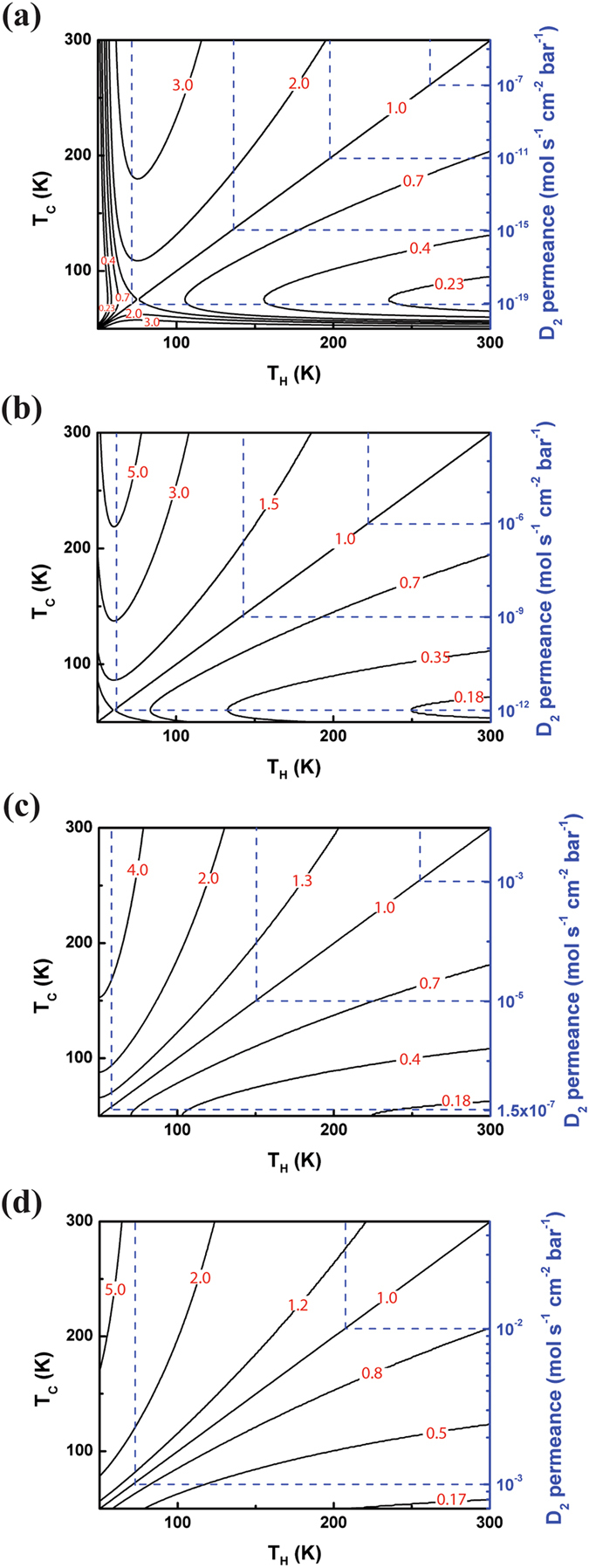
Thermally-driven separation factor r TST+Q indicated by black solid contour at low temperature regime and the corresponding D2 permeance by the blue dotted contours labeled on the right axis. (a) for strain of 0%, (b) for strain of 2%, (c) for strain of 4% and (d) for strain of 6%.
Discussion
Different from previous strategies employing potential well confinement for hydrogen isotopologues separation, we here make use of a potential barrier by a 2D membrane. Both kinetic and equilibrium quantum sieving with competitive separation efficiency can be easily achieved in an already synthesized C2N-h2D membrane under suitable strain, which provides an alternate approach for hydrogen isotopologues separation. More importantly, the C2N-h2D membrane exhibits intrinsic confinement to the hydrogen isotopologues, without the need of post-modifications or precise control of the material structure during manufacture.
The proper potential barrier provided by the strained C2N-h2D membrane ensures both high selectivity and high permeance, which also sets up a suitable window for highly-efficient hydrogen isotopologues separation. The barrier-based quantum sieving effect may also hold in other 2D porous membranes for this utility. Furthermore, the strain-tunable quantum sieving of 2D membranes offers a convenient manner for improving separation efficiency under various conditions.
In conclusion, by first-principles calculations, we show that both kinetic and equilibrium quantum sieving for D2 enrichment can be obtained via tunneling through a potential barrier in a strained C2N-h2D membrane. The competition between the ZPE effect and quantum tunneling effect leads to high separation efficiency with industrial acceptable selectivity and permeance. Our results provide an experimentally available 2D porous membrane as a superior quantum sieving that holds promise for both scientific and industrial applications.
Methods
Our first-principles calculations were performed in the framework of density functional theory (DFT) using the plane-wave pseudopotential approach as implemented in the Vienna Ab initio Simulation Package (VASP)27, 28, 36. The electron-electron interactions were treated using a generalized gradient approximation (GGA) in the form of Perdew-Burke-Ernzerhof (PBE) for the exchange-correlation functional36. The van der Waals (vdW) interactions were included explicitly by using the empirical correction scheme of Grimme (DFT-D2)37. The energy cutoff of the plane waves was set to 500 eV with an energy precision of 10−4 eV. The atomic coordinates were fully relaxed using a conjugate gradient scheme without any symmetry restrictions until the maximum force on each ion was smaller than 0.02 eV/Å. Vacuum space larger than 15 Å was used to avoid the interaction between adjacent images. The Monkhorst-Pack meshes of 7 × 7 × 1 were used in sampling the Brillouin zone for the 2 × 2 supercells of C2N-h2D lattice.
The ZPE correction was calculated by the density functional perturbation theory (DFPT) implemented in VASP. In this part of calculation, the energy cutoff of the plane waves was set to 500 eV with an energy precision of 10−8 eV and the maximum force on each ion was set to be 0.001 eV/Å.
The quantum tunneling probability calculations were performed using a 1D finite difference method. The grid density was set to be 0.01 Å and a region of 1 Å located 5 Å away from the peak of the barrier was chosen for the incident planewaves, where the barriers is lower than 0.001 eV.
Electronic supplementary material
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Nos 11504204, 21433006), the 111 project (No. B13029), the Fundamental Research Funds of Shandong University (Grant No. 2015HW012), the Technological Development Program in Shandong Province Education Department (Grant No. J14LJ03), and the National Super Computing Centre in Jinan.
Author Contributions
Y.Q. and F.L. performed the calculations and analyzed the data. Y.Q. and M.Z. conceived the research. Y.Q. and M.Z. wrote the paper.
Competing Interests
The authors declare that they have no competing interests.
Footnotes
Electronic supplementary material
Supplementary information accompanies this paper at doi:10.1038/s41598-017-01488-8
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Alekseev IA, et al. Heavy water detritiation by combined electrolysis catalytic exchange at the experimental industrial plant. Fusion Eng. Des. 2003;69:33–37. doi: 10.1016/S0920-3796(03)00230-8. [DOI] [Google Scholar]
- 2.Richter FM, et al. Isotopic fractionation of the major elements of molten basalt by chemical and thermal diffusion. Geochim. Cosmo. Ac. 2009;73:4250–4263. doi: 10.1016/j.gca.2009.04.011. [DOI] [Google Scholar]
- 3.Lis G, Wassenaar LI, Hendry MJ. High-Precision laser spectroscopy D/H and 18O/16O measurements of microliter aatural water samples. Anal. Chem. 2008;80:287–293. doi: 10.1021/ac701716q. [DOI] [PubMed] [Google Scholar]
- 4.Degtyareva OF, Bondareva LT. Gas-chromatographic analysis of mixtures of hydrogen Isotopes. J. of Anal. Chem. 2004;59:442–446. doi: 10.1023/B:JANC.0000026235.63109.f1. [DOI] [Google Scholar]
- 5.Hu S, et al. Hydrophobic Pt catalysts with different carbon substrates for the interphase hydrogen isotope separation. Sep. Purif. Technol. 2011;77:214–219. doi: 10.1016/j.seppur.2010.12.008. [DOI] [Google Scholar]
- 6.Wang Q, Challa SR, Sholl DS, Johnson JK. Quantum sieving in carbon nanotubes and zeolites. Physical Review Letters. 1999;82:956–959. doi: 10.1103/PhysRevLett.82.956. [DOI] [Google Scholar]
- 7.Kagita H, et al. Quantum molecular sieving effects of H2 and D2 on bundled and nonbundled single-walled carbon nanotubes. J. Phys. Chem. C. 2012;116:20918–20922. doi: 10.1021/jp3065085. [DOI] [Google Scholar]
- 8.Tanaka H, Kanoh H, Yudasaka M, Iijima S, Kaneko K. Quantum effects on hydrogen Isotope adsorption on single-wall carbon nanohorns. J. Am. Chem. Soc. 2005;127:7511–7516. doi: 10.1021/ja0502573. [DOI] [PubMed] [Google Scholar]
- 9.Noguchi D, et al. Quantum sieving effect of three-dimensional Cu-based organic framework for H2 and D2. J. Am. Chem. Soc. 2008;130:6367–6372. doi: 10.1021/ja077469f. [DOI] [PubMed] [Google Scholar]
- 10.Hankel M, Jiao Y, Du A, Gray SK, Smith SC. Asymmetrically decorated, doped porous graphene as an effective membrane for hydrogen isotope separation. J. Phys. Chem. C. 2012;116:6672–6676. doi: 10.1021/jp211930a. [DOI] [Google Scholar]
- 11.Teufel J, et al. MFU-4 – a metal-organic framework for highly effective H2/D2 separation. Adv. Mater. 2013;25:635–639. doi: 10.1002/adma.201203383. [DOI] [PubMed] [Google Scholar]
- 12.Beenakker JJM, Borman VD, Krylov SY. Molecular transport in subnanometer pores: zero-point energy, reduced dimensionality and quantum sieving. Chem. Phys. Lett. 1995;232:379–382. doi: 10.1016/0009-2614(94)01372-3. [DOI] [Google Scholar]
- 13.Wang Y, Bhatia SK. Simulation of quantum separation of binary hydrogen isotope mixtures in carbon slit pores. Mol. Simulat. 2009;35:162–171. doi: 10.1080/08927020802267394. [DOI] [Google Scholar]
- 14.Tanaka H, et al. Quantum effects on hydrogen isotopes adsorption in nanopores. J. Low Temp. Phys. 2009;157:352–373. doi: 10.1007/s10909-009-9917-8. [DOI] [Google Scholar]
- 15.Challa SR, Sholl DS, Johnson JK. Adsorption and separation of hydrogen isotopes in carbon nanotubes: Multicomponent grand canonical Monte Carlo simulations. J. Chem. Phys. 2002;116:814–824. doi: 10.1063/1.1423665. [DOI] [Google Scholar]
- 16.Hankel M, et al. Kinetic modelling of molecular hydrogen transport in microporous carbon materials. Phys. Chem. Chem. Phys. 2011;13:7834–7844. doi: 10.1039/c0cp02235g. [DOI] [PubMed] [Google Scholar]
- 17.Kumar AVA, Bhatia SK. Quantum effect induced reverse kinetic molecular sieving in microporous materials. Phys. Rev. Lett. 2005;95:245901. doi: 10.1103/PhysRevLett.95.245901. [DOI] [PubMed] [Google Scholar]
- 18.Hauser AW, Schwerdtfeger P. Nanoporous graphene membranes for efficient 3He/4He separation. J. Phys. Chem. Lett. 2012;3:209–213. doi: 10.1021/jz201504k. [DOI] [PubMed] [Google Scholar]
- 19.Bartolomei M, et al. Graphdiyne pores:‘Ad hoc’ openings for helium separation applications. J. Phys. Chem. C. 2014;118:29966–29972. doi: 10.1021/jp510124e. [DOI] [Google Scholar]
- 20.Li F, Qu Y, Zhao M. Efficient helium separation of graphitic carbon nitride membrane. Carbon. 2015;95:51–57. doi: 10.1016/j.carbon.2015.08.013. [DOI] [Google Scholar]
- 21.Qu Y, Li F, Zhou H, Zhao M. Highly efficient quantum sieving in porous graphene-like carbon nitride for light isotopes separation. Sci. Rep. 2016;6:19952. doi: 10.1038/srep19952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Schrier J, McClain J. Thermally-driven isotope separation across nanoporous graphene. Chem. Phys. Lett. 2012;521:118–124. doi: 10.1016/j.cplett.2011.11.069. [DOI] [Google Scholar]
- 23.Igor Poltavsky, L. Z., Mortazavi, M. & Tkatchenko, A. Quantum tunneling of thermal protons through pristine graphene. doi:arXiv: 1605.06341[physica.chem-ph] (2016). [DOI] [PubMed]
- 24.Lozada-Hidalgo M, et al. Sieving hydrogen isotopes through two-dimensional crystals. Science. 2016;351:68–70. doi: 10.1126/science.aac9726. [DOI] [PubMed] [Google Scholar]
- 25.Kroes JM, Fasolino A, Katsnelson MI. Density functional based simulations of proton permeation of graphene and hexagonal boron nitride. Phys. Chem. Chem. Phys. 2017;19:5813–5817. doi: 10.1039/C6CP08923B. [DOI] [PubMed] [Google Scholar]
- 26.Hauser AW, Schrier J, Schwerdtfeger P. Helium tunneling through nitrogen-functionalized graphene pores: pressure- and temperature-driven approaches to isotope separation. J. Phys. Chem. C. 2012;116:10819–10827. doi: 10.1021/jp302498d. [DOI] [Google Scholar]
- 27.Kohn W, Sham LJ. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965;140:1133–1138. doi: 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
- 28.Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B. 1996;54:11169–11186. doi: 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
- 29.Mahmood, J. et al. Nitrogenated holey two-dimensional structures. Nat. Commun. 6 (2015). [DOI] [PMC free article] [PubMed]
- 30.Henkelman G, Uberuaga BP, Jónsson H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000;113:9901–9904. doi: 10.1063/1.1329672. [DOI] [Google Scholar]
- 31.Henkelman G, Jónsson H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 2000;113:9978–9985. doi: 10.1063/1.1323224. [DOI] [Google Scholar]
- 32.Cedillo A. Quantum mechanical tunneling through barriers: A spreadsheet approach. J. Chem. Educ. 2000;77:528. doi: 10.1021/ed077p528. [DOI] [Google Scholar]
- 33.Schrier J. Helium separation using porous graphene membranes. J. Phys. Chem. Lett. 2010;1:2284–2287. doi: 10.1021/jz100748x. [DOI] [Google Scholar]
- 34.Zhu Z. Permeance should be used to characterize the productivity of a polymeric gas separation membrane. J.Membrane Sci. 2006;281:754–756. doi: 10.1016/j.memsci.2006.04.040. [DOI] [Google Scholar]
- 35.Mehio N, Dai S, Jiang D-e. Quantum mechanical basis for kinetic diameters of small gaseous molecules. J. Phys. Chem. A. 2014;118:1150–1154. doi: 10.1021/jp412588f. [DOI] [PubMed] [Google Scholar]
- 36.Hohenberg P, Kohn W. Inhomogeneous electron gas. Phys. Rev. 1964;136:B864–B871. doi: 10.1103/PhysRev.136.B864. [DOI] [Google Scholar]
- 37.Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006;27:1787–1799. doi: 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


