A SMART Data Analysis Method for Constructing Adaptive Treatment Strategies for Substance Use Disorders

Abstract

Aims

To demonstrate how Q-learning, a novel data analysis method, can be used with data from a sequential, multiple assignment, randomized trial (SMART) to construct empirically an adaptive treatment strategy (ATS) that is more tailored than the ATSs already embedded in a SMART.

Method

We use Q-learning with data from the Extending Treatment Effectiveness of Naltrexone (ExTENd) SMART (N=250) to construct empirically an ATS employing naltrexone, behavioral intervention, and telephone disease management to reduce alcohol consumption over 24 weeks in alcohol dependent individuals.

Results

Q-learning helped to identify a subset of individuals who, despite showing early signs of response to naltrexone, require additional treatment to maintain progress.

Conclusions

Q-learning can inform the development of more cost-effective, stepped-care strategies for treating substance use disorders.

Introduction

The cyclical and heterogeneous nature of many substance use disorders highlights the need to adapt the type or the dose of treatment to accommodate the specific and changing needs of individuals. [1–6] Adaptive treatment strategies (ATSs) are suited for guiding this type of sequential and tailored treatment decision making. [1,7–10] An ATS is a treatment design in which treatment options are tailored based not only on baseline characteristics (e.g., patient demographics), but also on information that is likely to change over time in the course of treatment (e.g., early signs of non-response). This is similar to clinical decision making whereby care providers tailor the type/dose of treatment repeatedly in the course of clinical care based on ongoing information regarding patient progress in treatment. In an ATS, such tailoring is operationalized (formalized) via decision rules that specify what type/dose of treatment should be offered, for whom and when, so as to enable replicability and evaluation. The sequential, multiple assignment, randomized trial (SMART) was developed specifically for constructing empirically-supported ATSs. [11,12] A SMART is an experimental design, which involves multiple stages of randomization. Each randomization stage provides an opportunity to inform how best to tailor the treatment at a specific stage of an ATS.

Several sequences of treatments of scientific interest are embedded in a SMART by design; these often use a single tailoring variable, such as the individual’s early response status—offering different subsequent treatments to individuals who show early signs of non-response to initial treatments than to those who respond well. However, investigators are often interested in using data from a SMART to construct ATSs that are more tailored. That is, investigators often collect additional information concerning baseline (e.g., baseline severity) and time-varying status of individuals (e.g., adherence to treatment) and plan to use this information to investigate whether and how treatment could be further tailored according to these variables. Drawn from computer science, Q-learning [13,14] is a novel methodology that can be used for this purpose.

The current manuscript provides an overview of Q-learning to investigators in the area of substance use disorders (SUDs). Despite the growing use of SMART studies in the area of SUDs, [15] there are no published applications of Q-learning in this area. Further, existing illustrations of Q-learning are mainly geared towards statisticians (e.g., [16,17]). To close this gap, we use data from the Extending Treatment Effectiveness of Naltrexone (ExTENd) trial—a 24-week study employing a SMART to inform the development of an ATS for supporting naltrexone medication in the treatment of alcohol dependence (N=250; D. Oslin, P.I. [18–20]). Previous analyses of data from ExTENd compared the relatively simple ATSs embedded in this SMART [18,21]. Here, these data are used for the first time with Q-learning to construct a more tailored ATS. The goal of this application is to demonstrate the scientific yield gained by applying Q-learning to inform the construction of ATSs for SUDs. Key terms and definitions are provided in Table 1.

Table 1.

Key terms and definitions

Key term	Definition
Tailoring	Individualization, namely the use of information from the individual to select when and how to offer treatment.
Tailoring variables	Information concerning the individual that is used for individualization (i.e., to decide when and/or how to offer treatment).
Adaptive Treatment Strategy (ATS)	A treatment design in which treatment options are tailored not only based on baseline characteristics, but also based on time-varying information about the individual, namely information that is likely to change over time in the course of treatment. An ATS involves a sequence of decision rules. The decision rules link the treatment options and tailoring variables in a systematic way.
The Sequential, Multiple Assignment, Randomized Trial (SMART)	A multi-stage randomized trial. Participants progress through the stages and are potentially randomly assigned to one of several treatment options at each stage. Each stage of randomization is designed to address scientific questions concerning the type, dose, mode of delivery, or tailoring of treatments at a specific stage of an ATS. While most clinical trials are designed to evaluate or compare two or more treatments, SMART aims to provide data to construct and optimize an ATS.
Embedded Adaptive Treatment Strategies	Tailored sequences of treatments of scientific interest that are embedded in a SMART by design. These ATSs are often relatively simple, in that they use a single tailoring variable—the individual’s early response status.
Q-learning Regression	A data analysis method drawn from computer science that can be used with SMART data to investigate whether and how certain covariates are useful for developing an ATS or improving an existing one. In other words, this method can be used to identify new tailoring variables beyond those used in a SMART by design. The “Q” in Q-learning indicates that this method is used to assess the relative quality of different treatment options in a sequence of tailored treatments.

Adaptive Treatment Strategies

Consider the development of an ATS to treat alcohol dependence using oral naltrexone (NTX)–an opioid receptor antagonist that blocks the pleasurable effects resulting from endogenous opioid neurotransmitters released by alcohol consumption in some people. [22,23] While NTX is efficacious for treating alcohol dependence, clinical use of NTX has been limited, [24] in part because of substantial heterogeneity in treatment response; [25] this heterogeneity is attributed to multiple factors, such as poor adherence, biological response to alcohol and the medication, poor coping skills, and poor social support. Hence, a natural ATS might include treatment components aimed to address these multiple factors, such as the Combined Behavioral Intervention (CBI), an in-person intervention targeting adherence to pharmacotherapy, motivation for change, and coping skills; and telephone disease management (TDM), targeting similar factors via basic (minimal) telephone-delivered clinical support. [26,27]

The following is an example ATS in this setting: At the first stage, alcohol dependent individuals are provided NTX, and their drinking behaviors are monitored weekly for eight weeks. At the second stage, the type of treatment is adapted based on the number of heavy drinking days (HDDs)ⁱ in the past week. Specifically, individuals who experience five or more HDDs during weeks two to eight are considered to be non-responding; as soon an individual is non-responding, s/he enters the second stage and is offered a rescue intervention: switching to CBI. Individuals who never experience five or more HDDs up to and including week eight (i.e., responders) are offered a maintenance intervention: adding TDM at the end of week eight. An ATS involves a sequence of decision rules; this ATS uses the decision rules in ATS#1 (Table 2).

Table 2.

Adaptive treatment strategies

ATS #1	ATS #2: A more tailored ATS
At entry into the program   First-stage treatment = [NTX] At the end of every week from week 3 to 8 of the initial NTX treatment   If response status = nonresponse (HDD ≥ 5)     Then, second-stage treatment = [Switch to CBI immediately]   Else if response status = response (HDD < 5)     Then, continue first-stage treatment and re-assess non-response in the following week, and at week 8 move to second-stage treatment = [add TDM]	At entry into the program   Stage 1 treatment = [NTX] By the end of week 3 of initial NTX treatment   Choose between a stringent or lenient criterion for weekly response/non-response At the end of every week from week 3 to 8 of the initial NTX treatment   If response status = non-response     Then, second-stage treatment = [offer CBI or NTX+CBI]   Else if response status = response     Then, continue stage 1 treatment and re-assess non-response in the following week, and, at week 8       If the proportion of non-abstinence days during first-stage > 10%         Then, move to second-stage treatment = [NTX+TDM]       Else if the proportion of non-abstinence days during first-stage ≤ 10%         Then, move to second-stage treatment = [NTX+TDM or NTX alone]
Estimated percentage of abstinence days over the entire study duration among ExTENd participants following this ATS: 78%	Estimated percentage of abstinence days over the entire study duration among ExTENd participants following this ATS: 77%

The decision rules for this example ATS involve a single tailoring variable–the individual’s response status. Here, different second-stage treatments are offered to responders than to non-responders. The first-stage treatment and the criterion for non-response are not tailored; they are the same for all individuals.

Traditionally, the sequence of decision rules underlying ATSs used in practice are constructed based on clinical experience, empirical evidence and literature reviews. However, in many cases, there are open questions concerning the best treatment option at specific stages of an ATS, which tailoring variables to use, and how to best use them. For example, in the context of the example ATS above, there may be insufficient evidence to inform (a) the amount of drinking behavior that reflects non-response to NTX, (b) the type of rescue tactic that would be most useful for non-responders, and (c) the type of maintenance tactic that would be most useful in reducing the chance of relapse among responders. The SMART is a clinical trial design that can be used to efficiently obtain data to address scientific questions such as these.

The Sequential, Multiple Assignment, Randomized Trial (SMART)

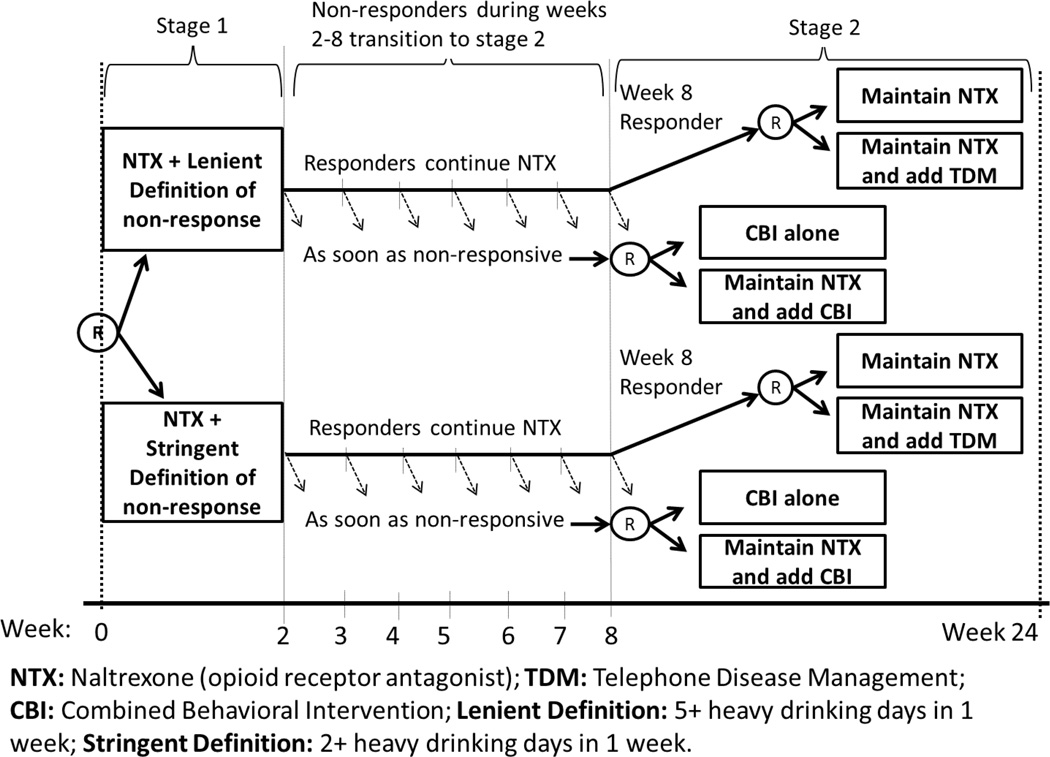
Consider the following simplified version of the ExTENd SMART (Figure 1). In this 24-week trial, NTX was offered to all individuals. The first-stage randomization was to one of two criteria for early non-response: (1) a stringent criterion, in which an individual was classified as a non-responder as soon as s/he had two or more HDDs during the first eight weeks of NTX treatment; or (2) a lenient criterion, in which an individual was classified as a non-responder as soon as s/he reported having five or more HDDs during the first eight weeks of NTX treatment. Individuals were assessed weekly for drinking behavior. Starting at week two, as soon as the individual met his/her assigned criterion for non-response, s/he was immediately re-randomized to one of the two rescue tactics: (1) adding CBI (NTX+CBI) or (2) CBI alone (CBI). Individuals who did not meet their assigned non-response criterion by the end of week eight (i.e., responders), were re-randomized at that point (i.e., at week 8) to one of two maintenance tactics: (1) adding TDM (NTX+TDM) or (2) NTX alone (NTX). The primary outcomes were based on weekly assessments of the number of drinking days.

Figure 1.

ExTENd SMART study

Eight ATSs are embedded in ExTENd (see [18]); one is described above (ATS#1). Each embedded ATS utilizes one tailoring variable–the individual’s early response status. This is because, by design, different second-stage treatments were offered to responders than to non-responders. Various methods can be employed to compare and select the best ATSs among the eight that are embedded in ExTENd (e.g., [28–30]). In previous analyses [18], ATS#1 was found to be the best among the eight embedded ATSs in terms of the probability of drinking during the second stage of treatment.

However, investigators often wish to explore whether other variables, beyond response status, could be tailoring variables. For example, in ExTENd, it would be useful to explore whether the non-response criterion should be tailored to the individual’s baseline years of alcohol consumption. This is driven by empirical evidence suggesting that individuals with more severe histories of alcohol use problems are prone to faster relapse, requiring a more stringent definition of non-response [31,32]. Additionally, it would be useful to explore whether the maintenance tactic for responders should be based on the proportion of non-abstinence (i.e., any use) days during the initial NTX treatment. This is based on the idea that even in those categorized as responders, failure to achieve complete abstinence places the individual at greater risk for poor long-term outcomes, hence requiring additional support in order to maintain long-term improvement [33–35]. In the following section we demonstrate how Q-learning can be used to conduct these analyses.

Q-learning

Q-learning [13,14] is a multi-stage regression approach that can be used with data from a SMART to investigate whether and how certain covariates are useful for developing an ATS or improving an existing one. Investigators first select a set of covariates at each stage that are hypothesized to be useful tailoring variables for the randomized treatment options at that stage. Such candidate tailoring variables may include any collection of baseline and time-varying variables measured prior to the randomization at each stage. In Q-learning, a regression is used at each stage to investigate whether and how the average treatment effect (i.e., the difference between treatment options) at that stage varies as a function of the candidate tailoring variables, while appropriately controlling for the effects of optimal future tailored treatments. Q-learning resembles moderated regression analyses [14], making it familiar and, therefore, easy to understand and implement. However, standard moderated regression analyses typically cannot be used to examine time-varying covariates as candidate tailoring variables for the purpose of empirically developing an ATS. For example, Nahum-Shani et al. [14] demonstrate how, compared to Q-learning, using a single standard moderated regression analysis to investigate time-varying candidate tailoring variables in a sequential treatments setting can lead to bias and, therefore, misleading conclusions.

Here we describe the application of Q-learning to data from the ExTENd SMART study. As discussed above, we examine the following two candidate tailoring variables: (a) the individual’s baseline years of alcohol consumption, denoted O₁₁; and (b) the proportion of non-abstinence days during the first stage, denoted O₂₁. Notice that O₂₁ is an outcome of the first-stage treatment, rather than a baseline measure.

The outcome, Y, is the proportion of abstinence days over 24 weeks (high values are desirable). Let A₁ denote the randomized non-response criteria at the first randomization, coded -1 for the stringent criterion and 1 for lenient; A_2R denotes the randomized maintenance tactics for responders at the second randomization, coded -1 for NTX alone and 1 for NTX+TDM; and A_2NR denotes the randomized rescue tactics for non-responders at the second randomization, coded -1 for CBI alone and 1 for NTX+CBI. To apply Q-learning in this context, we use two regressions, one for each randomization stage. Technical details concerning the regression models are provided in Appendix (1); here, we provide a more accessible presentation.

The first regression of Y on terms involving the predictors (O₁₁, A₁, O₂₁, A_2R, A_2NR) focuses on the effects of the second-stage randomized treatment options for responders (A_2R), and non-responders (A_2NR). This regression includes not only treatment effects for the maintenance (A_2R) and rescue (A_2NR) tactics, but also an interaction between A_2R and the proportion of non-abstinence days during the first stage (O₂₁). This is because our goal is to assess the usefulness of O₂₁ in tailoring the best maintenance tactic for responders (A_2R). No candidate tailoring variables are considered for the rescue tactics (A_2NR).

If the coefficient for the interaction between A_2R and O₂₁ is different from zero, then the average effect of A_2R differs by levels of O₂₁. To further investigate how this effect varies, we attend to the conditional effect [36] of A_2R, namely the expected difference between responders offered NTX+TDM (A_2R = 1) and those offered NTX alone (A_2R = −1), for varying levels of O₂₁. This is a simple linear combination of the regression coefficients for A_2R and the interaction between A_2R and O₂₁. For a given level of O₂₁, if this conditional effect is positive, it means that the expected outcome is higher for responders offered NTX+TDM, compared to NTX alone; if it is negative, it means that the expected outcome is higher for responders offered NTX alone compared to NTX+TDM. Recall that higher values of Y (proportion of abstinence days over 24 weeks) are more desirable. Hence, for a given level of O₂₁, if the conditional effect of A_2R is positive, an ATS based on this model should recommend NTX+TDM for responders with this particular level of the tailoring variable; if the conditional effect is negative, the ATS should recommend NTX alone for responders with this particular level of the tailoring variable.

For non-responders, because no candidate tailoring variables are considered for the rescue tactics, we attend to the regression coefficient for A_2NR to select the best rescue tactic. If this coefficient is positive, it means that the expected outcome is higher for non-responders offered NTX+CBI (A_2NR = 1), compared to CBI alone (A_2NR = −1); hence, an ATS based on this model should recommend NTX+CBI for non-responders. If the coefficient for A_2NR is negative, it means that the expected outcome is higher for non-responders offered CBI alone, compared to NTX+CBI; hence, the ATS should recommend CBI alone to non-responders.

After we have estimated the regression coefficients and assessed the evidence regarding the second-stage randomized treatment options and candidate tailoring variables, we move to a second regression that focuses on the effects of the first-stage randomized treatment options (A₁). Here, we examine the effects of the non-response criteria (A₁), presuming that in the future we would employ the optimal second-stage treatment options for responders and non-responders. This is done by using an adjusted Y that takes into account the optimal estimated second-stage tactics based on the first regression. This adjustment is straightforward; see Appendix (1).

The second regression of the adjusted Y on terms involving the predictors (O₁₁, A₁), includes not only the effect of the non-response criteria (A₁), but also an interaction between A₁ and the individual’s baseline years of alcohol consumption (O₁₁). This is because our goal is to assess the usefulness of O₁₁ in tailoring the best non-response criteria (A₁). If the coefficient for the interaction between A₁ and O₁₁ is different from zero, it means that the average effect of A₁ differs by levels of O₁₁. To further understand how this effect varies, we attend to the conditional effect of A₁, namely the difference between the lenient (A₁ = 1) and the stringent (A₁ = −1) criterion, for varying levels of O₁₁. This is a simple linear combination of the regression coefficients for A₁ and the interaction between A₁ and O₁₁. For a given level O₁₁, if this conditional effect is positive, it means that the expected outcome under the optimal second-stage treatment option is higher for individuals receiving the lenient, rather than the stringent criterion; if the conditional effect is negative, it means that the expected outcome under the optimal second-stage treatment option is higher for individuals receiving the stringent, rather than the lenient criterion. Hence, for a given level of the tailoring variable, if the conditional effect of A₁ is positive, it means that an ATS based on this regression model should recommend the lenient criterion for individuals with this particular level of the tailoring variable; if the conditional effect is negative, the ATS should recommend the stringent criterion for these individuals.

Illustrative Analysis of the ExTENd Data

The procedure described above was implemented to analyze data from the ExTENd study, using the ‘qlearning’ package in R [37]. Information from a total of 250 study participants was used in this analysis. In both the first- and second-stage regressions we included an indicator of gender (female = 1) as a covariate. Appendix (2) provides information concerning the baseline characteristics of study participants. Appendix (3) provides information concerning the rates and patterns of missing values in the data. A multiple imputation method specifically adapted for SMART ([38]) was used to generate ten imputed datasets. Each imputed dataset was analyzed in the same way; results across the imputed datasets were summarized using standard formulae (see [39] for a more detailed discussion of multiple imputation methodologies).

Measures

Weekly time-line follow-back (TLFB) assessments of the number of standard drinks recorded per day were used to calculate (a) the primary outcome (Y)—the proportion of abstinence days over the study duration—by dividing the number of non-drinking days by the duration of the study; and (b) the proportion of non-abstinence days during the initial NTX treatment (O₂₁), by dividing the number of drinking days by the total number of days the participant was provided the initial NTX treatment (i.e., the total number of days in the first stage prior to re-randomization). Baseline years of alcohol consumption (O₁₁) was self-reported by participants prior to initial randomization. Individuals were asked to indicate the number of years they consumed alcohol (i.e., any use) prior to entering the study. Appendix (2) includes sample distributions of variables.

Results

Table 3 includes the results for the first regression, which focuses on the effects of the second-stage randomized treatment options for responders (A_2R), and non-responders (A_2NR). The interaction between A_2R and O₂₁ (the candidate tailoring variable) was significantly different from zero (Estimate = .14; CI = [.06,.24]), indicating that the effect of maintenance tactics for responders varies depending on the proportion of non-abstinence days during initial NTX treatment (O₂₁). Estimates of the conditional effect of A_2R for various levels of O₂₁ indicate that for responders who consumed alcohol during 10% or fewer of days during the initial NTX treatment, the conditional effect of A_2R is not significantly different from zero (e.g., for 10% drinking days, Estimate = .04; CI = [−.002,.06]). However, for responders who consumed alcohol during more than 10% of days during the initial NTX treatment, the conditional effect of A_2R was positive and significantly different from zero (e.g., for 20% drinking days, Estimate = 0.06; CI = [.02,.12]). For these responders (33% of all study responders), NTX+TDM leads to at least a 6% increase in the percentage of abstinence days over the entire study duration (i.e., 10 days on average), relative to NTX alone. The coefficient of A_2NR was not significantly different from zero (Estimate = −.02; CI = [−.06,.04]), indicating inconclusive evidence with respect to the difference between the two rescue tactics for non-responders.

Table 3.

Results for the first regression, which focuses on the effects of the second-stage randomized treatment options for responders (A_2R), and non-responders (A_2NR); and estimated conditional effects of the second-stage randomized treatment options for responders

Parameter	Estimate	90% CI ii
Intercept	−0.06	−0.15	−0.03
Gender	−0.03	−0.08	0.02
O11: Baseline years of alcohol consumption	−0.003	−0.02	0.02
A1: Nonresponse criterion	0.01	−0.01	0.03
O21: Proportion of drinking days during stage 1	−1.07	−1.20	−0.96
A2R: Maintenance tactic for responders	0.003	−0.02	0.02
A2NR : Rescue tactic for non-responders	−0.02	−0.06	0.04
A2R × O21: Maintenance tactic for responders × Proportion of drinking days during stage 1	0.14	0.06	0.24
Estimated Conditional Effects of Maintenance Tactics	Estimate	90% CI ii
Percent drinking days during stage 1 = 0 (24% of responders had O21=0)	0.006	−0.04	0.04
Percent drinking days during stage 1 = 10% (43% of responders had 0< O21 ≤0.1)	0.04	−0.002	0.06
Percent drinking days during stage 1 = 20% (14% of responders had 0.1< O21 ≤0.2)	0.06	0.02	0.12
Percent drinking days during stage 1 = 30% (10% of responders had 0.2< O21 ≤0.3; and 9% had 0.3< O21)	0.10	0.04	0.16

ⁱⁱThe estimated regression coefficients and associated lower and upper limit of the 90% confidence intervals (CI) are summarized across ten imputed datasets. We set the Type I error rate to 0.10, rather than 0.05, given the illustrative nature of this analysis. Moreover, the aim of the analysis is to generate hypotheses about useful tailoring variables. Hence, from a clinical standpoint, it is sensible to tolerate a greater probability of detecting a false effect in order to improve the ability to detect true effects (see Collins et al. [50]; Dziak et al. [51]; McKay et al.,[52]).

Table 4 includes the results for the second regression, which focuses on the effects of the first-stage randomized treatment options (A₁). The results show that neither the effect of A₁, or the interaction between A₁ and O₁₁ (the candidate tailoring variable) were significantly different from zero. Hence, evidence is inconclusive with respect to the difference between the two non-response criteria, as well as with respect to the usefulness of baseline years of alcohol consumption for tailoring the best non-response criterion.

Table 4.

Results for the second regression, which focuses on the effects of the first-stage randomized treatment options (A₁); and estimated conditional effects of the first-stage randomized treatment options

Parameter	Estimate	90% CIii
Intercept	−0.21	−0.37	−0.19
Gender	−0.06	−0.15	0.02
O11 : Baseline years of alcohol consumption	−0.0001	−0.02	0.03
A1 : Nonresponse criteria	0.01	−0.02	0.03
A1 X O11 : Non-response criteria X Baseline years of alcohol consumption	−0.01	−0.02	0.01
Estimated Conditional Effects of Non-Response Criterion	Estimate	90% CIii
For patients with low number of baseline years of alcohol consumption (i.e., O11 = −1, namely 1 SD below sample mean)	0.04	−0.02	0.10
For patients with high number of baseline years of alcohol consumption (i.e., O11 = 1, namely 1 SD above sample mean)	0.004	−0.06	0.06

ⁱⁱThe estimated regression coefficients and associated lower and upper limit of the 90% confidence intervals (CI) are summarized across ten imputed datasets. We set the Type I error rate to 0.10, rather than 0.05, given the illustrative nature of this analysis. Moreover, the aim of the analysis is to generate hypotheses about useful tailoring variables. Hence, from a clinical standpoint, it is sensible to tolerate a greater probability of detecting a false effect in order to improve the ability to detect true effects (see Collins et al. [50]; Dziak et al. [51]; McKay et al.,[52]).

The ATS proposed based on the results above is presented in Table 2 (ATS #2). The percentage of abstinence days over the entire study duration among individuals following ATS#2 was estimated to be 77%. In additional analyses we found ATS#1 (Table 2) to be the best of the 8 ATSs embedded in ExTENd in terms of the proportion of abstinence days over the entire study duration; that is, consistent with previous studies [18], ATS#1 was the best among the 8 ATSs in which response status was used as the sole tailoring variable. The percentage of abstinence days over the entire study duration among participants following ATS#1 was estimated to be 78%, similar to ATS#2 which is more tailored.

Discussion

The results of the Q-learning analysis suggests that ATS #2 is advantageous; this strategy recommends adding TDM only to a subset of responders, namely those for whom the percentage of non-abstinence days during the initial NTX treatment was larger than 10%. Hence, while ATS #1 recommends that TDM should be added to all responders, the more tailored ATS (ATS #2) recommends TDM to only 33% of responders. Although TDM is a cost-effective and potentially cost-saving strategy for treating SUDs compared to face-to-face alternatives [40], costs per session are estimated at $30.24 for the client and $30.55 for the health system [41]. Hence, employing the more tailored ATS (ATS#2) may result in substantially lower cost of treatment, while achieving outcomes similar to ATS#1.

This has potential implications on both the scalability of the ATS as well as on treatment adherence. First, offering more costly treatments only to those who need it most should lead to greater cost-effectiveness, enhancing the scalability of substance abuse treatments [6]. Second, providing no more intervention than needed will reduce treatment burden, hence improve treatment adherence [42]. This demonstrates how ATSs generated by Q-learning have the potential to improve the treatment of SUDs beyond ATSs that are embedded in a SMART study, informing the development of more tailored treatment protocols that optimize outcomes while reducing cost and treatment burden [3]. As with standard linear regression, a potential limitation of Q-learning is that it requires that the linear models be correctly specified [16].

As with any study, the sample size for ExTENd was based on having adequate power to address its primary objective [43], which was to test the effect of CBI alone versus CBI + NTX among individuals who are non-responsive to NTX. Specifically, the total sample size (N=300) was selected to detect (at least) a moderate standardized difference of 0.55 [44] in change in the number of abstinent days following the second randomization between non-responders who were offered CBI alone vs. those offered NTX+CBI, with at least 80% power (calculations were based on a Type-I error rate of 5%, an exchangeable correlation structure assuming a within-person correlation of 0.5, 33% non-response rate, and 15% attrition rate by the end of the study). Sample size calculators exist for other primary objectives that are typical for SMART studies, such as the comparison of first-stage treatments or the comparison of ATSs that are embedded within the trial (e.g., [30]).

As with standard randomized trials, investigating additional ways to tailor treatment (such as the investigation we have conducted here with Q-learning regression) is often a secondary objective in a SMART. Such an objective is often of great interest to investigators designing a SMART [45]. Yet given the exploratory (or hypothesis-generating) nature of this objective, it is still rare for the sample size in a SMART, or in any standard randomized trial, to be planned based on this objective. Recent methodological work in the single-stage setting using data from standard randomized trials has begun to address this gap. [46]

Conclusion

Our application of Q-learning demonstrates that even responders to SUD treatment can be heterogeneous, with some exhibiting less progress than others during treatment. This information can be useful in identifying those individuals who respond well initially, but require more support to maintain progress. These insights can contribute to the development of more cost-effective, stepped-care strategies for treating SUDs. Currently, there is growing interest in developing methods that go beyond Q-learning, as implemented here, to identify new ways to tailor treatments (e.g., [47–49]). The straightforward application of Q-learning provided here represents a promising first-step towards the implementation of other novel methodologies to empirically develop more tailored ATSs in SUDs.