Do Different Methods for Modeling Age-Graded Trajectories Yield Consistent and Valid Results?

John R Warren; Liying Luo; Andrew Halpern-Manners; James M Raymo; Alberto Palloni

doi:10.1086/681962

. Author manuscript; available in PMC: 2017 May 15.

Published in final edited form as: AJS. 2015 May;120(6):1809–1856. doi: 10.1086/681962

Do Different Methods for Modeling Age-Graded Trajectories Yield Consistent and Valid Results?

John R Warren ¹, Liying Luo ², Andrew Halpern-Manners ³, James M Raymo ⁴, Alberto Palloni ⁵

PMCID: PMC5431596 NIHMSID: NIHMS856365 PMID: 28515496

Abstract

Data on age-sequenced trajectories of individuals’ attributes are used for a growing number of research purposes. However, there is no consensus about which method to use to identify the number of discrete trajectories in a population or to assign individuals to a specific trajectory group. We modeled real and simulated trajectory data using “naïve” methods, optimal matching, grade of membership models, and three types of finite mixture models. We found that these methods produced inferences about the number of trajectories that frequently differ (1) from one another and (2) from the truth as represented by simulation parameters. We also found that they differed in the assignment of individuals to trajectory groups. In light of these findings, we argue that researchers should interpret results based on these methods cautiously, neither reifying point estimates about the number of trajectories nor treating individuals’ trajectory group assignments as certain.

Investigators across a wide range of disciplines are concerned with characteristics and processes that vary systematically with subjects’ age. In recent years, researchers have studied age-sequenced patterns of delinquent behaviors (e.g., Miller, Malone and Dodge 2010), family and work roles (e.g., Rindfuss et al. 2010), chronic disabilities (e.g., Gill et al. 2010; Stallard et al. 2010), popularity (e.g., Moody et al. 2011), research productivity (e.g., Hunter and Leahey 2010), income (e.g., Rippeyoung and Noonan 2012), and academic achievement (e.g., Pianta et al. 2009), to name just a few substantive topics. In these and other areas of inquiry, scholars utilize ideas about trajectories of individual-level attributes, where trajectories are age-sequenced observations that reflect career, life course, or developmental patterns of stability and change for a particular focal attribute.¹

Despite this widespread interest in trajectories, and despite the growing availability of rich age-graded data, there is no consensus about how to describe and model trajectories in the social sciences. When faced with similar data structures—repeated observation of some individual-level attribute(s) across ages—different researchers employ different assumptions and empirical strategies. In some cases, they assume there is a single underlying trajectory (around which individuals’ observations deviate) and estimate hierarchical or growth curve models. In other cases, researchers assume there are a small number of underlying latent trajectories that describe individuals’ experiences. In the latter case, analysts face two specific challenges: How should they identify and enumerate those latent trajectories? How should they determine which latent trajectory best describes each individual’s age-sequenced observations? As reviewed below, a variety of statistical approaches are used to meet these challenges. In practice, researchers typically choose just one of these approaches without considering the consequences of this choice for the validity and reliability of substantive conclusions.

In this article, we are concerned with applications in which researchers aim to identify and characterize a discrete set of latent trajectories and to classify individuals according to which trajectory best describes their age-graded observations. Our goal is to compare the relative validity and reliability of several alternative methods for identifying and describing trajectories and for assigning individuals to them. To this end, we pose four questions: (1) Do these methods lead to similar inferences about the number of latent trajectories that exist in a particular population? (2) Do they yield similar descriptions of the characteristics or qualities of those trajectories? (3) Do they lead to similar decisions about which trajectory best describes each individual’s age-graded observations? (4) Under what circumstances do these alternative methods yield the same conclusions and—perhaps most importantly—under what circumstances do they yield correct conclusions?

On one hand, it would be reassuring if the various methods all yielded valid and equivalent conclusions about the number and qualities of trajectories or about which trajectory best describes each individual’s age-graded observations. We would have greater confidence in the soundness of any number of substantive scientific projects that have (more or less uncritically) elected to use just one of these various methods. On the other hand, if the choice of method does matter for substantive conclusions, and especially if some methods yield more accurate conclusions than others, then it will be imperative to understand (1) whether there are situations in which the choice of methods is particularly consequential and (2) whether certain methods produce more valid results under particular empirical conditions. Our research is designed to address both of these issues.

Background

Interest in studying age-graded trajectories has long outpaced the quality of the data available to study them. Careful analysis in any number of substantive domains generally calls for detailed data collected at short age intervals over long age spans. Until recently, however, researchers usually settled for data collected at wide intervals and/or over truncated age spans. For example, theories about trajectories of children’s reading ability suggest the need for data collected at multiple points each academic year and from early childhood through the teenage years. In practice, researchers evaluating these theories have often had to rely on data collected annually (or less frequently) and for just a few academic years. Recently, however, improved computer and data storage technologies, new methods for collecting data, and major investments in longitudinal social and economic surveys have combined to produce much richer age-graded data sufficient to describe trajectories more completely. Across many substantive domains, it is now increasingly possible to utilize data collected at frequent age intervals over longer spans of the life course or career.

Many analysts assume—at least implicitly, and with limited theoretical rationale—that there is just one underlying trajectory of the age-graded attribute of interest, and that individuals’ patterns of observations deviate around this single latent trajectory (Kreuter and Muthén 2008). Using multilevel or hierarchical linear models, researchers nest age-graded observations within individuals and explicitly consider the extent to which focal outcomes vary within individuals (i.e., with age) and across individuals (Bryk and Raudenbush 1987). Using structural equation models (SEMs), researchers estimate latent growth curves by modeling the means, variances, and co-variances of repeated (across ages) measures (Duncan, Duncan and Strycker 2006; MacCallum and Austin 2000; McArdle and Epstein 1987). For example, Judge and Cable (2011) recently used this multilevel modeling approach to estimate gender differences in relationships between trajectories of weight and trajectories of earnings, and Gibbons et al. (2012) used an SEM approach to examine the relationship between trajectories of experience with discrimination and trajectories of African American adolescents’ self-control. In many cases, the goal of such analyses is to explain between-person variation in patterns of stability and change in age-graded attributes.

In many other cases, researchers assume or hypothesize that more than one latent trajectory may underlie observed age-sequenced data. As we argue below, these studies are generally characterized by inductive reasoning, with little or no theoretical basis for expectations about how many trajectories there should be, what they should look like, or how individuals might be distributed across them. For example, there is considerable interest in identifying and describing distinct life course patterns of criminal offending (e.g., Besemer and Farrington 2012; Moffitt 1993) and the consequences for individuals of following particular criminal pathways (e.g., Piquero et al. 2010). Likewise, scholars in a number of related disciplines are interested in identifying and describing discrete types of labor force careers in an effort to test ideas about things like social mobility (e.g., Chan 1995), the transition to adulthood (Macmillan and Eliason 2003), and cross-national differences in labor market structures (e.g., Biemann and Wolf 2009).

When researchers assume or hypothesize that a discrete number of latent trajectories underlie their observed age-graded data, they have several methodological options for enumerating, identifying, and describing those latent trajectories and for deciding which trajectory best describes each individual’s series of observations. In the section that follows, we review six different techniques: “Naïve” classification, three variants of finite mixture models (specifically, latent class analysis, group-based trajectory models, and growth mixture models), optimal matching analysis, and grade of membership models. Our discussion of these techniques is meant to be as accessible and non-technical as possible; for more detailed descriptions of these methods, including relevant formulas, the interested reader should refer to Bollen and Curran (2006a), Abbott and Tsay (2000), Collins and Lanza (2010), and Manton et al. (1992). We end the section by arguing that researchers typically select from among these and other available methods without good reason and that this choice of method may be consequential for substantive results.

Naïve Approaches

One popular option for modeling trajectory data is to dictate, a priori, that there is some fixed number of trajectories and to use some logical algorithm to classify individual biographies into a discrete number of trajectories. For example, Gustafsson et al. (2010) began with measures of individuals’ socioeconomic status (SES) at four points between ages 16 and 43. After dichotomizing those measures, there were 2⁴ = 16 possible SES trajectories. However, these were “reduced to 5 mutually exclusive categories to increase the number of participants in subgroups” (p. 615); the five were labeled “Stable high,” “Early high/downward mobility,” “High mobility,” “Early low/upward mobility,” and “Stable low.” Likewise, Hicks et al. (2010) began with measures of individuals’ alcohol dependence at four points between ages 17 and 29 and assigned individuals to one of five “rationally derived groups” (p. 821) based on the ages at which they began and ended their dependence on alcohol. More recently, Frech and Damaske (2012) classified women’s work pathways as either “steady work,” “pulled back, or part-time work,” “interrupted, or repeatedly unemployed worker,” or “stay-at-home mother” based on their hours and weeks worked and experiences with unemployment over their careers.

Although such naïve approaches are widely used, Nagin (1999: 141) identifies three major problems with them. First, there is no way to falsify empirically the number or definition of trajectories; they must be assumed a priori. Second, there is “the risk of simultaneously over- and under-fitting the data, thus creating trajectory groups that reflect only random variation and failing to identify unusual, but still real, developmental patterns” (141). Third, such approaches offer no way to assess the certainty with which individuals are assigned to trajectory groups. That is, naïve approaches provide no empirically falsifiable way to determine the trajectory that best describes any given individual’s observations. Despite these shortcomings, Nagin (1999) concedes that in many substantive applications—at least within criminology, which was his focus—the logic used to define trajectories and to assign individuals to them seem “generally reasonable” (p. 141). The frequency with which naïve estimation strategies are used in the social sciences suggests that this is a widely held view.

Finite Mixture Models

In recent years, many researchers have turned to finite mixture models as a useful alternative to such naïve approaches (e.g., Cheadle, Amato and King 2010; Halpern-Manners, Warren and Brand 2009; McLeod and Fettes 2007; Mustillo, Hendrix and Schafer 2012; Petts 2009; Thomas 2011; Wagmiller et al. 2006; Zimmer et al. 2012). Latent class analysis (LCA), group-based trajectory models (GBTMs), and growth mixture models (GMMs) are three different types of finite mixture model (e.g., Clogg 1995; Muthén 2004).² In all three cases, individuals are assigned to latent trajectory groups on the basis of their observed experiences or behaviors.³ Each trajectory group represents a qualitatively distinct latent subpopulation within the data, composed of individuals with relatively similar measurements on some age-sequenced variable (e.g., employment status or criminal offending or marital status). GMMs allow for residual variation within these trajectory groups (i.e., within-class heterogeneity or random effects), whereas LCA and GBTMs assume homogeneity conditional on trajectory group membership.

In these models, the number of underlying trajectories, their shape, their prevalence within the population, and the assignment of individuals to them are all inferred from the data; see Bollen and Curran (2006a), Muthén (2004), Nagin (2005), and Appendix A for technical details and relevant formulas. Models with increasing numbers of trajectory classes are typically fit in an iterative fashion. The “preferred model” is then determined using a combination of formal and informal criteria. In many applications, researchers base decisions about the number of trajectories on measures of model fit (e.g., BIC, AIC, and/or the Lo-Mendell-Rubin Likelihood Ratio Test), the share of cases assigned to the smallest trajectory group, interpretability, and model convergence (e.g., Halpern-Manners, Warren and Brand 2009; Henselmans et al. 2010; Marcell et al. 2011). This reliance on multiple criteria may reflect the fact that the best-fitting model according to formal criteria can sometimes lead to a large number of groups, many of which contain few individuals and/or substantively similar trajectories. In some cases, even formal criteria can lead researchers to overestimate the number of latent trajectory classes (e.g., Bauer and Curran 2003).

Optimal Matching Analysis

Optimal matching (OM) or “sequence analysis” is a method of classifying sequences of observations with respect to their similarity. Although we focus on applications in which those sequences are age-graded observations of individuals’ attributes, OM was initially developed for analysis of protein and DNA sequences and has been applied in a wide variety of other substantive contexts. Abbott introduced OM for use in social science and historical research in the 1980s (Abbott 1983; 1995; Abbott and Forrest 1986; Abbott and Hrycak 1990). Although used for a variety of social science applications, OM has most frequently been employed to study trajectories or sequences of professional or working careers (e.g., Abbott and Hrycak 1990; Biemann, Fasang and Grunow 2011; Chan 1995; Halpin and Chan 1998; Han and Moen 1999; Stovel, Savage and Bearman 1996).

OM analyses usually proceed in two steps. First, every pair of age-graded sequences is compared with respect to their “distances,” or the costs associated with transforming one sequence into the other via a series of insertions, deletions, and/or substitutions. Those insertion, deletion, and substitution costs can be determined a priori by the analyst using theory or prior knowledge, or they can be determined posteriorly using observed transition rates or similar criteria (e.g., Lesnard 2008; 2010). These pairwise comparisons of the n sequences yield an n×n matrix of distance scores. Second, in most social science applications, researchers then subject that matrix to some form of cluster analysis in order to group sequences into a discrete (< n) number of trajectory categories. The result is a finite set of trajectory groups with relatively little within-group variation in distance scores. As with finite mixture models, determining the optimal number of distinct trajectory groups is typically based on both model fit statistics and informal criteria like interpretability and the size of the smallest group. Most recent OM analyses have constructed distance matrices using the R package TraMineR (Gabadinho et al. 2011) and subjected those matrices to some form of hierarchical cluster analysis (Ward 1963). See Appendix A for more details.

As noted by Stovel et al. (1996: 394), “[t]he assignment of transformation costs haunts all optimal matching analyses.” The distance between any two trajectories is a function of the costs assigned to insertions, deletions, and substitutions, and in many applications, there is no clear theoretical or applied basis for setting those costs. Abbott and Tsay (2000: 11) point out that some researchers simply set all of those costs equal to a single value “on the grounds that they lacked any theoretical reason for doing otherwise.” Wu (2000) discusses several theoretical and conceptual issues that arise by virtue of the need to pre-assign insertion, deletion, and substitution costs. For example, he notes that “[a] peculiar property of the OM part of sequence analysis is that one obtains the same distance between trajectories if the trajectories move ‘forward’ or ‘backward’ in time.” Lesnard (2010) provides guidance about how costs might be more thoughtfully determined, especially in the context of analyzing sequences of temporally-ordered observations. However, it seems that most analysts are neither fully aware of the issues described by Wu (2000) nor as careful or strategic as Lesnard (2010) argues they should be.

Grade of Membership Models

Grade of membership (GoM) models were originally developed to summarize multiple measures of health status into a small number of empirically and statistically meaningful groups or “pure types” and to identify the extent to which observed individuals belong to each of those groups (Manton, Woodbury and Tolley 1994; Woodbury and Manton 1982). Like finite mixture models, GoM analysis is used to estimate the probability of a specific value for a variable conditional on belonging to a “pure type.” Unlike finite mixture models, GoM models also estimate coefficients representing the degree to which each individual belongs to each pure type (rather than the probability of belonging to a given class). See Appendix A for more details.

GoM can be used to summarize multiple, discrete measures of any characteristic, but most social scientific applications to date have focused on physical and mental health. Previous efforts to use GoM to summarize repeated measures of the same variable to generate age-graded trajectories are rare (see Manton et al. 1987), but application to this type of data is straightforward. Estimated probabilities of a positive response on a given variable for each pure type provide the shape of the trajectories and grade of membership scores (ranging from 0.0 to 1.0 and summing to 1.0) provide respondent-specific indicators of the degree of (partial) membership in each trajectory. As with other methods, the number of pure types (or trajectories) is ascertained by comparing the fit of models with k and k+1 trajectories. The number of estimated parameters equals [N*(k−1)] + (x*k), where N is the number of observations, k is the number of groups or pure types, and x is the number of (usually health) indicators, making these models far less parsimonious than latent class analysis or other methods of data reduction.

Unlike most applications of the other methods considered in this article, the goal of GoM analysis is not to assign individuals to a single group or trajectory. Indeed, the fundamental motivation underlying GoM, derived from fuzzy set logic, is that heterogeneity in individual profiles implies simultaneous membership in multiple groups (pure types) for many people (Manton, Woodbury and Tolley 1994). Information about this heterogeneity that is lost when individuals are “forced” into or “assigned” to a single group is retained in GoM, where the primary output of interest is the estimated affiliation (grade of membership) with each of the pure types. In many cases, this affiliation is very strong and it is clear to which group an individual belongs, but in other cases, it is less clear, with meaningful membership in multiple groups (usually two). Most applications of GoM have thus focused on describing characteristics associated with degree of (usually health) profile membership (e.g., Andreotti et al. 2009) or have used estimated GoM scores as independent variables in analyses of subsequent outcomes (e.g., Portrait, Lindeboom and Deeg 1999). However, some studies have classified individuals into the single group for which estimated grade of membership is strongest (e.g., Cassidy, Pieper and Carroll 2001) or into categories that allow for membership in multiple groups (e.g., Berkman, Singer and Manton 1989).

Interchangeable Alternatives?

When analysts assume or hypothesize that there are multiple latent trajectories underlying some age-sequenced observations, how do they select from among the several methodological tools described above? In some cases, researchers seek to replicate and extend prior work; in these cases, it may be reasonable and productive to use the same data and/or analytic techniques. For example, because efforts to identify life-course trajectories of criminal offending have so consistently used GBTMs (e.g., Besemer and Farrington 2012; Nagin, Farrington and Moffitt 1995; Nagin and Land 1993), analysts who wish to engage this literature might reasonably use GBTMs as well. The same is true of the use of GoM to summarize large numbers of health indicators (e.g., Andreotti et al. 2009; Berkman et al. 1989; Portrait et al. 1999). However, we suspect that most analysts choose from among the alternatives listed above based on which method they first learned, on the availability of colleagues to assist them in utilizing the methods, or on their facility with the software packages that implement them.

Whatever the reason that researchers choose one from among these alternative methods, it is clear that few consider the substantive consequences of this choice. Would Besemer and Farrington’s (2012) conclusions about the intergenerational transmission of criminal behavior have differed had they used OM instead of GBTMs? Would Muller et al.’s (2011) conclusions about the life course trajectories of people with psychiatric disorders have differed had they used GBTMs instead of OM? Would either set of authors’ findings have been markedly different had they used what we label “naïve” approaches? Or GoM, LCA, or GMMs?

We know of little published research that has formally considered whether the choice of method for analyzing age-graded trajectory data matters for substantive findings. Robette and Bry (2012) recently compared results obtained using different forms of sequence analysis (of which OM is the most widely used), and identified variants that converged on consistent results in analyses of a simulated dataset. Barban and Billari (2012) analyzed both real and simulated datasets to compare results obtained from OM and LCA. They concluded that “the two techniques give consistent results in classifying life course trajectories” (pg. 781). These two examples are limited in scope, focusing mainly on variants of sequence analysis.

We noted above that “naïve” approaches to identifying latent trajectories (and to determining which individuals’ lives are best described by particular latent trajectories) are not empirically falsifiable. We also noted that questions about establishing insertion, deletion, and substation costs “haunt” OM analyses; Wu (2000) and others have raised other serious conceptual and theoretical issues about this method. Bauer and Curran (2003) have raised questions about the overestimation of the number of latent trajectories in GMMs. Analysts who use GBTMs, OM, GMMs, LCA and GoM sometimes base decisions about the number of latent trajectory groups in their data on decidedly informal criteria like interpretability and membership size of groups. Furthermore, these various methods utilize distinct empirical estimating strategies for identifying and populating latent trajectory groups. All of this suggests that (1) there may be no single “right” way to model trajectory data, and (2) the choice of method for modeling trajectory data may be consequential for substantive findings.

Do these six methods lead to similar inferences about the number of latent trajectories that exist in a particular dataset? Do they yield similar descriptions of the characteristics or qualities of those various trajectories? Do they lead to similar decisions about which trajectory best describes each individual’s age-graded observations? Beyond these questions—which speak to the reliability of empirical findings across methods—under what circumstances do these methods typically yield correct conclusions?

We suspect that—when analyzing the same data—these six methods will yield different inferences about the number of underlying latent trajectories, about the characteristics of those trajectories, and about the assignment of individuals to trajectory groups. We also suspect that the extent to which this is true will depend on four specific dimensions of the data and on the concept represented by the data. First, we hypothesize that the reliability and validity of results across methods will depend on the number of latent trajectories that actually exist. If there is a small number of latent trajectories, then it seems more plausible that they can be identified using “naïve” approaches, and differences in the way that model selection criteria using GBTMs, OM, GMMs, LCA, and GoM are influenced by the number of trajectories would seem less problematic than when the actual number of trajectories is large. Second, we expect the consistency and accuracy of results across methods to depend on the relative size of trajectory groups. We suspect that each method will have more difficulty accurately identifying smaller trajectory groups; thus if individuals are more evenly distributed across groups, we expect greater agreement and accuracy across methods. Third, we expect greater agreement across methods when there is less within-trajectory group variability in age-graded observations. Put another way, each method would seem to have an easier time assigning individuals to trajectory groups if their age-graded observations more closely resemble the average experience of trajectory group members. Fourth, we expect results to be more consistent across methods when observations are made at shorter time intervals. For example, when modeling data collected across 20 years of individuals’ working careers, we would expect more consistent and accurate results from analyses based on data collected annually than we would from analyses based on data collected every four or five years. This is a matter of the reliability of within-individual observations.

Our empirical analyses will make one very basic, but important, contribution: We will establish whether “naïve” approaches, GBTMs, OM, GoM, GMMs, and LCA yield the same results when analyzing the same data. As described below, our empirical strategy is also such that we will be able to say something about which methods yield correct results. Importantly, our empirical strategy will also permit conclusions about the conditions under which the choice of method for analyzing trajectory data may matter for substantive results.

Data and Methods

If we were only interested in whether these six methods yield the same results, we could select any existing dataset with age-graded observations, estimate the number of latent trajectories, make inferences about which individuals belong to each trajectory group, and compare results across methods; indeed we carry out this exercise below. However, this strategy has two important shortcomings. First, it does not allow us to say anything about whether agreement across methods varies as a function of important aspects of the data being analyzed. Perhaps our conclusions about the substantive consequences of selecting one method over another are a function of the actual number of latent trajectory groups, of the distribution of individuals across groups, of the amount of within-trajectory group variability in age-graded attributes, and/or of the frequency with which observations are made. If so, conclusions based on just one dataset could be misleading. Second, the use of real data precludes evaluation of the extent to which (and the conditions under which) different methods produce valid results. This is because it is impossible to know with certainty the true number of latent trajectories or the trajectory that actually describes each individual’s age-graded observations using real data.

For the bulk of our analyses we have thus opted to follow Barban and Billari (2012) in generating and modeling simulated trajectory data. This strategy has two key advantages. First, we can simulate multiple datasets that vary systematically with respect to the true number of latent trajectories, the distribution of individuals across trajectories, the amount of within-trajectory group variability, and the frequency with which each individual’s attributes are observed. By modeling multiple simulated datasets that vary along these dimensions, we can determine whether there are particular conditions under which different methods produce more (or less) accurate results; this may be useful information for analysts who have only one “real” data set to work with. Second, by modeling simulated data we can compare method-specific inferences—about the number of trajectory groups, about the characteristics of those trajectories, and about the assignment of individuals to trajectory groups—to the “truth” that was used to generate the simulated data.

Because “naïve” approaches are based primarily on background information about the focal substantive topic, we have simulated trajectory data that have some basis in reality. Specifically, each of our simulated data sets represents women’s employment status (0 = not employed, 1 = employed) between ages 16 and 63. Because employment status at time t + 1 is not independent of employment status at time t, we used a two-state (employed vs. not employed) Markov chain to simulate women’s employment trajectories. Because the probability of transitioning from one employment status to another varies over the life course, we establish a set of transition matrices in the Markov chain. The baseline parameters—employment probabilities and transition matrices—were based loosely on age- and sex-specific employment rates as observed in the cross-section in recent years of the Current Population Survey. Those parameters were then allowed to vary across simulations as described below. Each of our simulated datasets includes 2,000 “women” whose employment statuses are observed across a 48-year span of their lives. The simulated data sets suffer from no sample attrition or missing data.⁴ In Appendix B we provide a more technical description of our simulation procedures, as well as an example of the R code used to create the simulated data.

We simulated data sets that varied along four dimensions. First, we simulated datasets that differed with respect to T, the number of latent trajectories that actually underlie the data. T was equal to 1, 2, 4, or 6 across the several data sets. Second, we simulated datasets that varied with respect to D, the distribution of individuals across trajectory groups. In half of the datasets, D was “highly skewed” such that most observations fell into just one trajectory group; in the other half of the datasets, D was “uniform” such that individuals were distributed evenly across trajectories; of course, the value of D is not defined when T = 1. Third, we simulated datasets that differed with respect to C, the certainty with which individual observations were assigned to trajectory groups. In half of the datasets, C was “high” such that there was very little within-trajectory group variability in age-sequenced observations; in the other half of the datasets, C was relatively low. Finally, the simulated datasets varied with respect to t, the number of within-individual observations. In half of the datasets, t equaled 48, such that women’s employment status was observed annually between ages 16 and 63. In the other half of the datasets, t equaled six, such that employment status was observed every 8 years. Because there were four values of T, two values of D, two values of C, and two values of t, we might have simulated 4 × 2 × 2 × 2 = 32 datasets. However, the four data sets with T = 1 all have, by definition, the same value of D, and so we are left with 28 data sets. Each dataset was de-identified so that we could perform our analyses without knowledge of the true values of T, D, or C for any datasets; however, the value of t could be deduced from the size of the data files and is information required to estimate the various models.

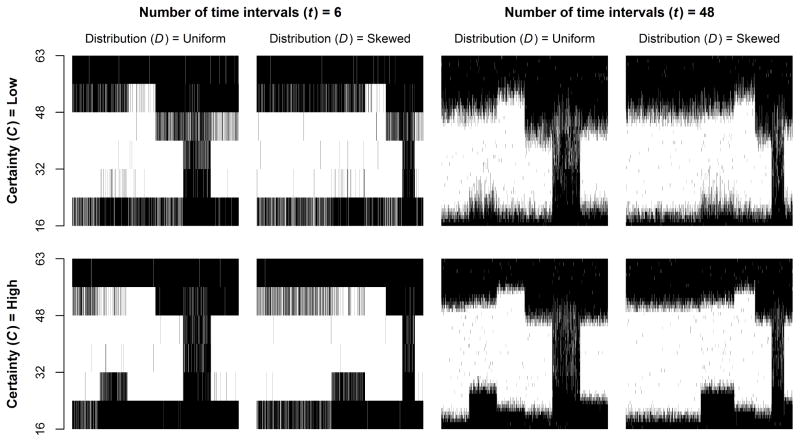
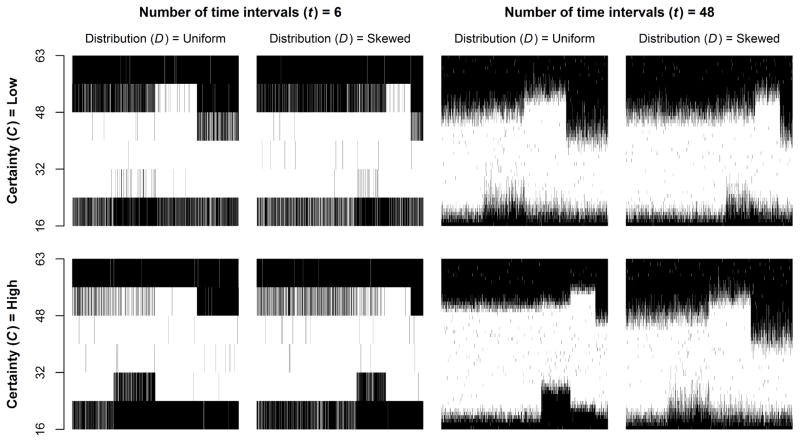
Figures 1 through 4 depict each observation in the simulated datasets when T = 1, 2, 4, and 6, respectively. In each dataset, each woman’s employment history between ages 16 and 63 is represented by a vertical line, where dark segments represent times when she is not employed and white segments represent times when she is employed. Within datasets, women are first sorted by true latent trajectory group membership and then at random within trajectory groups. Each figure depicts datasets that vary by the uniformity of the distribution of observations across trajectory groups (D), the certainty with which observations are assigned to trajectory groups (C), and the age frequency with which observations are made (t). Figure 1 has only four figures because D is a constant when T = 1.

Simulated data, by number of time intervals (t), uniformity of distribution across trajectories (D), and certainty of trajectory group assignment (C). All simulated data sets include T = 1 trajectory group. Each figure depicts 2,000 women’s employment histories from ages 16 through 63. For each woman, dark line segments represent spells of not being employed and white line segments represent spells of employment. See text for details about how these simulated data were generated.

“Naïve” Approach

For our “naïve” analyses, we begin by considering three key periods of the life course: Young Adulthood (ages 16 through 31), Mid-Life (ages 32 through 47), and Late Adulthood (ages 48 through 63). For simulated datasets in which we observe women’s employment status each year (t = 48), we thus observe that variable 16 times per life course period. For datasets in which we observe employment status every eight years, we observe that variable only twice per life course period. Within each of these three life course periods, we classify women as “mostly employed” during that period if they worked more than 75% of the time (which is to say, 2 out of 2 times when t = 6 and 13 or more out of 16 times when t = 48). Because women could be “mostly employed” or “not mostly employed” at each of three periods of the life course, their employment histories always followed one of 2³ = 8 possible “trajectories.” However, not all of these trajectories are actually observed in each dataset, and some are only infrequently observed. Consequently, within each dataset we collapse all trajectories that were observed in fewer than 5% of the 2,000 cases into a single “Other” category. In general, this procedure yielded between two and four trajectories in each dataset. For most datasets, the most frequently observed trajectory was one in which women were “mostly employed” in Mid-Life but not in Young Adulthood or Late Adulthood.

Finite Mixture Models

Our GBTM, LCA, and GMM analyses used Mplus version 6.12 (Muthén and Muthén 2010). For all 28 simulated datasets, we iteratively estimated models with T = 1, 2, …, 8 latent trajectory classes.⁵ Across models within datasets, we then compared model fit using a variety of formal statistical criteria (e.g., BIC, sample-size adjusted BIC, AIC, the entropy index, the Lo-Mendell-Rubin adjusted likelihood-ratio test, and the Vuong-Lo-Mendell-Rubin likelihood-ratio test). ⁶ When these statistical criteria failed to converge on a common solution, we gave preference to specifications that produced adequately populated classes (e.g., no fewer than 5 percent of all cases) with fewer trajectory groups. All models were estimated using maximum likelihood, with maximization performed via the EM algorithm. See Appendix Tables C1 through C3 for further details concerning class enumeration and model fit for GBTMs, GMMs, and LCA, respectively.

A key concern when estimating finite mixture models is the presence of local maxima (Hipp and Bauer 2006; McLachlan and Peel 2000). Likelihood functions for mixture models are exceedingly complex (e.g., not always concave), which can sometimes lead to false solutions and/or non-convergence problems (e.g., Jung and Wickrama 2007; Muthén 2004; Nagin 2005). In an effort to guard against these possibilities, we randomly generated at least 400 sets of starting values for every GBTM, LCA, and GMM that we estimated, using the automated STARTS routine available in recent versions of Mplus (Muthén and Muthén 2010). We then optimized the 100 best sets, as identified by a comparison of the log-likelihoods. Our final estimates were obtained from model estimates in which the highest log-likelihood was replicated at least once, suggesting that the global maximum likelihood solution was successfully reached.⁷ This approach is widely used in substantive applications (e.g., McLeod and Fettes 2007).

Optimal Matching Analyses

We began our OM analyses by setting the substitution cost of switching between “employed” and “not employed” equal to the transition rates between employment states observed in each simulated dataset. Specifically, the transition rate from state i to state j is the probability of observing state j at time t+1 given that state i has been observed at time t. Separately for each dataset, we then generated an n×n distance matrix—describing the distance between every pair of observed employment history sequences—using the R package TraMineR (Gabadinho et al. 2011). Next, and again separately for each dataset, we performed cluster analysis on these distance matrices in R using the Ward hierarchical clustering method (Ward 1963).⁸ We iteratively estimated models with 1, 2, … 20 clusters for each dataset. Decisions about the optimal number of trajectories were based on the Cali ski-Harabasz (1974) pseudo F-statistic.⁹ However, as in some published applications, we found that the preferred solution using only formal fit statistics led to many trajectory groups that looked very similar and that had small numbers of observations. Consequently, as with our finite mixture models, if increasing from k to k+1 trajectory groups led to only trivial improvement in model fit and/or yielded trajectory groups that included fewer than 5% of the observations, we decided in favor of the model with k trajectory groups.¹⁰ See Appendix Table C4 for more details on our OM models.

Grade of Membership Models

GoM models were estimated using the GOM3 program (Charpentier 1996). As with finite mixture models and OM analyses, the preferred model was chosen by comparing the fit of models with k and k+1 trajectories. Following standard procedure, we used likelihood ratio tests to assess improvements in model fit. We do not use BIC here because it often suggests a model with one trajectory given the large number of parameters estimated for each additional k (Manton, Woodbury and Tolley 1994; Portrait, Lindeboom and Deeg 1999). See Appendix Table C5 for further details concerning class enumeration and model fit.

The fundamental logic of GoM models is not consistent with the allocation of individuals to a single group, except in cases where the grade of membership in a given pure type is complete (Manton, Woodbury and Tolley 1994) or at least very strong (Berkman, Singer and Manton 1989). However, previous studies have assigned individuals to particular groups and used that group membership as an indicator of (usually) health in regression models (e.g., Berkman, Singer and Manton 1989; Cassidy, Pieper and Carroll 2001). We adopt a similar strategy to facilitate comparison with the other methods considered. Specifically, we assign cases to the trajectory group for which the ratio of their GoM score to the mean GoM score for that trajectory group is highest (Cassidy, Pieper and Carroll 2001). See Appendix Table C5 for additional details.

Results

Table 1 reports—separately for each of the 28 datasets—true simulation parameters (i.e., the values of T, D, C, and t) and four sets of results for each of the six analytic methods: The inferred number of latent trajectory groups (T’), the difference between the inferred and actual numbers of trajectory groups (T’-T), and two values of the Rand Index (Rand 1971). We use the Rand Index to assess the performance of models with respect to correctly classifying individuals to trajectory groups. Specifically, for any pair of individuals, if the simulation dictated that both members of the pair have the same (or different) underlying employment trajectory and the focal analytic method correctly assigned them to the same (or different) trajectory groups, this measure adds 1/(2000*1999) to the index for that pair (and 0 otherwise). This process is repeated for all of the 2000*1999 pairs of simulated women. If the Rand Index (RI) equals 1.00, then the method has correctly classified every observation for that dataset. Any deviation from 1.00 reflects classification errors. We report two different values of the Rand Index for each dataset and for each method: RI equals the value for the best fitting model, and RI* equals the value for a model that specifies the correct number of trajectory groups (T).

Table 1.

Inferred Number of Trajectory Groups and Accuracy of Sorting of Observations into Trajectory Groups, by Analytic Method and Specification of Simulation Parameters

Simulation Parameters				Inferred Results
T = # of Underlying Trajectory Groups	D = Distribution of Cases Over Groups	C = Certainty of Trajectory Group Assignment	t = # of Age Intervals	“Naïve” Approach				Group-Based Trajectory Models				Optimal Matching
T = # of Underlying Trajectory Groups	D = Distribution of Cases Over Groups	C = Certainty of Trajectory Group Assignment	t = # of Age Intervals	T′	T′-T	RI	RI*	T′	T′-T	RI	RI*	T′	T′-T	RI	RI*
1	n/a	High	6	2	1	0.956	1.000	1	0	1.000	1.000	3	2	0.529	1.000
1	n/a	Low	6	2	1	0.873	1.000	3	2	0.784	1.000	4	3	0.495	1.000
1	n/a	High	48	2	1	0.998	1.000	3	2	0.390	1.000	2	1	0.500	1.000
1	n/a	Low	48	3	2	0.749	1.000	3	2	0.341	1.000	2	1	0.513	1.000
2	Skewed	High	6	3	1	0.618	0.622	3	1	0.449	0.922	5	3	0.469	0.637
2	Uniform	High	6	3	1	0.517	0.516	3	1	0.599	0.833	6	4	0.667	0.716
2	Skewed	Low	6	3	1	0.510	0.516	2	0	0.809	0.809	4	2	0.446	0.503
2	Uniform	Low	6	3	1	0.556	0.555	3	1	0.554	0.558	3	1	0.533	0.503
2	Skewed	High	48	2	0	0.501	0.501	2	0	0.999	0.999	2	0	0.999	0.999
2	Uniform	High	48	2	0	0.602	0.602	2	0	0.998	0.998	2	0	0.998	0.998
2	Skewed	Low	48	3	1	0.479	0.510	5	3	0.347	0.528	2	0	0.534	0.534
2	Uniform	Low	48	3	1	0.611	0.624	3	1	0.589	0.645	5	3	0.557	0.531
4	Skewed	High	6	3	−1	0.405	0.405	3	−1	0.520	0.561	4	0	0.624	0.624
4	Uniform	High	6	3	−1	0.319	0.319	3	−1	0.655	0.552	5	1	0.460	0.475
4	Skewed	Low	6	3	−1	0.516	0.516	2	−2	0.616	0.635	5	1	0.627	0.623
4	Uniform	Low	6	4	0	0.565	0.565	2	−2	0.598	0.722	5	1	0.463	0.461
4	Skewed	High	48	3	−1	0.458	n/a¹	3	−1	0.899	0.962	5	1	0.795	0.761
4	Uniform	High	48	3	−1	0.422	n/a¹	4	0	0.944	0.944	4	0	0.577	0.577
4	Skewed	Low	48	4	0	0.575	0.575	4	0	0.725	0.725	2	−2	0.573	0.606
4	Uniform	Low	48	4	0	0.658	0.658	4	0	0.767	0.767	2	−2	0.501	0.443
6	Skewed	High	6	4	−2	0.433	0.433	4	−2	0.642	0.626	5	−1	0.719	0.712
6	Uniform	High	6	3	−3	0.470	n/a¹	3	−3	0.621	0.623	5	−1	0.804	0.811
6	Skewed	Low	6	4	−2	0.581	0.581	4	−2	0.624	0.562	6	0	0.677	0.677
6	Uniform	Low	6	4	−2	0.630	n/a¹	4	−2	0.665	0.607	6	0	0.785	0.785
6	Skewed	High	48	3	−3	0.504	n/a¹	5	−1	0.941	0.862	5	−1	0.952	0.882
6	Uniform	High	48	3	−3	0.538	n/a¹	5	−1	0.919	0.957	2	−4	0.442	0.916
6	Skewed	Low	48	4	−2	0.652	n/a¹	5	−1	0.737	0.745	3	−3	0.624	0.733
6	Uniform	Low	48	4	−2	0.721	n/a¹	5	−1	0.832	0.842	3	−3	0.664	0.788

Simulation Parameters				Inferred Results
T = # of Underlying Trajectory Groups	D = Distribution of Cases Over Groups	C = Certainty of Trajectory Group Assignment	t = # of Age Intervals	Grade of Membership				Growth Mixture Models				Latent Class Analysis
T = # of Underlying Trajectory Groups	D = Distribution of Cases Over Groups	C = Certainty of Trajectory Group Assignment	t = # of Age Intervals	T′	T′-T	RI	RI*	T′	T′-T	RI	RI*	T′	T′-T	RI	RI*
1	n/a	High	6	2	1	0.741	1.000	1	0	1.000	1.000	1	0	1.000	1.000
1	n/a	Low	6	2	1	0.667	1.000	1	0	1.000	1.000	1	0	1.000	1.000
1	n/a	High	48	2	1	0.500	1.000	5	4	0.207	1.000	5	4	0.242	1.000
1	n/a	Low	48	2	1	0.545	1.000	5	4	0.206	1.000	6	5	0.173	1.000
2	Skewed	High	6	3	1	0.447	0.918	2	0	0.500	0.500	2	0	0.951	0.951
2	Uniform	High	6	2	0	0.834	0.834	2	0	0.518	0.518	3	1	0.753	0.834
2	Skewed	Low	6	2	0	0.517	0.517	2	0	0.806	0.806	1	−1	0.820	0.821
2	Uniform	Low	6	2	0	0.558	0.558	2	0	0.543	0.543	2	0	0.523	0.523
2	Skewed	High	48	4	2	0.459	0.999	4	2	0.581	0.500	7	5	0.340	0.999
2	Uniform	High	48	3	1	0.873	0.998	4	2	0.769	0.874	6	4	0.670	0.998
2	Skewed	Low	48	4	2	0.377	0.540	3	1	0.443	0.501	5	3	0.371	0.540
2	Uniform	Low	48	4	2	0.571	0.640	4	2	0.578	0.554	4	2	0.569	0.641
4	Skewed	High	6	2	−2	0.541	0.513	2	−2	0.514	0.521	2	−2	0.647	0.641
4	Uniform	High	6	3	−1	0.463	0.446	2	−2	0.540	0.784	2	−2	0.545	0.752
4	Skewed	Low	6	4	0	0.625	0.625	2	−2	0.615	0.533	2	−2	0.618	0.639
4	Uniform	Low	6	4	0	0.478	0.478	2	−2	0.447	0.722	2	−2	0.454	0.737
4	Skewed	High	48	4	0	0.839	0.839	3	−1	0.743	0.676	7	3	0.759	0.868
4	Uniform	High	48	4	0	0.579	0.579	7	3	0.868	0.818	5	1	0.934	0.954
4	Skewed	Low	48	5	1	0.680	0.676	3	−1	0.572	0.578	7	3	0.662	0.682
4	Uniform	Low	48	5	1	0.450	0.488	3	−1	0.640	0.691	5	1	0.767	0.793
6	Skewed	High	6	4	−2	0.722	0.713	2	−4	0.404	n/a¹	3	−3	0.637	0.620
6	Uniform	High	6	2	−4	0.436	0.798	3	−3	0.621	0.622	3	−3	0.617	0.756
6	Skewed	Low	6	2	−4	0.402	0.636	2	−4	0.381	0.613	3	−3	0.534	0.562
6	Uniform	Low	6	2	−4	0.412	0.718	3	−3	0.665	0.746	4	−2	0.688	0.689
6	Skewed	High	48	5	−1	0.914	0.860	3	−3	0.723	n/a¹	8	2	0.848	0.869
6	Uniform	High	48	5	−1	0.916	0.956	4	−2	0.704	0.769	6	0	0.968	0.968
6	Skewed	Low	48	6	0	0.744	0.744	2	−4	0.564	0.629	5	−1	0.745	0.744
6	Uniform	Low	48	5	−1	0.831	0.831	4	−2	0.715	0.719	6	0	0.841	0.841

Open in a new tab

Note: Each row pertains to a different simulated dataset that includes records for 2,000 women whose employment status (1=employed, 0=not employed) was observed between ages 16 and 63. These 24 datasets vary with respect to the number of actual latent trajectories that describe women’s employment histories (T), the uniformity of the distribution of women across those trajectories (D), the certainty with which women were assigned to trajectories (C), and the number of times that women’s employment status was observed between ages 16 and 63 (t). For each of the methods used to model these trajectories, we report the inferred number of latent trajectories (T′), the difference between the actual and inferred number of trajectories (T′-T), the value of the Rand Index for the best fitting model (RI), and the value of the Rand Index for the model that specifies the correct number of trajectories (RI*). The Rand Index indicates how accurately each method allocates women to trajectory groups, where 1.0 indicates perfectly accurate sorting. See text for details of the simulation technique and the modeling strategies.

In these instances, it was not possible to compute the Rand Index for the model that specifies the correct number of trajectories.

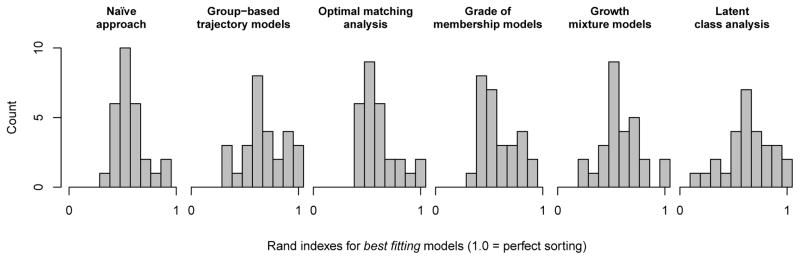
How often do our six analytic methods yield the same estimate of the number of latent trajectories underlying these 28 data sets? As shown in Table 1, across the 28 datasets the six methods never all infer the same number of trajectories (T’). Even excluding the “naïve” analyses, the five more statistically rigorous methods never all infer the same number of trajectories. Focusing on any pairwise comparison of two methods, there is only one instance—the comparison of “naïve” analyses with GBTMs—in which two methods agree more than half the time across the 28 datasets about the inferred number of trajectories. Unfortunately, “naïve” analyses and GBTMs most often agree that there are three trajectory groups—which is never a valid inference. Even the three variants of finite mixture modeling—GBTMs, GMMs, and LCA—infer the same number of trajectories only about a third of the time.

How often do these methods yield correct results—that is, how often do their inferences about the number of trajectories agree with the simulation parameter T that dictated the true number of trajectories? GoM analyses correctly inferred the number of latent trajectories for 8 of the 28 datasets; all the other methods performed even worse. Figure 5 presents histograms of the values of T’- T as reported in Table 1. Most of the time, each method inferred a number of latent trajectories that was within plus or minus two of the true value; none of the six methods appears to perform any better or worse than the others in this regard. These are relatively “clean” datasets—with no missing data, with no sample attrition, with employment histories of uniform length, and with a seemingly straightforward dichotomous outcome—and so it seems unlikely that these methods would perform much better when analyzing “real” data.

Comparison of inferred to actual number of trajectory groups, by analytic method. The x-axis reflects differences between our preferred solution and the actual number of trajectories that were used to generate the simulated data. See text for more details.

The accuracy of these methods with respect to making inferences about the number of underlying trajectory groups varies somewhat as a function of the simulation parameters used to generate the data. First, as shown in Table 1, all six methods tended to underestimate the number of trajectories when the true number of trajectories was higher and to overestimate the number of trajectories when the true number of trajectories was lower. Second, each method generally inferred a larger number of trajectories when the outcome was observed annually (as compared to when it was observed every 8 years). This seems to be particularly true for the less parsimonious GoM models which do not perform as well when the number of “internal variables” (observations of employment status in this case) is small (Manton et al. 1992). Overall, this suggests that these methods are more likely to produce valid inferences about the number of trajectories when age intervals are narrow and when there are few latent trajectories underlying the data. Unfortunately, analysts of real data usually have no way of knowing a priori whether the latter condition is met.

Putting aside the inferred number of trajectories, how often do these methods correctly sort individuals into trajectory groups? That is, how well do these methods perform with respect to trajectory assignment? In Figure 6, we present histograms of the Rand Index across the 28 datasets for each method; these values are also included in Table 1. The value of the Rand Index tends to be lower and less variable for the “naïve” approach; the more statistically rigorous methods tend to produce similar Rand Index values. In general, each method is more successful at allocating individuals to trajectory groups when age intervals are narrower; when certainty of trajectory group assignment was higher; and when individuals were distributed uniformly across trajectory groups.

Comparison of Rand Index values, by analytic method, for our best fitting models. Rand Indexes of 1 represent perfect sorting (i.e., zero classification errors). See text for more details.

To provide a closer inspection of these empirical patterns, we carried out a separate set of analyses in which we calculated the mean Rand Index value by simulation parameter and methodology. We then ran one-way ANOVAs to test whether these means varied significantly across methodologies, holding particular simulation parameters constant. Results from these analyses—which are shown graphically in Figure 7—suggest that the estimators in question produce a similar (and fairly large) number of classification errors, regardless of the empirical conditions that we imposed. Mean Rand Index values never exceeded 0.7 and the hypothesis tests that we performed were not significant (at least by conventional standards). Under these conditions, it is difficult to identify clear-cut “best” and “worst” methods.

Mean Rand Index values by methdology and simulation parameter. Point estimates are given by the solid circles; 50% and 95% confidence intervals are given by the thick and thin lines, respectively. The solid gray lines provide the mean Rand Index values *across* methodologies. P-values from one-way ANOVAs are given in the lower right-hand corner of each plot. The null hypothesis is that the means are equal within plots. The results for Trajectories = 4 (which we do no show to conserve space) were similar to those given above. See text for more details.

Part of the misallocation of individuals to trajectory groups can be attributed to errors in inferring the correct number of trajectory groups. The value of the Rand Index cannot equal 1.00 when the inferred number of trajectories is incorrect. To more clearly assess the ability of each method to allocate individuals to trajectories (net of their accuracy in inferring the number of trajectories), we have computed the Rand Index for each dataset and for each method for models that stipulate the correct number of trajectories; these values are also reported in Table 1. Distributions of the resulting Rand Indexes are shown in Figure 8. The Rand Index values are uniformly higher (except when the model initially inferred the correct number of trajectories), but are still not very high. If we excluded the four data sets in which the true number of trajectory groups (T) equals one—and thus where the Rand Index must equal 1.00—the results presented in Figure 8 would look very much like the results presented in Figure 6.

Comparison of Rand Index values, by analytic method, for models where we specified the correct number of trajectories. Rand Indexes of 1 represent perfect sorting (i.e., zero classification errors). See text for more details.

Do the trajectories produced by these several methods look qualitatively similar? Looking beyond errors in inferences about the number of trajectories and some misclassification of individuals across trajectory groups, do the methods yield trajectories that follow similar pathways? Our inspection of trends in age-specific employment rates suggests that when methods infer the same number of trajectory groups and have relatively high Rand Index values, the characteristics of the resulting trajectories are qualitatively similar to one another; descriptively, they also look similar to the truth as specified by the simulation parameters. That is, conditional on inferring the correct number of trajectories and on reasonably accurate sorting, each method yields similar and valid substantive stories about what the trajectories look like. Of course, in practice researchers typically have no way to assess whether those conditions are satisfied.

Supplemental Analyses of Real Data

Although we have argued that there are distinct analytic advantages to modeling simulated data to address our main research questions, we also recognize the importance of ascertaining how the several methods perform using real data. Could the divergent results we reported in Table 1 and Figures 5 and 6 be due to the ultimately artificial nature of our simulated data? Although we cannot assess the accuracy of each method using real data generated by processes that we obviously cannot observe or control, might the several methods yield more consistent results when the application involves real data analysis?

To address this question, we analyzed data from the Cambridge Study in Delinquent Development (CSDD) (Farrington 1999). Initiated in 1961, the CSDD was a prospective study that followed 411 (403 in our analysis due to 8 deaths) working-class boys in London from age 8/9 through age 31/32. For each single year of age from 10 through 32, the data indicate whether or not each of these 403 boys was convicted of some criminal offense; the most common offenses were thefts, burglaries, and stolen cars. The original data provided annual conviction counts, which we then dichotomized for the purposes of our analyses (1 = had a conviction in the past year; 0 = otherwise). The Cambridge data have been used prominently by D’Unger et al. (1998), Muthen (2004), Nagin (1999) and others in widely-cited work on trajectory methods.

Using the same six methods—and following the same model fitting, model selection, and other inferential procedures described above—we analyzed the Cambridge data to infer the optimal number of latent trajectories of criminal convictions, to describe the shape of these trajectories, and to allocate the 403 boys to their most likely latent trajectory group. Figure 9 depicts our results by showing the number of trajectory groups, the percentage of cases that were allocated to each group, and the average cumulative number of years with convictions at each age for members of those groups, separately by estimation strategy. The estimated group sizes for each trajectory are provided in the upper left-hand corner of each plot, along with generic letter names which we use to refer to the groups in the discussion below.

Number and shape of age trajectories of convictions, by analytic method. The data used in these analyses are from the Cambridge Study in Delinguent Development (Farrington 1999). See text for more details.

The naïve approach yielded six trajectory groups that differed qualitatively with respect to when boys were first convicted and whether or not they ever desisted. The largest group of boys (Group A, which included an estimated 64% of the sample) was never convicted. On the other hand, both GoM and OM inferred that there were only two distinct trajectory groups—a very large one (with more than 90% of the boys) that experienced few convictions, and a much smaller one (Group B) that experienced a large and growing number of convictions over time. The GoM and OM solutions do not distinguish between boys who were never convicted and those who experienced only a few convictions.

Each of the three finite mixture modeling approaches (GBTMs, GMMs, and LCA) inferred three trajectory groups, including one large group of boys who were never convicted (Group A); the estimated size of that group ranges from 65% to 75% of the sample. However, the profile of the other groups varies considerably across these three methods. Whereas LCA and GBTMs identified one small group of boys that was convicted a large number of times (Group B, accounting for between 4% and 11% of the sample depending on the methodology), GMMs inferred two moderate sized groups (19% of 16%) that experienced similar cumulative numbers of convictions. Unlike the other five methodologies (and the other two types of finite mixture models), GMMs did not identify a “high” conviction group.

In short, these six methods produced results that differ with respect to the number of latent trajectory groups; their relative size; and the qualitative attributes of those groups. Although we cannot compare these results to the “truth” (since that truth is unobserved), we can conclude that the choice of method for analyzing the Cambridge data has important implications for the substantive conclusions one draws about trajectories of criminal convictions.

Discussion

Our goal in this article was to assess the relative validity and reliability of six methods for identifying and describing latent age-graded trajectories and for assigning individuals to those trajectories. To this end, we posed four questions. In this section, we review the answers to these four specific questions before turning to the limitations of our analyses, describing future directions for methodological work, and drawing broader conclusions.

First, do “naïve” approaches, finite mixture models, optimal matching analyses (OM), and grade of membership (GoM) models lead to the same inferences about the number of latent trajectories that exist in a population? Here, the answer is a decided “no.” Across 28 simulated datasets, the methods never drew the same inferences about the number of trajectories. Even the more statistically sophisticated methods—all but the “naïve” analyses—never agreed with one another. Comparing any two methods, those methods rarely agreed on the number of latent trajectories more than a third of the time. The methods also produced dissimilar results when we analyzed “real” data. Clearly, analysts who draw substantive or theoretical conclusions based on the exact number of latent trajectories that underlie some age-graded phenomenon need to recognize that their inferences about that number are affected by their choice of methodology.

Not only did these methods not make the same inferences about the number of trajectories underlying simulated data, they also usually produced inferences that were incorrect. GoM inferred the correct number of trajectories for 8 of the 28 datasets, but all the other methods performed worse. Most of the time, these methods “missed” by one or two latent trajectories, but as we argue below many substantive analyses draw major substantive or theoretical conclusions based on the existence, size, or attributes of just one or two latent trajectory groups. To be fair, the developers of these several statistical methods recognize and quantify uncertainty in inferences about the number of latent trajectories (e.g., Nagin and Tremblay 2005). Most applied researchers, however, tend to reify the point estimate and overlook this uncertainty; for example, very few conclude that there are “between three and six” latent trajectories.

Second, under what conditions or circumstances do these alternative methods yield the same conclusions and—perhaps most importantly—under what circumstances do they yield correct conclusions? We found that all six methods tended to underestimate the number of trajectories when the true number of trajectories underlying the simulated data was relatively high (six) and to overestimate the number of trajectories when the true number was low (one or two). Of course, substantive researchers have no way of knowing in advance how many latent trajectories underlie some age-graded sequence of observations; consequently, they have no way of knowing whether they are likely under- or over-estimating the number of trajectories. We also found that each method tended to yield more accurate results when the age interval of observation was relatively narrow (i.e., when there were more frequently observations over the age range being observed). This finding should trouble the many substantive researchers who have relied on data collected on just a handful of occasions over a wide range of ages. All of this implies that these methods may be more likely to produce valid inferences about the number of trajectories only when age intervals are narrow and when there is good reason to believe that there are few latent trajectories underlying the data. On the other hand, when there was actually just one latent trajectory the various methods generally inferred that there were two or more.

Third, do these methods lead to the same decisions about which trajectory best describes each individual’s age-graded observations? Again, the answer is “no.” In part, this is because any disagreement between two methods about the inferred number of latent trajectories will necessarily lead to discrepancies in which individuals are assigned to the same trajectory groups. However, putting this aside, the Rand Index indicated that these methods differed with respect to the accuracy of their assignments of individuals to trajectory groups. As we note below, this inaccuracy in sorting individuals can lead to problems for researchers who use trajectory group membership as an independent variable in models predicting subsequent outcomes. Once again, the developers of the several statistical methods we considered recognize and quantify uncertainty or “fuzziness” in the assignment of individuals to trajectory groups—indeed this is a fundamental property of GoM models. Here again, applied researchers sometimes overlook this uncertainty.

Fourth, do those methods yield similar descriptions of the characteristics or qualities of those various trajectories? In this case the answer is “yes,” at least when they agree about the number of latent trajectories and about the assignment of individuals to them. Our simulated data represented women’s employment status histories, and in general, the several methods painted the same broad picture. However, substantive conclusions about population heterogeneity in these patterns—for example, about the existence and attributes of relatively uncommon ideal-typical life pathways—will be incorrect when the method used errs in inferring the number of trajectories or in sorting individuals into them. In practice, researchers have no way of knowing whether this is the case.

We might have expanded the scope of our analyses in ways that would make results even more useful for substantive researchers as they explore the best method for modeling age-graded trajectory data. First, we have focused only on methods that are used for drawing inferences about the discrete number of latent trajectories that underlie observed age-graded data. A more basic question—and one that we have not here addressed—is when and how researchers might more confidently reject the hypothesis that there is only one latent trajectory from which each individual’s biography deviates to some degree. Many researchers simply start by assuming that there is actually a single latent trajectory around which individual sequences vary, and then utilize growth curve models in multilevel or structural equation model frameworks. Our results do not speak to this more basic issue: When should researchers employ any method(s) from this entire class of models? Second, and more practically, all of our analyses pertain to outcomes measured dichotomously. Whether our basic findings would hold for count or continuous measures remains to be seen—but see Bauer and Curran (2003) in this regard. Third, our “naïve” analyses might be particularly “naïve.” We found that “naïve” approaches did about as well as more sophisticated methods in inferring the number of trajectories—although they did not do as well at sorting individuals into trajectory groups—but actual analysts would likely have been more thoughtful in how they performed “naïve” analysis. For example, they would likely have also considered the mean or total number of years employed in constructing their group taxonomy.

Our conclusions should be disconcerting for researchers who analyze age-graded trajectory data using just one method. Scholars in any number of disciplines and specialties draw key substantive and theoretical conclusions based on the number and attributes of latent trajectories that appear to underlie their data. We find that those conclusions may be determined, at least in part, by the choice that those scholars make about which method to use and that those methods frequently produce invalid results. What is more, many researchers employ these methods as a first step in their empirical work, as an effort to construct a key dependent or independent variable. They infer that there are k trajectory groups, and they then regress some outcome Y on a series of indicators of trajectory group membership. However, our findings suggest that there is often a substantial amount of misallocation of individuals to trajectory groups. This means that, for many applications, researchers’ key independent variables are measured with an amount of error that is generally difficult for them to quantify or correct. Even if these researchers infer the correct number of trajectory groups, their substantive results may thus still be biased by virtue of having utilized one of these methods. We should note that these disconcerting conclusions are based on analyses of data that are unrealistically “clean” in important respects: Our simulated datasets do not suffer from problems associated with missing data, censored or truncated observations, or panel attrition, for example. In analyses of “real data,” these additional complications and potential sources of bias are overlaid on top of the methodological problems we have identified.

A more fundamental implication of our work is that we need better theory about discrete, latent trajectory population subgroups in particular empirical situations. Most sociological and other analyses use the methods we have considered in a purely inductive manner, letting the data and model reveal the number of population subgroups, their membership, and their attributes. A more theoretically-based and deductive approach would begin with specific hypotheses about how many population subgroups there are, what sorts of individuals belong to those subgroups, and what the character of those subgroups’ trajectories might be. In this situation, the methods we examined might be used to confirm or disconfirm theoretically-motivated hypotheses. Of course, given our empirical findings, analysts would need to be cautious about basing tests of such hypotheses on just one of the analytic methods we consider.

Applied researchers should realize that their choice of method for modeling age-graded trajectory data has potentially important consequences for their substantive results. Regardless of which method(s) they use, they also need to take seriously uncertainty in inferred numbers of trajectory groups and uncertainty in trajectory group assignment. As we noted earlier, the developers of the various methods we consider are much clearer about these forms of uncertainty and about what the results of these forms of analysis mean and do not mean. However, users of these methods too often reify point estimates about the number of latent trajectories, overstate the certainty with which individuals “belong” to trajectory groups, and assume (at least implicitly) that they would get basically the same results had the selected a different method. Until new and better-validated techniques are available, we urge researchers to—at a minimum—verify their substantive results by replicating their analyses using multiple methods and then take seriously the uncertainty built into those results. We also encourage them to develop stronger theories about whether discrete, latent trajectories can be said to actually and meaningfully exist in particular substantive contexts, or whether the clusters of observations they are detecting using these methods are simply useful summaries of complex longitudinal data.

Acknowledgments

This project benefited from support provided by the Minnesota Population Center, which receives core support (5R24HD041023) from the Eunice Kennedy Shriver National Institute for Child Health and Human Development (NICHD). We are grateful to Shawn Bauldry, Ken Bollen, Ross Macmillan, Samir Soneji, Geoff Wodtke, and several anonymous reviewers for their comments and assistance. However, all errors omissions are the responsibility of the authors.

APPENDIX A (To Be Provided Online)

The technical details of the models used in this paper have been explicated at length elsewhere (Abbott and Hrycak 1990; Bauer and Curran 2003; Clogg 1995; Jones and Nagin 2007; Manton et al. 1992; Manton, Woodbury and Tolley 1994; Muthén 2004; Muthén and Shedden 1999; Nagin 2005; Wu 2000). In this section, we provide basic estimating equations and associated formulae in an effort to (1) spell out their underlying assumptions and (2) provide further details about how they are implemented in typical social science applications. The interested reader is encouraged to consult the extensive methodological literature on growth mixture models (Muthén 2004), group-based trajectory models (Nagin 2005), latent class analysis (Collins and Lanza 2010), grade of membership models (Manton et al. 1992), and optimal matching analysis (Lesnard 2010) for a more comprehensive treatment of these topics.

Growth mixture models and group-based trajectory models

Growth mixture models and group-based trajectory models can be expressed in general terms using SEM matrix notation (Bollen and Curran 2006b):

y = \sum_{g = 1}^{G} P_{i}^{(g)} [Λ^{(g)} η^{(g)} + ε^{(g)}]

(1)

η^{(g)} = μ_{η}^{(g)} + ζ^{(g)}

(2)

where y is the longitudinal attribute of interest (e.g., employment status across the life course); $P_{i}^{(g)}$ is the probability that individual i belongs to latent group g (where $P_{i}^{(g)} \geq 0$ and $\sum_{g = 1}^{G} P_{i}^{(g)} = 1$ ) ; Λ is a matrix of constants and factor loadings; η is a vector of growth parameters that includes intercepts, slopes, and (in our analyses) quadratic terms; and ε is vector of error terms.

The superscripts in Equations 1 and 2 indicate that the growth parameters that define the shape of each trajectory are free to vary across the g trajectory groups. When GMMs are fit, the within-class variance components in Equation 2 are freely estimated, allowing for residual variation within trajectory groups (i.e., random effects). When GBTMs are estimated, the within-class variance components are fixed to zero (ζ = 0), implying that individuals’ experiences (y) are homogeneous within groups. In some cases, researchers pursue a hybrid approach where certain variance components are fixed to 0 and/or constrained to be equal across trajectories (see, e.g., McLeod and Fettes 2007). This is the approach that we employed when fitting GMMs.

Latent class analysis

In the mixture modeling approaches described above growth parameters are used to characterize change over time in the attribute of interest. In latent class analysis, change is not characterized using polynomials and is instead modeled non-parametrically. This is especially useful when respondents’ trajectories are thought to oscillate over time and/or contain sharp discontinuities. The basic model for binary outcomes (dropping individual subscripts) can be written as:

P (Y = y) = \sum_{g - 1}^{G} P (g) P (y_{1} = 1 ∣ g) \dots P (y_{k} = 1 ∣ g)

(3)

where P(Y = y) is the joint probability of all of the y’s (1,…,k); P(g) is the probability of latent class g; and P(y_k = 1| g) is the probability that y_k = 1, conditional on membership in class g.

Classification probabilities—the latent class equivalent to factor scores—can be calculated for LCA models using Bayes’ theorem:

P (g ∣ y) = \frac{P (g) P (y_{1} ∣ g) \dots P (y_{k} ∣ g)}{P (y_{1}, \dots, y_{k})},

(4)

where P(g | y) represents the posterior probability of membership in latent class g, conditional on response pattern y (i.e., the likelihood that an individual belongs to a certain latent class given their actual sequence of measurements). The classification probabilities expressed in Equation 4 can take on any value between 0 and 1, and may be nonzero for more than one latent class. This is true for the two estimation strategies described above, as well.

Grade of membership analysis

Grade of membership models are similar to latent class models (Erosheva 2005; Manton, Woodbury and Tolley 1994) and are typically expressed as:

P (y = l_{j} ∣ k) = \sum_{k = 1}^{K} g_{k} λ_{kjl} .

(5)

Here, P(y=l_j|k) is the probability that the value of dichotomous variable y is equal to l for a given polytomous outcome j (e.g., the age-specific observations of employment status in our application) conditional on membership in class (or type) k. G are the so-called GoM scores which range from 0 to 1 and denote individual i’s degree of (partial) membership in state k. The GoM scores are similar to the term P(g) in Equations 3 and 4 and, as in latent class models, g_k≥0 and $\sum_{k = 1}^{K} g_{k} = 1$ . Rather than “latent classes,” k are referred to as “pure types” or “extreme profiles” in the GoM literature, reflecting the emphasis on partial membership in different states or classes. λ_kjl are the estimated probabilities of response l for outcome j for hypothetical individuals who belong completely to a single pure state (i.e., λ_kjl=P(y_jl=1 | g_k=1.0). λ are thus similar to p(y_k|g) in Equations 3 and 4 above. Given the focus on partial membership (or grade of membership) in multiple states, GoM models do not provide estimates of the probability that an individual belongs to a single profile, but some researchers have used the estimates of partial membership to assign individuals to one profile or pure type (e.g., Berkman, Singer and Manton 1989; Cassidy, Pieper and Carroll 2001). To facilitate comparison with the other methods used in this paper, we adopt a similar approach, allocating individuals to the state (trajectory) with the highest GoM score (g).

Optimal Matching Analysis

Optimal matching (OM) classifies sequences of observations based on their similarity and dissimilarity. OM analyses usually proceed in two steps. The first step assesses similarity and dissimilarity between two sequences by counting the steps of transforming one sequence into another. Let y_k = (s₁, s₂, s₃, …, s_t) be a sequence of attributes, where s_t (k = 1, 2, …, T) denotes the tth attribute of sequence y_k (i = 1, 2, …, K). OM algorithms are based on three algebras—substitution, deletion, and insertion—that transform one sequence to another. Let $a_{s_{t}}^{sub}, a_{s_{t}}^{del}$ and $a_{s_{t}}^{insert}$ denote substitution, deletion, and insertion algebras for sequence transformation, respectively. The key procedure is to decide the values of the cost for substitution, deletion, and insertion, denoted by $c (a_{s_{t}}^{sub}), c (a_{s_{t}}^{del})$ and $c (a_{s_{t}}^{ins})$ , respectively. Let A_ij = a₁, a₂, a₃, …, a_L be a series of operator algebras that can be used to transform y_i to y_j for i ≠ j so that the cost of this transformation is $c (A_{i j}) = \sum_{l = 1}^{L} a_{l}$ . Because there may be more than one way to transform y_i to y_j, the “optimal” cost is min[c(A_ij)]. These pairwise comparisons of the K sequences yield a cost or distance matrix of dimension K × K.

Second, in most social science applications, researchers then subject that distance matrix to some form of cluster analysis in order to group sequences into a discrete (<K) number of trajectory categories. In this article, we used the Ward’s method, a criterion that can be applied in agglomerative hierarchical clustering procedure. Hierarchical clustering procedures do not estimate the number of the groups in the data. Agglomerative hierarchical cluster analysis begins with assuming that there are K groups in the data where each individual is in its own cluster and repeats the process by merging individuals so that there are K − 1, K − 2,…,1 groups. To merge individuals, the Ward’s method defines the distance between two clusters, A and B, as follows:

Δ (A, B) = \sum_{k \in A \cup B} {‖ y_{k} - m_{A \cup B} ‖}^{2} - \sum_{k \in A} {‖ y_{k} - m_{A} ‖}^{2} - \sum_{k \in B} {‖ y_{k} - m_{B} ‖}^{2} = \frac{n_{A} n_{B}}{n_{A} + n_{B}} {‖ m_{A} - m_{B} ‖}^{2}

(6)

where y_k is a longitudinal attribute of interest; m_A and m_B is the center of cluster A and B, respectively; and n_A and n_B is the number of y in cluster A and B, respectively.

Equation 6 shows that the Ward hierarchical clustering method minimizes the increase in the total within-cluster variance. This method tends to merge clusters with a small number of individuals; may be biased toward yielding clusters with similar number of individuals; and is sensitive to outliers (Milligan 1980).

Selecting the optimal number of groups

Techniques for identifying the optimal number of trajectory groups vary across methods. For GMMs, GBTMS, and LCA, we fit models in a stepwise fashion that included increasing numbers of latent trajectories. We then compared model fit using a variety of statistical criteria (e.g., BIC, sample-size adjusted BIC, AIC, the entropy index, the Lo-Mendell-Rubin LR test, and the Vuong-Lo-Mendell-Rubin LR test). When these criteria failed to converge on a common solution, we gave preference to specifications that produced adequately populated classes (e.g., no fewer than 5 percent of all cases) with substantively distinct trajectory groups. Because information criteria do not work well for the relatively unparsimonious GoM models—each additional pure type requires N additional parameters where N is the sample size—we used likelihood ratio tests and the t test proposed by Manton, Woodbury, and Tolley (1994) to select the optimal number of groups. For OM analyses, following Aassve, Billari, and Piccarretta (2007), Anyadike-Danes and McVicar (2010) and Gauthier et al. (2010), the decisions about the optimal number of trajectories were based on the Cali ski-Harabasz (1974) pseudo F-statistic.

APPENDIX B (To Be Provided Online)

In this section we provide more technical detail concerning the method used to simulate the 28 data sets; below we provide the R code used to simulate one of them. Depending on her previous employment status (0=not employed, 1=employed), the current employment status for a simulated woman has a Bernoulli distribution with parameters q₀₁ and q₁₀, where q₀₁ and q₁₀ are elements of the time-dependent transition matrix for a two-state Markov chain procedure. The key step of this simulation procedure is to define a series of 2×2 transition matrices $Q (t) = [\begin{array}{l} q_{00} (t) & q_{01} (t) \\ q_{10} (t) & q_{11} (t) \end{array}]$ to generate different trajectories of employment statuses. In these matrices, q₀₀ is the probability of remaining unemployed for a woman who was unemployed at the preceding age; q₀₁ is the probability of becoming employed for a woman who was unemployed at the preceding age; q₁₀ is the probability of becoming unemployed for a woman who was employed at the preceding age, and q₁₁ the probability of remaining employed for a woman who was employed at the preceding age. In fact, we only need to define q₀₁ and q₁₀ because q₀₀ + q₀₁ = 1 and q₁₁ + q₁₀ = 1. The transition matrix, Q(t), varies across ages, so it is sometimes called a non-homogeneous Markov process. By manipulating (a) the values of q₀₁ and q₁₀; (b) the ways in which they differ across ages; and (c) the share of the 2,000 women assigned to follow each trajectory, we produce the 28 datasets depicted in Figures 1 through 4.

Below we provide the R code used to produce the data set that has T=2 latent trajectory groups in which there are 48 observation per women (t=48), in which women are uniformly distributed across the two trajectory groups (D=uniform), and in there is relatively little within trajectory-group heterogeneity (C=high).

##### FIRST TRAJECTORY GROUP #####
library(Rlab);
t = 48                      #define t (the number of within-individual observations)
tr = t-1
n = 1000;                #define D (the distribution of individuals across groups)
t1=18-17                #define C (the certainty with which individual observations
t2=24-17                #were assigned to trajectory groups) by specifying a set of
t3=49-17                #”critical” ages when employment status begins to change.
t4=55-17;
q01=rep(0.001,tr)
q10=rep(0.003,tr);
q01[(t1+1):t2]=c(1:(t2-t1)/(t2-t1))
q01[(t2+1):t3]=c(rep(0.999, (t3-t2)))
q01[(t3+1):tr]=c(rep(0.0001, (tr-t3)));
q10[(t3+1):t4]=c(1:(t4-t3)/(t4-t3))
q10[(t4+1):tr]=c(rep(0.999, (tr-t4)));
y1  =  array(rep(0,t*n),dim=c(n,t));
for (li in 1:n)
{
       for (lj in 2:tr)
          {
                          y1[li,lj]          =       y1[li,lj-1]-ifelse(y1[li,lj-1],rbern(1,q10[lj-
                          1]),rbern(1,q01[lj-1]))*(2*y1[li,lj-1]-1);
         }
}
##### SECOND TRAJECTORY GROUP #####
t = 48                     #define t (the number of within-individual observations)
tr = t-1
n = 1000;               #define D (the distribution of individuals across groups)
t1=26-17               #define C (the certainty with which individual observations
t2=32-17               #were assigned to trajectory groups) by specifying a set of
t3=50-17               #”critical” ages when employment status begins to change.
t4=56-17;
q01=rep(0.0001,tr)
q10=rep(0.008,tr);
q01[(t1+1):t2]=c(1:(t2-t1)/(t2-t1))
q01[(t2+1):t3]=c(rep(0.995, (t3-t2)))
q01[(t3+1):tr]=c(rep(0.0001, (tr-t3)));
q10[(t3+1):t4]=c(1:(t4-t3)/(t4-t3))
q10[(t4+1):tr]=c(rep(0.999, (tr-t4)));
y4 = array(rep(0,t*n),dim=c(n,t));
for   (li in 1:n)
{
         for (lj in 2:tr)
        {
        y4[li,lj]                    =        y4[li,lj-1]-ifelse(y4[li,lj-1],rbern(1,q10[lj-
1]),rbern(1,q01[lj-1]))*(2*y4[li,lj-1]-1);
         }
}
data1     = rbind(y1, y4);

Appendix Table C1.

Fit Statistics for Group-Based Trajectory Models

(FOR PEER REVIEW ONLY; TO BE AVAILABLE ON-LINE UPON PUBLICATION)

Data Set #	Simulation Parameters					Fit Statistics
Data Set #	T	D	C	t	T′	Smallest Group	AIC	BIC	aBIC	Entropy	VLMR p	LMR p
1	2	Uniform	High	48	1	100%	49286.2	49303.0	49293.5	—	—	—
					2	50%	27591.8	27631.0	27608.8	1.00	0.00	0.00
					3	24%	27018.3	27079.9	27044.9	0.87	0.00	0.00
					4	22%	26470.0	26554.1	26506.4	0.80	0.07	0.07
					5	15%	25986.7	26093.1	26032.8	0.81	0.00	0.00
					6	9%	25514.1	25642.9	25569.8	0.84	0.00	0.00
					7	9%	25165.8	25317.0	25231.3	0.84	0.00	0.00
					8	9%	24796.5	24970.1	24871.6	0.85	0.00	0.00
2	2	Uniform	High	6	1	100%	7591.0	7607.8	7598.2	—	—	—
					2	41%	6715.6	6754.8	6732.5	0.55	0.00	0.00
					3	10%	6706.3	6767.9	6733.0	0.85	0.00	0.00
					4	3%	6710.1	6794.1	6746.5	0.85	0.59	0.59
					5	1%	6717.6	6824.1	6763.7	0.78	0.79	0.80
					6	0%	6725.5	6854.3	6781.3	0.79	0.66	0.66
					7	1%	6733.5	6884.7	6798.9	0.76	0.34	0.34
					8	0%	6741.5	6915.1	6816.6	0.80	—	0.01
3	2	Skewed	High	48	1	100%	34794.3	34811.1	34801.5	—	—	—
					2	10%	27151.3	27190.6	27168.3	1.00	0.00	0.00
					3	10%	26086.6	26148.2	26113.3	0.78	0.00	0.00
					4	10%	25299.0	25383.0	25335.4	0.78	0.00	0.00
					5	10%	24577.0	24683.4	24623.1	0.82	0.00	0.00
					6	10%	24215.5	24344.4	24271.3	0.86	0.00	0.00
					7	7%	24008.2	24159.5	24073.7	0.87	0.00	0.00
					8	6%	23741.6	23915.2	23816.7	0.92	0.01	0.01
4	2	Skewed	High	6	1	100%	6110.4	6127.2	6117.6	—	—	—
					2	15%	6005.5	6044.7	6022.4	0.61	0.00	0.00
					3	10%	5995.3	6056.9	6022.0	0.73	0.00	0.00
					4	10%	5996.9	6080.9	6033.2	0.65	0.04	0.04
					5	4%	6002.6	6109.0	6048.7	0.54	0.12	0.13
					6	1%	6010.5	6139.3	6066.2	0.65	1.00	1.00
					7	0%	6018.5	6169.7	6083.9	0.69	0.99	0.99
					8	0%	6026.5	6200.1	6101.6	0.65	—	0.00
5	2	Uniform	Low	48	1	100%	41354.5	41371.3	41361.7	—	—	—
					2	34%	36184.4	36223.6	36201.4	0.85	0.04	0.04
					3	24%	32899.8	32961.4	32926.4	0.87	0.00	0.00
					4	18%	31603.6	31687.6	31640.0	0.87	0.00	0.00
					5	9%	30692.4	30798.8	30738.5	0.87	0.00	0.00
					6	9%	30009.1	30137.9	30064.9	0.86	0.04	0.04
					7	7%	29357.1	29508.3	29422.5	0.87	0.01	0.01
					8	8%	28678.2	28851.9	28753.4	0.88	0.00	0.00
6	2	Uniform	Low	6	1	100%	5281.1	5297.9	5288.4	—	—	—
					2	18%	5197.2	5236.4	5214.2	0.88	0.00	0.00
					3	8%	5164.7	5226.3	5191.3	0.77	0.00	0.00
					4	0%	5169.9	5253.9	5206.2	0.63	0.00	0.00
					5	2%	5176.9	5283.4	5223.0	0.44	0.61	0.61
					6	2%	5184.8	5313.6	5240.5	0.40	0.39	0.39
					7	0%	5192.8	5344.0	5258.2	0.43	—	0.68
					8	0%	5200.8	5374.4	5275.9	0.51	0.02	0.02
7	2	Skewed	Low	48	1	100%	35605.2	35622.0	35612.5	—	—	—
					2	43%	31313.6	31352.8	31330.6	0.82	0.00	0.00
					3	23%	29969.9	30031.5	29996.6	0.82	0.00	0.01
					4	15%	28853.1	28937.1	28889.4	0.82	0.01	0.01
					5	11%	28128.9	28235.3	28175.0	0.85	0.02	0.02
					6	6%	27546.2	27675.0	27601.9	0.86	0.06	0.06
					7	5%	26949.2	27100.5	27014.7	0.86	0.00	0.00
					8	5%	26536.2	26709.9	26611.4	0.86	0.14	0.14
8	2	Skewed	Low	6	1	100%	4940.6	4957.4	4947.9	—	—	—
					2	7%	4850.4	4889.6	4867.4	0.75	0.00	0.00
					3	6%	4851.3	4912.9	4877.9	0.76	0.22	0.23
					4	4%	4853.7	4937.8	4890.1	0.79	0.00	0.00
					5	3%	4860.7	4967.1	4906.7	0.82	0.00	0.00
					6	0%	4868.6	4997.4	4924.3	0.81	1.00	1.00
					7	1%	4876.6	5027.8	4942.0	0.71	—	0.45
					8	0%	4884.6	5058.2	4959.7	0.83	—	1.00
9	4	Uniform	High	48	1	100%	51241.9	51258.7	51249.1	—	—	—
					2	48%	39770.1	39809.3	39787.0	0.98	0.00	0.00
					3	25%	32039.9	32101.5	32066.6	0.99	0.00	0.00
					4	20%	29390.7	29474.7	29427.0	0.97	0.00	0.00
					5	9%	28911.4	29017.8	28957.4	0.94	0.05	0.05
					6	6%	28585.4	28714.3	28641.2	0.94	0.00	0.00
					7	6%	28256.1	28407.4	28321.6	0.94	0.00	0.00
					8	6%	28005.2	28178.9	28080.4	0.91	0.02	0.02
10	4	Uniform	High	6	1	100%	6161.8	6178.6	6169.1	—	—	—
					2	38%	5970.8	6010.0	5987.8	0.37	0.00	0.00
					3	5%	5966.0	6027.6	5992.7	0.63	0.00	0.00
					4	12%	5969.0	6053.0	6005.3	0.53	0.08	0.08
					5	2%	5974.1	6080.5	6020.1	0.65	0.03	0.04
					6	0%	5982.1	6110.9	6037.8	0.69	0.00	0.00
					7	0%	5990.1	6141.3	6055.5	0.71	0.96	0.96
					8	0%	5998.1	6171.7	6073.2	0.73	0.01	0.01
11	4	Skewed	High	48	1	100%	44300.1	44316.9	44307.3	—	—	—
					2	33%	34760.3	34799.5	34777.3	0.97	0.00	0.00
					3	16%	29790.2	29851.8	29816.9	0.99	0.00	0.00
					4	6%	28557.8	28641.8	28594.2	0.97	0.00	0.00
					5	8%	27775.0	27881.5	27821.1	0.88	0.02	0.02
					6	10%	27242.1	27370.9	27297.8	0.87	0.01	0.01
					7	6%	26656.9	26808.1	26722.4	0.89	0.01	0.01
					8	5%	26357.7	26531.3	26432.8	0.90	0.00	0.00
12	4	Skewed	High	6	1	100%	6176.1	6192.9	6183.4	—	—	—
					2	30%	5980.6	6019.8	5997.6	0.42	0.00	0.00
					3	6%	5973.1	6034.7	5999.8	0.71	0.00	0.00
					4	8%	5977.0	6061.0	6013.4	0.74	0.00	0.00
					5	0%	5981.9	6088.4	6028.0	0.75	0.10	0.10
					6	4%	5989.8	6118.6	6045.5	0.65	0.57	0.58
					7	0%	5997.7	6148.9	6063.1	0.58	0.06	0.06
					8	0%	6005.7	6179.3	6080.8	0.62	0.00	0.00
13	4	Uniform	Low	48	1	100%	56951.4	56968.2	56958.7	—	—	—
					2	47%	43879.7	43918.9	43896.7	0.92	0.00	0.00
					3	17%	39254.3	39315.9	39281.0	0.94	0.00	0.00
					4	13%	36747.5	36831.5	36783.8	0.93	0.01	0.01
					5	14%	35186.5	35292.9	35232.6	0.91	0.00	0.00
					6	3%	34393.4	34522.2	34449.2	0.92	0.01	0.01
					7	3%	33483.5	33634.7	33549.0	0.92	0.08	0.08
					8	3%	32743.3	32917.0	32818.5	0.92	0.00	0.00
14	4	Uniform	Low	6	1	100%	7584.2	7601.0	7591.5	—	—	—
					2	38%	7020.8	7060.0	7037.8	0.74	0.00	0.00
					3	4%	6994.0	7055.6	7020.6	0.77	0.00	0.00
					4	10%	6988.0	7072.1	7024.4	0.57	0.03	0.04
					5	7%	6992.6	7099.0	7038.7	0.75	0.08	0.09
					6	0%	6999.6	7128.4	7055.3	0.76	0.12	0.13
					7	0%	7007.4	7158.6	7072.8	0.76	0.27	0.27
					8	0%	7015.3	7188.9	7090.4	0.68	0.20	0.20
15	4	Skewed	Low	48	1	100%	46810.4	46827.2	46817.7	—	—	—
					2	37%	38569.2	38608.4	38586.1	0.89	0.00	0.00
					3	19%	35989.0	36050.7	36015.7	0.87	0.01	0.01
					4	11%	33347.7	33431.7	33384.0	0.91	0.00	0.00
					5	5%	31577.2	31683.7	31623.3	0.91	0.01	0.02
					6	3%	30770.5	30899.3	30826.3	0.92	0.00	0.00
					7	5%	30036.1	30187.3	30101.5	0.91	0.01	0.01
					8	5%	29374.0	29547.6	29449.1	0.90	0.00	0.00
16	4	Skewed	Low	6	1	100%	6249.7	6266.5	6257.0	—	—	—
					2	29%	6154.1	6193.3	6171.1	0.66	0.00	0.00
					3	3%	6135.9	6197.5	6162.5	0.87	0.00	0.00
					4	1%	6123.4	6207.4	6159.8	0.92	0.00	0.00
					5	0%	6125.8	6232.2	6171.9	0.85	0.12	0.12
					6	0%	6130.2	6259.0	6185.9	0.85	1.00	1.00
					7	0%	6137.1	6288.3	6202.6	0.86	0.04	0.04
					8	0%	6145.0	6318.6	6220.1	0.83	0.64	0.64
17	6	Uniform	High	48	1	100%	77862.9	77879.7	77870.2	—	—	—
					2	16%	50821.3	50860.5	50838.2	1.00	0.00	0.00
					3	16%	42307.2	42368.8	42333.9	0.98	0.00	0.00
					4	16%	36699.2	36783.2	36735.6	0.98	0.00	0.00
					5	16%	33287.0	33393.4	33333.0	0.97	0.00	0.00
					6	11%	31975.8	32104.7	32031.6	0.97	0.00	0.00
					7	5%	30764.2	30915.4	30829.6	0.97	0.00	0.00
					8	2%	30220.6	30394.2	30295.7	0.97	0.10	0.11
18	6	Uniform	High	6	1	100%	9239.3	9256.1	9246.6	—	—	—
					2	16%	7289.4	7328.6	7306.4	0.96	0.00	0.00
					3	16%	7048.5	7110.1	7075.2	0.78	0.00	0.00
					4	3%	7030.3	7114.3	7066.6	0.90	0.00	0.00
					5	2%	7033.9	7140.3	7079.9	0.88	0.22	0.23
					6	0%	7038.7	7167.5	7094.5	0.74	0.03	0.03
					7	0%	7044.6	7195.8	7110.0	0.82	0.46	0.47
					8	0%	7051.2	7224.8	7126.3	0.78	0.21	0.21
19	6	Skewed	High	48	1	100%	64248.1	64264.9	64255.4	—	—	—
					2	7%	46829.9	46869.1	46846.8	1.00	0.00	0.00
					3	7%	37878.7	37940.3	37905.4	0.97	0.00	0.00
					4	7%	32860.9	32945.0	32897.3	0.98	0.00	0.00
					5	7%	30141.7	30248.1	30187.7	0.97	0.00	0.00
					6	7%	29529.9	29658.7	29585.6	0.91	0.00	0.00
					7	6%	29098.0	29249.2	29163.5	0.91	0.09	0.09
					8	5%	28476.3	28649.9	28551.4	0.92	0.00	0.00
20	6	Skewed	High	6	1	100%	8303.2	8320.0	8310.5	—	—	—
					2	7%	7232.6	7271.8	7249.5	0.98	0.00	0.00
					3	7%	6984.3	7045.9	7011.0	0.70	0.00	0.00
					4	7%	6958.3	7042.3	6994.7	0.80	0.00	0.00
					5	2%	6964.1	7070.5	7010.2	0.67	0.18	0.19
					6	1%	6971.4	7100.2	7027.2	0.70	0.02	0.02
					7	0%	6979.3	7130.5	7044.8	0.58	1.00	1.00
					8	2%	6987.1	7160.8	7062.3	0.70	1.00	1.00
21	6	Uniform	Low	48	1	100%	78487.2	78504.0	78494.4	—	—	—
					2	16%	57761.3	57800.5	57778.3	1.00	0.00	0.00
					3	17%	46037.7	46099.3	46064.4	0.96	0.00	0.00
					4	16%	42600.1	42684.1	42636.4	0.95	0.00	0.00
					5	13%	40255.8	40362.2	40301.9	0.95	0.00	0.00
					6	13%	39129.9	39258.7	39185.7	0.93	0.13	0.14
					7	8%	38385.7	38536.9	38451.1	0.93	0.12	0.12
					8	5%	37443.1	37616.8	37518.3	0.93	0.02	0.02
22	6	Uniform	Low	6	1	100%	9914.8	9931.6	9922.0	—	—	—
					2	14%	8708.5	8747.7	8725.5	0.95	0.00	0.00
					3	16%	8250.9	8312.5	8277.6	0.76	0.00	0.00
					4	5%	8211.1	8295.1	8247.4	0.83	0.00	0.00
					5	4%	8200.1	8306.6	8246.2	0.90	0.00	0.00
					6	3%	8202.4	8331.2	8258.2	0.84	0.54	0.54
					7	3%	8209.5	8360.7	8274.9	0.87	0.09	0.10
					8	2%	8217.3	8390.9	8292.4	0.81	0.76	0.76
23	6	Skewed	Low	48	1	100%	63448.6	63465.5	63455.9	—	—	—
					2	8%	50010.4	50049.6	50027.4	1.00	0.00	0.00
					3	8%	41983.1	42044.7	42009.8	0.94	0.00	0.00
					4	8%	39009.0	39093.0	39045.3	0.92	0.00	0.00
					5	7%	36391.9	36498.3	36437.9	0.93	0.03	0.03
					6	3%	35899.6	36028.4	35955.4	0.94	0.41	0.42
					7	7%	34380.4	34531.6	34445.8	0.90	0.06	0.07
					8	3%	33725.6	33899.3	33800.8	0.91	0.00	0.00
24	6	Skewed	Low	6	1	100%	8307.6	8324.4	8314.8	—	—	—
					2	7%	7456.1	7495.3	7473.1	0.97	0.00	0.00
					3	7%	7303.1	7364.7	7329.8	0.78	0.00	0.00
					4	7%	7278.8	7362.8	7315.1	0.80	0.00	0.00
					5	0%	7274.5	7380.9	7320.5	0.87	0.00	0.00
					6	2%	7273.0	7401.8	7328.8	0.86	0.78	0.79
					7	0%	7278.5	7429.7	7344.0	0.72	0.00	0.00
					8	0%	7283.9	7457.6	7359.1	0.70	1.00	1.00

Open in a new tab

Bolded Results Indicate Preferred Model

Appendix Table C2.

Fit Statistics for Growth Mixture Models

(FOR PEER REVIEW ONLY; TO BE AVAILABLE ON-LINE UPON PUBLICATION)

Data Set #	Simulation Parameters					Fit Statistics
Data Set #	T	D	C	t	T′	Smallest Group	AIC	BIC	aBIC	Entropy	VLMR p	LMR p
1	2	Uniform	High	48	1	100%	27131.2	27181.6	27153.0	—	—	—
					2	43%	25893.5	25966.3	25925.0	0.96	0.06	0.07
					3	19%	24758.8	24854.0	24800.0	0.96	0.00	0.00
					4	12%	24581.6	24699.2	24632.5	0.91	0.00	0.00
					5	8%	24573.1	24713.1	24633.6	0.86	0.18	0.19
					6	3%	24365.7	24528.2	24436.0	0.85	0.49	0.50
					7	0%	24375.0	24559.8	24454.9	0.88	—	0.51
					8	4%	24144.3	24351.5	24234.0	0.90	0.00	0.00
2	2	Uniform	High	6	1	100%	6718.2	6768.6	6740.0	—	—	—
					2	6%	6712.8	6785.6	6744.3	0.91	0.00	0.00
					3	7%	6715.4	6810.6	6756.6	0.82	0.01	0.01
					4	3%	6722.0	6839.6	6772.9	0.85	0.01	0.01
					5	1%	6729.8	6869.8	6790.4	0.73	1.00	1.00
					6	0%	6737.7	6900.1	6808.0	0.87	0.51	0.51
					7	0%	6745.8	6930.7	6825.8	0.72	1.00	1.00
					8	0%	6753.5	6960.8	6843.2	0.79	0.00	0.00
3	2	Skewed	High	48	1	100%	25442.9	25493.3	25464.7	—	—	—
					2	41%	24551.8	24624.6	24583.3	0.78	0.48	0.49
					3	7%	24307.8	24403.0	24349.0	0.89	0.00	0.00
					4	6%	24227.2	24344.8	24278.1	0.81	0.00	0.00
					5	3%	24021.3	24161.3	24081.9	0.86	0.12	0.12
					6	6%	23856.7	24019.1	23927.0	0.83	—	0.98
					7	10%	23760.7	23945.5	23840.7	0.82	—	1.00
					8	1%	23647.8	23855.0	23737.4	0.84	0.00	0.00
4	2	Skewed	High	6	1	100%	6011.7	6062.1	6033.5	—	—	—
					2	31%	6000.4	6073.2	6031.9	0.67	0.00	0.00
					3	9%	6003.9	6099.1	6045.1	0.49	0.48	0.48
					4	3%	6008.6	6126.2	6059.5	0.53	0.23	0.23
					5	1%	6014.7	6154.8	6075.3	0.61	0.00	0.00
					6	2%	6022.7	6185.1	6093.0	0.43	0.00	0.00
					7	1%	6030.7	6215.5	6110.7	0.64	0.00	0.00
					8	1%	6038.6	6245.8	6128.3	0.54	1.00	1.00
5	2	Uniform	Low	48	1	100%	27600.2	27650.6	27622.0	—	—	—
					2	40%	27083.5	27156.4	27115.0	0.76	0.00	0.00
					3	15%	26813.1	26908.3	26854.3	0.77	0.03	0.03
					4	9%	26744.8	26862.4	26795.7	0.83	0.09	0.09
					5	9%	26613.2	26753.3	26673.8	0.76	0.26	0.27
					6	0%	26628.4	26790.8	26698.7	0.86	—	0.86
					7	0%	26535.4	26720.2	26615.4	0.75	0.23	0.23
					8	4%	26347.3	26554.6	26437.0	0.81	0.00	0.00
6	2	Uniform	Low	6	1	100%	5189.8	5240.2	5211.6	—	—	—
					2	11%	5175.6	5248.4	5207.1	0.83	0.00	0.00
					3	9%	—	—	—	0.77	—	—
					4	1%	5182.0	5299.6	5232.9	0.69	0.00	0.00
					5	0%	5189.1	5329.1	5249.7	0.49	0.52	0.53
					6	1%	5197.1	5359.5	5267.4	0.52	0.00	0.00
					7	0%	5205.0	5389.8	5285.0	0.46	—	0.99
					8	2%	5212.9	5420.1	5302.6	0.37	—	0.17
7	2	Skewed	Low	48	1	100%	26353.2	26403.6	26375.0	—	—	—
					2	45%	25912.0	25984.9	25943.6	0.76	0.00	0.00
					3	20%	25714.9	25810.1	25756.1	0.76	0.04	0.05
					4	2%	25623.4	25741.1	25674.4	0.83	0.46	0.47
					5	2%	25389.4	25529.5	25450.0	0.84	0.15	0.16
					6	0%	25329.7	25492.1	25400.0	0.82	0.11	0.12
					7	2%	25392.4	25577.2	25472.3	0.88	—	0.93
					8	0%	25285.1	25492.4	25374.8	0.81	—	0.96
8	2	Skewed	Low	6	1	100%	4861.4	4911.8	4883.2	—	—	—
					2	11%	4858.1	4931.0	4889.7	0.64	0.00	0.00
					3	2%	4859.5	4954.7	4900.7	0.73	0.00	0.00
					4	1%	4866.1	4983.7	4917.0	0.75	0.00	0.00
					5	2%	4872.9	5012.9	4933.5	0.54	0.00	0.00
					6	0%	4880.7	5043.1	4951.0	0.53	0.00	0.00
					7	0%	4888.7	5073.5	4968.7	0.72	1.00	1.00
					8	0%	4896.7	5103.9	4986.4	0.61	—	1.00
9	4	Uniform	High	48	1	100%	30148.5	30198.9	30170.3	—	—	—
					2	20%	28612.1	28684.9	28643.6	0.98	0.00	0.00
					3	9%	27937.2	28032.4	27978.4	0.93	0.00	0.00
					4	19%	27187.6	27305.3	27238.5	0.91	0.00	0.00
					5	0%	27047.6	27187.7	27108.2	0.92	0.00	0.00
					6	10%	26458.5	26620.9	26528.8	0.90	0.00	0.00
					7	6%	26429.0	26613.8	26508.9	0.87	0.00	0.00
					8	1%	26450.7	26658.0	26540.4	0.86	0.10	0.11
10	4	Uniform	High	6	1	100%	5980.3	6030.7	6002.1	—	—	—
					2	18%	5971.9	6044.7	6003.4	0.69	0.01	0.01
					3	24%	5975.2	6070.4	6016.4	0.33	0.02	0.03
					4	14%	5981.1	6098.7	6032.0	0.48	0.43	0.44
					5	2%	5986.2	6126.2	6046.8	0.59	1.00	1.00
					6	3%	5994.2	6156.7	6064.5	0.52	0.24	0.24
					7	0%	6002.2	6187.1	6082.2	0.66	—	0.02
					8	0%	6010.1	6217.4	6099.8	0.61	1.00	1.00
11	4	Skewed	High	48	1	100%	28460.6	28511.0	28482.4	—	—	—
					2	47%	26897.8	26970.6	26929.3	0.95	0.00	0.00
					3	13%	26415.2	26510.4	26456.4	0.92	0.00	0.00
					4	6%	26022.2	26139.8	26073.1	0.85	0.60	0.61
					5	4%	25783.2	25923.3	25843.8	0.96	0.00	0.00
					6	3%	25757.2	25919.6	25827.5	0.93	0.89	0.89
					7	4%	25554.8	25739.6	25634.8	0.83	—	0.87
					8	2%	25492.2	25699.4	25581.8	0.87	0.22	0.23
12	4	Skewed	High	6	1	100%	5990.8	6041.2	6012.6	—	—	—
					2	23%	5980.0	6052.8	6011.5	0.67	0.00	0.00
					3	7%	5981.3	6076.5	6022.5	0.75	0.00	0.00
					4	4%	5986.9	6104.5	6037.8	0.72	0.32	0.33
					5	3%	5994.2	6134.2	6054.7	0.59	0.86	0.86
					6	1%	6002.1	6164.5	6072.4	0.60	—	0.00
					7	0%	6010.0	6194.9	6090.0	0.60	—	0.98
					8	0%	6018.1	6225.3	6107.8	0.68	—	0.86
13	4	Uniform	Low	48	1	100%	30406.0	30456.4	30427.9	—	—	—
					2	41%	29500.0	29572.8	29531.5	0.83	0.00	0.00
					3	20%	29185.3	29280.5	29226.5	0.84	0.00	0.00
					4	18%	28894.1	29011.7	28945.0	0.77	—	0.93
					5	5%	28550.2	28690.2	28610.8	0.83	0.42	0.43
					6	4%	28321.8	28484.2	28392.1	0.81	0.14	0.15
					7	2%	28366.5	28551.3	28446.4	0.81	0.23	0.23
					8	0%	28143.1	28350.3	28232.7	0.81	0.07	0.07
14	4	Uniform	Low	6	1	100%	7101.1	7151.5	7122.9	—	—	—
					2	14%	7003.9	7076.7	7035.4	0.80	0.00	0.00
					3	4%	6998.6	7093.8	7039.8	0.86	0.01	0.01
					4	10%	7000.1	7117.7	7051.0	0.57	1.00	1.00
					5	0%	7005.3	7145.3	7065.9	0.64	1.00	1.00
					6	0%	7012.1	7174.5	7082.4	0.63	0.03	0.03
					7	0%	7020.1	7205.0	7100.1	0.66	—	0.95
					8	5%	7027.9	7235.2	7117.6	0.47	—	0.00
15	4	Skewed	Low	48	1	100%	27564.5	27614.9	27586.4	—	—	—
					2	44%	26811.0	26883.8	26842.5	0.74	0.02	0.02
					3	16%	26478.7	26573.9	26519.9	0.77	0.00	0.00
					4	2%	26358.2	26475.8	26409.1	0.78	0.70	0.71
					5	4%	26227.9	26367.9	26288.5	0.90	0.55	0.55
					6	2%	26136.4	26298.8	26206.7	0.75	0.42	0.42
					7	2%	26041.0	26225.8	26121.0	0.68	0.18	0.18
					8	1%	25926.7	26134.0	26016.4	0.86	0.55	0.55
16	4	Skewed	Low	6	1	100%	6166.0	6216.4	6187.8	—	—	—
					2	22%	6140.2	6213.0	6171.7	0.89	0.00	0.00
					3	4%	6130.3	6225.5	6171.5	0.54	0.00	0.00
					4	0%	6134.7	6252.3	6185.6	0.62	0.00	0.00
					5	0%	6139.2	6279.2	6199.8	0.80	1.00	1.00
					6	0%	6142.4	6304.8	6212.7	0.63	1.00	1.00
					7	0%	6150.2	6335.0	6230.2	0.86	—	0.69
					8	0%	6159.0	6366.2	6248.7	0.48	—	0.00
17	6	Uniform	High	48	1	100%	30650.6	30701.0	30672.4	—	—	—
					2	37%	29507.6	29580.4	29539.1	0.87	0.00	0.00
					3	13%	28826.0	28921.2	28867.2	0.83	0.00	0.00
					4	14%	28014.0	28131.6	28064.9	0.84	0.00	0.00
					5	3%	28031.1	28171.1	28091.7	0.88	0.01	0.01
					6	0%	27941.0	28103.5	28011.3	0.89	0.00	0.00
					7	4%	27441.7	27626.5	27521.7	0.88	0.00	0.00
					8	0%	27287.9	27495.2	27377.6	0.84	—	0.52
18	6	Uniform	High	6	1	100%	7369.2	7419.6	7391.0	—	—	—
					2	41%	7056.2	7129.0	7087.7	0.85	0.00	0.00
					3	16%	7041.0	7136.2	7082.2	0.75	0.01	0.01
					4	6%	7040.2	7157.8	7091.1	0.82	0.00	0.00
					5	3%	7044.7	7184.8	7105.3	0.67	0.25	0.25
					6	0%	7051.0	7213.5	7121.3	0.87	0.09	0.09
					7	0%	7057.0	7241.8	7137.0	0.84	—	0.00
					8	0%	7065.9	7273.2	7155.6	0.85	—	0.00
19	6	Skewed	High	48	1	100%	28901.3	28951.7	28923.1	—	—	—
					2	17%	27592.9	27665.8	27624.5	0.94	0.00	0.00
					3	15%	26517.1	26612.3	26558.3	0.88	0.00	0.00
					4	0%	26421.8	26539.4	26472.7	0.87	0.00	0.00
					5	4%	26305.5	26445.5	26366.1	0.85	0.38	0.39
					6	0%	26145.9	26308.4	26216.2	0.77	—	0.31
					7	0%	25930.7	26115.5	26010.7	0.91	0.01	0.01
					8	3%	25733.5	25940.7	25823.2	0.88	0.01	0.01
20	6	Skewed	High	6	1	100%	7213.6	7264.0	7235.4	—	—	—
					2	7%	6978.4	7051.2	7009.9	0.99	0.00	0.00
					3	7%	6966.0	7061.2	7007.2	0.94	0.00	0.00
					4	7%	6969.5	7087.1	7020.4	0.74	—	0.55
					5	2%	6975.7	7115.8	7036.3	0.76	0.24	0.25
					6	2%	6983.9	7146.3	7054.2	0.62	—	0.78
					7	2%	6991.5	7176.3	7071.5	0.59	—	0.57
					8	0%	6999.6	7206.8	7089.3	0.70	1.00	1.00
21	6	Uniform	Low	48	1	100%	34128.1	34178.5	34149.9	—	—	—
					2	24%	33068.5	33141.3	33100.0	0.95	0.00	0.00
					3	11%	32050.5	32145.7	32091.7	0.83	0.00	0.00
					4	9%	31690.3	31807.9	31741.2	0.79	0.00	0.00
					5	0%	31482.4	31622.5	31543.0	0.82	0.42	0.42
					6	4%	31437.7	31600.2	31508.0	0.82	0.00	0.00
					7	0%	31195.9	31380.7	31275.9	0.82	—	0.96
					8	2%	30826.7	31033.9	30916.4	0.80	0.23	0.23
22	6	Uniform	Low	6	1	100%	8507.9	8558.3	8529.7	—	—	—
					2	29%	8270.1	8342.9	8301.6	0.64	0.00	0.00
					3	18%	8205.3	8300.5	8246.5	0.76	0.62	0.63
					4	9%	8187.1	8304.8	8238.0	0.75	0.03	0.03
					5	9%	8198.8	8338.9	8259.4	0.58	0.65	0.65
					6	5%	8196.0	8358.4	8266.3	0.58	1.00	1.00
					7	5%	8201.7	8386.6	8281.7	0.54	0.22	0.22
					8	0%	8215.9	8423.1	8305.6	0.50	—	0.24
23	6	Skewed	Low	48	1	100%	30682.2	30732.6	30704.1	—	—	—
					2	48%	29495.1	29567.9	29526.6	0.75	0.00	0.00
					3	18%	29209.7	29304.9	29250.9	0.75	0.24	0.24
					4	6%	28989.5	29107.1	29040.4	0.74	0.03	0.04
					5	2%	28799.0	28939.0	28859.6	0.83	0.12	0.12
					6	2%	28712.9	28875.4	28783.2	0.71	0.59	0.60
					7	0%	28593.5	28778.3	28673.5	0.80	0.00	0.00
					8	2%	28422.7	28630.0	28512.4	0.80	0.77	0.77
24	6	Skewed	Low	6	1	100%	7373.8	7424.2	7395.6	—	—	—
					2	6%	7308.7	7381.5	7340.2	0.96	0.00	0.00
					3	8%	7283.9	7379.1	7325.1	0.63	0.00	0.00
					4	6%	7275.9	7393.5	7326.8	0.89	0.00	0.00
					5	0%	7278.5	7418.5	7339.1	0.73	0.00	0.00
					6	0%	7284.7	7447.2	7355.0	0.74	—	0.03
					7	0%	7290.3	7475.1	7370.3	0.81	—	0.00
					8	0%	7298.4	7505.6	7388.0	0.79	0.76	0.76

Open in a new tab

Bolded Results Indicate Preferred Model

Appendix Table C3.

Fit Statistics for Latent Class Analyses

(FOR PEER REVIEW ONLY; TO BE AVAILABLE ON-LINE UPON PUBLICATION)

Data Set #	Simulation Parameters					Fit Statistics
Data Set #	T	D	C	t	T′	Smallest Group	AIC	BIC	aBIC	Entropy	VLMR p	LMR p
1	2	Uniform	High	48	1	100%	41572.1	41840.9	41688.4	—	—	—
					2	50%	25037.1	25580.4	25272.2	1.00	0.00	0.00
					3	23%	24145.3	24963.1	24499.2	1.00	0.00	0.00
					4	23%	23319.6	24411.7	23792.2	0.99	0.00	0.00
					5	13%	22772.0	24138.6	23363.4	1.00	0.00	0.00
					6	13%	22399.3	24040.4	23109.5	0.99	0.00	0.00
					7	8%	22232.8	24148.3	23061.7	0.96	0.13	0.13
					8	7%	22052.1	24242.1	22999.9	0.95	0.00	0.00
2	2	Uniform	High	6	1	100%	7034.0	7067.6	7048.5	—	—	—
					2	44%	6708.4	6781.3	6740.0	0.60	0.00	0.00
					3	25%	6711.3	6823.3	6759.8	1.00	0.00	0.00
					4	22%	6718.9	6870.1	6784.3	0.70	0.04	0.04
					5	0%	6732.5	6923.0	6814.9	0.74	0.64	0.65
					6	1%	6746.3	6976.0	6845.7	0.67	0.68	0.68
					7	0%	6760.3	7029.2	6876.7	0.71	0.90	0.90
					8	0%	6774.3	7082.4	6907.6	0.84	0.22	0.22
3	2	Skewed	High	48	1	100%	31211.3	31480.2	31327.7	—	—	—
					2	10%	24259.0	24802.3	24494.1	1.00	0.00	0.00
					3	10%	22744.8	23562.6	23098.7	1.00	0.00	0.00
					4	10%	21845.1	22937.3	22317.7	0.99	0.00	0.00
					5	10%	21430.6	22797.3	22022.1	0.99	0.03	0.03
					6	7%	21239.0	22880.1	21949.2	0.98	0.00	0.00
					7	8%	21078.6	22994.1	21907.6	0.98	0.00	0.00
					8	5%	20941.9	23131.9	21889.7	0.97	0.76	0.76
4	2	Skewed	High	6	1	100%	6081.9	6115.5	6096.4	—	—	—
					2	11%	5990.8	6063.6	6022.3	0.85	0.00	0.00
					3	14%	5996.8	6108.8	6045.3	0.84	0.78	0.79
					4	7%	6006.8	6158.0	6072.2	0.79	0.23	0.23
					5	5%	6017.8	6208.2	6100.2	0.60	0.10	0.10
					6	1%	6031.1	6260.8	6130.5	0.66	0.17	0.17
					7	0%	6045.0	6313.8	6161.3	0.58	0.39	0.39
					8	0%	6059.0	6367.0	6192.3	0.55	1.00	1.00
5	2	Uniform	Low	48	1	100%	39904.6	40173.4	40020.9	—	—	—
					2	34%	33865.6	34408.9	34100.7	0.98	0.00	0.00
					3	24%	30342.8	31160.5	30696.7	0.98	0.00	0.00
					4	19%	28857.2	29949.4	29329.9	0.96	0.00	0.00
					5	10%	27793.2	29159.9	28384.7	0.97	0.11	0.11
					6	10%	27042.1	28683.2	27752.3	0.98	0.74	0.74
					7	11%	26438.9	28354.4	27267.8	0.97	0.71	0.71
					8	8%	26108.0	28298.0	27055.7	0.98	0.00	0.00
6	2	Uniform	Low	6	1	100%	5155.4	5189.0	5170.0	—	—	—
					2	34%	5131.2	5204.1	5162.8	0.28	0.01	0.01
					3	4%	5139.1	5251.2	5187.6	0.57	0.00	0.00
					4	4%	5150.6	5301.9	5216.1	0.63	0.31	0.31
					5	1%	5164.0	5354.5	5246.4	0.79	0.68	0.69
					6	1%	5177.8	5407.4	5277.1	0.86	0.11	0.11
					7	1%	5191.7	5460.5	5308.0	0.97	0.04	0.04
					8	0%	5205.7	5513.7	5339.0	0.85	0.48	0.48
7	2	Skewed	Low	48	1	100%	33586.7	33855.5	33703.0	—	—	—
					2	37%	28776.0	29319.3	29011.1	1.00	0.00	0.00
					3	16%	26984.0	27801.7	27337.9	0.95	0.00	0.00
					4	10%	25549.6	26641.8	26022.2	0.99	0.00	0.00
					5	8%	24746.7	26113.3	25338.1	0.99	0.01	0.01
					6	5%	24205.9	25846.9	24916.1	0.99	0.00	0.00
					7	4%	23835.2	25750.7	24664.2	0.98	0.77	0.77
					8	4%	23676.0	25866.0	24623.7	0.98	0.00	0.00
8	2	Skewed	Low	6	1	100%	4806.2	4839.8	4820.8	—	—	—
					2	8%	4804.1	4876.9	4835.6	0.68	0.13	0.14
					3	11%	4812.0	4924.0	4860.5	0.54	0.05	0.06
					4	1%	4824.8	4976.0	4890.2	0.63	0.37	0.38
					5	1%	4838.2	5028.6	4920.6	0.99	0.21	0.22
					6	0%	4852.1	5081.7	4951.5	0.88	0.81	0.82
					7	0%	4866.1	5134.9	4982.4	0.72	0.43	0.44
					8	1%	4880.0	5188.1	5013.4	0.85	0.04	0.04
9	4	Uniform	High	48	1	100%	49758.7	50027.6	49875.1	—	—	—
					2	48%	37563.6	38106.9	37798.8	0.98	0.00	0.00
					3	25%	29696.5	30514.2	30050.4	1.00	0.00	0.00
					4	21%	26825.4	27917.6	27298.1	1.00	0.00	0.00
					5	13%	26309.8	27676.4	26901.2	1.00	0.00	0.00
					6	9%	25897.5	27538.5	26607.6	0.99	0.79	0.79
					7	11%	25588.9	27504.4	26417.9	0.97	0.00	0.00
					8	8%	25268.0	27458.0	26215.7	0.99	0.16	0.16
10	4	Uniform	High	6	1	100%	6058.4	6092.0	6073.0	—	—	—
					2	21%	5951.9	6024.7	5983.4	1.00	0.00	0.00
					3	8%	5956.2	6068.2	6004.7	0.53	0.03	0.03
					4	13%	5967.7	6118.9	6033.1	0.69	0.16	0.17
					5	0%	5980.2	6170.7	6062.7	0.83	0.42	0.43
					6	0%	5994.0	6223.6	6093.3	0.74	0.84	0.84
					7	1%	6007.9	6276.8	6124.3	0.55	0.09	0.10
					8	0%	6021.9	6330.0	6155.2	0.65	0.99	0.99
11	4	Skewed	High	48	1	100%	42538.5	42807.3	42654.8	—	—	—
					2	33%	32496.0	33039.3	32731.2	0.98	0.00	0.00
					3	16%	27484.5	28302.2	27838.3	1.00	0.00	0.00
					4	15%	25774.0	26866.2	26246.7	1.00	0.00	0.00
					5	6%	24780.7	26147.4	25372.2	0.99	0.00	0.00
					6	6%	24132.3	25773.4	24842.5	0.98	0.00	0.00
					7	5%	23875.9	25791.5	24704.9	0.98	0.00	0.00
					8	6%	23677.1	25867.0	24624.8	0.98	0.81	0.81
12	4	Skewed	High	6	1	100%	6096.6	6130.2	6111.2	—	—	—
					2	29%	5972.5	6045.3	6004.0	0.49	0.00	0.00
					3	2%	5979.6	6091.6	6028.0	0.80	0.00	0.00
					4	0%	5989.3	6140.5	6054.7	0.64	0.20	0.21
					5	0%	5999.5	6189.9	6081.9	0.69	0.47	0.48
					6	0%	6010.9	6240.5	6110.2	0.70	0.21	0.21
					7	0%	6024.8	6293.6	6141.1	0.79	0.57	0.57
					8	0%	6038.7	6346.8	6172.1	0.82	0.39	0.40
13	4	Uniform	Low	48	1	100%	53569.2	53838.0	53685.5	—	—	—
					2	45%	41862.0	42405.3	42097.1	0.99	0.00	0.00
					3	22%	36984.8	37802.5	37338.6	0.99	0.00	0.00
					4	17%	34389.0	35481.2	34861.7	0.98	0.00	0.00
					5	12%	32717.6	34084.2	33309.0	0.99	0.00	0.00
					6	10%	31777.8	33418.8	32487.9	0.98	0.76	0.76
					7	11%	31009.8	32925.3	31838.7	0.98	0.00	0.00
					8	6%	30399.7	32589.6	31347.4	0.98	0.01	0.01
14	4	Uniform	Low	6	1	100%	7233.3	7266.9	7247.8	—	—	—
					2	34%	7015.8	7088.7	7047.4	0.50	0.00	0.00
					3	4%	6985.7	7097.7	7034.2	0.66	0.00	0.00
					4	16%	6996.0	7147.2	7061.4	0.70	0.43	0.43
					5	3%	7007.5	7197.9	7089.9	0.78	0.11	0.11
					6	2%	7020.8	7250.5	7120.2	0.54	0.37	0.37
					7	1%	7034.6	7303.5	7151.0	0.91	0.66	0.67
					8	0%	7048.6	7356.7	7181.9	0.73	0.01	0.01
15	4	Skewed	Low	48	1	100%	44721.5	44990.3	44837.8	—	—	—
					2	45%	36573.9	37117.2	36809.0	1.00	0.00	0.00
					3	25%	33340.2	34158.0	33694.1	0.98	0.00	0.00
					4	13%	30804.5	31896.7	31277.2	0.98	0.00	0.00
					5	5%	28985.5	30352.1	29576.9	0.99	0.00	0.00
					6	5%	28200.7	29841.8	28910.9	0.98	0.00	0.00
					7	5%	27545.5	29461.0	28374.4	0.99	0.01	0.01
					8	5%	26926.6	29116.5	27874.3	0.98	0.06	0.06
16	4	Skewed	Low	6	1	100%	6176.3	6209.9	6190.9	—	—	—
					2	24%	6116.7	6189.6	6148.2	0.96	0.00	0.00
					3	2%	6109.7	6221.7	6158.2	0.97	0.01	0.01
					4	2%	6116.6	6267.8	6182.0	0.74	0.14	0.14
					5	1%	6124.2	6314.7	6206.7	0.74	0.08	0.08
					6	1%	6134.2	6363.9	6233.6	0.79	0.17	0.17
					7	1%	6147.9	6416.7	6264.2	0.67	0.62	0.62
					8	0%	6161.7	6469.8	6295.1	0.71	0.31	0.31
17	6	Uniform	High	48	1	100%	77048.8	77317.7	77165.2	—	—	—
					2	16%	48806.1	49349.4	49041.2	1.00	0.00	0.00
					3	17%	40524.5	41342.2	40878.3	0.99	0.00	0.00
					4	16%	35150.1	36242.3	35622.7	1.00	0.00	0.00
					5	16%	31385.5	32752.1	31976.9	0.98	0.00	0.00
					6	13%	29963.7	31604.8	30673.9	1.00	0.00	0.00
					7	5%	28730.6	30646.1	29559.6	0.99	0.78	0.78
					8	2%	28278.7	30468.6	29226.4	1.00	0.72	0.72
18	6	Uniform	High	6	1	100%	9148.8	9182.4	9163.3	—	—	—
					2	17%	7190.6	7263.4	7222.1	0.98	0.00	0.00
					3	16%	7027.4	7139.4	7075.8	0.98	0.00	0.00
					4	0%	7028.4	7179.6	7093.8	0.96	0.01	0.01
					5	0%	7037.8	7228.2	7120.2	0.81	0.20	0.21
					6	0%	7049.4	7279.0	7148.8	0.85	0.08	0.09
					7	0%	7062.5	7331.4	7178.9	0.84	0.27	0.28
					8	0%	7076.4	7384.5	7209.7	0.69	0.56	0.56
19	6	Skewed	High	48	1	100%	62766.2	63035.0	62882.5	—	—	—
					2	8%	45172.5	45715.8	45407.6	1.00	0.00	0.00
					3	7%	36272.7	37090.5	36626.6	1.00	0.00	0.00
					4	7%	31492.8	32584.9	31965.4	0.99	0.00	0.00
					5	7%	28159.0	29525.6	28750.4	0.99	0.00	0.00
					6	7%	27380.1	29021.1	28090.3	0.99	0.00	0.00
					7	6%	26858.7	28774.2	27687.7	0.99	0.00	0.00
					8	6%	26345.9	28535.9	27293.7	0.98	0.00	0.00
20	6	Skewed	High	6	1	100%	8281.3	8314.9	8295.8	—	—	—
					2	7%	7084.0	7156.8	7115.5	0.99	0.00	0.00
					3	7%	6963.6	7075.6	7012.0	0.96	0.00	0.00
					4	7%	6969.5	7120.7	7034.9	0.98	0.09	0.10
					5	4%	6979.1	7169.5	7061.5	0.89	0.11	0.11
					6	4%	6991.1	7220.8	7090.5	0.88	0.02	0.02
					7	3%	7004.5	7273.3	7120.8	0.90	0.63	0.63
					8	1%	7018.3	7326.4	7151.6	0.78	0.84	0.84
21	6	Uniform	Low	48	1	100%	77093.4	77362.3	77209.8	—	—	—
					2	17%	54259.1	54802.4	54494.2	1.00	0.00	0.00
					3	17%	44196.4	45014.1	44550.3	1.00	0.00	0.00
					4	16%	40457.3	41549.5	40930.0	0.99	0.00	0.00
					5	11%	38060.7	39427.4	38652.2	0.99	0.00	0.00
					6	10%	36801.4	38442.4	37511.6	0.99	0.00	0.00
					7	5%	35566.4	37481.9	36395.3	0.99	0.22	0.23
					8	5%	34881.3	37071.3	35829.0	0.98	0.72	0.72
22	6	Uniform	Low	6	1	100%	9821.3	9854.9	9835.9	—	—	—
					2	16%	8387.9	8460.7	8419.4	0.94	0.00	0.00
					3	16%	8194.9	8306.9	8243.4	0.97	0.00	0.00
					4	11%	8177.6	8328.8	8243.0	0.98	0.00	0.00
					5	4%	8184.6	8375.0	8267.0	0.83	0.01	0.01
					6	4%	8195.5	8425.1	8294.8	0.70	0.24	0.25
					7	4%	8207.0	8475.9	8323.4	0.69	0.15	0.15
					8	0%	8221.0	8529.0	8354.3	0.71	0.14	0.14
23	6	Skewed	Low	48	1	100%	62075.6	62344.4	62191.9	—	—	—
					2	8%	47873.8	48417.1	48109.0	1.00	0.00	0.00
					3	8%	40128.7	40946.4	40482.6	1.00	0.00	0.00
					4	8%	36752.0	37844.2	37224.7	1.00	0.00	0.00
					5	7%	34224.7	35591.4	34816.2	0.99	0.00	0.00
					6	7%	32803.8	34444.9	33514.0	0.97	0.72	0.72
					7	7%	32003.1	33918.7	32832.1	0.99	0.84	0.84
					8	5%	31313.2	33503.1	32260.9	0.99	0.75	0.75
24	6	Skewed	Low	6	1	100%	8260.0	8293.6	8274.5	—	—	—
					2	7%	7337.0	7409.8	7368.5	0.97	0.00	0.00
					3	8%	7286.7	7398.8	7335.2	0.98	0.00	0.00
					4	4%	7276.5	7427.8	7342.0	0.99	0.00	0.00
					5	0%	7282.1	7472.5	7364.5	0.72	0.25	0.26
					6	0%	7288.3	7517.9	7387.7	0.98	0.03	0.03
					7	0%	7299.5	7568.3	7415.8	0.75	0.28	0.28
					8	0%	7311.6	7619.7	7444.9	0.76	0.11	0.11

Open in a new tab

Bolded Results Indicate Preferred Model

Appendix Table C4.

Fit Statistics for Optimal Matching Models

(FOR PEER REVIEW ONLY; TO BE AVAILABLE ON-LINE UPON PUBLICATION)

Data Set #	Simulation Parameters					Fit Statistics
	Simulation Parameters					Substitution Costs Based on Transition Rates, Ward Clustering		Substitution Costs Based on Transition Rates, K-Means Clustering		Substitution Costs Based on Constant Rates, Ward Clustering		Substitution Costs Based on Constant Rates, K-Means Clustering

	T	D	C	t	T′	F^a	Smallest Group	F^a	Smallest Group	F^a	Smallest Group	F^a	Smallest Group
1	2	Uniform	High	48	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	7833.1	49.9%	10863.1	49.9%	7243.7	49.9%	9852.5	49.9%
					3	5066.6	24.8%	7538.2	19.3%	4385.6	12.4%	6060.4	15.9%
					4	4576.2	21.3%	7420.2	19.3%	3610.6	11.8%	4825.6	15.4%
2	2	Uniform	High	6	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	1326.9	34.2%	1813.5	41.4%	1836.6	37.4%	1827.9	41.4%
					3	2493.5	27.9%	2445.6	32.6%	2432.4	9.5%	2620.4	32.7%
					4	3856.1	9.5%	2991.4	8.2%	4111.0	9.5%	3270.1	8.2%
					5	5612.4	8.0%	6462.3	8.2%	5727.0	8.0%	6136.4	8.2%
					6	6841.3	4.6%	10612.1	4.7%	6664.3	4.6%	10928.7	4.7%
					7	8182.3	0.8%	11496.7	0.7%	8283.0	0.8%	11759.7	0.7%
					8	10597.2	0.5%	13961.5	0.7%	10596.1	0.5%	14205.6	0.7%
3	2	Skewed	High	48	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	2689.7	10.0%	3991.1	10.1%	2537.9	10.0%	3883.5	10.0%
					3	2650.0	10.0%	3511.3	10.0%	2073.5	10.0%	2696.6	10.0%
					4	2419.4	10.0%	3148.2	10.0%	2040.5	10.0%	2175.9	10.0%
4	2	Skewed	High	6	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	1129.5	13.9%	2340.8	43.0%	1249.8	48.3%	2345.1	43.0%
					3	2275.0	13.9%	2491.4	14.2%	2411.6	13.9%	2416.0	14.3%
					4	3782.8	8.4%	3635.2	7.0%	3952.6	8.4%	3581.3	7.0%
					5	4536.7	6.4%	5540.0	6.5%	4666.8	6.4%	5712.6	6.5%
					6	5120.9	1.6%	7526.2	1.4%	5098.8	0.8%	7587.3	1.4%
					7	6271.8	0.8%	8213.8	0.8%	6504.5	0.8%	8242.1	0.8%
5	2	Uniform	Low	48	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	936.0	12.9%	1060.1	38.3%	1114.0	26.0%	847.1	48.6%
					3	1248.9	12.9%	948.9	28.6%	1256.2	23.8%	864.8	24.9%
					4	1219.3	12.9%	942.9	18.1%	1140.9	23.7%	885.7	17.5%
					5	1306.2	9.8%	---	---	1073.7	7.0%	739.1	14.9%
					6	1250.1	6.7%	---	---	---	---	677.6	12.7%
					7	1199.7	4.2%	---	---	---	---	---	---
6	2	Uniform	Low	6	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	1428.3	16.7%	1541.2	21.3%	1535.8	16.7%	1500.7	21.3%
					3	3201.7	16.7%	3289.0	15.0%	3033.9	16.7%	3370.6	15.0%
					4	4423.9	4.3%	4086.9	4.3%	4808.8	4.3%	3879.1	4.3%
					5	5632.4	2.9%	6484.9	2.9%	5976.9	2.9%	5713.0	2.9%
7	2	Skewed	Low	48	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	1460.0	31.5%	1154.8	35.7%	953.0	44.2%	809.6	45.8%
					3	1255.5	24.5%	1116.7	26.8%	1063.6	11.9%	781.4	23.4%
					4	1111.7	10.6%	869.5	18.0%	1000.2	11.9%	589.2	21.8%
					5	---	------	---	---	947.0	11.9%	---	---
8	2	Skewed	Low	6	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	1850.7	40.4%	2998.4	31.4%	1576.8	13.9%	2770.0	31.4%
					3	5131.4	13.9%	5728.8	14.5%	5064.2	13.9%	5466.3	14.5%
					4	6230.9	4.6%	8652.9	4.6%	5692.1	4.6%	8528.6	4.6%
					5	6615.9	1.0%	9210.4	1.0%	6573.4	1.0%	8634.5	1.0%
					6	7728.2	0.8%	11600.1	0.8%	8607.9	0.8%	9926.1	0.8%
9	4	Uniform	High	48	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	1627.0	47.6%	1610.2	31.2%	1753.9	49.7%	1460.2	30.3%
					3	2700.7	25.0%	2347.0	25.0%	3013.5	25.0%	2663.4	24.8%
					4	3233.3	22.4%	2716.9	23.2%	3495.0	23.1%	2806.7	22.9%
					5	2951.4	10.5%	2369.5	14.5%	2965.4	11.7%	2284.8	13.4%
					6	2785.1	10.5%	2217.0	9.3%	2666.1	10.7%	2068.8	8.5%
10	4	Uniform	High	6	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	1723.2	21.6%	2190.3	39.4%	1869.0	21.0%	2235.7	39.4%
					3	2855.1	21.6%	3449.3	21.3%	2758.3	21.0%	3505.2	21.3%
					4	3900.9	5.1%	3866.7	4.8%	4052.3	5.1%	4004.5	4.8%
					5	4998.9	4.7%	6770.4	4.8%	4998.3	4.7%	6776.9	4.8%
					6	5752.2	0.8%	9049.5	2.2%	5900.0	0.8%	9206.1	2.2%
					7	6960.3	0.6%	9310.1	0.4%	7238.6	0.6%	9334.0	0.4%
11	4	Skewed	High	48	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	2018.4	17.4%	2699.3	18.9%	1741.0	32.5%	1993.5	20.0%
					3	2217.7	17.4%	2413.9	18.0%	2483.9	15.1%	2412.6	17.5%
					4	2243.7	16.3%	2133.5	16.5%	2339.8	5.7%	2037.4	16.4%
					5	2373.2	5.5%	---	---	2339.5	5.7%	1948.8	15.4%
					6	2322.0	5.5%	---	---	---	---	---	---
					7	2242.0	5.5%	---	---	---	---	---	---
12	4	Skewed	High	6	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	1159.5	14.5%	2180.6	38.2%	1384.6	40.3%	2213.6	38.2%
					3	1761.2	14.5%	2543.9	14.6%	1818.0	9.6%	2575.7	14.6%
					4	4095.3	9.7%	4028.3	9.7%	4162.6	9.6%	3997.3	9.8%
					5	4235.9	4.4%	5225.0	4.6%	4235.9	4.4%	5150.9	4.6%
					6	4971.3	2.4%	8505.8	2.4%	4857.9	2.4%	8518.0	2.4%
					7	---	---	10274.1	0.7%	---	---	10337.4	0.7%
13	4	Uniform	Low	48	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	2089.2	39.3%	1846.9	49.8%	977.1	14.3%	1336.5	42.9%
					3	1746.5	18.3%	1878.2	20.3%	1264.7	14.3%	1490.6	19.9%
					4	1783.5	17.6%	1556.1	18.8%	1330.2	11.1%	1183.3	18.7%
					5	---	---	1603.4	15.7%	1426.2	11.1%	1116.5	15.9%
					6	---	---	---	---	1346.8	11.1%	---	---
					7	---	---	---	---	1343.4	11.1%	---	---
14	4	Uniform	Low	6	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	1522.8	43.3%	1494.1	32.7%	1869.3	31.7%	1399.7	32.7%
					3	1965.8	17.0%	1802.7	15.4%	2481.5	15.1%	1656.9	15.4%
					4	3467.4	15.3%	2394.2	11.6%	3227.7	11.9%	2349.9	11.6%
					5	3758.0	5.7%	3377.6	5.9%	3628.6	5.7%	3183.7	5.9%
					6	4993.3	3.2%	4338.6	3.8%	5156.9	3.2%	4339.8	3.8%
					7	7673.8	3.2%	7673.8	3.2%	7543.3	3.2%	7345.7	3.2%
15	4	Skewed	Low	48	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	1604.4	33.4%	1126.9	40.4%	1146.7	40.5%	961.8	39.3%
					3	1328.1	5.0%	1272.1	24.8%	1095.3	12.3%	839.6	18.5%
					4	1337.7	5.0%	884.0	23.7%	1155.2	5.5%	671.2	19.2%
					5	---	---	1130.5	5.9%	1114.2	5.5%	---	---
					6	---	---	---	---	1129.8	5.5%	---	---
16	4	Skewed	Low	6	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	1750.7	24.5%	1338.0	26.6%	1900.3	24.5%	1442.1	26.6%
					3	2831.9	19.8%	2426.3	21.1%	2508.6	19.5%	2521.5	21.1%
					4	3487.8	5.5%	2745.8	5.6%	3324.1	5.5%	2876.1	5.6%
					5	4716.7	5.4%	4179.1	4.0%	4064.7	5.4%	4021.6	4.0%
					6	5811.8	2.0%	6661.5	2.3%	4706.5	2.0%	5572.4	2.3%
					7	6825.4	1.5%	---	---	6426.8	0.7%	---	---
17	6	Uniform	High	48	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	6244.1	16.6%	8424.7	16.2%	4575.1	16.6%	6686.7	16.2%
					3	6067.5	16.6%	9226.6	16.0%	4142.5	16.6%	4749.2	15.5%
					4	5855.9	16.6%	7166.3	15.4%	4397.3	16.6%	5327.8	15.5%
					5	---	---	6588.5	15.4%	4843.2	16.6%	---	---
					6	---	---	---	---	4595.7	3.2%	---	---
					7	---	---	---	---	4643.9	3.2%	---	---
18	6	Uniform	High	6	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	3109.6	12.9%	4479.7	16.4%	2783.5	12.7%	631.4	40.6%
					3	3815.3	12.9%	5687.3	16.4%	3682.9	12.7%	4936.2	16.4%
					4	5261.3	12.9%	7427.3	15.4%	4419.7	12.7%	6462.8	15.4%
					5	6159.2	5.4%	7150.8	3.6%	4868.2	7.7%	6684.0	3.6%
					6	7081.5	2.8%	6981.1	1.9%	6016.1	2.8%	6563.1	2.0%
					7	8955.9	1.9%	---	---	8338.4	2.8%	---	---
19	6	Skewed	High	48	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	4312.8	7.5%	6602.1	7.5%	3073.1	7.5%	4829.9	7.5%
					3	5247.9	7.5%	8640.6	7.2%	3329.0	7.5%	5333.4	7.4%
					4	5163.6	7.5%	7344.5	7.2%	3659.5	7.5%	5203.8	7.2%
					5	5660.6	7.5%	6580.3	7.2%	4273.0	7.5%	4708.6	7.2%
					6	5310.0	7.5%	---	---	4042.7	7.5%	---	---
					7	5071.2	2.8%	---	---	3910.5	7.5%	---	---
20	6	Skewed	High	6	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	2135.4	7.6%	875.5	46.7%	1836.1	7.7%	981.6	46.7%
					3	2353.1	7.6%	2962.3	7.2%	2286.3	7.7%	2707.8	7.2%
					4	3530.8	7.6%	3911.0	7.2%	2927.7	7.7%	3609.8	7.2%
					5	6024.6	7.6%	5664.3	7.2%	5804.2	7.7%	4903.9	7.2%
					6	7042.7	4.0%	7627.7	4.1%	6507.8	4.0%	6682.3	4.1%
					7	8677.2	3.9%	10107.1	3.9%	7597.8	3.9%	9700.2	3.9%
21	6	Uniform	Low	48	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	4003.7	16.2%	4969.5	15.7%	3036.2	15.3%	4149.0	15.8%
					3	4158.3	16.2%	5651.4	15.5%	2996.6	15.3%	3951.7	15.6%
					4	4083.2	16.2%	4991.1	15.6%	2850.4	15.3%	3337.5	15.6%
					5	3727.9	7.8%	4343.7	11.1%	---	---	---	---
22	6	Uniform	Low	6	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	2460.5	18.5%	2578.7	15.1%	2277.2	18.6%	2187.0	15.1%
					3	2680.1	18.5%	2573.2	14.9%	2557.5	18.6%	2127.6	14.9%
					4	2809.9	13.9%	3052.0	14.9%	2805.8	11.2%	2551.8	14.9%
					5	3326.8	6.9%	3587.4	11.1%	3092.5	11.2%	2996.5	11.1%
					6	5039.2	6.9%	3882.8	3.9%	4152.1	7.5%	3132.7	3.9%
					7	5636.1	3.7%	4742.6	3.3%	4471.1	3.7%	3548.6	3.1%
					8	6338.1	3.1%	---	---	5127.2	3.7%	---	---
23	6	Skewed	Low	48	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	2897.7	7.1%	4331.0	7.1%	2207.7	7.1%	3474.4	7.2%
					3	3067.6	7.1%	3957.2	7.0%	2105.3	7.1%	2826.2	7.2%
					4	2972.4	7.1%	4303.1	7.0%	2038.8	7.1%	2474.4	7.0%
					5	2972.4	7.1%	3485.0	7.0%	---	---	---	---
					6	---	---	3106.4	7.0%	---	---	---	---
					7	---	---	3064.2	7.0%	---	---	---	---
24	6	Skewed	Low	6	1	---	100.0%	---	100.0%	---	100.0%	---	100.0%
					2	1678.5	6.8%	450.7	21.9%	1435.8	7.2%	480.5	21.9%
					3	2171.7	6.8%	1894.6	7.1%	1691.7	7.2%	503.3	16.5%
					4	3175.9	6.8%	2628.0	7.1%	2150.0	7.2%	2426.2	7.1%
					5	3631.4	6.8%	3347.7	7.1%	2988.9	7.2%	2874.2	6.4%
					6	3987.7	4.5%	4241.3	4.7%	3569.9	3.5%	3499.1	4.7%
					7	4735.8	3.4%	5425.4	3.3%	4111.4	3.5%	4217.7	2.4%
					8	5323.5	2.1%	6023.8	2.1%	---	---	5408.0	2.1%
					8	0.0				7018.3	7326.4 #	0.8	0.84

Open in a new tab

Bolded Results Indicate Preferred Model

^aCaliński-Harabasz (1974) pseudo F-statistic

Appendix Table C5.

Fit Statistics for Grade of Membership Analyses

(FOR PEER REVIEW ONLY; TO BE AVAILABLE ON-LINE UPON PUBLICATION)

Data Set #	Simulation Parameters					Fit Statistics
Data Set #	T	D	C	t	T′	LL = Log Likelihood	df	2 × Change in LL, Model w/T′ vs Model w/T′-1	Change in df, Model w/T′ vs Model w/T′-1	LR Test, Model w/T′ vs Model w/T′-1	t Test^a Model w/T′ vs Model w/T′-1
1	2	Uniform	High	48	1	−20,738	2,047	—	—	—	—
					2	−10,758	4,094	19,960.5	2,047	0.00	135.8
					3	−9,486	6,141	2,543.2	2,047	0.00	7.3
					4	−8,438	8,188	2,095.9	2,047	0.22	0.8
					5	−7,699	10,235	1,477.7	2,047	1.00	(9.6)
					6	−6,834	12,282	1,730.4	2,047	1.00	(5.2)
					7	−6,389	14,329	889.9	2,047	1.00	(21.8)
					8	−6,045	16,376	688.8	2,047	1.00	(26.9)
2	2	Uniform	High	6	1	−3,511	2,005	—	—	—	—
					2	−1,924	4,010	3,174.2	2,005	0.00	16.4
					3	−1,013	6,015	1,822.3	2,005	1.00	(3.0)
					4	−758	8,020	509.8	2,005	1.00	(31.4)
					5	−686	10,025	143.8	2,005	1.00	(46.4)
					6	−438	12,030	496.8	2,005	1.00	(31.8)
					7	−215	14,035	445.5	2,005	1.00	(33.5)
					8	−245	16,040	(59.6)	2,005	n/a^b	n/a^b
3	2	Skewed	High	48	1	−15,558	2,047	—	—	—	—
					2	−10,898	4,094	9,318.5	2,047	0.00	72.5
					3	−8,896	6,141	4,005.5	2,047	0.00	25.5
					4	−7,629	8,188	2,533.8	2,047	0.00	7.2
					5	−7,020	10,235	1,217.4	2,047	1.00	(14.6)
					6	−6,361	12,282	1,317.1	2,047	1.00	(12.7)
					7	−5,961	14,329	801.0	2,047	1.00	(24.0)
					8	−5,671	16,376	580.8	2,047	1.00	(29.9)
4	2	Skewed	High	6	1	−3,035	2,005	—	—	—	—
					2	−2,330	4,010	1,408.9	2,005	1.00	(10.2)
					3	−937	6,015	2,787.7	2,005	0.00	11.3
					4	−501	8,020	871.0	2,005	1.00	(21.6)
					5	−405	10,025	192.4	2,005	1.00	(43.7)
					6	−187	12,030	436.3	2,005	1.00	(33.8)
					7	−121	14,035	131.8	2,005	1.00	(47.1)
					8	−78	16,040	86.0	2,005	1.00	(50.2)
5	2	Uniform	Low	48	1	−19,904	2,047	—	—	—	—
					2	−14,596	4,094	10,616.5	2,047	0.00	81.7
					3	−12,049	6,141	5,094.1	2,047	0.00	37.0
					4	−10,532	8,188	3,034.1	2,047	0.00	13.9
					5	−9,602	10,235	1,859.9	2,047	1.00	(3.0)
					6	−8,701	12,282	1,802.9	2,047	1.00	(3.9)
					7	−8,195	14,329	1,010.4	2,047	1.00	(19.0)
					8	−7,636	16,376	1,119.0	2,047	1.00	(16.7)
6	2	Uniform	Low	6	1	−2,572	2,005	—	—	—	—
					2	−1,499	4,010	2,145.3	2,005	0.01	2.2
					3	−1,164	6,015	669.9	2,005	1.00	(26.7)
					4	−347	8,020	1,634.5	2,005	1.00	(6.2)
					5	−520	10,025	(346.0)	2,005	n/a^b	n/a^b
					6	−226	12,030	588.2	2,005	1.00	(29.0)
					7	−132	14,035	188.1	2,005	1.00	(43.9)
					8	−129	16,040	5.5	2,005	1.00	(60.1)
7	2	Skewed	Low	48	1	−16,745	2,047	—	—	—	—
					2	−12,641	4,094	8,209.5	2,047	0.00	64.2
					3	−10,511	6,141	4,260.2	2,047	0.00	28.3
					4	−9,170	8,188	2,680.4	2,047	0.00	9.2
					5	−8,127	10,235	2,087.4	2,047	0.26	0.6
					6	−7,566	12,282	1,121.3	2,047	1.00	(16.6)
					7	−7,096	14,329	940.8	2,047	1.00	(20.6)
					8	−6,763	16,376	665.0	2,047	1.00	(27.5)
8	2	Skewed	Low	6	1	−2,397	2,005	—	—	—	—
					2	−1,140	4,010	2,514.6	2,005	0.00	7.6
					3	−415	6,015	1,450.1	2,005	1.00	(9.5)
					4	−339	8,020	152.0	2,005	1.00	(45.9)
					5	−271	10,025	135.3	2,005	1.00	(46.9)
					6	−152	12,030	237.3	2,005	1.00	(41.6)
					7	−88	14,035	128.2	2,005	1.00	(47.3)
					8	−150	16,040	(122.7)	2,005	n/a^b	n/a^b
9	4	Uniform	High	48	1	−24,831	2,047	—	—	—	—
					2	−16,600	4,094	16,462.1	2,047	0.00	117.5
					3	−11,727	6,141	9,746.4	2,047	0.00	75.6
					4	−9,478	8,188	4,498.8	2,047	0.00	30.9
					5	−8,858	10,235	1,239.0	2,047	1.00	(14.2)
					6	−8,280	12,282	1,157.0	2,047	1.00	(15.9)
					7	−7,781	14,329	996.7	2,047	1.00	(19.3)
					8	−7,304	16,376	954.5	2,047	1.00	(20.3)
10	4	Uniform	High	6	1	−3,023	2,005	—	—	—	—
					2	−1,921	4,010	2,203.9	2,005	0.00	3.1
					3	−747	6,015	2,347.6	2,005	0.00	5.2
					4	−578	8,020	339.2	2,005	1.00	(37.3)
					5	−346	10,025	463.0	2,005	1.00	(32.9)
					6	−545	12,030	(396.4)	2,005	n/a^b	n/a^b
					7	−122	14,035	845.5	2,005	1.00	(22.2)
					8	−223	16,040	(203.2)	2,005	n/a^b	n/a^b
11	4	Skewed	High	48	1	−21,221	2,047	—	—	—	—
					2	−14,183	4,094	14,076.3	2,047	0.00	103.8
					3	−10,948	6,141	6,470.5	2,047	0.00	49.8
					4	−9,161	8,188	3,573.6	2,047	0.00	20.6
					5	−8,351	10,235	1,620.7	2,047	1.00	(7.1)
					6	−7,500	12,282	1,700.4	2,047	1.00	(5.7)
					7	−7,125	14,329	750.6	2,047	1.00	(25.2)
					8	−6,699	16,376	852.7	2,047	1.00	(22.7)
12	4	Skewed	High	6	1	−3,042	2,005	—	—	—	—
					2	−1,576	4,010	2,932.1	2,005	0.00	13.3
					3	−894	6,015	1,365.4	2,005	1.00	(11.1)
					4	−976	8,020	(164.6)	2,005	n/a^b	n/a^b
					5	−319	10,025	1,314.5	2,005	1.00	(12.1)
					6	−291	12,030	54.6	2,005	1.00	(52.9)
					7	−736	14,035	(888.9)	2,005	n/a^b	n/a^b
					8	−235	16,040	1,001.6	2,005	1.00	(18.6)
13	4	Uniform	Low	48	1	−26,737	2,047	—	—	—	—
					2	−18,689	4,094	16,095.5	2,047	0.00	115.4
					3	−15,374	6,141	6,630.4	2,047	0.00	51.2
					4	−12,750	8,188	5,247.1	2,047	0.00	38.5
					5	−11,521	10,235	2,457.6	2,047	0.00	6.1
					6	−10,705	12,282	1,633.1	2,047	1.00	(6.8)
					7	−9,949	14,329	1,510.6	2,047	1.00	(9.0)
					8	−9,194	16,376	1,511.1	2,047	1.00	(9.0)
14	4	Uniform	Low	6	1	−3,611	2,005	—	—	—	—
					2	−2,213	4,010	2,795.8	2,005	0.00	11.5
					3	−1,930	6,015	566.0	2,005	1.00	(29.7)
					4	−677	8,020	2,504.8	2,005	0.00	7.5
					5	−455	10,025	445.4	2,005	1.00	(33.5)
					6	−348	12,030	213.4	2,005	1.00	(42.7)
					7	−268	14,035	160.3	2,005	1.00	(45.4)
					8	−323	16,040	(109.5)	2,005	n/a^b	n/a^b
15	4	Skewed	Low	48	1	−22,313	2,047	—	—	—	—
					2	−16,269	4,094	12,087.8	2,047	0.00	91.5
					3	−13,910	6,141	4,718.5	2,047	0.00	33.2
					4	−11,396	8,188	5,028.0	2,047	0.00	36.3
					5	−10,059	10,235	2,674.1	2,047	0.00	9.1
					6	−9,184	12,282	1,749.7	2,047	1.00	(4.8)
					7	−8,438	14,329	1,491.1	2,047	1.00	(9.4)
					8	−8,039	16,376	797.9	2,047	1.00	(24.0)
16	4	Skewed	Low	6	1	−3,082	2,005	—	—	—	—
					2	−1,907	4,010	2,350.8	2,005	0.00	5.2
					3	−1,645	6,015	523.8	2,005	1.00	(31.0)
					4	−535	8,020	2,219.6	2,005	0.00	3.3
					5	−627	10,025	(184.8)	2,005	n/a^b	n/a^b
					6	−279	12,030	697.7	2,005	1.00	(26.0)
					7	−226	14,035	104.8	2,005	1.00	(48.9)
					8	−224	16,040	4.1	2,005	1.00	(60.6)
17	6	Uniform	High	48	1	−38,476	2,047	—	—	—	—
					2	−22,091	4,094	32,771.7	2,047	0.00	192.0
					3	−16,186	6,141	11,808.7	2,047	0.00	89.7
					4	−12,512	8,188	7,349.5	2,047	0.00	57.3
					5	−9,861	10,235	5,301.4	2,047	0.00	39.0
					6	−9,075	12,282	1,572.4	2,047	1.00	(7.9)
					7	−8,574	14,329	1,000.7	2,047	1.00	(19.3)
					8	−8,287	16,376	574.8	2,047	1.00	(30.1)
18	6	Uniform	High	6	1	−4,568	2,005	—	—	—	—
					2	−2,368	4,010	4,401.6	2,005	0.00	30.5
					3	−1,370	6,015	1,995.2	2,005	0.56	(0.2)
					4	−604	8,020	1,532.9	2,005	1.00	(8.0)
					5	−396	10,025	415.9	2,005	1.00	(34.5)
					6	−364	12,030	63.7	2,005	1.00	(52.1)
					7	−272	14,035	184.5	2,005	1.00	(44.1)
					8	−252	16,040	40.0	2,005	1.00	(54.4)
19	6	Skewed	High	48	1	−31,335	2,047	—	—	—	—
					2	−20,658	4,094	21,355.0	2,047	0.00	142.7
					3	−14,534	6,141	12,246.8	2,047	0.00	92.5
					4	−11,315	8,188	6,438.0	2,047	0.00	49.5
					5	−9,265	10,235	4,100.5	2,047	0.00	26.6
					6	−8,460	12,282	1,610.0	2,047	1.00	(7.2)
					7	−8,058	14,329	803.6	2,047	1.00	(23.9)
					8	−7,321	16,376	1,474.7	2,047	1.00	(9.7)
20	6	Skewed	High	6	1	−4,135	2,005	—	—	—	—
					2	−2,691	4,010	2,887.3	2,005	0.00	12.7
					3	−1,894	6,015	1,594.4	2,005	1.00	(6.9)
					4	−812	8,020	2,163.5	2,005	0.01	2.5
					5	−404	10,025	815.4	2,005	1.00	(22.9)
					6	−678	12,030	(547.1)	2,005	n/a^b	n/a^b
					7	−141	14,035	1,073.2	2,005	1.00	(17.0)
					8	−227	16,040	(171.3)	2,005	n/a^b	n/a^b
21	6	Uniform	Low	48	1	−38,499	2,047	—	—	—	—
					2	−24,205	4,094	28,586.8	2,047	0.00	175.1
					3	−17,713	6,141	12,984.7	2,047	0.00	97.2
					4	−15,299	8,188	4,828.1	2,047	0.00	34.3
					5	−13,290	10,235	4,017.6	2,047	0.00	25.7
					6	−12,502	12,282	1,575.5	2,047	1.00	(7.9)
					7	−11,644	14,329	1,717.0	2,047	1.00	(5.4)
					8	−10,866	16,376	1,555.4	2,047	1.00	(8.2)
22	6	Uniform	Low	6	1	−4,905	2,005	—	—	—	—
					2	−2,824	4,010	4,160.8	2,005	0.00	27.9
					3	−2,088	6,015	1,473.1	2,005	1.00	(9.0)
					4	−1,333	8,020	1,510.5	2,005	1.00	(8.4)
					5	−1,112	10,025	441.4	2,005	1.00	(33.6)
					6	−933	12,030	358.4	2,005	1.00	(36.6)
					7	−846	14,035	173.3	2,005	1.00	(44.7)
					8	−842	16,040	8.5	2,005	1.00	(59.3)
23	6	Skewed	Low	48	1	−30,990	2,047	—	—	—	—
					2	−21,065	4,094	19,850.4	2,047	0.00	135.3
					3	−16,075	6,141	9,978.8	2,047	0.00	77.3
					4	−14,002	8,188	4,147.1	2,047	0.00	27.1
					5	−11,903	10,235	4,198.0	2,047	0.00	27.6
					6	−10,767	12,282	2,270.5	2,047	0.00	3.4
					7	−10,142	14,329	1,250.0	2,047	1.00	(14.0)
					8	−9,323	16,376	1,639.6	2,047	1.00	(6.7)
24	6	Skewed	Low	6	1	−4,124	2,005	—	—	—	—
					2	−2,645	4,010	2,958.4	2,005	0.00	13.6
					3	−2,263	6,015	762.9	2,005	1.00	(24.3)
					4	−1,510	8,020	1,506.3	2,005	1.00	(8.4)
					5	−733	10,025	1,554.2	2,005	1.00	(7.6)
					6	−611	12,030	243.8	2,005	1.00	(41.3)
					7	−323	14,035	577.5	2,005	1.00	(29.3)
					8	−304	16,040	36.6	2,005	1.00	(54.8)

Open in a new tab

Bolded Results Indicate Preferred Model

t-test as per Manton, Woodbury, and Tolley (1994: 173)

Test cannot be performed.

Footnotes

Following Elder, Johnson, and Crosnoe (2003), we define trajectories as time-ordered sequences of states or roles. In social science research, time is typically age or calendar year; depending on the unit of observation, states usually describe the conditions of people (e.g., married, HIV positive, college graduate), countries (e.g., independent, in recession), or other units. In most social science applications, researchers are interested in the timing and frequency of transitions between states or roles. Trajectories are thus defined by the states of which they are comprised and the time-ordered transitions between them.

GBTMs are sometimes referred to as latent class growth models (e.g., Muthén 2004). For the purposes of this article, we use the acronym GBTM to prevent any confusion with LCA.

Posterior probabilities are used for assignment purposes. These probabilities provide the likelihood that an individual belongs to a particular class given their observed sequence of measurements.

⁴

We have simulated the data in such a way that at least ten women are employed and at least ten are not employed at every age. Using some of our methods, models could not be estimated when all individuals were in the same state (e.g., not employed) at specific ages (e.g., 16).

⁵

For the GBTMs and GMMs, we used intercept, slope, and quadratic growth factors to model the shape of each latent trajectory. To reduce computational burden and to speed up the estimation process, we allowed for residual variation within classes in the GMM analysis (on the intercept and slope terms), but we did not allow the variance to vary between classes. This strategy is fairly common in the empirical literature (e.g., Cheadle, Amato and King 2010).

⁶

Technical descriptions of these model fit statistics and their relative performance in finite mixture modeling settings can be found in Nylund et al. (2007). Note that we did not examine McLachlan and Peel’s (2000) parametric bootstrapped likelihood-ratio test—which has been shown to perform well in simulation studies—because it was too computationally demanding and because the volume of models being fitted (24 simulated data sets × 8 model specifications = 192 models per estimator) was too large.

⁷

If the best log-likelihood was not replicated, we increased the number of start values to 1000 and the number of second-stage optimizations to 250, and then re-estimated the model.

⁸

We also experimented with three other combinations of substitution costs (e.g., transition rates and a constant rate) and clustering methods (e.g., the Ward method and K-means), and the results are available upon request. Although model selection decisions vary somewhat depending on these combinations of methods, answers to our research questions remain unchanged.

⁹

That F-statistic is calculated as (SS_b/(k−1))/(SSw/(n−k)), where SS_b is the between-cluster sum of squares, SSw is the within-cluster sum of squares, k is the number of clusters, and n is the number of observations. Higher values of this measure correspond to improved model fit.

¹⁰

Separately for each data set, for two strategies for setting substitution costs, and for two methods of clustering, Appendix Table C4 reports Caliński-Harabasz (1974) pseudo F-statistics and the size of the smallest trajectory group for models with 2, 3, … 8 trajectory groups. We use boldface type to indicate our preferred model.

Earlier versions of this paper were presented at the annual meetings of the Population Association of America (May 2012, San Francisco) and at the annual meetings of the American Sociological Association (August 2012, Denver).

Contributor Information

John R. Warren, Minnesota Population Center, Department of Sociology, University of Minnesota

Liying Luo, Minnesota Population Center, Department of Sociology, University of Minnesota.

Andrew Halpern-Manners, Department of Sociology, Indiana University.

James M. Raymo, Department of Sociology, University of Wisconsin-Madison

Alberto Palloni, Department of Sociology, University of Wisconsin-Madison.

References

Aassve Arnstein, Billari Francesco, Piccarretta Raffaella. Strings of Adulthood: A Sequence Analysis of Young British Women’s Work-Family Trajectories. European Journal of Population. 2007;23:369–88. [Google Scholar]
Abbott Andrew. Sequences of Social Events: Concepts and Methods for the Analysis of Order in Social Processes. Historical methods. 1983;16(4):129–47. [Google Scholar]
Abbott Andrew. Sequence Analysis: New Methods for Old Ideas. ANnual Review of Sociology. 1995;21:93–113. [Google Scholar]
Abbott Andrew, Forrest John. Optimal Matching Methods for Historical Sequences. The Journal of Interdisciplinary History. 1986;16(3):471–94. [Google Scholar]
Abbott Andrew, Hrycak Alexandra. Measuring Resemblance in Sequence Data: An Optimal Matching Analysis of Musicians’ Careers. American Journal of Sociology. 1990;96(1):144–85. [Google Scholar]
Abbott Andrew, Tsay Angela. Sequence Analysis and Optimal Matching Methods in Sociology: Review and Prospect. Sociological Methods & Research. 2000;29(1):3–33. [Google Scholar]
Andreotti Alessandra, Minicuci Nadia, Kowal Paul, Chatterji Somnath. Multidimensional Profiles of Health Status: An Application of the Grade of Membership Model to the World Health Survey. PloS one. 2009;4(2):e4426. doi: 10.1371/journal.pone.0004426. [DOI] [PMC free article] [PubMed] [Google Scholar]
Anyadike-Danes M, McVicar D. My Brilliant Career: Characterizing the Early Labor Market Trajectories of British Women From Generation X. Sociological Methods & Research. 2010;38(3):482–512. [Google Scholar]
Barban Nicola, Billari Francesco C. Classifying Life Course Trajectories: A Comparison of Latent Class and Sequence Analysis. Journal of the Royal Statistical Society: Series C (Applied Statistics) 2012;61(5):765–84. [Google Scholar]
Bauer Daniel J, Curran Patrick J. Distributional Assumptions of Growth Mixture Models: Implications for Overextraction of Latent Trajectory Classes. Psychological Methods. 2003;8(3):338–63. doi: 10.1037/1082-989X.8.3.338. [DOI] [PubMed] [Google Scholar]
Berkman Lisa, Singer Burton, Manton Kenneth. Black/White Differences in Health Status and Mortality Among the Elderly. Demography. 1989;26(4):661–78. [PubMed] [Google Scholar]
Besemer Sytske, Farrington David P. Intergenerational Transmission of Criminal Behaviour: Conviction Trajectories of Fathers and their Children. European Journal of Criminology. 2012;9(2):120–41. [Google Scholar]
Biemann Torsten, Fasang Anette Eva, Grunow Daniela. Do Economic Globalization and Industry Growth Destabilize Careers? An Analysis of Career Complexity and Career Patterns Over Time. Organization Studies. 2011;32(12):1639–63. [Google Scholar]
Biemann Torsten, Wolf Joachim. Career Patterns of Top Management Team Members in Five Countries: An Optimal Matching Analysis. The International Journal of Human Resource Management. 2009;20(5):975–91. [Google Scholar]
Bollen Kenneth A, Curran Patrick J. Curve Models: A Structural Equation Perspective. Hoboken, NJ: John Wiley and Sons; 2006a. [Google Scholar]
Bollen Kenneth A, Curran Patrick J. Latent Curve Models: A Structural Equation Perspective. New Jersey: John Wiley & Sons; 2006b. [Google Scholar]
Bryk Anthony S, Raudenbush Stephen W. Application of Hierarchical Linear Models to Assessing Change. Psychological Bulletin. 1987;101(1):147–58. [Google Scholar]
Caliński RB, Harabasz J. A Dendrite Method for Cluster Analysis. Communications in Statistics. 1974;3(1):1–27. [Google Scholar]
Cassidy Frederick, Pieper Carl F, Carroll Bernard J. Subtypes of Mania Determined by Grade of Membership Analysis. Neuropsychopharmacology. 2001;25(3):373–83. doi: 10.1016/S0893-133X(01)00223-8. [DOI] [PubMed] [Google Scholar]
Chan Tak Wing. Optimal Matching Analysis: A Methodological Note on Studying Career Mobility. Work and Occupations. 1995;22(4):467–90. [Google Scholar]
Charpentier Peter. GOM3 (Version 3.4): Freeware. 1996 Available online at http://lib.stat.cmu.edu/DOS/general/.index.html.
Cheadle Jacob, Amato Paul R, King Valerie. Patterns of Nonresident Father Contact. Demography. 2010;47(1):205–25. doi: 10.1353/dem.0.0084. [DOI] [PMC free article] [PubMed] [Google Scholar]
Clogg Clifford C. Latent Class Models. In: Arminger Gerhard, Clogg Clifford C, Sobel Michael E., editors. Handbook of Statistical Modeling for the Social and Behavioral Sciences. New York: Plenum Press; 1995. pp. 311–59. [Google Scholar]
Collins Linda M, Lanza Stephanie T. Latent class and latent transition analysis : with applications in the social behavioral, and health sciences. Hoboken, N.J: Wiley; 2010. [Google Scholar]
D’Unger Amy V, Land Kenneth C, McCall Patricia L, Nagin Daniel S. How Many Latent Classes of Delinquent/Criminal Careers? Results from Mixed Poisson Regression Analyses. American Journal of Sociology. 1998;103:1593–630. [Google Scholar]
Duncan Terry E, Duncan Susan C, Strycker Lisa A. An Introduction to Latent Variable Growth Curve Modeling: Concepts, Issues, and Applications. Mahwah, NJ: Lawrence Earlbaum Associates, Inc; 2006. [Google Scholar]
Elder Glen H, Jr, Johnson Monica Kirkpatrick, Crosnoe Robert. The Emergence and Development of Life Course Theory. In: Mortimer Jeylan T, Shanahan Michael J., editors. Handbook of the Life Course. New York: Springer; 2003. pp. 3–19. [Google Scholar]
Erosheva E. Comparing latent structures of the Grade of Membership, Rasch, and latent class models. Psychometrika. 2005;70(4):619–28. [Google Scholar]
Farrington David P. Cambridge Study in Delinquent Development [Great Britain], 1961–1981. Ann Arbor, MI: Inter-University Consortium for Political and Social Research; 1999. ICPSR 8488. [Google Scholar]
Frech Adrianne, Damaske Sarah. The Relationships between Mothers’ Work Pathways and Physical and Mental Health. Journal of Health and Social Behavior. 2012;53(4):396–412. doi: 10.1177/0022146512453929. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gabadinho Alexis, Ritschard Gilbert, Müller Nicolas S, Studer Matthias. Analyzing and Visualizing State Sequences in R with TraMineR. Journal of Statistical Software. 2011;40(4) [Google Scholar]
Gauthier JA, Widmer ED, Bucher P, Notredame C. Multichannel Sequence Analysis Applied to Social Science Data. Sociological Methodology, Vol 40. 2010;40:1–38. [Google Scholar]
Gibbons Frederick X, O’Hara Ross E, Stock Michelle L, Gerrard Meg, Weng Chih-Yuan, Wills Thomas A. The Erosive Effects of Racism: Reduced Self-Control Mediates the Relation Between Perceived Racial Discrimination and Substance Use in African American Adolescents. Journal of Personality and Social Psychology. 2012;102:1089–104. doi: 10.1037/a0027404. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gill Thomas M, Gahbauer Evelyne A, Han Ling, Allore Heather G. Trajectories of Disability in the Last Year of Life. New England Journal of Medicine. 2010;362(13):1173–80. doi: 10.1056/NEJMoa0909087. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gustafsson Per E, Janlert Urban, Theorell Töres, Hammarström Anne. Life-course Socioeconomic Trajectories and Diurnal Cortisol Regulation in Adulthood. Psychoneuroendocrinology. 2010;35(4):613–23. doi: 10.1016/j.psyneuen.2009.09.019. [DOI] [PubMed] [Google Scholar]
Halpern-Manners Andrew, Warren John Robert, Brand Jennie E. Dynamic Measures of Primary and Secondary School Characteristics: Implications for School Effects Research. Social Science Research. 2009;38(2):397–411. [Google Scholar]
Halpin Brendan, Chan Tak Wing. Class Careers as Sequences. European Sociological Review. 1998;14:111–30. [Google Scholar]
Han Shin-Kap, Moen Phyllis. Clocking Out: Temporal Patterning of Retirement. American Journal of Sociology. 1999;105(1):191–236. [Google Scholar]
Henselmans Inge, Helgeson Vicki S, Seltman Howard, de Vries Jakob, Sanderman Robbert, Ranchor Adelita V. Identification and Prediction of Distress Trajectories in the First Year After a Breast Cancer Diagnosis. Health Psychology. 2010;29(2):160–68. doi: 10.1037/a0017806. [DOI] [PubMed] [Google Scholar]
Hicks Brian M, Iacono William G, McGue Matt. Consequences of an Adolescent Onset and Persistent Course of Alcohol Dependence in Men: Adolescent Risk Factors and Adult Outcomes. Alcoholism: Clinical and Experimental Research. 2010;34(5):819–33. doi: 10.1111/j.1530-0277.2010.01154.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hipp John R, Bauer Daniel J. Local Solutions in the Estimation of Growth Mixture Models. Psychological Methods. 2006;11:36–53. doi: 10.1037/1082-989X.11.1.36. [DOI] [PubMed] [Google Scholar]
Hunter Laura A, Leahey Erin. Parenting and Research Productivity: New Evidence and Methods. Social Studies of Science. 2010;40(3):433–51. [Google Scholar]
Jones Bobby L, Nagin Daniel S. Advances in Group-Based Trajectory Modeling and an SAS Procedure for Estimating Them. Sociological Methods & Research. 2007;35(4):542–70. [Google Scholar]
Judge Timothy A, Cable Daniel M. When it Comes to Pay, Do the Thin Win? The Effect of Weight on Pay for Men and Women. Journal of Applied Psychology. 2011;96(1):95–112. doi: 10.1037/a0020860. [DOI] [PubMed] [Google Scholar]
Jung Tony, Wickrama KAS. An Introduction to Latent Class Growth Analysis and Growth Mixture Modeling. Social and Personality Psychology Compass. 2007;2(1):302–17. [Google Scholar]
Kreuter Frauke, Muthén Bengt. General Growth Mixture Analysis with Antecedents and Consequences of Change. Journal of Quantitative Criminology. 2008;24(1):1–31. [Google Scholar]
Lesnard Laurent. Off-Scheduling within Dual-Earner Couples: An Unequal and Negative Externality for Family Time. American Journal of Sociology. 2008;114(2):447–90. [Google Scholar]
Lesnard Laurent. Setting Cost in Optimal Matching to Uncover Contemporaneous Socio-Temporal Patterns. Sociological Methods & Research. 2010;38(3):389–419. [Google Scholar]
MacCallum Robert C, Austin James T. Applications of Structural Equation Modeling in Psychological Research. Annual Review of Psychology. 2000;51(1):201–26. doi: 10.1146/annurev.psych.51.1.201. [DOI] [PubMed] [Google Scholar]
Macmillan Ross, Eliason Scott R. Characterizing the Life Course as Role Configurations and Pathways: A Latent Structure Approach. In: Mortimer Jeylan T, Shanahan Michael J., editors. Handbook of the Life Course. New York: Kluwer Academic/Plenum; 2003. pp. 529–54. [Google Scholar]
Manton Kenneth G, Stallard Eric, Woodbury MA, Tolley HD. Grade-of-Membership Techniques for Studying Complex Event History Processes with Unobserved Covariates. Sociological Methodology 1987. 1987;17:309–46. [Google Scholar]
Manton Kenneth G, Woodbury Max A, Stallard Eric, Corder Larry S. The Use of Grade-of-Membership Techniques to Estimate Regression Relationships. Sociological Methodology. 1992;22:321–81. [Google Scholar]
Manton Kenneth, Woodbury MA, Tolley HD. Statistical Applications Using Fuzzy Sets. New York: John Wiley & Sons; 1994. [Google Scholar]
Marcell Arik V, Eftim Sorina E, Sonenstein Freya L, Pleck Joseph H. Associations of Family and Peer Experiences with Masculinity Attitude Trajectories at the Individual and Group Level in Adolescent and Young Adult Males. Men and Masculinities. 2011;14(5):565–87. doi: 10.1177/1097184X11409363. [DOI] [PMC free article] [PubMed] [Google Scholar]
McArdle JJ, Epstein David. Latent Growth Curves within Developmental Structural Equation Models. Child Development. 1987;58(1):110–33. [PubMed] [Google Scholar]
McLachlan Geoffrey, Peel David. Finite Mixture Models. New York: John Wiley & Sons; 2000. [Google Scholar]
McLeod Jane D, Fettes Danielle L. Trajectories of Failure: The Educational Careers of Children with Mental Health Problems. American Journal of Sociology. 2007;113(3):653–701. doi: 10.1086/521849. [DOI] [PMC free article] [PubMed] [Google Scholar]
Miller Shari, Malone Patrick S, Dodge Kenneth A. Developmental Trajectories of Boys’ and Girls’ Delinquency: Sex Differences and Links to Later Adolescent Outcomes. Journal of Abnormal Child Psychology. 2010;38(7):1021–32. doi: 10.1007/s10802-010-9430-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
Milligan GW. An Examination of the Effect of 6 Types of Error Perturbation on 15 Clustering Algorithms. Psychometrika. 1980;45(3):325–42. [Google Scholar]
Moffitt Terrie E. Adolescence-Limited and Life-Course-Persistent Antisocial Behavior: A Developmental Taxonomy. Psychological Review. 1993;100(4):674–701. [PubMed] [Google Scholar]
Moody James, Brynildsen Wendy D, Wayne Osgood D, Feinberg Mark E, Gest Scott. Popularity Trajectories and Substance Use in Early Adolescence. Social Networks. 2011;33(2):101–12. doi: 10.1016/j.socnet.2010.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
Müller Nicolas S, Sapin Marlène, Jacques-Antoine Gauthier, Orita Alina, Widmer Eric D. Pluralized Life Courses? An Exploration of the Life Trajectories of Individuals with Psychiatric Disorders. International Journal of Social Psychiatry. 2011;58(3):266–77. doi: 10.1177/0020764010393630. [DOI] [PubMed] [Google Scholar]
Mustillo Sarah A, Hendrix Kimber L, Schafer Markus H. Trajectories of Body Mass and Self-Concept in Black and White Girls: The Lingering Effects of Stigma. Journal of Health and Social Behavior. 2012;53(1):2–16. doi: 10.1177/0022146511419205. [DOI] [PubMed] [Google Scholar]
Muthén Bengt. Latent Variable Analysis: Growth Mixture Modeling and Related Techniques for Longitudinal Data. In: Kaplan David., editor. The Sage Handbook of Quantitative Methodology for the Social Sciences. Newbury Park, CA: Sage; 2004. pp. 345–68. [Google Scholar]
Muthén Bengt, Shedden Kerby. Finite Mixture Modeling with Mixture Outcomes Using the EM Algorithm. Biometrics. 1999;55(2):463–69. doi: 10.1111/j.0006-341x.1999.00463.x. [DOI] [PubMed] [Google Scholar]
Muthén Linda, Muthén Bengt. Mplus User’s Guide. Los Angeles: Muthén and Muthén; 2010. [Google Scholar]
Nagin Daniel S. Analyzing Developmental Trajectories: A Semiparametric, Group-Based Approach. Psychological Methods. 1999;4:139–57. doi: 10.1037/1082-989x.6.1.18. [DOI] [PubMed] [Google Scholar]
Nagin Daniel S. Group-Based Modeling of Development. Cambridge: Harvard University Press; 2005. [Google Scholar]
Nagin Daniel S, Farrington David P, Moffitt Terrie E. Life-Course Trajectories Of Different Types Of Offenders. Criminology. 1995;33(1):111–39. [Google Scholar]
Nagin Daniel S, Land Kenneth C. Age, Criminal Careers, and Population Heterogeneity: Specification and Estimation of a Nonparametric, Mixed Poisson model. Criminology. 1993;31:327–62. [Google Scholar]
Nagin Daniel S, Tremblay Richard E. Developmental Trajectory Groups: Fact or Useful Statistical Fiction? Criminology. 2005;43(4):873–904. [Google Scholar]
Nylund Karen L, Asparouhov Tihomir, Muthén Bengt. Deciding on the Number of Classes in Latent Class Analysis and Growth Mixture Modeling: A Monte Carlo Simulation Study. Structural Equation Modeling. 2007;14(4):535–69. [Google Scholar]
Petts Richard J. Family and Religious Characteristics’ Influence on Delinquency Trajectories from Adolescence to Young Adulthood. American Sociological Review. 2009;74(3):465–83. [Google Scholar]
Pianta Robert C, Belsky Jay, Vandergrift Nathan, Houts Renate, Morrison Fred J. Classroom Effects on Children’s Achievement Trajectories in Elementary School. American Educational Research Journal. 2009;45(2):365–97. [Google Scholar]
Piquero Alex R, Farrington David P, Nagin Daniel S, Moffitt Terrie E. Trajectories of Offending and Their Relation to Life Failure in Late Middle Age: Findings from the Cambridge Study in Delinquent Development. Journal of Research in Crime and Delinquency. 2010;47(2):151–73. [Google Scholar]
Portrait France, Lindeboom Maarten, Deeg Dorly. Health and Mortality of the Elderly: The Grade of Membership Method, Classification and Determination. Health Economics. 1999;8(5):441–58. doi: 10.1002/(sici)1099-1050(199908)8:5<441::aid-hec452>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
Rand William M. Objective Criteria for the Evaluation of Clustering Methods. Journal of the American Statistical Association. 1971;66(336):846–50. [Google Scholar]
Rindfuss Ronald R, Choe Minja Kim, Kabamalan Maria Midea M, Tsuya Noriko O, Bumpass Larry L. Order Amidst Change: Work and Family Trajectories in Japan. Advances in Life Course Research. 2010;15(2–3):76–88. doi: 10.1016/j.alcr.2010.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
Rippeyoung Phyllis LF, Noonan Mary C. Is Breastfeeding Truly Cost Free? Income Consequences of Breastfeeding for Women. American Sociological Review. 2012;77(2):244–67. [Google Scholar]
Robette Nicolas, Bry Xavier. Harpoon or Bait? A Comparison of Various Metrics in Fishing for Sequence Patterns. Bulletin of Sociological Methodology. 2012;116(1):5–24. [Google Scholar]
Stallard Eric, Kinosian Bruce, Zbrozek Arthur S, Yashin Anatoliy I, Glick Henry A, Stern Yaakov. Estimation and Validation of a Multiattribute Model of Alzheimer Disease Progression. Medical Decision Making. 2010;30(6):625–38. doi: 10.1177/0272989X10363479. [DOI] [PMC free article] [PubMed] [Google Scholar]
Stovel Katherine, Savage Michael, Bearman Peter. Ascription Into Achievement. American Journal of Sociology. 1996;102:358–99. [Google Scholar]
Thomas Patricia A. Trajectories of Social Engagement and Limitations in Late Life. Journal of Health and Social Behavior. 2011;52(4):430–43. doi: 10.1177/0022146511411922. [DOI] [PubMed] [Google Scholar]
Wagmiller Robert L, Lennon Mary Clare, Kuang Li, Alberti Philip M, Lawrence Aber J. The Dynamics of Economic Disadvantage and Children’s Life Chances. American Sociological Review. 2006;71(5):847–66. [Google Scholar]
Ward Joe H., Jr Hierarchical Grouping to Optimize an Objective Function. Journal of the American Statistical Association. 1963;58(301):236–44. [Google Scholar]
Woodbury Max A, Manton Kenneth G. A New Procedure of Analysis of Medical Classification. Methods of Information in Medicine. 1982;21(4):210–20. [PubMed] [Google Scholar]
Wu Lawrence L. Some Comments on “Sequence Analysis and Optimal Matching Methods in Sociology: Review and Prospect. Sociological Methods & Research. 2000;29(1):41–64. [Google Scholar]
Zimmer Zachary, Martin Linda G, Nagin Daniel S, Jones Bobby L. Modeling Disability Trajectories and Mortality of the Oldest-Old in China. Demography. 2012;49:291–314. doi: 10.1007/s13524-011-0075-7. [DOI] [PubMed] [Google Scholar]

[R1] Aassve Arnstein, Billari Francesco, Piccarretta Raffaella. Strings of Adulthood: A Sequence Analysis of Young British Women’s Work-Family Trajectories. European Journal of Population. 2007;23:369–88. [Google Scholar]

[R2] Abbott Andrew. Sequences of Social Events: Concepts and Methods for the Analysis of Order in Social Processes. Historical methods. 1983;16(4):129–47. [Google Scholar]

[R3] Abbott Andrew. Sequence Analysis: New Methods for Old Ideas. ANnual Review of Sociology. 1995;21:93–113. [Google Scholar]

[R4] Abbott Andrew, Forrest John. Optimal Matching Methods for Historical Sequences. The Journal of Interdisciplinary History. 1986;16(3):471–94. [Google Scholar]

[R5] Abbott Andrew, Hrycak Alexandra. Measuring Resemblance in Sequence Data: An Optimal Matching Analysis of Musicians’ Careers. American Journal of Sociology. 1990;96(1):144–85. [Google Scholar]

[R6] Abbott Andrew, Tsay Angela. Sequence Analysis and Optimal Matching Methods in Sociology: Review and Prospect. Sociological Methods & Research. 2000;29(1):3–33. [Google Scholar]

[R7] Andreotti Alessandra, Minicuci Nadia, Kowal Paul, Chatterji Somnath. Multidimensional Profiles of Health Status: An Application of the Grade of Membership Model to the World Health Survey. PloS one. 2009;4(2):e4426. doi: 10.1371/journal.pone.0004426. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R8] Anyadike-Danes M, McVicar D. My Brilliant Career: Characterizing the Early Labor Market Trajectories of British Women From Generation X. Sociological Methods & Research. 2010;38(3):482–512. [Google Scholar]

[R9] Barban Nicola, Billari Francesco C. Classifying Life Course Trajectories: A Comparison of Latent Class and Sequence Analysis. Journal of the Royal Statistical Society: Series C (Applied Statistics) 2012;61(5):765–84. [Google Scholar]

[R10] Bauer Daniel J, Curran Patrick J. Distributional Assumptions of Growth Mixture Models: Implications for Overextraction of Latent Trajectory Classes. Psychological Methods. 2003;8(3):338–63. doi: 10.1037/1082-989X.8.3.338. [DOI] [PubMed] [Google Scholar]

[R11] Berkman Lisa, Singer Burton, Manton Kenneth. Black/White Differences in Health Status and Mortality Among the Elderly. Demography. 1989;26(4):661–78. [PubMed] [Google Scholar]

[R12] Besemer Sytske, Farrington David P. Intergenerational Transmission of Criminal Behaviour: Conviction Trajectories of Fathers and their Children. European Journal of Criminology. 2012;9(2):120–41. [Google Scholar]

[R13] Biemann Torsten, Fasang Anette Eva, Grunow Daniela. Do Economic Globalization and Industry Growth Destabilize Careers? An Analysis of Career Complexity and Career Patterns Over Time. Organization Studies. 2011;32(12):1639–63. [Google Scholar]

[R14] Biemann Torsten, Wolf Joachim. Career Patterns of Top Management Team Members in Five Countries: An Optimal Matching Analysis. The International Journal of Human Resource Management. 2009;20(5):975–91. [Google Scholar]

[R15] Bollen Kenneth A, Curran Patrick J. Curve Models: A Structural Equation Perspective. Hoboken, NJ: John Wiley and Sons; 2006a. [Google Scholar]

[R16] Bollen Kenneth A, Curran Patrick J. Latent Curve Models: A Structural Equation Perspective. New Jersey: John Wiley & Sons; 2006b. [Google Scholar]

[R17] Bryk Anthony S, Raudenbush Stephen W. Application of Hierarchical Linear Models to Assessing Change. Psychological Bulletin. 1987;101(1):147–58. [Google Scholar]

[R18] Caliński RB, Harabasz J. A Dendrite Method for Cluster Analysis. Communications in Statistics. 1974;3(1):1–27. [Google Scholar]

[R19] Cassidy Frederick, Pieper Carl F, Carroll Bernard J. Subtypes of Mania Determined by Grade of Membership Analysis. Neuropsychopharmacology. 2001;25(3):373–83. doi: 10.1016/S0893-133X(01)00223-8. [DOI] [PubMed] [Google Scholar]

[R20] Chan Tak Wing. Optimal Matching Analysis: A Methodological Note on Studying Career Mobility. Work and Occupations. 1995;22(4):467–90. [Google Scholar]

[R21] Charpentier Peter. GOM3 (Version 3.4): Freeware. 1996 Available online at http://lib.stat.cmu.edu/DOS/general/.index.html.

[R22] Cheadle Jacob, Amato Paul R, King Valerie. Patterns of Nonresident Father Contact. Demography. 2010;47(1):205–25. doi: 10.1353/dem.0.0084. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R23] Clogg Clifford C. Latent Class Models. In: Arminger Gerhard, Clogg Clifford C, Sobel Michael E., editors. Handbook of Statistical Modeling for the Social and Behavioral Sciences. New York: Plenum Press; 1995. pp. 311–59. [Google Scholar]

[R24] Collins Linda M, Lanza Stephanie T. Latent class and latent transition analysis : with applications in the social behavioral, and health sciences. Hoboken, N.J: Wiley; 2010. [Google Scholar]

[R25] D’Unger Amy V, Land Kenneth C, McCall Patricia L, Nagin Daniel S. How Many Latent Classes of Delinquent/Criminal Careers? Results from Mixed Poisson Regression Analyses. American Journal of Sociology. 1998;103:1593–630. [Google Scholar]

[R26] Duncan Terry E, Duncan Susan C, Strycker Lisa A. An Introduction to Latent Variable Growth Curve Modeling: Concepts, Issues, and Applications. Mahwah, NJ: Lawrence Earlbaum Associates, Inc; 2006. [Google Scholar]

[R27] Elder Glen H, Jr, Johnson Monica Kirkpatrick, Crosnoe Robert. The Emergence and Development of Life Course Theory. In: Mortimer Jeylan T, Shanahan Michael J., editors. Handbook of the Life Course. New York: Springer; 2003. pp. 3–19. [Google Scholar]

[R28] Erosheva E. Comparing latent structures of the Grade of Membership, Rasch, and latent class models. Psychometrika. 2005;70(4):619–28. [Google Scholar]

[R29] Farrington David P. Cambridge Study in Delinquent Development [Great Britain], 1961–1981. Ann Arbor, MI: Inter-University Consortium for Political and Social Research; 1999. ICPSR 8488. [Google Scholar]

[R30] Frech Adrianne, Damaske Sarah. The Relationships between Mothers’ Work Pathways and Physical and Mental Health. Journal of Health and Social Behavior. 2012;53(4):396–412. doi: 10.1177/0022146512453929. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R31] Gabadinho Alexis, Ritschard Gilbert, Müller Nicolas S, Studer Matthias. Analyzing and Visualizing State Sequences in R with TraMineR. Journal of Statistical Software. 2011;40(4) [Google Scholar]

[R32] Gauthier JA, Widmer ED, Bucher P, Notredame C. Multichannel Sequence Analysis Applied to Social Science Data. Sociological Methodology, Vol 40. 2010;40:1–38. [Google Scholar]

[R33] Gibbons Frederick X, O’Hara Ross E, Stock Michelle L, Gerrard Meg, Weng Chih-Yuan, Wills Thomas A. The Erosive Effects of Racism: Reduced Self-Control Mediates the Relation Between Perceived Racial Discrimination and Substance Use in African American Adolescents. Journal of Personality and Social Psychology. 2012;102:1089–104. doi: 10.1037/a0027404. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R34] Gill Thomas M, Gahbauer Evelyne A, Han Ling, Allore Heather G. Trajectories of Disability in the Last Year of Life. New England Journal of Medicine. 2010;362(13):1173–80. doi: 10.1056/NEJMoa0909087. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R35] Gustafsson Per E, Janlert Urban, Theorell Töres, Hammarström Anne. Life-course Socioeconomic Trajectories and Diurnal Cortisol Regulation in Adulthood. Psychoneuroendocrinology. 2010;35(4):613–23. doi: 10.1016/j.psyneuen.2009.09.019. [DOI] [PubMed] [Google Scholar]

[R36] Halpern-Manners Andrew, Warren John Robert, Brand Jennie E. Dynamic Measures of Primary and Secondary School Characteristics: Implications for School Effects Research. Social Science Research. 2009;38(2):397–411. [Google Scholar]

[R37] Halpin Brendan, Chan Tak Wing. Class Careers as Sequences. European Sociological Review. 1998;14:111–30. [Google Scholar]

[R38] Han Shin-Kap, Moen Phyllis. Clocking Out: Temporal Patterning of Retirement. American Journal of Sociology. 1999;105(1):191–236. [Google Scholar]

[R39] Henselmans Inge, Helgeson Vicki S, Seltman Howard, de Vries Jakob, Sanderman Robbert, Ranchor Adelita V. Identification and Prediction of Distress Trajectories in the First Year After a Breast Cancer Diagnosis. Health Psychology. 2010;29(2):160–68. doi: 10.1037/a0017806. [DOI] [PubMed] [Google Scholar]

[R40] Hicks Brian M, Iacono William G, McGue Matt. Consequences of an Adolescent Onset and Persistent Course of Alcohol Dependence in Men: Adolescent Risk Factors and Adult Outcomes. Alcoholism: Clinical and Experimental Research. 2010;34(5):819–33. doi: 10.1111/j.1530-0277.2010.01154.x. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R41] Hipp John R, Bauer Daniel J. Local Solutions in the Estimation of Growth Mixture Models. Psychological Methods. 2006;11:36–53. doi: 10.1037/1082-989X.11.1.36. [DOI] [PubMed] [Google Scholar]

[R42] Hunter Laura A, Leahey Erin. Parenting and Research Productivity: New Evidence and Methods. Social Studies of Science. 2010;40(3):433–51. [Google Scholar]

[R43] Jones Bobby L, Nagin Daniel S. Advances in Group-Based Trajectory Modeling and an SAS Procedure for Estimating Them. Sociological Methods & Research. 2007;35(4):542–70. [Google Scholar]

[R44] Judge Timothy A, Cable Daniel M. When it Comes to Pay, Do the Thin Win? The Effect of Weight on Pay for Men and Women. Journal of Applied Psychology. 2011;96(1):95–112. doi: 10.1037/a0020860. [DOI] [PubMed] [Google Scholar]

[R45] Jung Tony, Wickrama KAS. An Introduction to Latent Class Growth Analysis and Growth Mixture Modeling. Social and Personality Psychology Compass. 2007;2(1):302–17. [Google Scholar]

[R46] Kreuter Frauke, Muthén Bengt. General Growth Mixture Analysis with Antecedents and Consequences of Change. Journal of Quantitative Criminology. 2008;24(1):1–31. [Google Scholar]

[R47] Lesnard Laurent. Off-Scheduling within Dual-Earner Couples: An Unequal and Negative Externality for Family Time. American Journal of Sociology. 2008;114(2):447–90. [Google Scholar]

[R48] Lesnard Laurent. Setting Cost in Optimal Matching to Uncover Contemporaneous Socio-Temporal Patterns. Sociological Methods & Research. 2010;38(3):389–419. [Google Scholar]

[R49] MacCallum Robert C, Austin James T. Applications of Structural Equation Modeling in Psychological Research. Annual Review of Psychology. 2000;51(1):201–26. doi: 10.1146/annurev.psych.51.1.201. [DOI] [PubMed] [Google Scholar]

[R50] Macmillan Ross, Eliason Scott R. Characterizing the Life Course as Role Configurations and Pathways: A Latent Structure Approach. In: Mortimer Jeylan T, Shanahan Michael J., editors. Handbook of the Life Course. New York: Kluwer Academic/Plenum; 2003. pp. 529–54. [Google Scholar]

[R51] Manton Kenneth G, Stallard Eric, Woodbury MA, Tolley HD. Grade-of-Membership Techniques for Studying Complex Event History Processes with Unobserved Covariates. Sociological Methodology 1987. 1987;17:309–46. [Google Scholar]

[R52] Manton Kenneth G, Woodbury Max A, Stallard Eric, Corder Larry S. The Use of Grade-of-Membership Techniques to Estimate Regression Relationships. Sociological Methodology. 1992;22:321–81. [Google Scholar]

[R53] Manton Kenneth, Woodbury MA, Tolley HD. Statistical Applications Using Fuzzy Sets. New York: John Wiley & Sons; 1994. [Google Scholar]

[R54] Marcell Arik V, Eftim Sorina E, Sonenstein Freya L, Pleck Joseph H. Associations of Family and Peer Experiences with Masculinity Attitude Trajectories at the Individual and Group Level in Adolescent and Young Adult Males. Men and Masculinities. 2011;14(5):565–87. doi: 10.1177/1097184X11409363. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R55] McArdle JJ, Epstein David. Latent Growth Curves within Developmental Structural Equation Models. Child Development. 1987;58(1):110–33. [PubMed] [Google Scholar]

[R56] McLachlan Geoffrey, Peel David. Finite Mixture Models. New York: John Wiley & Sons; 2000. [Google Scholar]

[R57] McLeod Jane D, Fettes Danielle L. Trajectories of Failure: The Educational Careers of Children with Mental Health Problems. American Journal of Sociology. 2007;113(3):653–701. doi: 10.1086/521849. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R58] Miller Shari, Malone Patrick S, Dodge Kenneth A. Developmental Trajectories of Boys’ and Girls’ Delinquency: Sex Differences and Links to Later Adolescent Outcomes. Journal of Abnormal Child Psychology. 2010;38(7):1021–32. doi: 10.1007/s10802-010-9430-1. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R59] Milligan GW. An Examination of the Effect of 6 Types of Error Perturbation on 15 Clustering Algorithms. Psychometrika. 1980;45(3):325–42. [Google Scholar]

[R60] Moffitt Terrie E. Adolescence-Limited and Life-Course-Persistent Antisocial Behavior: A Developmental Taxonomy. Psychological Review. 1993;100(4):674–701. [PubMed] [Google Scholar]

[R61] Moody James, Brynildsen Wendy D, Wayne Osgood D, Feinberg Mark E, Gest Scott. Popularity Trajectories and Substance Use in Early Adolescence. Social Networks. 2011;33(2):101–12. doi: 10.1016/j.socnet.2010.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R62] Müller Nicolas S, Sapin Marlène, Jacques-Antoine Gauthier, Orita Alina, Widmer Eric D. Pluralized Life Courses? An Exploration of the Life Trajectories of Individuals with Psychiatric Disorders. International Journal of Social Psychiatry. 2011;58(3):266–77. doi: 10.1177/0020764010393630. [DOI] [PubMed] [Google Scholar]

[R63] Mustillo Sarah A, Hendrix Kimber L, Schafer Markus H. Trajectories of Body Mass and Self-Concept in Black and White Girls: The Lingering Effects of Stigma. Journal of Health and Social Behavior. 2012;53(1):2–16. doi: 10.1177/0022146511419205. [DOI] [PubMed] [Google Scholar]

[R64] Muthén Bengt. Latent Variable Analysis: Growth Mixture Modeling and Related Techniques for Longitudinal Data. In: Kaplan David., editor. The Sage Handbook of Quantitative Methodology for the Social Sciences. Newbury Park, CA: Sage; 2004. pp. 345–68. [Google Scholar]

[R65] Muthén Bengt, Shedden Kerby. Finite Mixture Modeling with Mixture Outcomes Using the EM Algorithm. Biometrics. 1999;55(2):463–69. doi: 10.1111/j.0006-341x.1999.00463.x. [DOI] [PubMed] [Google Scholar]

[R66] Muthén Linda, Muthén Bengt. Mplus User’s Guide. Los Angeles: Muthén and Muthén; 2010. [Google Scholar]

[R67] Nagin Daniel S. Analyzing Developmental Trajectories: A Semiparametric, Group-Based Approach. Psychological Methods. 1999;4:139–57. doi: 10.1037/1082-989x.6.1.18. [DOI] [PubMed] [Google Scholar]

[R68] Nagin Daniel S. Group-Based Modeling of Development. Cambridge: Harvard University Press; 2005. [Google Scholar]

[R69] Nagin Daniel S, Farrington David P, Moffitt Terrie E. Life-Course Trajectories Of Different Types Of Offenders. Criminology. 1995;33(1):111–39. [Google Scholar]

[R70] Nagin Daniel S, Land Kenneth C. Age, Criminal Careers, and Population Heterogeneity: Specification and Estimation of a Nonparametric, Mixed Poisson model. Criminology. 1993;31:327–62. [Google Scholar]

[R71] Nagin Daniel S, Tremblay Richard E. Developmental Trajectory Groups: Fact or Useful Statistical Fiction? Criminology. 2005;43(4):873–904. [Google Scholar]

[R72] Nylund Karen L, Asparouhov Tihomir, Muthén Bengt. Deciding on the Number of Classes in Latent Class Analysis and Growth Mixture Modeling: A Monte Carlo Simulation Study. Structural Equation Modeling. 2007;14(4):535–69. [Google Scholar]

[R73] Petts Richard J. Family and Religious Characteristics’ Influence on Delinquency Trajectories from Adolescence to Young Adulthood. American Sociological Review. 2009;74(3):465–83. [Google Scholar]

[R74] Pianta Robert C, Belsky Jay, Vandergrift Nathan, Houts Renate, Morrison Fred J. Classroom Effects on Children’s Achievement Trajectories in Elementary School. American Educational Research Journal. 2009;45(2):365–97. [Google Scholar]

[R75] Piquero Alex R, Farrington David P, Nagin Daniel S, Moffitt Terrie E. Trajectories of Offending and Their Relation to Life Failure in Late Middle Age: Findings from the Cambridge Study in Delinquent Development. Journal of Research in Crime and Delinquency. 2010;47(2):151–73. [Google Scholar]

[R76] Portrait France, Lindeboom Maarten, Deeg Dorly. Health and Mortality of the Elderly: The Grade of Membership Method, Classification and Determination. Health Economics. 1999;8(5):441–58. doi: 10.1002/(sici)1099-1050(199908)8:5<441::aid-hec452>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]

[R77] Rand William M. Objective Criteria for the Evaluation of Clustering Methods. Journal of the American Statistical Association. 1971;66(336):846–50. [Google Scholar]

[R78] Rindfuss Ronald R, Choe Minja Kim, Kabamalan Maria Midea M, Tsuya Noriko O, Bumpass Larry L. Order Amidst Change: Work and Family Trajectories in Japan. Advances in Life Course Research. 2010;15(2–3):76–88. doi: 10.1016/j.alcr.2010.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R79] Rippeyoung Phyllis LF, Noonan Mary C. Is Breastfeeding Truly Cost Free? Income Consequences of Breastfeeding for Women. American Sociological Review. 2012;77(2):244–67. [Google Scholar]

[R80] Robette Nicolas, Bry Xavier. Harpoon or Bait? A Comparison of Various Metrics in Fishing for Sequence Patterns. Bulletin of Sociological Methodology. 2012;116(1):5–24. [Google Scholar]

[R81] Stallard Eric, Kinosian Bruce, Zbrozek Arthur S, Yashin Anatoliy I, Glick Henry A, Stern Yaakov. Estimation and Validation of a Multiattribute Model of Alzheimer Disease Progression. Medical Decision Making. 2010;30(6):625–38. doi: 10.1177/0272989X10363479. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R82] Stovel Katherine, Savage Michael, Bearman Peter. Ascription Into Achievement. American Journal of Sociology. 1996;102:358–99. [Google Scholar]

[R83] Thomas Patricia A. Trajectories of Social Engagement and Limitations in Late Life. Journal of Health and Social Behavior. 2011;52(4):430–43. doi: 10.1177/0022146511411922. [DOI] [PubMed] [Google Scholar]

[R84] Wagmiller Robert L, Lennon Mary Clare, Kuang Li, Alberti Philip M, Lawrence Aber J. The Dynamics of Economic Disadvantage and Children’s Life Chances. American Sociological Review. 2006;71(5):847–66. [Google Scholar]

[R85] Ward Joe H., Jr Hierarchical Grouping to Optimize an Objective Function. Journal of the American Statistical Association. 1963;58(301):236–44. [Google Scholar]

[R86] Woodbury Max A, Manton Kenneth G. A New Procedure of Analysis of Medical Classification. Methods of Information in Medicine. 1982;21(4):210–20. [PubMed] [Google Scholar]

[R87] Wu Lawrence L. Some Comments on “Sequence Analysis and Optimal Matching Methods in Sociology: Review and Prospect. Sociological Methods & Research. 2000;29(1):41–64. [Google Scholar]

[R88] Zimmer Zachary, Martin Linda G, Nagin Daniel S, Jones Bobby L. Modeling Disability Trajectories and Mortality of the Oldest-Old in China. Demography. 2012;49:291–314. doi: 10.1007/s13524-011-0075-7. [DOI] [PubMed] [Google Scholar]

PERMALINK

Do Different Methods for Modeling Age-Graded Trajectories Yield Consistent and Valid Results?

John R Warren

Liying Luo

Andrew Halpern-Manners

James M Raymo

Alberto Palloni

Abstract

Background

Naïve Approaches

Finite Mixture Models

Optimal Matching Analysis

Grade of Membership Models

Interchangeable Alternatives?

Data and Methods

Figure 1.

Figure 4.

“Naïve” Approach

Finite Mixture Models

Optimal Matching Analyses

Grade of Membership Models

Results

Table 1.

Figure 5.

Figure 6.

Figure 7.

Figure 8.

Supplemental Analyses of Real Data

Figure 9.

Discussion

Figure 2.

Figure 3.

Acknowledgments

APPENDIX A (To Be Provided Online)

Growth mixture models and group-based trajectory models

Latent class analysis

Grade of membership analysis

Optimal Matching Analysis

Selecting the optimal number of groups

APPENDIX B (To Be Provided Online)

Appendix Table C1.

Appendix Table C2.

Appendix Table C3.

Appendix Table C4.

Appendix Table C5.

Footnotes

Contributor Information

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases