Model based inference from microvascular measurements: Combining experimental measurements and model predictions using a Bayesian probabilistic approach

Abstract

Objective

In vivo imaging of the microcirculation and network-oriented modeling have emerged as powerful means of studying microvascular function and understanding its physiological significance. Network-oriented modeling may provide the means of summarizing vast amounts of data produced by high-throughput imaging techniques in terms of key, physiological indices. To estimate such indices with sufficient certainty, however, network-oriented analysis must be robust to the inevitable presence of uncertainty due to measurement errors as well as model errors.

Methods

We propose the Bayesian probabilistic data analysis framework as a means of integrating experimental measurements and network model simulations into a combined and statistically coherent analysis. The framework naturally handles noisy measurements and provides posterior distributions of model parameters as well as physiological indices associated with uncertainty.

Results

We applied the analysis framework to experimental data from three rat mesentery networks and one mouse brain cortex network. We inferred distributions for more than five hundred unknown pressure and hematocrit boundary conditions. Model predictions were consistent with previous analyses, and remained robust when measurements were omitted from model calibration.

Conclusion

Our Bayesian probabilistic approach may be suitable for optimizing data acquisition and for analyzing and reporting large datasets acquired as part of microvascular imaging studies.

1 Introduction

The study of hemodynamics and solute transport within microvascular networks is typically based on experimental observations which are then subjected to theoretical modeling. This sequential approach has been crucial for our current understanding of the biophysical properties of the microcirculation and revealed phenomena which could not be gleaned from in vivo measurements alone [32].

Technological advances now permit high-throughput in vivo measurement of structural and functional network properties. These include high-resolution, three-dimensional imaging of microvascular networks, measurements of blood flow, RBC velocity and flux with high spatio-temporal resolution, and measurements of oxygen partial pressure in blood and tissue [14,15,30,33,35]. With this leap in spatio-temporal resolution comes a need to summarize vast data quantities in meaningful ways. Currently, data are typically reported as summary statistics across typical vessel types, e.g. average changes in capillary RBC flux or capillary diameter evoked by functional activation, but see [29]. While such analysis provides important information about the function of individual vessels, it falls short of addressing the net, biophysical effect of these changes [23,25,39], for example in terms of the change in nutrient availability for the tissue supplied by the microvasculature.

The complex topology and morphology of microvascular networks give rise to considerable heterogeneity, for example in terms of the distribution of blood [22,23], and inference regarding solute transport within these networks must therefore account for this heterogeneity [22]. Accordingly, network-oriented analysis seemingly resolves the discrepancies encountered when tracer uptake data are fitted to compartmental models which assume identical capillary extraction properties across all capillaries [23,28]. Network-oriented data analysis combines microvascular measurements and model simulations to predict blood flow and solute extraction at the scale of the experimental data at hand, and has been used to estimate intrinsic network quantities or parameters which cannot be inferred directly from the experimental measurements [22,23,25].

To simulate blood flow through microvascular networks, microscopy-based topological and morphological information (in the form of vascular graphs) is typically combined with physical laws governing blood flow, and empirical descriptions of rheological effects [25]. The interconnected nature of microvascular networks, however, presents a challenge [4,16,25]. Typical vascular graphs have a considerable number of open ends or boundary nodes. The choice of pressure or flow and hematocrit values for these boundary nodes is critical, in that simulated flow patterns are very sensitive to such boundary conditions [16,25]. Pries and co-workers compared experimental measurements of blood flow velocity and hematocrit with model simulations and found that boundary conditions required manual adjustments to achieve satisfactory correspondence [25,26]. Recent approaches determine pressure boundary conditions by minimizing the difference between observed and modeled flow directions or velocity, or between literature and modeled pressures and vessel wall shear stresses [4,17,36].

The information which can be obtained by combining model simulations with experimental measurements in a network-oriented analysis is limited by the uncertainties which inevitably arise from measurement errors and uncertainties regarding vascular topology, morphology, and model structural and parameter uncertainty. In this study we present a Bayesian probabilistic approach to address this challenge. Bayesian probabilistic analysis provides a rigorous framework in which sources of uncertainty can be incorporated by their respective probability distributions. Accordingly, our aim was to demonstrate that this framework (i) combines microcirculatory experimental measurement, literature data, and model predictions in a statistically coherent way, (ii) handles noisy measurements, (iii) can be used to infer distributions for uncertain model quantities (we focus on boundary conditions in this report), and (iv) assigns uncertainties to model predictions.

The present work is to the best of our knowledge the first to integrate experimental measurements and network model simulations into a Bayesian analysis. We use experimental data from rat mesentery and mouse cerebral cortex to illustrate the performance of the analysis and show that the analysis approach (i) gives results consistent with previous analyses of a comprehensive data set with measurements of blood flow velocity and hematocrit available in all vessel segments, up to 546 segments and 40 boundary nodes, and (ii) is robust to the omission of measurements available for model calibration. The utility of the framework is then demonstrated in the brain cortex data – a large network with 1878 segments and 295 boundary nodes and only a limited number of velocity measurements. Finally, we discuss our results and outline how the framework might guide the acquisition and interpretation of experimental microcirculation data.

Materials & Methods

Simulation model

We use a simulation model which was originally developed to describe blood flow in rat mesentery networks [21,25,26] and later also proven to apply to other tissue types, including the brain [7,16]. The simulation model is partly based on physical principles regarding flow-pressure relationships and mass conservation at bifurcations, and partly on empirical descriptions of rheological effects. Accordingly, flow resistance is modeled with Poiseuille’s law, which describes flow resistance in terms of vessel length, vessel diameter, and fluid viscosity. The non-Newtonian nature of blood is incorporated by considering an apparent viscosity [5,20,21,26]. Apparent viscosity, in turn, is modeled according to an empirical relationship as a function h_FL(d, hct_D; θ) of vessel diameter d and vessel discharge hematocrit hct_D (θ denotes parameters of the empirical function). Apparent viscosity decreases with vessel diameter down to ~5 μm but then increases for lower diameters (Fåhræus-Lindqvist effect). The reduction in tube hematocrit relative to discharge hematocrit is modeled by an empirical relationship h_F(d, hct_D; θ) as a function of vessel diameter and discharge hematocrit (Fåhræus effect) [5,25]. RBC concentrations at bifurcation outflow branches are usually not equal to bulk flow rates (phase-separation effect), and this disproportionate distribution of RBC flow at bifurcations is modeled by an empirical function h_PS(q_m, q_α, q_β, d_m, d_α, d_β; θ) where q denote segment blood flow, and subscripts m, α, and β denote mother vessel and daughter vessels respectively [18,21]. In addition to vessel morphology, topology, and the empirical descriptions of rheological effect, the model depends on a series of boundary conditions, ζ. Specifically, pressures, or equivalently blood flow rates, must be specified for all boundary nodes except one, and discharge hematocrit must be specified for all inflow nodes. An iterative procedure for flow simulation is required, since the rheological descriptions impose interdependence between blood flow and flow resistance. The simulation model predicts pressure, blood flow rate, hematocrit, and flow resistance for all vessel segments, and a series of subsequent parameters can be derived from these [22]. The simulation model is fully specified by vessel topology, morphology ϕ = (d, l), parameters of the empirical functions θ, and boundary conditions ζ. While topology and morphology are readily available from the vascular graph (although potentially confounded by uncertainties and measurement errors), the prescription of appropriate pressure and hematocrit boundary conditions is less straightforward. In the following we address how this challenge can be confronted by adopting a Bayesian probabilistic analysis strategy.

Bayesian probabilistic analysis

While microcirculatory measurements originate from a complicated microvascular system, the simulation model represents the underlying complex physiological phenomena in terms of relatively simple mathematical expressions. An example of such imposed simplicity is the empirical rheological functions that represent parametric fits to experimental data rather than explicit descriptions of the physics underlying the rheological phenomena. Such approximations inevitably introduce discrepancies between the observations and the model’s predictions from several error sources, including observation or measurement errors, model parameter errors, and model structural errors [26]. Therefore, a combined analysis of experimental measurements and model simulations requires adjustment of the model’s parameters to establish correspondence between the model’s predictions and the measurements, taking into account the presence of errors.

Let y be a vector of n observations of some microvascular quantities of interest, e.g. blood flow velocity, hematocrit, and blood flow direction, and let f(x) denote a vector of the simulation model’s predictions of the corresponding quantities, where x signifies the dependence on a series of (unknown) parameters, e.g. boundary conditions. The vector of errors or residuals ε = y − f(x) measures the mismatch between the observations and the model’s predictions and lumps together all sources of errors. A common strategy to achieve correspondence between model and observations, from an optimization perspective, is to obtain an estimate of the unknown parameters x̂ so that the sum of squared residuals is minimized (least-squares solution), or more generally, to use weighted- or generalized least-squares to allow for different weighting of individual measurements. From a statistical perspective, such least-squares solutions correspond to maximum likelihood solutions under Gaussian error models [2]. Least-squares estimation has indeed proven useful in a series of studies focused on combining microcirculatory measurements and literature knowledge with model simulations [4,6,25,36]. However, in the presence of incomplete and imperfect experimental data, this optimization problem may become underdetermined and further (strong) assumptions are required, e.g. to search for a solution that minimizes the Euclidean norm of the residuals [36], or to impose exact literature boundary conditions [6]. Furthermore, optimization leads to a single estimate of the best parameter values, and the uncertainties of the model’s predictions are therefore not directly available.

An alternative to parameter identification by optimization is to adopt a Bayesian analysis strategy. Bayesian analysis provides a rigorous framework for incorporating literature or prior knowledge (and their associated uncertainties) and observations into a combined analysis, it yields an estimate of the probability density function of x rather than a single point estimate x̂, and finally, it provides estimates of the uncertainties in the simulation model’s predictions. Bayesian analysis typically involves (i) inferences on a set of uncertain parameters, (ii) predictions based on in-sample and out-of-sample data, and (iii) model comparison, selection, and averaging [1,8].

Observations, model predictions, and model parameters are treated as random variables governed by probability distributions. These distributions are combined by use of probability rules to yield information on any quantity of interest. The Bayes’ theorem yields the posterior distribution of model parameters given the observations as a combination of the prior beliefs regarding model parameters and the probability density of the observations given parameter values

$$p(x\mid y,m)=\frac{p(y\mid x,m)p(x\mid m)}{p(y\mid m)}\propto L(x\mid y,m)p(x\mid m),$$ (1)

where p(x|y, m) is the posterior distribution of x, p(x|m) is the prior distribution of x, L(x|y, m) = p(y|x, m) is the likelihood function of x, and p(y|m) is Bayesian evidence for model m acting as a normalization constant. Here, m signifies assumptions regarding the structure of the simulation model as well as the structure of the probabilistic models. The Bayesian evidence is of particular interest in the context of model comparison, selection, and averaging, but is not necessarily required for posterior inference. The predictive distribution governing the model predictions can be found by integrating over the uncertain model parameters

$$p(y\mid m)=\int p(y\mid x,m)p(x\mid m)dx.$$ (2)

The probabilistic description of the observed data and prior knowledge allows the modeler to incorporate assumptions regarding errors via the likelihood function and assumptions regarding unknown model parameters and their uncertainties via the prior distribution and combine these in a statistically coherent way by Bayes’ theorem. The modeler faces practical challenges when applying Bayesian analysis, namely (i) the specification of the likelihood function and the prior distribution and (ii) inference of the posterior distribution of model parameters. These topics will be addressed in the following.

Likelihood functions

To formulate the likelihood function we partition observations into three observation types: y_vel (blood flow velocity), y_hct (discharge hematocrit), and y_dir (blood flow direction), and partition model predictions correspondingly, with dimensions n_vel, n_hct, and n_dir, respectively. We assume that the likelihood function decomposes as L(x|y, m) = L_vel(x|y_vel, m) × L_hct (x|y_hct, m) × L_dir (x|y_dir, m). Blood flow velocity errors and hematocrit errors (ε_vel and ε_hct) are assumed to be Gaussian distributed, uncorrelated, and with identical error variances within each observation type (i.e. homoscedasticity within observation type)

$$L_i\left(x,{\sigma }_i\mid y_i\right)\propto \prod _{j=1}^{n_i}\frac{1}{{\sigma }_i}exp\left[-\frac{1}{2{\sigma }_i^2}{\left(y_{i,j}-f_{i,j}(x)\right)}^2\right],i\in \left\{\text{vel},\text{hct}\right\},$$ (3)

To model the likelihood associated with blood flow direction we define a “success” to be the event of correspondence between observed and predicted flow direction, and model the likelihood associated with flow direction as a sequence of n_dir independent Bernoulli trails, each with probability of success γ

$$L_{\text{dir}}\left(x,\gamma \mid y_{\text{dir}}\right)=\prod _{j=1}^{n_{\text{dir}}}{\gamma }^{I(y_{\text{dir},j}=f_{\text{dir},j}(x))}{(1-\gamma )}^{I(y_{\text{dir},j}\ne f_{\text{dir},j}(x))},$$ (4)

where I(·) is the indicator function that returns one if the argument is true and zero elsewhere.

Priors governing simulation model (boundary conditions)

We model the pressure boundary conditions and hematocrit boundary conditions by scaled shifted beta distributions

$$p(x\mid \alpha ,\beta ,a,b)\propto \prod _{j=1}^{n_x}{\left(x_j-a_j\right)}^{{\alpha }_j-1}{\left(b_j-x_j\right)}^{{\beta }_j-1}$$ (5)

where α and β are shape hyper-parameters, a and b are hyper-parameters defining the bounds of feasible parameter spaces, and n_x is the dimension of x. The use of beta distributions allows the parameters to be constrained to physiologically conceivable ranges while also allowing the parameter distribution to have relatively flexible shapes depending on the particular choice of scale hyper-parameters.

Priors governing likelihood functions

The use of Gaussian distributions for blood flow velocity errors and hematocrit errors introduce associated noise components σ_i into the likelihood functions eq. 3 and hence also into the Bayes’ theorem eq. 1. However, the noise variances are unknown and therefore modeled as uncertain parameters. Prior distributions governing blood flow velocity errors and discharge hematocrit errors are modeled by scaled inverse chi-square distributions

$$p\left({\sigma }_i^2\right)\propto \frac{1}{{\sigma }_i^{n_{0,i}+2}}exp\left(-\frac{n_{0,i}{s}_{0,i}^2}{2{\sigma }_i^2}\right),i\in \left\{\text{vel},\text{hct}\right\},$$ (6)

with n₀ and s₀ being hyper-parameters. Combination of Gaussian error models with scaled inverse chi-square distributions for noise variance is convenient, since this not only leads to an analytical solution to the posterior of the noise variance, but also allows for integrating the noise variances out of the inference equations by analytical means [1,13].

The prior distribution of the probability of correctly predicting blood flow direction is modeled as a beta distribution

$$p(\gamma \mid \alpha ,\beta )\propto {(\gamma )}^{\alpha -1}{(1-\gamma )}^{\beta -1}$$ (7)

with α and β being hyper-parameters. This choice permits an analytical solution to the posterior of the probability of predicting correct flow direction.

Model inference

The objective of model inference is to infer the posterior distribution of model parameters p(x|y,m), (eq. 1). According to the Bayes’ theorem eq. 1 this posterior distribution is proportional to the product of the likelihood and the prior distribution, and it is straightforward to combine the likelihood and prior to form a mathematical expression for the posterior distribution. Similarly, evaluating the likelihood function and the prior distribution for a given parameter value x̃ is also straightforward (although potentially numerically expensive). However, an analytical expression for p(x|y,m) cannot be derived, partly because of the mathematical forms of the likelihood and the prior, and partly because x enters the likelihood function via the nonlinear simulation model f(x). Instead we use Markov chain Monte Carlo (MCMC) simulation [8]. MCMC generates a sequence of samples while exploring the parameter space. Samples are drawn such that they mimic samples from p(x|y,m), and can be used to represent the posterior distribution, to calculate moments with respect to it (e.g. mean and median), and to approximate intractable integrals by empirical averages in the context of prediction (eq. 2). A MCMC sampling iteration proceeds as follows: Let x_t−1 denote the current state of a chain. A trial move to a proposal state x_p is generated. The flow simulation model is run with the proposed parameters and the un-normalized posterior density L(x|y, m)p(x|m) is evaluated, i.e. the simulation model’s predictions are compared to the observations via the likelihood function and the proposed parameters are compared to the prior distribution. The proposed state is then either accepted or rejected according to the Metropolis rule

$$u_1=min\left\{\frac{L(x_p\mid y,m)p(x_p\mid m)}{L(x_{t-1}\mid y,m)p(x_{t-1}\mid m)},1\right\}.$$ (8)

A random value u is sampled uniformly on the interval [0, 1]. If u < u₁, the proposed sample is accepted (x_t = x_p), otherwise the sample is rejected (x_t = x_t−1). This iterative procedure of generating, and then accepting or rejecting the proposed samples, is repeated until either a desired number of evolution steps is achieved, or the iterations are stopped according to appropriate convergence diagnostics.

We use the DREAM_(ZS) algorithm [38,41,42] to generate proposal samples. DREAM_(ZS) is a multiple-chain method that uses differential evolution adaptive Metropolis with sampling from an archive of past states for posterior exploration. Three chains are iterated in parallel, and proposal points are generated from a joint archive of past states that is periodically updated for each 100^th iterations as the chains explore parameter space. DREAM_(ZS) automatically adapts the scale and orientation of the proposal distribution, and constantly introduces new sampling directions in parameter space by self-adaptive randomized subspace sampling [38,41,42].

Convergence of the MCMC chains to the posterior distribution is judged by computing the Gelman-Rubin R̂ convergence diagnostic from the multiple chains iterated in parallel [9,42].

We use the samples to quantify two types of uncertainties - prediction uncertainty due to model parameter uncertainty, and total predictive uncertainty. Prediction uncertainty due to model parameter uncertainty is computed by propagating the individual samples through the flow simulation model, thereby providing a distribution over the simulation model’s predictions. Total predictive uncertainty is calculated by adding, to the simulation model’s predictions, noise contributions sampled from Gaussian distributions with zero means and variances sampled form the posterior distributions of noise variances [8].

Case study data sets

Mesentery data

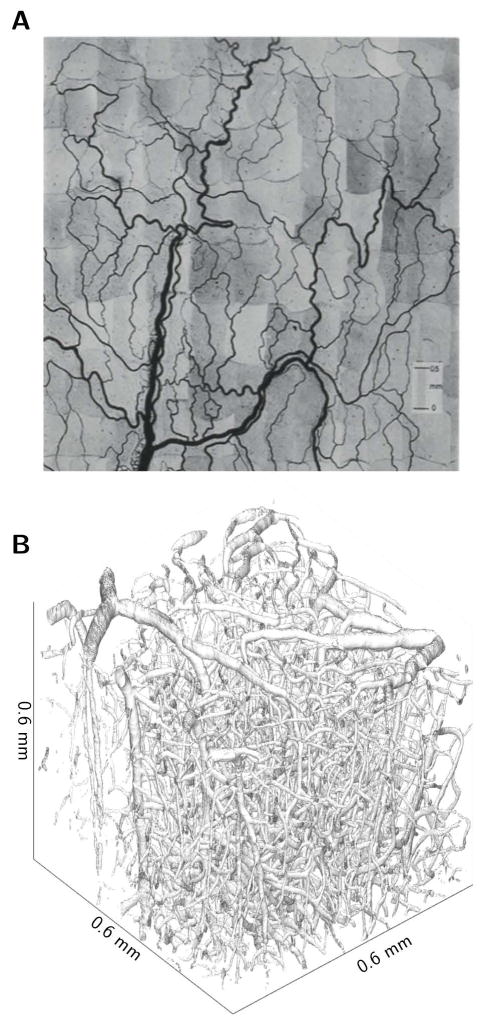
The mesentery data originates from experimental observations of the mesenteric microvasculature in rats [25,26]. In these experiments, the vascular networks were observed using intravital microscopy. The diameter and length of each vessel segment (between bifurcations) and the topological connectivity were determined from photographs (Figure 1A). Quantification of discharge hematocrit, blood flow direction, and blood flow velocity were based on video recordings. This resulted in measurements of discharge hematocrit and blood flow velocity/direction in all vessel segments. Here we include data from three networks for which measurements of both hematocrit and velocity are available. Vessel segments were grouped into arterioles, capillaries, and venules by an algorithm classifying vessel type without requiring flow information [34]. Summary statistics regarding network morphology and physiology are available in Table 1.

Figure 1.

Representations of microvascular networks. (A) Mesenteric network from rat, photomontage assembled from individual photographs [19], and (B) brain network from mouse cortex, surface based representation of angiogram acquired with two-photon microscopy using fluorescently labelled dextran.

Table 1.

Geometrical properties and measurement availability for the four microvascular networks. Measurement availability: mesentery networks - velocity and hematocrit are available in all mesentery segments, brain network - 17 OCT velocity measurements and 236 literature values available in venules and 44 literature values in arterioles.

Network	Mesentery 1	Mesentery 2	Mesentery 3	Brain 1
Number of nodes (boundary nodes)	288 (40)	270 (22)	388 (36)	1436 (295)
Number of segments (art/cap/ven)	392 (79/225/88)	383 (35/258/90)	546 (48/319/179)	1878 (49/1580/249)
Total segment volume (art/cap/ven) nL	25 (9/4/12)	21 2/6/13	44 (3/5/35)	4.3 (0.7/2.2/1.5)
Total segment length (art/cap/ven) mm	133 (34/71/29)	110 (10/72/29)	159 (16/93/50)	124 (4/108/11)
Average segment velocity (art/cap/ven)	1.6 (2.9/1.3/1.3)	0.9 (1.9/0.8/0.8)	1.4 (4.3/1.2/1.1)	1.3 (3.2/-/1.0)
Average segment hematocrit (art/cap/ven)	0.3 (0.3/0.3/0.3)	0.4 (0.4/0.4/0.4)	0.4 (0.4/0.4/0.4)	-

The mesentery data was used in three analyses: (i) To investigate the extent to which the Bayesian analysis framework can infer distributions of the unknown network pressure and hematocrit boundary conditions, (ii) to construct informative prior distributions for pressure and hematocrit, and (iii) to investigate the extent to which the Bayesian analysis framework can reconstruct local as well as global network flow patterns, even when measurements are incomplete.

Brain cortex data

The brain cortex data originates from experimental observations of the cortical microvasculature in mice and stems from two separate experiments (but with identical mouse strain and anesthetic regime): First, measurements of network morphology and topology based on an angiogram from TPM imaging (Figure 1B) and accompanying measurements of blood flow velocity in venules based on OCT imaging [6,29], and second, measurements of arteriolar and venular centerline RBC speed based on TPM imaging [31]. In these data, the diameter and length of all vessels, as well as their topological connectivity, were determined from the angiogram [29], and vessel segments were manually classified into arterioles, capillaries, and venules. Vessel diameters estimated from the angiogram may not reflect the entire luminal diameter, since the vasculature was imaged using fluorescently labelled dextran which labels free flowing plasma without staining the ESL [24,40]. Since the rheological descriptions used in the simulation model are calibrated using bright-field measurements that are more likely to reflect the entire luminal diameter, we performed a simple zeroth-order correction of the diameters to account for the potential underestimation of vessel diameters. Specifically, in the absence of comprehensive data to allow more detailed modeling, 1 μm was added to all segment diameters corresponding to an assumed width of ESL of 0.5 μm [24]. Due to limitations in resolution and readout rate of the OCT system, the OCT measurements were limited to large venules with diameter >13 μm. This resulted in 17 velocity measurements in seven ascending venules. To expand the amount of data available for calibration, we first defined flow direction in large descending arterioles and ascending venules and their first order branches in which the flow direction also could be defined with relatively high confidence based on network topology. We then added speed information by interpolating measurements of arteriolar and venular speeds [31] according to the diameters of the segments for which flow direction was known. This resulted in 280 (literature) velocity “measurements” in 280 segments. The literature velocity measurements were pooled with the OCT velocity measurements leading to 297 velocity measurements in total. Average blood velocity was estimated from centerline velocities and OCT maximum velocities assuming a blunting index of 3.5 [31,37]. Summary statistics regarding network structure and measurement availability are available in Table 1.

The data set obtained in brain cortex was used to examine the scalability of the Bayesian framework to current state-of-the-art datasets with close to six hundred unknown boundary conditions, and to illustrate how the framework allows for the incorporation of measured data and literature data in a combined analysis in the absence of comprehensive experimental measurements.

Results

Mesentery data - Inferring distributions of boundary conditions

We first calibrated the simulation model within the Bayesian analysis framework against all available measurement data (one model for each network). We used relatively weak priors for boundary pressures and boundary hematocrit, since a large number of observations were available to constrain the parameters. Specifically, we set the hyper-parameters {α, β, a, b} of the priors governing boundary pressure (in mmHg) and boundary hematocrit to {1, 1, 4, 130} and {1, 1, 0, 1} respectively. This amounts to uniform distributions over the intervals [4 mmHg, 130 mmHg] and [0, 1] respectively. The hyper-parameters {n₀, s₀} of the distributions governing blood flow velocity error and hematocrit error were both set to {0.001, 0.001}, corresponding to fairly “uninformative” priors. The hyper-parameter {α, β} of the distribution governing the probability of correct prediction of blood flow direction was set to {10, 1}, reflecting fairly strong prior belief in the accuracy of the measured flow directions.

The flow simulation model and Bayesian analysis was implemented as a computer program using C++. The MCMC simulation resulted in sequences of samples from the posterior distributions governing pressure and hematocrit at boundary nodes. Figure 2A shows the Gelman-Rubin R̂ convergence diagnostic versus the number of function evaluations (a function evaluation corresponds to running the flow simulation model with a given parameter settings). Convergence for all parameter chains in the three mesentery networks was reached after approximately 200,000 function evaluations whereas convergence for 99% of the parameters was reached after approximately 140,000 function evaluations. Running 3 million function evaluations (corresponding to 1,000,000 MCMC iterations of each of the three parallel chains) took less than an hour for each network on a laptop with an Intel i7 2.6 GHz processor.

Figure 2.

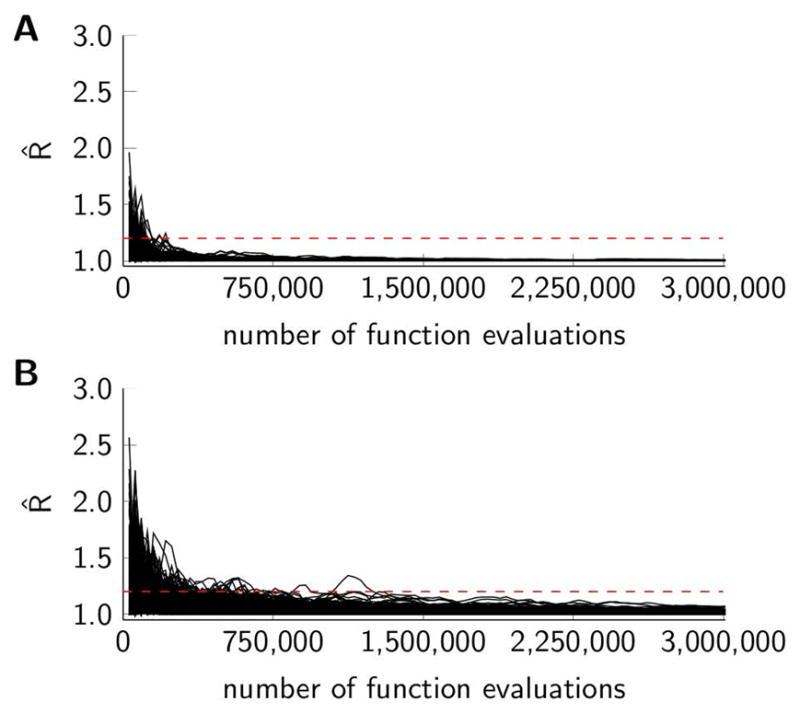
Evolution of the Gelman-Rubin R̂ convergence statistics versus the number of function evaluations (three chains iterated in parallel each with 1,000,000 MCMC iterations leading to a total of 3,000,000 function evaluations). Black curves represent individual parameters, and the dashed horizontal line indicates a convergence threshold of 1.2. (A) Three mesentery networks, 196 parameters. (B) Brain cortex network, 590 parameters.

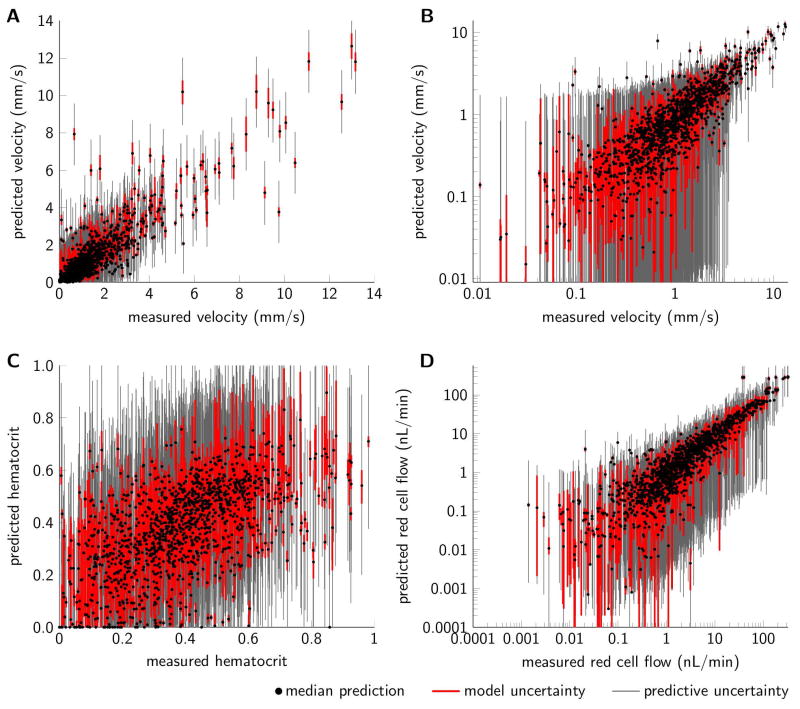
The individual samples were propagated through the flow simulation model to yield model predictions. Figure 3(A–C) show segment-by-segment comparisons between measured and predicted values of blood flow velocity and hematocrit. We observed good agreement between predictions and measurements for velocity, whereas the agreement between measured and predicted hematocrit is more moderate. Boundary condition uncertainty results in relatively large uncertainties in hematocrit predictions, whereas corresponding uncertainties in velocity predictions are smaller. The uncertainties in blood flow velocity and hematocrit can further be propagated to reflect uncertainties in other quantities, and Figure 3D illustrates how uncertainties in blood flow velocity and hematocrit propagate to uncertainties in red cell flow estimates.

Figure 3.

Scatterplots comparing (A) measured and predicted blood flow velocity, (B) blood flow velocity on log scale to enhance visual judgement of low velocity data, (C) measured and predicted hematocrit, and (D) measured and predicted red cell flow for the three mesentery networks (n=1321 segments). Red cell flow was calculated as the product between blood flow velocity, hematocrit, and vessel cross sectional area. Black dots mark median model predictions, red and gray bars mark prediction uncertainty due to model parameter uncertainty and total predictive uncertainty respectively (95% credible intervals). Model predictions correspond to the calibration setup with all measurements available for calibration and “non-informative” broad priors.

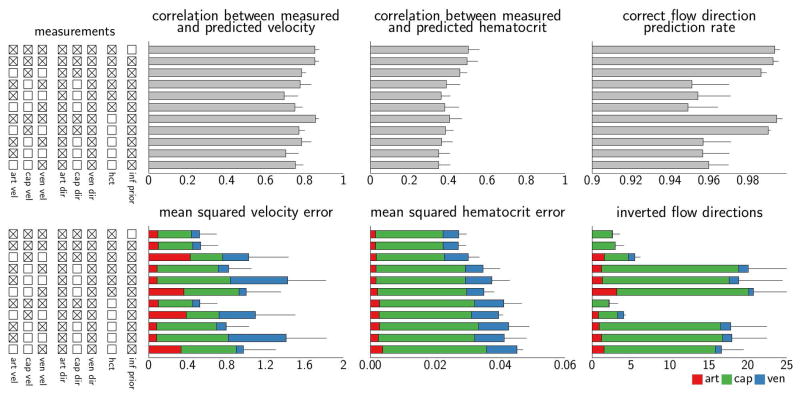
Quantitative metrics comparing the experimental measurements to model predictions are reported in Figure 4 (top bar in each plot). The mean squared velocity error and mean squared hematocrit error were 0.52 and 0.027, respectively, and the average number of wrong flow directions was 2.6. The noise contributions, corresponding to the random errors added to the model simulations to calculate total predictive uncertainty, were squared and averaged across the vessel segments. Across the MCMC samples these estimated errors were 0.52 [0.48 0.61] and 0.027 [0.024 0.031] for velocity and hematocrit, respectively (medians and credible intervals). Predictive performance is consistent with previous analysis reporting a mean square deviation of measured flow velocities of approximately 0.6 and approximately five wrong flow directions [21]. Additionally, for network 3, we observed a median of two wrong flow directions compared to nine wrong flow directions in previous reports [17]. It should be noted that network flow patterns were inferred without any manual intervention and with very weak assumptions regarding boundary conditions.

Figure 4.

Quantitative evaluation of the predictive performance in a series of calibration setups for the mesentery data set. Tick boxes (left column) indicate data available for model calibration. Metrics reported in the bottom row are decomposed into contributions from arterioles, capillaries, and venules. Error bars correspond to the standard deviation of the mean computed across the three networks. Note different scales in the plots.

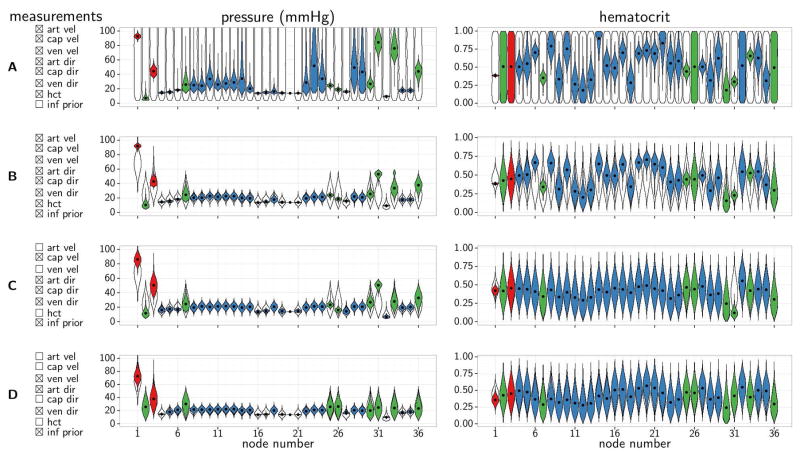
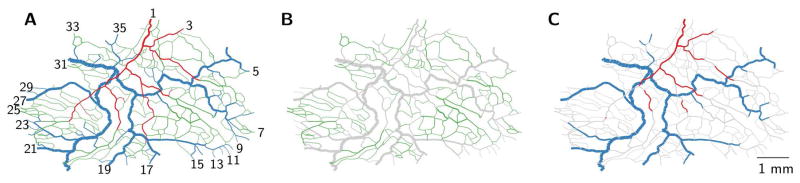
The marginal posterior distributions for boundary pressure and boundary hematocrit for mesentery network 3 are shown in Figure 5A. We observed narrow posterior distributions for boundary pressures in arterioles and larger venules – see Figure 6A for spatial representation and node numbers. Of note, pressure is relatively low for node 2, and relatively high for nodes 31 and 33 (all of which are boundary nodes of capillary segments). These three nodes are located either near the main input or near the main output (node 1 and 32 respectively). Therefore they primarily feed/drain localized parts of the network, and the inferred boundary pressures reflect the model’s attempt to match relatively high observed blood flow rates in these segments. Posterior distributions of boundary hematocrit fall into three categories; i) the main feeding arteriole (node 1) has a relatively narrow distribution, ii) the majority of nodes have more broad but still localized distributions, and iii) the posterior distributions of node 2, 3, 26, 32 and 36 resemble the prior distributions, since these are outlet nodes rendering the boundary hematocrit irrelevant. Note, however, that boundary nodes for which boundary hematocrit is irrelevant (outlets) cannot be specified prior to the analysis and hence excluded from the parameter inference, unless flow direction at such nodes are known with arbitrarily high confidence.

Figure 5.

Posterior distributions for boundary pressures (center column) and boundary hematocrit (right column) for four calibration setups in the mesentery network 3. Tick boxes (left column) indicate data available for model calibration. Colored “violins” represent marginal posterior distributions for individual parameters, black dots are medians, and black outlines represent prior distributions. Node numbers correspond to node numbers in Figure 6.

Figure 6.

Visualization of the spatial structure for mesentery network 3. (A) All 546 vessel segments colored according to vessel type classification; arterioles are red, capillaries are green, and venules are blue. Boundary nodes are labeled with numbers ordered clockwise from the main feeding arteriole (only uneven numbers shown). (B) Variant of complete network with capillaries highlighted. (C) Variant of complete network with arterioles and venules with diameters greater than 15 μm highlighted. Segment diameters are doubled to enhance visibility.

To summarize, Figure 4 and 5 illustrate, that the Bayesian inference framework successfully (i) yields distributions governing unknown pressure and hematocrit boundary conditions based on information from the experimental measurements and prior beliefs regarding the boundary conditions and (ii) provided predictions consistent with previous analyses of the mesentery data set [17,21,26].

Mesentery data - Constructing informative prior distributions

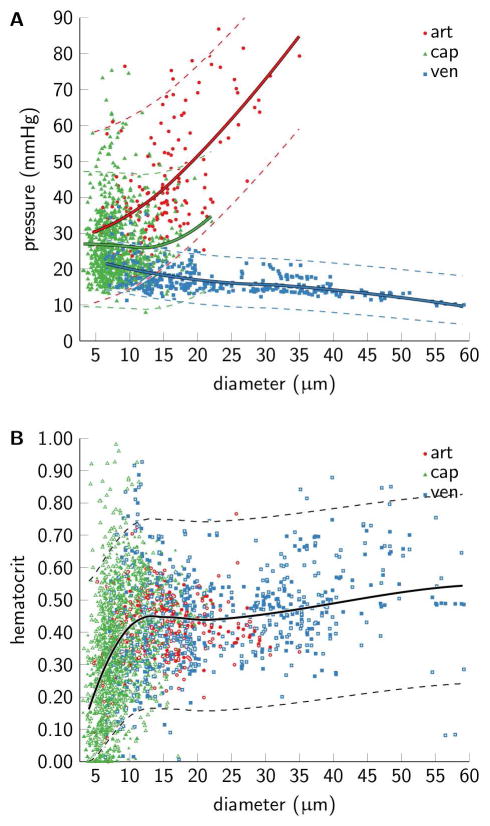
Mid-segment pressure and segment hematocrit versus diameter are shown in Figure 7; model simulations are shown for mid-segment pressure and experimental measurements as well as model simulations for hematocrit. We observe considerable heterogeneity in mid-segment pressure for a given segment diameter for both arterioles and capillaries, whereas venous pressures are more homogeneous. Pressures in arterioles(venules) increase(decrease) with their diameter. Note that the slight increase in capillary mid-segment pressure with diameter is supported by only relatively few observations. Hematocrit is relatively heterogeneous within segment classes and increase with diameter for all segment classes.

Figure 7.

Distributions of (A) mid-segment pressure and (B) segment hematocrit in the three mesentery networks. Arteriolar segments are red, capillary segments are green, and venular segments are blue. Scatter points correspond to median model predictions for segment pressure (n=1321 segments), and median hematocrit based on both predictions and measurements (n=2642) (measurements marked with white dots). Model predictions correspond to the calibration setup with all measurements available for calibration and “non-informative” priors. Solid lines are local polynomial regression fits of the data [3]. These fits were used as mean values of the “informative” priors, and the dashed lines mark 95 percentiles of the prior distributions.

Based on these observations, we derived empirical relationships that describe both pressure and hematocrit as a function of segment diameter in order to construct informative prior distributions. Pressure behaved differently as a function of diameter across segment classes, and three separate fits were therefore adopted to describe pressure for the three segment types. Conversely, hematocrit shows more similar behavior across segment class, and a single fit to data pooled across segment classes was used. These empirical fits served as the mean values governing the informative prior distributions. The corresponding variances of the prior distributions were estimated from the residuals (deviation between empirical model fits and observations). These means and variances define the shape hyper-parameters of the informative prior distributions which govern boundary conditions.

Mesentery data - Model inference in scenarios with limited data availability

We defined subsets of network segments in order to mimic experimental scenarios in which experimental measurements of physiological variables (blood flow velocity, flow direction, and hematocrit) are only partially available. Three vessel groups were defined; arterioles with diameter >15 μm, venules with diameter >15 μm, and capillaries (Figure 6B,C). Based on this partition, we generated ten data sets with various amounts of experimental information available. For information about these data sets, refer to Figure 4, left column. Calibration of the simulation model was based on observation data available within each of the ten data sets. Model predictive performance was evaluated by comparing model predictions to all observations, thereby considering calibration/in-sample performance as well as validation/out-of-sample performance. To constrain the model in the absence of comprehensive observation data in all segments, we used the informative prior distributions derived from the initial analysis as priors for the boundary conditions. Hyper-parameters of distributions governing blood flow velocity error, hematocrit error, and the probability of correct prediction of blood flow direction were set as in the initial calibration analysis.

Quantitative metrics comparing measurements and model predictions are reported in Figure 4. The use of an informative prior was associated with a negligible performance loss in comparison to the use of a weak prior on the data set with all observation available for calibration (first two bars in individual plots). Notably, model performance with respect to predicted velocity and flow direction was generally preserved although hematocrit measurements were lacking, although this of course lead to reduced performance with respect to hematocrit predictions. In addition, the simulation model maintains the capability of predicting velocity even when observations in segment subgroups were disregarded from the calibration stage. Note that increases in error for the disregarded subgroups do not necessarily imply decreased model performance as such, since these errors represent validation/out-of-sample errors rather than calibration/in-sample errors. Model simulations maintain good performance also in data sets where blood flow velocities in main feeding and draining vessels are disregarded in the calibration stage.

Marginal posterior distributions for boundary pressure and boundary hematocrit in network 3 are shown for four of the scenarios in Figure 5 (left column shows measurements available for model calibration). There is strong consistency between the inferred pressure distributions when inference is based on broad priors (Figure 5A) and more informative priors (Figure 5B). Note that there is sufficient evidence in the measurements to allow the posterior distributions to diverge from the prior distribution (nodes 1, 2, 3, 31, 33, and 36 in particular). Similarly, there is strong consistency between posterior distributions governing hematocrit for the broad and informative prior (Figure 5A,B right column). If velocity measurements in arterioles were disregarded in calibration, then the posterior distributions of boundary pressures for arterioles (nodes 1 and 3) approach the prior distributions (Figure 5C,D). For capillary boundary nodes (nodes 2, 31, 33, and 36), availability of capillary flow velocities in the calibration step leads to a departure from the prior distributions for pressure (Figure 5A,B,C). Note that hematocrit is decreased for node 31, probably in an attempt by the model to reproduce the relatively high observed blood flow velocity observed in the vicinity of node 31. Figure 5D shows posterior distributions inferred when only measurements of venous velocities and specification of arteriolar flow direction are available for model calibration. Most posterior distributions of boundary pressures and hematocrit largely resemble the prior distributions, whereas pressures of large venules are characterized by quite localized posterior distributions. Overall, Figure 5 shows that the modeling framework can adapt to limited calibration data availability when it includes the informative prior.

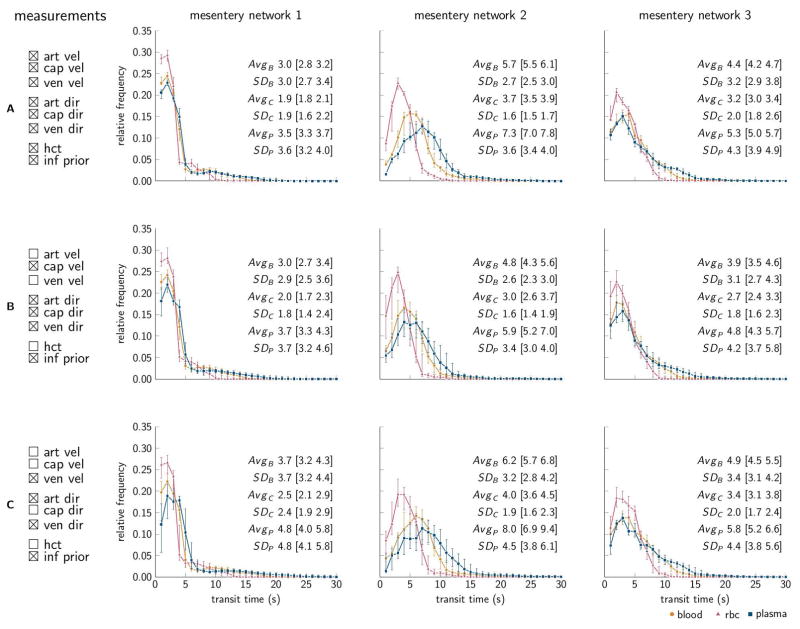
Combining analysis of experimental measurements with model simulations can potentially yield more information than one can glean from raw measurement data. To illustrate such additional information, we derived A-V blood transit time distributions (Figure 8). Overall, the averages and standard deviation of A-V transit times agree with previous reports [22]. Furthermore we observe a diversity of the distributions across networks (separate columns). The overall transit times tend to increase as observations are disregarded; however the diversity across networks is preserved when disregarding observations available for model calibration (Figure 8B,C).

Figure 8.

Frequency distributions of arteriovenous (A-V) transit times for the mesentery data, for blood, RBC, and plasma, subscript B, C, and P respectively. Individual networks are ordered in columns, and three different calibration setups are ordered in rows, tick boxes indicate data available for model calibration. Intervals with 1 s width and 1 s steps were used to estimate the distributions. Markers denote median predictions and error bars mark 95% credible intervals representing model parameter uncertainty. Avg and SD summarize the distributions by average and standard deviation, and numbers in brackets denote 95% credible intervals. All quantities are flow weighted.

Brain cortex data – Large vascular network and limited measurement availability

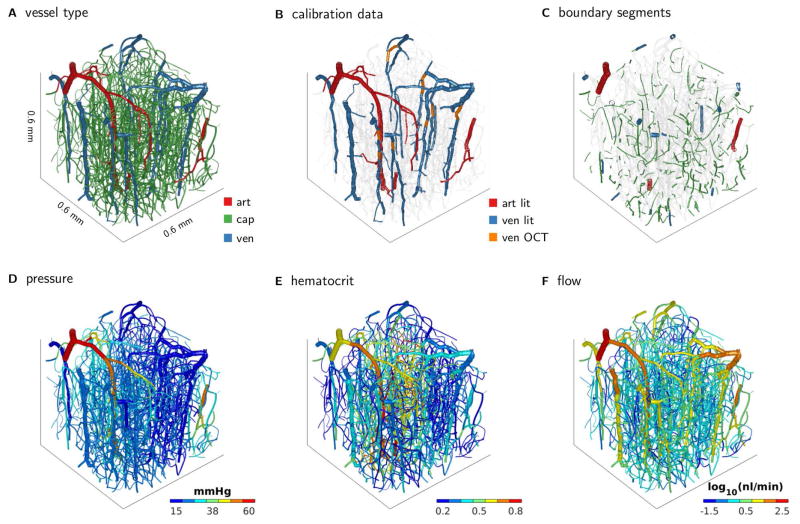
Using the Bayesian framework, our simulation model was calibrated to network data from the brain cortex (Figure 9A), with only a limited number of measurements available for calibration (Figure 9B) and close to six hundred unknown pressure and hematocrit boundary conditions (Figure 9C).

Figure 9.

Brain network from mouse cortex. (A) Segments colored according to vessel classification. (B) Colored segments indicate segments for which velocity data was available for model calibration. Velocity data origins partially from literature data and partially from Doppler OCT measurements. (C) Colored segments indicate boundary segments for which unknown boundary pressures and hematocrit were inferred. Markov chain Monte Carlo simulation was used to infer distributions of the unknown boundary conditions, and model predictions are obtained by propagating the individual samples through the flow simulation model. Plots in the bottom row summarize model predictions by showing mean model predictions of (D) flow, (E) hematocrit, and (F) flow.

Figure 2B shows the Gelman-Rubin R̂ convergence diagnostic versus the number of function evaluations. Convergence for all parameter chains was reached after approximately 1,200,000 function evaluations, whereas convergence for 99% of the parameters was reached after approximately 500,000 function evaluations. Three million function evaluations took about 13 hours.

The combined analysis of model simulations and experimental measurements yields predictions of pressure, flow, and hematocrit throughout the network (Figure 9D,E,F). Note that the Bayesian analysis leads to distributions over these quantities while the plots summarize these distributions by showing their mean only.

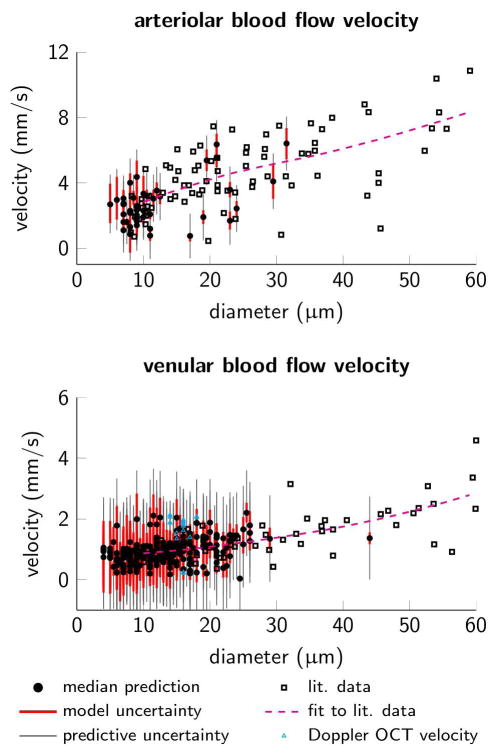
Figure 10 compares the simulation model’s prediction of velocity in arterioles and venules (Figure 9B) to experimental measurements as a function of diameter. Model predictions qualitatively agree with measurements and show decreased velocity with diameter. Additionally, there is quantitative agreement between the model’s predictions and actual measurements, while the uncertainty related to the model’s predictions shows a relative good coverage of measurement points.

Figure 10.

Blood flow velocity versus diameter. (A) Arteriolar segments and (B) venular segments, note different scales on the velocity axes. Black squares mark empirical measurements of blood flow velocities (literature data from another experiment but same mouse strain and anesthetic regime) [31] and the dashed magenta lines are local polynomial regression fits of the literature data [3]. Cyan triangles mark 17 Doppler OCT velocity measurements available in ascending venules. Black dots mark median model predictions, red and gray bars mark prediction uncertainty due to model parameter uncertainty and total predictive uncertainty respectively (95% credible intervals).

Finally, Figure 11 shows A-V blood transit time distributions. Similar to the mesentery networks, we observe a considerable heterogeneity in blood, RBC, and plasma A-V transit times.

Figure 11.

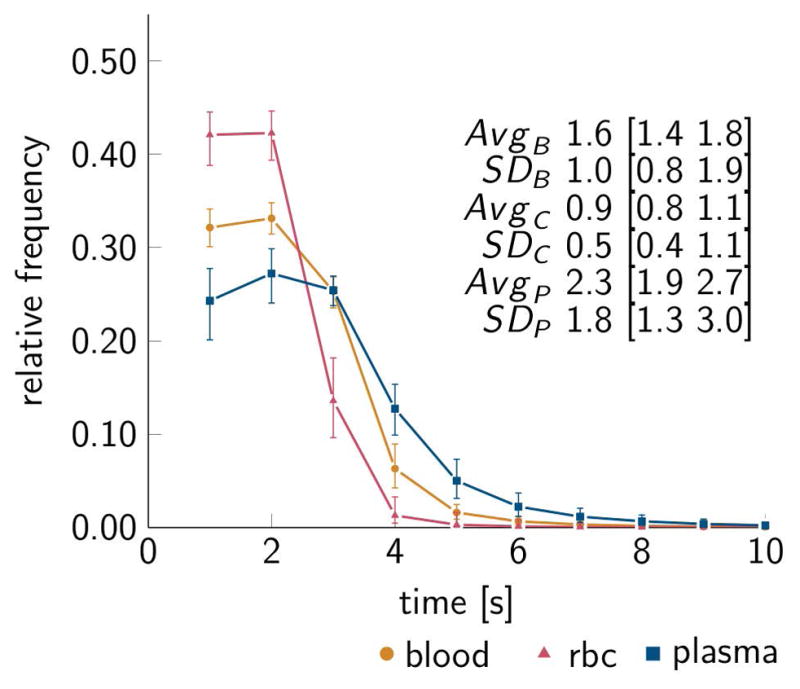
Frequency distribution of arteriovenous (A-V) transit times for the brain cortex data, for blood, RBC, and plasma, subscript B, C, and P respectively. Data representation corresponding to Figure 8.

In summary, the analysis of the brain cortex data illustrates that (i) the analysis framework works well on state-of-the-art data sets which contain hundreds of unknown pressure and hematocrit boundary conditions, (ii) the analysis framework allows calibration of simulation models against a data base containing both actual measurement data and also literature data, and (iii) the analysis framework extends the amount of information directly available from experimental measurements (Figure 9D,E,F, 10,11 versus Figure 9B).

Discussion

In this study we propose the Bayesian probabilistic data analysis framework as a means of integrating experimental measurements and network model simulations into a combined and statistically coherent analysis.

Modeling sources of uncertainties

Measurements and model predictions are associated with uncertainties and errors, including observation or measurement errors, model parameter errors, and errors concerning the model structure. A Bayesian probabilistic analysis approach allows for a formal incorporation of these uncertainties into a combined analysis. Recent analysis approaches combine observations and simulations by directly incorporating observations into simulation models as “hard constraints” in the system of governing equations [4,6,17]. While being relatively simple and easy to implement, this strategy also has inherent limitations. First, from a statistical point of view, the hard constraint approach introduces the assumption that measurements reflect the underlying physiological variable without any error or uncertainty. Second, hard constraints may lead to violations of flow/mass conservation in cases where measurements, with some degree of measurement error, are available for all segments connected at a bifurcation, or multiple measurements are available for the same segment. Error analysis revealed a significant presence of measurement error [26], rendering the assumption about arbitrary high measurement confidence questionable. The probabilistic analysis framework relaxes assumptions with regard to the accuracy of measurements and naturally incorporates the presence of uncertainty via the likelihood function. We have assumed the residuals to be Gaussian, uncorrelated and homoscedastic. This simplistic assumption is unlikely to fully describe the apparent complicated spatio-temporal correlation structure characterizing microcirculatory flow patterns. While being comprehensive from an experimental point of view, the mesentery data set can be argued to be limited from a data analytic point of view. A single observation of blood flow velocity and hematocrit is available for each segment, and hence the available data can be considered as a single (multidimensional) realization of the underlying biological system. Based on this, the noise model, which was applied in in this study, was deemed appropriate. It should be noted that residual analysis is an important element of the evaluation and further development of probabilistic models. Generalized error models that allow for non-Gaussian, correlated, and heteroscedastic errors can be developed based on future analyses.

Parameter inference and model identifiability

Bayesian inference yields distributions of parameters governed by uncertainties. Based on all available data and broad prior distributions, the analysis framework provided well-localized posterior distributions of boundary pressures and boundary hematocrit (Figure 5A). Hence, the complete data sets contained sufficient information to constrain the boundary conditions. In addition, informative prior distributions were constructed based on the initial analysis results, and a high degree of similarity was observed between inferred boundary conditions using broad- and the more informative priors respectively. Importantly, the informative priors were sufficiently broad to allow posterior distributions to diverge from the prior distributions when data contained information supporting this (Figure 5B,C,D). Conversely, the absence of experimental information resulted in posterior distributions resembling prior distributions (Figure 5B,C,D). It should be noted that a strict Bayesian analysis requires the prior to be defined before observations are considered. Construction of the informative prior distributions governing boundary pressures and hematocrit based on the initial analysis therefore imposes some degree of circularity to the analysis. An alternative strategy would be to repeatedly hold out one data set, estimate informative priors from the two other data sets, and apply this prior to the held out data set. However, circularity is already present to some extent since the viscosity model was developed based on the mesentery data [21,26]. To simplify, we based the informative prior on all three mesentery data sets. We speculate, that the impact of these circularities may not be overly severe, partly because relatively few global parameters were estimated, and partly because the informative priors were constructed to be relatively broad (Figure 5B,C,D and Figure 7).

Other approaches to constrain boundary conditions include the use of literature values for boundary conditions [6], ensuring identifiability by searching for a “minimum-norm solution” [36], and constraining boundary conditions by minimizing the deviance between simulated segment pressures and shear stresses and literature values [4]. Exact literature boundary conditions could easily be incorporated into the probabilistic analysis framework by defining corresponding boundary prior distributions as Dirac delta functions located at the exact literature values. Likewise, the minimization of the deviance between model predictions and literature target values could be incorporated by considering the literature target values as data observations which enter the analysis through the likelihood function, while choosing broad non-informative priors for the boundary conditions. Hence, the proposed analysis framework is quite flexible with regard to incorporating concepts underlying existing analysis procedures.

In the present study we have focused on modeling the uncertainty associated with pressure and hematocrit boundary conditions. However, parameters governing the rheological models as well as the simulation model’s inputs (vessel lengths and diameters) are also associated with uncertainty. Pries et. al [26] adopted a noise perturbation analysis to decompose the total deviation between experimental measurements and model simulations into contributions from errors related to (i) model inputs, (ii) parameters of the phase separation model, (iii) the structure of the viscosity model, and (iv) measurement errors. Within the Bayesian analysis framework, parameters such as those of the rheological models could also be ascribed with uncertainties. The rheological models include more than twenty parameters, and a sensible strategy could be to identify critical and identifiable parameters and then model uncertainty governing such parameters.

Model predictions

The probabilistic analysis resulted in posterior distributions of model predictions. Considering velocity prediction (Figure 3), there is a relatively high degree of correspondence between the measured and predicted velocities. With regard to hematocrit, there is considerable scatter in the plot of measured hematocrit versus predicted hematocrit (Figure 3), in agreement with previous analyses [25,26]. The presence of errors due to parameter uncertainties and model structural errors (e.g. in the model of phase separation at bifurcations) will result in an accumulation of errors throughout the network [25]. This accumulation of errors appears to have greater impact on hematocrit predictions than on velocity predictions. Whereas the model’s ability to reproduce spatially localized hematocrit measurements is moderate, the model has been shown to be capable of producing global hematocrit statistics (e.g. distributions, means, and variances) with good correspondence between hematocrit measurements and predictions [26].

The analysis framework maintained relatively good correspondence between measured and predicted velocities and flow directions as observations were disregarded from the calibration stage (Figure 4,9). It should be cautioned, however, that the model evaluation metrics (mean squared error, correlation coefficient, and correct flow direction prediction rate) largely reflect calibration or in-sample metrics, rather than validation or out-of-sample errors metrics. Consequently, the exact numerical values of the reported metrics may be characterized by some degree of over-optimism. However, this concern is not only related to our present analysis but applies to many existing studies. Future model evaluation can be conducted within well-established re-sampling frameworks.

Inferring latent network properties

The presence of heterogeneity in topological, structural, and hemodynamic parameters complicates the analysis of experimental measurements acquired at isolated spatial locations, because of the difficulty in generalizing from single measurements to overall or global functional properties of the microvasculature [22,23,28,39]. Whereas the typical vessel analysis approach is inherently limited to metrics that can be derived directly form the measurements, the network-oriented approach naturally appreciates the presence of heterogeneities. The probabilistic analysis approach naturally renders modeled uncertainties to be reflected also in derived latent parameters or indices, where uncertainties increase as fewer observations were available for model calibration. As an example, Figure 8 and 11 illustrate transit time distributions obtained from the analysis combining experimental measurements with model simulations. Overall, the averages and standard deviation of A-V transit times for the mesentery data set agree with previous reports [22]. Diversity in transit time distributions was observed across the three mesentery networks, and this diversity was preserved as experimental measurements were disregarded from model calibration. For the A-V transit times in mouse brain cortex we observe some discrepancy when comparing with estimates based on a plasma tracer technique that reported average transit time of about 0.5s to 1.2 s [11]. This may be explained by differences in assumptions underlying the two estimation techniques, including the structure and parameter values of the rheological descriptions used the simulation model. Future comprehensive measurements, in arterioles, capillaries, and venules of the mouse cortex, are needed to ascertain whether recalibration of the rheological descriptions to brain cortex is required.

Applicability of the analysis framework

In this study we show that Bayesian probabilistic data analysis framework provides a means to integrate experimental measurements and model simulations into a combined and statistically coherent framework. We wish to highlight some practical advantages of using this analysis framework in an experimental setting:

• The probabilistic analysis provides an alternative approach for parameter estimation in the analysis of network flows and provides not only point estimates of optimal parameters but also allows for quantification of model parameter uncertainty. This is an important feature in microvascular modeling since model inputs and parameters (e.g. pressure and hematocrit boundary conditions) are typically not directly observable but at the same time have profound impact on the simulation model’s performance [26]. Furthermore, this parameter uncertainty can be propagated through the simulation model to quantify uncertainty related to the model’s predictions.

• Although being computationally expensive compared to existing analysis methodologies [4,6,26,36] the Bayesian analysis coupled with MCMC sampling requires a rather reasonable runtime on a standard computer, i.e. the analysis will not be a significant bottleneck in the microcirculatory data acquisition and processing chain. Exploration of high-dimensional parameter spaces by MCMC is challenging [41]. In the present study we successfully applied the modeling framework to networks with up to 1878 vessel segments and 295 boundary nodes corresponding to nearly a 600-dimensional parameter space. Even in simulations considering large scale networks with >10,000 segments and thousands of boundary segments it is recognized, that relative choices regarding boundary conditions influence the simulated blood flows [10,16]. Future empirical work will establish whether the present modeling framework remains powerful in such large scale networks.

• The analysis of the mesentery data set demonstrated that the Bayesian probabilistic analysis approach support parameter identifiability in scenarios with limited measurement availability. Recent microvascular measurement techniques produce extensive amounts of measurements, albeit typically an incomplete representation of the complete microvascular flow patterns. Combining measurements with model simulations in a network-oriented analysis allows for reconstruction of the complete network flow pattern and also allows the modeler to derive latent network parameters or physiological indices, e.g. transit time distributions as illustrated here. Such “global” indices serve as inputs to recent macroscopic models that aim to make claims about oxygenation at the “tissue level” [12,27]. The probabilistic analysis readily identifies such indices, and provides estimates of their uncertainty intervals.

• While we assumed rheological model parameters to be fixed in this study, these parameters could also be associated with uncertainty. For studies of blood flow, e.g. in inflammation, aging, or other conditions modeled in the experimental animals being studied by high-throughput imaging, a probabilistic network-oriented analysis would potentially reveal the simulation model’s inability to explain measurement data and the model’s attempt to adjust rheological model parameters in order to comply with the measurements. Based on such analysis, inadequate aspects of the model could be identified, the model could be refined, and this iterative cycle could potentially provide novel insights into the rheology of blood in microvascular systems.

In conclusion, the analysis framework presented here will support the development and use of network-oriented analyses of microcirculatory measurements.

Perspectives

Combination of measurements acquired from microcirculatory networks using high-throughput imaging techniques and network-oriented modeling provide means of summarizing vast amounts of data in terms of key, physiological indices. To estimate such indices with sufficient certainty, however, network-oriented analysis must be robust to the inevitable presence of uncertainty due to measurement errors as well as model inadequacies. We propose the Bayesian probabilistic approach as a means for optimizing data acquisition and for analyzing and reporting large datasets acquired as part of microvascular imaging studies.

Abbreviations

Art

arteriolar

Cap

capillary

Dir

direction

ESL

endothelial surface layer

MCMC

Markov chain Monte Carlo

OCT

optical coherence tomography

RBC

red blood cell

TPM

two photon microscopy

Ven

venular