Abstract
Renal hypoxia could result from a mismatch in renal oxygen supply and demand, particularly in the renal medulla. Medullary hypoxic damage is believed to give rise to acute kidney injury, which is a prevalent complication of cardiac surgery performed on cardiopulmonary bypass (CPB). To determine the mechanisms that could lead to medullary hypoxia during CPB in the rat kidney, we developed a mathematical model which incorporates (i) autoregulation of renal blood flow and glomerular filtration rate, (ii) detailed oxygen transport and utilization in the renal medulla and (iii) oxygen transport along the ureter. Within the outer medulla, the lowest interstitial tissue P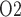 , which is an indicator of renal hypoxia, is predicted near the thick ascending limbs. Interstitial tissue P
, which is an indicator of renal hypoxia, is predicted near the thick ascending limbs. Interstitial tissue P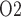 exhibits a general decrease along the inner medullary axis, but urine P
exhibits a general decrease along the inner medullary axis, but urine P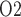 increases significantly along the ureter. Thus, bladder urinary P
increases significantly along the ureter. Thus, bladder urinary P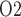 is predicted to be substantially higher than medullary P
is predicted to be substantially higher than medullary P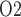 . The model is used to identify the phase of cardiac surgery performed on CPB that is associated with the highest risk for hypoxic kidney injury. Simulation results indicate that the outer medulla's vulnerability to hypoxic injury depends, in part, on the extent to which medullary blood flow is autoregulated. With imperfect medullary blood flow autoregulation, the model predicts that the rewarming phase of CPB, in which medullary blood flow is low but medullary oxygen consumption remains high, is the phase in which the kidney is most likely to suffer hypoxic injury.
. The model is used to identify the phase of cardiac surgery performed on CPB that is associated with the highest risk for hypoxic kidney injury. Simulation results indicate that the outer medulla's vulnerability to hypoxic injury depends, in part, on the extent to which medullary blood flow is autoregulated. With imperfect medullary blood flow autoregulation, the model predicts that the rewarming phase of CPB, in which medullary blood flow is low but medullary oxygen consumption remains high, is the phase in which the kidney is most likely to suffer hypoxic injury.
Keywords: hypoxia, kidney, metabolism, cardiopulmonary bypass, cardiac surgery
1. Introduction
Hospital-acquired acute kidney injury (AKI) is a serious clinical complication. In particular, patients who have undergone cardiac surgery that requires cardiopulmonary bypass (CPB) are at elevated risk of AKI (Karkouti et al., 2009). Cardiac surgery on CPB may be associated with mismatched changes in renal oxygen delivery and oxygen consumption (Evans et al., 2013). Mean arterial pressure is low during CPB (50–70 mmHg) (Andersson et al., 1994), which is below the lower limit of renal autoregulation, i.e. during CPB kidneys are unable to maintain a stable blood flow. The resulting reduction in renal blood flow and thus oxygen supply (Andersson et al., 1994) likely contributes to the risk of hypoxia and AKI. Furthermore, the CPB circuit is primed with a blood cell free solution, resulting in haemodilution which limits the systemic and renal oxygen delivery even further (Rosner et al., 2008).
Much of the oxygen consumed by the kidney is used to drive transport work, including the reabsorption of more than 99% of the filtered sodium under normal physiologic conditions. Renal blood flow is highly compartmentalized, with flow in the cortex (the outer portion of the kidney) substantially higher than that in the medulla (the innermost portion of the kidney). Blood flow is further compartmentalized within the medulla. The blood vessels that deliver oxygen to the medulla, i.e. the descending vasa recta (DVR), are sequestered within tightly packed vascular bundles, away from the renal tubules. This arrangement results in low oxygen tension (P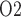 ) outside the vascular bundles and contributes to the vulnerability of the medullary thick ascending limbs (TALs) of the loops of Henle to hypoxic injury. TALs have high metabolic demand due to the Na
) outside the vascular bundles and contributes to the vulnerability of the medullary thick ascending limbs (TALs) of the loops of Henle to hypoxic injury. TALs have high metabolic demand due to the Na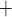 /K
/K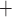 -ATPase pumps, which in fact account for the majority of the energy consumption in the renal medulla. Because the thick limbs are found outside of the vascular bundles, their oxygen supply is severely limited. When oxygen supply is reduced below normal, medullary hypoxic injury can develop. This is illustrated by the kidney's response to ischemia reperfusion which reveals widespread tubular epithelial necrosis and vascular congestion in the outer medulla (Brezis & Rosen, 1995; Okusa et al., 1999). Thus, a goal of this study is to determine the medullary tissue oxygenation levels under physiological and surgical conditions.
-ATPase pumps, which in fact account for the majority of the energy consumption in the renal medulla. Because the thick limbs are found outside of the vascular bundles, their oxygen supply is severely limited. When oxygen supply is reduced below normal, medullary hypoxic injury can develop. This is illustrated by the kidney's response to ischemia reperfusion which reveals widespread tubular epithelial necrosis and vascular congestion in the outer medulla (Brezis & Rosen, 1995; Okusa et al., 1999). Thus, a goal of this study is to determine the medullary tissue oxygenation levels under physiological and surgical conditions.
Diagnosis of AKI is usually based on either an elevation of serum creatinine or the detection of oliguria (production of abnormally small amounts of urine) (Mehta & Chertow, 2003). Serum creatinine is a poor marker of early renal dysfunction, because serum concentration is greatly influenced by numerous non-renal factors (e.g. body weight, race, age, gender, total body volume, drugs, muscle metabolism and protein intake) (Bjornsson, 1979). The utility of serum creatinine is worse in the setting of surgery, because the patients are not in steady state; hence, serum creatinine lags far behind renal injury. As a result, substantial increases in serum creatinine are often not witnessed until 48–72 h after the initial insult to the kidney (Star, 1998; Mehta & Chertow, 2003). In addition, significant renal disease can exist with minimal or no change in creatinine clearance because of renal reserve, enhanced tubular secretion of creatinine or other factors (Bosch, 1995; Herrera & Rodríguez-Iturb e, 1998). Thus, serum creatinine is a poor biomarker of AKI and an alternative that is easily measured, unaffected by other biological variables and capable of both early detection and risk stratification would substantially assist the diagnosis of AKI.
It has been suggested that urine P in the collecting ducts (CDs) would equilibrate with tissue P
in the collecting ducts (CDs) would equilibrate with tissue P of the inner medulla (Evans et al., 2014). Accordingly, the P
of the inner medulla (Evans et al., 2014). Accordingly, the P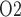 of urine in the renal pelvis may change in response to stimuli that are expected to alter the oxygenation of the renal medulla. To investigate the potential of urinary P
of urine in the renal pelvis may change in response to stimuli that are expected to alter the oxygenation of the renal medulla. To investigate the potential of urinary P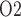 as a biomarker of the risk of AKI in hospital settings, we use a mathematical model of the rat kidney and ureter to assess the extent to which urinary P
as a biomarker of the risk of AKI in hospital settings, we use a mathematical model of the rat kidney and ureter to assess the extent to which urinary P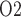 equilibrates with the inner medullary tissue P
equilibrates with the inner medullary tissue P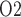 . As previously noted, the renal structures that are most susceptible to hypoxic injuries are the TALs in the outer medulla (Fry et al., 2014). Thus, a secondary goal of this study is to use model simulations to determine the relation between outer-medullary tissue P
. As previously noted, the renal structures that are most susceptible to hypoxic injuries are the TALs in the outer medulla (Fry et al., 2014). Thus, a secondary goal of this study is to use model simulations to determine the relation between outer-medullary tissue P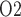 and urinary P
and urinary P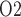 .
.
In a recent study (Sgouralis et al., 2015), we utilized a mathematical model of a single nephron to investigate the extent to which changes in systemic oxygenation during the surgical procedures performed on CPB might alter the medullary oxygenation. Simulations indicate that medullary oxygen extraction is substantially increased during the CPB rewarming phase. Because of the simplicity of that model we were unable to quantify oxygen levels in terms of medullary P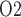 . By applying a much more detailed mathematical model of the renal medulla in this study, we aim to predict tissue and urine P
. By applying a much more detailed mathematical model of the renal medulla in this study, we aim to predict tissue and urine P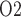 and to elaborate on our previous study.
and to elaborate on our previous study.
2. Mathematical model
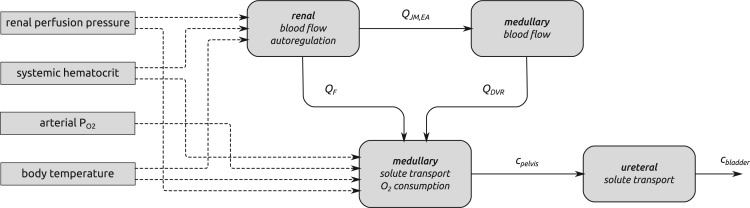
The model represents solute transport in the renal cortex, medulla and ureter of the rat kidney and is based on our previously applied mathematical models of renal haemodynamics (Sgouralis & Layton, 2013, 2014), urine concentrating mechanism (Layton et al., 2012; Moss & Layton, 2014), and oxygen transport (Fry et al., 2014). We combined these models and extended the resulting model to represent oxygen transport along the ureter. For a schematic diagram illustrating the model components and key variables see Fig. 1. Below we highlight key model equations.
FIG. 1.
A summary of the combined model. 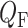 , glomerular filtration rate;
, glomerular filtration rate; 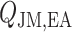 , efferent arteriole blood flow of juxtamedullary nephrons;
, efferent arteriole blood flow of juxtamedullary nephrons; 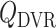 , DVR inflow;
, DVR inflow; 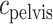 , pelvic, O
, pelvic, O concentration;
concentration;  , bladder O
, bladder O concentration. For details see main text.
concentration. For details see main text.
2.1. Modelling renal blood flow and autoregulation
The cortical component of the model simulates renal blood flow and autoregulation. The model represents afferent arterioles that respond to signals initiated by the myogenic response and tubuloglomerular feedback, which are triggered by variations in vascular blood pressure and macula densa Cl concentrations, respectively (Sgouralis & Layton,2015a). The model afferent arterioles are formed by series of vascular smooth muscle cells, which set the local vascular tone. The local vascular tone may change when an activating signal, initiated by the autoregulatory mechanisms, perturbs the smooth muscle membrane potential. The vascular tone of the smooth muscles is the main determinant of the resistance of the afferent arteriole
concentrations, respectively (Sgouralis & Layton,2015a). The model afferent arterioles are formed by series of vascular smooth muscle cells, which set the local vascular tone. The local vascular tone may change when an activating signal, initiated by the autoregulatory mechanisms, perturbs the smooth muscle membrane potential. The vascular tone of the smooth muscles is the main determinant of the resistance of the afferent arteriole  . Model details can be found in (Chen et al., 2011; Sgouralis et al., 2012; Sgouralis & Layton, 2014, 2015b).
. Model details can be found in (Chen et al., 2011; Sgouralis et al., 2012; Sgouralis & Layton, 2014, 2015b).
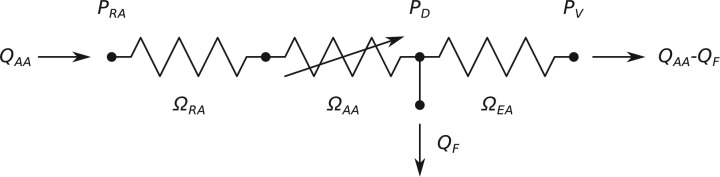
Afferent arteriolar blood flow, 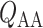 , is determined by pressure drop and vascular resistance according to Poiseuille's law
, is determined by pressure drop and vascular resistance according to Poiseuille's law
| (2.1) |
where 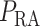 is the renal perfusion pressure (RPP),
is the renal perfusion pressure (RPP), 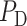 is the blood pressure in the glomerular capillaries,
is the blood pressure in the glomerular capillaries,  is the resistance of the pre-afferent arteriole vasculature (assumed constant) and
is the resistance of the pre-afferent arteriole vasculature (assumed constant) and 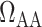 is the resistance of the afferent arteriole, Fig. 2. The latter depends on blood viscosity
is the resistance of the afferent arteriole, Fig. 2. The latter depends on blood viscosity 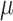 and the radius profile
and the radius profile 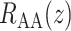 along the afferent arterioles
along the afferent arterioles
| (2.2) |
FIG. 2.
Schematic diagram of the model vasculature. A pre-afferent arteriole vascular resistor (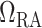 ) delivers blood to the afferent arteriole (
) delivers blood to the afferent arteriole (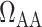 ). At the glomerulus, which is located at the exit of the afferent arteriole, blood is divided between the proximal tubule of the associated nephron (not shown) and the efferent arteriole (
). At the glomerulus, which is located at the exit of the afferent arteriole, blood is divided between the proximal tubule of the associated nephron (not shown) and the efferent arteriole (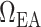 ).
). 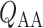 and
and 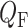 denote blood flow through the afferent arteriole and SNGFR, respectively.
denote blood flow through the afferent arteriole and SNGFR, respectively.  ,
, 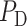 and
and 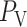 denote the renal perfusion pressure, glomerular capillary pressure and renal venous pressure, respectively.
denote the renal perfusion pressure, glomerular capillary pressure and renal venous pressure, respectively.
Similarly, glomerular capillary pressure 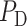 is computed by Poiseuille's law, which, along the efferent arteriole, takes the form
is computed by Poiseuille's law, which, along the efferent arteriole, takes the form
| (2.3) |
where 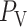 is the pressure in the renal vein (assumed constant),
is the pressure in the renal vein (assumed constant), 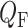 is the single nephron glomerular filtration rate (SNGFR) and
is the single nephron glomerular filtration rate (SNGFR) and 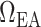 is the resistance of the efferent arteriole.
is the resistance of the efferent arteriole.
2.2. Modelling solute transport and oxygen consumption in the medulla
Based on the predicted blood flow 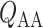 and glomerular capillary pressure
and glomerular capillary pressure 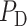 , a glomerular filtration model (Sgouralis & Layton, 2014) is used to predict the SNGFR. The glomerular filtrate is fed into the proximal tubules of the nephrons. The model proximal tubules are assumed to reabsorb a fixed fraction of the filtered water and Na
, a glomerular filtration model (Sgouralis & Layton, 2014) is used to predict the SNGFR. The glomerular filtrate is fed into the proximal tubules of the nephrons. The model proximal tubules are assumed to reabsorb a fixed fraction of the filtered water and Na load and to deliver the remaining load to the descending limbs of the model nephrons, which are located within the renal medulla (details can be found in Moss & Layton (2014)).
load and to deliver the remaining load to the descending limbs of the model nephrons, which are located within the renal medulla (details can be found in Moss & Layton (2014)).
The medullary component of the model simulates tubular transport and oxygen consumption. The model includes loops of Henle, CDs and vasa recta. Tubules and vessels are represented as rigid tubes; some extending from the cortico-medullary boundary to the papillary tip (e.g. the CDs and the longest loops of Henle) and some extending from the cortico-medullary boundary and terminating within the medulla (e.g. the superficial or ‘short’ loops of Henle which turn at the outer-inner medullary boundary). The solutes explicitly considered in the model are Na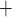 , urea, deoxy- and oxy-haemoglobin (Hb and HbO
, urea, deoxy- and oxy-haemoglobin (Hb and HbO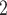 ), O
), O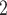 , NO, HbNO and O
, NO, HbNO and O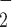 . Together, the cortical and medullary components of the model predict steady-state fluid and solute flows along the renal tubules and interstitial tissue P
. Together, the cortical and medullary components of the model predict steady-state fluid and solute flows along the renal tubules and interstitial tissue P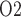 at all levels of the medulla.
at all levels of the medulla.
Detailed transport equations can be found in our previous study (Fry et al., 2015) and the references therein. In general, conservation of solute 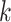 along a tubule or vessel
along a tubule or vessel 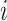 is given by
is given by
| (2.4) |
where 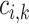 denotes solute concentration,
denotes solute concentration, 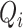 denotes fluid flow,
denotes fluid flow, 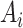 denotes tubular cross-sectional area and
denotes tubular cross-sectional area and 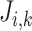 denotes transmural solute flux. For a non-reactive solute (e.g. Na
denotes transmural solute flux. For a non-reactive solute (e.g. Na and urea), the reaction term
and urea), the reaction term 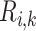 is set to zero; for others,
is set to zero; for others,  includes production, consumption and biochemical reactions.
includes production, consumption and biochemical reactions.
Along some of the nephron segments, e.g. the proximal straight tubules (PSTs), TALs and CDs, Na is actively reabsorbed via basolateral Na
is actively reabsorbed via basolateral Na /K
/K -ATPase pumps. The model assumes that T
-ATPase pumps. The model assumes that T -to-Q
-to-Q (TQ, where T
(TQ, where T denotes the moles of Na
denotes the moles of Na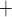 transported and QO2 denotes the moles of oxygen consumed) ratios are fixed at 18 for the TALs and PSTs and 12 for the CDs, based on tubular epithelial transport simulations (Weinstein, 1998; Nieves-Gonzalez et al., 2013). We further assume that below some critical P
transported and QO2 denotes the moles of oxygen consumed) ratios are fixed at 18 for the TALs and PSTs and 12 for the CDs, based on tubular epithelial transport simulations (Weinstein, 1998; Nieves-Gonzalez et al., 2013). We further assume that below some critical P (denoted
(denoted 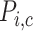 for tubule
for tubule 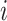 ), anaerobic metabolism maintains some fraction (denoted
), anaerobic metabolism maintains some fraction (denoted 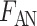 ) of the energy required to actively transport Na
) of the energy required to actively transport Na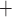 . The rate of active oxygen consumption in the epithelia of the PSTs, TALs and CDs is then given by
. The rate of active oxygen consumption in the epithelia of the PSTs, TALs and CDs is then given by
| (2.5) |
where TQ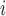 is the TQ ratio,
is the TQ ratio, 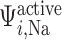 is the Na
is the Na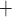 active transport rate and
active transport rate and 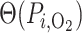 is the fraction that is supported by aerobic respiration. The latter is given by
is the fraction that is supported by aerobic respiration. The latter is given by
| (2.6) |
The active Na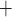 transport rate
transport rate 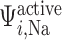 is characterized by Michaelis–Menten kinetics
is characterized by Michaelis–Menten kinetics
| (2.7) |
where 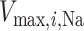 is the maximal rate of Na
is the maximal rate of Na transport (in unit of nmol/(cm
transport (in unit of nmol/(cm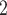 s)) and
s)) and  is the Michaelis constant (in unit of mM).
is the Michaelis constant (in unit of mM).
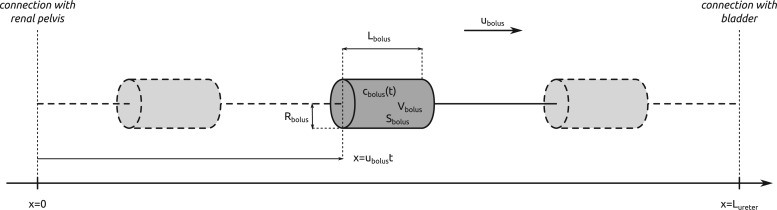
2.3. Modelling solute transport along the ureter
To predict bladder urinary P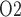 , we extended the renal model to represent oxygen transport along the ureter. The model ureter extends between
, we extended the renal model to represent oxygen transport along the ureter. The model ureter extends between 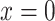 (connection with the renal pelvis) and
(connection with the renal pelvis) and 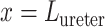 (connection with the bladder); see Fig. 3. Urine is transported along the ureter in boluses by peristaltic pumping of the ureter walls. The ureter is water impermeable (Kreft et al., 2010); thus, as the urine bolus moves through the ureter, its volume (
(connection with the bladder); see Fig. 3. Urine is transported along the ureter in boluses by peristaltic pumping of the ureter walls. The ureter is water impermeable (Kreft et al., 2010); thus, as the urine bolus moves through the ureter, its volume (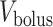 ) remains unchanged. In contrast, oxygen may diffuse across the ureter epithelium. We assume a uniform oxygen concentration in the urine bolus, denoted
) remains unchanged. In contrast, oxygen may diffuse across the ureter epithelium. We assume a uniform oxygen concentration in the urine bolus, denoted 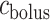 and seek to track its change as the bolus moves from the CD (i.e. renal pelvis) to the bladder. Bolus oxygen conservation is given by
and seek to track its change as the bolus moves from the CD (i.e. renal pelvis) to the bladder. Bolus oxygen conservation is given by
| (2.8) |
where 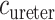 is the oxygen concentration along the ureter walls, assumed uniform throughout the length of the ureter.
is the oxygen concentration along the ureter walls, assumed uniform throughout the length of the ureter. 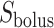 denotes the surface area of the bolus, and
denotes the surface area of the bolus, and 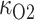 is the oxygen permeability of the ureter epithelium. The initial time (
is the oxygen permeability of the ureter epithelium. The initial time (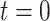 ) is taken to be the time that the bolus exits the collecting duct. Thus
) is taken to be the time that the bolus exits the collecting duct. Thus 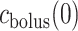 is equal to the oxygen concentration of the CD outflow (denoted
is equal to the oxygen concentration of the CD outflow (denoted 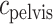 ), which is predicted by the medullary model.
), which is predicted by the medullary model.
FIG. 3.
Schematic diagram of the model ureter. Peristaltic boluses of volume 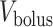 and contact area
and contact area 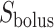 travel from the renal pelvis (left) to the bladder (right) at a speed
travel from the renal pelvis (left) to the bladder (right) at a speed 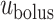 .
. 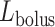 and
and 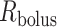 characterize the bolus' dimensions.
characterize the bolus' dimensions.
We assume that the bolus travels at a uniform speed of 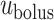 , which corresponds to the speed of the peristaltic wave. Thus, the time needed for a bolus to reach the bladder is
, which corresponds to the speed of the peristaltic wave. Thus, the time needed for a bolus to reach the bladder is 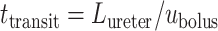 . Integrating (2.8), we determine the urinary oxygen concentration in the bladder (i.e.
. Integrating (2.8), we determine the urinary oxygen concentration in the bladder (i.e. 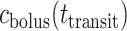 , denoted
, denoted 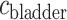 ) to be
) to be
| (2.9) |
If one assumes that the model bolus is a column of fluid with radius 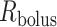 and length
and length 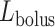 , as shown on Fig. 3, then
, as shown on Fig. 3, then 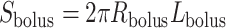 and
and 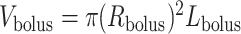 , which implies
, which implies 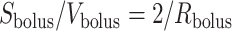 . Thus, (2.9) becomes
. Thus, (2.9) becomes
| (2.10) |
Typical values for the rat ureter are 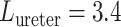 cm (Onyeanusi et al., 2009) and
cm (Onyeanusi et al., 2009) and 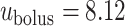 mm/s (Tillig & Constantinou, 1996). We use
mm/s (Tillig & Constantinou, 1996). We use 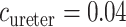 mM that corresponds to a tissue P
mM that corresponds to a tissue P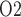 of 30 mmHg. Oxygen permeability is computed by
of 30 mmHg. Oxygen permeability is computed by 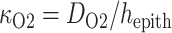 , where
, where 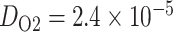 cm
cm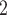 /s is the oxygen diffusion coefficient, and
/s is the oxygen diffusion coefficient, and 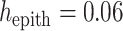 mm is the thickness of the ureter epithelium in rats (Wolf et al., 1996). Bolus radius
mm is the thickness of the ureter epithelium in rats (Wolf et al., 1996). Bolus radius 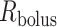 is taken to be 0.36 mm, which, given a baseline urine flow of
is taken to be 0.36 mm, which, given a baseline urine flow of 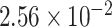 ml/min, as predicted by the medullary model at baseline, corresponds to a bolus length of 3.1 mm (Tillig & Constantinou,1996).
ml/min, as predicted by the medullary model at baseline, corresponds to a bolus length of 3.1 mm (Tillig & Constantinou,1996).
2.4. Modelling medullary blood flow
A major determinant of medullary oxygen levels is medullary blood flow, which is modulated by vasopressin, the antidiuretic hormone (Cowley, 2000). The degree to which medullary blood flow is autoregulated appears to depend on the hydration status of the animal (Cupples & Marsh, 1988; Roman et al., 1988; Mattson et al., 1991, 1993; Franchini et al., 1997), and has not been well characterized for patients or animals undergoing surgery performed under CPB. Given that uncertainty, we assume that medullary blood flow depends linearly on the efferent arteriole blood flow of the juxtamedullary nephrons, denoted QJM,EA, which the oxygen-supplying DVR stem from. That is, DVR inflow (specified at the cortico-medullary boundary) is given by
| (2.11) |
The reference DVR flow 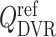 and juxtamedullary efferent arteriolar flow
and juxtamedullary efferent arteriolar flow 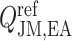 are taken to be 8 and 300 nl/min, respectively, in agreement with the baseline values of our previous modelling study (Fry et al., 2014). The case where
are taken to be 8 and 300 nl/min, respectively, in agreement with the baseline values of our previous modelling study (Fry et al., 2014). The case where 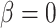 corresponds to perfect autoregulation of medullary blood flow, in which
corresponds to perfect autoregulation of medullary blood flow, in which 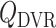 is independent of renal blood flow. The case where
is independent of renal blood flow. The case where 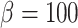 % corresponds to complete absence of medullary blood flow autoregulation, in which
% corresponds to complete absence of medullary blood flow autoregulation, in which 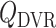 depends on renal blood flow.
depends on renal blood flow.
2.5. Modelling the effects of hypothermia
During the main phase of the cardiac surgery, the patient's body temperature is usually lowered (Andersson et al., 1994). Body temperature has multiple systemic and renal effects, as discussed in Sgouralis et al. (2015). Notably, body temperature has a profound effect on the metabolic rate. In the context of renal function, body temperature affects the active reabsorption of Na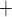 . This is represented in the model as a linear dependence of the maximum transport rate, i.e.
. This is represented in the model as a linear dependence of the maximum transport rate, i.e. 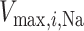 in (2.7), on body temperature (
in (2.7), on body temperature (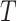 ):
):
| (2.12) |
where 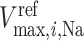 denotes the maximum Na
denotes the maximum Na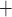 transport rate at a baseline body temperature of
transport rate at a baseline body temperature of 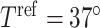 C and
C and 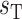 characterizes the sensitivity to
characterizes the sensitivity to 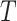 . We use
. We use 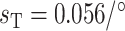 C such that the predicted Na
C such that the predicted Na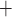 excretion at 28
excretion at 28 C increases
C increases 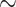 3.1-fold from baseline, consistent with the experimental data in Broman & Källskog (1995).
3.1-fold from baseline, consistent with the experimental data in Broman & Källskog (1995).
Other temperature-dependent effects of hypothermia that are incorporated in the model include (i) elevation of afferent arteriole myocyte cytosolic [Ca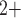 ], which affects the vascular tone of the afferent arteriolar smooth muscles and thus the resistance
], which affects the vascular tone of the afferent arteriolar smooth muscles and thus the resistance  ; (ii) vasoconstriction of the efferent arteriole, which affects efferent arteriole vascular resistance
; (ii) vasoconstriction of the efferent arteriole, which affects efferent arteriole vascular resistance  ; (iii) increase in plasma and tubular fluid viscosities, which also affects afferent and efferent arteriole vascular resistances
; (iii) increase in plasma and tubular fluid viscosities, which also affects afferent and efferent arteriole vascular resistances  and
and 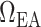 as well as glomerular filtration and (iv) decrease in glomerular ultrafiltration coefficient, which also affects glomerular filtration (Broman & Källskog, 1995). A detailed description of how these effects are modelled can be found in Sgouralis et al. (2015).
as well as glomerular filtration and (iv) decrease in glomerular ultrafiltration coefficient, which also affects glomerular filtration (Broman & Källskog, 1995). A detailed description of how these effects are modelled can be found in Sgouralis et al. (2015).
We have validated our approach of modelling hypothermia; a detailed summary of model predictions and a comparison with the available data reported in Broman & Källskog (1995) can be found in the Supplemental Materials.
3. Results
3.1. Baseline predictions
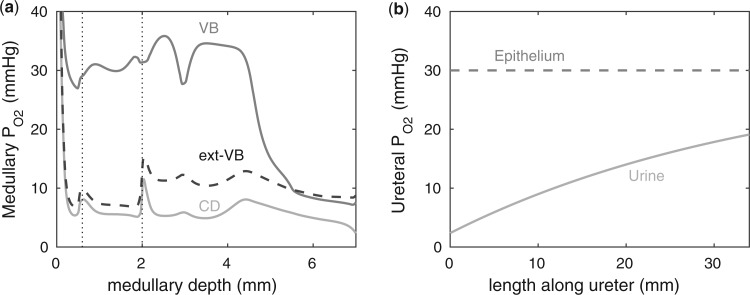
We first compute model solutions for a rat kidney, in anti-diuretic status, under baseline haemodynamics conditions (for haemodynamics parameters see Table 1, column labelled ‘Baseline’). Figure 4a shows medullary P profiles for the interstitial fluid near the long DVR (which are located centrally within the vascular bundles; curve labelled ‘VB’), for the interstitial fluid exterior to the vascular bundles (where the medullary TALs are located; curve labelled ‘ext-VB’) and for the luminal fluid along the CD (curve labelled ‘CD’).
profiles for the interstitial fluid near the long DVR (which are located centrally within the vascular bundles; curve labelled ‘VB’), for the interstitial fluid exterior to the vascular bundles (where the medullary TALs are located; curve labelled ‘ext-VB’) and for the luminal fluid along the CD (curve labelled ‘CD’).
We first consider the myogenic response (i.e. upper 2 mm of the medulla). Because of the sequestration of the DVR within the vascular bundles, away from the TALs which have high metabolic demands, a substantial P radial gradient can be observed in the outer medulla, as indicated by the difference between interstitial fluid P
radial gradient can be observed in the outer medulla, as indicated by the difference between interstitial fluid P inside and outside the vascular bundle (compare ‘VB’ and ‘ext-VB’). In the outer medulla, the lowest interstitial P
inside and outside the vascular bundle (compare ‘VB’ and ‘ext-VB’). In the outer medulla, the lowest interstitial P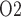 , which is 6.8 mmHg, is predicted in the interbundle region in inner stripe (i.e. upper 0.6 mm). %Interstitial P
, which is 6.8 mmHg, is predicted in the interbundle region in inner stripe (i.e. upper 0.6 mm). %Interstitial P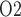 over the deepest 0.2 mm of the inner stripe decrease from 31.9 mmHg (region R1) to 6.9 mmHg (region R4). Over the same spatial domain, P
over the deepest 0.2 mm of the inner stripe decrease from 31.9 mmHg (region R1) to 6.9 mmHg (region R4). Over the same spatial domain, P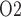 in the short ascending limb (profile not shown) is 5.2 mmHg, and in the collecting duct 5.4 mmHg.
in the short ascending limb (profile not shown) is 5.2 mmHg, and in the collecting duct 5.4 mmHg.
In the myogenic response (i.e. the lower 5 mm of the medulla), the thin ascending limbs do not engage in active Na transport. Nonetheless, a P
transport. Nonetheless, a P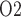 radial gradient can also be found in the upper inner medulla, where the DVR are separated from the CDs that have substantial Na
radial gradient can also be found in the upper inner medulla, where the DVR are separated from the CDs that have substantial Na /K
/K -ATPase activities. In the lowest 1.5 mm of the inner medulla, the arrangement of tubules and vessel becomes homogeneous (Pannabecker et al., 2004) and the P
-ATPase activities. In the lowest 1.5 mm of the inner medulla, the arrangement of tubules and vessel becomes homogeneous (Pannabecker et al., 2004) and the P radial gradient vanishes. The CD luminal fluid P
radial gradient vanishes. The CD luminal fluid P varies substantially along the inner medulla, decreasing from 5.2 mmHg near the inner-outer medullary boundary to 2.4 mmHg at the papillary tip (i.e. the lowest point in medulla).
varies substantially along the inner medulla, decreasing from 5.2 mmHg near the inner-outer medullary boundary to 2.4 mmHg at the papillary tip (i.e. the lowest point in medulla).
Figure 4b shows urinary P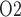 along the myogenic response. The ureter is contiguous with the inner-medullary CD, thus urinary P
along the myogenic response. The ureter is contiguous with the inner-medullary CD, thus urinary P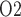 at the ureter entrance is the same as that of CD outflow. Because the ureter is situated in a well-perfused region, the P
at the ureter entrance is the same as that of CD outflow. Because the ureter is situated in a well-perfused region, the P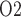 of the ureter walls is relatively high, at 30 mmHg. The resulting diffusive entry of oxygen raises urinary P
of the ureter walls is relatively high, at 30 mmHg. The resulting diffusive entry of oxygen raises urinary P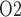 from 2.4 to 19.1 mmHg within the bladder. Thus, baseline bladder P
from 2.4 to 19.1 mmHg within the bladder. Thus, baseline bladder P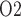 is 12.3 mmHg higher than the lowest interstitial P
is 12.3 mmHg higher than the lowest interstitial P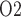 in the inner stripe. That difference is attributed in large part to the P
in the inner stripe. That difference is attributed in large part to the P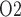 increase in the urine as it travels along the ureter.
increase in the urine as it travels along the ureter.
3.2. Effects of systemic factors on renal function and oxygenation
In the next set of simulations, we investigate the effects of varying systemic factors on renal blood flow, renal oxygenation and urinary P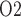 . Specifically, we consider the effects of RRP (
. Specifically, we consider the effects of RRP (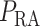 in (2.1)), systemic haematocrit (the fraction of arterial blood
in (2.1)), systemic haematocrit (the fraction of arterial blood 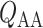 that is accounted for by red blood cells), arterial P
that is accounted for by red blood cells), arterial P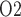 and body temperature; these parameters correspond to haemodynamics factors that play a key role in renal health following cardiac surgery under CPB (Andersson et al., 1994; Sgouralis et al., 2015). Given the uncertainty in the degree of medullary blood flow autoregulation (see Section 2.4), we consider three cases: myogenic response, where we assume perfect autoregulation of medullary blood flow by setting
and body temperature; these parameters correspond to haemodynamics factors that play a key role in renal health following cardiac surgery under CPB (Andersson et al., 1994; Sgouralis et al., 2015). Given the uncertainty in the degree of medullary blood flow autoregulation (see Section 2.4), we consider three cases: myogenic response, where we assume perfect autoregulation of medullary blood flow by setting 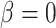 in (2.11) (referred to as ‘perfect autoreg’); myogenic response, where we set
in (2.11) (referred to as ‘perfect autoreg’); myogenic response, where we set 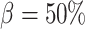 , leading to imperfect medullary blood flow autoregulation (‘partial autoreg’) and myogenic response, where we assume no autoregulation so that medullary blood flow changes proportionally to renal blood flow by setting
, leading to imperfect medullary blood flow autoregulation (‘partial autoreg’) and myogenic response, where we assume no autoregulation so that medullary blood flow changes proportionally to renal blood flow by setting 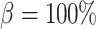 (‘no autoreg’).
(‘no autoreg’).
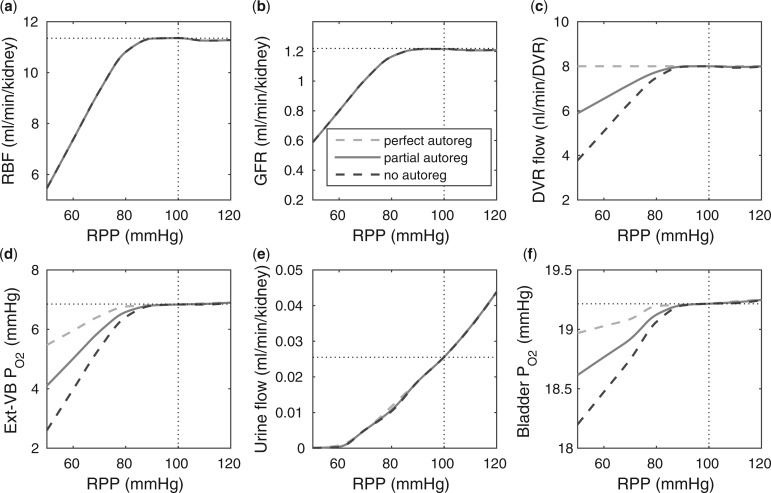
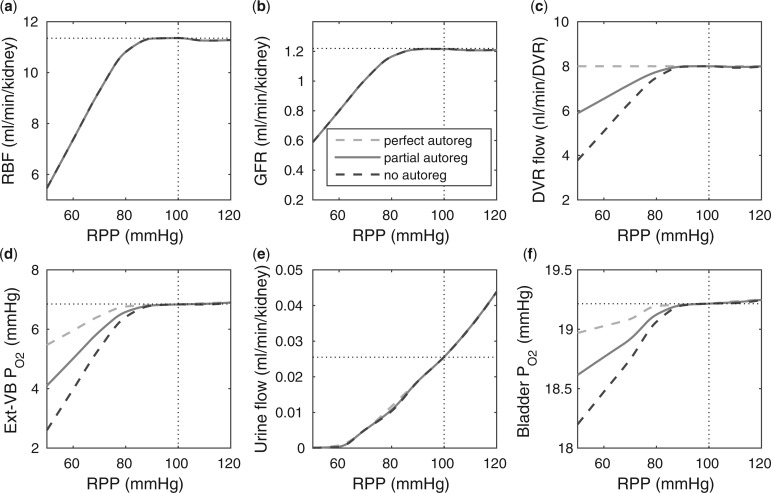
Renal perfusion pressure.
We varied RPP over the range of 50–120 mmHg. For RPP above  80 mmHg, the autoregulatory response of the afferent arterioles sufficiently compensates to maintain a stable renal blood flow and glomerular filtration rate (see Fig. 5a and b), resulting in essentially no change in medullary oxygenation and urinary P
80 mmHg, the autoregulatory response of the afferent arterioles sufficiently compensates to maintain a stable renal blood flow and glomerular filtration rate (see Fig. 5a and b), resulting in essentially no change in medullary oxygenation and urinary P (Fig. 5d and f). The increase in urine flow as RPP increases (Fig. 5e) is due to the pressure natriuresis/diuresis response, which reduces proximal tubule Na
(Fig. 5d and f). The increase in urine flow as RPP increases (Fig. 5e) is due to the pressure natriuresis/diuresis response, which reduces proximal tubule Na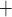 and water reabsorption as blood pressure increases. For RPP above 80 mmHg, all three cases predict essentially the same trends.
and water reabsorption as blood pressure increases. For RPP above 80 mmHg, all three cases predict essentially the same trends.
FIG. 5.
Effects of variations in RPP on: (a), renal blood flow; (b) glomerular filtration rate; (c) DVR flow at the cortico-medullary boundary; (d) interstitial fluid P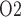 in the lower inner stripe outside the vascular bundles; (e) urine flow and (f) urinary P
in the lower inner stripe outside the vascular bundles; (e) urine flow and (f) urinary P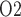 in the bladder. Results were computed for three different scenarios of medullary blood flow autoregulation. Dotted lines indicate baseline values.
in the bladder. Results were computed for three different scenarios of medullary blood flow autoregulation. Dotted lines indicate baseline values.
For RPP below 80 mmHg, the afferent arterioles' autoregulatory response fails to completely compensate, resulting in lower arteriolar flow, glomerular filtration rate and urine flow (Fig. 5a, b, and e). The effect on medullary oxygenation depends on how medullary blood flow is regulated (compare the three curves in Fig. 5c). As RPP is reduced, medullary and urine P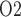 decrease less drastically when medullary blood flow is better regulated (Fig. 5d and f). In particular, although in the ‘no autoreg’ case bladder urinary P
decrease less drastically when medullary blood flow is better regulated (Fig. 5d and f). In particular, although in the ‘no autoreg’ case bladder urinary P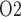 decreases approximately linearly from 19.3 to 18.3 mmHg as RPP decreases from 100 to 50 mmHg, the ‘perfect autoreg’ case and, to a lesser extent, the ‘partial autoreg’ case predict lower changes in bladder's urinary PO2(∼0.3 and ∼0.5 mmHg, respectively, see Fig. 5f).
decreases approximately linearly from 19.3 to 18.3 mmHg as RPP decreases from 100 to 50 mmHg, the ‘perfect autoreg’ case and, to a lesser extent, the ‘partial autoreg’ case predict lower changes in bladder's urinary PO2(∼0.3 and ∼0.5 mmHg, respectively, see Fig. 5f).
Systemic hematocrit.
As in our previous study (Sgouralis et al., 2015), we assume a linear relationship between systemic and medullary hematocrits, denoted Htc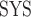 and Htc
and Htc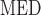 , respectively. Given that under baseline conditions, Htc
, respectively. Given that under baseline conditions, Htc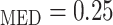 and Htc
and Htc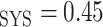 , we assume that systemic and medullary hematocrits vary myogenic response according to
, we assume that systemic and medullary hematocrits vary myogenic response according to
| (3.1) |
Key model results are shown in Fig. 6. A higher hematocrit leads to elevated blood viscosity (Pries et al., 1994) and thus reduced blood flow (Fig. 6a), lower glomerular filtration (Fig. 6b), and lower urine flow (Fig. 6e). It is noteworthy that the ‘perfect autoreg’ and the ‘no autoreg’ cases predict different trends in medullary and urinary P . Increasing hematocrit in the ‘no autoreg’ case has two competing effects on medullary oxygenation: the elevated blood viscosity reduces arteriolar flow and thus medullary blood flow (Fig. 6c), but the oxygen-carrying capacity of the blood is increased. These two opposing effects result in limited changes in medullary and bladder P
. Increasing hematocrit in the ‘no autoreg’ case has two competing effects on medullary oxygenation: the elevated blood viscosity reduces arteriolar flow and thus medullary blood flow (Fig. 6c), but the oxygen-carrying capacity of the blood is increased. These two opposing effects result in limited changes in medullary and bladder P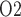 ; see Fig. 6d and f. In contrast, when medullary blood flow is fixed (in the ‘perfect autoreg’ case), a higher hematocrit increases medullary oxygen delivery, resulting in elevated medullary and urinary P
; see Fig. 6d and f. In contrast, when medullary blood flow is fixed (in the ‘perfect autoreg’ case), a higher hematocrit increases medullary oxygen delivery, resulting in elevated medullary and urinary P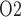 ; see Fig. 6c and f. Predictions of the ‘partial autoreg’ case lie between the two extreme cases.
; see Fig. 6c and f. Predictions of the ‘partial autoreg’ case lie between the two extreme cases.
FIG. 6.
Effects of variations in systemic hematocrit (Htc) on: (a) renal blood flow; (b) glomerular filtration rate; (c) DVR flow at the cortico-medullary boundary; (d) interstitial fluid P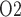 in the lower inner stripe outside the vascular bundles; (e) urine flow and (f) urinary P
in the lower inner stripe outside the vascular bundles; (e) urine flow and (f) urinary P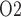 in the bladder. Results were computed for three different scenarios of medullary blood flow autoregulation. Dotted lines indicate baseline values.
in the bladder. Results were computed for three different scenarios of medullary blood flow autoregulation. Dotted lines indicate baseline values.
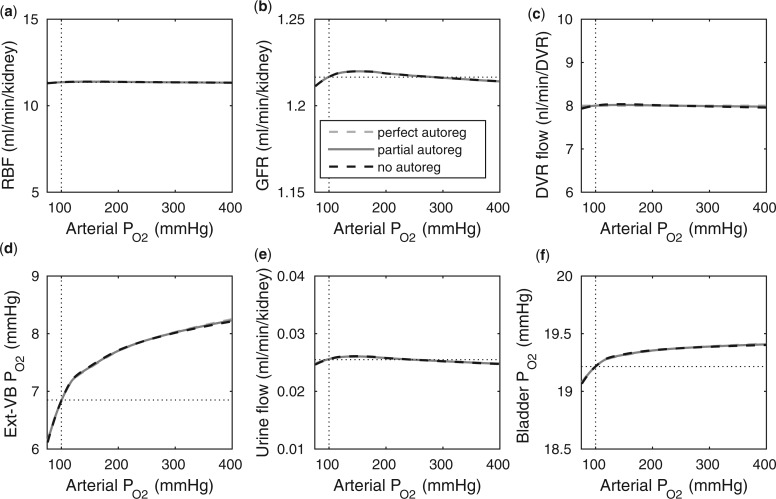
Arterial P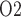 .
.
To model the effects of arterial P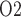 , we assume that plasma and RBC P
, we assume that plasma and RBC P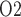 of the model DVR depend linearly on the P
of the model DVR depend linearly on the P of the arterial blood. We assume that under baseline conditions, DVR plasma and RBC P
of the arterial blood. We assume that under baseline conditions, DVR plasma and RBC P (denoted
(denoted 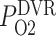 ) is 60% that of the arterial blood P
) is 60% that of the arterial blood P (denoted
(denoted 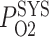 ) (Chen et al., 2009). When arterial P
) (Chen et al., 2009). When arterial P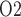 deviates from its baseline value, DVR P
deviates from its baseline value, DVR P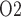 varies proportionally, i.e.
varies proportionally, i.e. 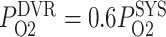 . Arterial P
. Arterial P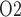 was varied from 75 to 400 mmHg; key model results are shown in Fig. 7.
was varied from 75 to 400 mmHg; key model results are shown in Fig. 7.
FIG. 7.
Effects of variations in arterial P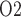 on: (a) renal blood flow; (b) glomerular filtration rate; (c) DVR flow at the cortico-medullary boundary; (d) interstitial fluid P
on: (a) renal blood flow; (b) glomerular filtration rate; (c) DVR flow at the cortico-medullary boundary; (d) interstitial fluid P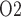 in the lower inner stripe outside the vascular bundles; (e) urine flow and (f) urinary P
in the lower inner stripe outside the vascular bundles; (e) urine flow and (f) urinary P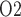 in the bladder. Results were computed for three different scenarios of medullary blood flow autoregulation. Dotted lines indicate baseline values.
in the bladder. Results were computed for three different scenarios of medullary blood flow autoregulation. Dotted lines indicate baseline values.
Because arterial P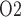 has no effect on renal blood flow (Fig. 7a), all three cases predict essentially the same results: glomerular filtration rate, medullary blood flow, and urine flow are minimally affected by variations in arterial P
has no effect on renal blood flow (Fig. 7a), all three cases predict essentially the same results: glomerular filtration rate, medullary blood flow, and urine flow are minimally affected by variations in arterial P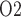 (Fig. 7b, c, and e), whereas medullary P
(Fig. 7b, c, and e), whereas medullary P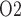 and urinary P
and urinary P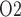 increase as arterial P
increase as arterial P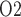 increases (Fig. 7d and f).
increases (Fig. 7d and f).
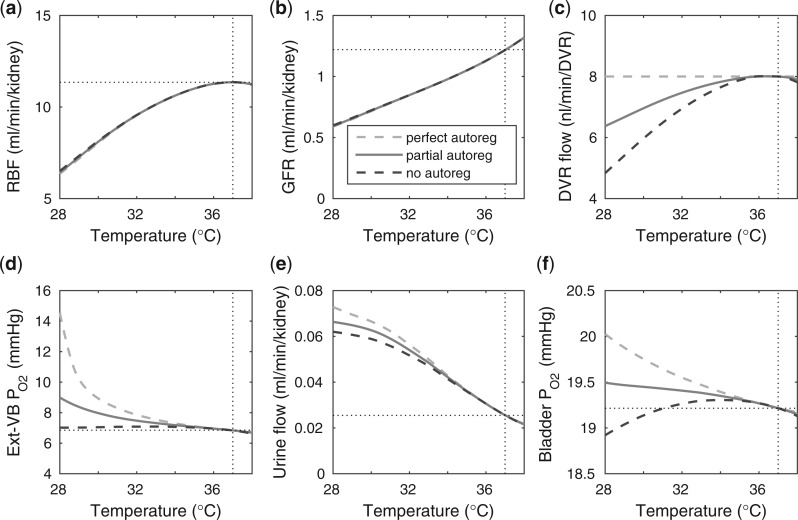
Body temperature.
Key simulation results that characterize the effects of body temperature on medullary oxygenation and renal function are shown in Fig. 8. At cooler temperatures, blood viscosity increases and vascular smooth muscles constrict (Broman & Källskog, 1995; Sgouralis et al., 2015), resulting in reduced blood flow (see Fig. 8a) and GFR (see Fig. 8b). But, perhaps more importantly, the body's metabolism slows down at lower temperatures. In the context of renal function, this leads to reduced active Na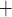 transport rate, which impedes water withdrawal from the CD, resulting in higher urine flow (Fig. 8e).
transport rate, which impedes water withdrawal from the CD, resulting in higher urine flow (Fig. 8e).
FIG. 8.
Effects of variations in body temperature on (a) renal blood flow; (b) glomerular filtration rate; (c) DVR flow at the cortico-medullary boundary; (d) interstitial fluid P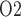 in the lower inner stripe outside the vascular bundles; (e), urine flow and (f), urinary P
in the lower inner stripe outside the vascular bundles; (e), urine flow and (f), urinary P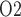 in the bladder. Results were computed for three different scenarios of medullary blood flow autoregulation. Dotted lines indicate baseline values.
in the bladder. Results were computed for three different scenarios of medullary blood flow autoregulation. Dotted lines indicate baseline values.
Interestingly, the ‘perfect autoreg’ case and the ‘no autoreg’ case predict opposite effects on medullary and urinary P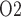 as body temperature is lowered. As previously noted, the active Na
as body temperature is lowered. As previously noted, the active Na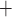 transport rate and the associated oxygen consumption decrease at lower temperature. Thus, in the ‘perfect autoreg’ case, where medullary blood flow and oxygen supply are fixed, medullary P
transport rate and the associated oxygen consumption decrease at lower temperature. Thus, in the ‘perfect autoreg’ case, where medullary blood flow and oxygen supply are fixed, medullary P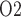 doubles and urinary P
doubles and urinary P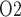 increases by
increases by 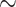 1 mmHg as temperature decreases from 37 to 28
1 mmHg as temperature decreases from 37 to 28 C. In contrast, in the ‘no autoreg’ case, medullary blood flow reflects the decrease in renal blood flow at lower temperature (Fig. 8c). The competing effects of reduced oxygen consumption and reduced oxygen supply result in a relatively constant medullary P
C. In contrast, in the ‘no autoreg’ case, medullary blood flow reflects the decrease in renal blood flow at lower temperature (Fig. 8c). The competing effects of reduced oxygen consumption and reduced oxygen supply result in a relatively constant medullary P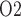 and decreasing urinary P
and decreasing urinary P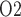 at sufficiently lower temperatures. Predictions of the ‘partial autoreg’ case lie between the two extreme cases.
at sufficiently lower temperatures. Predictions of the ‘partial autoreg’ case lie between the two extreme cases.
3.3. Renal oxygenation under CPB
In the next set of simulations, we aim to identify the phase of the cardiac surgery performed under CPB when the kidney is most vulnerable to hypoxic injury. As in our previous study (Sgouralis et al., 2015), four CPB phases were considered: (i) pre-CPB, defined as the period following induction of anaesthesia and prior to initiation of CPB; (ii) CPB-hypothermia, the hypothermic period of the surgery (iii) CPB-rewarming, the normothermic period of the surgery; and (iv) post-CPB, the post-surgical period in which the effects of haemodilution and anaesthesia persist. Because of the uncertainty on the degree of medullary blood flow autoregulation, we repeated every simulation for the three cases of Section 3.2. Namely, these cases are ‘perfect autoreg’, ‘partial autoreg’, and ‘no autoreg’.
Model parameters for the CPB phases are given in Table 1. The chosen values are typical of those encountered during CPB in humans (Andersson et al., 1994). In particular, during the hypothermic CPB phase, body temperature is lowered to 28  C.1 Other differences among the four CPB phases include:
C.1 Other differences among the four CPB phases include:
(1) In part due to the effects of anaesthesia, RPP is lower than baseline in all four phases but particularly so during the hypothermic and rewarming phases during which the patient‘s circulation is externally driven (Andersson et al., 1994).
(2) Except for the pre-CPB phase, systemic haematocrit is substantially lower than normal due to the requirement of a priming solution within the extracorporeal circuit (Andersson et al., 1994).
(3) During the hypothermic and rewarming CPB phases, the impact of haemodilution on oxygen delivery is partially compensated by the ventilation of the patient with almost 100% oxygen.
Table 1.
Summary of simulated baseline and CPB phases. These values are typical of those encountered during CPB surgery (Andersson et al., 1994).
| Parameter | Baseline | Pre-CPB | Hypo-CPB | Rewarm-CPB | Post-CPB | Units |
|---|---|---|---|---|---|---|
| RPP | 100 | 75 | 50 | 50 | 75 | mmHg |
| Arterial PO2 | 100 | 100 | 400 | 400 | 100 | mmHg |
| Systemic hematocrit | 45 | 45 | 25 | 25 | 25 | % |
| Body temperature | 37 | 37 | 28 | 37 | 37 | °C |
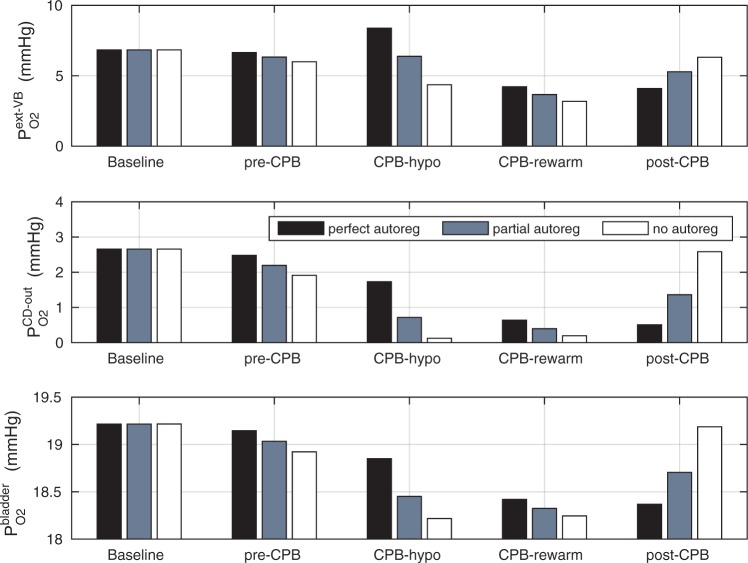
A comparison of renal oxygenation is shown on Fig. 9. One may view the P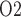 of the extra-bundle region in the inner stripe as an indicator for the risk of AKI, inasmuch as the inner stripe is the least oxygenated region of the outer medulla and contains the vulnerable medullary TALs. In terms of the relative risk for AKI during the CPB phases, it is interesting that the model yields rather different predictions depending on the degree to which medullary blood flow is regulated.
of the extra-bundle region in the inner stripe as an indicator for the risk of AKI, inasmuch as the inner stripe is the least oxygenated region of the outer medulla and contains the vulnerable medullary TALs. In terms of the relative risk for AKI during the CPB phases, it is interesting that the model yields rather different predictions depending on the degree to which medullary blood flow is regulated.
FIG 9.
Renal oxygenation during CPB surgery. Top panel, interstitial fluid P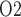 in the interbundle region in the lower inner stripe of the outer medulla. Middle panel, fluid P
in the interbundle region in the lower inner stripe of the outer medulla. Middle panel, fluid P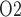 at the CD outlet (i.e. renal pelvis). Bottom panel, urinary P
at the CD outlet (i.e. renal pelvis). Bottom panel, urinary P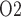 in the bladder. Results were obtained for the five phases of Table 1 each for three different degrees of medullary blood flow regulation.
in the bladder. Results were obtained for the five phases of Table 1 each for three different degrees of medullary blood flow regulation.
Pre-CPB phase.
When perfect medullary blood flow autoregulation is assumed, the model predicts slight reductions during the pre-CPB phase in the inner stripe, CD and bladder urine P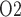 (
( 0.2, 0.2, 0.1 mmHg, respectively). The pre-CPB phase differs from baseline only in having a lower RPP (75 vs. 100 mmHg), which, owing to the compensatory response of the autoregulatory mechanisms, results in minimal change in glomerular filtration rate and no change in medullary blood flow (fixed in the ‘perfect autoreg’ case). Reductions in P
0.2, 0.2, 0.1 mmHg, respectively). The pre-CPB phase differs from baseline only in having a lower RPP (75 vs. 100 mmHg), which, owing to the compensatory response of the autoregulatory mechanisms, results in minimal change in glomerular filtration rate and no change in medullary blood flow (fixed in the ‘perfect autoreg’ case). Reductions in P become more substantial as the degree of autoregulation decreases. In the absence of medullary blood flow autoregulation, the pre-CPB phase is predicted to yield substantially lower medullary and bladder urine P
become more substantial as the degree of autoregulation decreases. In the absence of medullary blood flow autoregulation, the pre-CPB phase is predicted to yield substantially lower medullary and bladder urine P than baseline (
than baseline ( 0.6 and 0.2 mmHg, respectively). At a RPP of 75 mmHg, the ‘no autoreg’ model predicts 9% and 8% reductions in medullary blood flow and glomerular filtration rate, respectively. Together, these changes result in a 12% reduction in inner-stripe interstitial fluid P
0.6 and 0.2 mmHg, respectively). At a RPP of 75 mmHg, the ‘no autoreg’ model predicts 9% and 8% reductions in medullary blood flow and glomerular filtration rate, respectively. Together, these changes result in a 12% reduction in inner-stripe interstitial fluid P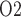 .
.
CPB-hypothermic phase.
Haemodilution begins during the hypothermic phase of CPB. Taken in isolation, the lower blood viscosity in haemodilution would increase blood flow. However, during surgery RPP is further reduced to 50 mmHg, at which point renal autoregulation can no longer compensate for the pressure variations and stabilize glomerular filtration rate. Altogether, these factors result in a 39% reduction in arteriolar blood flow and a 62% reduction in glomerular filtration rate. With medullary blood flow fixed (‘perfect autoreg’), haemodilution leads to a 45% reduction in medullary oxygen delivery. But interestingly, the model predicts that inner-stripe P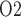 is the highest during the hypothermic CPB phase. In fact, the predicted inner-stripe P
is the highest during the hypothermic CPB phase. In fact, the predicted inner-stripe P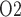 exceeds even that of base case. This counter-intuitive result may be attributed to hypothermia, which substantially reduces active Na
exceeds even that of base case. This counter-intuitive result may be attributed to hypothermia, which substantially reduces active Na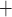 transport and oxygen consumption and to the model‘s assumption that medullary blood flow remains at baseline value. In the hypothermic CPB phase, the oxygen consumption due to thick limb active Na
transport and oxygen consumption and to the model‘s assumption that medullary blood flow remains at baseline value. In the hypothermic CPB phase, the oxygen consumption due to thick limb active Na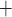 drops drastically to 13% that of base case. Thus, even with haemodilution, the model predicts that only 23% of the medullary oxygen supply is consumed, with the net result being an increase in medullary oxygen levels. However, P
drops drastically to 13% that of base case. Thus, even with haemodilution, the model predicts that only 23% of the medullary oxygen supply is consumed, with the net result being an increase in medullary oxygen levels. However, P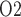 of the CD outflow and bladder urine are lower than base case. This is because the hypothermia induced reduction in TAL Na
of the CD outflow and bladder urine are lower than base case. This is because the hypothermia induced reduction in TAL Na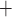 transport impairs water reabsorption from water-permeable nephron segments and leads to diuresis, which limits the concentration (but not the amount) of oxygen in the CD.
transport impairs water reabsorption from water-permeable nephron segments and leads to diuresis, which limits the concentration (but not the amount) of oxygen in the CD.
The prediction in the ‘perfect autoreg’ case that during the hypothermic CPB phase medullary P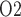 exceeds even baseline seems rather counter-intuitive and is indeed inconsistent with model predictions when medullary blood flow is insufficiently autoregulated. As previously noted, at RPP of 50 mmHg, renal autoregulation fails to compensate. Even with a reduced blood viscosity due to haemodilution, medullary blood flow decreases to 6.5 and 4.8 nl/min/DVR in the ‘partial autoreg’ and ‘no autoreg’ cases, respectively, compared to 8 nl/min/DVR in the base case (or ‘perfect autoreg’ case). For the ‘no autoreg’ case, the lowered medullary blood flow and hemodilution decrease medullary oxygen delivery to 34% of baseline. This is accompanied by a 27% reduction in oxygen consumption by the TALs, induced by the lowering of body temperature to 28
exceeds even baseline seems rather counter-intuitive and is indeed inconsistent with model predictions when medullary blood flow is insufficiently autoregulated. As previously noted, at RPP of 50 mmHg, renal autoregulation fails to compensate. Even with a reduced blood viscosity due to haemodilution, medullary blood flow decreases to 6.5 and 4.8 nl/min/DVR in the ‘partial autoreg’ and ‘no autoreg’ cases, respectively, compared to 8 nl/min/DVR in the base case (or ‘perfect autoreg’ case). For the ‘no autoreg’ case, the lowered medullary blood flow and hemodilution decrease medullary oxygen delivery to 34% of baseline. This is accompanied by a 27% reduction in oxygen consumption by the TALs, induced by the lowering of body temperature to 28 C. Together, these factors result in medullary oxygen extraction of 55% and an inner-stripe interstitial fluid P
C. Together, these factors result in medullary oxygen extraction of 55% and an inner-stripe interstitial fluid P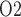 of 4.3 mmHg, which is 36% lower than baseline. Bladder urine P
of 4.3 mmHg, which is 36% lower than baseline. Bladder urine P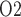 decreases from its baseline value of 19.1 to 18.3 mmHg. The analogous inner-stripe and bladder urine P
decreases from its baseline value of 19.1 to 18.3 mmHg. The analogous inner-stripe and bladder urine P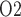 are predicted to be 6.3 and 18.5 mmHg, respectively, for the ‘partial autoreg’ case.
are predicted to be 6.3 and 18.5 mmHg, respectively, for the ‘partial autoreg’ case.
CPB-rewarming and post-CPB phases.
With the transition to the rewarming phase of CPB, body temperature is restored to 37 C. A particularly notable effect of a higher body temperature is the increase in TAL active transport of Na
C. A particularly notable effect of a higher body temperature is the increase in TAL active transport of Na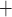 . Consequently, medullary oxygen consumption is
. Consequently, medullary oxygen consumption is 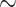 50% greater than in the hypothermic phase of CPB. The ‘perfect autoreg’ case predicts that the lowest inner-stripe P
50% greater than in the hypothermic phase of CPB. The ‘perfect autoreg’ case predicts that the lowest inner-stripe P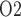 is obtained during the CPB rewarming and post-CPB phases (4.2 and 4.1 mmHg, respectively). Here, oxygen demand increases as body temperature is raised, but medullary oxygen levels remain low due to haemodilution; consequently, medullary oxygen extraction increases to 83%. The same trend can be seen in the P
is obtained during the CPB rewarming and post-CPB phases (4.2 and 4.1 mmHg, respectively). Here, oxygen demand increases as body temperature is raised, but medullary oxygen levels remain low due to haemodilution; consequently, medullary oxygen extraction increases to 83%. The same trend can be seen in the P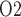 of collecting duct outflow, which drops to
of collecting duct outflow, which drops to 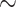 0.7 and
0.7 and 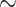 0.5 mmHg}, and bladder urine, which drops to
0.5 mmHg}, and bladder urine, which drops to 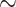 18.4 and
18.4 and 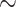 18.3 mmHg, respectively}. Thus, the model predicts that if the autoregulation of medullary blood flow is perfect during the surgery, then the patient is at similarly high risk of AKI during the rewarming and the post-CPB phases.
18.3 mmHg, respectively}. Thus, the model predicts that if the autoregulation of medullary blood flow is perfect during the surgery, then the patient is at similarly high risk of AKI during the rewarming and the post-CPB phases.
When medullary blood flow autoregulation is less than perfect, the model predicts substantially different P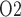 levels in the CPB rewarming and post-CPB phases. Both the ‘partial autoreg’ case and the ‘no autoreg’ case predict that the rewarming phase, during which RPP remains low at 50 mmHg, yields the lowest inner-stripe P
levels in the CPB rewarming and post-CPB phases. Both the ‘partial autoreg’ case and the ‘no autoreg’ case predict that the rewarming phase, during which RPP remains low at 50 mmHg, yields the lowest inner-stripe P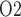 (3.7 and 3.1 mmHg, respectively, compared to 6.8 mmHg in baseline) among all four phases and a low bladder urine P
(3.7 and 3.1 mmHg, respectively, compared to 6.8 mmHg in baseline) among all four phases and a low bladder urine P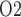 (18.4 and 18.3 mmHg, respectively, compared to 19.1 mmHg in baseline). It is noteworthy that in the ‘no autoreg’ case the CD outflow and bladder urine P
(18.4 and 18.3 mmHg, respectively, compared to 19.1 mmHg in baseline). It is noteworthy that in the ‘no autoreg’ case the CD outflow and bladder urine P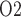 values are slightly higher in the rewarming phase than in the hypothermic phase, even though the inner-stripe P
values are slightly higher in the rewarming phase than in the hypothermic phase, even though the inner-stripe P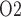 is lower in the rewarming phase. This discrepancy can be attributed to the higher TAL Na
is lower in the rewarming phase. This discrepancy can be attributed to the higher TAL Na transport in the rewarming phase, which results in a lower Na
transport in the rewarming phase, which results in a lower Na load downstream and consequently lower Na
load downstream and consequently lower Na active transport and oxygen consumption along the inner-medullary CD.
active transport and oxygen consumption along the inner-medullary CD.
In the post-CPB phase, medullary blood flow increases in the ‘partial autoreg’ and ‘no autoreg’ cases as RPP is restored to the pre-CPB levels. Consequently, the model predicts inner-stripe, CD outflow and bladder urinary P that are slightly lower than baseline and that are more similar to the pre-CPB levels.
that are slightly lower than baseline and that are more similar to the pre-CPB levels.
In summary, the model simulations suggest that the extent to which medullary blood flow is autoregulated may have a substantial impact on the relative risk of medullary hypoxic injury during the different phases of the cardiac surgery.
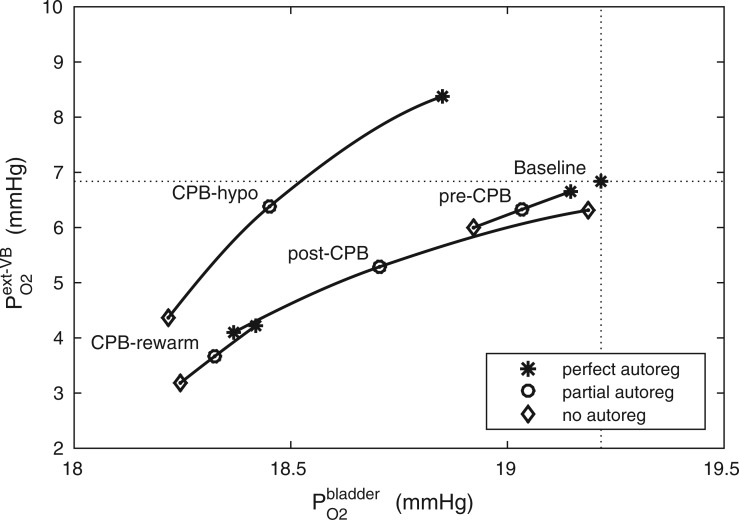
The relationship between inner-stripe extrabundle interstitial P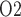 and bladder urine P
and bladder urine P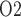 during the different CPB phases is summarized in Fig. 10. Generally, low medullary P
during the different CPB phases is summarized in Fig. 10. Generally, low medullary P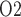 values are associated with low bladder urinary P
values are associated with low bladder urinary P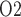 values. However, the precise relationship depends on the prevailing systemic factors of each phase. Further, the degree of medullary blood flow autoregulation induces a substantial variation in the predicted relationship, especially during the hypothermic and post-surgical phases.
values. However, the precise relationship depends on the prevailing systemic factors of each phase. Further, the degree of medullary blood flow autoregulation induces a substantial variation in the predicted relationship, especially during the hypothermic and post-surgical phases.
FIG 10.
Relationship between lower inner stripe P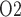 and urinary bladder P
and urinary bladder P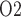 . Results were obtained for the five phases of Table 1 each for different degrees of medullary blood flow regulation that ranges from
. Results were obtained for the five phases of Table 1 each for different degrees of medullary blood flow regulation that ranges from 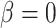 (perfect autoreg) to
(perfect autoreg) to 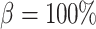 (no autoreg).
(no autoreg).
4. Discussion
Despite receiving approximately 25% of the cardiac output, the mammalian kidney is susceptible to hypoxia. The low medullary P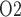 may be attributable, in part, to the high metabolic demand of the Na
may be attributable, in part, to the high metabolic demand of the Na /K
/K -ATPase pumps, which accounts for the majority of the energy consumption in the kidney. A principal goal of this study was to determine regional P
-ATPase pumps, which accounts for the majority of the energy consumption in the kidney. A principal goal of this study was to determine regional P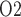 in a rat kidney and urinary tract. Of particular interest are the inner stripe, the papillary tip and the bladder. In the inner stripe of the rodent kidney, the oxygen-carrying DVR are isolated within tightly packed vascular bundles, separated from the metabolically demanding TALs. The structural organization of the tubules and vessels, which has been identified in rats, mice and human (Kriz, 1967; Kriz et al., 1972; Kriz & Koepsell, 1974; Jamison & Kriz, 1982), likely results in a substantial radial gradient in P
in a rat kidney and urinary tract. Of particular interest are the inner stripe, the papillary tip and the bladder. In the inner stripe of the rodent kidney, the oxygen-carrying DVR are isolated within tightly packed vascular bundles, separated from the metabolically demanding TALs. The structural organization of the tubules and vessels, which has been identified in rats, mice and human (Kriz, 1967; Kriz et al., 1972; Kriz & Koepsell, 1974; Jamison & Kriz, 1982), likely results in a substantial radial gradient in P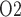 . The present model indeed predicts such a radial gradient in interstitial P
. The present model indeed predicts such a radial gradient in interstitial P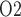 , from an average of
, from an average of 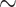 30 mmHg in the core of the vascular bundle, to an average P
30 mmHg in the core of the vascular bundle, to an average P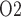 of
of 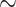 7.5 mmHg in the interbundle region, Fig. 4a.
7.5 mmHg in the interbundle region, Fig. 4a.
FIG. 4.
Baseline model predictions. (a) Interstitial fluid P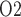 profiles in selected regions along the model medulla: VB, interstitial fluid P
profiles in selected regions along the model medulla: VB, interstitial fluid P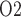 within the vascular bundles; Ext-VB, interstitial fluid P
within the vascular bundles; Ext-VB, interstitial fluid P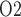 external to the vascular bundles and CD, collecting duct luminal fluid P
external to the vascular bundles and CD, collecting duct luminal fluid P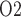 . Dotted lines indicate the boundaries of inner/outer stripes (at
. Dotted lines indicate the boundaries of inner/outer stripes (at 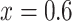 mm) and inner/outer medulla (at
mm) and inner/outer medulla (at 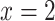 mm). (b) Urine P
mm). (b) Urine P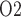 along the ureter. Dashed line indicates P
along the ureter. Dashed line indicates P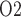 along the ureter walls.
along the ureter walls.
Under baseline conditions, the DVR deliver  23% of the medullary oxygen supply to the inner medulla. Thus, P
23% of the medullary oxygen supply to the inner medulla. Thus, P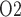 in the inner medulla is even lower than in the outer medulla. The model predicts that, under baseline conditions, urinary P
in the inner medulla is even lower than in the outer medulla. The model predicts that, under baseline conditions, urinary P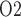 at the papillary tip is 2.4 mmHg, which is 4.1 mmHg below the interstitial fluid P
at the papillary tip is 2.4 mmHg, which is 4.1 mmHg below the interstitial fluid P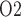 near the inner-outer medullary boundary. Along the ureter, urine becomes increasingly oxygenated owing to oxygen diffusion, reaching a P
near the inner-outer medullary boundary. Along the ureter, urine becomes increasingly oxygenated owing to oxygen diffusion, reaching a P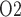 of 19.1 mmHg in the Fig. 4b. These results point to a large difference in bladder urinary P
of 19.1 mmHg in the Fig. 4b. These results point to a large difference in bladder urinary P and medullary P
and medullary P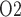 .
.
The predicted medullary P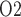 is in general agreement with tissue P
is in general agreement with tissue P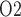 measured in the rat kidney, at least under the relatively antidiuretic conditions modelled in this study (Epsteinein et al., 1994; Palm et al., 2003). In contrast, substantially higher medullary tissue P
measured in the rat kidney, at least under the relatively antidiuretic conditions modelled in this study (Epsteinein et al., 1994; Palm et al., 2003). In contrast, substantially higher medullary tissue P (
( 30 mmHg) has been reported in unanaesthetized sheep (Calzavacca et al., 2015). Similarly high renal pelvic urine P
30 mmHg) has been reported in unanaesthetized sheep (Calzavacca et al., 2015). Similarly high renal pelvic urine P values have been reported in anaesthetized dogs (27 mmHg) (Rennie et al., 1958) and in humans (28 mmHg) (Lenhardt & Landes, 1963). Notably, Lenhardt & Landes (1963) reported that urinary P
values have been reported in anaesthetized dogs (27 mmHg) (Rennie et al., 1958) and in humans (28 mmHg) (Lenhardt & Landes, 1963). Notably, Lenhardt & Landes (1963) reported that urinary P decreases along the ureter, in direct contradiction with our model‘s prediction, which indicates a substantial increase (see Fig. 4b). Indeed, on the basis of their findings, Lenhardt & Landes (1965) concluded that urinary P
decreases along the ureter, in direct contradiction with our model‘s prediction, which indicates a substantial increase (see Fig. 4b). Indeed, on the basis of their findings, Lenhardt & Landes (1965) concluded that urinary P ‘reflects the interstitial P
‘reflects the interstitial P in the medulla,’ again in contrast to our conclusion. These discrepancies suggest that there may be fundamental differences in renal haemodynamics and medullary oxygenation between the rat and larger animals like sheep and human. For example, given the low tissue P
in the medulla,’ again in contrast to our conclusion. These discrepancies suggest that there may be fundamental differences in renal haemodynamics and medullary oxygenation between the rat and larger animals like sheep and human. For example, given the low tissue P in the inner medulla (
in the inner medulla ( 10 mmHg) (Epsteinein et al., 1994), it seems unlikely that pelvic urinary P
10 mmHg) (Epsteinein et al., 1994), it seems unlikely that pelvic urinary P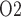 can rise to 50 mmHg, the value measured in human (Lenhardt & Landes, 1963). To reconcile these differences, one would need a better understanding of the anatomic structures and of renal and medullary blood flow autoregulation in humans. It should also be noted that there are very little available data regarding the relative changes in medullary and urinary P
can rise to 50 mmHg, the value measured in human (Lenhardt & Landes, 1963). To reconcile these differences, one would need a better understanding of the anatomic structures and of renal and medullary blood flow autoregulation in humans. It should also be noted that there are very little available data regarding the relative changes in medullary and urinary P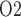 that occur under physiological and pathophysiological conditions. However, a recent study in unanaesthetized sheep showed a strong correlation between tissue P
that occur under physiological and pathophysiological conditions. However, a recent study in unanaesthetized sheep showed a strong correlation between tissue P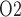 in the medulla and the P
in the medulla and the P of urine in the bladder during development of septic AKI (Lankadeva et al., 2016). Thus, the potential for urinary P
of urine in the bladder during development of septic AKI (Lankadeva et al., 2016). Thus, the potential for urinary P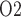 to be used as a biomarker of risk of AKI may still merit further investigation.
to be used as a biomarker of risk of AKI may still merit further investigation.
Another goal of this study was to determine the phase or phases of cardiac surgery performed under CPB during which the outer medulla and the TALs are most susceptible to hypoxia and the underlying renal haemodynamic and functional factors that contribute to this susceptibility. Given the low baseline medullary P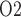 , the TALs likely operate near anoxia. Thus, a clinically important question is: When renal oxygen delivery is reduced during cardiac surgery performed under CPB, how likely are the thick limbs to become hypoxic?
, the TALs likely operate near anoxia. Thus, a clinically important question is: When renal oxygen delivery is reduced during cardiac surgery performed under CPB, how likely are the thick limbs to become hypoxic?
Model simulations suggest that the outer medulla‘s relative vulnerability to hypoxic injury during the different phases of the surgery depends, in part, on the extent to which medullary blood flow is autoregulated. There is evidence that indicates a link between increased renal interstitial hydrostatic pressure and elevated medullary blood flow, which is in turn modulated by vasopressin, the antidiuretic hormone (Cowley, 2000). In general, medullary blood flow is known to be strongly autoregulated in antidiuretic rats (Cupples & Marsh, 1988; Mattson et al., 1993; Franchini et al., 1997) and weakly regulated in diuretic rats (Roman et al., 1988; Mattson et al., 1991; Franchini et al., 1997). However, the degree to which medullary blood flow is regulated when a patient or an animal is undergoing surgery performed under CPB is not well characterized.
If medullary blood flow is perfectly autoregulated, then outer medullary P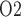 is predicted to be the lowest during the rewarming and post-surgical phases of CPB, when medullary oxygen supply is low due to haemodilution but medullary oxygen consumption remains high (Fig. 9). The model predicts that during the rewarming phase 83% of the medullary oxygen supply is consumed, resulting in tubular fluid P
is predicted to be the lowest during the rewarming and post-surgical phases of CPB, when medullary oxygen supply is low due to haemodilution but medullary oxygen consumption remains high (Fig. 9). The model predicts that during the rewarming phase 83% of the medullary oxygen supply is consumed, resulting in tubular fluid P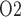 as low as 2.3 mmHg in the inner-stripe segment of the superficial TALs. Similar results were obtained for the post-CPB phase. It is noteworthy that even though medullary oxygen supply exceeds consumption by a comfortable margin, the risk of medullary hypoxia can still be substantial. This apparent paradox is explained by the anatomic structure of the outer medulla, as discussed above. However, with medullary blood flow assumed fixed, the model yields the somewhat counter-intuitive prediction that during the hypothermic CPB phase, when medullary TAL transport and oxygen consumption dramatically decrease, medullary oxygenation exceeds baseline levels (Fig. 9).
as low as 2.3 mmHg in the inner-stripe segment of the superficial TALs. Similar results were obtained for the post-CPB phase. It is noteworthy that even though medullary oxygen supply exceeds consumption by a comfortable margin, the risk of medullary hypoxia can still be substantial. This apparent paradox is explained by the anatomic structure of the outer medulla, as discussed above. However, with medullary blood flow assumed fixed, the model yields the somewhat counter-intuitive prediction that during the hypothermic CPB phase, when medullary TAL transport and oxygen consumption dramatically decrease, medullary oxygenation exceeds baseline levels (Fig. 9).
In contrast, if the assumption of perfect autoregulation is relaxed so that medullary blood flow is linked to renal blood flow, then model simulations identify the rewarming phase of CPB, in which medullary blood flow is low but medullary oxygen consumption remains high, as the phase in which the kidney is the most vulnerable to hypoxic injury (Fig. 9). The model predicts that during the rewarming phase of CPB, 93% of the medullary O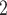 supply is consumed, resulting, in the ‘no autoreg’ case, P
supply is consumed, resulting, in the ‘no autoreg’ case, P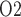 of 1.6 and 3.2 mmHg in the TAL luminal fluid and the surrounding interstitial fluid, respectively.
of 1.6 and 3.2 mmHg in the TAL luminal fluid and the surrounding interstitial fluid, respectively.
Renal tubules consist of a single layer of epithelial cells, with different transporters expressed on the apical and basolateral membranes. For example, for Na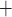 to be reabsorbed by the TALs, it may go through either the transcellular or paracellular pathway. For transcellular transport, the Na
to be reabsorbed by the TALs, it may go through either the transcellular or paracellular pathway. For transcellular transport, the Na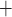 must first pass through the apical membrane (likely via the Na
must first pass through the apical membrane (likely via the Na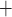 -K
-K -2 Cl
-2 Cl or NKCC, transporter) and then through the basolateral membrane (likely via the Na
or NKCC, transporter) and then through the basolateral membrane (likely via the Na -K
-K -ATPase). Alternatively, the Na
-ATPase). Alternatively, the Na may be reabsorbed through the tight junction, driven by a favourable electrochemical gradient. In contrast, for simplicity the present model represents single-barrier transport, where TAL Na
may be reabsorbed through the tight junction, driven by a favourable electrochemical gradient. In contrast, for simplicity the present model represents single-barrier transport, where TAL Na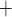 transport is determined by the Michaelis–Menten kinetics. Thus, the model cannot distinguish between transcellular transport (which consumes O
transport is determined by the Michaelis–Menten kinetics. Thus, the model cannot distinguish between transcellular transport (which consumes O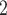 ) and paracellular transport (which does not). Instead, it assumes that the TQ ratio is known a priori. This limitation applies to all nephron segments that engage in active Na
) and paracellular transport (which does not). Instead, it assumes that the TQ ratio is known a priori. This limitation applies to all nephron segments that engage in active Na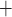 transport. To overcome this limitation and to improve the accuracy of the predicted T
transport. To overcome this limitation and to improve the accuracy of the predicted T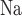 and Q
and Q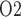 , the model nephron could be replaced by an epithelial-based model (e.g. Edwards et al., 2014; Layton et al., 2016), although this extension is by no means trivial.
, the model nephron could be replaced by an epithelial-based model (e.g. Edwards et al., 2014; Layton et al., 2016), although this extension is by no means trivial.
As previously noted, there appears to be substantial differences between the predictions of the present model, which is based on a rat kidney, and measurements in human. In fact, urine P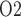 in patients undergoing cardiac surgery performed on CPB was measured to be
in patients undergoing cardiac surgery performed on CPB was measured to be  50 mmHg (Kainuma et al., 1996). It is clear that there are important differences between the rat and human kidneys beyond their sizes. % ADD HERE COMMENTS ABOUT DIFFERENCES rat VS human Because of the scarcity of data (anatomic, transport, electrochemical, etc.) in the human kidney relative to the rat, all detailed mathematical models of the mammalian kidney have been built for the rat (Chen et al., 2009; Layton, 2011; Layton & Layton, 2011; Edwards & Layton, 2012, 2014; Layton & Bankir, 2013; Weinstein, 2015a,b). Nonetheless, the large discrepancies between the rat model and human data clearly indicate the limit of knowledge that one can gain from a rat model and that a better understanding of the relationship between urinary and medullary P
50 mmHg (Kainuma et al., 1996). It is clear that there are important differences between the rat and human kidneys beyond their sizes. % ADD HERE COMMENTS ABOUT DIFFERENCES rat VS human Because of the scarcity of data (anatomic, transport, electrochemical, etc.) in the human kidney relative to the rat, all detailed mathematical models of the mammalian kidney have been built for the rat (Chen et al., 2009; Layton, 2011; Layton & Layton, 2011; Edwards & Layton, 2012, 2014; Layton & Bankir, 2013; Weinstein, 2015a,b). Nonetheless, the large discrepancies between the rat model and human data clearly indicate the limit of knowledge that one can gain from a rat model and that a better understanding of the relationship between urinary and medullary P in the human kidney might benefit from a model of the human kidney.
in the human kidney might benefit from a model of the human kidney.
Supplementary Material
Footnotes
1 Patient body temperature is lowered to different degrees depending on the nature of the surgery and varies between institutions. The model predicts qualitatively similar results (not shown) at different body temperatures.
Funding
This work was conducted while I.S. is a Postdoctoral Fellow at the National Institute for Mathematical and Biological Synthesis, an Institute sponsored by the National Science Foundation through NSF Award DBI1300426, with additional support from the National Institutes of Health, National Institute of Diabetes and Digestive and Kidney Diseases, via grant R01DK089066 to A.L.
Supplementary material
Supplementary material is available at http://imammb.oxfordjournals.org.
References
- Andersson L.G., Bratteby L.E., Ekroth R., Hallhagen S., Joachimsson P.O., van der Linden J. & Wesslén, O. (1994)Renal function during cardiopulmonary bypass: influence of pump flow and systemic blood pressure. Eur. J. Cardiothorac. Surg., 8, 597–602. [DOI] [PubMed] [Google Scholar]
- Bjornsson T.D. (1979). Use of serum creatinine concentrations to determine renal function. Clin. Pharmacokinet., 4, 200–22, 1979. [DOI] [PubMed] [Google Scholar]
- Bosch J.P. (1995). Renal reserve: a functional view of glomerular filtration rate. Semin. Nephrol., 15, 381–5. [PubMed] [Google Scholar]
- Brezis M. & Rosen S.. (1995). Hypoxia of the renal medulla—its implications for disease. N. Engl. J. Med., 332, 647–655. [DOI] [PubMed] [Google Scholar]
- Broman M. & Källskog O.. (1995). The effects of hypothermia on renal function and haemodynamics in the rat. Acta Physiol. Scand., 153, 179–84. [DOI] [PubMed] [Google Scholar]
- Calzavacca P., Evans R.G., Bailey M., Lankadeva Y.R., Bellomo R. & May C.N.. (2015). Long-term measurement of renal cortical and medullary tissue oxygenation and perfusion in unanesthetized sheep. Am. J. Physiol. Regu. Integr. Comp. Physiol., 308, R832–R839. [DOI] [PubMed] [Google Scholar]
- Chen J., Layton A.T. & Edwards A.. (2009). A mathematical model of oxygen transport in the rat outer medulla: I. model formulation and baseline results. Am. J. Physiol. Renal. Physiol., 297, F517–F536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J., Sgouralis I., Moore L.C., Layton H.E. & Layton A.T.. (2011). A mathematical model of the myogenic response to systolic pressure in the afferent arteriole. Am. J. Physiol. Renal. Physiol., 300, F669–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowley A.W., Jr. (2000)Control of the renal medullary circulation by vasopressin v1 and v2 receptors in the rat. Exp. Physiol., 85, 223–231. [DOI] [PubMed] [Google Scholar]
- Cupples W.A. & Marsh D.J.. (1988). Autoregulation of blood flow in renal medulla of the rat: no role for angiotensin II. Can. J. Physiol. Pharmacol., 66, 833–836. [DOI] [PubMed] [Google Scholar]
- Edwards, A. & Layton, A. T.. (2012). Impacts of nitric oxide-mediated vasodilation on outer medullary NaCl transport and oxygenation. Am. J. Physiol. Renal. Physiol., 303, F907–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards A. & Layton A.T.. (2014). Calcium dynamics underlying the afferent arteriole myogenic response. Am. J. Physiol. Renal. Physiol., 306, F34–F48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards A., Castrop H., Laghmani K., Vallon V. & Layton A.T.. (2014). Effects of NKCC2 isoform regulation on nacl transport in thick ascending limb and macula densa: a modeling study. Am. J. Physiol. Renal. Physiol., 307, F137–F146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Epsteinein F.H., Agmon Y. & Brezis M.. (1994). Physiology of renal hypoxia. Ann. N. Y. Acad. Sci., 718, 72—82. [PubMed] [Google Scholar]
- Evans R.G., Ince C., Joles J.A., Smith D.W., May C.N., O’Connor P.M. & Gardiner B.S.. (2013). Haemodynamic influences on kidney oxygenation: clinical implications of integrative physiology. Clin. Exp. Pharmacol. Physiol., 40, 106–22. [DOI] [PubMed] [Google Scholar]
- Evans R.G., Smith J.A., Wright C., Gardiner B.S., Smith D.W. & Cochrane A.D.. (2014). Urinary oxygen tension: a clinical window on the health of the renal medulla? Am. J. Physiol. Regul. Integr. Comp. Physiol., 306, R45–50. [DOI] [PubMed] [Google Scholar]
- Franchini K.G., Mattson D.L. & Cowley A.W., Jr. (1997)Vasopressin modulation of medullary blood flow and pressure-natriuresis-diuresis in the decerebrated rat. Am. J. Physiol. Regul. Integr. Comp. Physiol., 272, R1472–R1479. [DOI] [PubMed] [Google Scholar]
- Fry B.C., Edward A., & Layton A.T.. (2015). Impact of nitric oxide and superoxide on renal medullary oxygen transport and urine concentration. Am. J. Physiol. Renal. Physiol., 308, F967–F980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fry B.C., Edwards A., Sgouralis I. & Layton A.T.. (2014). Impact of renal medullary three-dimensional architecture on oxygen transport. Am. J. Physiol. Renal. Physiol., 307, F263–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrera J. & Rodŕiguez-Iturbe, B.. (1998). Stimulation of tubular secretion of creatinine in health and in conditions associated with reduced nephron mass. Evidence for a tubular functional reserve. Nephrol. Dial. Transplant., 13, 623–9. [DOI] [PubMed] [Google Scholar]
- Jamison R.L. & Kriz W.. (1982). Urinary Concentrating Mechanism: Structure and Function . New York: Oxford University Press. [Google Scholar]
- Kainuma M.,Yamada M. & Miyake T.. (1996). Continuous urine oxygen tension monitoring in patients undergoing cardiac surgery. J. Cardiothorac. Vasc. Anesth., 10, 603–608. [DOI] [PubMed] [Google Scholar]
- Karkouti K., Wijeysundera D.N., Yau T.M., Callum J.L., Cheng D.C., Crowther M., Dupuis, J.-Y., Fremes S.E., Kent B., Laflamme, C., Lamy A., Legare, J.-F., Mazer C.D., McCluskey S.A., Rubens F.D., Sawchuk C. & Beattie W.S.. (2009). Acute kidney injury after cardiac surgery: focus on modifiable risk factors. Circulation, 119, 495–502. [DOI] [PubMed] [Google Scholar]
- Kreft M.E., Hudoklin S., Jezernik K. & Romih R.. (2010). Formation and maintenance of blood-urine barrier in urothelium. Protoplasma, 246, 3–14. [DOI] [PubMed] [Google Scholar]
- Kriz W. (1967). Der architektonische and funktionelle Aufbau der Rattenniere. Z. Zellforsch., 82, 495–535. [PubMed] [Google Scholar]
- Kriz W. & Koepsell H.. (1974). The structural organization of the mouse kidney. Z. Anat. Entwickl.-Gesch., 144, 137–163. [DOI] [PubMed] [Google Scholar]
- Kriz W., Schnermann J. & Koepsell H.. (1972). The position of short and long loops of Henle in the rat kidney. Z. Anat. Entwickl.-Gesch., 138, 301–319. [DOI] [PubMed] [Google Scholar]
- Lankadeva Y., Kosaka J., Evans R., Bailey S., Bellomo R. & May C.. (2016). Intra-renal and urinary oxygenation during norepinephrine resuscitation in ovine septic acute kidney injury. Kidney Int . [DOI] [PubMed] [Google Scholar]
- Layton A.T., Vallon V. & Edwards A.. (2016). Predicted consequences of diabetes and SGLT inhibition on transport and oxygen consumption along a rat nephron. Am. J. Physiol. Renal. Physiol., ajprenal–00543, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Layton A.T. (2011). A mathematical model of the urine concentrating mechanism in the rat renal medulla: I. Formulation and base-case results. Am. J. Physiol. Renal. Physiol., 300, F356–F371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Layton A.T. & Bankir L.. (2013). Impacts of active urea secretion into pars recta on urine concentration and urea excretion rate. Physiol. Rep., 1, e00034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Layton A.T., Dantzler W.H. & Pannabecker T.L.. (2012). Urine concentrating mechanism: impact of vascular and tubular architecture and a proposed descending limb urea-na+ cotransporter. Am. J. Physiol. Renal. Physiol., 302, F591–605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Layton A.T. & Layton H.E.. (2011). Countercurrent multiplication may not explain the axial osmolality gradient in the outer medulla of the rat kidney. Am. J. Physiol. Renal. Physiol., 301, F1047–F1056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenhardt K.O. & Landes R.R.. (1963). Oxygen tension of the urine and renal structures. N. Eng. J. Med., 269, 115–121. [DOI] [PubMed] [Google Scholar]
- Lenhardt K.O. & Landes R.R.. (1965). Urinary oxygen pressure in renal parenchymal and vascular disease. J. Am. Med. Assoc., 194, 345–350. [PubMed] [Google Scholar]
- Mattson D.L., Lu S., Roman R.J. & Cowley A.W., Jr. (1993)Relationship between renal perfusion pressure and blood flow in different regions of the kidney. Am. J. Physiol. Regul. Integr. Comp. Physiol., 264, R578–R583. [DOI] [PubMed] [Google Scholar]
- Mattson D.L., Raff H. & Roman R.J.. (1991). Influence of angiotensin II on pressure natriuresis and renal hemodynamics in volume-expanded rats. Am. J. Physiol. Regul. Integr. Comp. Physiol., 260, R1200–R1209. [DOI] [PubMed] [Google Scholar]
- Mehta R.L. & Chertow G.M.. (2003). Acute renal failure definitions and classification: time for change? J. Am. Soc. Nephrol., 14, 2178–87. [DOI] [PubMed] [Google Scholar]
- Moss R. & Layton A.T.. (2014). Dominant factors that govern pressure natriuresis in diuresis and antidiuresis: a mathematical model. Am. J. Physiol. Renal. Physiol., 306, F952–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nieves-Gonzalez A., Clausen C., Layton A.T., Layton H.E. & Moore L.C.. (2013). Transport efficiency and workload distribution in a mathematical model of the thick ascending limb. Am. J. Physiol. Renal. Physiol., 304, F653–F664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okusa MD M.D., Linden J., MacDonald T. & Huang L.. (1999). Selective A2A adenosine receptor activation reduces ischemia-reperfusion injury in rat kidney. Am. J. Physiol. Renal. Physiol., 277, F404–F412. [DOI] [PubMed] [Google Scholar]
- Onyeanusi B.I., Adeniyi A.A., Ayo J.O., Ibe C.S., Onyeanusi C.G., et al. (2009)A comparative study of the urinary system of the African giant rat (Cricetomys gambianus Waterhouse) and the Wistar rat. Pak. J. Nutr., 8, 1043–1047. [Google Scholar]
- Palm F., Cederberg J., Hansell P., Liss P. & Carlsson P.O.. (2003). Reactive oxygen species cause diabetes-induced decrease in renal oxygen tension. Diabetologia, 46, 1153–1160. [DOI] [PubMed] [Google Scholar]
- Pannabecker T.L., Abbott D.E. & Dantzler W.H.. (2004). Three-dimensional functional reconstruction of inner medullary thin limbs of Henle’s loop. Am. J. Physiol. Renal. Physiol., 286, F38–F45. [DOI] [PubMed] [Google Scholar]
- Pries A.R., Secomb T.W., Gessner T., Sperandio M.B., Gross J.F. & Gaehtgens, P.. (1994). Resistance to blood flow in microvessels in vivo. Circ. Res., 75, 904–15. [DOI] [PubMed] [Google Scholar]
- Rennie D.W., Reeves R.B. & Pappenheimer J.R.. (1958). Oxygen pressure in urine and its relation to intrarenal blood flow. Am. J. Physiol, 195, 120–132. [DOI] [PubMed] [Google Scholar]
- Roman, R J., Cowley JR A.W., Garcia-Estan, J. & Lombard J.H.. (1988). Pressure-diuresis in volume-expanded rats, cortical and medullary hemodynamics. Hypertension, 12, 168–176. [DOI] [PubMed] [Google Scholar]
- Rosner M.H., Portilla D. & Okusa M.D.. (2008). Cardiac surgery as a cause of acute kidney injury: pathogenesis and potential therapies. J. Intensive Care Med., 23, 3–18. [DOI] [PubMed] [Google Scholar]
- Sgouralis I., Evans R.G., Gardiner B.S., Smith J.A., Fry B.C. & Layton A.T.. (2015). Renal hemodynamics, function & oxygenation during cardiac surgery performed on cardiopulmonary bypass: a modeling study. Physiol. Rep., 3,e12260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sgouralis I. & Layton A.T.. (2013). Control and modulation of fluid flow in the rat kidney. Bull. Math. Biol., 75, 2551–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sgouralis I. & Layton A.T.. (2014). Theoretical assessment of renal autoregulatory mechanisms. Am. J. Physiol. Renal. Physiol, 306, F1357–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sgouralis I. & Layton A.T.. (2015a). Conduction of feedback-mediated signal in a computational model of coupled nephrons. Math. Med. Biol, 33, 87–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sgouralis I. & Layton A.T.. (2015b). Mathematical modeling of renal hemodynamics in physiology and pathophysiology. Math. Biosci., 264, 8–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sgouralis I., Kosaka J., Evans R., Bailey S., Bellomo R. & May C.. (2012). Autoregulation and conduction of vasomotor responses in a mathematical model of the rat afferent arteriole. Am. J. Physiol. Renal. Physiol., 303, F229–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Star R.A. (1998). Treatment of acute renal failure. Kidney Int., 54, 1817–31. [DOI] [PubMed] [Google Scholar]
- Tillig B. & Constantinou C.E.. (1996). Videomicroscopic imaging of ureteral peristaltic function in rats during cystometry. J. Pharmacol. Toxicol. Methods, 35, 191–202. [DOI] [PubMed] [Google Scholar]
- Weinstein A.M. (1998). A mathematical model of the inner medullary collecting duct of the rat: pathways for Na and K transport. Am. J. Physiol. (Renal. Physiol. 43), 274, F841–F855. [DOI] [PubMed] [Google Scholar]
- Weinstein A.M. (2015a). A mathematical model of rat proximal tubule and loop of Henle. Am. J. Physiol. Renal. Physiol., 308, F1076–F1097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinstein A.M. (2015b). A mathematical model of the rat nephron: glucose transport. Am. J. Physiol. Renal. Physiol., 308, F1098–F1118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolf J.S., Humphrey P.A., Rayala H.J., Gardner S.M., Mackey R.B. & Clayman R.V.. (1996). Comparative ureteral microanatomy. J. Endourol., 10, 527–531. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.