Abstract
The viscoelastic properties of tissues are altered during pathogenesis of numerous diseases and can therefore be a useful indicator of disease status and progression. Several elastography studies have utilized the mechanical frequency response and the resonance frequencies of tissue samples to characterize their mechanical properties. However, using the resonance frequency as a source of mechanical contrast in heterogeneous samples is complicated because it not only depends on the viscoelastic properties but also on the geometry and boundary conditions. In an elastography technique called magnetomotive optical coherence elastography (MM-OCE), the controlled movement of magnetic nanoparticles (MNPs) within the sample is used to obtain the mechanical properties. Previous demonstrations of MM-OCE have typically used point measurements in elastically homogeneous samples assuming a uniform concentration of MNPs. In this study, we evaluate the feasibility of generating MM-OCE elastograms in heterogeneous samples based on a spectroscopic approach which involves measuring the magnetomotive response at different excitation frequencies. Biological tissues and tissue-mimicking phantoms with two elastically distinct regions placed in side-by-side and bilayer configurations were used for the experiments, and finite element method (FEM) simulations were used to validate the experimental results.
1. INTRODUCTION
The evaluation of the mechanical properties of tissues is important in many areas of medicine and biology (Kennedy et al., 2014; Carstensen et al., 2008; Dieter et al., 2007; Sinkus et al., 2005). Typically, in elastography measurements, the sample is perturbed by an excitation source and the resulting response is measured and processed to extract the mechanical properties (Parker et al., 2011; Kennedy et al., 2014; Greenleaf et al., 2003). The spatial and temporal characteristics of the mechanical stimulus play an important role in elastography. The mechanical excitation can either be applied through different types of external force transducers (Chan et al., 2006) or by generating the force internally in the sample through techniques such as acoustic radiation force (Nightingale, 2011) or magnetomotive forces (Crecea et al., 2009). Temporally, the sample can be perturbed by a static force or a dynamic force in the form of a pulse, chirp or harmonic excitations. A wide variety of techniques and imaging modalities including magnetic resonance elastography (MRE) (Muthupillai et al., 1995),ultrasound elastography (UE) (Yamakoshi et al., 1990) and optical coherence elastography (OCE) (Kennedy et al., 2014) have been used to measure the resulting deformation and response of the sample under a mechanical excitation. Optical coherence elastography (OCE) has the advantage of providing high resolution and displacement sensitivity compared to MRE and UE, which makes OCE a preferable technique for tissue samples with small dimensions or high heterogeneity (Kennedy et al., 2014).
In a technique called magnetomotive optical coherence elastography (MM-OCE), the controlled movement of magnetic nanoparticles (MNPs), which act as internal force transducers, is used to evaluate the tissues mechanical properties (Crecea et al., 2009; Crecea et al., 2013; Ahmad et al., 2014b). These MNPs can either be injected in the sample of interest, targeted to a diseased location, or in ex vivo specimens, can diffuse inside the tissues. MM-OCE has several advantages compared to other elastography techniques. Unlike contact-based methods which use external force transducers (Liang et al., 2008; Wang et al., 2006), the non-contact nature and small-scale localized displacements in MM-OCE alleviate modeling and inertia problems associated with contact-based methods, making it an attractive technique for measuring the elastic properties of soft materials (Crecea et al., 2009). Traditional compressional elastography techniques (Wang et al., 2006; Kennedy et al., 2013) which use the strain or the strain rate as a substitute for elastic modulus (under the assumption of uniform stress throughout the sample) are not directly applicable in MM-OCE as the estimation of the stress distribution within the sample is non-trivial (Kennedy et al., 2013). Unlike traditional elastography techniques, in MM-OCE, the total force acting on the sample depends not only on the applied force but also on the concentration of the magnetic particles within the sample. The determination of the applied magnetomotive force on the tissue would therefore require precise measurements of the magnetic field characteristics of the coil, and the estimation of the concentration, distribution, and the magnetic properties of the magnetic particles. Although these can potentially be determined by simulations and careful calibration, their precise determination in scenarios of different geometries and boundary conditions would be challenging. Moreover, MNPs, when targeted to a desired location, might not necessarily be uniformly distributed throughout the volume, making precise quantification of the force extremely challenging. Therefore, MM-OCE relies primarily on the temporal dynamics of the magnetomotive response rather than on the absolute scale of displacements (Crecea et al., 2009; Oldenburg and Boppart, 2010).
Mechanical resonances have been found useful for non-destructive evaluation of materials (Migliori et al., 1993) and measuring the mechanical properties. Techniques such as resonant ultrasound elastography, vibro-acoustic spectrography (Fatemi and Greenleaf, 1998) and shear-wave induced resonance elastography (Henni et al., 2010) have been developed over the years that exploit the mechanical resonances in the sample to infer its mechanical properties as the resonances are dependent on the viscoelastic properties of the material. Resonances have also been exploited to amplify small displacements (Henni et al., 2010), which is especially useful in techniques such as MM-OCT where the SNR can significantly be improved by operating near the resonance frequency of the sample (Oldenburg et al., 2008). In OCE several recent studies have explored the use of mechanical frequency response and resonance frequency of the sample as a source of relative mechanical contrast (Qi et al., 2013; Adie et al., 2010; Oldenburg and Boppart, 2010; Liang et al., 2010; Wang et al., 2013). The measured frequency response not only depends on the viscoelastic properties but also on the geometry and boundary conditions. Although the use of mechanical resonance frequency of the sample with known sizes and shapes has been well-established, the merit of the technique in heterogeneous samples has not been fully explored. The analysis of the mechanical frequency response in elastically heterogeneous samples is challenging due to complex mechanical coupling between regions of different geometries and mechanical properties, which are possibly subjected to different boundary conditions. It is hypothesized that elastically distinct regions in the sample based on differences in geometry, boundary conditions, and viscoelastic properties will have distinct mechanical resonance frequencies.
Previously, MM-OCE has been demonstrated using a step or a chirped excitation waveform, where the resulting magnetomotive response is inherently dependent on the resonant frequency of the sample (Oldenburg and Boppart, 2010; Crecea et al., 2013; Crecea et al., 2009). In this study, we investigate the feasibility of MM-OCE to image the local mechanical properties in elastically heterogeneous samples. This is an extension of previously performed MM-OCE studies that have invariably used samples with homogenous mechanical properties and typically performed point measurements at a single spatial location (Crecea et al., 2009; Crecea et al., 2013; Oldenburg and Boppart, 2010). We use a spectroscopic approach where cross-sectional magnetomotive images are acquired using a range of frequencies and the magnetomotive response at these frequencies is quantified. By measuring the response at different frequencies, mechanically distinct regions in a heterogeneous sample can be potentially identified based on the mechanical contrast provided by MM-OCE measurements. To explore the impact of elastic heterogeneities on the measured frequency response, we used tissue-mimicking phantoms with two elastically distinct regions placed in a side-by-side and a bilayer configuration. In addition, we employed finite element method (FEM) simulations to validate the experimental results.
2. METHODS
2.1 Experimental setup
A 1310 nm spectral-domain OCT system as shown in Figure 1(a) was used in this study (Ahmad et al., 2014b). The light source was a superluminescent diode (LS2000B, Thorlabs) and the measured axial and transverse resolutions (full width at half max) of the system were 6 μm and 16 μm, respectively. A 1024-pixel InGaAs line-scan camera (SU-LDH2, Goodrich) was used in the spectrometer providing an optical imaging depth of 2.2 mm. Although the system can acquire data at 91,912 A-lines per second, lower scan rates of up to 5000 A-lines per second were used to prevent excessive oversampling and to obtain a higher signal-to-noise ratio by capturing sufficient number of magnetic modulation cycles within each cross-sectional frame consisting of 4000 A-lines. MM-OCE measurements were performed by driving an electromagnetic coil placed in the OCT sample arm with the specimen containing the magnetic particles placed underneath the coil, as can be seen in Figure 1(a). The magnetomotive force acting on the MNPs would be proportional to the square of the magnetic field gradient i.e. F ∝ ∇ |B|2. Hence to obtain a sinusoidal displacement of the MNPs, a unipolar square root sinusoidal voltage, was applied to the coil through a computer controlled power supply where V0 is the peak voltage and fb is the applied modulation frequency. Cross-sectional magnetomotive images were acquired by sweeping fb over a range from 20–500 Hz with a frequency interval of 5 Hz, as shown in Figure 1(b). The magnetic field strength from the coil (I.D. 12 mm, O.D. 22 mm) at the surface of the sample was measured to be 400 Gauss. The variation in the magnetic field strength within the range of measurement frequencies (20–500 Hz) was found to be ± 5 %.
Figure 1.
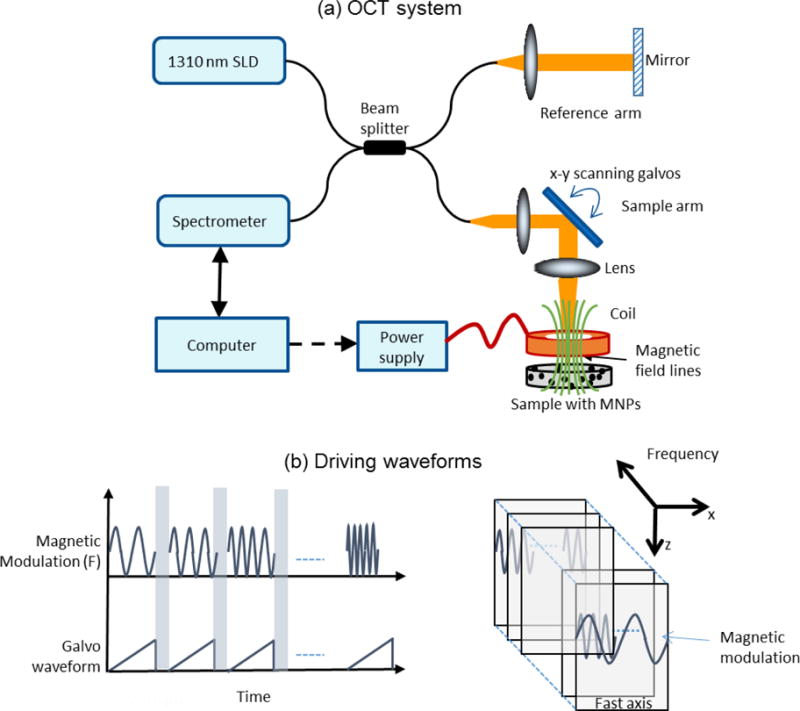
Experimental setup. (a) Magnetomotive optical coherence elastography setup. An electromagnetic coil was placed in the sample arm and (b) Square root of sinusoidal waveforms were used to drive the coil. Cross-sectional images were acquired at different modulation frequencies.
2.2 Tissue phantom preparation
Tissue mimicking phantoms were prepared by mixing a polydimethylsiloxane (PDMS) liquid with the curing agent RTVA and cross linker RTVB with ratios ranging from 200:10:1 to 50:10:1 (PDMS:RTVA:RTVB), providing an elastic modulus range of 0.8–50 kPa similar to that of soft tissues (John et al., 2010; Chen et al., 1996). Titanium dioxide scattering particles (size < 5 μm, 2 mg/ml) were added to the mixture to increase the optical scattering and the solution was sonicated for an hour. MNPs were then added to the solution to obtain a concentration of 2 mg/g (MNP/solution). The solution was again sonicated for 4 hours and subsequently left in the oven for 8 hours at 80 °C for curing (Crecea et al., 2009). The side-by-side and the bilayer phantoms were prepared in a two-step process, where one of the layer/side was allowed to cure in the oven before pouring in the other layer/side. All the phantoms had cylindrical geometry with 38 mm diameter and 5 mm height. The measured scattering coefficients of representative phantoms varied between μ = 0.8 – 1.2 mm−1 which is within the range of low scattering tissues (Kholodnykh et al., 2003; Zhang et al., 2014). The scattering was kept relatively low to obtain a higher SNR signal from deeper regions within the phantom.
2.3 Data processing
The data was analyzed using standard MM-OCT data processing techniques as described in previous studies (Oldenburg et al., 2008). Briefly, after the standard OCT processing (i.e. background subtraction, resampling, dispersion compensation and FFT), the phase differences between the adjacent A-scans were computed. Subsequently, a lateral FFT was taken to bandpass filter the response at the driving frequency. After one-sided bandpass filtering, the envelope of the complex analytical signal was computed and scaled to obtain the displacement amplitudes. One dataset was acquired with the magnetic field on and another with the field off. The median values of the relative displacements from a user-defined region-of-interest (ROI) are shown in the mechanical frequency spectrum plots in this paper.
2.4 FEM simulations
FEM techniques have been widely employed in numerous elastography studies and more recently in OCE (Kennedy et al., 2013), (Ilg et al., 2012; Chin et al., 2014). Using FEM, the impact of variations in boundary conditions, sample geometries, and mechanical properties can be conveniently investigated. In this study, FEM simulations were performed using COMSOL Multiphysics (v4.4). Each sample was modeled as an isotropic, linear viscoelastic medium with a fixed bottom boundary and free side boundaries with no-slip boundary conditions. A Kelvin-Voigt model (sample dependent stiffness and a viscosity value of 0.5 Pa·s) with Rayleigh damping was used for the viscoelastic medium. A distributed body force was applied along the axial direction throughout the sample volume assuming that the MNPs are uniformly distributed within the sample and they contribute negligible inertia. The simulation plots shown in the paper were obtained using a frequency domain analysis in COMSOL, which was performed over a 10– 500 Hz frequency range.
3. RESULTS
3.1 Homogeneous tissue mimicking samples
Dynamic modulation of MNPs by applying a harmonic excitation waveform has been used to obtain a magnetomotive response in MM-OCT (Oldenburg et al., 2008), where the modulation frequency is typically chosen to be close to the mechanical resonance frequency of the sample (Crecea et al., 2013; John et al., 2010). The capability of spectroscopic MM-OCE to measure distinct resonant frequencies was investigated by preparing elastically homogenous PDMS-based phantoms with different degrees of stiffness that were loaded with uniform concentration of MNPs. Cross-sectional magnetomotive images were acquired while sweeping the frequency over a range from 20–500 Hz and the relative displacements at these frequencies were subsequently estimated. The frequency response for the different tissue phantoms are shown in Figure 2(a), where distinct resonant frequencies can be seen for different tissue phantoms with varying elastic properties. The experimental results are in good agreement with the FEM simulations shown in Figure 2(b). The elastic modulus values of the phantoms were measured using a spherical indentation measurement device (Texture Technologies Corp., Algonquin, IL) and were plotted against the measured resonance frequency using spectroscopic MM-OCE in Figure 2(c). The linear fit (R2=0.996) verifies the linear relationship between the resonance frequency, fn, and the square root of the elastic modulus (E), i.e. , for samples with a fixed geometry and constant damping coefficient (Liang et al., 2008; Qi et al., 2013).
Figure 2.
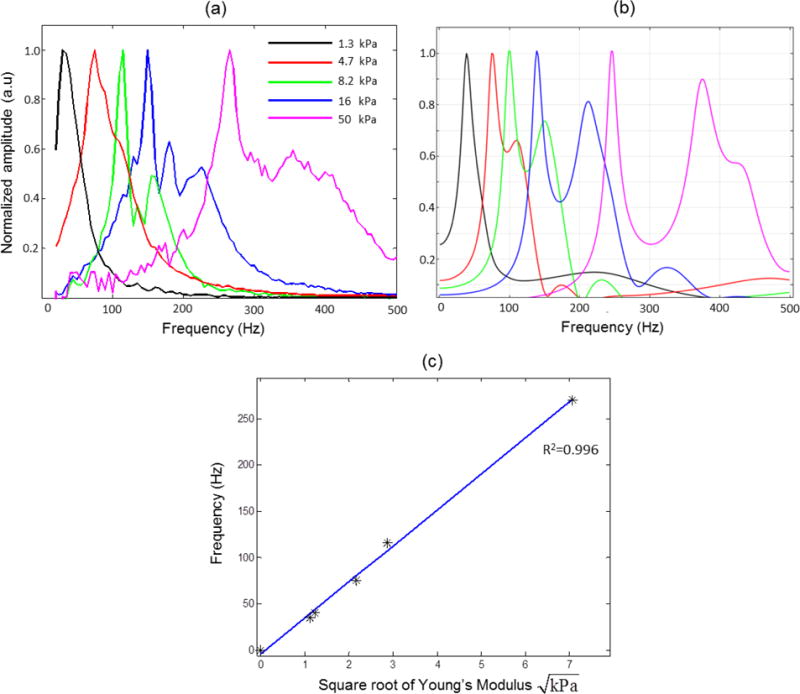
Mechanical resonance frequency in homogeneous phantoms. (a) Experiments. (b) FEM simulations. (c) The measured natural frequency is proportional to the square root of the elastic modulus. The elastic modulus values were measured with a spherical indentation measurement device (model TA.XT Plus Texture Analyzer, Texture Technologies Corp., Algonquin, IL). The blue line represents a linear fit to the data with a R2=0.996.
3.2 Heterogeneous tissue mimicking samples
Various factors such as the anisotropy in material mechanical properties, heterogeneities within the sample, geometry, and boundary conditions can influence the mechanical spectroscopic response. In the subsequent experiments, we keep the overall sample geometry the same while introducing elastically heterogeneous regions within the phantoms with known mechanical properties. Elastically heterogeneous phantoms in two configurations were prepared by making phantoms with two different degrees of stiffness placed in a (i) side-by-side and (ii) bi-layered fashion. In these configurations, the two materials having different mechanical properties are mechanically coupled with one another and the ability of MM-OCE to distinguish these mechanically coupled regions is investigated.
3.2.1 Side-by-side configuration phantoms
A side-by-side phantom in a cylindrical container (diameter = 38 mm, height = 5 mm) with a stiff region corresponding to E ~ 50 kPa and a soft region with E ~ 1.5 kPa was used to obtain the results shown in Figure 3 and 4. A 3-D geometry of the model shown in Figure 3(a) was used for the COMSOL simulations. Experiments were performed by acquiring a series of cross-sectional magnetomotive images by incrementing the frequency over the range 20 Hz to 500 Hz (with 5 Hz increments) as shown in Figure 3(b). The ability of MM-OCE based measurements to distinguish between separate regions of different stiffness is evident in Figure 3(c), where regions of different stiffness can be seen to have different frequency responses. The interface between the soft and the stiff media is visible in the OCT structural image in Figure 3(c), which correlates well with the magnetomotive response of the soft and the stiff medium. The soft part of the sample responds more strongly at a lower frequency range (as shown in the panel corresponding to 30 Hz in Figure 3(c)) while the stiff part gives a stronger magnetomotive signal at higher frequencies (as shown in the panel corresponding to 315 Hz in Figure 3(c)). In the side-by-side phantom, distinct resonance frequencies corresponding to the stiff (~ 200 Hz; left) and soft (~ 40 Hz; right) regions were observed.
Figure 3.
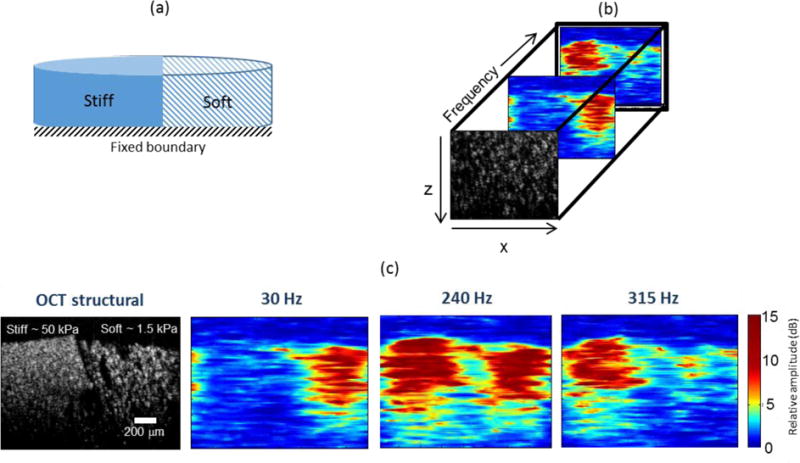
Spectroscopic MM-OCE in a heterogeneous side-by-side configuration phantom. (a) Geometrical model. (b) MM-OCE response at different excitation frequencies. (c) At lower frequencies (30 Hz) the soft region within the simple gives a higher magnetomotive response while at higher frequencies (315 Hz) the stiff region gives a higher magnetomotive signal.
Figure 4.
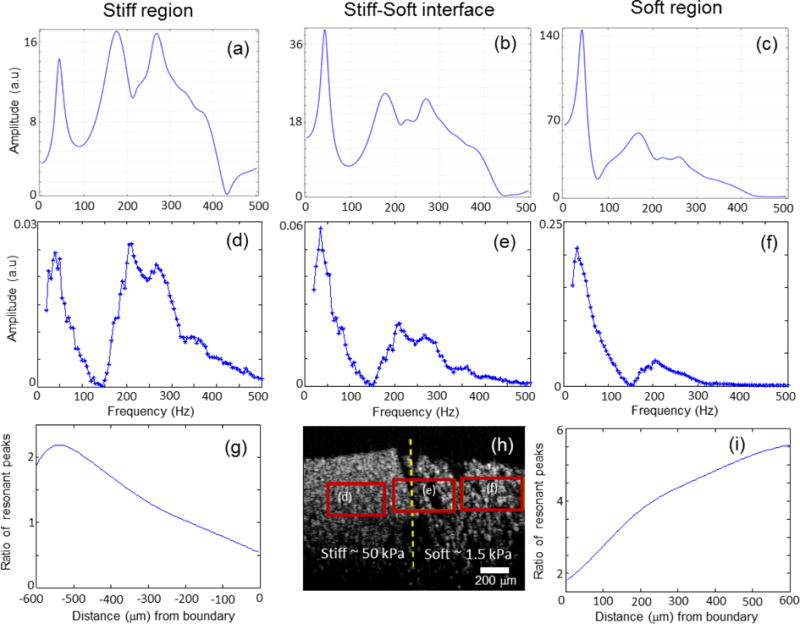
Spectroscopic magnetomotive data at different frequencies (5 Hz increments). (a) FEM simulations within the (a) stiff region (b) stiff-soft interface (c) soft region. A larger force was applied in the soft region due to a higher concentration of MNPs in this soft region. (d–f) show the experimental signal levels from the boxed regions in the PDMS phantom shown in (h). Note the differences in vertical scales, which were chosen to emphasize the differences in peak heights and relative ratios of the two resonant frequencies. (g) and (i) show that as one moves away from the interface marked by the dotted line in (h), the ratio of the resonant peaks increases, indicating diminishing boundary (interface) effects. The ratio of the resonant peak was defined as the peak amplitude of the soft over the stiff for (g) and the stiff over the soft for (i).
To evaluate how the mechanical spectrum changes at different distances away from the material interface, the spectra in localized rectangular regions at and away from the interface were estimated as shown in Figure 4(d, e, f). The differences in the scale of displacement between the stiff and soft regions can be seen in these plots. As the displacement in any localized region will depend on the concentration of the MNPs in that particular region, the relative ratios between the peaks corresponding to the two materials were used for analysis. The mechanical spectrum obtained at each spatial location were averaged over a moving window of size 250 um (width) × 25 um (height) to improve the SNR. The maximum value within the frequency range of 30–45 Hz was chosen as the soft peak while between 190 – 220 Hz was chosen as the stiff peak. It is seen that as one moves away from the interface, the ratio of the peaks of the two resonance frequencies increases (Figure 4(g, i)), indicating that at a certain distance away from the interface, distinct mechanical regions can be seen. The FEM simulation results, seen in Figure 4(a, b, c), show the same general trend and are in good agreement with the experimental results.
3.2.2 Bilayer configuration
In the next set of experiments, bilayer tissue phantoms were prepared by allowing the first layer to cure in the oven before pouring the second layer over it. Experiments were performed by changing the relative thicknesses of the stiff (~ 8 kPa) and the soft (~ 1.2 kPa) layers while keeping the overall height fixed at 5 mm. Data was taken by sweeping through a frequency range of 20–300 Hz and the relative displacement amplitudes are plotted in the figures. Figure 5(a) shows experimental results with bilayer phantoms where the soft layer is on the bottom and the stiff layer is at the top. For the same amount of force, the displacement amplitudes depend on the stiffness of the material, i.e. the softer the material, the higher the displacement values. However, for the purpose of comparing the mechanical spectroscopic response across different samples, the displacement amplitudes were all normalized to the maximum displacement value in the spectroscopic response.
Figure 5.
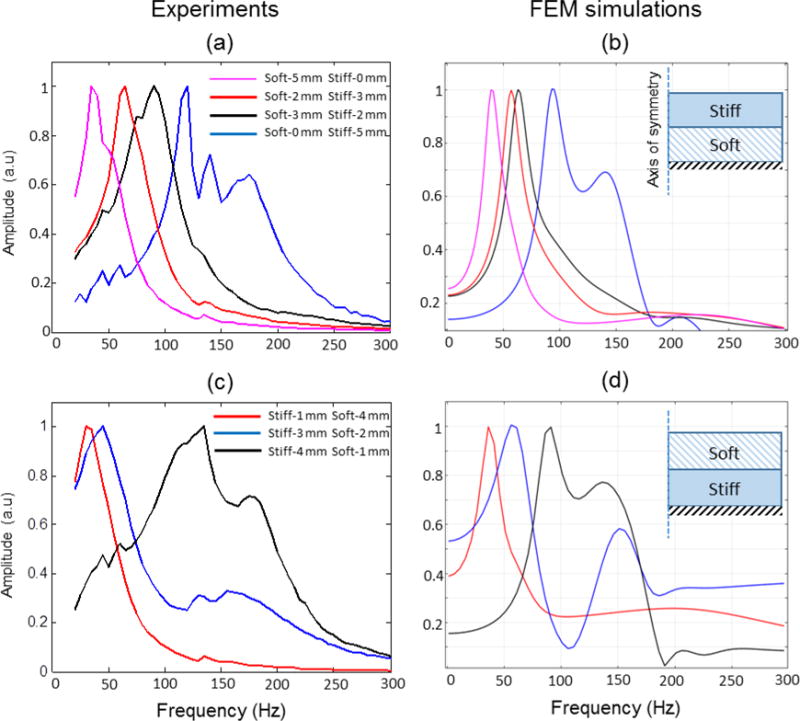
Spectroscopic MM-OCE data from bi-layer phantom having a uniform distribution of MNPs. The geometry of the samples used for simulations are illustrated in the inset. The heights of the stiff and the soft layers were varied from 0 to 5 mm while the overall height was kept constant at 5 mm. (a) Experiments and (b) FEM simulations for a soft-bottom and stiff-top phantom. (c) Experiments and (d) FEM simulations for a stiff-bottom and soft-top phantom.
These plots show a dominant peak (rather than two frequencies corresponding to the soft and stiff part of the material), suggesting that the bulk mechanical response across the axial dimension (depth) of the sample is being measured. As both these layers have a uniform distribution of MNPs and the thickness of the sample allows the magnetomotive force to act on both layers, the entire sample will respond in bulk with a resonance frequency dependent on the relative thickness of the two layers. It can be clearly seen that the resonance peaks shift from low frequencies to high frequencies as the relative thicknesses of the soft layers decreases. FEM simulation using a 2-D axisymmetric model (shown in the inset) was performed and the results shown in Figure 5(b) are in good agreement with the experimental results. The experiments were then repeated with the soft layer now placed on the top and the stiff layer at the bottom. The experimental results with this configuration shown in Figure 5(c) and simulations in Figure 5(d) show a similar trend where the resonance frequency peak shifts to high frequencies with a decrease in the relative thickness of the soft layers.
3.3 Biological samples
Finally, MM-OCE measurements were performed with biological specimens. The MNPs (#637106, average diameter 25 nm, Sigma Aldrich, Inc., St. Louis, Missouri) were allowed to diffuse into the tissues by soaking them in a MNP solution with a concentration of 10 mg∕ml (where the solvent is PBS) for a period of 4 hours. Distinct mechanical resonances from rat muscle and lung tissues at frequencies of approximately 105 Hz and 65 Hz respectively can be seen in Figure 6(a, b). These measured values are close to 99.6 ±8.9 Hz for the muscle tissue and 57.5±4.7 Hz for the lung tissue reported in an earlier study using a step magnetomotive excitation in rabbit tissues (Crecea et al., 2013). Results using a heterogeneous human tissue sample containing adipose and tumor tissues are shown in Figure 6(c, d). The excised human breast tissue was collected from the patient right after surgery, soaked in a MNP solution for 4 hours and fixed in formalin prior to the experiment. The mechanical spectroscopic responses (blue-adipose and red-tumor) in the plots in Figure 6(c) were obtained from the regions corresponding to the colored boxes shown in the OCT structural image. Several previous studies have noted the tumor tissue to be stiffer than the surrounding normal tissue (Liang et al., 2008; Wang et al., 2012). For a stiffer region like tumor, we expect a stronger magnetomotive signal at higher frequencies, as can be seen in Figure 6(c). The magnetomotive images at 20 Hz and 160 Hz excitation frequencies in Figure 6(d) clearly show the adipose tissue exhibiting a stronger response at lower frequencies while the tumor region giving a stronger signal at higher frequencies. The results that a higher resonance frequency corresponds to a medium with higher elastic modulus should be interpreted with cautious in heterogeneous samples. As the mechanical resonance frequency also depends on the geometry of the medium it might be possible that differences in the geometry between the soft and stiff parts might cause a higher elastic modulus material to have a lower mechanical resonance than that of the soft material.
Figure 6.
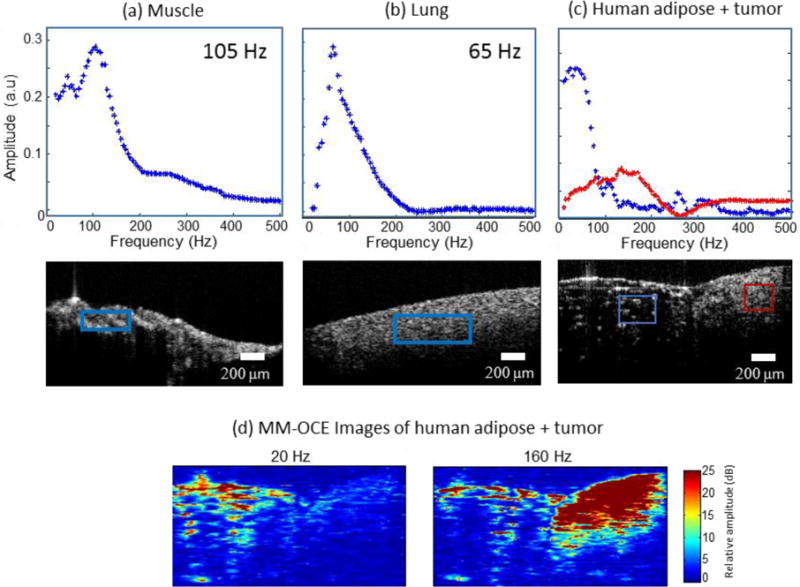
Mechanical resonance frequencies in rat and human tissue samples. (a) Rat muscle and (b) rat lung tissue. (c) Human adipose tissue and tumor. The red and blue boxes indicate the spatial regions from which the displacement amplitudes shown in the plots were calculated. (d) MM-OCE images of human adipose and tumor. At low magnetomotive frequency (20 Hz shown) the adipose is highlighted while at higher frequencies (160 Hz shown) the stiffer tumor region gives a higher magnetomotive signal.
4. DISCUSSION AND CONCLUSION
In this study, we demonstrated MM-OCE in biological tissues and samples with known heterogeneous configurations by utilizing MNPs. We demonstrated relative changes in the mechanical vibration spectrum that depend on the elastic properties of the specimen. However, obtaining quantitative estimates of the tissue mechanical properties using the current method is non-trivial especially in heterogeneous or multi-layered samples where the interpretation of the results can often be challenging. The results of our study indicate that predictable trends can be observed that agree with simulations, suggesting the possibility of obtaining quantitative estimates in future studies by using a priori information about the sample geometry and boundary conditions along with utilizing more complex models (Doyley, 2012).
In techniques such as MRE, the relative size of the excitation region is small compared to the overall size of the sample so inherently MRE perturbs a local tissue region and the propagation properties of the generated shear waves are measured to extract the local mechanical properties. However, in the present study using MM-OCE we are using small sized-samples with uniformly distributed MNPs throughout the sample. This gives a large excitation volume compared to the size of the sample and the resulting bulk movement of the sample makes the resonances more pronounced. The experimental results in this paper suggest that in the side-by-side configuration the soft and stiff parts of the medium are more easily distinguishable and distinct resonance peaks more apparent. We hypothesize that in the side-by-side configuration the two sides act “independently” of one another as the applied magnetomotive force is along the vertical (axial) direction. However, in the bi-layer configuration the vibrations are more closely coupled (one vibrating layer will result in vibration of the other layer as they are on top of each other) and we are possibly measuring the bulk excitation of the sample along the axial dimension. In future studies characterizing the local region over which resonance is sensitive would be an important parameter. This would depend on a number of factors such as the spatial extent of the applied force, elastic properties of the medium, damping within the system and the geometry of the sample etc. Further experiments and simulations are needed to gain a better understanding of the interplay of all these factors. The FEM simulations used in this study were limited to structural mechanics. However, a multi-physics simulation approach would be highly desirable. In future studies, the spatial variations in the magnetic field gradients and the noise attributes of the displacement estimates can be taken into account and combined with the structural mechanics simulations to potentially give more accurate and realistic results (Chin et al., 2014).
In this study, we have shown mechanical contrast in MM-OCE images based on the magnetomotive signal strength at different frequencies. However, it is to be noted that the magnetomotive response in a given region is also dependent on the local concentration of the MNPs, hence the magnetomotive response normalized to the MNP concentration within a given region is likely to provide more quantitative results. These differences in concentration can be due to many factors such as tissue dependent diffusion of MNPs and the biological functions and properties of the cells and tissues. The current tissue phantom study was done by varying the elastic modulus. We note that these silicone-based phantoms have lower damping as compared to that of the tissues (Crecea et al., 2013). Higher damping and viscosity will result in broadening of the resonant peaks and can result in merging of peaks that are close to one another. In future studies the effect of damping can be investigated either through simulations or by preparing a different set of phantoms where viscosity can be changed in a controlled manner (Nguyen et al., 2014).
In the spectroscopic approach described in this study, a large amount of data (one cross-sectional image per frequency) is acquired for a given sample. However, more useful information can potentially be extracted or the large acquired datasets can be represented in more meaningful ways by exploiting hyperspectral imaging techniques commonly used in remote sensing (Plaza et al., 2009). Furthermore, in scenarios where elastography over a tissue volume may be desired, the data acquisition can be improved by utilizing a volumetric MM-OCT scan scheme (Ahmad et al., 2014a).
The clinical utilization of spectroscopic MM-OCE would be challenging as the sample of interest is required to be loaded with MNPs. However, this technique might be applicable as an additional source of contrast in clinical scenarios such as in magnetic hyperthermia treatment (Moroz et al., 2002) or MNP-based contrast enhancement in MRI in which the tissue might already be loaded with MNPs (Shubayev et al., 2009). Moreover, the diffusion of the MNPs in tissues needs to be characterized and their toxicity better understood before it can be a viable technique for clinical applications.
Acknowledgments
This research was supported in part by grants from the National Institutes of Health (1 R01 EB009073, 1 R01 EB012479, S.A.B.). Dr. Jongsik Kim was funded by a Carle Foundation Hospital-Beckman Institute fellowship. The authors thank Eric Chaney and Dr. Marina Marjanovic for providing and preparing the tissue samples used in this study. Animal tissue specimens were acquired under a protocol approved by the Institutional Animal Care and Use Committee at the University of Illinois at Urbana-Champaign. Human tissue specimens were acquired under a protocol approved by the Institutional Review Boards at the University of Illinois at Urbana-Champaign and Carle Foundation Hospital. We would also like to thank Yue Wang from the Department of Bioengineering at the University of Illinois at Urbana-Champaign for the valuable discussions related to this work. We also thank Darold Spillman for providing operations and information technology support. Additional information can be found at http://biophotonics.illinois.edu.
References
- Adie SG, Liang X, Kennedy BF, John R, Sampson DD, Boppart SA. Spectroscopic optical coherence elastography. Opt Express. 2010;18:25519–34. doi: 10.1364/OE.18.025519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahmad A, Kim J, Shemonski ND, Marjanovic M, Boppart SA. Volumetric full-range magnetomotive optical coherence tomography. J Biomed Opt. 2014a;19:126001. doi: 10.1117/1.JBO.19.12.126001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahmad A, Kim J, Sobh NA, Shemonski ND, Boppart SA. Magnetomotive optical coherence elastography using magnetic particles to induce mechanical waves. Biomed Opt Express. 2014b;5:2349–61. doi: 10.1364/BOE.5.002349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carstensen EL, Parker KJ, Lerner RM. Elastography in the Management of Liver Disease. Ultrasound Med Biol. 2008;34:1535–46. doi: 10.1016/j.ultrasmedbio.2008.03.002. [DOI] [PubMed] [Google Scholar]
- Chan QCC, Li G, Ehman RL, Grimm RC, Li R, Yang ES. Needle shear wave driver for magnetic resonance elastography. Magn Reson Med. 2006;55:1175–9. doi: 10.1002/mrm.20856. [DOI] [PubMed] [Google Scholar]
- Chen EJ, Novakofski J, Jenkins WK, O’Brien WD., Jr Young’s modulus measurements of soft tissues with application to elasticity imaging. Ultrasonics, Ferroelectrics, and Frequency Control, IEEE Transactions on. 1996;43:191–4. [Google Scholar]
- Chin L, Curatolo A, Kennedy BF, Doyle BJ, Munro PRT, McLaughlin RA, Sampson DD. Analysis of image formation in optical coherence elastography using a multiphysics approach. Biomed Opt Express. 2014;5:2913–30. doi: 10.1364/BOE.5.002913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crecea V, Ahmad A, Boppart SA. Magnetomotive optical coherence elastography for microrheology of biological tissues. J Biomed Opt. 2013;18:121504. doi: 10.1117/1.JBO.18.12.121504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crecea V, Oldenburg AL, Liang X, Ralston TS, Boppart SA. Magnetomotive nanoparticle transducers for optical rheology of viscoelastic materials. Opt Express. 2009;17:23114–22. doi: 10.1364/OE.17.023114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dieter K, Uwe H, Patrick A, Jürgen B, Ingolf S. Noninvasive assessment of the rheological behavior of human organs using multifrequency MR elastography: a study of brain and liver viscoelasticity. Phys Med Biol. 2007;52:7281. doi: 10.1088/0031-9155/52/24/006. [DOI] [PubMed] [Google Scholar]
- Doyley MM. Model-based elastography: a survey of approaches to the inverse elasticity problem. Phys Med Biol. 2012;57:R35. doi: 10.1088/0031-9155/57/3/R35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fatemi M, Greenleaf JF. Ultrasound-Stimulated Vibro-Acoustic Spectrography. Science. 1998;280:82–5. doi: 10.1126/science.280.5360.82. [DOI] [PubMed] [Google Scholar]
- Greenleaf JF, Fatemi M, Insana M. Selected methods for imaging elastic properties of biological tissues. Annu Rev Biomed Eng. 2003;5:57–78. doi: 10.1146/annurev.bioeng.5.040202.121623. [DOI] [PubMed] [Google Scholar]
- Henni AH, Schmitt C, Cloutier G. Shear wave induced resonance elastography of soft heterogeneous media. J Biomech. 2010;43:1488–93. doi: 10.1016/j.jbiomech.2010.01.045. [DOI] [PubMed] [Google Scholar]
- Ilg J, Rupitsch SJ, Sutor A, Lerch R. Determination of Dynamic Material Properties of Silicone Rubber Using One-Point Measurements and Finite Element Simulations. IEEE Trans Instrum Meas. 2012;61:3031–8. [Google Scholar]
- John R, Chaney EJ, Boppart SA. Dynamics of magnetic nanoparticle-based contrast agents in tissues tracked using magnetomotive optical coherence tomography. IEEE J Sel Topics Quantum Electron. 2010;16:691–7. doi: 10.1109/JSTQE.2009.2029547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennedy BF, Kennedy KM, Sampson DD. A review of optical coherence elastography: fundamentals, techniques and prospects. IEEE J Sel Topics Quantum Electron. 2014;20:272–88. [Google Scholar]
- Kennedy KM, Ford C, Kennedy BF, Bush MB, Sampson DD. Analysis of mechanical contrast in optical coherence elastography. J Biomed Opt. 2013;18:121508. doi: 10.1117/1.JBO.18.12.121508. [DOI] [PubMed] [Google Scholar]
- Kholodnykh AI, Petrova IY, Motamedi M, Esenaliev RO. Accurate measurement of total attenuation coefficient of thin tissue with optical coherence tomography. Selected Topics in Quantum Electronics, IEEE Journal of. 2003;9:210–21. [Google Scholar]
- Liang X, Adie SG, John R, Boppart SA. Dynamic spectral-domain optical coherence elastography for tissue characterization. Opt Express. 2010;18:14183–90. doi: 10.1364/OE.18.014183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang X, Oldenburg AL, Crecea V, Chaney EJ, Boppart SA. Optical micro-scale mapping of dynamic biomechanical tissue properties. Opt Express. 2008;16:11052–65. doi: 10.1364/oe.16.011052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Migliori A, Sarrao JL, Visscher WM, Bell TM, Lei M, Fisk Z, Leisure RG. Resonant ultrasound spectroscopic techniques for measurement of the elastic moduli of solids. Physica B: Condensed Matter. 1993;183:1–24. [Google Scholar]
- Moroz P, Jones SK, Gray BN. Magnetically mediated hyperthermia: current status and future directions. Int J Hyperthermia. 18(2002):267–84. doi: 10.1080/02656730110108785. [DOI] [PubMed] [Google Scholar]
- Muthupillai R, Lomas DJ, Rossman PJ, Greenleaf JF, Manduca A, Ehman RL. Magnetic resonance elastography by direct visualization of propagating acoustic strain waves. Science. 1995;269:1854–7. doi: 10.1126/science.7569924. [DOI] [PubMed] [Google Scholar]
- Nguyen MM, Zhou S, Robert JL, Shamdasani V, Xie H. Development of oil-in-gelatin phantoms for viscoelasticity measurement in ultrasound shear wave elastography. Ultrasound Med Biol. 2014;40:168–76. doi: 10.1016/j.ultrasmedbio.2013.08.020. [DOI] [PubMed] [Google Scholar]
- Nightingale K. Acoustic radiation force impulse (ARFI) imaging: a review. Curr Med Imaging Rev. 2011;7:328–39. doi: 10.2174/157340511798038657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oldenburg AL, Boppart SA. Resonant acoustic spectroscopy of soft tissues using embedded magnetomotive nanotransducers and optical coherence tomography. Phys Med Biol. 2010;55:1189–201. doi: 10.1088/0031-9155/55/4/019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oldenburg AL, Crecea V, Rinne SA, Boppart SA. Phase-resolved magnetomotive OCT for imaging nanomolar concentrations of magnetic nanoparticles in tissues. Opt Express. 2008;16:11525–39. [PMC free article] [PubMed] [Google Scholar]
- Parker KJ, Doyley MM, Rubens DJ. Imaging the elastic properties of tissue: the 20 year perspective. Phys Med Biol. 2011;56:R1–R29. doi: 10.1088/0031-9155/56/1/R01. [DOI] [PubMed] [Google Scholar]
- Plaza A, Benediktsson JA, Boardman JW, Brazile J, Bruzzone L, Camps-Valls G, Chanussot J, Fauvel M, Gamba P, Gualtieri A, Marconcini M, Tilton JC, Trianni G. Recent advances in techniques for hyperspectral image processing. Remote Sens Environ. 2009;113(Supplement 1):S110–S22. [Google Scholar]
- Qi W, Li R, Ma T, Li J, Kirk Shung K, Zhou Q, Chen Z. Resonant acoustic radiation force optical coherence elastography. Appl Phys Lett. 2013;103:103704. doi: 10.1063/1.4820252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shubayev VI, Pisanic TR, II, Jin S. Magnetic nanoparticles for theragnostics. Adv Drug Deliv Rev. 2009;61:467–77. doi: 10.1016/j.addr.2009.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinkus R, Tanter M, Xydeas T, Catheline S, Bercoff J, Fink M. Viscoelastic shear properties of in vivo breast lesions measured by MR elastography. Magn Reson Imaging. 2005;23:159–65. doi: 10.1016/j.mri.2004.11.060. [DOI] [PubMed] [Google Scholar]
- Wang RK, Ma Z, Kirkpatrick SJ. Tissue Doppler optical coherence elastography for real time strain rate and strain mapping of soft tissue. Appl Phys Lett. 2006;89:144103–3. [Google Scholar]
- Wang S, Aglyamov S, Karpiouk A, Li J, Emelianov S, Manns F, Larin K. Assessing the mechanical properties of tissue-mimicking phantoms at different depths as an approach to measure biomechanical gradient of crystalline lens. Biomed Opt Express. 2013;4:2769–80. doi: 10.1364/BOE.4.002769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S, Li J, Manapuram RK, Menodiado FM, Ingram DR, Twa MD, Lazar AJ, Lev DC, Pollock RE, Larin K. Noncontact measurement of elasticity for the detection of soft-tissue tumors using phase-sensitive optical coherence tomography combined with a focused air-puff system. Opt Lett. 2012;37:5184–6. doi: 10.1364/OL.37.005184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamakoshi Y, Sato J, Sato T. Ultrasonic imaging of internal vibration of soft tissue under forced vibration. IEEE Trans Ultrason, Ferroelectr, Freq Control. 1990;37:45–53. doi: 10.1109/58.46969. [DOI] [PubMed] [Google Scholar]
- Zhang QQ, Wu XJ, Wang C, Zhu SW, Wang YL, Gao BZ, Yuan XC. Scattering coefficients of mice organs categorized pathologically by spectral domain optical coherence tomography. BioMed research international. 2014;2014:471082. doi: 10.1155/2014/471082. [DOI] [PMC free article] [PubMed] [Google Scholar]


