Reduced-cost linear-response CC2 method based on natural orbitals and natural auxiliary functions

Abstract

A reduced-cost density fitting (DF) linear-response second-order coupled-cluster (CC2) method has been developed for the evaluation of excitation energies. The method is based on the simultaneous truncation of the molecular orbital (MO) basis and the auxiliary basis set used for the DF approximation. For the reduction of the size of the MO basis, state-specific natural orbitals (NOs) are constructed for each excited state using the average of the second-order Møller–Plesset (MP2) and the corresponding configuration interaction singles with perturbative doubles [CIS(D)] density matrices. After removing the NOs of low occupation number, natural auxiliary functions (NAFs) are constructed [M. Kállay, J. Chem. Phys. 141, 244113 (2014)], and the NAF basis is also truncated. Our results show that, for a triple-zeta basis set, about 60% of the virtual MOs can be dropped, while the size of the fitting basis can be reduced by a factor of five. This results in a dramatic reduction of the computational costs of the solution of the CC2 equations, which are in our approach about as expensive as the evaluation of the MP2 and CIS(D) density matrices. All in all, an average speedup of more than an order of magnitude can be achieved at the expense of a mean absolute error of 0.02 eV in the calculated excitation energies compared to the canonical CC2 results. Our benchmark calculations demonstrate that the new approach enables the efficient computation of CC2 excitation energies for excited states of all types of medium-sized molecules composed of up to 100 atoms with triple-zeta quality basis sets.

I. INTRODUCTION

The excited states of molecular systems are important for many areas of chemistry, biology, and physics. Not only well-established disciplines, such as spectroscopy, photochemistry, or photobiology, but also emerging fields like energy conversion and storage utilize some phenomenon related to excited states. Consequently, the development of efficient theoretical methods for excited states is one of the major objectives of modern quantum chemistry.

Nowadays the most accurate electronic structure theory is the coupled-cluster approach introduced by Čížek a half a century ago.¹ The hierarchical coupled-cluster (CC) methods based on the exponential parameterization of the wave function, that is, the CC singles and doubles (CCSD), the CC singles, doubles, and triples (CCSDT), …, enable the consideration of electron correlation with arbitrary accuracy. The CC methods can also be generalized to excited states, but it is not a trivial task. One option is to invoke linear-response (LR) theory, which was first extended to CC theory by Monkhorst and co-workers^2,3 and later by Koch et al.^4,5 An alternative approach, which is equivalent to LR-CC theory for excitation energies, is the equation-of-motion (EOM) CC method developed by Bartlett and co-workers.^6,7 The theory, implementation, and performance of the various LR-CC and EOM-CC methods are reviewed in several publications in the literature.^8–11 Concerning bigger molecules, even the relatively cheap CCSD approach is too expensive, and further approximations are required. A simple approximate CCSD approach is the second-order CC (CC2) method proposed and first implemented by Christiansen et al.^12–14 and later perfected by Hättig and co-workers.^15–17 The CC2 method supplies excitation energies and transition moments with a moderate error, at least for valence states, with respect to higher-order CC methods.^18,19 It is also worth mentioning the configuration interaction singles with perturbative doubles [CIS(D)] approach introduced by Head-Gordon et al.,²⁰ which can also be regarded as an approximate CC2 method.²¹ The CIS(D) approach improves the configuration interaction singles (CIS) excitation energy with a perturbative correction for the double excitations and scales as the fifth power of the systems size as the CC2 method, but, in practice, it is considerably less expensive than CC2. Another closely related approach is the second-order algebraic diagrammatic construction [ADC(2)] method of Schirmer,^22,23 which has been recently extensively studied by Hättig²¹ and Dreuw and co-workers.²⁴ The ADC(2) approach can be regarded as an iterative, Hermitized generalization of CIS(D), which is close in accuracy to CC2.

Despite the excellent numerical results, the applicability of CC methods is limited due to the steep scaling of their costs with the system size. Thus, for excited states of extended molecular systems, currently the time-dependent density functional theory (TD-DFT)²⁵ is the method of choice, even if the reliability of the TD-DFT results is frequently in question,^26,27 especially for Rydberg and charge transfer (CT) excitations, just as for conjugated π-electron systems. An alternative solution is the reduction of computational expenses of CC methods, such as CC2, which provides results consistently better than TD-DFT.^28–30 In the case of most reduced-cost CC2 approaches, the bottleneck related to the processing of four-center electron repulsion integrals (ERIs) is removed exploiting density fitting (DF) or Cholesky-decomposition (CD) techniques, which can also be combined with Laplace transform (LT) approximations. In the DF approach introduced by Shavitt and co-workers³¹ and further developed by Whitten³² and Dunlap,³³ the four-center ERIs are approximated as products of three- and two-center integrals with the aid of an auxiliary (fitting) basis set. For electron correlation methods, this significantly decreases the expenses of the integral transformation steps as well as the memory demand and the number of input-output (I/O) operations for the correlation calculations.^15,34 The DF approximation was adapted for CC2 by Hättig and co-workers,¹⁵ who also developed analytic gradients for CC2 employing DF.^16,17 In the tensor hypercontraction (THC) scheme of Sherrill, Martínez, and their co-workers, which is a generalization of the DF technique, an even lower-order representation of the ERI tensor is used.^35–37 The method was also successfully applied to ground-³⁸ and excited-state³⁹ CC2 calculations. In the CD approach proposed by Koch et al.,^40,41 the four-center ERI tensor is decomposed as a product of triangular matrices neglecting the columns/rows that give negligible contributions. The efficiency of the approximation was also demonstrated for CC2.^42–44 The LT approximation developed by Almlöf and Häser^45–47 eliminates the orbital energy denominators appearing in many-body methods like CC2. Together with the DF and further approximations, it can be efficiently used for the scaling reduction of the CC2 method.^48,49

The computational costs of CC2 calculations can also be brought down by local approximations pioneered by Pulay and co-workers.^50,51 Although the literature of local correlation methods is intensively growing, applications to excited states are relatively scarce. The first excited-state local approach was proposed by Crawford et al.,^52,53 who generalized the ground-state local CCSD method of Werner and co-workers⁵⁴ to EOM-CCSD. Subsequently several excited-state CC methods utilizing local approximations were published by Korona, Schütz, and their associates.^49,55–60 First, a local EOM-CCSD method was developed, in which the dominant configurations contributing to the given excited state were identified by analyzing the CIS wave function.⁵⁵ In later publications, the development of local CC2 methods was reported,⁵⁶ which was also extended to the calculation of molecular properties⁵⁷ and combined with LT techniques.^49,58–60 It is also worthwhile mentioning the local CC2 methods of Hättig et al. utilizing pair natural orbitals^61–63 and the recent local framework for calculating excitation energies (LoFEx) approach of Baudin and Kristensen,⁶⁴ as well as the chain of spheres exchange⁶⁵ and pair natural orbitals⁶⁶ CCSD method of Izsák et al.

A widely used technique for decreasing the costs of CC calculations, the frozen natural orbital (NO) approach, is based on the reduction of the size of the molecular orbital (MO) space where the corresponding equations are solved. In this method, a one-particle density matrix is constructed using a more approximate correlation method, the matrix is diagonalized, and the orbitals with small occupation number, i.e., eigenvalue, are dropped from the resulting NO basis.^67–69 While the approach is extensively used for ground-state CCSD and higher-order CC calculations,^70–73 only a couple of applications have been reported for excited states,^53,74 and, to the best of knowledge, no attempt has been made so far to accelerate CC2 calculations with frozen NO approximations. Motivated by the NO technique, a related approach was recently put forward by one of us for the reduction of the auxiliary function basis set employed in DF methods.⁷⁵ The so-called natural auxiliary function (NAF) approach constructs a fitting basis that is optimal for the given integrals and thereby allows us to shrink the basis to as small as possible. It was successfully applied to the cost reduction of the second-order Møller–Plesset (MP2) method and the direct random-phase approximation (dRPA)⁷⁵ also in combination with local correlation approximations.^76–78 Although it was anticipated in Ref. 75 that significant speedup can also be achieved for CC2 calculations, the NAF technique has not yet been utilized for the CC2 method.

In this paper, we report the development of an efficient and robust reduced-cost LR-CC2 method which is based on the combination of the NO and NAF approaches. The errors introduced are analyzed in detail, and the applicability of the method is demonstrated for representative examples.

II. THEORY

A. The linear-response CC2 approach

The CC2 correlation energy for a restricted Hartree–Fock (HF) reference can be expressed as

$$\mathrm{\Delta }{E}_{\mathrm{CC2}}=\sum _{aibj}[2(ai|bj)-(aj|bi)](t_{ij}^{ab}+t_i^a{t}_j^b),$$ (1)

where $i,j,\mathrm{\dots }$ $(a,b,\mathrm{\dots })$ denote the occupied (virtual) spatial orbitals, and (ai|bj) is a two-electron integral in the Mulliken notation. The equations for the $t_i^a$ single and $t_{ij}^{ab}$ double excitation amplitudes were derived retaining the CCSD singles equations, while approximating the doubles equations to be correct through first order with assuming the singles to be zeroth-order parameters.¹² The resulting equations read as

$${\mathrm{\Omega }}_{{\mu }_1}=⟨{\mu }_1|\widehat{H}+[\widehat{H},T_2]|\mathrm{HF}⟩=0,$$ (2)

$${\mathrm{\Omega }}_{{\mu }_2}=⟨{\mu }_2|\widehat{H}+[F,T_2]|\mathrm{HF}⟩=0,$$ (3)

where $\mathrm{\Omega }$ is the CC2 residual, $|\mathrm{HF}⟩$ denotes the HF determinant, and $|{\mu }_n⟩$ stands for n-fold excited determinants. $T_2=\frac{1}{4}{\sum }_{aibj}{t}_{ij}^{ab}{a}^{+}{b}^{+}{i}^{-}{j}^{-}$ is the cluster operator of double excitations with a⁺ and i⁻ as the creation and annihilation operators corresponding to MOs a and i, respectively. For convenience, the T₂ operator together with the single excitation cluster operator, $T_1={\sum }_{ai}{t}_i^a{a}^{+}{i}^{-}$, will be denoted in a general form as T_n = $\frac{1}{{(n!)}^2}{\sum }_{{\mu }_n}{t}_{{\mu }_n}{\tau }_{{\mu }_n}$, where $t_{{\mu }_n}$ is the cluster amplitude associated with the ${\tau }_{{\mu }_n}$ excitation operator. In the above equations, F is the Fockian, while $\widehat{H}$ is the similarity-transformed Hamiltonian, which is obtained from the original Hamiltonian H as

$$\widehat{H}={\mathrm{e}}^{-T_1}H{\mathrm{e}}^{T_1}.$$ (4)

The T₁-transformed two-electron MO integrals can be expressed in a closed form as

$$(pq\widehat{|}rs)=\sum _{tuxy}{(\text{𝟏}-{\text{𝐭}}_1^{\mathrm{T}})}_{tp}{(\text{𝟏}+{\text{𝐭}}_1)}_{uq}{(\text{𝟏}-{\text{𝐭}}_1^{\mathrm{T}})}_{xr}{(\text{𝟏}+{\text{𝐭}}_1)}_{ys}(tu|xy),$$ (5)

where $p,q,\mathrm{\dots }$ are the generic orbital indices, and t₁ is an $n_{\mathrm{b}}\times n_{\mathrm{b}}$ matrix with n_b as the size of the basis. The elements of matrix t₁ are zero except for its virtual-occupied block, where they are equal to the $t_{{\mu }_1}$ amplitudes.

The simple equations for the doubles amplitudes, Eq. (3), can be regarded as the doubles equations of the MP2 method with an effective Hamiltonian, and the doubles amplitudes can simply be expressed as

$$t_{ij}^{ab}=\frac{(ai\widehat{|}bj)}{{\epsilon }_i\hspace{0.17em}+\hspace{0.17em}{\epsilon }_j\hspace{0.17em}-\hspace{0.17em}{\epsilon }_a\hspace{0.17em}-\hspace{0.17em}{\epsilon }_b}=\frac{(ai\widehat{|}bj)}{D_{ij}^{ab}},$$ (6)

where ${\epsilon }_p$ is the corresponding orbital energy. Substituting these into Eq. (2), it is obvious that the doubles amplitudes can be calculated on-the-fly, and their storage can be avoided.¹⁵ In practice, the equations for the single excitation amplitudes,

$${\mathrm{\Omega }}_{ai}=\sum _{bjc}(jb\widehat{|}ac){\widehat{t}}_{ij}^{cb}-\sum _{bjk}(jb\widehat{|}ik){\widehat{t}}_{kj}^{ab}+\sum _{bj}{\widehat{F}}_{jb}{\widehat{t}}_{ij}^{ab}+{\widehat{F}}_{ai}+({\epsilon }_a-{\epsilon }_i)t_i^a=0,$$ (7)

are iterated, where ${\widehat{t}}_{ij}^{ab}=\mathrm{\hspace{0.17em}2}{t}_{ij}^{ab}-t_{ji}^{ab}$, and the matrix elements of the similarity-transformed Fock-operator can be calculated as

$${\widehat{F}}_{jb}=\sum _{ai}[2(bj|ai)-(aj|bi)]t_i^a,$$ (8)

$${\widehat{F}}_{ai}=\sum _{bj}[2(ai|jb)-(ab|ji)]t_j^b-\sum _{bjk}[2(bj|ik)-(bk|ij)]t_k^a{t}_j^b+\sum _{bjc}[2(bj|ca)-(ba|cj)]t_j^b{t}_i^c-\sum _{bjck}[2(ck|bj)-(bk|cj)]t_k^c{t}_i^b{t}_j^a.$$ (9)

Introducing the DF approximation, the four-center ERIs can be written in the

$$(pq|rs)=\sum _{PQ}(pq|P){(P|Q)}^{-1}(Q|rs)$$ (10)

form, where P and Q stand for the elements of the auxiliary basis, whereas (pq|P) and (P|Q) are the three- and two-center Coulomb integrals, respectively, and (P|Q)⁻¹ is a simplified notation for the corresponding element of the inverse of the two-center Coulomb integral matrix. In practice, the latter inverse matrix is factorized and rewritten, e.g., as the product of the inverse square root matrices. The four-center ERIs can then be recast in the

$$(pq|rs)=\sum _Q{J}_{pq}^Q{J}_{rs}^Q$$ (11)

form with

$$J_{pq}^Q=\sum _P(pq|P){(P|Q)}^{-1/2}.$$ (12)

Alternatively, we can also use the CD of the inverse matrix for the factorization. The similarity-transformed two-electron integrals, $(pq\widehat{|}rs)$, can also be written in a form similar to Eq. (11) since the singles amplitudes can be absorbed into the elements of the J list as

$${\widehat{J}}_{pq}^Q=\sum _{rs}{(\text{𝟏}-{\text{𝐭}}_1^{\mathrm{T}})}_{rp}{(\text{𝟏}+{\text{𝐭}}_1)}_{sq}{J}_{rs}^Q.$$ (13)

Note that the occupied-virtual block of $\widehat{\text{𝐉}}$ is not affected by the similarity transformation, that is, ${\widehat{J}}_{ia}^P$ = $J_{ia}^P$, while the other blocks loose their permutational symmetries because ${\widehat{J}}_{pq}^P$ $\ne$ ${\widehat{J}}_{qp}^P$ any more.

Our implementation of the ground-state CC2 equations is based on the algorithm of Hättig and co-workers.¹⁵ Since our intention is to decrease the costs of the CC2 method partly by reducing the MO space, the important difference is that our implementation uses MO integrals as opposed to the atomic orbital-based algorithm of Ref. 15. This required the slight modification of the working equations and the algorithm, which are presented in Table I together with the scaling of the various steps given in terms of the number of occupied (n_occ) and virtual (n_virt) orbitals and the number of auxiliary functions (n_aux). The rate-determining step of the procedure is still the construction of the $(ai\widehat{|}bj)$ integral list (step 6) and the contraction of the doubles amplitudes (step 7), the operation count of which scales as $n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}^2{n}_{\mathrm{aux}}$.

TABLE I.

Working equations and their scaling for the CC2 algorithm.

Step	Scaling
1 Construct intermediates ${\widehat{X}}_{ai}^Q$ and ${\widehat{X}}_{ij}^Q$
${\widehat{X}}_{ai}^Q={\sum }_b{J}_{ab}^Q{t}_i^b$	$n_{\mathrm{occ}}{n}_{\mathrm{virt}}^2{n}_{\mathrm{aux}}$
${\widehat{X}}_{ij}^Q={\sum }_a{J}_{ai}^Q{t}_j^a$	$n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}{n}_{\mathrm{aux}}$
2 Compute the ${\widehat{J}}_{ji}^Q$ and ${\widehat{J}}_{ai}^Q$ lists and the contribution of one term in ${\widehat{F}}_{ai}$ to ${\mathrm{\Omega }}_{ai}$
${\widehat{J}}_{ij}^Q={\widehat{X}}_{ij}^Q+J_{ij}^Q$	$n_{\mathrm{occ}}^2{n}_{\mathrm{aux}}$
${\mathrm{\Omega }}_{ai}\leftarrow -{\sum }_{Qj}{\widehat{X}}_{aj}^Q{\widehat{J}}_{ji}^Q$	$n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}{n}_{\mathrm{aux}}$
${\widehat{J}}_{ai}^Q={\widehat{X}}_{ai}^Q+J_{ai}^Q-{\sum }_j{\widehat{J}}_{ij}^Q{t}_j^a$	$2n_{\mathrm{occ}}{n}_{\mathrm{virt}}{n}_{\mathrm{aux}}+n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}{n}_{\mathrm{aux}}$
3 Construct intermediate XQ
$X^Q={\sum }_{ai}{J}_{ai}^Q{t}_i^a$	noccnvirtnaux
4 Compute further contributions of ${\widehat{F}}_{ai}$ to ${\mathrm{\Omega }}_{ai}$
${\mathrm{\Omega }}_{ai}\leftarrow {\sum }_{Qj}({\sum }_k{\widehat{X}}_{jk}^Q{t}_k^a){\widehat{J}}_{ji}^Q$	$2n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}{n}_{\mathrm{aux}}$
${\mathrm{\Omega }}_{ai}\leftarrow {\sum }_Q{\widehat{J}}_{ai}^Q{X}^Q+t_i^a({\epsilon }_a-{\epsilon }_i)$	noccnvirtnaux + noccnvirt
5 Calculate ${\widehat{F}}_{jb}$
${\widehat{F}}_{jb}={\sum }_Q{\widehat{J}}_{bj}^Q{X}^Q-{\sum }_{Qi}{\widehat{X}}_{ji}^Q{J}_{bi}^Q$	$n_{\mathrm{occ}}{n}_{\mathrm{virt}}{n}_{\mathrm{aux}}+n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}{n}_{\mathrm{aux}}$
6 Construct the $(ai\widehat{|}bj)$ list
$(ai\widehat{|}bj)={\sum }_Q{\widehat{J}}_{ai}^Q{\widehat{J}}_{bj}^Q$	$n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}^2{n}_{\mathrm{aux}}$
7 Compute and contract ${\widehat{t}}_{ij}^{ab}$, calculate the contributions of ${\widehat{F}}_{jb}$ to ${\mathrm{\Omega }}_{ai}$
${\widehat{t}}_{ij}^{ab}=[2(ai\widehat{|}bj)-(aj\widehat{|}bi)]/D_{ij}^{ab}$	$n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}^2$
${\widehat{Y}}_{ai}^Q={\sum }_{bj}{\widehat{t}}_{ij}^{ab}{J}_{bj}^Q$	$n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}^2{n}_{\mathrm{aux}}$
${\mathrm{\Omega }}_{ai}\leftarrow {\sum }_{bj}{\widehat{t}}_{ij}^{ab}{\widehat{F}}_{jb}$	$n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}^2$
8 Calculate further contributions of ${\widehat{t}}_{ij}^{ab}$ to ${\mathrm{\Omega }}_{ai}$
${\mathrm{\Omega }}_{ai}\leftarrow {\sum }_{Qb}({\sum }_j{J}_{bj}^Q{t}_j^a+J_{ba}^Q){\widehat{Y}}_{bi}^Q={\sum }_{Qb}{\widehat{J}}_{ba}^Q{\widehat{Y}}_{bi}^Q$	$2n_{\mathrm{occ}}{n}_{\mathrm{virt}}^2{n}_{\mathrm{aux}}+n_{\mathrm{virt}}^2{n}_{\mathrm{aux}}$
${\mathrm{\Omega }}_{ai}\leftarrow -{\sum }_{Qj}{\widehat{J}}_{ji}^Q{\widehat{Y}}_{aj}^Q$	$n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}{n}_{\mathrm{aux}}$
9 Calculate CC2 correlation energy
$\mathrm{\Delta }{E}_{\mathrm{CC2}}={\sum }_{Qai}({\widehat{J}}_{ai}^Q+X^Q{t}_i^a-{\sum }_j{\widehat{X}}_{ij}^Q{t}_j^a){\widehat{Y}}_{ai}^Q$	$4n_{\mathrm{occ}}{n}_{\mathrm{virt}}{n}_{\mathrm{aux}}+n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}{n}_{\mathrm{aux}}$

Concerning excited states, the CC LR theory calculates the excitation energies as the eigenvalues of the Jacobi-matrix which is defined by the derivative of the residual with respect to the cluster amplitudes as

$$\begin{array}{cc}{A}_{{\mu }_i,{\nu }_j}\hfill & =\frac{\partial {\mathrm{\Omega }}_{{\mu }_i}}{\partial t_{{\nu }_j}}\hfill \\ & =\left(\begin{array}{cc}\hfill ⟨{\mu }_1|[\widehat{H},{\tau }_{{\nu }_1}]+[[\widehat{H},{\tau }_{{\nu }_1}],T_2]|\mathrm{HF}⟩\hfill & \hfill ⟨{\mu }_1|[\widehat{H},{\tau }_{{\nu }_2}]|\mathrm{HF}⟩\hfill \\ \hfill ⟨{\mu }_2|[\widehat{H},{\tau }_{{\nu }_1}]|\mathrm{HF}⟩\hfill & \hfill {\delta }_{{\mu }_2{\nu }_2}{\epsilon }_{{\mu }_2}\hfill \end{array}\right),\hfill \end{array}$$ (14)

where ${\epsilon }_{{\mu }_2}=-D_{ij}^{ab}$. Similar to the ground-state problem, the storage of the doubles amplitudes can also be avoided at the solution of the eigenvalue equation of matrix A if an effective Jacobian,

$$A_{{\mu }_1{\nu }_1}^{\mathrm{eff}}({\omega }_{\mathrm{CC2}})=A_{{\mu }_1{\nu }_1}-\frac{A_{{\mu }_1{\gamma }_2}{A}_{{\gamma }_2{\nu }_1}}{{\epsilon }_{{\gamma }_2}-{\omega }_{\mathrm{CC2}}},$$ (15)

is introduced, where ${\omega }_{\mathrm{CC2}}$ is the CC2 excitation energy.¹⁵ The pseudo-eigenvalue equation of matrix A^eff,

$$\sigma ({\omega }_{\mathrm{CC2}},\text{𝐫})={\text{𝐀}}^{\mathrm{eff}}({\omega }_{\mathrm{CC2}})\text{𝐫}={\omega }_{\mathrm{CC2}}\text{𝐫},$$ (16)

is only solved in the space spanned by the single excitations, whose coefficients are included in vector r. The working equations for the $\sigma$ vector can be derived by straightforward differentiation of Eq. (7) with respect to $t_{{\mu }_1}$. The structure of the resulting expressions is very similar to that of the corresponding ground-state terms, thus, the excited-state equations can be solved by defining intermediates of the same type. Only the number of intermediates will be higher since each term in Eq. (7) including n pieces of $t_{{\mu }_1}$ amplitudes results in n terms of similar structure upon differentiation. Consequently, the algorithm presented in Table I is also applicable mutatis mutandis to the evaluation of the σ vector.

An important feature of matrix A^eff is that it also depends on the excitation energy of the given excited state, and hence, the eigenvalue equation cannot be solved simultaneously for all the considered states using the conventional Davidson-type diagonalization techniques. We implemented a modified version of the algorithm proposed by Hättig and co-workers.¹⁵ In the first step, an integral direct, multi-state DF-CIS calculation is run, and the corresponding CIS excitation energies and vectors will be used as initial guess in the subsequent calculations. Then, for each excited state, the eigenvector is preoptimized by a modified Davidson algorithm using the root-following technique⁷⁹ to avoid convergence to a wrong solution. Finally, the non-linear problem is solved by a direct inversion in the iterative subspace (DIIS) algorithm, which is also applied to solve the ground-state CC2 equations. Our experience showed that in particular cases, the above algorithm finds the wrong root, that is, we arrive at the same CC2 solution starting from different CIS eigenvectors. We could overcome this problem by projecting out the single excitation part of the CC2 eigenvectors converged previously from the initial guess CIS vectors.

B. Natural orbitals

In the NO approximation, a lower-level wave function is chosen, let us denote it by Ψ, and the virtual-virtual block of the one-particle density matrix,

$$D_{ab}=⟨\mathrm{\Psi }|a^{+}{b}^{-}|\mathrm{\Psi }⟩,$$ (17)

as well as the occupied-occupied block of the hole density matrix,

$${\overline{D}}_{ij}=⟨\mathrm{\Psi }|i^{-}{j}^{+}|\mathrm{\Psi }⟩,$$ (18)

are constructed. The eigenvectors of these matrices are referred to as the virtual (VNOs) and occupied NOs (ONOs), respectively, whereas the corresponding eigenvalues are interpreted as the occupation numbers of the orbitals. It is supposed that the orbitals of low population give a small contribution to the correlation and can be dropped. The corresponding truncation thresholds for the virtual and occupied NO sets will be denoted by ${\epsilon }_{\mathrm{VNO}}$ and ${\epsilon }_{\mathrm{ONO}}$, respectively.

For the construction of the NOs for ground-state CC2 calculations, the MP2 density matrix is a plausible choice. For excited states, the selection of an appropriate wave function $\mathrm{\Psi }$ is less trivial. Here the CIS(D) approach seems to be a good choice since it is an excited-state generalization of the MP2 method and accounts for about the same amount of correlation for the excited state as the MP2 method does for the ground state. Moreover, the calculation of CIS(D) density matrices is relatively cheap, and the computation time required is similar to that of a CC2 iteration. Of course, we should keep in mind that the ground-state CC2 amplitudes are also necessary to solve the equations for the excited states, and it is highly desirable to solve both equations in the same MO basis. For this reason, we construct a state-specific MO basis for each excited state in which both the ground- and excited-state equations are solved. Consequently, a single, “state-averaged” (hole) density matrix is required for each excited state for the construction of the NOs. For this purpose, we simply take the average of the MP2 (D^MP2) and CIS(D) (D^CIS(D)) densities, i.e., we diagonalize the D = (D^MP2 + D^CIS(D))/2 density matrices, and the similar expression holds for the hole densities. After the diagonalization of the (hole) density matrices and the selection of the NOs of sufficiently high occupation number, the truncated NO basis is canonicalized so that we will be able to employ the equations derived for canonical MOs. The elements of the latter basis will be denoted by $\stackrel{\sim }{a}$, $\stackrel{\sim }{i}$, $\mathrm{\dots }$, and $\stackrel{\sim }{\text{𝐉}}$ will stand for the J list, the MO indices of which are transformed to the canonicalized NO basis.

The required blocks of the one-particle MP2 (hole) density matrices can be calculated as

$${\overline{D}}_{ij}^{\mathrm{MP2}}=\sum _{kab}\left(2T_{ik}^{ab}{T}_{jk}^{ab}-T_{ik}^{ab}{T}_{jk}^{ba}\right),$$ (19)

$$D_{ab}^{\mathrm{MP2}}=\sum _{ijc}\left(2T_{ij}^{ca}{T}_{ij}^{cb}-T_{ij}^{ca}{T}_{ij}^{bc}\right),$$ (20)

where $T_{ij}^{ab}$ is a first-order doubles amplitude defined as

$$T_{ij}^{ab}=\frac{(ai|bj)}{D_{ij}^{ab}}.$$ (21)

The algorithm for the construction of MP2 densities is presented in Table II. The bottleneck is the assembly of the (ai|bj) integral list, which scales as $n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}^2{n}_{\mathrm{aux}}$. There are two other fifth-power scaling operations in the algorithm. The evaluation of the virtual-virtual block of the density matrix scaling as $n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}^3$ is also relatively expensive, while the computation time needed for the calculation of the occupied-occupied block of the hole density matrix is in general considerably shorter. Please note that the MP2 densities must be constructed only once, independently of the number of excited states.

TABLE II.

Working equations and their scaling for the evaluation of MP2 density matrices.

Step	Scaling
1 Assemble (ai|bj) list
$(ai|bj)={\sum }_Q{J}_{ai}^Q{J}_{bj}^Q$	$n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}^2{n}_{\mathrm{aux}}$
2 Compute $T_{ij}^{ab}$
$T_{ij}^{ab}=(ai|bj)/D_{ij}^{ab}$	$n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}^2$
3 Compute intermediate $X_{ij}^{ab}$
$X_{ij}^{ab}=2T_{ij}^{ab}-T_{ij}^{ba}$	$n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}^2$
4 Compute density matrices
${\overline{D}}_{ij}^{\mathrm{MP2}}={\sum }_{kab}{T}_{ik}^{ab}{X}_{jk}^{ab}$	$n_{\mathrm{occ}}^3{n}_{\mathrm{virt}}^2$
$D_{ab}^{\mathrm{MP2}}={\sum }_{ijc}{T}_{ij}^{ca}{X}_{ij}^{cb}$	$n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}^3$

The CIS(D) density matrix can be split up as the sum of the CIS density matrix and the contribution of the perturbative (D) correction, D^CIS(D) = D^CIS + D^(D). The CIS density matrices read as

$${\overline{D}}_{ij}^{\mathrm{CIS}}=\sum _a{c}_i^a{c}_j^a,$$ (22)

$$D_{ab}^{\mathrm{CIS}}=\sum _i{c}_i^a{c}_i^b,$$ (23)

where $c_i^a$ is a CIS coefficient, while we define D^(D) analogously to its MP2 counterpart as

$${\overline{D}}_{ij}^{(\mathrm{D})}=\sum _{kab}(2c_{ik}^{ab}{c}_{jk}^{ab}-c_{ik}^{ab}{c}_{jk}^{ba}),$$ (24)

$$D_{ab}^{(\mathrm{D})}=\sum _{ijc}(2c_{ij}^{ca}{c}_{ij}^{cb}-c_{ij}^{ca}{c}_{ij}^{bc})$$ (25)

with $c_{ij}^{ab}$ as a CIS(D) doubles coefficient. The latter were given by Head-Gordon and co-workers²⁰ in a spin-orbital basis. The corresponding expression for spatial orbitals can easily be derived by spin-integration and exploiting the relationships of doubles amplitudes⁸⁰ and reads as

$$c_{ij}^{ab}=\frac{{\sum }_c[(ac|bj)c_i^c\hspace{0.17em}+\hspace{0.17em}(ac|bi)c_j^c]\hspace{0.17em}-\hspace{0.17em}{\sum }_k[(kj|ai)c_k^b\hspace{0.17em}+\hspace{0.17em}(kj|bi)c_k^a]}{D_{ij}^{ab}\hspace{0.17em}+\hspace{0.17em}{\omega }_{\mathrm{CIS}}},$$ (26)

where ${\omega }_{\mathrm{CIS}}$ stands for the CIS excitation energy. The calculation of CIS(D) densities follows the route shown in Table III. As it can be seen, similar to the evaluation of the MP2 densities, the rate-determining operation is the construction of a four-index intermediate as a product of three-index quantities, which scales as $n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}^2{n}_{\mathrm{aux}}$. However, in addition to the inexpensive CIS contribution, there are two further fourth-power scaling terms (step 2) in contrast to the MP2 density matrices, where the occupied-occupied and virtual-virtual blocks of the three-center integral list are contracted with CIS coefficients. Since the CIS(D) coefficients, and thus the density matrices, are state-dependent, these quantities have to be evaluated for each excited state.

TABLE III.

Working equations and their scaling for the evaluation of CIS(D) density matrices.

Step	Scaling
1 Construct CIS contribution to density matrices
${\overline{D}}_{ij}^{\mathrm{CIS}(\mathrm{D})}\leftarrow {\sum }_a{c}_i^a{c}_j^a$	$n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}$
$D_{ab}^{\mathrm{CIS}(\mathrm{D})}\leftarrow {\sum }_i{c}_i^a{c}_i^b$	$n_{\mathrm{occ}}{n}_{\mathrm{virt}}^2$
2 Compute intermediate $Y_{ai}^Q$
$Y_{ai}^Q\leftarrow {\sum }_c{J}_{ac}^Q{c}_i^c$	$n_{\mathrm{occ}}{n}_{\mathrm{virt}}^2{n}_{\mathrm{aux}}$
$Y_{ai}^Q\leftarrow -{\sum }_j{J}_{ij}^Q{c}_j^a$	$n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}{n}_{\mathrm{aux}}$
3 Compute intermediate $V_{ij}^{ab}$
$V_{ij}^{ab}={\sum }_Q{Y}_{ai}^Q{J}_{bj}^Q$	$n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}^2{n}_{\mathrm{aux}}$
4 Calculate $c_{ij}^{ab}$ coefficients
$c_{ij}^{ab}=(V_{ij}^{ab}+V_{ji}^{ba})/(D_{ij}^{ab}+{\omega }_{\mathrm{CIS}})$	$n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}^2$
5 Compute intermediate $X_{ij}^{ab}$
$X_{ij}^{ab}=2c_{ij}^{ab}-c_{ij}^{ba}$	$n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}^2$
6 Compute density matrices
${\overline{D}}_{ij}^{\mathrm{CIS}(\mathrm{D})}\leftarrow {\sum }_{kab}{c}_{ik}^{ab}{X}_{jk}^{ab}$	$n_{\mathrm{occ}}^3{n}_{\mathrm{virt}}^2$
$D_{ab}^{\mathrm{CIS}(\mathrm{D})}\leftarrow {\sum }_{ijc}{c}_{ij}^{ca}{X}_{ij}^{cb}$	$n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}^3$

Our numerical experience showed that further approximations can be introduced at the construction of the D^MP2 and D^CIS(D) matrices. As it will be demonstrated in Sec. III B, the calculated excitation energies hardly change if we neglect the exchange-like contributions to the density matrices, that is, instead of Eqs. (19), (20), (24), and (25), we define the density matrices as

$${\overline{D}}_{ij}^{\mathrm{MP2}}=\sum _{kab}2T_{ik}^{ab}{T}_{jk}^{ab},$$ (27)

$$D_{ab}^{\mathrm{MP2}}=\sum _{ijc}2T_{ij}^{ca}{T}_{ij}^{cb},$$ (28)

$${\overline{D}}_{ij}^{(\mathrm{D})}=\sum _{kab}2c_{ik}^{ab}{c}_{jk}^{ab},$$ (29)

$$D_{ab}^{(\mathrm{D})}=\sum _{ijc}2c_{ij}^{ca}{c}_{ij}^{cb}.$$ (30)

The advantage of these equations is that the evaluation of intermediates $X_{ij}^{ab}$ (see Tables II and III) can be avoided, and the calculation of the density matrices can be reduced to the multiplication of a matrix with its transpose, whose operation can be efficiently performed. Furthermore, a simple and fast algorithm can be designed for the evaluation of the above equations if the $T_{ij}^{ab}$ or $c_{ij}^{ab}$ list does not fit into the memory. In this case, at the construction of the MP2 densities (see Table II), one of the virtual indices of the doubles amplitudes is split up into blocks, hereafter denoted by $\mathcal{A}$, so that the amplitudes with the remaining three indices can be kept in the memory. The outmost loop in the algorithm runs over $\mathcal{A}$, and in the inner loops, the doubles amplitudes with one virtual index in the given index range are calculated, and their contribution to the density matrices is computed.

The evaluation of the CIS(D) density matrices deserves somewhat more attention (see Table III) since the size of the $J_{ab}^Q$ list can also easily exceed the size of the available memory. In this case, the list is blocked according to its auxiliary index so that the $J_{ab}^Q$ integrals with Q in a block can be held in the memory, and the first contribution to intermediate $Y_{ai}^Q$ (step 2) is evaluated within a loop performed over the blocks. Analogously to the MP2 algorithm, one of the virtual indices of the four-index intermediates is also restricted, and the subsequent steps (steps 3 to 6) are carried out in a loop running over the corresponding $\mathcal{A}$ blocks. A further difficulty is that the symmetrization of intermediate $V_{ij}^{ab}$ is necessary to obtain the $c_{ij}^{ab}$ coefficients (step 4), and it requires the recalculation of particular $V_{ij}^{ab}$ matrix elements if the out-of-core algorithm is executed.

C. Natural auxiliary functions

With the aid of the NAF approach,⁷⁵ the size of the auxiliary basis set can be reduced in a way reminiscent of the NO technique via a rank reduction of the corresponding three-center integral matrix J. If the latter is regarded as a two-index matrix with composite row index pq and column index Q, we can, in principle, perform its singular value decomposition (SVD) as

$$\text{𝐉}=\text{𝐌}\mathrm{\Sigma }{\text{𝐍}}^{\mathrm{T}},$$ (31)

where M and N are the matrices composed of the left and right singular vectors (SVs), and Σ is a diagonal matrix with the singular values on its diagonal. In practice, we only need the singular values and right SVs of J, which are identical, respectively, to the square root of the eigenvalues and eigenvectors of matrix

$$\text{𝐖}={\mathbf{J}\mathbf{J}}^{\mathrm{T}}$$ (32)

and can be more efficiently obtained by diagonalizing W than by performing the SVD of matrix J. The eigenvectors of matrix W, that is, the right SVs of J, can be considered as the linear combination coefficients of new auxiliary functions, which we call the NAFs. Similar to the NO approach, the NAFs with eigenvalues lower than a threshold (${\epsilon }_{\mathrm{NAF}}$) are dropped, and the remaining ${\overline{n}}_{\mathrm{aux}}$ pieces of eigenvectors are collected in matrix $\overline{\text{𝐍}}$. If the auxiliary function index of matrix J is now transformed by matrix $\overline{\text{𝐍}}$ as

$$\overline{\text{𝐉}}=\text{𝐉}\overline{\text{𝐍}},$$ (33)

the resulting $\overline{\text{𝐉}}$ matrix is the best rank ${\overline{n}}_{\mathrm{aux}}$ approximation of J in the least-squares sense.

The most computation-intensive operation of a CC2 calculation scales as $n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}^2{\overline{n}}_{\mathrm{aux}}$ (see Table I), but the scaling of the other expensive terms is also linear in ${\overline{n}}_{\mathrm{aux}}$. Furthermore, the storage requirements also grow linearly with the number of fitting functions. Consequently, using a NAF basis, the decrease in the computation time is expected to be proportional to the ${\overline{n}}_{\mathrm{aux}}/n_{\mathrm{aux}}$ ratio.

An important question is at what stage the NAF basis should be constructed and what J should be used for that purpose. In principle, we can change for a NAF basis right at the beginning of the calculation, prior to the evaluation of the MP2 and CIS(D) density matrices. The advantage of this strategy would be that the expenses of the latter steps would also be reduced. However, as it is discussed in Ref. 75, the NAF basis is an auxiliary basis that is optimal for the given MO basis, and hence, it is expedient to construct the NAFs from the J matrix whose MO indices are already transformed to the final MO basis, in our case from matrix $\stackrel{\sim }{\text{𝐉}}$. The second question is what block of $\stackrel{\sim }{\text{𝐉}}$ is to be used for the determination of the NAFs. Of course, the NAFs constructed from the entire $\stackrel{\sim }{\text{𝐉}}$ will be the exact right SVs of the matrix. However, we can also build approximate NAF bases from particular blocks of $\stackrel{\sim }{\text{𝐉}}$, for instance, we can compute matrix W only from the ${\stackrel{\sim }{J}}_{ai}^Q$ or ${\stackrel{\sim }{J}}_{pi}^Q$ integrals. In this way, we can reduce the time spent on the construction of the NAF basis, but probably more NAFs have to be retained to obtain results of similar accuracy as the NAFs computed, e.g., from the ${\stackrel{\sim }{J}}_{ai}^Q$ list will be lower-quality fitting functions for the (ab|ij)-type integrals. These aspects will be analyzed in Sec. III B.

D. General algorithm

To conclude this section, we overview our general algorithm for the present reduced-cost LR-CC2 approach, which is as follows:

• 1.Solve HF equations
• 2.Solve CIS equations for all the excited states using a multi-state, integral-direct algorithm
• 3.
  Loop over excited states

  • 3.a.
    Compute state-averaged one-particle density matrices (Tables II and III)
  • 3.b.
    Transform the MO indices of J to the pseudo-canonical NO basis
  • 3.c.
    Evaluate matrix W from $\stackrel{\sim }{\text{𝐉}}$ [Eq. (32)], select NAFs to be retained
  • 3.d.
    Transform the auxiliary function index of $\stackrel{\sim }{\text{𝐉}}$ to the NAF basis [Eq. (33)]
  • 3.e.
    Save integral list $\overline{\text{𝐉}}$ to disk

  End loop

• 4.
  Loop over excited states

  • 4.a.
    Retrieve integral list $\overline{\text{𝐉}}$ from disk
  • 4.b.
    Solve the ground- and excited-state CC2 equations (Table I)

  End loop

Note that the CC2 equations are solved in a different loop than the one in which the densities, the NAF basis, and the transformed integrals are constructed. The rationale behind this is that, in the first loop, it enables the design of an algorithm where the original J list is read from a disk or recalculated only once for the integral transformation. The transformed $\overline{\text{𝐉}}$ integral list is saved to the disk and retrieved in the second loop. However, the size of the $\overline{\text{𝐉}}$ lists is significantly, by more than an order of magnitude smaller than that of matrix J, thus the reading and processing of the $\overline{\text{𝐉}}$ list do not cause any complication in the CC2 calculations.

III. RESULTS

A. Computational details

The proposed reduced-cost CC2 approach has been implemented in the Mrcc suite of quantum chemical programs and is available in the current release of the package.⁸¹

For the test calculations, Dunning’s correlation consistent basis sets augmented with diffuse functions (aug-cc-pVXZ, where X = D, T, Q) were used,^82–84 and the corresponding auxiliary bases developed by Weigend et al. were employed in both the HF and the subsequent calculations.^85–87 In the CIS and CC2 calculations, the core orbitals were kept frozen.

For monitoring the convergence of the excitation energies with the truncation thresholds, a test set of small molecules was assembled including acetone, acetamide, benzene, butadiene, formaldehyde, and formamide from the benchmark set of Thiel and co-workers,^88,89 as well as the ethylene-tetrafluoroethylene system (at separations of 5 and 10 Å) from Dreuw et al.⁹⁰ We endeavored to consider all important types of excitations. The valence excited states ($n\to {\pi }^{*}$, $\sigma \to {\pi }^{*}$, and $\pi \to {\pi }^{*}$, including also the $\pi \to {\pi }^{*}$ states of the conjugated butadiene and the aromatic benzene) were those identified by Thiel and co-workers;^88,89 to consider CT excitations, the ones assigned by Dreuw et al.⁹⁰ for the ethylene-tetrafluoroethylene system were chosen, whereas the Rydberg states of formamide and acetamide were selected by us.

To also gain some insight into the performance of the new method for medium-sized molecules, another test set was also used, which is representative of all the important excitations types as well. The geometries of 6,6′-difluoro-indigo,⁹¹ a bithiophene derivative,²⁸ and N-methyl-2,3-benzcarbaxole²⁸ were taken from the literature, while those for the remaining azobenzene, diphenylamine, hydrazone dye, and 4-(N,N-dimethylamino)-3-hydroxyflavone molecules were optimized with the Mrcc program at the DFT level applying the B3LYP⁹² functional and the cc-pVDZ basis set. Further benchmark calculations were carried out for even larger systems to demonstrate the applicability of the approach. In these calculations, the bisimide derivative studied by Grimme and co-workers⁹¹ as well as the phenothiazine-isoalloxazine dyad,⁵⁶ two borondipyrromethene-flavin derivatives [Flv(a) and Flv(b)],⁵⁷ and the cyanoacrylic acid derivative (D21L6)⁵⁸ test system of Schütz et al. was considered. The structural formulas of the molecules and the coordinates for the molecules optimized by us are available in the supplementary material.

The reported computation times are wall-clock times measured on a computer with 128 GB of main memory and a 6-core 3.5 GHz Intel Xeon E5-1650 processor.

B. Convergence with the truncation thresholds

First, we analyze the convergence of the CC2 excitation energies with the cutoff parameters, ${\epsilon }_{\mathrm{VNO}}$ and ${\epsilon }_{\mathrm{NAF}}$, of the VNOs and NAFs for the small-molecule test set using the aug-cc-pVTZ basis. The effect of the truncation of the ONO space will be studied later for bigger systems because even for the largest molecules (benzene and the ethylene-tetrafluoroethylene model) considered here the number of occupied orbitals is rather small and cannot be decreased. We focus on the results obtained with the aug-cc-pVTZ basis since at least triple-ζ basis sets including diffuse functions are required for semi-quantitative excitation energies, while the quadruple-ζ and bigger basis sets are usually not worth using together with the simplistic CC2 approach and are not practical for large molecules. Nevertheless, results calculated with double- and quadruple-ζ basis sets will also be presented later.

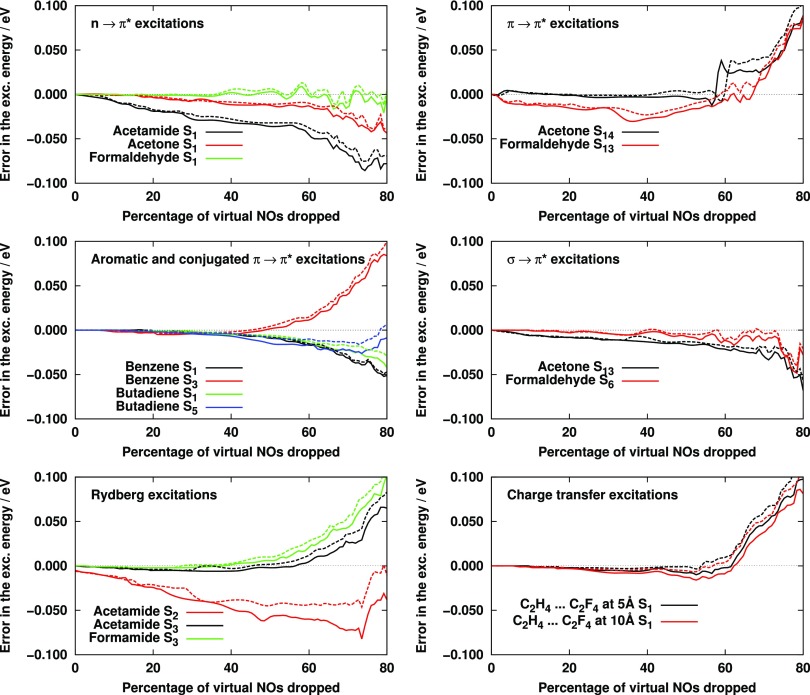
To study the convergence with the number of virtual orbitals, the VNO space constructed by diagonalizing the density matrices including (Eqs. (20) and (25)) or excluding (Eqs. (28) and (30)) the exchange-like terms were gradually decreased, and the error with respect to the canonical CC2 excitation energy was calculated. The results are visualized in Fig. 1. Inspecting the plots we can observe that the error introduced by dropping the VNOs is moderate and only slightly increases in most cases up to a truncation of about 60%, where the mean absolute error (MAE) obtained with density matrices including (excluding) the exchange-like terms is only 0.016 (0.019) eV, and the maximum absolute error (MAX) still does not exceed 0.044 (0.060) eV. For the $\pi \to {\pi }^{*}$, Rydberg, and CT excitations, the error starts increasing steeply at around 60%, while for the excited states of other types, the results deteriorate more slowly. The increase of the errors, apart from small fluctuations on the meV scale, is monotonic up to 60%; however, the sign of the errors can differ even for different states of the same molecule or different excited states of the same type. The difference of the results obtained with and without the exchange contributions is very small. The average difference is 2 to 3 meV for any truncation of the VNO space with the S₂ state of acetamide exhibiting the largest deviation, 0.030 eV, at the truncation of 73%, which causes too large error anyway to be used in practical applications. As a consequence, the exchange-excluding density matrices can safely be employed.

FIG. 1.

Error of CC2 excitation energies as a function of the number of VNOs dropped with the aug-cc-pVTZ basis set. Dashed (solid) line: results obtained with density matrices including (excluding) the exchange-like contributions.

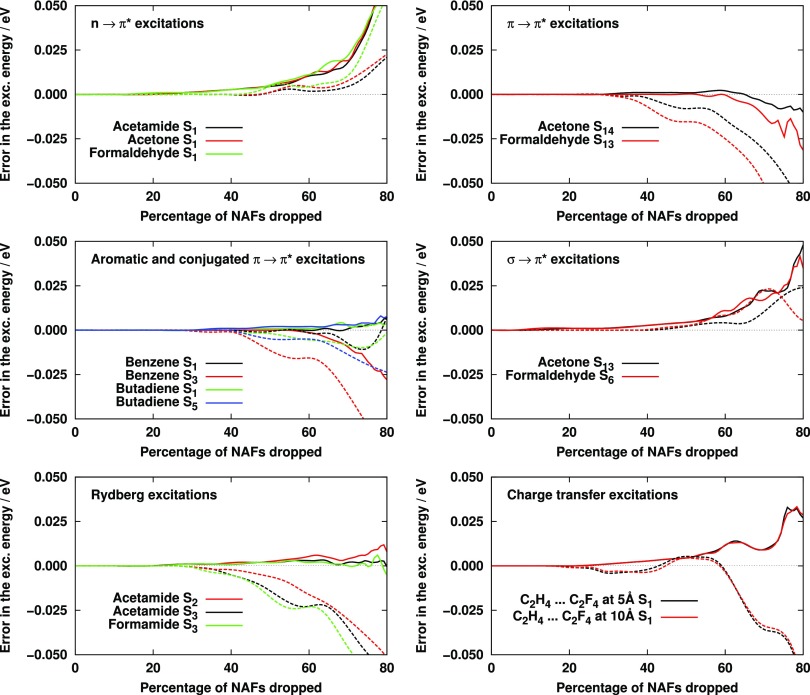
The behavior of the excitation energies as a function of the size of the NAF basis was analyzed similarly, first without any truncation of the VNO space. The NAFs constructed from the $J_{ai}^Q$, $J_{pi}^Q$, and $J_{pq}^Q$ lists were tested, however, the results calculated using the first integral list are relatively poor and not discussed here. The errors of the approximate CC2 excitation energies with respect to the canonical ones are displayed in Fig. 2. As it can be seen, in contrast to the VNOs, the NAF approximation introduces a very small error up to 40% truncation, where the MAE (MAX) is 0.002 (0.004) eV with NAFs derived from the $J_{pi}^Q$ list, while the corresponding value for the case of the $J_{pq}^Q$ list is just 0.001 (0.002) eV. Dropping further NAFs, the approach based on the $J_{pq}^Q$ integrals is obviously more robust, with the exception of the $n\to {\pi }^{*}$ excitations, and the error for the latter scheme is significantly lower than with the approach using the $J_{pi}^Q$ list. At the truncation of 60%, the MAE (MAX) is 0.005 (0.011) eV with the $J_{pq}^Q$-based and 0.010 (0.024) eV with the $J_{pi}^Q$-based approach. Beyond 60%, the quality of the results drops rapidly for most types of excited states, especially with the latter scheme. These results suggest that it is worthwhile constructing the NAF basis from the $J_{pq}^Q$ list even if $n_{\mathrm{virt}}^2{n}_{\mathrm{aux}}^2$ additional operations are required to calculate matrix W [Eq. (32)] with respect to the case when W is computed just from the $J_{pi}^Q$ integrals.

FIG. 2.

Error of CC2 excitation energies as a function of the number of NAFs dropped with the aug-cc-pVTZ basis set. Dashed (solid) line: results obtained with W matrices calculated from the $J_{pi}^Q$ ($J_{pq}^Q$) lists.

Since our intention is to combine the NO and NAF approaches, it is also important to study their joint effect, which also facilitates the selection of reliable default values for our truncation thresholds. As it is discussed in Sec. II C, if the NO and NAF approximations are applied simultaneously, it is more beneficial to construct first the NO basis then the NAFs. Accordingly, taking into account the above results, we first calculate the VNOs from the density matrices excluding the exchange terms and truncate the VNO space using threshold ${\epsilon }_{\mathrm{VNO}}$. Then, we construct the NAF basis with the ${\stackrel{\sim }{J}}_{\stackrel{\sim }{p}\stackrel{\sim }{q}}^Q$ integral list and truncate it according to ${\epsilon }_{\mathrm{NAF}}$. At the determination of the default truncation threshold, our main purpose was to develop a robust method and to keep the MAE of the approach about an order of magnitude smaller than the intrinsic error of the CC2 method, that is, 0.2 to 0.3 eV.^93,94 We tested numerous combinations of the ${\epsilon }_{\mathrm{VNO}}$ and ${\epsilon }_{\mathrm{NAF}}$ thresholds with the considered values corresponding close to 60% truncations in Figs. 1 and 2. Relying on the results of these numerical experiments, which are presented in the supplementary material, we propose ${\epsilon }_{\mathrm{VNO}}=\mathrm{\hspace{0.17em}7.5}\times {10}^{-5}$ and ${\epsilon }_{\mathrm{NAF}}=\mathrm{\hspace{0.17em}0.1}$ a.u. as the default values of the cutoff parameters.

The errors of the computed excitation energies and the number of the neglected VNOs and NAFs with the default thresholds are presented in Table IV for the small-molecule test. Looking at the results we can conclude that the MAE (MAX) of the joint NO and NAF approach is 0.023 (0.052) eV, which is considerably lower than the error of the CC2 method itself. The percentage of the dropped VNOs is rather system independent and falls in the narrow range of 56% to 65%. The ratio of the neglected NAFs is even more stable, and it fluctuates in an interval of about 5%. As expected, in the truncated NO basis, considerably fewer auxiliary functions are necessary, and in average, 82.3% of the NAFs can be removed. Being aware of these results, we can envisage a speedup of about 35 for the rate-determining step of the CC2 calculations scaling as $n_{\mathrm{occ}}^2{n}_{\mathrm{virt}}^2{n}_{\mathrm{aux}}$, and a reduction of also about 35-times is foreseen in the size of the largest quantity to be stored, the virtual-virtual block of matrix J.

TABLE IV.

Canonical CC2 excitation energies (in eV), the error of CC2 excitation energies computed with the present approach (in eV), and the percentage of VNOs and NAFs dropped using the default thresholds with the aug-cc-pVTZ basis set for small molecules.

Molecule	Character	State	${\omega }_{\mathrm{CC2}}$	Error	Dropped VNOs	Dropped NAFs
Acetamide	$n\to {\pi }^{*}$	S1	5.605	−0.033	63.6	82.9
	Rydberg	S2	5.917	−0.031	61.5	82.7
	Rydberg	S3	6.456	0.034	61.8	82.6
Acetone	$n\to {\pi }^{*}$	S1	4.454	−0.001	65.0	83.4
	$\sigma \to {\pi }^{*}$	S13	9.110	−0.007	64.7	83.6
	$\pi \to {\pi }^{*}$	S14	9.212	0.052	62.4	83.4
Benzene	$\pi \to {\pi }^{*}$	S1	5.220	−0.017	63.4	84.0
	$\pi \to {\pi }^{*}$	S3	6.452	0.035	63.9	84.5
Butadiene	$\pi \to {\pi }^{*}$	S1	6.134	−0.009	63.2	83.7
	$\pi \to {\pi }^{*}$	S5	7.064	−0.004	63.8	84.6
Formaldehyde	$n\to {\pi }^{*}$	S1	3.996	0.041	58.8	80.3
	$\sigma \to {\pi }^{*}$	S6	9.191	0.010	59.2	80.6
	$\pi \to {\pi }^{*}$	S13	10.698	0.022	57.7	81.2
Formamide	Rydberg	S3	6.697	0.034	58.5	80.9
CTa at 5Å	CT	S1	6.728	0.013	56.1	79.5
CTa at 10Å	CT	S1	6.740	0.020	56.8	79.7
Average				0.023b	61.3	82.3
Maximum				0.052c	65.0	84.6
Minimum				0.001d	56.1	79.5

^aEthylene-tetrafluoroethylene model.

^bMean absolute error.

^cMaximum absolute error.

^dMinimum absolute error.

To gain some impression of the basis set dependence of the results, we also performed test calculations for the small-molecule test set with the aug-cc-pVDZ and aug-cc-pVQZ basis sets using the default thresholds (${\epsilon }_{\mathrm{VNO}}=\mathrm{\hspace{0.17em}7.5}\times {10}^{-5}$ and ${\epsilon }_{\mathrm{NAF}}=\mathrm{\hspace{0.17em}0.1}$ a.u.). The error measures, such as the MAE, MAX, and the minimum absolute error (MIN), for the excitation energies are summarized in Table V, while the detailed results can be found in the supplementary material. As we can presume, with the double-ζ basis in average, a smaller number of VNOs are dropped (32.9%) than with the triple-ζ one (61.3%), while with the quadruple-ζ basis, more VNOs are neglected (78.5%). The tendency is similar but not so pronounced for the NAFs, where the average number of dropped functions only changes with a couple of percents when increasing the cardinal number of the basis set. The MAE and MAX are about twice as large with aug-cc-pVDZ and aug-cc-pVQZ basis sets than with aug-cc-pVTZ but are still moderate and remarkably lower than the intrinsic error of CC2. We note that with the aug-cc-pVQZ basis set, the truncation of the VNO and NAF spaces is expected to result in a speedup of about 190 for the most expensive operations and a reduction of about 190-times in the size of the integral list.

TABLE V.

Error measures for the CC2 excitation energies (in eV) and the average, maximum, minimum percentage of VNOs and NAFs dropped using the default thresholds with various basis sets for small molecules.

	Error			Dropped VNOs			Dropped NAFs
Basis	MAE	MAX	MIN	Avg.	Max.	Min.	Avg.	Max.	Min.
aug-cc-pVDZ	0.051	0.100	0.022	32.9	39.2	25.0	81.4	83.1	80.0
aug-cc-pVTZ	0.023	0.052	0.001	61.3	65.0	56.1	82.3	84.6	79.5
aug-cc-pVQZ	0.047	0.106	0.004	78.5	81.0	75.8	88.6	90.5	86.7

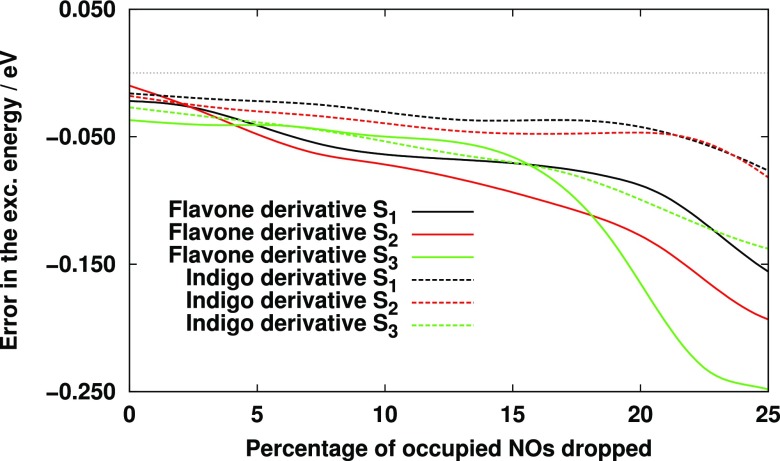
We also investigated the truncation of the ONO basis. To this intent, we selected two bigger molecules, 6,6′-difluoro-indigo and 4-(N,N-dimethylamino)-3-hydroxyflavone, for which the number of correlated occupied orbitals is sufficiently high, 53 for both molecules. Fixing the VNO and NAF truncation thresholds to their default values, the number of neglected ONOs was systematically varied. The errors of the CC2 excitation energies with respect to the canonical ones are shown in Fig. 3. The error that arose at the 10% reduction of the ONO space is in average as large as the combined error of the VNO and NAF approximations (0.02 eV, see Table VI) even if the latter spaces are much more aggressively truncated. Thus, at around 10%, the overall error of the three approximations is about 0.05 eV, but it starts growing rapidly after the truncation of 15%. It means that only a couple of occupied orbitals can be dropped, and unfortunately the gain in the computation time is rather limited. The approximation is probably more efficient for large systems, for which, however, CC2 calculations are currently not feasible even with the present reduced-cost scheme. Therefore, in the following test calculations, the occupied MO space will not be truncated.

FIG. 3.

Error of CC2 excitation energies as a function of the number of ONOs dropped with the aug-cc-pVTZ basis set using ${\epsilon }_{\mathrm{VNO}}=\mathrm{\hspace{0.17em}7.5}\times {10}^{-5}$ and ${\epsilon }_{\mathrm{NAF}}=0.1$ a.u. thresholds.

TABLE VI.

Canonical CC2 excitation energies (in eV), the error of CC2 excitation energies computed with the present approach (in eV), and the percentage of VNOs and NAFs dropped using the default thresholds with the aug-cc-pVTZ basis set for bigger molecules.

Molecule	Number of atoms	Number of basis functions	State	Character	${\omega }_{\mathrm{CC2}}$	Error	Dropped VNOs	Dropped NAFs	Speedup
Hydrazone dye	21	828	S1	$\pi$ $\to {\pi }^{*}$	3.562	−0.012	58.1	80.7	14.1
			S2	CT	3.924	−0.016	59.0	80.9
			S3	$n,\sigma$ $\to {\pi }^{*}$	3.947	−0.015	58.9	80.8
			S4	$\pi$ $\to {\pi }^{*}$	4.180	−0.019	57.8	80.4
			S5	$n,\sigma$ $\to {\pi }^{*}$	4.527	−0.011	58.9	80.8
			S6	$n,\sigma$ $\to {\pi }^{*}$	4.543	−0.006	58.8	80.8
Diphenylamine	24	851	S1	$\pi$ $\to {\pi }^{*}$	4.334	−0.015	63.3	83.9	17.9
			S2	$\pi$ $\to {\pi }^{*}$	4.460	−0.024	63.3	83.7
			S3	Rydberg	4.627	0.014	63.4	83.8
			S4	Rydberg	4.994	0.048	63.3	83.9
			S5	Rydberg	5.084	0.037	63.2	84.0
			S6	Rydberg	5.229	0.026	63.2	83.9
Azobenzene	24	874	S1	$n,\sigma$ $\to {\pi }^{*}$	2.785	0.014	63.7	83.6	12.3
			S2	$\pi$ $\to {\pi }^{*}$	4.071	−0.018	62.6	83.3
			S3	$\pi$ $\to {\pi }^{*}$	4.427	−0.029	62.5	83.2
			S4	$\pi$ $\to {\pi }^{*}$	4.435	−0.029	62.6	83.3
			S5	$\pi$ $\to {\pi }^{*}$	5.155	−0.042	62.2	83.1
			S6	Rydberg	6.057	0.021	62.0	83.5
6,6′-difluoro-indigo	28	1150	S1	$\pi$ $\to {\pi }^{*}$	2.952	−0.016	58.3	80.9	12.8
			S2	$\pi$ $\to {\pi }^{*}$	3.436	−0.018	58.2	80.8
			S3	$\pi$ $\to {\pi }^{*}$	3.684	−0.027	58.2	80.9
			S4	$\pi$ $\to {\pi }^{*}$	3.725	−0.027	58.2	80.9
			S5	$\pi$ $\to {\pi }^{*}$	4.274	−0.023	58.1	80.9
			S6	$\pi$ $\to {\pi }^{*}$	4.775	−0.037	58.1	80.9
Bithiophene derivative	29	1135	S1	$\pi$ $\to {\pi }^{*}$	3.843	−0.026	59.4	82.3	17.8
			S2	$\pi$ $\to {\pi }^{*}$	4.631	−0.025	59.4	82.3
			S3	$\pi$ $\to {\pi }^{*}$	4.940	−0.034	59.2	82.2
			S4	$\pi$ $\to {\pi }^{*}$	5.446	0.002	59.2	82.4
			S5	Rydberg	5.538	0.009	59.1	82.3
			S6	$\pi$ $\to {\pi }^{*}$	5.602	−0.027	59.2	82.3
N-methyl-2,3-benzcarbaxole	31	1127	S1	$\pi$ $\to {\pi }^{*}$	3.332	−0.013	63.3	83.6	20.5
			S2	$\pi$ $\to {\pi }^{*}$	4.062	−0.021	63.4	83.6
			S3	Rydberg	4.468	0.020	63.1	83.8
			S4	$\pi$ $\to {\pi }^{*}$	4.510	−0.037	63.1	83.6
			S5	Rydberg	4.835	0.011	63.2	83.9
			S6	Rydberg	4.898	−0.017	63.2	83.9
Hydroxyflavone derivative	36	1311	S1	CT	3.382	−0.022	63.0	83.1	28.1
			S2	$\pi$ $\to {\pi }^{*}$	4.124	−0.030	63.0	83.1
			S3	$n,\sigma$ $\to {\pi }^{*}$	4.154	−0.020	63.0	83.2
			S4	$\pi$ $\to {\pi }^{*}$	4.227	−0.010	63.1	83.2
			S5	Rydberg	4.330	0.018	62.7	83.3
			S6	Rydberg	4.866	−0.037	62.6	83.3
Average						0.022a	61.1	82.6	17.6
Maximum						0.048b	63.7	84.0	28.1
Minimum						0.002c	57.8	80.4	12.3

^aMean absolute error.

^bMaximum absolute error.

^cMinimum absolute error.

C. Representative examples

Our approach was further tested for bigger molecules to check if the conclusions drawn for the small systems are also valid in the general case. The set includes dye molecules which are well-established test molecules from the literature.^30,95,96 The 6,6′-difluoro-indigo, the bithiophene derivative, and the N-methyl-2,3-benzcarbaxole molecules stem from the test suite of Grimme and co-workers;^28,91,97 the azobenzene, the diphenylamine, and the hydrazone dye were collected from the work of Matsuura et al.;⁹⁸ whereas the 4-(N,N-dimethylamino)-3-hydroxyflavone molecule featuring a dominant CT excited state was taken from the studies of Mély and co-workers.^99,100 Applying our default settings, for each molecule the six lowest singlet states were considered, among which all important types of excited state can be found including several Rydberg and two CT states. The numerical results are collected in Table VI.

The MAE (MAX) of the computed excitation energies with respect to the canonical results is 0.022 (0.048) eV, which is practically identical to the corresponding value, 0.023 (0.051) eV, obtained for the small-molecule test set. The same holds for the average number of the neglected VNOs and NAFs, which are 61.1% and 82.6%, respectively, for these molecules, while for the smaller ones, the 61.3% and 82.3% values were found. The spread of the results is also similar for the smaller and the bigger systems: the deviations of the minimum and maximum number of dropped VNOs and NAFs are 6% and 4%, respectively, which should be compared to the differences of 9% and 5% obtained for the small-molecule test set. These data support that the errors introduced by our approximations are rather stable and independent of the system size, and our approach with the default settings can be applied as a black-box method for arbitrary excited states of extended systems.

As it has been discussed above, a theoretical speedup of 35 can be expected in the most expensive step of a CC2 iteration with the aug-cc-pVTZ basis, however, the overhead due to evaluation of the density matrices is notable. To estimate the overall speedup factors for our approach, we measured the wall-clock times for the canonical CC2 calculations including the CIS iterations, the solution of the ground-state CC2, and the six response equations. These values were divided by the wall times measured for the entire reduced-cost CC2 calculations excluding the solution of the HF equations, that is, the wall time spent on the CIS calculation, the construction of the MP2 and the six CIS(D) density matrices, the integral transformations, reading and writing of the $\overline{\text{𝐉}}$ integral list, and the solution of the ground- and excited-state CC2 equations for each excited state. The calculated speedups are also reported in Table VI. The average speedup with respect to the canonical run is about 18, but in particular cases much larger increase in the speed of the calculation can be observed. Of course, we would await that the speedup factors vary in a tighter interval since the number of the neglected VNOs and NAFs does so. However, the number of iterations needed to converge the CC2 equations can significantly change when working in the reduced spaces. Anyway, the computation time is reduced by an order of magnitude even in the worst cases, and it is easy to see that the speedup is even better if more excited states are targeted.

To further demonstrate the applicability of our approach, benchmark calculations were carried out for even larger systems. The considered molecules, that is, the bisimide derivative;^28,91,96 the flavin derivatives, Flv(a) and Flv(b);⁵⁷ the phenothiazine-isoalloxazine dyad;^49,56,58,64 and the cyanoacrylic acid derivative D21L6^58,59 were previously studied in the literature at the CC2 level using small bases, however, CC2 calculations with the aug-cc-pVTZ or similar basis sets have not been possible so far. The results are compiled in Table VII.

TABLE VII.

CC2 excitation energies computed with the present approach (in eV), the percentage of VNOs and NAFs dropped, and computation times (in min) using the default thresholds with the aug-cc-pVTZ basis set for big molecules.

Molecule	Number of atoms	Number of basis functions	State	Character	${\omega }_{\mathrm{CC2}}$	Dropped VNOs	Dropped NAFs	tCISa	$t_{\overline{\text{𝐉}}}$ b	tCC2c
Flv(a)	51	2001	S1	$\pi \to {\pi }^{*}$	2.750	60.9	82.1	15.5	81.6	3.7
			S2	$\pi \to {\pi }^{*}$	2.995	60.8	82.0		81.6	3.6
			S3	$n,\sigma \to {\pi }^{*}$	3.339	61.1	82.1		81.6	3.4
			S4	$\pi \to {\pi }^{*}$	3.613	60.9	82.0		81.6	3.5
Dyad	53	2051	S1	$\pi \to {\pi }^{*}$	3.063	61.4	82.7	15.4	84.1	3.5
			S2	CT	3.373	61.7	82.8		84.1	3.5
			S3	$\pi \to {\pi }^{*}$	3.506	61.2	82.6		84.1	3.4
			S4	CT	3.826	61.2	82.7		84.1	3.5
Bisimide derivative	60	2346	S1	$\pi \to {\pi }^{*}$	2.543	61.5	82.5	24.6	179.3	7.0
			S2	$\pi \to {\pi }^{*}$	3.438	61.5	82.6		178.7	6.7
			S3	$\pi \to {\pi }^{*}$	3.707	61.5	82.6		179.2	6.4
			S4	$\pi \to {\pi }^{*}$	3.793	61.5	82.6		178.9	6.4
Flv(b)	78	2829	S1	$\pi \to {\pi }^{*}$	2.603	63.8	83.3	53.9	416.3	12.9
			S2	$\pi \to {\pi }^{*}$	2.978	63.9	83.3		416.2	12.9
			S3	$n,\sigma \to {\pi }^{*}$	3.279	64.0	83.4		416.2	13.0
			S4	$\pi \to {\pi }^{*}$	3.329	63.8	83.3		415.9	13.0
D21L6	98	3412	S1	CT	2.622	65.2	84.4	42.8	1093.2	29.1
			S2	$\pi \to {\pi }^{*}$	3.442	65.1	84.3		1092.9	30.0
Average						62.3	82.9
Maximum						65.2	84.4
Minimum						60.8	82.0

^aAverage wall time for a CIS iteration using a multi-state, integral-direct algorithm.

^bAverage wall time for the construction of the $\overline{\text{𝐉}}$ integral list. The calculation of the MP2 density is distributed equally among the excited states, that is, $t_{\overline{\text{𝐉}}}=t_{\mathbf{\text{CIS(D)}}}+t_{\text{𝐌𝐏𝟐}}/n+t_{\text{𝐖}}+t_{\mathrm{Int}}$, where t_CIS(D), t_MP2, and t_W are the wall times required for the evaluation of the CIS(D) and MP2 density matrices and the W matrix, respectively, n stands for the number of excited states, and t_Int is the wall time required for the integral transformations.

^cAverage wall time for a CC2 iteration.

The computed excitation energies and the assignation of the excited states are in line with the results available in the literature. The percentage of the VNOs and NAFs dropped is still close to what we obtain for the smaller molecules but seems to slightly increase with the size of the system. The basis set includes at least 2000 atomic orbitals for all the molecules, and the number of basis functions far exceeds 3000 for the most extended system. Looking at the wall times required for the CIS and CC2 iterations, we can see that the expenses of the solution of the CC2 equations in the reduced spaces are similar to those of the initial canonical CIS calculation. In addition to the calculation of the state-averaged density matrices, two integral transformations and, for the construction of the NAF basis, the evaluation of matrix W are required. The time of these operations amounts to 10% to 15% of the computation time spent on the calculation of the densities. Our timings show that the excitation energy of a single excited state can be computed within less than a day for a molecule of more than 80 atoms with around 3000 basis functions.

IV. CONCLUSIONS

An efficient approach has been presented for the calculation of CC2 excitation energies. Our scheme successfully combines the natural orbital and natural auxiliary function approximations. For the calculation of the NOs, state-averaged density matrices are constructed using approximate MP2 and CIS(D) densities for the ground and excited state, respectively. For the calculation of NAFs, the use of the entire integral list turned out to be the most advantageous choice.

The errors introduced by the various approximations have been analyzed for a representative test set including all important types of excitations. The thresholds for the selection of NOs and NAFs have been determined. Our results suggest that the average error obtained with the proposed cutoff parameters is low, 0.02 eV, with a triple-$\zeta$ basis and practically independent of the system size. In average, 60% and 80% of the virtual NOs and NAFs can be dropped, respectively, and these numbers also seem system-independent. For these calculations, the CC2 iterations are by about a factor of 35 faster, and even if the evaluation of the density matrices requires some extra time, the overall speedup is of more than an order of magnitude.

Our results demonstrate that the proposed approach enables the routine use of the CC2 method for molecules of more than 50 atoms with basis sets including more than 2000 basis functions. We have also carried out CC2 excitation energy calculations with reliable basis sets for systems of about 100 atoms on a single workstation computer. Such calculations were previously not possible within an acceptable time frame.

SUPPLEMENTARY MATERIAL

See supplementary material for molecular structures and geometries and excitation energies computed with various thresholds and basis sets.