Abstract
We propose a model of an adaptive network of spiking neurons that gives rise to a hypernetwork of its dynamic states at the upper level of description. Left to itself, the network exhibits a sequence of transient clustering which relates to a traffic in the hypernetwork in the form of a random walk. Receiving inputs the system is able to generate reproducible sequences corresponding to stimulus-specific paths in the hypernetwork. We illustrate these basic notions by a simple network of discrete-time spiking neurons together with its FPGA realization and analyse their properties.
This article is part of the themed issue ‘Mathematical methods in medicine: neuroscience, cardiology and pathology’.
Keywords: adaptive network, spiking neuron, hypernetwork, transient sequence, cluster state, map-based model
1. Introduction
The interest in multiagent systems with entangled structures and non-trivial dynamics known as complex networks is stimulated by their prevalence in nature, technical applications and society, and by the common mathematical language mainly based on graph theory, statistical physics and nonlinear dynamics [1–3]. The most promising application field of the complex network view is neuroscience [4–8]. Revealing the architecture of structural links in neuronal structures as well as functional relations between anatomically remote brain regions allows formulating basic principles of the organization of the central nervous system in terms of complex networks and nonlinear dynamics [9,10]. New findings in neuroscience require developing novel concepts in mathematical descriptions; for example, the hierarchical structure and activity in brain stimulates generalizations in network science, e.g. temporal, multiplex, multilayer, multilevel networks [11–14] and hypernetworks [15,16].
The ever-changing synaptic couplings lead to studying adaptive or evolving dynamical networks [17–20], impermanent nature of most perception and cognitive processes require shifting focus in nonlinear dynamics from attractors to transients [21,22]. The transient dynamics of spatio-temporal patterns and evolving architectures of synaptic links seem to be basic properties underlying most complex brain functions [23–25]. Many studies of anatomical structures and physiological processes support the idea that cognitive processes relate to interactions among distributed neuronal populations and brain areas [26,27]. It was hypothesized and experimentally shown that during each perception or cognitive act there emerges an assembly of spatially distributed neurons—the dynamic core—that operates in a coordinated manner [28–33]. The neurons within the assembly preferentially communicate with each other giving rise to some integration activity. This process is highly transient which enables the neuronal network to rapidly change the activation pattern reflecting the multitasking property of brain and functional segregation [34–37]. Uncovering biophysical and dynamical mechanisms underlying a rich functional repertoire of the brain circuit at the micro-, meso- and macrolevels remains a non-trivial challenge for both experimentalists and theoreticians. Understanding the principles of relating cognitive functions to coordinated activities of neuronal substrates is still in its infancy and needs to be described by an appropriate mathematical language. In this paper, we propose a descriptive model for emerging complex behaviours in a hypernetwork—at the upper level with respect to a basic network with coevolving coupling structure and nodal dynamics. This approach is used to provide an example of how a simple structured network of coupled oscillators gives rise to the traffic in the hypernetwork.
2. Results
(a). A hypernetwork generated by an adaptive network
We propose a paradigmatic model based on the concept of hypernetworks [15,16]; this model captures how network dynamics and structure evolution can lead to the emergence of a new level of description which may be considered as an emergence of functions from evolving dynamical structures. The model gives a sketch, a mathematical image of how a small oscillatory network with coevolving structure and dynamics generates a new—functional—structure at an upper level of description. Simple transient dynamics of activity clusters result in a special form of traffic in this new structure that we refer to as a hypernetwork [38].
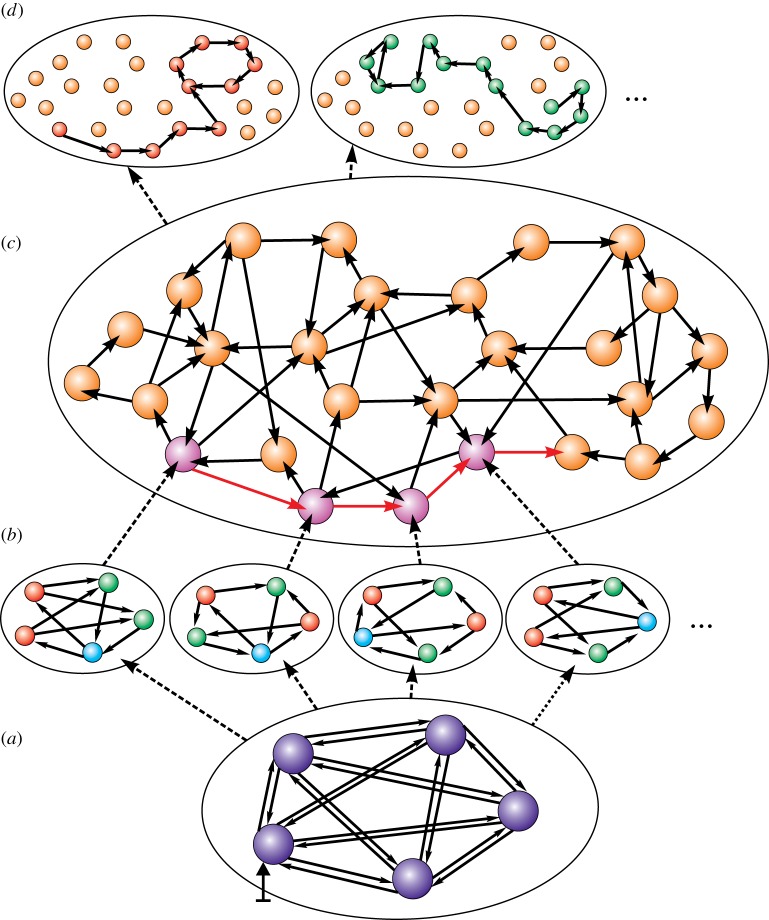
The outline of the model is shown in figure 1. First, we consider a neuronal population as a network of interacting nodes–oscillators coupled by directed links. This is the bottom level presented schematically in figure 1a. The nodal dynamics as well as the activity of links are governed by some deterministic evolutionary operators (for details, see Material and methods). Depending on nodal dynamics the links become active or inactive thus forming different structural patterns in the network. Physiologically this can mean that some synaptic links become strong while others tend to be weak. A structural pattern results in a specific spatio-temporal activity in the form of synchronous or asynchronous clusters. Depending on the internal state as well as external conditions the network can adapt to different stimuli and reconfigure the structure of strong and weak couplings thus changing the spatio-temporal pattern. Different perception stimuli or cognitive tasks give rise to the activation of different distributed neuronal groups or to a different order of sequential activation of various brain areas. We relate this distributed neuronal group specified by the common task to a corresponding hypersimplex. Hypersimplices are ordered, or structured, sets of nodes with an explicit relation; in other words, they exist at a higher level of representation than network nodes (figure 1b). In our model, hypersimplices are specified by the coupling topology that leads to a certain cluster activity. By a cluster activity, we mean the form of collective behaviour exhibited by oscillators. For example, in figure 1b nodes with a same colour denote one cluster, i.e. they tend to fire synchronously while other nodes are silent. Different colours relate to different clusters, i.e. these groups of oscillators do not fire simultaneously. The cluster activity which is a functional attribute of the network is directly specified by the current hypersimplex which is a structural attribute of the network. As time progresses, the network in figure 1a can exhibit different configurations corresponding to particular hypersimplices in figure 1b, i.e. at each moment only one hypersimplex can be found in the network. All possible hypersimplices realized in the network form a simplicial family.
Figure 1.
The network at the bottom level (a) generates a family of relational simplices (b) that appear sequentially due to the coevolution of structure and dynamics. The set of hypersimplices, or simplicial family, are connected to each other by directed links thus constituting a hypernetwork (c). Different paths in the hypernetwork (d) occur according to different stimuli (the vertical arrow) coming to the bottom level (a). (Online version in colour.)
A structured set of hypersimplices determines a hypernetwork (figure 1c) where the connections between hypersimplices describe their functional relations. In our model, we assume that two hypersimplices are connected if the network can change its state from one hypersimplex to another due to the evolutionary rules governing its structure and dynamics. Internal as well as external conditions usually tend to slowly evolve or drastically change which causes the network to adapt by reconfiguring the structure of its links. In general, this leads to rewiring and a new hypersimplex appears in the system. Hence the coevolution of structure and dynamics at the bottom-level network in figure 1a gives rise to a kind of traffic at the upper level—in the hypernetwork (figure 1c). The complexity of the hypernetwork and potential transitions in it depend on the dynamical principles and evolutionary rules that govern the constituents of the basic network. An actual path in the hypernetwork depends on the joint action of external inputs and the network’s internal state. Sensory information and task requirements activate some subset in the hypernetwork thus transforming it to a simpler structure that enables movement along the hypernetwork by a specific path. Each such path is a unique pattern of transient cluster activity for a given task performance and is robust in non-stationary environments.
(b). Example: 5-node oscillatory network with inhibitory connections
We illustrate this general paradigm by a model in the form of a 5-node dynamical network. The nodes–oscillators are coupled by inhibitory links in such a way that they can generate a rather simple but non-trivial form of activity: sequential clusters that appear cyclically. This is due to a chosen scheme of coupling where some two nodes inhibit the other two nodes, the latter inhibit the last node, and this one inhibits the former two nodes. The nodes–oscillators are tuned to have a property of post-inhibitory rebound: an oscillator receives an inhibitory input and then is released from it after which the oscillator fires a post-inhibitory burst of spikes. Inhibitory links sent by some oscillators to others allow suppression of the activity of the latter while the former are active. Thus, the network can produce a three-step cycle of clusters (which we refer to as a cluster state) where first two nodes synchronously fire, then the other two generate synchronous bursts, after that the remaining one becomes active, and finally it starts all over again. For example, at the cluster state s1 nodes 1 and 2 fire synchronously first while the others are silent, then nodes 3 and 4 generate synchronous bursts, and finally node 5 fires while the other four are below the threshold. Totally there are 30 cluster states si, i=1…30, and corresponding topologies having the described properties (for more details, see Material and methods and [19]).
The coupling structure is static for some time interval, thus enabling production of several identical cluster cycles. After that the structure switches to another one that depends on the dynamics exhibited by the oscillators. The new structure has the same symmetric properties as the previous one reflecting the homeostasis inherent to biological networks. In the new state, the network also generates three cyclic clusters but they comprise other oscillators; in other words, the clusters mix during the structure switching by swapping the nodes between each other. We assume that the new topology depends on what cluster is active at the moment of switching; since we have three clusters there are three different topologies which can be established after the switching. From time to time, the network moves from a current cluster state to one of three others. The system is basically an adaptive network where the connection topology determines the form of nodal activity while the oscillatory dynamics influences the network structure affecting the subsequent coupling scheme after the switching. As we discussed in the previous subsection, a structured set of nodes which determines a cyclic cluster sequence can be regarded as a hypersimplex. Therefore, we consider all 30 possible three-cluster states in our network as a simplicial family. Being connected by directed links they form a hypernetwork of cluster states where some path is activated during the time course of the network coevolution (figure 1).
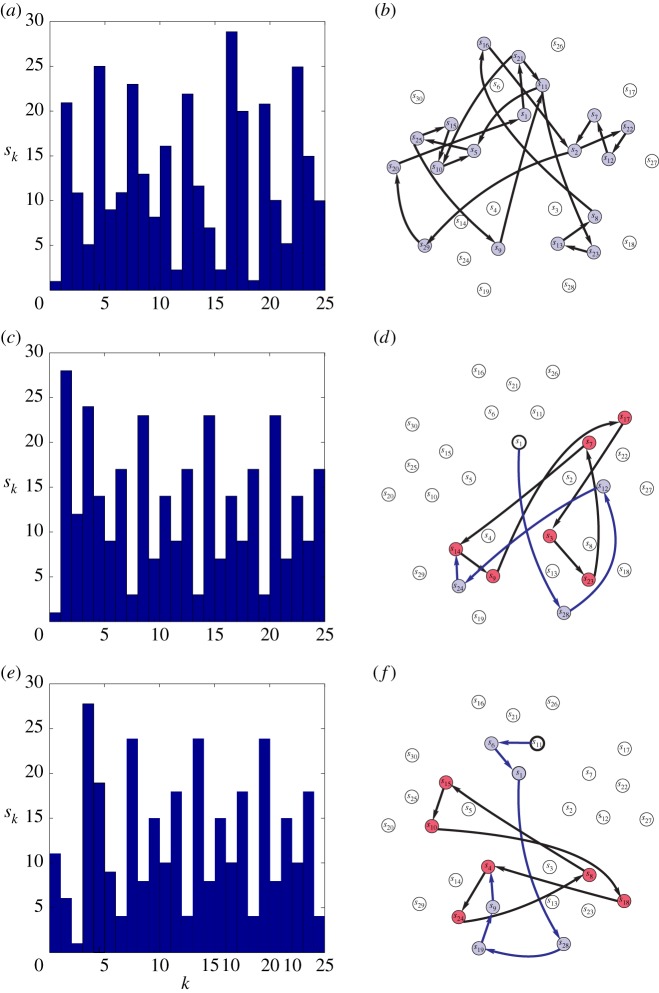
We studied the coevolution of the network in an autonomous case and under the effect of constant stimuli. Left to itself, the network generates a sequence of different cluster states and the path in the corresponding hypernetwork is a random walk shown in figure 2a,b. If an input is applied to the network then the path becomes stimulus-specified. The analysis of the network dynamics showed that the path depends on an internal network state—its topology—and the external stimulus, namely on what node it is applied to. In general, in the non-autonomous case the path in the hypernetwork after several steps comes to some cycle consisting of six cluster states and remains there until a new input comes. In the example shown in figure 2c,d the network initially is in the state s1 and the constant input is applied to node 1. The trajectory in the hypernetwork goes through the sequence s1,s28,s12,s24 and comes to the cycle s14,s9,s17,s3,s23,s7. When the input is applied to node 2 and the network is in the state s11 at the beginning, the trajectory in the hypernetwork goes through the sequence s11,s6,s1,s28,s19,s9 and comes to the other cycle s4,s24,s8,s15,s10,s18 shown in figure 2e,f.
Figure 2.
The sequences of cluster states {sk} (a,c,e) and the corresponding paths in the hypernetwork (b,d,f) for the autonomous case (a,b) and under constant inputs (c–f). In the autonomous case, one observes a random walk in the hypernetwork (b). In the case of constant stimuli there are different scenarios: for example, when the stimulus is applied to the first node and the network is initially in the state s1 (c,d) one obtains a path that after four steps comes to the six-cycle of cluster states (red or grey circles) s14,s9,s17,s3,s23,s7; when the stimulus is applied to the second node and the network is initially in the state s11 (e,f) there is a path that after six steps comes to the six-cycle of cluster states s4,s24,s8,s15,s10,s18. (Online version in colour.)
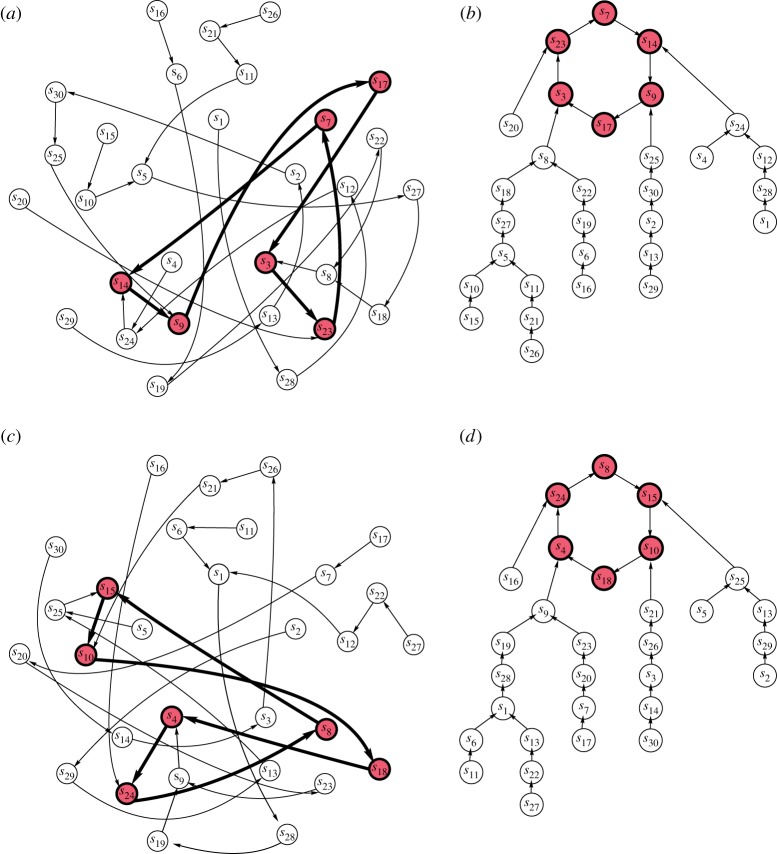
We found that the application of a constant stimulus to a network node specifies the subset of active directed links in the hypernetwork which govern the coevolution while other links become inactive. In this new hypernetwork, each hypersimplex has only one outward link so the path becomes specified and there is a limiting path—a six-cycle—attracting all other trajectories. For example, the application of a stimulus to node 1 results in a reduced hypernetwork shown in figure 3a. Starting from some cluster state si, a trajectory moves along a well-determined path towards a six-cycle of states s14,s9,s17,s3,s23,s7. For a better visualization the same reduced hypernetwork is shown in figure 3b where it is seen how different branches of the reduced hypernetwork converge to the same six-cycle. An input to node 2 leads to another reduced hypernetwork with a similar structure (figure 3c,d).
Figure 3.
The application of a constant stimulus to node 1 (a) and node 2 (c) specifies active links in the hypernetwork; thus this reduced hypernetwork governs transitions until node 1 (respectively, node 2) remains under the stimulus. In both cases, all the trajectories come to cycles of six cluster states shown by red (grey) circles. The same reduced hypernetworks can be presented in an untangled way (b,d). (Online version in colour.)
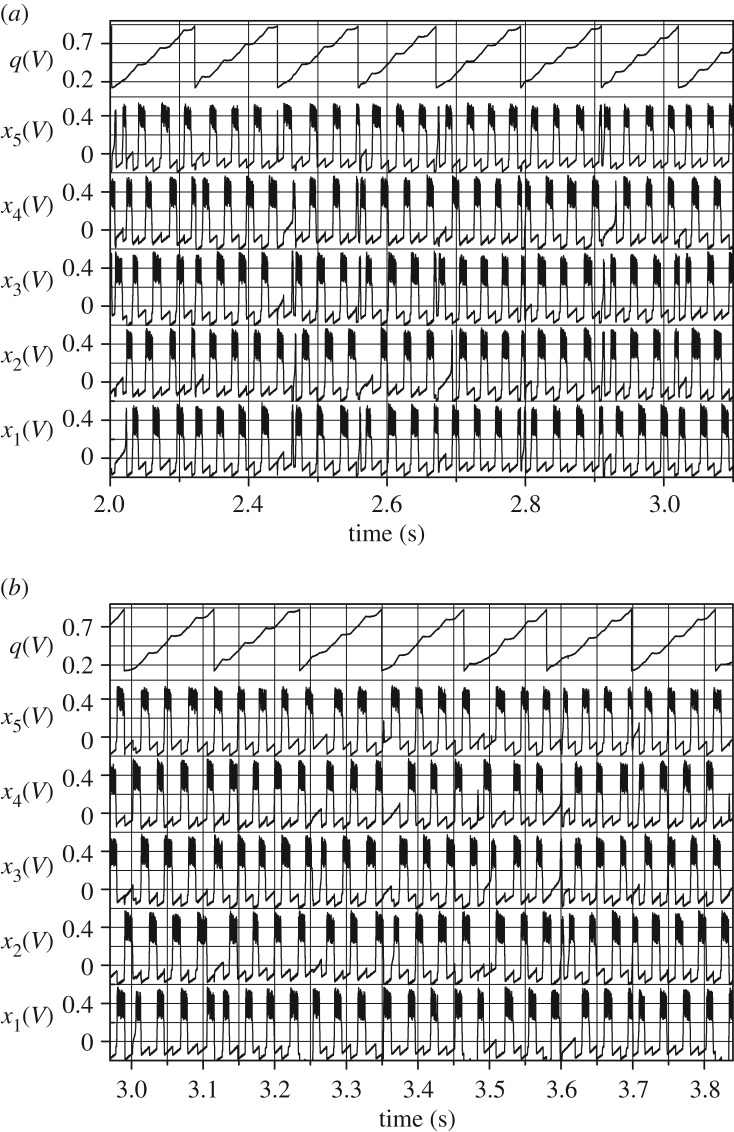
To create a real-time functioning 5-node dynamical network with inhibitory connections, we realized its electronic model on FPGA Xilinx Artix-7. The FPGA electronic model allows one to process external (sensory, informational) signals in this network in real time. Owing to the real-time processing and parameter scalability of the electronic model, we have the opportunity to apply it to different types of interfaces (a human–machine interface, a brain–computer interface, an artificial neural network interface, etc.). The analysis shows a full agreement of theoretical and numerical predictions with experimental data. Without external inputs the experimental set-up displays random transitions between different cluster states; an example is shown in figure 4a. In the case of an input application, the network demonstrates transitions relating to the corresponding reduced hypernetwork where each hypersimplex has only one outward link and all paths are converged to a six-cycle. For example, when an input is applied to node 1 the network activity gives rise to a transition in the hypernetwork towards the cyclic sequence s23,s7,s14,s9,s17,s3,s23, etc., shown in figure 4b.
Figure 4.
Dynamics of the mean-field-based quantity q and nodal variables xi (i=1,…,5) which represent transitions between different cluster states realized on FPGA Xilinx Artix-7. Time graphs are registered from a multi-channel acquisition system. Waveforms in (a) correspond to a random walk in the hypernetwork in an autonomous case. Waveforms in (b) relate to the case of a stimulus-specific traffic in the hypernetwork (an input is applied to node 1) when the trajectory came to the six-cycle s23,s7,s14,s9,s17,s3,s23.
3. Conclusion
In this paper, we proposed a paradigmatic model of how a network of spiking neurons can create complex responses at the higher level of representation—in the corresponding hypernetwork. Despite the simplicity of the coupling structure, the neuron model, and the evolutionary operator, we show the basic idea: how dynamics of the adaptive oscillatory network of spiking neurons leads to the emergence of various transient behaviours in the hypernetwork. Consecutive switchings between different hypersimplices mean that each cluster state is unstable due to the evolutionary rules governing the system but applying inputs results in a robust stimulus-specific path in the hypernetwork. This is similar to dynamics exhibited by systems with the ‘winnerless competition’ principle in [39–42]; however, the dynamic mechanism of the coevolving topology and dynamics in our case is completely different from the stable heteroclinic channel in these works. Besides fundamental issues concerning the dynamic origin of relational simplices in large-scale neural networks there are several items relating to the case study model to be addressed in further research. For example, the influence of more complicated than constant inputs, the role of noise and parameters detuning on temporal properties of sequences in the hypernetwork [43,44], the appearance of topology switching from local internodal interactions and others. These problems remain beyond the scope of this paper and provide a baseline for future studies.
4. Material and methods
(a). Nodal dynamics
The activity of nodes–oscillators is described by the following map [45,46]:
 |
4.1 |
where n=0,1,2,… is discrete time, and the variables xi,n and yi,n characterize the state of the ith node at the moment of n. The nonlinear function FH(x)=x(x−a)(1−x)−βH(x−d), where H(x) is the Heaviside step function: H(x)=1 if x≥0 and H(x)=0 otherwise; the parameters a, β and d control an oscillatory regime, in particular, β and d determine chaotic activity. The parameter ε determines the rate for the variable yi and the parameter Ji characterizes the excitatory properties of the nodes. The term Ii,n takes into account the additive noise and the impact on the ith node from the other network nodes (inhibitory links); the latter is given by
 |
4.2 |
where the coefficient g defines the coupling strength, aij,n are the elements of an adjacency matrix A={aij} (see below) at the moment of n, ν is the so-called reversal parameter, and θ is the threshold parameter. In our simulations, we fix the parameters a=0.1, β=0.3, d=0.45, ε=10−3, g=0.15, ν=−0.5 and θ=0.2. For these values, the nodes described by (4.1) and (4.2) display subthreshold activity in the absence of an input (Ii,n=0) and generate chaotic bursts as a result of the inhibition by the connected nodes (for more details, see [45,46]). The map-based approach in modelling neuronal networks is described in more detail in [47–50]. The system (4.1) was used in a number of research papers for modelling the collective activity of different neuronal systems [51–56] and studying rather theoretical issues on chaotic dynamics in maps [57,58]. Note that the chaos itself is not necessarily needed to generate a hypernetwork and the general results in §2 do not depend on whether chaotic or regular dynamics is exhibited by the network. We use in our example chaotic oscillators to demonstrate the robustness of switching activity in adaptive networks of spiking neurons even in the case of irregular dynamics.
(b). Dynamical network and cluster states
We considered a network consisting of five nodes–oscillators. The connections are directed and described by the adjacency matrix A={aij}, where aij=1 if node j sends a link to node i and aij=0 otherwise. We consider the simplest nontrivial cluster states in this network, two clusters consist of two oscillators, and the remaining oscillator forms the third cluster. As a result, the network exhibits a cyclic sequence 〈(i1,i2),(i3,i4),i5〉 which means that first two nodes with numbers (i1,i2) fire synchronously (the first cluster), then nodes (i3,i4) generate synchronous bursts, after that node i5 fires and the sequence repeats. To obtain this configuration, we choose the elements aij in a specific way. We take ai1i5=ai2i5=1, ai3i1=ai3i2=ai4i1=ai4i2=1, ai5i3=ai5i4=1, and the other elements of A are equal to 0. The complete list of possible three-cluster sequences of this configuration is presented in table 1 where each column is generated by cyclic permutation of the indexes 〈(i1,i2),(i3,i4),i5〉 in the top state.
Table 1.
List of the cluster states in the 5-node network.
| s1=〈(1,2),(3,4),5〉 | s6=〈(1,3),(2,4),5〉 | s11=〈(1,4),(2,3),5〉 |
| s2=〈(2,3),(4,5),1〉 | s7=〈(2,4),(3,5),1〉 | s12=〈(2,5),(3,4),1〉 |
| s3=〈(3,4),(5,1),2〉 | s8=〈(3,5),(4,1),2〉 | s13=〈(3,1),(4,5),2〉 |
| s4=〈(4,5),(1,2),3〉 | s9=〈(4,1),(5,2),3〉 | s14=〈(4,2),(5,1),3〉 |
| s5=〈(5,1),(2,3),4〉 | s10=〈(5,2),(3,1),4〉 | s15=〈(5,3),(1,2),4〉 |
| s16=〈(2,3),(1,4),5〉 | s21=〈(2,4),(1,3),5〉 | s26=〈(3,4),(1,2),5〉 |
| s17=〈(3,4),(2,5),1〉 | s22=〈(3,5),(2,4),1〉 | s27=〈(4,5),(2,3),1〉 |
| s18=〈(4,5),(3,1),2〉 | s23=〈(4,1),(3,5),2〉 | s28=〈(5,1),(3,4),2〉 |
| s19=〈(5,1),(4,2),3〉 | s24=〈(5,2),(4,1),3〉 | s29=〈(1,2),(4,5),3〉 |
| s20=〈(1,2),(5,3),4〉 | s25=〈(3,1),(5,2),4〉 | s30=〈(2,3),(5,1),4〉 |
(c). Coevolution of nodal dynamics and coupling topology
The coupling topology evidentally influences the nodal dynamics as it directly determines the form and order of clusters. To take into account the impact of the dynamics on the coupling topology we use the following algorithm. We introduce an auxiliary variable q which defines the moment n=n* of topology switching in the following way:
 |
4.3 |
It follows from equations (4.3) that q is increasing on the average starting from zero up to the threshold q=1 with the rate determined by the network behaviour (the mean field X) and a small parameter μ (0<μ≪1). The dynamics of X is chaotic due to the chaotic activity of xi, i=1,…,5, which leads to small perturbations of q. After reaching the threshold, the value of q is reset to zero and begins to grow according to equation (4.3). The topology rewiring occurs at the moment n=n* of resetting of q.
At the moment of rewiring, two nodes are chosen, one from the current active cluster, and another from the previous active cluster. The indexes of these nodes, k and l, determine how the coupling topology is changed according to the rule
| 4.4 |
Which numbers k and l are chosen depends on the following algorithm. Suppose at the moment of rewiring n=n* the nodes with indexes (i3,i4) are active, and before that the nodes (i1,i2) were active. In the clockwise ordered set starting from i5 there is a pair of nodes ik*∈(i3,i4) and il*∈(i1,i2) that have a minimum index distance determined from the clockwise ordering of the nodes. For example, the index clockwise distance between nodes 2 and 3 is 1 while between 3 and 2 it is 4. The indexes ik* and il* specify the numbers k=k* and l=l* in equation (4.4). The matrix Tkl is obtained by swapping row k and row l of the identity 5×5 matrix with 1’s on the main diagonal and 0’s elsewhere. Thus Tkl makes a row-switching transformation, i.e. TklA is the matrix produced by exchanging row k and row l of A. The product TklATkl is thus a matrix where firstly the rows k and l are exchanged and then in the obtained matrix the columns k and l are swapped.
(d). Experimental set-up
The discrete-time systems describing the nodal and coupling dynamics in equations (4.1) and (4.2) as well as the evolutionary rule governing the topology switching in equations (4.3) and (4.4) were realized on FPGA Xilinx Artix-7. The signal from each oscillator of the network and the signal corresponding to average variable q were registered from the FPGA through 12-bit digital-to-analogue convertors. One discrete time step for this network is equal 50 μs, the average spike duration is about 10–20 discrete steps (approx. 0.5–1 ms), and the burst lasts about 25 ms. Such timings correspond well to time scales of real neurons. The parameters are equal to μ=0.001, ε=0.001, J=0.05, β=0.3, a=0.1, d=0.45, θ=0.2, ν=−0.5 and g=0.07.
Authors' contributions
O.V.M. performed simulations and drafted the manuscript. D.S.S. carried out the experiments. V.I.N. conceived of and designed the study, and drafted the manuscript. All authors read and approved the manuscript.
Competing interests
The authors declare that they have no competing interests.
Funding
This work was supported by the Russian Science Foundation (project no. 16-42-01043).
References
- 1.Newman ME. 2003. The structure and function of complex networks. SIAM Rev. 45, 167–256. ( 10.1137/S003614450342480) [DOI] [Google Scholar]
- 2.Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang D-U. 2006. Complex networks: structure and dynamics. Phys. Rep. 424, 175–308. ( 10.1016/j.physrep.2005.10.009) [DOI] [Google Scholar]
- 3.Arenas A, Díaz-Guilera A, Kurths J, Moreno Y, Zhou C. 2008. Synchronization in complex networks. Phys. Rep. 469, 93–153. ( 10.1016/j.physrep.2008.09.002) [DOI] [Google Scholar]
- 4.Bullmore E, Sporns O. 2009. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 10, 186–198. ( 10.1038/nrn2575) [DOI] [PubMed] [Google Scholar]
- 5.Rubinov M, Sporns O. 2010. Complex network measures of brain connectivity: uses and interpretations. Neuroimage 52, 1059–1069. ( 10.1016/j.neuroimage.2009.10.003) [DOI] [PubMed] [Google Scholar]
- 6.Hagmann P, Cammoun L, Gigandet X, Meuli R, Honey CJ, Wedeen VJ, Sporns O. 2008. Mapping the structural core of human cerebral cortex. PLoS Biol. 6, e159 ( 10.1371/journal.pbio.0060159) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sporns O, Chialvo DR, Kaiser M, Hilgetag CC. 2004. Organization, development and function of complex brain networks. Trends Cognit. Sci. 8, 418–425. ( 10.1016/j.tics.2004.07.008) [DOI] [PubMed] [Google Scholar]
- 8.Jirsa VK. 2004. Connectivity and dynamics of neural information processing. Neuroinformatics 2, 183–204. ( 10.1385/NI:2:2:183) [DOI] [PubMed] [Google Scholar]
- 9.Sporns O. 2010. Networks of the brain. Cambridge, MA: MIT Press. [Google Scholar]
- 10.Rabinovich MI, Varona P, Selverston AI, Abarbanel HD. 2006. Dynamical principles in neuroscience. Rev. Mod. Phys. 78, 1213–1265. ( 10.1103/RevModPhys.78.1213) [DOI] [Google Scholar]
- 11.Holme P, Saramäki J. 2012. Temporal networks. Phys. Rep. 519, 97–125. ( 10.1016/j.physrep.2012.03.001) [DOI] [Google Scholar]
- 12.De Domenico M, Solé-Ribalta A, Cozzo E, Kivelä M, Moreno Y, Porter MA, Gómez S, Arenas A. 2013. Mathematical formulation of multilayer networks. Phys. Rev. X 3, 041022 ( 10.1103/PhysRevX.3.041022) [DOI] [Google Scholar]
- 13.Boccaletti S, Bianconi G, Criado R, DelGenio CI, Gómez-Gardeñes J, Romance M, Sendiña-Nadal I, Wang Z, Zanin M. 2014. The structure and dynamics of multilayer networks. Phys. Rep. 544, 1–122. ( 10.1016/j.physrep.2014.07.001) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kivelä M, Arenas A, Barthelemy M, Gleeson JP, Moreno Y, Porter MA. 2014. Multilayer networks. J. Complex Netw. 2, 203–271. ( 10.1093/comnet/cnu016) [DOI] [Google Scholar]
- 15.Johnson J. 2013. Hypernetworks in the science of complex systems, vol. 3. Singapore: World Scientific. [Google Scholar]
- 16.Johnson J. 2016. Hypernetworks: multidimensional relationships in multilevel systems. Eur. Phys. J. Spec. Top. 225, 1037–1052. ( 10.1140/epjst/e2016-02653-4) [DOI] [Google Scholar]
- 17.Gorochowski TE, Bernardo MD, Grierson CS. 2012. Evolving dynamical networks: a formalism for describing complex systems. Complexity 17, 18–25. ( 10.1002/cplx.20386) [DOI] [Google Scholar]
- 18.Belykh I, di Bernardo M, Kurths J, Porfiri M. 2014. Evolving dynamical networks. Phys. D Nonlinear Phenom. 267, 1–6. ( 10.1016/j.physd.2013.10.008) [DOI] [Google Scholar]
- 19.Maslennikov OV, Nekorkin VI. 2015. Evolving dynamical networks with transient cluster activity. Commun. Nonlinear Sci. Numer. Simul. 23, 10–16. ( 10.1016/j.cnsns.2014.11.019) [DOI] [Google Scholar]
- 20.Maslennikov OV, Nekorkin VI. In press Adaptive dynamical networks. Physics-Uspekhi. ( 10.3367/UFNe.2016.10.037902) [DOI]
- 21.Rabinovich M, Huerta R, Laurent G. 2008. Transient dynamics for neural processing. Science 321, 48–50. ( 10.1126/science.1155564) [DOI] [PubMed] [Google Scholar]
- 22.Rabinovich MI, Friston KJ, Varona P. 2012. Principles of brain dynamics: global state interactions. Cambridge, MA: MIT Press. [Google Scholar]
- 23.Hutchison RM. et al. 2013. Dynamic functional connectivity: promise, issues, and interpretations. Neuroimage 80, 360–378. ( 10.1016/j.neuroimage.2013.05.079) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Petersen SE, Sporns O. 2015. Brain networks and cognitive architectures. Neuron 88, 207–219. ( 10.1016/j.neuron.2015.09.027) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Mišić B, Sporns O. 2016. From regions to connections and networks: new bridges between brain and behavior. Curr. Opin. Neurobiol. 40, 1–7. ( 10.1016/j.conb.2016.05.003) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Park H-J, Friston K. 2013. Structural and functional brain networks: from connections to cognition. Science 342, 1238411 ( 10.1126/science.1238411) [DOI] [PubMed] [Google Scholar]
- 27.Sporns O. 2014. Contributions and challenges for network models in cognitive neuroscience. Nat. Neurosci. 17, 652–660. ( 10.1038/nn.3690) [DOI] [PubMed] [Google Scholar]
- 28.Tononi G, Edelman GM. 1998. Consciousness and complexity. Science 282, 1846–1851. ( 10.1126/science.282.5395.1846) [DOI] [PubMed] [Google Scholar]
- 29.Thompson E, Varela FJ. 2001. Radical embodiment: neural dynamics and consciousness. Trends Cognit. Sci. 5, 418–425. ( 10.1016/S1364-6613(00)01750-2) [DOI] [PubMed] [Google Scholar]
- 30.Varela F, Lachaux J-P, Rodriguez E, Martinerie J. 2001. The brainweb: phase synchronization and large-scale integration. Nat. Rev. Neurosci. 2, 229–239. ( 10.1038/35067550) [DOI] [PubMed] [Google Scholar]
- 31.Le Van Quyen M. 2003. Disentangling the dynamic core: a research program for a neurodynamics at the large-scale. Biol. Res. 36, 67–88. ( 10.4067/S0716-97602003000100006) [DOI] [PubMed] [Google Scholar]
- 32.Edelman GM. 2003. Naturalizing consciousness: a theoretical framework. Proc. Natl Acad. Sci. USA 100, 5520–5524. ( 10.1073/pnas.0931349100) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tononi G. 2004. An information integration theory of consciousness. BMC Neurosci. 5, 42 ( 10.1186/1471-2202-5-42) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Buonomano DV, Maass W. 2009. State-dependent computations: spatiotemporal processing in cortical networks. Nat. Rev. Neurosci. 10, 113–125. ( 10.1038/nrn2558) [DOI] [PubMed] [Google Scholar]
- 35.Buzsáki G. 2010. Neural syntax: cell assemblies, synapsembles, and readers. Neuron 68, 362–385. ( 10.1016/j.neuron.2010.09.023) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Rigotti M, Barak O, Warden MR, Wang X-J, Daw ND, Miller EK, Fusi S. 2013. The importance of mixed selectivity in complex cognitive tasks. Nature 497, 585–590. ( 10.1038/nature12160) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Stokes MG, Kusunoki M, Sigala N, Nili H, Gaffan D, Duncan J. 2013. Dynamic coding for cognitive control in prefrontal cortex. Neuron 78, 364–375. ( 10.1016/j.neuron.2013.01.039) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Anokhin KV. 2016. In 17th Conf. on Nonlinear Waves, Nizhny Novgorod, Russia, 27 February–4 March 2016.
- 39.Afraimovich V, Zhigulin V, Rabinovich M. 2004. On the origin of reproducible sequential activity in neural circuits. Chaos 14, 1123–1129. ( 10.1063/1.1819625) [DOI] [PubMed] [Google Scholar]
- 40.Afraimovich VS, Rabinovich MI, Varona P. 2004. Heteroclinic contours in neural ensembles and the winnerless competition principle. Int. J. Bifurcation Chaos 14, 1195–1208. ( 10.1142/S0218127404009806) [DOI] [Google Scholar]
- 41.Afraimovich V, Tristan I, Huerta R, Rabinovich MI. 2008. Winnerless competition principle and prediction of the transient dynamics in a Lotka–Volterra model. Chaos 18, 043103 ( 10.1063/1.2991108) [DOI] [PubMed] [Google Scholar]
- 42.Afraimovich VS, Young TR, Rabinovich MI. 2014. Hierarchical heteroclinics in dynamical model of cognitive processes: chunking. Int. J. Bifurcation Chaos 24, 1450132 ( 10.1142/S0218127414501326) [DOI] [Google Scholar]
- 43.Wordsworth J, Ashwin P. 2008. Spatiotemporal coding of inputs for a system of globally coupled phase oscillators. Phys. Rev. E 78, 066203 ( 10.1103/PhysRevE.78.066203) [DOI] [PubMed] [Google Scholar]
- 44.Ashwin P, Coombes S, Nicks R. 2016. Mathematical frameworks for oscillatory network dynamics in neuroscience. J. Math. Neurosci. 6, 65 ( 10.1186/s13408-015-0033-6) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Nekorkin V, Vdovin L. 2007. Diskretnaya model neyronnoy aktivnosti. Izvest vys ucheb zaved Prikladnaya nelinejnaya dinamika 15, 36–60. [Google Scholar]
- 46.Courbage M, Nekorkin V, Vdovin L. 2007. Chaotic oscillations in a map-based model of neural activity. Chaos 17, 043109 ( 10.1063/1.2795435) [DOI] [PubMed] [Google Scholar]
- 47.Courbage M, Nekorkin VI. 2010. Map based models in neurodynamics. Int. J. Bifurcation Chaos 20, 1631–1651. ( 10.1142/S0218127410026733) [DOI] [Google Scholar]
- 48.Ibarz B, Casado JM, Sanjuán MA. 2011. Map-based models in neuronal dynamics. Phys. Rep. 501, 1–74. ( 10.1016/j.physrep.2010.12.003) [DOI] [Google Scholar]
- 49.Girardi-Schappo M, Tragtenberg M, Kinouchi O. 2013. A brief history of excitable map-based neurons and neural networks. J. Neurosci. Methods 220, 116–130. ( 10.1016/j.jneumeth.2013.07.014) [DOI] [PubMed] [Google Scholar]
- 50.Maslennikov OV, Nekorkin VI. 2014. Map-based approach to problems of spiking neural network dynamics. In Nonlinear dynamics and complexity, pp. 143–161. Berlin, Germany: Springer.
- 51.Nekorkin V, Maslennikov O. 2011. Spike-burst synchronization in an ensemble of electrically coupled discrete model neurons. Radiophys. Quant. Electron. 54, 56–73. ( 10.1007/s11141-011-9271-y) [DOI] [Google Scholar]
- 52.Courbage M, Maslennikov O, Nekorkin V. 2012. Synchronization in time-discrete model of two electrically coupled spike-bursting neurons. Chaos Solitons Fractals 45, 645–659. ( 10.1016/j.chaos.2011.12.018) [DOI] [Google Scholar]
- 53.Maslennikov O, Nekorkin V. 2012. Discrete model of the olivo-cerebellar system: structure and dynamics. Radiophys. Quant. Electron. 55, 198–214. ( 10.1007/s11141-012-9360-6) [DOI] [Google Scholar]
- 54.Maslennikov OV, Kasatkin DV, Rulkov NF, Nekorkin VI. 2013. Emergence of antiphase bursting in two populations of randomly spiking elements. Phys. Rev. E 88, 042907 ( 10.1103/PhysRevE.88.042907) [DOI] [PubMed] [Google Scholar]
- 55.Maslennikov OV, Nekorkin VI. 2014. Modular networks with delayed coupling: synchronization and frequency control. Phys. Rev. E 90, 012901 ( 10.1103/PhysRevE.90.012901) [DOI] [PubMed] [Google Scholar]
- 56.Maslennikov OV, Nekorkin VI, Kurths J. 2015. Basin stability for burst synchronization in small-world networks of chaotic slow-fast oscillators. Phys. Rev. E 92, 042803 ( 10.1103/PhysRevE.92.042803) [DOI] [PubMed] [Google Scholar]
- 57.Maslennikov OV, Nekorkin VI. 2013. Dynamic boundary crisis in the Lorenz-type map. Chaos 23, 023129 ( 10.1063/1.4811545) [DOI] [PubMed] [Google Scholar]
- 58.Maslennikov OV, Nekorkin VI. 2016. Attractors of relaxation discrete-time systems with chaotic dynamics on a fast time scale. Chaos 26, 073104 ( 10.1063/1.4955084) [DOI] [PubMed] [Google Scholar]