On detecting ecological impacts of extreme climate events and why it matters

Abstract

There is growing interest in identifying the impacts of extreme climate events on natural systems. Two principles of such detection are that it should be based on a scientific understanding of the processes by which climate affects the system of interest and that non-climate factors that also affect the system should be controlled for. Using a simple temperature-dependent predator–prey model, this paper illustrates the importance of these principles in the context of establishing a link between temperature and population extremes. The results suggest that a naive approach based only on the co-occurrence of temperature and population extremes may fail. In the second part of the paper, some reasons for focusing attention on the ecological impacts of extreme climate events are briefly reviewed. It is suggested that, while extreme ecological events may be important for society, this does not imply that an analysis aimed at connecting them to extreme climate events should necessarily be based on extreme events themselves.

This article is part of the themed issue ‘Behavioural, ecological and evolutionary responses to extreme climatic events’.

1. Introduction

With the debate about the reality of anthropogenic climate change essentially settled, the attention of scientists and policy makers is turning increasingly to its likely impacts on human society and natural systems. Much of this attention has focused on the impacts of extreme climate events like heatwaves and droughts—first, because their impacts are themselves likely to be extreme and, second, because the frequency of such events is projected to increase, possibly disproportionately, as the Earth warms [1]. Although numerous studies have considered ecological impacts of climate change, including shifts in phenology [2–4] and in species distributions [5–7], fewer have focused on the impact of extreme events—a notable exception being a special issue of the Journal of Ecology in 2011. The purpose of this paper is to discuss two general issues connected to the impact of extreme climate events on biological populations: the detection of such an impact and why it matters.

2. Why it matters

In this section, I will briefly review some practical reasons why understanding the ecological impacts of extreme climate events matters.

One reason that is sometimes given or implied for studying the impact of extreme events in the current climate is that they serve as a proxy for normal conditions in the future climate and therefore have predictive value. This is the case, for example, in studies of the impact of climate on human conflict [8]. This approach is problematic for human systems that are likely to adapt to future conditions and the same may be true of natural systems. Indeed, shifts in phenology or in species distributions presumably represent such adaptations.

A second reason is connected to assessing the cost of climate change to human society. To the extent that the ecological impacts of extreme climate events are costly to society, the predicted increase in the frequency of these events implies increased cost. This should be figured among the total cost of climate change and therefore play a role in the underlying policy calculus.

On a related note, some of the ecological systems that will be affected by an increase in the frequency of extreme climate events are managed or manageable by humans. These include exploited populations like fisheries and unexploited populations like pests. A third reason for understanding these impacts is to inform management strategies that may avoid or ameliorate the negative impacts [9].

There is a fourth, arguably less creditable, reason for focusing on the impacts of extreme events. Some scientists see it as their role to galvanize an uninformed public against the dangers of climate change. In doing so, there is a temptation to use so-called disaster narratives that are seen as especially galvanizing [10]. Extreme ecological events fall into this category in the same way that extreme climate events do.

3. Detecting ecological impacts of extreme climate events

The detection of the impact of climate change (or climate variability generally) on a human or natural system refers to the identification of an effect on the system that can be attributed to climate change. Because detection focuses on real-world systems, it is non-experimental. This is not at all to say that experimental approaches have no value in understanding or predicting such impacts [11], only that the real world is not an experiment. While there is no single approach to detecting climate change impacts, some general principles were discussed in the recent report of the Intergovernmental Panel on Climate Change [12]. One of these principles is that detection should be based on an understanding of the underlying process by which such an impact is likely to arise rather than, say, on simple correlations. In part, this is intended to narrow the search for climate change impacts and, among other things, to avoid fishing expeditions. A second principle is that the analysis must control for factors other than climate that have an impact on the system of interest. These principles—a failure which to follow can lead to spurious detection or non-detection—may seem obvious but they are not always followed. For example, empirical studies of the impact of climate change on civil conflict have been criticized for not being based on an understanding of the processes underlying such conflict [13]. Some studies of boundary shifts in species ranges fail to control for factors like changes in overall abundance and sampling effort [14].

In this section, I will use a simple population model to illustrate the importance of these principles in the context of detecting the impact of extreme climate events on the density of an animal population. Consider a predator–prey system governed by the stochastic discrete-time model:

3.1

and

3.2

where U_t is the abundance or density of the prey in period t, V_t is the abundance or density of the predator in period t, X_t is temperature in period t, and r is a positive, monotonically increasing function. For a fixed temperature, in the absence of the predator, prey density follows a logistic model with carrying capacity of 1, with the presence of the predator reducing prey density. In the absence of prey, predator density declines geometrically, with the presence of prey increasing predator density.

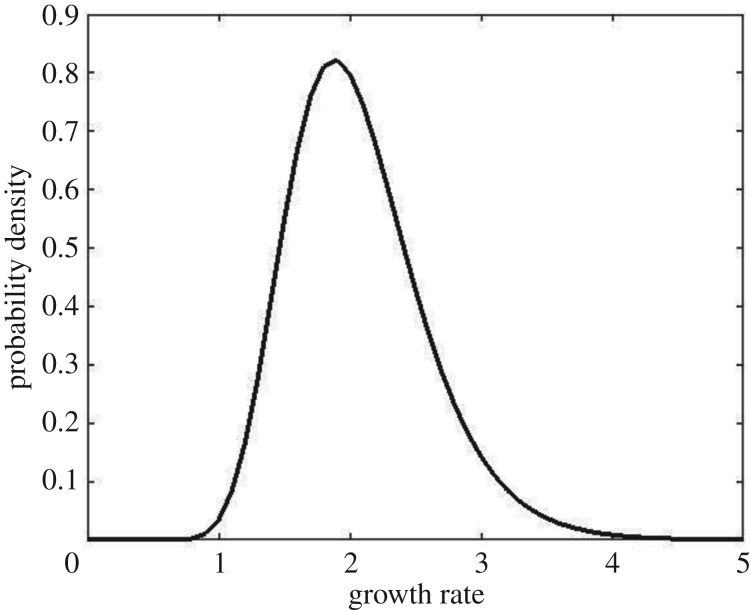
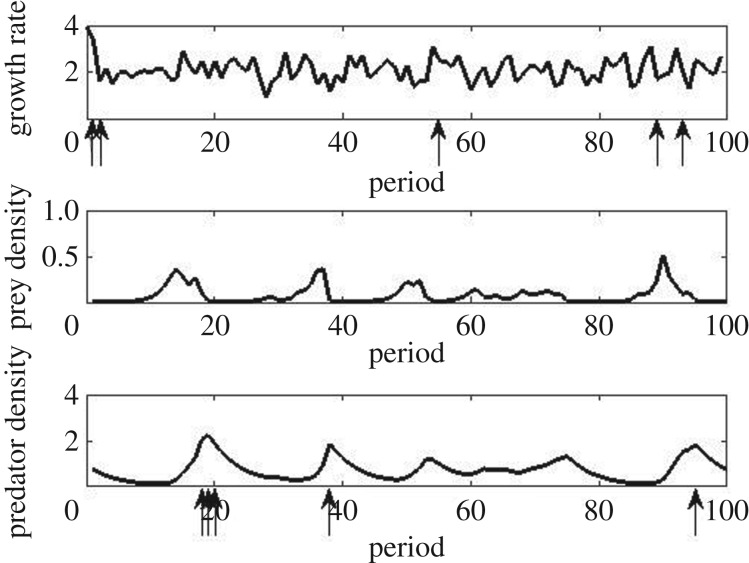
Stochasticity enters this model through X_t which I will treat as a random variable. Throughout this paper, I will define an extreme event as an exceedance by a random variable of the upper 0.05-quantile of its distribution so that, on average, extreme events occur 5% of the time. The monotonicity of the function r ensures that the intrinsic prey growth rate r(X_t) is extreme if and only if X_t is extreme. Here, I will assume that the random variable r(X_t) follows a lognormal distribution with median 2.0 and coefficient of variation 0.5. The corresponding probability density function is shown in figure 1. In figure 2, 100 successive simulated values of the intrinsic prey growth rate and the densities of prey and predator are plotted, with the five highest values of the first and the last indicated by arrows.

Figure 1.

Probability density function of the intrinsic prey growth rate.

Figure 2.

Simulated time series of length 100 of the intrinsic prey growth rate (top), prey density (middle), and predator density (bottom). The five highest values of growth rate and predator density are indicated by arrows.

For concreteness, I will focus here on the problem of determining whether temperature extremes lead to extremes in the density of the predator. The predator density in this model can be written as:

3.3

Thus, there is a direct relationship between a temperature extreme in period t − 2 and an extreme predator density in period t other things being equal. The other things that must be equal are the density of the predator in period t − 1 and of the predator and the prey in period t − 2. In keeping with the principles of detection outlined above, this would be revealed by fitting a temperature-dependent predator–prey model to sufficiently long time series observations of temperature and predator and prey densities. In practice, of course, the form of the model (including the form of the function r) would be unknown and the usual challenge of model specification would have to be addressed [15].

What would be the consequences of ignoring these detection principles? A naive approach that does would be based on the frequency with which temperature extremes and extremes in predator density co-occur. To examine this approach in detail, let the binary random variable I_t take the value 1 if predator density V_t in period t is extreme and 0 otherwise and, similarly, let the binary random variable J_t take the value 1 if temperature X_t (and therefore the intrinsic prey growth rate r(X_t)) in period t is extreme and 0 otherwise. Define the conditional probability:

3.4

With this notation, the naive approach would focus on the conditional probability p₁₁(0) of an extreme predator density in period t given an extreme temperature in the same period. For the model outlined above, predator density is independent of temperature in the same period so p₁₁(0) is just 0.05. The same is true of p₁₁(1). If a 2-period lag is considered, then p₁₁(2)—as approximated by a long simulation—jumps to 0.14. To avoid occasional population crashes in this simulation, prey density was not allowed to fall below 0.01. A probability of 0.14 is not large in absolute terms: only 1 in 7 temperature extremes is followed 2 periods later by an extreme predator density. For example, the highest temperature in figure 2 occurs at t = 2, but because it occurs when prey density is very low, predator density actually declines between periods 3 and 4. It is important to point out that this approach is not all that naive as it is based on scientific knowledge of the 2-period lag between temperature and predator density.

An even less naive approach would be to compare p₁₁(2) to the conditional probability p₁₀(2) of an extreme predator density given that the temperature 2 periods earlier is not extreme. This latter probability is around 0.045. The finding that the probability of an extreme predator density is more than 3 times greater 2 periods after an extreme temperature than 2 periods after a non-extreme temperature certainly constitutes the detection of an ecological impact of extreme temperature. Again, this approach is based on knowledge of the 2-period lag between temperature and predator density.

In practice, of course, these conditional probabilities are not known and detection must be based on time series of temperature and predator density. A natural way to do this is the following. Consider time series of temperature and predator density of length n + 2 so that there are n paired observations of temperature and predator density 2 periods later. Let the count N_ij = #{I_t = i, J_t−2 = j} so that, for example, N₁₁ is the number of times that a temperature extreme in period t − 2 is followed by a predator density extreme in period t. These counts can be arranged in a 2-by-2 contingency table:

3.5

and detection can be based on testing the null hypothesis of independence in this table. This approach was taken in a similar context in Palmer et al. [16]. By virtue of the way in which I have defined extremes, the row sums are fixed at 0.95 n and 0.05 n and similarly for the column sums, so the appropriate procedure is Fisher's exact test [17]. The power of this test depends on n and on the unknown conditional probabilities p_ij(2). For values of n typical of population studies—almost always less than 100—this power is low unless p₁₁(2) is very different from p₁₀(2) [18]. Power would not be high for the conditional probabilities of 0.140 and 0.045 reported above.

There is, in addition, a technical problem with the contingency table approach outlined here. Standard tests of independence in this contingency table (including Fisher's exact test) assume that successive observations of (I_t, J_t−2) are independent. This is clearly not the case for observations following the model outlined above. In principle, it is possible to account for dependence in the analysis of a contingency table (and in statistical inference generally), but getting this right requires knowledge of the form of the dependence and this, in turn, requires a scientific understanding of the dynamics of this system.

4. Discussion

One of the more robust predictions about climate change is that it will lead to an increase in the frequency of certain types of extreme climate events. There are good scientific and, as pointed out in the previous section, practical reasons to understand the ecological impacts of such events. One way to gain insight on this issue is to identify ecological impacts of extreme climate events in the historical record.

The results of §2 underscore the importance of scientific understanding—for example, as encapsulated in a population model—in detecting the impact of an extreme climate event on a population. Real-world systems are more complicated than the simple model I have used to illustrate this point. However, there is no a priori reason to believe that more complication makes the detection of climate impacts easier. Indeed, one might expect the opposite. Modelling ecological systems in all their complexity can be extremely difficult and inference must typically be based on a simplified model (e.g. [19]). It is a good question how much simplification is possible before the results of the analysis become unreliable. Of course, this question is pertinent to all of population modelling, not just that part aimed at the impacts of extreme climate events. Among other things, the answer will depend on what is being asked of the model: a simplified model may provide reliable qualitative results even if it does not provide accurate quantitative predictions.

The discussion in the previous section about the contingency table approach raises another important point. By their nature, extreme climate events are rare. As a general proposition, basing inference about extreme events and their impacts solely on the events themselves may involve a substantial loss of power [20,21]. The sensitivity of a population to an extreme temperature event is a form of temperature-dependence. By modelling this dependence across the full range of temperatures, it may be possible to predict the population effect of a temperature extreme even when relatively few temperature extremes are observed. It is possible, however, that the ecological effect of a temperature extreme is qualitatively different from the effect of a non-extreme temperature, so that a statistical analysis must be restricted to extreme events themselves. In such cases, it is all the more important to bring to bear scientific understanding of the system in question.

Competing interests

I have no competing interests.

Funding

I received no funding for this study.