Abstract
Climate changes include concurrent changes in environmental mean, variance and extremes, and it is challenging to understand their respective impact on wild populations, especially when contrasted age-dependent responses to climate occur. We assessed how changes in mean and standard deviation of sea surface temperature (SST), frequency and magnitude of warm SST extreme climatic events (ECE) influenced the stochastic population growth rate log(λs) and age structure of a black-browed albatross population. For changes in SST around historical levels observed since 1982, changes in standard deviation had a larger (threefold) and negative impact on log(λs) compared to changes in mean. By contrast, the mean had a positive impact on log(λs). The historical SST mean was lower than the optimal SST value for which log(λs) was maximized. Thus, a larger environmental mean increased the occurrence of SST close to this optimum that buffered the negative effect of ECE. This ‘climate safety margin’ (i.e. difference between optimal and historical climatic conditions) and the specific shape of the population growth rate response to climate for a species determine how ECE affect the population. For a wider range in SST, both the mean and standard deviation had negative impact on log(λs), with changes in the mean having a greater effect than the standard deviation. Furthermore, around SST historical levels increases in either mean or standard deviation of the SST distribution led to a younger population, with potentially important conservation implications for black-browed albatrosses.
This article is part of the themed issue ‘Behavioural, ecological and evolutionary responses to extreme climatic events’.
Keywords: climate safety margin, matrix population model, seabird, population persistence
1. Introduction
The Intergovernmental Panel on Climate Change (IPCC) research group outlined that special attention should be put forth on the impact of extreme climatic events (ECE) on human societies and ecosystems [1]. Marked temperature anomalies and associated heatwaves may become more of a common environmental feature by the end of the century that our society and wild populations will have to adjust to, in conjunction with an adjustment to overall global warming [2]. Yet, assessing changes in ECE remains challenging given their rarity by definition [3] and the difficulty to model and understand their ecological effects at different spatio-temporal scales and biological levels [4–6]. Extreme events can be defined in many ways; throughout this paper, a climatological definition will be used as the occurrence of a value as rare as or rarer than the 5th and 95th percentile of the distribution of observed values in a climatic variable of interest (e.g. temperature and precipitation) over a specific historical time period [7].
The effects of climate change on wild populations have been extensively studied but most studies focused on the effect of changes in mean temperature and/or precipitation regimes on phenology, physiology, behaviour and demography [8–10]. In recent years, the number of studies investigating the effects of ECE in wild populations has been increasing [11–13]. There is now empirical evidence that ECE can have strong ecological effects as they can lead to local extinctions [14], changes in sex ratio [15], disease proliferation [16] and even reset community composition [17]. However, understanding the respective biological responses to the effects of changes in mean climate and climate variability—especially ECE—requires more research [7,18–22]. Projections of population responses based on mean temperature changes alone can differ substantially from those incorporating changes to the variability, including extreme events [23,24].
Furthermore, different life-history stages, phenotypes or age-classes can respond differently to the same climatic variable [25–27]. For example, Jenouvrier et al. [28] showed that extreme sea ice years affected foraging behaviour, body condition, vital rates and population growth rate of the southern fulmar (Fulmarus glacialoides), and individuals of higher quality were less impacted by these extreme events. Therefore, changes in ECE can strongly alter not only the population growth rate, but also the structure of populations. A textbook example is the contrasted effect of ECE according to age in human populations. Specifically, during the 2003 heatwave in Europe, more than 70 000 human deaths were recorded, with the most vulnerable persons being young and older individuals [29], which affected the age pyramid.
Here, we focus on the long-lived black-browed albatross (Thalassarche melanophris) using a 50 year longitudinal dataset including 4235 individuals. Previous studies have shown that survival and fecundity of black-browed albatrosses breeding in Kerguelen, French Sub-Antarctic territories, varied in response to changes in sea surface temperature (SST) in their foraging zones during the breeding season [30–32]. Pardo et al. [33] showed that fecundity and survival responses to changes in SST were different between age classes, with larger effects on young and old breeders than on middle-aged birds. To understand the respective impacts of increasing mean and variability of SST, as well as frequency and magnitude of extreme SST events on population growth and structure, we constructed an age-structured stochastic matrix population model in which young, middle-aged and old breeders responded differently to changes in SST. We had three specific aims (figure 1, bottom) as follows.
(1) Determine the influence of changes in the mean and standard deviation of the historical SST distribution on the frequency and magnitude of warm SST ECE.
(2) Determine the influence of changes in the mean and standard deviation of the historical SST distribution on the stochastic population growth rate and stable age distribution.
(3) Study the effects of ECE on stochastic population growth rate and stable age distribution.
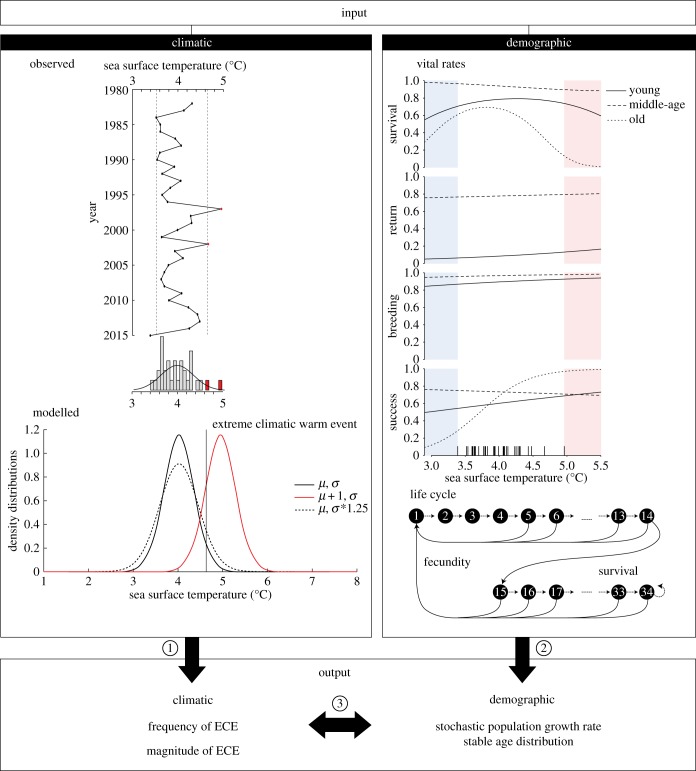
Figure 1.
Sketch explaining the approach followed in this paper. Input environmental data consist of SST sampled from a normal distribution (middle-left). The observed SST from 1982 to 2015 was used to determine a threshold of warm ECE (top-left in red). We defined the ECE frequency as the occurrence of ECE, and the ECE magnitude as the maximum SST values occurring in the simulated environment. The population model projects the number of individuals within each age-class and is described by an age-structured life cycle (middle-right) where vital rates depend on both age and SST (top-right). Vertical traits on the x-axis represent the occurrence of historical SST. The outputs are of two kinds (bottom): climatic, to measure the influence of SST distribution parameters on the frequency and magnitude of warm SST ECE (1), and demographic, to measure the influence of SST distribution parameters on the stochastic population growth rate and on the stable age distribution (2). The two outputs were also combined (3).
We address these questions at two different scales of variation in SST that contrast the historical versus future climate change ranges: (i) at the local scale around the historical SST distribution by using a sensitivity analysis based on the partial derivative method and (ii) an analysis over a wider range of climatic parameters with various scenarios of change in the mean or standard deviation of the SST distribution using scatter plots.
2. Material and methods
(a). Species life cycle
Black-browed albatross are large Procellariiforms (3–4 kg, 2–2.5 m wingspan) that breed on Sub-Antarctic islands during the austral summer. Birds arrive in September and lay a single egg in October that will hatch in December. Both parents alternate care at the nest during incubation of the egg and brooding of the young chick, then provision the large chick that fledges in late March at a size similar to that of an adult. This study focuses on black-browed albatross breeding at Canyon des Sourcils Noirs (49.4° S–70.1° E), Kerguelen Islands. Each year since 1978, pair members were identified with a stainless steel band. In addition, all fledglings, unringed breeding individuals and non-breeding individuals attending the colony were marked. The average age at first breeding is 9.7 and can range from 5 to 15 years old [34]. During breeding, black-browed albatrosses forage in northeast and southeast regions of the peri-insular Kerguelen shelf [30–32]. Their diet at that period is composed of fish (73%), penguin carrion (14%) and squids (10%) [35]. They are known to strongly interact with long-line and trawl fisheries targeting Patagonian toothfish (Dissostichus eleginoides) and mackerel icefish (Champsocephalus gunnari) to feed on discards and baits [36]. Such interactions can affect black-browed albatross demography and dynamics (e.g. increase their breeding success, diminish adult and juvenile survival) [37]. In winter, breeding adults migrate to southeast Australia and north of Tasmania in less than a week, where they remain until the next breeding season and occasionally follow longliners fishing for southern bluefin tuna (Thunnus thynnus) and other tuna species in their wintering zone [38].
(b). Sea surface temperature
Historical SST were extracted from satellite data from 1982 to 2015 in a spatial sector where most birds from this colony forage during the breeding season (from October to March; International Research Institute for Climate and Society, http://iridl.ldeo.columbia.edu/; see map in Pardo et al. [33]). SST is thought to be a proxy of food availability in the marine environment and has been found in several studies to have an influence on breeding parameters as well as survival rates in this population [30,32,39].
Seasonal means in historical SST data over 34 years were used to determine thresholds of ECE, so that values below the 5th percentile (3.52°C) were considered as cold SST ECEs and above the 95th percentile (4.63°C) as warm SST ECE (figure 1, top left panel). As the IPCC predicts an increase in Earth surface temperature (including SST) and an increase in the frequency and magnitude of heatwaves in particular, here we focused on the influence of the warmer temperatures [1].
The historical SST followed a normal distribution (Anderson–Darling test: p = 0.13) with two parameters: the mean (μ = 3.95°C at baseline conditions based on the historical data) and the standard deviation (σ = 0.35 at baseline conditions; figure 1, bottom left panel). We derived various scenarios based on the normal distribution fitted on historical SST data: the baseline scenario; a scenario when mean temperature increased up to μ + 1°C in accordance with IPCC predictions [1], which is a 25% increase relative to the historical mean of 3.95°C; and a scenario when standard deviation increased by 25%. Thus, the range of change in the mean and standard deviation relative to their historical values are directly comparable. These scenarios resulted in demographic rates that were in a realistic range of variations (electronic supplementary material, A). Two characteristics of warm ECE were calculated from an SST vector obtained by sampling into the fitted distributions (SST vector length of 10 000): the frequency and magnitude. The frequency of warm ECE was calculated as the number of extreme years divided by the total number of years multiplied by 100 (baseline frequency of warm ECE = 2.86%), and the magnitude of warm ECE was the warmest temperature (i.e. maximum value of the SST vector, baseline magnitude of warm ECE = 5.28°C).
(c). Population model
To calculate the population growth rate and structure, we constructed an age-structured matrix model using a pre-breeding census [40] based on a life cycle of 34 age classes where individuals older than 34 years remain in the last stage (figure 1, bottom right panel). We projected the population between time t and t + 1 using the following equation: n(t+1) = At n(t), where n(t) is the population vector at time t including the 34 age classes and At is the projection matrix containing the age-specific vital rates [40]. The projection matrix At depended on SST in each year, with vital rates projected from the specific functional relationships from Pardo et al. [33] (figure 1, top right panel).
Vital rates were projected using linear and quadratic functional relationships with SST on the logit scale for four different vital rates (figure 1, top right panel): apparent survival probability, return probability to the breeding grounds, breeding probability (laying an egg) given return, and breeding success probability (chick fledged) given breeding. Survival, return, breeding and success probabilities were estimated for all individuals according to their age. Vital rates and effect of SST varied between the following age classes: young from 5 to 10 years old; middle-aged from 11 to 26 years old for return, breeding and success probabilities and from 11 to 29 for survival probability [33]. After age 26 for success probability or 29 for survival probability, birds were in the old-age class until the maximum age observed (i.e. 34 years old). There was no old-age class for return and breeding probabilities (electronic supplementary material, B). Breeding experience was not included in this study.
Fecundity was defined as the product of age-dependent return, breeding and success probabilities multiplied by the sex ratio at birth (assumed unity [37]) and juvenile survival. We used an estimate of juvenile survival probability from Nevoux et al. [41] assuming that juvenile survival (Sj) was constant over the first 5 years (Sj0–5 = Sj0–1*Sj1–2*Sj2–3*Sj3–4*Sj4–5 = 0.281). There was no data to estimate annual variation of juvenile survival before recruitment because young birds stay at sea permanently from fledging until first return on land. Thus, annual juvenile survival was set to constant (Sj = 0.776 [fifth root of 0.281 for Sj0 to Sj5]). Apparent survival can be an underestimation of true survival due to permanent emigration but in highly philopatric species such as albatrosses, we do not expect this bias to be large (less than 2%; [42]). Rolland et al. [37] estimated the annual immigration rate at 0.044 and as we had no information on how it might be linked with SST or age, we focused on local population dynamics.
An SST value was drawn randomly 10 000 times from the normal distribution fitted on historical SST data and altered to simulate more ECE. The stochastic population growth rate log(λs) and the stable age distribution (asymptotic proportion of individuals in each age class) were then calculated following the approach described in chapter 14.1 of Caswell [39] using numerical simulation. All analyses were performed in the program MATLAB [43].
(d). Local sensitivity analysis
We first performed a local sensitivity analysis by estimating the partial derivative of frequency and magnitude of warm ECE events (climatic output y) over 10 000 time steps with respect to the mean and standard deviation of the normal distribution fitted on historical SST data (Aim 1, figure 1, bottom panel). In addition, we performed a local sensitivity analysis of the growth rate and stable age distribution (demographic output y) with respect to SST parameters following the same approach (Aim 2, figure 1, bottom panel).
We evaluated the sensitivity of a climatic or demographic output of the model (y) with respect to the mean or standard deviation of the SST distribution (input x) by calculating numerically the partial derivative dx/dy. We perturbed the input by a small perturbation such as the perturbed input is xp = x(1 ± 0.001). We performed 100 simulations for each positive and negative perturbation, and estimated as dx/dy = (y − yp)/(x − xp) for each simulation and perturbation. The sensitivity is measured as the average of dx/dy over 200 simulations.
(e). Effect of sea surface temperature on stochastic population growth rate
Since the results of the sensitivity analysis based on the partial derivative were very local, we performed an analysis over a wider range of the SST distribution parameters similar to a global sensitivity analysis. Our aim was to illustrate the contrasted effects of changes in SST distribution parameters between the historical and future projected ranges of SST. Thus, we chose a simple but useful approach computing the scatter plots of the stochastic population growth rate against SST distribution parameters as well as the frequency and magnitude of ECE (Aim 3, figure 1, bottom panel). Starting from the baseline parameters of the SST distribution, we varied the mean by up to 1°C [1] and the standard deviation up to an increase of 25% relative to the baseline value (σ = 0.45). Changes in the mean and standard deviation of the distribution were varied independently.
3. Results
(a). Sensitivity of climatic output (Aim 1)
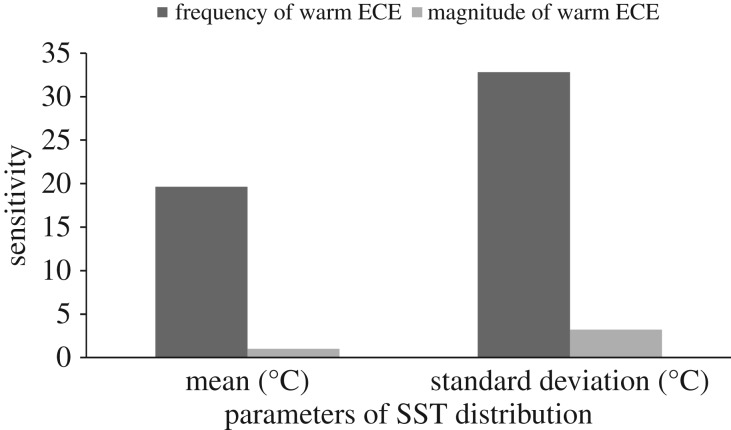
The local sensitivity analysis of climatic output showed the relative effects of a unit of change in the two parameters of the historical SST distribution (μ,σ) on the frequency and magnitude of warm ECE (figure 2). Increasing the mean or standard deviation increased the frequency and magnitude of warm ECE. A unit of change in standard deviation (σ) had a larger effect on both frequency (1.6 times larger) and magnitude of warm ECE (3 times larger) than a unit of change in the mean (μ) (both μ and σ parameters are in °C).
Figure 2.
Sensitivity of the frequency and magnitude of warm SST ECE with respect to the two parameters of a normal distribution (mean and standard deviation) of SST. The distribution was fitted on 34 years of historical SST averaged in the foraging areas of Kerguelen black-browed albatrosses during the breeding season.
(b). Sensitivity of demographic output (Aim 2)
The sensitivity of log(λs) with respect to the standard deviation was negative while the sensitivity of log(λs) with respect to the mean was positive (figure 3). A unit of change in standard deviation (σ) had a larger effect on log(λs) (approx. 3 times larger) than a unit of change in the mean (μ) (figure 3).
Figure 3.
Sensitivity of the stochastic population growth rate log(λs) with respect to the two parameters of a normal SST distribution (mean and standard deviation).
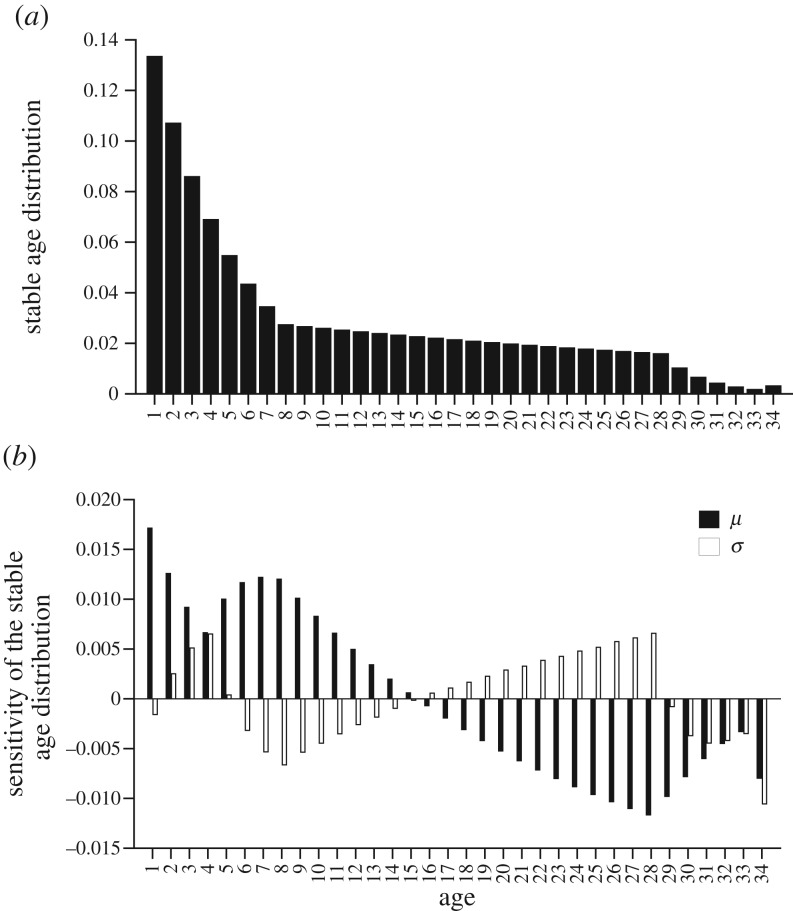
Considering the stable age distribution, in the baseline conditions 44% of the population was 5 years old or less (figure 4a). The sensitivity analysis revealed that changes in mean or standard deviation of the SST distribution affected the proportion of individuals in all age classes (figure 4b). A unit change in mean had a larger influence than a unit change in the standard deviation, and their relative effects had opposite sign in middle-aged classes. However, the sensitivities of the stable age distribution with respect to a unit change in mean and/or standard deviation were both positive for age classes from 2 to 5 years old and both negative for old-age classes from 28 to 34+ years old (figure 4b). To summarize, the number of individuals in the immature age classes (under 5 years old) increased and the number of individuals in the oldest age classes decreased when mean or standard deviation of the SST distribution increased, resulting in a younger population.
Figure 4.
Baseline stable age distribution (a) and sensitivity of the stable age distribution (b) with respect to the two parameters of a normal distribution (mean (μ) and standard deviation (σ)) of SST.
(c). Relationship between extreme climatic event, population growth and sea surface temperature distribution parameters (Aim 3)
In the baseline conditions, the stochastic growth rate was log(λs) = −0.033 meaning that the local population of black-browed albatross is currently decreasing annually by 3.3%.
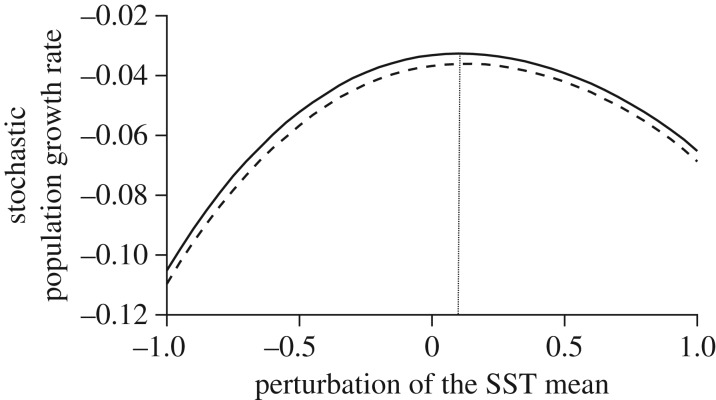
As the previous sensitivity analysis was very local, we also investigated the relationships, relative to baseline levels, between log(λs) and the climatic ECE characteristics on a wider range of change in SST distribution parameters (electronic supplementary material, C; figure 5). First, figure 5 shows that log(λs) was maximized at slightly warmer values of mean SST than present (i.e. observed mean + 0.1°C), with an optimal value of log(λs) of −0.032. Log(λs) declined as mean SST became warmer or colder. Interestingly, the effect of colder SST was stronger than the effect of warmer SST (figure 5). There was a large plateau around the optimal log(λs) value (−0.2°C to +0.4°C; figure 5). Over the range of mean SST values shown here, the effect of standard deviation was negative, lowering log(λs) by up to 0.005.
Figure 5.
Stochastic population growth rate as a function of SST mean (x-axis) and standard deviation (plot lines) of the normal SST distribution. The mean and standard deviation vary over a similar range: up to 25% change relative to their historical value, but these changes lead to a very different SST distribution (figure 1). Specifically, the mean varies ± 1°C from its historical value, and the standard deviation by a 25% increase relative to its historical value (dashed line). The solid line represents the historical standard deviation and the dotted line represents the optimal (maximum) stochastic population growth rate.
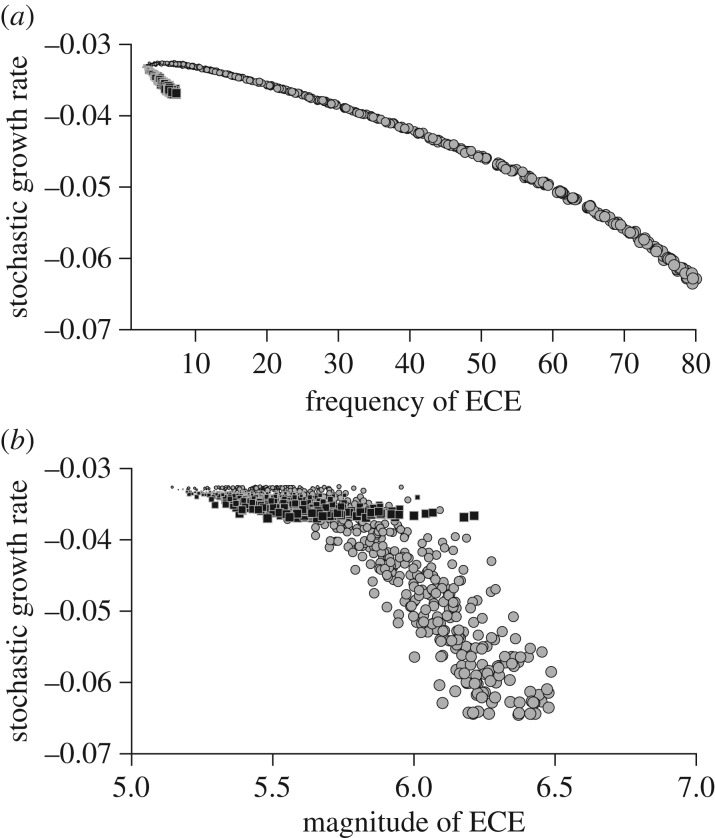
Second, figure 6 shows: (i) how changes to baseline SST distribution parameters (up to 25% increase for both mean and standard deviation relative to their historical values) lead to increased climatic ECE characteristics (frequency and magnitude on the x-axis, but see also the electronic supplementary material, C) and (ii) how changes in the frequency and magnitude of ECE lead to changes in log(λs) (y-axis). Mean and standard deviation parameters both influenced the frequency and magnitude of warm ECE. Mean SST had by far the strongest impact on the frequency of ECE (figure 6a; electronic supplementary material, C) after a small plateau around historical level up to 8% ECE frequency. For an increase of 1°C (i.e. 25% increase in the mean relative to historical level), log(λs) declined to −0.064 when 80% of SST were considered extreme according to the historical climatological definition. Changes in the standard deviation affected the frequency of warm ECE to a much lesser extent for the range explored here (up to 10% extreme event frequency for a 25% increase in the standard deviation relative to historical level) and the minimum log(λs) reached −0.037 (figure 6a). Similarly, with the magnitude of warm ECE (figure 6b), a steeper decline in log(λs) occurred when changes in the magnitude were caused by a change in mean SST further from historical value rather than a change in standard deviation. The mean of the SST distribution had a greater effect on the magnitude of ECE than the standard deviation, especially for values far from the historical range (electronic supplementary material, C). However, the difference between the impact of mean and standard deviation on the magnitude of ECE is smaller than for the impact on the frequency of ECE.
Figure 6.
Relationships between the stochastic population growth rate log(λs) and frequency (a) and magnitude (b) of warm SST ECE according to changes of the two parameters of a normal distribution (mean (μ) increasing up to 1°C, grey circles; and standard deviation (σ) multiplied by up to 1.25, black squares; see also the electronic supplementary material, C).
To summarize, for changes in SST around the historical levels observed since 1982, the standard deviation of the SST distribution had a larger and negative impact on log(λs) compared to a change in the mean. However, for a larger range, changes in the mean had a stronger effect on both the frequency and magnitude of ECE and the stochastic population growth rate.
4. Discussion
Using a black-browed albatross demographic model incorporating age- and SST-dependent vital rates, we have characterized the impact of changes in the mean and standard deviation of the climatic distribution on the frequency and magnitude of ECE as well as on the population growth and structure. We highlighted opposite effects of changes in mean and standard deviation on the growth rate and some age classes of the population. In addition, we showed how the impact of ECE frequency and magnitude on population growth rate is mediated through change in mean or standard deviation of the SST distribution. Below, we discuss how our study complements previous studies on ECE and speculate on the resilience of the albatross population to climate change and fisheries in this novel age-dependent framework. Some methodological aspects of our approach are also discussed along with how future studies could build on our approach towards a more comprehensive understanding of the impact of ECE in wild populations.
(a). Effect of changes in the parameters of the sea surface temperature distribution on the stochastic population growth rate
Several recent theoretical studies have emphasized that the relative effects of environmental standard deviation and mean on stochastic population growth rate log(λs) are expected from the curvature of the population growth response to the environment (referred to as the population response function): a concave response results in a negative effect of environmental standard deviation on log(λs) while the opposite occurs for a convex response (see review by Lawson et al. [21]). Figure 5 depicts such a population response function for the black-browed albatross and shows that the response is concave around historical levels. As expected, the effect of SST standard deviation was negative on black-browed albatross log(λs).
We demonstrated that, around the historical values of SST, a change in the standard deviation of the SST distribution had a larger effect on the black-browed albatross log(λs) than a change in SST mean. García-Carreras & Reuman [44] concluded that many populations close to their optimal environment are likely to be more sensitive to a change in the variability of the environment rather than the mean. By contrast, changes in mean conditions are likely to have a greater impact than changes in variability on populations far from their optimal environment. Our results at both the historical (figure 3) and a wider range of SST distribution parameters (figure 5) are in agreement with these theoretical expectations because: (i) we observed a single-peaked response function of the black-browed albatross log(λs) to SST and (ii) the historical variation of SST are close the optimal value for the black-browed albatross.
Noteworthy, the sensitivity of the black-browed albatross log(λs) with respect to the SST standard deviation was negative while its sensitivity with respect to the SST mean was positive. This pattern is expected [44] because the log(λs) is maximized at warmer values of mean SST than present (i.e. SSTOPT = SSTHISTORICAL + 0.1°C). As a result, larger environmental standard deviation would cause more SST values far from the optimum, while larger mean would cause more SST values close to the optimum. This pattern echoes results from empirical studies on ectotherms [45,46]: a positive shift in mean temperature (T) will decrease mean fitness in tropical ectothermic species, but will increase fitness at higher latitudes because tropical species are experiencing mean annual temperatures (THISTORICAL) very close to their optimal temperatures (TOPT), while the opposite occurs at higher latitudes [45]. Specifically, ectothermic species ‘thermal safety margins’ (TOPT − THISTORICAL) are typically 1–4°C in the tropics and increase markedly with latitude, up to 10°C or more at higher latitudes. Therefore, a species would be less severely impacted by warmer mean temperatures depending on how much historical SST are below the optimal SST.
(b). Effect of extreme climatic event on the stochastic population growth rate
The frequency and magnitude of warm ECE depended on the two parameters of the normal SST historical distribution. Thus, it is not straightforward to understand the respective effect of ECE through their response to a change in the environmental mean and standard deviation. Around the historical value, our local sensitivity analysis of the climate outputs showed that both the frequency and magnitude of ECE were more influenced by a change in the standard deviation rather than the mean of the SST distribution (figure 2). However, over a wider range of parameters (figure 6; electronic supplementary material, C), the SST mean had a stronger impact on the frequency and magnitude of warm ECE, especially beyond SSTOPT.
The effect of warm ECE was negative on the black-browed albatross log(λs) (figure 5). In addition, higher frequency and magnitude of ECE mostly decreased log(λs), although it depended on the path through which such changes occurred—i.e. changes in the mean, or standard deviation and the amplitude of the deviation from SSTOPT. Noteworthy, a change in the mean of the SST distribution increased black-browed albatross log(λs) despite increasing the frequency and magnitude of ECE (lower dots on figure 5). The positive sign of the sensitivity of log(λs) to the mean occurred because the historical SST mean was lower than the optimal value for the black-browed albatross, and there is a large plateau around the optimal value in the population response function. As a result larger environmental mean increased the occurrence of SST close to the optimal value that buffered the negative effect of ECE. The ‘climate safety margin’ (i.e. the difference between the optimal climatic conditions and the historical climatic conditions) and the specific shape of the response function for a species may determine how ECE affects the stochastic population growth rate through a change in environmental mean. Single peak response functions like those reported here are common in the wild [44], such as thermal performance curves in ectothermic species [46,47] (figure 5). A theoretical framework using such response functions [44] could shed light on the buffering role of the environmental mean against ECE as a function of the climate safety margins, the maximum height of the response function, the width of the range of optimal values, the rate of fall off from the optimal environment, as well as the asymmetry of the response function. Species with a large climate safety margin, a wide optimum range and a slow rate of fall off from the optimal environment are likely to be less sensitive to ECE, especially when climate changes are dominated by a shift in the mean rather than a change in the standard deviation.
(c). Age-dependent demographic responses to climate change
Individuals differ in their quality, age, sex and other characteristics that may mediate the effects of ECE on population growth and structure. We found that for local changes, the population structure was altered by increases in both mean and standard deviation of SST, with opposed effects in middle-aged individuals, leading to a higher proportion of young individuals in the population. Old individuals were particularly affected by both changes in mean and standard deviation, suggesting a particular vulnerability to the frequency of ECE as reported in humans [29]. These changes were driven by the age-specific nonlinear relationships between vital rates and SST, more particularly by the decreasing survival of old individuals in both cold and warm SST ECE, the increasing breeding probability of young and middle-aged individuals, and the increasing breeding success of young and old individuals when SST increased.
With future climate change, new concerns may arise for this black-browed albatross population, because the structure of the population is projected to change with a higher proportion of juveniles, which are highly sensitive to other anthropogenic activities. Juveniles are known to represent a significant part of birds accidentally killed in long-line fisheries [36,38]. Rolland et al. [37] demonstrated relationships between SST and fisheries impact on the growth rate of this same population. The stochastic population growth rate remains negative even when incorporating immigration in the young and middle-aged classes which is consistent with previous models and observations since 1976 [37]. This suggests that even at optimal values of SST, the population is likely affected by fisheries bycatch [37]. Mitigating the effect of fisheries with a warmer climate with limited change in environmental inter-annual variations may allow the population to recover. This will probably occur only for a short time as the climate safety margin (0.1°C) is relatively narrow compared to projected SST changes reported by the IPCC (≈1°C, [48]). A shift in mean SST by 1°C is not unlikely according to the IPCC projections. However, this would lead to a frequency of warm event of approximately 80%, and whether black-browed albatross will adapt to these conditions remains an open question. To predict the impact of extreme events and inform policy and management decisions, models linking IPCC climate projections to a demographic model would be required [23].
(d). Methodological considerations
The normal distribution is one possible distribution among many to address the relative impact in mean, variability as well as ECE. This distribution is symmetrical and thus does not account for the positive skewness that may result from climate change (i.e. more extreme warm than cold events or when the mean of the distribution shifts [1]). To understand the effect of an increasing frequency of warm events, one could have used asymmetrical climate distributions, such as the generalized extreme value (GEV) distribution developed within the extreme value theory, which are designed to address the data sparseness problems in the tails of the distribution due to the rarity of extreme events [10,49]. In our case study, we could not apply such a distribution because our functional relationships between SST and vital rates were based on SST averaged over large temporal and spatial scales. Within extreme value theory, GEV distributions are used to model the largest or smallest observations. For example, one can use the maximum SST recorded within a season or a spatial sector—the data are known as block maxima. For species such as ectotherms that are very sensitive to temperature daily minima or maxima, GEV distributions are very valuable [10]. However, long-lived endothermic species, such as black-browed albatross, are likely to escape cold spells or heatwaves because of their wide foraging range, their relatively good fasting abilities, or their ability to skip or abandon reproduction during extremely unfavourable events on the breeding grounds instead of jeopardizing their survival [13,50]. Thus, we believe that extreme environmental conditions for black-browed albatross more likely consist of persistent warmer SST over the entire breeding season and over a wide spatial sector, whereby their average value is extreme (i.e. a compound ECE, see [7]).
Our framework was based on the normal distribution, because it was the distribution that best fitted our historical SST. However, one could apply the t-location-scale distribution that has heavier tails, meaning that it is more prone to producing ECE values to study the impact of the shape of a climate distribution on the population growth and structure (electronic supplementary material, D).
While previous studies have shed light on the respective role of the mean and standard deviation of the environment, few have focused on the shape of the distribution of the environmental variables. The effects of a change in the shape of the tail of the distribution set by the skew were generally small relative to those of environmental means or standard deviations [21,24]. Vasseur et al. [24] applied a transformation of an (initially) normally distributed temperature distribution to study the respective effects of the mean, standard deviation and positive skewness on the thermal performance of 38 ectothermic invertebrate species. They found that a change in the mean temperature distribution had a larger impact than a change in variability and skewness (their fig. 2).
Models are very useful tools to understand the effect of climatic extremes that are rare, even if such projections require projecting beyond historical ranges of variability. Our study has indeed revealed contrasted patterns between values around the historical range and a wider range that depend on the climate safety margin. Although, we have projected the vital rates using functional relationships obtained with a robust capture–recapture analysis [33], to limit unrealistic demographic rates beyond the observed range, we have limited our wider range of climate parameters to few scenarios where we varied the two parameters of the SST distribution independently. Thus, we could not conduct a global sensitivity analysis that would require varying several model inputs simultaneously to account for interactions among parameters [51].
Finally, our approach focused on the effect of frequency and magnitude of extreme events on the long-term demography. But other ECE characteristics like the duration of a given ECE or a particular sequence of ECE (i.e. environmental auto-correlation) might also be important for the population [10]. Although the duration and sequence of ECE may affect greatly the transient population dynamics [52], they are likely to have little effect on the long-term population growth and structure for a long-lived species [4,53,54].
5. Conclusion
Our empirical study suggests how the direction and strength of change in population growth rate and population structure are determined by the mean and standard deviation of an environmental distribution, and shows that changes in the frequency and to a lesser extent the magnitude of ECE impact the demography of this black-browed albatross population. Interestingly, our results indicate that a shift in environmental mean can buffer and even reverse the effects of ECE on stochastic population growth rate. Species might therefore be able to cope with ECE. This depends on the magnitude of climate shift and variation in relation to a species' optimal environmental conditions.
Supplementary Material
Acknowledgements
We are extremely grateful to all fieldworkers involved in the monitoring program of black-browed albatrosses at Kerguelen for 50 years. We thank Dominique Besson and Karine Delord for data management, Philippe Naveau, Jimmy Garnier, Hal Caswell, Lise Aubry, Dave Koon, Loreleï Guéry and Jean-Dominique Lebreton for fruitful discussions as well as D.P.'s PhD committee: Emmanuelle Cam, Daniel Oro, Jean-Michel Gaillard, Bernard Cazelles and Michael Schaub. We also thank Woods Hole Oceanographic Institution's guest student program, Jamie Oliver from the British Antarctic Survey for help with the figures, Martjin van de Pol and two anonymous reviewers for advice on how to improve this manuscript.
Ethics
All experiments with albatrosses were approved by the Ethic Committee of the French Polar Institute (IPEV) and by the Comité de l'Environnement Polaire.
Data accessibility
Data is available as electronic supplementary material at https://dx.doi.org/10.6084/m9.figshare.c.3723961.
Authors' contributions
C.B. initiated the idea and H.W. supervised the long-term data necessary to this project. The model was conceived and designed by S.J., D.P. and. C.B. The analyses were performed by D.P. and S.J. in consultation with C.B. and D.P., S.J. and C.B. wrote manuscript, and H.W. provided comments.
Competing interests
We have no competing interests.
Funding
Work carried out at Canyon des Sourcils Noirs was supported by Institut Paul Emile Victor (IPEV program no.109) and Terres Australes et Antarctiques Françaises. S.J. thanks support from NSF-Antarctic Sciences Division (project no. 1246407), the Grayce B. Kerr Fund and the Penzance Endowed Fund in Support of Assistant Scientists. D.P. PhD was supported by a grant from the French Research Minister CNRS-INEE.
References
- 1.Field CB et al. (eds). 2017. Managing the risks of extreme events and disasters to advance climate change adaptation. A special report of working groups I and II of the intergovernmental panel on climate change. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 2.Moreno J, Moller AP. 2011. Extreme climatic events in relation to global change and their impact on life histories. Curr. Zool. 57, 375–389. ( 10.1093/czoolo/57.3.375) [DOI] [Google Scholar]
- 3.Stephenson DB, Casati B, Ferro CAT, Wilson CA. 2008. The extreme dependency score: a non-vanishing measure for forecasts of rare events. Meteorol. Appl. 15, 41–50. ( 10.1002/met.53) [DOI] [Google Scholar]
- 4.Palmer G, et al. 2017. Climate change, climatic variation and extreme biological responses. Phil. Trans. R. Soc. B 372, 20160144 ( 10.1098/rstb.2016.0144) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Felton AJ, Smith MD. 2017. Integrating plant ecological responses to climate extremes from individual to ecosystem levels. Phil. Trans. R. Soc. B 372, 20160142 ( 10.1098/rstb.2016.0142) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Altwegg R, Visser V, Bailey LD, Erni B. 2017. Learning from single extreme events. Phil. Trans. R. Soc. B 372, 20160141 ( 10.1098/rstb.2016.0141) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.van de Pol M, Jenouvrier S, Cornelissen JHC, Visser ME. 2017. Behavioural, ecological and evolutionary responses to extreme climatic events: challenges and directions. Phil. Trans. R. Soc. B 372, 20160134 ( 10.1098/rstb.2016.0134) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Parmesan C, et al. 1999. Poleward shifts in geographical ranges of butterfly species associated with regional warming. Nature 399, 579–583. ( 10.1038/21181) [DOI] [Google Scholar]
- 9.Crick HQP, Dudley C, Glue DE, Thomson DL. 1997. UK birds are laying eggs earlier. Nature 388, 526 ( 10.1038/41453) [DOI] [Google Scholar]
- 10.Kingsolver JG, Buckley LB. 2017. Quantifying thermal extremes and biological variation to predict evolutionary responses to changing climate. Phil. Trans. R. Soc. B 372, 20160147 ( 10.1098/rstb.2016.0147) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bailey LD, van de Pol M. 2016. Tackling extremes: challenges for ecological and evolutionary research on extreme climatic events. J. Anim. Ecol. 85, 85–96. ( 10.1111/1365-2656.12451) [DOI] [PubMed] [Google Scholar]
- 12.Jentsch A, Kreyling J, Beierkuhnlein C. 2007. A new generation of climate-change experiments: events, not trends. Front. Ecol. Environ. 5, 365–374. ( 10.1890/1540-9295(2007)5%5B365:ANGOCE%5D2.0.CO;2) [DOI] [Google Scholar]
- 13.Jenouvrier S, Péron C, Weimerskirch H. 2015. Extreme climate events and individual heterogeneity shape life-history traits and population dynamics. Ecol. Monogr. 85, 605–624. ( 10.1890/14-1834.1) [DOI] [Google Scholar]
- 14.Sanz-Aguilar A, Daniel Anadon J, Gimenez A, Ballestar R, Gracia E, Oro D. 2011. Coexisting with fire: the case of the terrestrial tortoise Testudo graeca in mediterranean shrublands. Biol. Conserv. 144, 1040–1049. ( 10.1016/j.biocon.2010.12.023) [DOI] [Google Scholar]
- 15.Bull JJ, Vogt RC. 1979. Temperature-dependent sex determination in turtles. Science 206, 1186–1188. ( 10.1126/science.505003) [DOI] [PubMed] [Google Scholar]
- 16.Glass GE, et al. 2000. Anticipating risk areas for hantavirus pulmonary syndrome with remotely sensed data: re-examination of the 1993 outbreak. Emerg. Infect. Dis. 6, 238–247. ( 10.3201/eid0603.000303) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Thibault KM, Brown JH. 2008. Impact of an extreme climatic event on community assembly. Proc. Natl Acad. Sci. USA 105, 3410 ( 10.1073/pnas.0712282105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.van de Pol M, et al. 2010. Do changes in the frequency, magnitude and timing of extreme climatic events threaten the population viability of coastal birds? J. Appl. Ecol. 47, 720–730. ( 10.1111/j.1365-2664.2010.01842.x) [DOI] [Google Scholar]
- 19.van de Pol M, Vindenes Y, Saether B.-E., Engen S, Ens BJ, Oosterbeek K, Tinbergen JM. 2010. Effects of climate change and variability on population dynamics in a long-lived shorebird. Ecology 91, 1192–1204. ( 10.1890/09-0410.1) [DOI] [PubMed] [Google Scholar]
- 20.Jenouvrier S, Holland M, Stroeve J, Barbraud C, Weimerskirch H, Serreze M, Caswell H. 2012. Effects of climate change on an emperor penguin population: analysis of coupled demographic and climate models. Glob. Change Biol. 18, 2756–2770. ( 10.1111/j.1365-2486.2012.02744.x) [DOI] [PubMed] [Google Scholar]
- 21.Lawson CR, Vindenes Y, Bailey L, van de Pol M. 2015. Environmental variation and population responses to global change. Ecol. Lett. 18, 724–736. ( 10.1111/ele.12437) [DOI] [PubMed] [Google Scholar]
- 22.Frederiksen M, Daunt F, Harris MP, Wanless S. 2008. The demographic impact of extreme events: stochastic weather drives survival and population dynamics in a long-lived seabird. J. Anim. Ecol. 77, 1020–1029. ( 10.1111/j.1365-2656.2008.01422.x) [DOI] [PubMed] [Google Scholar]
- 23.Jenouvrier S. 2013. Impacts of climate change on avian populations. Glob. Change Biol. 19, 2036–2057. ( 10.1111/gcb.12195) [DOI] [PubMed] [Google Scholar]
- 24.Vasseur DA, DeLong JP, Gilbert B, Greig HS, Harley CDG, McCann KS, Savage V, Tunney TD, O'Connor MI. 2014. Increased temperature variation poses a greater risk to species than climate warming. Proc. R. Soc. B 281, 20132612 ( 10.1098/rspb.2013.2612) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Chan KS, Mysterud A, Øritsland NA, Severinsen T, Stenseth NC. 2005. Continuous and discrete extreme climatic events affecting the dynamics of a high-arctic reindeer population. Oecologia 145, 556–563. ( 10.1007/s00442-005-0157-6) [DOI] [PubMed] [Google Scholar]
- 26.Jackson ST, Betancourt JL, Booth RK, Gray ST. 2009. Ecology and the ratchet of events: climate variability, niche dimensions, and species distributions. Proc. Natl Acad. Sci. USA 106, 19 685–19 692. ( 10.1073/pnas.0901644106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Vindenes Y, Edeline E, Ohlberger J, Langangen Ø, Winfield IJ, Stenseth NC, Vøllestad LA, Neubert AEMG, Bronstein EJL. 2014. Effects of climate change on trait-based dynamics of a top predator in freshwater ecosystems. Am. Nat. 183, 243–256. ( 10.1086/674610) [DOI] [PubMed] [Google Scholar]
- 28.Jenouvrier S, Barbraud C, Weimerskirch H. 2003. Effects of climate variability on the temporal population dynamics of southern fulmars. J. Anim. Ecol. 72, 576–587. ( 10.1046/j.1365-2656.2003.00727.x) [DOI] [PubMed] [Google Scholar]
- 29.Stafoggia M, et al. 2006. Vulnerability to heat-related mortality: a multicity, population-based, case-crossover analysis. Epidemiology 17, 315–323. ( 10.1097/01.ede.0000208477.36665.34) [DOI] [PubMed] [Google Scholar]
- 30.Pinaud D, Weimerskirch H. 2002. Ultimate and proximate factors affecting the breeding performance of a marine top-predator. Oikos 99, 141–150. ( 10.1034/j.1600-0706.2002.990114.x) [DOI] [Google Scholar]
- 31.Nevoux M, Weimerskirch H, Barbraud C. 2007. Environmental variation and experience-related differences in the demography of the long-lived black-browed albatross. J. Anim. Ecol. 76, 159–167. ( 10.1111/j.1365-2656.2006.01191.x) [DOI] [PubMed] [Google Scholar]
- 32.Rolland V, Barbraud C, Weimerskirch H. 2008. Combined effects of fisheries and climate on a migratory long-lived marine predator. J. Appl. Ecol. 45, 4–13. ( 10.1111/j.1365-2664.2007.01360.x) [DOI] [Google Scholar]
- 33.Pardo D, Barbraud C, Authier M, Weimerskirch H. 2013. Evidence for an age-dependent influence of environmental variations on a long-lived seabird's life-history traits. Ecology 94, 208–220. ( 10.1890/12-0215.1) [DOI] [PubMed] [Google Scholar]
- 34.Weimerskirch H, Jouventin P.. 1998. Changes in population sizes and demographic parameters of six albatross species breeding on the French sub-Antarctic islands. In Albatross biology and conservation (eds Robertson G, Gales R), pp. 84–91. Chipping Norton, Australia: Surrey Beatty and Sons. [Google Scholar]
- 35.Cherel Y, Weimerskirch H, Trouv C. 2000. Food and feeding ecology of the neritic-slope forager black-browed albatross and its relationships with commercial fisheries in Kerguelen waters. Mar. Ecol. Prog. Ser. 207, 183–199. ( 10.3354/meps207183) [DOI] [Google Scholar]
- 36.Weimerskirch H, Capdeville D, Duhamel G. 2000. Factors affecting the number and mortality of seabirds attending trawlers and long-liners in the Kerguelen area. Polar Biol. 23, 236–249. ( 10.1007/s003000050440) [DOI] [Google Scholar]
- 37.Rolland V, Nevoux M, Barbraud C, Weimerskirch H. 2009. Respective impact of climate and fisheries on the growth of an albatross population. Ecol. Appl. 19, 1336–1346. ( 10.1890/08-1060.1) [DOI] [PubMed] [Google Scholar]
- 38.Gales R, Brothers N, Reid T. 1998. Seabird mortality in the Japanese tuna longline fishery around Australia, 1988–1995. Biol. Conserv. 86, 37–56. ( 10.1016/S0006-3207(98)00011-1) [DOI] [Google Scholar]
- 39.Nevoux M, Forcada J, Barbraud C, Croxall J, Weimerskirch H. 2010. Bet-hedging response to environmental variability, an intraspecific comparison. Ecology 91, 2416–2427. ( 10.1890/09-0143.1) [DOI] [PubMed] [Google Scholar]
- 40.Caswell H. 2001. Matrix population models: construction, analysis and interpretation. Sunderland, MA: Sinauer. [Google Scholar]
- 41.Nevoux M, Weimerskirch H, Barbraud C. 2010. Long- and short-term influence of environment on recruitment in a species with highly delayed maturity. Oecologia 162, 383–392. ( 10.1007/s00442-009-1482-y) [DOI] [PubMed] [Google Scholar]
- 42.Inchausti P, Weimerskirch H. 2002. Dispersal and metapopulation dynamics of an oceanic seabird, the wandering albatross, and its consequences for its response to long-line fisheries. J. Anim. Ecol. 71, 765–770. ( 10.1046/j.1365-2656.2002.00638.x) [DOI] [Google Scholar]
- 43.The MathWorks. 2010. MATLAB v. 7.10.0. Natick, MA: The MathWorks, Inc. [Google Scholar]
- 44.García-Carreras B, Reuman DC. 2013. Are changes in the mean or variability of climate signals more important for long-term stochastic growth rate? PLoS ONE 8, e63974 ( 10.1371/journal.pone.0063974) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Deutsch CA, Tewksbury JJ, Huey RB, Sheldon KS, Ghalambor CK, Haak DC, Martin PR. 2008. Impacts of climate warming on terrestrial ectotherms across latitude. Proc. Natl Acad. Sci. USA 105, 6668–6672. ( 10.1073/pnas.0709472105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Kingsolver JG, Diamond SE, Buckley LB. 2013. Heat stress and the fitness consequences of climate change for terrestrial ectotherms. Funct. Ecol. 27, 1415–1423. ( 10.1111/1365-2435.12145) [DOI] [Google Scholar]
- 47.Lloret F, Escudero A, Iriondo JM, Martínez-Vilalta J, Valladares F. 2012. Extreme climatic events and vegetation: the role of stabilizing processes. Glob. Change Biol. 18, 797–805. ( 10.1111/j.1365-2486.2011.02624.x) [DOI] [Google Scholar]
- 48.Collins M, et al. 2013. Long-term climate change: projections, commitments and irreversibility.
- 49.Coles S. 2001. An introduction to statistical modeling of extreme values. Berlin, Germany: Springer. [Google Scholar]
- 50.Barbraud C, Delord K, Weimerskirch H.. 2015. Extreme ecological response of a seabird community to unprecedented sea ice cover. R. Soc. Open Sci. 2, 140456 ( 10.1098/rsos.140456) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Aiello-Lammens ME, Akçakaya HR. 2016. Using global sensitivity analysis of demographic models for ecological impact assessment. Conserv. Biol. 31, 116–125. ( 10.1111/cobi.12726) [DOI] [PubMed] [Google Scholar]
- 52.Koons DN, Grand JB, Zinner B, Rockwell RF. 2005. Transient population dynamics: relations to life history and initial population state. Ecol. Model. 185, 283–297. ( 10.1016/j.ecolmodel.2004.12.011) [DOI] [Google Scholar]
- 53.Jenouvrier S, Barbraud C, Weimerskirch H, Caswell H. 2009. Limitation of population recovery: a stochastic approach to the case of the emperor penguin. Oikos 118, 1292–1298. ( 10.1111/j.1600-0706.2009.17498.x) [DOI] [Google Scholar]
- 54.Ferguson JM, Carvalho F, Murillo-García O, Taper ML, Ponciano JM. 2016. An updated perspective on the role of environmental autocorrelation in animal populations. Theor. Ecol. 9, 129–148. ( 10.1007/s12080-015-0276-6) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data is available as electronic supplementary material at https://dx.doi.org/10.6084/m9.figshare.c.3723961.