We found that human whole body self-motion direction-recognition thresholds measured during dynamic roll tilts were significantly lower than those predicted by a conventional maximum-likelihood weighting of the roll angular velocity and quasistatic roll tilt cues. Here, we show that two models can each match this “apparent” better-than-optimal performance: 1) inclusion of a somatosensory contribution and 2) inclusion of a dynamic sensory interaction between canal and otolith cues via a Kalman filter model.
Keywords: multisensory integration, vestibular, semicircular canals, otolith organs
Abstract
When making perceptual decisions, humans have been shown to optimally integrate independent noisy multisensory information, matching maximum-likelihood (ML) limits. Such ML estimators provide a theoretic limit to perceptual precision (i.e., minimal thresholds). However, how the brain combines two interacting (i.e., not independent) sensory cues remains an open question. To study the precision achieved when combining interacting sensory signals, we measured perceptual roll tilt and roll rotation thresholds between 0 and 5 Hz in six normal human subjects. Primary results show that roll tilt thresholds between 0.2 and 0.5 Hz were significantly lower than predicted by a ML estimator that includes only vestibular contributions that do not interact. In this paper, we show how other cues (e.g., somatosensation) and an internal representation of sensory and body dynamics might independently contribute to the observed performance enhancement. In short, a Kalman filter was combined with an ML estimator to match human performance, whereas the potential contribution of nonvestibular cues was assessed using published bilateral loss patient data. Our results show that a Kalman filter model including previously proven canal-otolith interactions alone (without nonvestibular cues) can explain the observed performance enhancements as can a model that includes nonvestibular contributions.
NEW & NOTEWORTHY We found that human whole body self-motion direction-recognition thresholds measured during dynamic roll tilts were significantly lower than those predicted by a conventional maximum-likelihood weighting of the roll angular velocity and quasistatic roll tilt cues. Here, we show that two models can each match this “apparent” better-than-optimal performance: 1) inclusion of a somatosensory contribution and 2) inclusion of a dynamic sensory interaction between canal and otolith cues via a Kalman filter model.
many behavioral tasks involve sensing and controlling multidimensional movement. For instance, humans are especially adept at minimizing sideways sway while walking (Bauby and Kuo 2000). To help control head orientation, the vestibular system’s semicircular canals and otolith organs sense head rotation, translation, and tilt. While the structural and functional segregation of the vestibular organs maximizes directional specificity, the brain combines these various signals to estimate the magnitude and direction of motion (Goldberg et al. 2012). In this study, we investigate how the brain combines vestibular signals indicating rotation and tilt to yield reliable perception.
When incoming sensory information is independent, studies show that human multisensory thresholds are consistent with maximum-likelihood (ML) estimators (Ernst and Banks 2002; Hillis et al. 2002). Such ML estimators: 1) weight sensory signals inversely with the sensory noise variance (Angelaki et al. 2009; Butler et al. 2010; Ernst and Banks 2002; Fetsch et al. 2010; Hillis et al. 2002; Landy et al. 1995), 2) yield variance estimates that approach maximum precision (Cramer-Rao lower bound) (Kay 1993), and 3) match performance of optimal Bayesian estimators given a uniform prior distribution of the estimated variable (Gelb 1974). Other studies have shown that, when such signals are accompanied by additional information in the form of nonuniform prior distributions (also called Bayesian priors), performance matches maximum a posteriori (MAP) estimators (Gelb 1974; Kalman and Bucy 1961). ML/MAP estimators are optimal for noisy signals and provide a performance limit that cannot be surpassed for a linear system.
However, differences between vestibular neurophysiology and perception regarding the optimality of the integration of rotation and translation cues have been suggested. For instance, electrophysiological studies showed that the activities of neurons, which receive and integrate rotation and translation signals, are suboptimal (Carriot et al. 2015), yet it has been suggested that human perceptual thresholds in response to eccentric rotation were better than optimal (Soyka et al. 2015). Given this discrepancy, we performed a study of self-motion sensory integration that includes incoming sensory information that interacts dynamically.
When the incoming sensory information is dynamically interacting, the knowledge of the physical relationship between the signals is relevant, and conventional “nondynamic” ML/MAP models that do not include such dynamic interaction might not always be sufficient to match human performance. For example, for linear dynamic systems, Kalman filters improve performance by using information about the relationship between the time-varying measurement history and the states of a system (Gelb 1974; Kalman and Bucy 1961). This augments the a priori and the likelihood function of the ML/MAP models, which yields dynamic Bayesian optimal performance (Gelb 1974; Kalman and Bucy 1961) that can yield a better performance than conventional ML/MAP models that do not consider dynamic sensory interaction.
Kalman filters and internal models are well established in the vestibular literature (Angelaki et al. 1999; Glasauer 1992; Lacquaniti et al. 2014; MacNeilage et al. 2008; Merfeld et al. 2005b, 1993a, 1999) and have specifically been suggested to contribute to suprathreshold vestibular perception (Glasauer 1992; Merfeld et al. 2005b) and vestibuloocular reflex (VOR) (Angelaki et al. 1999; Merfeld et al. 1993a, 1999) responses. Similarly, here we hypothesize that the internal model can further enhance perceptual performance by including the dynamic interactions among the neural signals. To test this hypothesis, we measured roll tilt direction-recognition thresholds in the dark. We chose a roll tilt paradigm because a number of studies have shown that rotation signals from the semicircular canals and gravitational tilt signals from otolith organs interact via an internal model during roll tilt (Angelaki et al. 1999; Glasauer 1992; Merfeld et al. 2005b, 1999). Furthermore, a recent study showed that higher roll tilt thresholds were correlated with failure to complete a standard Romberg test of balance (Bermúdez Rey et al. 2016). We report roll tilt thresholds significantly below (P < 0.01 for all subjects) those predicted by a nondynamic ML/MAP linear weighting of the available rotation signals and tilt signals when the two signals have comparable magnitudes. To explain our findings, we explore 1) a vestibular-only dynamic Kalman filter model, 2) alternative noninteracting models that include noise correlations, and 3) somatosensory contributions.
METHODS
General psychophysical methods mimic those recently published (Karmali et al. 2014; Valko et al. 2012); more details than provided below can be found in these earlier publications. The Massachusetts Eye and Ear Infirmary Human Studies Committee approved the study, and informed consent was obtained. We used a repeated-measures design. Six normal volunteers (4 females, 2 males, mean age 39, range 27–59 yr) completed the entire test series that consisted of 42 different tests over at least 20 separate test sessions. Four other normal subjects began testing but declined further testing before completing all tests in this demanding experimental protocol; only control data from these subjects were used. Other than these incomplete datasets, no data were discarded for any reason. Each normal subject was screened via a detailed clinical vestibular examination. Screening consisted of a short questionnaire inquiring about any history of dizziness/vertigo in addition to caloric, Hallpike testing, angular VOR, and posture control measures. Two patients (39 and 59 yr of age) suffering severe idiopathic bilateral vestibular loss, confirmed by clinical testing, also participated in limited control testing.
Task.
We measured thresholds using a standard one-interval, two-response recognition paradigm (Chaudhuri et al. 2013; Karmali et al. 2014; Macmillan and Creelman 2005; Valko et al. 2012), which we refer to as “direction recognition.” All motion stimuli were applied with a Moog 6 degrees of freedom (DOF) motion platform. As described in detail below, the following three different motions were used: 1) slow unidirectional constant-velocity (“quasistatic”) roll tilts, 2) unidirectional single-cycle sinusoidal roll rotation about an earth vertical axis, and 3) unidirectional single-cycle sinusoidal roll tilts.
Subjects were trained to push a button in their left hand to indicate leftward motion or their right hand to indicate rightward motion. Subjects were instructed to respond only after hearing a pure tone indicating the offset of a motion stimulus. Each test series began with ~5–10 practice trials. We used a 3-down, 1-up staircase paradigm that targets a stimulus level at which the subject correctly recognizes motion direction 79.4% of the time (Leek 2001). A single condition/frequency was tested at a time; multiple staircases were never interleaved (Benson et al. 1989, 1986; Grabherr et al. 2008). Testing began well above threshold and continued until there were five direction reversals in the adaptive track (3 minima and 2 maxima).
As for earlier studies (Benson et al. 1989, 1986; Grabherr et al. 2008; Valko et al. 2012), we varied frequency as a primary independent variable. While some earlier threshold studies have investigated optimal integration by degrading the precision of one or more of the cues (Ernst and Banks 2002; Fetsch et al. 2010), we chose to vary frequency as for our earlier threshold study that investigated optimal integration of visual and vestibular cues (Karmali et al. 2014), taking advantage of the fact that self-motion thresholds naturally vary as a function of frequency (Benson et al. 1989, 1986; Grabherr et al. 2008; Valko et al. 2012). In other words, stimulus duration was controlled as duration is defined as the inverse of frequency.
Quasistatic roll tilt stimuli (“otolith”).
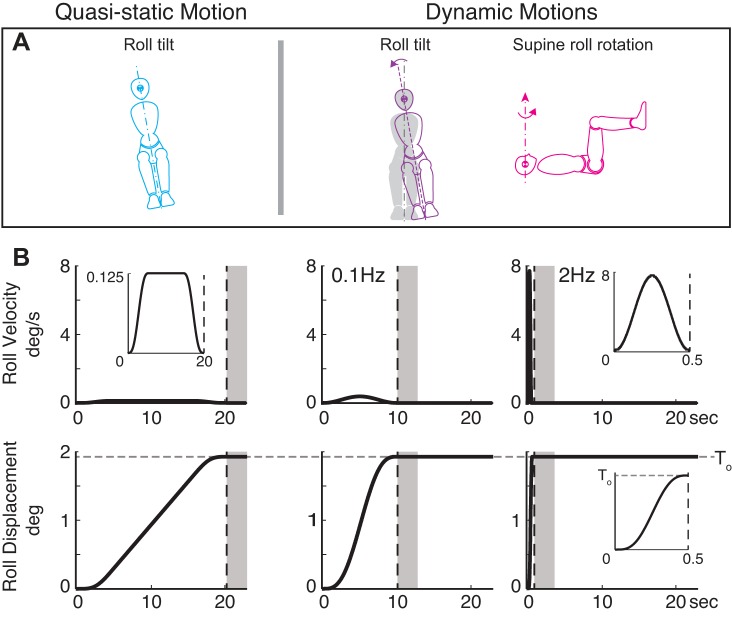
Subjects were seated upright and were tilted in roll about a head-centered earth-horizontal axis (Fig. 1A, left) using unidirectional constant-velocity smoothed trapezoids of varying duration. These motion stimuli, called “quasistatic tilts” (Fig. 1A, left) because the canal cues were subthreshold, mimic those used previously (Bringoux et al. 2002). Minimizing the canal cue also had a secondary effect of minimizing the canal-otolith sensory interaction. After each trial, subjects returned to the initial vertical position before the next trial. Quasistatic tilt velocity and displacement profiles are shown in Fig. 1B, left. The plateau angular velocity was 0.125°/s (Fig. 1 top left), which was almost four times lower than the lowest roll rotation averaged threshold (0.42°/s plateau; see Fig. 4A), and the peak angular acceleration and angular jerk were 0.05°/s2 and 0.03°/s3. These parameters were selected to provide subthreshold rotation stimuli, confirmed by findings reported herein, forcing subjects to focus on the tilt angle to recognize tilt direction. To reduce measurement error, this test was repeated on four different days for each subject.
Fig. 1.
Roll tilt velocity and displacement motion profiles with final tilt equal to mean quasistatic tilt threshold. Eq. 1 relates final displacement and peak velocity of single-cycle sinusoid acceleration motion. Note that the peak velocity for quasistatic motion is very small compared with dynamic roll tilt velocity. The horizontal dashed gray lines are identical to the dashed cyan line in Fig. 4B. Subjects were encouraged to press a button after motion (shaded area); end of motion is indicated by the vertical dashed line. Insets expand the time scale to show motion profiles.
Fig. 4.
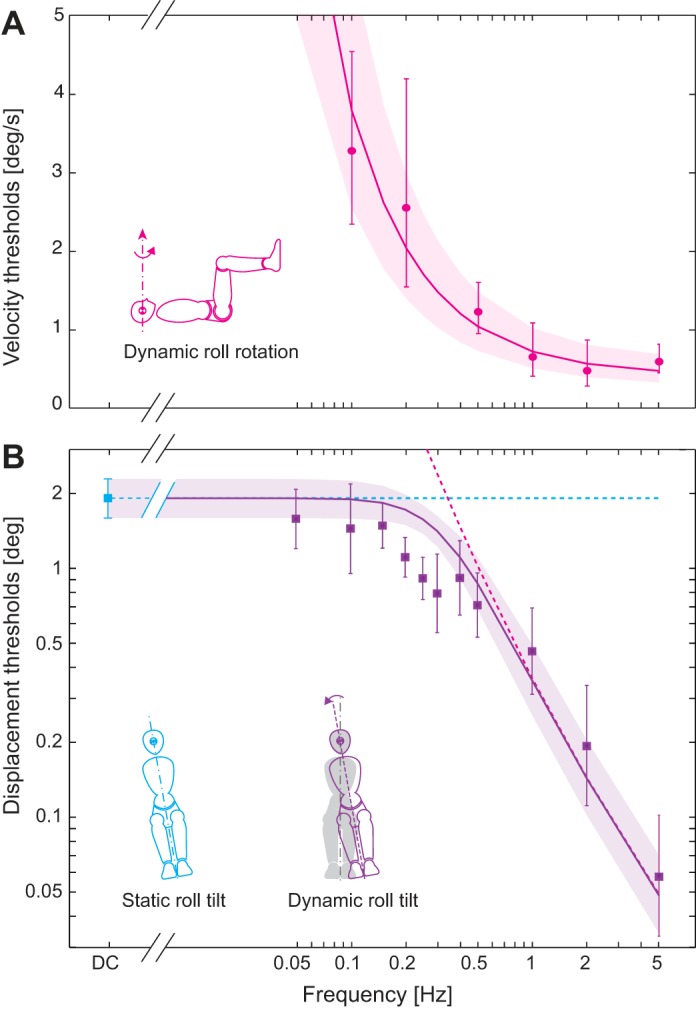
Human roll rotation (A) and roll tilt (B) perceptual thresholds. A: supine roll rotation velocity thresholds for 0.1–5 Hz. Magenta circles show average thresholds, and the error bars show 95% confidence intervals (95% CI). Magenta line shows the average high-pass filter model (model 4) (Lim and Merfeld 2012) fit. B: roll tilt thresholds (purple squares) across frequencies. The blue square shows the average quasistatic roll tilt threshold. Error bars show 95% CI. Dashed magenta curve shows the velocity threshold (°/s) fit from a scale to show the displacement threshold in degrees. Blue dashed line represents that the otolith cue at the end of a roll tilt is independent of frequency (i.e., is constant, see text). Purple solid line indicates the thresholds predicted by an ML sensory fusion of the rotation and tilt thresholds using Eq. 3.
We also performed an additional control test, using a different task, in which the subjects were not returned to the vertical position after each trial. Motion stimuli were the same smoothed trapezoidal motion profiles described in the previous paragraph; however, each motion commenced from the end point of the previous trial. For these trials, the subjects were explicitly trained to indicate the direction they were tilted at the end of the trial. For example, if the subject started out tilted to the left by 2.5° and then rotated to the right by 1°, they would be tilted 1.5° to the left, so the objectively correct response would be “left.” A technical reason for choosing quasistatic tilt over dynamic linear translation is that translation requires large distances that exceed the track length of our available equipment. Scientific reasons are discussed in the discussion.
Dynamic roll tilt stimuli (“canal-otolith”).
Subjects were seated upright and were tilted in roll about a head-centered earth-horizontal axis using single cycles of sinusoidal angular acceleration like those we have used in previous studies (Benson et al. 1989, 1986; Grabherr et al. 2008; Karmali et al. 2014; Valko et al. 2012; Zupan and Merfeld 2008). After each trial, subjects returned to the initial vertical position before the next trial (Fig. 1A, center). Frequencies were 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.4, 0.5, 1, 2, and 5 Hz. These correspond to durations ranging between 0.2 and 20 s. The magnitude of the peak acceleration (αp), peak velocity (ωp), and displacement (Δθ) are related as:
| (1) |
Figure 1 highlights the differences between quasistatic tilt, slow dynamic tilt, and fast dynamic tilt motions.
To reduce measurement error, repeat testing at each frequency was performed on two different days for each subject.
Dynamic roll rotation stimuli (“canal”).
Unidirectional roll rotation motion was identical to the rotation motion during roll tilts, except that subjects were supine with the rotations about a nasooccipital earth-vertical axis. Frequencies were 0.1, 0.2, 0.5, 1, 2, and 5 Hz. To reduce measurement error, repeat testing at each frequency was performed on two different days for each subject.
Data analysis.
Thresholds were determined using psychometric curve fits. A Gaussian cumulative distribution was fit to each data block (Haburcakova et al. 2012; Zupan and Merfeld 2008). For simulated data acquired using nonadaptive sampling, ML fits were performed using a generalized linear model (GLM) and probit link function. This fit was performed using the MATLAB function call [b, dev, stats] = glmfit (θ, y, “binomial,” “link,” “probit”), where θ is a vector of trial displacements, y is a vector indicating the subjects’ responses (0 leftward, 1 rightward), and b is a two-element parameter fit vector. The underlying Gaussian probability distribution is described by “vestibular bias”μ = −b(1)/b(2), which represents a subjective offset from zero, and “sigma” σ = 1/b(2), which represents the noise standard deviation (Dobson and Barnett 2011; Haburcakova et al. 2012; Merfeld 2011). We report all thresholds as “1-sigma thresholds,” i.e., t = σ. For experimental data acquired using adaptive staircases, the fits were performed using the MATLAB function call [b, dev, stats] = brglmfit (θ, y, binomial, link, probit), where brglmfit (Chaudhuri and Merfeld 2013) implements a bias-reduced GLM fit developed to correct for underestimation of the slope of the psychometric function (Chaudhuri and Merfeld 2013).
Consistent with earlier vestibular threshold studies (Benson et al. 1989, 1986; Grabherr et al. 2008), Kolmogorov-Smirnov tests did not reveal significant departures from a lognormal distribution across subjects, so final averaging across subjects was performed in logarithmic units, which is sometimes called the “geometric mean.” Results, both mean and 95% confidence interval (95% CI), were transformed back to physical units for presentation. Error bars shown in Figs. 1–6 and error values in text represent the 95% CI.
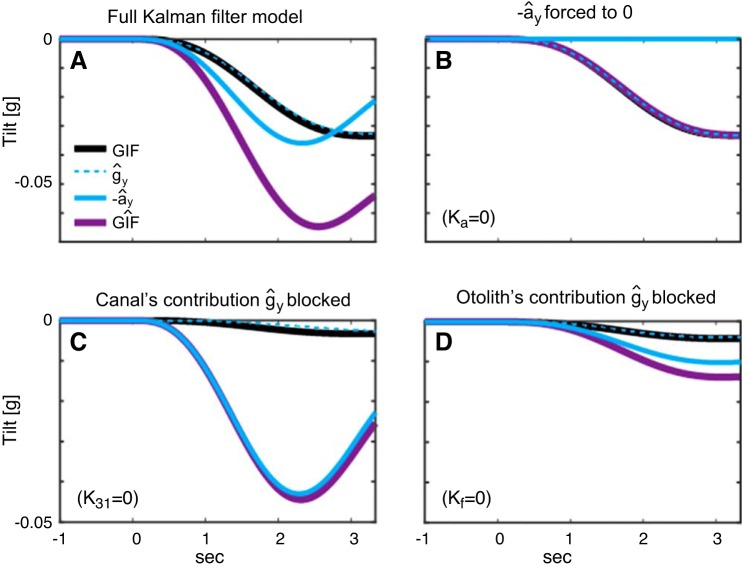
Fig. 6.
Internal estimates of tilt components resulting from various Kalman gain manipulations. A: normal Kalman filter with the Kalman gains in Fig. 3. B: translation estimate is forced to 0 (cyan horizontal line) while keeping other Kalman gains the same as in A. Internal estimate of GIF is nearly perfect. C: the Kalman gain gating the canal’s error signal to GIF estimate is forced to 0. Compared with the small underestimation of ĝy resulting from such manipulation, overestimation of ây is marked by great magnitude. D: the Kalman gain modulating the otolith’s contribution to ĝy is forced to zero. In this case, the tilt signal is completely determined by the canal’s rotation signal that is integrated over time to yield rotational displacement.
Roll rotation threshold transfer function fit.
Single-cycle sinusoids do not yield steady-state responses; fitting a transfer function must take this into account (Lim and Merfeld 2012; Soyka et al. 2012). We did this using model 4 of the cross-frequency fitting approach described in detail in an earlier publication (Lim and Merfeld 2012). Because the details are published, we briefly describe the implementation here. To determine the high-pass transfer function most consistent with the roll rotation (“canal-only”) thresholds, angular velocity trajectories mimicking those used experimentally were input to a MATLAB Simulink model of a high-pass filter. For each subject, the input amplitude was set to the threshold at each of the six roll rotation test frequencies. The filter output then represented the high-pass-filtered neural signal at each of the six frequencies tested. The cut-off frequency was varied using “fmincon” in MATLAB to minimize variations in the peak filter output at threshold as a function of frequency. This minimization calculates the cut-off frequency that yields the peak neural signal after filtering that varies the least (i.e., is maximally “constant”) across the frequencies tested. This calculation is justified by the fact that a threshold is defined in signal detection theory (Green and Swets 1966) when the neural signal representing the stimulus exceeds some fraction of the noise, which we assume constant. This fit does not assume steady state and yields the transfer function that the nervous system would implement to yield the measured responses. Conceptually, this high-pass transfer function can be interpreted as a perceptual filter, HPFc, estimated based on the external motion stimuli (Merfeld et al. 2015).
ML estimation weighting.
In appendix a, we derive a minimum variance unbiased (MVU) estimator that yields the exact same relationships as earlier ML estimators (Ernst and Banks 2002; Hillis et al. 2002) when the noise is Gaussian. We chose an MVU estimator because it does not require Gaussian noise and because it was then straightforward to consider the influence of correlated noise (see appendix a).
Consistent with earlier studies (Ernst and Banks 2002; Hillis et al. 2002), the assumption of uncorrelated noise is justified by the following facts: 1) the canal and otolith sensors are physically distinct from one another, 2) independent afferent populations consisting of thousands of neurons innervate each vestibular end organ, and 3) the canals and otoliths transduce qualitatively different specific energies (gravity and angular velocity).
Under these assumptions, a relatively simple equation (Eq. 2) shows how to combine the variances from two sensory signals ( and ) to calculate the reduced variance () when these two signals are optimally combined via an ML (Ernst and Banks 2002; Hillis et al. 2002) or MVU (Gelb 1974) estimator:
| (2) |
where σc represents the canal threshold, σo the otolith/graviceptor threshold, and σco the combined threshold.
Because thresholds are linearly proportional to standard deviations (Ti = λσi), this relationship can be substituted into the variance equation to yield an equation that relates the threshold for the combined signals to the thresholds for the individual signals:
| (3) |
where Tc is the canal threshold, To the otolith/graviceptor threshold, Tco the combined threshold, and f explicitly emphasizes frequency dependence. Because the proportionality constant λ cancels, note that Eqs. 2 and 3 have identical forms and can be obtained by substituting T for σ and vice versa. See Ernst and Banks (2002) for an excellent derivation and description of Eqs. 2 and 3.
Similarly, the combined threshold Tvp resulting from the integration of vestibular and somatosensory cues can be calculated from , where Ts is somatosensation thresholds. Because it is not feasible to measure somatosensory-only roll tilt thresholds in normal subjects, roll tilt thresholds from well-compensated total bilateral-loss patients (Valko et al. 2012) were used. Because these patients had years to compensate for their vestibular loss, these patients likely learned to fully use all available somatosensory cues, so these thresholds may provide a lower bound on somatosensory thresholds for normal subjects.
As noted above, the assumption of uncorrelated noise seems reasonable. Nonetheless, noise correlations might play a role (Averbeck et al. 2006), so we include models with and without noise correlations. We can generalize Eq. 3 to include correlated noise that the brain is unaware of during estimation (Gelb 1974). The derivation included in appendix a shows that, under these assumptions:
| (4) |
where ρ is the noise correlation coefficient. For simplicity, we have removed the notation that explicitly showed that thresholds vary with frequency.
We can also include correlated noise that the brain is aware of and fully considers during estimation. Under these assumptions, following Gelb (1974), we calculate the combined threshold as:
| (5) |
A derivation of the influence of correlated noise (Eqs. 4 and 5) on thresholds is included in appendix a. Note that with no correlation (ρ = 0), Eqs. 3, 4, and 5 are all the same.
Statistics.
With the use of Eq. 3, roll tilt thresholds as a function of frequency were calculated for each subject using each subject’s fitted roll rotation thresholds as a function of frequency and each subject’s static roll tilt threshold. Because this model has been used extensively to define optimal integration (Ernst and Banks 2002; Fetsch et al. 2010; Hillis et al. 2002; Karmali et al. 2014), we call this estimator (Eq. 3) the conventional nondynamic ML model. To determine errors for roll rotation, static tilt, and nondynamic ML model fits (cf., Fig. 4), we used bootstrap resampling (Chaudhuri and Merfeld 2013; Wichmann and Hill 2001). Based on the resulting estimated psychometric function, 1,000 response vectors were randomly generated while keeping the stimuli vectors identical to the experimental sequence (i.e., nonadaptive), i.e., bootstrap resampled (Wichmann and Hill 2001). To estimate the variance of the predicted threshold for each individual at each frequency, the resulting simulated responses were refitted 1,000 times using the standard GLM fit in MATLAB because such nonadaptive paradigms yield unbiased threshold estimates (Chaudhuri and Merfeld 2013; Fetsch et al. 2010).
Because we used a repeated-measures experiment design, we used within-subject repeated-measures statistics. Specifically, two tests were performed to compare the nondynamic ML model predictions with the experimental data. First, we calculated the residual at each frequency and then summed these residuals across all frequencies for each subject. A Wilcoxon ranked-sign test was then used to determine if these summed residuals for each subject demonstrated a significant overall tendency for underestimation or overestimation by the model. Because nonnarametric statistical tests are more robust and simpler than parametric statistical tests, and make fewer assumptions about the error distribution, these nonparametric tests are more conservative than parametric tests. Second, a Chi square test was performed across frequencies of specific interest (0.2–0.5 Hz) to determine whether the measured thresholds and the nondynamic ML model predictions for each subject were significantly different. Once a statistical difference was shown, a sign test was performed using the differences between the observed and modeled thresholds across subjects to determine whether the experimental result was significantly less or greater than the nondynamic ML model prediction.
Kalman filter model.
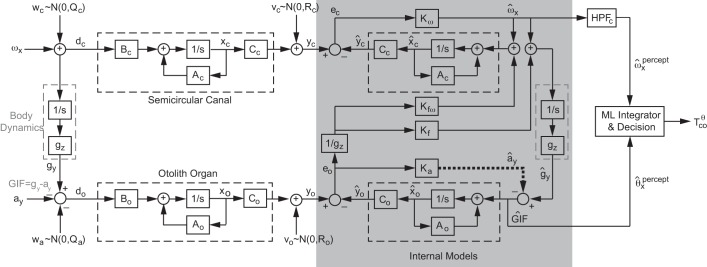
To investigate how thresholds might be influenced by the dynamic convergence of roll rotation and tilt cues, we simplified a previously published vestibular model (Karmali and Merfeld 2012, 1999; Selva and Oman 2012) by linearizing it for small angles. Figure 2 shows the block diagram of the proposed model that includes a standard Kalman filter. The model consists of the following three partitions: 1) real body and sensory dynamics (shown on left), 2) internal copies of body and sensory dynamics (gray box in middle), and 3) perceptual threshold fusion of the internal estimates of the two sensory cues (far right). The first two partitions show the entire Kalman filter, including sensor dynamics, which is just a linearized version of the preexisting observer model (Merfeld et al. 1999; Selva and Oman 2012). The rightmost partition represents a high-pass filter that contributes to direction-recognition decision-making (Aston-Jones and Cohen 2005; Merfeld et al. 2015) (also see discussion) and standard ML weighting (Eq. 3). To simplify the Kalman filter for our application, we first eliminated the pitch, yaw, and forward-backward translation components from the original 6 DOF model since our study focused exclusively on roll rotation and lateral tilt. We then linearized the nonlinear observer model, which was justifiable since the tilt thresholds we measured experimentally were <2° in normal subjects.
Fig. 2.
Detailed block diagram of the Kalman filter model. Incoming roll tilt velocity stimulus (ωx), which is impacted by the process noise (wc),is transformed to tilt displacement by body dynamics (gray dashed box on far left). For tilts, otolith organs cannot distinguish between the interaural component of gravity and interaural acceleration. Hence, the interaural component of the tilt (gy) is measured as gravitoinertial force (GIF = gy − ay), which is impacted by the interaural acceleration process noise wa. Noisy rotation and GIF are transduced by the semicircular canals and otolith organs (black dashed boxes), respectively. The transduced signals yc and yo, analogous to the afferent signals from the canal and otolith in physiology, include intrinsic sensory (measurement) noise characterized by vc and vo. To estimate the external roll tilt stimulus based on the noisy afferent signals, the brain maintains internal copies (gray box) of sensory and body dynamics. To optimally use two different signals, the brain may weigh each error signal (ec and eo) differently depending on the precision and dynamics of the signals to update the state estimates of rotation , ω, and GIF = ĝy − ây. In Kalman filters, this optimization is accomplished via the Kalman gains (K with various subscripts). In our Kalman filter model, Kω is the gain for the rotational velocity, Kf corresponds to the gravity vector gain, and Ka corresponds to the translational acceleration gain. Kfω weights the slow change in the gravity vector signal to compensate for the high-pass filtering of the canal that cannot transduce low-frequency rotations. Two state estimates ( and ĝy − ây) emerge from this Kalman filter internal model. These estimates are then processed as part of the decision-making operations (far right) that include a perceptual high-pass-filter (HPFc) for the transient rotation signal (Lim and Merfeld 2012), which are combined with the gravitoinertial estimate via a simple standard maximum-likelihood (ML) model (Ernst and Banks 2002; Fetsch et al. 2010; Karmali et al. 2014) (Eq. 3) to yield a decision, which is finally measured in the form of dynamic roll tilt perception thresholds (). Superscript θ indicates that the threshold measurements were done in the angular displacement domain.
Specifically, roll tilt input movement was linearized such that the roll tilt displacement is represented as the lateral component gy of the gravity vector that is approximated by integrating the noisy roll angular velocity input dc over time.
| (6) |
The semicircular canals can be modeled as a second-order band-pass filter (Fernandez and Goldberg 1971; Karmali and Merfeld 2012). We follow Karmali’s derivation (Karmali and Merfeld 2012) (see appendix b) starting with a transfer function representation,
| (7) |
where yc is the output canal afferent firing rate, dc is the angular velocity input signal, and s is the Laplace variable ( = j2πf). Here, τ1 characterizes high-pass dynamics having the value of 5.7 s (cutoff frequency 0.028 Hz), resulting from the canal’s fluid dynamics (Fernandez and Goldberg 1971). τ2 characterizing the low-pass dynamics was set at 0.005 s (32 Hz), which is identical to that used in the recent model (Karmali and Merfeld 2012). As a consequence, the rotational velocity input between 0.028 and 32 Hz is transduced fairly accurately, whereas the motions outside these frequencies are attenuated.
In Merfeld’s original observer model (Merfeld et al. 1993a), the otolith organ dynamics were modeled with unity gain. To allow modeling using the state-space formulation, the otolith dynamics were modeled using a first-order low-pass filter with the cutoff chosen so that it behaved like a unity transfer function for motion stimuli well below the cutoff frequency. Like another recent Kalman filter model (Selva and Oman 2012), we modeled otolith organ dynamics as a first-order low pass:
| (8) |
where yo is an output otolith afferent firing rate, and do is the noisy gravito-inertial force (GIF = gy − ay) input. Here, τ2 was arbitrarily chosen to equal 0.016 s (10 Hz), which approximately yields a unity gain for all stimulus frequencies tested. (In other words, this specific choice for this free parameter is not crucial.)
Another characteristic that distinguishes a Kalman filter from an observer model is that the Kalman gains are determined from the prior knowledge of the system dynamics and noise (Gelb 1974; Kalman and Bucy 1961). Hence, given the dynamic model parameters (e.g., Eqs. 7 and 8) and noise variances, the steady-state Kalman gains can be found by solving the Riccati equation (Gelb 1974). (Detailed state-space representations are provided in appendix b.) The state-space representation of the resulting internal estimates can be expressed as the following (see Figs. 2 and 3 for nomenclature).
| (9) |
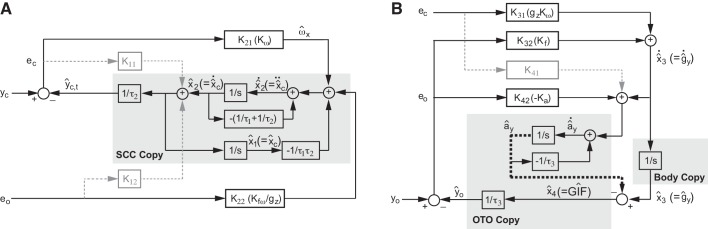
In Eq. 9, the dynamics of the internal states are governed by the 4x4 matrix while the canal and the otolith error signals ec and eo contribute to the internal states after being multiplied by the Kalman gain matrix (the 4 × 2 matrix containing Kω, Kfω, Kf, and Ka). To observe how the individual Kalman gains mediate the sensory interaction and the resolution of the tilt translation ambiguity, the individual component of the internal models is broken down to separate diagrams in Fig. 3. In Fig. 3, the subscripts assigned to Kalman gains indicate row-column element numbers in the Kalman gain matrix in Eq. 9. These Kalman gains are found through a fitting process described in the following paragraph.
Fig. 3.
Internal models with individual Kalman gain elements. Canal internal model (A) and otolith internal models (B) in Fig. 2 are drawn separately to show the sensory interactions among the rotation (), translation (ây), and tilt (ĝy) estimates. The sensory interactions are mediated by Kalman gains that gate canal and otolith error signals (ec and eo) contributing to the internal estimates.
Table 1 summarizes the free parameters found in this Kalman filter ML model that provides dynamic canal-otolith interaction. The resulting Kalman gains were Kω = 3.0, Kfω = 0.22, Kf = 2.1, and Ka = −62. The process we used to find these four Kalman gains follows. For our Kalman filter model, like earlier studies (Karmali and Merfeld 2012; Merfeld et al. 1993b; Selva and Oman 2012), we assumed that the brain knows the distribution of the external (process) noise and the internal (sensory) noise; each noise was assumed to be band-limited (0~400 Hz) Gaussian white noise (Karmali and Merfeld 2012). The four noise sources (rotation process noise, acceleration process noise, canal measurement noise, and otolith measurement noise) were assumed uncorrelated with one another. As for the previously published model (Karmali and Merfeld 2012), model parameters were fitted based on four known constraints (Karmali and Merfeld 2012): canal afferent noise/threshold (Sadeghi et al. 2007), rotational VOR gain (Dimitri et al. 2001), otolith afferent noise/threshold (Yu et al. 2012), and human dynamic roll tilt thresholds (Fig. 4B, purple squares). First, while having the total noise in yc equal to the canal afferent noise variance of 4.0 (deg/s)2 (Sadeghi et al. 2007), the ratio between the canal process and measurement noise variances Qc and Rc that generated the rotational gain Kω of 3.0 was found (Dimitri et al. 2001; Karmali and Merfeld 2012). Next, while keeping the noise ratio (Qc /Rc = 15) constant, Qc and Rc were fine tuned to fit the canal afferent noise variance. Next, while having the total otolith noise in yo constrained by the otolith afferent noise (0.03 G2) (Yu et al. 2012), the otolith measurement noise variance Ro (0.0047 G2) was found, and, through manual optimization via grid search, the ratio of the otolith noise variance Qo to Ro of 2.9 that minimized the root mean square error (RMSE) between the dynamic Kalman filter model and the observed roll tilt thresholds (Fig. 4B) was found, both across all frequencies (0~5 Hz) and between 0.2 and 0.5 Hz. All of these parameters were found by passing zero-mean white noise through the Kalman filter model.
Table 1.
Model free parameters
| SCC | Otolith | Constraints | |
|---|---|---|---|
| Internal model sensory dynamics | |||
| Time constants | τ1 = 5.7 s | τ3 = 0.16 s | (Fernandez and Goldberg 1971; Fernández and Goldberg 1976) |
| τ2 = 0.005 s | |||
| Kalman filter | |||
| Process noise variance Q | Qc = 7.6 × 102 (°/s)2 | Qo = 1.4 × 10−2 (G)2 | VOR gain (Dimitri et al. 2001), Roll tilt thresholds (Fig. 4B) |
| Measurement noise variance R | Rc = 52 (°/s)2 | Ro = 4.7 × 10−3 (G)2 | Afferent noise (Sadeghi et al. 2007; Yu et al. 2012) |
| Perceptual processing inferred from the observed thresholds | |||
| Perception filter | fHPF = 0.44 Hz | Unity gain function | |
VOR, vestibuloocular reflex.
In addition to the Kalman filter model described above that combines signals optimally using internal models, we wanted a “control” model that simulated the absence of dynamic interaction between the canal and otolith signals. To accomplish this, the acceleration estimate (arrow with thick dashed line labeled ây in Fig. 2) in the internal model of the same Kalman filter model was forced to zero. This, in effect, made for all tilts, emulating the external acceleration input (ây = 0, GIF = gy) perfectly, in turn yielding results identical to the ML model in isolation (solid purple in Fig. 4B). Hereafter, this model is called the noninteracting Kalman filter model. This noninteracting Kalman filter model was further used to examine the influence of noise correlation between rotation and tilt signals.
Predicting perception thresholds based on internal estimates.
To calculate perception thresholds from the Kalman filter outputs (internal estimates), we used the relationship among thresholds, signal variance, and gain (Jamali et al. 2013; Lim and Merfeld 2012). Here, the goal is not to verify the relationship between the physiological noise and perceptual noise. Instead, physiological noise and perceptual noise are considered separately. For instance, we use the physiological noise to find parameters for the existing physiological model in Fig. 2. With the use of this model, the ratio of the peak input and peak output was obtained for noise-free threshold motion profiles for different frequencies. Next, this ratio at each frequency was multiplied by the perceptual noise variance to calculate the perception threshold estimate as a function of frequency; this calculation is based on the signal detection theory assumption that perceptual thresholds are directly proportional to noise variance. Such utilization of perceptual noise and frequency response ratios has been used similarly in previous work modeling perceptual threshold dynamics (Lim and Merfeld 2012) and vestibular afferent neural thresholds (Eq. 5 in Jamali et al. 2013). We used the perceptual thresholds (calculated at 1σ, horizontal asymptote for the magenta curve in Fig. 4A and cyan dashed line in Fig. 4B) to provide the noise variance estimations in our model. As presented in results, thresholds predicted by such simulations exactly matched those predicted theoretically, which also helps verify these simulation methods.
The resulting rotation and tilt threshold curves were then combined using the standard ML model (Eq. 3) to obtain the dynamic roll tilt perception threshold estimation curves for ρ = 0 (both dynamic Kalman filter model and noninteracting Kalman filter model). For correlated noise (i.e., Eqs. 4 and 5 and the noninteracting Kalman filter model) the noise correlation ρ is a free parameter. Noise correlation model fits were performed using the fmincon command in MATLAB to minimize square error.
RESULTS
During roll tilts, the semicircular canals primarily provide a velocity cue and the otolith organs primarily provide a displacement cue; changing the frequency of motion allows the relative size of displacement and velocity to be modulated. Because multisensory integration is most apparent when sensory cues have similar precision (e.g., Ernst and Banks 2002), we measured thresholds as a function of frequency (Karmali et al. 2014) across a broad range of frequencies that ensured that there would be a frequency range where a robust multisensory integration effect would be observed.
To determine individual cue precision, we measured roll rotation thresholds with supine subjects that primarily stimulated canals and measured quasistatic roll tilt thresholds with very slow motions that primarily stimulated the otolith organs. Figure 4 shows our measured threshold data. The shaded areas represent the 95% CI across the six subjects. Roll rotation (canal) velocity thresholds (Tc) were measured using earth-vertical rotation with each subject supine (Fig. 4A, sketch). As previously reported for yaw rotation, we found that the average velocity threshold decreased as stimulus frequency (f) increased (Benson et al. 1989; Grabherr et al. 2008; Valko et al. 2012). This pattern of roll rotation thresholds is consistent with the influence of a high-pass filter on the rotational signal from the canals (Grabherr et al. 2008; Haburcakova et al. 2012; Lim and Merfeld 2012). Therefore, we fit these data (Fig. 4A) by high-pass filtering the angular velocity (model 4 in Lim and Merfeld 2012). We found that a high-pass filter (HPFc) with a cut-off frequency (fHPF) of 0.44 Hz (+0.11/−0.07) best matched the data with a plateau velocity of 0.42°/s (+0.10/−0.06). This model leads to threshold parameter estimates that are similar to those previously reported for yaw rotation (Grabherr et al. 2008; Lim and Merfeld 2012; Valko et al. 2012).
We measured an average graviceptor (otolith) tilt threshold of 1.91° (+0.20/−0.16) by tilting vertical (“upright”) subjects using quasistatic tilt stimuli. Additionally, we performed three control tests to show that these primarily represent otolith thresholds and minimally reflect other sensory cues. First, to show that the semicircular canals were not contributing, we used a tilt paradigm that decoupled the otolith cue from the canal cue. In this paradigm, subjects were tilted without ever returning to the vertical position, and the subject’s task was to indicate the final tilted position. (See methods for details.) Here we found an average tilt threshold of 1.56° (+0.37/−0.24) for the same six subjects tested in this control condition; this threshold value is indistinguishable (P = 0.57, paired t-test) from that measured using our quasistatic tilt paradigm. Second, we verified that sensory signals other than those due to gravity were subthreshold by testing subjects using the same quasistatic roll rotation motion stimuli with the subjects supine; we found that without otolith cues quasistatic thresholds were more than an order of magnitude greater (>20°) than when upright. Third, to confirm that this tilt threshold was predominantly due to the otoliths and not other graviceptor cues, we also measured quasistatic tilt thresholds in two patients with severe bilateral vestibular hypofunction. The measured patient thresholds were roughly two to three times greater than normal (4.00° and 6.42° for quasistatic tilt, 4.08° and 4.97° at 0.1 Hz), which is qualitatively consistent with roll tilt thresholds measured in total bilateral loss patients (Valko et al. 2012).
The average rotation displacements at threshold (dashed magenta curve), calculated from the velocity threshold curve shown in Fig. 4A, are shown vs. frequency in Fig. 4B. Because a recent analysis showed that both regular and irregular otolith afferent thresholds are constant over the frequency range we tested (Jamali et al. 2013) and because the gravitational tilt cue depends only on the final tilt angle regardless of the frequency, we assumed that the otolith threshold in isolation would be the same across all frequencies, which is represented by the horizontal dashed blue line in Fig. 4B. (See the discussion for consideration of otolith dynamics.) The solid purple line in Fig. 4B shows the theoretical thresholds predicted when noisy rotation and tilt signals were combined using a conventional ML model (Eq. 3). Similar to earlier models (Ernst and Banks 2002; Hillis et al. 2002), this model has no free parameters; the noise variances are determined from the measured thresholds.
To test this ML integration model, we measured dynamic roll tilt (canal-otolith) thresholds (Tco) by tilting subjects in roll (Fig. 4B, purple squares), again using single cycle sinusoids. The data fell significantly below the thresholds predicted by the conventional ML model (P = 0.012, 1-sided Wilcoxon signed-rank test, n = 11 frequencies). More specifically, at the five intermediate frequencies (0.2–0.5 Hz), the average thresholds were significantly lower than predicted by the ML model (P = 0.016, 1-sided sign test, n = 6 subjects). In fact, the thresholds for each of the six individual subjects across (or “at each of”) these five frequencies were significantly lower than predicted by the ML model (P < 0.01 for each subject, Chi square test). Between 0.05 and 0.15 Hz the average measured thresholds had a tendency to be lower than the blue line representing the otolith threshold, but individual subjects’ thresholds did not differ significantly from the predicted thresholds (P > 0.05 for 5 subjects, Chi square test). Similarly, at 1.0, 2.0, and 5.0 Hz, the measured roll tilt threshold (purple squares) did not differ significantly from the magenta curve representing the measured roll rotation threshold (P = 0.25, 1-sided sign test, n = 6).
That the measured roll tilt thresholds were significantly lower than those predicted by a vestibular-only ML model (Fig. 4B) from 0.2 through 0.5 Hz is our primary experimental finding. We next show that two independent models, both a nondynamic ML model including somatosensory contribution and a vestibular-only dynamic Kalman filter model, can match this finding. We then show that noise correlation is an unlikely explanation.
Optimal vestibulosomatosensory integration.
To assess the contribution of somatosensory cues, we used bilateral-loss patients’ (n = 3) thresholds that were previously published by Valko et al. (2012) to estimate the vestibulosomatosensory integration thresholds (Fig. 5, green dashed line). This fit, like the Kalman filter fit in the next section, yielded predictions that closely matched the dynamic roll tilt thresholds. The RMSE between the data and the vestibule-somatosensory ML model was 0.22 for all test frequencies between 0.05 and 5 Hz. At five midfrequencies between 0.2 and 0.5 Hz, where the difference between the experimental data (purple squares in Fig. 4) and the vestibular-only standard ML model (solid purple curve in Fig. 4) is most evident, lower RMSE of 0.16 is achieved (see Table 2 for the list of RMSEs for all models).
Fig. 5.
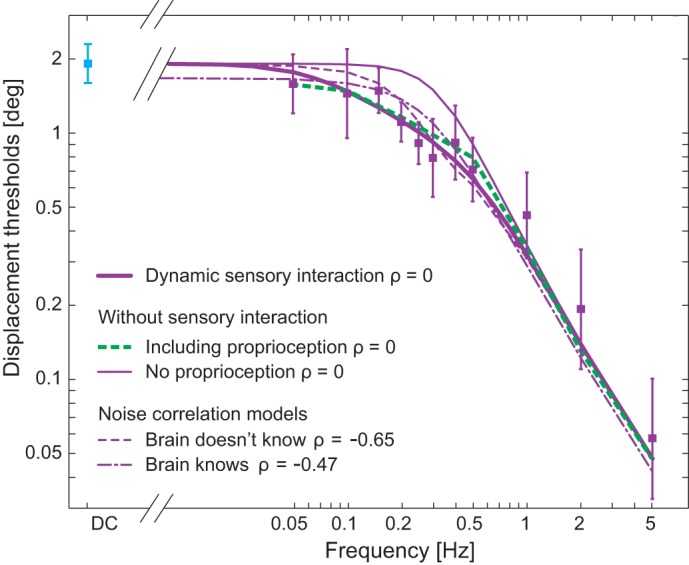
Thresholds predicted by Kalman filter and correlated noise models. Thin and thick solid purple curves show the predictions for uncorrelated noise generated by the Kalman filter ML and noninteracting Kalman filter ML models, respectively. Green dashed curve includes the contribution of somatosensation, which was estimated using roll tilt thresholds of three bilateral loss patients (Valko et al. 2012) without any sensory interaction. The dashed purple line indicates the conventional ML integration of the canal and otolith signals if the brain does not know that the noise is correlated and performs conventional ML integration assuming no correlation; the dash-dot purple line shows optimal conventional ML sensory fusion for correlated noise when the brain knows the noise correlation and determines the optimal weighting given that known noise correlation.
Table 2.
RMSEs for the model fits
| Model Category | Model Condition | RMSE0.05~5Hz | RMSE0.2~0.5Hz |
|---|---|---|---|
| Nondynamic ML model | Vestibular only | 0.24 | 0.25 |
| Vestibulosomatosensory | 0.22 | 0.16 | |
| Noise correlation ML model | Brain unaware of noise correlation | 0.21 | 0.17 |
| Brain aware of noise correlation | 0.22 | 0.17 | |
| Dynamic Kalman filter ML model | Interacting (canal-otolith) | 0.20* | 0.15* |
| Noninteracting | 0.24 | 0.25 |
RMSE, root-mean squared errors; ML, maximum likelihood. *Best RMSE values.
Kalman filter.
To determine whether our perceptual thresholds were consistent with the brain performing dynamic optimal estimation while taking into account the physical relationship of sensory organs, we made predictions using a Kalman filter (Gelb 1974; Kalman and Bucy 1961; Karmali and Merfeld 2012) combined with an ML estimator (Fig. 2 in methods). While details are presented in methods, this Kalman filter uses head angular velocity signals to reorient estimated gravity with respect to the head, mimicking the real-world kinematics that angular velocity of the head during head tilt reorients gravity with respect to the head. This internal model yields “promotion” to common units as suggested by earlier analyses (Landy et al. 1995). Because roll rotation thresholds demonstrated the influence of a high-pass filter (Fig. 4A), our model includes a perceptual high-pass filter (HPFc) with the cut-off frequency (fHPF) matching that found experimentally for the roll rotation signal (Fig. 2, top right, and in methods). Inclusion of the roll rotation and roll tilt sensory interaction pathway before threshold calculation yields model predictions (Fig. 5, thick solid purple line) that both quantitatively and qualitatively match the measured roll tilt thresholds better than when the interaction between the canal and the otolith signals is blocked in the internal model, called the “noninteracting Kalman filter ML model” (Fig. 5, thin solid purple line). In the noninteracting Kalman filter ML model, the lateral acceleration estimate is forced to zero such that ây = 0 (thick dashed path in Figs. 2 and 3). This in effect emulates the perfect resolution of tilt-translation ambiguity, blocking the sensory interaction between the tilt and translation estimates. As the result, only the ĝy contributes to the tilt perception (i.e., ), making the model prediction equivalent to the conventional ML model prediction. In fact, the noninteracting Kalman filter ML model yields thresholds (Fig. 5, thin solid line) that are indistinguishable from those predicted by the conventional ML model (Fig. 4B, thin solid purple line) for all frequencies, which serves as a check on the implementation of both models. For all frequencies between 0.05 and 5 Hz, RMSE between the data and the dynamic Kalman filter ML model was 0.20. On the other hand, the RMSE between the data and the noninteracting Kalman filter ML model was 0.24, which also equals the RMSE of the conventional nondynamic ML model fit. The fit improvement is more pronounced at the five frequencies (0.2–0.5 Hz) where the difference between the ML model predictions and data is evident. In this frequency range, the RMSE for the Kalman filter ML model was 0.15, whereas the RMSE for the noninteracting Kalman filter ML model was 0.25.
Correlated noise.
To determine whether our results could be caused by correlated noise, we also compared our results with predictions made with an ML estimator when the rotation noise and tilt noise were correlated. The following two correlated noise situations were considered: 1) when the brain does not know that the noise is correlated (Eq. 4 in methods) and tries to combine signals optimally and 2) when the brain knows and fully uses the noise correlation (Eq. 5 in methods). In Fig. 4, the dashed purple curve shows the best fit (RMSE0.05~5Hz 0.21 and RMSE0.2~0.5Hz 0.17) to the observed data when the brain does not know that the noise is correlated (correlation coefficient ρ = −0.65), and the dash-dot purple curve shows the best fit (RMSE0.05~5Hz 0.22 and RMSE0.2~0.5Hz 0.17) when the brain knows the noise correlation (ρ = −0.47). There are three notable observations regarding the correlated noise models. First, very large negative correlations, with noise correlation coefficients of −0.47 and −0.65, are required to mimic the data. Second, qualitatively, the shapes of the correlated noise curves do not match the data as well as the Kalman filter. Third, despite the correlation coefficients being selected to best fit the data, the RMSEs for the correlated noise models are higher than for the Kalman filter, which shows that providing an additional degree of freedom, a nonzero noise correlation coefficient, improves the fit but not nearly as much as the Kalman filter ML model.
DISCUSSION
We found that the thresholds measured during dynamic roll tilt were significantly lower than those predicted by a conventional ML weighting (Ernst and Banks 2002; Hillis et al. 2002) of the perception thresholds measured during roll rotation and quasistatic roll tilt. Here, we define the conventional ML weighting model as an ML estimator that does not include dynamic interaction between canal and otolith cues. On the surface, this experimental finding seems to indicate that human performance can exceed optimal performance limits provided by simple ML models that combine available vestibular cues. We consider two models that plausibly explain this performance. 1) Self-motion sensory integration includes the contribution of other sensory cues (e.g., somatosensation). 2) Canal and otolith neural integration is performed via internal models. Inclusion of other sensory cues (estimated from total bilateral loss patients’ data from Valko et. al. 2013) yielded thresholds that matched the observed dynamic roll tilt thresholds. This is consistent with the brain optimally combining canal, otolith, and somatosensory cues. Furthermore, simulations showed that a Kalman filter including dynamic sensory interaction as part of the estimation process can also match the observed human performance even without considering the somatosensory contributions. This is consistent with the brain enhancing the perceptual precision by using indirect information (knowledge of dynamic sensory interactions) and direct sensory cues. Discussion of the findings and both explanations follows.
Somatosensory contributions.
During roll tilts, additional somatosensory information becomes available that is not present in supine roll rotation. For instance, body fluid and weight shift due to gravity during roll tilts but not during supine roll rotations. Two steps were taken to investigate the somatosensory contributions. First, quasistatic thresholds were measured in two patients diagnosed with severe bilateral hypofunction although not total bilateral vestibular loss. These patients had thresholds that were about four times greater than normal. This result suggests that the vestibular system provides roll tilt information with a higher signal-to-noise ratio than all other information sources combined. The quasistatic tilt thresholds we measured in patients (4.00 and 6.42°) are also consistent with those measured in patients (average 4.4°) using a time-to-detect task (Mann 1951). At the same time, the quasistatic thresholds we measured in normal subjects (1.91°) are lower than when using their time-to-detect task (5.1°) (Bringoux et al. 2002). This difference is probably task dependent, since normal subjects performing time-to-detect tasks can (and often do) wait until they are confident before responding. To avoid such criterion issues, we performed a forced-choice direction-recognition task in which subjects responded after each trial.
Second, the somatosensory contributions during dynamic motions to dynamic roll tilt motion thresholds were estimated using thresholds published by Valko et. al. (2012) for three total vestibular loss patients. These studies were conducted on the same motion device and chair and used the same direction-recognition task. Valko and colleagues reported patient performance that was between 1.5 and 3 times worse than normal depending on frequency. This is roughly consistent with our finding in the two patients diagnosed with bilateral hypofunction included herein.
All of these patients (3 total bilateral loss patients and 2 bilateral hypofunction patients) suffered from vestibular loss symptoms for no less than two years. Because such chronic exposure to vestibular dysfunction provided them an extended opportunity to adapt and compensate for the vestibular loss, it is reasonable to suggest (and can certainly be argued) that the predicted thresholds estimated using the patient data provide an upper limit of the contribution of somatosensation to dynamic roll tilt perception in normal human subjects. While the patient data provide insights to somatosensory contributions, the number of patient subjects is not sufficient to separate somatosensory cues from vestibular cues, with which a vestibular-only model can be developed and tested. A future study focused on decoupling somatosensory and vestibular contribution is further discussed in the next subsection.
Kalman filter.
We found that the Kalman filter estimate of gravitoinertial force ( in Figs. 2 and 3) matched our tilt threshold data better than either of the Kalman filter estimates of gravity or linear acceleration alone. For instance, whereas it was shown that the low-frequency tilt threshold converges toward the gravity-cue only (quasistatic) threshold, it was also shown that the gravity cue is not sufficient to explain the midfrequency data. On the other hand, because the linear acceleration approaches zero, bringing the tilt threshold toward zero with decreasing frequency, the assumption of the linear acceleration cue being the sole contributor does not match the data. Altogether, this implies that the brain may not perfectly resolve tilt-translation ambiguity, which is consistent with earlier findings in tilt perception and modeling studies (Merfeld et al. 2005a). These studies reported that gradual low-frequency GIF changes are more likely to be interpreted as tilt, whereas rapid high-frequency GIF changes are more likely to be interpreted as translation when subjects know that motion includes both translation and tilt. In fact, during roll tilt experiments, we explicitly informed all subjects that all motion stimuli were roll tilts with no translation. Consistent with an earlier study showing that cognition can influence tilt/translation processing (Wertheim et al. 2001), this cognitive knowledge could have influenced the subjects to learn to attribute all pertinent signals as tilt.
Second, we found that the internal model generally overestimates the translational component of tilt motion at higher frequency. Such overestimation of translation increases the overall GIF estimate, which improves the signal-to-noise ratio. Inversely, this is equivalent to reduction of noise-to-signal ratio or, i.e., improved precision, resulting in lower thresholds. More importantly, the model predicts a nonzero estimate even when the actual translation is near zero during dynamic tilt (Fig. 6; see appendix c for further discussion). Based on the model simulations, we attribute this phenomenon to relatively greater weighting of the translational pathway (marked with ây in Figs. 2 and 3) relative to the tilt pathway (marked with ĝy in Figs. 2 and 3). A high translation-to-tilt gain ratio accentuates the dynamic component (e.g., single-cycle acceleration) over the static component (e.g., final tilt position) at higher frequency (Fig. 6A). This is consistent with the earlier finding that the nervous system can generate an illusory translation estimate in response to postrotatory tilts (Merfeld et al. 1999). Moreover, this is also consistent with more recent neural recordings from the cerebellar neurons coding tilt and translation that show increased translational weighting during prolonged dynamic off-vertical rotation (Laurens et al. 2013). Additional experiments with dynamic linear translation may verify these simulation results. However, there is a confound that the inertial force gradient in linear motions is different from tilt motions. For instance, the inertial force in linear translations is constant across head to toe, whereas it is greater in the toes and near zero in the head for the head-centered roll tilts. Considering that canal-otolith integration does not match optimal sensory integration in altered gravity-gradient via eccentric rotation (Soyka et al. 2015), such additional experiment necessitates other control studies that decouple vestibular and nonvestibular cues in linear translation motions. Along with deeper scrutinization of the somatosensory contribution and its accompanying models, sensory integration of dynamic translation and rotation would be meaningful to be investigated in a future study.
Although the underlying mechanisms that lead to the otolith gain ratio () required to fit the data are unclear and need further verification, it may be clinically relevant for understanding vestibular migraine (VM). Earlier studies of VM patients showed dynamic roll tilt thresholds at 0.1 Hz that were significantly lower than in a normal population (Lewis et al. 2011). Our Kalman filter ML model suggests that such frequency-selective lowering of thresholds can be generated when , which may be interpreted as a dysfunctional sensory interaction in the central circuitry. In short, our model predicts that the multisensory perceptual sensitivity is modulated by the ratio of the internal model gains, both in normal and pathological populations. This is consistent with earlier behavioral findings that canal and otolith inputs are combined centrally (Angelaki et al. 1999; Merfeld et al. 2005b, 1999). Although nonlinearities have been observed in central vestibular pathways (Massot et al. 2012, Newlands and Wei 2013, Newlands et al. 2014), we minimized these contributions by using very small (near-threshold) stimuli and never mixing low- and high-frequency stimuli.
Our model shares some characteristics of an earlier threshold model (Zupan and Merfeld 2008). For example, we showed that our noninteracting Kalman filter ML model, which requires eliminating all sensory interactions, is equivalent to the conventional ML threshold model. However, the earlier model included sensory fusion only after the perception formation; this contrasts with our finding that dynamic sensory interaction before perception formation is essential to explain frequency-selective enhancement of perceptual precision within the context of the internal model.
Correlated noise.
Noise correlation models, as in Eqs. 4 and 5, predict that a negative noise correlation is required to lower thresholds to match experimental results (Fig. 5). Any positive noise correlation yielded increased threshold predictions, which is inconsistent with our results. To approach our data, the correlation between the angular velocity noise and the tilt noise needed to be about −0.65 if the brain ignored the correlation and −0.47 if the brain took the correlation into account. Such high noise correlations for separate vestibular neuron populations have not been reported. In fact, consistent with other sensory systems, fairly small average noise correlations (~0.05) have been reported for pairs of neurons carrying vestibular signals related to perceptual thresholds in MSTd (Gu et al. 2010). Several papers have noted that small correlations between individual neurons can theoretically lead to large effects in a single population of many neurons (Averbeck et al. 2006; Zohary et al. 1994). This may prove to be true, but we are considering something different, that two separate populations of neurons, one representing tilt and one representing angular velocity, have strongly correlated noise.
In the Kalman filter model, such strong noise correlations can be simulated by setting either process or measurement noise to have a perfect correlation (ρ = 1) between the canal and otolith pathways. Positively correlated (ρ = 1) process noise while keeping measurement noise uncorrelated (ρ = 0) yielded almost negligible negative correlation between the tilt and the rotation perception signals (P = −0.01). This shows that the canal-otolith interaction included in the Kalman filter model does not structurally yield correlated noise. Of course, positively correlated (ρ = 1) measurement noise yielded substantial positive correlation in the perceptual signal noise (ρ = 0.96). This suggests that the two peripheral afferent populations would need to have large negative measurement noise correlations (ρ approximately −0.6) for peripheral noise correlations to cause large correlations in perceptual signals. We are not aware of any directly relevant data suggesting that any vestibular signals demonstrate such large negative noise correlations, let alone different neural populations (e.g., otolith and canal afferents).
It is also possible that noise correlation can be combined with the Kalman filter model. Simulations showed that positive noise correlations of ρ = 0.17 and ρ = 0.25 for the brain not knowing and knowing the noise correlation, respectively, yield the optimal fit to the data, but the fit improvement is minimal. In both cases, RMSE is 0.20°, the same as the dynamic model with ρ = 0. This indicates that adding a large noise correlation minimally improves the fit. Therefore, while correlated noise could, in theory, explain our threshold data, our data do not strongly support this explanation, especially when dynamic internal models (e.g., observers, Kalman filters), using neural mechanisms already shown to influence such vestibular processing (Angelaki et al. 1999; Merfeld et al. 1999), can explain the data with one fewer degree of freedom.
Tilt dynamics.
We found empirically that the thresholds at the lowest frequencies tested (0.05 and 0.1 Hz) did not differ significantly from the quasistatic otolith threshold. This is reasonable because the maximum gravitational shear force transduced by the otolith organs occurs at the end of the motion trajectory. Hence, the final steady-state gravitational cue is independent of the motion frequency used to reach a given tilt angle (Fig. 1, row on bottom). Also, recent analyses showed that both regular and irregular otolith afferent thresholds are constant over this frequency range (Jamali et al. 2013). Combining these two observations directly corroborates our assumption that otolith thresholds in isolation for our roll tilt paradigm are constant over the frequency range tested.
It has been shown that both vestibular perception and direction-recognition thresholds match predictions made by internal models (Glasauer 1992; Merfeld et al. 2005a, 2005b; Zupan and Merfeld 2008); hence, otolith afferent sensitivity can contribute to perception through such internal models. Therefore, we investigated if adding a lead operator, previously used to model high-frequency otolith regular afferent dynamics (Fernández and Goldberg 1976), to our noninteracting Kalman filter ML model contributes to the threshold reduction we observed as frequency increased. For our noninteracting Kalman filter ML model, the regular afferent dynamics had almost no impact (RMSE0.05~5Hz = 0.24) relative to using a constant-gain otolith model as described earlier (RMSE0.05~5Hz also equals 0.24). On the other hand, for our dynamic Kalman filter ML model, the regular afferent dynamics lowered thresholds in the midfrequency range. These results are consistent with our conclusion that the dynamic sensory interaction is necessary to match the reduced thresholds between 0.2 and 0.5 Hz. Furthermore, these results also demonstrate the flexibility of the Kalman filter model that naturally takes peripheral dynamics into account. This in turn maximizes the precision of the internal signals while eliminating the need for separate parallel pathways (Orban de Xivry et al. 2013).
High-pass dynamics in perception.
Although not the primary focus of this paper, we found roll rotation thresholds that decreased substantially, by a factor of four between 0.1 and 1 Hz, as frequency increased, which is consistent with earlier yaw rotation threshold reports (Grabherr et al. 2008; Lim and Merfeld 2012; Valko et al. 2012). Such frequency effects would occur if the signal decreased substantially and/or the noise increased substantially as frequency decreased. For small threshold-level stimuli, changes in peripheral (Goldberg and Fernandez 1971) and central spike rates and spike variability (Sadeghi et al. 2007) are small. Coupled with this, the push/pull inhibitory/excitatory balance of canal responses would tend to yield no average change in spike rate for small threshold-level rotations and, hence, no variability change that might be associated with changes in average spike rate. More directly, VOR thresholds actually decrease slightly at lower frequencies (Haburcakova et al. 2012). None of these facts are consistent with the hypothesis that vestibular noise increases substantially for lower stimulus frequencies.
We therefore suggest that the rotation signals, already high-pass filtered by the semicircular canal mechanics (Goldberg et al. 2012), might be further high-pass filtered as part of the decision-making processes (Merfeld et al. 2015). Such dynamic effects have previously been reported in the threshold literature. For transient self-motion stimuli, like bell-shaped yaw angular velocity (Benson et al. 1989; Grabherr et al. 2008; Soyka et al. 2012; Valko et al. 2012) or linear velocity (Benson et al. 1986; Valko et al. 2012) trajectories, thresholds increase as frequency decreases below 0.5 Hz. This has been modeled via dynamic elements that high-pass filter the perceptual velocity signal with a time constant <1 s (Lim and Merfeld 2012; Soyka et al. 2012). This high-pass filtering hypothesis is also consistent with recently reported vestibular aftereffect data where a lingering effect from a stimulus impacts the response to a subsequent stimulus (Crane 2012). These aftereffects were also modeled with time constants of ~1 s (Coniglio and Crane 2014). Although our supine roll rotation threshold data (Fig. 4A) do not prove the contributions of such a high-pass filter to decision-making, they are empirically consistent with such filtering. Similar phasic characteristics have been recorded in locus coeruleus neurons (Aston-Jones and Cohen 2005) associated with task-related decision processes, not unlike the direction-recognition decision processes required for our task, but could also arise anywhere along human vestibulocortical projections (e.g, thalamus, cortex).
As for the otolith signals, it is not straightforward to see how the otolith signals indicating tilt might similarly be processed using a high-pass filter (i.e., as discussed earlier for the roll rotation thresholds). On first consideration, this may even appear nonsensical, since it seems to suggest an inability to determine static tilt direction, which conflicts with our data (not to mention personal experience). However, it is important to remember that, in contrast to the transient motion signals described above for roll rotation, afferent signals from the otolith organs were maintained until after the decision was made in our paradigm. Decision-making never took more than a few seconds, so so-called peripheral adaptation effects, having time constants in the order of 100 s (Goldberg et al. 2012), would have little impact. For such sustained signals, it has been reported that the brain accumulates information until the decision is made (Gold and Shadlen 2007), but limits to this evidence accumulation have been noted (Ratcliff 2006). Evidence accumulation has been modeled (Cain et al. 2013) as an integration process (i.e, , where e(t) represents the evidence being accumulated). Integration combined with a decisionmaking high-pass filter like those described above yields a low-pass filter. In fact, consistent with this hypothesized low-pass filter, several studies (Hintzman and Curran 1997; Reed 1973) have shown that evidence accumulation can be dynamically modeled as an exponential function (1 − e−t/τ), which is the step response of a low-pass filter. The time constant for this evidence accumulation is ~0.5 s, roughly the same as the time constants reported above for transient stimuli. For a more extended discussion of decision-making dynamics, see our recent review (Merfeld et al. 2015).
If the otolith evidence accumulation for tilt decision-making is impacted by such hypothetical low-pass filtering (i.e., leaky integration) or even pure accumulation (i.e., integration), it would yield tilt thresholds that increase with increasing frequency because the signal passed by the low-pass filter would be attenuated at higher frequencies. Hence, the combined canal and otolith thresholds predicted by a conventional ML model (shown to be equivalent to our simulated noninteracting Kalman filter ML model) would be higher at midfrequencies, not lower as observed experimentally. In the end, any such low-pass dynamics would therefore increase the level of statistical significance of our primary finding that human performance exceeds the optimal predictions of noninteracting models.
GRANTS
This work was supported by NIH/NIDCD Grants R01-DC-04158 (to K. Lim, F. Karmali, and D. M. Merfeld) and R01-DC-014924 (to D. M. Merfeld). KN was supported by the Swiss National Science Foundation and Swiss Foundation for Grants in Biology and Medicine.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
K.L. and K.N. performed experiments; K.L. and F.K. analyzed data; K.L. and D.M.M. interpreted results of experiments; K.L. prepared figures; K.L. and D.M.M. drafted manuscript; K.L., F.K., and D.M.M. edited and revised manuscript; K.L., F.K., K.N., and D.M.M. approved final version of manuscript.
ACKNOWLEDGMENTS
We thank our subjects for their time and assistance. We thank Drs. R. Lewis and A. Priesol for help recruiting patients and Dr. A. Natapoff for statistical guidance. We thank Drs. R. A. Eatock, R. Lewis, F. Mast, M. Shelhamer, S. Wood, and C. M. Oman for comments on preliminary drafts.
appendix a
Minimum variance unbiased estimator: Uncorrelated noise.
The following derivation follows the minimum variance unbiased (MVU) derivation in chapter one of Gelb (1974). We assume two neural signals (z1, z2) representative of roll tilt. Each of these two tilt signals is the sum of a representation of the actual tilt (x) and noise: z1 = x + v1 and z2 = x + v2. We assume that the noises are random, unbiased (), and uncorrelated (), where E represents the expected value operator. It is worth noting that, if the noise includes bias, one can define this bias as part of the signal, so this assumption is not restrictive. (Furthermore, our data show thresholds below those predicted by the MVU estimator, while any such bias would lead to increased thresholds.) The variances are defined as and .
Because our task is direction recognition, we are interested in combining z1 and z2 to determine the sign of the tilt. We define a scalar variable to be the scaled sum of z1 and z2: , where and are scalar constants. We define the estimation error as . We desire an unbiased estimator, which means that the expected value of the estimation error must be zero: , which yields the relationship k2 = 1 − k1.
Combining the above equations, we can calculate the variance of the estimator as . To determine the value of that minimizes the variance, we differentiate with respect to and set the resulting equation equal to zero: , which yields and Therefore, the MVU estimator for tilt is:
| (A1) |
Substituting, we can now find our tilt estimation error,
| (A2) |
Therefore, the variance for the combined signals is,
| (A3) |
Thresholds are linearly proportional to the SD of the noise (), which can be substituted into the variance equation. This yields an equation that relates the threshold for the combined signals to the thresholds for the individual signals:
| (A4) |
The above results for combined variance (Eq. A3) and threshold (Eq. A4) exactly match the ML calculations for similar problems (Ernst and Banks 2002), but this MVU derivation does not assume Gaussian noise. For context, a few additional words regarding MVU and ML estimators are warranted. MVU estimators cannot always be found and may not exist. For this relatively simple problem, we derived an MVU estimator, which proves its existence. When an MVU estimator does not exist or cannot be found, ML estimators are usually implemented, since ML estimators, which are asymptotically optimal, can be found via “turn-the-crank” procedures. In summary, the two approaches yield the minimum variance unbiased estimator for this particular problem, which explains the identical answers. The MVU approach is somewhat more powerful, since the MVU estimator does not require Gaussian noise. See Ernst and Banks (2002) for a clear derivation and description of the ML estimator for a similar problem. See Kay (1993) for more details regarding MVU and ML estimators.
MVU estimator: Correlated noise.
We now show similar calculations for when the noises are correlated (E[v1,v2] = ρσ1σ2), where ρ is the correlation coefficient. We first assume that the brain does not realize that the noise is correlated; this means that we only need to recalculate the variance and thresholds when the signals are combined. Starting with Eq. A1 and substituting as shown in Eqs. A2 and A3 but now using E[v1,v2] = ρσ1σ2, we find that the variance of this estimator with correlated noise is:
| (A5) |
As above, the relationship between the thresholds can then be written:
| (A6) |
For the second approach with correlated noise, we assume that the noises are correlated and that the brain knows this correlation and takes it into account. Taking the same approach outlined above, Gelb (1974) reports that the variance of this MVU estimator is:
| (A7) |
As above, the relationship between the thresholds can then be written:
| (A8) |
Note that with ρ = 0, Eqs. A5 through A8 reduce to Eqs. A3 and A4, respectively.
appendix b
Kalman filter model.
Equations 7 and 8 in methods can be rearranged in standard differential state-space form
| (B1) |
where x(t) is the time-varying state vector, d(t) is the time-varying input vector, and y(t) is the time-varying output vector. A, B, and C are matrexes that define the system dynamics. To assist with the derivation of a state-space representation, Eqs. 7 and 8 are first expanded:
| (B2a) |
| (B2b) |
where dc = ωx + wc, and do = gy − (ay + way). Here wc and way are process noise associated with roll rotation and lateral translation, respectively, and ay (= 0 for roll tilt) is lateral acceleration that contributes to the total gravitoinertial force (GIF) that the otolith organs sense. Substituting for yc and for yo yields
| (B3a) |
| (B2b) |
Differentiating Eq. 6 yields:
| (B3c) |
To arrange Eqs. B3a, B3b, and B3c into state-space form, let x1 = xc, , x3 = gy, and x4 = xo. Then,
| (B4a) |
| (B4b) |
Rearranging Eqs. B4a and B4b into state-space form as in Eq. B1 yields,
| (B5a) |
| (B5b) |
where From Eqs. B5a and B5b, matrixes A, B, and C can be defined as
In state-space form, the estimated state vector is
| (B6) |
where , and K is a 4 × 2 matrix containing the Kalman gains, in which Kω = K21, Kfω = gzK22, Kf = K32, and Ka = −K42. Solving the steady-state Riccati equation yields the Kalman gain matrix. To solve for the steady-state Kalman gain, the MATLAB function care (AT, CT, BQBT, R) was used. Q and R are covariance matrixes of the process and measurement noise such that , and , where the noise is assumed to be normally distributed with zero mean. Note that the rotation noise found in the semicircular canal pathway is not correlated with the lateral acceleration noise found in the otolith pathway.
appendix c
To more specifically observe how Kalman gains affect sensory interactions, the gains gating the sensory interactions [K22(Kfω), K31(gzKω), K32(Kf), and K42(Ka)] were sequentially set to zero, and the internal estimates were observed. Eliminating the otolith-to-canal contribution (K22 = 0) had no impact on the internal estimates for frequencies greater than 0.05 Hz (data not shown). On the other hand, eliminating other sensory interactions had substantial effects on the estimated GIF (), particularly on the estimated linear acceleration () as can be seen in Fig. 6, B, C, and D. Specifically, it can be seen from Fig. 6C that K31 plays a substantial role in interpreting the otolithic cue. In other words, because of the large translational gain (Ka), a greater portion of otolith input can be interpreted as translation without the assistance of the canal input. This leads to grossly overestimated as shown by purple in Fig. 6A. Also, the Kalman filter allows a separate gain adjustment of K31, therefore achieving a more accurate tilt estimate (ĝy, dotted blue curve matching the input in black). In addition to K31, ĝy is also driven by the otolith error signal through Kf. Figure 6D shows the internal estimates when Kf is manipulated to zero, which generates greater ây From this manipulation, it can be inferred that allowing a portion of the otolith signal to be interpreted as tilt also has a suppressive effect on ây.
REFERENCES
- Angelaki DE, Klier EM, Snyder LH. A vestibular sensation: probabilistic approaches to spatial perception. Neuron 64: 448–461, 2009. doi: 10.1016/j.neuron.2009.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Angelaki DE, McHenry MQ, Dickman JD, Newlands SD, Hess BJ. Computation of inertial motion: neural strategies to resolve ambiguous otolith information. J Neurosci 19: 316–327, 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aston-Jones G, Cohen JD. An integrative theory of locus coeruleus-norepinephrine function: adaptive gain and optimal performance. Annu Rev Neurosci 28: 403–450, 2005. doi: 10.1146/annurev.neuro.28.061604.135709. [DOI] [PubMed] [Google Scholar]
- Averbeck BB, Latham PE, Pouget A. Neural correlations, population coding and computation. Nat Rev Neurosci 7: 358–366, 2006. doi: 10.1038/nrn1888. [DOI] [PubMed] [Google Scholar]
- Bauby CE, Kuo AD. Active control of lateral balance in human walking. J Biomech 33: 1433–1440, 2000. doi: 10.1016/S0021-9290(00)00101-9. [DOI] [PubMed] [Google Scholar]
- Benson AJ, Hutt EC, Brown SF. Thresholds for the perception of whole body angular movement about a vertical axis. Aviat Space Environ Med 60: 205–213, 1989. [PubMed] [Google Scholar]
- Benson AJ, Spencer MB, Stott JR. Thresholds for the detection of the direction of whole-body, linear movement in the horizontal plane. Aviat Space Environ Med 57: 1088–1096, 1986. [PubMed] [Google Scholar]
- Bringoux L, Schmerber S, Nougier V, Dumas G, Barraud PA, Raphel C. Perception of slow pitch and roll body tilts in bilateral labyrinthine-defective subjects. Neuropsychologia 40: 367–372, 2002. doi: 10.1016/S0028-3932(01)00103-8. [DOI] [PubMed] [Google Scholar]
- Butler JS, Smith ST, Campos JL, Bülthoff HH. Bayesian integration of visual and vestibular signals for heading. J Vis 10: 23, 2010. doi: 10.1167/10.11.23. [DOI] [PubMed] [Google Scholar]
- Cain N, Barreiro AK, Shadlen M, Shea-Brown E. Neural integrators for decision making: a favorable tradeoff between robustness and sensitivity. J Neurophysiol 109: 2542–2559, 2013. doi: 10.1152/jn.00976.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carriot J, Jamali M, Brooks JX, Cullen KE. Integration of canal and otolith inputs by central vestibular neurons is subadditive for both active and passive self-motion: implication for perception. J Neurosci 35: 3555–3565, 2015. doi: 10.1523/JNEUROSCI.3540-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaudhuri SE, Karmali F, Merfeld DM. Whole body motion-detection tasks can yield much lower thresholds than direction-recognition tasks: implications for the role of vibration. J Neurophysiol 110: 2764–2772, 2013. doi: 10.1152/jn.00091.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaudhuri SE, Merfeld DM. Signal detection theory and vestibular perception: III. Estimating unbiased fit parameters for psychometric functions. Exp Brain Res 225: 133–146, 2013. doi: 10.1007/s00221-012-3354-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coniglio AJ, Crane BT. Human yaw rotation aftereffects with brief duration rotations are inconsistent with velocity storage. J Assoc Res Otolaryngol 15: 305–317, 2014. doi: 10.1007/s10162-013-0438-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crane BT. Roll aftereffects: influence of tilt and inter-stimulus interval. Exp Brain Res 223: 89–98, 2012. doi: 10.1007/s00221-012-3243-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dimitri PS, Wall C III, Rauch SD. Multivariate vestibular testing: laterality of unilateral Ménière’s disease. J Vestib Res 11: 405–412, 2001-2002. [PubMed] [Google Scholar]
- Dobson AJ, Barnett A. An Introduction to Generalized Linear Models. Boca Raton, FL: CRC, 2011. [Google Scholar]
- Ernst MO, Banks MS. Humans integrate visual and haptic information in a statistically optimal fashion. Nature 415: 429–433, 2002. doi: 10.1038/415429a. [DOI] [PubMed] [Google Scholar]
- Fernandez C, Goldberg JM. Physiology of peripheral neurons innervating semicircular canals of the squirrel monkey. II. Response to sinusoidal stimulation and dynamics of peripheral vestibular system. J Neurophysiol 34: 661–675, 1971. [DOI] [PubMed] [Google Scholar]
- Fernández C, Goldberg JM. Physiology of peripheral neurons innervating otolith organs of the squirrel monkey. III. Response dynamics. J Neurophysiol 39: 996–1008, 1976. [DOI] [PubMed] [Google Scholar]
- Fetsch CR, Deangelis GC, Angelaki DE. Visual-vestibular cue integration for heading perception: applications of optimal cue integration theory. Eur J Neurosci 31: 1721–1729, 2010. doi: 10.1111/j.1460-9568.2010.07207.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelb A. Applied Optimal Estimation. Cambridge, MA: MIT, 1974. [Google Scholar]
- Glasauer S. Interaction of semicircular canals and otoliths in the processing structure of the subjective zenith. Ann N Y Acad Sci 656: 847–849, 1992. doi: 10.1111/j.1749-6632.1992.tb25272.x. [DOI] [PubMed] [Google Scholar]
- Gold JI, Shadlen MN. The neural basis of decision making. Annu Rev Neurosci 30: 535–574, 2007. doi: 10.1146/annurev.neuro.29.051605.113038. [DOI] [PubMed] [Google Scholar]
- Goldberg JM, Fernandez C. Physiology of peripheral neurons innervating semicircular canals of the squirrel monkey. I. Resting discharge and response to constant angular accelerations. J Neurophysiol 34: 635–660, 1971. [DOI] [PubMed] [Google Scholar]
- Goldberg JM, Wilson VJ, Cullen KE, Angelaki DE, Broussard DM, Buttner-Ennever J, Fukushima K, Minor LB. The Vestibular System: A Sixth Sense. Oxford, UK: Oxford Scholarship Online, 2012. doi: 10.1093/acprof:oso/9780195167085.001.0001. [DOI] [Google Scholar]
- Grabherr L, Nicoucar K, Mast FW, Merfeld DM. Vestibular thresholds for yaw rotation about an earth-vertical axis as a function of frequency. Exp Brain Res 186: 677–681, 2008. doi: 10.1007/s00221-008-1350-8. [DOI] [PubMed] [Google Scholar]
- Green DM, Swets JA. Signal Detection Theory and Psychophysics. New York, NY: Wiley, 1966, p. xi. [Google Scholar]
- Gu Y, Fetsch CR, Adeyemo B, Deangelis GC, Angelaki DE. Decoding of MSTd population activity accounts for variations in the precision of heading perception. Neuron 66: 596–609, 2010. doi: 10.1016/j.neuron.2010.04.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haburcakova C, Lewis RF, Merfeld DM. Frequency dependence of vestibuloocular reflex thresholds. J Neurophysiol 107: 973–983, 2012. doi: 10.1152/jn.00451.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hillis JM, Ernst MO, Banks MS, Landy MS. Combining sensory information: mandatory fusion within, but not between, senses. Science 298: 1627–1630, 2002. doi: 10.1126/science.1075396. [DOI] [PubMed] [Google Scholar]
- Hintzman DL, Curran T. Comparing retrieval dynamics in recognition memory and lexical decision. J Exp Psychol Gen 126: 228–247, 1997. doi: 10.1037/0096-3445.126.3.228. [DOI] [Google Scholar]
- Jamali M, Carriot J, Chacron MJ, Cullen KE. Strong correlations between sensitivity and variability give rise to constant discrimination thresholds across the otolith afferent population. J Neurosci 33: 11302–11313, 2013. doi: 10.1523/JNEUROSCI.0459-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalman RE, Bucy RS. New results in linear filtering and prediction theory. J Fluids Eng 83: 95–108, 1961. [Google Scholar]
- Karmali F, Lim K, Merfeld DM. Visual and vestibular perceptual thresholds each demonstrate better precision at specific frequencies and also exhibit optimal integration. J Neurophysiol 111: 2393–2403, 2014. doi: 10.1152/jn.00332.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karmali F, Merfeld DM. A distributed, dynamic, parallel computational model: the role of noise in velocity storage. J Neurophysiol 108: 390–405, 2012. doi: 10.1152/jn.00883.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kay SM. Fundamentals of Statistical Signal Processing: Estimation Theory. Upper Saddle River, NJ: Prentice Hall, 1993, p. 625. [Google Scholar]
- Lacquaniti F, Bosco G, Gravano S, Indovina I, La Scaleia B, Maffei V, Zago M. Multisensory integration and internal models for sensing gravity effects in primates. BioMed Res Int 2014: 615854, 2014. doi: 10.1155/2014/615854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landy MS, Maloney LT, Johnston EB, Young M. Measurement and modeling of depth cue combination: in defense of weak fusion. Vision Res 35: 389–412, 1995. doi: 10.1016/0042-6989(94)00176-M. [DOI] [PubMed] [Google Scholar]
- Laurens J, Meng H, Angelaki DE. Neural representation of orientation relative to gravity in the macaque cerebellum. Neuron 80: 1508–1518, 2013. doi: 10.1016/j.neuron.2013.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leek MR. Adaptive procedures in psychophysical research. Percept Psychophys 63: 1279–1292, 2001. doi: 10.3758/BF03194543. [DOI] [PubMed] [Google Scholar]
- Lewis RF, Priesol AJ, Nicoucar K, Lim K, Merfeld DM. Abnormal motion perception in vestibular migraine. Laryngoscope 121: 1124–1125, 2011. doi: 10.1002/lary.21723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lim K, Merfeld DM. Signal detection theory and vestibular perception: II. Fitting perceptual thresholds as a function of frequency. Exp Brain Res 222: 303–320, 2012. doi: 10.1007/s00221-012-3217-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macmillan NA, Creelman CD. Detection Theory: A User’s Guide. Mahwah, NJ: Lawrence Erlbaum Associates, 2005, p. xix. [Google Scholar]
- MacNeilage PR, Ganesan N, Angelaki DE. Computational approaches to spatial orientation: from transfer functions to dynamic Bayesian inference. J Neurophysiol 100: 2981–2996, 2008. doi: 10.1152/jn.90677.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mann CW. The effects of auditory-vestibular nerve pathology on space perception. J Exp Psychol 42: 450–456, 1951. doi: 10.1037/h0060080. [DOI] [PubMed] [Google Scholar]
- Merfeld DM. Signal detection theory and vestibular thresholds: I. Basic theory and practical considerations. Exp Brain Res 210: 389–405, 2011. doi: 10.1007/s00221-011-2557-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merfeld DM, Clark TK, Lu YM, Karmali F. Dynamics of individual perceptual decisions. J Neurophysiol 115: 39-59, 2016. doi: 10.1152/jn.00225.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merfeld DM, Park S, Gianna-Poulin C, Black FO, Wood S. Vestibular perception and action employ qualitatively different mechanisms. I. Frequency response of VOR and perceptual responses during Translation and Tilt. J Neurophysiol 94: 186–198, 2005a. doi: 10.1152/jn.00904.2004. [DOI] [PubMed] [Google Scholar]
- Merfeld DM, Park S, Gianna-Poulin C, Black FO, Wood S. Vestibular perception and action employ qualitatively different mechanisms. II. VOR and perceptual responses during combined Tilt&Translation. J Neurophysiol 94: 199–205, 2005b. doi: 10.1152/jn.00905.2004. [DOI] [PubMed] [Google Scholar]
- Merfeld DM, Young LR, Oman CM, Shelhamer MJ. A multidimensional model of the effect of gravity on the spatial orientation of the monkey. J Vestib Res 3: 141–161, 1993a. [PubMed] [Google Scholar]
- Merfeld DM, Young LR, Paige GD, Tomko DL. Three dimensional eye movements of squirrel monkeys following postrotatory tilt. J Vestib Res 3: 123–139, 1993b. [PubMed] [Google Scholar]
- Merfeld DM, Zupan L, Peterka RJ. Humans use internal models to estimate gravity and linear acceleration. Nature 398: 615–618, 1999. doi: 10.1038/19303. [DOI] [PubMed] [Google Scholar]
- Orban de Xivry JJ, Coppe S, Blohm G, Lefèvre P. Kalman filtering naturally accounts for visually guided and predictive smooth pursuit dynamics. J Neurosci 33: 17301–17313, 2013. doi: 10.1523/JNEUROSCI.2321-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R. Modeling response signal and response time data. Cognit Psychol 53: 195–237, 2006. doi: 10.1016/j.cogpsych.2005.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reed AV. Speed-accuracy trade-off in recognition memory. Science 181: 574–576, 1973. doi: 10.1126/science.181.4099.574. [DOI] [PubMed] [Google Scholar]
- Sadeghi SG, Chacron MJ, Taylor MC, Cullen KE. Neural variability, detection thresholds, and information transmission in the vestibular system. J Neurosci 27: 771–781, 2007. doi: 10.1523/JNEUROSCI.4690-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selva P, Oman CM. Relationships between observer and Kalman Filter models for human dynamic spatial orientation. J Vestib Res 22: 69–80, 2012. doi: 10.3233/VES-2012-0451. [DOI] [PubMed] [Google Scholar]
- Soyka F, Barnett-Cowan M, Robuffo Giordano P, Bülthoff H. Integration of Translational and Rotational Vestibular Cues for Direction Detection during Eccentric Rotations. In: 12th Conference of Junior Neuroscientists of Tübingen (NeNA 2011). Tübingen, Germany, 2011. [Google Scholar]
- Soyka F, Bülthoff HH, Barnett-Cowan M. Integration of Semi-Circular Canal and Otolith Cues for Direction Discrimination during Eccentric Rotations. PLoS One 10: e0136925, 2015. doi: 10.1371/journal.pone.0136925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soyka F, Giordano PR, Barnett-Cowan M, Bülthoff HH. Modeling direction discrimination thresholds for yaw rotations around an earth-vertical axis for arbitrary motion profiles. Exp Brain Res 220: 89–99, 2012. doi: 10.1007/s00221-012-3120-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valko Y, Lewis RF, Priesol AJ, Merfeld DM. Vestibular labyrinth contributions to human whole-body motion discrimination. J Neurosci 32: 13537–13542, 2012. doi: 10.1523/JNEUROSCI.2157-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wertheim AH, Mesland BS, Bles W. Cognitive suppression of tilt sensations during linear horizontal self-motion in the dark. Perception 30: 733–741, 2001. doi: 10.1068/p3092. [DOI] [PubMed] [Google Scholar]
- Wichmann FA, Hill NJ. The psychometric function: II. Bootstrap-based confidence intervals and sampling. Percept Psychophys 63: 1314–1329, 2001. doi: 10.3758/BF03194545. [DOI] [PubMed] [Google Scholar]
- Yu XJ, Dickman JD, Angelaki DE. Detection thresholds of macaque otolith afferents. J Neurosci 32: 8306–8316, 2012. doi: 10.1523/JNEUROSCI.1067-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zohary E, Shadlen MN, Newsome WT. Correlated neuronal discharge rate and its implications for psychophysical performance. Nature 370: 140–143, 1994. doi: 10.1038/370140a0. [DOI] [PubMed] [Google Scholar]
- Zupan LH, Merfeld DM. Interaural self-motion linear velocity thresholds are shifted by roll vection. Exp Brain Res 191: 505–511, 2008. doi: 10.1007/s00221-008-1540-4. [DOI] [PMC free article] [PubMed] [Google Scholar]