NMR Assignments of Sparsely Labeled Proteins Using a Genetic Algorithm

Abstract

Sparse isotopic labeling of proteins for NMR studies using single types of amino acid (¹⁵N or ¹³C enriched) has several advantages. Resolution is enhanced by reducing numbers of resonances for large proteins, and isotopic labeling becomes economically feasible for glycoproteins that must be expressed in mammalian cells. However, without access to the traditional triple resonance strategies that require uniform isotopic labeling, NMR assignment of crosspeaks in heteronuclear single quantum coherence (HSQC) spectra is challenging. We present an alternative strategy which combines readily accessible NMR data with known protein domain structures. Based on the structures, chemical shifts are predicted, NOE cross-peak lists are generated, and residual dipolar couplings (RDCs) are calculated for each labeled site. Simulated data are then compared to measured values for a trial set of assignments and scored. A genetic algorithm uses the scores to search for an optimal pairing of HSQC crosspeaks with labeled sites. While none of the individual data types can give a definitive assignment for a particular site, their combination can in most cases. Four test proteins previously assigned using triple resonance methods and a sparsely labeled glycosylated protein, Robo1, previously assigned by manual analysis, are used to validate the method and develop a criterion for identifying sites assigned with high confidence.

INTRODUCTION

In the structural biology field, NMR is most noted for its ability to produce de novo structures of proteins in solution. Its contributions are significant in that solution better represents a physiological environment and many structures produced involve proteins that have resisted crystallization. Nevertheless, most systems studied have involved small proteins expressible in bacterial hosts where uniform enrichment in ¹⁵N and ¹³C (required for assignment by triple resonance methods) is practical. However, interest of the structural biology community is shifting to larger proteins, multi-protein complexes, and proteins that are natively glycosylated. While perdeuteration allows extension to some of the larger systems, this is not an option when glycoproteins are involved. For glycoproteins with native glycosylation expression in mammalian cells is preferred, and deuterated media inhibit mammalian cell growth. The need to supplement media for these cells with labeled amino acids, instead of labeled glucose and ammonium chloride, also makes uniform labeling extraordinarily expensive. However, sparse labeling with single or small subsets of isotopically labeled amino acids is still possible. Certain subsets of isotopically labeled amino acids are relatively inexpensive, making application to glycoproteins economical, and the reduction in numbers of resonances increases resolution for larger proteins (Goto and Kay 2000; Kainosho et al. 2006; Prestegard et al. 2014). Even with fewer labeled sites chemical shift perturbation can provide information on ligand binding or protein-protein association (Williamson 2014), and residual dipolar couplings (RDCs) can constrain relative orientation of structural units in multiple domain proteins or protein-protein complexes (Chen and Tjandra 2012; Lipsitz and Tjandra 2004). The only prerequisite is the replacement of triple resonance assignment methods with an alternative strategy. Here we present a strategy based on collection of data readily obtained on sparsely labeled sites and describe a convenient software implementation that uses a genetic algorithm to search for an optimal set of assignments.

The types of data that can be acquired on sparsely labeled proteins include heteronuclear single quantum coherence (HSQC) spectra from which chemical shifts of both protons and heteronuclei (¹⁵N or¹³C) can be measured. HSQC experiments also provide the basis for collection of ¹⁵N- or ¹³C-edited nuclear Overhauser effects (NOEs) (Ikura et al. 1990) and one-bond residual dipolar couplings (RDCs) (Lipsitz and Tjandra 2004). When structures are available for at least the domains comprising multi-domain proteins, or the proteins comprising multi-protein complexes, it is possible to predict each of these data types in a site specific manner. There are now several different chemical shift prediction programs (Han et al. 2011; Li and Bruschweiler 2015; Sahakyan et al. 2011; Shen and Bax 2010) that are based on the existence of three dimensional structures for protein domains. The NOE vectors associated with a given crosspeak in the 2–3 plane of a 3D NOESY-HSQC can also be predicted from a three dimensional structure, assuming a 1/r⁶ dependence of NOE intensity on inter-proton distances, and RDCs can be predicted using programs such as REDCAT (Valafar and Prestegard 2004) or PALES (Zweckstetter 2008), provided a sufficient number of RDCs are available to simultaneously evaluate the level and direction of partial orientation.

It is clear that comparison of any of the above data types with predictions can be used to facilitate assignments. The automated assignment of some NOE peaks in the course of structure determination is quite common (Buchner and Guntert 2015; Lange et al. 2012; Linge et al. 2003), and there are several examples of the use of NOEs for structural characterization without explicit NOE crosspeak assignments (Grishaev et al. 2005; Orts et al. 2016). There is also increasing use of both NOE and chemical shift data to validate or extend assignments made by traditional triple resonance methods (Dashti et al. 2016; Huang et al. 2015; Piai et al. 2016). However, most of these procedures rely to some extent on uniform isotope labeling. For sparsely labeled systems there has been some prior effort at resonance assignment. We have attempted to use amide exchange rate correlations in NMR and MS data to achieve assignments of ¹⁵N labeled sites (Feng et al. 2007; Nkari and Prestegard 2009). There have also been approaches that label proteins with combinations of amino acids to make assignments based on connectivities similar to those seen in triple resonance experiments (Kato et al. 2010; Lohr et al. 2015; Maslennikov and Choe 2013), and of course, assignment in sparsely labeled proteins can be facilitated by mutating residues to remove crosspeaks from labeled sites one at a time (Tzakos et al. 2006). However, these approaches are labor intensive. ¹³C-methy labeling of large proteins can also be seen as a type of sparse labeling, and this has fostered the development of assignment strategies that depend on data that can be collected via these sites, primarily methyl-methyl NOEs (Xiao et al. 2015) and paramagnetic effects (John et al. 2007). It has also stimulated exploration of probabilistic approaches to assignment using these and other types of data (Chao et al. 2014; Mishra and Frueh 2015).

Recently, we utilized the data types described above, namely chemical shifts, RDCs and NOEs, to assign a glycoprotein sparsely labeled with ¹⁵N enriched amino acids. Resonance assignment used a largely manual approach in which each type of prediction is sequentially used to exclude possible assignments (Gao et al. 2016). However, it is difficult to set strict exclusion limits in a sequential strategy. In principle, it is better to assign a score based on agreement between measurement and prediction of all data types and use these scores in a search over all possible pairings of labeled sites with measured crosspeaks. A systematic search over all possibilities would be feasible with modern computers and a small number of sites, but this quickly becomes unmanageable. Even at 12 sparsely labeled sites, the number of possible assignments is enormous; 12! = 470,001,600. Instead we use a procedure based on evolutionary algorithms, more specifically a genetic algorithm (Schmitt 2001).

Genetic algorithms have been used previously to facilitate NMR assignments (Lin et al. 2005; Yang et al. 2013), but not for the assignment of sparsely labeled proteins. They are particularly advantageous for NP-Hard problems where direct search methods become impractical. They are also well suited to problems where the search surface is not continuous, as in our assignment problem. However, there are limitations. The primary one is that there is no guarantee that the best assignment (global minimum of a scoring function) will be found; trapping in a local minimum is always a possibility. The initial selection of chromosomes (each showing possible assignments of all resonances to particular sites), crossover rates and mutation rates all affect the efficiency and generality of the search. Optimizing these parameters for a particular problem is the subject of ongoing research that points to coupled parallel searches starting from different chromosome sets (Tsoulos et al. 2016) and adaptive control of parameters during the search process (Aleti and Moser 2016). We have not specifically implemented these recent advances, but in an effort to make our search space more inclusive, we do loop through a set of crossover and mutation rates with each loop having a new chromosome selection.

We test our implementation of a genetic algorithm search for an optimal assignment on a set of proteins for which the required data and assignments have been deposited. Four of the test proteins come from a recent summary of X-ray/NMR structure pairs produced by the Northeast Structural Genomics group (NESG) (Everett et al. 2016). The existing assignments in this case are by traditional triple resonance methods on uniformly labeled proteins, but we mimic a sparsely labeled set by selecting resonances for a subset of amino acids. We also test the procedure on a sparsely labeled two domain fragment of the Robo1 protein whose assignment is achieved by a sequential approach (Gao et al. 2016). Robo1 is a glycosylated protein whose activity in developmentally related cell-signaling is regulated by interaction with certain heparan sulfate (HS) epitopes. Assignment was critical to locating the HS binding site and modeling an HS-Robo1 complex.

The new procedure proves to be quite successful. It is relatively fast, requiring from several minutes to a few hours of computational time. In three of the five cases the completely correct assignment is found among the 5 top scoring solutions (chromosomes), and the correct assignment is always found in the set of solutions having scores less than a score corresponding to measurements falling within one or two standard deviations of predictions. Many crosspeaks are also assigned consistently to correct sites within most of this solution set. Based on this consistency we suggest a criterion for identification of crosspeaks which can be assigned with high confidence in the absence of known assignments. The procedure, therefore, provides a robust means of assigning NMR spectra and sets the stage for answering questions involving ligand binding and complex assembly for some of the more challenging structural biology systems.

MATERIALS and METHODS

Test set selection

Four test proteins were chosen from the 40 pairs of NMR-X-ray structures produced by the Northeast Structural Genomics group, imposing the additional requirement that the resolution of the X-ray structures be below 2 Å (Everett et al. 2016). The NMR data for Robo1-Ig1–2 are from our paper reporting its interaction with heparan sulfate (Gao et al. 2016). There are several X-ray structures for the Ig1–2 construct, but these show significant differences in inter-domain orientation. For the purpose of this application domain motions were simulated in a long MD trajectory (1μs) (Gao et al. 2016) and an x-ray structure (PDB 2V9R) was selected that closely approximated the domain orientation in the most highly populated state of this trajectory. The PDB accession codes for the structures and a summary of experimental data used for all test proteins are summarized in Table 1.

Table 1.

Structure and experimental information on chosen test proteins and a glycoprotein.

PDB		Total Residues	Labeled Sites	Available RDC Data	Inter-residue NOE crosspeaks per residue
X-ray (resolution Å)	NMR
3C4S (1.70)	2JZ2	58*	Ala 4, Val 8	12	4.8
3CWI (1.90)	2K5P	70	Ala 7, Val 9	11	7.9
3LMO (2.00)	2KW2	93	Ala 12, Lys 6	17	6.4
3FIA (1.45)	2KHN	111	Ala 8, Lys 6	8	8.2
2V9R (2.00)	NA	212	Lys 12, Phe 5	17	7.4

^*3C4S is a dimer. Monomer A with 58 residues was used.

Experimental and predicted data

Selection of labeled sites

Because RDC analysis requires at least 5 measurements to fit order parameters before data can be used to assess quality of alignment or crosspeak assignment, we strove to have at least 10 isotopically labeled sites. Based on the expression construct for Robo1-Ig1–2, lysine and phenylalanine would yield 17 measurements, but two lysine crosspeaks were not observed. One N-terminal site is missing due to proteolysis, as confirmed by mass spectral analysis. The other unobserved site was identified as K137 by a selective mutation that produced no change in the number of HSQC crosspeaks. The two sites were thus eliminated from assignment consideration. Data for one phenylalanine was also not used because it exhibited high levels of internal motion, consistent with its being very near the end of the non-structured C-terminus (absent in some crystal structures). Hence, 14 of the 17 sites were subject to assignment by our methodology. To mimic a similar level of sparse labeling in the 4 uniformly labeled test proteins, we selected data from alanine and valine or alanine and lysine. The specific numbers of sites are listed in Table 1.

¹⁵N-¹H HSQC chemical shifts

Experimental measurement of ¹⁵N and ¹H chemical shifts from HSQC spectra is straightforward. Errors are all small compared to chemical shift prediction errors and will, therefore, be neglected. There are several program options for the prediction of chemical shift data (Han et al. 2011; Li and Bruschweiler 2015; Shen and Bax 2010), and they have very similar estimated precision for amide N and H shifts. Here, we chose PPM_one (Li and Bruschweiler 2015) to perform chemical shift prediction. Both backbone amide nitrogen and proton chemical shifts of the labeled sites were predicted using the crystal structures listed in Table 1. Errors for predicted ¹H and ¹⁵N chemical shifts were taken to be 0.17 ppm and 1 ppm respectively, numbers consistent with limits suggested by the authors of prediction programs (Han et al. 2011; Li and Bruschweiler 2015).

Nuclear Overhauser Effects (NOEs)

Experimental NOE data to be used for ¹H-¹⁵N crosspeak assignment are most useful when both chemical shifts and intensities of NOE crosspeaks are available. For most deposited NOE data only peak lists containing chemical shifts and constraint files containing upper and lower distance limits for proton pairs are available. However, there is no reliable way to work back from distance limits to a crosspeak intensity. Therefore, we chose cases where the original ¹⁵N-filtered NOE peak lists included the intensity of each crosspeak. Because the crosspeaks from intra-residue contacts are less useful in making assignments, we removed these by considering crosspeaks from a ¹⁵N-edited TOCSY spectrum. NOE crosspeaks at corresponding chemical shifts were eliminated from the list. Experimental amide proton NOE vectors containing only inter-residue data were then constructed by spreading intensity over a range of chemical shift equal to the estimated accuracy of predicted shifts. Since the vectors mimic columns emanating from ¹⁵N-¹H crosspeaks in 3D NOESY-HSQC data sets, it is also possible to take vectors directly from the columns in the 3D data sets when these are available.

For predicted NOE data the intensities for peaks in amide proton NOE vectors were predicted using a $\frac{1}{r^6}$ dependence on interproton distances derived from crystal structures. This would be correct for a rigid spherical protein with NOEs measured from initial slopes. We cannot assume the selected data meet these conditions, but since we are not seeking perfect scores, just best scores, we believe the treatment is adequate. The intensities were placed in predicted amide proton inter-residue NOE vectors at the chemical shift positions predicted by PPM_1 and spread over a range equal to the estimated chemical shift accuracy.

Residual Dipolar Couplings (RDCs)

¹⁵N-¹H Residual dipolar couplings (RDCs) reflect the orientation of each H-N bond vector relative to the magnetic field; hence, they are very dependent on the structure of each site. Experimental RDCs (8–17 in number) were obtained along with their estimated errors (typically 1Hz for the 4 uniformly labeled test proteins, and 2–5 Hz for the Robo1 set). Unlike the previous data types, predicted values could not be obtained independently for each site, because the data must be used to determine the five order parameters in addition to the RDCs. Therefore, for each possible set of assignments, all RDCs were used simultaneously, in combination with coordinates for nitrogen and proton pairs at potential sites, to calculate order parameters by singular value decomposition. A set of predicted RDCs were then back-calculated using the parameters and compared to measurements.

Missing and substandard data

It is not always possible to have complete data sets or data sets with uniform high quality. Sometimes crosspeaks are not observed in HSQC spectra, because of motional contributions to line widths, interference from solvent and other contaminants, or accidental overlap of a pair of crosspeaks. Sometimes there is supplementary information that makes the interpretation of certain measurements suspect, and one would choose to disregard the data. For example, spin relaxation data may suggest a high level of internal motion that would compromise the interpretation of RDCs. As the number of measurements of a given type must always equal the number of sites, the software package described below handles missing measurements by entering 999 as a default measurement. The package also handles too many measurements by entering 999 for null sites. The package also handles cases where the number of measurements exceeds the number of sites by entering 999 for null sites.

Program development

Our implementation of a genetic algorithm search for correct assignments of HSQC crosspeaks is based on routines available in MATLAB (Chipperfield and Fleming 1995; Sumathi and Surekha 2010). The complete package, “ASSIGNments for Sparsely Labeled Proteins”, ASSIGN_SLP, can be downloaded from the internet site http://tesla.ccrc.uga.edu/software/. The program executing the genetic algorithm search is designated ASSIGN_SLP.mat. Detailed information of program implementation, execution and analysis can be found in the Supplemental Materials.

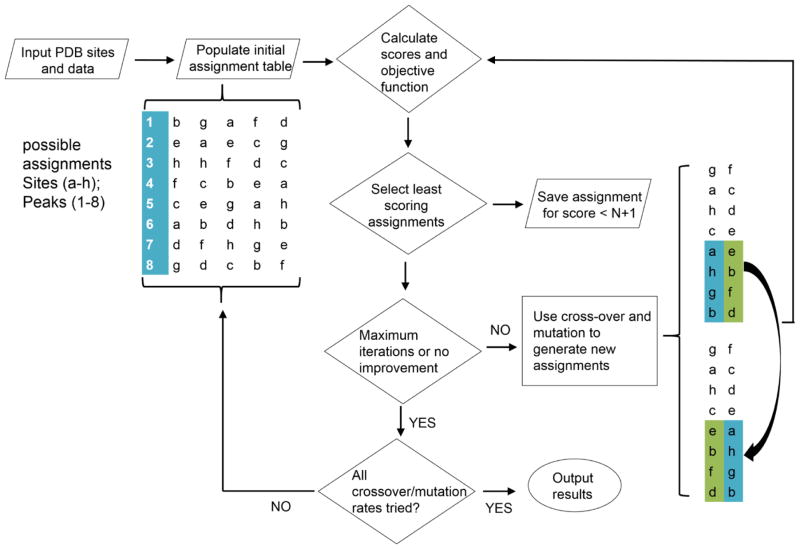
The work flow through the primary program is depicted in Figure 1. Input includes: the pdb file, a list of sites to be assigned (a–h in the flow chart), output from chemical shift programs, output from the NOE vector script and other experimental data with estimates of errors. Coordinates are extracted by the provided script from the pdb file for the calculation of predicted RDCs and NOEs, and predicted chemical shifts for the relevant sites are extracted from output files of PPM_1 or SHIFTX2.

Figure 1.

Work flow of the assignment strategy using a genetic algorithm. The sparsely labeled sites are represented by letters a–h and the HSQC crosspeaks are numbered 1–8. The region where certain mutations happened is labeled by blue and green.

One of the most important aspects of the search program is the objective function, in our case a sum of scores for different data types. It must minimize at a global optimal solution, weight each data type appropriately and provide a useful limit on what we regard as an acceptable solution. For most data types (RDCs and chemical shifts) our scores are based on a root mean square deviation (RMSD) between the predicted value for each site (pred(i)) and the experimental value being assigned to that site, exp(q(i)). See Equation 1.

$$\frac{1}{\sqrt{n}}\sqrt{{\sum }_{i=1}^n\raisebox{1ex}{$(exp(q(i))-\mathit{pred}{(i)))}^2$}\!\left/ \!\raisebox{-1ex}{${(\mathit{error}(q(i)))}^2$}\right.}$$ (1)

The error estimate, error(q(i)), is used to scale each score contribution by a number that reflects the information content of the measurement type. For example, in the case of chemical shifts, the error is from the estimated precision of predictions supplied by the authors of the prediction programs. If the range of measurements (largest deviation of prediction and measurement) is divided by the error, we have an estimate of the information content. As measurements assigned to particular sites begin to approximate predicted values, their contribution to the score is reduced. When the differences between experiment and prediction are at the estimated error, the score for each measurements type would equal one, and any total score less than one or two times the number of measurements types should be considered acceptable. Hence, the scaling provides both a weighting by information content and a convenient cut off for acceptable solutions.

In calculating an RMSD the number of comparisons contributing to the mean for a given measurement type (n) is normally the total number of independent measurements. For chemical shifts this is just the number of measurements, but for RDCs the number of independent measurements is less than the number of experimental data by five because of the order parameters that must be determined. In the case of missing data there should also be an additional subtraction for the number of data points entered as 999. This would appropriately make the errors seem somewhat larger. However, we must also consider information content. This is particularly important for RDCs. As the number of RDCs approaches 5, the five parameters will, in most cases, allow a perfect match of predicted to experimental data, and the information content for assignment will actually approach zero. Hence, we have added an additional scaling factor of (n-5)/n to the RDC part of the scoring function.

There are some limitations to the above RMSD-based procedure. First, it is hard to define an RMSD for some types of measurement, NOEs, for example. NOEs from 3D NOESY-HSQC data sets are best represented as vectors containing intensity information rising from each HSQC crosspeak. Both intensity of crosspeaks (volumes from the 3D set) and the chemical shift positions for various crosspeaks are variables. Therefore, we calculate a Pearson correlation coefficient that compares the predicted and experimental NOE vectors, yielding a single number for each vector. This has the additional advantage of making the absolute intensity of the vectors irrelevant; only NOE patterns matter. The coefficient, R, is 1 for a perfect match between experimental and predicted NOE vectors and zero for no correlation. To mimic an RMSD that goes to zero for a perfect match we use the square of (1-R) averaged over all NOE vectors. To replace the estimate of error we use data from the four uniformly labeled test proteins, where we know correct assignments, to estimate NOE information content. To do this we calculate heat maps (see below). When predicted and experimental NOEs are listed in the correct order the scores on the diagonal represent correct pairings and the scores off the diagonal represent those for incorrect pairings. The ratios of the averages on and off the diagonal are about 5 for the test proteins and this is what we used for a weighting factor (equivalent to using an error estimate of about 0.2).

The above procedures, particularly those that simply use error estimates as opposed to a heat map analysis, are not perfect. Improper weighting relative to information content can still occur. This is often recognizable in an ordered list of acceptable solutions that includes contributions to total scores from individual data types. A contribution from one particular data type may consistently have an unusually small or large contribution, or its contributions may fall continuously through the list indicating that is dominating the algorithm. It is possible in these cases to further adjust weighting factors to eliminate this behavior.

Scores can also be adjusted to take into account additional knowledge about pairings. Since sparse labeling often includes data from samples labeled with different amino acids, we know that a specific set of crosspeaks must be associated with sites having a particular amino acid type. Adding 100 to experimental and predicted chemical shifts for one amino acid type forces incorrect associations to have unacceptable scores. Other types of knowledge, for example, knowledge about surface versus interior location can be introduced in a similar fashion.

The objective function is evaluated for each of the trial assignments (chromosomes). Chromosomes with a total score less than a user specified value is saved in an output file; this maximum score usually is set to two to three times the number of measurement types. Detailed information on chromosome selection and mutation rate determination are described in the Supplemental Materials. Chromosomes are then selected from the entire pool with a frequency biased toward high scores, which means farther from the best individual score, and these are subjected to modification. There are two general processes used, a permutation mutation and a pairwise crossover process, as illustrated in the flow chart. The frequencies with which the processes are used is governed by rate constants which are normally tuned for a particular application. As we intend our program to be applicable to a range of different data types we attempted to eliminate the normal tuning process by looping through a combination of rates (0.2, 0.4, 0.6 and 0.8 for both mutation and crossover). An initial set of rates is selected, a new set of chromosomes is generated, the new set is re-scored and it is subjected to another cycle. This cycle is continued for a given crossover and mutation rate until a convergence criterion is reached. In our case, the convergence criterion is that the lowest score does not change after 100 iterations or that a set maximum number of 500 iterations is reached. The program then selects another set of mutation and crossover rates, generates another set of random assignments and starts the process over. When all pairs of rates have been used the program ends.

The raw output is a MATLAB file in a “cell array,” which is a Java data class used by MATLAB. The output contains possible solutions generated in each of the mutation/crossover cycles that have scores less than a user specification. In addition to detailing the match of crosspeaks to sites, contributions of each data type to the total score are given along with information that allows a direct comparison of predicted to experimental values.

RESULTS

Assignments for our four uniformly labeled test proteins and one glycoprotein have been produced using the programs introduced above. The four uniformly labeled test proteins range in size from 55 to 212 amino acids. Different mixes of secondary structures are represented, including those rich in alpha-helix, rich in beta-sheet and a combination of both. There are instances of missing data and different levels of internal motion. For the two domain construct from Robo1, our example of a sparsely labeled glycoprotein, ¹⁵N-¹H HSQC spectra for the lysine and phenylalanine labeled versions are shown in Supplementary Materials Figure S1 (Gao et al. 2016). These spectra give examples of the resolution that can be expected for a sparsely labeled, non-deuterated 23 kDa protein.

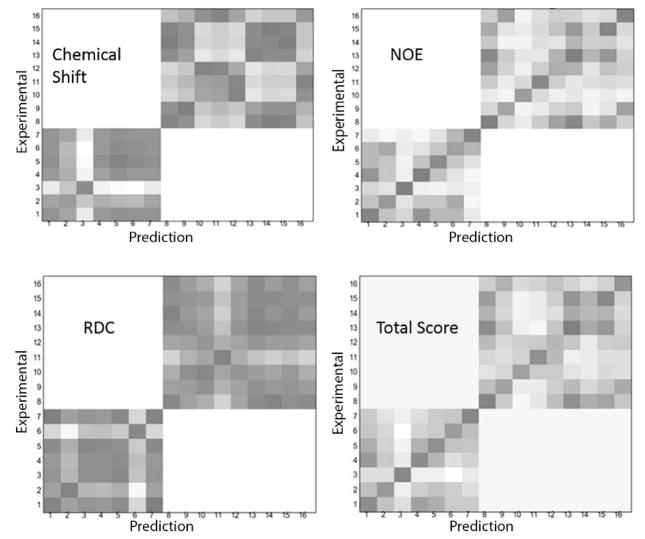
Working with the first four proteins, for which assignments are well documented by traditional methods, provides an opportunity to evaluate the degree to which each measurement type contributes to the assignment process. Their contributions can be visualized in the heatmaps similar to those generated by the auxiliary statistical analysis program. The examples shown in Figure 2 use the X-ray structure, 2K5P, for prediction and the deposited information for the NMR structure, 3CWI, for experimental data. Experimental assignments are listed on the y axis and predicted assignments are listed on the x axis, both ordered with respect to increasing residue numbers. Correct assignments fall on the diagonal. The contributions to the total score from each data type have been generated using an in-house MATLAB script (available at the ASSIGN_SLP download site). The values are represented on the plots in gray-scale, with black representing zero (best score) and white a normalized score of 1. The amino acids represented are 7 alanines and 9 valines. Since we do not allow cross-assignments between the amino acid types, white regions exist for coordinates1–7, 8–16 and 8–16, 1–7. The first 3 panels are heatmaps of the scores for individual data types; chemical shifts, NOEs and RDCs. From these heatmaps, it is clear that NOEs are the most informative since the darkest spots for most possible assignments fall on the diagonal. However, it is also obvious that there are cases with little distinction between pairs of possible assignments (scores for peaks 1, 6, and 13), and an incorrect assignment would be indicated for peaks 9 and 12. Data for RDCs and chemical shifts are typically less definitive, but still useful. Adding all the scores together produces a plot in which the diagonal box is darkest for all but one possible site. The heatmaps have already been used to extract an error estimate for NOEs, but they could be used to evaluate the proper weighting for all data types. We will examine this possibility in the future.

Figure 2.

Heatmaps comparing predicted and experimental values of each type of measurement (chemical shift, NOEs and RDCs) and total score contribution. Each number on both X and Y axes represent one labeled residue. The amino acid type is assumed to be known for the two sets of crosspeaks.

An example of the output of our assignment program for the 3CWI-2K5P protein is shown in Table 2. The output contains not only all the possible assignments but also the solution rank and the score contributions from each type of measurement. There is a comparison of experimental and predicted RDC data for each site. For chemical shifts the experimental data are given for each site; the predicted data are given in the output header. For NOEs individual score contributions in terms of (1-R)² are given. In the example presented, the first rank solution is a single-swap of two residue assignments (peak 3 should assigned to 48 and peak 4 should assigned to 32); peak 3 has no RDC data, making assignments for this pair somewhat ambiguous.

Table 2.

First rank solution for assignments of 3CWI-2K5P.

Solution Rank	1
Peak number	2	5	1	3	4	7	6	12	15	9	14	11	8	13	16	10
Residue number	15	26	30	32	48	51	59	5	12	20	29	35	37	43	54	60
Exp.RDC	2.69	7.24	0.96	999	0.74	−9.87	3.33	−3.24	999	3.2	9.5	999	−0.17	999	−1.28	999
Calculated RDC	3.04	8.41	−0.14	0	0.42	−8.94	1.1	−1.92	0	3.5	9.6	0	0.15	0	0.11	0
Exp. shift (N)	121.2	126.1	131.1	120.2	119.9	119.5	121.1	226*	225*	217.9*	219.2*	221.2*	227.6*	226.8*	226.2*	221.8*
Exp. shift (H)	7.36	8.71	8.54	8.01	8.03	7.54	8.33	108.56 *	108.56 *	107.81 *	107.58 *	107.33 *	109.62 *	108.87 *	109.22 *	109.06 *
NOE score	0.01	0.2	0	0.11	0.23	0.1	0.01	0.05	0.05	0.15	0.03	0.2	0	0.43	0	0
Data type	RDC	N	H	NOE	Sum/Score
Total score	1.48	0.99	1.19	1.52	5.19

^*100 is automatically added to the chemical shift for the second type of amino acid so that different types of amino acid will not be cross-assigned. 999 is used to indicate data that are not available. The incorrect assignment is colored in gray; 3 and 4 should be interchanged

The results of application of our assignment program to all four uniformly labeled test cases are summarized in Table 3. In all cases ¹H and ¹⁵N chemical shifts, NOE peak lists for HSQC crosspeaks, and a single set of RDCs were available. The top score solutions contain at least 70% of correct assignments (case 3FIA) and can reach 100% of correct assignments (case 3C4S). The correct solution is always found near the top of the list; the worst case is number 11 out of 7493 solutions for 3FIA which has 6 missing RDCs.

Table 3.

Assignment summary of four test protein cases.

PDB	3C4S	3CWI	3LMO	3FIA
Labeled Sites and Number	Ala 4, Val 8	Ala 7, Val 9	Ala 12, Lys 6	Ala 8, Lys 6
Number of Acceptable Solutions*	260	1376	14006	7493
Top Score Solution (correct/total)	12/12	14/16	16/18	10/14
Correct Solution Rank	1	4	2	11
Consistently Assigned Crosspeaks (correct/total)	7/12	10/16	15/18	10/14
Missing Data	0	5 RDCs	1 RDCs	6 RDCs

^*If the lowest score for an application is below 4, all the solutions with a score under 5 are collected. If the lowest score is above four, all the solutions with a score more than the lowest score plus 1.0 are collected.

The application to Robo1-Ig1–2 deserves a separate discussion. Robo1-Ig1–2 is both larger than the other test proteins, (212 residues), it has the potential complication of internal motion between domains, and it is a glycoprotein where sparse labeling with individual amino acids is necessary. The top ranked assignment from an initial run (having a score of 4.09) contains 10 correct assignments and the completely correct solution was solution number 366. However, the Robo1 protein is a good example of using some intelligence in changing the weights of the contributions in the objective function to improve performance. The calculation using initial error estimates had high chemical shift contributions to the scores and several of the RDC’s did not agree with the back calculation of individual contributions. By increasing the errors of the chemical shift terms to lessen their importance in the objective function, the correct solution moved from a rank of 366 to a rank of 18 in a list of 354 acceptable solutions with scores less than 5.09. The top ranked solution still had 10 correct assignments.

For Robo1-Ig1–2 it is possible to see some of the reason for the four missed assignments in the top ranked solution. The RDC degeneracy makes it hard to distinguish peak 4 from 9, peak 6 from 7 and peak 13 from 14. Therefore, swaps between assignments for these pairs might have been expected. 10 correct out of 14 is in fact not a bad result. We might also have expected the RDC data to be compromised in the Robo1-Ig1–2 case by the existence of inter-domain motion. This could have led to different alignment tensors for the two domains and completely incorrect RDC predictions when assuming a rigid structure and extracting a single set of alignment parameters. The fact that RDCs fit reasonably well may mean that motions are fairly restricted in the presence of the large attached glycan. The crystal structures showing large variations in inter-domain geometry were all produced on non-glycosylated material.

It may seem convenient to focus on top-ranked solutions, however, this is not particularly valuable for a protein for which there is not prior knowledge of the correct assignment Identifying sites which are assigned with high confidence is actually more important than obtaining a complete assignment. For example, in applications to ligand binding by chemical shift perturbation, one only needs to know the assignment of the perturbed peak, and for domain orientation using RDC measurements, one only needs an adequate number of confident assignments to use RDCs.

One approach to assessing the probability of a correct assignment is to look at the frequency with which a crosspeak is assigned to the same site in solutions which fall within a standard deviation or so of satisfying experimental data. Since we have tried to scale scores relative to estimated error for each data type, the cut-off for solutions to examine should be roughly equal to the number of data types used. Our test cases had 4 data types. We would expect to see a significant number of solutions with scores below 4. Two of the test proteins fall in this class, 3CWI had a best solution score of 3.66 and 3FIA had a best solution score of 3.87. The other 3 had best scores of 4.45, 5.38, and 4.09. The higher scores could represent an underestimate of error, a systematic deviation in some data due to internal motion, or minor differences in structure between solution and crystal. To get an adequate sampling of solutions we will examine solutions with scores less than 5.0 if the minimum score is less than 4 and one plus the minimum when the minimum score is larger or equal to 4. We consider these to be acceptable assignments.

A visual way of presenting this analysis is shown in Figure 3 using protein 3CWI as an example. Other examples are contained in the Supplemental Materials Figure S2. Histograms show the number of times a crosspeak is assigned to each site. If we take consistency to be assignment of the same residue to a given crosspeak in more than 50% of the acceptable assignments, we find the following: of the 60 assignments which we can compare to the results of traditional triple resonance assignments, we would assign with confidence 35 peaks or about 60% of them. We find that among these 35 we would make one mistake. This would correspond to being correct 97% of the time, something close to a 95% confidence limit. The Robo1 system is a little different because we have good reason to believe that the structural model may be inadequate. Nevertheless, applying the same criteria we find that we can assign 7 of the14 peaks with confidence and all of these agree with our manual assignment.

Figure 3.

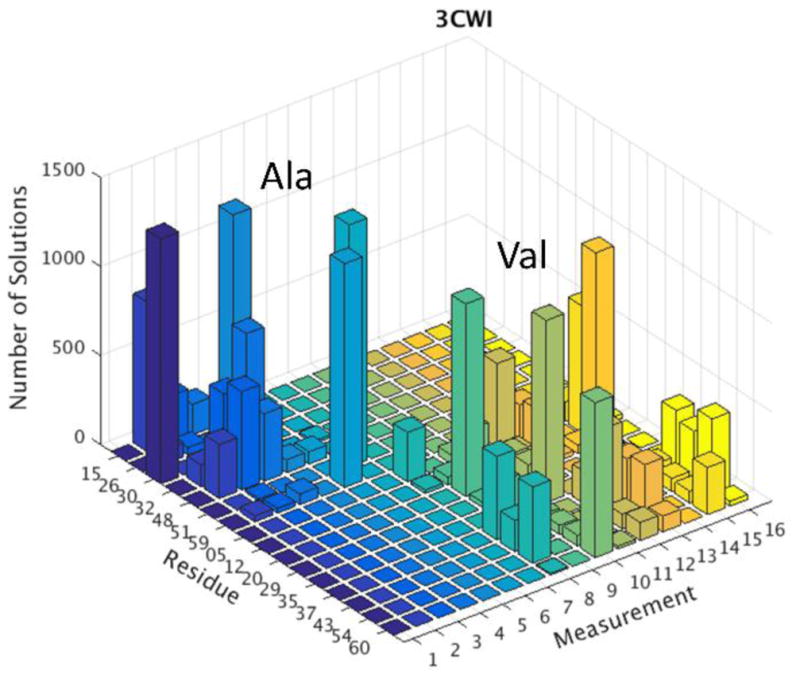
Histogram showing the frequency with which each crosspeak (measurement) is assigned to each site (residue) for the protein with NMR structure 3CWI.

DISCUSSION

Thus, we have clearly demonstrated an alternate procedure for assignments of HSQC crosspeaks from sparsely labeled proteins. This is particularly useful for glycoproteins that may have to be expressed in mammalian cell culture. Certain isotopically labeled amino acids are only moderately expensive. Drop-out media for mammalian cell culture is available and procedures for expression using 100–300 mg/L of labeled amino acid have been described (Barb et al. 2012). The basic experiments for data collection are straightforward and not extremely time consuming. For Robo1-Ig1–2 only a single protein sample was needed for a complete set of experiments on each amino acid type; this is less than that typically required for a complete set of traditional 3D NMR experiments. The computation times are also modest, and more importantly, do not require personnel time. For the proteins studied, each required 5 hours or less to cover all cross-over mutation rates (0.1, 0.2, 0.4, 0.6 and 0.8) on a Xeon E5-2640 CPU.

We have emphasized the use of ¹⁵N-enriched amino acids, but methods are equally applicable to ¹³C-enriched amino acids. Metabolic labeling in methyl groups of isoleucine, leucine and valine, combined with perdeuteration, has become a popular approach to NMR-based structural work on large proteins (Tugarinov et al. 2006). Some alternate assignment strategies have also been developed for these systems (Chao et al. 2014; John et al. 2007; Mishra and Frueh 2015; Xiao et al. 2015), but we believe the approach described here could offer some advantages. Labeling with ¹³C-methyl alanine provides the same excellent sensitivity and resolution, but it also provides RDCs that are backbone centered, much like ¹⁵N-¹H amide RDCs. These can be used in our assignment strategy. Complete deuteration of large proteins would have to be sacrificed to collect the type of NOE data we use, but there is precedent for collection of NOEs on partially deuterated proteins that give well resolved spectra (Kay and Gardner 1997) (Nietlispach et al. 1996).

The procedure we describe does require structures for at least the individual domains comprising a protein, or proteins comprising a multi-protein complex. Structures for many of the proteins of interest today have been produced by X-ray crystallography or NMR and are available through readily accessible databanks. In principle, many other proteins can be modeled from homologous proteins in databanks (Bordoli et al. 2009; Webb and Sali 2014). We have not examined the use of modeled protein structures. However, it is likely that high quality structures will be required, as RDCs, NOEs and chemical shifts are all highly sensitive to three dimensional structure. Some limitations may also arise, because, NOEs are not sensitive just to an average structure or minimum energy structure, but to all structures sampled on the timescale of an NMR measurement. Accounting for conformational sampling using molecular dynamics trajectories remains one of the most promising options for improving predictions of chemical shifts, RDCs and NOEs. There have already been attempts to improve both chemical shift predictions and NOE predictions using these trajectories.

We have used just four types of data in this presentation. However, addition of other data types is relatively straightforward. Pseudo contact shifts have the same geometry dependence as RDCs and can be predicted with the same single value decomposition algorithms used for RDCs. A precedent for use of these in resonance assignment has been established (John et al. 2007; Skinner et al. 2013). Paramagnetic relaxation enhancements (PREs) also have the same dependence as an NOE. There are other types of readily accessible data that would require design of distinctly different scoring functions. Amide protein exchange rates, for example, are easily measured from ¹⁵N-¹H HSQCs, and there have been some attempts at making predictions based on structure (McAllister and Konermann 2015). These additions promise significant improvements in the applicability of our sparse-label assignment strategy in the future.

In summary, we have successfully demonstrated an NMR resonance assignment strategy that does not rely on triple resonance experiments and is applicable to proteins that benefit from sparse isotope labeling as opposed to uniform isotopic labeling. A program, “ASSIGNments for Sparsely Labeled Proteins”, that uses a genetic algorithm to search for the best match of readily accessible experimental data to data predicted from known domain structures, has been developed. While a set of relatively small, previously assigned, proteins has been used to validate methods, the approach is applicable to larger proteins and a growing number of glycoproteins that are proving important in the study of human physiology and disease.

Supplementary Material

10858_2017_101_MOESM1_ESM

Figure S1. 2D ^I5N-¹H HSQC spectra of (A) ¹⁵N Lys labeled Robol-Ig1-2 and (B) ¹⁵N-Phe labeled Robol-Ig1-2. The protein is at 140 μM in 25 mM Tris-HCl and 100 mM KCl buffer at pH 7, 27 °C. Figure is adapted from: Gao, Q. C., C.Y.; Zong, C; Wang, S; Ramiah, A; Prabhakar, P; Morris, L.; Boons, G-J; Moremen, K.M; Prestegard. J.H., Structural Aspects of Heparan Sulfate Binding to Robol-Ig1-2. ACS Chemical Biology 2016 (DOI: 10.1021/acschembio.6b00692).

Figure S2. Histograms showing the frequency with which each crosspeak (measurement) is assigned to each site (residue) for three uniformly labeled test proteins and sparsely labeled glycoprotein Robol.