SUMMARY
Combinatorial control of gene expression is presumed to be mediated by molecular interactions between coincident transcription factors (TFs). While information on the genome-wide locations of TFs is available, the genes they regulate and whether they function combinatorially often remain open questions. Here, we developed a mechanistic, rather than statistical, modeling approach to elucidate TF control logic from gene expression data. Applying this approach to hundreds of genes in 85 datasets measuring the transcriptional responses of murine fibroblasts and macrophages to cytokines and pathogens, we found that stimulus-responsive TFs generally function sequentially in logical OR gates or singly. Logical AND gates were found between NFκB-responsive mRNA synthesis and MAPKp38-responsive control of mRNA half-life, but not between temporally coincident TFs. Our analyses identified the functional target genes of each of the pathogen-responsive TFs and prompts a revision of the conceptual underpinnings of combinatorial control of gene expression to include sequentially acting molecular mechanisms that govern mRNA synthesis and decay.
eTOC blurb
An iterative systems modeling approach reveals how the pathogen-responsive transcriptome of murine fibroblasts and macrophages is specified by combinations of nuclear transcription factors and cytoplasmic mRNA half-life regulators.
INTRODUCTION
Mammalian cells express genetic information in a manner that is both cell-type specific and responsive to environmental cues. The notion that combinations of transcription factors (TFs) may control gene expression by functioning together, or combinatorially, was established by observations that TF binding sites are often clustered within promoters and enhancers (Zhu et al., 2002), that some TFs may bind cooperatively (Johnson et al., 1979), or that they may show transcriptional synergy (Carey et al., 1990), possibly mediated by multiple TF interaction domains in coactivators such as CBP/p300 (Vo and Goodman, 2001). Boolean logic gates (Buchler et al., 2003), including graded versions using thermodynamic formulations (Bintu et al., 2005b), emerged as a useful conceptual framework and theoretical considerations emphasized the capacity of combinatorial control logic to produce a large variety of gene expression programs with a smaller number of available TFs (Arkin and Ross, 1994; Mayo et al., 2006; Morris et al., 2010). However, despite the availability of genome-wide technologies to probe transcriptional responses and TF binding events, whether and how the notions of combinatorial control of gene expression actually apply to cellular gene expression programs has not been investigated in an unbiased manner on a genome-wide scale.
A key difficulty for elucidating TF logic functions or construct predictive gene regulatory network (GRN) models that account for these logic functions is that in mammalian genomes, neither the presence of a consensus TF binding site nor an experimentally confirmed TF binding event is reliably predictive for function (Jaimovich and Friedman, 2011); indeed, functionally relevant TF-binding events may be far from the transcription start site due to extensive looping of the native chromatin fiber (Jin et al., 2011; Lieberman-Aiden et al., 2009). Detailed single-gene studies utilizing CRISPR/Cas9-directed mutagenesis of specific binding sites are beginning to provide answers but such approaches have not been successfully scaled to expression programs involving hundreds of genes. One consequence of lacking a mechanistic genome-scale GRN model is that the seemingly simple question of what the functionally relevant target genes of a given TF are remains largely unanswered.
A well-studied model system for stimulus-responsive gene expression is the innate immune and inflammatory response. Exposure to pathogen leads to dramatic changes in the transcriptome of myeloid and fibroblastoid cells (Nau et al., 2002; Novershtern et al., 2011; Ramirez-Carrozzi et al., 2009; Ramsey et al., 2008; Ravasi et al., 2010). These cells function as sentinels and initiators of multi-tiered immune responses; in response to pathogen exposure they induce the expression of genes that mediate cell intrinsic defenses, the coordinated recruitment of professional innate immune cells (e.g. neutrophils and macrophages), the initiation of an adaptive immune response (via dendritic cells and T-cells), and tissue remodeling for pathogen clearance and subsequent wound healing. A large body of research has identified numerous molecular factors that form complex Signal Regulatory Networks (SRNs) and Gene Regulatory Networks (GRNs) to regulate these pathogen-responsive gene expression programs (Amit et al., 2009; Cheng et al., 2011; Gilchrist et al., 2006; Nau et al., 2002; Novershtern et al., 2011; Ramsey et al., 2008; Ravasi et al., 2010). Key pathogen-responsive, so-called signal-dependent TFs (SDTFs), whose dynamic activities are controlled by SRNs, are AP1, NFκB, and IRF. For specific SRNs, particularly NFκB (Basak et al., 2012), mathematical modeling has provided key insights into how a variety of biochemical mechanisms function together to regulate activation and inactivation. To understand how pathogen-responsive gene expression is controlled, DNA sequence motifs, chromatin-signatures, and SDTF binding events have been characterized both genome-wide and for subsets of highly induced genes (Garber et al., 2012; Heinz et al., 2013; Jin et al., 2011; Ramirez-Carrozzi et al., 2009); (Bhatt et al., 2012); (Tong et al., 2016), but predictive GRN models that allow for an understanding of how combinations of these SDTFs function have only been produced for individual genes of interest (Amit et al., 2009; Cheng et al., 2011; Gilchrist et al., 2006).
Here, we report the development of GRN models underlying the pathogen-responsive transcriptome for the purposes of examining how the prominent pathogen-responsive SDTFs AP1, NFκB, and IRF function combinatorially. The modeling approach allows integration of diverse functional gene expression datasets in successive cycles of model simulation/prediction, experimental testing, and model refinement, but side-steps the challenge of charactering the functional relevance of specific physical TF-enhancer binding events. By tracking the performance of the models at single gene resolution, we could identify the best performing GRN model for each cluster of co-regulated genes. Interestingly, we found no evidence for synergy (logical AND gates) between these SDTFs, but identified numerous logical OR gates of sequentially acting NFκB and ISGF3 and AND gates between sequentially acting NFκB-driven nuclear mRNA synthesis and cytoplasmic p38-driven mRNA half-life control.
RESULTS
Identifying GRN architectures
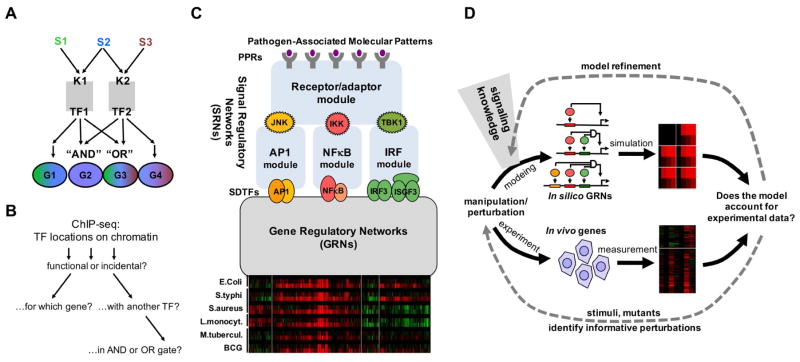
A hallmark of the notion of combinatorial TF control is that a relatively small number of regulators can provide for a larger number of different gene expression responses through the use of AND and OR gates (Figure 1A). However, delineating the combinatorial control logic on actual mammalian genes is difficult in part because genome-wide TF location analyses do not readily provide functional information about the binding event (Figure 1B). We sought to leverage knowledge about the signal regulatory networks (SRNs) responsive to pathogens to develop models of the gene regulatory networks (GRNs) that underlie pathogen-responsive gene expression programs (Figure 1C). We pursued the systems biology approach of iterative modeling and experimentation (Ideker et al., 2001) to test increasingly sophisticated model formulations of Boolean, thermodynamic or kinetic formulations of GRNs involving combinations of TFs with an increasing set of experimental data (Figure 1D).
Figure 1. Dissecting the combinatorial control logic underlying the pathogen-responsive transcriptome.
(A) Schematic of how combinatorial control of kinases (K) signal-dependent transcription factors (TFs) can mediate stimulus (S)-specific gene (G) expression programs. In this example the presence of AND and OR gates allows two TFs to mediate four distinct stimulus-responsive gene expression programs.
(B) While ChIP-seq studies enable genome-wide location analysis of TFs, it remains challenging to determine whether these binding events are functional or incidental, which gene or transcription start site they may regulate, and whether they function in conjunction with other TFs nearby or at a distance, in potential AND or OR gates.
(C) Schematic of key signal regulatory networks (SRNs) that control pathogen-responsive gene expression programs, exemplified by clusters of co-regulated genes (re-analysis of data by (Nau et al., 2002)). Prior studies of these SRNs have resulted in computational models of the molecular mechanisms (blue boxes) that recapitulate observed stimulus-responsive activation of the signal-dependent transcription factors (SDTFs) AP1, NFκB, and IRF. How these SDTF activities are interpreted to produce pathogen responsive gene expression programs is determined by the gene regulatory networks (GRNs), for which no mechanistic model has been developed (grey box).
(D) Schematic of the workflow for iteratively refining a mathematical model that recapitulates pathogen-responsive inflammatory and immune gene expression programs. Model formulations of increasing complexity are constructed and refined based on prior knowledge of the signaling network, and assessed by comparison to experimental data. With each round of simulation and experimentation of additional conditions the model is iteratively refined.
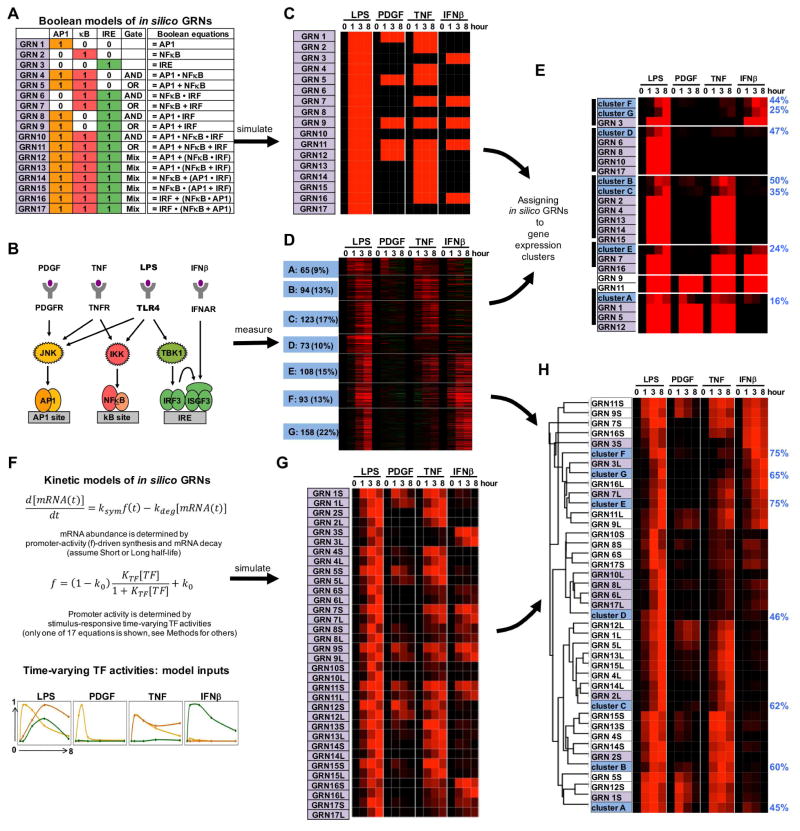
We first focused on the three prominent pathogen-responsive SDTFs, the families designated AP1, NFκB, and IRF, and enumerated 17 possible GRNs including Boolean logic AND and OR gates (Figure 2A). To elucidate the Boolean logic functions of actual genes we reasoned that experiments involving subsets of these SDTFs would be informative. Prior knowledge of the upstream SRNs suggested that this is possible with a panel of cellular cytokines or growth factors (Figure 2B): Platelet-derived growth factor B (PDGFβ), the major growth factor in blood serum, is known to activate the JNK pathway and AP1 (Tallquist and Kazlauskas, 2004), the inflammatory cytokine tumor necrosis factor (TNF) activates AP1 and NFκB (Bradley, 2008), and interferon-β (IFNβ), the important antiviral autocrine regulator, activates the IRF transcription factor ISGF3 (Borden et al., 2007). Based on this knowledge, we used each of the 17 hypothetical GRNs for simulations that predicted the mRNA response pattern to the panel of stimuli (Figure 2C).
Figure 2. Assigning combinatorial GRN models to endotoxin-responsive gene expression clusters.
(A) Combinatorial control by three pathogen responsive SDTFs AP1, NFκB, and IRF described by Boolean logic gates. Considering AND and OR gates, 17 possible GRNs (indicated in purple) can be enumerated.
(B) Knowledge of the pathogen-responsive SRNs indicates that subsets of pathogen-responsive SDTFs may be activated by cytokines (TNF, IFNβ) and growth factor (PDGF).
(C) Heatmap of the gene expression patterns predicted by the Boolean GRN models of panel (A) responding to the SDTF-inducing stimuli schematized in panel (B).
(D) Heatmap of experimental mRNA expression data of 714 genes inducible by endoxin in MEFs. MEFs were stimulated with PDGFβ (50 ng/ml), TNF (10 ng/ml), IFNβ (500 units/ml) and LPS (100 ng/ml) for the indicated times. Expression fold changes (log2) were analyzed by K-means clustering following row-normalization, yielding 7 clusters of co-regulated genes (A to G, indicated in blue). Data is representative of three experiments in which all conditions were performed in parallel.
(E) Hierarchical clustering of experimental cluster average profiles (D) and predicted expression profiles of the Boolean GRN model (C). Many Boolean GRN models lead to indistinguishable expression profiles hindering the assignment of a GRN model to experimentally determined gene expression clusters. Further, the percentage (blue on right) of in vivo gene expression profiles that are accounted for by the assigned in silico GRN (Spearman rank correlation-based “good fit” criterion. See methods) is generally low.
(F) Formulation of 17 kinetic in silico models of potential GRNs with two mRNA half-lives. Promoter activity f is a function of thermodynamic interactions of TFs with their cognate binding sites; combinations of these may form AND or OR gates (figure S1) (Bintu et al., 2005a). As TF abundances change over time (bottom), promoter activity and the resulting mRNA synthesis rate ksyn.f will change accordingly. Abundances of mature mRNAs may then be calculated with a differential equation accounting for mRNA synthesis and decay.
(G) Heatmap of the predicted expression profiles of the kinetic GRN models (panel F) in response to the SDTF-inducing stimuli (panel B). Each GRN is represented twice with a short (S) or long (L) mRNA half-life (1 vs. 6 hrs). Simulations employed SDTF activity profiles measured biochemically (figure S2).
(H) Hierarchical clustering of experimental average profiles (D) and predicted expression profiles of the GRN models (G). Best fit GRNs are highlighted in purple, and the percentage of in vivo gene expression profiles that are accounted for by the assigned in silico GRN (Spearman correlation-based “good fit” criteria. See methods) is indicated in blue on the right. GRNs shaded in purple best match the experimental data thus far.
To characterize actual cellular gene expression programs responsive to each stimulus, we performed genome-wide expression analyses in wild-type primary mouse fibroblasts (MEF) with aforementioned stimuli. K-means clustering of the MEF expression data of 714 endotoxin inducible genes identified seven distinct clusters of co-expressed genes (Figure 2D). We attempted to assign in silico GRNs to the mean profiles of these gene expression clusters, but because many Boolean GRNs shows indistinguishable expression patterns, assignments were generally not unique, and the fraction of genes in a cluster that were accounted for by the model simulations were generally below 50% (Figure 2E).
The poor fit-scores suggested that more detailed information was required; indeed, gene expression timecourses provide quantitative information over time that was not used by the Boolean digital logic model. We therefore constructed thermodynamic versions (Bintu et al., 2005b; Mayo et al., 2006) of aforementioned 17 GRNs (including logical AND and OR gates, Figure S1A) that drive the synthesis of mRNA transcripts, characterized by either long (L) or short (S) decay half-lives (Figure 2F), resulting in 34 GRN models (see Methods). As TF activities show stimulus-specific temporal profiles, we measured these in timecourse studies in response to each of the four stimuli (Figure S1B, Table S1), allowing us to generate numerical inputs (Figure 2F) for GRN model simulations of stimulus-responsive gene expression (Figure 2G).
Hierarchical clustering the GRN model simulations with the mean expression profiles of the seven experimentally determined expression clusters suggested an initial assignment of an in silico GRN model to each experimental expression cluster (Figure 2H). Two clusters were assigned combinatorial GRNs: cluster E was predicted to be an OR-gate GRN (GRN7L) in which transcription factors function independently, and cluster D was assigned an AND-gate GRN (GRN10L) in which TFs are predicted to function cooperatively. (While GRN6L, 8L, 10L 17L do reasonably capture cluster D patterns, GRN10L was slightly preferred due to the complete lack of response to IFNβ.) Comparison between the simulated and measured temporal expression profiles showed that generally more than 60% of genes passed a “good fit” criterion based on rank correlations for time-course data under different conditions (Spearman correlation; see Methods).
Testing the model: physical and functional characteristics of assigned GRNs
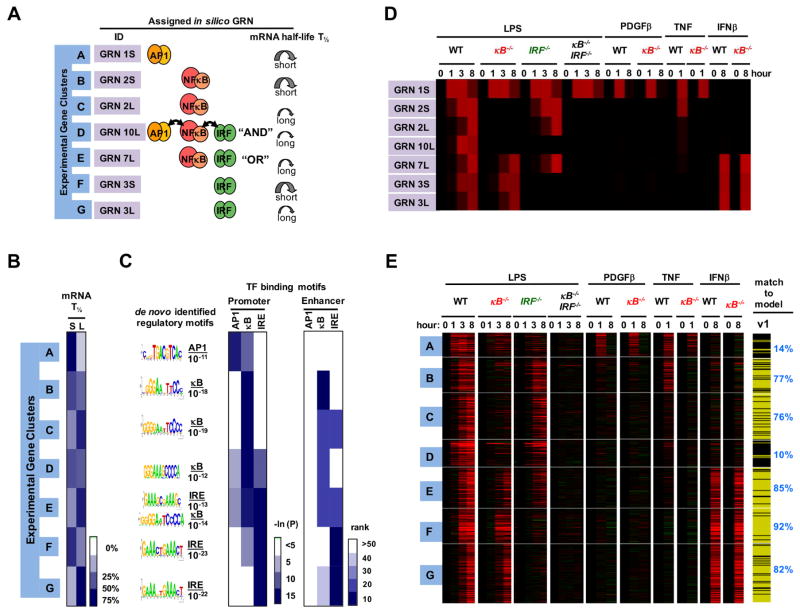
Based on this analysis, genes in cluster A were predicted to be AP1 targets (Figure 3A), genes in cluster B and cluster C were predicted to be NFκB target genes with either short or long mRNA half-lives, and cluster F and cluster G were predicted to be IRF/ISGF3 target genes with either short or long mRNA half-lives. Cluster E was predicted to consist of genes that may be induced by either NFκB or IRF/ISGF3, while cluster D’s expression pattern was most consistent with promoters synergistically controlled by combinations of AP1, NFκB, and IRF/ISGF3. We next tested these model predictions with respect to physical and functional characteristics of the GRNs.
Figure 3. Testing predicted physical and functional properties of GRNs.
(A) Summary of GRN assignments. For each in vivo gene expression cluster the assigned in silico GRN is shown in terms of associated TF logic gate architecture and fast or slow mRNA turnover rate (short or long half-life, T1/2).
(B) Results of experimental genome-wide mRNA half-life measurements using Actinomycin D, represented by percentage of genes in each cluster that have short (S) (< 6 hr) or long (L) (≥ 6 hr) mRNA half-lives on the indicated white-blue scale.
(C) De novo motif analyses identified the most highly enriched motifs (with indicated p-values) within −1.0 kb to 0.3 kb of transcriptional start sites. Similarly, the occurrence frequency of known motifs was evaluated from promoter regions as well as enhancers identified by the presence of H3K4me1 and absence of H3K4me3 peaks (ENCODE data).
(D) In silico gene expression profiles predicted by kinetic model v1 for the indicated stimuli and knockout conditions.
(E) Results from experimental genome-wide mRNA expression measurements to test the conditions simulated in (D). This dataset was obtained with primary wild-type (“WT”), IRF-deficient (ifnar−/−), NFκB-deficient (rela−/−crel−/−, rela−/−relb−/−crel−/−), and compound deficient (rela−/−crel−/−irf3−/−) MEFs stimulated with PDGFβ, TNF, IFNβ and LPS for 0, 1, 3 and 8 hours, as indicated. Whether the kinetic model v1 recapitulated the expression profile of each gene was assessed with the Spearman goodness of fit criterion and indicated on the right with yellow indicating passing and black not passing. This analysis indicated that model v1 does not well account for the expression profiles of gene clusters A and D.
Physical characteristics of GRNs include the presence of TF binding sites and the half-life of the mRNA. We measured mRNA half-lives using the transcription inhibitor actinomycin D; transcriptome-wide measurements (Figure S3) confirmed model predictions that clusters B and F contained predominantly short mRNA half-life genes, in contrast to clusters C and G (Figure 3B); however, for cluster D, there was poor agreement between model (long half-life) and experiment (mostly short). We then tested predictions regarding the presence of specific TF binding sites bioinformatically; unbiased de novo motif analysis of promoters found that the most over-represented sequences in cluster A conform to AP1 binding sites (Figure 3C), and motif searches with known TF binding matrices showed little enrichment of κB or IRE sequences in either promoter or enhancer sequences. In similar support of the model’s predictions, we found κB-sites enriched in clusters B and C, IREs in clusters F and G, and both IRE and κB sites in cluster E. However, we found only one sequence (conforming to a κB site) highly enriched in cluster D, although the model had predicted cluster D to contain AND gate genes controlled also by AP1 and IRF.
We further tested the model functionally by comparing predicted expression patterns following TF-deletion (Figure 3D) with expression profiles observed in cells with corresponding genetic perturbations (Figure 3E). We prepared primary MEFs from mouse embryos deficient in NFκB (NFκB−/−), IRF (IRF−/−), or both (NFκB−/−IRF−/−), each involving complex combination knockouts to ensure minimal residual activty by family members (see Methods), and profiled the transcriptome following stimulation with LPS and cytokines (Supplementary Table 2). Consistent with the model, NFκB−/− cells showed no LPS-induced activation of NFκB target genes (clusters B, C and D) and, as predicted by the simulations, only partial activation of the OR gate genes (cluster E). Similarly, IRF−/− cells showed no activation of IRF/ISGF3 target genes (clusters F and G), and only partial activation of the OR gate genes (cluster E); indeed, cluster E gene expression was only abolished in the compound NFκB−/−IRF−/− mutant cells. Remarkably, model fit scores for most clusters remained well above 70% with this extended dataset, supporting the original assignments for those clusters. However, cluster A and D fit scores dropped to 14 and 10%, respectively, indicating that the initial GRN assignments were likely incorrect.
Iterative model refinement: identification of a feedforward loop
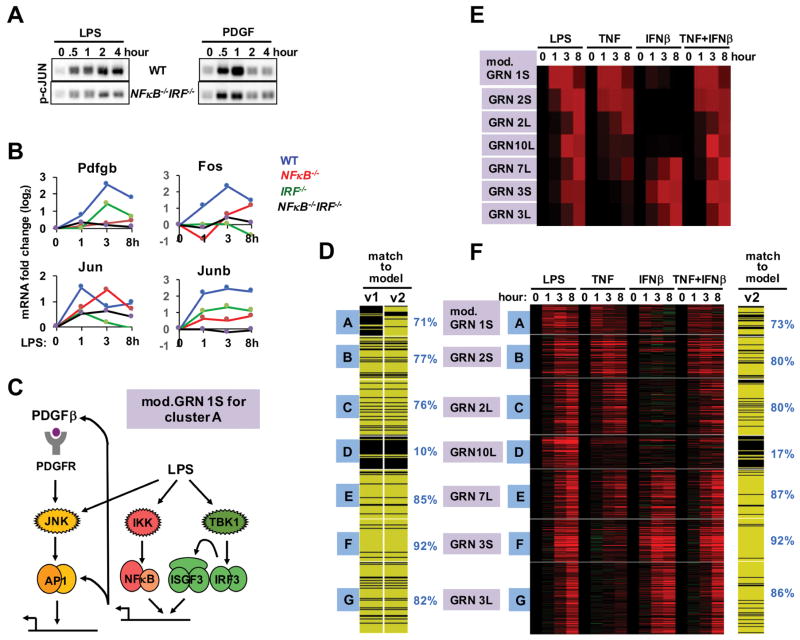
Addressing cluster A, we noted that gene expression was unexpectedly reduced in NFκB−/− and IRF−/− cells (Figure 3E). Testing for the activation of the relevant TF, AP1, we found deficiency in NFκB/IRF knockout cells in response to LPS, particularly at the later timepoints (2 and 4 hrs), and also, but to a lesser degree, in response to PDGF treatment (Figure 4A). As endogenous PDGF was reported to function in an autocrine manner during the LPS response (Chow et al., 2005), we examined whether IRF and NFκB contribute to the expression of the Pdgfb gene. We found a partial dependence on IRF and a severe dependence on NFκB (Figure 4B). In addition, NFκB and IRF was found to control the expression of AP-1 family members Jun, Fos, and JunB. These data suggest that NFκB, and to a lesser degree IRF, form a feedforward loop by inducing the expression of PDGFβ and AP1 components, thus amplifying and extending AP1 activity (Figure 4C). Including the NFκB-dependent feedforward activation of AP1 in response to LPS in the model significantly improved the fit for cluster A genes from 14% to 71% (Figure 4D).
Figure 4. A GRN involving coherent feedforward TF control.
(A) AP1 activity is NFκB- and IRF-dependent. Immunoblot of p-c-Jun using cell extracts prepared from WT and NFκB/IRF compound deficient (rela−/−crel−/−irf3−/−) MEFs stimulated with LPS (left) or PDGF (right) for the indicated times (representative of four experiments).
(B) Expression of PDGF and AP1 constituents is NFκB- and IRF-dependent. Microarray measurements of Pdgfb mRNA expression in WT (blue), NFκB-deficient (red, rela−/−crel−/−), IRF-deficient (green, ifnar−/−), or NFκB/IRF compound deficient (black, rela−/−crel−/−irf3−/−) MEFs stimulated with LPS (0.1 μg/ml) for 1, 3 and 8 hours were plotted as expression fold changes (log2) relative to unstimulated cells.
(C) Schematic of the modified GRN 1S, which depicts that cluster A is controlled by AP1, but that AP1 activity requires NFκB and IRF by controlling autocrine PDGF and AP1 constituents, forming coherent feedforward loop.
(D) Inclusion of interdependent TF control into model v2 increases the number of genes in cluster A that pass (yellow) the Spearman goodness of fit criterion.
(E) Testing the validity of GRN10L assigned to cluster D. Heatmap of predicted gene expression profiles of TNF and IFNβ co-stimulation, using model v2. The model predicts that the AND-gate containing GRN10L (thought to control cluster D) is responsive to the co-stimulation condition.
(F) Heatmap of experimental transcriptome data from wild-type MEFs in response to TNF and IFNβ co-stimulation at indicated times. Genes that passed (yellow lines) or did not pass (black lines) the goodness of fit criterion for model v2 including the co-stimulation dataset (percent of genes shown on the right). This analysis indicates that GRN10L does not represent the true regulatory logic underlying the expression control of cluster D.
Addressing cluster D, the GRN model of an AND gate between NFκB (or AP1) and IRF/ISGF3 fared poorly with the extended expression data (only 10% passed the fit threshold). We decided to address the AND gate hypothesis directly using a mixed TNF/IFNβ co-stimulation protocol in which both NFκB and IRF/ISGF3 are activated, mimicking the SDTF activation profiles in response to LPS (Figure S3). Indeed, such co-stimulation leads to a transcriptome that closely resembles that induced by LPS (Figure 4E), including cluster E, which our analysis suggests is governed by an OR-gate GRN between NFκB and IRF. However, contrary to model prediction, cluster D genes were not induced by the TNF/IFNβ co-stimulation protocol (Figure 4F). Drilling down into the fit of individual gene profiles to model predictions indicated that Spearman Rho correlation score distributions for each of the clusters were highest for the assigned GRN (Figure S4A), confirming that assignments of the available models were optimal, but that a large number of cluster D genes scored below the established threshold fit (Figure S4B). These genes did not score better with the OR gate model (GRN 7L), unlike the genes in cluster E, whose expression control was generally better accounted for by the OR gate model than the equivalent AND gate GRN 6L (Figure S4C).
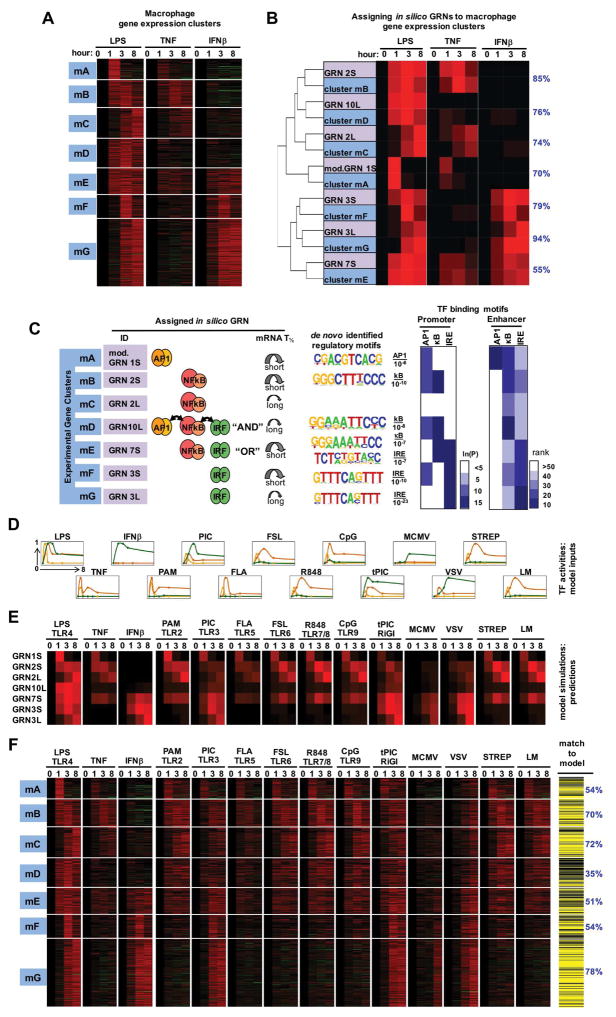
The SDTF GRN logic also applies to macrophage transcriptomes induced by pathogens
We next addressed whether the GRN models identified in fibroblasts may be applied to other cells also. Although fibroblasts have the experimental advantage that they can be isolated from mouse embryos and thus from genotypes that are embryonic lethal (e.g. NFκB knockouts), macrophages are considered the primary innate immune cells. Pathogen-responsive SRNs controlling SDTF activities are qualitatively conserved between fibroblasts and macrophages. To examine whether the GRNs identified in fibroblasts may also account for the endotoxin-responsive gene expression programs in macrophages, we analyzed transcriptomes in murine bone-marrow-derived macrophages (BMDMs) in response to LPS, TNF and IFNβ by next-generation RNA-sequencing (RNA-seq). We identified seven co-regulated gene clusters (mA to mG, Figure 5A), which showed distinct gene-ontology terms (Figure S5). We determined the inputs for the previously identified GRNs by measuring the SDTF activation profiles in macrophages as we had done for MEFs (Table S2), and produced GRN outputs of gene expression. By co-clustering expression profiles of measured gene clusters and GRNs, we found that the SDTF logic previously determined in MEFs well-matched measured gene expression profiles in macrophages, producing fit scores ranging from 55% to 94% (Figure 5B). Testing these predicted assignments by regulatory motif analysis in promoters and enhancers (Figure 5C) we confirmed that the mA cluster contained AP1 binding sites, mB and mC clusters contained κB sites, mF and mG contained IRE sites, and mE, the predicted GRN7L OR gate cluster, contained both κB and IRE motifs. However the predicted GRN10L AND gate cluster mD showed primarily a preponderance of only κB sites, as was also seen in the corresponding MEF cluster D.
Figure 5. Testing GRN models in predicting the transcriptomes of macrophages responding to diverse stimuli and pathogens.
(A) Gene expression clusters of endotoxin-induced transcriptome dissected by cytokine stimuli TNF and IFNβ. Bone marrow-derived macrophages (BMDMs) were stimulated with 100 ng/ml LPS, 10 ng/ml TNF, and 100 U/ml IFNβ; isolated mRNA was subjected to RNA-seq. Expression profiles from 782 genes, induced by LPS ≥3 fold at least one timepoint, were subjected to k-means clustering.
(B) Clusters of co-regulated genes were assigned best-matched GRNs by co-clustering GRN model outputs (using SDTF activity profiles as inputs) and the means of clusters mA - mG identified in (A). Shown on right in blue in the percentage of the in vivo gene expression profiles that are accounted for by the assigned in silico GRN (see methods).
(C) Summary of GRN assignments. For each in vivo gene expression cluster the assigned in silico GRN is shown in terms of TF logic gate architectures and mRNA half-life. De novo motif analyses identified the most highly enriched motifs (with indicated p-values) within −1.0 kb to 0.3 kb from transcriptional start sites. Similarly, the occurrence frequency of known motifs was evaluated from promoter regions as well as enhancers identified by the presence of H3K4me1 and absence of H3K4me3 peaks (ENCODE data).
(D) Measured SDTF activities in cells exposed to indicated stimuli and pathogens. Experimental data (table S2) is normalized to maximum.
(E) Computational simulations using the indicated GRN models and the TF activities depicted in (D) used as inputs.
(F) Testing GRN model predictions with new experimental datasets. Heatmap depicts the fold induction based on RNA-seq analysis of each of the 782 genes in each of the indicated are conditions. Genes that passed (yellow lines) or did not pass (black lines) the goodness of fit criterion (figure S5B) are shown on the right. Note that more than 50% of genes pass the Spearman fit score criterion in all clusters but mD (35%), to which the AND gate GRN10L was assigned.
To test whether these GRN models may be used to predict gene expression in response to a wider range of PAMPs as well as live pathogens, we measured macrophage SDTF activation profiles in response to each of seven additional PAMPs that are ligands for various members of the TLR family and the cytosolic sensor Rig-I, as well as the bacterial pathogens Strepococcus pneumoniae (STREP), and viral pathogens Listeria monocytogenes (LM), murine cytomegalovirus (MCMV), or vesicular stomatitis virus (VSV). Quantified SDTF trajectories (Figure 5D) were used as inputs for simulations with each of the seven models to produce predicted gene expression profiles (Figure 5E). We then measured the macrophage transcriptomic responses to these stimuli by RNA-seq with internal controls to allow for cross-comparisons (Figure 5F). In this manner we challenged the GRN models with 33 additional datasets. Remarkably, these diverse stimulation conditions elicited gene expression profiles that were largely accounted for by the previously assigned GRN models, with fit scores mostly remaining well above 50%, indicating that the identified GRN logic have broad relevance in accounting for pathogen-responsive gene expression programs.
However, the predicted GRN10L (AND gate) for cluster mD fared poorly, with fewer than 35% genes passing the Spearman fit score test. Thus both MEF and BMDM datasets contained a cluster of co-regulated genes that did not conform to the initially identified AND gate model GRN10 (Figure S6B), prompting further studies to develop a better model.
Iterative model refinement: an AND gate of nuclear and cytoplasmic control mechanisms
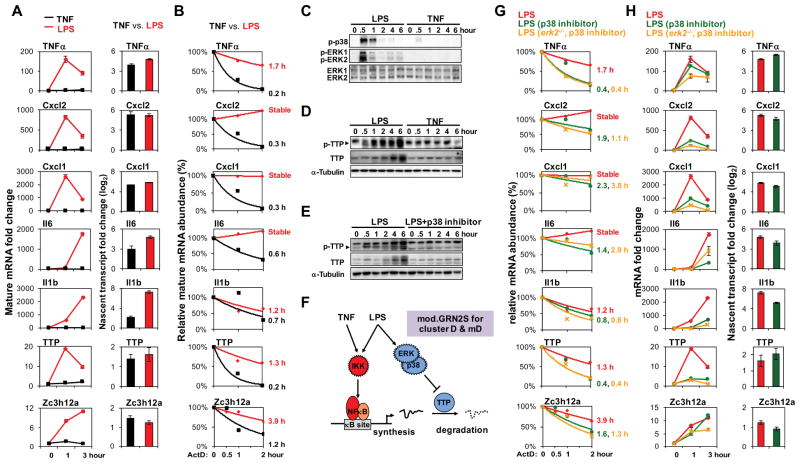
To investigate the regulatory mechanisms underlying cluster mD gene control, we examined the expression of a few representative genes (also present in corresponding MEF cluster D) by quantitative PCR. Their mRNA levels were indeed highly induced by LPS but not by TNF (Figure 6A). To examine expression control of these genes in more detail we measured nascent transcript levels and found to our surprise that several (e.g. TNFα, Cxcl2, Cxcl1) were equally induced by LPS and TNF, and for some others (e.g. IL6, IL1β) the difference was smaller than that observed for the mature mRNA. These data did not support the model of an AND gate controlling promoter activity and transcription, but instead suggested a post-transcriptional regulatory mechanism involving mRNA stability. We tested whether regulation might occur at the mRNA stability level by measuring mRNA half-lives using actinomycin D following TNF or LPS stimulation. Indeed, the aforementioned mRNAs showed very short half-lives in TNF-stimulated cells but LPS stimulation led to their stabilization (Figure 6B). mRNA stabilization may be regulated by p38- and ERK-dependent phosphorylation of the ARE binding protein TTP (Mahtani et al., 2001), which inhibits its interaction with the RNA decay machinery (Sandler and Stoecklin, 2008). Interestingly, in our analysis LPS induced much stronger activation of p38 and ERK than TNF (Figure 6C). Phosphorylation of TTP was specific to LPS (Figure 6D) and p38-dependent (Figure 6E). These results suggested a logical AND gate not of two TFs, but of two sequentially acting pathways: NFκB-driven pre-mRNA synthesis and p38-dependent mRNA stabilization (Figure 6F). Such a model is also consistent with a more detailed analysis recently described for the control of TNF expression (Caldwell et al., 2014), and several genes in this cluster contain AU-rich elements that are targeted by TTP in their UTRs. (However, other genes are known to be targets of other RNA decay mechanisms, mediated, for example, by Regnase/Zc3h12a.) Importantly, replacing the GRN10 AND gate of TFs with an AND gate model that combined stimulus-induced transcription and half-life stabilization (dubbed mod.GRN2) increased the percentage of genes that passed the goodness of fit threshold from 39 to 76%.
Figure 6. A GRN governed by an AND gate of stimulus-responsive mRNA synthesis and half-life control.
(A) Mature and nascent mRNA expression fold changes in BMDMs stimulated with TNF (10 ng/ml) or LPS (100 ng/ml). The shown data are representative of three independent experiments. The same stimulation conditions are used in all subsequent experiments.
(B) mRNA half-life measurements using the synthesis inhibitor actinomycin D in BMDMs stimulated with TNF (black) or LPS (red) for 30 minutes. The underlying qRT-PCR data was representative of three independent experiments. All mRNA half-lives were calculated within a 50% standard error by exponential regression analysis.
(C) Phospho-p38 (Thr180/Tyr182) and phospho-ERK1/ERK2 (Thr202/Tyr204) revealed by immunoblot of whole cell lysates prepared from stimulated BMDMs. ERK1 and ERK2 immunoblots are shown as loading controls. This is representative of three independent experiments performed by different individuals.
(D) and (E) Phospho-TTP (arrowhead), TTP and α-Tubulin (loading control) were analyzed by immunoblotting of whole cell lysates prepared from stimulated BMDMs with and without a p38 inhibitor (2.5 μM, SB202190). This is representative of three independent experiments performed by different individuals.
(F) A schematic of the AND gate between NFκB-driven transcription and LPS-specific activation of a p38/ERK- and TTP-dependent mRNA stabilization pathway. This is referred to as mod.GRN 2S, and its inclusion results in model v3.
(G) mRNA half-life measurements as in (B) in wild-type and erk2−/− BMDMs stimulated with LPS (red) for 30 minutes or in the presence of p38 inhibitor (green for wild-type and yellow for erk2−/−). The shown data are representative of three independent experiments.
(H) Mature and nascent mRNA expression fold changes in wild-type or erk2−/− BMDMs stimulated with LPS, in the absence (red) or presence of p38 inhibitor (green for wild-type and yellow for erk2−/−). The shown data are representative of three independent experiments.
Consistent with this model, we determined that LPS-induced mRNA stabilization was p38/ERK-dependent (Figure 6G). We found that LPS-specific induction of mRNAs was attenuated by p38 inhibitors in WT or erk2−/− BMDMs, while LPS-induced nascent transcript induction of TNFα, Cxcl2, Cxcl1, and TTP was unaffected (Figure 6H). Nascent transcript induction of IL6 and IL1β was slightly reduced by p38 inhibition and may relate to their control via a p38-dependent TF (Kim et al., 2008).
Delineating the GRN logics that decode pathogen-responsive intra-cellular signals
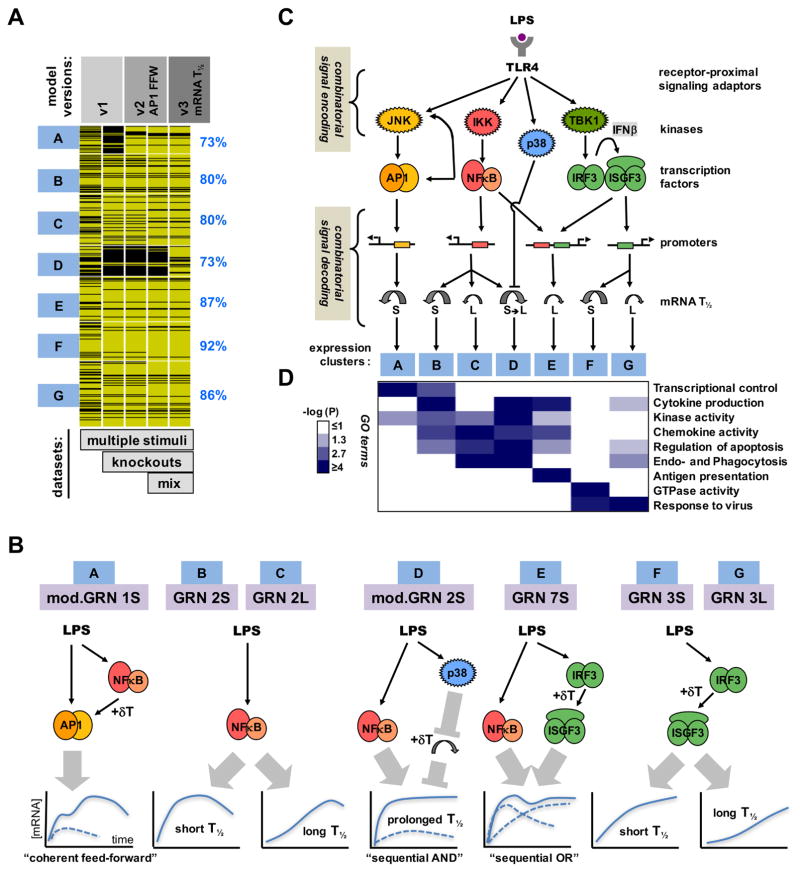
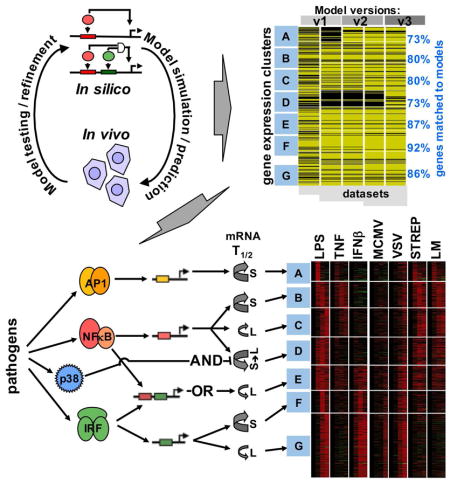
Using simple kinetic models we analyzed an expanding expression dataset of endotoxin-induced genes (714 in MEFs and 782 in BMDMs) in response to diverse stimuli and genetic knockout scenarios. In MEFs, the performance of the models improved with each iteration as ascertained by the increased rank correlations over a larger number of datasets to be satisfied (Figure 7A and Figure S7A). The last model of this series accounted for the observed timecourses of induction of the majority of LPS-responsive genes (84%) in 27 different conditions involving diverse stimulus and genetic perturbations. According to our resutls, most GRNs appear to be responsive to just one of the three SDTFs (Figure 7B): AP1 (cluster A), NFκB (clusters B, C and D) and IRF/ISGF3 (clusters F and G), with differences in mRNA half-life providing for further diversification in stimulus-responsiveness. Only cluster E shows combinatorial control by SDTFs; the OR gate logic implies that NFκB and IRF/ISGF3 function independently rather than cooperatively, though it is coordinated: NFκB and ISGF3 engage with the OR gate sequentially, prompting the term “sequential OR gate”. Two other gene clusters appear to be controlled by logic gates that were not initially considered: Cluster A involves an NFκB-dependent pathway for enabling AP1 activation, and thus may be described as a “coherent feedforward gate”; it allows signal integration at the level of JNK or AP1 rather than at the target gene DNA. Cluster D is controlled by an unconventional AND gate formed by NFκB and the p38 signaling axis which controls mRNA half-life in a stimulus-specific manner. Signal integration does not occur on the target gene promoter but within the sequential enzymatic steps of the reaction cascade that determines the abundance of mature mRNA, hence prompting the term “sequential AND gate”.
Figure 7. Iterative modeling of pathogen-responsive GRNs reveals combinatorial control mediated by sequentially acting regulatory mechanisms.
(A) Tracking the performance of iterative models with increasing datasets. Genes associated with expression clusters A to G passed (yellow lines) or did not pass (black lines) the Spearman goodness of fit criterion in successive GRN model versions and an increasing number of experimental “-omic” datasets generated in indicated perturbation studies, such as “multiple stimuli” (Figure 2), “knockouts” (Figure 3), and “mixed” stimuli (Figure 4). The fraction of genes that pass the goodness of fit Spearman correlation criterion for model v3 (including mod.GRN1S and mod.GRN2S) is shown on the right.
(B) Schematics of the GRNs that govern expression of genes in clusters A to G in MEFs and macrophages. (Schematic expression profiles are indicated as a solid blue line for wild-type cells, or as dashed lines in cells lacking one of the modifying pathway.) Cluster A expression is driven by AP1 which is controlled by a “coherent feed-forward” gate involving NFκB-driven autocrine PDGF which introduces a delay relative to the direct activation pathway. Clusters B, C and D are NFκB-driven, but specificity is generated by distinct mRNA half-life control. LPS-responsive p38-mediated inhibition of mRNA decay combines with LPS-responsive NFκB-mediated mRNA synthesis to form a “sequential AND” gate in the GRN for cluster D. Cluster E is driven by NFκB and IRF, forming a “sequential OR” gate between a rapidly activated immediate-early TF (NFκB) and a delayed, protein-synthesis-dependent TF (ISGF3). Cluster F and G are ISGF3-driven, but specificity is generated by distinct mRNA decay rates.
(C) A summary schematic of signal encoding and decoding via SRNs and GRNs, respectively. Combinatorially encoded signals are decoded not only by the promoter architecture of TF binding sites, but also by signal-responsive mRNA half-life control.
(D) Gene expression clusters are associated with distinct physiological functions. Highly enriched gene ontology (GO) terms were evaluated based on -log10 p-values as indicated on the white-blue scale.
The resulting functional network map (Figure 7C) allows us to pinpoint key molecular mechanisms involved in the processing and interpretation of intracellular signals that transduce the presence of endotoxin to produce complex gene expression programs. SRNs determine which precise combination of signal transducers is activated in response to each stimulus; they “encode” a combinatorial code of signaling pathways via the TLR4-associated adaptors MyD88 and TRIF. Our results reveal that GRNs “decode” this combinatorial code not only via the TF binding sites within promoters, but also through cytoplasmic events that control mRNA half-life (e.g. cluster D, that may be described as a “sequential AND” gate).
DISCUSSION
The unresolved challenge of relating physical genome-wide TF-DNA interactions to the expression of genes (Jaimovich and Friedman, 2011) is thought to be a key impediment for the development of predictive GRN models. We focused here on the functional inputs and output of GRNs, i.e. SDTF activity and mRNA abundance measurements, and found that the inclusion of cytoplasmic and cross-regulatory events is critical for developing predictive models of pathogen-responisve gene expression programs. By iteratively testing a series of models with an expanding sets of expression data, we began to delineate how signaling activities generated by receptor-proximal SRNs are interpreted by GRNs to produce mRNA. Specifically, we delineated the combinatorial logic of signal-dependent regulatory mechanisms and found that they function sequentially rather than coincidently within logical OR and AND gates.
Our analysis indicated that none of the seven clusters of co-regulated genes involve synergistic or cooperative functions between the SDTFs NFκB and ISGF3. Similarly, studies of the multi-κB site-containing IκBα gene failed to provide support for cooperative NFκB function (Giorgetti et al., 2010), and recent biophysical (Panne et al., 2007) and genetic studies (Wang et al., 2010; Wang et al., 2007) of the interferon-β gene do not support the notion that cooperative and coincident binding of NFκB, IRF and AP1 control this enhancer. However, our study supports a broader notion of a combinatorial code that is not restricted to coincident molecular events but in fact involves sequential molecular events, such as NFκB-responisve transcription and p38-responsive halfllife control (cluster D), or NFκB-responsive and then ISGF3-responsive transcriptional control in (cluster E). This broader notion of combinatoral control of gene expression was previously proposed (Herschlag and Johnson, 1993) and suggests that combinations of TF binding sites found frequently in the genome (Ravasi et al., 2010) may mediate control at sequential steps in the regulation of gene expression, and not necessarily imply direct cooperative interactions between the TFs.
The kinetic notion of how combinatorial control of gene expression is achieved calls for both renewed experimental and theoretical efforts to develop a predictive understanding of gene expression. Specifically, further work needs to develop appropriate theoretical frameworks that go beyond the thermodynamic formalism employed here (Bintu et al., 2005a; Bintu et al., 2005b). Instead of assuming that there is a single rate limiting recruitment step, our work suggests that we need a mathematical formalism that accounts for the multi-step control of gene expression control, including explicit formulation of enhancer formation, preinitiation complex (PIC) formation, transcription initiation, elongation, or pre-mRNA processing (e.g. (Scholes et al., 2016)). Experimentally, the kinetic notion of combinatorial contol of gene expression calls for a systematic categorization of TFs based on the kinetic step that they accelerate to control gene expression (e.g. establishing poised enhancers, enhancer-promoter interactions, accelerating initiation, or transcriptional elongation). One might expect that TFs affecting distinct steps are more likely to function synergistically to provide stimulus-specific control of gene expression, whereas TFs affecting the same step are more likely to form OR gates to regulate the temporal changes in mRNA abundance (as NFκB and ISGF3 on cluster E). Interestingly, the Smale group recently found that IRF3 has the propensity to open chromatin on the CCL5 locus which then facilitates the binding of NFκB to activate transcription (Tong et al., 2016); though the IRF3 requirement is not complete and thus did not emerge as an AND gate in our analysis, the new data illustrates the need for a kinetic formalism in which multiple steps may potentially be “rate-limiting”.
We applied the described systems biology workflow to the transcriptomic responses in two cell types that function as sentinels for the pathogen response, and produce partially overlapping gene expression programs. Although the gene expression programs are distinct, the majority of genes induced in both cell types (but not all) show the same control logic (Figure S7B). Those that show distinct regulatory logic may potentially involve distinct enhancers in the two cell types. Overall, our results suggest that differences between stimulus-responsive gene expression in MEFs and BMDMs are primarily due to lineage-determing transcription factors (LDTF)-mediated establishment of cell type-specific enhancer landscapes (Ghisletti et al., 2010; Heinz et al., 2010; Jin et al., 2011; Natoli et al., 2011) rather than SDTF control. Nevertheless, we note that fit-scores to the macrophage dataset, which involved a greater variety of stimuli, were generally lower than the MEF dataset, indicating that additional SDTFs and regulatory mechanisms may play a more important role in macrophages than in MEFs.
The mathematical models presented here constitute sufficiency tests, identifying regulatory mechanisms that together are sufficient to account for a given set of experimental observations. We have used these models to make testable predictions, allowing for iterative refinement. Thus datasets from additional pertubation studies may lead to the inclusion of additional TFs and regulatory mechanisms in future iterations of the models. For example, this may reveal distinctions in transcriptional control by NFκB family members RelA vs cRel vs RelB (Almaden et al., 2016; Alves et al., 2014) or IRF3 vs ISGF3 (Ourthiague et al., 2015). Further, challenging the model to account for longer timecourses may require inclusion of a variety of late inducible TFs such as ATF3 (Gilchrist et al., 2006), CEBPβ and CEBPδ (Litvak et al., 2009) as well as LDTFs leading to the establishment of poised enhancers and promoters (Garber et al., 2012; Kaikkonen et al., 2013; Miele and Dekker, 2008). Further, the functional description of GRNs responsible for gene control provides a starting point for the ultimate goal of developing gene-specific mechanistic models based on physical TF binding events within promoters and enhancers connected by looped chromatin structure. However, the coarse level modeling achieved here also has advantages: as the functional GRN models described here use numerically defined inputs of TF activity profiles (based on experimental measurements), they are easily linked to models of associated SRNs whose outputs are those same TF activities (e.g.; (Basak et al., 2012; Caldwell et al., 2014) paving the way for whole cell models that account for the cellular response to pathogens.
STAR Methods
CONTACT FOR REAGENTS AND RESOURCE SHARING
The Lead Contact A.H. is willing to distribute all materials, datasets, software and analysis tools, and protocols used in the manuscript. Requests should be made directly to Alexander Hoffmann at ahoffmann@ucla.edu or by mail at Institute for Quantitative and Computational Biosciences, University of California Los Angeles, 611 S Charles E. Young Dr. Los Angeles, CA 90095.
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Fibroblast Cell Culture
Primary MEFs were prepared from male or female E12–E14 embryos from C57BL/6 mice that were WT (wild-type), NFκB−/− (rela−/−crel−/− or rela−/−relb−/−crel−/−), IRF−/− (ifnar−/−) and NFκB−/−IRF−/− (rela−/−crel−/−irf3−/−), and cultured in DMEM containing 10% BCS for 5–6 passages before being stimulated (Werner et al., 2005).
Macrophage Cell Culture
Primary BMDMs were prepared by culturing bone marrow cells from femurs of male or female 8–12 week old WT mice in L929-conditioned medium by standard methods (Cheng et al., 2011; Ourthiague et al., 2015). BMDMs were stimulated on day 8.
Animal Use
Animals were housed in isolator cages and regularly confirmed to be pathogen-free. The animal protocols for this study were approved by the University of California, San Diego Animal Care and Use Committee.
METHOD DETAILS
Mathematical Modeling
We developed a series models to describe the Gene regulatory Networks (GRNs) controlling the cellular transcriptomic response to LPS. Version 1 (v1) refers to the initial suite of 17 GRN models, some of which were found to adequately account for experimentally determined gene expression profiles in a variety of conditions. v2 includes a feedforward loop in model GRN1S by which NFκB and IRF control AP1 activation to describe the gene expression behavior of cluster A genes. v3 includes LPS-specific control of mRNA half-life in GRN2S to describe the gene expression behavior of cluster D genes. The models were coded in Mathematica 7.0 (Wolfram Research, Urbana, IL), and are available for download (Data S1).
GRN Model Formulation
We developed a suite of 17 GRN models that combine a thermodynamic expression for promoter activity and a kinetic expression for promoter-driven mRNA synthesis and first order mRNA degradation.
Briefly, mRNA abundance for gene i is described by an ordinary differential equation (ODE):
| (S1) |
where fi(t)is the fractional (≥ 0, ≤1) promoter activity at time t, kisyn is the maximal synthesis rate constant, and kideg is equal to ln(2)/half-life of the mRNA. Parameter kisyn was assigned a numerical value equal to kideg to normalize mRNA abundance levels regardless of mRNA half-life.
Promoter activity fi for each GRN was modeled with thermodynamic expressions (Bintu et al., 2005a; Mayo et al., 2006), describing logical gates (f1, f2AND, f2OR, f3AND, f3OR, and combined gates), in which TF1, TF2, TF3 could be any of AP1, NFκB or IRF, thus yielding 17 possible GRN models.
| (S2) |
| (S3) |
| (S4) |
| (S5) |
| (S6) |
| (S7) |
| (S8) |
| (S9) |
GRN Model Simulations
Piecewise functions based on experimental measurements of TF activities (Tables S1 and S2) were used as model simulation inputs. In all cases, we scaled the temporal profiles of TF activities to span a range of 0.05 to 1 (20-fold) in arbitrary units to avoid assay-specific reductions of dynamic range. Initial model simulations used an ad-hoc parameter value of 0.5 for each KTF (TF-DNA binding site interactions) to ensure that the scaled inputs fall within the responsive range of the GRN model dose-response curve. To simulate the transcription factor activity in knockout cells we eliminated the corresponding activation profile from the inputs; for instance NFκB activity was set to zero for all stimuli for the NFκB knockouts.
Assignments of GRN Models to Experimental Gene Expression Clusters
Initial GRN assignment was based on the best fit between GRN simulations of mRNA profiles and the average of each experimentally determined gene expression cluster. Co-clustering of in vivo and in silico gene expression profiles (Figure 2E, 2H, 5B) was performed by hierarchical clustering (Manhattan distance). For comparisons with the preliminary Boolean model (Figure 2C), in vivo expression data were digitized based on whether the maximum expression level within each timecourse passed above the threshold of 0.5.
GRN Model Maturation
GRN models were matured through parameter optimization to maximize the fit score. Optimal values for KTF’s and kideg were determined by simultaneous minimization of the total deviation between the time-dependent normalized average mRNA levels for the clusters and the normalized mRNA levels produced by the assigned GRN models. Optimization was performed simultaneously for the LPS, PDGF, TNF, and IFN conditions. Numerical minimization was performed with the NMinimize function using the Nelder-Mead algorithm. For each transcription factor, affinity (KTF) was treated as a free parameter but the same value was used for all GRN models.
Evaluating the Goodness of Model Fits
Spearman rank correlation coefficient (rho) was used to evaluate the goodness of fit between the model and individual mRNA measurements comprising each cluster. Briefly, for each individual gene, a vector was built containing normalized mRNA measured at various time points for the collection of conditions (stimuli, perturbation, etc.) specified for each model iteration (see main text). The Spearman correlation coefficient was calculated by comparing this vector with a similar one built out of mRNA levels predicted by the model assigned to the cluster containing the gene being evaluated. Fits with Spearman rho values over 0.5 within a 1% confidence level (Fisher CI test) were considered good. For reference, mRNA dynamics experimentally determined for individual genes are compared with predicted GRN activity in figure S4B and S6B. Despite intra-cluster variability in the expression levels for individual genes, the patterns of expression for the various conditions are remarkably similar justifying the choice of a rank test as an adequate metric for goodness of fit.
Iterative model refinement from version 1 to versions 2 and 3
Following evaluation of model v1 (Figure 3 and 4), refinements led to two successive model versions. In model v2, AP1 activity was reduced 10-fold in the NFκB KO and NFκB/IRF3 KO scenarios. In model v3, for cluster D GRN10L was replaced by mod.GRN2S, which is a GRN2S model in which the half-life was extended to 8hs at t=0 in all simulations in which the Myd88-pathway is activated.
Experimental Procedures
Fibroblast stimulation conditions
MEFs were stimulated with 0.1 μg/ml LPS, 500 U/ml murine IFNβ, 50 ng/ml human PDGFB/B, or 10 ng/ml murine TNF.
Macrophage stimulation conditions
BMDMs were stimulated with 0.1 μg/ml LPS, 100 U/ml murine IFNβ, or 10 ng/ml murine TNF, as well as with a TLR2/1 agonist, the synthetic triacylated lipoprotein Pam3CSK4 (PAM) (3 μg/ml); a TLR2/6 agonist, a synthetic lipoprotein derived from Mycoplasma salivarium, FSL-1 (FSL) (50 ng/ml); a TLR3 agonist, low molecular weight polyinosine-polycytidylic acid (Poly(I:C) (PIC), 50 μg/ml); a TLR5 agonist, recombinant flagellin (FLA) from Salmonella typhimurium (30 ng/ml); a TLR7/8 agonist, the imidazoquinoline compound R848 (5 μg/ml); a TLR9 agonist, the synthetic CpG ODN 1668 (CpG, 100 mM); the Rig-I agonist transfected Poly(I:C) (tPIC) using the Lipofectamine 2000 kit per the manufacturer’s instructions (Poly(I:C) 50 μg/ml, Life Technologies); live Strepococcus pneumoniae (MOI 1.0), live Listeria monocytogenes (LM) (MOI 1.0), murine cytomegalovirus (MCMV, MOI 5.0), or vesicular stomatitis virus (VSV, MOI 1.0).
Biochemical assays
Western blotting analysis and EMSAs were conducted with standard methods as described previously for fibroblasts (Basak et al., 2007; Hoffmann et al., 2003) and macrophages (Cheng et al., 2011). Briefly, whole cell lysates were made with RIPA buffer; nuclear extracts by hypotonic cell lysis and high salt extraction of nuclear proteins. Experimental measurements of TF activities (Figure S2) triggered by LPS, TNF, PDGF and IFNβ stimulation are provided in Table S1 for MEFs. Table S2 lists the TF activation profiles for all stimuli used for BMDMs.
Fibroblast Transcriptome Analyses
MEF RNA was isolated with Qiagen RNeasy kit and hybridized to Illumina mouse RefSeq Sentrix-8 V1.1 BeadChips at the UCSD Biogem facility. Microarray data were normalized, and probes with ≥ 2 fold change in expression with LPS stimulation in all three wild-type samples were selected (Table S3, S4). All array data was deposited at GEO under accession number GSE35521. Genes showing a ≥2 fold increase at any one time point upon LPS stimulation were selected for subsequent analysis.
Macrophage Transcriptome Analyses
BMDM RNA was isolated with Qiagen RNeasy kit, mature mRNA was purified from 2 μg total RNA using oligo(dT) magnetic beads and fragmented at high temperature using divalent cations. The cDNA library was generated using the Illumina TruSeq kits and quantitation was performed using Roche Light Cycler 480. Sequencing was performed on Illumina’s HiSeq 2000 according to the manufacturer’s recommendations by the University of California, San Diego Biogem facility. Paired-end 100 nt reads were subjected to quality control steps (adaptor sequences were removed with cutadapt, ends with poor quality scores were trimmed with scythe) before alignment to the mouse genome mm10 with gencode vM4 annotations using the STAR aligner. Post alignment quality control was done to remove multimappers, low-quality mappers (< 30) and ribosomal RNA reads. htseq-count (union mode) was used to determine the per-gene raw read counts. For subsequent analyses raw reads counts were normalized to counts per million (cpm) values, and genes showing a ≥3 fold increase in BMDMs at any timepoint upon LPS stimulation were selected (Table S5). All RNA-seq raw and processed data was deposited at GEO under accession number GSE68318.
Quantitative PCR analyses
Total RNA was isolated using Qiagen RNeasy kit from MEFs or BMDMs that had been treated as indicated. RNA was reverse transcribed with Superscript II reverse transcriptase (Invitrogen) and resulted cDNA was used for real-time qPCR analysis (SYBRgreen). Nascent transcript assays were conducted as described previously (Giorgetti et al., 2010) with BMDMs stimulated for 30 minutes or 2 hours with 0.1 μg/ml LPS or 10 ng/ml TNF. Chromatin-associated transcripts were extracted with TRIzol reagent (Invitrogen) and treated with DNase I before the RT reaction. qPCR primers were specific for pre-mRNA. Primer sequences are shown in Table S6.
QUANTIFICATION AND STATISTICAL ANALYSIS
Expression analysis
Fold changes were clustered (in log2 scale) by K-means using absolute Pearson correlation as a similarity metric with manual curation. Co-clustering of in vivo and in silico gene expression profiles (Figure 2E, 2H, 5B) was performed by hierarchical clustering (Manhattan distance) comparing model simulation outputs with mean expression level of the in vivo expression clusters relative to basal wild-type. For comparisons with the preliminary Boolean model (Figure 2C), in vivo expression data were digitized based on whether the maximum expression level within each timecourse passed above the threshold of 0.5.
mRNA hall-life analysis
Half-lives of mRNAs (Figure 3B, 6B, 6G) were determined by fitting a first order exponential decay equation to qPCR or microarray expression measurements from unstimulated MEFs or BMDMs stimulated with 10 ng/ml TNF or 0.1 μg/ml LPS for 2 hours then treated with Actinomycin D for 1 hour or in the indicated timecourse. Genes for which mRNA levels increased by the first timepoint of Actinomycin treatment (presumably due to confounding drug-induced stress responses) were removed from the calculations.
Motif analysis
De novo motif searches and known motif searches using JASPAR matrixes were performed with the promoter sequences 1 kb upstream and 0.3 kb downstream of the transcription start site with the motif search program Homer (Heinz et al., 2010). An in-depth description and benchmarking of this software suite can be found at homer.salk.edu/homer. Enhancer-based motif search: Enhancers were identified by the presence of H3K4me1 and absence of H3K4me3 peaks (Mouse ENCODE datasets for MEFs and BMDMs, available at www.mouseencode.org). Regions proximal to the TSS (1 kb upstream and 0.3 kb downstream), which had already been used for motif analysis in promoters, were excluded from the enhancer definition. Known motif analysis was performed using Homer, using all enhancers as background, and only enhancers within 50 kb from the TSS of genes regulated by a given GRNs as foreground. The 264 known motifs searched by Homer were ranked by p-value, then scaled to a 1–100 range in order to report a rank percentile. In Homer’s database, AP1 is represented by motifs AP1(bZIP) and Jun-AP1(bZIP); p65 NFκB by motifs NFκB-p65(RHD) and NFκB-p65-Rel(RHD); and IRF/IRE by motifs ISRE(IRF) and T1ISRE(IRF). TF rankings resulted from averaging the rankings of related motifs.
Gene ontology (GO) analysis
GO term enrichment was performed using DAVID with the entire mouse genome as the background, and P values represent a Bonferroni-corrected modified Fisher’s exact test. The 1–2 most enriched GO terms were selected for each cluster.
DATA AND SOFTWARE AVAILABILITY
All array data was deposited at GEO under accession numbers GSE35521 and GSE68318. The model code in Mathematica and R is available upon request. The Mathematica file containing the mechanistic modeling approach is available for download (Data S1).
Supplementary Material
HIGHLIGHTS.
Model-aided analysis identifies the TF logic controlling pathogen-responsive genes
Combinatorial TF logic seems to not involve coincident, but sequential interactions
Gene expression models must include post-transcriptional regulatory processes
Kinetic models may be iteratively refined and applied to different cell types
Acknowledgments
We thank Dr. Chris Benner for guidance in using the Homer motif search program, Dr. Gioacchino Natoli (IFOM-IEO, Italy) for the nascent transcript protocol, Dr. Paul Anderson (Brigham and Women’s Hospital) for the phospho-TTP antibody, Dr. Jiahuai Han (Scripps Research Institute) for the TTP antibody, Chiung-Fang Chang and Steven M. Hedrick for ERK-deficient cells, Aakash K. Patel and Bing Xia for technical assistance, and Paul Loriaux, Chris Glass, and Bing Ren for helpful suggestions. The work was supported by NIH grants P50 GM085763, P50 AR063020, U01 AI124319, R01 AI127864, R01 GM117134 (A.H.), a Department of Defense Breast Cancer Predoctoral Training Fellowship (C.S.C.), a Cancer Research Institute postdoctoral fellowship (M.B.), and a Quantitative and Computational Biosciences (QCB) Collaboratory Fellowship (R.S.).
Footnotes
AUTHOR CONTRIBUTIONS
A.H., C.S.C. and M.B. designed the study. C.S.C. undertook all experiments, except for those shown in Figure 5, which were done by K.F. M.B. developed the model fitting and evaluation workflow. G.S. applied the modeling to macrophage datasets. C.S.C., M.B., G.S. and R.S. did bioinformatics analyses. A.H., C.S.C. and M.B. wrote the manuscript.
Supplemental Information includes seven figures and five tables and can be found with this article online at
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Almaden JV, Liu YC, Yang E, Otero DC, Birnbaum H, Davis-Turak J, Asagiri M, David M, Goldrath AW, Hoffmann A. B-cell survival and development controlled by the coordination of NF-kappaB family members RelB and cRel. Blood. 2016;127:1276–1286. doi: 10.1182/blood-2014-10-606988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alves BN, Tsui R, Almaden J, Shokhirev MN, Davis-Turak J, Fujimoto J, Birnbaum H, Ponomarenko J, Hoffmann A. IkappaBepsilon is a key regulator of B cell expansion by providing negative feedback on cRel and RelA in a stimulus-specific manner. J Immunol. 2014;192:3121–3132. doi: 10.4049/jimmunol.1302351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amit I, Garber M, Chevrier N, Leite AP, Donner Y, Eisenhaure T, Guttman M, Grenier JK, Li W, Zuk O, et al. Unbiased reconstruction of a mammalian transcriptional network mediating pathogen responses. Science. 2009;326:257–263. doi: 10.1126/science.1179050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arkin A, Ross J. Computational functions in biochemical reaction networks. Biophys J. 1994;67:560–578. doi: 10.1016/S0006-3495(94)80516-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basak S, Behar M, Hoffmann A. Lessons from mathematically modeling the NF-kappaB pathway. Immunol Rev. 2012;246:221–238. doi: 10.1111/j.1600-065X.2011.01092.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basak S, Kim H, Kearns JD, Tergaonkar V, O’Dea E, Werner SL, Benedict CA, Ware CF, Ghosh G, Verma IM, et al. A fourth IkappaB protein within the NF-kappaB signaling module. Cell. 2007;128:369–381. doi: 10.1016/j.cell.2006.12.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhatt DM, Pandya-Jones A, Tong AJ, Barozzi I, Lissner MM, Natoli G, Black DL, Smale ST. Transcript dynamics of proinflammatory genes revealed by sequence analysis of subcellular RNA fractions. Cell. 2012;150:279–290. doi: 10.1016/j.cell.2012.05.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bintu L, Buchler NE, Garcia HG, Gerland U, Hwa T, Kondev J, Kuhlman T, Phillips R. Transcriptional regulation by the numbers: applications. Curr Opin Genet Dev. 2005a;15:125–135. doi: 10.1016/j.gde.2005.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bintu L, Buchler NE, Garcia HG, Gerland U, Hwa T, Kondev J, Phillips R. Transcriptional regulation by the numbers: models. Curr Opin Genet Dev. 2005b;15:116–124. doi: 10.1016/j.gde.2005.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borden EC, Sen GC, Uze G, Silverman RH, Ransohoff RM, Foster GR, Stark GR. Interferons at age 50: past, current and future impact on biomedicine. Nat Rev Drug Discov. 2007;6:975–990. doi: 10.1038/nrd2422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bradley JR. TNF-mediated inflammatory disease. J Pathol. 2008;214:149–160. doi: 10.1002/path.2287. [DOI] [PubMed] [Google Scholar]
- Buchler NE, Gerland U, Hwa T. On schemes of combinatorial transcription logic. Proc Natl Acad Sci U S A. 2003;100:5136–5141. doi: 10.1073/pnas.0930314100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caldwell AB, Cheng Z, Vargas JD, Birnbaum HA, Hoffmann A. Network dynamics determine the autocrine and paracrine signaling functions of TNF. Genes Dev. 2014;28:2120–2133. doi: 10.1101/gad.244749.114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carey M, Lin YS, Green MR, Ptashne M. A mechanism for synergistic activation of a mammalian gene by GAL4 derivatives. Nature. 1990;345:361–364. doi: 10.1038/345361a0. [DOI] [PubMed] [Google Scholar]
- Cheng CS, Feldman KE, Lee J, Verma S, Huang DB, Huynh K, Chang M, Ponomarenko JV, Sun SC, Benedict CA, et al. The specificity of innate immune responses is enforced by repression of interferon response elements by NF-kappaB p50. Sci Signal. 2011;4:ra11. doi: 10.1126/scisignal.2001501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chow EK, O’Connell RM, Schilling S, Wang XF, Fu XY, Cheng G. TLR agonists regulate PDGF-B production and cell proliferation through TGF-beta/type I IFN crosstalk. EMBO J. 2005;24:4071–4081. doi: 10.1038/sj.emboj.7600867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garber M, Yosef N, Goren A, Raychowdhury R, Thielke A, Guttman M, Robinson J, Minie B, Chevrier N, Itzhaki Z, et al. A high-throughput chromatin immunoprecipitation approach reveals principles of dynamic gene regulation in mammals. Mol Cell. 2012;47:810–822. doi: 10.1016/j.molcel.2012.07.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghisletti S, Barozzi I, Mietton F, Polletti S, De Santa F, Venturini E, Gregory L, Lonie L, Chew A, Wei CL, et al. Identification and characterization of enhancers controlling the inflammatory gene expression program in macrophages. Immunity. 2010;32:317–328. doi: 10.1016/j.immuni.2010.02.008. [DOI] [PubMed] [Google Scholar]
- Gilchrist M, Thorsson V, Li B, Rust AG, Korb M, Roach JC, Kennedy K, Hai T, Bolouri H, Aderem A. Systems biology approaches identify ATF3 as a negative regulator of Toll-like receptor 4. Nature. 2006;441:173–178. doi: 10.1038/nature04768. [DOI] [PubMed] [Google Scholar]
- Giorgetti L, Siggers T, Tiana G, Caprara G, Notarbartolo S, Corona T, Pasparakis M, Milani P, Bulyk ML, Natoli G. Noncooperative interactions between transcription factors and clustered DNA binding sites enable graded transcriptional responses to environmental inputs. Mol Cell. 2010;37:418–428. doi: 10.1016/j.molcel.2010.01.016. [DOI] [PubMed] [Google Scholar]
- Heinz S, Benner C, Spann N, Bertolino E, Lin YC, Laslo P, Cheng JX, Murre C, Singh H, Glass CK. Simple combinations of lineage-determining transcription factors prime cis-regulatory elements required for macrophage and B cell identities. Mol Cell. 2010;38:576–589. doi: 10.1016/j.molcel.2010.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heinz S, Romanoski CE, Benner C, Allison KA, Kaikkonen MU, Orozco LD, Glass CK. Effect of natural genetic variation on enhancer selection and function. Nature. 2013;503:487–492. doi: 10.1038/nature12615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herschlag D, Johnson FB. Synergism in transcriptional activation: a kinetic view. Genes Dev. 1993;7:173–179. doi: 10.1101/gad.7.2.173. [DOI] [PubMed] [Google Scholar]
- Hoffmann A, Leung TH, Baltimore D. Genetic analysis of NF-kappaB/Rel transcription factors defines functional specificities. EMBO J. 2003;22:5530–5539. doi: 10.1093/emboj/cdg534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ideker T, Galitski T, Hood L. A new approach to decoding life: systems biology. Annu Rev Genomics Hum Genet. 2001;2:343–372. doi: 10.1146/annurev.genom.2.1.343. [DOI] [PubMed] [Google Scholar]
- Jaimovich A, Friedman N. From large-scale assays to mechanistic insights: computational analysis of interactions. Curr Opin Biotechnol. 2011;22:87–93. doi: 10.1016/j.copbio.2010.10.017. [DOI] [PubMed] [Google Scholar]
- Jin F, Li Y, Ren B, Natarajan R. PU.1 and C/EBP{alpha} synergistically program distinct response to NF-{kappa}B activation through establishing monocyte specific enhancers. Proc Natl Acad Sci U S A. 2011;108:5290–5295. doi: 10.1073/pnas.1017214108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson AD, Meyer BJ, Ptashne M. Interactions between DNA-bound repressors govern regulation by the lambda phage repressor. Proc Natl Acad Sci U S A. 1979;76:5061–5065. doi: 10.1073/pnas.76.10.5061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaikkonen MU, Spann NJ, Heinz S, Romanoski CE, Allison KA, Stender JD, Chun HB, Tough DF, Prinjha RK, Benner C, et al. Remodeling of the enhancer landscape during macrophage activation is coupled to enhancer transcription. Mol Cell. 2013;51:310–325. doi: 10.1016/j.molcel.2013.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim C, Wilcox-Adelman S, Sano Y, Tang WJ, Collier RJ, Park JM. Antiinflammatory cAMP signaling and cell migration genes co-opted by the anthrax bacillus. Proc Natl Acad Sci U S A. 2008;105:6150–6155. doi: 10.1073/pnas.0800105105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieberman-Aiden E, van Berkum NL, Williams L, Imakaev M, Ragoczy T, Telling A, Amit I, Lajoie BR, Sabo PJ, Dorschner MO, et al. Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science. 2009;326:289–293. doi: 10.1126/science.1181369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Litvak V, Ramsey SA, Rust AG, Zak DE, Kennedy KA, Lampano AE, Nykter M, Shmulevich I, Aderem A. Function of C/EBPdelta in a regulatory circuit that discriminates between transient and persistent TLR4-induced signals. Nat Immunol. 2009;10:437–443. doi: 10.1038/ni.1721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahtani KR, Brook M, Dean JL, Sully G, Saklatvala J, Clark AR. Mitogen-activated protein kinase p38 controls the expression and posttranslational modification of tristetraprolin, a regulator of tumor necrosis factor alpha mRNA stability. Mol Cell Biol. 2001;21:6461–6469. doi: 10.1128/MCB.21.9.6461-6469.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayo AE, Setty Y, Shavit S, Zaslaver A, Alon U. Plasticity of the cis-regulatory input function of a gene. PLoS Biol. 2006;4:e45. doi: 10.1371/journal.pbio.0040045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miele A, Dekker J. Long-range chromosomal interactions and gene regulation. Mol Biosyst. 2008;4:1046–1057. doi: 10.1039/b803580f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris MK, Saez-Rodriguez J, Sorger PK, Lauffenburger DA. Logic-based models for the analysis of cell signaling networks. Biochemistry. 2010;49:3216–3224. doi: 10.1021/bi902202q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Natoli G, Ghisletti S, Barozzi I. The genomic landscapes of inflammation. Genes Dev. 2011;25:101–106. doi: 10.1101/gad.2018811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nau GJ, Richmond JF, Schlesinger A, Jennings EG, Lander ES, Young RA. Human macrophage activation programs induced by bacterial pathogens. Proc Natl Acad Sci U S A. 2002;99:1503–1508. doi: 10.1073/pnas.022649799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novershtern N, Subramanian A, Lawton LN, Mak RH, Haining WN, McConkey ME, Habib N, Yosef N, Chang CY, Shay T, et al. Densely interconnected transcriptional circuits control cell States in human hematopoiesis. Cell. 2011;144:296–309. doi: 10.1016/j.cell.2011.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ourthiague DR, Birnbaum H, Ortenlof N, Vargas JD, Wollman R, Hoffmann A. Limited specificity of IRF3 and ISGF3 in the transcriptional innate-immune response to double-stranded RNA. J Leukoc Biol. 2015;98:119–128. doi: 10.1189/jlb.4A1014-483RR. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Panne D, Maniatis T, Harrison SC. An atomic model of the interferon-beta enhanceosome. Cell. 2007;129:1111–1123. doi: 10.1016/j.cell.2007.05.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramirez-Carrozzi VR, Braas D, Bhatt DM, Cheng CS, Hong C, Doty KR, Black JC, Hoffmann A, Carey M, Smale ST. A unifying model for the selective regulation of inducible transcription by CpG islands and nucleosome remodeling. Cell. 2009;138:114–128. doi: 10.1016/j.cell.2009.04.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsey SA, Klemm SL, Zak DE, Kennedy KA, Thorsson V, Li B, Gilchrist M, Gold ES, Johnson CD, Litvak V, et al. Uncovering a macrophage transcriptional program by integrating evidence from motif scanning and expression dynamics. PLoS Comput Biol. 2008;4:e1000021. doi: 10.1371/journal.pcbi.1000021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ravasi T, Suzuki H, Cannistraci CV, Katayama S, Bajic VB, Tan K, Akalin A, Schmeier S, Kanamori-Katayama M, Bertin N, et al. An atlas of combinatorial transcriptional regulation in mouse and man. Cell. 2010;140:744–752. doi: 10.1016/j.cell.2010.01.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sandler H, Stoecklin G. Control of mRNA decay by phosphorylation of tristetraprolin. Biochem Soc Trans. 2008;36:491–496. doi: 10.1042/BST0360491. [DOI] [PubMed] [Google Scholar]
- Scholes C, DePace AH, Sanchez A. Integrating regulatory information via combinatorial control of the transcription cycle. Cell Systems. 2016 doi: 10.1016/j.cels.2016.11.012. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tallquist M, Kazlauskas A. PDGF signaling in cells and mice. Cytokine Growth Factor Rev. 2004;15:205–213. doi: 10.1016/j.cytogfr.2004.03.003. [DOI] [PubMed] [Google Scholar]
- Tong AJ, Liu X, Thomas BJ, Lissner MM, Baker MR, Senagolage MD, Allred AL, Barish GD, Smale ST. A Stringent Systems Approach Uncovers Gene-Specific Mechanisms Regulating Inflammation. Cell. 2016;165:165–179. doi: 10.1016/j.cell.2016.01.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vo N, Goodman RH. CREB-binding protein and p300 in transcriptional regulation. J Biol Chem. 2001;276:13505–13508. doi: 10.1074/jbc.R000025200. [DOI] [PubMed] [Google Scholar]
- Wang J, Basagoudanavar SH, Wang X, Hopewell E, Albrecht R, Garcia-Sastre A, Balachandran S, Beg AA. NF-kappa B RelA subunit is crucial for early IFN-beta expression and resistance to RNA virus replication. J Immunol. 2010;185:1720–1729. doi: 10.4049/jimmunol.1000114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X, Hussain S, Wang EJ, Li MO, Garcia-Sastre A, Beg AA. Lack of essential role of NF-kappa B p50, RelA, and cRel subunits in virus-induced type 1 IFN expression. J Immunol. 2007;178:6770–6776. doi: 10.4049/jimmunol.178.11.6770. [DOI] [PubMed] [Google Scholar]
- Werner SL, Barken D, Hoffmann A. Stimulus specificity of gene expression programs determined by temporal control of IKK activity. Science. 2005;309:1857–1861. doi: 10.1126/science.1113319. [DOI] [PubMed] [Google Scholar]
- Zhu Z, Pilpel Y, Church GM. Computational identification of transcription factor binding sites via a transcription-factor-centric clustering (TFCC) algorithm. J Mol Biol. 2002;318:71–81. doi: 10.1016/S0022-2836(02)00026-8. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.