Spatial Resolution Requirements for Accurate Identification of Drivers of Atrial Fibrillation

Supplemental Digital Content is available in the text.

Abstract

Background—

Recent studies have demonstrated conflicting mechanisms underlying atrial fibrillation (AF), with the spatial resolution of data often cited as a potential reason for the disagreement. The purpose of this study was to investigate whether the variation in spatial resolution of mapping may lead to misinterpretation of the underlying mechanism in persistent AF.

Methods and Results—

Simulations of rotors and focal sources were performed to estimate the minimum number of recording points required to correctly identify the underlying AF mechanism. The effects of different data types (action potentials and unipolar or bipolar electrograms) and rotor stability on resolution requirements were investigated. We also determined the ability of clinically used endocardial catheters to identify AF mechanisms using clinically recorded and simulated data. The spatial resolution required for correct identification of rotors and focal sources is a linear function of spatial wavelength (the distance between wavefronts) of the arrhythmia. Rotor localization errors are larger for electrogram data than for action potential data. Stationary rotors are more reliably identified compared with meandering trajectories, for any given spatial resolution. All clinical high-resolution multipolar catheters are of sufficient resolution to accurately detect and track rotors when placed over the rotor core although the low-resolution basket catheter is prone to false detections and may incorrectly identify rotors that are not present.

Conclusions—

The spatial resolution of AF data can significantly affect the interpretation of the underlying AF mechanism. Therefore, the interpretation of human AF data must be taken in the context of the spatial resolution of the recordings.

WHAT IS KNOWN

• It is unclear whether the different reported causes of persistence of atrial fibrillation—focal and rotational drivers, and multiple wavelets—are the result of different underlying mechanisms or result from different scales and resolutions of recording devices and interpretations of the electrographic data they produce.

WHAT THE STUDY ADDS

• This study determined the minimum resolution required to accurately identify rotors and focal sources, and to avoid false detections, as a function of the spatial wavelength (the distance between wavefronts) of the arrhythmia.

• Stationary rotors are more reliably identified compared to meandering trajectories, for any given spatial resolution.

• All clinical high-resolution multipolar catheters are of sufficient resolution to accurately detect and track rotors when placed over the rotor core, though the low-resolution basket catheter is prone to false detections and may incorrectly identify rotors that are not present.

Recent studies have demonstrated conflicting mechanisms underlying persistent atrial fibrillation (AF), with the spatial resolution of data often cited as a potential reason for the disagreement. The hierarchical model of AF states that disturbances are sustained by drivers, in the form of rotors or focal sources.¹ Evidence for rotors as drivers of human AF is inferred from termination through ablation of putative stable rotor sites, mapped with basket catheters,^2,3 as well as ablation of regions with a high probability of transient rotors, identified using a noninvasive body surface mapping technology.⁴ Despite these data, the rotor paradigm is neither confirmed nor universally accepted,^5–7 with recent studies raising questions about the efficacy of rotor-targeted ablation.^8,9 The contrasting multiple-wavelet hypothesis of AF, proposed by Moe et al¹⁰ in the 1960s, states that AF is sustained by multiple, self-perpetuating, randomly propagating activation wavelets. This is supported by Allessie et al¹¹ and de Groot et al¹² who found no evidence for the presence of stable focal sources or rotors using a small high-resolution spoon-shaped mapping device. Similarly, the Waldo laboratory found no evidence of rotational activity using an epicardial electrode array (interelectrode spacing, 5.2–7.0 mm); in this case, AF was maintained by wavefronts from foci and breakthrough sites.¹³

These contradictory results have spawned intense debate^5,7 with findings attributed to the divergent methods used. One source of variation arises from differences in scale (global versus regional) and electrode density and therefore spatial resolution of the mapping techniques. A second difference is the approach used to analyze fibrillatory wavefront dynamics, using either phase mapping¹⁴ or activation time.¹² Correct interpretation of AF mechanisms is critical for effective diagnosis and delivery of ablation therapy.

In this study, we systematically investigated the hypothesis that the variation in spatial resolution of mapping systems may lead to misinterpretation of mechanism in persistent AF. We determined, through computer simulation, the minimum resolution required to accurately identify rotors and focal sources and to avoid false detections, using unipolar and bipolar reconstructed electrograms from 5 clinical catheter configurations. These were compared against action potential data requirements for computational modeling data. We considered stationary versus meandering rotors. Finally, we compared clinical phase maps and detected singularities for data measured during AF.

Methods

The Methods are briefly described here with full details in the Data Supplement.

Simulation Data

We initially determined resolution requirements on a regularly spaced 2-dimensional (2D) homogeneous grid for a stable rotor or focal source, before testing on more complicated arrhythmias with spatially varying activation and repolarization properties, realistic geometries, and catheter electrode arrangements.

Monodomain simulations of rotors and focal sources were performed using the Courtemanche-Ramirez-Nattel human atrial cell model, with changes representing electrical remodeling in AF.¹⁵ To generate a physiological range of spatial wavelengths in a 10 cm×10 cm sheet, the conduction velocity (CV)¹⁶ and local atrial rate^17,18 were varied by modifying tissue diffusivity (0.0005, 0.001, and 0.0015 cm²/ms) and I_K1 conductance (g_K1; 0.09, 0.135, and 0.18 nS/pF), resulting in CVs of 0.26, 0.36, and 0.43 m/s and action potential (AP) durations of 121, 142, and 181 ms (considered as 9 combinations; Tables I and II and Section 1.1.1 in the Data Supplement).

The effects of simulated data type and rotor stability were tested using an atrial bilayer model.^19,20 These simulations included interstitial fibrosis as microstructural discontinuities,²⁰ with distributions based on late-gadolinium intensity values from patients with persistent AF²¹ used to infer probabilities for fibrosis inclusion in the model, resulting in heterogeneous anisotropic conduction. For 1 simulation, areas of fibrosis also included reduced conductivity and changes to the ionic properties. Unipolar electrograms were calculated 1 mm off the endocardium with bipolar electrograms calculated as differences between paired unipoles with 4 mm spacing. Full model details are given in Section 1.1.2 in the Data Supplement.

High-density catheters were simulated, including a circular (Lasso), spiral (AFocus II), and 2 variations of a 5-spline (PentaRay) catheter with different interelectrode spacings, all of diameter 2 cm. Lower resolution basket catheters (median interelectrode spacing, 10.2 mm; lower quartile, 5.9 mm; upper quartile, 16.2 mm) were simulated in an anatomically accurate human left atrial model for 30 seconds of AF for 2 parameter sets, corresponding to short (45.2 mm) and long (75.2 mm) wavelength activity (Section 1.1.3 in the Data Supplement).

Clinical Data

All data were obtained with informed consent under ethical approval from the UK Health Research Authority Ref 13/LO1169. Electrograms and electrode locations were recorded during AF from the left atrium of 11 patients (6–17 catheter recording locations per patient; 127 total) at the beginning of ablation procedures, using multipolar AFocus II catheters and the Ensite Velocity electroanatomic mapping system (St Jude Medical, Inc). Unipolar and bipolar electrograms were recorded for 16 to 106 seconds (mean, 34 seconds). To investigate the effects of resolution on phase singularity (PS) detection, analysis was performed for random subsets of 4 to 19 electrograms, and the number of missing and false PS detections were calculated.

Identifying Rotors and Focal Sources

Figure 1A outlines our methodology. AP and bipolar and unipolar electrogram data were downsampled, phase was calculated for each modality²² and interpolated, singularities were identified, and statistics were calculated on a regional basis. PSs were located by calculating the topological charge²³ and were tracked over time, with those lasting >120 ms defined to be rotors.²⁰

Figure 1.

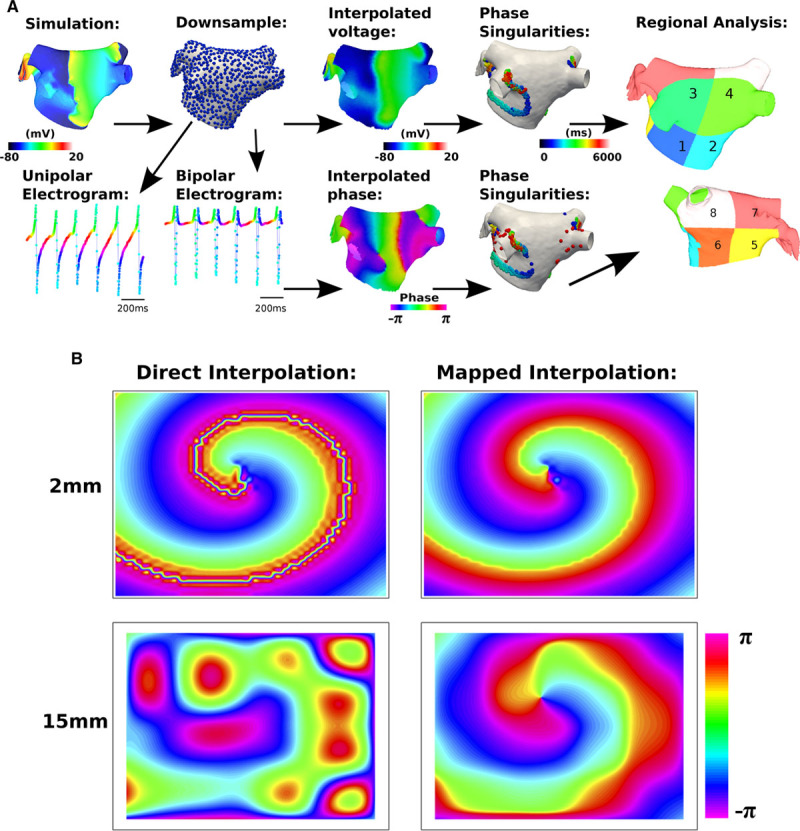
Methods schematic. A, Action potential (AP) data were computed at a mesh resolution (MR) of 0.34 mm edge length (93 927 points). Data were then downsampled: 1.62 to 17.1 mm (4813–36 points). Voltages were interpolated (to MR=1.62 mm), and phase was calculated. Unipolar electrograms were calculated at AP point distribution. Bipolar electrograms were calculated from paired unipolar electrograms with 4-mm interelectrode spacing. Phase of unipolar and bipolar electrograms was calculated and interpolated to MR=1.62 mm. Phase singularities were tracked over time (>120 ms trajectories tagged as rotors), and regional assessment was performed. B, A mapping is introduced for phase interpolation. Direct interpolation of the phase angle θ leads to issues when interpolating, in the instance that neighboring points are close to π and −π (left). Mapping to the exponential form (e^iϑ), interpolating this and then converting back to a phase angle, removes the issue with phase angle discontinuities (right). The errors become larger as the grid spacing is increased (bottom). The domain size shown here is 10 cm-by-10 cm.

Resolution requirements were determined for the 10 cm×10 cm sheet by uniformly spatially downsampling voltage data to different resolutions, ranging from 1 to 25 mm. For the atrial bilayer model, we considered subsets of nodes corresponding to the average distance between nodes, termed mesh resolution (MR), of 1.62 to 17.1 mm.

To compare results between different resolutions, downsampled phase (uniformly downsampled resolutions: 1–25 mm) was interpolated using cubic splines to full grid resolution (0.1 mm) for the 2D sheet (Figure 1B) or to 1.62 mm MR for the bilayer model (MR=1.62–17.1 mm, 4813–36 points). Phase rather than voltage was interpolated (Section 1.2 in the Data Supplement) because electrograms vary in magnitude (particularly bipoles) making their interpolation challenging.

For focal source identification, we calculated the divergence of the CV field²⁴ (Figure I in the Data Supplement). For each AP, activation time was calculated as the location of the maximum temporal derivative. CV vectors were calculated by differencing the activation times of four neighboring points.²⁵ The point of maximum divergence of the normalized CV field identified the origin of focal sources.

Criteria for Determining Required Resolutions

The accuracy of rotor identification was assessed using 2 measures: (1) visual inspection of isopotential plots over time and (2) error in the center of the rotor trajectory calculated using phase (time-averaged center error criterion; success if within an ablation catheter diameter of 4 mm). For (2), PS locations were calculated as detailed above. To separate these PSs into rotor PSs and false detections, a rotor PS was seeded in an initial frame of the simulation and tracked over time subject to a movement threshold to detect rotor PSs over the simulation duration. Other PSs were then defined to be false detections (Figure 2B). To assess the influence of false detections on correct rotor identification, both the number and distribution of falsely identified PSs were assessed.

Figure 2.

Methodology for defining success or failure of rotor identification. Left column (A, C, and E): successful identification at 7-mm spacing; right column (B, D, and F): failed identification at 17-mm spacing. A and B, Phase singularity (PS) locations corresponding to the rotor core (green) and false detections (red and blue, coloured depending on spin). C and D, Rotor core PSs (green), showing the time-averaged center of the full-resolution rotor trajectory (black) and the time-averaged center of the given resolution rotor trajectory (purple). The distance between these gives the time-averaged center error (C: 0.9 mm, success; D: 4.3 mm, failure of the time-averaged center error criterion). E and F, Histogram of number of PSs plotted as a function of distance from the full-resolution time-averaged rotor center. At 7 mm (E), there is a single peak corresponding to the true rotor center, whereas at 17 mm (F), there are 2 peaks in the histogram corresponding to a failure of the false PS detection histogram criterion because the false detections may be misidentified as a rotor core.

A methodology for determining an appropriate threshold for the number of permissible false detections was developed by considering the number of PSs as a function of distance from the true rotor core location, which was taken to be the time-averaged full-resolution rotor core location (Figure 2C). A resolution is considered to fail the false PS detection histogram criterion if the resulting histogram contains multiple peaks (Figure 2F), corresponding to additional spatial clusters of PSs that represent false detections. These spatial clusters could be misidentified as rotor locations.

Example resolutions for which identification is successful and unsuccessful for each of the 3 criteria are shown in Figure 2.

Focal sources were identified using the same measures as for rotors, except the center of the focal source was identified using the maximum divergence of the velocity. There were no false detections of positive divergence.

Wavelength Estimation

We express resolution requirements in terms of the number of recording points (N) needed within 1 spatial wavelength (λ), the distance between consecutive wavefronts.

The wavelength associated with each parameter set was automatically determined from full-resolution data by calculating the distance between arms of spiral wavefronts of a rotor or consecutive circular wavefronts of a focal source, using isopotential lines²⁶ (Figure 3A; Section 1.4.1 in the Data Supplement).

Figure 3.

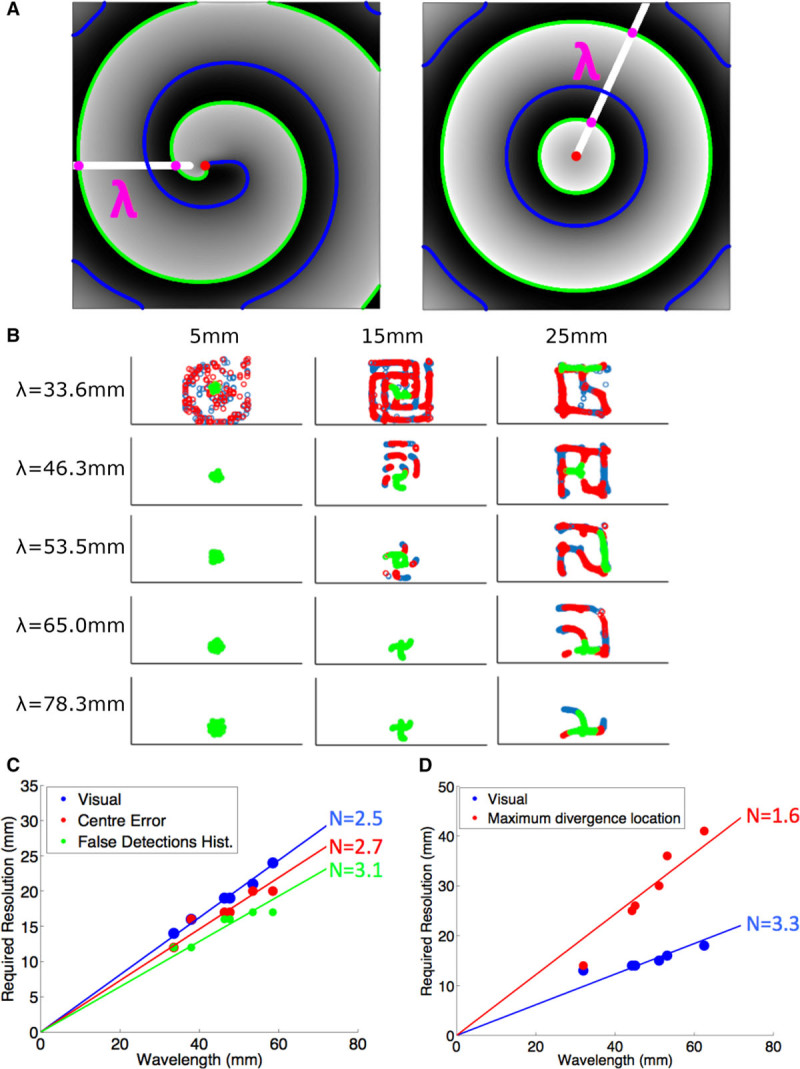
Resolution requirements for spiral wave detection and focal source detection depend on spatial wavelength. A, Technique to calculate wavelength of a spiral or focal wavefront. Isopotential lines at −60 mV with positive (green) and negative (blue) gradient. Intersections of the ray (white line) with the isopotential lines of positive gradient are shown (purple dots). B, Distributions of PSs over time for rotor simulations at different resolution and wavelengths. Phase singularities corresponding to a rotor core location are shown in green. Number of false detections (chirality shown in blue and red) increased as wavelength decreased and as grid spacing increased. C, Minimum N necessary to identify a rotor for each criterion. D, Minimum N necessary to identify a focal source for each criterion.

Where measurements are sparse, we define λ as the product of mean CV (Section 1.4.2 and Figure II in the Data Supplement) and mean cycle length: λ≈CV×cycle length. For bilayer simulations, λ was estimated for all nodes at MR=1.62 mm by calculating mean CV and cycle length over the simulation duration for data within a 2-cm diameter.

Results

Resolution Required for Correct Identification of Rotors and Focal Sources Is a Function of Spatial Wavelength

For each assessment criteria, the minimum measuring points, N, per wavelength was determined for each sheet simulation parameter set, as the reciprocal of the gradient of the line of best fit for each identification criterion. Figure 3B illustrates that resolution and wavelength clearly influence the accuracy of rotor core detection. We found that N=2.5 for visual identification, N=2.7 for the time-averaged center error criterion, and N=3.1 for the false PS detection histogram criterion, as shown in Figure 3C.

There must necessarily be a 3×3 grid of measuring points between consecutive wavefronts for focal source identification using maximum divergence to be successful. Because the distance between wavefronts decreases for shorter wavelengths, correspondingly finer grid spacing is necessary (Figure III in the Data Supplement). For accurate identification, N=3.3 for visual inspection and N=1.6 when using the maximum divergence criterion (Figure 3D).

Rotor Localization Errors Are Larger for Electrogram Data Than for AP Data

Figure 4A shows an area of high PS density in an area of high fibrosis in an anatomically accurate simulation of 2 rotors. Wavelength varies spatially (range, 21.5–108.1; mean 67.8±15.5 mm) because of the heterogeneous CV (range, 0.12–0.60 m/s; mean 0.37±0.09 m/s), where slow conduction is seen in areas of high fibrosis. The 3 modeled elements of fibrosis all decreased CV. As such, resolution requirements also varied spatially.

Figure 4.

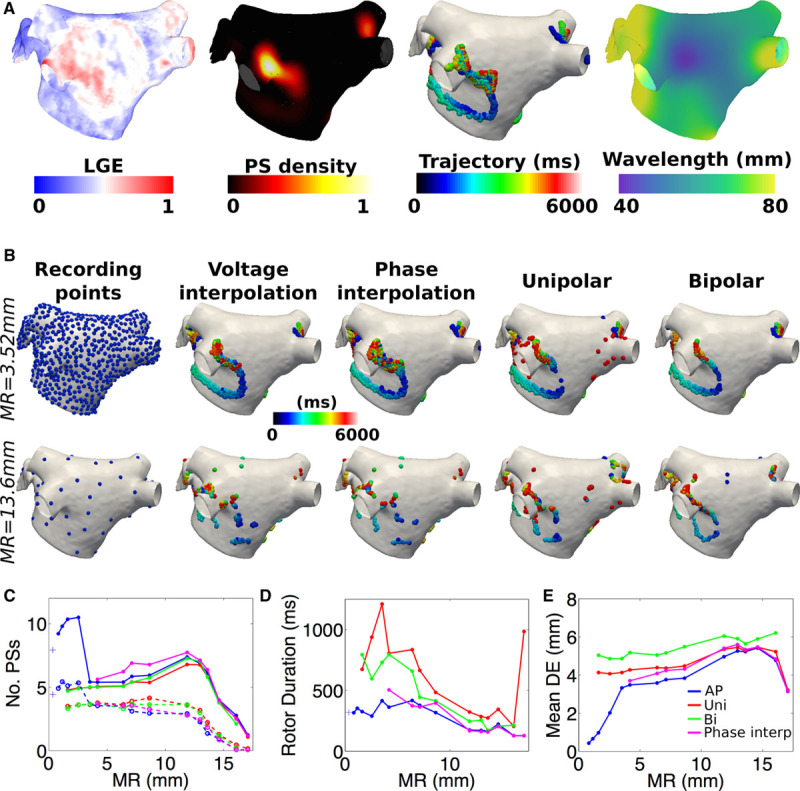
Phase singularity (PS) distributions and characteristics for different data modalities. A, Normalized late gadolinium enhancement (LGE)-magnetic resonance imaging data for a patient with persistent atrial fibrillation was used to infer probabilities for fibrosis inclusion in the model; high PS density is seen to coincide with high fibrosis density; PS locations over time show rotor trajectories; wavelength varies spatially. B, Comparison of detected PS locations for mesh resolutions (MRs) of 3.52 mm (top) and 13.6 mm (bottom), for different AP interpolations and electrogram modalities. C, Number of PSs (solid lines) and rotors (dashed lines), (D) rotor durations, and (E) distance errors as a function of MR.

For a given resolution, Figure 4B shows that PS distributions were visually similar across data types, as were the number of PSs, number of rotors and rotor duration, as shown in Figure 4C. For computational efficiency, electrograms were only calculated at MR≥1.6 mm, whereas AP interpolation was only calculated for MR≥3.5 mm. The mean localization error was generally higher for both types of electrogram phase than for AP phase. Results for AP phase were similar when using either voltage or phase interpolation.

Stationary Rotors Are More Reliably Identified Compared With Meandering Trajectories

We analyzed simulation data in which 1 rotor anchored to an area of high fibrosis intensity on the posterior wall (Figure 5A, compare PS density and late gadolinium enhancement maps), and a second rotor meandered across the anterior wall covering a larger area (Figure 5B). The CV is again heterogeneous (range, 0.21–0.59 and 0.44±0.08 m/s), leading to heterogeneous wavelength (39.7–110.1 and 81.2±13.9 mm), with shorter wavelengths in areas of fibrosis (Figure 5A).

Figure 5.

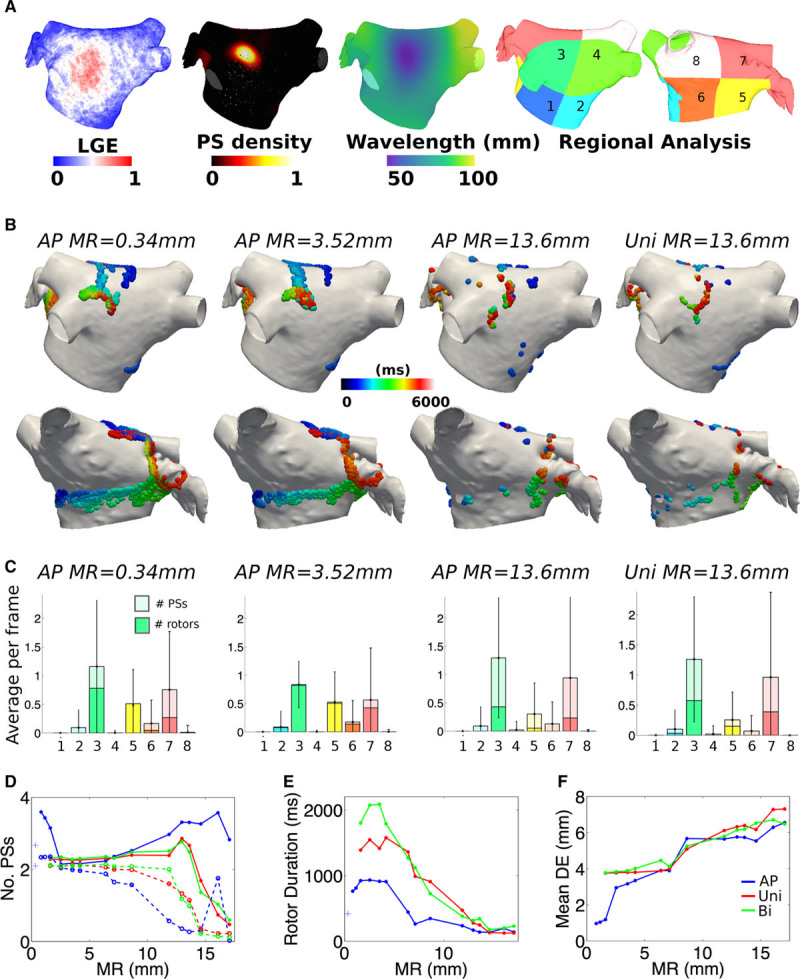
Stationary rotors are more reliably identified compared with meandering trajectories. A, Average late gadolinium enhancement (LGE)-magnetic resonance imaging map, phase singularity (PS) density, and local wavelengths, as well as numbered regions used for regional analysis. B, PS distributions shown on the posterior (top) and anterior (bottom) walls for different resolutions and modalities. C, Regional analysis showing mean number of phase singularities and rotors in each region (error bars indicate SD for the number of phase singularities). D, Number of PSs (solid lines) and rotors (dashed lines), (E) rotor durations, and (F) distance errors as a function of mesh resolution (MR).

On reducing resolution, PSs are still identified near the stable rotor, but the meandering rotor trajectory breaks up with both AP and unipolar data (Figure 5B). This is apparent in the regional analysis (Figure 5C) in which region 3, corresponding to the stable rotor, is a high driver region across all resolutions (top PS region for AP data for all resolutions), whereas regions 5 and 6, corresponding to the meandering rotor, decrease in importance for MR≥11.9 mm for AP data.

The average number of PSs and rotors detected decreased with coarser MR (Figure 5D) as did rotor duration (Figure 5E). PS location error increased at coarser MR for all data types.

Multipolar Catheters Are of Sufficient Resolution to Accurately Detect and Track Rotors If Placed Over the Rotor Core

We investigated whether electrode arrangements of commonly used high-density clinical mapping catheters satisfy the resolution requirements identified above for reliably identifying rotors at the shortest wavelength (33.6 mm). Illustrative isophase maps and rotor core PS trajectories are shown in Figure 6A.

Figure 6.

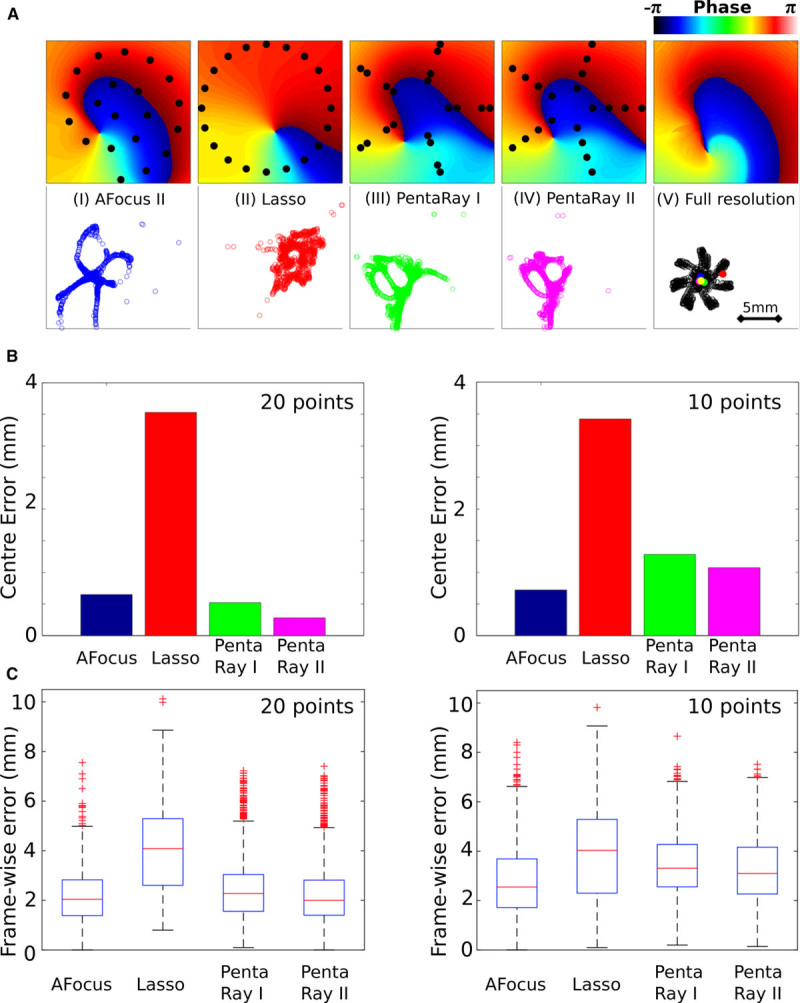
Multipolar catheters are of sufficient resolution to accurately detect and track rotors. A, Top: Example isophase maps interpolated from the recording points shown in black (I–IV), with the phase from the full-resolution simulation data shown in (V). Bottom: Rotor core phase singularity (PS) trajectories for each catheter type calculated using the interpolated phase. Examples are shown for spiral (AFocus II), circular (Lasso), and 2 five-spline electrode arrangements (PentaRay I and PentaRay II). B, Errors in the time-averaged estimated center location compared with the time-averaged location computed from the raw simulation data. Catheters are configured as either 20 unipoles or 10 bipoles. C, Box plots to show frame-wise difference in estimated PS location compared with the location computed from raw simulation data. The boxes indicate the interquartile range (IQR) and median (red line) of the data; the whiskers extend to a maximum of 1.5×IQR; and the crosses represent outliers.

For 20 unipole configurations, the circular (Lasso) catheter produced the largest time-averaged center location error (3.5 mm) with respect to full-resolution (0.1 mm) simulated data. Other catheters gave significantly lower errors (Figure 6B). Corresponding frame-wise errors in PS location are shown in Figure 6C, where the circular catheter again had the largest error.

For the 10 bipole configuration, formed from 20 unipolar signals, the spiral (AFocus II) catheter produced the smallest location errors (quantified in Figure 6B and 6C). The circular catheter gave similar errors with either 20 unipoles or 10 bipoles, whereas the accuracy of the other catheters decreased as the number of data points was reduced.

Low-Resolution Basket Catheters Are Prone to False Detections

In contrast to the high-density catheters examined above, basket catheters provide global coverage at a lower electrode density.² Geodesic distances between each basket electrode and its 4 neighboring electrodes are shown in Figure 7A. The majority of interelectrode distances satisfy our requirements for accurately locating rotor cores (time-averaged center error criterion): 99.1% for the longer wavelength (75.2 mm) resolution requirement of 27.9 mm (75.2/2.7=27.9) and 79.3% for the shorter wavelength (45.2 mm) resolution requirement of 16.7 mm. Fewer interelectrode distances satisfied the requirements to avoid false detections (false PS detection histogram criterion): 96.4% for the longer wavelength resolution requirement of 24.4 mm and 64.0% for the shorter wavelength resolution requirement of 14.5 mm.

Figure 7.

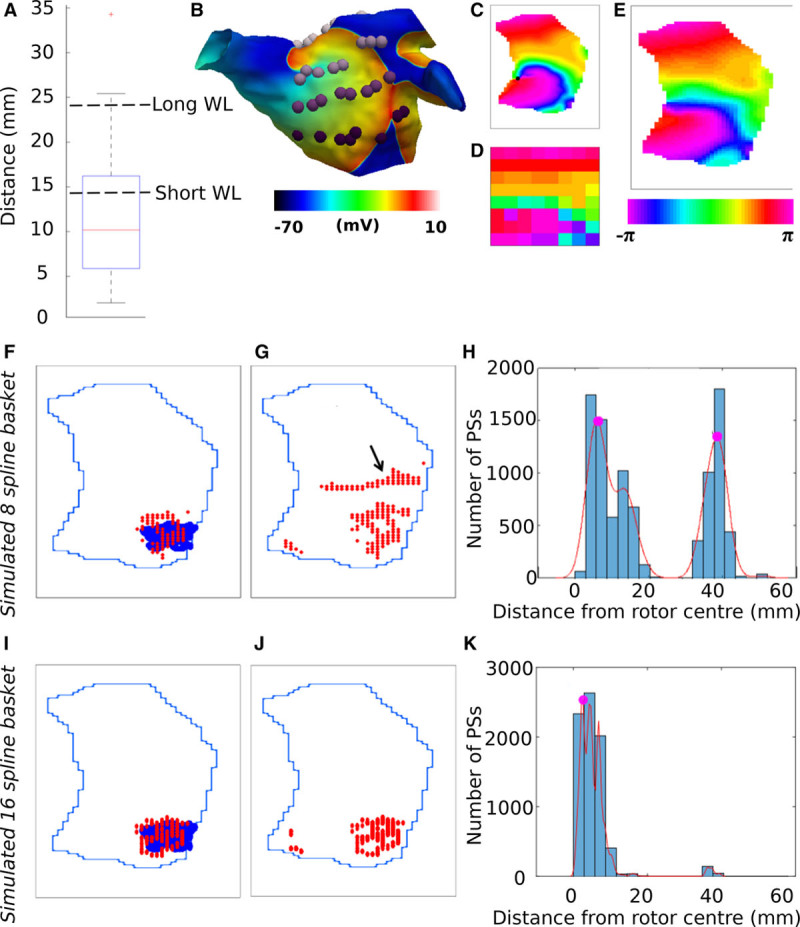
Low-resolution basket catheters are prone to false detections. A, Interelectrode distances in an 8-spline basket catheter. Resolution requirements for avoiding false detections for the 2 wavelengths (45.2 and 75.2 mm) are marked. B, Example isopotential map for longer wavelength simulation with basket electrodes marked. C, High-resolution phase map generated from phase at mesh vertices. Phase singularity (PS) marked as a black dot. D, Phase of electrodes as arranged on a regular 8×8 grid. E, Interpolated phase from basket arrangement of electrodes. F, Rotor PS locations computed from high-resolution data (blue) and the 8-spline basket electrodes (red) for the short wavelength simulation. Only PSs that correspond to the rotor are shown. G, All detected PSs of 8-spline basket catheter. H, PS detection histogram for 8-spline catheter. I, Rotor PS locations, (J) all PSs, and (K) PS detection histogram for a simulated 16-spline catheter—double the clinical resolution.

Interpolated phase maps were qualitatively similar to the high-resolution phase maps, as shown in Figure 7C and 7E. The rotor core was accurately located for the short wavelength simulation (1.3 mm time-averaged center error). For the long wavelength simulation, 2 rotor cores were present in the mapping area for much of the simulation. The first was located with sufficient accuracy (3.6 mm time-averaged center error; 2.6% of frames missing rotor core detections), whereas the second rotor had a time-averaged center error greater than the 4-mm threshold (5.4 mm) because many PSs were along the edge of the full-resolution area of coverage and as such were not picked up by the basket arrangement (40.2% of frames missing rotor core detections).

For the short wavelength simulation, many false detections were observed. For example, Figure 7G shows an additional cluster of PSs close to the main rotor for the short wavelength simulation. This aligned with a larger interelectrode spacing between electrodes vertically. Subsequently, this led to a secondary peak in the PS distribution histogram (Figure 7H). When a basket catheter with double the number of splines (ie, 16 splines of 8 electrodes) was simulated, the cluster of false detections was no longer present, as shown in Figure 7J and 7K.

In addition, the average rotor path is accurate; however, the PS trajectory showed a larger rotor meander area for the basket resolution data than for the high-resolution data (Section 2.3 and Figure IV in the Data Supplement).

For Clinical AF Data, Reducing the Number of Electrodes in Mapping Catheters Increased the Number of Missing and False PS Detections

We determined the ability of multipolar catheters to detect PSs as electrodes were removed. Clinical catheter recordings with different degrees of rotational activity were analyzed, ranging from planar activity to curved rotor cores: overall mean number of PSs for unipolar catheters 0.47±0.20, range 0 to 0.91 and for bipolar 0.36±0.16, range 0 to 0.73. Figure 8 shows box plots for the percentage of missing PSs (percentage of full-resolution PSs not present in downsampled data) and the percentage of false detections (percentage of downsampled data PSs not present in full-resolution data), which both increase as the number of recording points is reduced.

Figure 8.

For clinical atrial fibrillation (AF) data, reducing the number of electrodes in high-density mapping catheters increased the number of missing and false phase singularity (PS) detections. A, Box plots to show the percentage of full-resolution PSs not present in downsampled data measured across 127 catheter recordings, for unipolar and bipolar electrode recordings. B, Box plots to show the percentage of PSs in downsampled data not present in full-resolution data. In all cases, the boxes indicate the interquartile range (IQR) and median of the data (red line); the whiskers extend to a maximum of 1.5×IQR; and the crosses represent outliers.

Discussion

Main Findings

In this study, we demonstrated that sufficient spatial resolution is essential for the accurate detection of rotors and focal sources and propose that insufficient resolution may be responsible for the conflicting findings of recent human studies.^2,12,27 An estimate of the resolution requirements as a function of the spatial wavelength was found for spiral wavefronts (rotors) and circular wavefronts (focal sources) using different criteria. For regularly spaced grids, the minimum resolution required is a ratio of spatial wavelength to number of measuring points per wavelength (λ/N). For rotors, N=2.5 (visual inspection), N=2.7 (rotor core time-averaged center error), and N=3.1 (to avoid false detections). For focal sources, N=3.3 (visual inspection) and N=1.6 (maximum divergence calculation of focal source origin location). The results suggest that although the basket catheter has adequate resolution to track rotors, it has inadequate resolution to avoid false detections.

We found that although stationary rotors may be identified at coarse resolutions, meandering rotors are lost. For atrial bilayer simulations, regional analyses at all resolutions considered identified the same region as having the highest PS density, whereas rotor localization error was unacceptable for MR≥11.9 mm. This suggests that standard mapping modalities offer sufficient resolution for ablation guided by regional driver density²⁷ although localization of meandering rotors may not be possible. In addition, resolution requirements are similar for unipolar and bipolar electrogram data. Correct PS identification for clinical spiral (AFocus II) mapping catheter recordings is sensitive to the number of electrodes used in the analysis.

Spatial Wavelengths in Human AF

We simulated 9 different wavelengths for rotors and focal sources to determine the relationship between resolution requirements and wavelength. Based on previous reports, the expected range of spatial wavelengths in human AF is 44 to 127 mm, because of the varying degree of electric remodeling in patients with AF. This range was estimated as CV divided by dominant frequency, where CVs are in the range 0.38±0.1 to 0.61±0.06 m/s,¹⁶ and dominant frequency ranges from 4.8 to 8.6 Hz.^17,18 The wavelengths of the spiral waves simulated in this study cover a subset of this range from 33 to 78 mm. Wavelength may vary spatially (Figures 4A and 5A) because of conduction or repolarization heterogeneities, leading to spatially varying resolution requirements. This is particularly important as rotors may anchor to areas of slow conduction.

Away from a rotor core, 7 points were required for an accurate and reliable estimate of spatial wavelength if located within 1 wavelength (Section 2.1 in the Data Supplement). High-density mapping catheters fulfill this criterion because wavelengths in human AF are estimated to be longer than their diameters.

Required Resolution for Regular Grids

The Nyquist criterion states that interelectrode spacing must be less than half the smallest spatial wavelength of interest,²⁸ corresponding to N=2. This study aimed to extend the work of Rappel and Narayan,²⁹ where a theoretical approach determined that the resolution required to identify stable rotors and focal sources is of the form λ/N; their study identified wave patterns visually and the required value of N was not quantitatively determined. In our study, we find that the resolution requirements are linear in λ, suggesting that the resolution required does follow λ/N.

Four of the identification criteria suggest a slightly higher value of N than the theoretical Nyquist criterion is needed in practice, whereas the maximum divergence location suggests a smaller value. This criterion was applied for focal sources where the grid was centered over the focal source, which is the optimal arrangement; off-center arrangements and placements away from the source will require a higher N.

Required Resolution for Clinically Used Catheters

The most stringent spatial resolution requirement found for identification of rotors in human AF is 44/3.1=14.2 mm. The interelectrode spacings of all high-density mapping catheters considered (AFocus II 4 mm, Lasso 6 mm, PentaRay 4 mm, or 6 mm) are smaller than this distance, suggesting the ability of these catheters to accurately locate PSs if placed over the rotor core. For 20 recording points, the circular Lasso catheter gave the largest error in estimating rotor center location (Figure 6B). Similarly, Weber³⁰ found that a simulated circular catheter performed worse than spiral and 5-spline catheters because it could not identify focal sources, but rather, the radial basis function interpolation showed a planar wave. For clinical data, correct PS identification was sensitive to the number of points used for interpolation from a high-density spiral AFocus II mapping catheter (Figure 8).

A major disadvantage of mapping catheters is their localized coverage; as such, rotor tracking is only possible if the catheter is fortuitously placed over a rotor that does not meander outside the margins of the catheter poles. If the catheter does not lie over the rotor core, techniques presented by Roney et al³¹ could be used to direct the catheter toward the rotor, but these techniques are dependent on some degree of organization of wavefronts remote from the driver. In addition, it may be necessary to consider the activity of surrounding electrograms to differentiate rotors from interactions around lines of block.³²

Unlike the catheters mentioned above, basket catheters provide global coverage, which is a possible reason why studies using them^2,33 were able to detect rotors in human AF, whereas studies using catheters with only regional coverage⁷ were not. Our results confirm that basket catheters can accurately detect rotors (Figure 7) and faithfully track PS trajectories (Figure IV in the Data Supplement).

Berenfeld and Oral³³ comment that some areas of interpolation for basket mapping have interspline difference of >20 mm; for the basket catheter used in this study, 12.6% of interelectrode distances are >20 mm. Laughner et al³⁴ found that equatorial bunching of basket catheter splines often occurred, leading to a wide range of interspline distances within the basket, and this varied between patients. In addition, coverage of the pulmonary veins, left septum, and left lateral wall was limited, with only 55% of the atrial surface covered, as observed by Benharash et al,⁸ explaining the large number of missing rotor detections in our study.

Low-Resolution Basket Catheters Are Prone to False Detection of PSs

The basket catheter, however, was found to be inadequate to avoid spurious rotors. Only 63.1% of the interelectrode distances are less than the resolution requirement of 14.2 mm, corresponding to 3.1 points per spatial wavelength. This is likely the cause of the false PS detections, where the simulated basket data failed the false PS detection histogram criterion.

The tendency of basket catheters with inadequate resolution to detect nonexistent PSs may explain the discrepancy between recent clinical studies, where studies using basket catheters report stable rotors,² whereas regional, higher-resolution mapping do not report stable rotors.^12,35 This may explain, in part, the large incidence of rotors reported by Narayan et al,² a low termination rate,⁸ and poor long-term success⁹ for ablating rotors detected by basket catheters. The modeled 16-spline basket catheter did not suffer from false PS detections although good endocardial contact of such a catheter may be difficult to achieve in practice.

Our study comparing resolution requirements for stationary and meandering rotors found that rotor trajectories may be lost at resolutions for which stable rotors are still identifiable (Figure 5), which may explain differences in findings on rotor stability with basket catheters identifying stable rotors and noninvasive electrocardiographic imaging identifying transient meandering rotors.^27,36

Effect of Datatype

Resolution requirements for AP, unipolar electrogram, and bipolar electrogram data (Figure 4) were similar. Localization errors were larger for electrogram data than for AP data and always larger than the 4-mm threshold, corresponding to an ablation catheter diameter, used for rotor location error, perhaps also because of rotor meander and irregular point spacing on the surface mesh (compared with the regular 2D grid).

Limitations

The limitations of our study include (1) we assume the presence of rotors, (2) our tissue is simplified and we do not model endocardial–epicardial dissociation. Furthermore, in the simulations for the clinically used catheters, all electrograms were noise free, representing perfect data. In reality, electrograms will contain noise, motion artifacts, and may have unsatisfactory tissue contact.³³

Conclusions

We determined the minimum spatial resolution requirements, as a function of AF wavelength, to correctly identify the underlying AF mechanism. All clinically used catheters assessed in our study possess adequate spatial resolution to identify and track rotor core location for the range of wavelengths occurring in human AF if covering the location of the rotor PS. However, the low resolution of basket catheters renders them prone to false detections. Resolution requirements depend on rotor meander and AF spatial wavelength, but are similar for AP, unipolar electrogram, and bipolar electrogram data. Overall, the spatial resolution of AF data can significantly affect the interpretation of the underlying AF mechanism.

Acknowledgments

We thank Dr Hubert Cochet for the late gadolinium enhancement (LGE)-magnetic resonance imaging data used in this study.

Sources of Funding

This work was supported by funding awarded from the British Heart Foundation (FS/11/22/28745 and RG/16/3/32175); the ElectroCardioMaths Programme of the Imperial BHF Centre of Research Excellence; the National Institute for Health Research. Dr Ng is funded by National Institute for Health Research Clinical Lectureship (1716). Dr Roney is funded by a Lefoulon-Delalande Foundation fellowship administered by the Institute of France. In addition, this study was supported through the Investment of the Future grant, ANR-10-IAHU-04, and the grant Equipex MUSIC ANR-11-EQPX-0030. Computer time for this study was provided by the computing facilities Mésocentre de Calcul Intensif Aquitain of the Université de Bordeaux and of the Université de Pau et des Pays de l’Adour.

Disclosures

None

Supplementary Material

hae-10-e004899-s001.pdf ^{(2.8MB, pdf)}